Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-24T02:59:28.075Z Has data issue: false hasContentIssue false
  • English
  • Français

Weak amenability of free products of hyperbolic and amenable groups

Part of: Noncompact transformation groups Selfadjoint operator algebras Abstract harmonic analysis Special aspects of infinite or finite groups Structure and classification of infinite or finite groups

Published online by Cambridge University Press:  06 January 2022

Ignacio Vergara Open the ORCID record for Ignacio Vergara [Opens in a new window]
Ignacio Vergara*
Affiliation:
Leonhard Euler International Mathematical Institute, Saint-Petersburg State University, 14th Line 29B, Vasilyevsky Island, St. Petersburg, 199178, Russia. E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

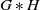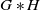We show that if G is an amenable group and H is a hyperbolic group, then the free product $G\ast H$ is weakly amenable. A key ingredient in the proof is the fact that $G\ast H$ is orbit equivalent to 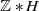$\mathbb{Z}\ast H$ .

Keywords

Weak amenabilityfree productsorbit equivalence

MSC classification

Primary: 46L07: Operator spaces and completely bounded maps
Secondary: 20E06: Free products, free products with amalgamation, Higman-Neumann-Neumann extensions, and generalizations 43A07: Means on groups, semigroups, etc.; amenable groups 20F67: Hyperbolic groups and nonpositively curved groups 22F10: Measurable group actions
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 64 , Issue 3 , September 2022 , pp. 698 - 701
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Glasgow Mathematical Journal Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bożejko, M. and Picardello, M. A., Weakly amenable groups and amalgamated products, Proc. Amer. Math. Soc. 117(4) (1993), 1039–1046.CrossRefGoogle Scholar
Brown, N. P. and Ozawa, N., $C^*$ -algebras and finite-dimensional approximations, Graduate Studies in Mathematics, vol. 88 (American Mathematical Society, Providence, RI, 2008).Google Scholar
Cowling, M. and Haagerup, U., Completely bounded multipliers of the Fourier algebra of a simple Lie group of real rank one, Invent. Math. 96(3) (1989), 507–549.CrossRefGoogle Scholar
Cowling, M. and Zimmer, R. J., Actions of lattices in ${\rm Sp}(1,n)$ , Ergodic Theory Dyn. Syst. 9(2) (1989), 221–237.CrossRefGoogle Scholar
de Cannière, J. and Haagerup, U., Multipliers of the Fourier algebras of some simple Lie groups and their discrete subgroups, Amer. J. Math. 107(2) (1985), 455–500.CrossRefGoogle Scholar
Furman, A., A survey of measured group theory, in Geometry, rigidity, and group actions, Chicago Lectures in Mathematics (University of Chicago Press, Chicago, IL, 2011), 296–374.Google Scholar
Guentner, E., Reckwerdt, E. and Tessera, R., Proper actions and weak amenability for classical relatively hyperbolic groups, Preprint.Google Scholar
Ishan, I., Von neumann equivalence and group approximation properties, arXiv preprint arXiv:2107.11335 (2021).Google Scholar
Ishan, I., Peterson, J. and Ruth, L., Von neumann equivalence and properly proximal groups, arXiv preprint arXiv:1910.08682 (2019).Google Scholar
Jolissaint, P., Approximation properties for measure equivalent groups, Preprint (2001).Google Scholar
Löh, C., Geometric group theory (Universitext, Springer, Cham, 2017).Google Scholar
Ornstein, D. S. and Weiss, B., Ergodic theory of amenable group actions. I. The Rohlin lemma, Bull. Amer. Math. Soc. (N.S.) 2(1) (1980), 161–164.CrossRefGoogle Scholar
Ozawa, N., Weak amenability of hyperbolic groups, Groups Geom. Dyn. 2(2) (2008), 271–280.CrossRefGoogle Scholar
Ricard, É. and Xu, Q., Khintchine type inequalities for reduced free products and applications, J. Reine Angew. Math. 599 (2006), 27–59.Google Scholar