No CrossRef data available.
Article contents
Some characterizations of expanding and steady Ricci solitons
Part of:
Global differential geometry
Published online by Cambridge University Press: 13 March 2023
Abstract
In this short note, we deal with complete noncompact expanding and steady Ricci solitons of dimension 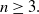 $n\geq 3.$ More precisely, under an integrability assumption, we obtain a characterization for the generalized cigar Ricci soliton and the Gaussian Ricci soliton.
$n\geq 3.$ More precisely, under an integrability assumption, we obtain a characterization for the generalized cigar Ricci soliton and the Gaussian Ricci soliton.
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of Glasgow Mathematical Journal Trust
Footnotes
Dedicated to my daughter Aurora Vitória.
References
Bryant, R. L., Ricci flow solitons in dimension three with so(3)-symmetries. Available at www.math.duke.edu/bryant/3DRotSymRicciSolitons.pdf (2005).Google Scholar
Catino, G., P. Mastrolia D. Monticelli, Classification of expanding and steady Ricci solitons with integral curvature decay, Geom.
Topol. 20 (2016), 2665–2685.Google Scholar
Chan, P. Y., Curvature estimates and gap theorems for expanding Ricci solitons, arXiv:2001.11487 (2021).10.1093/imrn/rnab257CrossRefGoogle Scholar
Chen, B.-L., Strong uniqueness of the Ricci flow, J. Differ. Geom. 82(2) (2009), 363–382.10.4310/jdg/1246888488CrossRefGoogle Scholar
Deruelle, A., Steady gradient Ricci soliton with curvature in L1, Comm. Anal. Geom. 20(1) (2012), 31–53.CrossRefGoogle Scholar
Hamilton, R. S., The Ricci flow on surfaces, Cont. Math. 71 (1998), 237–261.10.1090/conm/071/954419CrossRefGoogle Scholar
Lott, J., On the long-time behavior of type-III Ricci flow solutions, Math. Ann. 339(3) (2007), 627–666.CrossRefGoogle Scholar
Ma, L., Expanding Ricci solitons with pinched Ricci curvature, Kodai Math. J. 34(1) (2011), 140–143.10.2996/kmj/1301576768CrossRefGoogle Scholar
Petersen, P. and Wylie, W., On the classification of gradient Ricci solitons, Geom. Topol. 14(4) (2010), 2277–2300.10.2140/gt.2010.14.2277CrossRefGoogle Scholar
Petersen, P. and Wylie, W., Rigidity of gradient Ricci solitons, Pac. J. Math. 241(2) (2009), 329–345.CrossRefGoogle Scholar
Schulze, F. and Simon, M., Expanding solitons with non-negative curvature operator coming out of cones, Math. Z. 275(1–2) (2013), 625–639.CrossRefGoogle Scholar
Yau, S. T., Some function-theoretic properties of complete Riemannian manifolds and their applications to geometry, Indiana Univ. Math. J. 25 (1976), 659–670.CrossRefGoogle Scholar



