Published online by Cambridge University Press: 10 May 2022
In this work, we study foliations of arbitrary codimension
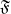 $\mathfrak{F}$
with integrable normal bundles on complete Riemannian manifolds. We obtain a necessary and sufficient condition for
$\mathfrak{F}$
with integrable normal bundles on complete Riemannian manifolds. We obtain a necessary and sufficient condition for
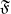 $\mathfrak{F}$
to be totally geodesic. For this, we introduce a special number
$\mathfrak{F}$
to be totally geodesic. For this, we introduce a special number
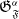 $\mathfrak{G}_{\mathfrak{F}}^{\alpha}$
that measures when the foliation ceases to be totally geodesic. Furthermore, applying some maximum principle we deduce geometric properties for
$\mathfrak{G}_{\mathfrak{F}}^{\alpha}$
that measures when the foliation ceases to be totally geodesic. Furthermore, applying some maximum principle we deduce geometric properties for
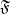 $\mathfrak{F}$
. We conclude with a geometrical version of Novikov’s theorem (Trans. Moscow Math. Soc. (1965), 268–304), for Riemannian compact manifolds of arbitrary dimension.
$\mathfrak{F}$
. We conclude with a geometrical version of Novikov’s theorem (Trans. Moscow Math. Soc. (1965), 268–304), for Riemannian compact manifolds of arbitrary dimension.