The Logic of Proportionality: Reasoning with Non-Numerical Magnitudes

Giovanni Sartor

doi:10.1017/S2071832200002339

1 See Pollock, John L., Cognitive Carpentry: A Blueprint for How to Build a Person (1995) [hereinafter Cognitive Carpentry]; John L. Pollock, Thinking About Acting: Logical Foundations for Rational Decision Making (2006) [hereinafter Thinking About Acting]. See also Cristiano Castelfranchi & Fabio Paglieri, The Role of Beliefs in Goal Dynamics: Prolegomena to a Constructive Theory of Intention, 15 Synthese 237–63 (2007) (arguing that intentions and values are not primitive notions, given that they may be analyzed into combinations of goals and beliefs).Google Scholar

2 See Amartya, Sen, Rational Fools: A Critique of Behavioral Foundation of Economic Theory, 6 Phil. & Pub. Aff. 317 (1977).Google Scholar

3 Simon, Herbert A., Reason in Human Affairs 63 (1983). For a discussion of the idea of satisficing, as developed by theorists of bounded rationality, see Herbert A. Simon, The Sciences of the Artificial 139 (2d. 1981).Google Scholar

We cannot within practicable computational limits generate all the admissible alternatives and compare their respective merits. Nor can we recognize the best alternative, even if we are fortunate enough to generate it early, until we have seen all of them. We satisfice by looking for alternatives in such a way that we can generally find an acceptable one after only moderate search.

Id.

4 Simon, Herbert A., Administrative Behavior: A Study of Decision-Making Processes in Administrative Organizations 63 (2d ed. 1957).Google Scholar

The fact that goals may be dependent for their force on other more distant ends leads to the arrangement of these goals in a hierarchy each level to be considered as an end relative to the levels below it and as a means relative to the levels above it. Through the hierarchical structure of ends, behavior attains integration and consistency, for each member of a set of behavior alternatives is then weighed in terms of a comprehensive scale of values, the ultimate ends. In actual behavior, a high degree of conscious integration is seldom attained. Instead of a single branching hierarchy, the structure of conscious motives is usually a tangled web, or more precisely, a disconnected collection of elements only weakly and incompletely tied together; and the integration of these elements becomes progressively weaker as the higher levels of the hierarchy the more final ends are reached.

Id.

5 This can also be expressed by saying that a plan operates as an exclusionary reason with regard to the values that were considered in its adoption, though this terminology may be misleading. See, e.g., Joseph Raz, Practical Reason and Norms (1975).Google Scholar

6 Let me clarify this issue with an economic example. Assume that the choice to switch to a new product in a company would cause a loss of 100 for the abandonment of the old product, which still has some market, and a gain of 150 from the new product. Then we can say that the plan would provide a net gain of 50. Now if we were to consider whether to adopt the plan by comparing the net gain it provides (50), with the loss it causes (100) it seems that we should not implement the change, since the loss is higher than the benefit provided by the plan, so the result of the plan seems to be negative: 50 – 100 = –50. But this calculation is wrong, because we have double-counted the loss: first, we subtracted it to compute the net outcome of the plan, and then we subtracted it again when comparing the net outcome of the plan against the loss it causes. The same kind of reasoning applies when losses and gains concern different values. Assume for instance that a decision has to be taken concerning whether to endow an existing power plant with new expensive anti-pollution measures. Assume that environmental benefit outweighs the additional costs, providing a utility 1.5 times bigger than such costs. By comparing the net benefit of the plan (0.5 times the costs) against its costs (1 times themselves), it seems again that the power plant should not be endowed with the anti-pollution measures, since the wrong computation gives a negative result: 0.5 – 1 = –0.5.Google Scholar

7 See Atienza, Manuel & Manero, Juan Ruiz, Permissions, Principles and Rights. A Paper on Statements Expressing Constitutional Liberties, 9 Ratio Juris 236 (1996), which discusses the distinction between action-norms and norms having a purposive content, which they call policies.Google Scholar

8 Alexy, Robert, A Theory of Constitutional Rights 44–110 (2002).Google Scholar

9 Luhmann, Niklas, Das Recht der Gesellschaft 195 (1996).Google Scholar

10 See id. at 198.Google Scholar

11 See Sartor, Giovanni, Fundamental Legal Concepts: A Formal and Teleological Characterisation, 21 Artificial Intelligence & L. 101 (2006).Google Scholar

12 For a discussion on the different norms related to a constitutional right, see Atienza & Manero, supra note 7.Google Scholar

13 Nozick, Robert, Anarchy, State and Utopia 30 (1974), 28.Google Scholar

14 I use the term number to refer only to the cases where a quantity is expressed with the symbols, the numerals, or a particular number system. When a quantity is represented, e.g. graphically, or mentally, without the use of such symbols, I use the term magnitude. Google Scholar

15 According to the so-called Morgenstern-Von Neumann representation theorem, if we have a set of preferences among alternatives, and these preferences are complete, transitive, independent and continuous, then we can build an utility function assigning a numerical utility to each alternative, in such a way that any alternative being strictly preferred to another would have a higher utility that the latter.Google Scholar

16 This does not exclude that the methods of decision theory and cost-benefit analysis can be usefully deployed in many cases. For a technical account of multi-criteria decision-making, see Ralph L. Keeney & Howard Raiffa, Decisions with Multiple Objectives: Preferences and Value Trade Offs (1993).Google Scholar

17 C.R. Gallistel, Rochel Gelman & Cordes, Sara, The Cultural and Evolutionary History of the Real Numbers, in Evolution and Culture: A Tyssen Foundation Symposium 247, 255 (Stephen C. Levinson & Pierre Jaisson eds., 2006).Google Scholar

18 Id. at 259.Google Scholar

19 Gallistel, C. R. & Gelman, Rochel, Mathematical Cognition, in The Cambridge Handbook of Thinking and Reasoning 559 (Keith J. Holyoak & Robert G. Morrison eds., 2005).Google Scholar

20 Thus, apparently, these findings of contemporary cognitive science seem to validate Leibniz's principle of continuity, often expressed by the saying natura non facit saltus, at least with regard to the mental processing of quantitative information. See Nicholas Rescher, G.W. Leibniz's Monadology: An Edition for Students § 10 (1991): “I also take it for granted that every created being is subject to change … and even that this change is continuous in each.”Google Scholar

21 Pollock, , Thinking About Acting, supra note 1, at 37–54.Google Scholar

22 Using a logical notation to make our concept more precise, we may write Real_v (s) to denote the realisation-quantity of value v in situation s. We correspondingly denote as Real_v (s_c ), or simply Real_v, the level of realisation of v in the current situation s_c (the present state of affairs). Thus Real_v = q means that in the current situation the value v is realized in quantity q. Google Scholar

23 We write Ut_v s to denote the utility that is obtained with regard to value v, in situation s, i.e., the utility that is delivered by the fact that v is realised up to extent denoted by Real_v (s). Thus, Ut_v s = q means that such utility is quantity q. Google Scholar

24 In particular, I do not assume a utilitarian approach, according to which utility is to be viewed as happiness or preference satisfaction. On the contrary, here utility refers to the sum of all impacts on all legally relevant, communal and individual, values, and may be specified in such a way that the distribution of individual opportunities is subject to some fairness requirements.Google Scholar

25 In mathematical terms, we can say the relation between the realisation of a value and the corresponding utility is a monotonic function, and indeed a strictly increasing one. However, we take this only as a defeasible assumption, which expresses what is usually the case, and does not exclude that in certain cases over realisation of a value can be counterproductive.Google Scholar

26 In other words, if Real_v (S ₁) Real< v (S ₂), then Ut_v (S ₁) _Ut< v (S ₂).Google Scholar

27 Let us denote the outcome of action α, namely, the situation resulting from its performance, in the current situation, as out (α) and the realisation impact, the differential realisation, of an action α on a value v, as ΔReal_v (α). Then ΔReal_v (α) = Real_v, out(α) — Real_v out(Ψ).Google Scholar

28 ΔReal_v (α) > 0.+0.>Google Scholar

29 ΔReal_v (α) < 0.Google Scholar

30 Let us denote the utility impact of an action α on a value v, as ΔUt_v (α). Then ΔUt_v (α) = Ut_v out (α) — Ut_v out(Ψ).Google Scholar

31 In other words, if and only if .Google Scholar

32 In other words, since (1) ΔReal_v α > ΔReal_v β entails ΔUt_v α > ΔUt_v β and (2) the latter entails α > _v β, we can conclude (3) that ΔReal_v α > ΔReal_v β entails α > _v β. This is an application of the propositional inference according to which premises A → B and B → C entail conclusion A → C. +ΔReal+v+β+entails+ΔUt+v+α+>+ΔUt+v+β+and+(2)+the+latter+entails+α+>+v+β,+we+can+conclude+(3)+that+ΔReal+v+α+>+ΔReal+v+β+entails+α+>+v+β.+This+is+an+application+of+the+propositional+inference+according+to+which+premises+A+→+B+and+B+→+C+entail+conclusion+A+→+C.>Google Scholar

33 ΔReal _vα > ΔReal_v β entails α > _v β. +ΔReal+v+β+entails+α+>+v+β.>Google Scholar

34 On how to handle cases when this assumption does not hold, see Pollock, Thinking About Acting, supra note 1, at 13.Google Scholar

35 In other words, .Google Scholar

36 In other words, α is Pareto-superior to β with regard to a value-set {v ₁, …, v_n } if (a) there exists a v_i ∊ {v ₁, …, v_n } such that ΔReal_vi α > ΔReal_vi β and (b) for all .+ΔReal+vi+β+and+(b)+for+all+.>Google Scholar

37 Whenever some x_i is such than x_i > y_i and for all x_j is such that x_j ≥ y_j , then . Thus if α is Pareto-superior to β with regard to {v ₁, …, v_n } then .+yi+and+for+all+xj+is+such+that+xj+≥+yj+,+then+.+Thus+if+α+is+Pareto-superior+to+β+with+regard+to+{v+1,+…,+vn+}+then+.>Google Scholar

38 In the concrete reasoning of a decision-maker the two steps do not need to be clearly distinguished. They may be merged in the intuitive assessment of the importance of the negative or positive impact on the value at issue, an assessment that also reflects emotional responses.Google Scholar

39 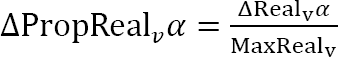, where MaxReal_v is the maximum, reasonably achievable, realisation of v. Google Scholar

40 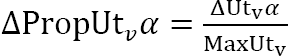.Google Scholar

41 In mathematical terms, we would say that the function connecting a value to its utility is such that its second derivative is negative. This too, however, has to be taken as what happens in most of the cases, namely, as a defeasible assumption.Google Scholar

42 Let us denote the weight of a value v with w_v. Google Scholar

43 Amartya Sen observes that there are facts that there are “reasonable variations, or inescapable ambiguities, in the choice of relative weights” does not exclude a shared assessment, with sufficient precision, from being made under many circumstances. In particular, agreement on the fact that the weights at issue fall within certain ranges is often sufficient. For some references to more technical contributions, see Amartya Sen, The Idea of Justice 297 (2009).Google Scholar

44 ΔUt_v α = ΔPropUt_v α * = w_v. Google Scholar

45 .Google Scholar

46 The positive impact can be expressed as follows: . The negative impact is correspondingly: . We use positive quantities for negative impacts—given that the absolute value |-x| a negative number -x, is the positive number (x)—since we want to express the negative impact through a positive quantity, which can be compared with the quantity of the positive impact.Google Scholar

47

48

49

50

51

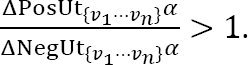
52

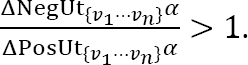
53 See Alexy, supra note 8, at 388. Alexy provides the proportion between negative and positive impacts on two values, in a particular case, through the formula 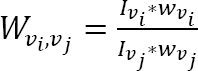, where v_i is the promoted value and v_j is the demoted value, and are the intensities of the interference on the two values, and and are the abstract weights of such values, and expresses, in Alexy's terminology, the “concrete weight” of the demoted value v_i relatively to the promoted value v_j. In the framework here presented, the intensity of the interference of an action α on a value v corresponds to ΔPropUt_v α, i.e., the proportional utility of α concerning v. By multiplying ΔPropUt_v α for v's weight w_v we obtain the utility of α concerning v, i.e., ΔUt_v α. Thus, in our framework Alexy's “concrete weight” of a demoted value v_i relatively to a promoted value v_j becomes the proportion 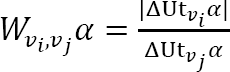., which amounts to 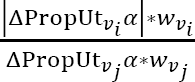. This proportion gives a number larger than 1 when α's negative utility-impact concerning v_i is larger than α's positive utility-impact concerning v_i. Google Scholar

54

55 if and only if .Google Scholar

56 More precisely, given an option set and a value-set {v ₁, …, v_n } it is possible that there is an option such that for every but there is no v_j ∊ {v ₁, …, v_n } such that for every .Google Scholar

57 This happens when and .Google Scholar

58 Alexy, Robert, Constitutional Rights, Balancing, and Rationality, 16 Ratio Juris 131, 135 (2003) (role of proportionality in judicial practice). See also Alec Stone Sweet & Jud Mathews, Proportionality Balancing and Global Constitutionalism, 47 Colum. J. Transnat'l L. 68 (2008).Google Scholar

59 Id. at 135.Google Scholar

60 Id. Google Scholar

61 Id. Google Scholar

62 , which entails .Google Scholar

63 , and there exist no β such that and .Google Scholar

64 .Google Scholar

65 There exists no β such that and .Google Scholar

66 Some aspects have been addressed in Giovanni Sartor, Doing Justice to Rights and Values: Teleological Reasoning and Proportionality, 18 Artificial Intelligence & L. 175 (2010).Google Scholar

67 More exactly, in our framework, the utility impact of a decision on two values is the sum of its utility impacts on each of them, where each utility impact is the result of the proportional impact on a value for the weight of that value: . Thus the condition for the first term—in hypothesis, the negative impact—to be bigger than the second term is that which is equivalent to 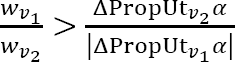. This inequality can be falsified even when the weight of value v ₁ is much larger than the weight of v ₂. This happens when the proportion between , and is larger than the proportion between and .Google Scholar

68 Barak, Aharon, Proportionality and Principled Balancing, 4 L. & Ethics of Hum. Rts. 1, 8 (2010).Google Scholar

69 In Alexy's terms this would be the passage from the application of principles to the application of rules, in Luhmann's terms, the passage from goal-programs to conditional-programsGoogle Scholar

70 On the need to complement proportionality with deontological considerations, see Mattias Kumm, Political Liberalism and the Structure of Rights: On the Place and Limits of the Proportionality Requirement, in Law, Rights and Discourse: The Legal Philosophy of Robert Alexy 131 (George Pavlakos, ed., 2007). Such deontological worries, however, can be addressed, I would argue, by applying proportionality analysis at a higher level, namely, at the level of the justification of adopting an action-rule.Google Scholar

71 On the idea of fit, see Ronald Dworkin, Law's Empire 225–75 (1986). On the connection between value-based reasoning and the interpretation of rules or the determination of their priorities, see Trevor Bench-Capon & Giovanni Sartor, A Model of Legal Reasoning with Cases Incorporating Theories and Values, 150 Artificial Intelligence 97 (2003); Henry Prakken, An Exercise in Formalising Teleological Case-Based Reasoning, 10 Artificial Intelligence & L. 113 (2000).Google Scholar

72 This follows from inequalities and . In fact, such inequalities entail that , i.e., that . Since we know that the α's utility () is superior to 0 (α is proportionate), and that β's utility () is superior to α's, it follows that also β's utility is superior to 0, namely, that also β is proportionate.Google Scholar

73 This follows from inequalities and . Such inequalities entail that , i.e., that . Since we know that the α's utility is inferior to 0, α being disproportionate, and that the β's utility is inferior to α's, it follows that also β's utility is inferior to 0, namely, that also β is disproportionate.Google Scholar

74 Whether , where v_d is the demoted value, i.e., privacy, while v_p is the promoted value, i.e., security.Google Scholar

75

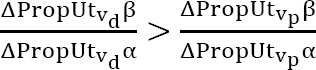
76 On the basis of the previous definitions we have the following equalities: . We know from the previous assessment that was unbalanced, i.e., that . This entails that the negative quantity is greater, in absolute value, than the positive quantity . Thus, whatever quantities and we attribute to the weight of and consistently with the precedent, it must be the case that . We also know that the new decision decreases privacy to a larger proportion than it increases security, in comparison to 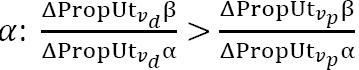. Then by multiplying for 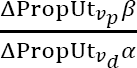and simplifying we get , and similarly by multiplying for 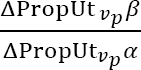and simplifying we get . Thus we must conclude that also these results must be, in absolute value, such as the first one is bigger than the second: . This follows indeed from the fact that for all numbers a ₁, a ₂, b ₁, b ₂, if a ₁, > b ₁, and a ₂ > b ₂ then also a ₁, * a ₂, > b ₁, * b ₂. Therefore also the second sum must give a negative result: . This means that , i.e., that β is unbalanced too.+b+1,+and+a+2+>+b+2+then+also+a+1,+*+a+2,+>+b+1,+*+b+2.+Therefore+also+the+second+sum+must+give+a+negative+result:+.+This+means+that+,+i.e.,+that+β+is+unbalanced+too.>Google Scholar

77 For some critical observations on teleological reasoning in the law and value-based constitutional review in the law, see Jurgen Habermas, Between Facts and Norms: Contributions to a Discourse Theory of Law and Democracy 259 (1999); Niklas Luhmann, Zweckbegriff und Systemrationalität: über die Funktion von Zwecken in sozialen Systemen (1973); Bernhard Schlink, Der Grundsatz der Verhältnismäßigkeit, in Festschrift 50 Jahre Bundesverfassungsgericht 445 (Peter Badura & Horst Dreier eds., 2001).Google Scholar

78 See Wojciech Zaluski, Evolutionary Theory and Legal Philosophy (2009); 5 Studies in Philosophy of Law: Law and Biology (Jerzy Stelmach, Bartosz Brożek & Marta Soniewicka eds., 2011).Google Scholar

Article contents

The Logic of Proportionality: Reasoning with Non-Numerical Magnitudes

Extract

References

This article has been cited by the following publications. This list is generated based on data provided by Crossref.

Article contents

The Logic of Proportionality: Reasoning with Non-Numerical Magnitudes

Extract

References

Save article to Kindle

Save article to Dropbox

Save article to Google Drive

Reply to: Submit a response

Your details

You have entered the maximum number of contributors

Conflicting interests