Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-25T16:33:43.748Z Has data issue: false hasContentIssue false
  • English
  • Français

Using known QTLs to detect directional epistatic interactions

Published online by Cambridge University Press:  22 February 2012

MONTGOMERY SLATKIN  and
MARK KIRKPATRICK
MONTGOMERY SLATKIN*
Affiliation:
Department of Integrative Biology, University of California, Berkeley, CA 94720-3140, USA
MARK KIRKPATRICK
Affiliation:
Section of Integrative Biology, University of Texas, Austin, TX 78712, USA
*
*Corresponding author: [email protected]; Fax: 510-643-6264.
Rights & Permissions [Opens in a new window]

Summary

Epistasis plays important roles in evolution, for example in the evolution of recombination, but each of the current methods to study epistasis has limitations. Here, we propose a new strategy. If a quantitative trait locus (QTL) affecting a quantitative character has been identified, individuals who have the same genotype at that QTL can be regarded as comprising a subpopulation whose response to selection depends in part on interactions with other loci affecting the character. We define the marginal differences to be the differences in the average phenotypes of individuals with different genotypes of that QTL. We show that the response of the marginal differences to directional selection on the quantitative character depends on epistatic gene interactions. For a model with no interactions, the marginal differences do not differ on average from their starting values once linkage equilibrium has been re-established. If there is directional epistasis, meaning that interactions between the QTL and other loci tend to increase or decrease the character more than under an additive model, then the marginal differences will tend to increase or decrease accordingly when larger values of the character are selected for. We develop a likelihood ratio test for significant changes in the marginal differences and show that it has some power to detect directional epistasis for realistic sample sizes. We also show that epistatic interactions which affect the evolution of the marginal differences do not necessarily result in a substantial epistatic component of the genetic variance.

Type
Research Papers
Information
Genetics Research , Volume 94 , Issue 1 , February 2012 , pp. 39 - 48
Copyright
Copyright © Cambridge University Press 2012

Gene interactions are commonly found in genetic experiments but their overall importance for quantitative genetics is not well understood (Phillips, Reference Phillips2008; Flint & Mackay, Reference Flint and Mackay2009). In this paper, we introduce a new way of testing for epistatic interactions when one or more QTLs affecting a quantitative character have been identified. For a specific QTL, the marginal averages, defined to be the character averages in individuals with each of the QTL genotypes, depend on other loci affecting the character. After the marginal averages are estimated in the initial population, selection can be applied. Changes in the marginal averages in the selected population reflect interactions with other loci affecting the character. In particular, the differences in the marginal averages, which we call the marginal differences, increase or decrease if interactions tend to increase or decrease the character from the expectation under additivity. Such interactions are called directional epistatic interactions by Hansen & Wagner (Reference Hansen and Wagner2001). They can affect the evolutionary dynamics of a trait even when they do not result in a substantial epistatic component of genetic variance.

Directional epistatic interactions have been discussed extensively in the context of loci affecting fitness. If alleles that increase fitness have negative interactions (i.e. overall fitness is less than would be predicted by the individual effects), then negative linkage disequilibrium results. Under some conditions, this situation can favour the evolution of increased recombination and sexual reproduction (reviewed in Otto, Reference Otto2009). This theoretical prediction has motivated a substantial number of experiments searching for consistent patterns in the sign of epistasis. No clear trend has emerged (de Visser & Elena, Reference de Visser and Elena2007; Kouyos et al., Reference Kouyos, Silander and Bonhoeffer2007). Those results, however, largely rest on two experimental paradigms: constructing genotypes with known combinations of mutations, and following changes in time and differences between mutation accumulation lines. These and other approaches used to quantify epistasis, however, have a variety of limitations that we review in the Discussion. It would therefore be useful to have other experimental strategies that could be applied to other genes, organisms and traits.

Early work on the effects of epistasis on quantitative traits was led by Cockerham (Reference Cockerham1954) and Kempthorne (Reference Kempthorne1954), who first worked out the theory for estimating epistatic components of genetic variance from the resemblance between relatives. Since then, many specific models of epistasis have been developed and analysed, some based on the deviations from additivity expressed in algebraic terms (Lewontin & Kojima, Reference Lewontin and Kojima1960) and others based on explicit assumptions about interactions of gene products (Kacser & Burns, Reference Kacser and Burns1981). In most cases, explicit models of gene interactions do not result in much epistatic variance (Keightley, Reference Keightley1989). Hansen and Wagner (Reference Hansen and Wagner2001), Barton and Turelli (Reference Barton and Turelli2004) and others have explored the properties of general models of epistasis. Pavlicev et al. (Reference Pavlicev, Le Rouzic, Cheverud, Wagner and Hansen2010) implemented the Hansen and Wagner theory and found evidence for directional epistasis between QTLs affecting several characters in inbred mice. Le Rouzic et al. (Reference Le Rouzic, Skaug and Hansen2010) developed a statistical method for estimating epistatic effects by analysing data from selection experiments. Although they did not assume that QTL frequencies could be monitored in the same experiment, their method could be adapted to allow for that possibility.

In this paper, we propose a strategy to detect directional epistasis using selection experiments. Our method differs from that used by Pavlicev et al. (Reference Pavlicev, Le Rouzic, Cheverud, Wagner and Hansen2010) because it is designed to detect directional epistasis between a previously identified QTL and all other QTLs affecting the same character, including both those that have been identified and those that are still unknown. The method used by Pavlicev et al. (Reference Pavlicev, Le Rouzic, Cheverud, Wagner and Hansen2010) tests for directional epistasis between only those QTLs that have been identified. We begin by describing a null model of additive effects across loci (i.e. no epistasis). We next define three simple models of gene interactions that will allow us to illustrate our results. The first is a completely symmetric model of epistasis for which the theory is relatively simple. We then consider two other models for epistasis in which one locus, representing a known QTL, is distinguished from the others. We then turn to detecting epistasis. Using analysis and simulation of the models, we show that with directional epistasis the average differences between the genotypes at a QTL changes following selection. We propose a statistical test for detecting these changes and examine its power.

Model assumptions

We assume that a quantitative character, x, is determined by the genotype at L unlinked diallelic loci. At each locus, the allele that tends to increase x is denoted by +. The genotype of an individual is represented by a vector k={k 1, …kL }, where ki =0, 1 or 2, indicates the number of+alleles at that locus. In general,

(1)
x \equals f\,\lpar {\bi k}\rpar \comma

where f(k) is the phenotype map that specifies the average phenotype associated with each genotype. In general, f depends on 3L parameters, one for each genotype.

Our reference by which to judge the effects of epistasis is the additive model. It assumes that the contributions of each locus add:

(2)
f\,\lpar k_{\setnum{1}} \comma \ldots \comma k_{L} \rpar \equals f_{\setnum{1}} \lpar k_{\setnum{1}} \rpar \plus \ldots \plus f_{L} \lpar k_{L} \rpar .

The first and simplest of our three models that include epistasis is the symmetric model. It assumes that all+alleles are equivalent in their effect on the character, which implies that f depends only on the total number of+alleles:

(3)
f\,\lpar k_{\setnum{1}} \comma \ldots \comma k_{L} \rpar \equals h_{i} \comma

where i \equals \sum _{j \equals \setnum{1}}^{L} k_{j} . If hi is a linear function of i, then the symmetric model is also additive. In later analysis, we will assume quadratic functional dependence on i: h_{i} \equals \beta {i} \plus \gamma {i} ^{\setnum{2}} . A generalization of the symmetric model assumes that a random interaction term, e k is added with probability q to each genotype:

(4)
f\,\lpar {\bi k}\rpar \equals \beta {i} \plus \gamma {i} ^{\setnum{2}} \plus e_{\bi k} .

The parameter q allows us to vary the sparseness of the additional epistatic terms. We will assume that each e k is drawn independently from a distribution with mean 0 and standard deviation σI.

We next consider cases in which a focal locus, which we take to be locus 1 without loss of generality, is distinguished from the others. Locus 1 represents a QTL that has already been identified in a mapping study. In our second model for epistasis, which we call conditional additive, locus 1 interacts additively with all other loci considered together, but the other loci interact among themselves:

f\,\lpar k_{\setnum{1}} \comma \ldots \comma k_{L} \rpar \equals f_{\setnum{1}} \lpar k_{\setnum{1}} \rpar \plus f_{\setnum{2} \minus L} \lpar k_{\setnum{2}} \comma \ldots \comma k_{L} \rpar .

In our third and final model for epistasis, which we call conditional epistatic, locus 1 interacts with each other locus epistatically but the other loci do not interact with one another:

(6)
\eqalign{ f\,\lpar k_{\setnum{1}} \comma \ldots \comma k_{L} \rpar \equals \tab f_{\setnum{1}} \lpar k_{\setnum{1}} \rpar \plus \ldots \plus f_{L} \lpar k_{L} \rpar \plus f_{\setnum{12}} \lpar k_{\setnum{1}} \comma k_{\setnum{2}} \rpar \cr \tab \hskip-2pt \plus \ldots\plus f_{\setnum{1}L} \lpar k_{\setnum{1}} \comma k_{L} \rpar . \cr}

The conditional epistatic model allows for directional epistasis in an especially simple context.

Population properties

The mean and total genetic variance of x in the population are

(7)
\bar{x} \equals \mathop\sum\limits_{\bi k} {{\rm Pr} \lpar {\bi k}\rpar f\lpar {\bi k}\rpar }

and

(8)
V_{G} \equals \mathop\sum\limits_{\bi k} {{\rm Pr} \lpar {\bi k}\rpar \left[ {f\lpar {\bi k}\rpar \minus \bar{x}} \right]^{\setnum{2}} } \comma

where Pr(k) is the frequency of genotype k in the population.

We assume there is a base population in which the frequency of the + allele at locus j is pj and the loci are in Hardy–Weinberg and linkage equilibrium. Then we allow directional selection on x to be applied. Continued random mating will ensure Hardy–Weinberg genotype frequencies each generation, but selection will create linkage disequilibrium even between unlinked loci. We will assume that selection is applied for t 1 generations and then t 2 generations of random mating occur without selection in order to allow linkage equilibrium to be restored.

We calculated the components of genetic variance in the standard way (Falconer & Mackay, Reference Falconer and Mackay1996; Lynch & Walsh, Reference Lynch and Walsh1998). The total genetic variance is V G (eqn 8). We compute a_{j} \equals \lpar \bar{x}_{\setnum{2}\comma j} \minus \bar{x}_{\setnum{0}\comma j} \rpar \sol 2 and d_{j} \equals \bar{x}_{\setnum{1}\comma j} \minus \lpar \bar{x}_{\setnum{2}\comma j} \plus \bar{x}_{\setnum{0}\comma j} \rpar \sol 2, where \bar{x}_{k\comma j} are the marginal averages for locus j. Then, V_{A} \equals \sum _{j \equals \setnum{1}}^{L} 2p_{j} <$> <$>\lpar 1 \minus p_{j} \rpar \lsqb a_{j} \plus d_{j} \lpar 1 \minus 2p_{j} \rpar \rsqb ^{\setnum{2}} , V_{D} \equals \sum _{j \equals \setnum{1}}^{L} \lsqb 2p_{j} \lpar 1 \minus p_{j} \rpar d_{j} \rsqb ^{\setnum{2}} and VI =VG −VA −VD .

Marginal averages and marginal differences

Our test for epistasis depends on changes in the differences between the average phenotypes produced by genotypes at the focal QTL. The marginal averages for that QTL (locus 1) are the expectations of x, given the genotype at locus 1:

(9)
\bar{x}_{k} \equals \mathop\sum\limits_{k_{\setnum{2}} \ldots k_{L} } {\Pr \lpar k_{\setnum{2}} \comma \ldots \comma k_{L} \vert k_{\setnum{1}} \equals k\rpar f\lpar k\comma k_{\setnum{2}} \comma \ldots \comma k_{L} \rpar } .

where k=0, 1, 2 corresponds to the number of+alleles at the focal locus. At linkage equilibrium, the conditional probabilities do not depend on k.

We define the marginal differences for locus 1 to be \rmDelta _{\setnum{1}} \equals \bar{x}_{\setnum{2}} \minus \bar{x}_{\setnum{1}} and \rmDelta _{\setnum{0}} \equals \bar{x}_{\setnum{1}} \minus \bar{x}_{\setnum{0}} . These quantities are the key to the test we propose for detecting directional epistasis: as we will see in the following sections, changes in allele frequencies cause the marginal differences to change under some types of epistasis. If the marginal differences for a locus do change that will alter the additive genetic variance the locus contributes to the trait. To see this, write the additive genetic effect of locus 1 in terms of the marginal differences:

(10)
\alpha \equals {{\rmDelta _{\setnum{1}} \plus \rmDelta _{\setnum{0}} } \over 2} \minus \lpar 1 \minus 2p\rpar {{\rmDelta _{\setnum{1}} \minus \rmDelta _{\setnum{0}} } \over 2}.

The marginal differences are therefore of interest for two reasons: they provide an opportunity to test for epistasis, and changes in their values alter the contribution of a locus to the additive genetic variance for a trait.

We now consider the properties of the marginal differences under the conditional additive and conditional epistatic model, where simple analytic results can be obtained, and under the symmetric model, where we rely on numerical analysis.

The conditional additive model

In the conditional additive model, the effect of locus 1 is added to the net effect of the other L–1 loci, which may interact among themselves. It is easy to see that the expectations of the marginal averages do not depend on the allele frequencies at the other loci at linkage equilibrium. From eqn (9),

(11)
\eqalign{ \hskip1pt\bar{x}_{k} \equals \tab \mathop\sum\limits_{k_{\setnum{2}} \ldots k_{L} } {{\rm Pr} \lpar k_{\setnum{2}} \comma \ldots \comma k_{L} \vert k_{\setnum{1}} \equals k\rpar \; f \; \lpar k\comma k_{\setnum{2}} \comma \ldots \comma k_{L} \rpar } \cr \equals \tab \mathop\sum\limits_{k_{\setnum{2}} \ldots k_{L} }^{} {{\rm Pr} \lpar k_{\setnum{2}} \comma \ldots \comma k_{L} \vert k_{\setnum{1}} \equals k\rpar } \left[ {f_{\setnum{1}} \lpar k\rpar \plus f_{\setnum{2}\comma L} \lpar k_{\setnum{2}} \comma \ldots \comma k_{L} \rpar } \right] \cr \equals \tab f_{\setnum{1}} \lpar k\rpar \plus \mathop\sum\limits_{k_{\setnum{2}} \ldots k_{L} } {{\rm Pr} \lpar k_{\setnum{2}} \comma \ldots \comma k_{L} \rpar f_{\setnum{2}\comma L} \lpar k_{\setnum{2}} \comma \ldots \comma k_{L} \rpar } \cr}

because, at linkage equilibrium, Pr(k 2, …, kL |k 1=k) is independent of k. Therefore, \rmDelta _{\setnum{1}} \equals \bar{x}_{\setnum{2}} \minus \bar{x}_{\setnum{1}} \equals f_{\setnum{1}} \lpar 2\rpar \minus f_{\setnum{1}} \lpar 1\rpar and \rmDelta _{\setnum{0}} \equals \bar{x}_{\setnum{1}} \minus \bar{x}_{\setnum{0}} \equals f_{\setnum{1}} \lpar 1\rpar \minus f_{\setnum{1}} \lpar 0\rpar . The conclusion is that the marginal differences at locus 1 are independent of the allele frequencies at the other loci. In fact, all that is required for this result is that there should be linkage equilibrium between locus 1 and the others, even if there is linkage disequilibrium among the other loci.

The conditional epistasis model

A different result holds under the conditional epistasis model. If locus 1 interacts with the other loci, the marginal differences may change. Substituting into eqn (9), we obtain

(12)
\eqalign{ \hskip-1.5pt\bar{x}_{k} \equals \tab f_{\setnum{1}} \lpar k\rpar \plus \mathop\sum\limits_{k_{\setnum{2}} \; \ldots \; k_{L} } {{\rm Pr} \lpar k_{\setnum{2}} \comma \ldots \comma k_{L} \vert k_{\setnum{1}} \equals k\rpar } \cr \tab \left[ {\,f_{\setnum{2}} \lpar k_{\setnum{2}} \rpar \plus \ldots \plus f_{L} \lpar k_{L} \rpar \plus f_{\setnum{12}} \lpar k\comma k_{\setnum{2}} \rpar \plus \ldots \plus f_{\setnum{1}L} \lpar k\comma k_{L} \rpar } \right]. \cr}

Subtracting and assuming linkage equilibrium yields

(13)
\rmDelta _{\setnum{1}} \equals f_{\setnum{1}} \lpar 2\rpar \minus f_{\setnum{1}} \lpar 1\rpar \plus \mathop\sum\limits_{i \equals \setnum{2}}^{L} {\mathop\sum\limits_{k_{i} \equals \setnum{0}}^{\setnum{2}} {{\rm Pr} \lpar k_{i} \rpar \left[ {f_{\setnum{1}i} \lpar 2\comma k_{i} \rpar \minus f_{\setnum{1}i} \lpar 1\comma k_{i} \rpar } \right]} }

and

(14)
\rmDelta _{\setnum{0}} \equals f_{\setnum{1}} \lpar 1\rpar \minus f_{\setnum{1}} \lpar 0\rpar \plus \mathop\sum\limits_{i \equals \setnum{2}}^{L} {\mathop\sum\limits_{k_{i} \equals \setnum{0}}^{\setnum{2}} {{\rm Pr} \lpar k_{i} \rpar \left[ {f_{\setnum{1}i} \lpar 1\comma k_{i} \rpar \minus f_{\setnum{1}i} \lpar 0\comma k_{i} \rpar } \right]} } .

The third terms on the right-hand sides of these expressions represent the net effects of the epistatic interactions between locus 1 and the others. These expressions show that the marginal differences at locus 1 are functions of the allele frequencies at the other loci.

A special case of the conditional epistasis model is that in which fi (ki )=ki and f 1i(k 1,ki )=βik 1ki . Then

(15)
\rmDelta _{\setnum{1}} \equals \rmDelta _{\setnum{0}} \equals 1 \plus 2\mathop\sum\limits_{i \equals \setnum{2}}^{L} {\beta _{i} p_{i} } .

Thus, the changes in the marginal averages are proportional to the changes in allele frequency at the other loci, weighted by the βi.

The key conclusion that emerges from the conditional epistasis model is that the marginal differences for the focal QTL will change if there are allele frequency changes at other loci with which the focal locus has directional epistatic interactions. This motivates the experimental test proposed below, in which the allele frequencies change in response to artificial selection.

The symmetric model

The general model is not analytically or even numerically tractable for more than a few loci. This situation motivates the symmetric model, in which the frequency and effect of the + allele is assumed to be the same at all loci. These assumptions lead to a relatively simple theory that can be analysed numerically for larger numbers of loci.

Our analysis is based on that of Barton (Reference Barton1992) . We assume an infinitely large population and ignore the effects of genetic drift. The population is characterized by the frequencies of gametes carrying i+alleles. A generation consists of the random union of gametes, then selection based on the number of+alleles in zygotes, and finally free recombination to create the next generation of gametes. After one generation

(16)
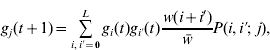
g_{j} \lpar t \plus 1\rpar \equals \mathop\sum\limits_{i\comma i \prime \equals \setnum{0}}^{L} {g_{i} \lpar t\rpar g_{i \prime} \lpar t\rpar {{w\lpar i \plus i'\rpar } \over {\bar{w}}}} P\lpar i\comma i \prime \semi \ j\rpar \comma

where gi (t) is the frequency of gametes carrying i+alleles in generation t, w(i+i′) is the relative fitness of an individual with i+i′+alleles, \bar{w} is the average fitness in the population and P(i,i′;j) is the probability that an individual with gametes carrying i and i′+alleles will produce a gamete with j+alleles. Barton (Reference Barton1992) derived the expression for P by assuming all configurations of+alleles are equally probable in a gamete carrying i+alleles:

(17)
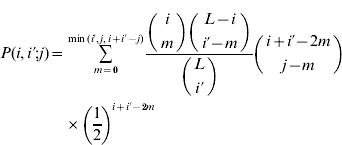
\eqalign{ P\lpar i\comma i \prime \semi j\rpar \equals \tab \mathop\sum\limits_{m \equals \setnum{0}}^{\min \lpar i \prime \comma j\comma i \plus i \prime \minus j\rpar } {{{\left( {\matrix{ i \cr m \cr} } \right)\left( {\matrix{ {L \minus i} \cr {i \prime \minus m} \cr} } \right)} \over {\left( {\matrix{ L \cr {i \prime } \cr} } \right)}}} \left( {\matrix{ {i \plus i \prime \minus 2m} \cr {j \minus m} \cr} } \right) \cr \tab \times \left( {{1 \over 2}} \right)^{i \plus i \prime \minus \setnum{2}m} \cr}

if i′⩽i and max(i+i′−L)⩽j⩽min(i+i′−L). By symmetry P(i,i′; j)=P(i′,i; j). Because the ratio of binomial coefficients in the sum is the same as the ratio in the hypergeometric probability distribution, this model is sometimes called the hypergeometric model. We compute the marginal differences and the variance components for the symmetric model as described in Appendix A. A Mathematica program that carries out these calculations is available on request.

There is no closed form solution for this model, but it is easy to iterate numerically for an arbitrary fitness function, w. Here we will assume truncation selection for larger x and let αx be the fraction of zygotes that survive to breed. Our interest is with the dependence on the marginal differences on the phenotype map, hi .

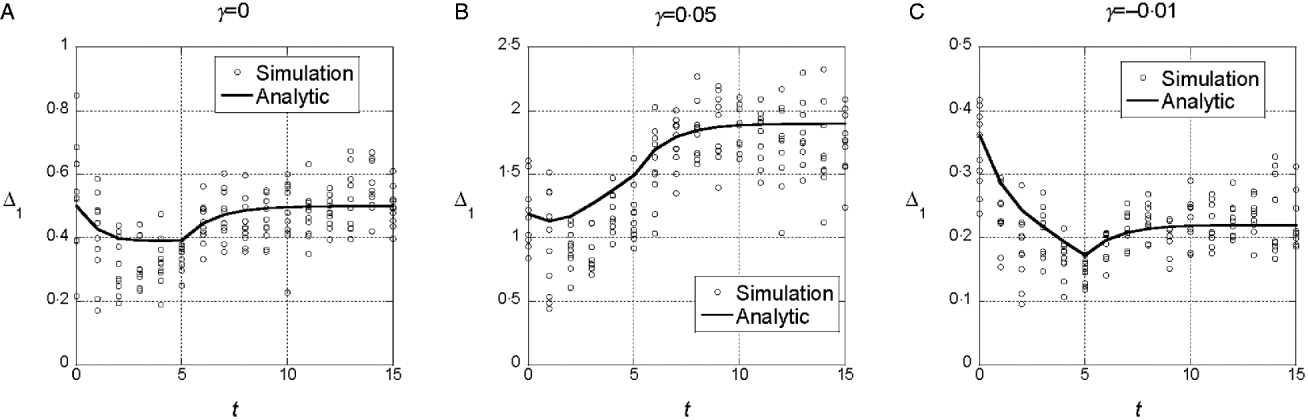
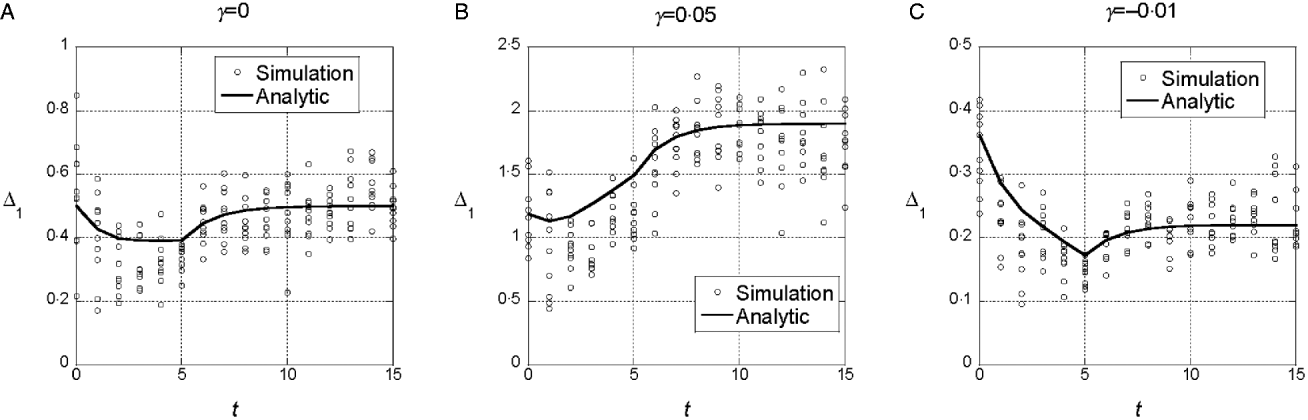
We assumed a quadratic phenotype map, h_{i} \equals \beta {i} \plus \gamma {i} ^{\setnum{2}} , in order to contrast the results for the additive model (γ=0) with models that assume synergistic (γ>0) and antagonistic (γ<0) interactions of+alleles. Figure 1 shows typical results for experiments in which five generations of truncation selection with αx=0·5 are followed by 10 generations with no selection. In the additive model, the marginal differences initially decrease because of the accumulation of linkage disequilibrium, but then return to their original values after 10 generations of random mating. In contrast, if γ>0, the marginal differences are larger than their initial values after linkage equilibrium has been re-established (Fig. 1 b), and if γ<0, the marginal differences are smaller than their initial values (Fig. 1 c).

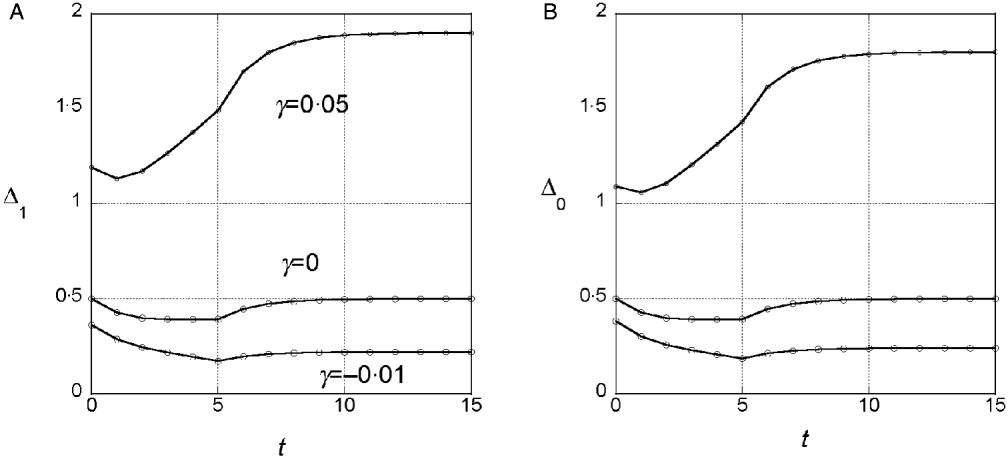
Fig. 1. Time dependence of the marginal differences, Δ1 and Δ0, after five generations of truncation selection with αx=1/2. The phenotype map in each case is h_{i} \equals \beta {i} \plus \gamma {i} ^{\setnum{2}} . In all cases, β=0·5. Generation 0 is the initial population assumed to be in Hardy–Weinberg and linkage equilibrium with p=0·3 at all 10 loci. Selection was applied in generations 0–4 followed by 10 generations of random mating without selection.

This trend in the results does not require much synergistic or antagonistic interaction and these interactions do not create much interaction variance once linkage equilibrium is re-established. The final values of V I/V G are 0·002 for γ=0·05 and 0·015 for γ=−0·01.

We conclude from these numerical results that the marginal differences are sensitive to relatively weak gene interactions and that they are sensitive to gene interactions that do not create significant interaction components of the genetic variance.

Statistical test for changes in marginal differences

The symmetric model shows that the marginal differences depend on directional epistatic interactions between a QTL and other loci. To detect a significant change in the marginal differences, either in real or simulated data, a statistical test is needed. We developed a likelihood ratio test that is described in Appendix B. The test compares the genotype-specific distributions of the character in the initial and final populations. The data are in six vectors, {xki } for the starting population and {yki } for the final population, where k=0, 1, 2 is the number of copies of the+allele at the QTL. We assume that the elements of each vector are drawn from a normal distribution with means μkx or μky and variances Vkx or Vky . Our test is of whether \mu _{\setnum{2}x} \minus \mu _{\setnum{1}x} \equals \mu _{\setnum{2}y} \minus \mu _{\setnum{1}y} and \mu _{\setnum{1}x} \minus \mu _{\setnum{0}x} \equals \mu _{\setnum{1}y} \minus \mu _{\setnum{0}y} under the assumption that the variances can take any values. Our test assumes that twice ratio of likelihoods computed under the assumption of no constraints on the means and under the assumption of these two constraints has a χ2 distribution with two degrees of freedom. The P-value reported is the tail probability of this distribution.

Like any statistical test, the power of this test increases with sample size. The power can be increased by accumulating data from several generations before and after selection is performed. In this way, larger total sample sizes can be obtained without having to increase the total size of the populations studied.

Simulations

The numerical analysis of the symmetric model assumes that selection is performed in infinitely large populations and that allele frequencies at all loci are the same in each generation. We wrote a simulation program for finite populations to test whether the trends seen in those analyses can be detected in selection experiments and to analyse other models for epistasis.

The simulation program assumes that a population of 2N gametes is formed into N zygotes. A phenotype x is assigned to each zygote according the specified phenotype map. Then the Ns =αxN individuals with the largest x are chosen to breed. Meiosis was modelled by randomly choosing individuals with replacement 2N times from the breeding pool and generating a random gamete from each, assuming no linkage. Because the gametes are paired randomly into zygotes, this method is equivalent to allowing self-fertilization.

In each generation, we recorded the marginal differences and the genetic, additive, dominance and epistatic components of the genetic variance. After t 1+t 2 generations, we tested for significant changes in the marginal differences at locus 1 to obtain a P-value of the test that there was no change in the marginal differences.

Simulation results for the symmetric model

Figure 2 shows the simulation results for the marginal differences in the symmetric model for the same parameter values used in Fig. 1. The numerical results from Fig. 1 are included for comparison. In Fig. 2, the marginal differences for all 10 loci are plotted for each generation. In the symmetric model, all loci are equivalent, and hence variation among loci represents the variation among replicates for a single locus. The simulation results are consistent on average with the results for an infinitely large population and they illustrate that there is substantial stochastic variation even with N=1000. It is worth noting that the stochastic variation seen is not the result of the instability of allele frequencies caused by selection. Although the equality of allele frequencies in a symmetric model may be unstable to some kinds of selection (Barton & Shpak, Reference Barton and Shpak2000), that is not the case with the selection model we used. In these and other simulation results for the symmetric model, allele frequencies at different loci do not vary more than would be expected under genetic drift alone acting for the same number of generations. Instead, the variation in the marginal differences results from stochastic variation in linkage disequilibrium among the loci.

Fig. 2. Time dependence of Δ1 and Δ0 for all 10 loci in a population of N=1000 individuals. The parameter values are the same as in Fig. 1. The predictions of the analytic theory from Fig. 1 are plotted with solid lines for comparison with the simulations.

To determine whether significant changes in the marginal differences can be detected with the test described above, we ran 100 replicates each with the same parameter values used in the three cases shown in Fig. 2 but with \sigma _{e}^{2} chosen so that the heritability in each case is roughly 1/2: \sigma _{e}^{\setnum{2}} =1.1 for γ=0, 3·0 for γ=0·5 and 0·9 for γ=−0·1. For 3A (linear model), 5% had a significant change in the marginal differences at the 5% level. For 3B (synergistic), 31% were significant at the 5% level and for 3C (antagonistic) 14% were significant.

These simulation results confirm that the average behaviour predicted by the analytic theory is seen in populations of finite size and that there is some power to detect significant changes in the marginal differences. The symmetric model we analysed is not a realistic model for interactions affecting quantitative character, however, because all interactions are in the same direction. As a consequence, V G is predicted to change systematically in a way not seen in selection experiments. With γ=0·05, V G almost doubles and if γ=−0·01, it decreases by almost a half.

Simulation results for other models

The results from the symmetric model indicate that deviations from the additive model of the same sign (either synergistic or antagonistic) tend to have consistent effects on the marginal differences. To determine whether those results are sensitive to additional random epistatic effects, we simulated the model with the randomly generated interaction term, eqn (4). Figure 3(a) shows that if γ=0, selection on x does not tend to change the marginal differences, even though the additional interaction terms create a substantial interaction component of the variance. After linkage equilibrium is re-established, V I/V G≈0·25. With both synergistic (γ>0) and antagonistic (γ<0), the trends in the marginal differences persist (Fig. 3 b and c). In sets of 100 replicate simulations for each set of parameter values, we tested whether the marginal differences changed significantly at the 5% level. In 100 replicates, we found 10% significant changes in the marginal differences for the parameters in 3A (with \sigma _{e}^{\setnum{2}} \equals 1{\cdot}4), 56% for 3B (with \sigma _{e}^{\setnum{2}} \equals 9) and 5% for 3C (with \sigma _{e}^{\setnum{2}} \equals 0{\cdot}9)

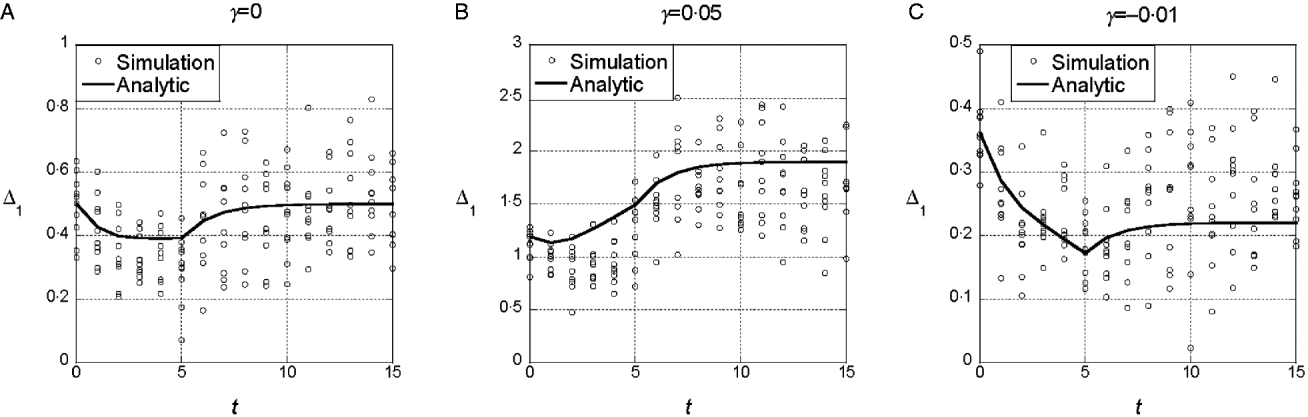
Fig. 3. Time dependence of Δ1 and Δ0 in the model with random epistatic terms added to the quadratic dependence on i (cf. eqn (4)). The parameter values are the same as in Figs 1 and 2. The additional epistatic term for each genotype was drawn with probability q=0.5 from a normal distribution with mean 0 and standard deviation σI =1. The predictions of the analytic theory from Fig. 1 are plotted with solid lines for comparison.

We determined the power of the likelihood ratio test for the conditional epistasis model with f 1i(k 1, ki )=βi1ki . Table 1 shows some results for L=10, pi =0·2 initially, and the same β used for i=2, …, 10. With the parameter values used, the average pi was approximately 0·8 in the final population. Therefore, from eqn (15) the expected change in the marginal differences is 2\beta \lpar L \minus 1\rpar \lpar p_{i}^{{\rm final}} \minus p_{i}^{{\rm initial}} \rpar or approximately 10·6β. We can see there is some power to detect significant changes in marginal differences, particularly if N=1000.

Table 1. Power to detect significant changes in the marginal differences (Δ1 and Δ0) for the conditional epistasis model. In all cases, 100 replicate simulations were run, αx=0·5, L=10, f1(k1)=k1, the frequency of the+allele was initially 0·2 at every locus, and the same value of βi was assumed for loci i=2, …, 10. If the+allele became fixed after selection, the test could not be performed. The numbers shown are the fractions of replicates for which the likelihood ratio test was performed and P⩽0·05. The numbers in parentheses are the numbers of tests performed

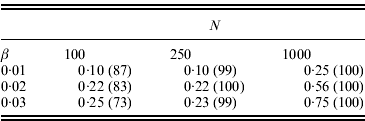
As mentioned above, the power of our test can be increased if information is accumulated over several generations before and after selection. To illustrate, we ran additional simulations for the middle cell in Table 1 (N=250 and β=0·02). With data taken in one generation before and after selection was performed, 22% of the replicates had a significant change in the marginal differences at the 5% level. With data accumulated over three generations before and after, 47% of the replicates were significant and over five generations before and after 62% were significant.

Discussion and conclusions

Four research strategies are currently used to study epistasis among genes affecting quantitative traits, each with its strengths and weaknesses. The total genetic variance can be decomposed to determine the contribution from epistasis (Cockerham, Reference Cockerham1954; Kempthorne, Reference Kempthorne1954). Limitations of this approach are that it does not give information about the form of epistasis, or how epistasis will affect evolutionary dynamics. A second approach is to construct known genotypes to study interactions between loci (Flint & Mackay, Reference Flint and Mackay2009). This strategy has the virtues that it can directly identify loci that interact, and allows the interactions to be quantified in detail and studied experimentally. It is limited to organisms in which appropriate mutations have been characterized and by the number of mutant combinations that can be constructed and analysed. A third strategy is to analyse replicated mutation accumulation lines (Elena & Lenski, Reference Elena and Lenski1997). The dynamics of trait values (such as fitness) within lines and differences between lines can be used to estimate parameters of epistasis. The strength of this method is that it can in principle detect the effects of epistasis at loci throughout the genome, and these loci do not need to be identified a priori. A major limitation is that it quantifies only the epistatic effects of spontaneous mutations, which may not be typical of genes segregating in natural populations. A fourth method used to study epistasis is QTL mapping (Manichaikul et al., Reference Manichaikul, Moon, Sen, Yandell and Broman2010). This approach identifies the QTLs involved, but is constrained by statistical power to detecting only strong epistatic interactions.

This paper proposes a new strategy for studying epistasis that complements these other methods. Its strengths are that it can detect contributions to epistasis from naturally segregating variation at loci throughout the genome. Its limitations are that it requires a large replicated selection experiment and is sensitive to only certain types of epistasis. The principle of our method depends on the fact that the marginal effects of a known QTL depend on the epistatic interactions of that locus with other loci affecting the same character. Changes in allele frequencies at those loci change the genetic environment for the QTL (Phillips, Reference Phillips2008). This generalization implies that changes in the marginal effects of a known QTL can provide evidence of interactions that tend to be in one direction, either synergistic or antagonistic. Furthermore, interactions that affect the marginal differences do not necessarily lead to a substantial interaction component of the genetic variance and therefore might not be detected by studies that focus on variance components.

Our method is not able to detect all types of epistatic interactions, only those that result in a net directional component. As shown in Fig. 3(a), interactions can be present and can generate a substantial interaction component of the variance and yet will not result in a net change in the marginal differences because their effects tend to cancel.

Our numerical and simulation results show that synergistic and antagonistic interactions result in predictable changes in the marginal differences, on average. At first sight, it may seem unlikely that epistatic interactions would show a bias towards synergistic or antagonistic interactions. It is, however, well established that dominance interactions often display directionality. Deleterious mutations are typically partly recessive (Eyre-Walker & Keightley, Reference Eyre-Walker and Keightley2007), and consistent dominance patterns have been seen for other kinds of traits, a phenomenon called ‘directional dominance’ (Falconer & Mackay, Reference Falconer and Mackay1996, p. 250). If dominance (i.e. interactions between alleles at a single locus) can show consistent patterns, it is plausible that epistasis (which is interactions between alleles at different loci) will also. Metabolic control theory gives support to that view (Keightley, Reference Keightley1989).

In our analysis, we have assumed that QTLs are unlinked. In that case a few generations of random mating with no selection will restore linkage equilibrium. Our conclusions are still true if there is very close linkage between the focal QTL and others. In the time scale of the experiment, very closely linked QTLs would behave as a single QTL because recombination between them would be unlikely. Complications arise if there is weaker linkage between the focal QTL and one or more unseen QTLs. Even if they are in linkage equilibrium in the initial population, directional selection would create LD between them that would not decay in a few generations of random mating. The remaining LD could create a false signal of directional epistasis that would decline if more generations of random mating were allowed. If a signal of significant directional epistasis were found in an experiment, it would be necessary to test for the presence of a linked QTL by doing controlled crosses.

Our method tests for directional epistasis between a specific QTL and others. If there were directional epistasis between all QTLs in the same direction, as in our symmetric model, then the directionality of the interactions would also be indicated by the response of the character mean to selection (an outcome that can also result from dominance). The mean would increase more than linearly in response to selection. In that case, the directionality could be removed by changing the scale of measurement so that the selection response is linear. The situation is different if the focal QTL interacts with others but they do not interact among themselves, as in our conditional epistasis model. Even when there are significant changes in the marginal differences, we found that the average response to selection is not distinguishable from linear. In a model in which there are positive directional interactions with one QTL and negative interactions with another, the effect of the directional interactions would cancel on average while directionality for each QTL could in principle be detected with our method.

It may be difficult to detect epistatic interactions by the approach explored in this paper because of the large stochastic fluctuations in the marginal differences. These stochastic fluctuations reflect the fact that the marginal differences are the difference in the averages of two distributions that are quite similar unless the QTL accounts for a substantial fraction of the genetic variance. Nevertheless, changes in marginal differences after selection reflect kinds of epistatic interactions that cannot be detected by other means.

Although relatively large sample sizes are required to detect significant directional epistasis between a known QTL and other QTLs that affect the same character, that is a problem for classical tests of epistatic interactions as well. Large sample sizes are needed to estimate additive by additive and other components of genetic variance from breeding experiments (Hill et al., Reference Hill, Goddard and Visscher2008). Estimates for the genetic variance resulting from epistasis, however, cannot predict evolutionary consequences, for example how the selection response will change as allele frequencies evolve.

Our method will not be effective in detecting directional epistasis caused by interactions with low frequency alleles. Changes in the marginal differences result from changes in the frequency of unseen QTLs because of directional selection, and low frequency alleles will respond very slowly to directional selection. However, low frequency alleles would be expected to contribute little to directional epistasis (cf. eqn 15), just as they contribute little to the interaction variance (Hill et al., Reference Hill, Goddard and Visscher2008). Epistatic interactions with more common QTLs may not contribute much to the interaction component of the genetic variance, even if they can be detected from changes in the marginal differences.

Our results also suggest a way to detect loci strongly affected by epistatic interactions. The idea is to perform a genome-wide association study (GWAS) for a quantitative character in an initial population and again after several generations of directional selection on the character. An experiment of this type was carried out by Burke et al. (Reference Burke, Dunham, Shahrestani, Thornton, Rose and Long2010) . They selected for accelerated development in Drosophila melanogaster and tested for significant differences in single nucleotide polymorphism (SNP) frequencies between selected and unselected (control) populations in order to identify SNPs associated with development time. In such an experiment, SNPs for which the marginal differences change substantially would likely be closely linked to loci that are affected by epistatic interactions. Although the statistical problems arising in the analysis of such data are formidable and complications would arise because linkage disequilibrium between the SNPs surveyed and causative genes could change, data from independent replicates would give increasing power to detecting interacting loci if they are present. Decreasing costs of genotyping on a genome wide scale will make such experiments increasingly feasible.

Acknowledgements

We thank J. Felsenstein and Y. S. Song for helpful discussions of this topic and comments on a draft of this paper. M. S. was supported in part by NIH Grant R01-GM40282 and M. K. was supported in part by NSF Grant DEB-0819901.

Appendix A. Formulae for symmetric model

We show here the formulae for calculating the marginal averages and components of genetic variance for the symmetric model with equal allele frequencies. From the distribution of the number of+alleles in gametes, gi . the distribution in zygotes is the convolution of gi with itself:

\phi _{i} \equals \mathop\sum\limits_{j \equals {\rm max}\lpar \setnum{0}\comma i \minus L\rpar }^{{\rm min}\lpar i\comma L\rpar } {g_{j} g_{i \minus j} } .

Therefore,

\bar{x} \equals \mathop\sum\limits_{i \equals \setnum{0}}^{\setnum{2}L} {h_{i} \phi _{i} }

and

V_{G} \equals \mathop\sum\limits_{i \equals \setnum{0}}^{\setnum{2}L} {\left( {h_{i} \minus \bar{x}} \right)^{\setnum{2}} \phi _{i} } .

The distribution of i in gametes, given that one of the loci has k=0 or 1+alleles, is

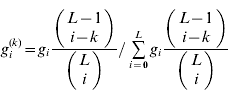
g_{i}^{\lpar k\rpar } \equals g_{i} {{\left( {\matrix{ {L \minus 1} \cr {i \minus k} \cr} } \right)} \over {\left( {\matrix{ L \cr i \cr} } \right)}}\sol \mathop\sum\limits_{i \equals \setnum{0}}^{L} {g_{i} {{\left( {\matrix{ {L \minus 1} \cr {i \minus k} \cr} } \right)} \over {\left( {\matrix{ L \cr i \cr} } \right)}}}

(i=0, …, L), where the binomial coefficients are assumed to be 0 if either of the arguments is negative. The marginal averages are then

\bar{x}_{\setnum{0}} \equals \mathop\sum\limits_{i\comma j \equals \setnum{0}}^{L} {g_{i}^{\lpar \setnum{0}\rpar } g_{j}^{\lpar \setnum{0}\rpar } h_{i \plus j} } \comma
\bar{x}_{\setnum{1}} \equals \mathop\sum\limits_{i\comma j \equals \setnum{0}}^{L} {g_{i}^{\lpar \setnum{1}\rpar } g_{j}^{\lpar \setnum{0}\rpar } h_{i \plus j} }

and

\bar{x}_{\setnum{2}} \equals \mathop\sum\limits_{j\comma k \equals \setnum{0}}^{L} {g_{i}^{\lpar \setnum{1}\rpar } g_{j}^{\lpar \setnum{1}\rpar } h_{i \plus j} } .

The marginal differences, Δ1 and Δ0, are obtained by subtraction. For each locus, a \equals \lpar \rmDelta _{\setnum{1}} \plus \rmDelta _{\setnum{0}} \rpar \sol 2 and d \equals \lpar \rmDelta _{\setnum{0}} \minus \rmDelta _{\setnum{1}} \rpar \sol 2. Substituting these into the expressions given in the text, V A, V D and V I are obtained.

Appendix B. Likelihood ratio test for a change in the marginal differences

In the initial population, there are mk individuals with k+alleles at locus 1 and nk in the final population. In the initial population, the phenotypes of individuals with each of the three genotypes are vectors with elements xki (k=0, 1, 2 and i=1, …, mk ) and in the final population they are yki (k=0, 1, 2 and i=1, …, nk ). We assume the x's and y's are normally distributed with arbitrary means and variances.

In the unconstrained model, the parameters of the normal distributions for xki are μkx and Vkx and for yki the parameters are μky and Vky .

The likelihood expressed as a function of these means and variances is

\eqalign{ \hskip-3pt L \equals\hskip-2pt \tab \prod\limits_{k \equals \setnum{0}}^{\setnum{2}} {\left( {{1 \over {2\pi V_{kx} }}} \right)^{\hskip-2pt m_{k} \sol \setnum{2}} \prod\limits_{i \equals \setnum{1}}^{m_{k} } {\exp \left[ {{{ \minus \lpar x_{ki} \minus \mu _{kx} \rpar ^{\setnum{2}} } \over {2V_{kx} }}} \right]}\hskip-2pt \left( {{1 \over {2\pi V_{ky} }}} \right)^{\hskip-2pt n_{k} \sol \setnum{2}} } \cr \tab \times \prod\limits_{i \equals \setnum{1}}^{n_{k} } {\exp \left[ {{{ \minus \lpar y_{ki} \minus \mu _{ky} \rpar ^{\setnum{2}} } \over {2V_{ky} }}} \right]} . \cr}

For the unconstrained model, the maximum likelihood estimates of the means and variances are the same as for three independent normal distributions:

\hat{\mu }_{kx} \equals {1 \over {m_{k} }}\mathop\sum\limits_{i \equals \setnum{1}}^{m_{k} } {x_{ki} }

with similar expressions for μky, and

\hat{V}_{kx} \equals {1 \over {m_{k} }}\mathop\sum\limits_{i \equals \setnum{1}}^{m_{k} } {\lpar x_{ki} -\hat{\mu }_{kx} \rpar ^{\setnum{2}} } .

(k=0, 1, 2) with similar expressions for the Vky .

The marginal differences at the beginning of the experiment are \rmDelta _{\setnum{1}} \equals \mu _{\setnum{2}x} \minus \mu _{\setnum{1}x} and \rmDelta _{\setnum{0}} \equals \mu _{\setnum{1}x} \minus \mu _{\setnum{0}x} and at the end of the experiment they are \rmDelta \prime_{\setnum{1}} \equals \mu _{\setnum{2}y} \minus \mu _{\setnum{1}y} and \rmDelta \prime_{\setnum{0}} \equals \mu _{\setnum{1}y} \minus \mu _{\setnum{0}y} . We want to test the hypothesis that \rmDelta _{\setnum{1}} \equals \rmDelta \prime_{\setnum{1}} and \rmDelta _{\setnum{0}} \equals \rmDelta \prime_{\setnum{0}} . To do so, we find the maximum likelihood estimates for a model in which the variances can take any value but the means are constrained to satisfy \rmDelta _{\setnum{1}} \equals \rmDelta \prime_{\setnum{1}} and \rmDelta _{\setnum{0}} \equals \rmDelta \prime_{\setnum{0}} .

For the constrained model, the six equations for the variances, given the means, are the same as for the unconstrained model. We parameterize the constrained model by setting \mu _{\setnum{2}x} \equals \mu _{\setnum{1}x} \plus \rmDelta _{\setnum{1}} , \mu _{\setnum{0}x} \equals \mu _{\setnum{1}x} \minus \rmDelta _{\setnum{0}} , \mu _{\setnum{2}y} \equals \mu _{\setnum{1}y} \plus \rmDelta _{\setnum{1}} and \mu _{\setnum{0}y} \equals \mu _{\setnum{1}y} \minus \rmDelta _{\setnum{0}} . We find that the maximum likelihood estimates of μ1x, μ1y, Δ1 and Δ0 have to satisfy the following four equations:

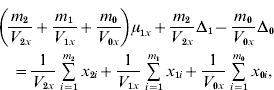
\eqalign{ \tab \left( {{{m_{\setnum{2}} } \over {V_{\setnum{2}x} }} \plus {{m_{\setnum{1}} } \over {V_{\setnum{1}x} }} \plus {{m_{\setnum{0}} } \over {V_{\setnum{0}x} }}} \right)\mu _{\setnum{1}x} \plus {{m_{\setnum{2}} } \over {V_{\setnum{2}x} }}\rmDelta _{\setnum{1}} \minus {{m_{\setnum{0}} } \over {V_{\setnum{0}x} }}\rmDelta _{\setnum{0}} \cr \tab \quad\equals {1 \over {V_{\setnum{2}x} }}\mathop\sum\limits_{i \equals \setnum{1}}^{m_{\setnum{2}} } {x_{\setnum{2}i} } \plus {1 \over {V_{\setnum{1}x} }}\mathop\sum\limits_{i \equals \setnum{1}}^{m_{\setnum{1}} } {x_{\setnum{1}i} } \plus {1 \over {V_{\setnum{0}x} }}\mathop\sum\limits_{i \equals \setnum{1}}^{m_{\setnum{0}} } {x_{\setnum{0}i} } \comma \cr}
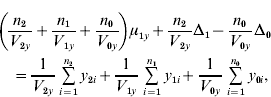
\eqalign{ \tab \left( {{{n_{\setnum{2}} } \over {V_{\setnum{2}y} }} \plus {{n_{\setnum{1}} } \over {V_{\setnum{1}y} }} \plus {{n_{\setnum{0}} } \over {V_{\setnum{0}y} }}} \right)\mu _{\setnum{1}y} \plus {{n_{\setnum{2}} } \over {V_{\setnum{2}y} }}\rmDelta _{\setnum{1}} \minus {{n_{\setnum{0}} } \over {V_{\setnum{0}y} }}\rmDelta _{\setnum{0}} \cr \tab \quad\equals {1 \over {V_{\setnum{2}y} }}\mathop\sum\limits_{i \equals \setnum{1}}^{n_{\setnum{2}} } {y_{\setnum{2}i} } \plus {1 \over {V_{\setnum{1}y} }}\mathop\sum\limits_{i \equals \setnum{1}}^{n_{\setnum{1}} } {y_{\setnum{1}i} } \plus {1 \over {V_{\setnum{0}y} }}\mathop\sum\limits_{i \equals \setnum{1}}^{n_{\setnum{0}} } {y_{\setnum{0}i} } \comma \cr}
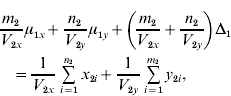
\eqalign{ \tab {{m_{\setnum{2}} } \over {V_{\setnum{2}x} }}\mu _{\setnum{1}x} \plus {{n_{\setnum{2}} } \over {V_{\setnum{2}y} }}\mu _{\setnum{1}y} \plus \left( {{{m_{\setnum{2}} } \over {V_{\setnum{2}x} }} \plus {{n_{\setnum{2}} } \over {V_{\setnum{2}y} }}} \right)\rmDelta _{\setnum{1}} \cr \tab \quad\equals {1 \over {V_{\setnum{2}x} }}\mathop\sum\limits_{i \equals \setnum{1}}^{n_{\setnum{2}} } {x_{\setnum{2}i} } \plus {1 \over {V_{\setnum{2}y} }}\mathop\sum\limits_{i \equals \setnum{1}}^{m_{\setnum{2}} } {y_{\setnum{2}i} } \comma \cr}
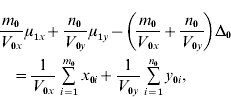
\eqalign{ \tab {{m_{\setnum{0}} } \over {V_{\setnum{0}x} }}\mu _{\setnum{1}x} \plus {{n_{\setnum{0}} } \over {V_{\setnum{0}y} }}\mu _{\setnum{1}y} \minus \left( {{{m_{\setnum{0}} } \over {V_{\setnum{0}x} }} \plus {{n_{\setnum{0}} } \over {V_{\setnum{0}y} }}} \right)\rmDelta _{\setnum{0}} \cr \tab \quad\equals {1 \over {V_{\setnum{0}x} }}\mathop\sum\limits_{i \equals \setnum{1}}^{m_{\setnum{0}} } {x_{\setnum{0}i} } \plus {1 \over {V_{\setnum{0}y} }}\mathop\sum\limits_{i \equals \setnum{1}}^{n_{\setnum{0}} } {y_{\setnum{0}i} } \comma \cr}

where the carats have been omitted for notational convenience.

In the constrained model, the estimates of the variances depend on the means and the estimates of the μs and Δs depend on the variances. To solve all 10 equations, we used an EM algorithm that starts with the means and variances from the unconstrained model, estimates the means by solving the above four equations, re-estimates the variances from the new means, and continues until the maximum change in any of the estimates in one cycle is less than a specified small value (10−8). This procedure converged in a few iterations in all cases ran. We then computed the logarithm of the ratio of likelihoods under the unconstrained and constrained models and computed a P-value from a χ2 distribution with two degrees of freedom. We found in a simulation test of a null model that this test rejected the null hypothesis at the 5% level roughly 5% of the time.

References

Barton, N. H. (1992). On the spread of new gene combinations in the 3rd phase of Wright's shifting-balance. Evolution 46, 551–557.Google Scholar
Barton, N. H. & Shpak, M. (2000). The stability of symmetric solutions to polygenic models. Theoretical Population Biology 57, 249–263.CrossRefGoogle ScholarPubMed
Barton, N. H. & Turelli, M. (2004). Effects of genetic drift on variance components under a general model of epistasis. Evolution 58, 2111–2132.Google Scholar
Burke, M. K., Dunham, J. P., Shahrestani, P., Thornton, K. R., Rose, M. R. & Long, A. D. (2010). Genome-wide analysis of a long-term evolution experiment with Drosophila. Nature 467, 587–590.CrossRefGoogle ScholarPubMed
Cockerham, C. C. (1954). An extension of the concept of partitioning hereditary variance for analysis of covariances among relatives when epistasis is present. Genetics 39, 859–882.CrossRefGoogle ScholarPubMed
de Visser, J. A. G. M. & Elena, S. F. (2007). The evolution of sex: empirical insights into the roles of epistasis and drift. Nature Reviews Genetics 8, 139–149.CrossRefGoogle ScholarPubMed
Elena, S. F. & Lenski, R. E. (1997). Test of synergistic interactions among deleterious mutations in bacteria. Nature 390, 395–398.CrossRefGoogle ScholarPubMed
Eyre-Walker, A. & Keightley, P. D. (2007). The distribution of fitness effects of new mutations. Nature Reviews Genetics 8, 610–618.CrossRefGoogle ScholarPubMed
Falconer, D. S. & Mackay, T. F. C. (1996). Introduction to Quantitative Genetics. Longman, Essex.Google Scholar
Flint, J. & Mackay, T. F. C. (2009). Genetic architecture of quantitative traits in mice, flies, and humans. Genome Research 19, 723–733.CrossRefGoogle ScholarPubMed
Hansen, T. F. & Wagner, G. P. (2001). Modeling genetic architecture: a multilinear theory of gene interaction. Theoretical Population Biology 59, 61–86.CrossRefGoogle ScholarPubMed
Hill, W. G., Goddard, M. E. & Visscher, P. M. (2008). Data and theory point to mainly additive genetic variance for complex traits. PLoS Genetics 4, e1000008.CrossRefGoogle ScholarPubMed
Kacser, H. & Burns, J. A. (1981). The molecular basis of dominance. Genetics 97, 639–666.CrossRefGoogle ScholarPubMed
Keightley, P. D. (1989). Models of quantitative variation of flux in metabolic pathways. Genetics 121, 869–876.CrossRefGoogle ScholarPubMed
Kempthorne, O. (1954). The correlation between relatives in a random mating population. Proceedings of the Royal Society of London Series B. Biological Sciences 143, 103–113.Google Scholar
Kouyos, R. D., Silander, O. K. & Bonhoeffer, S. (2007). Epistasis between deleterious mutations and the evolution of recombination. Trends in Ecology and Evolution 22, 308–315.CrossRefGoogle ScholarPubMed
Le Rouzic, A., Skaug, H. J. & Hansen, T. F. (2010). Estimating genetic architectures from artificial-selection responses: a random-effect framework. Theoretical Population Biology 77, 119–130.CrossRefGoogle ScholarPubMed
Lewontin, R. C. & Kojima, K. (1960). The evolutionary dynamics of complex polymorphisms. Evolution 14, 458–472.Google Scholar
Lynch, M. & Walsh, B. (1998). Genetics and Analysis of Quantitative Traits. Sinauer Associates, Sunderland, MA.Google Scholar
Manichaikul, A., Moon, J. Y., Sen, S., Yandell, B. S. & Broman, K. W. (2010). A model selection approach for the identification of quantitative trait loci in experimental crosses, allowing epistasis. Genetics 184, 607–607.Google Scholar
Otto, S. P. (2009). The evolutionary enigma of sex. American Naturalist 174, S1–S14.CrossRefGoogle ScholarPubMed
Pavlicev, M., Le Rouzic, A., Cheverud, J. M., Wagner, G. P. & Hansen, T. F. (2010). Directionality of epistasis in a murine intercross population. Genetics 185, 1489–1505.CrossRefGoogle Scholar
Phillips, P. C. (2008). Epistasis – the essential role of gene interactions in the structure and evolution of genetic systems. Nature Reviews Genetics 9, 855–867.CrossRefGoogle ScholarPubMed
Figure 0

Fig. 1. Time dependence of the marginal differences, Δ1 and Δ0, after five generations of truncation selection with αx=1/2. The phenotype map in each case is h_{i} \equals \beta {i} \plus \gamma {i} ^{\setnum{2}} . In all cases, β=0·5. Generation 0 is the initial population assumed to be in Hardy–Weinberg and linkage equilibrium with p=0·3 at all 10 loci. Selection was applied in generations 0–4 followed by 10 generations of random mating without selection.

Figure 1

Fig. 2. Time dependence of Δ1 and Δ0 for all 10 loci in a population of N=1000 individuals. The parameter values are the same as in Fig. 1. The predictions of the analytic theory from Fig. 1 are plotted with solid lines for comparison with the simulations.

Figure 2

Fig. 3. Time dependence of Δ1 and Δ0 in the model with random epistatic terms added to the quadratic dependence on i (cf. eqn (4)). The parameter values are the same as in Figs 1 and 2. The additional epistatic term for each genotype was drawn with probability q=0.5 from a normal distribution with mean 0 and standard deviation σI=1. The predictions of the analytic theory from Fig. 1 are plotted with solid lines for comparison.

Figure 3

Table 1. Power to detect significant changes in the marginal differences (Δ1 and Δ0) for the conditional epistasis model. In all cases, 100 replicate simulations were run, αx=0·5, L=10, f1(k1)=k1, the frequency of the+allele was initially 0·2 at every locus, and the same value of βi was assumed for loci i=2, …, 10. If the+allele became fixed after selection, the test could not be performed. The numbers shown are the fractions of replicates for which the likelihood ratio test was performed and P⩽0·05. The numbers in parentheses are the numbers of tests performed