Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-25T17:38:12.852Z Has data issue: false hasContentIssue false
  • English
  • Français

Theoretical study on genetic variation in multigene families*

Published online by Cambridge University Press:  14 April 2009

Tomoko Ohta
Tomoko Ohta
Affiliation:
National Institute of Genetics, Mishima, 411, Japan
Rights & Permissions [Opens in a new window]

Summary

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Genetic variation contained in a multigene family was theoretically investigated from the standpoint of population genetics. Unequal crossover is assumed to be responsible for the coincidental evolution of mutant genes in a chromosome. When the allowed latitude of the duplicated or deleted number of gene units at unequal crossover is 10 ˜ 15% of the total gene number in a chromosome, the arrangement of gene lineage in a chromosome is shown to be roughly random. The equilibrium properties of genetic variation or the probability of identity of two genes within a family (clonality) were studied under mutation, unequal crossover, interchromosomal crossover and sampling of gametes. The clonality of a multigene family within a chromosome is shown to be approximately

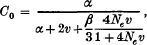
in which α = 2k/n2 with k = effective number of cycles of unequal crossover and with n = number of gene units in a family, v is the mutation rate per gene unit, β is the rate of interchromosomal crossover per family and Ne is the effective size of the population, all measured by the rate per generation. The clonality of a gene family between two different chromosomes becomes approximately C1 = C0/(l + 4Neν). Some models of natural selection which lowers the clonality or increases genetic variation in a multigene family were investigated. It was shown that natural selection may be quite effective in increasing genetic variation in a gene family.

Type
Research Article
Information
Genetics Research , Volume 31 , Issue 1 , February 1978 , pp. 13 - 28
Copyright
Copyright © Cambridge University Press 1978

References

REFERENCES

Capra, J. D. & Edmundson, A. B. (1977). The antibody combining site. Scientific American 236 (1), 50–59.CrossRefGoogle ScholarPubMed
Crow, J. F. & Kimura, M. (1970). An Introduction to Population Genetics Theory. New York: Harper & Row.Google Scholar
Fisher, R. A. (1930). The Genetical Theory of Natural Selection. Oxford: Clarendon Press.CrossRefGoogle Scholar
Hood, L., Campbell, J. H. & Elgin, S. C. R. (1975). The organization, expression, and evolution of antibody genes and other multigene families. Annual Reviev of Genetics 9, 305–353.CrossRefGoogle ScholarPubMed
Kimura, M. (1964). Diffusion models in population genetics. Journal of Applied Probability 1, 177–232.Google Scholar
Kimura, M. & Crow, J. F. (1964). The number of alleles that can be maintained in a finite population. Genetics 49, 725–738.CrossRefGoogle Scholar
Kimura, M. & Ohta, T. (1969 a). The average number of generations until fixation of a mutant gene in a finite population. Genetics 61, 763–771.CrossRefGoogle Scholar
Kimura, M. & Ohta, T. (1969 b). The average number of generations until extinction of an individual mutant gene in a finite population. Genetics 63, 701–709.CrossRefGoogle Scholar
Nei, M. (1968). Evolutionary change of linkage intensity. Nature 218, 1160–1161.CrossRefGoogle ScholarPubMed
Nei, M. (1975). Molecular Population Genetics and Evolution. Amsterdam, Oxford, New York: North-Holland/American Elsevier.Google ScholarPubMed
Ohta, T. (1976). A simple model for treating the evolution of multigene families. Nature 263, 74–76.CrossRefGoogle ScholarPubMed
Ohta, T. (1977). Genetic variation in multigene families Nature 267, 515–517.CrossRefGoogle ScholarPubMed
Ohta, T. (1978). A model of directional selection with multigene families. Journal of Molecular Evolution (submitted).Google Scholar
Perelson, A. S. & Bell, G. I. (1977). Mathematical models for the evolution of multigene families by unequal crossing over. Nature 265, 304–310.CrossRefGoogle ScholarPubMed
Smith, G. P. (1974). Unequal crossover and the evolution of multigene families. Cold Spring Harbor Symposia on Quantitative Biology 38, 507–513.CrossRefGoogle ScholarPubMed
Stewart, F. M. (1976). Variability in the amount of heterozygosity maintained by neutral mutations. Theoretical Population Biology 9, 188–201.CrossRefGoogle ScholarPubMed
Tartof, K. D. (1975). Redundant genes. Annual Review of Genetics 9, 355–385.CrossRefGoogle ScholarPubMed
Wellauer, P. K., Reeder, R. H., Dawid, I. B. & Brown, D. D. (1976). The arrangement of length heterogeneity in repeating units of amplified and chromosomal ribosomal DNA from Xenopus leavis. Journal of Molecular Biology 105, 487–505.CrossRefGoogle Scholar
Wright, S. (1969). Evolution and the Genetics of Populations Vol. 2. The Theory of Gene Frequencies. University of Chicago Press.Google Scholar