1. INTRODUCTION
A challenge when predicting future phenotypes (or total genetic values) for complex quantitative traits is that phenotypic variation often reflects the concerted action of a large number of genes (quantitative trait loci (QTLs)) with small allelic effects (Risch, Reference Risch2000). QTLs acting together may affect the trait in a cryptic manner, inducing non-additivity in relationships between phenotypes and QTLs (Gianola & de los Campos, Reference Gianola and de los Campos2008; Mackay, Reference Mackay2008; Yamamoto et al., Reference Yamamoto, Zwarts, Callaerts, Norga, Mackay and Anholt2008). Since QTL genotypes are not usually observable, molecular markers such as single nucleotide polymorphisms (SNPs) are used as proxies.
Standard linear parametric models that assume linear relationships between phenotypes and markers may have poor predictive ability in the presence of interaction. To take into account non-additive gene action (e.g. epistasis), interaction effects can be added to some additive linear model. However, in a whole-genome analysis, this usually produces an over-saturated model, due to the large number of markers (p) and a small sample size (N), with N≪p. One solution is using random-effects models with a Bayesian treatment. For example, Xu & Jia (Reference Xu and Jia2007) used an empirical Bayes method to estimate main effects of 127 markers and interactions between all marker pairs simultaneously. If more markers and higher order interactions are considered, a large sample is needed for these parametric linear models to produce stable estimates (e.g. of additive and epistatic effects).
For phenotypic prediction under cryptic forms of epistasis, model-free non-parametric approaches have been proposed by Gianola et al. (Reference Gianola, Fernando and Stella2006), Gianola & van Kaam (Reference Gianola and van Kaam2008), Gianola & de los Campos (Reference Gianola and de los Campos2008) and de los Campos et al. (Reference de los Campos, Gianola and Rosa2009a). In non-parametric regression, no assumption is made regarding the form of the genotype–phenotype relationship. Rather, this relationship is described by a smoothing function and driven primarily by the data. For example, non-parametric methods based on reproducing kernel Hilbert spaces (RKHS) regression require finding a suitable kernel, a semi-positive definite matrix that is used instead of the standard incidence matrix X in regression. Recently, Bennewitz et al. (Reference Bennewitz, Solberg and Meuwissen2009) applied non-parametric additive models to evaluate breeding value (BV) prediction with simulated data, and found that their accuracy was moderate to high, and in some cases slightly higher than BLUP.
Another non-parametric approach is radial basis function (RBF) regression (Powell, Reference Powell1987). RBF regression uses a linear combination of a set of RBFs, each of them centred at a training data point. Because of its capability of approximating complex non-linear functions, RBF regression has been used in signal processing Hu & Hwang, Reference Hu and Hwang2001). The genotype–phenotype relationship is expected to be complex as well, which makes this method appealing.
In this study, RBF regression methods for predicting genetic values of quantitative traits were developed and examined. Two types of RBF models were considered: one had a common weight parameter for all SNPs, and the other one had SNP-specific parameters and was thus more general. For comparison, a method known as Bayes A (Meuwissen et al., Reference Meuwissen, Hayes and Goddard2001) was used as a benchmark. First, a toy example was developed, in which an arbitrary non-linear relationship between eight SNPs and the phenotype was created. Then, two chicken datasets representing body weight (BW) and food conversion rate (FCR, the ratio of BW gain to the amount of feed fed) were used in a real data analysis. Finally, a large-scale whole genome simulation was carried out to compare RBF and Bayes A under three different gene action modes: pure additive, additive+dominance and pure epistasis.
The paper is organized as follows. Section 2 is methodological and provides a description of RBF regression methods and related techniques. Two RBF models are proposed and a Bayesian implementation is formulated. Section 3 describes briefly the Bayes A model. Criteria used for checking model predictive ability and a principal component analysis (PCA) for SNP dimension reduction are described in sections 4 and 5, respectively. Simulation and data analysis are presented in sections 6 and 7, followed by a discussion of implications, limitations and scope for RBF regression in section 8. Concluding remarks are given in section 9.
2. RBF REGRESSION MODELS
RBF regression is an approach to approximation problems in high-dimensional spaces (Powell, Reference Powell1987; Broomhead & Lowe, Reference Broomhead and Lowe1988; Poggio & Girosi, Reference Poggio and Girosi1990). The expectation function (given x) in a RBF regression model takes the form
where {k(‖x−xj‖)|j=1, 2, … , m} is a set of m RBFs, which are fixed and non-linear on x, and ‖·‖ denotes the Euclidean norm. Each xj∊ℝp is a training point (e.g. a vector of SNP covariates on individual j) taken as centre of the RBFs, and p is the dimension of the input, e.g., the number of SNPs. A regression coefficient αj is associated with each basis function. The functions k(·) are called ‘radial’ because their value depends only on the distance (r) from the origin (x) to the centre point xj, i.e., r=‖x−xj‖. Examples are the multiquadric ![]() for some c⩾0, the thin-plate-spline k(r)=r 2 log r, and the Gaussian k(r)=exp(−θr 2) for some θ⩾0.
for some c⩾0, the thin-plate-spline k(r)=r 2 log r, and the Gaussian k(r)=exp(−θr 2) for some θ⩾0.
(i) k-medoids clustering algorithm for finding centres
Given N observations or training data points, one possibility is using each training data point xj as a centre in (1), so N=m. This can be computationally expensive for a large number of observations, since computation grows polynomially with N (Haykin, Reference Haykin1999). Besides, this may produce over-fitting unless regularization is imposed (Ripley, Reference Ripley1996; Haykin, Reference Haykin1999). Therefore, a number (m) of representative centres smaller than N is often used, to reduce model complexity. Moody & Darken (Reference Moody and Darken1989) used k-means clustering for selecting centres, which chooses m<N centres or centroids in the input space such that the sum of squared distances from each training point to its nearest centroid is minimum. In k-means clustering, a centroid's coordinates are the mean of coordinates of the points in the cluster. This is not suitable for discrete coordinates, such as SNPs, because SNP covariates are coded using the number of allele copies, and thus cannot be a fractional number as it would be if means were taken. To overcome this restriction, a variant called the k-medoids algorithm (Kaufman & Rousseeuw, Reference Kaufman and Rousseeuw1990) chooses an existing data point, or medoid, for each cluster. The objective function to be minimized is the sum of distances from each data point to its closest medoid.
(ii) Bayesian Gaussian RBF models
In this study, phenotypes were approximated with a RBF regression model incorporating SNP information. A Bayesian analysis was adopted to infer all parameters in model (1) simultaneously. The RBF chosen was Gaussian, expressed as
![\eqalign{ k_{\bimtheta } \lpar {\bi x}_{i} \comma {\bi x}_{j} \rpar \equals \tab \exp\left[ { \minus \mathop \sum\limits_{k \equals \setnum{1}}^{p} \,\theta _{k} {\left( {x_{i}^{\lsqb k\rsqb } \minus x_{j}^{\lsqb k\rsqb } } \right)}\nolimits^{\setnum{2}} } \right] \cr \equals \tab \exp\left[ { \minus \lpar {\bi x}_{i} \minus {\bi x}_{j} \rpar \prime \rmSigma ^{ \minus \setnum{1}} \lpar {\bi x}_{i} \minus {\bi x}_{j} \rpar } \right]. \hfill](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20160920235843672-0896:S0016672310000157:S0016672310000157_eqn2.gif?pub-status=live)
Here θ=(θ1, θ2, … , θp)′ is a vector of unknown and non-negative weights and p is the number of SNPs. Genotypes at each SNP were coded as x=0, 1 and 2 for A 2A 2, A 1A 2 and A 1A 1, respectively, and xi contained the p codes for genotypes of individual i. The weights θ can be viewed as inverse variances for each input SNP, and the ‘covariance’ matrix Σ, which was common to all centres, was ![]() . The larger the value of a particular θk, the more relevant the associated input (SNP) is to the outcome. Conversely, zero or a very small value of θk implicitly excludes that SNP from the basis functions. When p is large, as in the case of genome-wide association studies involving tens of thousands of SNPs, only a small portion is expected to be relevant. While it may be necessary to assume different weights for each SNP a priori, p distinct θ values may lead to an exceedingly greedy specification when p is large, as discussed later.
. The larger the value of a particular θk, the more relevant the associated input (SNP) is to the outcome. Conversely, zero or a very small value of θk implicitly excludes that SNP from the basis functions. When p is large, as in the case of genome-wide association studies involving tens of thousands of SNPs, only a small portion is expected to be relevant. While it may be necessary to assume different weights for each SNP a priori, p distinct θ values may lead to an exceedingly greedy specification when p is large, as discussed later.
If an equal weight (variance) is assumed for all SNPs, the RBF reduces to
In this case, only a single θ needs to be estimated. RBFs that take the forms of (2) and (3) will be denoted as RBF I and RBF II, respectively, in what follows.
Given N observations with p SNPs each, a linear model with m (m⩽N) RBFs is
Here,
- β:
nuisance parameter vector
- wi:
incidence vector linking β to observation i
- xi:
p×1 input vector for observation i
- α={αj|j=1, 2, … , m}:
m×1 vector of non-parametric regression coefficients
- k θ(xi, xj):
RBF based on xi, xj
- θ={θk|k=1, 2, … , p}:
p×1 vector of weights
and e~N(0, Iσe2) is a vector of residuals, where σe2 is the residual variance. It is important to note that this model is linear in α but not in θ. In matrix notation,
where y={y i|i=1, 2, … , N} is a vector of phenotypic values, W={wi′|i=1, 2, … , N}, and the radial basis matrix Kθ of order N×m is
![\hfill \hskip112pt{\bi K}_{\bimtheta } \equals \left[ {\matrix{ {\exp\left[ { \minus \mathop \sum\limits_{k \equals \setnum{1}}^{p} \,\theta _{k} \mathop {\left( {x_{\setnum{1}}^{\lsqb k\rsqb } \minus x_{\setnum{1}}^{\lsqb k\rsqb } } \right)}\nolimits^{\setnum{2}} } \right]} \tab \cdots \tab {\exp\left[ { \minus \mathop \sum\limits_{k \equals \setnum{1}}^{p} \,\theta _{k} \mathop {\left( {x_{\setnum{1}}^{\lsqb k\rsqb } \minus x_{m}^{\lsqb k\rsqb } } \right)}\nolimits^{\setnum{2}} } \right]} \cr \vdots \tab \cdots \tab \vdots \cr \vdots \tab \cdots \tab \vdots \cr {\exp\left[ { \minus \mathop\sum\limits_{k \equals \setnum{1}}^{p} \,\theta _{k} \mathop {\left( {x_{N}^{\lsqb k\rsqb } \minus x_{\setnum{1}}^{\lsqb k\rsqb } } \right)}\nolimits^{\setnum{2}} } \right]} \tab \cdots \tab {\exp\left[ { \minus \mathop\sum\limits_{k \equals \setnum{1}}^{p} \,\theta _{k} \mathop {\left( {x_{N}^{\lsqb k\rsqb } \minus x_{m}^{\lsqb k\rsqb } } \right)}\nolimits^{\setnum{2}} } \right]} \cr} } \right].](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20160920235843672-0896:S0016672310000157:S0016672310000157_eqn6.gif?pub-status=live)
The above formulation is for RBF I; RBF II is obtained by replacing the weight vector θ by a scalar variable θ, which is common to all input SNPs.
The conditional likelihood for the Bayesian hierarchical model is
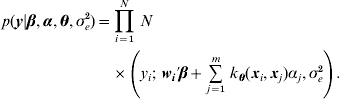
Park & Casella (Reference Park and Casella2008) suggested assigning a double exponential prior to each of the regression coefficients, αi, in (1), due to its equivalence to regularization with an l 1 norm penalty as in the (least absolute shrinkage and selection operator LASSO) method (Tibshirani, Reference Tibshirani1996). Specifically, α was assigned a product of double exponential distributions with density
where λ is a positive parameter. Since θk (k=1, 2, … , p), is non-negative, this parameter was assigned an exponential prior with parameter ρ, i.e.
Priors for all parameters and fully conditional distributions are provided in Appendix A.
3. BENCHMARK MODEL: BAYES A
Bayes A poses the linear model
where W and β are as in (5); matrix X links additive SNP effects to the phenotypes, with element X ij being the genotype code (as for the RBF models) of individual i at SNP locus j (j=1, 2, … , p); g is a vector of additive SNP effects. Bayes A assumes a priori that ![]() are independent, and that the variance of marker effect (
are independent, and that the variance of marker effect (![]() ) differs for every locus j. Further, the prior distribution assigned to
) differs for every locus j. Further, the prior distribution assigned to ![]() in Bayes A is a scaled inverted chi-square distribution, χ−2(ν, S), for all SNPs, where S and ν are the scale and degrees of freedom, respectively. In our Bayes A implementation, instead of using a scaled inverted chi-square distribution, a uniform (0, u) distribution was assigned to each
in Bayes A is a scaled inverted chi-square distribution, χ−2(ν, S), for all SNPs, where S and ν are the scale and degrees of freedom, respectively. In our Bayes A implementation, instead of using a scaled inverted chi-square distribution, a uniform (0, u) distribution was assigned to each ![]() . The value of u was determined using information on phenotypic variance, number of SNP loci and allele frequency at each locus (see Appendix C). It was found that the two priors (scaled inverted chi-square and uniform) resulted in virtually the same predictive performance on a toy example and the two chicken data sets (see Appendix D). For β, a flat prior was used, and an Inverse Gamma (0·001, 0·001) distribution was assigned to the residual variance σe2.
. The value of u was determined using information on phenotypic variance, number of SNP loci and allele frequency at each locus (see Appendix C). It was found that the two priors (scaled inverted chi-square and uniform) resulted in virtually the same predictive performance on a toy example and the two chicken data sets (see Appendix D). For β, a flat prior was used, and an Inverse Gamma (0·001, 0·001) distribution was assigned to the residual variance σe2.
4. PREDICTIVE ABILITY
Predictive performance on a test data set (i.e. a sample not used for model training) was used to compare models. Given M posterior samples of the parameter vector obtained with the training data set, M predicted values of the response variable were obtained for each test individual. Given the mth (m=1, 2, … , M) posterior draw of the parameter vector (βm, αm, θm, etc.), the two RBF models generate a predicted value for test individual i as
where wi′ is a nuisance covariate vector pertaining to individual i, and ![]() is the ith row of the rectangular radial basis matrix linking test and training observations,
is the ith row of the rectangular radial basis matrix linking test and training observations, ![]() . For Bayes A, the predicted response value was
. For Bayes A, the predicted response value was
Here, wi′ and ![]() are as in (11) and xi′ is the genotype coding of individual i. After (11) or (12) was computed for each test individual i, its final predicted response, ŷ i, was the average of M predicted values, which were used for computing the following criteria.
are as in (11) and xi′ is the genotype coding of individual i. After (11) or (12) was computed for each test individual i, its final predicted response, ŷ i, was the average of M predicted values, which were used for computing the following criteria.
Correlations. Two types of correlations were of interest. (1) Correlation between expected phenotype E(y|x, w) using true values of the parameters, and its predicted value ŷ. This correlation is denoted as corr(E(y), ŷ) hereinafter. In the absence of nuisance covariates, the expected phenotype can be regarded as true genomic value, and corr(E(y), ŷ) represents accuracy of marker-assisted prediction of genomic value. (2) Correlation between observed and predicted phenotype, denoted by corr(y, ŷ). When E(y) is known, corr(E(y), ŷ) is a better measure than corr(y, ŷ), for the observed phenotype (y) is a noisy version of the expected phenotype E(y). Since only in a simulation study one knows E(y), the measure corr(E(y), ŷ) was used only in simulation settings, and corr(y, ŷ) used only in the real data analysis.
Predictive mean squared errors (PMSE). Two different PMSE measures were used, depending on whether y (observed phenotype) or E(y) (expected phenotype) was the target. The two PMSE criteria were: PMSE1![]() and PMSE2
and PMSE2![]() , where n test is the number of observations in the testing set. PMSE1 was used for the simulation study and PMSE2 was used for the real data analysis.
, where n test is the number of observations in the testing set. PMSE1 was used for the simulation study and PMSE2 was used for the real data analysis.
5. PCA FOR REDUCING SNP DIMENSIONALITY
In the BW and FCR datasets, the number (thousands) of SNPs made RBF I implementation computationally intensive, because weights (θ′s) need to be sampled from a non-standard distribution for every SNP and Kθ has to be reconstructed accordingly. For Bayes A, computational burden was also heavy but less so because X is fixed in the course of iteration. For RBF II, this was not an issue, because only one θ needs to be estimated, regardless of the number of SNPs. To alleviate computations, SNP dimensionality was reduced prior to applying the three methods (RBF I, RBF II and Bayes A). This was done by means of a PCA, where principal components of the original SNP incidence matrix X were found and used to form a number of ‘mega-SNPs’, which was much smaller than the number of SNPs. PCA as a data reduction technique has been widely used in population genetics (e.g. McVean, Reference McVean2009) and genetic association studies (e.g. Price et al., Reference Price, Patterson, Plenge, Weinblatt, Shadick and Reich2006). For example, principal components can be used to represent ancestry differences among individuals in a case-control study, and adjusting for them is necessary prior to association tests. Procedures of PCA-based modelling and prediction in the current study are given below.
(i) PCA-based modelling of RBF I, RBF II and Bayes A
The method of PCA (Manly, Reference Manly2005; Varmuza & Filzmoser, Reference Varmuza and Filzmoser2009) used is described briefly here. Let X be the N×p SNP incidence matrix, where each column (x1, … , xp) represents genotypes of an SNP locus over N individuals. Performing PCA on matrix X gives
Here, P (p×p) is a loading matrix containing in its columns all eigenvectors (i.e., principal components) of the covariance matrix of X. T is the score matrix (N×p) whose columns are uncorrelated score vectors. Each score vector in T can be regarded as a regressor for a given mega-SNP. Note that for each eigenvector in P, its associated eigenvalue corresponds to the variance of the associated score vector in T. Usually columns of P are ordered in a way that the eigenvalues decrease. Since the primary aim of PCA is dimension reduction, the number of mega-SNPs used in PCA regressions is as small as possible, provided that a large proportion of the total variance of X can be explained. The score matrix containing the first a mega-SNPs is
where Pa consists of the first a columns in P. Therefore, the dimension of SNP inputs is reduced from p to a, where a (number of mega-SNPs) can be much less than p. Subsequent modelling (RBF I, RBF II and Bayes A) was based on this mega-SNP incidence matrix Ta, rather than on the original SNP matrix X.
For RBF models, the k-medoids algorithm used to reduce the number of basis functions from N to m was applied to Ta instead of X; each entry in the radial basis matrix Kθ in (6) was computed using mega-SNP distance between two individuals. In Bayes A, X in (10) was replaced with Ta, and the vector of SNP effects g was replaced with a vector of mega-SNP effects, denoted by m. This yields a principal component regression, but cast in a Bayesian framework.
(ii) Mega-SNP grouping for RBF I
As noted, assigning SNP-specific weights as in RBF I is appealing but greedy. An alternative consists of grouping SNPs first, and then assigning group-specific weights. In the context of mega-SNPs, a natural grouping criterion is the variances accounted for by them. To do this, eigenvalues corresponding to each of the mega-SNPs were ordered and cut-points were chosen to divide them into a few groups, with the range of eigenvalues in each group being roughly equal. Then, a common θ-parameter was assigned to mega-SNPs within a group. Thus, the number of weights to be inferred reduced to the number of groups, which was arbitrarily set to four for both BW and FCR data.
(iii) Prediction using mega-SNPs
RBF models. Observations from the test data were first projected onto the space of principal components obtained from the training data to form a score matrix for the test data. That is,
where Pa is the loading matrix defined previously, computed using training data; Xtest is the SNP incidence matrix for the test data. Based on the training and testing score matrices (Ta and Ttest), a test-to-training radial basis matrix (e.g. (11)) can be built for prediction using RBF models.
Bayes A. For Bayes A-based prediction, a modification was needed. Bayes A becomes (for simplicity nuisance covariates are omitted here)
where m is a vector of mega-SNP effects defined earlier. Note that Ta=XPa as in (14), so that
where g=Pam. Hence, ![]() . This means that SNP effects (g) can be estimated by transforming estimates of mega-SNP effects (m) using the loading matrix (Pa). Therefore, predictions on testing observations can be made using the original SNP genotypes directly.
. This means that SNP effects (g) can be estimated by transforming estimates of mega-SNP effects (m) using the loading matrix (Pa). Therefore, predictions on testing observations can be made using the original SNP genotypes directly.
6. Data analysis
(i) Outline
The Bayesian analysis was performed using the R package R2WinBUGS (Sturtz et al., Reference Sturtz, Ligges and Gelman2005), which provides functions to call WinBUGS from R. The study consisted of three parts. First, a toy example with eight SNPs was used to illustrate the behaviour of RBF I and RBF II, as compared to Bayes A, under a hypothetical non-linear genotype–phenotype relationship. Subsequently, the three models were applied to two chicken datasets (provided by Aviagen Ltd) for BW and FCR, respectively. In the chicken data analysis, predictors in each model were not the original thousands of SNPs, but a smaller number of mega-SNPs derived from PCA. This was so because handling thousands of SNPs in our current implementation of RBF I with WinBUGS was too computationally intensive, so some reduction in input dimension was required. Although RBF II and Bayes A did not face this issue, mega-SNPs were used as predictors, to keep consistency between methods. A third part of the data analysis was a simulation-based whole genome marker-assisted prediction of genetic value. As with the chicken data, dense markers (about 2000) were used for prediction. In the simulation, total genetic value was determined by QTL in different manners, and model comparison was made correspondingly. In this part, the two models being compared were RBF II and Bayes A.
In the toy example and chicken data analysis, the number of basis functions was fixed at about 1/6 of training sample size; this was unlikely to produce overfitting according to our experience. The effect of the number of basis functions on RBF's predictive performance was investigated further in the whole genome simulation study, where RBF II was fitted using different numbers of basis functions.
(ii) A toy example
The simulated training data set had 300 unrelated individuals. Each observation consisted of two nuisance covariates (w 1 and w 2), eight SNP covariates (x 1, x 2, … , x 8) and a phenotypic value. Only three SNPs had effects on the phenotype. The phenotype for individual i (y i) was generated as
Here, regression coefficients on w i1 and w i2 are 1 and 2, respectively; x i1, x i2 and x i3 are the genotypic codes for the three relevant SNPs among all eight SNPs, with a non-linear effect on phenotype, and e i is a residual, distributed as N(0, σe2). The covariates were drawn by independent sampling from w i1~uniform(−1, 1), w i2~uniform(0, 2), and x ip was sampled independently with equal probability (1/3) from {0, 1, 2}, for p=1, 2, … , 8. Hence, the eight SNPs were in linkage equilibrium, and five SNPs were completely uninformative about the genetic signal in the phenotype.
The residual variance was specified such that the ratio of genetic variance (caused by signal SNP variations) to residual variance, σG2:σe2, would take the following five different values: 1:9 (scenario 1); 1:3 (scenario 2); 1:1 (scenario 3); 3:1 (scenario 4) and 9:1 (scenario 5). These scenarios correspond to broad sense heritabilities of about 0·10, 0·25, 0·50, 0·75 and 0·90, respectively. To assess σG2, the variance of the term involving x 1, x 2, x 3 in (19), which is a non-linear function over the space of (x 1, x 2, x 3), was calculated. Parameter σG2 was estimated empirically, by generating a large number (100 000) of realizations of e xi1 sin(x i2−0·5) x i32, and their variance was taken as an indication of genetic variance in the population. Subsequently, σe2 was adjusted accordingly. A testing data set with sample size n test=500 was simulated for each of the five scenarios under the same data generating distribution as for the training set.
Predictors in all three models were the eight SNPs (x 1, x 2, … , x 8) and the two nuisance covariates (w 1, w 2). RBF I assigned a specific θ to each of the eight SNPs, whereas RBF II assigned a common θ to them. The number of basis functions chosen by the k-medoids clustering algorithm was 50. The Bayes A was fitted in three different ways: (1) containing only additive effects of the eight SNPs (Bayes AA); (2) containing additive and dominance effects of each SNP locus (Bayes AAD); and (3) containing additive and dominance effects at each SNP locus, and their pair-wise epistatic interactions (Bayes AADE). The latter two were an enrichment to the first one by introducing non-additive marker effects. Bayes AA was as in (10); Bayes AAD and Bayes AADE were obtained by expanding the columns of the X matrix to represent all additive, dominance and epistasis terms needed. For example, in the case of two loci, the genetic value assumed by Bayes AADE can be represented as (Cordell, Reference Cordell2002)
Here, x i and z i are dummy variables coding additive and dominant effects at locus i, respectively. One can set x i=1, z i=−0·5 for one homozygote, x i=−1, z i=−0·5 for the other homozygote and x i=0, z i=0·5 for a heterozygote. Coefficients a and d represent additive and dominance effects, respectively; i aa, i ad, i da and i dd correspond to epistatic effects. Following assumptions of Bayes A, all coefficients were assigned normal priors with heterogeneous variances.
For the toy example data, the length of the Markov chain was 20 000, and the first half was discarded as burn-in. Chains were then thinned at a rate of 5, such that 2000 samples were saved for inference.
(iii) BW and FCR data analysis
BW control is a key factor in rearing meat-type poultry and efficiency of food conversion is economically important in poultry production (Bell & Weaver, Reference Bell and Weaver2002). Heritability is 0·3 for BW and 0·2 for FCR, as used in the genetic evaluation program in Aviagen Ltd. Both datasets contained information on whole genome SNPs and these were used to predict the two traits.
BW data consisted of mean 42-day BWs of the progeny of each of 200 sires. Birds were raised in a low-hygiene environment, representing a commercial production setting. Phenotypic values of each sire were adjusted progeny means. Specifically, for each progeny of a sire, its phenotype was adjusted with estimates of fixed effects, maternal environmental random effects and of dam's BV, using best linear unbiased prediction. That is, adjusted phenotype=phenotype−fixed effect−maternal random effect−1/2 dam's BV. Then, a sire's phenotype was the average of its offspring's adjusted phenotypes. To make the analysis more reliable, sires with less than 20 progeny records were removed, leaving 192 sires. These 192 sires were further partitioned into a training set (143 sires) and testing set (49 sires), such that sires in the testing set were sons of those in the training set. Phenotypic means (standard deviations) of the training and testing sets were 4·43 (6·00) and 5·57 (6·45), respectively. SNPs with monomorphic genotypes or minor allele frequency (MAF) less than 0·05 were removed, leaving 6947 SNPs for each sire.
FCR data were adjusted progeny means of FCR records of 394 sires from a commercial broiler line. The adjustment procedure was as for the BW records. The FCR data have been used by González-Recio et al. (Reference González-Recio, Gianola, Rosa, Weigel and Kranis2009), where predictive ability of Bayes A was compared against that of RKHS. Training data contained 333 sires and the test data contained 61 sires that were sons of sires in the training set. SNPs with monomorphic genotypes or MAF less than 0·05 were removed, leaving 3481 SNPs. Means (standard deviations) of sire phenotypes in the training and testing sets were 1·23 (0·10) and 1·21 (0·08), respectively.
For both datasets, PCA was applied to the SNP incidence matrix (143×6947 for BW and 333×3481 for FCR) of the training set, and mega-SNPs were formed after extracting the minimum number of principal components that could explain about 90% of the total variance. The RBF models and Bayes A (the one that assumes additivity only) fitted to the training data were based on mega-SNPs, and a mega-SNP grouping strategy was adopted for RBF I, as described earlier. Since phenotypic values were pre-adjusted for other effects, only an intercept was included in each model along with SNP genotypes. For RBF I and RBF II, the number of basis functions was set to 25 for BW data (training sample size=143), and 50 for FCR data (training sample size=333). Residuals in each model were assumed to be independently distributed normal random variables, with zero mean and different variances depending on the number of progeny of each sire. That is, for sire i with N i progeny that were used to compute its mean, its residual variance was σe2/N i. As before, the length of Markov chain was 20 000, with the first half as burn-in. Chains were thinned at a rate of 5, giving 2000 samples for inference.
(iv) Whole genome simulation
The simulation basically followed that of Meuwissen et al. (Reference Meuwissen, Hayes and Goddard2001) and Solberg et al. (Reference Solberg, Sonesson, Woolliams and Meuwissen2008). The simulated genome contained 10 chromosomes, each of 1 Morgan length. Along each chromosome, there were in total 302 loci (202 SNP markers and 100 putative QTLs) equi-distantly spaced. Markers (M) and QTL (Q) were positioned as
The population evolved during 1000 generations of random mating and random selection, with a population size of 100 (50 males and 50 females) in each generation. Mutation rates at QTL and SNP markers were 2·5×10−5 and 2·5×10−3, respectively. After 1000 generations, the population size was increased to 1000 at generation t=1001 by mating each sire with 20 dams, with one offspring per mating pair. In t=1002, 1000 offspring were born from random mating of individuals in t=1001. This resulted in 57 segregating QTL (5·7% of the total number of QTLs) and 2004 segregating SNP markers (99% of the total number of markers) in generations t=1001 and t=1002.
The total genetic values resulting from the QTL were generated for individuals in generations t=1001 and t=1002. Three hypothetical gene action scenarios were considered.
(1) Purely additive: each QTL locus had an additive effect only, without dominance or epistasis.
(2) Additive+dominance: each QTL had an additive as well as a dominance effect, and there was no epistasis between QTLs.
(3) Pure epistasis: there was no additive or dominance effects at any of the individual QTLs. Epistasis existed only between pairs of QTLs. The forms of epistasis included additive×dominance (a×d), dominance×additive (d×a) and dominance×dominance (d×d). Additive and a×a epistasis effects were excluded, to prevent the additive variance from dominating the total genetic variance.
Given the genetic values and the genetic variance (estimated empirically from the genetic values generated), the error variance was chosen to keep heritability (in a broad sense) at 0·37 for each scenario. In scenario 1, the total genetic variance was completely additive. In scenario 2, 38% of the genetic variance was additive and the remaining 62% was due to dominance. In scenario 3, 42% of the variance was additive, 36% was dominance and 22% was epistatic. Note that there was additive genetic variance even though gene action was completely non-additive. Details of this simulation as well as variance component estimation are in Appendix B.
The training set was formed by randomly picking 300 individuals from generation t=1001. The testing set was formed by randomly picking 500 individuals from t=1002. The training (testing) set was repeatedly sampled from t=1001 (t=1002) 50 times and, for each replicate, RBF II and Bayes A (assuming additivity) were used to predict genetic values of individuals in the testing set using SNP markers. Specifically, RBF II was fitted with a varying number of basis functions (50, 100, 150, 200, 250 and 300) to allow for an examination of its effect on model's prediction accuracy. Results of the 50 replications were averaged for a final evaluation of each method. This procedure was performed for each of the three gene action scenarios described earlier. The Markov chain in the Bayesian implementation of the two models was run for 100 000 iterations, with the first half as burn-in. Thinning rate was 10, yielding 5000 samples for inference.
7. RESULTS
(i) Toy example
Table 1 shows correlation (corr(E(y), ŷ)) and PMSE1 on the test data (sample size=500) for the five competing models (RBF I, RBF II, Bayes AA, Bayes AAD and Bayes AADE). RBF I presented the best predictive ability in the five heritability scenarios. Even at low heritability (scenarios 1 and 2 with heritability of 0·1 and 0·25, respectively), RBF I attained large prediction correlations (0·72 and 0·86). RBF II was worse than RBF I, indicating that assigning SNP-specific weights improved ability to infer non-linear signals and enhanced prediction accuracy. Bayes AA and Bayes AAD were similar in correlation and PMSE1, indicating that introducing dominance effects in addition to additive effects was not helpful. Prediction correlation was improved by Bayes AADE, especially for moderate to high heritability (⩾0·25). There, correlations of Bayes AADE increased by about 40–50% over those of Bayes AA and Bayes AAD, and were about 5–25% higher than RBF II. Concerning PMSE, RBF I was clearly superior and RBF II was better than any of the Bayes A versions except when heritability was 0.75 and 0.9.
Table 1. Correlation and PMSE1 on test data in the toy example. Five scenarios (1–5) of broad sense heritability are 0·1, 0·25, 0·5, 0·75 and 0·9, respectively. corr (E(y), ŷ): correlation between expected and predicted phenotype; PMSE1 ![]() , where ntest=500 is sample size in the testing set. Bayes AA, Bayes AAD and Bayes AADE represent a Bayes A model that contains additive marker effects only, additive + dominance effects and additive + dominance + pair-wise epistatic effects, respectively.
, where ntest=500 is sample size in the testing set. Bayes AA, Bayes AAD and Bayes AADE represent a Bayes A model that contains additive marker effects only, additive + dominance effects and additive + dominance + pair-wise epistatic effects, respectively.
Overall, Bayes AA and Bayes AAD seemed inadequate for dealing with the datasets used in the toy example, which were generated in a non-linear and interactive manner. Bayes AADE further accommodated interaction effects and improved Bayes A's predictive ability considerably, but it was still inferior to RBF I.
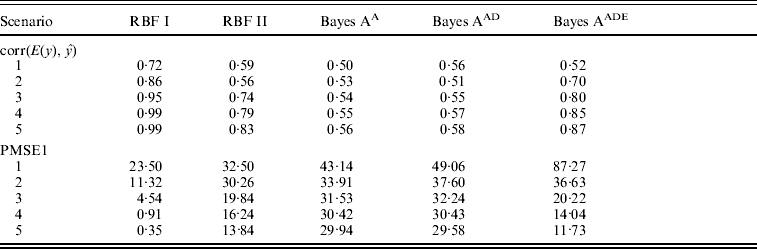
Absolute values of estimates of SNP effects g in Bayes AA can be regarded as signal intensities of each SNP. A larger absolute value implies a greater relevance to the phenotype. Similarly, values of θ in RBF I can be used as relevance measure also. Figure 1 shows ‘signals’ of the eight SNPs, as inferred by RBF I and Bayes AA. RBF I was able to pick the three truly relevant SNPs (1–3) and to flag the other five as irrelevant, especially in scenarios 3–5, where the signal:noise ratio was large. Even in the two noisiest scenarios (1 and 2), SNPs 1–3 still stood out. For Bayes AA, ambiguity existed due to large absolute values of estimates of some irrelevant SNPs. For example, SNP 7 appeared to be ‘relevant’ across scenarios 2 through 5. This indicated that Bayes A was not able to infer SNP effects accurately when the underlying relationship between genotype and phenotype was not additive. This is consistent with its poorer predictive ability.
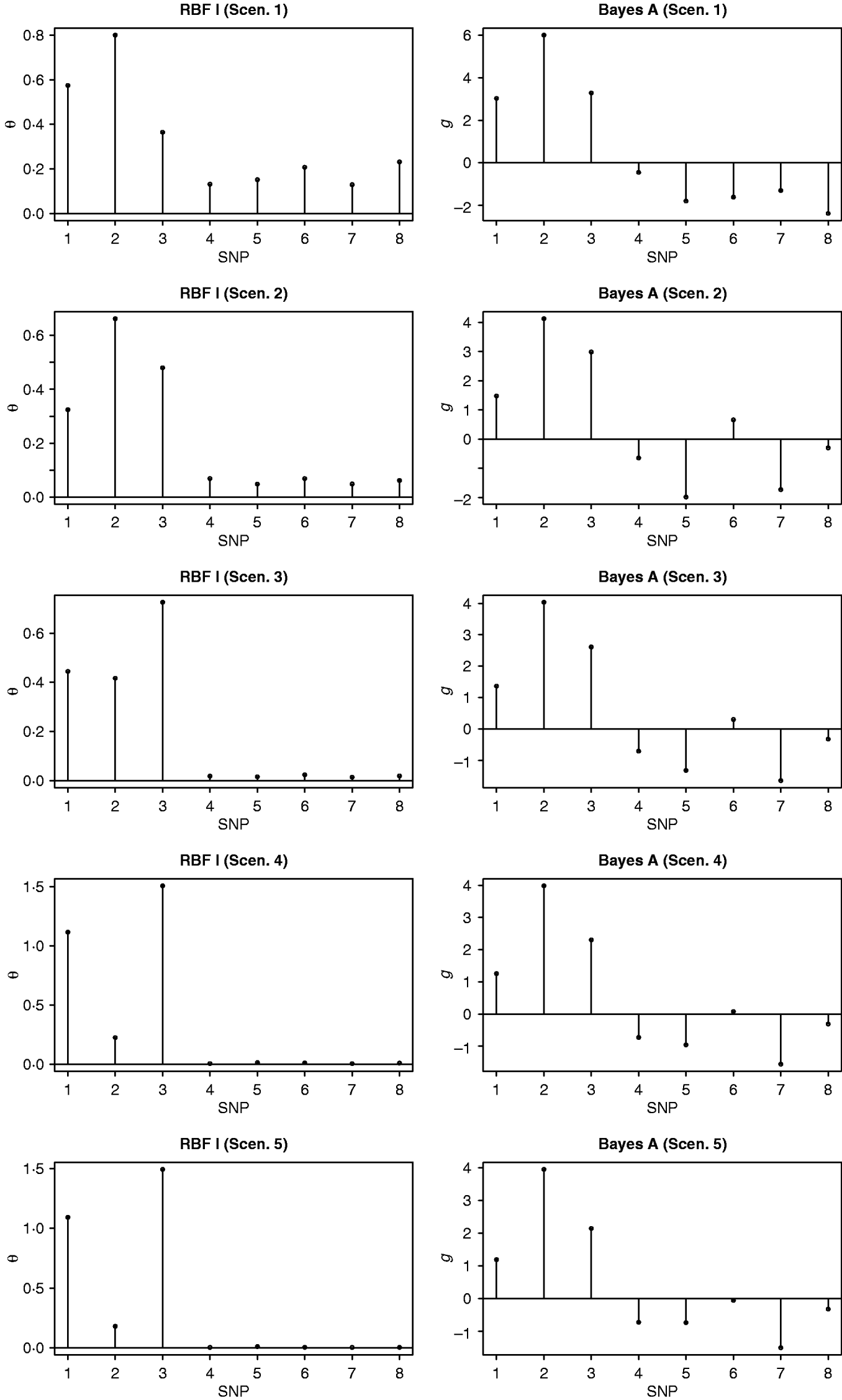
Fig. 1. Posterior means of θ in RBF I and of SNP effects g in Bayes A in the toy example. The five scenarios correspond to different ratios between the genetic and residual variances (1–1:9; 2–1:3; 3–1:1; 4–3:1 and 5–9:1).
(ii) BW and FCR data
In the BW analysis, about 90% of the total variance of the SNP training incidence matrix (143×6947) was explained by 105 principal components, resulting in 105 mega-SNPs. The range of their eigenvalues was 8·2–102·6. Cut-points for a roughly ‘equal-interval’ division of mega-SNPs (for RBF I) were 32, 56 and 80, resulting in four groups and, therefore, 4 θ's. Using the 105 mega-SNPs, all three models were fitted to the training data (143 sires). Predictive performance on the testing data (49 sires) is summarized in Table 2. The highest predictive correlation (corr(y, ŷ)) was achieved by RBF I (0·49), followed by RBF II (0·45). Bayes A produced the lowest correlation (0·35). PMSE2 was smallest with RBF I (32·5) and larger in RBF II (35·5) and Bayes A (35·9). Overall, RBF I and RBF II were better than Bayes A.
Table 2. Correlation and PMSE2 in the testing sets of BW and FCR data. corr(y, ŷ): correlation between observed and predicted phenotype. PMSE2 ![]() , where ntest is the sample size in the testing set.
, where ntest is the sample size in the testing set.
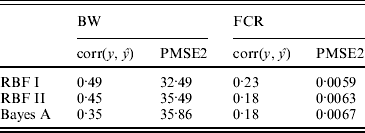
In the FCR analysis, 220 mega-SNPs (explaining 90% of the total variance of the training set 333×3481X matrix) were formed; the range of the associated eigenvalues was 1·7–35·4. Cut-points for a roughly ‘equal-interval’ division (for RBF I) were 10, 20 and 30, yielding four groups and therefore 4 θ's, as in the BW data. Prediction results on the testing data (61 sires) are given in Table 2. RBF I had the best performance (corr(y, ŷ)=0·23, PMSE2=0·0059). RBF II and Bayes A were the same in correlation (0·18) but RBF II had a slightly smaller value for PMSE2 (0·0063) than Bayes A (0·0067).
(iii) Whole genome simulation
As in the toy example, corr(E(y), ŷ) and PMSE1 were used, and the former can be interpreted as accuracy of marker-assisted prediction of total genetic value. Both metrics were summarized from all 50 replications, and density plots are presented in Figs 2 and 3 for prediction accuracy and PMSE1, respectively. The corresponding summaries are given in Table 3.
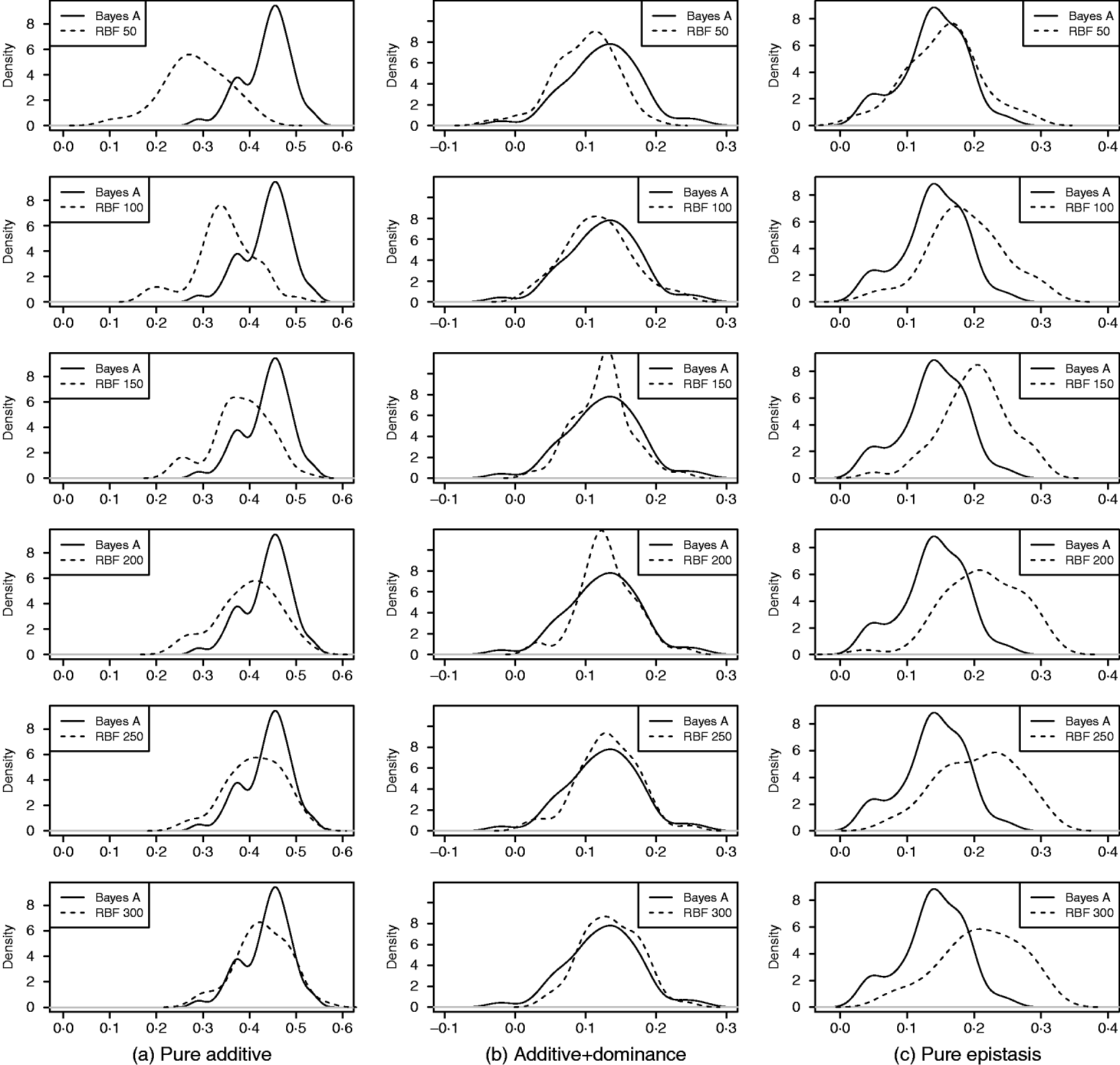
Fig. 2. Density of prediction accuracy of Bayes A and RBF II in the whole genome simulation (based on 50 replications), for each of the three scenarios (pure additive, additive+dominance and pure epistasis). Prediction accuracy is corr(E(y), ŷ). RBF50–RBF300 indicate RBF II with 50–300 basis functions, respectively.
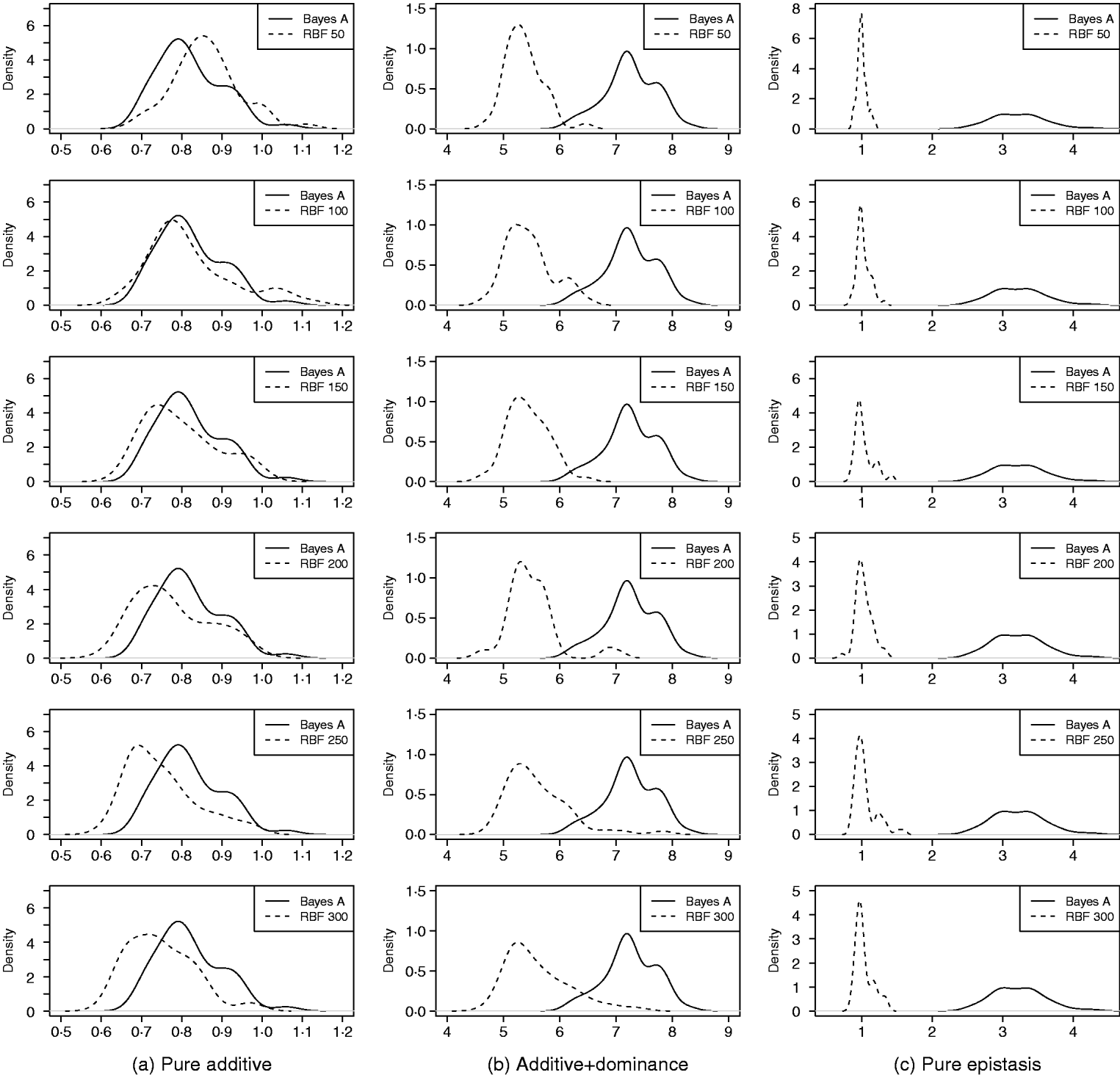
Fig. 3. Density of PMSE1 of Bayes A and RBF II in the whole genome simulation (based on 50 replications), for each of the three scenarios (pure additive, additive+dominance and pure epistasis). PMSE1 ![]() , where n test=500 is sample size in the testing set. RBF50–RBF300 indicate RBF II with 50–300 basis functions, respectively.
, where n test=500 is sample size in the testing set. RBF50–RBF300 indicate RBF II with 50–300 basis functions, respectively.
Table 3. Prediction accuracy and PMSE1 for the three scenarios (pure additive, additive+dominance and pure epistasis) in the whole genome simulation. Prediction accuracy is corr(E(y), ŷ). PMSE1 ![]() , where ntest=500 is the sample size in the testing set. RBF50–RBF300 indicate RBF II with 50–300 basis functions, respectively. Results were averages of 50 replications, with standard deviations given in parentheses.
, where ntest=500 is the sample size in the testing set. RBF50–RBF300 indicate RBF II with 50–300 basis functions, respectively. Results were averages of 50 replications, with standard deviations given in parentheses.
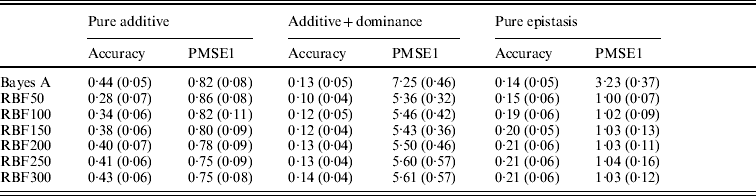
In the scenario of pure additivity, Bayes A had an average accuracy of 0·44, whereas RBF II with 300 basis functions (i.e. using each observation as the centre of a basis function) achieved an average accuracy of 0·43. Increasing the number of basis functions in RBF II gradually from 50 to 300 increased accuracy from 0·28 to 0·43. The improvement was relatively large from 50 to 100 basis functions. Beyond that, the change was small. The PMSE1 of Bayes A was 0·82; RBF II attained a PMSE1 from 0·86 with 50 basis functions moving down to 0·75 with 300 basis functions. Using an appropriate number of basis functions, RBF II can be as accurate as Bayes A or even better than Bayes A in PMSE.
In additive+dominance scenario, there was no major difference between Bayes A and RBF II in accuracy. Both were able to make predictions with an average accuracy of 0·13–0·14. Increasing the number of basis functions increased RBF II's accuracy somehow, but not much. PMSE1 was larger in Bayes A than in RBF II: PMSE 1 was 7·25 for Bayes A, whereas it ranged from 5·36 (50 basis functions) to 5·61 (300 basis functions) with RBF II. The overall performance of RBF II was therefore better than that of Bayes A.
In the scenario of pure epistasis, the accuracy of Bayes A was 0·14. For RBF II with 50 basis functions, the accuracy was 0·15, and increased to 0·19 and 0·20 with 100 and 150 basis functions, respectively. Then, accuracy stabilized at 0·21 with 200, 250 and 300 basis functions. The PMSE1 was clearly smaller for RBF II (about 1) than for Bayes A (3·23). In short, RBF II was superior to Bayes A in predictive ability.
8. DISCUSSION
The Bayes A method of Meuwissen et al. (Reference Meuwissen, Hayes and Goddard2001) is a linear model that assumes additive marker effects with each marker assigned a different variance, a priori. This produces heterogeneous shrinkage of marker effects, which may be more realistic than assuming equal variances and homogenous shrinkage for all markers, e.g., a BLUP model (Meuwissen et al., Reference Meuwissen, Hayes and Goddard2001; de los Campos et al., Reference de los Campos, Naya, Gianola, Crossa, Legarra, Manfredi, Weigel and Cotes2009b). However, an additive model may not work well in the presence of non-linear phenotype–genotype relationships (e.g. dominance or epistasis), in which case a substantial portion of genetic variance might be non-additive. In theory, one can include all possible forms of gene actions (additive, dominance and epistasis) in a Bayes A model but this becomes infeasible with hundreds of thousands of markers as model dimensionality is intractable. On the other hand, as pointed out by Gianola et al. (Reference Gianola, Fernando and Stella2006), non-parametric regression on marker genotypes does not make strong assumptions about the form of the marker–phenotype relationships and is expected to capture all possible forms of interaction. In the toy example where an arbitrary non-linear function was used to model genotype–phenotype relationship, RBFs attained a reasonably high accuracy whereas Bayes A was useful only when it contained additive, dominant and epistatic effects. In the analysis of two chicken datasets (offspring–parent settings), RBFs also outperformed a Bayes A that assumed additivity. Notably, model dimension of RBF II is independent of the number of markers, an important advantage over Bayes A.
In order to assess the value of RBF in various scenarios of gene action including pure additivity, a high level of dominance and pure epistasis, a whole genome simulation study was carried out. The training data simulated contained 2000 SNPs and 300 individuals so as to make it a ‘large p small n’ problem. Genetic value was generated by QTL but was predicted using SNP markers, relying on linkage disequilibrium (LD) between QTL and markers. Due to computational reasons discussed below, RBF I could not be considered so the comparison was between RBF II and Bayes A. It was found that RBF II, which makes no assumption of additivity of marker effects, was competitive for genetic value prediction relative to Bayes A (which assumed additivity) even when genetic values were purely additive. When dominance plus additive effects were considered (leading to 38% of the total genetic variance being additive and 62% being due to dominance), RBF II showed some advantage over Bayes A, especially in PMSE. Furthermore, when epistatic effects were simulated (42% additive variance, 36% dominance variance and 22% epistasis variance), RBF II was clearly better than Bayes A.
Increasing the number of SNPs increases computing time for RBF I because SNP-specific weights need to be estimated. When sampling from their conditional posterior distribution, every time a single weight is updated, the entire radial basis matrix has to be recomputed, making the process more time-consuming than RBF II. For example, with WinBUGS, RBF I with 50 basis functions and eight SNPs required 11 h for running 20 000 iterations, while RBF II spent only 4·9 h. It must be noted that this software is not tailored for large-scale calculation, so computational requirements may be lowered considerably if problem-specific software were developed. The WinBUGS environment limits the scope of RBF I unless some data reduction is done with respect to SNP dimension. For instance, in our analysis of BW and FCR, instead of using SNP-specific weights, group-specific weights were used, so that the effective number of weights to be estimated was reduced from the number of SNPs to the number of groups. Grouping can be done on the basis of chromosome, LD, or some other measure. LD was not useful for grouping here. Pairwise LD (Fig. 4) among SNPs was very weak for both BW and FCR data, as estimated by the r 2 measure (squared correlation between two SNP loci). This means that LD-based grouping would produce almost as many groups as there are SNPs. Instead, PCA-based grouping was adopted, which consisted of two steps: forming mega-SNPs and then grouping mega-SNPs based on their eigenvalues.
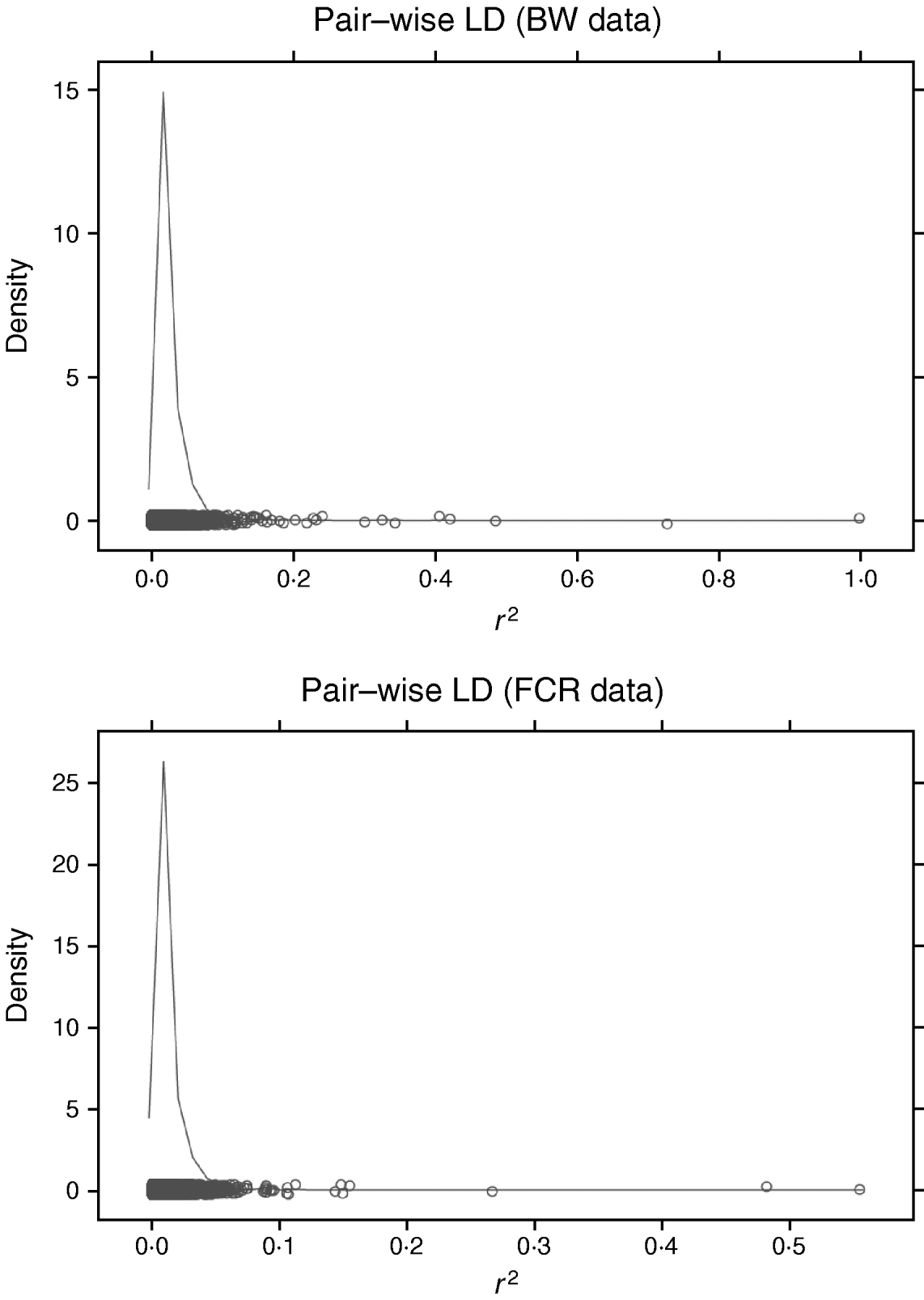
Fig. 4. Density plots of r 2 (squared correlation between two SNP loci) of pairwise SNP LD in BW and FCR data. Exhaustive pairwise computations were not feasible (24 126 931 pairs from 6947 SNPs in BW; 6 056 940 pairs from 3481 SNPs in FCR), so repeated sampling of all SNPs was used. Each repetition consisted of randomly sampling 50 SNPs, and pairwise r 2 was calculated. Values of r 2 from all repetitions were collected to approximate the LD level among the SNPs, and used for plotting. Here, 10 repetitions were performed for each dataset.
To compare mega-SNPs with real SNPs, Bayes A and RBF II were also fitted to BW and FCR data using real SNPs. Results indicated that the two yielded similar prediction performance. For example, Bayes A with real SNPs had correlations of 0·36 (BW) and 0·19 (FCR), very close to those obtained from using mega-SNPs: 0·35 (BW) and 0·18 (FCR). Likewise, RBF II with real SNPs had correlations of 0·41 (BW) and 0·17 (FCR), close to those from using mega-SNPs: 0·45 (BW) and 0·18 (FCR).
RBF I tended to have better predictive ability than RBF II. Also, by assigning SNP-specific weights, RBF I successfully flagged the three relevant SNPs in the toy example (Fig. 1). Nonetheless, RBF II is a promising, simpler, non-parametric method for making predictions. It achieved reasonably high accuracy in the toy example across a wide range of heritabilities. Although slightly worse, RBF II had similar prediction accuracy to RBF I in the real data analysis. More importantly, RBF II outperformed Bayes A when the underlying data generating system was far from additive.
As suggested by the whole genome simulation study, increasing the number of basis functions in RBF can improve prediction accuracy in general. However, the improvement gets smaller as more basis functions are included. At some point, accuracy reaches a plateau. Hence, one may not need as many basis functions as there are observations in order to get satisfactory predictions, provided that a smaller number of basis functions are properly chosen.
When all training data points are to be used as centres for the RBFs, some smoothness (regularization) must be imposed on the regression coefficients α in the model y=1μ+Kα+e, in order to avoid over-fitting. In a Bayesian treatment, regularization is done via a prior over the regression coefficients. In the present study, α was assigned a double exponential prior which puts more mass near 0 and in the tails, relative to a normal prior (Tibshirani, Reference Tibshirani1996). With a normal prior N(0, K−1σα2) on α, the model becomes a RKHS regression model (e.g. Wahba, Reference Wahba2002) from a Bayesian point of view (Gianola & van Kaam, Reference Gianola and van Kaam2008), in which a scaled inverted chi-square distribution is usually assigned as a prior to σα2. RKHS requires the kernel matrix (equivalently radial basis matrix in RBF) K to be semi-positive definite. RBF regression does not require so. González-Recio et al. (Reference González-Recio, Gianola, Long, Weigel, Rosa and Avendano2008, Reference González-Recio, Gianola, Rosa, Weigel and Kranis2009) presented applications of RKHS to mortality and FCR in broilers, and their results suggested that RKHS regression using SNPs can produce more reliable predictions of genomic value than standard parametric additive model currently in use.
In addition to RBF and RKHS, another non-parametric method for modelling genotypic data is kernel regression, introduced by Gianola et al. (Reference Gianola, Fernando and Stella2006). When interest is in additive effects, kernel regression can be built in an additive manner, in which the total genetic value is the sum of non-parametric function values at each locus. In this way, additive and dominance effects at each of the loci can be captured, but not epistatic interactions (Gianola & van Kaam, Reference Gianola and van Kaam2008). Bennewitz et al. (Reference Bennewitz, Solberg and Meuwissen2009) compared additive kernel regression with a BLUP model, and found that with differential amount of smoothing for the markers, the kernel regression was better than BLUP in predicting genomic BVs.
Since additive effects are central in selection improvement, it is sensible to ask whether or not it is useful to accommodate non-additivity in the model. Further, as shown by Hill et al. (Reference Hill, Goddard and Visscher2008), and corroborated here, a large portion of the genetic variance turns out to be additive. Our research indicates that non-parametric methods have similar or even better predictive ability than additive parametric models. Further, they are more general in situations in which prediction of performance is a focal point, such as in personalized medicine or genome-assisted management programmes.
9. CONCLUSION
Non-parametric RBF regressions were investigated by simulation and analysis of two broiler datasets. In the presence of a complex genotype–phenotype relationship (i.e. non-linearity and non-additivity), the RBF models outperformed a linear additive model, Bayes A, in predicting total genetic values of quantitative traits using SNP markers. The RBF methods had similar or even better predictive ability when gene action was purely additive. A RBF model with SNP-specific weights (RBF I) was generally better than one with a common weight for every SNP (RBF II). There is a potential for RBF I to discover relevant markers from a large pool of genetic markers scattered across the entire genome. When dealing with a massive number of markers, computational demand in RBF I is intensive, which remains an issue to be addressed.
APPENDIX A. BAYESIAN HIERARCHICAL RBF MODEL
The priors for all parameters in the Bayesian hierarchical model (see (5) and (7)) are as follows
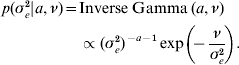
The residual variance σe2 was assigned a vague Inverse Gamma(a=0·001, ν=0·001) prior, throughout; the Gamma distribution parameters for λ and ρ were tuned to ensure convergence in all analyses. The joint posterior density of all parameters is proportional to the product of (7)–(A.6). The fully conditional distributions can be shown to be:
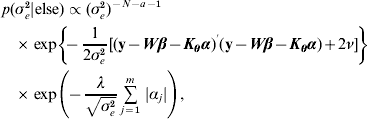
![\eqalign {\tab p\lpar \bimalpha \vert {\rm else}\rpar \hskip-1pt \propto \hskip-1pt\exp\left[ \hskip-2pt{ \minus {1 \over {2\sigma _{e}^{\setnum{2}} }}\lpar {\bf y} \minus {\bi W}\bimbeta \minus {\bi K}_{\bimtheta } \bimalpha \rpar ^\prime\lpar {\bf y} \minus {\bi W}\bimbeta \minus {\bi K}_{\bimtheta } \bimalpha \rpar } \right]\, \cr \tab\quad \times \prod\limits_{j \equals \setnum{1}}^{m} \, \exp\left( {\hskip-2pt \minus {{\lambda \vert \alpha _{j} \vert } \over {\sqrt {\sigma _{e}^{\setnum{2}} } }}} \right)\comma}](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20160920235843672-0896:S0016672310000157:S0016672310000157_eqn29.gif?pub-status=live)
![\eqalign{ p\lpar \lambda \vert {\rm else}\rpar \tab\propto \lambda ^{m \plus \gamma _{\setnum{1}} \minus \setnum{1}} \exp\left[ { \minus \left( {\mathop \sum\limits_{j \equals \setnum{1}}^{m} \,{{\vert \alpha _{j} \vert } \over {\sqrt {\sigma _{e}^{\setnum{2}} } }} \plus \delta _{\setnum{1}} } \right)\lambda } \right] \cr \tab \equals {\rm Gamma}\,\left( {m \plus \gamma _{\setnum{1}} \comma \mathop \sum\limits_{j \equals \setnum{1}}^{m} \,{{\vert \alpha _{j} \vert } \over {\sqrt {\sigma _{e}^{\setnum{2}} } }} \plus \delta _{\setnum{1}} } \right) \comma \cr}](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20160920235843672-0896:S0016672310000157:S0016672310000157_eqn30.gif?pub-status=live)
![\scale92%\eqalign{\tab p\lpar \bimtheta \vert {\rm else}\rpar \cr \tab\enspace\propto\exp \left[ { \hskip-3pt\minus {1 \over {2\sigma _{e}^{\setnum{2}} }}\lpar {\bf y} \minus {\bi W}\bimbeta \minus {\bi K}_{\bimtheta } \bimalpha \rpar \prime\lpar {\bf y} \minus {\bi W}\bimbeta \minus {\bi K}_{\bimtheta } \bimalpha \rpar \minus \rho \mathop \sum\limits_{k \equals \setnum{1}}^{p} \,\theta _{k} } \right]\comma}](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20160920235843672-0896:S0016672310000157:S0016672310000157_eqn31.gif?pub-status=live)
Hence, not all fully conditionals are recognizable distributions. For parameters with recognized distributions (β, λ and ρ), Gibbs sampling (i.e. using the fully conditionals as proposal distributions) can be used. For the other parameters, Metropolis–Hastings sampling can be employed.
APPENDIX B. GENERATING GENETIC VALUES AND EVALUATING ADDITIVE GENETIC VARIANCE IN THE WHOLE GENOME SIMULATION
Pure additive. The additive effect (a) was equal to the allele substitution effect, such that for genotypes A 1A 1, A 1A 2 and A 2A 2, their genotypic values were 2a, a and 0, respectively. The value of a at each QTL locus was sampled from a normal distribution with mean 0 and variance 0·1.
Additive+dominance. The additive effects were as in the pure additive scenario. To simulate a marked dominance effect, its value (d) assigned to each QTL locus was obtained by multiplying the additive effect (a) at that locus by arandom number sampled from uniform (−5, 5) distribution. For a QTL locus with additive effect a and dominance effect d, its genotypic values were 2a for A 1A 1, a+d for A 1A 2, and 0 for A 2A 2. If genotypic frequencies at that locus are p 2, 2pq and q 2 for A 1A 1, A 1A 2 and A 2A 2, respectively, the total genetic variance can be decomposed into additive (σA2) and dominance variance (σD2) as follows (Falconer & Mackay, Reference Falconer and Mackay1996):
For simplicity, independence between QTLs was assumed and, as a result, the total additive (dominance) variance was summed over all loci.
Pure epistasis. Only segregating QTLs were involved in epistatic interactions. Among the 57 segregating QTLs, 56 were randomly chosen to form 28 QTL pairs. Each pair was assigned an a×d interaction effect i ad, a d×a effect i da and a d×d effect i d×d. The absolute value of each of i ad, i da and i dd was the same, and set to mean of |a 1|, |d 1|, |a 2| and |d 2|, where a 1 and d 1 were additive and dominance effects at the first locus, and a 2 and d 2 were those at the second locus. The sign of each of the three epistatic effects was sampled from {1, −1} with probability 0·5.
Given a pair of QTLs (i=1, 2), its epistatic value was given by i adx 1z 1+i daz 1x 2+i ddz 1z 2, where x i and z i were additive and dominance codes at locus i, respectively. For A 1A 1 genotype, x i=1, z i=−0·5; for A 1A 2, x i=0, z i=0·5; and for A 2A 2, x i=−1, z i=−0·5 (Cordell, Reference Cordell2002).
The total genetic value was the sum of epistatic values produced by each of the 28 QTL pairs. The procedure of estimating additive and epistatic variance components followed Cockerham (Reference Cockerham1954), assuming independence between two loci of each QTL pair and between QTL pairs.
APPENDIX C. DETERMINE u IN THE UNIFORM PRIOR DISTRIBUTION (0, u) FOR VARIANCES OF MARKER EFFECTS IN BAYES A
The construction of the prior distribution was based on some assumptions and approximations. The purpose was getting a rough value of the marker variance ![]() , which was the variance of the prior distribution for marker effect
, which was the variance of the prior distribution for marker effect ![]() . The assumptions were:
. The assumptions were:
1. Allele frequencies at all loci come from the same distribution. Similarly, marker effects at all loci come from the same distribution g j~N(0, σg2).
2. Consider only additive genetic variance at each locus j, which is 2p jq jg j2 (p j, q j are allele frequencies and g j is additive marker effect at locus j).
3. The total genetic value (G) of an individual is assumed to be obtained by adding genetic values at all marker loci, with marker loci treated as independent (no LD). Then, the variance of the total genetic value (var(G)) is the sum of variances at individual loci.
4. Approximate var(G) by the variance of observed phenotypic values (var(y)). This leads to an overstatement of genetic variance and, thus, of the variance of each marker. As a prior, this allows a wide range of values for marker variance.
Based on assumptions 1 and 3, the expectation of the variance contributed by each of the p loci is the same. Hence,
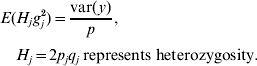
Because H j and g j2 are independent,
E(H j) was estimated by averaging H j across all p loci (due to assumption 1) and var(y) was calculated from the empirical distribution of phenotypic values. Thus, σg2 was available. Finally, the upper bound u in the uniform (0, u) distribution was set to be twice as large as the estimated value of σg2, to make the mean of this uniform distribution equal to the estimated σg2.
This procedure was also applied to the principal component regression, as used for the two broiler datasets. In that case, the variance of the prior distribution of mega-SNP effects m (16) was the target. The expectation of the variance caused by each of the a mega-SNPs (tj, j=1, … , a) was approximated as
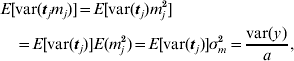
and E[var(tj)] was estimated by averaging var(tj) across all a mega-SNPs. Thus, σm2 was available.
APPENDIX D. COMPARE BAYES A WITH UNIFORM PRIOR AND SCALED INVERTED CHI-SQUARE PRIOR ON THE VARIANCES OF MARKER EFFECTS
The uniform prior was described in the preceding section. For the scaled inverted chi-square distribution, its degrees of freedom (ν) was fixed at 4·2, and the scale S was chosen so as to make the mean of the distribution equal the estimated value of σg2, as for the uniform prior. Bayes A (additive effects only) with each of the two priors was fitted to the five simulated data used in the toy example, as described in section 6(ii), and to the two chicken datasets (BW and FCR) using real SNPs. Predictive correlations (corr(E(y), ŷ)) obtained with each of the two priors were similar.

Support by the Wisconsin Agriculture Experiment Station, and by grants NRICGP/USDA 2003-35205-12833, NSF DEB-0089742 and NSF DMS-044371 is acknowledged. Two anonymous reviewers and the editor are thanked for useful comments.









