1. Introduction
Loss of genetic diversity or increase of inbreeding is of special concern in either captive or selected populations. In order to monitor and manage genetic diversity the genealogical information is usually condensed into a few parameters such as average inbreeding coefficients (![]() ; Wright, Reference Wright1922), average kinship (Malécot, Reference Malécot1948) or coancestry (
; Wright, Reference Wright1922), average kinship (Malécot, Reference Malécot1948) or coancestry (![]() ; Cockerham, Reference Cockerham and K.1970), effective population size (Wright, Reference Wright1931), founder equivalents, founder genome equivalent (Lacy, Reference Lacy1989), effective number of ancestors, and founders and non-founders (Boichard et al., Reference Boichard, Maignel and Verrier1997; Caballero & Toro, Reference Caballero and Toro2000). The most relevant indicator of genetic variability is
; Cockerham, Reference Cockerham and K.1970), effective population size (Wright, Reference Wright1931), founder equivalents, founder genome equivalent (Lacy, Reference Lacy1989), effective number of ancestors, and founders and non-founders (Boichard et al., Reference Boichard, Maignel and Verrier1997; Caballero & Toro, Reference Caballero and Toro2000). The most relevant indicator of genetic variability is ![]() , including self-coancestries (Ballou & Lacy, Reference Ballou, Lacy, Ballou, Gilpin and Foose1995; Caballero & Toro, Reference Caballero and Toro2000; Fernandez et al., Reference Fernandez, Toro and Caballero2003). Selection for minimum coancestry has been shown to reduce the loss of genetic variation or the rate of inbreeding in the long term more effectively than other strategies such as equalizing the founder contributions or minimizing immediate inbreeding (Ballou & Lacy, Reference Ballou, Lacy, Ballou, Gilpin and Foose1995; Meuwissen, Reference Meuwissen1997; Caballero et al., Reference Caballero, Santiago and Toro1996; Caballero & Toro, Reference Caballero and Toro2000; Sanchez et al., Reference Sanchez, Bijma and Woolliams2003).
, including self-coancestries (Ballou & Lacy, Reference Ballou, Lacy, Ballou, Gilpin and Foose1995; Caballero & Toro, Reference Caballero and Toro2000; Fernandez et al., Reference Fernandez, Toro and Caballero2003). Selection for minimum coancestry has been shown to reduce the loss of genetic variation or the rate of inbreeding in the long term more effectively than other strategies such as equalizing the founder contributions or minimizing immediate inbreeding (Ballou & Lacy, Reference Ballou, Lacy, Ballou, Gilpin and Foose1995; Meuwissen, Reference Meuwissen1997; Caballero et al., Reference Caballero, Santiago and Toro1996; Caballero & Toro, Reference Caballero and Toro2000; Sanchez et al., Reference Sanchez, Bijma and Woolliams2003).
Examination of detailed contributions of ancestors gives a better understanding of the development of inbreeding or coancestry over time, in terms of the origin of genes, in general, or the origin of genetic gains in selected populations. The expression ‘origin of genes’ is sometimes misleading in the literature when it refers to non-founder ancestors. Strictly speaking, unless there are mutations, only founder genes are segregating. Instead, ‘origin of breeding values (BVs)’ may be preferred, where BVs concern a hypothetical polygenic neutral trait. Throughout the following text, the term ‘BV’ will refer to the BV for this latent trait.
Some studies (e.g., Woolliams & Thompson, Reference Woolliams and Thompson1994) have insisted on the prominent role played by Mendelian sampling components of BVs. Basically, considering such a trait is quite relevant because covariances between individuals for this trait are equal to twice the coancestry coefficient, when genetic variance is 1. Following this rationale, inbreeding coefficients can be expressed in terms of contributions of parents and Mendelian sampling variances (MSVs) over generations (Woolliams & Thompson, Reference Woolliams and Thompson1994; Woolliams et al., Reference Woolliams, Bijma and Villanueva1999). Conceptually, contribution of an ancestor to an individual quantifies the fraction of ancestral Mendelian sampling components of BV passed to this individual (James & McBride, Reference James and McBride1958). In this context, Caballero & Toro (Reference Caballero and Toro2000) gave the expression of ![]() or
or ![]() in a population in terms of contribution of MSVs from founders and subsequent ancestors. Here contributors are common ancestors (CAs). Later on, this approach will be denoted as the ‘conventional’ approach.
in a population in terms of contribution of MSVs from founders and subsequent ancestors. Here contributors are common ancestors (CAs). Later on, this approach will be denoted as the ‘conventional’ approach.
Wright (Reference Wright1922) presented the first method to compute coefficients of inbreeding and relationships. In contrast to the conventional method, this coalescence probabilistic method partitions inbreeding into contributions of genes of ancestors, through a recursive path counting process. This approach can be used for partitioning ![]() or
or ![]() in a population, but it is time-consuming. The most striking consequence of using this approach is that the list of contributors is modified, and basically shortened, because the upward search can be stopped as soon as coalescence is obtained (i.e., inbreeding in an intermediate ancestor is encountered). Then, Wright's approach consists of determining the most recent occurrences of inbreeding, irrespective of the genes being inbred. Remaining contributors can be called ‘nodal common ancestors’ (NCAs). The other CAs can be considered as ‘absorbed CAs’ (ACAs) because their genes contribute to inbreeding or coancestry through the NCAs. Probability of absorption increases when age of ancestors increases, because probability of direct access to inbreeding by older ancestors decreases.
in a population, but it is time-consuming. The most striking consequence of using this approach is that the list of contributors is modified, and basically shortened, because the upward search can be stopped as soon as coalescence is obtained (i.e., inbreeding in an intermediate ancestor is encountered). Then, Wright's approach consists of determining the most recent occurrences of inbreeding, irrespective of the genes being inbred. Remaining contributors can be called ‘nodal common ancestors’ (NCAs). The other CAs can be considered as ‘absorbed CAs’ (ACAs) because their genes contribute to inbreeding or coancestry through the NCAs. Probability of absorption increases when age of ancestors increases, because probability of direct access to inbreeding by older ancestors decreases.
In the present article, the results of Wright's method can be fully recovered by a non-probabilistic method, analytically linked with Caballero & Toro's (Reference Caballero and Toro2000) method, still considering the conventional approach or MSVs. Wright's decomposition is denoted ‘proximal’ because NCAs are usually younger and less numerous than CAs in the conventional analysis, due to a backward or coalescence decomposition process. Finally, the efficiency of past management of simulated selected populations will be examined by the conventional and the proximal analyses.
2. Materials and methods
(i) Recovering Wright's decomposition from Caballero & Toro's decomposition
Caballero & Toro's decomposition method can be shown to be obtained exactly after multiplication of Wright's decomposition by an upper triangular matrix, and then that the reverse can be carried out easily and very fast, due to this simplicity.
Statistics of interest are average pairwise coancestry (![]() ) or average inbreeding (
) or average inbreeding (![]() ) for a group of individuals. The relationship matrix (A) can be decomposed as:
) for a group of individuals. The relationship matrix (A) can be decomposed as:
where C={c ij}=(I−T)−1 is the contribution matrix, a unit lower triangular matrix containing the fraction of genes that individual j passed to descendant i (contribution of j to i in the sense of James & McBride, Reference James and McBride1958), T is a unit lower triangular sparse matrix consisting of only −0·5 at positions where individual i is linked to its sire and dam, D=diag {d ii} is a diagonal matrix containing the MSVs of individuals. The MSV for individual i is ![]() , where
, where ![]() and
and ![]() are inbreeding coefficients of the sire and dam of individual i, respectively (Quaas, Reference Quaas1976). Now
are inbreeding coefficients of the sire and dam of individual i, respectively (Quaas, Reference Quaas1976). Now ![]() can be decomposed into vector m={m j}, where m j is the contribution of MSV of ancestor j. Such a decomposition is referred to as the m-decomposition. Following Caballero & Toro (Reference Caballero and Toro2000), vector m is:
can be decomposed into vector m={m j}, where m j is the contribution of MSV of ancestor j. Such a decomposition is referred to as the m-decomposition. Following Caballero & Toro (Reference Caballero and Toro2000), vector m is:
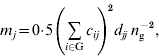
where n g is the size of the group. The term ![]() can be readily obtained by the indirect method (Colleau, Reference Colleau2002), which requires tracing back the pedigree only once. Figure 1 shows an example pedigree for illustrating the method.
can be readily obtained by the indirect method (Colleau, Reference Colleau2002), which requires tracing back the pedigree only once. Figure 1 shows an example pedigree for illustrating the method.

Fig. 1. Example pedigree.
Let the group in question be individuals 9 and 10. Then vector m for ![]() is:
is:
The contribution of MSV of ancestor j to ![]() can be derived in the same manner:
can be derived in the same manner:

To obtain vector m for ![]() using the indirect method, the pedigree should be traced back twice the number of sires of the group considered, because the sum corresponding to a given sire can be obtained from two back explorations of the population pedigree (Colleau, Reference Colleau2002; Sargolzaei et al., Reference Sargolzaei, Iwaisaki and Colleau2005). Vector m for the
using the indirect method, the pedigree should be traced back twice the number of sires of the group considered, because the sum corresponding to a given sire can be obtained from two back explorations of the population pedigree (Colleau, Reference Colleau2002; Sargolzaei et al., Reference Sargolzaei, Iwaisaki and Colleau2005). Vector m for the ![]() of the group consisting of individuals 9 and 10 is then:
of the group consisting of individuals 9 and 10 is then:
The probabilistic approach of path counting (Wright, Reference Wright1922) is theoretically well suited to partition the inbreeding coefficients into contributions of genes of NCAs. An NCA can be defined as an ancestor who connects the sire and dam lines that arise from the individual of interest or from its NCA(s). The NCA makes an inbreeding loop in which no individual is present more than once. The details of the path counting method are presented in Appendix A.
Now, let the results of the path counting method be represented by the known vector w={w i}, where w i indicates the contribution of genes of NCA i to the statistics of interest to be partitioned. For simplicity, in the following development, ![]() is used as the statistic of interest. However, the derivation holds for
is used as the statistic of interest. However, the derivation holds for ![]() because
because ![]() can be considered as
can be considered as ![]() resulting from a factorial mating design between members of the group investigated.
resulting from a factorial mating design between members of the group investigated.
The relation ![]() is well known. Note that
is well known. Note that ![]() is the MSV of individual i. Then, recursive decomposition of the genetic variances of parents of i across generations, leads one to find that 1 is the sum of a series involving MSVs of all the ancestors of individual i. Appendix B shows that this development is also the development of one certain occurrence of inbreeding in individual i in terms of MSV.
is the MSV of individual i. Then, recursive decomposition of the genetic variances of parents of i across generations, leads one to find that 1 is the sum of a series involving MSVs of all the ancestors of individual i. Appendix B shows that this development is also the development of one certain occurrence of inbreeding in individual i in terms of MSV.
The decomposition of parental variances is carried out using corresponding rows of matrix C, which can be computed by tracing back the pedigree of each parent. Let column vector ψi={ψki} represent the coefficients of this development, where ψki indicates the contribution of ancestor k to inbreeding in i, given the contribution of elder ancestors. Because these weights sum up to 1 (1′ψi=1), they can be directly interpreted as the relative probability of origin of the inbreeding for a gene of a given individual, when inbreeding is certain.
If inbreeding through a given individual has probability w i, then the contribution of individual i to vector m is w iψi and finally:
where the transition matrix Ψ from w to m gathers all the involved coefficients and is an upper triangular matrix. Off-diagonal elements of column i of matrix Ψ are:
and diagonal elements of matrix Ψ are simply d kk. Matrix Ψ for the example pedigree is shown below:
![{\bmPsi } \equals \left[ {\matrix{ {1{\cdot}0000} \tab {0{\cdot}0000} \tab {0{\cdot}0000} \tab {0{\cdot}2500} \tab {0{\cdot}3125} \tab {0{\cdot}0000} \tab {0{\cdot}1406} \tab {0{\cdot}1406} \tab {0{\cdot}0703} \tab {0{\cdot}0703} \cr {0{\cdot}0000} \tab {1{\cdot}0000} \tab {0{\cdot}0000} \tab {0{\cdot}2500} \tab {0{\cdot}0625} \tab {0{\cdot}2500} \tab {0{\cdot}0781} \tab {0{\cdot}0781} \tab {0{\cdot}0703} \tab {0{\cdot}0703} \cr {0{\cdot}0000} \tab {0{\cdot}0000} \tab {1{\cdot}0000} \tab {0{\cdot}0000} \tab {0{\cdot}0000} \tab {0{\cdot}2500} \tab {0{\cdot}0625} \tab {0{\cdot}0625} \tab {0{\cdot}0313} \tab {0{\cdot}0313} \cr {0{\cdot}0000} \tab {0{\cdot}0000} \tab {0{\cdot}0000} \tab {0{\cdot}5000} \tab {0{\cdot}1250} \tab {0{\cdot}0000} \tab {0{\cdot}0313} \tab {0{\cdot}0313} \tab {0{\cdot}0156} \tab {0{\cdot}0156} \cr {0{\cdot}0000} \tab {0{\cdot}0000} \tab {0{\cdot}0000} \tab {0{\cdot}0000} \tab {0{\cdot}5000} \tab {0{\cdot}0000} \tab {0{\cdot}1250} \tab {0{\cdot}1250} \tab {0{\cdot}0625} \tab {0{\cdot}0625} \cr {0{\cdot}0000} \tab {0{\cdot}0000} \tab {0{\cdot}0000} \tab {0{\cdot}0000} \tab {0{\cdot}0000} \tab {0{\cdot}5000} \tab {0{\cdot}1250} \tab {0{\cdot}1250} \tab {0{\cdot}0625} \tab {0{\cdot}0625} \cr {0{\cdot}0000} \tab {0{\cdot}0000} \tab {0{\cdot}0000} \tab {0{\cdot}0000} \tab {0{\cdot}0000} \tab {0{\cdot}0000} \tab {0{\cdot}4375} \tab {0{\cdot}0000} \tab {0{\cdot}1094} \tab {0{\cdot}1094} \cr {0{\cdot}0000} \tab {0{\cdot}0000} \tab {0{\cdot}0000} \tab {0{\cdot}0000} \tab {0{\cdot}0000} \tab {0{\cdot}0000} \tab {0{\cdot}0000} \tab {0{\cdot}4375} \tab {0{\cdot}1094} \tab {0{\cdot}1094} \cr {0{\cdot}0000} \tab {0{\cdot}0000} \tab {0{\cdot}0000} \tab {0{\cdot}0000} \tab {0{\cdot}0000} \tab {0{\cdot}0000} \tab {0{\cdot}0000} \tab {0{\cdot}0000} \tab {0{\cdot}4688} \tab {0{\cdot}0000} \cr {0{\cdot}0000} \tab {0{\cdot}0000} \tab {0{\cdot}0000} \tab {0{\cdot}0000} \tab {0{\cdot}0000} \tab {0{\cdot}0000} \tab {0{\cdot}0000} \tab {0{\cdot}0000} \tab {0{\cdot}0000} \tab {0{\cdot}4688} \cr} } \right].](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary-alt:20160627181914-07270-mediumThumb-S0016672307009202_eqnU15.jpg?pub-status=live)
A remarkable result is that for finding w, the equation above does not involve MSVs, but only contributions. This is apparent after dividing each row k of the linear system by the corresponding d kk.
Solve for w as w=Ψ−1m. The inverse of matrix Ψ is sparse but cannot be readily obtained because the distribution of non-null terms depends on the unknown situation concerning vector w, the issue to be solved. However, Ψ is upper triangular and w can be obtained efficiently from m by Gaussian elimination because each column of Ψ can be formed separately by tracing back the pedigrees of the two parents involved. Starting from the vector m pertaining to decomposition of the average inbreeding coefficient of individuals 9 and 10,
i.e., exactly the result obtained by the path counting method (see Appendix A). For each individual, distinct computations of contribution vectors of sires and dams are needed, which might be time-consuming in large populations. However, substantial computation time can be saved if the number of sires is much less than the number of dams (a very frequent situation) and if the population is subdivided into pseudo-generations (Colleau, Reference Colleau2002). In this situation, solutions for w during Gaussian elimination can be obtained simultaneously by blocks and updating of the right-hand side needs only one trace back per sire involved in this pseudo-generation. The m-decomposition includes the effect of self-coancestries of the individuals of the current population, when the statistic considered is the average relationship. If the weighted average coancestry between parents of the current population is preferred because this bias is avoided, the corresponding modified w-decomposition is easy to implement (see Appendix C).
(ii) Defining a proximal model of breeding values
In the conventional context, let g i be the BV of individual i, c ik is the contribution of ancestor k to individual i and δik is the Mendelian sampling deviation of ancestor k, then ![]() . The model for BVs is straightforward and leads one naturally to decomposition of variances or covariances, as presented above.
. The model for BVs is straightforward and leads one naturally to decomposition of variances or covariances, as presented above.
In the proximal context, introduced by Wright's decomposition, quite the reverse occurs: partitioning of variances or covariances is obtained without explicitly defining the model for BVs. A model based on the conventional model is proposed, where the independent genetic variables are deviations of BVs of proximal ancestors (or NCA) from their expectations given BVs of all older proximal ancestors. In contrast, in the conventional model, BVs are only conditioned on parental BVs (two individuals) for providing Mendelian sampling BV. Then, the corresponding regression coefficients are the proximal contributions, i.e., ![]() , where k is the rank number in the list of proximal ancestors and δk* is the deviation of BV of ancestor k from its expectation given BVs of proximal ancestors 1,…, k−1. In this model, variances of the random variables can be much more heterogeneous than in the conventional model. Regression coefficients and conditional variances in this context cannot be easily linked to terms of the w-decomposition, because proximal ancestors can have one or even both parents not included in the list of proximal ancestors. Basically, they should be obtained by a numerical method, such as Cholesky decomposition of the relationship matrix of the proximal ancestors.
, where k is the rank number in the list of proximal ancestors and δk* is the deviation of BV of ancestor k from its expectation given BVs of proximal ancestors 1,…, k−1. In this model, variances of the random variables can be much more heterogeneous than in the conventional model. Regression coefficients and conditional variances in this context cannot be easily linked to terms of the w-decomposition, because proximal ancestors can have one or even both parents not included in the list of proximal ancestors. Basically, they should be obtained by a numerical method, such as Cholesky decomposition of the relationship matrix of the proximal ancestors.
For the example pedigree, if the cohort of interest contains individuals 9 and 10 then C* matrix is:
![\eqalign{\tab \quad \quad\matrix{ {\hskip-22{\rm NCA}} \tab {\hskip8{\rm 1 }} \quad \quad \tab {\!\!{\rm 2 }}\quad \quad \quad \tab {\hskip-12{\rm 5 }}\quad \quad \quad \tab {\hskip-10{\rm 6 }}\quad \quad \quad \tab {\hskip-13{\rm 7 }}\quad \quad \tab {\hskip-4{\rm 8 }}\quad \quad \quad \tab {\hskip-15{\rm 9 }}\quad \quad \tab {\hskip-10{\rm 10}} \cr} \cr \tab {\bf C}\ast \equals \left[ {\matrix{ {1{\cdot}000} \tab {0{\cdot}000} \tab {0{\cdot}000} \tab {0{\cdot}000} \tab {0{\cdot}000} \tab {0{\cdot}000} \tab {0{\cdot}000} \tab {0{\cdot}000} \cr {0{\cdot}000} \tab {1{\cdot}000} \tab {0{\cdot}000} \tab {0{\cdot}000} \tab {0{\cdot}000} \tab {0{\cdot}000} \tab {0{\cdot}000} \tab {0{\cdot}000} \cr {0{\cdot}750} \tab {0{\cdot}250} \tab {1{\cdot}000} \tab {0{\cdot}000} \tab {0{\cdot}000} \tab {0{\cdot}000} \tab {0{\cdot}000} \tab {0{\cdot}000} \cr {0{\cdot}000} \tab {0{\cdot}500} \tab {0{\cdot}000} \tab {1{\cdot}000} \tab {0{\cdot}000} \tab {0{\cdot}000} \tab {0{\cdot}000} \tab {0{\cdot}000} \cr {0{\cdot}375} \tab {0{\cdot}375} \tab {0{\cdot}395} \tab {0{\cdot}433} \tab {1{\cdot}000} \tab {0{\cdot}000} \tab {0{\cdot}000} \tab {0{\cdot}000} \cr {0{\cdot}375} \tab {0{\cdot}375} \tab {0{\cdot}395} \tab {0{\cdot}433} \tab {0{\cdot}000} \tab {1{\cdot}000} \tab {0{\cdot}000} \tab {0{\cdot}000} \cr {0{\cdot}375} \tab {0{\cdot}375} \tab {0{\cdot}395} \tab {0{\cdot}433} \tab {0{\cdot}331} \tab {0{\cdot}331} \tab {1{\cdot}000} \tab {0{\cdot}000} \cr {0{\cdot}375} \tab {0{\cdot}375} \tab {0{\cdot}395} \tab {0{\cdot}433} \tab {0{\cdot}331} \tab {0{\cdot}331} \tab {0{\cdot}000} \tab {1{\cdot}000} \cr} } \right]. \cr}](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20160405022600524-0606:S0016672307009202_eqnU20.gif?pub-status=live)
In selected populations, the origin of genetic gain can be re-examined in a proximal perspective, analogously to Woolliams et al. (Reference Woolliams, Bijma and Villanueva1999) for the conventional model. The contribution of ancestor k to genetic gain is equal to, ![]() , where
, where ![]() and δk* are obtained based on the Cholesky decomposition.
and δk* are obtained based on the Cholesky decomposition.
When BVs of the trait under selection are estimated by best linear unbiased prediction (BLUP), then we also have ![]() . Finally, the estimated contribution of ancestor k to genetic gain is equal to
. Finally, the estimated contribution of ancestor k to genetic gain is equal to ![]() . Furthermore, the efficiency of the breeding scheme can be examined in retrospect. In the next section, the proximal decomposition is compared to the conventional decomposition of
. Furthermore, the efficiency of the breeding scheme can be examined in retrospect. In the next section, the proximal decomposition is compared to the conventional decomposition of ![]() to assess the maximal estimated genetic gain possible while constraining this coancestry to the observed value.
to assess the maximal estimated genetic gain possible while constraining this coancestry to the observed value.
(iii) Measuring the retrospective efficiency of a breeding scheme
The inefficiency of a selection breeding scheme for balancing genetic gain and ![]() can be measured by the discrepancy between the observed genetic gain and the maximum genetic gain that could have been generated considering the ancestors of the current population and constraining
can be measured by the discrepancy between the observed genetic gain and the maximum genetic gain that could have been generated considering the ancestors of the current population and constraining ![]() to its observed value. Ideal contributions for producing maximum genetic gains can be determined either by the conventional approach or by the proximal approach. Conventional BLUP selection considers a fixed number of breeding individuals selected based only on their EBVs without any other consideration. In contrast, optimized schemes such as those defined by Meuwissen (Reference Meuwissen1997) allow contributions of selected breeding individuals to fluctuate permanently according to the balance between their EBVs and the extra coancestry they could generate.
to its observed value. Ideal contributions for producing maximum genetic gains can be determined either by the conventional approach or by the proximal approach. Conventional BLUP selection considers a fixed number of breeding individuals selected based only on their EBVs without any other consideration. In contrast, optimized schemes such as those defined by Meuwissen (Reference Meuwissen1997) allow contributions of selected breeding individuals to fluctuate permanently according to the balance between their EBVs and the extra coancestry they could generate.
Simulation was carried out to assess the respective potential of the conventional or proximal methods of back-optimization when applied to breeding schemes implementing various degrees of optimization. The founder population consisted of 25 sires and 50 dams, and 15 discrete generations were considered (founder generation being generation 0). Selection was carried out on a single trait with heritability of 0·2 (initial genetic variance set to 1), expressed by both sexes. In BLUP selection schemes, each sire is mated to two dams at random according to a hierarchical design. Each dam produces four progeny. In optimized breeding schemes, a hierarchical design and random mating were maintained, whereas the number of progeny per sire and per dam was allowed to vary. Four intermediate schemes were added starting with BLUP and switching towards an optimized scheme at generations 14, 11, 8 and 5. One hundred replicates of the six schemes were simulated by sextuplets. For increasing the efficiency of comparison between schemes, the same set of founders was considered for each member of a given sextuplet. Furthermore, intermediate schemes were initiated from the data of the BLUP member until the switch. Optimized and intermediate breeding schemes of a given sextuplet were constrained to produce, at each generation, the same coancestry as their BLUP counterpart.
For each breeding scheme and each replicate, the maximum genetic gain obtained in retrospect was determined analytically by maximizing a Lagrange function where unknowns were optimal contributions as the main constraint, so the coancestry between parents of generation 15 should be equal to that observed. For the optimization in retrospect based on conventional contributions, additional constraints were introduced. Firstly, sums of contributions per generation×sex combination should obviously equal 0·5. Secondly, contributions of CA with a single progeny in the list of CAs were constrained to be equal to 0·5 contributions of respective progeny: in our simulations, because these CAs were always found to be the ACAs. Detailed algorithms can be found in Appendix D.
3. Results
Table 1 shows the results obtained in generation 15 for BLUP and optimized schemes. Coancestry coefficients were similar in both schemes as expected, 27·5 and 27·6%, respectively. Genetic gain (average of true breeding values) was 39% higher (8·8 vs 6·3) in the optimized breeding scheme in comparison to BLUP. In both schemes, the number of proximal ancestors of the last generation was substantially lower than the number of ancestors given by the conventional approach, by about 42%. As expected, ancestors found by the proximal approach were also younger (by about 1 generation). Estimated genetic gains were directly obtained based on the EBV for the selected trait. They were 6·28 for BLUP schemes and 8·82 for optimized schemes, i.e., very close to the true genetic gains. Maximum estimated genetic gains obtained by optimizing in retrospect based on conventional contributions were 7·61 (+21%) for BLUP and 9·21 (+5%) for optimized. Using the proximal approach would have yielded 7·79 (+24%) for BLUP and 9·02 (+2%) for optimized. Results given by both approaches were similar. The optimal genetic gain obtained in retrospect was far from the gain exhibited by permanent optimization, thus illustrating the impact of drift and the loss of valuable ancestors before the optimization in retrospect.
Table A1. Implementation of the tabular algorithm to decompose the average inbreeding of individuals 9 and 10 of the example pedigree
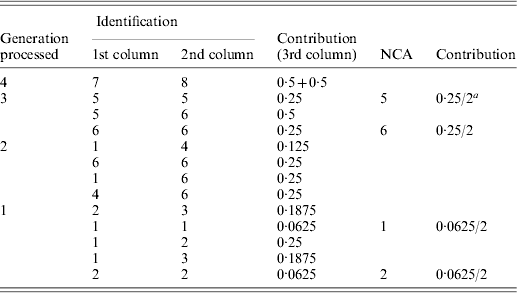
a2 is the number of individuals in the group considered.
Table 1. Results of simulations (generation 15)
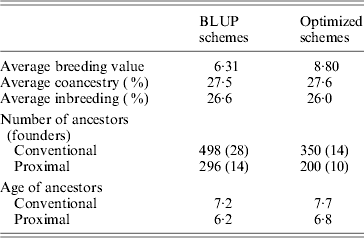
Intermediate schemes showed an interesting pattern. At the generation corresponding to the switch, a lift was observed (approximately doubling the instantaneous genetic gain) and, afterwards, rates of gain were quite similar to those of the optimized schemes. The estimated genetic gains for these four schemes (very close to the true genetic gains), of increasing efficiency, were 6·7, 7·1, 7·7 and 8·3. Corresponding maximal genetic gains were 7·7 (+14%), 7·9 (+12%), 8·3 (+9%) and 8·7 (+5%) according to the conventional decomposition and 7·7 (+14%), 7·9 (+12%), 8·2 (+8%) and 8·6 (+4%) according to the proximal decomposition. Once again, both decompositions gave similar results. The overall comparison of the six schemes confirmed that the efficiency of a breeding programme can be safely assessed by the discrepancy between the estimated genetic gain and the one of back optimization: when efficiency increased, discrepancy decreased.
4. Conclusion
Wright's (Reference Wright1922) method for decomposing inbreeding and coancestry could be linked exactly with the conventional approach summarized by Caballero & Toro (Reference Caballero and Toro2000). Wright's decomposition led exactly to the well-established conventional decomposition. Analytical calculations were relatively straightforward. However, Wright's coalescence approach yielded fewer and younger ancestors, and hence was called a ‘proximal’ approach. If the same information was given by a smaller number of ancestors, then this meant that information given by the absorbed ancestors was totally dependent on the information given by the remaining ancestors, as a special consequence of drift. In the general situation, involving overlapping generations, identification of absorbed ancestors required the full analytical calculations presented above. Prediction of status (ACA vs NCA) by simple methods would be highly desirable for understanding the mechanisms involved and also to skip useless calculations. However, early attempts failed and further research is needed in this area.
Simulation showed that the discrepancy between both approaches in terms of number of ancestors could be substantial. Inbreeding and coancestry could be explained parsimoniously by fewer ancestors capturing the whole information due to genetic drift. For selected populations, contributions of ancestors to genetic gains should be considered too. Simulation on discrete generations showed that evaluation of the past efficiency of breeding schemes through back-optimization was quite similar using both decompositions. However, in the context of discrete generations, constraints occurring on conventional contributions could be identified clearly. For overlapping generations, in contrast, the proximal approach might be more robust in such a situation. Research is needed in this area.
Appendix A. Tabular implementation of Wright's method
The basic formula for computing inbreeding coefficients, which is based on computation of contributions of genes of NCAs, is:

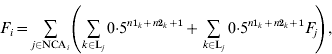
where F i and F j are inbreeding coefficients of individuals i and j, respectively, NCAi is a set of identification numbers of NCAs of individual i, and Lj is a set of inbreeding loops for NCA j of individual i; n1k and n2k are the number of generations from sire and dam of individual i, respectively, to NCA j in loop k. The first term is the contribution of genes of individual j regardless of its inbreeding and the second term is the contribution of genes of NCAs of individual j to inbreeding of individual i. Inbreeding coefficients of the NCA can be expressed in the same way and therefore (A1) can be expanded recursively. After expansion, each term would be the contribution of genes of the corresponding NCA (regardless of its inbreeding) to the inbreeding of individual i.
As an example, take the pedigree of individual 10 (Fig. 1). There are three NCAs for individual 10, namely 5, 6 and 2. From these three, only individual 5 is inbred. So, in addition, we need to consider individual 1, who is the only NCA of individual 5. The NCAs 1, 2, 5 and 6 contribute 0·03125, 0·03125, 0·125 and 0·125 to the inbreeding coefficient of individual 10 (F10=0·3125). Contributions of individuals 1 and 2 are marginal.
The same results as those by Wright's method can be recovered by using an upward exploration method, faster but still storage-demanding. The method is tabular and adapted to partition ![]() or
or ![]() for a specified group of individuals. The outline of the algorithm is as follows:The identifications (ID) should be consecutive integers and parents precede progeny.
for a specified group of individuals. The outline of the algorithm is as follows:The identifications (ID) should be consecutive integers and parents precede progeny.
1. Define a table of three columns and initialize all elements to 0.
2. Set the first and the second columns for the m first rows to the ID of two parents of m individuals in question. Add the minimum ID in the first column.
3. Set the third column of the m rows to 0·5.
4. Process from the largest generation to 0.
For overlapping generations, consider pseudo-generations.
(i) For the 1st and 2nd columns, in turn, expand the table by adding two parents of individuals belonging to the current generation to the end of table while duplicating the corresponding ID in other column and adding half of the corresponding contribution to the 3rd column. Always place the minimum ID in the 1st column and avoid repeated rows by summing their contributions.
(ii) If IDs in the 1st and the 2nd columns are identical, then this is a NCA; therefore add its ID and contribution to the result table.
The resulting table will contain the ID and contribution of NCAs to the inbreeding of the individuals of interest. Table A1 shows the steps of the tabular algorithm applied to the example pedigree for decomposing the average inbreeding of individuals 9 and 10.
Appendix B. Detailed proof that m-decomposition can be recovered from w-decomposition
We partition one occurrence of inbreeding through individual i at locus k into link probabilities with inbred states of ancestors, given that the polygenic neutral trait involves L unlinked loci.
Transform the probability problems into problems of genetic variance decomposition. Sire of individual i is s i and its dam is d i with genetic values at locus k equal to ![]() and
and ![]() , respectively. Genetic and gametic variances at locus k are 1/L and 0·5/L, respectively. A gene sampled from the sire has an expected genetic value of
, respectively. Genetic and gametic variances at locus k are 1/L and 0·5/L, respectively. A gene sampled from the sire has an expected genetic value of ![]() and of sampling variance equal to
and of sampling variance equal to ![]() .
.
Then, conditioning on inbreeding occurring, the same gene from the sire is sampled twice so that the expectation of the sum of the genetic values is ![]() and its sampling variance is equal to
and its sampling variance is equal to ![]() . Because overall variance of the sum of the genetic values corresponding to these genes is equal to 2/L, we have:
. Because overall variance of the sum of the genetic values corresponding to these genes is equal to 2/L, we have:
The same is true when the gene comes from the dam. When the same gene is sampled twice, the probability for paternal or maternal origin is 0·5. Then, the conditioned variance of the BV at locus k is equal to 2/L and to
If w i is the probability that the gene sampled twice comes from ancestor i, then participation of ancestor i to drift at locus k is
Summing over all independent loci, with the same probability of inbreeding, shows that the overall contribution of ancestor i to drift is equal to
and after division by 2, because relationship coefficient is twice coancestry coefficient, we have another expression of the contribution of ancestor i to the average coancestry, i.e.,
Appendix C. Removing the effect of self-contributions from vector m
Let ![]() be the average BV of the current population,
be the average BV of the current population, ![]() and
and ![]() the average BVs of sires and dams. Then,
the average BVs of sires and dams. Then, ![]() , where
, where ![]() is the average Mendelian sampling BV. Drift due to parents is equal to the variance of the parental mean, i.e., the average weighted relationship coefficient between parents, where weights are proportional to progeny size and sum to 0·5 per sex. If we express drift in terms of coancestry (f), then this value should be multiplied by 0·5. A direct adaptation of the m-decomposition for
is the average Mendelian sampling BV. Drift due to parents is equal to the variance of the parental mean, i.e., the average weighted relationship coefficient between parents, where weights are proportional to progeny size and sum to 0·5 per sex. If we express drift in terms of coancestry (f), then this value should be multiplied by 0·5. A direct adaptation of the m-decomposition for ![]() is possible but still complicates calculation.
is possible but still complicates calculation.
Then, an indirect approach is proposed that is much simpler, where the m-decomposition of ![]() is still carried out, but where the effect of
is still carried out, but where the effect of ![]() is easily removed. If
is easily removed. If ![]() is the average contribution of ancestor k and δk is his Mendelian sampling BV, then
is the average contribution of ancestor k and δk is his Mendelian sampling BV, then ![]() . Index k includes the N indices l corresponding to the current population. For these indices, the direct impact of l is through c l equal to 1/N for any l (self-contribution). Then,
. Index k includes the N indices l corresponding to the current population. For these indices, the direct impact of l is through c l equal to 1/N for any l (self-contribution). Then,
The new m-decomposition is the decomposition of ![]() for l, and the new value is
for l, and the new value is ![]() . Given that
. Given that ![]() , then
, then ![]() .
.
Appendix D. Back-optimization of contributions
(i) Conventional contributions
The average coancestry between parents of the last generation is constrained to be ϕ. This coancestry is equal to 0·5x′Dx, where x is the vector of contributions of CA and where D is the diagonal matrix involving their MSVs. The second constraint on the sums per sex×generation can be written as P′x=0·51, where P is the incidence matrix relating the ancestors to the combined factor sex×generation, and the third constraint on CAs with one progeny can be written as K′x=0. For simplicity, we do not indicate the sizes of matrices and vectors involved. Given these constraints, the objective is to maximize the estimated genetic gain, i.e., ![]() , where
, where ![]() is the vector of the estimated Mendelian deviations for the trait under selection. Then, the Lagrange function to optimize is
is the vector of the estimated Mendelian deviations for the trait under selection. Then, the Lagrange function to optimize is
The solution is ![]() . Constraint 3 leads one to find that
. Constraint 3 leads one to find that ![]() and then that,
and then that, ![]() , where
, where ![]() and
and ![]() . The solution for θ is
. The solution for θ is ![]() and the solution for λ is+square root of the ratio
and the solution for λ is+square root of the ratio ![]() , where
, where ![]() and
and ![]() .
.
(ii) Proximal contributions
The Lagrange function to optimize is ![]() , with only a single constraint because other constraints on the solutions cannot be established analytically in the proximal model. Solutions are
, with only a single constraint because other constraints on the solutions cannot be established analytically in the proximal model. Solutions are ![]() with
with ![]() and maximum genetic gain equals
and maximum genetic gain equals ![]() .
.





