Phenotypic and genetic variations and correlations in multitrait developmental instability: a multivariate Bayesian model applied to Speckled Wood butterfly (Pararge aegeria) wing measurements

Summary

Phenotypic and genetic variation and covariation in developmental instability (DI) have been the subject of many debates. In this paper we develop and apply a statistical model in a Bayesian context to analyse different traits simultaneously in a multivariate model of DI. We apply the model to measurements of yellow spots on the front wing of the Speckled Wood butterfly (Pararge aegeria L.) in a full-sib breeding experiment. We estimated the posterior distribution of the broad-sense heritability of DI averaged across the five yellow spots, which had a median of 0·19 and a 95% credibility interval ranging between 0·04 and 0·64. Phenotypic and genetic correlations in DI could not be estimated accurately with the present sample size. Yellow spots 4 and 5 appeared to show some degree of developmental integration. The importance of this model and its possible extensions are discussed.

1. Introduction

The evolutionary potential of developmental instability (DI: the sensitivity of a developmental system to resist random perturbations during development; Klingenberg, 2003) and the extent to which DI is a property of an individual remain controversial topics (for a recent review see e.g. Van Dongen, 2006). In addition, its relationship to environmental stress remains equivocal. The phenotypic outcome of DI is that a trait's developmental pathway deviates from its expected trajectory – given the individual's genotype and prevailing environmental conditions – resulting in within-individual morphological variation. The most commonly used phenotypic measure of DI is random deviations from perfect symmetry in bilateral traits, the so-called fluctuating asymmetry (FA). The basic idea behind the use of FA as a measure of DI is that the two sides of bilaterally symmetrical organisms are controlled by the same genes and probably develop under identical environmental conditions. They therefore have the same expectation in the absence of DI (Klingenberg, 2003; Van Dongen, 2006). Any deviation from perfect symmetry is assumed to be the result of the inability of the developing system to buffer itself against random perturbations. In statistical analyses and theoretical work, the left and right trait values of each individual are often represented as two independent normal distributions with equal means on both sides, and variances reflecting individual specific levels of DI. FA, the difference between left and right, consequently follows a normal distribution with zero mean and variance equal to 2×DI (Whitlock, 1996). Although the validity of this normal assumption has been challenged repeatedly (e.g. Houle, 2000; Graham et al., 2003), there is evidence that it is a ‘reasonable approximation’ of reality (Van Dongen et al., 2005; Van Dongen & Møller, 2007).

For decades, the genetic basis of DI received considerable attention in the literature because FA and DI may reflect individual or population-level quality and health. Yet the evidence for heritable variation is scant and there is a growing awareness that the estimation of the heritability of DI (h ²_DI) is extremely challenging from an experimental point of view (Fuller & Houle, 2003; Leamy & Klingenberg, 2005; Van Dongen, 2006, 2007). Indeed, Van Dongen (2007) recently concluded that none of the existing studies estimating h ²_DI have been adequately designed. Furthermore, most estimates of h ²_DI have been obtained under optimal breeding conditions, while the highest values can be expected to emerge under stress, when indiviuals of low (genetic) quality are unmasked (Van Dongen, 2006). The main problem when analysing DI at the individual level is that the phenotypically observable degree of asymmetry correlates only poorly with the underlying process of interest (i.e. DI) (e.g. Whitlock, 1996, 1998; Houle, 2000; Van Dongen, 2006, 2007). This is because individual FA estimates a variance (i.e. DI) with only two data points. As a consequence very large sample sizes are needed in order to obtain accurate estimates of the heritability of DI and between-trait correlations. This problem can be circumvented to some extent by studying traits that develop more than twice within individuals, such as floral traits and leaves (e.g. Pelabon et al., 2004), yet are restricted to a limited set of species such as plants and clonal organisms. More accurate estimates of h ²_DI might be obtained by studying different traits in bilaterally symmetrical organisms simultaneously, and integrating that information into average heritabilities. At present, however, it is not clear how to interpret information integrated across traits biologically, because little is known about the relationship of levels of DI among traits. To overcome this problem, more research is required into phenotypic and genetic correlations in DI and how consistent associations with stress and fitness are among traits. Here we present a general Bayesian statistical framework to model phenotypic and genetic variation and covariation of DI in different traits to help fill this gap. It is, to our knowledge, the first multivariate model of DI.

Bayesian statistics are becoming increasingly popular for analysing complex models and have been shown to conveniently reflect uncertainty of parameters in the form of posterior distributions. These posteriors integrate all sources of error and can be viewed to provide an ‘honest’ way to express the amount of information available about model parameters. Recently, Bayesian statistical models were introduced in the area of FA and DI, thereby treating individual DI as a latent variable, where uncertainties due to measurement error, directional asymmetry and the weak associations between the observable levels of FA and the unobservable DI are adequately taken into account (e.g. Van Dongen, 2001, 2007; Van Dongen et al., 2005). Here we present a multivariate Bayesian model of DI to estimate genetic and phenotypic variations and covariations in DI of different traits. It can be applied to estimate genetic parameters, to compare levels of DI among samples, and to study associations between DI and other covariates. We apply this model to a full-sib breeding experiment with the Speckled Wood butterfly (Pararge aegeria), estimating broad-sense heritabilities (correcting for common environment effects and measurement error), genetic correlations in DI and comparing levels of DI among traits. Characteristics – yellow spot surface areas – of the front wing are studied because of their high degree of functional and presumed developmental integration, such that the integration of information on the genetic parameters of the different traits may be biologically relevant. Extensions of this model to more complex ANOVA designs, such as nested half-sib experiments which yield unbiased estimates of the narrow-sense heritability, are straightforward (see e.g. Van Dongen, 2007 for such a model in the univariate case for single-trait analyses). It is important to note here that the main objective of this paper is to develop the general statistical framework rather than to study the evolutionary potential of DI in detail. Limitations of the explored dataset and design considerations will be discussed.

2. Materials and methods

(i) Study species

The Speckled Wood is a common temperate-zone, satyrine butterfly. It has a pale to dark brown background colour on the dorsal surface of the wings with yellowish patches and a series of submarginal eyespots (Schwanwitsch, 1935; Fig. 1). Melanins are most plausibly the major pigments shaping this brown background colour (Talloen et al., 2004) and the development of this functionally integrated unit is expected to be developmentally integrated as well. Variation in the degree of presumed basal melanization of the dorsal surface of the wings has been shown to affect thermoregulation, as darker individuals heat up faster than pale brown ones (Van Dyck & Matthysen, 1998; Berwaerts et al., 2001). The yellowish patches and the submarginal eyespots are thought to be relevant to crypsis and antipredation when basking on the forest floor or vegetation or when flying (Van Dyck et al., 1998). The wing colour has been shown to be a phenotypically plastic trait (Nylin et al., 1995). Environmental variation in photoperiod and temperature can induce different developmental pathways that result in different morphologies (including different degrees of presumed melanization), which has been interpreted as adaptive seasonal plasticity. Environmental variation in host-plant drought stress causes resource constraints that in turn affect wing size and coloration (Talloen et al., 2004).

Fig. 1. Pararge aegeria right front wing indicating the five yellow spots on the dorsal side used in this study.

(ii) Experimental set-up

Full details on the experimental set-up are given in Talloen et al. (2004). Briefly, 52 field-inseminated female butterflies were collected, and their offspring were used as the parental generation to generate a second generation whereby brother–sister and multiple matings were ruled out. Second-generation offspring were used for the experiment. As the parental generation of the experimental individuals experienced identical ambient conditions in the laboratory, possible confounding parental effects on offspring development (e.g. age, nutritional condition) were minimized.

The breeding experiment consisted of a control and two drought-stress treatments imposed on the host plant Poa annua. Plants were sown on a standard sand substrate in plastic jars (18×18 cm) covered with white gauze held in place with a rubber band. Jars were randomly assigned to one of three treatments differing in water supply: host plants of the control group had full access to water, whereas the intermediate and extreme drought-stressed host plants had been deprived of water for 20 or 40 days, respectively, before first instar caterpillars from the breeding programme were transferred. Drought stress of the host plant affected its nutritional value, as leaf nitrogen, carbon and water concentrations decreased with increasing drought stress (Talloen et al., 2004). Host plant drought stress increased larval mortality and development time, and decreased the size and presumed melanization of the butterfly wings (Talloen et al., 2004). Two days after egg hatching, 581 full-sibling first instar larvae of 35 families were randomly divided over the three treatments, with three larvae reared per jar. As drought stress was expected to induce increased mortality, 163, 173 and 245 larvae were assigned to the control, intermediate and extreme drought stress treatment, respectively. All larvae exposed to different treatments were raised within the same climate room (temperature day/night: 21°C/8°C; photoperiod: LD 18:6 h). After pupation, pupae were transferred to small cups and checked twice a day for emergence. When emerged, adult butterflies were killed by freezing and stored at −18°C; hence wing wear caused by long periods of flight in small cages was avoided. In the analyses below, data from the three treatments were pooled to avoid numerical problems when estimating the posteriors for the complex model developed below. Morphological comparisons with the parental generation suggested that even the control group experienced stressful conditions during development (W. Talloen, unpublished results). This is therefore one of the few studies to estimate genetic variation in DI under stress.

(iii) Measurements

Frozen butterflies were placed in an incubator and dried to constant mass at 60°C for 24 h, after which wings were carefully removed from the thorax. All traits were measured with an Olympus 3030 digital camera connected to a Pentium PC with OPTIMAS 6.1 software. All colour measurements were taken under controlled light conditions (cold light source Leica CLS 50) on a standard green background. Area of the wing and of the 5 yellow wing spots were measured using a semi-automated procedure, such that measurement error could only be due to low resolution or variation in calibration and/or photographic conditions. A small subsample was remeasured with a second series of photographs so that measurement error could be taken into account in the analyses described below.

(iv) Bayesian model

The posterior distribution [p(θ|y)] in any Bayesian analysis is proportional to the product of the likelihood of the statistical model [p(y|θ)] and the prior distributions of the model parameters [p(θ)]. Any Bayesian analysis requires minimally four steps. First a statistical model is set up, then prior distributions are determined for each of the model parameters, after which the posterior distributions are estimated. Posteriors then need to be represented by summary statistics (Gelman et al., 1995). Next to the fact that Bayesian analyses allow the incorporation of prior knowledge, an important difference with likelihood methods is that the distribution of the model parameters θ is obtained conditional on the data. Thus, the posterior reflects what we know about the model parameters after the data were collected, while the prior reflects what we knew beforehand. The analytical evaluation of posterior distributions is often complex. Yet, Monte Carlo Markov Chain (MCMC) sampling methods allow the approximation of the posteriors in a wealth of situations, resulting in the recent application of Bayesian methods in many different areas of research (e.g. Congdon, 2003).

In the model developed and applied here, phenotypic variation and covariation in five yellow spots for a total of 387 offspring (N _tot=387) from 35 full-sib families (N _fam=35) raised in a total of 172 jars (N _jar=172) will be partitioned over different hierarchical levels. Each side of the bilaterally symmetrical traits was measured independently, while the wings of a subset of 18 individuals were measured twice from independent photographs, to allow modelling measurement error (ME). Assuming that ME is normally distributed with variance σ²_ME,t (i.e. a different degree of ME for each trait is assumed), the rth measurement (r=1…2) on side k (k=1, 2 for left and right sides, respectively) on trait t (t=1…5) of offspring i (i=1…N _tot) in jar j (j=1…N _jar) from family f (f=1…N _fam) can be represented as:

(1)

where

(2)

This model is closely related to the mixed regression model introduced by Van Dongen et al. (1999) in the area of asymmetry research and has been applied in a Bayesian context before (e.g. Van Dongen 2001; Van Dongen et al., 2005). In this model, β₀[t] reflects the overall intercepts estimating the average trait size for the five yellow spots respectively (t=1…5). The β₁[t] estimates the degrees of directional asymmetry (where side[1]=−0·5 and side[2]=0·5 for left and right respectively). Specifically for this dataset, between-sex differences in spot size (β_sex) were modelled and total wing area was added a covariate (β_area). Between-individual variation and covariation in trait size is modelled as a multivariate random effect where ind_size[f, j, i, t]∼N ₅(0, Σ₁). The true underlying level of FA is assumed to be a sample from a normal distribution with zero mean and variance equal to the individual- and trait-specific level of DI as follows:

(3)

where DI _ind.[f, j, i][t] represents the tth element of the vector DI _ind.[f, j, i], containing the five individual-specific levels of DI for the five yellow spots respectively. Variation in DI of the five yellow spots is treated as being family-, jar- and individual-specific in a hierarchically multivariate way on a log scale:

(4)

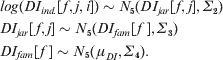
The overall average level of the natural logarithm of DI is represented by the vector μ_DI of length 5. The variance–covariance matrices Σ₂, Σ₃ and Σ₄ reflect (co) variation in log(DI) among individuals (nested within jars and family), jars (nested within families) and families, respectively. Between-individual variation in DI on the original scale can be represented as the coefficient of variation of the DI[f, j, i] values. We model variation in DI on the log scale as suggested by Fuller & Houle (2003), assuming that genetic effects occurred at this scale. The heritability of DI for each of the five yellow spots (h ² _DI[t]) can be obtained from the model parameters as . By evaluating h ²_DI[t] during each iteration in the MCMC, its posterior is obtained integrating the uncertainty in the estimation of the variance components. In addition, the mean heritability across yellow spots is also evaluated during the MCMC simulations.

As priors we used normal distributions with zero mean and variance equal to 1 million for β₀[t], β₁[t], β_area[t], β_sex[t] and μ_DI[t]. For all variance components we used a uniform distribution bounded between 0 and 1000 at the level of the standard deviation. For the variance–covariance matrices, an inverse wishart with 6 degrees of freedom was used. Posterior distributions were determined using MCMC techniques in OPENBUGS, called from R software using the BRugs package (version 0.2-6) (available free at http://cran.r-project.org/). We ran five independent MCMCs of 15 000 iterations each. The first 4000 were discarded, so that posterior distributions were based on 55 000 iterations. Visual inspection of the MCMCs and the use of Gelman and Rubin's shrink factor revealed slow mixing, yet no convergence problems in using this many iterations (Cowles & Carlin, 1996). The bugs code, a sample dataset and annotated output will be made available at the author's web page at http://www.ua.ac.be/stefan.vandongen.

3. Results

Spot numbers 3 and 4 appeared the largest and number 1 the smallest. Spot size increased with total wing area for spots 2 and 3, while for the three others there was little evidence for such a relationship. Yellow spots 1 and 3 showed a directional component where the spot on the right wing was significantly larger. Females had on average larger yellow spots than males, and this difference appeared to be larger towards the posterior part of the front wing (Table 1).

Table 1. Summary of posterior distributions of average spot size (for females) (β₀), directional asymmetry (DA: right minus left) (β₁), sexual dimorphism (male minus female) (β_sex) and the association of spot area with wing area (β_area)

Yellow spots 3 and 4 appeared to be measured with a lower accuracy (σ²_ME) relative to the others. Average degrees of DI (i.e. averages of DI _ind) appeared to be the lowest for yellow spots 1 and 3 (Fig. 2). Degrees of measurement error relative to the average degrees of DI, however, were highest for spots 1 and 3. In both cases the degree of ME was in the order of magnitude of the levels of DI. For spots 2, 4 and 5 levels of DI were 2 to 10 times higher than ME (Fig. 2). The degree of between-individual variation in DI was high (above 100% for each spot), yet was estimated with very low accuracy since the 95% credibility intervals were very wide (Fig. 2). Broad-sense heritabilities of DI of the yellow spots showed very wide posterior distributions for each spot except number 2 (medians and 95% credibility intervals: spot 1, 0·13 (0·01–1·18); spot 2, 0·03 (0·00–0·17); spot 3, 0·30 (0·02–1·71); spot 4, 0·09 (0·01–0·80); spot 5, 0·14 (0·03–0·72); Fig. 3). The mean heritability across the five yellow spots showed a median posterior of 0·19 with a 95% credibility interval ranging between 0·04 and 0·64 (Fig. 4). Applying a (traditionally applied) likelihood approach at the level of the unsigned FA (corrected for wing area), estimates of the broad-sense heritability equalled zero for all spots except number 1, where the estimate equalled 0·05. The latter was not statistically significant (χ²₁=1·2, P=0·14).

Fig. 2. Medians and 95% credibility intervals for the coefficients of variaton in developmental instability (top), mean levels of DI (middle) and degrees of measurement error (bottom) for the five yellow spots of the front wing of the Speckled Wood butterfly.

Fig. 3. Posterior distributions for the broad-sense heritabilities of developmental instability for the five yellow spots.

Fig. 4. Posterior distribution for the mean of the broad-sense heritabilities of developmental instability across the five yellow spots.

Phenotypic correlations in the average sizes of the yellow spots across sides (corrected for wing surface area) (Σ₁) were high and highest between spots 4 and 5 (Table 2). The medians of the posterior distributions of correlations in DI at the individual level (Σ₂) were very high as well, yet 95% credibility intervals were very wide, all including zero except for the correlation in DI between spots 4 and 5 (Table 2), in support of a shared DI, at least for these two spots. Correlations in individual DI among traits can result from two processes. On the one hand, DI may be a property of the individual, while on the other hand, developing traits may share common processes and their developmental errors such that they are developmentally integrated. The former results in phenotypic correlations in the unsigned FA only, while the latter produces correlations in the signed FA as well. This model does not allow separation between these two processes. Exploration of the correlations in the signed and unsigned asymmetry for the five yellow spots was therefore required and revealed that the correlations in the signed FA for spots 4 and 5 were highest (Fig. 5) and highly significant (P<0·001). Correlations in the unsigned FA were much weaker and only statistically significant for spots 3 and 4 and spots 4 and 5, respectively. None remained significant after correction for multiple testing (Fig. 6). Thus, the correlations in DI between spots 4 and 5 are more likely to be the result of developmental integration.

Fig. 5. Scatterplots of the signed asymmetries among the five yellow spots.

Fig. 6. Scatterplots of the unsigned asymmetries (i.e. absolute value of signed asymmetry) among the five yellow spots.

Table 2. Matrices of correlations among the five yellow spots. Top matrix: trait size (above diagonal) and developmental instability (below diagonal); the bottom matrix: response of DI to jar effects (above diagonal) and genetic correlations in DI (below diagonal)

Variation in DI among jars (diagonal elements of Σ₃) was generally low with very wide credibility intervals (Table 3). Correlations in the response of DI to the tray effect (Σ₃) and the genetic correlations (Σ₄) were relatively small and showed 95% credibility intervals nearly spanning the whole range of possible values (Table 2). This indicates that the current dataset contains no information to estimate correlations at these two levels of the analysis.

Table 3. Summary of posterior distributions of variation in developmental instability among jars

4. Discussion

Although of interest in ecology and evolutionary biology, the genetic basis of developmental instability remains poorly understood (Fuller & Houle, 2003; Leamy & Klingenberg, 2005; Van Dongen, 2006, 2007). Genetic variation and covariation of trait size, variation and developmental instability have been important topics in evolutionary biology research. More recently, the study of different parts of a morphologically and/or functionally integrated trait have shown very exciting promise in unravelling the importance of development and the existence of developmental modules in the evolution of complex traits. Butterfly wings and mandibles of small mammals have emerged as important model systems (e.g. Beldade & Brakefield, 2003; Badyaev & Foresman, 2005). While it has been proposed that canalization, developmental instability and morphological integration are the three main components of variability, it is at present unclear what role, if any, developmental instability could play in these processes. Crucial to our understanding is the amount of genetic variation and covariation of DI, of which little is known, mainly because the phenotypic outcome of DI, namely FA, only weakly reflects its underlying process (e.g. Van Dongen, 2006). Combining data from different traits measured within individuals could provide more robust results, and the model developed here can achieve this.

This paper supports a weak level of (broad-sense) heritability of developmental instability. Combining information from 5 traits in a multivariate model, and treating DI as a latent variable takes all sources of error and uncertainty into account and provides estimates of the available information on the parameters of interest. Analyses for both DI and unsigned FA of the individual yellow spots yielded very broad posteriors and non-significant heritabilities, respectively. Nevertheless, although the method provides more narrow posterior distributions and thus more information on the heritability of DI, it is important to note that the biological interpretation of such average heritabilities remains difficult. It is at present unclear to what extent levels of DI are related among traits, except for those which appear developmentally integrated. This is also highlighted in our analyses, where posterior distributions of genetic and phenotypic correlations in DI among yellow spots were generally very wide. In conclusion, we have developed a statistical model for gaining greater insight into the (genetic) variation and covariation of DI in a multivariate framework. It is widely applicable to both ecological and evolutionary applications. Our analyses of yellow spots in the Speckled Wood butterfly indicate that combining information from different traits provides more accurate heritability estimates. Similarly, comparisons of levels of DI may be done more accurately by combining measurements from different traits. However, the biological interpretation of such average estimates remains somewhat ambiguous. Further research into the phenotypic and genetic correlations in DI is required to evaluate the usefulness of integrating across different traits. However, the analyses here show that the latter requires very high sample sizes.