Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-28T00:31:40.649Z Has data issue: false hasContentIssue false
  • English
  • Français

On the maximum avoidance of inbreeding*

Published online by Cambridge University Press:  14 April 2009

Motoo Kimura  and
James F. Crow
Motoo Kimura
Affiliation:
University of Wisconsin, Madison, Wisconsin, U.S.A.
James F. Crow
Affiliation:
University of Wisconsin, Madison, Wisconsin, U.S.A.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Mating systems in which the least related individuals are mated have been designated by Wright as having maximum avoidance of inbreeding. For such systems the initial rate of decrease in heterozygosity is minimum. However, some other systems have a lower rate of decrease in later generations.

Circular mating, in which each individual is mated with the one to his right and to his left, leads to an asymptotic rate of decrease in heterozygosity of 1– λ ˜ π2/(2N + 4)2 compared with 1/4N for maximum avoidance systems. Circular pair mating, in which for example each male progeny is moved one cage to the right, leads to 1– λ ~ π2/(N + 12)2. Other similar systems are discussed.

For minimum gene frequency drift, a mating system should have a constant number of progeny per parent and the population should be broken up as rapidly as possible into the maximum number of lines. The gene frequency variance at generation T within a line is

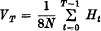
where N is the number in the line and Ht is the proportion of heterozygotes in generation t. Although the three mating systems, circular, circular pair, and maximum avoidance (and many others) have the same amount of random drift ultimately, at any generation circular mating has the smallest drift variance, VT, and circular pair next smallest.

Type
Research Article
Information
Genetics Research , Volume 4 , Issue 3 , November 1963 , pp. 399 - 415
Copyright
Copyright © Cambridge University Press 1963

References

REFERENCES

Falconer, D. S. (1960). Introduction to Quantitative Genetics. ix + 365 pp. New York: The Ronald Press.Google Scholar
Kimura, M. & Crow, J. F. (1963). The measurement of effective population number. Evolution (in press).CrossRefGoogle Scholar
Rutherford, D. E. (1952). Some continuant determinants arising in physics and chemistry. Proc. roy. Soc. Edinb. A, 63, 232–241.Google Scholar
Weight, S. (1921). Systems of mating. Genetics, 6, 111–178.Google Scholar
Wright, S. (1931). Evolution in mendelian populations. Genetics, 16, 97–159.CrossRefGoogle ScholarPubMed
Wright, S. (1951). The genetical structure of populations. Ann. Eugen. 15, 323–354.CrossRefGoogle ScholarPubMed