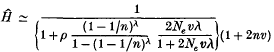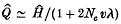Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Chapman, Robert W.
Stephens, J. Claiborne
Lansman, Robert A.
and
Avise, John C.
1982.
Models of mitochondrial DNA transmission genetics and evolution in higher eucaryotes.
Genetical Research,
Vol. 40,
Issue. 1,
p.
41.
Takahata, Naoyuki
1982.
Linkage disequilibrium, genetic distance and evolutionary distance under a general model of linked genes or a part of the genome.
Genetical Research,
Vol. 39,
Issue. 1,
p.
63.
Takahata, Naoyuki
1983.
Linkage disequilibrium of extranuclear genes under neutral mutations and random genetic drift.
Theoretical Population Biology,
Vol. 24,
Issue. 1,
p.
1.
Takahata, N.
and
Slatkin, M.
1983.
Evolutionary dynamics of extranuclear genes.
Genetical Research,
Vol. 42,
Issue. 3,
p.
257.
Takahata, Naoyuki
1983.
Population genetics of extranuclear genomes under the neutral mutation hypothesis.
Genetical Research,
Vol. 42,
Issue. 3,
p.
235.
Takahata, Naoyuki
1984.
A model of extranuclear genomes and the substitution rate under within-generation selection.
Genetical Research,
Vol. 44,
Issue. 1,
p.
109.
Solignac, Michel
Génermont, Jean
Monnerot, Monique
and
Mounolou, Jean-Claude
1984.
Genetics of mitochondria in Drosophila: mtDNA inheritance in heteroplasmic strains of D. mauritiana.
Molecular and General Genetics MGG,
Vol. 197,
Issue. 2,
p.
183.
Uyenoyama, Marcy K.
1985.
Quantitative models of hybrid dysgenesis: Rapid evolution under transposition, extrachromosomal inheritance, and fertility selection.
Theoretical Population Biology,
Vol. 27,
Issue. 2,
p.
176.
Takahata, Naoyuki
1985.
Introgression of extranuclear genomes in finite populations: nucleo-cytoplasmic incompatibility.
Genetical Research,
Vol. 45,
Issue. 2,
p.
179.
Clark, Andrew G.
1988.
DETERMINISTIC THEORY OF HETEROPLASMY.
Evolution,
Vol. 42,
Issue. 3,
p.
621.
Jiménez, J
Longo, E
and
Benítez, T
1988.
Induction of petite yeast mutants by membrane-active agents.
Applied and Environmental Microbiology,
Vol. 54,
Issue. 12,
p.
3126.
Ward, Robert D.
Billington, Neil
and
Hebert, Paul D. N.
1989.
Comparison of Allozyme and Mitochondrial DNA Variation in Populations of Walleye,Stizostedion vitreum.
Canadian Journal of Fisheries and Aquatic Sciences,
Vol. 46,
Issue. 12,
p.
2074.
1990.
Sex-biased mitochondrial DNA heteroplasmy in the marine musselMytilus.
Proceedings of the Royal Society of London. Series B: Biological Sciences,
Vol. 242,
Issue. 1305,
p.
149.
Brown, B. L.
and
Paynter, K. T.
1991.
Mitochondrial DNA analysis of native and selectively inbred Chesapeake Bay oysters,Crassostrea virginica.
Marine Biology,
Vol. 110,
Issue. 3,
p.
343.
Brown, Bonnie L.
and
Chapman, Robert W.
1991.
GENE FLOW AND MITOCHONDRIAL DNA VARIATION IN THE KILLIFISH,FUNDULUS HETEROCLITUS.
Evolution,
Vol. 45,
Issue. 5,
p.
1147.
Harris, Stephen A.
and
Ingram, Ruth
1991.
Chloroplast DNA and biosystematics: The effects of intraspecific diversity and plastid transmission.
TAXON,
Vol. 40,
Issue. 3,
p.
393.
Kondo, Rumi
Matsuura, Etsuko T.
and
Chigusa, Sadao I.
1992.
Further observation of paternal transmission ofDrosophilamitochondrial DNA by PCR selective amplification method.
Genetical Research,
Vol. 59,
Issue. 2,
p.
81.
Hastings, Ian M.
1992.
Population genetic aspects of deleterious cytoplasmic genomes and their effect on the evolution of sexual reproduction.
Genetical Research,
Vol. 59,
Issue. 3,
p.
215.
Zeviani, M.
1992.
Nucleus‐driven mutations of human mitochondrial DNA.
Journal of Inherited Metabolic Disease,
Vol. 15,
Issue. 4,
p.
456.
Meusel, Michael S.
and
Moritz, Robin F. A.
1993.
Transfer of paternal mitochondrial DNA during fertilization of honeybee (Apis mellifera L.) eggs.
Current Genetics,
Vol. 24,
Issue. 6,
p.
539.