Hostname: page-component-745bb68f8f-d8cs5 Total loading time: 0 Render date: 2025-01-12T12:05:16.576Z Has data issue: false hasContentIssue false
  • English
  • Français

Group selection and the ‘shifting balance’

Published online by Cambridge University Press:  14 April 2009

S. Rouhani  and
N. H. Barton
S. Rouhani
Affiliation:
Physics Department, Sharif University of Technology, and Institute for Studies in Theoretical Physics and Mathematics, Tehran, PO Box 11365-9161, Iran
N. H. Barton*
Affiliation:
Division of Biology, University of Edinburgh, King's Buildings, Edinburgh EH9 3JT, U.K.
*
*Corresponding author.
Rights & Permissions [Opens in a new window]

Summary

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We investigate the establishment and spread of new adaptive peaks within Wright's ‘shifting balance’. The third phase of the ‘shifting balance’ involves a kind of group selection, since demes in which a superior peak has been established contain more individuals, and so send out more migrants. We assume that population size, N, increases with mean fitness, , according to the exponential relation, 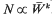. Here, k is a measure of the weakness of density-dependent regulation, and equals the inverse of the regression of log (fitness) on log(N). In the island model, we find that just as with soft selection (k = 0), two distinct types of behaviour exist: group selection makes no qualitative difference. With low numbers of migrants, demes fluctuate almost independently, and only one equilibrium exists. With large numbers of migrants, all the demes evolve towards the same adaptive peak, and so the whole population can move towards one or other of the peaks. Group selection can be understood in terms of an effective mean fitness function. Its main consequence is to increase the effect of selection relative to drift (Ns), and so increase the bias towards the fitter peak. However, this increased bias depends on the ratio between k and the deme size (k/N), and so is very small when density-dependence is reasonably strong.

Type
Research Article
Information
Genetics Research , Volume 61 , Issue 2 , April 1993 , pp. 127 - 135
Copyright
Copyright © Cambridge University Press 1993

References

Akin, E. (1979). The Geometry of Population Genetics. Lecture Notes in Biomathematics 31. Berlin: Springer-Verlag.Google Scholar
Barton, N. H. & Charlesworth, B. (1984). Genetic revolutions, founder effects and speciation. Annual Review of Ecology and Systematics 15, 133–164.Google Scholar
Barton, N. H. (1986). The effects of linkage and density-dependent regulation on gene flow. Heredity 57, 415–426.Google Scholar
Barton, N. H. (1992). On the spread of new gene combinations in the third phase of Wright's ‘shifting balance’. Evolution 46, 551–557.Google Scholar
Barton, N. H. & Hewitt, G. M. (1989). Adaptation, speciation and hybrid zones. Nature 341, 497–503.Google Scholar
Barton, N. H. & Rouhani, S. (1987). The frequency of peak shifts between alternative equilibria. Journal of Theoretical Biology 125, 397–418.Google Scholar
Barton, N. H. & Rouhani, S. (1993). Adaptation and the ‘shifting balance’. Genetical Research 61, 57–74.Google Scholar
Bengtsson, B. O. & Bodmer, W. F. (1976). The fitness of human translocation carriers. Annals of Human Genetics 40, 253–257.CrossRefGoogle ScholarPubMed
Christiansen, F. B. (1975). Hard and soft selection in a subdivided population. American Naturalist 109, 11–16.Google Scholar
Crow, J. F., Engels, W. R. & Denniston, C. (1989). Phase three of Wright's shifting balance theory. Evolution 44, 233–247.Google Scholar
Gardiner, C. W. (1983). Handbook of Stochastic Methods. Berlin: Springer-Verlag.Google Scholar
Kauffmann, S. & Levin, S. A. (1987). Towards a general theory of adaptive walks on a rugged landscape. Journal of Theoretical Biology 128, 11–46.CrossRefGoogle Scholar
Lande, R. (1976). Natural selection and random genetic drift in phenotypic evolution. Evolution 30, 314–334.Google Scholar
Lande, R. (1979). Effective deme size during long term evolution estimated from rates of chromosomal rearrangement. Evolution 33, 234–251.Google Scholar
Lande, R. (1985). The fixation of chromosomal rearrangements in a subdivided population with local extinction and colonization. Heredity 54, 323–332.Google Scholar
Nunney, L. (1985). Group selection, altruism, and structured-deme models. American Naturalist 126, 212–230.Google Scholar
Maynard, Smith J. (1964). Group selection and kin selection. Nature 201, 1145–1147.Google Scholar
Provine, W. (1986). Sewall Wright and Evolutionary Biology. University of Chicago Press, Chicago, Illinois.Google Scholar
Rouhani, S. & Barton, N. H. (1987). Speciation and the ‘shifting balance’ in a continuous population. Theoretical Population Biology 31, 465–492.Google Scholar
Wade, M. J. (1978). A critical review of the models of group selection. Quarterly Review of Biology 53, 101–114.CrossRefGoogle Scholar
Wade, M. J. & Goodnight, C. J. (1991). Wright's shifting balance theory -an experimental study. Science 253, 1015–1018.Google Scholar
Wright, S. (1931). Evolution in Mendelian populations. Genetics 16, 97–159.Google Scholar
Wright, S. (1932). The role of mutation, inbreeding crossbreeding and selection in evolution. Proceedings of the 6th International Congress of Genetics, 356–366.Google Scholar
Wright, S. (1941). The probability of fixation of reciprocal translocations. American Naturalist 75, 513–522.Google Scholar
Wright, S. (1949). Adaptation and selection. In Genetics, Paleontology, and Evolution (ed. Jepson, G.L., Simpson, G. G. and Mayr, E.), pp. 265–389. Princeton University Press.Google Scholar
Wright, S. (1977). Evolution and the Genetics of Populations. Vol. 3: Experimental Results and Evolutionary Deductions. University of Chicago Press.Google Scholar
Wright, S. (1988). Surfaces of selective value revisited. American Naturalist 131, 115–123.Google Scholar