Genome-wide interaction analysis of quantitative traits in outbred mice

Summary

With a large number of quantitative trait loci being identified in genome-wide association studies, researchers have become more interested in detecting interactions among genes or single nucleotide polymorphisms (SNPs). In this research, we carried out a two-stage model selection procedure to detect interacting gene pairs or SNP pairs associated with four important traits of outbred mice, including glucose, high-density lipoprotein cholesterol, diastolic blood pressure and triglyceride. In the first stage, a variance heterogeneity test was used to screen for candidate SNPs. In the second stage, the Lasso method and single pair analysis were used to select two-way interactions. Moreover, the shared Gene Ontology information about the selected interacting gene pairs was considered to study the interactions auxiliarily. Based on this method, we not only replicated the identification of important SNPs associated with each trait of outbred mice, but also found some SNP pairs and gene pairs with significant interaction effects on each trait. Simulation studies were also conducted to evaluate the performance of the two-stage method in different situations.

1. Introduction

There are various meanings for the term interaction, here it is defined as a joint SNP–SNP or gene–gene effect that can not be readily explained by their separate marginal effect (Kahn, 1983). As is known, interaction between genes or gene and environment is one of the main factors that contribute to a trait (i.e. disease). Many strategies and methods have been applied to genome-wide interaction studies (GWIS), such as regression, machine learning, Bayesian method and SNP filtering etc. (Mckinney et al., 2006; Zhang & Liu, 2007; Bai et al., 2012). Balancing computational load and statistical power, SNP filtering or screening that select candidate SNPs based on a priori information is a promising method for genome-wide data (Herold et al., 2009). Sources of the a priori information include statistical evidence (single marker association at a moderate level), genetic relevance (genomic location) and biologic relevance (SNP function class and pathway information).

Kooperberg & Leblanc (2008) proposed a two-stage analysis, in which they only test for interactions between SNPs that show some marginal effects. Some SNPs or genes may not show strong marginal associations when they affect disease risk through interactions with other SNPs or genes. As a result, these genes may not be identified by the single marker association screening method in GWIS. Considering both computational load and statistical power, Wu et al. (2009) conducted an exhaustive two-dimensional search in the first stage, which detected joint effects that may fail to emerge from single maker analysis, but may have an inflated type I error. Paré et al. (2010) demonstrated that, under plausible scenarios of genetic interaction, the variances of a quantitative trait are expected to differ among the three possible genotypes of a biallele SNP. Thus a variance heterogeneity test can be used to screen for potentially interacting SNPs. Then an exhaustive two-dimensional scan was conducted among the candidates identified in the first stage. Paré’s screening method has the advantage that the interacting covariants need not be known or measured for a SNP to be prioritized and independence between the two steps under the null hypothesis of no interaction can guarantee correct type I error.

In this study, we carried out genome-wide interaction association studies using 288 mice from a commercially available outbred stock with four traits and 44 428 SNPs (Zhang et al., 2012). The four traits including glucose (GLU), high-density lipoprotein cholesterol (HDL), diastolic blood pressure (DBP) and triglyceride (TG) are strongly associated with some complex diseases, such as diabetes, cardiovascular disease and adiposity. Detecting interacting SNP or gene pairs is of great significance for learning about the mechanisms of some complex diseases.

A two-stage model selection procedure was used to detect interacting SNP pairs or gene pairs for each trait. In the first stage, based on Paré’s idea, variance heterogeneity tests were used to screen for potentially interacting SNPs. As multiple genetic variants are expected to jointly affect a complex trait, the Lasso method (Tibshirani, 1996) and single pair analysis were both used to select significant interacting pairs among the candidates in the second stage. Several simulation scenarios were designed to evaluate the performance of the two-stage procedure, where Hardy-Weinberg equilibrium (HWE) and linkage equilibrium may be not satisfied.

2. Materials

The raw data set includes 288 NMRI mice with eight traits and 581 672 SNPs. Zhang et al. (2012) carried out some basic work on the data by excluding those SNPs whose HWE ${\chi ^2} \ge 20$ , minor allele frequencies <2% and missing values >40%, and collapsing identical SNPs within 2Mb intervals, resulting in a total of 44 428 unique SNPs in the final data.

These traits include systolic blood pressure (SBP), DBP, mean arterial pressure (MAP), GLU, TG, cholesterol (CHL), HDL and urinary albumin-to-creatinine ratio (ACR). All traits except ACR were approximately normally distributed. Since the lipid traits (HDL and CHL) and blood pressure traits (SBP, DBP and MAP) were highly correlated among themselves (r > 0·97), here we only report our analysis results of DBP, GLU, TG and HDL as representative of this group of traits.

3. Method

A two-stage method based on Paré’s idea is introduced in this section. In the first stage, equality of the conditional variances under three possible genotypes for each SNP is tested, which is equivalent to test interaction between this SNP and another covariant. Then the Lasso method and single pair analysis are both used to select SNP pairs among the candidates chosen before. The details of the two-stage approach are given in the following sections.

(i) Stage one: variance heterogeneity test

The objective of the first stage is to select SNPs that are likely to have interaction effects. In detail, if we want to test whether a SNP (G represents its genotype) has an interaction effect on a quantitative trait y with a covariant C (another SNP or environment factor), the follow linear model is considered:

$$y = {\beta _0} + {\beta _1}G + {\beta _2}C + {\beta _3}GC + \varepsilon \comma \;$$

then $Var\lpar y\vert G = g\rpar = {\lpar {\beta _2} + {\beta _3}g\rpar ^2}Var\lpar C\vert G = g\rpar + {\sigma ^2}$ . Under the assumption of independence between G and C, we further have:

$$Var\lpar y\vert G = g\rpar = {\lpar {\beta _2} + {\beta _3}g\rpar ^2}Var\lpar C\rpar + {\sigma ^2}.$$

It is clear that $Var\lpar y\vert G = 0\rpar = Var\lpar y\vert G =0\!\cdot\!5\rpar = Var\lpar y\vert G = 1\rpar $ if and only if ${\beta _3} = 0$ . Thus, testing the interaction effect between G and C is equivalent to testing the equality of the conditional variances (i.e. $\sigma _0^2 = \sigma _{0\cdot5}^2 = \sigma _1^2 $ , where $\sigma _i^2 = Var\lpar y\vert G = i\rpar $ ). The biggest character of this approach is that we do not need to know the covariant's information when judging whether one factor has an interaction effect with another covariant or not.

The Levene's test (Olkin et al., 1960) was applied to verify the equality of variances under different genotypes for each of 44 428 SNPs in the data set we considered. Suppose the sample size N can be divided into K subgroups and let ${N_i}$ denote the sample size of the ith group. The Levene's test statistic is defined as:

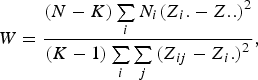$$W = \displaystyle{{\lpar N - K\rpar \sum\limits_i {{N_i}{{\lpar {Z_i}. - Z..\rpar }^2}} } \over {\lpar K - 1\rpar \sum\limits_i {\sum\limits_j {{{\lpar {Z_{ij}} - {Z_i.}\rpar }^2}} } }}\comma \;$$

where ${Z_{ij}} = \vert {Y_{ij}} - {Y_i.}\vert $ , and ${Y_{ij}}$ is the trait value for the jth individual of the ith group; Y _i . is the mean of the ith subgroup; Z _i . and Z.. are the subgroup mean and overall mean of Z _ij , respectively. Under the null hypothesis of variance homogeneity, the Levene's statistic follows a F distribution with K–1 and N–K degrees of freedom. In this paper we have K = 3 and N = 288.

(ii) Stage two: interaction test

The purpose of the second stage is to further identify interacting pairs among the candidate SNPs selected from the first stage. When building statistical models, the marginal association loci reported by Zhang et al. (2012) are included. Single pair scan and multiple marker analysis with the Lasso model are both used here. The details of the two linear models are as follows:

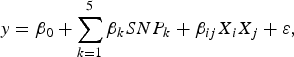(1) $$y = {\beta _0} + \sum\limits_{k = 1}^5 {{\beta _k}SN{P_k} + {\beta _{ij}}{X_i}{X_j} + \varepsilon \comma \; }$$

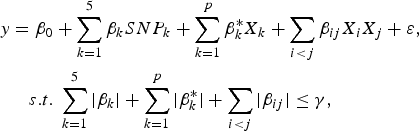(2) $$\eqalign{y & = {\beta _0} + \sum\limits_{k = 1}^5 {{\beta _k}SN{P_k} + \sum\limits_{k = 1}^p {\beta _k^\ast {X_k} + \sum\limits_{i \lt j} {{\beta _{ij}}{X_i}{X_j} + \varepsilon \comma \; } } } \cr & \quad s.t.\; \sum\limits_{k = 1}^5 {\vert {\beta _k}\vert + \sum\limits_{k = 1}^p {\vert \beta _k^\ast \vert + \sum\limits_{i \lt j} {\vert {\beta _{ij}}\vert } \le \gamma \comma \;}}}$$

where $SN{P_k}\comma \; \; 1 \le k \le 5$ represent the five main effect loci identified by Zhang et al. (2012), ${X_k}\comma \; \; 1 \le k \le p$ are genotypes of the SNPs selected in the first stage, X _i X _j is product of the candidate pair's genotype values and $\gamma \ge 0$ is a tuning parameter to be determined separately.

Although the single pair scan and multiple marker analysis may detect some different interacting SNP pairs in the second stage, we expect that the results from the analysis of the two strategies can supplement each other, since we do not want to miss any valuable interaction effect.

4. Results

(i) Results from stage one

In order to avoid filtering out interesting SNPs by the variance heterogeneity tests, a relaxed type I error or family wise error rate is allowed in stage one. In the real data analysis, significance level $\alpha = 0\!\cdot\!05$ was chosen for each SNP. Taking trait GLU as an example, there are 2487 SNPs showing significant variance heterogeneity (see the second line of Table 1).

Table 1. The number of selected SNPs and SNP pairs.

^a The number of significant SNPs in variance heterogeneity tests with significance level $\alpha = 0\!\cdot\!05$ .

^b The number of SNPs after collapsing those SNPs selected in the first stage with similar genotypes and close positions.

As some SNPs are very close in their locations on the chromosome, their genotypes are very similar among the 288 mice in the data set. For example, only three mouse genotypes are different on the three loci respectively located at 74104950bp, 74187929bp and 74201260bp on chromosome 1. In general, if one of them was significant in the variance heterogeneity test, then all would pass the first stage test. Therefore, the loci we picked up in the first stage would not be independent, and that would also increase the burden of multiple tests. So we combined those SNPs that were within 2Mb and gave the same genotype among more than 97·5% of the 288 mice. There are 779 SNPs left after reorganizing the 2487 SNPs for trait GLU (see the third line of Table 1). The allelic association between two SNP loci was used as a measure of linkage disequilibrium (LD). We observed a sharp decay in LD with increasing physical distance between the 779 SNPs on the same chromosome (see Fig. 1). The numbers of SNPs after reorganizing for each trait are listed in Table 1.

Fig. 1. LD plot for trait GLU. The allelic association between two SNP loci was used as a measure of LD. Each dot represents the LD value of a SNP pair on the same chromosome.

(ii) Results from stage two

(a) Single pair analysis based on model (1)

Taking trait GLU as an example, 779 SNPs were chosen from stage one and C ₇₉₉ ² SNP pairs were tested with model (1). After calculation, 199 SNP pairs among them have P-values smaller than 1E-4. The mean square error (MSE) reduction by including each interaction term in model (1) was also calculated, respectively. Tables S1–S4 in File 1 of the supplementary material give the annotations of SNP pairs with P-values <1E-4 and significant shared Gene Ontology (GO) information for the four traits. We listed some representative SNP pairs with validated interaction effects in model (1) for each trait in Table 2.

Table 2. The interacting information detected by the two-stage method via model (1).

^a P-value for model (1) containing five main effects loci and each single SNP pair.

^b N: Number of SNP pairs with P-value <5E-4 near the SNP pairs listed in each row.

^c The MSE reduction by including each interaction term in model (1).

^d -Epas1: The detected SNP is located within the intergenic region of a snRNA or miRNA and MGI gene Epas1.

(b) Multiple marker analysis based on model (2)

The goal of model (2) is to jointly select from the candidates. In total, 1784 variables were chosen as candidates for trait GLU, including five marginal association loci reported by Zhang et al. (2012), 779 unique SNPs selected in stage 1 and the top 1000 epistatic SNP pairs in model (1). Bayesian information criterion (Schwarz, 1978) was used as a criterion to choose the tuning parameter. The Lasso method generated 11 non-zero coefficients, including one marginal association locus on chromosome 5 reported before and ten interacting pairs (see Table 3). The total MSE has decreased by 26·4% compared with the previous main effect linear model. The most significant pair obtained by the single pair analysis was also selected by the Lasso method.

Table 3. SNP pairs selected by the two-stage method via Model (2).

^a The increased rate of MSE after deleting each pair from the final full model selected by the Lasso method.

For trait HDL, five terms were selected by the Lasso method, including two marginal association loci reported before and three interacting pairs (see Table 3). The total MSE has decreased by 15·9% compared with the main effect linear model. The first two SNP pairs in Table 3 for trait HDL are near the first two pairs based on model (1) listed in Table 2. The analysis results for traits DBP and TG can also be found in Table 3.

Comparing Table 2 with Table 3, we found that the single pair analysis may pick up many SNP pairs, but they are mostly nested within some narrow genomic regions. While in the joint analysis via the Lasso method, SNP pairs that have high correlation with those already included in the model are less likely to be added into the model again, which may help us to find more valuable regions. Furthermore, a final model that can well explain the variability of each trait can be found by the Lasso method.

The main reason that we considered two analysis strategies in the second stage is that the results obtained from the two strategies can supplement each other, i.e. the single pair analysis and the Lasso method also detected their own interacting SNP pairs as well as the common ones. We should not neglect any detected interacting SNP pairs, since the true model between the trait and the main and interaction effects of the SNPs is completely unknown.

5. Simulation studies

In this section, simulation studies are designed to investigate the effects of minor allele frequency (MAF), main effects, HWE and LD on the two-stage method we used in the real data analysis.

(i) Simulation design

We assumed that a quantitative trait (denoted Y) is affected by four causal SNPs, with two of them having main effects only (denoted X ₁ and X ₂) and two of them having interaction (denoted X ₃ and X ₄). Phenotype data were generated from the following linear model:

$$Y = {\beta _0} + \sum\limits_{k = 1}^4 {{\beta _k}{X_k}} + {\beta _{34}}{X_3}{X_4} + \varepsilon \comma \;$$

where $\varepsilon {\sim} N \lpar 0\comma \; {\sigma ^{2}} \rpar$ , ${\sigma ^2} = 10$ , ${\beta _0} = 3$ . The main effect of the ith SNP (denoted ${\beta _i}$ , i = 1,…,4) was chosen according to its heritability (denoted ${H_i}$ ), which means the proportion of the trait's variance is explained by the ith locus. As loci 1 and 2 do not have an interaction effect, we set ${H_1} = {H_2} = 10\% \; $ .

We considered four different situations of loci 3 and 4. For each scenario, 300 individuals were generated, which is similar to the previous real data set and the process was repeated 1000 times. If loci 3 and 4 both came through the variance heterogeneity test with a significant interaction effect in the linear model, we would conclude that an interacting pair has been discovered, and then the discovery rate among 1000 replications was calculated. Four different situations were considered, as discussed in the following sections.

(a) Situation 1: loci 3 and 4 are independent and have an interaction effect only (H ₃ = H ₄ = 0)

In this situation, ${\beta _3}$ and ${\beta _4}$ are set to zero and X _i can be encoded as -2q, 1-2q and 2-2q with probability ${p^2}$ , 2pq and ${q^2}$ , respectively, such that the mean genotypic value equals to zero. We can easily get:

$${H_i} = \displaystyle{{2pq\beta _i^2 } \over {Var\lpar Y\rpar }}\quad {\rm }i = 1\comma \; ...\comma \; 4\comma \; \quad \hbox{and}\quad H = \displaystyle{{4{\,p^2}{q^2}\beta _5^2 \over Var\lpar Y\rpar }}\comma \;$$

where $Var\lpar Y\rpar = 2pq\lpar \beta _1^2 + \beta _2^2 + \beta _3^2 + \beta _4^2 \rpar + 4{p^2}{q^2}\beta _5^2 + 10$ and H denotes the heritability of the interaction effect of loci 3 and 4.

For each MAF q, we respectively took H (%) = 10, 15, 20, 25, 30, 35, 50. For example, when q = 0·3, H = 10%, we can obtain β = 1·22, 1·22, 0, 0, 2·005, which satisfies the assumptions of heritabilities. As estimates of powers, the discovery rates among 1000 replications were presented in Table 4.

Table 4. The discovery rates of 1000 simulations in situation 1.

^a MAF.

^b The proportion of variance (heritability) explained by interaction effect of loci 3 and 4.

(b) Situation 2: loci 3 and 4 are independent and have main effects ( $\!{H_3} = {H_4} \ne 0$ )

In this situation, we investigate the influence of marginal effects of interacting factors on the power of the variance heterogeneity test. We fixed q at 0·3, because the effect of MAF has been studied in situation 1. For each H (%) (5, 7, 10, 15, 20), we respectively took H ₃ + H ₄ (%) = 10, 15, 20, 30, 40. The simulation results are listed in Table 5.

Table 5. The discovery rates of 1000 simulations with q = 0·3 in situation 2.

^a The total proportion of variance explained by the marginal effects of loci 3 and 4.

(c) Situation 3: loci 3 and 4 are independent and HWE is not satisfied for locus 3

Firstly, we define a measure of skew for HWE. Let A and a denote the two alleles of locus 3 with P(A) = p and P(a) = q. By fixing one of the three genotype probabilities, we can define skew coefficient of HWE according to the other two genotype probabilities. For example, Supposing P(Aa) = 2pq, skew coefficient r of HWE is defined by the following expressions:

$$p\lpar AA\rpar = {\,p^2} - r\comma \; P\lpar aa\rpar = {q^2} + r.$$

If $r \ge 0$ , then $r \lt {p^2}$ , otherwise $r \gt - {q^2}$ . r = 0 indicates that HWE holds. The simulation results of two different cases by respectively fixing P(Aa) = 2pq and $p\lpar aa\rpar = {q^2}$ are both given in Table 6.

Table 6. The discovery rates of 1000 simulations with different r in situation 3.

^a The skew coefficient of HWE when fixing P(Aa) = 2pq.

^b The skew coefficient of HWE when fixing $P\lpar aa\rpar = {q^2}$ .

(d) Situation 4: loci 3 and 4 are linked and have interaction effect only ( $\!{H_3} = {H_4} = 0$ )

The performance of the two-stage method on two linked loci with various LD coefficients θ is considered. The detailed information to chose genotypes of loci 3 and 4 and regression coefficients are listed in the supplementary material (File 2). For each H, we respectively took, 0 = 0·9, 0·85, 0·8, 0·75, 0·7, 0·65, 0·6, 0·55, 0·5. The simulation results are listed in Table 7.

Table 7. The discovery rates of 1000 simulations with q = 0·3 in situation 4.

^a The LD coefficient between loci 3 and 4.

(ii) Simulation results

The discovery rate among 1000 replicates is considered as an estimate of power. From Table 4, we can see that the powers increase with increasing interaction effect and MAF except when MAF is small. This result is intuitive. When MAF is 0·1, the power always stays at a low level, even if the interaction effect is highly significant (H = 50%). So the method we used may be ineffective in detecting interaction effects among rare variants.

Table 5 shows that the marginal effects of interacting factors can affect the power and the dependence is monotonic in most cases. While some violation may exist for small H. The reasons that contribute to this contra-intuitive phenomenon are explained as follows (Struchalin et al., 2010): from the linear model given before, we can get $\sigma_{AA}^2 = Var\lpar y\vert G = 1\rpar = {\lpar {\beta _2} + {\beta _3}\rpar ^2}+ {\sigma ^2}\comma\ \sigma _{Aa}^2 = Var\lpar y\vert G = 0\!\cdot\!5\rpar = {\lpar {\beta _2} + 0\!\cdot\!5{\beta _3}\rpar ^2} + {\sigma ^2}\comma\ \sigma _{aa}^2 = Var\lpar y\vert G = 0\rpar = \beta _2^2 + {\sigma ^2}$ . Let

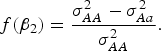$$f\lpar {\beta _2}\rpar = \displaystyle{{\sigma _{AA}^2 - \sigma _{Aa}^2 } \over {\sigma _{AA}^2 }}.$$

When MAF is small, $f\lpar {\beta _2}\rpar $ is one of the main factors that affects the power of the variance heterogeneity test, and interacting loci tend to be discovered with large $f\lpar {\beta _2}\rpar $ . So an optimum ${\beta _2}$ may exist.

From Table 6 we can see that there is no simple change of powers when HWE is not satisfied. As the skew coefficient r of HWE influences the distribution of the three genotypes, the power of detecting interaction would increase if the skew coefficient r makes the distribution more uniform, otherwise the power would decrease. For example, in the first case, where $P\lpar Aa\rpar = 2pq$ , $P\lpar AA\rpar = {p^2} - r$ and $P\lpar aa\rpar = {q^2} + r$ . When r > 0, P(aa) would increase r from ${q^2} = 0\!\cdot\!09$ and P(AA) would decrease from ${p^2} = 0\!\cdot\!49$ , which makes the three probabilities more close. So the power increases with the increasing of r.

It can be seen from Table 7 that the two-stage method performs poorly when independence assumption of loci is not satisfied. Even for H = 25%, the discovery rate is <10% and the discovery rate also decreases with the increasing of the LD coefficient θ.

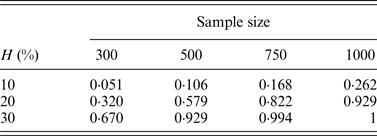
In addition, the performance of the two-stage method for cases of different sample sizes was also considered in our simulation. Table 8 lists the change of powers when we increase the number of individuals from 300 to 500, 750 and 1000, where q = 0·3.

Table 8. The discovery rates of 1000 simulations for different sample sizes.

6. Discussion

In this paper, a two-stage method based on Paré’s idea was used to conduct a genome-wide interaction analysis for four important traits of NMRI outbred mice. For each trait, we found some SNP pairs that are potentially valuable in further exploring the relationships between genes and these traits. From a bioinformatics point of view, the GO information was also used to auxiliarily explain the selected interacting pairs. Special simulation scenarios were also conducted in this research to evaluate the effects of practical factors such as HWE and LD on the two-stage screening method.

The NMRI outbred mice data set we used in this paper originated from a single population that descended from two males and seven females imported from Lausanne, Switzerland (Lynch, 1969). Therefore, it has minimal population structure and a small proportion of private alleles. Furthermore, all the mice are bred in the same situation, which can avoid wild factors. From this aspect, the population size needed is much smaller than would be needed in human association studies. Association mapping with a population of outbred mice is similar to human genome-wide association studies (GWAS) in many respects; therefore, we expect that the two-stage method and the analysis results in this paper can provide valuable reference for human GWAS.

Simulation results show that the power is affected by the MAF of a SNP and it grows sharply with increasing MAF. In the real data set, we just analysed SNPs with a MAF >2%, thus we may have neglected some rare variants with interaction effects. Fang et al. (2011) modified Paré’s two-stage approach such that it can be applied to rare variants. They just simply collapsed the rare variants in a gene to a part that is considered as a single variant, so the marginal effect of a rare variant can not be measured. Currently, the issues surrounding rare variant analysis are arousing many researchers’ attention.

In our statistical analysis of the mouse data, we assumed that all SNPs are independent. SNPs in different chromosomes may satisfy this assumption, while some SNPs in the same chromosome may have LD, especially for those whose positions are very close. In NMRI mice, there is probably no significant LD between markers approximately more than 10Mb apart (Zhang et al., 2012), and the distance is approximately 0·5Mb in humans (Dawson et al., 2002). So our statistical method may neglect some interacting SNPs that are located on the same chromosome and whose positions are very close. Our further research will be to test interaction effects among dependent variants.