Hostname: page-component-745bb68f8f-v2bm5 Total loading time: 0 Render date: 2025-01-12T21:48:28.506Z Has data issue: false hasContentIssue false
  • English
  • Français

Fixation time of overdominant alleles influenced by random fluctuation of selection intensity*

Published online by Cambridge University Press:  14 April 2009

Tomoko Ohta  and
Motoo Kimura
Tomoko Ohta
Affiliation:
National Institute of Genetics, Mishima, Japan
Motoo Kimura
Affiliation:
National Institute of Genetics, Mishima, Japan
Rights & Permissions [Opens in a new window]

Summary

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

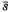It was demonstrated that the number of generations until fixation or loss of an overdominant alleles is influenced by random fluctuation of selection coefficients. When 2 < Vs, where 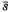is the mean selection coefficient against either homozygote and Vs is the between -generation variance of the selection coefficient, overdominance generally accelerates rather than retards fixation of segregating alleles. This finding should have important bearing on our consideration of the behaviour of polymorphic variants which are nearly neutral but have very slight overdominance. When the population size (Ne) is extremely large, not only Ne 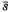but also 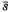/Vs have to be considered in discussing the effectiveness of overdominance.

Type
Research Article
Information
Genetics Research , Volume 20 , Issue 1 , August 1972 , pp. 1 - 7
Copyright
Copyright © Cambridge University Press 1972

References

REFERENCES

Ayala, F. J., Mourão, C. A., Pérez-Salas, S., Richmond, R. & Dobzhansky, Th. (1970). Enzyme variability in the Drosophila willistoni group. I. Genetic differentiation among sibling species. Proceedings of the National Academy of Sciences, U.S.A. 67, 225–232.CrossRefGoogle Scholar
Crow, J. F. (1972). Darwinian and non-Darwinian evolution. Proceedings of the 6th Berkeley Symposium on Mathematical Statistics and Probability. (In the Press.)CrossRefGoogle Scholar
Crow, J. F. & Kimura, M. (1970). An introduction to Population Genetics Theory. New York: Harper and Row.Google Scholar
Ewens, W. J. (1963). The diffusion equation and a pseudo-distribution in genetics. Journal of the Royal Statistical Society B 25, 405–412.Google Scholar
Ewens, W. J. & Thomson, G. (1970). Heterozygote selective advantage. Annals of Human Genetics 33, 365–376.CrossRefGoogle Scholar
Fincham, J. R. S. (1966). Genetic Complementation. New York: Benjamin.Google Scholar
Hill, W. G. & Robertson, A. (1966). The effect of linkage on limits to artificial selection. Genetical Research 8, 269–294CrossRefGoogle ScholarPubMed
Kimura, M. (1971). Theoretical foundation of population genetics at the molecular level. Theoretical Population Biology 2, 174–208.CrossRefGoogle ScholarPubMed
Ohta, T. (1972). Fixation probability of a mutant influenced by random fluctuation of selection intensity. Genetical Research 19, 33–38.CrossRefGoogle Scholar
Ohta, T. & Kimura, M. (1969). Linkage disequilibrium at steady state determined by random genetic drift and recurrent mutation. Genetics 63, 229–238.CrossRefGoogle ScholarPubMed
Ohta, T. & Kimura, M. (1970). Development of associative overdominance through linkage disequilibrium in finite populations. Genetical Research 16, 165–177.CrossRefGoogle ScholarPubMed
Ohta, T. & Kimura, M. (1971). Behaviour of neutral mutants influenced by associated overdominant loci in finite populations. Genetics 69, 247–260.CrossRefGoogle Scholar
Prakash, S., Lewontin, R. C. & Hubby, J. L. (1969). A molecular approach to the study of genetic heterozygosity in natural populations. IV. Pattern of genic variation in central, marginal and isolated populations of Drosophila pseudoobscura. Genetics 61, 841–858.CrossRefGoogle Scholar
Robertson, A. (1962). Selection for heterozygotes in small populations. Genetics 47, 1291–1300.CrossRefGoogle ScholarPubMed