Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-24T12:57:11.075Z Has data issue: false hasContentIssue false
  • English
  • Français

The effect of population subdivision on two loci without selection

Published online by Cambridge University Press:  14 April 2009

Marcus W. Feldman  and
Freddy Bugge Christiansen
Marcus W. Feldman
Affiliation:
Department of Biological Sciences, Stanford University, Stanford, California 94305
Freddy Bugge Christiansen
Affiliation:
Department of Biological Sciences, Stanford University, Stanford, California 94305
Rights & Permissions [Opens in a new window]

Summary

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This paper is devoted to the study of the effects of population subdivision on the evolution of two linked loci. Two simple deterministic models of population subdivision without selection are investigated. One is a finite linear ‘stepping stone’ model and the other is a finite linear stepping stone chain of populations stretching between two large populations of constant genetic constitution. At equilibrium in the first model the gene frequencies in each population are equal and there is linkage equilibrium in each population. 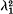The rate of decay to zero of the linkage disequilibrium functions is the larger of (1 – c) and , where λ1 is the rate of convergence of the gene frequencies to equilibrium and c is the recombination frequency. In the second model at equilibrium there will be a linear cline in gene frequencies connecting the two large constant populations. This cline will be accompanied by a ‘cline’ of linkage disequilibria. The rate of convergence to this equilibrium cline is independent of the recombination frequency, and, in fact, the gene frequencies and the linkage disequilibria converge to equilibrium at the same rate.

Type
Research Article
Information
Genetics Research , Volume 24 , Issue 2 , October 1974 , pp. 151 - 162
Copyright
Copyright © Cambridge University Press 1974

References

REFERENCES

Bodmer, W. F. & Cavalli-Sforza, L. L. (1968). A migration matrix model for the study of random genetic drift. Genetics 59, 565–592.CrossRefGoogle Scholar
Bodmer, W. F. & Felsenstein, J. (1967). Linkage and selection: Theoretical analysis of the deterministic two locus random mating model. Genetics 57, 237–265.CrossRefGoogle ScholarPubMed
Christiansen, F. B., Frydenberg, O. & Simonsen, V. (1973) Genetics of Zoarces populations. IV. Selection component analysis of an esterase polymorphism using population samples including mother-offspring combinations. Hereditas 73, 291–304.CrossRefGoogle ScholarPubMed
Feller, W. (1957). An introduction to probability theory and its applications, 2nd ed.New York: John Wiley.Google Scholar
Hill, W. G. & Robertson, A. (1968). Linkage disequilibrium in finite populations. Theoretical and Applied Genetics 38, 226–231.CrossRefGoogle ScholarPubMed
Karlin, S. & Feldman, M. W. (1970). Linkage and selection: Two locus symmetric viability model. Theoretical Population Biology 1, 39–71.CrossRefGoogle ScholarPubMed
Kidd, K. & Cavalli-Sforza, L. L. (1974). The role of genetic drift in the differentiation of Icelandic and Norwegian cattle. Evolution (to appear).CrossRefGoogle ScholarPubMed
Kimura, M. & Weiss, G. H. (1964). The steppibg stone model of population structure and the decrease of genetic correlation with distance. Genetics 49, 561–576.CrossRefGoogle ScholarPubMed
Lewontin, R. C. & Kojima, K. (1960). The evolutionary dynamics of complex polymorphisms. Evolution 14, 458–472.Google Scholar
Lewontin, R. C. & Krakuaer, J. (1973). Distribution of gene frequency as a test of the neutrality of polymorphisms. Genetics 74, 175–195.CrossRefGoogle ScholarPubMed
Malécot, G. (1950). Quelques schémas probabilistés sur la variabilité des populations naturelles. Annales Université de Lyon, Science Section A 13, 36–60,Google Scholar
Malécot, G. (1951). Un traitement stochastique des problemes linéares (mutation, linkage et migration en génétique de populations). Annales Université de Lyon, Science Section A 14, 79–117.Google Scholar
Malécot, G. (1967). Identical loci and relationship. Proceedings of the 5th Berkeley Symposium in Mathematical Statistics and Probability IV; 317–332.Google Scholar
Maruyama, T. (1971). The rate of decrease of heterozygosity in a population occupying a circular or linear habitat. Genetics 67, 437–454.CrossRefGoogle Scholar
Nei, M. & Li, W. (1973). Linkage disequilibrium in subdivided populations. Genetics 75, 213–219.CrossRefGoogle ScholarPubMed
Ohta, T. (1973). Effect of linkage on behaviour of mutant genes in finite populations. Theoretical Population Biology 4, 145–162.CrossRefGoogle Scholar
Prout, T. (1973). Appendix to: ′Population genetics of marine pelecypods. III. Epistasis between functionally related isoenzymes Ulytius edulua, by J. B. Mitten and R. C. Koehn. Genetics 73, 487–496.Google Scholar
Robbins, R. B. (1918). Some applications of mathematics to breeding problems: II. Genetics 3, 73–92.CrossRefGoogle Scholar
Sick, K. (1965). Haemoglobin polymorphism of cod in the Baltic and Danish Belt Sea. Hereditas 54, 19–48.CrossRefGoogle ScholarPubMed
Sinnock, P. & Sing, C. F. (1972). Analysis of multilocus genetic systems in Tecimsek Michigan. II. Consideration of the correlation between non-alleles in gametes. American Journal of Human Genetics 24, 393–415.Google Scholar
Sved, J. (1971). Linkage disequilibrium and homozygosity of chromosome segments in finite populations. Theoretical Population Biology 2, 125–141.CrossRefGoogle ScholarPubMed
Wahlund, S. (1928). Zusammensetzung von Populationen und Korrelations-escheinungen vom Standpunkt der Vererbungslehre aus betrachtet. Hereditas 11, 65–106.CrossRefGoogle Scholar
Wright, S. (1943). Isolation by distance. Genetics 28, 114–138.CrossRefGoogle ScholarPubMed