Bayesian model selection for multiple QTLs mapping combining linkage disequilibrium and linkage

Summary

Linkage disequilibrium (LD) mapping is able to localize quantitative trait loci (QTL) within a rather small region (e.g. 2 cM), which is much narrower than linkage analysis (LA, usually 20 cM). The multilocus LD method utilizes haplotype information around putative mutation and takes historical recombination events into account, and thus provides a powerful method for further fine mapping. However, sometimes there are more than one QTLs in the region being studied. In this study, the Bayesian model selection implemented via the Markov chain Monte Carlo (MCMC) method is developed for fine mapping of multiple QTLs using haplotype information in a small region. The method combines LD as well as linkage information. A series of simulation experiments were conducted to investigate the behavior of the method. The results showed that this new multiple QTLs method was more efficient in separating closely linked QTLs than single-marker association studies.

1. Introduction

Linkage analysis (LA) and linkage has been an important tool for quantitative trait loci (QTLs) mapping over the past two decades (Lander & Bostein, 1989; Zeng, 1994; Sillanpaa & Arjas, 1998; Xu, 2003; Yi et al., 2005), which utilizes recombination information from parents to offspring. Usually it is able to successfully localize QTLs within several centi-Morgan (cM) regions with a moderate sample size, but it fails to further fine map QTLs in this region because the recombination event is rather limited in pedigree. Compared with LA, historical recombination could be used by linkage disequilibrium (LD) analysis, so that more recombination events are able to be observed, which herein provides opportunities to narrow the credible interval of QTLs location.

LD mapping was initially used to search genes that affect human disease. The simplest method is to plot the LD values against marker position. The location with the highest LD value is estimated as the gene location (e.g. Devlin & Risch, 1995). These methods require a population that consists of patients with disease as well as healthy individuals. Luo et al. (2000) conceived a LD method for gene mapping. They infer the LD coefficient, D', and allele frequency of QTLs and test D' against zero. Wu et al. (2001, 2002) modified their method by combining LD and linkage information simultaneously for fine mapping. Lou et al. (2005) extended the method to disequilibrium association studies using multiple markers.

Hästbacka et al. (1992) developed another kind of disequilibrium mapping method; they assumed that a disease allele was produced on one chromosome 100 years ago and that it then spread through the population. The discovered population then undergoes exponential growth. Kaplan & Weil (1995) further refined this method by employing a Poisson branching process to mimic the population growth. These methods make good use of evolution information, so that the inference of the disequilibrium become less variable compared with methods using population information only (Meuwissen & Goddard, 2000). However, these methods are specifically designed for a disease population. For animal and plant geneticists, quantitative phenotype is well studied as it is economically interesting. A disequilibrium mapping method for QTLs was developed by Meuwissen & Goddard (2000), who assumed a causative mutation occurred 100 years ago on one chromosome and has a large effect on phenotypic variation (other genetic variation is assumed to have a negligible effect on phenotypic variation). After population evolution, the causative mutation remains in the present population. A gene-dropping method was developed by Meuwissen & Goddard (2000) to characterize the identity by descent (IBD) probability between haplotypes, which simulates a historical population (given the effective population size) since causative mutation occurred. Then the haplotype bearing the causative mutation decays according to the distance from the mutation due to recombination; therefore, if two haplotypes have a higher identity by state (IBS), they have a higher IBD at the causative mutation. After simulation, the IBD probabilities between two haplotypes can be estimated as the frequency of such haplotype pairs that are IBD at the causative mutation divided by the number of such haplotype pairs. After the construction of an IBD probability matrix between pair-wise haplotypes of individuals, the variance component model is employed to estimate the variance of the mutation. A LA combined with LD method was proposed by Meuwissen & Goddard (2001) to simultaneously utilize the linkage and LD information (LDLA). In a pedigree population, the LD-based IBD matrix between founders in pedigree (the individuals who have no record of parents) can be derived using estimated historical recombination information (a coalescent method was introduced that is faster than the gene-dropping method), and the IBD probabilities between offspring, and between offspring and parent can be derived using linkage information between parents and offspring. The LDLA method was also studied and extended by some researchers (Lund et al., 2003; Grapes et al., 2004; Goddard & Meuwissen, 2005; Zhao et al., 2007).

Recently, some studies have been carried out to fine map multiple QTLs (Lee & van der Werf, 2006). Lee & van der Werf (2006) developed a reversible jump MCMC method (RJMCMC) to search multiple QTLs simultaneously. They claimed that multiple QTLs mapping could more effectively separate close linked QTLs than the single QTL method. A stochastic search variable selection (SSVS) method was applied by Meuwissen & Goddard (2004) to estimate multiple QTLs and multiple trait effects. Uleberg & Meuwissen (2007) applied BayesB (Meuwissen et al., 2001) to localize multiple QTLs simultaneously.

Bayesian model selection with a variance component model has been developed to map multiple QTLs in LA (Fang et al., 2009, 2011), in which a huge number of random QTLs effects are intergrated out and the number of model parameters is reduced dramatically, so that it has excellent mixing character. In this research, we applied the Bayesian model selection to fine map multiple QTLs combined LD and LA information simultaneously. A series of simulation experiments were conducted to test the efficiency of the Bayesian model selection for fine mapping.

2. Materials and methods

(i) Data simulation

A small chromosome region of 2 cM was simulated. A total of 20 SNP markers were evenly spaced on this small region. Two QTLs were simulated at position 0·5 and 1·5 cM, respectively. Each marker had two alleles in the founder population with equal frequency, and each QTL allele had a unique number (the frequency of each allele is 1/2N _e). The pedigree was built on a founder population that was created 100 generations ago (T) with an effective population size (N _e) of 100 (50 males and 50 females). In the following 80 generations, 50 males and 50 females were randomly sampled and each mating resulted in two offspring. At each generation, the marker and QTL alleles were transmitted to the offspring according to Haldane's recombination rule without mutation. At generation 81, 10 males and 50 females were randomly selected and mated with each other to generate two offspring for each mating, so that overall 1000 (10 × 50 × 2) individuals were generated in this generation. The selection and mating pattern was carried out for 20 generations. The pedigree was recorded at the 100th and 101st generation. Marker genotypes and phenotypic values were available at the 101st generation. In the last generation, one of the QTL alleles that still existed with a frequency (π) of >0·1 and <0·9 was randomly sampled as the mutation allele with effect q, while all other QTL alleles were assumed to be the wild-type. The QTL allele effect was determined from σ _q ² = 2q² π(1−π), where QTLs variances of two simulated QTLs, σ _q ², were set as 0·08 and 0·05, respectively. The polygenic variance was 0·4 and the residual variance was 0·47. Therefore the heritabilities of two QTLs were 0·08 and 0·05, respectively. The overall mean was set as zero. The phenotypic value for each individual was generated by summing overall mean, QTLs effects and residual effect.

(ii) Multiple QTLs mapping

(a) Model

Let y be an n × 1 phenotypic vector, here n is the number of phenotypic observations, then the multiple QTLs model can be expressed as:

(1) $$y = {X_i} \beta + \sum\nolimits_{\,j = 1}^L \gamma_j a_j + g + e$$

where, β is a vector of covariate effects, which includes the effects of fixed factors; X _i is the corresponding design matrix; γ _j is the binary variable indicating the corresponding QTL effect is present (γ _j  = 1) or absent (γ _j  = 0) from model; a _j is jth QTL effect, which is assumed to be random and follows normal distribution, a _j ~N(0, Θ _j σ _j ²), where σ ² _j is the QTL variance and Θ _j is the IBD matrix; L is the maximum QTLs number; g is the polygenic effect and assumed to follow normal distribution, g  ~ N(0, A σ _A ²), where A is the additive relationship matrix and σ _A ² is the polygenic additive variance; e is the vector of random error with the distribution e ~ N(0,I σ _e ²), where I is the n × n identity matrix and σ _e ² is the residual variance. We assume QTLs effect and polygenic effect have no dominant effects. Then the variance component model can be expressed as:

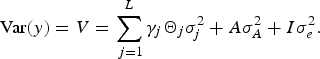(2) $$\hbox{Var} (y) = V = \sum\limits_{\,j = 1}^L \gamma_j {\it \Theta}_j {\it \sigma}_j^2 + A \sigma_A^2 +{I}{\it\sigma}_e^2.$$

(iii) IBD matrices construction

(a) IBD probabilities between two gametes

For the unrelated founder haplotypes (the corresponding individuals that had no parental records), the IBD probabilities between them are calculated using the method of Meuwissen & Goddard (2001), who inferred unknown historical recombination with coalescent theory. For individuals with parental records, the IBD probabilities were inferred using linkage information (see Meuwissen & Goddard (2001) for more details).

(b) Genotypic IBD matrices

To reduce the dimension of IBD matrices, the gametic IBD probability is transformed into genotypic probability using the equation:

(3) $$\eqalign{{\it \Theta}_{ii^{\prime}} &= \displaystyle{1 \over 2} \left[{\rm pr} \left(Q_i^{\rm p} \equiv Q_{i^{\prime}}^{\rm p} \left\vert G \right. \right) + {\rm pr} \left(Q_i^{\rm p} \equiv Q_{i^{\prime}}^{\rm M} \left\vert G \right. \right) \right. \cr &\quad \left. + {\rm pr}\left(Q_i^{\rm M} \equiv Q_{i^{\prime}}^{\rm p} \left\vert G \right. \right) + {\rm pr}\left(Q_i^{\rm M} \equiv Q_{i^{\prime}}^{\rm M} \left\vert G \right. \right) \right],}$$

where pr(Q _i ^p≡Q _i′ ^M|G) denotes the probability of the paternal allele (P) of an individual i being IBD to the maternal allele (M) of an individual i′, conditional on the marker information G; other terms have a similar explanation.

(iv) Prior and likelihood

The prior distribution of QTLs variance is assumed to follow scaled inverted Chi-squared distribution (Fang et al., 2009); the prior probability of the model indicator γ _j follows Bernoulli distribution, i.e., p(γ _j = 1) = l ₀/L, where l ₀ is the prior QTL number and L is the maximum QTL number. In our study, the expected QTL number was l ₀ = 1, and the maximum QTL number was L = 3, which results in the prior inclusion probability p(γ _j  = 1) = l ₀/L = 0.25. QTL position, λ _j , follows uniform distribution across all possible positions (the middle of each marker interval). The likelihood of variance component model can be expressed as:

(4) $$f\,(y) = \displaystyle{1 \over \sqrt{2\pi} \left\vert V^{1/2} \right\vert} \exp \left[(y - X_i \beta)^{\prime} V^{ - 1} (y - X_i \beta) \right].$$

(v) Posterior exploration

Given likelihood and prior distribution, the conditional posterior distribution can be inferred easily. If the prior distribution is conjugate, the posterior distribution can be derived directly, so one can sample it easily with Gibbs sampler; otherwise, the conditional posterior distribution could be simulated with the M–H algorithm.

(a) Updating model indicator variable

The model indicator variable {γ _j } _j=1 ^L is sampled from Gibbs sampler. The conditional posterior probability distribution is:

(5) $$p(\gamma_j = 1 \vert y, \cdot \cdot \cdot) = \displaystyle{\,p(\gamma_j = 1) \cdot f\,(y \vert \gamma_j = 1, \cdot \cdot \cdot) \over \sum\nolimits_{\kappa \in (0,1)} p(\gamma_j =\kappa) \cdot f\,(y \vert \gamma_j = \kappa, \cdot \cdot \cdot)}.$$

(b) Updating QTL position

The Metropolis–Hastings (M–H) algorithm (Metropolis et al., 1953; Hastings, 1970) is used to update QTL position λ _j . The new QTL position λ _j ^(*) is proposed around the old one λ _j ⁽⁰⁾, λ _j ^(*) = λ _j ⁽⁰⁾ + δ, where δ is the tuning parameter that is sampled uniformly from a small interval. When one position is proposed, the IBD probability matrix at position j, $\hat{\bi \Theta}_j^{\ast}$ is calculated using eqn 3. Then, if γ _j  = 1, the new position λ _j ^(*) is accepted with the probability:

(6) $$r = \displaystyle{\,f\,(y\vert {\rm \varphi}, \theta, \lambda_{-j},\lambda_j^{\ast}, \hat{\Theta}_{-j}, \hat{\Theta}_{-j}^{\ast}, A,X) \over f\,(y\vert \varphi, \theta, \lambda, \hat{\Theta}_j, A, X)},$$

otherwise, r = 1, because the new IBD matrix $\hat{\bi \Theta}_j^{\ast}$ would not contribute to likelihood when γ _j  = 0.

(c) Updating QTL variance and polygenic variance

QTL variance, polygenic variance and residual variance can be updated with any convenient M–H algorithm, but we update them using a random walk M–H algorithm (RWM–H) developed by us (Fang et al., 2009). The method generates a new proposal variance from scale inverted Chi-squared distribution conditional on the old variance, which would increase the mixing speed of Markov chain.

(vi) Bayes Factor to measure the importance of QTL

The Bayes Factor (BF) combines the posterior and prior information, which gives a reasonable way to measure the importance of a QTL. For each position λ _j , BF can be expressed as: bf $\ = \displaystyle{{\rm Post}(\lambda_j) \over 1 - {\rm Post}(\lambda_j)} \cdot \displaystyle{1 - {\rm Pr}(\lambda_j) \over {\rm Pr}(\lambda_j)}$ , where Post(λ _j ) and Pr(λ _j ) denote the posterior and prior probabilities of position λ _j , respectively (see Yi et al. (2005) for more details). Then the point estimate of the QTL position is at the peak of the BF profiles.

3. Results

(i) Effect of marker density

To study the effect of marker density, the marker number in a region was set as 10, 20 and 40 (marker density is 10, 20 and 40/cM), respectively, so that the distance between markers is 0·2, 0·1 and 0·05 cM, respectively. For each marker density, the simulated experiments were replicated 50 times. The average BF values over 50 experiments were summarized separately for each marker densities, the profiles are depicted in Fig. 1. It can be seen that the average positions are very close to the true positions; furthermore, with the increase of marker density, the BF values increase. The estimated standard deviation of the QTL positions are given in Table 1, it becomes smaller (more precise) when marker density increases.

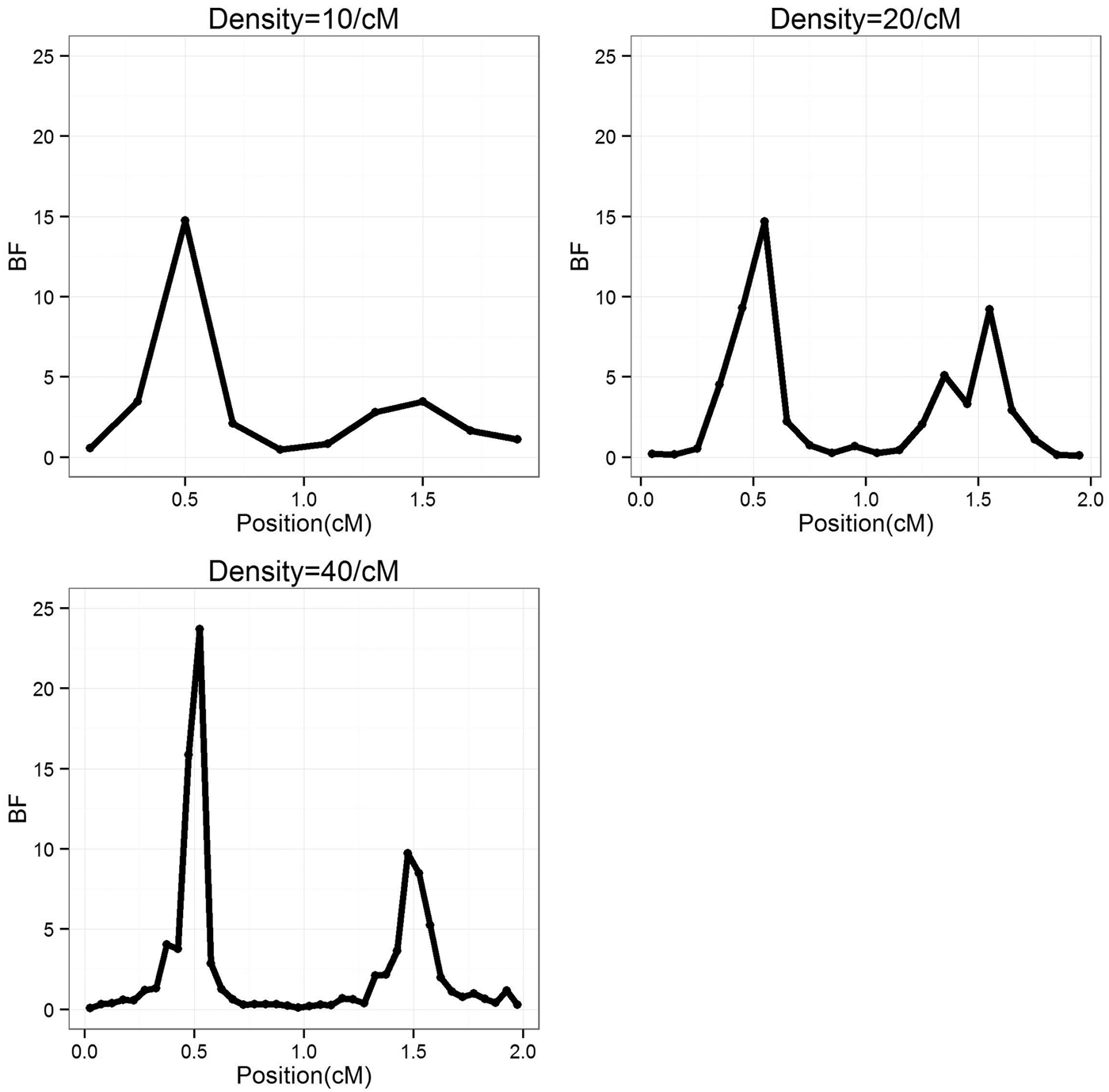
Fig. 1. The BF profiles for different marker density average over 50 replications. BF, Bayes Factor.

Table 1. The average estimates of QTL parameter over 50 replications with different marker density

The standard deviations are given in parenthesis. The true positions for QTL1 and QTL2 are 0·5 and 1·5; and the true variances

for QTL1 and QTL2 are 0·08 and 0·05, respectively.

QTL, quantitative trait locus.

(ii) Comparison with single QTL analysis

We also used single QTL analysis (based on a variance-component maximum-likelihood method) to study the simulated dataset with marker density fixed at 20/cM. The average log10 likelihood ratio (LOD) profiles across 50 replications are shown in Fig. 2. It can be seen that the single QTL analysis generates two peaks around the simulated QTL positions, but the signals of the two simulated QTLs are not separated clearly. In fact, in 18 out of 50 replications the signals of the two simulated QTLs were combined together and could not be distinguished, but a Bayesian method could separate them in all experiments, and usually generated two clear peaks at two simulated QTLs. We also summarized the estimated standard deviation of QTL position, and they were 0·38 and 0·41 cM for two simulated QTLs, respectively, which was much bigger than those from the Bayesian method (0·126 and 0·135 cM, respectively, see also Table 1).

Fig. 2. The LOD profile of single QTL method over 50 replications. LOD, log10 likelihood ratio; QTL, quantitative trait locus.

(iii) Effect of effective population size

The calculation of gametic IBD probability requires two population parameters, the past effective size N _e and mutation generation T, which are unknown and usually set before hand (Meuwissen & Goddard, 2000; Lee & van der Werf, 2006). T was set as equal to N _e here, so that a similar population equilibrium would be achieved (Lee & van der Werf, 2006). N _e was set as 10, 100, 400 and 2000. The average BF profiles over 50 replications are depicted in Fig. 3, which shows that the estimated QTLs positions are very close to the simulated positions for all N _e. It can also be seen that the profiles are similar, which suggests that the method is not very sensitive to N _e and T.

Fig. 3. The BF profiles for different N _e and T averages over 50 replications. BF, Bayes Factor.

(iv) Performance on single QTL situation

We simulated a single QTL at position 1·1 cM with a marker density of 20/cM. The profiles of BF and LOD over 50 replications with Bayesian method and maximum likelihood analysis are plotted in Fig. 4. The peaks are very close to the true positions for both methods. The standard deviations of the two methods are 0·112 and 0·128 cM, respectively, and they do not show a large difference.

Fig. 4. The BF and LOD profiles for simulating single QTL average over 50 replications. BF, Bayes Factor; LOD, log10 likelihood ratio 292; QTL, quantitative trait locus.

4. Discussion

A Bayesian model selection method is developed for fine-scale multiple QTLs mapping combining LD and linkage. The method performs model selection by introducing a model indicator for each QTL effect, which keeps model dimension fixed. The results show that the key feature of the proposed method is that it allows for easy separation of closely linked QTLs. With the single QTL method, approximately one out of three experiments fail to separate the simulated QTLs, but all the replications separated them with the proposed multiple QTLs method. Another advantage of the multiple QTLs method is that it can also give a more precise estimation for QTL position than the single QTL method.

The proposed method utilizes the historical recombination information together with linkage information across pedigree to fine-scale QTL mapping. The historical recombination information will result in a larger amount of recombination events even for a small chromosome region, which can be inferred from the surrounding markers and provides powerful information for separating QTLs. We used the Meuwissen & Goddard (2001) method to construct a LDLA-based IBD matrix. There are two parameters to be set beforehand, the effective population size, N _e, and the time since mutation occurred, T. Our results show that when N _e and T vary from 10 to 2000, the results have no clear difference. But this conclusion is different from those of Lee & van der Werf (2006), who report that different values of N _e and T will result in different powers, which is probably due to the large sample size that we used.

Although the Bayesian method shows striking performance in separating close linked QTLs, its computational time takes too long to finish one experiment (approximately 30 hours). Most of time is used to calculate the likelihood (or the inverse of matrix). Since the sample size used in simulation is not very large (2000 individuals), we directly calculated the inverse of the LDLA-based IBD matrix here. However, when the sample size is too large, the calculation of the inverse will be quickly forbidden. In this situation, some special techniques should be adopted. Mathew et al. (2012) proposed a method to calculate likelihood, which does not need the inverse of a variance–covariance matrix V. They firstly factorize V using Cholesky decomposition, V = LL′ (where L is the lower triangular), and then calculate the quadratic form with y′V ⁻¹ y = (L ⁻¹ y)′(L ⁻¹ y), where L ⁻¹ y is calculated by solving Z from the equation LZ = y. Furthermore, they also provide an approach to calculate the determinant of V with Cholesky decomposition by $\log (\det (V)) = 2\sum\nolimits_{i = 1}^n \log (L_{ii})$ . Their method avoids calculating the inverse of V, so it would be useful in our method when the sample size is large.

For convenience, we constructed an IBD matrix using the method of Meuwissen & Goddard (2001), which does not take the mutation of the marker into account. A novel IBD calculation method is proposed by Meuwissen & Goddard (2007), who take the SNP mutation into account, which would be more realistic in practice. There are also many methods for constructing a LD-based IBD matrix (e.g. Hill & Hernandez-Sanchez, 2007), each has its own advantages, but all can easily be applied in our Bayesian model selection framework.

We have studied the Bayesian method on a continuous trait. It is not difficult for this method to be extended to a binary or categorical trait, and an additional step is required to sample the underlying liabilities in MCMC iterations.