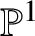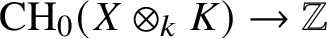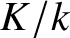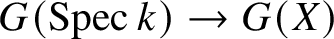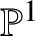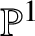1 Introduction
A proper smooth variety X over a field k is said to be universally ![]() ${\mathrm {CH}}_0$-trivial if for any field extension
${\mathrm {CH}}_0$-trivial if for any field extension ![]() $K/k$, the degree map of the Chow group of
$K/k$, the degree map of the Chow group of ![]() $0$-cycles induces an isomorphism
$0$-cycles induces an isomorphism  $\deg \colon {\mathrm {CH}}_0(X\otimes _kK)\xrightarrow {\simeq }\mathbb {Z}$. Basic examples of universally
$\deg \colon {\mathrm {CH}}_0(X\otimes _kK)\xrightarrow {\simeq }\mathbb {Z}$. Basic examples of universally ![]() ${\mathrm {CH}}_0$-trivial varieties include rational (and more generally stably rational) varieties, and this property may be considered a near-rationality condition. The condition plays a crucial role in the degeneration method established by Voisin [Reference Voisin32] and Colliot-Thélène and Pirutka [Reference Colliot-Thélène and Pirutka9], where counterexamples to the Lüroth problem are produced.
${\mathrm {CH}}_0$-trivial varieties include rational (and more generally stably rational) varieties, and this property may be considered a near-rationality condition. The condition plays a crucial role in the degeneration method established by Voisin [Reference Voisin32] and Colliot-Thélène and Pirutka [Reference Colliot-Thélène and Pirutka9], where counterexamples to the Lüroth problem are produced.
Now it is natural to ask how to disprove the universal ![]() ${\mathrm {CH}}_0$-triviality for a given variety X. In this direction, Merkurjev [Reference Merkurjev23, Theorem 2.11] proved that X is universally
${\mathrm {CH}}_0$-triviality for a given variety X. In this direction, Merkurjev [Reference Merkurjev23, Theorem 2.11] proved that X is universally ![]() ${\mathrm {CH}}_0$-trivial if and only if the function field
${\mathrm {CH}}_0$-trivial if and only if the function field ![]() $k(X)$ has trivial unramified cohomology – that is,
$k(X)$ has trivial unramified cohomology – that is, ![]() $M_*(k)\simeq M_*(k(X))_{{\mathrm {ur}}}$ for all Rost’s cycle modules
$M_*(k)\simeq M_*(k(X))_{{\mathrm {ur}}}$ for all Rost’s cycle modules ![]() $M_*$ over k. As a consequence, if
$M_*$ over k. As a consequence, if ![]() $\ell $ is a prime number different from the characteristic p of k, then
$\ell $ is a prime number different from the characteristic p of k, then ![]() $\ell $-primary torsion elements of the Brauer group
$\ell $-primary torsion elements of the Brauer group  $\operatorname {Br}(X):=H^2_{{\mathrm {\acute {e}t}}}(X,\mathbb {G}_m)$ not coming from
$\operatorname {Br}(X):=H^2_{{\mathrm {\acute {e}t}}}(X,\mathbb {G}_m)$ not coming from ![]() $\operatorname {Br}(k)$ obstruct the universal
$\operatorname {Br}(k)$ obstruct the universal ![]() ${\mathrm {CH}}_0$-triviality. This is because the
${\mathrm {CH}}_0$-triviality. This is because the ![]() $\ell $-primary torsion subgroups
$\ell $-primary torsion subgroups  $\operatorname {Br}(K)[\ell ^{\infty }]\simeq H^2_{{\mathrm {\acute {e}t}}}(K,\mathbb {Q}_{\ell }/\mathbb {Z}_{\ell }(1))$ for all field extensions
$\operatorname {Br}(K)[\ell ^{\infty }]\simeq H^2_{{\mathrm {\acute {e}t}}}(K,\mathbb {Q}_{\ell }/\mathbb {Z}_{\ell }(1))$ for all field extensions ![]() $K/k$ give rise to a cycle module
$K/k$ give rise to a cycle module  $M_*\colon K\mapsto \bigoplus _{i=0}^{\infty }H^{i+1}_{{\mathrm {\acute {e}t}}}(K,\mathbb {Q}_{\ell }/\mathbb {Z}_{\ell }(i))$, to which the theorem of Merkurjev can be applied.
$M_*\colon K\mapsto \bigoplus _{i=0}^{\infty }H^{i+1}_{{\mathrm {\acute {e}t}}}(K,\mathbb {Q}_{\ell }/\mathbb {Z}_{\ell }(i))$, to which the theorem of Merkurjev can be applied.
There are, however, more obstructions other than cycle modules. In [Reference Totaro28], Totaro adopted as an obstruction the sheaves of differential forms  $\Omega ^i_{X/k}$ to disprove the universal
$\Omega ^i_{X/k}$ to disprove the universal ![]() ${\mathrm {CH}}_0$-triviality for a wide class of hypersurfaces. In [Reference Auel, Bigazzi, Böhning and Graf von Bothmer3], Auel et al. used
${\mathrm {CH}}_0$-triviality for a wide class of hypersurfaces. In [Reference Auel, Bigazzi, Böhning and Graf von Bothmer3], Auel et al. used ![]() $\operatorname {Br}(-)[2^\infty ]$ in characteristic
$\operatorname {Br}(-)[2^\infty ]$ in characteristic ![]() $p=2$ to obtain a similar result for conic bundles over
$p=2$ to obtain a similar result for conic bundles over ![]() $\mathbb {P}^2$. Neither
$\mathbb {P}^2$. Neither ![]() $\Omega ^i$ nor
$\Omega ^i$ nor ![]() $\operatorname {Br}(-)[p^\infty ]$ in characteristic
$\operatorname {Br}(-)[p^\infty ]$ in characteristic ![]() $p>0$ constitutes a cycle module. In fact, it is not straightforward to extend Merkurjev’s result to
$p>0$ constitutes a cycle module. In fact, it is not straightforward to extend Merkurjev’s result to ![]() $\operatorname {Br}(-)[p^\infty ]$. This gap was filled in by the previous work of Auel et al. [Reference Auel, Bigazzi, Böhning and Graf von Bothmer2]:
$\operatorname {Br}(-)[p^\infty ]$. This gap was filled in by the previous work of Auel et al. [Reference Auel, Bigazzi, Böhning and Graf von Bothmer2]:
Theorem 1.1 [1, Theorem 1.1]
Let X be a smooth proper variety over a field k which is universally ![]() ${\mathrm {CH}}_0$-trivial. Then the structure morphism
${\mathrm {CH}}_0$-trivial. Then the structure morphism ![]() $X\to \operatorname {Spec} k$ induces an isomorphism
$X\to \operatorname {Spec} k$ induces an isomorphism  $\operatorname {Br}(k)\xrightarrow {\simeq }\operatorname {Br}(X)$.
$\operatorname {Br}(k)\xrightarrow {\simeq }\operatorname {Br}(X)$.
Our main result extends this theorem to more general invariants:
Theorem 1.2 see Corollary 3.3
Let X be a smooth proper variety over a field k which is universally ![]() ${\mathrm {CH}}_0$-trivial. Then the structure morphism
${\mathrm {CH}}_0$-trivial. Then the structure morphism ![]() $X\to \operatorname {Spec} k$ induces an isomorphism
$X\to \operatorname {Spec} k$ induces an isomorphism  $G(k)\xrightarrow {\simeq }G(X)$ for any
$G(k)\xrightarrow {\simeq }G(X)$ for any ![]() $\mathbb {P}^1$-invariant Nisnevich sheaf with transfers G in the sense of Definition 3.1.
$\mathbb {P}^1$-invariant Nisnevich sheaf with transfers G in the sense of Definition 3.1.
This theorem generalises Theorem 1.1, since the Brauer group has a structure of a ![]() $\mathbb {P}^1$-invariant Nisnevich sheaf with transfers (see Remark 1.5(1)). The conclusion of Theorem 1.2 for homotopy-invariant sheaves with transfers follows from Merkurjev’s result already cited. More recently, Binda et al. proved the same conclusion for another class of Nisnevich sheaves with transfers, called reciprocity sheaves [Reference Binda, Rülling and Saito5, Theorem 10.13, Remark 10.14]. Our main theorem also covers their result, since we have by [Reference Kahn, Saito and Yamazaki18, Theorems 3, 8]
$\mathbb {P}^1$-invariant Nisnevich sheaf with transfers (see Remark 1.5(1)). The conclusion of Theorem 1.2 for homotopy-invariant sheaves with transfers follows from Merkurjev’s result already cited. More recently, Binda et al. proved the same conclusion for another class of Nisnevich sheaves with transfers, called reciprocity sheaves [Reference Binda, Rülling and Saito5, Theorem 10.13, Remark 10.14]. Our main theorem also covers their result, since we have by [Reference Kahn, Saito and Yamazaki18, Theorems 3, 8]
Both implications are strict (see Remark 3.4). Note also that ![]() $\Omega ^i$ is a reciprocity sheaf by [Reference Kahn, Saito and Yamazaki18, Theorem A.6.2], hence Totaro’s method can be explained either by our results or those of Binda et al. The main technical issue in the proof of Theorem 1.2 is the comparison of
$\Omega ^i$ is a reciprocity sheaf by [Reference Kahn, Saito and Yamazaki18, Theorem A.6.2], hence Totaro’s method can be explained either by our results or those of Binda et al. The main technical issue in the proof of Theorem 1.2 is the comparison of ![]() $G(X)$ and
$G(X)$ and ![]() $h^0(G)(X)$, where
$h^0(G)(X)$, where ![]() $h^0(G)$ is the maximal homotopy-invariant subsheaf with transfers of G. We rephrase the problem in terms of algebraic cycles, and settle it by establishing a new moving lemma (Theorem 3.5).
$h^0(G)$ is the maximal homotopy-invariant subsheaf with transfers of G. We rephrase the problem in terms of algebraic cycles, and settle it by establishing a new moving lemma (Theorem 3.5).
The unramified logarithmic Hodge–Witt cohomology  $H^1_{\mathrm {ur}}\left (-, W_n \Omega ^i_{\log }\right )$ (see Section 6 for the definition) satisfies the hypothesis of Theorem 1.2. Although this fact can also be deduced from known results on reciprocity sheaves (see Remark 6.2), we will give a direct proof which depends on classical results [Reference Gros and Suwa12, Reference Izhboldin15] but not on reciprocity sheaves.
$H^1_{\mathrm {ur}}\left (-, W_n \Omega ^i_{\log }\right )$ (see Section 6 for the definition) satisfies the hypothesis of Theorem 1.2. Although this fact can also be deduced from known results on reciprocity sheaves (see Remark 6.2), we will give a direct proof which depends on classical results [Reference Gros and Suwa12, Reference Izhboldin15] but not on reciprocity sheaves.
Proposition 1.3 see Proposition 6.1
The unramified logarithmic Hodge–Witt cohomology  $H^1_{\mathrm {ur}}\left (-, W_n \Omega ^i_{\log }\right )$ is a
$H^1_{\mathrm {ur}}\left (-, W_n \Omega ^i_{\log }\right )$ is a ![]() $\mathbb {P}^1$-invariant Nisnevich sheaf with transfers (over a field of positive characteristic) for any integers
$\mathbb {P}^1$-invariant Nisnevich sheaf with transfers (over a field of positive characteristic) for any integers ![]() $n \ge 1$ and
$n \ge 1$ and ![]() $i \ge 0$.
$i \ge 0$.
As a corollary, we obtain a new proof of the following (known) result:
Theorem 1.4. Let X be a smooth proper variety over a field k of characteristic ![]() $p>0$. Assume that X is universally
$p>0$. Assume that X is universally ![]() ${\mathrm {CH}}_0$-trivial. Then the canonical map
${\mathrm {CH}}_0$-trivial. Then the canonical map
 $$ \begin{align*} H^1_{\mathrm{ur}}\left(\operatorname{Spec} k, W_n \Omega^i_{\log}\right) \to H^1_{\mathrm{ur}}\left(X, W_n \Omega^i_{\log}\right) \\[-15pt]\end{align*} $$
$$ \begin{align*} H^1_{\mathrm{ur}}\left(\operatorname{Spec} k, W_n \Omega^i_{\log}\right) \to H^1_{\mathrm{ur}}\left(X, W_n \Omega^i_{\log}\right) \\[-15pt]\end{align*} $$is an isomorphism for any integers ![]() $n \ge 1$ and
$n \ge 1$ and ![]() $i \ge 0$.
$i \ge 0$.
(1) Since
 $H^1_{{\mathrm {ur}}}\left (X,W_n\Omega ^1_{\log }\right )\simeq \operatorname {Br}(X)[p^n]$, Theorem 1.4 for
$H^1_{{\mathrm {ur}}}\left (X,W_n\Omega ^1_{\log }\right )\simeq \operatorname {Br}(X)[p^n]$, Theorem 1.4 for  $i=1$ follows from Theorem 1.1. For general i, Theorem 1.4 was posed as a problem by Auel et al. in [Reference Auel, Bigazzi, Böhning and Graf von Bothmer2, Problem 1.2] and previously proved in [Reference Binda, Rülling and Saito5] and [Reference Otabe24], as explained in the following.
$i=1$ follows from Theorem 1.1. For general i, Theorem 1.4 was posed as a problem by Auel et al. in [Reference Auel, Bigazzi, Böhning and Graf von Bothmer2, Problem 1.2] and previously proved in [Reference Binda, Rülling and Saito5] and [Reference Otabe24], as explained in the following.(2) Theorem 1.4 was shown by Binda et al. in [Reference Binda, Rülling and Saito5, Theorem 10.13, Remark 10.14] as a consequence of their general result on reciprocity sheaves already mentioned, along with the fact that
 $H^1_{{\mathrm {ur}}}\left (-,W_n\Omega ^i_{\log }\right )$ has a structure of reciprocity sheaf.
$H^1_{{\mathrm {ur}}}\left (-,W_n\Omega ^i_{\log }\right )$ has a structure of reciprocity sheaf.(3) Independent of [Reference Binda, Rülling and Saito5], almost at the same time, Otabe also obtained Theorem 1.4 for
 $n=1$ [Reference Otabe24, Theorem 1.2]. His proof is somewhat close to ours, but it is more cycle-module-theoretical. A tame subgroup of the unramified cohomology is used in place of
$n=1$ [Reference Otabe24, Theorem 1.2]. His proof is somewhat close to ours, but it is more cycle-module-theoretical. A tame subgroup of the unramified cohomology is used in place of  $h^0(G)$ in the present paper. The relation between these two subgroups is left for future research.
$h^0(G)$ in the present paper. The relation between these two subgroups is left for future research.(4) A similar statement to Theorem 1.4 holds when
 $H^1_{\mathrm {ur}}$ is replaced by
$H^1_{\mathrm {ur}}$ is replaced by  $H^j_{\mathrm {ur}}$ for any
$H^j_{\mathrm {ur}}$ for any  $j \in \mathbb {Z}$. Indeed, the cohomology groups in question are trivial unless
$j \in \mathbb {Z}$. Indeed, the cohomology groups in question are trivial unless  $j = 0, 1$, because the natural map
$j = 0, 1$, because the natural map  $H^j_{\mathrm {ur}}\left (X, W_n \Omega ^i_{\log }\right ) \to H^j_{\mathrm {ur}}\left (k(X), W_n \Omega ^i_{\log }\right )$ is injective (if X is connected), and the p-cohomology dimension of any field of characteristic
$H^j_{\mathrm {ur}}\left (X, W_n \Omega ^i_{\log }\right ) \to H^j_{\mathrm {ur}}\left (k(X), W_n \Omega ^i_{\log }\right )$ is injective (if X is connected), and the p-cohomology dimension of any field of characteristic  $p>0$ is at most
$p>0$ is at most  $1$. The case
$1$. The case  $j=0$ follows from the results of Bloch, Gabber and Kato [Reference Bloch and Kato6, Theorem 2.1] and Merkurjev [Reference Merkurjev23, Theorem 2.11].
$j=0$ follows from the results of Bloch, Gabber and Kato [Reference Bloch and Kato6, Theorem 2.1] and Merkurjev [Reference Merkurjev23, Theorem 2.11].
The organisation of this paper is as follows. In Section 2, we revisit the proof of Theorem 1.2 for homotopy-invariant Nisnevich sheaves with transfers due to Merkurjev [Reference Merkurjev23] and Kahn [Reference Kahn16] (see Corollary 2.4). In Section 3, we state the main result in a slightly more general form (see Theorem 3.2) and prove it while admitting the key moving lemma (Theorem 3.5). The proof of Theorem 3.5 occupies the next two sections.
In Section 4, we rephrase the problem in terms of algebraic cycles. To do so, we consider the Suslin complex ![]() $C_{\bullet }(X)$ and its variant
$C_{\bullet }(X)$ and its variant ![]() $\overline {C}_{\bullet }(X)$, where the latter is defined by replacing
$\overline {C}_{\bullet }(X)$, where the latter is defined by replacing ![]() $\mathbb {A}^n$ with
$\mathbb {A}^n$ with ![]() $\mathbb {P}^n$ in the former. Theorem 3.5 is then reduced to a comparison, up to Zariski sheafification, of their
$\mathbb {P}^n$ in the former. Theorem 3.5 is then reduced to a comparison, up to Zariski sheafification, of their ![]() $0$th homology presheaves (see Theorem 4.1). Its proof is given in Section 5, which is pivotal in our work.
$0$th homology presheaves (see Theorem 4.1). Its proof is given in Section 5, which is pivotal in our work.
In Section 6, we give a proof of Proposition 1.3. Finally, Appendix A provides a proof of basic properties of universally  $H_0^S$-trivial correspondences (see Definition 2.1).
$H_0^S$-trivial correspondences (see Definition 2.1).
We close this introduction with a brief discussion of related works. Shimizu [Reference Shimizu27] and Koizumi [Reference Koizumi21] have obtained some results resembling our moving lemma (Theorem 3.5) in ![]() $\mathbb {A}^1$-homotopy theory. Ayoub [Reference Ayoub4] has considered the notion of
$\mathbb {A}^1$-homotopy theory. Ayoub [Reference Ayoub4] has considered the notion of ![]() $\mathbb {P}^1$-localisation, which is much more sophisticated than our
$\mathbb {P}^1$-localisation, which is much more sophisticated than our ![]() $\mathbb {P}^n$-Suslin complex introduced in Section 4. The relation of their works to ours is to be explored. Kahn has communicated to us that Theorem 3.5 has implications in the theory of birational sheaves [Reference Kahn and Sujatha19], which should be an interesting topic for future research (see a brief comment in Remark 3.6).
$\mathbb {P}^n$-Suslin complex introduced in Section 4. The relation of their works to ours is to be explored. Kahn has communicated to us that Theorem 3.5 has implications in the theory of birational sheaves [Reference Kahn and Sujatha19], which should be an interesting topic for future research (see a brief comment in Remark 3.6).
2 Reminders on homotopy-invariant sheaves with transfers
We fix a field k. Let ![]() $\mathbf {Sch}$ be the category of separated k-schemes of finite type, and
$\mathbf {Sch}$ be the category of separated k-schemes of finite type, and ![]() $\mathbf {Sm}$ its full subcategory of smooth k-schemes. We write
$\mathbf {Sm}$ its full subcategory of smooth k-schemes. We write ![]() $\mathbf {Fld}_k$ for the category of fields over k, and
$\mathbf {Fld}_k$ for the category of fields over k, and  $\mathbf {Fld}_k^{\mathrm {gm}}$ for its full subcategory consisting of the k-fields which are isomorphic to the function field of some (irreducible)
$\mathbf {Fld}_k^{\mathrm {gm}}$ for its full subcategory consisting of the k-fields which are isomorphic to the function field of some (irreducible) ![]() $U \in \mathbf {Sm}$. For
$U \in \mathbf {Sm}$. For ![]() $K \in \mathbf {Fld}_k$ and
$K \in \mathbf {Fld}_k$ and ![]() $X \in \mathbf {Sch}$, we write
$X \in \mathbf {Sch}$, we write ![]() $X_K := X \otimes _k K$.
$X_K := X \otimes _k K$.
Let ![]() $\mathbf {Cor}$ be Voevodsky’s category of finite correspondences. By definition it has the same objects as
$\mathbf {Cor}$ be Voevodsky’s category of finite correspondences. By definition it has the same objects as ![]() $\mathbf {Sm}$, and for
$\mathbf {Sm}$, and for ![]() $U, V \in \mathbf {Sm}$ the space of morphisms
$U, V \in \mathbf {Sm}$ the space of morphisms ![]() $\operatorname {\mathbf {Cor}}(U, X)$ from U to V is the free abelian group on the set of integral closed subschemes of
$\operatorname {\mathbf {Cor}}(U, X)$ from U to V is the free abelian group on the set of integral closed subschemes of ![]() $U \times X$ which is finite and surjective over an irreducible component of U. An additive functor
$U \times X$ which is finite and surjective over an irreducible component of U. An additive functor ![]() $F : \mathbf {Cor}^{\mathrm {op}} \to \mathbf {Ab}$ is called a presheaf with transfers. Denote by
$F : \mathbf {Cor}^{\mathrm {op}} \to \mathbf {Ab}$ is called a presheaf with transfers. Denote by ![]() $\mathbf {PST}$ the category of presheaves with transfers. If S is a k-scheme that is written as a filtered limit
$\mathbf {PST}$ the category of presheaves with transfers. If S is a k-scheme that is written as a filtered limit  $S=\varprojlim _i S_i$ where
$S=\varprojlim _i S_i$ where ![]() $S_i \in \mathbf {Sm}$ and all transition maps are open immersions, then we define
$S_i \in \mathbf {Sm}$ and all transition maps are open immersions, then we define
 $$ \begin{align} F(S) = \varinjlim_i F(S_i) \quad (F \in \mathbf{PST}). \end{align} $$
$$ \begin{align} F(S) = \varinjlim_i F(S_i) \quad (F \in \mathbf{PST}). \end{align} $$ We abbreviate ![]() $F(R)=F(\operatorname {Spec} R)$ for a k-algebra R (when
$F(R)=F(\operatorname {Spec} R)$ for a k-algebra R (when ![]() $F(\operatorname {Spec} R)$ is defined). In particular, we may speak of
$F(\operatorname {Spec} R)$ is defined). In particular, we may speak of ![]() $F(K)$ for
$F(K)$ for  $K \in \mathbf {Fld}_k^{\mathrm {gm}}$ and
$K \in \mathbf {Fld}_k^{\mathrm {gm}}$ and ![]() $F\left (\mathcal {O}_{X, x}\right )$ for
$F\left (\mathcal {O}_{X, x}\right )$ for ![]() $x \in X \in \mathbf {Sm}$. We set
$x \in X \in \mathbf {Sm}$. We set ![]() $\mathbb {Z}_{\mathrm {tr}}(X):=\operatorname {\mathbf {Cor}}(-, X) \in \mathbf {PST}$ for
$\mathbb {Z}_{\mathrm {tr}}(X):=\operatorname {\mathbf {Cor}}(-, X) \in \mathbf {PST}$ for ![]() $X \in \mathbf {Sm}$.
$X \in \mathbf {Sm}$.
We say ![]() $F \in \mathbf {PST}$ is homotopy-invariant if the projection
$F \in \mathbf {PST}$ is homotopy-invariant if the projection ![]() $\mathrm {pr} : X \times \mathbb {A}^1 \to X$ induces an isomorphism
$\mathrm {pr} : X \times \mathbb {A}^1 \to X$ induces an isomorphism ![]() $\mathrm {pr}^* : F(X) \cong F\left (X \times \mathbb {A}^1\right )$ for any
$\mathrm {pr}^* : F(X) \cong F\left (X \times \mathbb {A}^1\right )$ for any ![]() $X \in \mathbf {Sm}$. We write
$X \in \mathbf {Sm}$. We write ![]() $\mathbf {HI}$ for the full subcategory of
$\mathbf {HI}$ for the full subcategory of ![]() $\mathbf {PST}$ of homotopy-invariant presheaves with transfers. We say
$\mathbf {PST}$ of homotopy-invariant presheaves with transfers. We say ![]() $F \in \mathbf {PST}$ is a Nisnevich sheaf with transfers if F composed with the inclusion (graph) functor
$F \in \mathbf {PST}$ is a Nisnevich sheaf with transfers if F composed with the inclusion (graph) functor ![]() $\mathbf {Sm} \to \mathbf {Cor}$ is a Nisnevich sheaf on
$\mathbf {Sm} \to \mathbf {Cor}$ is a Nisnevich sheaf on ![]() $\mathbf {Sm}$. We write
$\mathbf {Sm}$. We write ![]() $\mathbf {NST}$ for the full subcategory of
$\mathbf {NST}$ for the full subcategory of ![]() $\mathbf {PST}$ of Nisnevich sheaves with transfers. Set
$\mathbf {PST}$ of Nisnevich sheaves with transfers. Set ![]() $\mathbf {HI}_{\mathrm {Nis}}:=\mathbf {HI} \cap \mathbf {NST}$.
$\mathbf {HI}_{\mathrm {Nis}}:=\mathbf {HI} \cap \mathbf {NST}$.
We will use the following facts:
(V1) The inclusion functor
 $\mathbf {NST} \hookrightarrow \mathbf {PST}$ admits a left adjoint
$\mathbf {NST} \hookrightarrow \mathbf {PST}$ admits a left adjoint  $a_{\mathrm {Nis}} : \mathbf {PST} \to \mathbf {NST}$ and
$a_{\mathrm {Nis}} : \mathbf {PST} \to \mathbf {NST}$ and  $a_{\mathrm {Nis}}(\mathbf {HI}) \subset \mathbf {HI}_{\mathrm {Nis}}$ holds [Reference Mazza, Voevodsky and Weibel22, Corollary 11.2, Theorem 22.3]. We write
$a_{\mathrm {Nis}}(\mathbf {HI}) \subset \mathbf {HI}_{\mathrm {Nis}}$ holds [Reference Mazza, Voevodsky and Weibel22, Corollary 11.2, Theorem 22.3]. We write  $F_{\mathrm {Nis}} := a_{\mathrm {Nis}}(F)$. We have
$F_{\mathrm {Nis}} := a_{\mathrm {Nis}}(F)$. We have  $F_{\mathrm {Nis}}(K)=F(K)$ for any
$F_{\mathrm {Nis}}(K)=F(K)$ for any  $K \in \mathbf {Fld}_k^{\mathrm {gm}}$ (because fields are Henselian local).
$K \in \mathbf {Fld}_k^{\mathrm {gm}}$ (because fields are Henselian local).(V2) The inclusion functor
 $\mathbf {HI} \hookrightarrow \mathbf {PST}$ has a left adjoint
$\mathbf {HI} \hookrightarrow \mathbf {PST}$ has a left adjoint  $h_0$ given by the formula where we write
$h_0$ given by the formula where we write $$ \begin{align*} h_0(F)(U)=\operatorname{Coker}\left(i_0^* - i_1^* : F\left(U \times \mathbb{A}^1\right) \to F(U)\right) \quad (F \in \mathbf{PST}, \ U \in \mathbf{Sm}), \end{align*} $$
$$ \begin{align*} h_0(F)(U)=\operatorname{Coker}\left(i_0^* - i_1^* : F\left(U \times \mathbb{A}^1\right) \to F(U)\right) \quad (F \in \mathbf{PST}, \ U \in \mathbf{Sm}), \end{align*} $$ $i_\varepsilon ^*$ for the pullback along
$i_\varepsilon ^*$ for the pullback along  $U \to U \times \mathbb {A}^1,\, x \mapsto (x, \varepsilon )$, for
$U \to U \times \mathbb {A}^1,\, x \mapsto (x, \varepsilon )$, for  $\varepsilon =0, 1$. This is the maximal homotopy-invariant quotient of F [Reference Mazza, Voevodsky and Weibel22, Example 2.20]. For
$\varepsilon =0, 1$. This is the maximal homotopy-invariant quotient of F [Reference Mazza, Voevodsky and Weibel22, Example 2.20]. For  $X \in \mathbf {Sm}$, we write
$X \in \mathbf {Sm}$, we write  $h_0(X):=h_0(\mathbb {Z}_{\mathrm {tr}}(X))$. We call the
$h_0(X):=h_0(\mathbb {Z}_{\mathrm {tr}}(X))$. We call the $$ \begin{align*} H_0^S(X_K):=h_0(X)(K) = h_0(X)_{\mathrm{Nis}}(K) \end{align*} $$
$$ \begin{align*} H_0^S(X_K):=h_0(X)(K) = h_0(X)_{\mathrm{Nis}}(K) \end{align*} $$ $0$th Suslin homology of
$0$th Suslin homology of  $X_K$ for
$X_K$ for  $K \in \mathbf {Fld}_k^{\mathrm {gm}}$. There is a canonical surjective map
$K \in \mathbf {Fld}_k^{\mathrm {gm}}$. There is a canonical surjective map  $H_0^S(X_K) \to {\mathrm {CH}}_0(X_K)$, which is isomorphic if X is proper over k [Reference Mazza, Voevodsky and Weibel22, Exercise 2.21].
$H_0^S(X_K) \to {\mathrm {CH}}_0(X_K)$, which is isomorphic if X is proper over k [Reference Mazza, Voevodsky and Weibel22, Exercise 2.21].(V3) The inclusion functor
 $\mathbf {HI} \hookrightarrow \mathbf {PST}$ has a right adjoint
$\mathbf {HI} \hookrightarrow \mathbf {PST}$ has a right adjoint  $h^0$, given by the formula for
$h^0$, given by the formula for $$ \begin{align*} h^0(F)(U)={\operatorname{\mathbf{PST}}}(h_0(U), F) \end{align*} $$
$$ \begin{align*} h^0(F)(U)={\operatorname{\mathbf{PST}}}(h_0(U), F) \end{align*} $$ $F \in \mathbf {PST}, U \in \mathbf {Sm}$. This is the maximal homotopy-invariant subobject of F [Reference Rülling and Saito25, Section 4.34].
$F \in \mathbf {PST}, U \in \mathbf {Sm}$. This is the maximal homotopy-invariant subobject of F [Reference Rülling and Saito25, Section 4.34].(V4) Let
 $f : F \to G$ be a morphism in
$f : F \to G$ be a morphism in  $\mathbf {HI}_{\mathrm {Nis}}$. If f induces an isomorphism
$\mathbf {HI}_{\mathrm {Nis}}$. If f induces an isomorphism  $f^* : F(K) \cong G(K)$ for any
$f^* : F(K) \cong G(K)$ for any  $K \in \mathbf {Fld}^{\mathrm {gm}}_k$, then f is an isomorphism in
$K \in \mathbf {Fld}^{\mathrm {gm}}_k$, then f is an isomorphism in  $\mathbf {HI}_{\mathrm {Nis}}$ [Reference Mazza, Voevodsky and Weibel22, Corollary 11.2].
$\mathbf {HI}_{\mathrm {Nis}}$ [Reference Mazza, Voevodsky and Weibel22, Corollary 11.2].(V5) Given
 $F \in \mathbf {PST}$, we denote by
$F \in \mathbf {PST}$, we denote by  $F_{\mathrm {Zar}}$ the Zariski sheaf associated to the presheaf on
$F_{\mathrm {Zar}}$ the Zariski sheaf associated to the presheaf on  $\mathbf {Sm}$ obtained by restricting F along the graph functor
$\mathbf {Sm}$ obtained by restricting F along the graph functor  $\mathbf {Sm} \to \mathbf {Cor}$. In general, it does not admit a structure of presheaf with transfers, but if
$\mathbf {Sm} \to \mathbf {Cor}$. In general, it does not admit a structure of presheaf with transfers, but if  $F \in \mathbf {HI}$, then we have
$F \in \mathbf {HI}$, then we have  $F_{\mathrm {Zar}}=F_{\mathrm {Nis}}$ by [Reference Mazza, Voevodsky and Weibel22, Theorem 22.2], and hence
$F_{\mathrm {Zar}}=F_{\mathrm {Nis}}$ by [Reference Mazza, Voevodsky and Weibel22, Theorem 22.2], and hence  $F_{\mathrm {Zar}}$ acquires transfers by (V1). We say
$F_{\mathrm {Zar}}$ acquires transfers by (V1). We say  $F \in \mathbf {PST}$ is a Zariski sheaf with transfers if
$F \in \mathbf {PST}$ is a Zariski sheaf with transfers if  $F=F_{\mathrm {Zar}}$.
$F=F_{\mathrm {Zar}}$.
Another important fact can be stated as  $H^i_{\mathrm {Zar}}(-, F_{\mathrm {Zar}})=H^i_{\mathrm {Nis}}(-, F_{\mathrm {Nis}}) \in \mathbf {HI}$ for
$H^i_{\mathrm {Zar}}(-, F_{\mathrm {Zar}})=H^i_{\mathrm {Nis}}(-, F_{\mathrm {Nis}}) \in \mathbf {HI}$ for ![]() $F \in \mathbf {HI}$, assuming k is perfect [Reference Voevodsky30, Theorems 5.6, 5.7]. We will not use this in the sequel.
$F \in \mathbf {HI}$, assuming k is perfect [Reference Voevodsky30, Theorems 5.6, 5.7]. We will not use this in the sequel.
Definition 2.1. Let ![]() $X, Y \in \operatorname {\mathbf {Sm}}$. We say
$X, Y \in \operatorname {\mathbf {Sm}}$. We say ![]() $f \in \operatorname {\mathbf {Cor}}(X, Y)$ is universally
$f \in \operatorname {\mathbf {Cor}}(X, Y)$ is universally  $H_0^S$-trivial if the induced map
$H_0^S$-trivial if the induced map  $f_{K*} : H_0^S(X_K) \to H_0^S(Y_K)$ is an isomorphism for each
$f_{K*} : H_0^S(X_K) \to H_0^S(Y_K)$ is an isomorphism for each  $K \in \operatorname {\mathbf {Fld}}^{\operatorname {gm}}_k$.
$K \in \operatorname {\mathbf {Fld}}^{\operatorname {gm}}_k$.
Remark 2.2. This is an analogue of [Reference Colliot-Thélène and Pirutka9, Définition 1.1], where a proper morphism ![]() $f : X \to Y$ is said to be universally
$f : X \to Y$ is said to be universally ![]() ${\mathrm {CH}}_0$-trivial if the induced map
${\mathrm {CH}}_0$-trivial if the induced map ![]() $f_{K*} : {\mathrm {CH}}_0(X_K) \to {\mathrm {CH}}_0(Y_K)$ is an isomorphism for each
$f_{K*} : {\mathrm {CH}}_0(X_K) \to {\mathrm {CH}}_0(Y_K)$ is an isomorphism for each ![]() $K \in \mathbf {Fld}_k$. When X and Y are proper over k, a universally
$K \in \mathbf {Fld}_k$. When X and Y are proper over k, a universally ![]() ${\mathrm {CH}}_0$-trivial morphism is also universally
${\mathrm {CH}}_0$-trivial morphism is also universally  $H_0^S$-trivial by (V2). (We tacitly identify a morphism with its graph.) Note also that a smooth proper variety X is universally
$H_0^S$-trivial by (V2). (We tacitly identify a morphism with its graph.) Note also that a smooth proper variety X is universally ![]() ${\mathrm {CH}}_0$-trivial (in the sense of Theorem 1.4) if and only if the structure map
${\mathrm {CH}}_0$-trivial (in the sense of Theorem 1.4) if and only if the structure map ![]() $X \to \operatorname {Spec} k$ is universally
$X \to \operatorname {Spec} k$ is universally ![]() ${\mathrm {CH}}_0$-trivial.
${\mathrm {CH}}_0$-trivial.
The following result is due to Merkurjev [Reference Merkurjev23, Theorem 2.11] and Kahn [Reference Kahn16, Corollary 4.7]. We include a short proof here to keep self-containedness.
Proposition 2.3. Set ![]() $X, Y \in \mathbf {Sm}$. The following conditions are equivalent for
$X, Y \in \mathbf {Sm}$. The following conditions are equivalent for ![]() $f \in \operatorname {\mathbf {Cor}}(X, Y)$:
$f \in \operatorname {\mathbf {Cor}}(X, Y)$:
(1) The finite correspondence f is universally
 $H_0^S$-trivial.
$H_0^S$-trivial.(2) The induced map
 $f_* : h_0(X)_{\mathrm {Nis}} \to h_0(Y)_{\mathrm {Nis}}$ is an isomorphism in
$f_* : h_0(X)_{\mathrm {Nis}} \to h_0(Y)_{\mathrm {Nis}}$ is an isomorphism in  $\mathbf {HI}_{\mathrm {Nis}}$.
$\mathbf {HI}_{\mathrm {Nis}}$.(3) The induced map
 $f^* : F(Y) \to F(X)$ is an isomorphism for each
$f^* : F(Y) \to F(X)$ is an isomorphism for each  $F \in \mathbf {HI}_{\mathrm {Nis}}$.
$F \in \mathbf {HI}_{\mathrm {Nis}}$.
(Thanks to (V5), we may replace ![]() ${\mathrm {Nis}}$ by
${\mathrm {Nis}}$ by ![]() ${\mathrm {Zar}}$ in this statement.)
${\mathrm {Zar}}$ in this statement.)
Proof. The equivalence of (1) and (2) is a consequence of (V4). We have
for any ![]() $F \in \mathbf {HI}_{\mathrm {Nis}}$. Here we used, in order, Yoneda’s lemma, (V2) and (V1). Now another use of Yoneda’s lemma shows the equivalence of (2) and (3).
$F \in \mathbf {HI}_{\mathrm {Nis}}$. Here we used, in order, Yoneda’s lemma, (V2) and (V1). Now another use of Yoneda’s lemma shows the equivalence of (2) and (3).
Corollary 2.4. Let X be a smooth and proper scheme over a field k. If X is universally ![]() ${\mathrm {CH}}_0$-trivial, then we have
${\mathrm {CH}}_0$-trivial, then we have ![]() $F(k) \cong F(X)$ for any
$F(k) \cong F(X)$ for any ![]() $F \in \mathbf {HI}_{\mathrm {Nis}}$.
$F \in \mathbf {HI}_{\mathrm {Nis}}$.
We will generalise this result in Corollary 3.3.
Remark 2.5. We collect basic properties of universally  $H_0^S$-trivial correspondences. Since they are not used in the sequel, the proof will be given in Appendix A.
$H_0^S$-trivial correspondences. Since they are not used in the sequel, the proof will be given in Appendix A.
(1) If
 $f, g$ are composable finite correspondences and if two out of
$f, g$ are composable finite correspondences and if two out of  $f, g , f \circ g$ are universally
$f, g , f \circ g$ are universally  $H_0^S$-trivial, then so is the third.
$H_0^S$-trivial, then so is the third.(2) If
 $f : X \to Y$ and
$f : X \to Y$ and  $f' : X' \to Y'$ are universally
$f' : X' \to Y'$ are universally  $H_0^S$-trivial finite correspondences, then so is
$H_0^S$-trivial finite correspondences, then so is  $f \times f' : X \times X' \to Y \times Y'$.
$f \times f' : X \times X' \to Y \times Y'$.(3) Suppose k is perfect. Let
 $j : U \hookrightarrow X$ be an open dense immersion in
$j : U \hookrightarrow X$ be an open dense immersion in  $\mathbf {Sm}$. If
$\mathbf {Sm}$. If  $X \setminus j(U)$ is of codimension
$X \setminus j(U)$ is of codimension  $\ge 2$, then j is universally
$\ge 2$, then j is universally  $H_0^S$-trivial.
$H_0^S$-trivial.(4) Suppose k is perfect. A proper birational morphism in
 $\mathbf {Sm}$ is universally
$\mathbf {Sm}$ is universally  $H_0^S$-trivial.
$H_0^S$-trivial.
3  $\mathbb {P}^1$-invariance and the main result
$\mathbb {P}^1$-invariance and the main result
Recall from [Reference Voevodsky31, Section 3.2] that ![]() $\mathbf {PST}$ is equipped with a symmetric monoidal structure
$\mathbf {PST}$ is equipped with a symmetric monoidal structure ![]() $\otimes $ which is uniquely characterised by the facts that it is right exact and the Yoneda functor is monoidal (that is,
$\otimes $ which is uniquely characterised by the facts that it is right exact and the Yoneda functor is monoidal (that is, ![]() $\mathbb {Z}_{\mathrm {tr}}(X) \otimes \mathbb {Z}_{\mathrm {tr}}(Y)=\mathbb {Z}_{\mathrm {tr}}(X \times Y)$ for
$\mathbb {Z}_{\mathrm {tr}}(X) \otimes \mathbb {Z}_{\mathrm {tr}}(Y)=\mathbb {Z}_{\mathrm {tr}}(X \times Y)$ for ![]() $X, Y \in \mathbf {Sm}$). It admits a right adjoint
$X, Y \in \mathbf {Sm}$). It admits a right adjoint ![]() $\mathrm {\underline {Hom}}$ given by the formula
$\mathrm {\underline {Hom}}$ given by the formula
Definition 3.1. We say ![]() $G \in \mathbf {PST}$ is
$G \in \mathbf {PST}$ is ![]() $\mathbb {P}^1$-invariant if the structure map
$\mathbb {P}^1$-invariant if the structure map ![]() $\sigma : \mathbb {P}^1 \to \operatorname {Spec} k$ induces an isomorphism
$\sigma : \mathbb {P}^1 \to \operatorname {Spec} k$ induces an isomorphism  $G \overset {\cong }{\longrightarrow } \operatorname {\underline {Hom}}\left (\mathbb {Z}_{\mathrm {tr}}\left (\mathbb {P}^1\right ), G\right )$ – that is,
$G \overset {\cong }{\longrightarrow } \operatorname {\underline {Hom}}\left (\mathbb {Z}_{\mathrm {tr}}\left (\mathbb {P}^1\right ), G\right )$ – that is, ![]() $\sigma $ induces isomorphisms
$\sigma $ induces isomorphisms  $G(U) \overset {\cong }{\longrightarrow } G\left (U \times \mathbb {P}^1\right )$ for all
$G(U) \overset {\cong }{\longrightarrow } G\left (U \times \mathbb {P}^1\right )$ for all ![]() $U \in \mathbf {Sm}$. Denote by
$U \in \mathbf {Sm}$. Denote by ![]() $\mathbf {PI}_{\mathrm {Nis}}$ the full subcategory of
$\mathbf {PI}_{\mathrm {Nis}}$ the full subcategory of ![]() $\mathbf {PST}$ consisting of all Nisnevich sheaves with transfers which are
$\mathbf {PST}$ consisting of all Nisnevich sheaves with transfers which are ![]() $\mathbb {P}^1$-invariant.
$\mathbb {P}^1$-invariant.
Theorem 3.2. Suppose that ![]() $X, Y$ are smooth and proper schemes over a field k and
$X, Y$ are smooth and proper schemes over a field k and ![]() $f \in \operatorname {\mathbf {Cor}}(X, Y)$. Then the conditions in Proposition 2.3 are equivalent to the following:
$f \in \operatorname {\mathbf {Cor}}(X, Y)$. Then the conditions in Proposition 2.3 are equivalent to the following:
(4) The induced map
 $f^* : G(Y) \to G(X)$ is an isomorphism for each
$f^* : G(Y) \to G(X)$ is an isomorphism for each  $G \in \mathbf {PI}_{\mathrm {Nis}}$.
$G \in \mathbf {PI}_{\mathrm {Nis}}$.
As with Corollary 2.4, Theorem 3.2 has an immediate consequence:
Corollary 3.3. Let X be a smooth proper scheme over a field k. If X is universally ![]() ${\mathrm {CH}}_0$-trivial, then we have
${\mathrm {CH}}_0$-trivial, then we have ![]() $G(k) \cong G(X)$ for any
$G(k) \cong G(X)$ for any ![]() $G \in \mathbf {PI}_{\mathrm {Nis}}$.
$G \in \mathbf {PI}_{\mathrm {Nis}}$.
Remark 3.4. Let T be a smooth quasi-affine scheme over k. It follows from [Reference Kahn, Miyazaki, Saito and Yamazaki17, Theorem 6.4.1] that ![]() $\mathbb {Z}_{\mathrm {tr}}(T) \in \mathbf {PI}_{\mathrm {Nis}}$. On the other hand,
$\mathbb {Z}_{\mathrm {tr}}(T) \in \mathbf {PI}_{\mathrm {Nis}}$. On the other hand, ![]() $\mathbb {Z}_{\mathrm {tr}}(T)$ does not have reciprocity in general. (This follows, for example, from [Reference Kahn, Saito and Yamazaki18, Proposition 9.4.4].) We conclude that
$\mathbb {Z}_{\mathrm {tr}}(T)$ does not have reciprocity in general. (This follows, for example, from [Reference Kahn, Saito and Yamazaki18, Proposition 9.4.4].) We conclude that ![]() $\mathbb {P}^1$-invariance does not imply reciprocity (i.e., the converse of the second arrow in formula (1.1) does not hold). On the other hand, the conclusion of Corollary 3.3 is obvious for
$\mathbb {P}^1$-invariance does not imply reciprocity (i.e., the converse of the second arrow in formula (1.1) does not hold). On the other hand, the conclusion of Corollary 3.3 is obvious for ![]() $G=\mathbb {Z}_{\mathrm {tr}}(T)$. Indeed, it is not difficult to show
$G=\mathbb {Z}_{\mathrm {tr}}(T)$. Indeed, it is not difficult to show ![]() $\operatorname {\mathbf {Cor}}(\operatorname {Spec} k, T) \cong \operatorname {\mathbf {Cor}}(X, T)$ for any
$\operatorname {\mathbf {Cor}}(\operatorname {Spec} k, T) \cong \operatorname {\mathbf {Cor}}(X, T)$ for any ![]() $X \in \mathbf {Sm}$ which is connected and proper over k (but not necessary universally
$X \in \mathbf {Sm}$ which is connected and proper over k (but not necessary universally ![]() ${\mathrm {CH}}_0$-trivial).
${\mathrm {CH}}_0$-trivial).
For ![]() $F \in \mathbf {PST}$ we define
$F \in \mathbf {PST}$ we define
 $$ \begin{align} \overline{h}_0(F) := \operatorname{Coker}\left(i_0^* - i_1^* : \operatorname{\underline{Hom}}\left(\mathbb{Z}_{\mathrm{tr}}\left(\mathbb{P}^1\right), F\right) \to F\right). \end{align} $$
$$ \begin{align} \overline{h}_0(F) := \operatorname{Coker}\left(i_0^* - i_1^* : \operatorname{\underline{Hom}}\left(\mathbb{Z}_{\mathrm{tr}}\left(\mathbb{P}^1\right), F\right) \to F\right). \end{align} $$We write ![]() $\overline {h}_0(X):=\overline {h}_0(\mathbb {Z}_{\mathrm {tr}}(X))$ for
$\overline {h}_0(X):=\overline {h}_0(\mathbb {Z}_{\mathrm {tr}}(X))$ for ![]() $X \in \mathbf {Sm}$. The main part in the proof of Theorem 3.2 is the following:
$X \in \mathbf {Sm}$. The main part in the proof of Theorem 3.2 is the following:
Theorem 3.5 A moving lemma
The natural map ![]() $\overline {h}_0(X) \to h_0(X)$ yields an isomorphism
$\overline {h}_0(X) \to h_0(X)$ yields an isomorphism ![]() $\overline {h}_0(X)_{\mathrm {Zar}} \cong h_0(X)_{\mathrm {Zar}}$ for any smooth proper scheme X over a field k. (Hence we have
$\overline {h}_0(X)_{\mathrm {Zar}} \cong h_0(X)_{\mathrm {Zar}}$ for any smooth proper scheme X over a field k. (Hence we have ![]() $\overline {h}_0(X)_{\mathrm {Nis}} \cong h_0(X)_{\mathrm {Nis}}$ as well.)
$\overline {h}_0(X)_{\mathrm {Nis}} \cong h_0(X)_{\mathrm {Nis}}$ as well.)
The proof of Theorem 3.5 occupies the next two sections. In the rest of this section, we deduce Theorem 3.2 assuming Theorem 3.5.
Remark 3.6. For X as in Theorem 3.5, we have an explicit formula:
because we know ![]() $h_0(X)_{\mathrm {Nis}}(U) \cong {\mathrm {CH}}_0(X \otimes _k k(U))$ by [Reference Kahn and Sujatha19, Theorem 3.1.2] (and we have
$h_0(X)_{\mathrm {Nis}}(U) \cong {\mathrm {CH}}_0(X \otimes _k k(U))$ by [Reference Kahn and Sujatha19, Theorem 3.1.2] (and we have ![]() $h_0(X)_{\mathrm {Zar}} \cong h_0(X)_{\mathrm {Nis}}$ by (V2) and (V5)). In particular,
$h_0(X)_{\mathrm {Zar}} \cong h_0(X)_{\mathrm {Nis}}$ by (V2) and (V5)). In particular, ![]() $\overline {h}_0(X)_{\mathrm {Zar}}$ is birational in the sense of [Reference Kahn and Sujatha19, Definition 2.3.1] – that is, any open dense immersion
$\overline {h}_0(X)_{\mathrm {Zar}}$ is birational in the sense of [Reference Kahn and Sujatha19, Definition 2.3.1] – that is, any open dense immersion ![]() $V \hookrightarrow W$ induces an isomorphism
$V \hookrightarrow W$ induces an isomorphism ![]() $\overline {h}_0(X)_{\mathrm {Zar}}(W) \cong \overline {h}_0(X)_{\mathrm {Zar}}(V)$.
$\overline {h}_0(X)_{\mathrm {Zar}}(W) \cong \overline {h}_0(X)_{\mathrm {Zar}}(V)$.
Denote by ![]() $i_\varepsilon : \operatorname {Spec} k \to \mathbb {P}^1$ the closed immersion defined by a rational point
$i_\varepsilon : \operatorname {Spec} k \to \mathbb {P}^1$ the closed immersion defined by a rational point ![]() $\varepsilon \in \mathbb {P}^1(k)$.
$\varepsilon \in \mathbb {P}^1(k)$.
Definition 3.7. Set ![]() $F \in \mathbf {PST}$. We say F is
$F \in \mathbf {PST}$. We say F is ![]() $\mathbb {P}^1$-rigid if the two induced maps
$\mathbb {P}^1$-rigid if the two induced maps
 $$ \begin{align*} i_0^*, ~i_1^* : F\left(U \times \mathbb{P}^1\right) \to F(U) \end{align*} $$
$$ \begin{align*} i_0^*, ~i_1^* : F\left(U \times \mathbb{P}^1\right) \to F(U) \end{align*} $$are equal for any ![]() $U \in \mathbf {Sm}$. Denote by
$U \in \mathbf {Sm}$. Denote by ![]() $\mathbf {PRig}$ the full subcategory of
$\mathbf {PRig}$ the full subcategory of ![]() $\mathbf {PST}$ consisting of all
$\mathbf {PST}$ consisting of all ![]() $\mathbb {P}^1$-rigid presheaves with transfers.
$\mathbb {P}^1$-rigid presheaves with transfers.
Lemma 3.8. If ![]() $F \in \mathbf {PST}$ is
$F \in \mathbf {PST}$ is ![]() $\mathbb {P}^1$-invariant, then it is
$\mathbb {P}^1$-invariant, then it is ![]() $\mathbb {P}^1$-rigid. The converse holds if F is separated for Zariski topology.
$\mathbb {P}^1$-rigid. The converse holds if F is separated for Zariski topology.
Proof. See [Reference Kahn, Saito and Yamazaki18, Proposition 6.1.4].
(1) For
 $F \in \mathbf {PST}$, the following conditions are equivalent:
$F \in \mathbf {PST}$, the following conditions are equivalent:(a) F is
 $\mathbb {P}^1$-rigid.
$\mathbb {P}^1$-rigid.(b) The two induced maps
 $i_0^*, ~i_1^* : \operatorname {\underline {Hom}}\left (\mathbb {Z}_{\mathrm {tr}}\left (\mathbb {P}^1\right ), F\right ) \to F$ are equal.
$i_0^*, ~i_1^* : \operatorname {\underline {Hom}}\left (\mathbb {Z}_{\mathrm {tr}}\left (\mathbb {P}^1\right ), F\right ) \to F$ are equal.(c) The canonical surjection
 $F \to \overline {h}_0(F)$ is an isomorphism.
$F \to \overline {h}_0(F)$ is an isomorphism.(d) The canonical injection
 ${\operatorname {\mathbf {PST}}}\left (\overline {h}_0(U), F\right ) \to {\operatorname {\mathbf {PST}}}(\mathbb {Z}_{\mathrm {tr}}(U), F)$ is an isomorphism for each
${\operatorname {\mathbf {PST}}}\left (\overline {h}_0(U), F\right ) \to {\operatorname {\mathbf {PST}}}(\mathbb {Z}_{\mathrm {tr}}(U), F)$ is an isomorphism for each  $U \in \mathbf {Sm}$.
$U \in \mathbf {Sm}$.
(2) Rormula (3.2) defines a left adjoint
 $\overline {h}_0 : \mathbf {PST} \to \mathbf {PRig}$ of the inclusion functor
$\overline {h}_0 : \mathbf {PST} \to \mathbf {PRig}$ of the inclusion functor  $\mathbf {PRig} \hookrightarrow \mathbf {PST}$.
$\mathbf {PRig} \hookrightarrow \mathbf {PST}$.(3) We have
 $\mathbf {HI}_{\mathrm {Nis}} \subset \mathbf {PI}_{\mathrm {Nis}}$.
$\mathbf {HI}_{\mathrm {Nis}} \subset \mathbf {PI}_{\mathrm {Nis}}$.
Proof. (1) The equivalence of (a), (b) and (c) follows from formulas (3.1) and (3.2). If (c) holds, then any morphism ![]() $\mathbb {Z}_{\mathrm {tr}}(U) \to F$ factors as
$\mathbb {Z}_{\mathrm {tr}}(U) \to F$ factors as ![]() $\mathbb {Z}_{\mathrm {tr}}(U) \twoheadrightarrow \overline {h}_0(U) \to \overline {h}_0(F) \cong F$, whence (d). If (d) holds, then any morphism
$\mathbb {Z}_{\mathrm {tr}}(U) \twoheadrightarrow \overline {h}_0(U) \to \overline {h}_0(F) \cong F$, whence (d). If (d) holds, then any morphism ![]() $\mathbb {Z}_{\mathrm {tr}}(U) \to F$ factors as
$\mathbb {Z}_{\mathrm {tr}}(U) \to F$ factors as ![]() $\mathbb {Z}_{\mathrm {tr}}(U) \twoheadrightarrow \overline {h}_0(U) \to F$, whence (b).
$\mathbb {Z}_{\mathrm {tr}}(U) \twoheadrightarrow \overline {h}_0(U) \to F$, whence (b).
(2) We need to show  ${\operatorname {\mathbf {PST}}}\left (\overline {h}_0(G), F\right ) \cong {\operatorname {\mathbf {PST}}}(G, F)$ for any
${\operatorname {\mathbf {PST}}}\left (\overline {h}_0(G), F\right ) \cong {\operatorname {\mathbf {PST}}}(G, F)$ for any ![]() $F \in \mathbf {PRig}$ and
$F \in \mathbf {PRig}$ and ![]() $G \in \mathbf {PST}$. This is (d) if
$G \in \mathbf {PST}$. This is (d) if ![]() $G=\mathbb {Z}_{\mathrm {tr}}(U)$ for
$G=\mathbb {Z}_{\mathrm {tr}}(U)$ for ![]() $U \in \mathbf {Sm}$, to which the general case is reduced by taking a resolution of the form
$U \in \mathbf {Sm}$, to which the general case is reduced by taking a resolution of the form
 $$ \begin{align*} \bigoplus_\beta \mathbb{Z}_{\mathrm{tr}}\left(V_\beta\right) \to \bigoplus_\alpha \mathbb{Z}_{\mathrm{tr}}(U_\alpha) \to G \to 0, \end{align*} $$
$$ \begin{align*} \bigoplus_\beta \mathbb{Z}_{\mathrm{tr}}\left(V_\beta\right) \to \bigoplus_\alpha \mathbb{Z}_{\mathrm{tr}}(U_\alpha) \to G \to 0, \end{align*} $$where ![]() $U_\alpha , V_\beta \in \mathbf {Sm}$ [Reference Voevodsky31, Section 3.2].
$U_\alpha , V_\beta \in \mathbf {Sm}$ [Reference Voevodsky31, Section 3.2].
(3) Given ![]() $F \in \mathbf {PST}$, we have a chain of canonical surjections
$F \in \mathbf {PST}$, we have a chain of canonical surjections ![]() $F \twoheadrightarrow \overline {h}_0(F) \twoheadrightarrow h_0(F)$, and F is homotopy-invariant if and only if the composition is an isomorphism. It follows from (1) that
$F \twoheadrightarrow \overline {h}_0(F) \twoheadrightarrow h_0(F)$, and F is homotopy-invariant if and only if the composition is an isomorphism. It follows from (1) that ![]() $\mathbf {HI} \subset \mathbf {PRig}$. Now the assertion follows from Lemma 3.8.
$\mathbf {HI} \subset \mathbf {PRig}$. Now the assertion follows from Lemma 3.8.
Lemma 3.10. Suppose ![]() $G \in \mathbf {PST}$ is a Zariski sheaf. Then
$G \in \mathbf {PST}$ is a Zariski sheaf. Then ![]() $h^0(G)$ is a Nisnevich sheaf.
$h^0(G)$ is a Nisnevich sheaf.
Proof. This is essentially shown in [Reference Rülling and Saito25, Section 4.34], but we include a short proof for the sake of completeness. We consider a commutative diagram

The bottom arrow is injective, since the sheafification is exact. This shows the injectivity of j. Fact (V5) shows that ![]() $h^0(G)_{\mathrm {Zar}}=h^0(G)_{\mathrm {Nis}}$, and (V1) shows that it is homotopy-invariant. Hence j must be isomorphic, since
$h^0(G)_{\mathrm {Zar}}=h^0(G)_{\mathrm {Nis}}$, and (V1) shows that it is homotopy-invariant. Hence j must be isomorphic, since ![]() $h^0(G) \subset G$ is the maximal subobject in
$h^0(G) \subset G$ is the maximal subobject in ![]() $\mathbf {HI}$.
$\mathbf {HI}$.
Proof of Theorem 3.2, admitting Theorem 3.5. That (4) implies (3) follows from Lemma 3.9(3). To show the converse, we assume (3) and take ![]() $G \in \mathbf {PI}_{\mathrm {Nis}}$. Set
$G \in \mathbf {PI}_{\mathrm {Nis}}$. Set ![]() $F:=h^0(G)$. By Lemma 3.10 we find
$F:=h^0(G)$. By Lemma 3.10 we find ![]() $F \in \mathbf {HI}_{\mathrm {Nis}}$, and hence we have
$F \in \mathbf {HI}_{\mathrm {Nis}}$, and hence we have ![]() $f^* : F(Y) \cong F(X)$ by assumption (3). It remains to show
$f^* : F(Y) \cong F(X)$ by assumption (3). It remains to show ![]() $G(X)=F(X)$ for any proper
$G(X)=F(X)$ for any proper ![]() $X \in \mathbf {Sm}$. By Theorem 3.5 we have
$X \in \mathbf {Sm}$. By Theorem 3.5 we have ![]() $\overline {h}_0(X)_{\mathrm {Nis}}=h_0(X)_{\mathrm {Nis}} \in \mathbf {HI}_{\mathrm {Nis}} \subset \mathbf {PST}$. We now proceed as follows:
$\overline {h}_0(X)_{\mathrm {Nis}}=h_0(X)_{\mathrm {Nis}} \in \mathbf {HI}_{\mathrm {Nis}} \subset \mathbf {PST}$. We now proceed as follows:
 $$\begin{align*}\hspace{35pt}G(X) &={\operatorname{\mathbf{PST}}}(\mathbb{Z}_{\mathrm{tr}}(X), G)\kern-0.2pt\!\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad{\text{(Yoneda)}} \\ &={\operatorname{\mathbf{PST}}}\left(\overline{h}_0(X), G\right) \kern-0.8pt\quad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\, {\text{(Lemma 3.9(d))}} \\ &={\operatorname{\mathbf{PST}}}\left(\overline{h}_0(X)_{\mathrm{Nis}}, G\right) \kern-0.8pt\quad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\!{\text{(}G\ \text{is a Nisnevich sheaf)}} \\ &={\operatorname{\mathbf{PST}}}\left(h_0(X)_{\mathrm{Nis}}, G\right) \quad\qquad\qquad\qquad\qquad\qquad{\text{(}\overline{h}_0(X)_{\mathrm{Nis}}=h_0(X)_{\mathrm{Nis}}, \text{by Theorem~3.5)}} \\ &={\operatorname{\mathbf{PST}}}(h_0(X), G)\qquad\qquad\qquad\qquad\quad\quad\qquad\qquad\qquad\qquad\!{\text{(}G\ \text{is a Nisnevich sheaf)}} \\ &={\operatorname{\mathbf{HI}}}(h_0(X), F) \qquad\qquad\qquad\qquad\qquad\qquad\quad\ \kern0.5pt\,{\text{(}h^0\ \text{is a right adjoint to the inclusion)}} \\ &={\operatorname{\mathbf{PST}}}(\mathbb{Z}_{\mathrm{tr}}(X), F) \qquad\qquad\qquad\qquad\ \quad\qquad\qquad{\text{(}h_0\ \text{is a left adjoint to the inclusion)}} \\ &=F(X) \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\ \qquad\qquad\qquad\ \ \quad{\text{(Yoneda)}}. \end{align*}$$
$$\begin{align*}\hspace{35pt}G(X) &={\operatorname{\mathbf{PST}}}(\mathbb{Z}_{\mathrm{tr}}(X), G)\kern-0.2pt\!\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad{\text{(Yoneda)}} \\ &={\operatorname{\mathbf{PST}}}\left(\overline{h}_0(X), G\right) \kern-0.8pt\quad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\, {\text{(Lemma 3.9(d))}} \\ &={\operatorname{\mathbf{PST}}}\left(\overline{h}_0(X)_{\mathrm{Nis}}, G\right) \kern-0.8pt\quad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\!{\text{(}G\ \text{is a Nisnevich sheaf)}} \\ &={\operatorname{\mathbf{PST}}}\left(h_0(X)_{\mathrm{Nis}}, G\right) \quad\qquad\qquad\qquad\qquad\qquad{\text{(}\overline{h}_0(X)_{\mathrm{Nis}}=h_0(X)_{\mathrm{Nis}}, \text{by Theorem~3.5)}} \\ &={\operatorname{\mathbf{PST}}}(h_0(X), G)\qquad\qquad\qquad\qquad\quad\quad\qquad\qquad\qquad\qquad\!{\text{(}G\ \text{is a Nisnevich sheaf)}} \\ &={\operatorname{\mathbf{HI}}}(h_0(X), F) \qquad\qquad\qquad\qquad\qquad\qquad\quad\ \kern0.5pt\,{\text{(}h^0\ \text{is a right adjoint to the inclusion)}} \\ &={\operatorname{\mathbf{PST}}}(\mathbb{Z}_{\mathrm{tr}}(X), F) \qquad\qquad\qquad\qquad\ \quad\qquad\qquad{\text{(}h_0\ \text{is a left adjoint to the inclusion)}} \\ &=F(X) \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\ \qquad\qquad\qquad\ \ \quad{\text{(Yoneda)}}. \end{align*}$$This completes the proof.
4 Projective Suslin complex
Fix ![]() $X \in \mathbf {Sm}$ in this section. After a brief review of the definition of the Suslin complex of X, we define its variant using the projective spaces
$X \in \mathbf {Sm}$ in this section. After a brief review of the definition of the Suslin complex of X, we define its variant using the projective spaces ![]() $\mathbb {P}^n$. This will be used in the proof of the moving lemma in the next section. (We will use them only up to degree
$\mathbb {P}^n$. This will be used in the proof of the moving lemma in the next section. (We will use them only up to degree ![]() $2$.)
$2$.)
For each nonnegative integer n, we write
For ![]() $j=0, \dotsc , n$, we define
$j=0, \dotsc , n$, we define
 $$ \begin{align} i_{n, j} : \Delta^{n-1} \to \Delta^n; \quad (t_0, \dotsc, t_{n-1}) \mapsto \left(t_0, \dotsc, t_{j-1}, 0, t_j, \dotsc, t_{n-1}\right). \end{align} $$
$$ \begin{align} i_{n, j} : \Delta^{n-1} \to \Delta^n; \quad (t_0, \dotsc, t_{n-1}) \mapsto \left(t_0, \dotsc, t_{j-1}, 0, t_j, \dotsc, t_{n-1}\right). \end{align} $$The Suslin complex ![]() $C_\bullet (X)$ of X is a complex in
$C_\bullet (X)$ of X is a complex in ![]() $\mathbf {PST}$ defined by
$\mathbf {PST}$ defined by
 $$ \begin{align*} C_n(X)&:=\operatorname{\underline{Hom}}(\mathbb{Z}_{\mathrm{tr}}(\Delta^n), \mathbb{Z}_{\mathrm{tr}}(X)), \\ {\partial}_n &:= \sum_{j=0}^n (-1)^j i_{n, j}^* : C_n(X) \to C_{n-1}(X). \end{align*} $$
$$ \begin{align*} C_n(X)&:=\operatorname{\underline{Hom}}(\mathbb{Z}_{\mathrm{tr}}(\Delta^n), \mathbb{Z}_{\mathrm{tr}}(X)), \\ {\partial}_n &:= \sum_{j=0}^n (-1)^j i_{n, j}^* : C_n(X) \to C_{n-1}(X). \end{align*} $$Its homology is denoted by ![]() $h_n(X) \in \mathbf {PST}$. For
$h_n(X) \in \mathbf {PST}$. For ![]() $n=0$, it recovers
$n=0$, it recovers ![]() $h_0(X)$ from (V2).
$h_0(X)$ from (V2).
For each nonnegative integer n, we set
 $$ \begin{align*} \overline{\Delta}^n:= \operatorname{Proj} k[t_0, \dotsc, t_{n+1}]/(t_0+\dotsb+t_n-t_{n+1}) \cong \mathbb{P}^n. \end{align*} $$
$$ \begin{align*} \overline{\Delta}^n:= \operatorname{Proj} k[t_0, \dotsc, t_{n+1}]/(t_0+\dotsb+t_n-t_{n+1}) \cong \mathbb{P}^n. \end{align*} $$We have a canonical open immersion ![]() $\iota _n : \Delta ^n \hookrightarrow \overline {\Delta }^n$, which is isomorphic to
$\iota _n : \Delta ^n \hookrightarrow \overline {\Delta }^n$, which is isomorphic to ![]() $\mathbb {A}^n \hookrightarrow \mathbb {P}^n$. It induces a map in
$\mathbb {A}^n \hookrightarrow \mathbb {P}^n$. It induces a map in ![]() $\mathbf {PST}$
$\mathbf {PST}$
 $$ \begin{align} \overline{C}_n(X):=\operatorname{\underline{Hom}}\left(\mathbb{Z}_{\mathrm{tr}}\left(\overline{\Delta}^n\right), \mathbb{Z}_{\mathrm{tr}}(X)\right) \hookrightarrow C_n(X), \end{align} $$
$$ \begin{align} \overline{C}_n(X):=\operatorname{\underline{Hom}}\left(\mathbb{Z}_{\mathrm{tr}}\left(\overline{\Delta}^n\right), \mathbb{Z}_{\mathrm{tr}}(X)\right) \hookrightarrow C_n(X), \end{align} $$which is injective for any n and isomorphic for ![]() $n=0$. Indeed, its section over
$n=0$. Indeed, its section over ![]() $U \in \mathbf {Sm}$ is given by
$U \in \mathbf {Sm}$ is given by
 $$ \begin{align*} ({\mathrm{Id}}_U \times \iota_n)^* : \operatorname{\mathbf{Cor}}\left(U \times \overline{\Delta}^n, X\right) \to \operatorname{\mathbf{Cor}}(U \times \Delta^n, X), \end{align*} $$
$$ \begin{align*} ({\mathrm{Id}}_U \times \iota_n)^* : \operatorname{\mathbf{Cor}}\left(U \times \overline{\Delta}^n, X\right) \to \operatorname{\mathbf{Cor}}(U \times \Delta^n, X), \end{align*} $$which is injective in general and isomorphic for ![]() $n=0$. We regard
$n=0$. We regard ![]() $\overline {C}_n(X)$ as a subobject in
$\overline {C}_n(X)$ as a subobject in ![]() $\mathbf {PST}$ of
$\mathbf {PST}$ of ![]() $C_n(X)$. Since the morphisms
$C_n(X)$. Since the morphisms ![]() $i_{n, j}$ from formula (4.1) extend (uniquely) to morphisms
$i_{n, j}$ from formula (4.1) extend (uniquely) to morphisms ![]() $\overline {\Delta }^{n-1} \to \overline {\Delta }^{n}$, we obtain a subcomplex
$\overline {\Delta }^{n-1} \to \overline {\Delta }^{n}$, we obtain a subcomplex ![]() $\overline {C}_\bullet (X)$ of
$\overline {C}_\bullet (X)$ of ![]() $C_\bullet (X)$. We write its homology by
$C_\bullet (X)$. We write its homology by ![]() $\overline {h}_n(X) \in \mathbf {PST}$. For
$\overline {h}_n(X) \in \mathbf {PST}$. For ![]() $n=0$, it recovers
$n=0$, it recovers ![]() $\overline {h}_0(X)$ from formula (3.2).
$\overline {h}_0(X)$ from formula (3.2).
We write
for the quotient complex, and its homology presheaf is denoted by ![]() $H_n(Q_\bullet (X)) \in \mathbf {PST}$. We have
$H_n(Q_\bullet (X)) \in \mathbf {PST}$. We have ![]() $H_0(Q_\bullet (X))=0$, for formula (4.2) is isomorphic for
$H_0(Q_\bullet (X))=0$, for formula (4.2) is isomorphic for ![]() $n=0$. Since the sheafification is exact, we obtain an exact sequence
$n=0$. Since the sheafification is exact, we obtain an exact sequence
Theorem 3.5 is now reduced to the following:
Theorem 4.1. If ![]() $X \in \mathbf {Sm}$ is proper, then we have
$X \in \mathbf {Sm}$ is proper, then we have ![]() $H_1(Q_\bullet (X))_{\mathrm {Zar}}=0$.
$H_1(Q_\bullet (X))_{\mathrm {Zar}}=0$.
(1) In general,
 $\overline {h}_n(X)_{\mathrm {Zar}} \to h_n(X)_{\mathrm {Zar}}$ is not isomorphic for
$\overline {h}_n(X)_{\mathrm {Zar}} \to h_n(X)_{\mathrm {Zar}}$ is not isomorphic for  $n>0$. Indeed, one easily checks
$n>0$. Indeed, one easily checks  $H_2\left (Q_\bullet \left (\mathbb {P}^1\right )\right )_{\mathrm {Zar}}(k)=H_2\left (Q_\bullet \left (\mathbb {P}^1\right )\right )(k) \not = 0$.
$H_2\left (Q_\bullet \left (\mathbb {P}^1\right )\right )_{\mathrm {Zar}}(k)=H_2\left (Q_\bullet \left (\mathbb {P}^1\right )\right )(k) \not = 0$.(2) The properness assumption on X is essential. Indeed, it follows from [Reference Kahn, Miyazaki, Saito and Yamazaki17, Theorem 6.4.1] that if X is quasiaffine, then all the boundary maps of
 $\overline {C}_\bullet (X)$ are the zero maps.
$\overline {C}_\bullet (X)$ are the zero maps.
5 Moving lemma
We shall prove Theorem 4.1 in the following (equivalent) form:
Theorem 5.1. Let ![]() $X\in \mathbf {Sm} $ be proper. For every irreducible affine
$X\in \mathbf {Sm} $ be proper. For every irreducible affine ![]() $V\in \mathbf {Sm} $ and local scheme U at a closed point of V, the restriction map
$V\in \mathbf {Sm} $ and local scheme U at a closed point of V, the restriction map
is the zero map. (The target ![]() $H_1(Q_\bullet (X) )(U)$ is defined as a colimit – see equation (2.1).)
$H_1(Q_\bullet (X) )(U)$ is defined as a colimit – see equation (2.1).)
Note that in proving Theorem 5.1, we may assume k is infinite; for if k is finite, we can use the usual norm argument.
5.1 The bad locus
In the notation of Theorem 5.1, let ![]() $\Gamma \subset V\times X\times \Delta ^n$ be an irreducible closed subset which is finite and surjective over
$\Gamma \subset V\times X\times \Delta ^n$ be an irreducible closed subset which is finite and surjective over ![]() $V\times \Delta ^n$. Let
$V\times \Delta ^n$. Let ![]() $\overline \Gamma $ be its closure in
$\overline \Gamma $ be its closure in ![]() $V\times X\times {\overline \Delta }^{n}$. We call
$V\times X\times {\overline \Delta }^{n}$. We call
 $$ \begin{align} B(\Gamma ):=\left\{ p\in V\times {\overline\Delta}^{n} \,\middle\vert\, \overline\Gamma \to V\times {\overline\Delta}^{n} \text{ is not finite over}\ p \right\} \\[-15pt]\nonumber\end{align} $$
$$ \begin{align} B(\Gamma ):=\left\{ p\in V\times {\overline\Delta}^{n} \,\middle\vert\, \overline\Gamma \to V\times {\overline\Delta}^{n} \text{ is not finite over}\ p \right\} \\[-15pt]\nonumber\end{align} $$the bad locus of ![]() $\Gamma $, which witnesses how far
$\Gamma $, which witnesses how far ![]() $\Gamma $ is from being a member of
$\Gamma $ is from being a member of ![]() $\overline C _n(X)(V)$.
$\overline C _n(X)(V)$.
(1) We have
 $\Gamma \in C_n(X)(V)$ if and only if
$\Gamma \in C_n(X)(V)$ if and only if  $B(\Gamma )=\emptyset $.
$B(\Gamma )=\emptyset $.(2) The bad locus
 $B(\Gamma )$ is a closed proper subset of
$B(\Gamma )$ is a closed proper subset of  $V\times \left ({\overline \Delta }^{n}\setminus \Delta ^n\right )$.
$V\times \left ({\overline \Delta }^{n}\setminus \Delta ^n\right )$.(3) If
 $n\le 1$, the image of the projection
$n\le 1$, the image of the projection  $B(\Gamma )\to V$ is a closed proper subset.
$B(\Gamma )\to V$ is a closed proper subset.
Proof. Assertion (1) is clear from definitions, and put for later reference.
To prove (2), consider the set upstairs:
 $$ \begin{align*} \widetilde B\left(\overline\Gamma \right):= \left\{ x\in \overline\Gamma \,\middle\vert\, \text{locally around}\ x, \text{the fibre of}\ \overline\Gamma \to V\times {\overline\Delta}^{n}\ \text{has dimension}\ \ge 1 \right\}.\\[-15pt] \end{align*} $$
$$ \begin{align*} \widetilde B\left(\overline\Gamma \right):= \left\{ x\in \overline\Gamma \,\middle\vert\, \text{locally around}\ x, \text{the fibre of}\ \overline\Gamma \to V\times {\overline\Delta}^{n}\ \text{has dimension}\ \ge 1 \right\}.\\[-15pt] \end{align*} $$It is a closed subset of ![]() $V\times X\times {\overline \Delta }^{n}$ by Chevalley’s theorem [Reference Dieudonné and Grothendieck11, IV3 13.1.3]. It is contained in
$V\times X\times {\overline \Delta }^{n}$ by Chevalley’s theorem [Reference Dieudonné and Grothendieck11, IV3 13.1.3]. It is contained in ![]() $\overline \Gamma \setminus \Gamma $:
$\overline \Gamma \setminus \Gamma $:
 $$ \begin{align} \widetilde{B}\left(\overline\Gamma \right) \subset \overline\Gamma \setminus \Gamma ,\\[-15pt]\nonumber \end{align} $$
$$ \begin{align} \widetilde{B}\left(\overline\Gamma \right) \subset \overline\Gamma \setminus \Gamma ,\\[-15pt]\nonumber \end{align} $$because ![]() $\Gamma $ is assumed to be finite over
$\Gamma $ is assumed to be finite over ![]() $V\times \Delta ^n$. Since
$V\times \Delta ^n$. Since ![]() $B(\Gamma )$ is by definition the image of the map
$B(\Gamma )$ is by definition the image of the map  $\widetilde B\left (\overline \Gamma \right )\to V\times {\overline \Delta }^{n}$ which is proper because X is, it follows that
$\widetilde B\left (\overline \Gamma \right )\to V\times {\overline \Delta }^{n}$ which is proper because X is, it follows that ![]() $B(\Gamma )$ is a closed subset of
$B(\Gamma )$ is a closed subset of  $V\times \left ({\overline \Delta }^{n}\setminus \Delta ^n\right )$.
$V\times \left ({\overline \Delta }^{n}\setminus \Delta ^n\right )$.
To show that ![]() $B(\Gamma )$ is a proper subset of
$B(\Gamma )$ is a proper subset of  $V\times \left ({\overline \Delta }^{n}\setminus \Delta ^n\right )$, let
$V\times \left ({\overline \Delta }^{n}\setminus \Delta ^n\right )$, let  $\xi \in \widetilde B\left (\overline \Gamma \right )$ be an arbitrary point and
$\xi \in \widetilde B\left (\overline \Gamma \right )$ be an arbitrary point and ![]() $\eta \in B(\Gamma )$ its image. By formula (5.2) we have
$\eta \in B(\Gamma )$ its image. By formula (5.2) we have
 $$ \begin{align*} \dim \left(\overline\Gamma \setminus \Gamma \right)&\ge \operatorname{\mathbf{trdeg}} (k(\xi )/k) \\ &=\operatorname{\mathbf{trdeg}} (k(\xi )/k(\eta ) ) +\operatorname{\mathbf{trdeg}} (k(\eta )/k) \\ &\ge 1+\operatorname{\mathbf{trdeg}} (k(\eta )/k ),\\[-15pt] \end{align*} $$
$$ \begin{align*} \dim \left(\overline\Gamma \setminus \Gamma \right)&\ge \operatorname{\mathbf{trdeg}} (k(\xi )/k) \\ &=\operatorname{\mathbf{trdeg}} (k(\xi )/k(\eta ) ) +\operatorname{\mathbf{trdeg}} (k(\eta )/k) \\ &\ge 1+\operatorname{\mathbf{trdeg}} (k(\eta )/k ),\\[-15pt] \end{align*} $$and by  $\dim (V)+n-1 \ge \dim \left (\overline \Gamma \setminus \Gamma \right ) $ we obtain
$\dim (V)+n-1 \ge \dim \left (\overline \Gamma \setminus \Gamma \right ) $ we obtain
Since ![]() $\dim (B(\Gamma ))= \sup _{\eta \in B(\Gamma )} \operatorname {\mathbf {trdeg}} (k(\eta )/k)$, we conclude
$\dim (B(\Gamma ))= \sup _{\eta \in B(\Gamma )} \operatorname {\mathbf {trdeg}} (k(\eta )/k)$, we conclude  $\dim \left (V\times \left ({\overline \Delta }^{n} \setminus \Delta ^n\right )\right )>\dim (B(\Gamma ))$. We are done.
$\dim \left (V\times \left ({\overline \Delta }^{n} \setminus \Delta ^n\right )\right )>\dim (B(\Gamma ))$. We are done.
Assertion (3) is a direct consequence of (2) (or of formula (5.3)).
5.2 Affine-space case
In this subsection we consider the case ![]() $V=\mathbb {A} ^N$ of Theorem 5.1, with
$V=\mathbb {A} ^N$ of Theorem 5.1, with ![]() $N\ge 0$ an integer. Recall that we may assume k is infinite, which we do here.
$N\ge 0$ an integer. Recall that we may assume k is infinite, which we do here.
Let ![]() $\Gamma \in C_1(X)\left (\mathbb {A} ^N\right )$ be an arbitrary irreducible cycle. By a diagram chase in the following diagram (see formula (4.3) for the definition of
$\Gamma \in C_1(X)\left (\mathbb {A} ^N\right )$ be an arbitrary irreducible cycle. By a diagram chase in the following diagram (see formula (4.3) for the definition of ![]() $Q_\bullet (X)$), it suffices to find
$Q_\bullet (X)$), it suffices to find  $\widetilde \Gamma \in C_2(X)\left (\mathbb {A} ^N\right )$ such that
$\widetilde \Gamma \in C_2(X)\left (\mathbb {A} ^N\right )$ such that  $\left (\Gamma -\partial _2 \widetilde \Gamma \right )\rvert _U \in \overline C_1(X)(U)$:
$\left (\Gamma -\partial _2 \widetilde \Gamma \right )\rvert _U \in \overline C_1(X)(U)$:

For a vector ![]() $\boldsymbol{v}\in \mathbb {A}^N(k)$, consider the translation
$\boldsymbol{v}\in \mathbb {A}^N(k)$, consider the translation ![]() $+\boldsymbol{v} : \mathbb {A}^N \to \mathbb {A}^N$ by
$+\boldsymbol{v} : \mathbb {A}^N \to \mathbb {A}^N$ by ![]() $\boldsymbol{v}$. The next assertion suggests how it can be useful:
$\boldsymbol{v}$. The next assertion suggests how it can be useful:
Lemma 5.3. There is a closed proper subset ![]() $B\subset \mathbb {A}^N$ such that for every vector
$B\subset \mathbb {A}^N$ such that for every vector ![]() $\boldsymbol{v}\in \mathbb {A}^N(k)\setminus B$, if we denote by
$\boldsymbol{v}\in \mathbb {A}^N(k)\setminus B$, if we denote by ![]() $\tau _{\boldsymbol{v}}\colon \mathbb {A} ^N\times X\times \mathbb {A}^1\to \mathbb {A}^N\times X\times \mathbb {A}^1$ the base change of the translation
$\tau _{\boldsymbol{v}}\colon \mathbb {A} ^N\times X\times \mathbb {A}^1\to \mathbb {A}^N\times X\times \mathbb {A}^1$ the base change of the translation ![]() $\mathbb {A}^N \xrightarrow {+\boldsymbol{v}} \mathbb {A}^N$, then we have
$\mathbb {A}^N \xrightarrow {+\boldsymbol{v}} \mathbb {A}^N$, then we have
 $$ \begin{align*} \left(\tau _{\boldsymbol{v}}^*\Gamma \right)\rvert_U \in \overline C_1(X)(U).\\[-18pt] \end{align*} $$
$$ \begin{align*} \left(\tau _{\boldsymbol{v}}^*\Gamma \right)\rvert_U \in \overline C_1(X)(U).\\[-18pt] \end{align*} $$Proof. Let ![]() $s\in U$ be the unique closed point of V contained in U. Let
$s\in U$ be the unique closed point of V contained in U. Let  $B(\Gamma )\subset V\times {\overline \Delta }^{1}$ be as in formula (5.1). By Lemma 5.2 we know that its projection
$B(\Gamma )\subset V\times {\overline \Delta }^{1}$ be as in formula (5.1). By Lemma 5.2 we know that its projection ![]() $\operatorname {pr}_V (B(\Gamma ))\subset V=\mathbb {A} ^N $ is a closed proper subset. Consider the closed subset
$\operatorname {pr}_V (B(\Gamma ))\subset V=\mathbb {A} ^N $ is a closed proper subset. Consider the closed subset
 $$ \begin{align*} B_0:=\operatorname{pr}_V \left(B(\Gamma )_{k(s)}\right)-s = \left\{ \boldsymbol{v}\in \mathbb{A}^N_{k(s)} \,\middle\vert\, \boldsymbol{v}+s \in \operatorname{pr}_V B(\Gamma ) _{k(s)} \right\} \subsetneq \mathbb{A}^N_{k(s)}\\[-18pt] \end{align*} $$
$$ \begin{align*} B_0:=\operatorname{pr}_V \left(B(\Gamma )_{k(s)}\right)-s = \left\{ \boldsymbol{v}\in \mathbb{A}^N_{k(s)} \,\middle\vert\, \boldsymbol{v}+s \in \operatorname{pr}_V B(\Gamma ) _{k(s)} \right\} \subsetneq \mathbb{A}^N_{k(s)}\\[-18pt] \end{align*} $$and let B be its image by the finite projection  $\pi \colon \mathbb {A}^N_{k(s)}\to \mathbb {A}^N$:
$\pi \colon \mathbb {A}^N_{k(s)}\to \mathbb {A}^N$:
Take an arbitrary ![]() $\boldsymbol{v}\in \mathbb {A}^N(k) \setminus B$. By definitions, we know
$\boldsymbol{v}\in \mathbb {A}^N(k) \setminus B$. By definitions, we know ![]() $s+ \boldsymbol{v} \in \mathbb {A}^N\setminus \operatorname {pr}_V B(\Gamma )$. Since the right-hand side is an open subset of
$s+ \boldsymbol{v} \in \mathbb {A}^N\setminus \operatorname {pr}_V B(\Gamma )$. Since the right-hand side is an open subset of ![]() $\mathbb {A}^N$, this relation remains true if we replace s by any point specialising to s. In particular,
$\mathbb {A}^N$, this relation remains true if we replace s by any point specialising to s. In particular,
Let us denote by ![]() $\overline \tau _{\boldsymbol{v}}$ the endomorphism of
$\overline \tau _{\boldsymbol{v}}$ the endomorphism of  $\mathbb {A}^N \times X\times {\overline \Delta }^{1}$ obtained as the base change of the translation
$\mathbb {A}^N \times X\times {\overline \Delta }^{1}$ obtained as the base change of the translation ![]() $+\boldsymbol{v}$. By formula (5.5), the maps
$+\boldsymbol{v}$. By formula (5.5), the maps ![]() $\tau _{\boldsymbol{v}}$ and
$\tau _{\boldsymbol{v}}$ and ![]() $\overline \tau _{\boldsymbol{v}}$ restrict themselves as in the following commutative diagram:
$\overline \tau _{\boldsymbol{v}}$ restrict themselves as in the following commutative diagram:

The slanted arrow is finite because  $\overline \Gamma \to \mathbb {A}^N\times {\overline \Delta }^{1}$ is finite outside
$\overline \Gamma \to \mathbb {A}^N\times {\overline \Delta }^{1}$ is finite outside ![]() $B(\Gamma )$ precisely by definition (5.1), and we have the inclusion
$B(\Gamma )$ precisely by definition (5.1), and we have the inclusion  $\left (\mathbb {A}^N\setminus \operatorname {pr}_V B(\Gamma )\right )\times {\overline \Delta }^{1} \subset \left (\mathbb {A}^N\times {\overline \Delta }^{1}\right )\setminus B(\Gamma )$. It follows that
$\left (\mathbb {A}^N\setminus \operatorname {pr}_V B(\Gamma )\right )\times {\overline \Delta }^{1} \subset \left (\mathbb {A}^N\times {\overline \Delta }^{1}\right )\setminus B(\Gamma )$. It follows that ![]() $\overline \tau _{\boldsymbol{v}}^* \overline \Gamma $ is finite over
$\overline \tau _{\boldsymbol{v}}^* \overline \Gamma $ is finite over  $U\times {\overline \Delta }^{1}$. As a general fact about closure and continuity, we have the inclusion
$U\times {\overline \Delta }^{1}$. As a general fact about closure and continuity, we have the inclusion  $\overline {\left (\tau _{\boldsymbol{v}}^*\Gamma \right )}\subset \overline \tau _{\boldsymbol{v}}^* \overline \Gamma $. We conclude that
$\overline {\left (\tau _{\boldsymbol{v}}^*\Gamma \right )}\subset \overline \tau _{\boldsymbol{v}}^* \overline \Gamma $. We conclude that ![]() $\left (\tau _{\boldsymbol{v}}^*\Gamma \right )\rvert _{U}$ belongs to
$\left (\tau _{\boldsymbol{v}}^*\Gamma \right )\rvert _{U}$ belongs to ![]() $\overline C_1(X)(U)$, and this completes the proof.
$\overline C_1(X)(U)$, and this completes the proof.
Let B be as in Lemma 5.2 and fix a vector ![]() $\boldsymbol{v}\in \mathbb {A}^N(k)\setminus B$. Let
$\boldsymbol{v}\in \mathbb {A}^N(k)\setminus B$. Let ![]() $\varphi _{\boldsymbol{v}}\colon \mathbb {A}^N \times \mathbb {A}^1\to \mathbb {A}^N$ be the map
$\varphi _{\boldsymbol{v}}\colon \mathbb {A}^N \times \mathbb {A}^1\to \mathbb {A}^N$ be the map ![]() $(a,t)\mapsto a+t\boldsymbol{v}$ and let
$(a,t)\mapsto a+t\boldsymbol{v}$ and let
 $$ \begin{align*} \Phi _{\boldsymbol{v},n}\colon \mathbb{A}^N\times X\times \mathbb{A}^1\times \Delta ^n\to \mathbb{A}^N\times X\times \Delta ^n \end{align*} $$
$$ \begin{align*} \Phi _{\boldsymbol{v},n}\colon \mathbb{A}^N\times X\times \mathbb{A}^1\times \Delta ^n\to \mathbb{A}^N\times X\times \Delta ^n \end{align*} $$be its base change by ![]() $X\times \Delta ^n \to \operatorname {Spec} k$. Since finite morphisms are stable under base change, we know that
$X\times \Delta ^n \to \operatorname {Spec} k$. Since finite morphisms are stable under base change, we know that
 $$ \begin{align} \text{the inverse image }\Phi _{\boldsymbol{v},1}^{-1}\Gamma \subset \mathbb{A}^N\times X\times \mathbb{A}^1\times \Delta ^1 \text{ is finite over }\mathbb{A}^N\times \mathbb{A}^1\times \Delta ^1 .\end{align} $$
$$ \begin{align} \text{the inverse image }\Phi _{\boldsymbol{v},1}^{-1}\Gamma \subset \mathbb{A}^N\times X\times \mathbb{A}^1\times \Delta ^1 \text{ is finite over }\mathbb{A}^N\times \mathbb{A}^1\times \Delta ^1 .\end{align} $$We shall use the following triangulation maps, as in Figure 1:
 $$ \begin{align} \sigma _1,\sigma _2 \colon \Delta ^2 \xrightarrow{\cong } \mathbb{A}^1 \times \Delta ^1. \end{align} $$
$$ \begin{align} \sigma _1,\sigma _2 \colon \Delta ^2 \xrightarrow{\cong } \mathbb{A}^1 \times \Delta ^1. \end{align} $$
Figure 1 Triangulation.
Explicitly, the maps ![]() $\sigma _1, \sigma _2$ are the unique affine-linear ones satisfying
$\sigma _1, \sigma _2$ are the unique affine-linear ones satisfying
 $$ \begin{align*} &\sigma _1(u_0)=(v_0,0),& &\sigma _1(u_1)=(v_1,0),& &\sigma _1(u_2)=(v_1,1),& \\ &\sigma _2(u_0)=(v_0,0),& &\sigma _2(u_1)=(v_0,1),& &\sigma _2(u_2)=(v_1,1)& \end{align*} $$
$$ \begin{align*} &\sigma _1(u_0)=(v_0,0),& &\sigma _1(u_1)=(v_1,0),& &\sigma _1(u_2)=(v_1,1),& \\ &\sigma _2(u_0)=(v_0,0),& &\sigma _2(u_1)=(v_0,1),& &\sigma _2(u_2)=(v_1,1)& \end{align*} $$in ![]() $\left (\Delta ^1\times \mathbb {A}^1\right )(k)$, where
$\left (\Delta ^1\times \mathbb {A}^1\right )(k)$, where ![]() $v_j=i_{1, j}\left (\Delta ^0\right )$ for
$v_j=i_{1, j}\left (\Delta ^0\right )$ for ![]() $j=0, 1$ and
$j=0, 1$ and ![]() $u_0=i_{2, 2}(v_1), u_1=i_{2, 0}(v_1), u_2=i_{2, 1}(v_0)$.
$u_0=i_{2, 2}(v_1), u_1=i_{2, 0}(v_1), u_2=i_{2, 1}(v_0)$.
Let  $\Phi ^{(1)}_{\boldsymbol{v},1}, \Phi ^{(2)}_{\boldsymbol{v},1}\colon \mathbb {A}^N\times X\times \Delta ^2 \to \mathbb {A}^N\times X\times \Delta ^1$ be the composite maps
$\Phi ^{(1)}_{\boldsymbol{v},1}, \Phi ^{(2)}_{\boldsymbol{v},1}\colon \mathbb {A}^N\times X\times \Delta ^2 \to \mathbb {A}^N\times X\times \Delta ^1$ be the composite maps ![]() $\Phi _{\boldsymbol{v},1}\circ \left ({\mathrm {Id}} _{\mathbb {A}^N\times X}\times \sigma _i\right )$ (
$\Phi _{\boldsymbol{v},1}\circ \left ({\mathrm {Id}} _{\mathbb {A}^N\times X}\times \sigma _i\right )$ (![]() $i=1,2$). By fact (5.6), we conclude
$i=1,2$). By fact (5.6), we conclude  $\Phi ^{(1)*}_{\boldsymbol{v},1} \Gamma , \Phi ^{(2)*}_{\boldsymbol{v},1} \Gamma \in C_2(X)\left (\mathbb {A}^N\right )$. Now set
$\Phi ^{(1)*}_{\boldsymbol{v},1} \Gamma , \Phi ^{(2)*}_{\boldsymbol{v},1} \Gamma \in C_2(X)\left (\mathbb {A}^N\right )$. Now set
 $$ \begin{align*} \widetilde{\Gamma }:= \Phi ^{(1)*}_{\boldsymbol{v},1} \Gamma -\ \Phi ^{(2)*}_{\boldsymbol{v},1} \Gamma. \end{align*} $$
$$ \begin{align*} \widetilde{\Gamma }:= \Phi ^{(1)*}_{\boldsymbol{v},1} \Gamma -\ \Phi ^{(2)*}_{\boldsymbol{v},1} \Gamma. \end{align*} $$We want to show  $\left (\Gamma -\partial _2 \widetilde {\Gamma }\right )\rvert _U \in \overline C_1(X)(U)$.
$\left (\Gamma -\partial _2 \widetilde {\Gamma }\right )\rvert _U \in \overline C_1(X)(U)$.
By a routine calculation of ![]() $\partial _2 \widetilde {\Gamma }$, we have
$\partial _2 \widetilde {\Gamma }$, we have
 $$ \begin{align} \Gamma - \partial_2 \widetilde\Gamma = \tau _{\boldsymbol{v}}^*\Gamma +\Phi _{\boldsymbol{v},0}^*\left(i_{1,1}^*\Gamma \right) -\Phi _{\boldsymbol{v},0}^*\left(i_{1,0}^*\Gamma \right) .\end{align} $$
$$ \begin{align} \Gamma - \partial_2 \widetilde\Gamma = \tau _{\boldsymbol{v}}^*\Gamma +\Phi _{\boldsymbol{v},0}^*\left(i_{1,1}^*\Gamma \right) -\Phi _{\boldsymbol{v},0}^*\left(i_{1,0}^*\Gamma \right) .\end{align} $$By Lemma 5.3, for ![]() $\boldsymbol{v}\in \mathbb {A}^N(k)\setminus B $ we know that the first term of the right-hand side maps into
$\boldsymbol{v}\in \mathbb {A}^N(k)\setminus B $ we know that the first term of the right-hand side maps into ![]() $\overline C_1(X)(U)$. So it suffices to show the following, which we apply to
$\overline C_1(X)(U)$. So it suffices to show the following, which we apply to  $\gamma := i_{1,j}^*\Gamma $:
$\gamma := i_{1,j}^*\Gamma $:
Lemma 5.4. For every ![]() $\gamma \in C_0(X)\left (\mathbb {A}^N \right ) $, there is a closed proper subset
$\gamma \in C_0(X)\left (\mathbb {A}^N \right ) $, there is a closed proper subset ![]() $C\subsetneq \mathbb {A}^N$ such that for all
$C\subsetneq \mathbb {A}^N$ such that for all ![]() $\boldsymbol{v}\in \mathbb {A}^N(k)\setminus C$, the cycle
$\boldsymbol{v}\in \mathbb {A}^N(k)\setminus C$, the cycle ![]() $\Phi _{\boldsymbol{v},0}^*\gamma $ on
$\Phi _{\boldsymbol{v},0}^*\gamma $ on ![]() $\mathbb {A}^N\times X\times \Delta ^1$ belongs to
$\mathbb {A}^N\times X\times \Delta ^1$ belongs to  $\overline C_1(X)\left (\mathbb {A}^N\right )$.
$\overline C_1(X)\left (\mathbb {A}^N\right )$.
Proof. Let us observe that as long as ![]() $\boldsymbol{v}\neq 0$, the morphism
$\boldsymbol{v}\neq 0$, the morphism ![]() $\varphi _{\boldsymbol{v}}$ extends (uniquely) to a morphism
$\varphi _{\boldsymbol{v}}$ extends (uniquely) to a morphism
 $$ \begin{align} \overline\varphi _{\boldsymbol{v}}\colon \mathbb{A}^N\times \mathbb{P} ^1 &\to \mathbb{P}^N \notag\\ (a,[t_0:t_1])&\mapsto [t_0:t_0a+t_1\boldsymbol{v}]. \end{align} $$
$$ \begin{align} \overline\varphi _{\boldsymbol{v}}\colon \mathbb{A}^N\times \mathbb{P} ^1 &\to \mathbb{P}^N \notag\\ (a,[t_0:t_1])&\mapsto [t_0:t_0a+t_1\boldsymbol{v}]. \end{align} $$ For this proof, we may assume ![]() $\gamma $ is irreducible. Let
$\gamma $ is irreducible. Let ![]() $\overline \gamma \subset \mathbb {P}^N\times X$ be the closure of
$\overline \gamma \subset \mathbb {P}^N\times X$ be the closure of ![]() $\gamma $. Consider the set
$\gamma $. Consider the set
 $$ \begin{align} C_\infty := \left\{ a\in \mathbb{P}^N\setminus \mathbb{A}^N \,\middle\vert\, \overline\gamma \to \mathbb{P}^N \text{ is not finite over }a \right\}. \end{align} $$
$$ \begin{align} C_\infty := \left\{ a\in \mathbb{P}^N\setminus \mathbb{A}^N \,\middle\vert\, \overline\gamma \to \mathbb{P}^N \text{ is not finite over }a \right\}. \end{align} $$By the ![]() $V=\operatorname {Spec} (k)$ case of Lemma 5.2(2) (via
$V=\operatorname {Spec} (k)$ case of Lemma 5.2(2) (via ![]() $X\times {\overline \Delta }^{n} \cong \mathbb {P} ^N\times X$), we find that
$X\times {\overline \Delta }^{n} \cong \mathbb {P} ^N\times X$), we find that ![]() $C_\infty $ is a closed proper subset of
$C_\infty $ is a closed proper subset of ![]() $\mathbb {P}^N\setminus \mathbb {A}^N$. Let
$\mathbb {P}^N\setminus \mathbb {A}^N$. Let ![]() $C\subset \mathbb {A}^N$ be the cone associated to
$C\subset \mathbb {A}^N$ be the cone associated to ![]() $C_\infty $, namely,
$C_\infty $, namely,
 $$ \begin{align*} C:= \begin{cases} \{ 0 \} \cup q^{-1}(C_\infty) \subset \mathbb{A}^N & (N>0), \\ \emptyset & (N=0), \end{cases} \end{align*} $$
$$ \begin{align*} C:= \begin{cases} \{ 0 \} \cup q^{-1}(C_\infty) \subset \mathbb{A}^N & (N>0), \\ \emptyset & (N=0), \end{cases} \end{align*} $$where ![]() $q : \mathbb {A}^N\setminus \left \{ 0 \right \} \to \mathbb {P}^N\setminus \mathbb {A}^N$ is the projection with centre
$q : \mathbb {A}^N\setminus \left \{ 0 \right \} \to \mathbb {P}^N\setminus \mathbb {A}^N$ is the projection with centre ![]() $0$. This is a closed proper subset of
$0$. This is a closed proper subset of ![]() $\mathbb {A}^N$.
$\mathbb {A}^N$.
Now suppose ![]() $\boldsymbol{v}\in \mathbb {A}^N(k)\setminus C$. Then by formula (5.9) we see that
$\boldsymbol{v}\in \mathbb {A}^N(k)\setminus C$. Then by formula (5.9) we see that ![]() $\overline \varphi _{\boldsymbol{v}}$ maps
$\overline \varphi _{\boldsymbol{v}}$ maps ![]() $\mathbb {A}^N \times \mathbb {P}^1$ into
$\mathbb {A}^N \times \mathbb {P}^1$ into ![]() $\mathbb {P}^N\setminus C_\infty $. We obtain the following commutative diagram:
$\mathbb {P}^N\setminus C_\infty $. We obtain the following commutative diagram:

Since the slanted arrow is finite by the definition (5.10) of ![]() $C_\infty $, the inverse image
$C_\infty $, the inverse image ![]() $\left (\overline \varphi _{\boldsymbol{v}}\times {\mathrm {Id}} _X\right )^*\overline \gamma $ is finite over
$\left (\overline \varphi _{\boldsymbol{v}}\times {\mathrm {Id}} _X\right )^*\overline \gamma $ is finite over ![]() $\mathbb {A}^N \times \mathbb {P}^1$. By the inclusion
$\mathbb {A}^N \times \mathbb {P}^1$. By the inclusion  $\overline {\left (\Phi _{\boldsymbol{v},0}^*\gamma \right )}\subset \left (\overline \varphi _{\boldsymbol{v}}\times {\mathrm {Id}} _X\right )^*\overline \gamma $ of subsets of
$\overline {\left (\Phi _{\boldsymbol{v},0}^*\gamma \right )}\subset \left (\overline \varphi _{\boldsymbol{v}}\times {\mathrm {Id}} _X\right )^*\overline \gamma $ of subsets of ![]() $\mathbb {A}^N\times X\times \mathbb {P}^1$, we conclude that
$\mathbb {A}^N\times X\times \mathbb {P}^1$, we conclude that ![]() $\Phi _{\boldsymbol{v},0}^*\gamma $ belongs to
$\Phi _{\boldsymbol{v},0}^*\gamma $ belongs to  $\overline C_1(X)\left (\mathbb {A}^N\right )$, completing the proof.
$\overline C_1(X)\left (\mathbb {A}^N\right )$, completing the proof.
Lemmas 5.3 and 5.4 applied to equation (5.8) prove Theorem 5.1 in the case ![]() $V=\mathbb {A}^N$.
$V=\mathbb {A}^N$.
5.3 The general case
Let ![]() $V\in \mathbf {Sm} $ be affine and irreducible. Let
$V\in \mathbf {Sm} $ be affine and irreducible. Let ![]() $N=\dim (V)$ be its dimension. Fix a closed embedding
$N=\dim (V)$ be its dimension. Fix a closed embedding ![]() $V\hookrightarrow \mathbb {A}^{N'}$ into an affine space. For a technical reason (see Proposition 5.6), we assume it is obtained as the composition of a preliminary one
$V\hookrightarrow \mathbb {A}^{N'}$ into an affine space. For a technical reason (see Proposition 5.6), we assume it is obtained as the composition of a preliminary one ![]() $V\hookrightarrow \mathbb {A} ^{N^{\prime }_0}$ and the
$V\hookrightarrow \mathbb {A} ^{N^{\prime }_0}$ and the ![]() $2$-fold Veronese embedding
$2$-fold Veronese embedding ![]() $\mathbb {A} ^{N^{\prime }_0}\hookrightarrow \mathbb {A} ^{N'}$,
$\mathbb {A} ^{N^{\prime }_0}\hookrightarrow \mathbb {A} ^{N'}$,  $N':= \begin {pmatrix} N^{\prime }_0+2 \\ 2 \end {pmatrix} -1 $ defined by
$N':= \begin {pmatrix} N^{\prime }_0+2 \\ 2 \end {pmatrix} -1 $ defined by
 $$ \begin{align} (x_i)_{i=1,\dotsc ,N^{\prime}_0} \mapsto \left(x_1,\dotsc ,x_{N^{\prime}_0}; \left(x_ix_j\right)_{i\le j} \right). \end{align} $$
$$ \begin{align} (x_i)_{i=1,\dotsc ,N^{\prime}_0} \mapsto \left(x_1,\dotsc ,x_{N^{\prime}_0}; \left(x_ix_j\right)_{i\le j} \right). \end{align} $$Let ![]() $M_{NN'}\cong \mathbb {A}^{NN'}$ be the k-scheme parametrising
$M_{NN'}\cong \mathbb {A}^{NN'}$ be the k-scheme parametrising ![]() $N\times N'$ matrices. The choice of a k-rational point
$N\times N'$ matrices. The choice of a k-rational point ![]() $f\in M_{NN'}(k)$ determines a morphism, which we denote by the same symbol
$f\in M_{NN'}(k)$ determines a morphism, which we denote by the same symbol ![]() $f\colon \mathbb {A}^{N'}\to \mathbb {A}^N$.
$f\colon \mathbb {A}^{N'}\to \mathbb {A}^N$.
Proposition 5.5 Noether’s normalisation lemma
There is a closed proper subset ![]() $D_1\subset M_{NN'}$ such that the composite map
$D_1\subset M_{NN'}$ such that the composite map
 $$ \begin{align*} \pi _f \colon V\hookrightarrow \mathbb{A}^{N'}\xrightarrow[]{f}\mathbb{A}^N \end{align*} $$
$$ \begin{align*} \pi _f \colon V\hookrightarrow \mathbb{A}^{N'}\xrightarrow[]{f}\mathbb{A}^N \end{align*} $$is finite and flat whenever ![]() $f\in M_{NN'}(k)\setminus D_1$.
$f\in M_{NN'}(k)\setminus D_1$.
Proof. For the existence of ![]() $D_1$ which guarantees finiteness, see, for example, [Reference Atiyah and Macdonald1, p. 69] or [Reference Kai20, Section 3.1]. Flatness is then automatic by the smoothness of V and
$D_1$ which guarantees finiteness, see, for example, [Reference Atiyah and Macdonald1, p. 69] or [Reference Kai20, Section 3.1]. Flatness is then automatic by the smoothness of V and ![]() $\mathbb {A}^N$; see [Reference Hartshorne13, Exercise III-10.9, p. 276].
$\mathbb {A}^N$; see [Reference Hartshorne13, Exercise III-10.9, p. 276].
By Proposition 5.5, for ![]() $f\in M_{NN'}(k)\setminus D_1$ we have push-forward maps
$f\in M_{NN'}(k)\setminus D_1$ we have push-forward maps ![]() $\pi _{f*}\colon H_n(X)(V)\to H_n(X)\left (\mathbb {A}^N\right )$. Let
$\pi _{f*}\colon H_n(X)(V)\to H_n(X)\left (\mathbb {A}^N\right )$. Let ![]() $s\in U$ be the unique closed point of V contained in U. Let
$s\in U$ be the unique closed point of V contained in U. Let ![]() $U_0\subset \mathbb {A}^N$ be the local scheme at
$U_0\subset \mathbb {A}^N$ be the local scheme at ![]() $\pi _f (s)$. Since
$\pi _f (s)$. Since ![]() $\pi _f$ carries U into
$\pi _f$ carries U into ![]() $U_0$, we have the following commutative diagram:
$U_0$, we have the following commutative diagram:

Here the restriction map ![]() $(-)\rvert _{U_0}$ is the zero map by the conclusion of Section 5.2.
$(-)\rvert _{U_0}$ is the zero map by the conclusion of Section 5.2.
Now toward the proof of Theorem 5.1, let
be an irreducible cycle. The commutative diagram shows that  $ \left (\pi _f^*\pi _{f*} \Gamma \right )\rvert _U =0$ in
$ \left (\pi _f^*\pi _{f*} \Gamma \right )\rvert _U =0$ in ![]() $H_1(Q_\bullet (X))(U)$. In other words, we have
$H_1(Q_\bullet (X))(U)$. In other words, we have
 $$ \begin{align} \Gamma \rvert_U = \left(\Gamma - \pi _f^*\pi _{f*} \Gamma \right)\rvert_U \quad\text{in }H_1(Q_\bullet(X))(U). \end{align} $$
$$ \begin{align} \Gamma \rvert_U = \left(\Gamma - \pi _f^*\pi _{f*} \Gamma \right)\rvert_U \quad\text{in }H_1(Q_\bullet(X))(U). \end{align} $$This right-hand side turns out to be easier to handle.
Let  $\overline \Gamma \subset V\times X\times \overline \Delta ^1$ be the closure and let
$\overline \Gamma \subset V\times X\times \overline \Delta ^1$ be the closure and let  $B(\Gamma )\subset V\times {\overline \Delta }^{1}$ be the bad locus in formula (5.1). By Lemma 5.2, we know it is a closed proper subset of
$B(\Gamma )\subset V\times {\overline \Delta }^{1}$ be the bad locus in formula (5.1). By Lemma 5.2, we know it is a closed proper subset of ![]() $V\times \left \{ \infty \right \} $. Let
$V\times \left \{ \infty \right \} $. Let ![]() $\overline B (\Gamma )\subsetneq V$ be its projection (which is isomorphic to
$\overline B (\Gamma )\subsetneq V$ be its projection (which is isomorphic to ![]() $B(\Gamma )$).
$B(\Gamma )$).
Proposition 5.6. There is a closed proper subset ![]() $D_2\subsetneq M_{NN'}$ such that whenever
$D_2\subsetneq M_{NN'}$ such that whenever ![]() $f\in M_{NN'}(k)\setminus (D_2\cup D_1)$, we have the equality of zero cycles:
$f\in M_{NN'}(k)\setminus (D_2\cup D_1)$, we have the equality of zero cycles:
 $$ \begin{align} \pi _f^*\pi _{f*}s = s+\sum _{i=1}^m x_i \quad\text{on }V, \end{align} $$
$$ \begin{align} \pi _f^*\pi _{f*}s = s+\sum _{i=1}^m x_i \quad\text{on }V, \end{align} $$where ![]() $s,x_1,\dotsc ,x_m$ are distinct and
$s,x_1,\dotsc ,x_m$ are distinct and ![]() $x_i\in V\setminus \overline B(\Gamma )$ for all i.
$x_i\in V\setminus \overline B(\Gamma )$ for all i.
Proof. This can be shown using Chow’s techniques [Reference Chow8, pp. 458–460], [Reference Chevalley7, p. 3-08, Lemma 2]. We present a proof based on a more recent account [Reference Kai20].
First, since we are using the Veronese embedding (5.11), we can invoke [Reference Kai20, Propositions 3.2 and 3.3], which state that there is a closed proper subset ![]() $D'\subsetneq M_{NN'}$ such that for all
$D'\subsetneq M_{NN'}$ such that for all ![]() $f\in M_{NN'}(k)\setminus (D'\cup D_1)$, the map
$f\in M_{NN'}(k)\setminus (D'\cup D_1)$, the map ![]() $\pi _f\colon V\to \mathbb {A}^N $ is étale over
$\pi _f\colon V\to \mathbb {A}^N $ is étale over ![]() $\pi _f(s)$ and the restriction
$\pi _f(s)$ and the restriction ![]() $s\to \pi _f(s)$ is an isomorphism. This gives an equality of the form (5.14), with s and
$s\to \pi _f(s)$ is an isomorphism. This gives an equality of the form (5.14), with s and ![]() $x_i$s distinct.
$x_i$s distinct.
It remains to show that ![]() $x_i\in V\setminus \overline B(\Gamma )$. We need the following statement:
$x_i\in V\setminus \overline B(\Gamma )$. We need the following statement:
Proposition 5.7 a special case of [Reference Kai20, Proposition 3.5]
Let ![]() $B\subset V$ be a proper closed subset and
$B\subset V$ be a proper closed subset and ![]() $s\in V$ a closed point. Then there is a closed proper subset
$s\in V$ a closed point. Then there is a closed proper subset ![]() $D''\subsetneq M_{NN'}$ such that for all
$D''\subsetneq M_{NN'}$ such that for all ![]() $f\in M_{NN'}(k)\setminus D ''$, we have the equality of subsets of V:
$f\in M_{NN'}(k)\setminus D ''$, we have the equality of subsets of V:
 $$ \begin{align*} \left(\pi _f^{-1}\pi _f (s) \setminus \{ s \} \right) \cap B = \emptyset. \end{align*} $$
$$ \begin{align*} \left(\pi _f^{-1}\pi _f (s) \setminus \{ s \} \right) \cap B = \emptyset. \end{align*} $$ (To extract Proposition 5.7 from [Reference Kai20, Proposition 3.5], set ![]() $X:= V$,
$X:= V$, ![]() $Y:= \operatorname {Spec} (k)$,
$Y:= \operatorname {Spec} (k)$, ![]() $p=0$,
$p=0$, ![]() $W:=B$ and
$W:=B$ and ![]() $V:=\{ s \}$. Also note that the only topological space having dimension
$V:=\{ s \}$. Also note that the only topological space having dimension ![]() $\le -1$ is the empty set.)
$\le -1$ is the empty set.)
Now set ![]() $D_2:= D'\cup D'' $ and suppose
$D_2:= D'\cup D'' $ and suppose ![]() $f\in M_{NN'}(k)\setminus (D_1\cup D_2)$. Then we know
$f\in M_{NN'}(k)\setminus (D_1\cup D_2)$. Then we know  $\pi _f^{-1}\pi _f (s) \setminus \{ s \} = \left \{ x_1,\dotsc ,x_m \right \}$, by the first half of this proof. Applying Proposition 5.7 to
$\pi _f^{-1}\pi _f (s) \setminus \{ s \} = \left \{ x_1,\dotsc ,x_m \right \}$, by the first half of this proof. Applying Proposition 5.7 to ![]() $B:= \overline B(\Gamma )$, we get the desired result. This completes the proof of Proposition 5.6.
$B:= \overline B(\Gamma )$, we get the desired result. This completes the proof of Proposition 5.6.
Corollary 5.8. Take any ![]() $f\in M_{NN'}(k)\setminus (D_1\cup D_2)$ and form the fibre product
$f\in M_{NN'}(k)\setminus (D_1\cup D_2)$ and form the fibre product ![]() $V\times _{\mathbb {A}^N} U$ of
$V\times _{\mathbb {A}^N} U$ of ![]() $\pi _f\colon V\to \mathbb {A}^N$ and
$\pi _f\colon V\to \mathbb {A}^N$ and ![]() $\pi _f\rvert _U \colon U\to \mathbb {A}^N$. Then it decomposes as
$\pi _f\rvert _U \colon U\to \mathbb {A}^N$. Then it decomposes as
where ![]() $T $ is finite and étale over U by the second projection and maps into
$T $ is finite and étale over U by the second projection and maps into ![]() $V\setminus \overline B(\Gamma )$ along the first projection.
$V\setminus \overline B(\Gamma )$ along the first projection.
Proof. Since ![]() $\pi _f $ is finite and étale over
$\pi _f $ is finite and étale over ![]() $U_0$ by Proposition 5.6 and U maps into
$U_0$ by Proposition 5.6 and U maps into ![]() $U_0$, the second projection
$U_0$, the second projection ![]() $V\times _{\mathbb {A}^N} U \to U$ is étale (and finite by default, because
$V\times _{\mathbb {A}^N} U \to U$ is étale (and finite by default, because ![]() $f\in M_{NN'}(k)\setminus D_1$). Since it has the diagonal splitting
$f\in M_{NN'}(k)\setminus D_1$). Since it has the diagonal splitting ![]() $U\to V\times _{\mathbb {A}^N}U$, we have
$U\to V\times _{\mathbb {A}^N}U$, we have ![]() $V\times _{\mathbb {A}^N}U\cong U\sqcup T $. By Proposition 5.6, the set of its closed points can be computed as
$V\times _{\mathbb {A}^N}U\cong U\sqcup T $. By Proposition 5.6, the set of its closed points can be computed as ![]() $V\times _{\mathbb {A}^N} \{ s \} \cong \left \{ s,x_1,\dotsc ,x_m \right \}$, with the right-hand side having the reduced structure, and we know that
$V\times _{\mathbb {A}^N} \{ s \} \cong \left \{ s,x_1,\dotsc ,x_m \right \}$, with the right-hand side having the reduced structure, and we know that ![]() $x_i$s map into
$x_i$s map into ![]() $V\setminus \overline B(\Gamma )$ by the first projection. This completes the proof.
$V\setminus \overline B(\Gamma )$ by the first projection. This completes the proof.
Consider the following Cartesian diagram, where ![]() ${\mathrm {Id}} $ denotes
${\mathrm {Id}} $ denotes ![]() ${\mathrm {Id}} _{X\times \Delta ^1}$:
${\mathrm {Id}} _{X\times \Delta ^1}$:

The element  $\left (\pi _f^*\pi _{f*} \Gamma \right )\rvert _U $ in equation (5.13) is represented by the cycle
$\left (\pi _f^*\pi _{f*} \Gamma \right )\rvert _U $ in equation (5.13) is represented by the cycle ![]() $\left (\left (\pi _f\rvert _U\right )\times {\mathrm {Id}} \right )^*\left (\pi _f \times {\mathrm {Id}} \right )_* \Gamma $ on
$\left (\left (\pi _f\rvert _U\right )\times {\mathrm {Id}} \right )^*\left (\pi _f \times {\mathrm {Id}} \right )_* \Gamma $ on ![]() $U\times X\times \Delta ^1$. By a slight abuse of notation, let us omit
$U\times X\times \Delta ^1$. By a slight abuse of notation, let us omit ![]() ${\mathrm {Id}}$s from the notation in what follows; for example, the previous expression is shortened as
${\mathrm {Id}}$s from the notation in what follows; for example, the previous expression is shortened as ![]() $\left (\pi _f\rvert _U\right )^*\pi _{f*} \Gamma $. By the base-change formula for flat pullback and proper push-forward of algebraic cycles, we know this equals
$\left (\pi _f\rvert _U\right )^*\pi _{f*} \Gamma $. By the base-change formula for flat pullback and proper push-forward of algebraic cycles, we know this equals ![]() $\mathrm {pr} _{2*}\mathrm {pr} _1^*\Gamma $. Via the vertical isomorphism in diagram (5.15), if we write
$\mathrm {pr} _{2*}\mathrm {pr} _1^*\Gamma $. Via the vertical isomorphism in diagram (5.15), if we write ![]() $\mathrm {pr} _{iU}$ and
$\mathrm {pr} _{iU}$ and ![]() $\mathrm {pr} _{iT }$ (
$\mathrm {pr} _{iT }$ (![]() $i=1,2$) for the restrictions of the projections, we get
$i=1,2$) for the restrictions of the projections, we get
 $$ \begin{align} \left(\pi _f^*\pi _{f*} \Gamma \right)\rvert_U = \mathrm{pr} _{2U*}\mathrm{pr} _{1U} ^*\Gamma + \mathrm{pr} _{2T *}\mathrm{pr} _{1T } ^*\Gamma. \end{align} $$
$$ \begin{align} \left(\pi _f^*\pi _{f*} \Gamma \right)\rvert_U = \mathrm{pr} _{2U*}\mathrm{pr} _{1U} ^*\Gamma + \mathrm{pr} _{2T *}\mathrm{pr} _{1T } ^*\Gamma. \end{align} $$ We know that ![]() $\mathrm {pr} _{1U} \colon U\to V$ is the inclusion map and
$\mathrm {pr} _{1U} \colon U\to V$ is the inclusion map and ![]() $\mathrm {pr} _{2U}\colon U\to U$ is the identity map. Thus the first term is
$\mathrm {pr} _{2U}\colon U\to U$ is the identity map. Thus the first term is ![]() $\Gamma \rvert _U$. Therefore we can compute the right-hand side in equation (5.13) as
$\Gamma \rvert _U$. Therefore we can compute the right-hand side in equation (5.13) as
 $$ \begin{align} \left(\Gamma - \pi _f^*\pi _{f*} \Gamma \right)\rvert_U = -\mathrm{pr} _{2T *} \mathrm{pr} _{1T } ^*\Gamma. \end{align} $$
$$ \begin{align} \left(\Gamma - \pi _f^*\pi _{f*} \Gamma \right)\rvert_U = -\mathrm{pr} _{2T *} \mathrm{pr} _{1T } ^*\Gamma. \end{align} $$ By Corollary 5.8, we know that ![]() $\mathrm {pr} _{1T }$ maps
$\mathrm {pr} _{1T }$ maps ![]() $T $ into
$T $ into ![]() $V\setminus \overline B(\Gamma ) \subset V$. In the resulting commutative diagram
$V\setminus \overline B(\Gamma ) \subset V$. In the resulting commutative diagram

we know that  $\Gamma \rvert _{V\setminus \overline B(\Gamma )}$ belongs to the subgroup
$\Gamma \rvert _{V\setminus \overline B(\Gamma )}$ belongs to the subgroup  $ \overline C_1(X)\left (V\setminus \overline B(\Gamma )\right )$ by the definition of
$ \overline C_1(X)\left (V\setminus \overline B(\Gamma )\right )$ by the definition of ![]() $B (\Gamma )$. It follows that
$B (\Gamma )$. It follows that  $\mathrm {pr} _{1T }^*\Gamma \in \overline C_1(X)(T )$. Since
$\mathrm {pr} _{1T }^*\Gamma \in \overline C_1(X)(T )$. Since ![]() $\mathrm {pr} _{2T }\colon T \to U$ is finite, we conclude
$\mathrm {pr} _{2T }\colon T \to U$ is finite, we conclude  $\mathrm {pr} _{2T *}\mathrm {pr} _{1T }^*\Gamma \in \overline C_1(X)(U)$.
$\mathrm {pr} _{2T *}\mathrm {pr} _{1T }^*\Gamma \in \overline C_1(X)(U)$.
Combined with equations (5.13) and (5.17), this shows that ![]() $\Gamma \rvert _U =0 $ in
$\Gamma \rvert _U =0 $ in ![]() $H_1(Q_\bullet (X))(U)$. This completes the proof of Theorem 5.1.
$H_1(Q_\bullet (X))(U)$. This completes the proof of Theorem 5.1.
6 The unramified cohomology  $H_{\mathrm {ur}}^1\left (-, W_n\Omega ^j_{\log }\right )$
$H_{\mathrm {ur}}^1\left (-, W_n\Omega ^j_{\log }\right )$
The aim of this short section is to prove Proposition 6.1.
Let X be a scheme over ![]() $\mathbb {F}_p$. For any integer
$\mathbb {F}_p$. For any integer ![]() $n\ge 1$, let
$n\ge 1$, let ![]() $W_n\Omega ^{\bullet }_{X}$ denote the de Rham–Witt complex of
$W_n\Omega ^{\bullet }_{X}$ denote the de Rham–Witt complex of ![]() $X/\mathbb {F}_p$ (see [Reference Illusie14, I, 1.3]). For any morphism of
$X/\mathbb {F}_p$ (see [Reference Illusie14, I, 1.3]). For any morphism of ![]() $\mathbb {F}_p$-schemes
$\mathbb {F}_p$-schemes ![]() $f\colon Y\to X$, there exists a natural morphism of complexes of
$f\colon Y\to X$, there exists a natural morphism of complexes of ![]() $W_n(\mathcal {O}_Y)$-modules,
$W_n(\mathcal {O}_Y)$-modules,
 $$ \begin{align} f^{-1}W_n\Omega_X^{\bullet}\to W_n\Omega_Y^{\bullet} \end{align} $$
$$ \begin{align} f^{-1}W_n\Omega_X^{\bullet}\to W_n\Omega_Y^{\bullet} \end{align} $$(see [Reference Illusie14, I, (1.12.3)]), which is an isomorphism if f is étale (see [Reference Illusie14, I, Proposition 1.14]).
For any ![]() $i\ge 0$, we denote by
$i\ge 0$, we denote by  $W_n\Omega ^i_{X,\log }$ the logarithmic Hodge–Witt sheaf of X in the sense of [Reference Shiho26, Definition 2.6]. Namely, it is the étale sheaf on X defined as the image
$W_n\Omega ^i_{X,\log }$ the logarithmic Hodge–Witt sheaf of X in the sense of [Reference Shiho26, Definition 2.6]. Namely, it is the étale sheaf on X defined as the image
 $$ \begin{align*} W_n\Omega^i_{X,\log}:= \mathrm{im}\left(\left(\mathcal{O}_X^{\times}\right)^{\otimes i}\to W_n\Omega^i_X\right) \end{align*} $$
$$ \begin{align*} W_n\Omega^i_{X,\log}:= \mathrm{im}\left(\left(\mathcal{O}_X^{\times}\right)^{\otimes i}\to W_n\Omega^i_X\right) \end{align*} $$of the map  $\left (\mathcal {O}_X^{\times }\right )^{\otimes i}\to W_n\Omega ^i_X$;
$\left (\mathcal {O}_X^{\times }\right )^{\otimes i}\to W_n\Omega ^i_X$; ![]() $x_1\otimes \dotsm \otimes x_i\mapsto d\log [x_1]\wedge \dotsb \wedge d\log [x_i]$, where
$x_1\otimes \dotsm \otimes x_i\mapsto d\log [x_1]\wedge \dotsb \wedge d\log [x_i]$, where ![]() $[x]\in W_n\mathcal {O}_X$ is the Teichmüller representative of any local section
$[x]\in W_n\mathcal {O}_X$ is the Teichmüller representative of any local section ![]() $x\in \mathcal {O}_X$. If
$x\in \mathcal {O}_X$. If ![]() $f\colon Y\to X$ is a morphism of
$f\colon Y\to X$ is a morphism of ![]() $\mathbb {F}_p$-schemes, by the functoriality of the de Rham–Witt complexes (6.1) there exists a natural morphism of étale sheaves on Y,
$\mathbb {F}_p$-schemes, by the functoriality of the de Rham–Witt complexes (6.1) there exists a natural morphism of étale sheaves on Y,
 $$ \begin{align} f^{-1}W_n\Omega_{X,\log}^i\to W_n\Omega^i_{Y,\log}. \end{align} $$
$$ \begin{align} f^{-1}W_n\Omega_{X,\log}^i\to W_n\Omega^i_{Y,\log}. \end{align} $$Proposition 6.1. Fix ![]() $n>0$ and
$n>0$ and ![]() $i \ge 0$. We denote by
$i \ge 0$. We denote by  $H_{\mathrm {ur}}^1\left (-, W_n \Omega ^i_{\log }\right )$ the Zariski sheaf on
$H_{\mathrm {ur}}^1\left (-, W_n \Omega ^i_{\log }\right )$ the Zariski sheaf on ![]() $\mathbf {Sm}$ associated to
$\mathbf {Sm}$ associated to
 $$ \begin{align*} H^1\left(-, W_n \Omega^i_{\log}\right) : X \mapsto H_{\mathrm{\acute{e}t}}^1\left(X, W_n \Omega^i_{X, \log}\right). \end{align*} $$
$$ \begin{align*} H^1\left(-, W_n \Omega^i_{\log}\right) : X \mapsto H_{\mathrm{\acute{e}t}}^1\left(X, W_n \Omega^i_{X, \log}\right). \end{align*} $$Then  $H_{\mathrm {ur}}^1\left (-, W_n \Omega ^i_{\log }\right )$ is a
$H_{\mathrm {ur}}^1\left (-, W_n \Omega ^i_{\log }\right )$ is a ![]() $\mathbb {P}^1$-invariant Nisnevich sheaf, and has a structure of presheaf with transfers.
$\mathbb {P}^1$-invariant Nisnevich sheaf, and has a structure of presheaf with transfers.
Remark 6.2. As mentioned in the introduction, it is known that  $H_{\mathrm {ur}}^1\left (-, W_n \Omega ^i_{\log }\right )$ has reciprocity [Reference Binda, Rülling and Saito5, Section 11.1 (5)], hence it is
$H_{\mathrm {ur}}^1\left (-, W_n \Omega ^i_{\log }\right )$ has reciprocity [Reference Binda, Rülling and Saito5, Section 11.1 (5)], hence it is ![]() $\mathbb {P}^1$-invariant by [Reference Kahn, Saito and Yamazaki18, Theorem 8]. We shall give a direct proof of Proposition 6.1 which makes no use of the theory of reciprocity sheaves.
$\mathbb {P}^1$-invariant by [Reference Kahn, Saito and Yamazaki18, Theorem 8]. We shall give a direct proof of Proposition 6.1 which makes no use of the theory of reciprocity sheaves.
To ease the notation, for ![]() $q=0,1$ we set
$q=0,1$ we set
 $$ \begin{align*} F^{q,i} := H^q\left(-, W_n \Omega^i_{\log}\right), \qquad F^{q,i}_{\mathrm{ur}} := H^q_{\mathrm{ur}}\left(-, W_n \Omega^i_{\log}\right). \end{align*} $$
$$ \begin{align*} F^{q,i} := H^q\left(-, W_n \Omega^i_{\log}\right), \qquad F^{q,i}_{\mathrm{ur}} := H^q_{\mathrm{ur}}\left(-, W_n \Omega^i_{\log}\right). \end{align*} $$We have  $F^{q,i}(S)=F^{q,i}_{\mathrm {ur}}(S)$ for any local S.
$F^{q,i}(S)=F^{q,i}_{\mathrm {ur}}(S)$ for any local S.
Theorem 6.3. For any ![]() $X \in \mathbf {Sm}$ and any
$X \in \mathbf {Sm}$ and any ![]() $q=0,1$, we have an exact sequence
$q=0,1$, we have an exact sequence
 $$ \begin{align*} 0 \to F^{q,i}_{\mathrm{ur}}(X) \to \bigoplus_{x \in X^{(0)}} F^{q,i}(x) \to \bigoplus_{x \in X^{(1)}} G^{q,i}_x(X), \end{align*} $$
$$ \begin{align*} 0 \to F^{q,i}_{\mathrm{ur}}(X) \to \bigoplus_{x \in X^{(0)}} F^{q,i}(x) \to \bigoplus_{x \in X^{(1)}} G^{q,i}_x(X), \end{align*} $$where we set  $G_x^{q,i}(X):=H^{q+1}_x\left (X, W_n \Omega ^i_{X, \log }\right )$. Moreover, if
$G_x^{q,i}(X):=H^{q+1}_x\left (X, W_n \Omega ^i_{X, \log }\right )$. Moreover, if ![]() $q=0$ there exists a canonical isomorphism
$q=0$ there exists a canonical isomorphism
 $$ \begin{align*} \theta^{i}_x\colon F^{0,i-1}(k(x))\xrightarrow{\simeq}G_x^{0,i}(X) \end{align*} $$
$$ \begin{align*} \theta^{i}_x\colon F^{0,i-1}(k(x))\xrightarrow{\simeq}G_x^{0,i}(X) \end{align*} $$for any codimension ![]() $1$ point
$1$ point ![]() $x\in X^{(1)}$.
$x\in X^{(1)}$.
Proof. For the first assertion, see [Reference Gros and Suwa12, Theorem 1.4] or [Reference Shiho26, Theorem 4.1]. For the last assertion, see [Reference Shiho26, Theorem 3.2].
Proposition 6.4. The étale sheaf  $W_n\Omega _{\log }^i$ on
$W_n\Omega _{\log }^i$ on ![]() $\mathbf {Sm}$ has a structure of presheaf with transfers. Hence so does the étale cohomology group
$\mathbf {Sm}$ has a structure of presheaf with transfers. Hence so does the étale cohomology group  $H^j\left (-,W_n\Omega _{\log }^i\right )$ for any
$H^j\left (-,W_n\Omega _{\log }^i\right )$ for any ![]() $j\ge 0$.
$j\ge 0$.
Proof. According to [Reference Mazza, Voevodsky and Weibel22, 6.21], the second assertion is immediate from the first one. Therefore, it suffices to show that  $W_n\Omega ^i_{\log }\in \mathbf {PST}$. However, thanks to Theorem 6.3 together with the theorem of Bloch, Gabber and Kato [Reference Bloch and Kato6], for any
$W_n\Omega ^i_{\log }\in \mathbf {PST}$. However, thanks to Theorem 6.3 together with the theorem of Bloch, Gabber and Kato [Reference Bloch and Kato6], for any ![]() $X\in \mathbf {Sm}$ we have a natural exact sequence
$X\in \mathbf {Sm}$ we have a natural exact sequence
 $$ \begin{align*} 0\to H^0\left(X,W_n\Omega^i_{\log}\right)\to\bigoplus_{x \in X^{(0)}} K^{\textrm{M}}_i(k(x))/p^n \xrightarrow{\left(\partial^{\textrm{M}}_x\right)} \bigoplus_{x \in X^{(1)}}K_{i-1}^{\textrm{M}}(k(x))/p^n, \end{align*} $$
$$ \begin{align*} 0\to H^0\left(X,W_n\Omega^i_{\log}\right)\to\bigoplus_{x \in X^{(0)}} K^{\textrm{M}}_i(k(x))/p^n \xrightarrow{\left(\partial^{\textrm{M}}_x\right)} \bigoplus_{x \in X^{(1)}}K_{i-1}^{\textrm{M}}(k(x))/p^n, \end{align*} $$where ![]() $\partial _x^{\textrm {M}}$ is the tame symbol at each
$\partial _x^{\textrm {M}}$ is the tame symbol at each ![]() $x\in X^{(1)}$. This implies that the sheaf
$x\in X^{(1)}$. This implies that the sheaf  $W_n\Omega ^i_{\log }$ has a structure of (homotopy-invariant) presheaf with transfers (see [Reference Kahn16]). This completes the proof of the proposition.
$W_n\Omega ^i_{\log }$ has a structure of (homotopy-invariant) presheaf with transfers (see [Reference Kahn16]). This completes the proof of the proposition.
Proposition 6.5. Let ![]() $f : Y \to X$ be an étale morphism in
$f : Y \to X$ be an étale morphism in ![]() $\mathbf {Sm}$ which induces an isomorphism
$\mathbf {Sm}$ which induces an isomorphism ![]() $k(y) \cong k(x)$ for some
$k(y) \cong k(x)$ for some ![]() $y \in Y^{(1)}$ and
$y \in Y^{(1)}$ and ![]() $x:=f(y)$. Then for
$x:=f(y)$. Then for ![]() $q=0,1$, in the commutative diagram
$q=0,1$, in the commutative diagram

all maps are bijective.
Proof. For ![]() $q=0$, the assertion follows from the last claim of Theorem 6.3. So let us assume that
$q=0$, the assertion follows from the last claim of Theorem 6.3. So let us assume that ![]() $q=1$. Then the bijectivity of the left vertical map is a consequence of the localisation sequence
$q=1$. Then the bijectivity of the left vertical map is a consequence of the localisation sequence
 $$ \begin{align*} F^{1,i}\left(\mathcal{O}_{X, x}\right) \to F^{1,i}\left(\operatorname{Frac} \mathcal{O}_{X, x}\right) \to G_x^{1,i}(X) \to H^2\left(\mathcal{O}_{X, x}, W_n \Omega^i_{X, \log}\right)=0, \end{align*} $$
$$ \begin{align*} F^{1,i}\left(\mathcal{O}_{X, x}\right) \to F^{1,i}\left(\operatorname{Frac} \mathcal{O}_{X, x}\right) \to G_x^{1,i}(X) \to H^2\left(\mathcal{O}_{X, x}, W_n \Omega^i_{X, \log}\right)=0, \end{align*} $$and the same for the right vertical map. The statement for the upper horizontal map in the case when ![]() $n=1$ is a consequence of [Reference Totaro29, Theorem 4.3]. Indeed, given any discrete valuation ring over k, the cited theorem shows that there is an exhaustive filtration
$n=1$ is a consequence of [Reference Totaro29, Theorem 4.3]. Indeed, given any discrete valuation ring over k, the cited theorem shows that there is an exhaustive filtration ![]() $F^{1,i}(R)=U_{-1} \subset U_0 \subset U_1 \subset \dotsb \subset F^{1,i}(\operatorname {Frac} R)$ whose graded quotients are described solely in terms of the residue field. In our situation,
$F^{1,i}(R)=U_{-1} \subset U_0 \subset U_1 \subset \dotsb \subset F^{1,i}(\operatorname {Frac} R)$ whose graded quotients are described solely in terms of the residue field. In our situation, ![]() $F^{1,i}\left (\operatorname {Frac} \mathcal {O}_{X, x}\right ) \to F^{1,i}\left (\operatorname {Frac} \mathcal {O}_{Y, y}\right )$ respects this filtration because
$F^{1,i}\left (\operatorname {Frac} \mathcal {O}_{X, x}\right ) \to F^{1,i}\left (\operatorname {Frac} \mathcal {O}_{Y, y}\right )$ respects this filtration because ![]() $\mathcal {O}_{X, x} \to \mathcal {O}_{Y, y}$ is étale. Hence the desired bijectivity follows from the assumption
$\mathcal {O}_{X, x} \to \mathcal {O}_{Y, y}$ is étale. Hence the desired bijectivity follows from the assumption ![]() $k(y) \cong k(x)$. For
$k(y) \cong k(x)$. For ![]() $n>1$, thanks to the exact sequence
$n>1$, thanks to the exact sequence
 $$ \begin{align*} 0\to W_{n-1}\Omega^i_{X,\log}\to W_{n}\Omega^i_{X,\log}\to \Omega^i_{X,\log}\to 0 \end{align*} $$
$$ \begin{align*} 0\to W_{n-1}\Omega^i_{X,\log}\to W_{n}\Omega^i_{X,\log}\to \Omega^i_{X,\log}\to 0 \end{align*} $$for any regular scheme X over ![]() $\mathbb {F}_p$ (see [Reference Shiho26, Proposition 2.12]), one can inductively see the bijectivity of the map
$\mathbb {F}_p$ (see [Reference Shiho26, Proposition 2.12]), one can inductively see the bijectivity of the map ![]() $F^{1,i}\left (\operatorname {Frac} \mathcal {O}_{X, x}\right )/F^{1,i}\left (\mathcal {O}_{X, x}\right )\to F^{1,i}\left (\operatorname {Frac} \mathcal {O}_{Y, y}\right )/F^{1,i}\left (\mathcal {O}_{Y, y}\right )$. This completes the proof.
$F^{1,i}\left (\operatorname {Frac} \mathcal {O}_{X, x}\right )/F^{1,i}\left (\mathcal {O}_{X, x}\right )\to F^{1,i}\left (\operatorname {Frac} \mathcal {O}_{Y, y}\right )/F^{1,i}\left (\mathcal {O}_{Y, y}\right )$. This completes the proof.
Proof of Proposition 6.1. We first show that ![]() $F^{1,i}_{\mathrm {ur}}$ is a sheaf for Nisnevich topology. For this, we take a Cartesian diagram in
$F^{1,i}_{\mathrm {ur}}$ is a sheaf for Nisnevich topology. For this, we take a Cartesian diagram in ![]() $\mathbf {Sm}$
$\mathbf {Sm}$

where j is an open dense immersion and f is an étale morphism that is an isomorphism over ![]() $X \setminus j(U)$. By [Reference Mazza, Voevodsky and Weibel22, 12.7], it suffices to prove the exactness of the upper row in the commutative diagram
$X \setminus j(U)$. By [Reference Mazza, Voevodsky and Weibel22, 12.7], it suffices to prove the exactness of the upper row in the commutative diagram

The second row is exact for obvious reason, and all columns are exact by Theorem 6.3. The map ![]() $(*)$ is injective by Proposition 6.5 (and the assumption on f). Now the claim follows by diagram chasing. As a consequence, we can find that
$(*)$ is injective by Proposition 6.5 (and the assumption on f). Now the claim follows by diagram chasing. As a consequence, we can find that ![]() $F^{1,i}_{{\mathrm {ur}}}$ is the same as the Nisnevich sheaf associated with
$F^{1,i}_{{\mathrm {ur}}}$ is the same as the Nisnevich sheaf associated with ![]() $F^{1,i}\in \mathbf {PST}$ (see Proposition 6.4). Therefore, we conclude that
$F^{1,i}\in \mathbf {PST}$ (see Proposition 6.4). Therefore, we conclude that ![]() $F^{1,i}_{\mathrm {ur}} \in \mathbf {PST}$ by [Reference Mazza, Voevodsky and Weibel22, 13.1].
$F^{1,i}_{\mathrm {ur}} \in \mathbf {PST}$ by [Reference Mazza, Voevodsky and Weibel22, 13.1].
Finally, to show that ![]() $F^{1,i}_{{\mathrm {ur}}}$ is
$F^{1,i}_{{\mathrm {ur}}}$ is ![]() $\mathbb {P}^1$-invariant, we apply Lemma 6.6. Condition (1) is due to Izhboldin [Reference Izhboldin15] (see also [Reference Totaro29, Theorem 4.4]), and (2) is a part of Theorem 6.3.
$\mathbb {P}^1$-invariant, we apply Lemma 6.6. Condition (1) is due to Izhboldin [Reference Izhboldin15] (see also [Reference Totaro29, Theorem 4.4]), and (2) is a part of Theorem 6.3.
Lemma 6.6. Set ![]() $F \in \mathbf {PST}$. Suppose the following conditions hold:
$F \in \mathbf {PST}$. Suppose the following conditions hold:
(1) For any
 $K \in \mathbf {Fld}_k^{\mathrm {gm}}$,
$K \in \mathbf {Fld}_k^{\mathrm {gm}}$,  $\sigma _K^* : F(\operatorname {Spec} K) \cong F\left (\mathbb {P}^1_K\right )$ is an isomorphism, where
$\sigma _K^* : F(\operatorname {Spec} K) \cong F\left (\mathbb {P}^1_K\right )$ is an isomorphism, where  $\sigma _K$ denotes the base change of the structure morphism
$\sigma _K$ denotes the base change of the structure morphism  $\sigma : \mathbb {P}^1 \to \operatorname {Spec} k$.
$\sigma : \mathbb {P}^1 \to \operatorname {Spec} k$.(2) Any open immersion
 $U \hookrightarrow V$ in
$U \hookrightarrow V$ in  $\mathbf {Sm}$ induces an injection
$\mathbf {Sm}$ induces an injection  $F(V) \to F(U)$.
$F(V) \to F(U)$.
Then F is ![]() $\mathbb {P}^1$-invariant.
$\mathbb {P}^1$-invariant.
Proof. Define ![]() $G \in \mathbf {PST}$ by the formula
$G \in \mathbf {PST}$ by the formula
 $$ \begin{align} G(U) := \operatorname{Coker}\left(\sigma^* : F(U) \to \operatorname{\underline{Hom}}\left(\mathbb{Z}_{\mathrm{tr}}\left(\mathbb{P}^1\right), F\right)(U)=F\left(U \times \mathbb{P}^1\right)\right) \quad (U \in \mathbf{Sm}). \end{align} $$
$$ \begin{align} G(U) := \operatorname{Coker}\left(\sigma^* : F(U) \to \operatorname{\underline{Hom}}\left(\mathbb{Z}_{\mathrm{tr}}\left(\mathbb{P}^1\right), F\right)(U)=F\left(U \times \mathbb{P}^1\right)\right) \quad (U \in \mathbf{Sm}). \end{align} $$We have a direct sum decomposition ![]() $\operatorname {\underline {Hom}}\left (\mathbb {Z}_{\mathrm {tr}}\left (\mathbb {P}^1\right ), F\right ) \cong F \oplus G$ (provided by a k-rational point of
$\operatorname {\underline {Hom}}\left (\mathbb {Z}_{\mathrm {tr}}\left (\mathbb {P}^1\right ), F\right ) \cong F \oplus G$ (provided by a k-rational point of ![]() $\mathbb {P}^1$), and
$\mathbb {P}^1$), and ![]() $G(U)=0$ holds if and only if the map in formula (6.3) is an isomorphism. By (1), we have
$G(U)=0$ holds if and only if the map in formula (6.3) is an isomorphism. By (1), we have ![]() $G(\operatorname {Spec} K)=0$ for any
$G(\operatorname {Spec} K)=0$ for any  $K \in \mathbf {Fld}_k^{\mathrm {gm}}$. Property (2) for F implies the same property for
$K \in \mathbf {Fld}_k^{\mathrm {gm}}$. Property (2) for F implies the same property for ![]() $\operatorname {\underline {Hom}}\left (\mathbb {Z}_{\mathrm {tr}}\left (\mathbb {P}^1\right ), F\right )$ and hence for G. We conclude that
$\operatorname {\underline {Hom}}\left (\mathbb {Z}_{\mathrm {tr}}\left (\mathbb {P}^1\right ), F\right )$ and hence for G. We conclude that ![]() $G(U) \hookrightarrow G(k(U))=0$ for any (irreducible)
$G(U) \hookrightarrow G(k(U))=0$ for any (irreducible) ![]() $U \in \mathbf {Sm}$, which means F is
$U \in \mathbf {Sm}$, which means F is ![]() $\mathbb {P}^1$-invariant.
$\mathbb {P}^1$-invariant.
A Proof of Remark 2.5
We give a proof of Remark 2.5. Property (1) is obvious. Property (2) is a consequence of the formula ![]() $h_0(X \times X')=h_0(X) \otimes h_0(X')$. For (3) and (4), we shall freely use Voevodsky’s triangulated category
$h_0(X \times X')=h_0(X) \otimes h_0(X')$. For (3) and (4), we shall freely use Voevodsky’s triangulated category ![]() $\operatorname {\mathbf {DM}}^-_{\mathrm {eff}}(k) \subset D^-(\mathbf {NST})$ of effective motivic complexes over k [Reference Voevodsky31]. For
$\operatorname {\mathbf {DM}}^-_{\mathrm {eff}}(k) \subset D^-(\mathbf {NST})$ of effective motivic complexes over k [Reference Voevodsky31]. For ![]() $V \in \mathbf {Sm}$, we denote the motivic complex of V by
$V \in \mathbf {Sm}$, we denote the motivic complex of V by ![]() $M(V):=C_*(\mathbb {Z}_{\mathrm {tr}}(V)) \in \operatorname {\mathbf {DM}}^-_{\mathrm {eff}}(k)$. Recall that its homology sheaves
$M(V):=C_*(\mathbb {Z}_{\mathrm {tr}}(V)) \in \operatorname {\mathbf {DM}}^-_{\mathrm {eff}}(k)$. Recall that its homology sheaves ![]() $h_n(V):=H_n(M(V))$ are trivial if
$h_n(V):=H_n(M(V))$ are trivial if ![]() $n<0$, and for
$n<0$, and for ![]() $n=0$ it recovers
$n=0$ it recovers ![]() $h_0(V)$ defined in (V2).
$h_0(V)$ defined in (V2).
Lemma A.1. Let ![]() $c>0$ be a positive integer and let
$c>0$ be a positive integer and let ![]() $j : U \to X$ be an open immersion in
$j : U \to X$ be an open immersion in ![]() $\mathbf {Sm}$. Define
$\mathbf {Sm}$. Define ![]() $M(X/U)$ to be the cone of
$M(X/U)$ to be the cone of ![]() $j_*:M(U) \to M(X)$. If each component of
$j_*:M(U) \to M(X)$. If each component of ![]() $Z := (X \setminus U)_{\mathrm {red}}$ is of codimension
$Z := (X \setminus U)_{\mathrm {red}}$ is of codimension ![]() $\ge c$ in X, then
$\ge c$ in X, then ![]() $h_n(X/U):=H_n(M(X/U))$ vanishes for any
$h_n(X/U):=H_n(M(X/U))$ vanishes for any ![]() $n<c$.
$n<c$.
Proof. If Z is smooth over k, then by the Gysin triangle [Reference Mazza, Voevodsky and Weibel22, Theorem 15.15] we have
from which the statement follows. In general, let ![]() $Z' \subset Z$ be the singular locus of Z, and define
$Z' \subset Z$ be the singular locus of Z, and define ![]() $U':=X \setminus Z'$. There is a distinguished triangle
$U':=X \setminus Z'$. There is a distinguished triangle
Since each component of ![]() $Z'$ has codimension
$Z'$ has codimension ![]() $\ge c+1$ in X, we may assume
$\ge c+1$ in X, we may assume ![]() $h_n(X/U')=0$ for any
$h_n(X/U')=0$ for any ![]() $n \le c$ by induction. Since
$n \le c$ by induction. Since ![]() $U' \setminus U = Z \setminus Z'$ is smooth over k, we have shown
$U' \setminus U = Z \setminus Z'$ is smooth over k, we have shown ![]() $h_n(U'/U)=0$ for
$h_n(U'/U)=0$ for ![]() $n<c$. It follows that
$n<c$. It follows that ![]() $h_n(X/U)=0$ for
$h_n(X/U)=0$ for ![]() $n<c$.
$n<c$.
Now (3) immediately follows from Lemma A.1. To show (4), let ![]() $f : X \to Y$ be a proper birational morphism in
$f : X \to Y$ be a proper birational morphism in ![]() $\mathbf {Sm}$. Let
$\mathbf {Sm}$. Let ![]() $V \subset Y$ be the open dense subset on which
$V \subset Y$ be the open dense subset on which ![]() $f^{-1}$ is defined. Then f restricts to an isomorphism
$f^{-1}$ is defined. Then f restricts to an isomorphism  $U:=f^{-1}(V) \overset {\cong }{\longrightarrow } V$ and
$U:=f^{-1}(V) \overset {\cong }{\longrightarrow } V$ and ![]() $Y \setminus V$ has codimension
$Y \setminus V$ has codimension ![]() $\ge 2$ in Y. We have a commutative diagram
$\ge 2$ in Y. We have a commutative diagram

in which we used Lemma A.1 for the vanishing. This proves (4).
Acknowledgments
The second author would like to thank Tomoyuki Abe for fruitful discussions and suggestions, which brought him into Voevodsky’s theory of motives. Without that, this joint project would have never started. The authors thank Bruno Kahn for his intriguing comments on birational sheaves.
The first author is supported by a JSPS KAKENHI Grant (JP18K13382). The second author is supported by JSPS KAKENHI Grants (JP19J00366, JP21K20334). The third author is supported by JSPS KAKENHI Grants (JP18K03232, JP21K03153).
Conflict of Interest
None.