Article contents
Tropically constructed Lagrangians in mirror quintic threefolds
Published online by Cambridge University Press: 20 November 2020
Abstract
We use tropical curves and toric degeneration techniques to construct closed embedded Lagrangian rational homology spheres in a lot of Calabi-Yau threefolds. The homology spheres are mirror dual to the holomorphic curves contributing to the Gromov-Witten (GW) invariants. In view of Joyce’s conjecture, these Lagrangians are expected to have special Lagrangian representatives and hence solve a special Lagrangian enumerative problem in Calabi-Yau threefolds.
We apply this construction to the tropical curves obtained from the 2,875 lines on the quintic Calabi-Yau threefold. Each admissible tropical curve gives a Lagrangian rational homology sphere in the corresponding mirror quintic threefold and the Joyce’s weight of each of these Lagrangians equals the multiplicity of the corresponding tropical curve.
As applications, we show that disjoint curves give pairwise homologous but non-Hamiltonian isotopic Lagrangians and we check in an example that
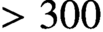 $>300$
mutually disjoint curves (and hence Lagrangians) arise. Dehn twists along these Lagrangians generate an abelian subgroup of the symplectic mapping class group with that rank.
$>300$
mutually disjoint curves (and hence Lagrangians) arise. Dehn twists along these Lagrangians generate an abelian subgroup of the symplectic mapping class group with that rank.
- Type
- Differential Geometry and Geometric Analysis
- Information
- Creative Commons
- This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
- Copyright
- © The Author(s), 2020. Published by Cambridge University Press
References
- 11
- Cited by



