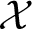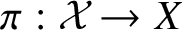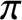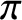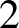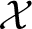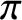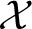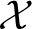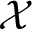1 Introduction
Let X be a variety with log-terminal singularities. Motivated by mirror symmetry for singular Calabi–Yau varieties, Batyrev introduced stringy Hodge numbers for X in [Reference BatyrevBat98], which are defined in terms of a resolution of singularities. In particular, if X admits a crepant resolution
![]() $Y \to X$
by a smooth projective variety Y, then the stringy Hodge numbers of X are equal to the usual Hodge numbers of Y. In [Reference Denef and LoeserDL02], Denef and Loeser defined the Gorenstein measure
$Y \to X$
by a smooth projective variety Y, then the stringy Hodge numbers of X are equal to the usual Hodge numbers of Y. In [Reference Denef and LoeserDL02], Denef and Loeser defined the Gorenstein measure
 $\mu ^{\mathrm {Gor}}_X$
on the arc scheme
$\mu ^{\mathrm {Gor}}_X$
on the arc scheme
![]() $\mathscr {L}(X)$
of X and used it to prove a McKay correspondence that refines the McKay correspondence conjectured by Reid in [Reference ReidRei92] and proved by Batyrev in [Reference BatyrevBat99]. The measure
$\mathscr {L}(X)$
of X and used it to prove a McKay correspondence that refines the McKay correspondence conjectured by Reid in [Reference ReidRei92] and proved by Batyrev in [Reference BatyrevBat99]. The measure
 $\mu ^{\mathrm {Gor}}_X$
takes values in a modified Grothendieck ring of varieties
$\mu ^{\mathrm {Gor}}_X$
takes values in a modified Grothendieck ring of varieties
 $\widehat {\mathscr {M}}_k\left [\mathbb {L}^{1/m}\right ]$
and is a refinement of the stringy Hodge numbers of X. If X admits a crepant resolution
$\widehat {\mathscr {M}}_k\left [\mathbb {L}^{1/m}\right ]$
and is a refinement of the stringy Hodge numbers of X. If X admits a crepant resolution
![]() $Y \to X$
, then
$Y \to X$
, then
 $\mu ^{\mathrm {Gor}}_X$
is essentially equivalent to the usual motivic measure
$\mu ^{\mathrm {Gor}}_X$
is essentially equivalent to the usual motivic measure
![]() $\mu _Y$
on
$\mu _Y$
on
![]() $\mathscr {L}(Y)$
as introduced by Kontsevich in [Reference KontsevichKon95].
$\mathscr {L}(Y)$
as introduced by Kontsevich in [Reference KontsevichKon95].
A major open question asks whether or not the stringy Hodge numbers of projective varieties are nonnegative, as conjectured by Batyrev in [Reference BatyrevBat98, Conjecture 3.10]. A stronger conjecture predicts that stringy Hodge numbers of projective varieties are equal to the dimensions of some kind of cohomology groups. In [Reference YasudaYas04], these conjectures were proved in the case where X has quotient singularites. Yasuda showed that in that case, if
![]() $\mathcal {X}$
is the canonical smooth Deligne–Mumford stack over X, then the stringy Hodge numbers of X are equal to the orbifold Hodge numbers of
$\mathcal {X}$
is the canonical smooth Deligne–Mumford stack over X, then the stringy Hodge numbers of X are equal to the orbifold Hodge numbers of
![]() $\mathcal {X}$
in the sense of Chen and Ruan [Reference Chen and RuanCR04]. To prove this result, Yasuda introduced a notion of motivic integration (further developed in [Reference YasudaYas06, Reference YasudaYas19]) for Deligne–Mumford stacks and proved a formula expressing
$\mathcal {X}$
in the sense of Chen and Ruan [Reference Chen and RuanCR04]. To prove this result, Yasuda introduced a notion of motivic integration (further developed in [Reference YasudaYas06, Reference YasudaYas19]) for Deligne–Mumford stacks and proved a formula expressing
 $\mu ^{\mathrm {Gor}}_X$
in terms of certain motivic integrals over arcs of
$\mu ^{\mathrm {Gor}}_X$
in terms of certain motivic integrals over arcs of
![]() $\mathcal {X}$
. When X is projective, those integrals over arcs of
$\mathcal {X}$
. When X is projective, those integrals over arcs of
![]() $\mathcal {X}$
compute the orbifold Hodge numbers of
$\mathcal {X}$
compute the orbifold Hodge numbers of
![]() $\mathcal {X}$
.
$\mathcal {X}$
.
In this paper, we initiate a similar program for varieties with singularities that are worse than quotient singularities. Such varieties never arise as the coarse space of a smooth Deligne–Mumford stack, so one is instead forced to consider Artin stacks. A major technicality is that such stacks are not separated. This leads us to define new functions
![]() $\operatorname {\mathrm {sep}}_{\pi , \mathcal {C}}$
, discussed later, which measure the degree to which an Artin stack is not separated. These functions play a key role in our theory.
$\operatorname {\mathrm {sep}}_{\pi , \mathcal {C}}$
, discussed later, which measure the degree to which an Artin stack is not separated. These functions play a key role in our theory.
The class of varieties we consider are those X occurring as the good moduli space (in the sense of [Reference AlperAlp13]) of a smooth Artin stack
![]() $\mathcal {X}$
; varieties of this form arise naturally in the context of geometric invariant theory. We require that the map
$\mathcal {X}$
; varieties of this form arise naturally in the context of geometric invariant theory. We require that the map
![]() $\pi \colon \mathcal {X} \to X$
induce an isomorphism over a nonempty open subset of X and that the exceptional locus of
$\pi \colon \mathcal {X} \to X$
induce an isomorphism over a nonempty open subset of X and that the exceptional locus of
![]() $\pi $
have codimension at least
$\pi $
have codimension at least
![]() $2$
. In other words, we want
$2$
. In other words, we want
![]() $\mathcal {X}$
to be a ‘small’ resolution of X. We conjecture a relationship between
$\mathcal {X}$
to be a ‘small’ resolution of X. We conjecture a relationship between
 $\mu ^{\mathrm {Gor}}_X$
and a motivic measure
$\mu ^{\mathrm {Gor}}_X$
and a motivic measure
![]() $\mu _{\mathcal {X}}$
on the arc stack
$\mu _{\mathcal {X}}$
on the arc stack
![]() $\mathscr {L}(\mathcal {X})$
of
$\mathscr {L}(\mathcal {X})$
of
![]() $\mathcal {X}$
. This relationship involves integrating
$\mathcal {X}$
. This relationship involves integrating
![]() $\operatorname {\mathrm {sep}}_{\pi , \mathcal {C}}: \mathscr {L}(X) \to \mathbb {N}$
against
$\operatorname {\mathrm {sep}}_{\pi , \mathcal {C}}: \mathscr {L}(X) \to \mathbb {N}$
against
 $\mu ^{\mathrm {Gor}}_X$
. This function
$\mu ^{\mathrm {Gor}}_X$
. This function
![]() $\operatorname {\mathrm {sep}}_{\pi , \mathcal {C}}$
counts the number of arcs of
$\operatorname {\mathrm {sep}}_{\pi , \mathcal {C}}$
counts the number of arcs of
![]() $\mathcal {X}$
(in some auxiliary measurable subset
$\mathcal {X}$
(in some auxiliary measurable subset
![]() $\mathcal {C}$
), up to isomorphism, above each arc of X, and can therefore be thought of as an invariant which measures the nonseparatedness of
$\mathcal {C}$
), up to isomorphism, above each arc of X, and can therefore be thought of as an invariant which measures the nonseparatedness of
![]() $\pi $
. We emphasise that this conjectural relationship is not ‘built into’ our definition of
$\pi $
. We emphasise that this conjectural relationship is not ‘built into’ our definition of
![]() $\mu _{\mathcal {X}}$
. In fact, our notion of
$\mu _{\mathcal {X}}$
. In fact, our notion of
![]() $\mu _{\mathcal {X}}$
is straightforward: it is more or less Kontsevich’s original motivic measure, except that various notions for schemes are replaced with the obvious analogues for Artin stacks. When the stabilisers of
$\mu _{\mathcal {X}}$
is straightforward: it is more or less Kontsevich’s original motivic measure, except that various notions for schemes are replaced with the obvious analogues for Artin stacks. When the stabilisers of
![]() $\mathcal {X}$
are special groups in the sense of SerreFootnote
1
and
$\mathcal {X}$
are special groups in the sense of SerreFootnote
1
and
![]() $\mathscr {L}(\pi ): \mathscr {L}(\mathcal {X}) \to \mathscr {L}(X)$
has finite fibres outside a set of measure
$\mathscr {L}(\pi ): \mathscr {L}(\mathcal {X}) \to \mathscr {L}(X)$
has finite fibres outside a set of measure
![]() $0$
, our conjectures imply a formula expressing the stringy Hodge numbers of X in terms of a certain motivic integral over
$0$
, our conjectures imply a formula expressing the stringy Hodge numbers of X in terms of a certain motivic integral over
![]() $\mathscr {L}(\mathcal {X})$
.
$\mathscr {L}(\mathcal {X})$
.
We prove that our conjectures hold when X is a toric variety and
![]() $\mathcal {X}$
is a fantastack – that is, a type of smooth toric Artin stack in the sense of [Reference Geraschenko and SatrianoGS15a, Reference Geraschenko and SatrianoGS15b]. Fantastacks are a broad class of toric stacks that allow one to simultaneously have any specified toric variety X as a good moduli space while also obtaining stabilisers with arbitrarily large dimension. An important special case of fantastacks (and their products with algebraic tori) is the so-called canonical stack
$\mathcal {X}$
is a fantastack – that is, a type of smooth toric Artin stack in the sense of [Reference Geraschenko and SatrianoGS15a, Reference Geraschenko and SatrianoGS15b]. Fantastacks are a broad class of toric stacks that allow one to simultaneously have any specified toric variety X as a good moduli space while also obtaining stabilisers with arbitrarily large dimension. An important special case of fantastacks (and their products with algebraic tori) is the so-called canonical stack
![]() $\mathcal {X}$
over a toric variety X. When X has quotient singularities,
$\mathcal {X}$
over a toric variety X. When X has quotient singularities,
![]() $\mathcal {X}$
is the canonical smooth Deligne–Mumford stack over X; when X has worse singularities, the good moduli space of
$\mathcal {X}$
is the canonical smooth Deligne–Mumford stack over X; when X has worse singularities, the good moduli space of
![]() $\mathcal {X}$
is still X, but
$\mathcal {X}$
is still X, but
![]() $\mathcal {X}$
is an Artin stack that is not Deligne–Mumford.
$\mathcal {X}$
is an Artin stack that is not Deligne–Mumford.
1.1 Conventions
Throughout this paper, k will be an algebraically closed field with characteristic
![]() $0$
. All Artin stacks will be assumed to have affine (geometric) stabilisers, and all toric varieties will be assumed to be normal. For any stack
$0$
. All Artin stacks will be assumed to have affine (geometric) stabilisers, and all toric varieties will be assumed to be normal. For any stack
![]() $\mathcal {X}$
over k, we will let
$\mathcal {X}$
over k, we will let
![]() $\lvert \mathcal {X}\rvert $
denote the topological space associated to
$\lvert \mathcal {X}\rvert $
denote the topological space associated to
![]() $\mathcal {X}$
, and for any k-algebra R, we will let
$\mathcal {X}$
, and for any k-algebra R, we will let
![]() $\overline {\mathcal {X}}(R)$
denote the set of isomorphism classes of the category
$\overline {\mathcal {X}}(R)$
denote the set of isomorphism classes of the category
![]() $\mathcal {X}(R)$
.
$\mathcal {X}(R)$
.
1.2 Conjectures
Our first conjecture predicts a relationship between
 $\mu ^{\mathrm {Gor}}_X$
and
$\mu ^{\mathrm {Gor}}_X$
and
![]() $\mu _{\mathcal {X}}$
. As already mentioned, our formula involves integrals weighted by functions
$\mu _{\mathcal {X}}$
. As already mentioned, our formula involves integrals weighted by functions
![]() $\operatorname {\mathrm {sep}}_{\pi , \mathcal {C}}$
that measure the degree to which
$\operatorname {\mathrm {sep}}_{\pi , \mathcal {C}}$
that measure the degree to which
![]() $\pi $
is not separated. We refer the reader to section 3 for precise definitions of the arc stack
$\pi $
is not separated. We refer the reader to section 3 for precise definitions of the arc stack
![]() $\mathscr {L}(\mathcal {X})$
and its motivic measure
$\mathscr {L}(\mathcal {X})$
and its motivic measure
![]() $\mu _{\mathcal {X}}$
, and to subsection 3.4 for the definition of
$\mu _{\mathcal {X}}$
, and to subsection 3.4 for the definition of
![]() $\operatorname {\mathrm {sep}}_{\pi , \mathcal {C}}$
and its integral
$\operatorname {\mathrm {sep}}_{\pi , \mathcal {C}}$
and its integral
 $\int _C \operatorname {\mathrm {sep}}_{\pi , \mathcal {C}} \mathrm {d}\mu ^{\mathrm {Gor}}_X$
.
$\int _C \operatorname {\mathrm {sep}}_{\pi , \mathcal {C}} \mathrm {d}\mu ^{\mathrm {Gor}}_X$
.
Conjecture 1.1. Let
![]() $\mathcal {X}$
be a smooth irreducible Artin stack over k admitting a good moduli space
$\mathcal {X}$
be a smooth irreducible Artin stack over k admitting a good moduli space
![]() $\pi : \mathcal {X} \to X$
, where X is a separated k-scheme and has log-terminal singularities. Assume that
$\pi : \mathcal {X} \to X$
, where X is a separated k-scheme and has log-terminal singularities. Assume that
![]() $\pi $
induces an isomorphism over a nonempty open subset of X, and that the exceptional locus of
$\pi $
induces an isomorphism over a nonempty open subset of X, and that the exceptional locus of
![]() $\pi $
has codimension at least
$\pi $
has codimension at least
![]() $2$
.
$2$
.
If
![]() $\mathcal {C} \subset \lvert \mathscr {L}(\mathcal {X})\rvert $
is a measurable subset such that
$\mathcal {C} \subset \lvert \mathscr {L}(\mathcal {X})\rvert $
is a measurable subset such that
![]() $\operatorname {\mathrm {sep}}_{\pi , \mathcal {C}}: \mathscr {L}(X) \to \mathbb {N} \cup \{\infty \}$
is finite outside a set of measure
$\operatorname {\mathrm {sep}}_{\pi , \mathcal {C}}: \mathscr {L}(X) \to \mathbb {N} \cup \{\infty \}$
is finite outside a set of measure
![]() $0$
, then
$0$
, then
![]() $\operatorname {\mathrm {sep}}_{\pi , \mathcal {C}}: \mathscr {L}(X) \to \mathbb {N} \cup \{\infty \}$
has measurable fibres, and for any measurable subset
$\operatorname {\mathrm {sep}}_{\pi , \mathcal {C}}: \mathscr {L}(X) \to \mathbb {N} \cup \{\infty \}$
has measurable fibres, and for any measurable subset
![]() $C \subset \mathscr {L}(X)$
, the set
$C \subset \mathscr {L}(X)$
, the set
![]() $\mathcal {C} \cap \mathscr {L}(\pi )^{-1}(C) \subset \lvert \mathscr {L}(\mathcal {X})\rvert $
is measurable and satisfies
$\mathcal {C} \cap \mathscr {L}(\pi )^{-1}(C) \subset \lvert \mathscr {L}(\mathcal {X})\rvert $
is measurable and satisfies
 $$ \begin{align*} \mu_{\mathcal{X}}\left(\mathcal{C} \cap \mathscr{L}(\pi)^{-1}(C)\right) = \int_C \operatorname{\mathrm{sep}}_{\pi, \mathcal{C}} \mathrm{d}\mu^{\mathrm{Gor}}_X \in \widehat{\mathscr{M}}_k\left[\mathbb{L}^{1/m}\right], \end{align*} $$
$$ \begin{align*} \mu_{\mathcal{X}}\left(\mathcal{C} \cap \mathscr{L}(\pi)^{-1}(C)\right) = \int_C \operatorname{\mathrm{sep}}_{\pi, \mathcal{C}} \mathrm{d}\mu^{\mathrm{Gor}}_X \in \widehat{\mathscr{M}}_k\left[\mathbb{L}^{1/m}\right], \end{align*} $$
where
![]() $m \in \mathbb {Z}_{>0}$
is such that
$m \in \mathbb {Z}_{>0}$
is such that
![]() $mK_X$
is Cartier.
$mK_X$
is Cartier.
This conjecture predicts that for the purpose of computing
 $\mu ^{\mathrm {Gor}}_X$
, the stack
$\mu ^{\mathrm {Gor}}_X$
, the stack
![]() $\mathcal {X}$
behaves like a crepant resolution of X, except we need to correct by
$\mathcal {X}$
behaves like a crepant resolution of X, except we need to correct by
![]() $\operatorname {\mathrm {sep}}_{\pi , \mathcal {C}}$
to account for the fact that
$\operatorname {\mathrm {sep}}_{\pi , \mathcal {C}}$
to account for the fact that
![]() $\mathcal {X}$
is not separated over X. Set
$\mathcal {X}$
is not separated over X. Set
Notice that Conjecture 1.1 implies, in particular, that the motivic measure
![]() $\mu _{\mathcal {X}}$
‘does not see’ how
$\mu _{\mathcal {X}}$
‘does not see’ how
 $\mu ^{\mathrm {Gor}}_X$
behaves on the set
$\mu ^{\mathrm {Gor}}_X$
behaves on the set
![]() $\operatorname {\mathrm {sep}}_\pi ^{-1}(0) \subset \mathscr {L}(X)$
. This set can have nonzero measure because
$\operatorname {\mathrm {sep}}_\pi ^{-1}(0) \subset \mathscr {L}(X)$
. This set can have nonzero measure because
![]() $\pi : \mathcal {X} \to X$
does not necessarily satisfy the ‘strict valuative criterion’ – that is, there may exist arcs of X (even outside a set of measure
$\pi : \mathcal {X} \to X$
does not necessarily satisfy the ‘strict valuative criterion’ – that is, there may exist arcs of X (even outside a set of measure
![]() $0$
) that do not lift to arcs of
$0$
) that do not lift to arcs of
![]() $\mathcal {X}$
. Thus in general we cannot use this conjecture to compute the total Gorenstein measure
$\mathcal {X}$
. Thus in general we cannot use this conjecture to compute the total Gorenstein measure
 $\mu ^{\mathrm {Gor}}_X(\mathscr {L}(X))$
, which specialises to the stringy Hodge numbers of X. This issue already occurs in the case where
$\mu ^{\mathrm {Gor}}_X(\mathscr {L}(X))$
, which specialises to the stringy Hodge numbers of X. This issue already occurs in the case where
![]() $\mathcal {X}$
is a Deligne–Mumford stack. For this reason, Yasuda uses a notion of ‘twisted arcs’ of
$\mathcal {X}$
is a Deligne–Mumford stack. For this reason, Yasuda uses a notion of ‘twisted arcs’ of
![]() $\mathcal {X}$
instead of usual arcs of
$\mathcal {X}$
instead of usual arcs of
![]() $\mathcal {X}$
, and this is why the inertia of
$\mathcal {X}$
, and this is why the inertia of
![]() $\mathcal {X}$
and orbifold Hodge numbers appear in Yasuda’s setting. We take a different approach, emphasising a setting in which the next conjecture predicts that almost all arcs of X lift to arcs of
$\mathcal {X}$
and orbifold Hodge numbers appear in Yasuda’s setting. We take a different approach, emphasising a setting in which the next conjecture predicts that almost all arcs of X lift to arcs of
![]() $\mathcal {X}$
.
$\mathcal {X}$
.
Conjecture 1.2. Let
![]() $\mathcal {X}$
be a finite-type Artin stack over k admitting a good moduli space
$\mathcal {X}$
be a finite-type Artin stack over k admitting a good moduli space
![]() $\pi : \mathcal {X} \to X$
. Assume that X is an irreducible k-scheme and that
$\pi : \mathcal {X} \to X$
. Assume that X is an irreducible k-scheme and that
![]() $\pi $
induces an isomorphism over a nonempty open subset of X. If the stabilisers of
$\pi $
induces an isomorphism over a nonempty open subset of X. If the stabilisers of
![]() $\mathcal {X}$
are all special groups, then
$\mathcal {X}$
are all special groups, then
![]() $\operatorname {\mathrm {sep}}_\pi ^{-1}(0) \subset \mathscr {L}(X)$
is measurable and
$\operatorname {\mathrm {sep}}_\pi ^{-1}(0) \subset \mathscr {L}(X)$
is measurable and
 $$ \begin{align*} \mu_X\left( \operatorname{\mathrm{sep}}_\pi^{-1}(0) \right) = 0, \end{align*} $$
$$ \begin{align*} \mu_X\left( \operatorname{\mathrm{sep}}_\pi^{-1}(0) \right) = 0, \end{align*} $$
where we note that
![]() $\mu _X$
is the usual (non-Gorenstein) motivic measure on
$\mu _X$
is the usual (non-Gorenstein) motivic measure on
![]() $\mathscr {L}(X)$
.
$\mathscr {L}(X)$
.
Remark 1.3. All special groups are connected, so if
![]() $\mathcal {X}$
is a Deligne–Mumford stack whose stabilisers are special groups, then its stabilisers are all trivial. Thus Conjecture 1.2 highlights a setting that is ‘orthogonal’ to the setting considered by Yasuda.
$\mathcal {X}$
is a Deligne–Mumford stack whose stabilisers are special groups, then its stabilisers are all trivial. Thus Conjecture 1.2 highlights a setting that is ‘orthogonal’ to the setting considered by Yasuda.
Our next question is motivated by the fact that if
![]() $\operatorname {\mathrm {sep}}_\pi $
is finite outside a set of measure
$\operatorname {\mathrm {sep}}_\pi $
is finite outside a set of measure
![]() $0$
, we may then consider the special case of Conjecture 1.1 where
$0$
, we may then consider the special case of Conjecture 1.1 where
![]() $\mathcal {C} = \lvert \mathscr {L}(\mathcal {X})\rvert $
.
$\mathcal {C} = \lvert \mathscr {L}(\mathcal {X})\rvert $
.
Question 1.4. Let
![]() $\mathcal {X}$
be a finite-type Artin stack over k admitting a good moduli space
$\mathcal {X}$
be a finite-type Artin stack over k admitting a good moduli space
![]() $\pi : \mathcal {X} \to X$
. Assume that X is an irreducible k-scheme and that
$\pi : \mathcal {X} \to X$
. Assume that X is an irreducible k-scheme and that
![]() $\pi $
induces an isomorphism over a nonempty open subset of X. When is
$\pi $
induces an isomorphism over a nonempty open subset of X. When is
 $$ \begin{align*} \mu_X\left(\operatorname{\mathrm{sep}}_\pi^{-1}(\infty)\right) = 0 \end{align*} $$
$$ \begin{align*} \mu_X\left(\operatorname{\mathrm{sep}}_\pi^{-1}(\infty)\right) = 0 \end{align*} $$
satisfied?
We now give an application of this framework to computing stringy Hodge numbers. In subsection 3.4, we introduce the function
![]() $\operatorname {\mathrm {sep}}_{\mathcal {X}} = 1/(\operatorname {\mathrm {sep}}_\pi \circ \mathscr {L}(\pi )): \lvert \mathscr {L}(\mathcal {X})\rvert \to \mathbb {Q}_{\geq 0} \cup \{\infty \}$
. We think of its integral
$\operatorname {\mathrm {sep}}_{\mathcal {X}} = 1/(\operatorname {\mathrm {sep}}_\pi \circ \mathscr {L}(\pi )): \lvert \mathscr {L}(\mathcal {X})\rvert \to \mathbb {Q}_{\geq 0} \cup \{\infty \}$
. We think of its integral
 $\int _{\mathscr {L}(\mathcal {X})} \operatorname {\mathrm {sep}}_{\mathcal {X}} \mathrm {d}\mu _{\mathcal {X}}$
as a kind of motivic class of
$\int _{\mathscr {L}(\mathcal {X})} \operatorname {\mathrm {sep}}_{\mathcal {X}} \mathrm {d}\mu _{\mathcal {X}}$
as a kind of motivic class of
![]() $\mathscr {L}(\mathcal {X})$
corrected by
$\mathscr {L}(\mathcal {X})$
corrected by
![]() $\operatorname {\mathrm {sep}}_{\mathcal {X}}$
to account for the fact that
$\operatorname {\mathrm {sep}}_{\mathcal {X}}$
to account for the fact that
![]() $\mathcal {X}$
is not separated. We refer the reader to subsection 3.4 for the precise definitions of
$\mathcal {X}$
is not separated. We refer the reader to subsection 3.4 for the precise definitions of
 $\int _{\mathscr {L}(\mathcal {X})} \operatorname {\mathrm {sep}}_{\mathcal {X}} \mathrm {d}\mu _{\mathcal {X}}$
and the ring
$\int _{\mathscr {L}(\mathcal {X})} \operatorname {\mathrm {sep}}_{\mathcal {X}} \mathrm {d}\mu _{\mathcal {X}}$
and the ring
 $\widehat {\mathscr {M}_k \otimes _{\mathbb {Z}} \mathbb {Q}}$
. The next proposition is then immediate:
$\widehat {\mathscr {M}_k \otimes _{\mathbb {Z}} \mathbb {Q}}$
. The next proposition is then immediate:
Proposition 1.5. With hypotheses as in Conjecture 1.1, if the stablisers of
![]() $\mathcal {X}$
are special groups and
$\mathcal {X}$
are special groups and
![]() $\mu _X\left (\operatorname {\mathrm {sep}}_\pi ^{-1}(\infty )\right ) = 0$
, then Conjecture 1.1 and Conjecture 1.2 imply that the fibres of
$\mu _X\left (\operatorname {\mathrm {sep}}_\pi ^{-1}(\infty )\right ) = 0$
, then Conjecture 1.1 and Conjecture 1.2 imply that the fibres of
![]() $\operatorname {\mathrm {sep}}_{\mathcal {X}}: \lvert \mathscr {L}(\mathcal {X})\rvert \to \mathbb {Q}_{\geq 0}$
are measurable and
$\operatorname {\mathrm {sep}}_{\mathcal {X}}: \lvert \mathscr {L}(\mathcal {X})\rvert \to \mathbb {Q}_{\geq 0}$
are measurable and
 $$ \begin{align*} \mu^{\mathrm{Gor}}_X(\mathscr{L}(X)) = \int_{\mathscr{L}(\mathcal{X})} \operatorname{\mathrm{sep}}_{\mathcal{X}} \mathrm{d}\mu_{\mathcal{X}} \in \widehat{\mathscr{M}_k \otimes_{\mathbb{Z}} \mathbb{Q}}. \end{align*} $$
$$ \begin{align*} \mu^{\mathrm{Gor}}_X(\mathscr{L}(X)) = \int_{\mathscr{L}(\mathcal{X})} \operatorname{\mathrm{sep}}_{\mathcal{X}} \mathrm{d}\mu_{\mathcal{X}} \in \widehat{\mathscr{M}_k \otimes_{\mathbb{Z}} \mathbb{Q}}. \end{align*} $$
Since the stringy Hodge–Deligne invariant of X is a specialisation of the image of
 $\mu ^{\mathrm {Gor}}_X(\mathscr {L}(X))$
in
$\mu ^{\mathrm {Gor}}_X(\mathscr {L}(X))$
in
 $\left (\widehat {\mathscr {M}_k \otimes _{\mathbb {Z}} \mathbb {Q}}\right )\left [\mathbb {L}^{1/m}\right ] \supset \widehat {\mathscr {M}_k \otimes _{\mathbb {Z}} \mathbb {Q}}$
, Proposition 1.5 provides a conjectural formula for the stringy Hodge numbers of X (when the stringy Hodge numbers exist – that is, when the stringy Hodge–Deligne invariant is a polynomial).
$\left (\widehat {\mathscr {M}_k \otimes _{\mathbb {Z}} \mathbb {Q}}\right )\left [\mathbb {L}^{1/m}\right ] \supset \widehat {\mathscr {M}_k \otimes _{\mathbb {Z}} \mathbb {Q}}$
, Proposition 1.5 provides a conjectural formula for the stringy Hodge numbers of X (when the stringy Hodge numbers exist – that is, when the stringy Hodge–Deligne invariant is a polynomial).
We envision a few potential applications of this framework. Noting that the good moduli space map
![]() $\pi : \mathcal {X} \to X$
is intrinsic to the stack
$\pi : \mathcal {X} \to X$
is intrinsic to the stack
![]() $\mathcal {X}$
and therefore so is the integral
$\mathcal {X}$
and therefore so is the integral
 $\int _{\mathscr {L}(\mathcal {X})} \operatorname {\mathrm {sep}}_{\mathcal {X}} \mathrm {d}\mu _{\mathcal {X}}$
, we hope that a cohomological interpretation of
$\int _{\mathscr {L}(\mathcal {X})} \operatorname {\mathrm {sep}}_{\mathcal {X}} \mathrm {d}\mu _{\mathcal {X}}$
, we hope that a cohomological interpretation of
 $\int _{\mathscr {L}(\mathcal {X})} \operatorname {\mathrm {sep}}_{\mathcal {X}} \mathrm {d}\mu _{\mathcal {X}}$
will lead to progress on Batyrev’s conjecture on the nonnegativity of stringy Hodge numbers. We also hope that by considering Proposition 1.5 as a kind of McKay correspondence, our conjectures will lead to new representation-theoretic statements for positive-dimensional algebraic groups.
$\int _{\mathscr {L}(\mathcal {X})} \operatorname {\mathrm {sep}}_{\mathcal {X}} \mathrm {d}\mu _{\mathcal {X}}$
will lead to progress on Batyrev’s conjecture on the nonnegativity of stringy Hodge numbers. We also hope that by considering Proposition 1.5 as a kind of McKay correspondence, our conjectures will lead to new representation-theoretic statements for positive-dimensional algebraic groups.
Remark 1.6. The hypothesis
![]() $\mu _X\left (\operatorname {\mathrm {sep}}_\pi ^{-1}(\infty )\right ) = 0$
in Proposition 1.5 allows us to make a canonical choice for
$\mu _X\left (\operatorname {\mathrm {sep}}_\pi ^{-1}(\infty )\right ) = 0$
in Proposition 1.5 allows us to make a canonical choice for
![]() $\mathcal {C}$
in Conjecture 1.1, specifically the choice
$\mathcal {C}$
in Conjecture 1.1, specifically the choice
![]() $\mathcal {C} = \lvert \mathscr {L}(\mathcal {X})\rvert $
. We hope that even when this hypothesis does not hold, one can still (after an appropriate generalisation of the notion of an arc) make a canonical choice for
$\mathcal {C} = \lvert \mathscr {L}(\mathcal {X})\rvert $
. We hope that even when this hypothesis does not hold, one can still (after an appropriate generalisation of the notion of an arc) make a canonical choice for
![]() $\mathcal {C}$
. This is a subject of our ongoing research.
$\mathcal {C}$
. This is a subject of our ongoing research.
1.3 Main results
Our first main result is that Conjecture 1.1 holds, and
![]() $\mu _X\left (\operatorname {\mathrm {sep}}_\pi ^{-1}(\infty )\right ) = 0$
, when
$\mu _X\left (\operatorname {\mathrm {sep}}_\pi ^{-1}(\infty )\right ) = 0$
, when
![]() $\mathcal {X}$
is a fantastack and
$\mathcal {X}$
is a fantastack and
![]() $\mathcal {C} = \lvert \mathscr {L}(\mathcal {X})\rvert $
. In particular, our framework applies to the Gorenstein measure of any toric variety X with log-terminal singularities.
$\mathcal {C} = \lvert \mathscr {L}(\mathcal {X})\rvert $
. In particular, our framework applies to the Gorenstein measure of any toric variety X with log-terminal singularities.
Theorem 1.7. Conjecture 1.1 holds and
![]() $\mu _X\left (\operatorname {\mathrm {sep}}_\pi ^{-1}(\infty )\right ) = 0$
when
$\mu _X\left (\operatorname {\mathrm {sep}}_\pi ^{-1}(\infty )\right ) = 0$
when
![]() $\mathcal {X}$
is a fantastack and
$\mathcal {X}$
is a fantastack and
![]() $\mathcal {C} = \lvert \mathscr {L}(\mathcal {X})\rvert $
.
$\mathcal {C} = \lvert \mathscr {L}(\mathcal {X})\rvert $
.
Remark 1.8. In fact, our techniques prove a more general result: the conclusions of Conjecture 1.1 hold when
![]() $\mathcal {C} = \lvert \mathscr {L}(\mathcal {X})\rvert $
and
$\mathcal {C} = \lvert \mathscr {L}(\mathcal {X})\rvert $
and
![]() $\mathcal {X}$
is a fantastack satisfying a certain combinatorial condition analogous to
$\mathcal {X}$
is a fantastack satisfying a certain combinatorial condition analogous to
![]() $\mathcal {X} \to X$
being ‘crepant’ (see Remark 2.20 for more details). It is important to note here that unlike the case of Deligne–Mumford stacks, defining
$\mathcal {X} \to X$
being ‘crepant’ (see Remark 2.20 for more details). It is important to note here that unlike the case of Deligne–Mumford stacks, defining
![]() $K_{\mathcal {X}}$
for Artin stacks is a subtle issue, so there is no a priori obvious definition one can take for
$K_{\mathcal {X}}$
for Artin stacks is a subtle issue, so there is no a priori obvious definition one can take for
![]() $\mathcal {X}\to X$
to be crepant.
$\mathcal {X}\to X$
to be crepant.
Remark 1.9. We note that the stacks
![]() $\mathcal {X}$
in Theorem 1.7 all have commutative stabilisers. In order to provide evidence that Conjecture 1.1 should not be limited to the setting of commutative stabilisers, we also verify that it holds in examples that involve
$\mathcal {X}$
in Theorem 1.7 all have commutative stabilisers. In order to provide evidence that Conjecture 1.1 should not be limited to the setting of commutative stabilisers, we also verify that it holds in examples that involve
![]() $\mathrm {SL}_2$
as a stabiliser (see section 10). These examples also demonstrate the flexibility in choosing the auxiliary set
$\mathrm {SL}_2$
as a stabiliser (see section 10). These examples also demonstrate the flexibility in choosing the auxiliary set
![]() $\mathcal {C} \subset \lvert \mathscr {L}(\mathcal {X})\rvert $
.
$\mathcal {C} \subset \lvert \mathscr {L}(\mathcal {X})\rvert $
.
Remark 1.10. Theorem 1.7 can be thought of as a motivic change-of-variables formula. We note that Balwe introduced versions of motivic integration for Artin n-stacks [Reference BalweBal08, Reference BalweBal15] and proved a change-of-variables formula [Reference BalweBal08, Theorem 7.2.5]. However, Theorem 1.7 cannot be obtained from Balwe’s result, as the map
![]() $\pi : \mathcal {X} \to X$
does not satisfy Balwe’s hypotheses: specifically,
$\pi : \mathcal {X} \to X$
does not satisfy Balwe’s hypotheses: specifically,
![]() $\pi $
is not ‘
$\pi $
is not ‘
![]() $0$
-truncated’.
$0$
-truncated’.
The three main steps of proving Theorem 1.7 are as follows. First, we give a combinatorial description of the fibres of the map
![]() $\mathscr {L}(\pi ): \mathscr {L}(\mathcal {X}) \to \mathscr {L}(X)$
. Second, we show that for sufficiently large n, the map of jets
$\mathscr {L}(\pi ): \mathscr {L}(\mathcal {X}) \to \mathscr {L}(X)$
. Second, we show that for sufficiently large n, the map of jets
![]() $\mathscr {L}_n(\pi ): \mathscr {L}_n(\mathcal {X}) \to \mathscr {L}_n(X)$
has constant fibres (after taking the fibres’ reduced structure) over certain combinatorially defined pieces of
$\mathscr {L}_n(\pi ): \mathscr {L}_n(\mathcal {X}) \to \mathscr {L}_n(X)$
has constant fibres (after taking the fibres’ reduced structure) over certain combinatorially defined pieces of
![]() $\mathscr {L}_n(X)$
. These two steps allow us to reduce Theorem 1.7 to the final step: verifying the case where the measurable sets C are certain combinatorially defined subsets of
$\mathscr {L}_n(X)$
. These two steps allow us to reduce Theorem 1.7 to the final step: verifying the case where the measurable sets C are certain combinatorially defined subsets of
![]() $\mathscr {L}(X)$
. A key ingredient in this final step is Theorem 3.9 and its corollary, Corollary 3.16, which show how to compute the motivic measure of the stack quotient of a variety by the action of a special group.
$\mathscr {L}(X)$
. A key ingredient in this final step is Theorem 3.9 and its corollary, Corollary 3.16, which show how to compute the motivic measure of the stack quotient of a variety by the action of a special group.
Our second main result is that Conjecture 1.2 holds for fantastacks.
Theorem 1.11. Conjecture 1.2 holds when
![]() $\mathcal {X}$
is a fantastack.
$\mathcal {X}$
is a fantastack.
An essential ingredient in proving Theorem 1.11 is Theorem 9.1, which may be of independent interest, as it provides a combinatorial criterion to check whether or not the stabilisers of a fantastack are special groups.
2 Preliminaries
In this section, we introduce notation and recall some facts about motivic integration for schemes and the Gorenstein measure, the Grothendieck ring of stacks and constructible subsets and toric Artin stacks.
2.1 Motivic integration for schemes
If X is a k-scheme, for each
![]() $n \in \mathbb {N}$
we will let
$n \in \mathbb {N}$
we will let
![]() $\mathscr {L}_n(X)$
denote the nth jet scheme of X; for each
$\mathscr {L}_n(X)$
denote the nth jet scheme of X; for each
![]() $n \geq m$
we will let
$n \geq m$
we will let
![]() $\theta ^n_m: \mathscr {L}_n(X) \to \mathscr {L}_m(X)$
denote the truncation morphism; we will let
$\theta ^n_m: \mathscr {L}_n(X) \to \mathscr {L}_m(X)$
denote the truncation morphism; we will let
 $\mathscr {L}(X) = \varprojlim _n\mathscr {L}_n(X)$
denote the arc scheme of X; and for each
$\mathscr {L}(X) = \varprojlim _n\mathscr {L}_n(X)$
denote the arc scheme of X; and for each
![]() $n \in \mathbb {N}$
we will let
$n \in \mathbb {N}$
we will let
![]() $\theta _n: \mathscr {L}(X) \to \mathscr {L}_n(X)$
denote the canonical morphism, which is also referred to as a truncation morphism. For any k-algebra R and k-scheme X, the map
$\theta _n: \mathscr {L}(X) \to \mathscr {L}_n(X)$
denote the canonical morphism, which is also referred to as a truncation morphism. For any k-algebra R and k-scheme X, the map
![]() is bijective by [Reference BhattBha16, Theorem 1.1], and we will often implicitly make this identification.
is bijective by [Reference BhattBha16, Theorem 1.1], and we will often implicitly make this identification.
We will let
![]() $K_0(\mathbf {Var}_k)$
denote the Grothendieck ring of finite type k-schemes; for each finite-type k-scheme X we will let
$K_0(\mathbf {Var}_k)$
denote the Grothendieck ring of finite type k-schemes; for each finite-type k-scheme X we will let
![]() $\mathrm {e}(X) \in K_0(\mathbf {Var}_k)$
denote its class; we will let
$\mathrm {e}(X) \in K_0(\mathbf {Var}_k)$
denote its class; we will let
 $\mathbb {L} = \mathrm {e}\left (\mathbb {A}_k^1\right ) \in K_0(\mathbf {Var}_k)$
denote the class of the affine line; and for each constructible subset C of a finite-type k-scheme we will let
$\mathbb {L} = \mathrm {e}\left (\mathbb {A}_k^1\right ) \in K_0(\mathbf {Var}_k)$
denote the class of the affine line; and for each constructible subset C of a finite-type k-scheme we will let
![]() $\mathrm {e}(C) \in K_0(\mathbf {Var}_k)$
denote its class.
$\mathrm {e}(C) \in K_0(\mathbf {Var}_k)$
denote its class.
We will let
![]() $\mathscr {M}_k$
denote the ring obtained by inverting
$\mathscr {M}_k$
denote the ring obtained by inverting
![]() $\mathbb {L}$
in
$\mathbb {L}$
in
![]() $K_0(\mathbf {Var}_k)$
. For each
$K_0(\mathbf {Var}_k)$
. For each
![]() $\Theta \in \mathscr {M}_k$
, let
$\Theta \in \mathscr {M}_k$
, let
![]() $\dim (\Theta ) \in \mathbb {Z} \cup \{-\infty \}$
denote the infimum over all
$\dim (\Theta ) \in \mathbb {Z} \cup \{-\infty \}$
denote the infimum over all
![]() $d \in \mathbb {Z}$
such that
$d \in \mathbb {Z}$
such that
![]() $\Theta $
is in the subgroup of
$\Theta $
is in the subgroup of
![]() $\mathscr {M}_k$
generated by elements of the form
$\mathscr {M}_k$
generated by elements of the form
![]() $\mathrm {e}(X)\mathbb {L}^{-n}$
with
$\mathrm {e}(X)\mathbb {L}^{-n}$
with
![]() $\dim (X) - n \leq d$
, and let
$\dim (X) - n \leq d$
, and let
![]() $\lVert \Theta \rVert = \exp (\dim (\Theta ))$
. We will let
$\lVert \Theta \rVert = \exp (\dim (\Theta ))$
. We will let
![]() $\widehat {\mathscr {M}}_k$
denote the separated completion of
$\widehat {\mathscr {M}}_k$
denote the separated completion of
![]() $\mathscr {M}_k$
with respect to the non-Archimedean seminorm
$\mathscr {M}_k$
with respect to the non-Archimedean seminorm
![]() $\lVert \cdot \rVert $
, and we will also let
$\lVert \cdot \rVert $
, and we will also let
![]() $\lVert \cdot \rVert $
denote the non-Archimedean norm on
$\lVert \cdot \rVert $
denote the non-Archimedean norm on
![]() $\widehat {\mathscr {M}}_k$
. For any
$\widehat {\mathscr {M}}_k$
. For any
![]() $m \in \mathbb {Z}_{>0}$
, we will let
$m \in \mathbb {Z}_{>0}$
, we will let
 $\widehat {\mathscr {M}}_k\left [\mathbb {L}^{1/m}\right ] = \widehat {\mathscr {M}}_k[t]/(t^m-\mathbb {L})$
, we will let
$\widehat {\mathscr {M}}_k\left [\mathbb {L}^{1/m}\right ] = \widehat {\mathscr {M}}_k[t]/(t^m-\mathbb {L})$
, we will let
![]() $\mathbb {L}^{1/m}$
denote the image of t in
$\mathbb {L}^{1/m}$
denote the image of t in
 $\widehat {\mathscr {M}}_k\left [\mathbb {L}^{1/m}\right ]$
and we will endow
$\widehat {\mathscr {M}}_k\left [\mathbb {L}^{1/m}\right ]$
and we will endow
 $\widehat {\mathscr {M}}_k\left [\mathbb {L}^{1/m}\right ]$
with the topology induced by the equality
$\widehat {\mathscr {M}}_k\left [\mathbb {L}^{1/m}\right ]$
with the topology induced by the equality
 $$ \begin{align*} \widehat{\mathscr{M}}_k\left[\mathbb{L}^{1/m}\right] = \bigoplus_{\ell = 0}^{m-1} \widehat{\mathscr{M}}_k \cdot \left(\mathbb{L}^{1/m}\right)^\ell, \end{align*} $$
$$ \begin{align*} \widehat{\mathscr{M}}_k\left[\mathbb{L}^{1/m}\right] = \bigoplus_{\ell = 0}^{m-1} \widehat{\mathscr{M}}_k \cdot \left(\mathbb{L}^{1/m}\right)^\ell, \end{align*} $$
where each summand
 $\widehat {\mathscr {M}}_k \cdot \left (\mathbb {L}^{1/m}\right )^\ell $
has the topology induced by the bijection
$\widehat {\mathscr {M}}_k \cdot \left (\mathbb {L}^{1/m}\right )^\ell $
has the topology induced by the bijection
 $$ \begin{align*} \widehat{\mathscr{M}}_k \to \widehat{\mathscr{M}}_k \cdot \left(\mathbb{L}^{1/m}\right)^\ell: \Theta \mapsto \Theta \cdot \left(\mathbb{L}^{1/m}\right)^\ell. \end{align*} $$
$$ \begin{align*} \widehat{\mathscr{M}}_k \to \widehat{\mathscr{M}}_k \cdot \left(\mathbb{L}^{1/m}\right)^\ell: \Theta \mapsto \Theta \cdot \left(\mathbb{L}^{1/m}\right)^\ell. \end{align*} $$
We note that in the foregoing and throughout this paper, if
![]() $\Theta $
is an element of
$\Theta $
is an element of
![]() $K_0(\mathbf {Var}_k)$
,
$K_0(\mathbf {Var}_k)$
,
![]() $\mathscr {M}_k$
or
$\mathscr {M}_k$
or
![]() $\widehat {\mathscr {M}}_k$
, we slightly abuse notation by also using
$\widehat {\mathscr {M}}_k$
, we slightly abuse notation by also using
![]() $\Theta $
to refer to its image under any of the ring maps
$\Theta $
to refer to its image under any of the ring maps
 $K_0(\mathbf {Var}_k) \to \mathscr {M}_k \to \widehat {\mathscr {M}}_k \to \widehat {\mathscr {M}}_k\left [\mathbb {L}^{1/m}\right ]$
.
$K_0(\mathbf {Var}_k) \to \mathscr {M}_k \to \widehat {\mathscr {M}}_k \to \widehat {\mathscr {M}}_k\left [\mathbb {L}^{1/m}\right ]$
.
If X is an equidimensional finite-type k-scheme and
![]() $C \subset \mathscr {L}(X)$
is a cylinder – that is,
$C \subset \mathscr {L}(X)$
is a cylinder – that is,
![]() $C =(\theta _n)^{-1}(C_n)$
for some
$C =(\theta _n)^{-1}(C_n)$
for some
![]() $n \in \mathbb {N}$
and some constructible subset
$n \in \mathbb {N}$
and some constructible subset
![]() $C_n \subset \mathscr {L}_n(X)$
– we will let
$C_n \subset \mathscr {L}_n(X)$
– we will let
![]() $\mu _X(C) \in \widehat {\mathscr {M}}_k$
denote the motivic measure of C, so by definition
$\mu _X(C) \in \widehat {\mathscr {M}}_k$
denote the motivic measure of C, so by definition
 $$ \begin{align*} \mu_X(C) = \lim_{n \to \infty} \mathrm{e}(\theta_n(C))\mathbb{L}^{-(n+1)\dim X} \in \widehat{\mathscr{M}}_k, \end{align*} $$
$$ \begin{align*} \mu_X(C) = \lim_{n \to \infty} \mathrm{e}(\theta_n(C))\mathbb{L}^{-(n+1)\dim X} \in \widehat{\mathscr{M}}_k, \end{align*} $$
where we note that each
![]() $\theta _n(C)$
is constructible (for example, by [Reference Chambert-Loir, Nicaise and SebagCLNS18, Chapter 5, Corollary 1.5.7(b)]) and this limit exists (for example, by [Reference Chambert-Loir, Nicaise and SebagCLNS18, Chapter 6, Theorem 2.5.1]). The motivic measure
$\theta _n(C)$
is constructible (for example, by [Reference Chambert-Loir, Nicaise and SebagCLNS18, Chapter 5, Corollary 1.5.7(b)]) and this limit exists (for example, by [Reference Chambert-Loir, Nicaise and SebagCLNS18, Chapter 6, Theorem 2.5.1]). The motivic measure
![]() $\mu _X$
can be extended to the class of so-called measurable subsets of
$\mu _X$
can be extended to the class of so-called measurable subsets of
![]() $\mathscr {L}(X)$
, whose definition we now recall.
$\mathscr {L}(X)$
, whose definition we now recall.
Definition 2.1. Let X be an equidimensional finite-type scheme over k, set
![]() $C \subset \mathscr {L}(X)$
and
$C \subset \mathscr {L}(X)$
and
![]() $\varepsilon \in \mathbb {R}_{>0}$
, let I be a set, let
$\varepsilon \in \mathbb {R}_{>0}$
, let I be a set, let
![]() $C^{(0)} \subset \mathscr {L}(X)$
be a cylinder and let
$C^{(0)} \subset \mathscr {L}(X)$
be a cylinder and let
 $\left \{C^{(i)}\right \}_{i \in I}$
be a collection of cylinders in
$\left \{C^{(i)}\right \}_{i \in I}$
be a collection of cylinders in
![]() $\mathscr {L}(X)$
.
$\mathscr {L}(X)$
.
The data
 $\left (C^{(0)}, \left (C^{i}\right )_{i \in I}\right )$
is called a cylindrical
$\left (C^{(0)}, \left (C^{i}\right )_{i \in I}\right )$
is called a cylindrical
![]() $\varepsilon $
-approximation of C if
$\varepsilon $
-approximation of C if
 $$ \begin{align*} \left(C \cup C^{(0)}\right) \setminus \left(C \cap C^{(0)}\right) \subset \bigcup_{i \in I} C^{(i)} \end{align*} $$
$$ \begin{align*} \left(C \cup C^{(0)}\right) \setminus \left(C \cap C^{(0)}\right) \subset \bigcup_{i \in I} C^{(i)} \end{align*} $$
and, for all
![]() $i \in I$
,
$i \in I$
,
 $$ \begin{align*} \left\lVert \mu_X\left(C^{(i)}\right) \right\rVert < \varepsilon. \end{align*} $$
$$ \begin{align*} \left\lVert \mu_X\left(C^{(i)}\right) \right\rVert < \varepsilon. \end{align*} $$
Definition 2.2. Let X be an equidimensional finite-type scheme over k, and set
![]() $C \subset \mathscr {L}(X)$
. The set C is called measurable if for any
$C \subset \mathscr {L}(X)$
. The set C is called measurable if for any
![]() $\varepsilon \in \mathbb {R}_{>0}$
there exists a cylindrical
$\varepsilon \in \mathbb {R}_{>0}$
there exists a cylindrical
![]() $\varepsilon $
-approximation of C. The motivic measure of a measurable subset
$\varepsilon $
-approximation of C. The motivic measure of a measurable subset
![]() $C \subset \mathscr {L}(X)$
is defined to be the unique element
$C \subset \mathscr {L}(X)$
is defined to be the unique element
![]() $\mu _X(C) \in \widehat {\mathscr {M}}_k$
such that for any
$\mu _X(C) \in \widehat {\mathscr {M}}_k$
such that for any
![]() $\varepsilon \in \mathbb {R}_{>0}$
and any cylindrical
$\varepsilon \in \mathbb {R}_{>0}$
and any cylindrical
![]() $\varepsilon $
-approximation
$\varepsilon $
-approximation
 $\left (C^{(0)}, \left (C^{(i)}\right )_{i \in I}\right )$
of C, we have
$\left (C^{(0)}, \left (C^{(i)}\right )_{i \in I}\right )$
of C, we have
 $$ \begin{align*} \left\lVert \mu_X(C) - \mu_X\left(C^{(0)}\right) \right\rVert < \varepsilon. \end{align*} $$
$$ \begin{align*} \left\lVert \mu_X(C) - \mu_X\left(C^{(0)}\right) \right\rVert < \varepsilon. \end{align*} $$
Such an element
![]() $\mu _X(C)$
exists by [Reference Chambert-Loir, Nicaise and SebagCLNS18, Chapter 6, Theorem 3.3.2].
$\mu _X(C)$
exists by [Reference Chambert-Loir, Nicaise and SebagCLNS18, Chapter 6, Theorem 3.3.2].
For the remainder of this subsection, let X be an integral finite-type separated k-scheme with log-terminal singularities. We will set notation relevant for the Gorenstein measure associated to X. We will let
![]() $K_X$
denote the canonical divisor on X. If
$K_X$
denote the canonical divisor on X. If
![]() $m \in \mathbb {Z}_{>0}$
is such that
$m \in \mathbb {Z}_{>0}$
is such that
![]() $mK_X$
is Cartier, we will let
$mK_X$
is Cartier, we will let
 $\omega _{X,m} = \iota _*\left ( \left (\Omega _{X_{\mathrm {sm}}}^{\dim X}\right )^{\otimes m} \right )$
, where
$\omega _{X,m} = \iota _*\left ( \left (\Omega _{X_{\mathrm {sm}}}^{\dim X}\right )^{\otimes m} \right )$
, where
![]() $\iota : X_{\mathrm {sm}} \hookrightarrow X$
is the inclusion of the smooth locus of X, and we will let
$\iota : X_{\mathrm {sm}} \hookrightarrow X$
is the inclusion of the smooth locus of X, and we will let
![]() $\mathscr {J}_{X,m}$
denote the unique ideal sheaf on X such that the image of
$\mathscr {J}_{X,m}$
denote the unique ideal sheaf on X such that the image of
 $\left (\Omega _X^{\dim X}\right )^{\otimes m} \to \omega _{X,m}$
is equal to
$\left (\Omega _X^{\dim X}\right )^{\otimes m} \to \omega _{X,m}$
is equal to
![]() $\mathscr {J}_{X,m} \omega _{X,m}$
. If
$\mathscr {J}_{X,m} \omega _{X,m}$
. If
![]() $C \subset \mathscr {L}(X)$
is measurable, we will let
$C \subset \mathscr {L}(X)$
is measurable, we will let
 $\mu ^{\mathrm {Gor}}_X(C)$
denote the Gorenstein measure of C, so by definition,
$\mu ^{\mathrm {Gor}}_X(C)$
denote the Gorenstein measure of C, so by definition,
 $$ \begin{align*} \mu^{\mathrm{Gor}}_X(C) &= \int_C \left(\mathbb{L}^{1/m}\right)^{\operatorname{\mathrm{ord}}_{\mathscr{J}_{X,m}}} \mathrm{d} \mu_X \\ &= \sum_{n = 0}^\infty \left(\mathbb{L}^{1/m}\right)^n \mu_X\left(\operatorname{\mathrm{ord}}_{\mathscr{J}_{X,m}}^{-1}(n) \cap C\right) \in \widehat{\mathscr{M}}_k\left[\mathbb{L}^{1/m}\right], \end{align*} $$
$$ \begin{align*} \mu^{\mathrm{Gor}}_X(C) &= \int_C \left(\mathbb{L}^{1/m}\right)^{\operatorname{\mathrm{ord}}_{\mathscr{J}_{X,m}}} \mathrm{d} \mu_X \\ &= \sum_{n = 0}^\infty \left(\mathbb{L}^{1/m}\right)^n \mu_X\left(\operatorname{\mathrm{ord}}_{\mathscr{J}_{X,m}}^{-1}(n) \cap C\right) \in \widehat{\mathscr{M}}_k\left[\mathbb{L}^{1/m}\right], \end{align*} $$
where
![]() $m \in \mathbb {Z}_{>0}$
is such that
$m \in \mathbb {Z}_{>0}$
is such that
![]() $mK_X$
is Cartier and
$mK_X$
is Cartier and
![]() $\operatorname {\mathrm {ord}}_{\mathscr {J}_{X,m}}: \mathscr {L}(X) \to \mathbb {N} \cup \{\infty \}$
is the order function of the ideal sheaf
$\operatorname {\mathrm {ord}}_{\mathscr {J}_{X,m}}: \mathscr {L}(X) \to \mathbb {N} \cup \{\infty \}$
is the order function of the ideal sheaf
![]() $\mathscr {J}_{X,m}$
. The following proposition is easy to check using the definition of
$\mathscr {J}_{X,m}$
. The following proposition is easy to check using the definition of
 $\mu ^{\mathrm {Gor}}_X$
and standard properties of
$\mu ^{\mathrm {Gor}}_X$
and standard properties of
![]() $\mu _X$
given in [Reference Chambert-Loir, Nicaise and SebagCLNS18, Chapter 6, Proposition 3.4.3]:
$\mu _X$
given in [Reference Chambert-Loir, Nicaise and SebagCLNS18, Chapter 6, Proposition 3.4.3]:
Proposition 2.3. Let
 $\left \{C^{(i)}\right \}_{i \in \mathbb {N}}$
be a sequence of pairwise disjoint measurable subsets of
$\left \{C^{(i)}\right \}_{i \in \mathbb {N}}$
be a sequence of pairwise disjoint measurable subsets of
![]() $\mathscr {L}(X)$
such that
$\mathscr {L}(X)$
such that
 $C = \bigcup _{i = 0}^\infty C^{(i)}$
is measurable. Then
$C = \bigcup _{i = 0}^\infty C^{(i)}$
is measurable. Then
 $$ \begin{align*} \lim_{i \to \infty} \mu^{\mathrm{Gor}}_X\left(C^{(i)}\right) = 0, \end{align*} $$
$$ \begin{align*} \lim_{i \to \infty} \mu^{\mathrm{Gor}}_X\left(C^{(i)}\right) = 0, \end{align*} $$
and
 $$ \begin{align*} \mu^{\mathrm{Gor}}_X(C) = \sum_{i =0}^\infty \mu^{\mathrm{Gor}}_X\left(C^{(i)}\right). \end{align*} $$
$$ \begin{align*} \mu^{\mathrm{Gor}}_X(C) = \sum_{i =0}^\infty \mu^{\mathrm{Gor}}_X\left(C^{(i)}\right). \end{align*} $$
2.2 The Grothendieck ring of stacks and constructible subsets
We will let
![]() $K_0(\mathbf {Stack}_k)$
denote the Grothendieck ring of stacks in the sense of [Reference EkedahlEke09], and for each finite-type Artin stack
$K_0(\mathbf {Stack}_k)$
denote the Grothendieck ring of stacks in the sense of [Reference EkedahlEke09], and for each finite-type Artin stack
![]() $\mathcal {X}$
over k, we will let
$\mathcal {X}$
over k, we will let
![]() $\mathrm {e}(\mathcal {X}) \in K_0(\mathbf {Stack}_k)$
denote the class of
$\mathrm {e}(\mathcal {X}) \in K_0(\mathbf {Stack}_k)$
denote the class of
![]() $\mathcal {X}$
. If
$\mathcal {X}$
. If
 $K_0(\mathbf {Var}_k)\left [\mathbb {L}^{-1}, \left \{(\mathbb {L}^n - 1)^{-1}\right \}_{n \in \mathbb {Z}_{>0}}\right ]$
is the ring obtained from
$K_0(\mathbf {Var}_k)\left [\mathbb {L}^{-1}, \left \{(\mathbb {L}^n - 1)^{-1}\right \}_{n \in \mathbb {Z}_{>0}}\right ]$
is the ring obtained from
![]() $K_0(\mathbf {Var}_k)$
by inverting
$K_0(\mathbf {Var}_k)$
by inverting
![]() $\mathbb {L}$
and
$\mathbb {L}$
and
![]() $(\mathbb {L}^n-1)$
for all
$(\mathbb {L}^n-1)$
for all
![]() $n \in \mathbb {Z}_{>0}$
, then the obvious ring map
$n \in \mathbb {Z}_{>0}$
, then the obvious ring map
![]() $K_0(\mathbf {Var}_k) \to K_0(\mathbf {Stack}_k)$
induces an isomorphism
$K_0(\mathbf {Var}_k) \to K_0(\mathbf {Stack}_k)$
induces an isomorphism
 $$ \begin{align*} K_0(\mathbf{Var}_k)\left[\mathbb{L}^{-1}, \left\{(\mathbb{L}^n - 1)^{-1}\right\}_{n \in \mathbb{Z}_{>0}}\right] \cong K_0(\mathbf{Stack}_k), \end{align*} $$
$$ \begin{align*} K_0(\mathbf{Var}_k)\left[\mathbb{L}^{-1}, \left\{(\mathbb{L}^n - 1)^{-1}\right\}_{n \in \mathbb{Z}_{>0}}\right] \cong K_0(\mathbf{Stack}_k), \end{align*} $$
by [Reference EkedahlEke09, Theorem 1.2]. Therefore there exists a unique ring map
whose composition with
![]() $K_0(\mathbf {Var}_k) \to K_0(\mathbf {Stack}_k)$
is the usual map
$K_0(\mathbf {Var}_k) \to K_0(\mathbf {Stack}_k)$
is the usual map
![]() $K_0(\mathbf {Var}_k) \to \widehat {\mathscr {M}}_k$
. If
$K_0(\mathbf {Var}_k) \to \widehat {\mathscr {M}}_k$
. If
 $\Theta \in K_0 (\mathbf {Stack}_k)$
, we will slightly abuse notation by also using
$\Theta \in K_0 (\mathbf {Stack}_k)$
, we will slightly abuse notation by also using
![]() $\Theta $
to refer to its image under
$\Theta $
to refer to its image under
![]() $K_0(\mathbf {Stack}_k) \to \widehat {\mathscr {M}}_k$
. By [Reference EkedahlEke09, Propositions 1.1(iii) and 1.4(i)], if G is a special group over k, then
$K_0(\mathbf {Stack}_k) \to \widehat {\mathscr {M}}_k$
. By [Reference EkedahlEke09, Propositions 1.1(iii) and 1.4(i)], if G is a special group over k, then
![]() $\mathrm {e}(G) \in K_0(\mathbf {Stack}_k)$
is a unit, and for any finite-type k-scheme X with G-action, the class of the stack quotient is
$\mathrm {e}(G) \in K_0(\mathbf {Stack}_k)$
is a unit, and for any finite-type k-scheme X with G-action, the class of the stack quotient is
Remark 2.4. Let G be an algebraic group over k. For each
![]() $n \in \mathbb {N}$
, we give
$n \in \mathbb {N}$
, we give
![]() $\mathscr {L}_n(G)$
the group structure induced by applying the functor
$\mathscr {L}_n(G)$
the group structure induced by applying the functor
![]() $\mathscr {L}_n$
to the group law
$\mathscr {L}_n$
to the group law
![]() $G \times _k G \to G$
. It is easy to verify that for each
$G \times _k G \to G$
. It is easy to verify that for each
![]() $n \in \mathbb {N}$
, we have a short exact sequence
$n \in \mathbb {N}$
, we have a short exact sequence
 $$ \begin{align*} 1 \to \mathfrak{g} \to \mathscr{L}_{n+1}(G) \xrightarrow{\theta^{n+1}_n} \mathscr{L}_n(G) \to 1, \end{align*} $$
$$ \begin{align*} 1 \to \mathfrak{g} \to \mathscr{L}_{n+1}(G) \xrightarrow{\theta^{n+1}_n} \mathscr{L}_n(G) \to 1, \end{align*} $$
where
![]() $\mathfrak {g}$
is the Lie algebra of G. Thus by induction on n, the fact that
$\mathfrak {g}$
is the Lie algebra of G. Thus by induction on n, the fact that
![]() $\mathbb {G}_a$
is special, the fact that extensions of special groups are special and the fact that
$\mathbb {G}_a$
is special, the fact that extensions of special groups are special and the fact that
![]() $\mathscr {L}_0(G) \cong G$
, we see that if G is a special group, then each jet scheme
$\mathscr {L}_0(G) \cong G$
, we see that if G is a special group, then each jet scheme
![]() $\mathscr {L}_n(G)$
is a special group.
$\mathscr {L}_n(G)$
is a special group.
To state the next result, we recall that if
![]() $\mathcal {X}$
is a finite-type Artin stack over k, then the topological space
$\mathcal {X}$
is a finite-type Artin stack over k, then the topological space
![]() $\lvert \mathcal {X}\rvert $
is Noetherian, so its constructible subsets are precisely those subsets that can be written as a finite union of locally closed subsets.
$\lvert \mathcal {X}\rvert $
is Noetherian, so its constructible subsets are precisely those subsets that can be written as a finite union of locally closed subsets.
Proposition 2.5. Let
![]() $\mathcal {X}$
be a finite-type Artin stack over k and let
$\mathcal {X}$
be a finite-type Artin stack over k and let
![]() $\mathcal {C} \subset \lvert \mathcal {X}\rvert $
be a constructible subset. Then there exists a unique
$\mathcal {C} \subset \lvert \mathcal {X}\rvert $
be a constructible subset. Then there exists a unique
![]() $\mathrm {e}(\mathcal {C}) \in K_0(\mathbf {Stack}_k)$
that satisfies the following property. If
$\mathrm {e}(\mathcal {C}) \in K_0(\mathbf {Stack}_k)$
that satisfies the following property. If
![]() $\{\mathcal {X}_i\}_{i \in I}$
is a finite collection of locally closed substacks
$\{\mathcal {X}_i\}_{i \in I}$
is a finite collection of locally closed substacks
![]() $\mathcal {X}_i$
of
$\mathcal {X}_i$
of
![]() $\mathcal {X}$
such that
$\mathcal {X}$
such that
![]() $\mathcal {C}$
is equal to the disjoint union of the
$\mathcal {C}$
is equal to the disjoint union of the
![]() $\lvert \mathcal {X}_i\rvert $
, then
$\lvert \mathcal {X}_i\rvert $
, then
 $$ \begin{align*} \mathrm{e}(\mathcal{C}) = \sum_{i \in I}\mathrm{e}(\mathcal{X}_i) \in K_0(\mathbf{Stack}_k). \end{align*} $$
$$ \begin{align*} \mathrm{e}(\mathcal{C}) = \sum_{i \in I}\mathrm{e}(\mathcal{X}_i) \in K_0(\mathbf{Stack}_k). \end{align*} $$
Proof. The proposition holds by the exact same proof used for the analogous statement for schemes in [Reference Chambert-Loir, Nicaise and SebagCLNS18, Chapter 2, Corollary 1.3.5].
If
![]() $\mathcal {X}$
is a finite-type Artin stack and
$\mathcal {X}$
is a finite-type Artin stack and
![]() $\mathcal {C} \subset \lvert \mathcal {X}\rvert $
is a constructible subset, we will let
$\mathcal {C} \subset \lvert \mathcal {X}\rvert $
is a constructible subset, we will let
![]() $\mathrm {e}(\mathcal {C})$
denote the class of
$\mathrm {e}(\mathcal {C})$
denote the class of
![]() $\mathcal {C}$
– that is,
$\mathcal {C}$
– that is,
![]() $\mathrm {e}(\mathcal {C})$
is as in the statement of Proposition 2.5.
$\mathrm {e}(\mathcal {C})$
is as in the statement of Proposition 2.5.
We end this subsection with a useful tool to compute the class of a stack.
Definition 2.6. Let S be a scheme, let Z be scheme over S, let
![]() $\mathcal {Y}$
and
$\mathcal {Y}$
and
![]() $\mathcal {F}$
be Artin stacks over S and let
$\mathcal {F}$
be Artin stacks over S and let
![]() $\xi : \mathcal {Y} \to Z$
be a morphism over S. We say
$\xi : \mathcal {Y} \to Z$
be a morphism over S. We say
![]() $\xi $
is a piecewise trivial fibration with fibre
$\xi $
is a piecewise trivial fibration with fibre
![]() $\mathcal {F}$
if there exists a finite cover
$\mathcal {F}$
if there exists a finite cover
![]() $\{Z_i\}_{i \in I}$
of Z consisting of pairwise disjoint locally closed subschemes
$\{Z_i\}_{i \in I}$
of Z consisting of pairwise disjoint locally closed subschemes
![]() $Z_i \subset Z$
such that for all
$Z_i \subset Z$
such that for all
![]() $i \in I$
,
$i \in I$
,
as stacks over
![]() $(Z_i)_{\mathrm {red}}$
.
$(Z_i)_{\mathrm {red}}$
.
Remark 2.7. Let Z be a finite-type scheme over k, let
![]() $\mathcal {Y}$
and
$\mathcal {Y}$
and
![]() $\mathcal {F}$
be finite-type Artin stacks over k and let
$\mathcal {F}$
be finite-type Artin stacks over k and let
![]() $\xi : \mathcal {Y} \to Z$
be a piecewise trivial fibration with fibre
$\xi : \mathcal {Y} \to Z$
be a piecewise trivial fibration with fibre
![]() $\mathcal {F}$
. Then by Proposition 2.5,
$\mathcal {F}$
. Then by Proposition 2.5,
The next proposition is well known in the case where
![]() $\mathcal {Y}$
is a scheme.
$\mathcal {Y}$
is a scheme.
Proposition 2.8. Let S be a Noetherian scheme, let Z be a finite-type scheme over S, let
![]() $\mathcal {Y}$
and
$\mathcal {Y}$
and
![]() $\mathcal {F}$
be finite-type Artin stacks over S and let
$\mathcal {F}$
be finite-type Artin stacks over S and let
![]() $\xi : \mathcal {Y} \to Z$
be a morphism over S. Then
$\xi : \mathcal {Y} \to Z$
be a morphism over S. Then
![]() $\xi $
is a piecewise trivial fibration with fibre
$\xi $
is a piecewise trivial fibration with fibre
![]() $\mathcal {F}$
if and only if for all
$\mathcal {F}$
if and only if for all
![]() $z \in Z$
, there exists an isomorphism
$z \in Z$
, there exists an isomorphism
of stacks over
![]() $k(z)$
, where
$k(z)$
, where
![]() $k(z)$
denotes the residue field of z.
$k(z)$
denotes the residue field of z.
Proof. If
![]() $\xi $
is a piecewise trivial fibration with fibre
$\xi $
is a piecewise trivial fibration with fibre
![]() $\mathcal {F}$
, then for every
$\mathcal {F}$
, then for every
![]() $z\in Z$
, there is a locally closed subset
$z\in Z$
, there is a locally closed subset
![]() $Z'\subseteq Z$
containing z for which
$Z'\subseteq Z$
containing z for which
![]() $(\mathcal {Y}\times _Z Z')_{\mathrm {red}}\cong (\mathcal {F}\times _S Z')_{\mathrm {red}}$
as
$(\mathcal {Y}\times _Z Z')_{\mathrm {red}}\cong (\mathcal {F}\times _S Z')_{\mathrm {red}}$
as
![]() $Z^{\prime }_{\mathrm {red}}$
-stacks. Then
$Z^{\prime }_{\mathrm {red}}$
-stacks. Then
 $$ \begin{align*} \begin{split} (\mathcal{Y}\times_Z \operatorname{\mathrm{Spec}} k(z))_{\mathrm{red}} &=\left((\mathcal{Y}\times_Z Z')_{\mathrm{red}}\times_{Z^{\prime}_{\mathrm{red}}} \operatorname{\mathrm{Spec}} k(z)\right)_{\mathrm{red}}\\ &\cong\left((\mathcal{F}\times_S Z')_{\mathrm{red}}\times_{Z^{\prime}_{\mathrm{red}}} \operatorname{\mathrm{Spec}} k(z)\right)_{\mathrm{red}}=(\mathcal{F}\times_S \operatorname{\mathrm{Spec}} k(z))_{\mathrm{red}}. \end{split} \end{align*} $$
$$ \begin{align*} \begin{split} (\mathcal{Y}\times_Z \operatorname{\mathrm{Spec}} k(z))_{\mathrm{red}} &=\left((\mathcal{Y}\times_Z Z')_{\mathrm{red}}\times_{Z^{\prime}_{\mathrm{red}}} \operatorname{\mathrm{Spec}} k(z)\right)_{\mathrm{red}}\\ &\cong\left((\mathcal{F}\times_S Z')_{\mathrm{red}}\times_{Z^{\prime}_{\mathrm{red}}} \operatorname{\mathrm{Spec}} k(z)\right)_{\mathrm{red}}=(\mathcal{F}\times_S \operatorname{\mathrm{Spec}} k(z))_{\mathrm{red}}. \end{split} \end{align*} $$
We now show that the converse holds. Since
for every
![]() $z\in Z$
, we can assume
$z\in Z$
, we can assume
![]() $\mathcal {Y}$
is reduced. By Noetherian induction on Z, we need only find a nonempty open subset
$\mathcal {Y}$
is reduced. By Noetherian induction on Z, we need only find a nonempty open subset
![]() $U\subseteq Z$
for which
$U\subseteq Z$
for which
![]() $(\mathcal {Y}\times _Z U)_{\mathrm {red}}\cong (\mathcal {F}\times _S U)_{\mathrm {red}}$
. Let
$(\mathcal {Y}\times _Z U)_{\mathrm {red}}\cong (\mathcal {F}\times _S U)_{\mathrm {red}}$
. Let
![]() $z\in Z$
be the generic point of an irreducible component of Z; replacing Z by an open affine neighbourhood of z, we may further assume Z is affine. Since
$z\in Z$
be the generic point of an irreducible component of Z; replacing Z by an open affine neighbourhood of z, we may further assume Z is affine. Since
![]() $\mathcal {O}_{Z,z}$
is a field,
$\mathcal {O}_{Z,z}$
is a field,
![]() $\mathcal {Y}\times _Z \operatorname {\mathrm {Spec}} k(z)$
is reduced and we hence have a surjective closed immersion
$\mathcal {Y}\times _Z \operatorname {\mathrm {Spec}} k(z)$
is reduced and we hence have a surjective closed immersion
Now,
![]() $\operatorname {\mathrm {Spec}}\mathcal {O}_{Z,z}=\lim _\lambda U_\lambda $
is the inverse limit of open affine neighbourhoods
$\operatorname {\mathrm {Spec}}\mathcal {O}_{Z,z}=\lim _\lambda U_\lambda $
is the inverse limit of open affine neighbourhoods
![]() $U_\lambda \subseteq Z$
of z. Since Z is affine, each map
$U_\lambda \subseteq Z$
of z. Since Z is affine, each map
![]() $U_\lambda \to Z$
is affine. Note also that
$U_\lambda \to Z$
is affine. Note also that
![]() $\mathcal {Y}$
is Noetherian, hence quasicompact and quasiseparated, and that
$\mathcal {Y}$
is Noetherian, hence quasicompact and quasiseparated, and that
![]() $\mathcal {F}\times _S \operatorname {\mathrm {Spec}} k(z)\to \operatorname {\mathrm {Spec}} k(z)$
is locally of finite presentation. [Reference RydhRyd15, Proposition B.2] then shows there is some index
$\mathcal {F}\times _S \operatorname {\mathrm {Spec}} k(z)\to \operatorname {\mathrm {Spec}} k(z)$
is locally of finite presentation. [Reference RydhRyd15, Proposition B.2] then shows there is some index
![]() $\lambda $
and a morphism
$\lambda $
and a morphism
![]() $\iota _\lambda \colon \mathcal {Y}\times _Z U_\lambda \to \mathcal {F}\times _S U_\lambda $
whose base change to
$\iota _\lambda \colon \mathcal {Y}\times _Z U_\lambda \to \mathcal {F}\times _S U_\lambda $
whose base change to
![]() $\operatorname {\mathrm {Spec}}\mathcal {O}_{Z,z}$
is
$\operatorname {\mathrm {Spec}}\mathcal {O}_{Z,z}$
is
![]() $\iota $
. Furthermore, since
$\iota $
. Furthermore, since
![]() $\mathcal {F}\times _S \operatorname {\mathrm {Spec}} k(z)\to \operatorname {\mathrm {Spec}} k(z)$
and
$\mathcal {F}\times _S \operatorname {\mathrm {Spec}} k(z)\to \operatorname {\mathrm {Spec}} k(z)$
and
![]() $\xi $
are both of finite presentation, [Reference RydhRyd15, Proposition B.3] shows that after replacing
$\xi $
are both of finite presentation, [Reference RydhRyd15, Proposition B.3] shows that after replacing
![]() $\lambda $
by a larger index if necessary, we can assume
$\lambda $
by a larger index if necessary, we can assume
![]() $\iota _\lambda $
is a surjective closed immersion, and hence defines an isomorphism
$\iota _\lambda $
is a surjective closed immersion, and hence defines an isomorphism
![]() $(\mathcal {Y}\times _Z U_\lambda )_{\mathrm {red}}\cong (\mathcal {F}\times _S U_\lambda )_{\mathrm {red}}$
.
$(\mathcal {Y}\times _Z U_\lambda )_{\mathrm {red}}\cong (\mathcal {F}\times _S U_\lambda )_{\mathrm {red}}$
.
2.3 Toric Artin stacks
In this subsection, we briefly review the theory of toric stacks introduced in [Reference Geraschenko and SatrianoGS15a], as well as establish some notation. Since the focus in our paper is on the toric variety X, and the toric stack
![]() $\mathcal {X}$
is viewed as a stacky resolution of X, we introduce some notational changes to emphasise this focus.
$\mathcal {X}$
is viewed as a stacky resolution of X, we introduce some notational changes to emphasise this focus.
Definition 2.9. A stacky fan is a pair
 $\left (\widetilde {\Sigma },\nu \right )$
, where
$\left (\widetilde {\Sigma },\nu \right )$
, where
![]() $\widetilde {\Sigma }$
is a fan on a lattice
$\widetilde {\Sigma }$
is a fan on a lattice
![]() $\widetilde {N}$
and
$\widetilde {N}$
and
![]() $\nu \colon \widetilde {N}\to N$
is a homomorphism to a lattice N so that the cokernel
$\nu \colon \widetilde {N}\to N$
is a homomorphism to a lattice N so that the cokernel
![]() $\operatorname {\mathrm {cok}}\nu $
is finite.
$\operatorname {\mathrm {cok}}\nu $
is finite.
A stacky fan
 $\left (\widetilde {\Sigma },\nu \right )$
gives rise to a toric stack as follows. Let
$\left (\widetilde {\Sigma },\nu \right )$
gives rise to a toric stack as follows. Let
![]() $X_{\widetilde \Sigma }$
be the toric variety associated to
$X_{\widetilde \Sigma }$
be the toric variety associated to
![]() $\widetilde {\Sigma }$
. Since
$\widetilde {\Sigma }$
. Since
![]() $\operatorname {\mathrm {cok}}\nu $
is finite,
$\operatorname {\mathrm {cok}}\nu $
is finite,
![]() $\nu ^*$
is injective, so we obtain a surjective homomorphism of tori
$\nu ^*$
is injective, so we obtain a surjective homomorphism of tori
 $$ \begin{align*} \widetilde{T}:=\operatorname{\mathrm{Spec}} k\left[\widetilde{N}^*\right]\longrightarrow\operatorname{\mathrm{Spec}} k[N^*]=:T. \end{align*} $$
$$ \begin{align*} \widetilde{T}:=\operatorname{\mathrm{Spec}} k\left[\widetilde{N}^*\right]\longrightarrow\operatorname{\mathrm{Spec}} k[N^*]=:T. \end{align*} $$
Let
![]() $G_\nu $
denote the kernel of this map. Since
$G_\nu $
denote the kernel of this map. Since
![]() $\widetilde {T}$
is the torus of
$\widetilde {T}$
is the torus of
![]() $X_{\widetilde \Sigma }$
, we obtain a
$X_{\widetilde \Sigma }$
, we obtain a
![]() $G_\nu $
-action on
$G_\nu $
-action on
![]() $X_{\widetilde \Sigma }$
via the inclusion
$X_{\widetilde \Sigma }$
via the inclusion
![]() $G_\nu \subset \widetilde {T}$
.
$G_\nu \subset \widetilde {T}$
.
Definition 2.10. With notation as in the previous paragraph, if
 $\left (\widetilde {\Sigma },\nu \right )$
is a stacky fan, the associated toric stack is defined to be
$\left (\widetilde {\Sigma },\nu \right )$
is a stacky fan, the associated toric stack is defined to be
 $$ \begin{align*} \mathcal{X}_{\widetilde{\Sigma},\nu}:=\left[X_{\widetilde{\Sigma}}/G_\nu\right]. \end{align*} $$
$$ \begin{align*} \mathcal{X}_{\widetilde{\Sigma},\nu}:=\left[X_{\widetilde{\Sigma}}/G_\nu\right]. \end{align*} $$
When
![]() $\widetilde {\Sigma }$
is the fan generated by the faces of a single cone
$\widetilde {\Sigma }$
is the fan generated by the faces of a single cone
![]() $\widetilde {\sigma }$
, we denote
$\widetilde {\sigma }$
, we denote
![]() $\mathcal {X}_{\widetilde {\Sigma },\nu }$
by
$\mathcal {X}_{\widetilde {\Sigma },\nu }$
by
![]() $\mathcal {X}_{\widetilde {\sigma },\nu }$
.
$\mathcal {X}_{\widetilde {\sigma },\nu }$
.
Example 2.11. If
![]() $\Sigma $
is a fan on a lattice N and we let
$\Sigma $
is a fan on a lattice N and we let
![]() $\nu $
be the identity map, then
$\nu $
be the identity map, then
![]() $\mathcal {X}_{\Sigma ,\nu }=X_\Sigma $
. Thus, every toric variety is an example of a toric stack.
$\mathcal {X}_{\Sigma ,\nu }=X_\Sigma $
. Thus, every toric variety is an example of a toric stack.
In this paper, we concentrate in particular on fantastacks introduced in [Reference Geraschenko and SatrianoGS15a, Section 4]. These play a particularly important role for us because they allow us to start with a toric variety
![]() $X_\Sigma $
and produce a smooth stack
$X_\Sigma $
and produce a smooth stack
![]() $\mathcal {X}$
with arbitrary degree of stackyness while maintaining the property that X is the good moduli space of
$\mathcal {X}$
with arbitrary degree of stackyness while maintaining the property that X is the good moduli space of
![]() $\mathcal {X}$
. In the following, we let
$\mathcal {X}$
. In the following, we let
![]() $e_1,\dotsc ,e_r$
be the standard basis for
$e_1,\dotsc ,e_r$
be the standard basis for
![]() $\mathbb {Z}^r$
.
$\mathbb {Z}^r$
.
Definition 2.12. Let
![]() $\Sigma $
be a fan on a lattice N, and let
$\Sigma $
be a fan on a lattice N, and let
![]() $\nu \colon \mathbb {Z}^r\to N$
be a homomorphism with finite cokernel so that every ray of
$\nu \colon \mathbb {Z}^r\to N$
be a homomorphism with finite cokernel so that every ray of
![]() $\Sigma $
contains some
$\Sigma $
contains some
![]() $v_i:=\nu (e_i)$
and every
$v_i:=\nu (e_i)$
and every
![]() $v_i$
lies in the support of
$v_i$
lies in the support of
![]() $\Sigma $
. For a cone
$\Sigma $
. For a cone
![]() $\sigma \in \Sigma $
, let
$\sigma \in \Sigma $
, let
![]() $\widetilde \sigma =\mathrm {cone}(\{e_i\mid v_i\in \sigma \})$
. We define the fan
$\widetilde \sigma =\mathrm {cone}(\{e_i\mid v_i\in \sigma \})$
. We define the fan
![]() $\widetilde \Sigma $
on
$\widetilde \Sigma $
on
![]() $\mathbb {Z}^r$
as the fan generated by all the
$\mathbb {Z}^r$
as the fan generated by all the
![]() $\widetilde \sigma $
. We define
$\widetilde \sigma $
. We define
Any toric stack isomorphic to some
![]() $\mathcal {F}_{\Sigma ,\nu }$
is called a fantastack. When
$\mathcal {F}_{\Sigma ,\nu }$
is called a fantastack. When
![]() $\Sigma $
is the fan generated by the faces of a cone
$\Sigma $
is the fan generated by the faces of a cone
![]() $\sigma $
, we denote
$\sigma $
, we denote
![]() $\mathcal {F}_{\Sigma ,\nu }$
by
$\mathcal {F}_{\Sigma ,\nu }$
by
![]() $\mathcal {F}_{\sigma ,\nu }$
.
$\mathcal {F}_{\sigma ,\nu }$
.
Remark 2.13. By [Reference Geraschenko and SatrianoGS15a, Example 6.24] (compare [Reference SatrianoSat13, Theorem 5.5]), the natural map
is a good moduli space morphism. Furthermore, fantastacks have moduli interpretations in terms of line bundles and sections, analogous to the moduli interpretation for
![]() $\mathbb {P}^n$
[Reference Geraschenko and SatrianoGS15a, Section 7].
$\mathbb {P}^n$
[Reference Geraschenko and SatrianoGS15a, Section 7].
The next two results will be useful later on.
Proposition 2.14. Let
![]() $\sigma $
be a pointed full-dimensional cone and suppose that the good moduli space map
$\sigma $
be a pointed full-dimensional cone and suppose that the good moduli space map
![]() $\pi \colon \mathcal {F}_{\sigma ,\nu }\to X_\sigma $
is an isomorphism over the torus T of
$\pi \colon \mathcal {F}_{\sigma ,\nu }\to X_\sigma $
is an isomorphism over the torus T of
![]() $X_\sigma $
. Then for any
$X_\sigma $
. Then for any
![]() $f \in F:=\widetilde {\sigma }^\vee \cap \widetilde {N}^*$
, there exists some
$f \in F:=\widetilde {\sigma }^\vee \cap \widetilde {N}^*$
, there exists some
![]() $f' \in F$
such that
$f' \in F$
such that
In particular, if
![]() $\psi \colon F\to \mathbb {N}\cup \{\infty \}$
is a morphism of monoids and
$\psi \colon F\to \mathbb {N}\cup \{\infty \}$
is a morphism of monoids and
![]() $\psi (P)\subset \mathbb {N}$
, then
$\psi (P)\subset \mathbb {N}$
, then
![]() $\psi (F)\subset \mathbb {N}$
.
$\psi (F)\subset \mathbb {N}$
.
Proof. Let
![]() $v_i=\beta (e_i)$
for
$v_i=\beta (e_i)$
for
![]() $1\leq i\leq r$
. Since
$1\leq i\leq r$
. Since
![]() $\pi $
is an isomorphism over T, each
$\pi $
is an isomorphism over T, each
![]() $v_i\neq 0$
. As
$v_i\neq 0$
. As
![]() $\sigma $
is pointed, there exists some
$\sigma $
is pointed, there exists some
![]() $p \in P$
such that
$p \in P$
such that
![]() $\langle v_i, p \rangle> 0$
for all i. Viewing p as an element of F via the inclusion
$\langle v_i, p \rangle> 0$
for all i. Viewing p as an element of F via the inclusion
![]() $P\subset F$
, we have
$P\subset F$
, we have
![]() $\langle e_i, p \rangle> 0$
.
$\langle e_i, p \rangle> 0$
.
Let
![]() $f_1, \dotsc , f_r$
be the basis of
$f_1, \dotsc , f_r$
be the basis of
![]() $\widetilde {M}$
dual to
$\widetilde {M}$
dual to
![]() $e_1, \dotsc , e_r$
. Since the
$e_1, \dotsc , e_r$
. Since the
![]() $f_i$
are generators of F, it suffices to prove the proposition for each
$f_i$
are generators of F, it suffices to prove the proposition for each
![]() $f_i$
. Note that
$f_i$
. Note that
Since
![]() $\langle e_i, p \rangle> 0$
, we see that
$\langle e_i, p \rangle> 0$
, we see that
 $$ \begin{align*} f^{\prime}_i:=(\langle e_i,p\rangle-1)f_i+\sum_{j\neq i}\left\langle e_j,p\right\rangle f_j\in F \end{align*} $$
$$ \begin{align*} f^{\prime}_i:=(\langle e_i,p\rangle-1)f_i+\sum_{j\neq i}\left\langle e_j,p\right\rangle f_j\in F \end{align*} $$
and that
![]() $f_i+f^{\prime }_i\in P$
.
$f_i+f^{\prime }_i\in P$
.
Proposition 2.15. Keep the notation and hypotheses of Proposition 2.14 and let
![]() $\beta \colon \widetilde \sigma \cap \widetilde {N}\to \sigma \cap N$
be the induced map. If
$\beta \colon \widetilde \sigma \cap \widetilde {N}\to \sigma \cap N$
be the induced map. If
![]() $w \in \sigma \cap N$
, then
$w \in \sigma \cap N$
, then
![]() $\beta ^{-1}(w)$
is a finite set.
$\beta ^{-1}(w)$
is a finite set.
Proof. Let
![]() $f_1, \dotsc , f_r$
be the minimal generators of the monoid F. By Proposition 2.14, there exist
$f_1, \dotsc , f_r$
be the minimal generators of the monoid F. By Proposition 2.14, there exist
![]() $f^{\prime }_1, \dotsc , f^{\prime }_r$
such that
$f^{\prime }_1, \dotsc , f^{\prime }_r$
such that
![]() $f_i + f^{\prime }_i \in P$
for all
$f_i + f^{\prime }_i \in P$
for all
![]() $i \in \{1, \dotsc , r\}$
. For any
$i \in \{1, \dotsc , r\}$
. For any
![]() $\widetilde {w} \in \beta ^{-1}(w)$
,
$\widetilde {w} \in \beta ^{-1}(w)$
,
 $$ \begin{align*} \left\langle \widetilde{w}, f_i \right\rangle \leq \left\langle \widetilde{w}, f_i + f^{\prime}_i \right\rangle = \left\langle w, f_i+f^{\prime}_i\right\rangle, \end{align*} $$
$$ \begin{align*} \left\langle \widetilde{w}, f_i \right\rangle \leq \left\langle \widetilde{w}, f_i + f^{\prime}_i \right\rangle = \left\langle w, f_i+f^{\prime}_i\right\rangle, \end{align*} $$
so there are only finitely many possible values for each
![]() $\left \langle \widetilde {w}, f_i \right \rangle $
. Thus
$\left \langle \widetilde {w}, f_i \right \rangle $
. Thus
![]() $\beta ^{-1}(w)$
is a finite set.
$\beta ^{-1}(w)$
is a finite set.
We end this section by discussing canonical stacks as defined in [Reference Geraschenko and SatrianoGS15a, Section 5].
Definition 2.16. If
![]() $\Sigma $
is a fan on a lattice N, let
$\Sigma $
is a fan on a lattice N, let
![]() $v_1,\dotsc ,v_r\in N$
be the first lattice points on the rays of
$v_1,\dotsc ,v_r\in N$
be the first lattice points on the rays of
![]() $\Sigma $
, let
$\Sigma $
, let
![]() $\nu \colon \mathbb {Z}^r\to N$
be the map
$\nu \colon \mathbb {Z}^r\to N$
be the map
![]() $\nu (e_i):=v_i$
and let
$\nu (e_i):=v_i$
and let
![]() $\widetilde \Sigma $
be as in Definition 2.12. If
$\widetilde \Sigma $
be as in Definition 2.12. If
![]() $N'$
is a direct complement of the support of
$N'$
is a direct complement of the support of
![]() $\Sigma $
and
$\Sigma $
and
![]() $\nu '\colon \mathbb {Z}^r\oplus N'\to N$
is given by
$\nu '\colon \mathbb {Z}^r\oplus N'\to N$
is given by
![]() $\nu '(v,n')=\nu (v)+n'$
, then
$\nu '(v,n')=\nu (v)+n'$
, then
![]() $\mathcal {X}_{\widetilde \Sigma ,\nu '}$
is the canonical stack of
$\mathcal {X}_{\widetilde \Sigma ,\nu '}$
is the canonical stack of
![]() $X_\Sigma $
.
$X_\Sigma $
.
Remark 2.17. With notation as in Definition 2.16, if the support of
![]() $\Sigma $
is N, the canonical stack of
$\Sigma $
is N, the canonical stack of
![]() $X_\Sigma $
is the fantastack
$X_\Sigma $
is the fantastack
![]() $\mathcal {F}_{\widetilde {\Sigma },\nu }$
.
$\mathcal {F}_{\widetilde {\Sigma },\nu }$
.
The next proposition, which is straightforward from the definition, says that canonical stacks are compatible with open immersions. This will be useful for us, as this proposition will allow us to reduce most of our work to the case of affine toric varieties defined by a d-dimensional cone in
![]() $N_{\mathbb {R}}$
.
$N_{\mathbb {R}}$
.
Proposition 2.18. Let
![]() $\Sigma $
be a fan consisting of pointed rational cones in
$\Sigma $
be a fan consisting of pointed rational cones in
![]() $N_{\mathbb {R}}$
, let
$N_{\mathbb {R}}$
, let
![]() $\sigma $
be a cone in
$\sigma $
be a cone in
![]() $\Sigma $
, let
$\Sigma $
, let
![]() $X(\Sigma )$
and
$X(\Sigma )$
and
![]() $X(\sigma )$
be the T-toric varieties associated to
$X(\sigma )$
be the T-toric varieties associated to
![]() $\Sigma $
and
$\Sigma $
and
![]() $\sigma $
, respectively, and let
$\sigma $
, respectively, and let
![]() $\iota : X(\sigma ) \hookrightarrow X(\Sigma )$
be the open inclusion. If
$\iota : X(\sigma ) \hookrightarrow X(\Sigma )$
be the open inclusion. If
![]() $\mathcal {X}(\Sigma )$
and
$\mathcal {X}(\Sigma )$
and
![]() $\mathcal {X}(\sigma )$
are the canonical stacks over
$\mathcal {X}(\sigma )$
are the canonical stacks over
![]() $X(\Sigma )$
and
$X(\Sigma )$
and
![]() $X(\sigma )$
, respectively, and
$X(\sigma )$
, respectively, and
![]() $\pi (\Sigma ): \mathcal {X}(\Sigma ) \to X(\Sigma )$
and
$\pi (\Sigma ): \mathcal {X}(\Sigma ) \to X(\Sigma )$
and
![]() $\pi (\sigma ): \mathcal {X}(\sigma ) \to X(\sigma )$
are the canonical maps, then there exists a map
$\pi (\sigma ): \mathcal {X}(\sigma ) \to X(\sigma )$
are the canonical maps, then there exists a map
![]() $\mathcal {X}(\sigma ) \to \mathcal {X}(\Sigma )$
such that
$\mathcal {X}(\sigma ) \to \mathcal {X}(\Sigma )$
such that

is a fibre product diagram.
For the remainder of this subsection, let
![]() $\sigma $
be a d-dimensional pointed rational cone in
$\sigma $
be a d-dimensional pointed rational cone in
![]() $N_{\mathbb {R}}$
, let X be the affine T-toric variety associated to
$N_{\mathbb {R}}$
, let X be the affine T-toric variety associated to
![]() $\sigma $
, let
$\sigma $
, let
![]() $\mathcal {X}$
be the canonical stack over X and let
$\mathcal {X}$
be the canonical stack over X and let
![]() $\pi : \mathcal {X} \to X$
be the canonical map. At points later in this paper, we will refer to the following list of notations when we want to set it, and we also set it for the remainder of this subsection:
$\pi : \mathcal {X} \to X$
be the canonical map. At points later in this paper, we will refer to the following list of notations when we want to set it, and we also set it for the remainder of this subsection:
Notation 2.19.
-
• Let
 $M = N^*$
.
$M = N^*$
. -
• Let
 $\widetilde {N}$
be the free abelian group with generators indexed by the rays of
$\widetilde {N}$
be the free abelian group with generators indexed by the rays of
 $\sigma $
.
$\sigma $
. -
• Let
 $\widetilde {M} = \widetilde {N}^*$
.
$\widetilde {M} = \widetilde {N}^*$
. -
• Let
 $\langle \cdot , \cdot \rangle $
denote both pairings
$\langle \cdot , \cdot \rangle $
denote both pairings
 $N \otimes _{\mathbb {Z}} M \to \mathbb {Z}$
and
$N \otimes _{\mathbb {Z}} M \to \mathbb {Z}$
and
 $\widetilde {N} \otimes _{\mathbb {Z}} \widetilde {M} \to \mathbb {Z}$
.
$\widetilde {N} \otimes _{\mathbb {Z}} \widetilde {M} \to \mathbb {Z}$
. -
• Let
 $\widetilde {T} = \operatorname {\mathrm {Spec}}\left (k\left [\widetilde {M}\right ]\right )$
be the algebraic torus with cocharacter lattice
$\widetilde {T} = \operatorname {\mathrm {Spec}}\left (k\left [\widetilde {M}\right ]\right )$
be the algebraic torus with cocharacter lattice
 $\widetilde {N}$
.
$\widetilde {N}$
. -
• Let
 $\widetilde {\sigma }$
be the positive orthant of
$\widetilde {\sigma }$
be the positive orthant of
 $\widetilde {N}_{\mathbb {R}}$
– that is,
$\widetilde {N}_{\mathbb {R}}$
– that is,
 $\widetilde {\sigma }$
is the positive span of those generators of
$\widetilde {\sigma }$
is the positive span of those generators of
 $\widetilde {N}$
that are indexed by the rays of
$\widetilde {N}$
that are indexed by the rays of
 $\sigma $
.
$\sigma $
. -
• Let
 $\widetilde {X}$
be the affine
$\widetilde {X}$
be the affine
 $\widetilde {T}$
-toric variety associated to
$\widetilde {T}$
-toric variety associated to
 $\widetilde {\sigma }$
.
$\widetilde {\sigma }$
. -
• Let
 $\beta : \widetilde {\sigma } \cap \widetilde {N} \to \sigma \cap N$
be the monoid map taking the generator of
$\beta : \widetilde {\sigma } \cap \widetilde {N} \to \sigma \cap N$
be the monoid map taking the generator of
 $\widetilde {N}$
indexed by a ray of
$\widetilde {N}$
indexed by a ray of
 $\sigma $
to the first lattice point of that ray.
$\sigma $
to the first lattice point of that ray. -
• Let
 $\widetilde {\pi }: \widetilde {X} \to X$
be the toric map associated to
$\widetilde {\pi }: \widetilde {X} \to X$
be the toric map associated to
 $\beta ^{\mathrm {gp}}: \widetilde {N} \to N$
.
$\beta ^{\mathrm {gp}}: \widetilde {N} \to N$
. -
• Let
 $P = \sigma ^\vee \cap M$
. Note that
$P = \sigma ^\vee \cap M$
. Note that
 $X = \operatorname {\mathrm {Spec}}(k[P])$
.
$X = \operatorname {\mathrm {Spec}}(k[P])$
. -
• Let
 $F = \widetilde {\sigma }^\vee \cap \widetilde {M}$
. Note that
$F = \widetilde {\sigma }^\vee \cap \widetilde {M}$
. Note that
 $\widetilde {X} = \operatorname {\mathrm {Spec}}(k[F])$
.
$\widetilde {X} = \operatorname {\mathrm {Spec}}(k[F])$
. -
• Identify P with its image under the injection
 $P \hookrightarrow F$
given by dualising
$P \hookrightarrow F$
given by dualising
 $\beta $
. Note that
$\beta $
. Note that
 $P \hookrightarrow F$
is injective because
$P \hookrightarrow F$
is injective because
 $\sigma $
is full-dimensional.
$\sigma $
is full-dimensional. -
• Let
 $A = F^{\mathrm {gp}}/P^{\mathrm {gp}} = \widetilde {M}/ M$
.
$A = F^{\mathrm {gp}}/P^{\mathrm {gp}} = \widetilde {M}/ M$
. -
• Let
 $G = \operatorname {\mathrm {Spec}}(k[A])$
be the kernel of the algebraic group homomorphism
$G = \operatorname {\mathrm {Spec}}(k[A])$
be the kernel of the algebraic group homomorphism
 $\widetilde {T} \to T$
obtained by restricting
$\widetilde {T} \to T$
obtained by restricting
 $\widetilde {\pi }$
, and let G act on
$\widetilde {\pi }$
, and let G act on
 $\widetilde {X}$
by restricting the toric action of
$\widetilde {X}$
by restricting the toric action of
 $\widetilde {T}$
on
$\widetilde {T}$
on
 $\widetilde {X}$
.
$\widetilde {X}$
.
By definition, the canonical stack
![]() $\mathcal {X}$
is equal to the stack quotient
$\mathcal {X}$
is equal to the stack quotient
 $\left [\widetilde {X}/G\right ]$
and the morphism
$\left [\widetilde {X}/G\right ]$
and the morphism
![]() $\widetilde {\pi }: \widetilde {X} \to X$
is the composition
$\widetilde {\pi }: \widetilde {X} \to X$
is the composition
 $\widetilde {X} \to \left [\widetilde {X} / G\right ] = \mathcal {X} \xrightarrow {\pi } X$
.
$\widetilde {X} \to \left [\widetilde {X} / G\right ] = \mathcal {X} \xrightarrow {\pi } X$
.
We note that because our focus is on singular varieties instead of on stacks, we simplify our exposition by focusing on canonical stacks over toric varieties instead of all fantastacks. The expositional advantage is that canonical stacks depend only on the toric variety and not on additional data, as is the case for other fantastacks. We end this section with two remarks which explain why we have not lost any generality by making this expositional simplification and discuss a generalisation of Theorem 1.7.
Remark 2.20. For Theorem 1.7, it is sufficient to consider canonical stacks, as these are precisely the fantastacks satisfying the hypotheses of Conjecture 1.1. Nonetheless, we note that with only superficial modifications to our techniques, one can actually prove a more general statement than Theorem 1.7, which we explain here.
With notation as in Definition 2.16, let
![]() $\mathcal {X}=\mathcal {F}_{\Sigma ,\nu }$
be a fantastack. Assume that
$\mathcal {X}=\mathcal {F}_{\Sigma ,\nu }$
be a fantastack. Assume that
![]() $X=X_\Sigma $
is
$X=X_\Sigma $
is
![]() $\mathbb {Q}$
-Gorenstein, so for each maximal cone
$\mathbb {Q}$
-Gorenstein, so for each maximal cone
![]() $\sigma \in \Sigma $
, there exist
$\sigma \in \Sigma $
, there exist
![]() $q_\sigma \in N^*$
and
$q_\sigma \in N^*$
and
![]() $m_\sigma \in \mathbb {Z}_{>0}$
such that the set
$m_\sigma \in \mathbb {Z}_{>0}$
such that the set
contains the first lattice point of every ray of
![]() $\sigma $
. We say the good moduli space map
$\sigma $
. We say the good moduli space map
![]() $\pi \colon \mathcal {X}\to X$
is combinatorially crepant if
$\pi \colon \mathcal {X}\to X$
is combinatorially crepant if
![]() $\nu (e_i)\in \bigcup _\sigma \mathcal {H}_\sigma $
for every
$\nu (e_i)\in \bigcup _\sigma \mathcal {H}_\sigma $
for every
![]() $i\in \{1,\dotsc ,r\}$
.
$i\in \{1,\dotsc ,r\}$
.
For example, the canonical stack is combinatorially crepant over X. Since Lemma 7.9 holds for all fantastacks that are combinatorially crepant over their good moduli space, the conclusions of Conjecture 1.1 hold for any fantastack that is combinatorially crepant over its good moduli space.
Remark 2.21. If
![]() $\mathcal {F}_{\Sigma , \nu }$
is a fantastack over X, then
$\mathcal {F}_{\Sigma , \nu }$
is a fantastack over X, then
![]() $\mathcal {F}_{\Sigma , \nu } \to X$
is an isomorphism over a nonempty open subset of X if and only if
$\mathcal {F}_{\Sigma , \nu } \to X$
is an isomorphism over a nonempty open subset of X if and only if
![]() $\nu $
does not send any standard basis vector to
$\nu $
does not send any standard basis vector to
![]() $0$
. Since Proposition 2.14 holds for every fantastack satisfying the hypotheses of Conjecture 1.2, our proofs show that Theorem 1.11 holds for any fantastack as well.
$0$
. Since Proposition 2.14 holds for every fantastack satisfying the hypotheses of Conjecture 1.2, our proofs show that Theorem 1.11 holds for any fantastack as well.
3 Motivic integration for stacks
For the remainder of this paper, by a quotient stack over k we will mean an Artin stack over k that is isomorphic to the stack quotient of a k-scheme by the action of a linear algebraic group over k.
Remark 3.1. Let G be a linear algebraic group over k acting on a k-scheme
![]() $\widetilde {X}$
, and let
$\widetilde {X}$
, and let
![]() $G \hookrightarrow G'$
be an inclusion of G as a closed subgroup of a linear algebraic group
$G \hookrightarrow G'$
be an inclusion of G as a closed subgroup of a linear algebraic group
![]() $G'$
over k. Then we have an isomorphism
$G'$
over k. Then we have an isomorphism
 $$ \begin{align*} \left[\widetilde{X} / G\right] \cong \left[\left(\widetilde{X} \times^G G'\right)/G'\right], \end{align*} $$
$$ \begin{align*} \left[\widetilde{X} / G\right] \cong \left[\left(\widetilde{X} \times^G G'\right)/G'\right], \end{align*} $$
where
![]() $\widetilde {X} \times ^G G'$
is the k-scheme with
$\widetilde {X} \times ^G G'$
is the k-scheme with
![]() $G'$
-action obtained from
$G'$
-action obtained from
![]() $\widetilde {X}$
by pushout along
$\widetilde {X}$
by pushout along
![]() $G \hookrightarrow G'$
. Thus any quotient stack is isomorphic to a stack quotient of a scheme by a general linear group, which in particular is a special group.
$G \hookrightarrow G'$
. Thus any quotient stack is isomorphic to a stack quotient of a scheme by a general linear group, which in particular is a special group.
In this section we define a notion of motivic integration for quotient stacks. On the one hand, our definition is straightforward: it is more or less identical to motivic integration for schemes, but in various places we need to replace notions for schemes with the obvious analogues for Artin stacks; in particular, our motivic integration for quotient stacks does not depend on a choice of presentation for the stack as a quotient. On the other hand, our notion allows explicit computations in terms of motivic integration for schemes, as long as one first writes the stack as a stack quotient of a scheme by a special group.
Definition 3.2. Let
![]() $\mathcal {X}$
be an Artin stack over k, and set
$\mathcal {X}$
be an Artin stack over k, and set
![]() $n \in \mathbb {N}$
. The nth jet stack of
$n \in \mathbb {N}$
. The nth jet stack of
![]() $\mathcal {X}$
, denoted
$\mathcal {X}$
, denoted
![]() $\mathscr {L}_n(\mathcal {X})$
, is the Weil restriction of
$\mathscr {L}_n(\mathcal {X})$
, is the Weil restriction of
![]() $\mathcal {X} \otimes _k k[t]/\left (t^{n+1}\right )$
with respect to the morphism
$\mathcal {X} \otimes _k k[t]/\left (t^{n+1}\right )$
with respect to the morphism
![]() $\operatorname {\mathrm {Spec}}\left (k[t]/\left (t^{n+1}\right )\right ) \to \operatorname {\mathrm {Spec}}(k)$
.
$\operatorname {\mathrm {Spec}}\left (k[t]/\left (t^{n+1}\right )\right ) \to \operatorname {\mathrm {Spec}}(k)$
.
Remark 3.3. Each jet stack
![]() $\mathscr {L}_n(\mathcal {X})$
is an Artin stack by [Reference RydhRyd11, Theorem 3.7(iii)].
$\mathscr {L}_n(\mathcal {X})$
is an Artin stack by [Reference RydhRyd11, Theorem 3.7(iii)].
Remark 3.4. Each jet stack
![]() $\mathscr {L}_n(\mathcal {X})$
has affine (geometric) stabilisers by the following argument. Let
$\mathscr {L}_n(\mathcal {X})$
has affine (geometric) stabilisers by the following argument. Let
![]() $y: \operatorname {\mathrm {Spec}}(k') \to \mathscr {L}_n(\mathcal {X})$
be a geometric point corresponding to
$y: \operatorname {\mathrm {Spec}}(k') \to \mathscr {L}_n(\mathcal {X})$
be a geometric point corresponding to
![]() $\psi _n: \operatorname {\mathrm {Spec}}\left (k'[t]/\left (t^{n+1}\right )\right ) \to \mathcal {X}$
. Because
$\psi _n: \operatorname {\mathrm {Spec}}\left (k'[t]/\left (t^{n+1}\right )\right ) \to \mathcal {X}$
. Because
![]() $\mathcal {X}$
has affine (geometric) stabilisers, the reduction of the stabiliser of
$\mathcal {X}$
has affine (geometric) stabilisers, the reduction of the stabiliser of
![]() $\psi _n$
is affine, so the stabiliser of
$\psi _n$
is affine, so the stabiliser of
![]() $\psi _n$
is affine. Thus the stabiliser of y, which is the Weil restriction of the stabiliser of
$\psi _n$
is affine. Thus the stabiliser of y, which is the Weil restriction of the stabiliser of
![]() $\psi _n$
, is affine.
$\psi _n$
, is affine.
The morphisms
![]() $k[t]/\left (t^{n+1}\right ) \to k[t]/\left (t^{m+1}\right )$
, when
$k[t]/\left (t^{n+1}\right ) \to k[t]/\left (t^{m+1}\right )$
, when
![]() $n \geq m$
, induce truncation morphisms
$n \geq m$
, induce truncation morphisms
![]() $\theta ^n_m: \mathscr {L}_n(\mathcal {X}) \to \mathscr {L}_m(\mathcal {X})$
for any Artin stack
$\theta ^n_m: \mathscr {L}_n(\mathcal {X}) \to \mathscr {L}_m(\mathcal {X})$
for any Artin stack
![]() $\mathcal {X}$
over k. Like in the case of schemes, we use these truncation morphisms to define arcs of
$\mathcal {X}$
over k. Like in the case of schemes, we use these truncation morphisms to define arcs of
![]() $\mathcal {X}$
and a stack parametrising them.
$\mathcal {X}$
and a stack parametrising them.
Definition 3.5. Let
![]() $\mathcal {X}$
be an Artin stack over k. The arc stack of
$\mathcal {X}$
be an Artin stack over k. The arc stack of
![]() $\mathcal {X}$
is the inverse limit
$\mathcal {X}$
is the inverse limit
 $\mathscr {L}(\mathcal {X}) = \varprojlim _n \mathscr {L}_n(\mathcal {X})$
, where the inverse limit is taken with respect to the truncation morphisms
$\mathscr {L}(\mathcal {X}) = \varprojlim _n \mathscr {L}_n(\mathcal {X})$
, where the inverse limit is taken with respect to the truncation morphisms
![]() $\theta ^n_m: \mathscr {L}_n(\mathcal {X}) \to \mathscr {L}_m(\mathcal {X})$
.
$\theta ^n_m: \mathscr {L}_n(\mathcal {X}) \to \mathscr {L}_m(\mathcal {X})$
.
Remark 3.6. The name arc stack is justified by the fact that
![]() $\mathscr {L}(\mathcal {X})$
is indeed a stack (see, for example, [Reference TalpoTal14, Proposition 2.1.9]). Since
$\mathscr {L}(\mathcal {X})$
is indeed a stack (see, for example, [Reference TalpoTal14, Proposition 2.1.9]). Since
![]() $\mathscr {L}(\mathcal {X})$
is a stack as opposed to an Artin stack, we use the symbol
$\mathscr {L}(\mathcal {X})$
is a stack as opposed to an Artin stack, we use the symbol
![]() $\lvert \mathscr {L}(\mathcal {X})\rvert $
to denote equivalence classes of points but do not define a topology on this set.
$\lvert \mathscr {L}(\mathcal {X})\rvert $
to denote equivalence classes of points but do not define a topology on this set.
Remark 3.7. Let
![]() $\mathcal {X}$
be an Artin stack over k, and let
$\mathcal {X}$
be an Artin stack over k, and let
![]() $k'$
be a field extension of k. The truncation morphism
$k'$
be a field extension of k. The truncation morphism
![]() induces a functor
induces a functor
![]() for each
for each
![]() $n \in \mathbb {N}$
, and these functors induce a functor
$n \in \mathbb {N}$
, and these functors induce a functor
![]() . Since
. Since
![]() $\mathcal {X}$
is an Artin stack, the functor
$\mathcal {X}$
is an Artin stack, the functor
![]() is an equivalence of categories, for example by Artin’s criterion for algebraicity. Throughout this paper, we will often implicitly make this identification.
is an equivalence of categories, for example by Artin’s criterion for algebraicity. Throughout this paper, we will often implicitly make this identification.
We will let each
![]() $\theta _n: \mathscr {L}(\mathcal {X}) \to \mathscr {L}_n(\mathcal {X})$
denote the canonical morphism, and we will also call these truncation morphisms.
$\theta _n: \mathscr {L}(\mathcal {X}) \to \mathscr {L}_n(\mathcal {X})$
denote the canonical morphism, and we will also call these truncation morphisms.
We will eventually define a notion of measurable subsets of
![]() $\lvert \mathscr {L}(\mathcal {X})\rvert $
and a motivic measure
$\lvert \mathscr {L}(\mathcal {X})\rvert $
and a motivic measure
![]() $\mu _{\mathcal {X}}$
that assigns an element of
$\mu _{\mathcal {X}}$
that assigns an element of
![]() $\widehat {\mathscr {M}}_k$
to each of these measurable subsets. We begin with an important special case of measurable subsets. Note that when
$\widehat {\mathscr {M}}_k$
to each of these measurable subsets. We begin with an important special case of measurable subsets. Note that when
![]() $\mathcal {X}$
is finite type over k, so is each
$\mathcal {X}$
is finite type over k, so is each
![]() $\mathscr {L}_n(\mathcal {X})$
, by [Reference RydhRyd11, Proposition 3.8(xv)].
$\mathscr {L}_n(\mathcal {X})$
, by [Reference RydhRyd11, Proposition 3.8(xv)].
Definition 3.8. Let
![]() $\mathcal {X}$
be a finite-type Artin stack over k, and set
$\mathcal {X}$
be a finite-type Artin stack over k, and set
![]() $\mathcal {C} \subset \lvert \mathscr {L}(\mathcal {X})\rvert $
. We call the subset
$\mathcal {C} \subset \lvert \mathscr {L}(\mathcal {X})\rvert $
. We call the subset
![]() $\mathcal {C}$
a cylinder if there exist some
$\mathcal {C}$
a cylinder if there exist some
![]() $n \in \mathbb {N}$
and a constructible subset
$n \in \mathbb {N}$
and a constructible subset
![]() $\mathcal {C}_n \subset \lvert \mathscr {L}_n(\mathcal {X})\rvert $
such that
$\mathcal {C}_n \subset \lvert \mathscr {L}_n(\mathcal {X})\rvert $
such that
![]() $\mathcal {C} = (\theta _n)^{-1}(\mathcal {C}_n)$
.
$\mathcal {C} = (\theta _n)^{-1}(\mathcal {C}_n)$
.
The next theorem, which we will prove later in this section, allows us to define a motivic integration for quotient stacks that is closely related to motivic integration for schemes.
Theorem 3.9. Let
![]() $\mathcal {X}$
be an equidimensional finite-type quotient stack over k, and let
$\mathcal {X}$
be an equidimensional finite-type quotient stack over k, and let
![]() $\mathcal {C} \subset \lvert \mathscr {L}(\mathcal {X})\rvert $
be a cylinder. Then the set
$\mathcal {C} \subset \lvert \mathscr {L}(\mathcal {X})\rvert $
be a cylinder. Then the set
![]() $\theta _n(\mathcal {C}) \subset \lvert \mathscr {L}_n(\mathcal {X})\rvert $
is constructible for each
$\theta _n(\mathcal {C}) \subset \lvert \mathscr {L}_n(\mathcal {X})\rvert $
is constructible for each
![]() $n \in \mathbb {N}$
, and the sequence
$n \in \mathbb {N}$
, and the sequence
 $$ \begin{align*} \left\{\mathrm{e}(\theta_n(\mathcal{C})) \mathbb{L}^{-(n+1)\dim\mathcal{X}}\right\}_{n \in \mathbb{N}} \subset \widehat{\mathscr{M}}_k \end{align*} $$
$$ \begin{align*} \left\{\mathrm{e}(\theta_n(\mathcal{C})) \mathbb{L}^{-(n+1)\dim\mathcal{X}}\right\}_{n \in \mathbb{N}} \subset \widehat{\mathscr{M}}_k \end{align*} $$
converges.
Furthermore, suppose that G is a special group over k and
![]() $\widetilde {X}$
is a k-scheme with G-action such that there exists an isomorphism
$\widetilde {X}$
is a k-scheme with G-action such that there exists an isomorphism
 $\left [\widetilde {X} / G\right ] \xrightarrow {\sim } \mathcal {X}$
, let
$\left [\widetilde {X} / G\right ] \xrightarrow {\sim } \mathcal {X}$
, let
![]() $\rho : \widetilde {X} \to \mathcal {X}$
be the composition of the quotient map
$\rho : \widetilde {X} \to \mathcal {X}$
be the composition of the quotient map
 $\widetilde {X} \to \left [\widetilde {X} / G\right ]$
with the isomorphism
$\widetilde {X} \to \left [\widetilde {X} / G\right ]$
with the isomorphism
 $\left [\widetilde {X} / G\right ] \xrightarrow {\sim } \mathcal {X}$
and let
$\left [\widetilde {X} / G\right ] \xrightarrow {\sim } \mathcal {X}$
and let
![]() $\widetilde {C} = \mathscr {L}(\rho )^{-1}(\mathcal {C})$
. Then
$\widetilde {C} = \mathscr {L}(\rho )^{-1}(\mathcal {C})$
. Then
![]() $\widetilde {C} \subset \mathscr {L}(\widetilde {X})$
is a cylinder, and
$\widetilde {C} \subset \mathscr {L}(\widetilde {X})$
is a cylinder, and
 $$ \begin{align*} \lim_{n \to \infty} \mathrm{e}(\theta_n(\mathcal{C}))\mathbb{L}^{-(n+1)\dim\mathcal{X}} = \mu_{\widetilde{X}} \left(\widetilde{C}\right) \mathrm{e}(G)^{-1} \mathbb{L}^{\dim G} \in \widehat{\mathscr{M}}_k. \end{align*} $$
$$ \begin{align*} \lim_{n \to \infty} \mathrm{e}(\theta_n(\mathcal{C}))\mathbb{L}^{-(n+1)\dim\mathcal{X}} = \mu_{\widetilde{X}} \left(\widetilde{C}\right) \mathrm{e}(G)^{-1} \mathbb{L}^{\dim G} \in \widehat{\mathscr{M}}_k. \end{align*} $$
Remark 3.10. Let G and
![]() $\widetilde {X}$
be as in the statement of Theorem 3.9. Since
$\widetilde {X}$
be as in the statement of Theorem 3.9. Since
 $\left [\widetilde {X}/G\right ]$
is equidimensional and G is geometrically irreducible,
$\left [\widetilde {X}/G\right ]$
is equidimensional and G is geometrically irreducible,
![]() $\widetilde {X}$
is equidimensional as well, and hence
$\widetilde {X}$
is equidimensional as well, and hence
![]() $\mu _{\widetilde {X}}$
is well defined.
$\mu _{\widetilde {X}}$
is well defined.
Before we prove Theorem 3.9, we will discuss some useful consequences. First, we can define the motivic measure
![]() $\mu _{\mathcal {X}}$
on cylinders.
$\mu _{\mathcal {X}}$
on cylinders.
Definition 3.11. Let
![]() $\mathcal {X}$
be an equidimensional finite-type quotient stack over k, and let
$\mathcal {X}$
be an equidimensional finite-type quotient stack over k, and let
![]() $\mathcal {C} \subset \lvert \mathscr {L}(\mathcal {X})\rvert $
be a cylinder. The motivic measure of
$\mathcal {C} \subset \lvert \mathscr {L}(\mathcal {X})\rvert $
be a cylinder. The motivic measure of
![]() $\mathcal {C}$
is
$\mathcal {C}$
is
 $$ \begin{align*} \mu_{\mathcal{X}}(\mathcal{C}) = \lim_{n \to \infty} \mathrm{e}(\theta_n(\mathcal{C}))\mathbb{L}^{-(n+1)\dim\mathcal{X}} \in \widehat{\mathscr{M}}_k. \end{align*} $$
$$ \begin{align*} \mu_{\mathcal{X}}(\mathcal{C}) = \lim_{n \to \infty} \mathrm{e}(\theta_n(\mathcal{C}))\mathbb{L}^{-(n+1)\dim\mathcal{X}} \in \widehat{\mathscr{M}}_k. \end{align*} $$
Remark 3.12. Let
![]() $\mathcal {X}$
be an equidimensional smooth Artin (not necessarily quotient) stack over k and let
$\mathcal {X}$
be an equidimensional smooth Artin (not necessarily quotient) stack over k and let
![]() $\mathcal {C} \subset \lvert \mathscr {L}(\mathcal {X})\rvert $
be a cylinder. One can verify that
$\mathcal {C} \subset \lvert \mathscr {L}(\mathcal {X})\rvert $
be a cylinder. One can verify that
![]() $\theta _n(\mathcal {C}) \subset \lvert \mathscr {L}_n(\mathcal {X})\rvert $
is constructible for each
$\theta _n(\mathcal {C}) \subset \lvert \mathscr {L}_n(\mathcal {X})\rvert $
is constructible for each
![]() $n \in \mathbb {N}$
and that
$n \in \mathbb {N}$
and that
 $\left \{\mathrm {e}(\theta _n(\mathcal {C})) \mathbb {L}^{-(n+1)\dim \mathcal {X}}\right \}_{n \in \mathbb {N}}$
stabilises for sufficiently large n, so Definition 3.11 also makes sense here. Although this is not used for the main results of this paper, our main conjectures are stated in the generality, so we provide the argument for completeness in subsection 3.5.
$\left \{\mathrm {e}(\theta _n(\mathcal {C})) \mathbb {L}^{-(n+1)\dim \mathcal {X}}\right \}_{n \in \mathbb {N}}$
stabilises for sufficiently large n, so Definition 3.11 also makes sense here. Although this is not used for the main results of this paper, our main conjectures are stated in the generality, so we provide the argument for completeness in subsection 3.5.
We now define measurable subsets analogously to the case of schemes.
Definition 3.13. Let
![]() $\mathcal {X}$
be an equidimensional finite-type quotient stack over k, set
$\mathcal {X}$
be an equidimensional finite-type quotient stack over k, set
![]() $\mathcal {C} \subset \lvert \mathscr {L}(\mathcal {X})\rvert $
and
$\mathcal {C} \subset \lvert \mathscr {L}(\mathcal {X})\rvert $
and
![]() $\varepsilon \in \mathbb {R}_{>0}$
, let I be a set, let
$\varepsilon \in \mathbb {R}_{>0}$
, let I be a set, let
![]() $\mathcal {C}^{(0)} \subset \lvert \mathscr {L}(\mathcal {X})\rvert $
be a cylinder and let
$\mathcal {C}^{(0)} \subset \lvert \mathscr {L}(\mathcal {X})\rvert $
be a cylinder and let
 $\left \{\mathcal {C}^{(i)}\right \}_{i \in I}$
be a collection of cylinders in
$\left \{\mathcal {C}^{(i)}\right \}_{i \in I}$
be a collection of cylinders in
![]() $\lvert \mathscr {L}(\mathcal {X})\rvert $
.
$\lvert \mathscr {L}(\mathcal {X})\rvert $
.
We say that
 $\left (\mathcal {C}^{(0)}, \left (\mathcal {C}^{(i)}\right )_{i \in I}\right )$
is a cylindrical
$\left (\mathcal {C}^{(0)}, \left (\mathcal {C}^{(i)}\right )_{i \in I}\right )$
is a cylindrical
![]() $\varepsilon $
-approximation of
$\varepsilon $
-approximation of
![]() $\mathcal {C}$
if
$\mathcal {C}$
if
 $$ \begin{align*} \left(\mathcal{C} \cup \mathcal{C}^{(0)}\right) \setminus \left(\mathcal{C} \cap \mathcal{C}^{(0)}\right) \subset \bigcup_{i \in I} \mathcal{C}^{(i)} \end{align*} $$
$$ \begin{align*} \left(\mathcal{C} \cup \mathcal{C}^{(0)}\right) \setminus \left(\mathcal{C} \cap \mathcal{C}^{(0)}\right) \subset \bigcup_{i \in I} \mathcal{C}^{(i)} \end{align*} $$
and, for all
![]() $i \in I$
,
$i \in I$
,
 $$ \begin{align*} \left\lVert\mu_{\mathcal{X}}\left(\mathcal{C}^{(i)}\right)\right\rVert < \varepsilon. \end{align*} $$
$$ \begin{align*} \left\lVert\mu_{\mathcal{X}}\left(\mathcal{C}^{(i)}\right)\right\rVert < \varepsilon. \end{align*} $$
Definition 3.14. Let
![]() $\mathcal {X}$
be an equidimensional finite-type quotient stack over k, and set
$\mathcal {X}$
be an equidimensional finite-type quotient stack over k, and set
![]() $\mathcal {C} \subset \lvert \mathscr {L}(\mathcal {X})\rvert $
. We say that
$\mathcal {C} \subset \lvert \mathscr {L}(\mathcal {X})\rvert $
. We say that
![]() $\mathcal {C}$
is measurable if for any
$\mathcal {C}$
is measurable if for any
![]() $\varepsilon \in \mathbb {R}_{>0}$
, there exists a cylindrical
$\varepsilon \in \mathbb {R}_{>0}$
, there exists a cylindrical
![]() $\varepsilon $
-approximation of
$\varepsilon $
-approximation of
![]() $\mathcal {C}$
.
$\mathcal {C}$
.
Remark 3.15. Let
![]() $\mathcal {X}$
be an equidimensional finite-type quotient stack over k, and let
$\mathcal {X}$
be an equidimensional finite-type quotient stack over k, and let
![]() $\mathcal {C} \subset \lvert \mathscr {L}(\mathcal {X})\rvert $
be a cylinder. Then for any
$\mathcal {C} \subset \lvert \mathscr {L}(\mathcal {X})\rvert $
be a cylinder. Then for any
![]() $\varepsilon \in \mathbb {R}_{>0}$
, we have that
$\varepsilon \in \mathbb {R}_{>0}$
, we have that
![]() $(\mathcal {C}, \emptyset )$
is a cylindrical
$(\mathcal {C}, \emptyset )$
is a cylindrical
![]() $\varepsilon $
-approximation of
$\varepsilon $
-approximation of
![]() $\mathcal {C}$
. In particular,
$\mathcal {C}$
. In particular,
![]() $\mathcal {C}$
is measurable.
$\mathcal {C}$
is measurable.
We now see that Theorem 3.9 allows us to extend
![]() $\mu _{\mathcal {X}}$
to measurable subsets.
$\mu _{\mathcal {X}}$
to measurable subsets.
Corollary 3.16. Let
![]() $\mathcal {X}$
be an equidimensional finite-type quotient stack over k, and let
$\mathcal {X}$
be an equidimensional finite-type quotient stack over k, and let
![]() $\mathcal {C} \subset \lvert \mathscr {L}(\mathcal {X})\rvert $
be a measurable subset. Then there exists a unique
$\mathcal {C} \subset \lvert \mathscr {L}(\mathcal {X})\rvert $
be a measurable subset. Then there exists a unique
![]() $\mu _{\mathcal {X}}(\mathcal {C}) \in \widehat {\mathscr {M}}_k$
such that for any
$\mu _{\mathcal {X}}(\mathcal {C}) \in \widehat {\mathscr {M}}_k$
such that for any
![]() $\varepsilon \in \mathbb {R}_{>0}$
and any cylindrical
$\varepsilon \in \mathbb {R}_{>0}$
and any cylindrical
![]() $\varepsilon $
-approximation
$\varepsilon $
-approximation
 $\left (\mathcal {C}^{(0)}, \left (\mathcal {C}^{(i)}\right )_{i \in I}\right )$
of
$\left (\mathcal {C}^{(0)}, \left (\mathcal {C}^{(i)}\right )_{i \in I}\right )$
of
![]() $\mathcal {C}$
,
$\mathcal {C}$
,
 $$ \begin{align*} \left\lVert\mu_{\mathcal{X}}(\mathcal{C}) - \mu_{\mathcal{X}}\left(\mathcal{C}^{(0)}\right)\right\rVert < \varepsilon. \end{align*} $$
$$ \begin{align*} \left\lVert\mu_{\mathcal{X}}(\mathcal{C}) - \mu_{\mathcal{X}}\left(\mathcal{C}^{(0)}\right)\right\rVert < \varepsilon. \end{align*} $$
Furthermore, suppose that
![]() $G, \widetilde {X}, \rho $
are as in the statement of Theorem 3.9 and
$G, \widetilde {X}, \rho $
are as in the statement of Theorem 3.9 and
![]() $\widetilde {C}=\mathscr {L}(\rho )^{-1}(\mathcal {C})$
. Then
$\widetilde {C}=\mathscr {L}(\rho )^{-1}(\mathcal {C})$
. Then
 $\widetilde {C} \subset \mathscr {L}\left (\widetilde {X}\right )$
is measurable, and
$\widetilde {C} \subset \mathscr {L}\left (\widetilde {X}\right )$
is measurable, and
 $$ \begin{align*} \mu_{\mathcal{X}}(\mathcal{C}) = \mu_{\widetilde{X}} \left(\widetilde{C}\right) \mathrm{e}(G)^{-1} \mathbb{L}^{\dim G} \in \widehat{\mathscr{M}}_k. \end{align*} $$
$$ \begin{align*} \mu_{\mathcal{X}}(\mathcal{C}) = \mu_{\widetilde{X}} \left(\widetilde{C}\right) \mathrm{e}(G)^{-1} \mathbb{L}^{\dim G} \in \widehat{\mathscr{M}}_k. \end{align*} $$
Proof. Let
![]() $G, \widetilde {X}, \rho , \widetilde {C}$
be as in the second part of the corollary. For any
$G, \widetilde {X}, \rho , \widetilde {C}$
be as in the second part of the corollary. For any
![]() $\varepsilon \in \mathbb {R}_{>0}$
and any cylindrical
$\varepsilon \in \mathbb {R}_{>0}$
and any cylindrical
![]() $\varepsilon $
-approximation
$\varepsilon $
-approximation
 $\left (\mathcal {C}^{(0)}, \left (\mathcal {C}^{(i)}\right )_{i \in I}\right )$
of
$\left (\mathcal {C}^{(0)}, \left (\mathcal {C}^{(i)}\right )_{i \in I}\right )$
of
![]() $\mathcal {C}$
, Theorem 3.9 implies that
$\mathcal {C}$
, Theorem 3.9 implies that
 $\left (\mathscr {L}(\rho )^{-1}\left (\mathcal {C}^{(0)}\right ), \left (\mathscr {L}(\rho )^{-1}\left (\mathcal {C}^{(i)}\right )\right )_{i \in I}\right )$
is a cylindrical
$\left (\mathscr {L}(\rho )^{-1}\left (\mathcal {C}^{(0)}\right ), \left (\mathscr {L}(\rho )^{-1}\left (\mathcal {C}^{(i)}\right )\right )_{i \in I}\right )$
is a cylindrical
 $\varepsilon \left \lVert \mathrm {e}(G) \mathbb {L}^{-\dim G}\right \rVert $
-approximation of
$\varepsilon \left \lVert \mathrm {e}(G) \mathbb {L}^{-\dim G}\right \rVert $
-approximation of
![]() $\widetilde {C}$
. Thus
$\widetilde {C}$
. Thus
![]() $\widetilde {C}$
is measurable, and for any cylindrical
$\widetilde {C}$
is measurable, and for any cylindrical
![]() $\varepsilon $
-approximation
$\varepsilon $
-approximation
 $\left (\mathcal {C}^{(0)}, \left (\mathcal {C}^{(i)}\right )_{i \in I}\right )$
of
$\left (\mathcal {C}^{(0)}, \left (\mathcal {C}^{(i)}\right )_{i \in I}\right )$
of
![]() $\mathcal {C}$
,
$\mathcal {C}$
,
 $$ \begin{align*} \left\lVert\mu_{\widetilde{X}} \left(\widetilde{C}\right)\right.& \left.\mathrm{e}(G)^{-1} \mathbb{L}^{\dim G} - \mu_{\mathcal{X}}\left(\mathcal{C}^{(0)}\right)\right\rVert\\ &= \left\lVert\mu_{\widetilde{X}} \left(\widetilde{C}\right) \mathrm{e}(G)^{-1} \mathbb{L}^{\dim G} - \mu_{\widetilde{X}} \left(\mathscr{L}(\rho)^{-1}\left(\mathcal{C}^{(0)}\right)\right) \mathrm{e}(G)^{-1} \mathbb{L}^{\dim G}\right\rVert\\ &\leq \left\lVert \mathrm{e}(G)^{-1} \mathbb{L}^{\dim G} \right\rVert \left\lVert \mu_{\widetilde{X}}\left(\widetilde{C}\right) - \mu_{\widetilde{X}}\left(\mathscr{L}(\rho)^{-1}\left(\mathcal{C}^{(0)}\right)\right) \right\rVert\\ &< \varepsilon \left\lVert \mathrm{e}(G)^{-1} \mathbb{L}^{\dim G} \right\rVert \left\lVert\mathrm{e}(G) \mathbb{L}^{-\dim G}\right\rVert, \end{align*} $$
$$ \begin{align*} \left\lVert\mu_{\widetilde{X}} \left(\widetilde{C}\right)\right.& \left.\mathrm{e}(G)^{-1} \mathbb{L}^{\dim G} - \mu_{\mathcal{X}}\left(\mathcal{C}^{(0)}\right)\right\rVert\\ &= \left\lVert\mu_{\widetilde{X}} \left(\widetilde{C}\right) \mathrm{e}(G)^{-1} \mathbb{L}^{\dim G} - \mu_{\widetilde{X}} \left(\mathscr{L}(\rho)^{-1}\left(\mathcal{C}^{(0)}\right)\right) \mathrm{e}(G)^{-1} \mathbb{L}^{\dim G}\right\rVert\\ &\leq \left\lVert \mathrm{e}(G)^{-1} \mathbb{L}^{\dim G} \right\rVert \left\lVert \mu_{\widetilde{X}}\left(\widetilde{C}\right) - \mu_{\widetilde{X}}\left(\mathscr{L}(\rho)^{-1}\left(\mathcal{C}^{(0)}\right)\right) \right\rVert\\ &< \varepsilon \left\lVert \mathrm{e}(G)^{-1} \mathbb{L}^{\dim G} \right\rVert \left\lVert\mathrm{e}(G) \mathbb{L}^{-\dim G}\right\rVert, \end{align*} $$
where the first equality follows from Theorem 3.9. Once
![]() $\mu _{\mathcal {X}}(\mathcal {C})$
is shown to exist, this chain of inequalities proves
$\mu _{\mathcal {X}}(\mathcal {C})$
is shown to exist, this chain of inequalities proves
 $\mu _{\mathcal {X}}(\mathcal {C}) = \mu _{\widetilde {X}} \left (\widetilde {C}\right ) \mathrm {e}(G)^{-1} \mathbb {L}^{\dim G}$
. To show the existence of
$\mu _{\mathcal {X}}(\mathcal {C}) = \mu _{\widetilde {X}} \left (\widetilde {C}\right ) \mathrm {e}(G)^{-1} \mathbb {L}^{\dim G}$
. To show the existence of
![]() $\mu _{\mathcal {X}}(\mathcal {C})$
, it suffices by Remark 3.1 to assume G is a general linear group, so this chain of inequalities and Lemma 3.17 finish the proof.
$\mu _{\mathcal {X}}(\mathcal {C})$
, it suffices by Remark 3.1 to assume G is a general linear group, so this chain of inequalities and Lemma 3.17 finish the proof.
Lemma 3.17. Let G be a general linear group over k. Then
 $$ \begin{align*} \left\lVert \mathrm{e}(G)^{-1} \mathbb{L}^{\dim G} \right\rVert \left\lVert\mathrm{e}(G) \mathbb{L}^{-\dim G}\right\rVert = 1. \end{align*} $$
$$ \begin{align*} \left\lVert \mathrm{e}(G)^{-1} \mathbb{L}^{\dim G} \right\rVert \left\lVert\mathrm{e}(G) \mathbb{L}^{-\dim G}\right\rVert = 1. \end{align*} $$
Proof. Using Euler–Poincaré polynomials, it is straightforward to check (see, for example, the proof of [Reference Chambert-Loir, Nicaise and SebagCLNS18, Chapter 2, Lemma 4.1.3]) that if
![]() $n_0 \in \mathbb {Z}$
and
$n_0 \in \mathbb {Z}$
and
![]() $\{c_n\}_{n \geq n_0}$
is a sequence of integers with
$\{c_n\}_{n \geq n_0}$
is a sequence of integers with
![]() $c_{n_0} \neq 0$
, then
$c_{n_0} \neq 0$
, then
 $$ \begin{align*} \left\lVert \sum_{n \geq n_0} c_n \mathbb{L}^{-n} \right\rVert = \exp(-n_0). \end{align*} $$
$$ \begin{align*} \left\lVert \sum_{n \geq n_0} c_n \mathbb{L}^{-n} \right\rVert = \exp(-n_0). \end{align*} $$
The lemma then follows from the fact that
![]() $\mathrm {e}(G)$
is a polynomial in
$\mathrm {e}(G)$
is a polynomial in
![]() $\mathbb {L}$
(see, for example, the proof of [Reference JoyceJoy07, Lemma 4.6]).
$\mathbb {L}$
(see, for example, the proof of [Reference JoyceJoy07, Lemma 4.6]).
Definition 3.18. Let
![]() $\mathcal {X}$
be an equidimensional finite-type quotient stack over k, and let
$\mathcal {X}$
be an equidimensional finite-type quotient stack over k, and let
![]() $\mathcal {C} \subset \lvert \mathscr {L}(\mathcal {X})\rvert $
be a measurable subset. The motivic measure of
$\mathcal {C} \subset \lvert \mathscr {L}(\mathcal {X})\rvert $
be a measurable subset. The motivic measure of
![]() $\mathcal {C}$
is defined to be
$\mathcal {C}$
is defined to be
![]() $\mu _{\mathcal {X}}(\mathcal {C}) \in \widehat {\mathscr {M}}_k$
, as in the statement of Corollary 3.16.
$\mu _{\mathcal {X}}(\mathcal {C}) \in \widehat {\mathscr {M}}_k$
, as in the statement of Corollary 3.16.
In the next two subsections, we will prove Theorem 3.9.
3.1 Jet schemes of quotient stacks
In this subsection, we describe the jet schemes of a stack quotient as stack quotients themselves. This is the first step in providing the relationship between motivic integration for quotient stacks and motivic integration for schemes. This description, Corollary 3.22, is a special case of the next proposition, which describes the Weil restriction of a stack quotient.
If
![]() $S'$
and S are schemes and
$S'$
and S are schemes and
![]() $S' \to S$
is a finite flat morphism of finite presentation, we will let
$S' \to S$
is a finite flat morphism of finite presentation, we will let
![]() $\mathscr {R}_{S'/S}$
denote the functor taking each stack over
$\mathscr {R}_{S'/S}$
denote the functor taking each stack over
![]() $S'$
to its Weil restriction with respect to
$S'$
to its Weil restriction with respect to
![]() $S' \to S$
, and we note that if
$S' \to S$
, and we note that if
![]() $\mathcal {X}$
is an Artin stack over
$\mathcal {X}$
is an Artin stack over
![]() $S'$
, then
$S'$
, then
![]() $\mathscr {R}_{S'/S}(\mathcal {X})$
is an Artin stack over S [Reference RydhRyd11, Theorem 3.7(iii)].
$\mathscr {R}_{S'/S}(\mathcal {X})$
is an Artin stack over S [Reference RydhRyd11, Theorem 3.7(iii)].
Proposition 3.20. Let
![]() $S'$
and S be schemes and
$S'$
and S be schemes and
![]() $S' \to S$
be a finite flat morphism of finite presentation. If
$S' \to S$
be a finite flat morphism of finite presentation. If
![]() $\widetilde {X}'$
is an
$\widetilde {X}'$
is an
![]() $S'$
-scheme with an action by a linear algebraic group
$S'$
-scheme with an action by a linear algebraic group
![]() $G'$
over
$G'$
over
![]() $S'$
, then there exists an isomorphism
$S'$
, then there exists an isomorphism
 $$ \begin{align*} \mathscr{R}_{S'/S}\left(\left[\widetilde{X}'/G'\right]\right)\xrightarrow{\sim} \left[\mathscr{R}_{S'/S}\left(\widetilde{X}'\right)/\mathscr{R}_{S'/S}(G')\right] \end{align*} $$
$$ \begin{align*} \mathscr{R}_{S'/S}\left(\left[\widetilde{X}'/G'\right]\right)\xrightarrow{\sim} \left[\mathscr{R}_{S'/S}\left(\widetilde{X}'\right)/\mathscr{R}_{S'/S}(G')\right] \end{align*} $$
such that

commutes.
Remark 3.21. In the statement of Proposition 3.20, the action of
![]() $\mathscr {R}_{S'/S}(G')$
on
$\mathscr {R}_{S'/S}(G')$
on
 $\mathscr {R}_{S'/S}\left (\widetilde {X}'\right )$
is obtained by applying
$\mathscr {R}_{S'/S}\left (\widetilde {X}'\right )$
is obtained by applying
![]() $\mathscr {R}_{S'/S}$
to the map
$\mathscr {R}_{S'/S}$
to the map
![]() $G' \times _{S'} \widetilde {X}' \to \widetilde {X}'$
defining the action of
$G' \times _{S'} \widetilde {X}' \to \widetilde {X}'$
defining the action of
![]() $G'$
on
$G'$
on
![]() $\widetilde {X}'$
.
$\widetilde {X}'$
.
Proof. We let
 $\mathcal {X}'=\left [\widetilde {X}'/G'\right ]$
,
$\mathcal {X}'=\left [\widetilde {X}'/G'\right ]$
,
![]() $\rho ': \widetilde {X}' \to \mathcal {X}'$
be the quotient map,
$\rho ': \widetilde {X}' \to \mathcal {X}'$
be the quotient map,
![]() $\mathcal {X}=\mathscr {R}_{S'/S}(\mathcal {X}')$
,
$\mathcal {X}=\mathscr {R}_{S'/S}(\mathcal {X}')$
,
 $\widetilde {X}=\mathscr {R}_{S'/S}\left (\widetilde {X}'\right )$
and
$\widetilde {X}=\mathscr {R}_{S'/S}\left (\widetilde {X}'\right )$
and
![]() $G=\mathscr {R}_{S'/S}(G')$
. Since
$G=\mathscr {R}_{S'/S}(G')$
. Since
![]() $\rho '\colon \widetilde {X}'\to \mathcal {X}'$
is a smooth cover,
$\rho '\colon \widetilde {X}'\to \mathcal {X}'$
is a smooth cover,
 $\mathscr {R}_{S'/S}(\rho ')\colon \widetilde {X}\to \mathcal {X}$
is as well, by [Reference RydhRyd11, Proposition 3.5(v)]. Since
$\mathscr {R}_{S'/S}(\rho ')\colon \widetilde {X}\to \mathcal {X}$
is as well, by [Reference RydhRyd11, Proposition 3.5(v)]. Since
![]() $\rho '$
is a
$\rho '$
is a
![]() $G'$
-torsor, the natural map
$G'$
-torsor, the natural map
![]() $G'\times _{S'} \widetilde {X}'\to \widetilde {X}'\times _{\mathcal {X}'} \widetilde {X}'$
induced by the
$G'\times _{S'} \widetilde {X}'\to \widetilde {X}'\times _{\mathcal {X}'} \widetilde {X}'$
induced by the
![]() $G'$
-action
$G'$
-action
![]() $G' \times _{S'} \widetilde {X}' \to \widetilde {X}'$
is an isomorphism, and applying Weil restriction, we see that the map
$G' \times _{S'} \widetilde {X}' \to \widetilde {X}'$
is an isomorphism, and applying Weil restriction, we see that the map
![]() $G\times _S \widetilde {X}\to \widetilde {X}\times _{\mathcal {X}} \widetilde {X}$
induced by the G-action
$G\times _S \widetilde {X}\to \widetilde {X}\times _{\mathcal {X}} \widetilde {X}$
induced by the G-action
![]() $G \times _S \widetilde {X} \to \widetilde {X}$
is an isomorphism as well. Thus,
$G \times _S \widetilde {X} \to \widetilde {X}$
is an isomorphism as well. Thus,
 $\mathscr {R}_{S'/S}(\rho ')\colon \widetilde {X}\to \mathcal {X}$
is a G-torsor, thereby inducing an isomorphism
$\mathscr {R}_{S'/S}(\rho ')\colon \widetilde {X}\to \mathcal {X}$
is a G-torsor, thereby inducing an isomorphism
 $\mathcal {X}\xrightarrow {\sim }\left [\widetilde {X}/G\right ]$
which makes the diagram in the statement of the proposition commute.
$\mathcal {X}\xrightarrow {\sim }\left [\widetilde {X}/G\right ]$
which makes the diagram in the statement of the proposition commute.
By the definition of jet stacks, the following is a special case of Proposition 3.20:
Corollary 3.22. Let G be a linear algebraic group over k acting on a k-scheme
![]() $\widetilde {X}$
, and set
$\widetilde {X}$
, and set
![]() $n \in \mathbb {N}$
. There exists an isomorphism
$n \in \mathbb {N}$
. There exists an isomorphism
 $$ \begin{align*} \mathscr{L}_n\left(\left[\widetilde{X}/G\right]\right) \xrightarrow{\sim} \left[\mathscr{L}_n\left(\widetilde{X}\right)/\mathscr{L}_n(G)\right], \end{align*} $$
$$ \begin{align*} \mathscr{L}_n\left(\left[\widetilde{X}/G\right]\right) \xrightarrow{\sim} \left[\mathscr{L}_n\left(\widetilde{X}\right)/\mathscr{L}_n(G)\right], \end{align*} $$
such that

commutes.
Remark 3.23. In the statement of Corollary 3.22, the action of
![]() $\mathscr {L}_n(G)$
on
$\mathscr {L}_n(G)$
on
 $\mathscr {L}_n\left (\widetilde {X}\right )$
is obtained by applying
$\mathscr {L}_n\left (\widetilde {X}\right )$
is obtained by applying
![]() $\mathscr {L}_n$
to the map
$\mathscr {L}_n$
to the map
![]() $G \times _{k} \widetilde {X} \to \widetilde {X}$
defining the G-action on
$G \times _{k} \widetilde {X} \to \widetilde {X}$
defining the G-action on
![]() $\widetilde {X}$
.
$\widetilde {X}$
.
3.2 Truncation morphisms and quotient stacks
Lemma 3.24. Let
![]() $\mathcal {X}$
be an Artin stack over k, let
$\mathcal {X}$
be an Artin stack over k, let
![]() $\widetilde {X}$
be a scheme over k and let
$\widetilde {X}$
be a scheme over k and let
![]() $\rho : \widetilde {X} \to \mathcal {X}$
be a smooth covering. Set
$\rho : \widetilde {X} \to \mathcal {X}$
be a smooth covering. Set
![]() $\mathcal {C} \subset \lvert \mathscr {L}(\mathcal {X})\rvert $
and
$\mathcal {C} \subset \lvert \mathscr {L}(\mathcal {X})\rvert $
and
 $\widetilde {C} = \mathscr {L}(\rho )^{-1}(\mathcal {C}) \subset \mathscr {L}\left (\widetilde {X}\right )$
. Then for all
$\widetilde {C} = \mathscr {L}(\rho )^{-1}(\mathcal {C}) \subset \mathscr {L}\left (\widetilde {X}\right )$
. Then for all
![]() $n \in \mathbb {N}$
,
$n \in \mathbb {N}$
,
 $$ \begin{align*} \mathscr{L}_n(\rho)^{-1}(\theta_n(\mathcal{C})) = \theta_n\left(\widetilde{C}\right). \end{align*} $$
$$ \begin{align*} \mathscr{L}_n(\rho)^{-1}(\theta_n(\mathcal{C})) = \theta_n\left(\widetilde{C}\right). \end{align*} $$
Proof. Set
![]() $n \in \mathbb {N}$
. Clearly,
$n \in \mathbb {N}$
. Clearly,
 $\theta _n\left (\widetilde {C}\right ) \subset \mathscr {L}_n(\rho )^{-1}(\theta _n(\mathcal {C}))$
.
$\theta _n\left (\widetilde {C}\right ) \subset \mathscr {L}_n(\rho )^{-1}(\theta _n(\mathcal {C}))$
.
To prove the opposite inclusion, let
![]() $k'$
be a field extension of k, and let
$k'$
be a field extension of k, and let
 $\widetilde {\psi }_n \in \mathscr {L}_n\left (\widetilde {X}\right )(k')$
and
$\widetilde {\psi }_n \in \mathscr {L}_n\left (\widetilde {X}\right )(k')$
and
![]() $\psi \in \mathscr {L}(\mathcal {X})(k')$
be such that the class of
$\psi \in \mathscr {L}(\mathcal {X})(k')$
be such that the class of
![]() $\psi $
in
$\psi $
in
![]() $\lvert \mathscr {L}(\mathcal {X})\rvert $
is contained in
$\lvert \mathscr {L}(\mathcal {X})\rvert $
is contained in
![]() $\mathcal {C}$
and
$\mathcal {C}$
and
 $\mathscr {L}_n(\rho )\left (\widetilde {\psi }_n\right ) \cong \theta _n(\psi )$
. We must show
$\mathscr {L}_n(\rho )\left (\widetilde {\psi }_n\right ) \cong \theta _n(\psi )$
. We must show
 $\widetilde {\psi }_n\in \theta _n\left (\widetilde {C}\right )$
. Since
$\widetilde {\psi }_n\in \theta _n\left (\widetilde {C}\right )$
. Since
![]() $\rho $
is smooth, by the infinitesimal lifting criterion, we have a dotted arrow filling in the following diagram:
$\rho $
is smooth, by the infinitesimal lifting criterion, we have a dotted arrow filling in the following diagram:

Then
![]() $\widetilde {\psi }\in \widetilde {C}$
, so
$\widetilde {\psi }\in \widetilde {C}$
, so
 $\widetilde {\psi }_n\in \theta _n\left (\widetilde {C}\right )$
.
$\widetilde {\psi }_n\in \theta _n\left (\widetilde {C}\right )$
.
We may now prove the next proposition, which by Remark 3.1 and Remark 3.10 implies Theorem 3.9.
Proposition 3.25. Let G be a special group over k, let
![]() $\widetilde {X}$
be an equidimensional finite-type scheme over k with G-action, let
$\widetilde {X}$
be an equidimensional finite-type scheme over k with G-action, let
 $\mathcal {X} = \left [\widetilde {X}/G\right ]$
, let
$\mathcal {X} = \left [\widetilde {X}/G\right ]$
, let
![]() $\rho : \widetilde {X} \to \mathcal {X}$
be the quotient map, let
$\rho : \widetilde {X} \to \mathcal {X}$
be the quotient map, let
![]() $\mathcal {C} \subset \lvert \mathscr {L}(\mathcal {X})\rvert $
be a cylinder and let
$\mathcal {C} \subset \lvert \mathscr {L}(\mathcal {X})\rvert $
be a cylinder and let
![]() $\widetilde {C} = \mathscr {L}(\rho )^{-1}(\mathcal {C})$
. Then
$\widetilde {C} = \mathscr {L}(\rho )^{-1}(\mathcal {C})$
. Then
![]() $\widetilde {C} \subset \mathscr {L}(\widetilde {X})$
is a cylinder, the set
$\widetilde {C} \subset \mathscr {L}(\widetilde {X})$
is a cylinder, the set
![]() $\theta _n(\mathcal {C}) \subset \lvert \mathscr {L}_n(\mathcal {X})\rvert $
is constructible for each
$\theta _n(\mathcal {C}) \subset \lvert \mathscr {L}_n(\mathcal {X})\rvert $
is constructible for each
![]() $n \in \mathbb {N}$
, and the sequence
$n \in \mathbb {N}$
, and the sequence
 $$ \begin{align*} \left\{\mathrm{e}(\theta_n(\mathcal{C})) \mathbb{L}^{-(n+1)\dim\mathcal{X}}\right\}_{n \in \mathbb{N}} \subset \widehat{\mathscr{M}}_k \end{align*} $$
$$ \begin{align*} \left\{\mathrm{e}(\theta_n(\mathcal{C})) \mathbb{L}^{-(n+1)\dim\mathcal{X}}\right\}_{n \in \mathbb{N}} \subset \widehat{\mathscr{M}}_k \end{align*} $$
converges to
 $$ \begin{align*} \mu_{\widetilde{X}} \left(\widetilde{C}\right) \mathrm{e}(G)^{-1} \mathbb{L}^{\dim G} \in \widehat{\mathscr{M}}_k. \end{align*} $$
$$ \begin{align*} \mu_{\widetilde{X}} \left(\widetilde{C}\right) \mathrm{e}(G)^{-1} \mathbb{L}^{\dim G} \in \widehat{\mathscr{M}}_k. \end{align*} $$
Remark 3.26. In the statement of Proposition 3.25, because G is irreducible, the irreducible components of
![]() $\widetilde {X}$
are G-invariant, so
$\widetilde {X}$
are G-invariant, so
![]() $\mathcal {X}$
is equidimensional.
$\mathcal {X}$
is equidimensional.
Proof. We first show that
 $\widetilde {C} \subset \mathscr {L}\left (\widetilde {X}\right )$
is a cylinder. Because
$\widetilde {C} \subset \mathscr {L}\left (\widetilde {X}\right )$
is a cylinder. Because
![]() $\mathcal {C}$
is a cylinder, there exist some
$\mathcal {C}$
is a cylinder, there exist some
![]() $n \in \mathbb {N}$
and some constructible subset
$n \in \mathbb {N}$
and some constructible subset
![]() $\mathcal {C}_n \subset \lvert \mathscr {L}_n(\mathcal {X})\rvert $
such that
$\mathcal {C}_n \subset \lvert \mathscr {L}_n(\mathcal {X})\rvert $
such that
![]() $\mathcal {C} = (\theta _n)^{-1}(\mathcal {C}_n)$
. Then
$\mathcal {C} = (\theta _n)^{-1}(\mathcal {C}_n)$
. Then
 $\widetilde {C} = (\theta _n)^{-1}\left (\mathscr {L}_n(\rho )^{-1}(\mathcal {C}_n)\right )$
is a cylinder.
$\widetilde {C} = (\theta _n)^{-1}\left (\mathscr {L}_n(\rho )^{-1}(\mathcal {C}_n)\right )$
is a cylinder.
Now we will show that for all
![]() $n \in \mathbb {N}$
, the set
$n \in \mathbb {N}$
, the set
![]() $\theta _n(\mathcal {C})$
is a constructible subset of
$\theta _n(\mathcal {C})$
is a constructible subset of
![]() $\mathscr {L}_n(\mathcal {X})$
. Each
$\mathscr {L}_n(\mathcal {X})$
. Each
 $\theta _n\left (\widetilde {C}\right )$
is a constructible subset of
$\theta _n\left (\widetilde {C}\right )$
is a constructible subset of
 $\mathscr {L}_n\left (\widetilde {X}\right )$
. Therefore each
$\mathscr {L}_n\left (\widetilde {X}\right )$
. Therefore each
![]() $\theta _n(\mathcal {C}) \subset \lvert \mathscr {L}_n(\mathcal {X})\rvert $
is constructible, by Chevalley’s theorem for Artin stacks [Reference Hall and RydhHR17, Theorem 5.2], Corollary 3.22 and Lemma 3.24.
$\theta _n(\mathcal {C}) \subset \lvert \mathscr {L}_n(\mathcal {X})\rvert $
is constructible, by Chevalley’s theorem for Artin stacks [Reference Hall and RydhHR17, Theorem 5.2], Corollary 3.22 and Lemma 3.24.
Then since G is a special group,
![]() $\mathscr {L}_n(G)$
is as well, by Remark 2.4. Then Corollary 3.22 and Lemma 3.24 imply that for each
$\mathscr {L}_n(G)$
is as well, by Remark 2.4. Then Corollary 3.22 and Lemma 3.24 imply that for each
![]() $n \in \mathbb {N}$
,
$n \in \mathbb {N}$
,
 $$ \begin{align*} \mathrm{e}(\theta_n(\mathcal{C})) = \mathrm{e}\left(\theta_n\left(\widetilde{C}\right)\right)\mathrm{e}(\mathscr{L}_n(G))^{-1} = \mathrm{e}\left(\theta_n\left(\widetilde{C}\right)\right) \mathrm{e}(G)^{-1} \mathbb{L}^{-n\dim G}, \end{align*} $$
$$ \begin{align*} \mathrm{e}(\theta_n(\mathcal{C})) = \mathrm{e}\left(\theta_n\left(\widetilde{C}\right)\right)\mathrm{e}(\mathscr{L}_n(G))^{-1} = \mathrm{e}\left(\theta_n\left(\widetilde{C}\right)\right) \mathrm{e}(G)^{-1} \mathbb{L}^{-n\dim G}, \end{align*} $$
where the second equality holds because G is smooth. Therefore,
 $$ \begin{align*} \mu_{\widetilde{X}}(\widetilde{C})\mathrm{e}(G)^{-1}\mathbb{L}^{\dim G} &= \lim_{n \to \infty} \mathrm{e}\left(\theta_n\left(\widetilde{C}\right)\right) \mathrm{e}(G)^{-1} \mathbb{L}^{\dim G -(n+1)\dim \widetilde{X}}\\ &= \lim_{n \to \infty} \mathrm{e}(\theta_n(\mathcal{C})) \mathbb{L}^{-(n+1)\dim\mathcal{X}}.\\[-36pt] \end{align*} $$
$$ \begin{align*} \mu_{\widetilde{X}}(\widetilde{C})\mathrm{e}(G)^{-1}\mathbb{L}^{\dim G} &= \lim_{n \to \infty} \mathrm{e}\left(\theta_n\left(\widetilde{C}\right)\right) \mathrm{e}(G)^{-1} \mathbb{L}^{\dim G -(n+1)\dim \widetilde{X}}\\ &= \lim_{n \to \infty} \mathrm{e}(\theta_n(\mathcal{C})) \mathbb{L}^{-(n+1)\dim\mathcal{X}}.\\[-36pt] \end{align*} $$
3.3 Properties of motivic integration for quotient stacks
We now state some basic properties of motivic integration for quotient stacks. We will use these properties later in this paper.
Proposition 3.27. Let
![]() $\mathcal {X}$
be an equidimensional finite-type quotient stack over k, let
$\mathcal {X}$
be an equidimensional finite-type quotient stack over k, let
 $\left \{\mathcal {C}^{(i)}\right \}_{i \in \mathbb {N}}$
be a sequence of pairwise disjoint measurable subsets of
$\left \{\mathcal {C}^{(i)}\right \}_{i \in \mathbb {N}}$
be a sequence of pairwise disjoint measurable subsets of
![]() $\lvert \mathscr {L}(\mathcal {X})\rvert $
and let
$\lvert \mathscr {L}(\mathcal {X})\rvert $
and let
 $\mathcal {C} = \bigcup _{i= 0}^\infty \mathcal {C}^{(i)}$
. If
$\mathcal {C} = \bigcup _{i= 0}^\infty \mathcal {C}^{(i)}$
. If
 $\lim _{i \to \infty } \mu _{\mathcal {X}}\left (\mathcal {C}^{(i)}\right ) = 0$
, then
$\lim _{i \to \infty } \mu _{\mathcal {X}}\left (\mathcal {C}^{(i)}\right ) = 0$
, then
![]() $\mathcal {C}$
is measurable and
$\mathcal {C}$
is measurable and
 $$ \begin{align*} \mu_{\mathcal{X}}(\mathcal{C}) = \sum_{i = 0}^\infty \mu_{\mathcal{X}}\left(\mathcal{C}^{(i)}\right). \end{align*} $$
$$ \begin{align*} \mu_{\mathcal{X}}(\mathcal{C}) = \sum_{i = 0}^\infty \mu_{\mathcal{X}}\left(\mathcal{C}^{(i)}\right). \end{align*} $$
Proof. The set
![]() $\mathcal {C}$
is measurable by the exact same proof used for the analogous statement for schemes in [Reference Chambert-Loir, Nicaise and SebagCLNS18, Chapter 6, Proposition 3.4.2]. The remainder of the proposition follows from Corollary 3.16 and the analogous statement for schemes [Reference Chambert-Loir, Nicaise and SebagCLNS18, Chapter 6, Proposition 3.4.3] applied to the scheme
$\mathcal {C}$
is measurable by the exact same proof used for the analogous statement for schemes in [Reference Chambert-Loir, Nicaise and SebagCLNS18, Chapter 6, Proposition 3.4.2]. The remainder of the proposition follows from Corollary 3.16 and the analogous statement for schemes [Reference Chambert-Loir, Nicaise and SebagCLNS18, Chapter 6, Proposition 3.4.3] applied to the scheme
![]() $\widetilde {X}$
in the statement of Corollary 3.16.
$\widetilde {X}$
in the statement of Corollary 3.16.
Proposition 3.28. Let
![]() $\mathcal {X}$
be an equidimensional finite-type quotient stack over k, and set
$\mathcal {X}$
be an equidimensional finite-type quotient stack over k, and set
![]() $\mathcal {C} \subset \mathcal {D} \subset \lvert \mathscr {L}(\mathcal {X})\rvert $
. If
$\mathcal {C} \subset \mathcal {D} \subset \lvert \mathscr {L}(\mathcal {X})\rvert $
. If
![]() $\mathcal {D}$
is measurable and
$\mathcal {D}$
is measurable and
![]() $\mu _{\mathcal {X}}(\mathcal {D}) = 0$
, then
$\mu _{\mathcal {X}}(\mathcal {D}) = 0$
, then
![]() $\mathcal {C}$
is measurable and
$\mathcal {C}$
is measurable and
![]() $\mu _{\mathcal {X}}(\mathcal {C}) = 0$
.
$\mu _{\mathcal {X}}(\mathcal {C}) = 0$
.
Proof. The proposition holds by the exact same proof used for the analogous statement for schemes in [Reference Chambert-Loir, Nicaise and SebagCLNS18, Chapter 6, Corollary 3.5.5(a)].
Proposition 3.29. Let
![]() $\mathcal {X}$
be an equidimensional finite-type quotient stack over k, and let
$\mathcal {X}$
be an equidimensional finite-type quotient stack over k, and let
![]() $\mathcal {C}, \mathcal {D}$
be measurable subsets of
$\mathcal {C}, \mathcal {D}$
be measurable subsets of
![]() $\lvert \mathscr {L}(\mathcal {X})\rvert $
. If
$\lvert \mathscr {L}(\mathcal {X})\rvert $
. If
![]() $\mathcal {C} \subset \mathcal {D}$
, then
$\mathcal {C} \subset \mathcal {D}$
, then
Proof. By Remark 3.1, there exist
![]() $G, \widetilde {X}, \rho $
as in the statement of Theorem 3.9 such that G is a general linear group. Let
$G, \widetilde {X}, \rho $
as in the statement of Theorem 3.9 such that G is a general linear group. Let
![]() $\widetilde {C} = \mathscr {L}(\rho )^{-1}(\mathcal {C})$
and
$\widetilde {C} = \mathscr {L}(\rho )^{-1}(\mathcal {C})$
and
![]() $\widetilde {D} = \mathscr {L}(\rho )^{-1}(\mathcal {D})$
. Then
$\widetilde {D} = \mathscr {L}(\rho )^{-1}(\mathcal {D})$
. Then
 $$ \begin{align*} \lVert \mu_{\mathcal{X}}(\mathcal{C}) \rVert &= \left\lVert \mu_{\widetilde{X}}\left(\widetilde{C}\right)\mathrm{e}(G)^{-1}\mathbb{L}^{\dim G} \right\rVert\\ &\leq \left\lVert \mathrm{e}(G)^{-1}\mathbb{L}^{\dim G}\right\rVert \left\lVert \mu_{\widetilde{X}}\left(\widetilde{C}\right)\right\rVert\\ &\leq \left\lVert \mathrm{e}(G)^{-1}\mathbb{L}^{\dim G}\right\rVert \left\lVert \mu_{\widetilde{X}}\left(\widetilde{D}\right)\right\rVert\\ &= \left\lVert \mathrm{e}(G)^{-1}\mathbb{L}^{\dim G}\right\rVert \left\lVert \mu_{\mathcal{X}}(\mathcal{D}) \mathrm{e}(G)\mathbb{L}^{-\dim G}\right\rVert\\ &\leq \left\lVert \mathrm{e}(G)^{-1} \mathbb{L}^{\dim G} \right\rVert \left\lVert\mathrm{e}(G) \mathbb{L}^{-\dim G}\right\rVert \lVert \mu_{\mathcal{X}}(\mathcal{D}) \rVert\\ &= \lVert \mu_{\mathcal{X}}(\mathcal{D}) \rVert, \end{align*} $$
$$ \begin{align*} \lVert \mu_{\mathcal{X}}(\mathcal{C}) \rVert &= \left\lVert \mu_{\widetilde{X}}\left(\widetilde{C}\right)\mathrm{e}(G)^{-1}\mathbb{L}^{\dim G} \right\rVert\\ &\leq \left\lVert \mathrm{e}(G)^{-1}\mathbb{L}^{\dim G}\right\rVert \left\lVert \mu_{\widetilde{X}}\left(\widetilde{C}\right)\right\rVert\\ &\leq \left\lVert \mathrm{e}(G)^{-1}\mathbb{L}^{\dim G}\right\rVert \left\lVert \mu_{\widetilde{X}}\left(\widetilde{D}\right)\right\rVert\\ &= \left\lVert \mathrm{e}(G)^{-1}\mathbb{L}^{\dim G}\right\rVert \left\lVert \mu_{\mathcal{X}}(\mathcal{D}) \mathrm{e}(G)\mathbb{L}^{-\dim G}\right\rVert\\ &\leq \left\lVert \mathrm{e}(G)^{-1} \mathbb{L}^{\dim G} \right\rVert \left\lVert\mathrm{e}(G) \mathbb{L}^{-\dim G}\right\rVert \lVert \mu_{\mathcal{X}}(\mathcal{D}) \rVert\\ &= \lVert \mu_{\mathcal{X}}(\mathcal{D}) \rVert, \end{align*} $$
where the first and fourth lines follow from Corollary 3.16, the third line follows from the analogous statement [Reference Chambert-Loir, Nicaise and SebagCLNS18, Chapter 6, Corollary 3.3.5] for schemes applied to
![]() $\widetilde {X}$
and the last line follows from Lemma 3.17.
$\widetilde {X}$
and the last line follows from Lemma 3.17.
Proposition 3.30. Let
![]() $\mathcal {X}$
be an equidimensional finite-type quotient stack over k, let
$\mathcal {X}$
be an equidimensional finite-type quotient stack over k, let
![]() $\mathcal {Y}$
be a closed substack of
$\mathcal {Y}$
be a closed substack of
![]() $\mathcal {X}$
with
$\mathcal {X}$
with
![]() $\dim \mathcal {Y} < \dim \mathcal {X}$
and let
$\dim \mathcal {Y} < \dim \mathcal {X}$
and let
![]() $\mathcal {C} \subset \lvert \mathscr {L}(\mathcal {X})\rvert $
be the image of
$\mathcal {C} \subset \lvert \mathscr {L}(\mathcal {X})\rvert $
be the image of
![]() $\lvert \mathscr {L}(\mathcal {Y})\rvert $
in
$\lvert \mathscr {L}(\mathcal {Y})\rvert $
in
![]() $\lvert \mathscr {L}(\mathcal {X})\rvert $
. Then
$\lvert \mathscr {L}(\mathcal {X})\rvert $
. Then
![]() $\mathcal {C}$
is measurable and
$\mathcal {C}$
is measurable and
![]() $\mu _{\mathcal {X}}(\mathcal {C}) = 0$
.
$\mu _{\mathcal {X}}(\mathcal {C}) = 0$
.
Proof. For each
![]() $n \in \mathbb {N}$
, let
$n \in \mathbb {N}$
, let
![]() $\mathcal {C}_n \subset \lvert \mathscr {L}_n(\mathcal {X})\rvert $
be the image of
$\mathcal {C}_n \subset \lvert \mathscr {L}_n(\mathcal {X})\rvert $
be the image of
![]() $\lvert \mathscr {L}_n(\mathcal {Y})\rvert $
in
$\lvert \mathscr {L}_n(\mathcal {Y})\rvert $
in
![]() $\lvert \mathscr {L}_n(\mathcal {X})\rvert $
, and let
$\lvert \mathscr {L}_n(\mathcal {X})\rvert $
, and let
![]() $\mathcal {C}^{(n)} = (\theta _n)^{-1}(\mathcal {C}_n)$
. By [Reference RydhRyd11, Proposition 3.5(vi)], each
$\mathcal {C}^{(n)} = (\theta _n)^{-1}(\mathcal {C}_n)$
. By [Reference RydhRyd11, Proposition 3.5(vi)], each
![]() $\mathcal {C}_n$
is a closed subset of
$\mathcal {C}_n$
is a closed subset of
![]() $\mathscr {L}_n(\mathcal {X})$
, so each
$\mathscr {L}_n(\mathcal {X})$
, so each
![]() $\mathcal {C}^{(n)}$
is a cylinder in
$\mathcal {C}^{(n)}$
is a cylinder in
![]() $\mathscr {L}(\mathcal {X})$
.
$\mathscr {L}(\mathcal {X})$
.
By Remark 3.1, there exist
![]() $G, \widetilde {X}, \rho $
as in the statement of Theorem 3.9. Let
$G, \widetilde {X}, \rho $
as in the statement of Theorem 3.9. Let
![]() $\widetilde {Y} = \widetilde {X} \times _{\mathcal {X}} \mathcal {Y}$
. Then
$\widetilde {Y} = \widetilde {X} \times _{\mathcal {X}} \mathcal {Y}$
. Then
![]() $\mathscr {L}_n(\rho )^{-1}(\mathcal {C}_n)$
is the underlying set of
$\mathscr {L}_n(\rho )^{-1}(\mathcal {C}_n)$
is the underlying set of
 $\mathscr {L}_n\left (\widetilde {Y}\right )$
. Thus by Theorem 3.9,
$\mathscr {L}_n\left (\widetilde {Y}\right )$
. Thus by Theorem 3.9,
 $$ \begin{align*} \mu_{\mathcal{X}}\left(\mathcal{C}^{(n)}\right) &= \mu_{\widetilde{X}} \left(\mathscr{L}(\rho)^{-1}\left(\mathcal{C}^{(n)}\right)\right) \mathrm{e}(G)^{-1} \mathbb{L}^{\dim G}\\ &= \mu_{\widetilde{X}}\left((\theta_n)^{-1}\left(\mathscr{L}_n\left(\widetilde{Y}\right)\right)\right)\mathrm{e}(G)^{-1} \mathbb{L}^{\dim G}. \end{align*} $$
$$ \begin{align*} \mu_{\mathcal{X}}\left(\mathcal{C}^{(n)}\right) &= \mu_{\widetilde{X}} \left(\mathscr{L}(\rho)^{-1}\left(\mathcal{C}^{(n)}\right)\right) \mathrm{e}(G)^{-1} \mathbb{L}^{\dim G}\\ &= \mu_{\widetilde{X}}\left((\theta_n)^{-1}\left(\mathscr{L}_n\left(\widetilde{Y}\right)\right)\right)\mathrm{e}(G)^{-1} \mathbb{L}^{\dim G}. \end{align*} $$
By [Reference Chambert-Loir, Nicaise and SebagCLNS18, Chapter 6, Proposition 2.3.1],
 $$ \begin{align*} \lim_{n \to \infty} \mu_{\widetilde{X}}\left((\theta_n)^{-1}\left(\mathscr{L}_n\left(\widetilde{Y}\right)\right)\right) = 0, \end{align*} $$
$$ \begin{align*} \lim_{n \to \infty} \mu_{\widetilde{X}}\left((\theta_n)^{-1}\left(\mathscr{L}_n\left(\widetilde{Y}\right)\right)\right) = 0, \end{align*} $$
so
 $$ \begin{align*} \lim_{n \to \infty} \mu_{\mathcal{X}}\left(\mathcal{C}^{(n)}\right) = 0. \end{align*} $$
$$ \begin{align*} \lim_{n \to \infty} \mu_{\mathcal{X}}\left(\mathcal{C}^{(n)}\right) = 0. \end{align*} $$
Therefore for any
![]() $\varepsilon \in \mathbb {R}_{>0}$
, we get that
$\varepsilon \in \mathbb {R}_{>0}$
, we get that
 $\left (\emptyset , \left (\mathcal {C}^{(n)}\right )\right )$
is a cylindrical
$\left (\emptyset , \left (\mathcal {C}^{(n)}\right )\right )$
is a cylindrical
![]() $\varepsilon $
-approximation of
$\varepsilon $
-approximation of
![]() $\mathcal {C}$
for sufficiently large n, and we are done, by the definition of
$\mathcal {C}$
for sufficiently large n, and we are done, by the definition of
![]() $\mu _{\mathcal {X}}$
.
$\mu _{\mathcal {X}}$
.
Proposition 3.31. Let
![]() $\mathcal {X}$
be an equidimensional finite-type quotient stack over k, and let
$\mathcal {X}$
be an equidimensional finite-type quotient stack over k, and let
![]() $\mathcal {C}$
and
$\mathcal {C}$
and
![]() $\mathcal {D}$
be measurable subsets of
$\mathcal {D}$
be measurable subsets of
![]() $\lvert \mathscr {L}(\mathcal {X})\rvert $
. Then the intersection
$\lvert \mathscr {L}(\mathcal {X})\rvert $
. Then the intersection
![]() $\mathcal {C} \cap \mathcal {D}$
, the union
$\mathcal {C} \cap \mathcal {D}$
, the union
![]() $\mathcal {C} \cup \mathcal {D}$
and the complement
$\mathcal {C} \cup \mathcal {D}$
and the complement
![]() $\mathcal {C} \setminus \mathcal {D}$
are all measurable subsets of
$\mathcal {C} \setminus \mathcal {D}$
are all measurable subsets of
![]() $\lvert \mathscr {L}(\mathcal {X})\rvert $
.
$\lvert \mathscr {L}(\mathcal {X})\rvert $
.
Proof. The proposition holds by the exact same proof used for the analogous statement for schemes in [Reference Chambert-Loir, Nicaise and SebagCLNS18, Chapter 6, Proposition 3.2.8].
Proposition 3.32. Let
![]() $\mathcal {X}$
be an equidimensional finite-type quotient stack over k, let
$\mathcal {X}$
be an equidimensional finite-type quotient stack over k, let
![]() $\iota : \mathcal {U} \hookrightarrow \mathcal {X}$
be the inclusion of an open substack and set
$\iota : \mathcal {U} \hookrightarrow \mathcal {X}$
be the inclusion of an open substack and set
![]() $\mathcal {C} \subset (\theta _0)^{-1}(\lvert \mathcal {U}\rvert ) \subset \lvert \mathscr {L}(\mathcal {X})\rvert $
. Then
$\mathcal {C} \subset (\theta _0)^{-1}(\lvert \mathcal {U}\rvert ) \subset \lvert \mathscr {L}(\mathcal {X})\rvert $
. Then
![]() $\mathcal {C}$
is a measurable subset of
$\mathcal {C}$
is a measurable subset of
![]() $\lvert \mathscr {L}(\mathcal {X})\rvert $
if and only if
$\lvert \mathscr {L}(\mathcal {X})\rvert $
if and only if
![]() $\mathscr {L}(\iota )^{-1}(\mathcal {C})$
is a measurable subset of
$\mathscr {L}(\iota )^{-1}(\mathcal {C})$
is a measurable subset of
![]() $\lvert \mathscr {L}(\mathcal {U})\rvert $
, and in that case,
$\lvert \mathscr {L}(\mathcal {U})\rvert $
, and in that case,
 $$ \begin{align*} \mu_{\mathcal{X}}(\mathcal{C}) = \mu_{\mathcal{U}}\left(\mathscr{L}(\iota)^{-1}(\mathcal{C})\right). \end{align*} $$
$$ \begin{align*} \mu_{\mathcal{X}}(\mathcal{C}) = \mu_{\mathcal{U}}\left(\mathscr{L}(\iota)^{-1}(\mathcal{C})\right). \end{align*} $$
Proof. As in the case of schemes, this is an easy consequence of the definitions and the fact that for all
![]() $n \in \mathbb {N}$
, the morphism
$n \in \mathbb {N}$
, the morphism
![]() $\mathscr {L}_n(\iota ): \mathscr {L}_n(\mathcal {U}) \to \mathscr {L}_n(\mathcal {X})$
is an open immersion by [Reference RydhRyd11, Proposition 3.5(vii)].
$\mathscr {L}_n(\iota ): \mathscr {L}_n(\mathcal {U}) \to \mathscr {L}_n(\mathcal {X})$
is an open immersion by [Reference RydhRyd11, Proposition 3.5(vii)].
3.4 Nonseparatedness functions
We now introduce notation for the nonseparatedness functions
![]() $\operatorname {\mathrm {sep}}_{\pi , \mathcal {C}}$
,
$\operatorname {\mathrm {sep}}_{\pi , \mathcal {C}}$
,
![]() $\operatorname {\mathrm {sep}}_\pi $
and
$\operatorname {\mathrm {sep}}_\pi $
and
![]() $\operatorname {\mathrm {sep}}_{\mathcal {X}}$
that were used in the statements of the main conjectures and theorems of this paper. Throughout this subsection, let
$\operatorname {\mathrm {sep}}_{\mathcal {X}}$
that were used in the statements of the main conjectures and theorems of this paper. Throughout this subsection, let
![]() $\mathcal {X}$
be an Artin stack over k, set
$\mathcal {X}$
be an Artin stack over k, set
![]() $\mathcal {C} \subset \lvert \mathscr {L}(\mathcal {X})\rvert $
, let X be a scheme over k and let
$\mathcal {C} \subset \lvert \mathscr {L}(\mathcal {X})\rvert $
, let X be a scheme over k and let
![]() $\pi : \mathcal {X} \to X$
be a map. For any field extension
$\pi : \mathcal {X} \to X$
be a map. For any field extension
![]() $k'$
of k, we will let
$k'$
of k, we will let
![]() $\overline {\mathcal {C}}(k')$
denote the subset of
$\overline {\mathcal {C}}(k')$
denote the subset of
![]() $\overline {\mathscr {L}(\mathcal {X})}(k')$
consisting of arcs whose classes in the set
$\overline {\mathscr {L}(\mathcal {X})}(k')$
consisting of arcs whose classes in the set
![]() $\lvert \mathscr {L}(\mathcal {X})\rvert $
are contained in
$\lvert \mathscr {L}(\mathcal {X})\rvert $
are contained in
![]() $\mathcal {C}$
.
$\mathcal {C}$
.
If
![]() $k'$
is a field extension of k and
$k'$
is a field extension of k and
![]() $\varphi \in \mathscr {L}(X)(k')$
, we set
$\varphi \in \mathscr {L}(X)(k')$
, we set
 $$ \begin{align*} \operatorname{\mathrm{sep}}_{\pi, \mathcal{C}}(\varphi) = \#\left(\overline{\mathcal{C}}(k') \cap \overline{\left(\mathscr{L}(\pi)^{-1}(\varphi)\right)}(k')\right) \in \mathbb{N} \cup \{\infty\}, \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{sep}}_{\pi, \mathcal{C}}(\varphi) = \#\left(\overline{\mathcal{C}}(k') \cap \overline{\left(\mathscr{L}(\pi)^{-1}(\varphi)\right)}(k')\right) \in \mathbb{N} \cup \{\infty\}, \end{align*} $$
which induces a map
![]() $\operatorname {\mathrm {sep}}_{\pi , \mathcal {C}}: \mathscr {L}(X) \to \mathbb {N} \cup \{\infty \}$
by considering each
$\operatorname {\mathrm {sep}}_{\pi , \mathcal {C}}: \mathscr {L}(X) \to \mathbb {N} \cup \{\infty \}$
by considering each
![]() $\varphi \in \mathscr {L}(X)$
as a point valued in its residue field. If, furthermore, we assume that X is integral, finite type and separated and has log-terminal singularities, that
$\varphi \in \mathscr {L}(X)$
as a point valued in its residue field. If, furthermore, we assume that X is integral, finite type and separated and has log-terminal singularities, that
![]() $\operatorname {\mathrm {sep}}_{\pi , \mathcal {C}}: \mathscr {L}(X) \to \mathbb {N} \cup \{\infty \}$
has measurable fibres and that
$\operatorname {\mathrm {sep}}_{\pi , \mathcal {C}}: \mathscr {L}(X) \to \mathbb {N} \cup \{\infty \}$
has measurable fibres and that
![]() $C \subset \mathscr {L}(X)$
is a measurable subset, then we can consider the motivic integral
$C \subset \mathscr {L}(X)$
is a measurable subset, then we can consider the motivic integral
 $$ \begin{align*} \int_C \operatorname{\mathrm{sep}}_{\pi, \mathcal{C}} \mathrm{d}\mu^{\mathrm{Gor}}_X = \sum_{n \in \mathbb{N}} n \mu^{\mathrm{Gor}}_X\left(\operatorname{\mathrm{sep}}_{\pi, \mathcal{C}}^{-1}(n) \cap C\right) \in \widehat{\mathscr{M}}_k\left[\mathbb{L}^{1/m}\right], \end{align*} $$
$$ \begin{align*} \int_C \operatorname{\mathrm{sep}}_{\pi, \mathcal{C}} \mathrm{d}\mu^{\mathrm{Gor}}_X = \sum_{n \in \mathbb{N}} n \mu^{\mathrm{Gor}}_X\left(\operatorname{\mathrm{sep}}_{\pi, \mathcal{C}}^{-1}(n) \cap C\right) \in \widehat{\mathscr{M}}_k\left[\mathbb{L}^{1/m}\right], \end{align*} $$
where
![]() $m \in \mathbb {Z}_{>0}$
is such that
$m \in \mathbb {Z}_{>0}$
is such that
![]() $mK_X$
is Cartier. Note that with these assumptions, the series defining
$mK_X$
is Cartier. Note that with these assumptions, the series defining
 $\int _C \operatorname {\mathrm {sep}}_{\pi , \mathcal {C}} \mathrm {d}\mu ^{\mathrm {Gor}}_X$
converges because
$\int _C \operatorname {\mathrm {sep}}_{\pi , \mathcal {C}} \mathrm {d}\mu ^{\mathrm {Gor}}_X$
converges because
 $$ \begin{align*} \lim_{n \to \infty} n \mu^{\mathrm{Gor}}_X\left(\operatorname{\mathrm{sep}}_{\pi, \mathcal{C}}^{-1}(n) \cap C\right) = 0, \end{align*} $$
$$ \begin{align*} \lim_{n \to \infty} n \mu^{\mathrm{Gor}}_X\left(\operatorname{\mathrm{sep}}_{\pi, \mathcal{C}}^{-1}(n) \cap C\right) = 0, \end{align*} $$
which follows from
 $$ \begin{align*} \lim_{n \to \infty} \mu^{\mathrm{Gor}}_X\left(\operatorname{\mathrm{sep}}_{\pi, \mathcal{C}}^{-1}(n) \cap C\right) = 0, \end{align*} $$
$$ \begin{align*} \lim_{n \to \infty} \mu^{\mathrm{Gor}}_X\left(\operatorname{\mathrm{sep}}_{\pi, \mathcal{C}}^{-1}(n) \cap C\right) = 0, \end{align*} $$
which itself, for example, is a consequence of Proposition 2.3.
Set
and
If, furthermore, we assume that
![]() $\mathcal {X}$
is an equidimensional and finite-type quotient stack over k and that
$\mathcal {X}$
is an equidimensional and finite-type quotient stack over k and that
![]() $\operatorname {\mathrm {sep}}_{\mathcal {X}}: \lvert \mathscr {L}(\mathcal {X})\rvert \to \mathbb {Q}_{\geq 0} \cup \{\infty \}$
has measurable fibres, we can consider the motivic integral
$\operatorname {\mathrm {sep}}_{\mathcal {X}}: \lvert \mathscr {L}(\mathcal {X})\rvert \to \mathbb {Q}_{\geq 0} \cup \{\infty \}$
has measurable fibres, we can consider the motivic integral
 $$ \begin{align*} \int_{\mathscr{L}(\mathcal{X})} \operatorname{\mathrm{sep}}_{\mathcal{X}} \mathrm{d}\mu_{\mathcal{X}} = \sum_{n \in \mathbb{Z}_{\geq 1}} (1/n) \mu_{\mathcal{X}}\left( \operatorname{\mathrm{sep}}_{\mathcal{X}}^{-1}(1/n) \right) \in \widehat{\mathscr{M}_k \otimes_{\mathbb{Z}} \mathbb{Q}}, \end{align*} $$
$$ \begin{align*} \int_{\mathscr{L}(\mathcal{X})} \operatorname{\mathrm{sep}}_{\mathcal{X}} \mathrm{d}\mu_{\mathcal{X}} = \sum_{n \in \mathbb{Z}_{\geq 1}} (1/n) \mu_{\mathcal{X}}\left( \operatorname{\mathrm{sep}}_{\mathcal{X}}^{-1}(1/n) \right) \in \widehat{\mathscr{M}_k \otimes_{\mathbb{Z}} \mathbb{Q}}, \end{align*} $$
where the ring
 $\widehat {\mathscr {M}_k \otimes _{\mathbb {Z}} \mathbb {Q}}$
is defined like
$\widehat {\mathscr {M}_k \otimes _{\mathbb {Z}} \mathbb {Q}}$
is defined like
![]() $\widehat {\mathscr {M}}_k$
in subsection 2.1 by replacing any mention of
$\widehat {\mathscr {M}}_k$
in subsection 2.1 by replacing any mention of
![]() $K_0(\mathbf {Var}_k)$
with
$K_0(\mathbf {Var}_k)$
with
![]() $K_0(\mathbf {Var}_k) \otimes _{\mathbb {Z}} \mathbb {Q}$
and any mention of ‘subgroup’ with ‘
$K_0(\mathbf {Var}_k) \otimes _{\mathbb {Z}} \mathbb {Q}$
and any mention of ‘subgroup’ with ‘
![]() $\mathbb {Q}$
-subspace’. With these assumptions, the series defining
$\mathbb {Q}$
-subspace’. With these assumptions, the series defining
 $\int _{\mathscr {L}(\mathcal {X})} \operatorname {\mathrm {sep}}_{\mathcal {X}} \mathrm {d}\mu _{\mathcal {X}}$
converges because
$\int _{\mathscr {L}(\mathcal {X})} \operatorname {\mathrm {sep}}_{\mathcal {X}} \mathrm {d}\mu _{\mathcal {X}}$
converges because
 $$ \begin{align*} \lim_{n \to \infty} (1/n) \mu_{\mathcal{X}}\left( \operatorname{\mathrm{sep}}_{\mathcal{X}}^{-1}(1/n) \right) = 0, \end{align*} $$
$$ \begin{align*} \lim_{n \to \infty} (1/n) \mu_{\mathcal{X}}\left( \operatorname{\mathrm{sep}}_{\mathcal{X}}^{-1}(1/n) \right) = 0, \end{align*} $$
which by the definition of the norm on
 $\widehat {\mathscr {M}_k \otimes _{\mathbb {Z}} \mathbb {Q}}$
follows from
$\widehat {\mathscr {M}_k \otimes _{\mathbb {Z}} \mathbb {Q}}$
follows from
 $$ \begin{align*} \lim_{n \to \infty} \mu_{\mathcal{X}}\left( \operatorname{\mathrm{sep}}_{\mathcal{X}}^{-1}(1/n) \right) = 0, \end{align*} $$
$$ \begin{align*} \lim_{n \to \infty} \mu_{\mathcal{X}}\left( \operatorname{\mathrm{sep}}_{\mathcal{X}}^{-1}(1/n) \right) = 0, \end{align*} $$
which itself follows from Corollary 3.16 and properties of motivic measures for schemes.
3.5 Motivic integration for smooth stacks via the cotangent complex
In this subsection, we prove that the motivic measure
![]() $\mu _{\mathcal {X}}$
is also well defined when
$\mu _{\mathcal {X}}$
is also well defined when
![]() $\mathcal {X}$
is an equidimensional smooth Artin (not necessarily quotient) stack over k. We only explicitly verify this for cylinders, but by a standard argument (identical to the one for schemes in [Reference Chambert-Loir, Nicaise and SebagCLNS18]), it leads to well-defined notions (that coincide with our definitions in the case where
$\mathcal {X}$
is an equidimensional smooth Artin (not necessarily quotient) stack over k. We only explicitly verify this for cylinders, but by a standard argument (identical to the one for schemes in [Reference Chambert-Loir, Nicaise and SebagCLNS18]), it leads to well-defined notions (that coincide with our definitions in the case where
![]() $\mathcal {X}$
is a quotient stack) of measurable subsets of
$\mathcal {X}$
is a quotient stack) of measurable subsets of
![]() $\lvert \mathscr {L}(\mathcal {X})\rvert $
and their motivic measures. The main result of this subsection is the following theorem, which immediately implies that Definition 3.11 makes sense in this setting:
$\lvert \mathscr {L}(\mathcal {X})\rvert $
and their motivic measures. The main result of this subsection is the following theorem, which immediately implies that Definition 3.11 makes sense in this setting:
Theorem 3.33. Let
![]() $\mathcal {X}$
be an equidimensional smooth Artin stack over k, and let
$\mathcal {X}$
be an equidimensional smooth Artin stack over k, and let
![]() $\mathcal {C} \subset \lvert \mathscr {L}(\mathcal {X})\rvert $
be a cylinder. Then the set
$\mathcal {C} \subset \lvert \mathscr {L}(\mathcal {X})\rvert $
be a cylinder. Then the set
![]() $\theta _n(\mathcal {C}) \subset \lvert \mathscr {L}_n(\mathcal {X})\rvert $
is constructible for each
$\theta _n(\mathcal {C}) \subset \lvert \mathscr {L}_n(\mathcal {X})\rvert $
is constructible for each
![]() $n \in \mathbb {N}$
, and the sequence
$n \in \mathbb {N}$
, and the sequence
 $$ \begin{align*} \left\{\mathrm{e}(\theta_n(\mathcal{C})) \mathbb{L}^{-(n+1)\dim\mathcal{X}}\right\}_{n \in \mathbb{N}} \subset K_0(\mathbf{Stack}_k) \end{align*} $$
$$ \begin{align*} \left\{\mathrm{e}(\theta_n(\mathcal{C})) \mathbb{L}^{-(n+1)\dim\mathcal{X}}\right\}_{n \in \mathbb{N}} \subset K_0(\mathbf{Stack}_k) \end{align*} $$
stabilises for sufficiently large n.
We first prove two lemmas, after which we prove this theorem.
Lemma 3.34. Let
![]() $\mathcal {X}$
be an equidimensional smooth Artin stack over k, and set
$\mathcal {X}$
be an equidimensional smooth Artin stack over k, and set
![]() $n \in \mathbb {N}$
. There exist some
$n \in \mathbb {N}$
. There exist some
![]() $\ell \in \mathbb {Z}_{>0}$
, a partition
$\ell \in \mathbb {Z}_{>0}$
, a partition
 $\lvert \mathscr {L}_n(\mathcal {X})\rvert = \bigsqcup _{i=1}^\ell \mathcal {C}_i$
of
$\lvert \mathscr {L}_n(\mathcal {X})\rvert = \bigsqcup _{i=1}^\ell \mathcal {C}_i$
of
![]() $\lvert \mathscr {L}_n(\mathcal {X})\rvert $
into constructible subsets
$\lvert \mathscr {L}_n(\mathcal {X})\rvert $
into constructible subsets
![]() $\mathcal {C}_i$
and some
$\mathcal {C}_i$
and some
![]() $r_1, \dotsc , r_\ell , j_1, \dotsc , j_\ell \in \mathbb {N}$
such that
$r_1, \dotsc , r_\ell , j_1, \dotsc , j_\ell \in \mathbb {N}$
such that
-
• for any
 $i \in \{1, \dotsc , \ell \}$
, we have
$i \in \{1, \dotsc , \ell \}$
, we have
 $r_i - j_i = \dim \mathcal {X}$
, and
$r_i - j_i = \dim \mathcal {X}$
, and -
• for any
 $i \in \{1, \dotsc , \ell \}$
, any field extension
$i \in \{1, \dotsc , \ell \}$
, any field extension
 $k'$
of k and any
$k'$
of k and any
 $\psi _n \in \mathscr {L}_n(\mathcal {X})(k')$
whose class in
$\psi _n \in \mathscr {L}_n(\mathcal {X})(k')$
whose class in
 $\lvert \mathscr {L}_n(\mathcal {X})\rvert $
is contained in
$\lvert \mathscr {L}_n(\mathcal {X})\rvert $
is contained in
 $\mathcal {C}_i$
, we have
$\mathcal {C}_i$
, we have  $$ \begin{align*} \left(\theta^{n+1}_n\right)^{-1}(\psi_n) \cong \mathbb{A}^{r_i}_{k'} \times_{k'} B\mathbb{G}_{a}^{j_i}. \end{align*} $$
$$ \begin{align*} \left(\theta^{n+1}_n\right)^{-1}(\psi_n) \cong \mathbb{A}^{r_i}_{k'} \times_{k'} B\mathbb{G}_{a}^{j_i}. \end{align*} $$
Proof. Fix
![]() $\xi _n\colon \operatorname {\mathrm {Spec}} k'\to \mathscr {L}_n(\mathcal {X})$
and let
$\xi _n\colon \operatorname {\mathrm {Spec}} k'\to \mathscr {L}_n(\mathcal {X})$
and let
![]() $\mathcal {Y}_{\xi _n}$
denote the fibre of the truncation map
$\mathcal {Y}_{\xi _n}$
denote the fibre of the truncation map
![]() $\mathscr {L}_{n+1}(\mathcal {X})\to \mathscr {L}_n(\mathcal {X})$
over
$\mathscr {L}_{n+1}(\mathcal {X})\to \mathscr {L}_n(\mathcal {X})$
over
![]() $\xi _n$
. For any
$\xi _n$
. For any
![]() $\alpha \colon \operatorname {\mathrm {Spec}} A\to \operatorname {\mathrm {Spec}} k'$
, the A-valued points
$\alpha \colon \operatorname {\mathrm {Spec}} A\to \operatorname {\mathrm {Spec}} k'$
, the A-valued points
![]() $\mathcal {Y}_{\xi _n}(A)$
are the category of lifts of
$\mathcal {Y}_{\xi _n}(A)$
are the category of lifts of
![]() $\xi _n\otimes _{k'}A$
to
$\xi _n\otimes _{k'}A$
to
![]() $\mathscr {L}_{n+1}(\mathcal {X})$
. For all
$\mathscr {L}_{n+1}(\mathcal {X})$
. For all
![]() $m\geq 0$
, let
$m\geq 0$
, let
![]() $\mathcal {X}_m=\mathcal {X}\otimes _k k[t]/\left (t^{m+1}\right )$
and let
$\mathcal {X}_m=\mathcal {X}\otimes _k k[t]/\left (t^{m+1}\right )$
and let
![]() $\alpha _m\colon \operatorname {\mathrm {Spec}} A[t]/\left (t^{m+1}\right )\to \operatorname {\mathrm {Spec}} k'[t]/\left (t^{m+1}\right )$
be the map induced by
$\alpha _m\colon \operatorname {\mathrm {Spec}} A[t]/\left (t^{m+1}\right )\to \operatorname {\mathrm {Spec}} k'[t]/\left (t^{m+1}\right )$
be the map induced by
![]() $\alpha $
; for
$\alpha $
; for
![]() $m\leq n$
, let
$m\leq n$
, let
![]() $\varphi _m\colon \operatorname {\mathrm {Spec}} k'[t]/\left (t^{m+1}\right )\to \mathcal {X}_m$
denote the map induced by
$\varphi _m\colon \operatorname {\mathrm {Spec}} k'[t]/\left (t^{m+1}\right )\to \mathcal {X}_m$
denote the map induced by
![]() $\xi _n$
. We then obtain a cartesian diagram
$\xi _n$
. We then obtain a cartesian diagram

where the curved arrow is the structure map. Let
![]() $\mathcal {J}_n$
denote the ideal sheaf of
$\mathcal {J}_n$
denote the ideal sheaf of
![]() $\operatorname {\mathrm {Spec}} k'[t]/\left (t^{n+1}\right )\to \operatorname {\mathrm {Spec}} k'[t]/\left (t^{n+2}\right )$
considered as a
$\operatorname {\mathrm {Spec}} k'[t]/\left (t^{n+1}\right )\to \operatorname {\mathrm {Spec}} k'[t]/\left (t^{n+2}\right )$
considered as a
![]() $k'$
-module. By [Reference OlssonOls06, Theorem 1.5] and the fact that
$k'$
-module. By [Reference OlssonOls06, Theorem 1.5] and the fact that
![]() $\mathcal {X}_{n+1}$
and
$\mathcal {X}_{n+1}$
and
![]() $A[t]/\left (t^{n+2}\right )$
are flat over
$A[t]/\left (t^{n+2}\right )$
are flat over
![]() $k[t]/(t^{n+2})$
, the obstruction to the existence of a dotted arrow in this diagram lives in
$k[t]/(t^{n+2})$
, the obstruction to the existence of a dotted arrow in this diagram lives in
 $$ \begin{align*} \operatorname{\mathrm{Ext}}^1\left(L(\alpha_0\varphi_0)^*L_{\mathcal{X}/k},\alpha_0^*\mathcal{J}_n\right)=\operatorname{\mathrm{Ext}}^1\left(L\varphi_0^*L_{\mathcal{X}/k},\mathcal{O}_{k'}\right)\otimes_{k'}\mathcal{J}_n\otimes_{k'}A. \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{Ext}}^1\left(L(\alpha_0\varphi_0)^*L_{\mathcal{X}/k},\alpha_0^*\mathcal{J}_n\right)=\operatorname{\mathrm{Ext}}^1\left(L\varphi_0^*L_{\mathcal{X}/k},\mathcal{O}_{k'}\right)\otimes_{k'}\mathcal{J}_n\otimes_{k'}A. \end{align*} $$
We will show that this group vanishes, and so by [Reference OlssonOls06, Theorem 1.5], the objects (resp., automorphisms) of
![]() $\mathcal {Y}_{\xi _n}(A)$
are parametrised by
$\mathcal {Y}_{\xi _n}(A)$
are parametrised by
 $\operatorname {\mathrm {Ext}}^n\left (L\varphi _0^*L_{\mathcal {X}/k},\mathcal {O}_{k'}\right )\otimes _{k'}\mathcal {J}_n\otimes _{k'}A$
where
$\operatorname {\mathrm {Ext}}^n\left (L\varphi _0^*L_{\mathcal {X}/k},\mathcal {O}_{k'}\right )\otimes _{k'}\mathcal {J}_n\otimes _{k'}A$
where
![]() $n=0$
(resp.,
$n=0$
(resp.,
![]() $n=-1$
). In particular, if V (resp., G) denotes the affine space (resp., algebraic vector group) over
$n=-1$
). In particular, if V (resp., G) denotes the affine space (resp., algebraic vector group) over
![]() $k'$
associated to the vector space
$k'$
associated to the vector space
 $\operatorname {\mathrm {Ext}}^n\left (L\varphi _0^*L_{\mathcal {X}/k},\mathcal {O}_{k'}\right )\otimes _{k'}\mathcal {J}_n$
with
$\operatorname {\mathrm {Ext}}^n\left (L\varphi _0^*L_{\mathcal {X}/k},\mathcal {O}_{k'}\right )\otimes _{k'}\mathcal {J}_n$
with
![]() $n=0$
(resp.,
$n=0$
(resp.,
![]() $n=-1$
), then we have
$n=-1$
), then we have
 $$ \begin{align*} \mathcal{Y}_{\xi_n}\cong V\times_{k'} G\cong \mathbb{A}^{r\left(\xi_n\right)}\times B\mathbb{G}_a^{j\left(\xi_n\right)}, \end{align*} $$
$$ \begin{align*} \mathcal{Y}_{\xi_n}\cong V\times_{k'} G\cong \mathbb{A}^{r\left(\xi_n\right)}\times B\mathbb{G}_a^{j\left(\xi_n\right)}, \end{align*} $$
where
 $r(\xi _n)=\dim \operatorname {\mathrm {Ext}}^0\left (L\varphi _0^*L_{\mathcal {X}/k},\mathcal {O}_{k'}\right )$
and
$r(\xi _n)=\dim \operatorname {\mathrm {Ext}}^0\left (L\varphi _0^*L_{\mathcal {X}/k},\mathcal {O}_{k'}\right )$
and
 $j(\xi _n)=\dim \operatorname {\mathrm {Ext}}^1\left (L\varphi _0^*L_{\mathcal {X}/k},\mathcal {O}_{k'}\right )$
. Note that this implies
$j(\xi _n)=\dim \operatorname {\mathrm {Ext}}^1\left (L\varphi _0^*L_{\mathcal {X}/k},\mathcal {O}_{k'}\right )$
. Note that this implies
 $$ \begin{align*} e\left(\mathcal{Y}_{\xi_n}\right)=\mathbb{L}^{r\left(\xi_n\right)-j\left(\xi_n\right)}. \end{align*} $$
$$ \begin{align*} e\left(\mathcal{Y}_{\xi_n}\right)=\mathbb{L}^{r\left(\xi_n\right)-j\left(\xi_n\right)}. \end{align*} $$
Therefore, to finish the proof of the theorem, it suffices to show that
 $$ \begin{align} \operatorname{\mathrm{Ext}}^1\left(L\varphi_0^*L_{\mathcal{X}/k},\mathcal{O}_{k'}\right)=0,\qquad r(\xi_n)-j(\xi_n)=\dim\mathcal{X}, \end{align} $$
$$ \begin{align} \operatorname{\mathrm{Ext}}^1\left(L\varphi_0^*L_{\mathcal{X}/k},\mathcal{O}_{k'}\right)=0,\qquad r(\xi_n)-j(\xi_n)=\dim\mathcal{X}, \end{align} $$
and that the locus of
![]() $\varphi _0\in \lvert \mathcal {X}\rvert $
where
$\varphi _0\in \lvert \mathcal {X}\rvert $
where
![]() $r(\xi _n)$
is constant is given by a constructible set. Since these remaining statements depend only on the dimension of the
$r(\xi _n)$
is constant is given by a constructible set. Since these remaining statements depend only on the dimension of the
![]() $\operatorname {\mathrm {Ext}}$
-groups over
$\operatorname {\mathrm {Ext}}$
-groups over
![]() $k'$
, it suffices to replace
$k'$
, it suffices to replace
![]() $k'$
with an extension field, and hence we can assume
$k'$
with an extension field, and hence we can assume
![]() $k'$
is algebraically closed.
$k'$
is algebraically closed.
Let
![]() $\rho \colon \widetilde {X}\to \mathcal {X}$
be a smooth cover. Since
$\rho \colon \widetilde {X}\to \mathcal {X}$
be a smooth cover. Since
![]() $k'$
is algebraically closed, we may fix a lift
$k'$
is algebraically closed, we may fix a lift
![]() $\phi _0\colon \operatorname {\mathrm {Spec}} k'\to \widetilde {X}$
of
$\phi _0\colon \operatorname {\mathrm {Spec}} k'\to \widetilde {X}$
of
![]() $\varphi _0$
. Since
$\varphi _0$
. Since
![]() $\widetilde {X}$
and
$\widetilde {X}$
and
![]() $\rho $
are smooth, we have an exact triangle
$\rho $
are smooth, we have an exact triangle
 $$ \begin{align*} p^*L_{\mathcal{X}/k}\to\Omega^1_{\widetilde{X}/k}\to\Omega^1_{\widetilde{X}/\mathcal{X}}, \end{align*} $$
$$ \begin{align*} p^*L_{\mathcal{X}/k}\to\Omega^1_{\widetilde{X}/k}\to\Omega^1_{\widetilde{X}/\mathcal{X}}, \end{align*} $$
from which we obtain an exact triangle
 $$ \begin{align*} \Gamma\left(\phi_0^*T_{\widetilde{X}/\mathcal{X}}\right)\to\Gamma\left(\phi_0^*T_{\widetilde{X}/k}\right)\to \mathrm{RHom}\left(L\varphi_0^*L_{\mathcal{X}/k},\mathcal{O}_{k'}\right). \end{align*} $$
$$ \begin{align*} \Gamma\left(\phi_0^*T_{\widetilde{X}/\mathcal{X}}\right)\to\Gamma\left(\phi_0^*T_{\widetilde{X}/k}\right)\to \mathrm{RHom}\left(L\varphi_0^*L_{\mathcal{X}/k},\mathcal{O}_{k'}\right). \end{align*} $$
In particular,
 $\operatorname {\mathrm {Ext}}^n\left (L\varphi _0^*L_{\mathcal {X}/k},\mathcal {O}_{k'}\right )=0$
for
$\operatorname {\mathrm {Ext}}^n\left (L\varphi _0^*L_{\mathcal {X}/k},\mathcal {O}_{k'}\right )=0$
for
![]() $n\neq 0,-1$
, and there is an exact sequence
$n\neq 0,-1$
, and there is an exact sequence
 $$ \begin{align} 0\to\operatorname{\mathrm{Ext}}^{-1}\left(L\varphi_0^*L_{\mathcal{X}/k},\mathcal{O}_{k'}\right)\to\Gamma\left(\phi_0^*T_{\widetilde{X}/\mathcal{X}}\right)\to\Gamma\left(\phi_0^*T_{\widetilde{X}/k}\right)\to\operatorname{\mathrm{Ext}}^0\left(L\varphi_0^*L_{\mathcal{X}/k},\mathcal{O}_{k'}\right)\to0. \end{align} $$
$$ \begin{align} 0\to\operatorname{\mathrm{Ext}}^{-1}\left(L\varphi_0^*L_{\mathcal{X}/k},\mathcal{O}_{k'}\right)\to\Gamma\left(\phi_0^*T_{\widetilde{X}/\mathcal{X}}\right)\to\Gamma\left(\phi_0^*T_{\widetilde{X}/k}\right)\to\operatorname{\mathrm{Ext}}^0\left(L\varphi_0^*L_{\mathcal{X}/k},\mathcal{O}_{k'}\right)\to0. \end{align} $$
Thus,
 $$ \begin{align*} r(\xi_n)-j(\xi_n)=\dim\Gamma\left(\phi_0^*T_{\widetilde{X}/k}\right)-\dim\Gamma\left(\phi_0^*T_{\widetilde{X}/\mathcal{X}}\right)= \dim\mathcal{X}, \end{align*} $$
$$ \begin{align*} r(\xi_n)-j(\xi_n)=\dim\Gamma\left(\phi_0^*T_{\widetilde{X}/k}\right)-\dim\Gamma\left(\phi_0^*T_{\widetilde{X}/\mathcal{X}}\right)= \dim\mathcal{X}, \end{align*} $$
thereby establishing equation (1). Finally, note from formula (2) that the cokernel of
 $\Gamma \left (\phi _0^*T_{\widetilde {X}/\mathcal {X}}\right )\to \Gamma \left (\phi _0^*T_{\widetilde {X}/k}\right )$
depends only on
$\Gamma \left (\phi _0^*T_{\widetilde {X}/\mathcal {X}}\right )\to \Gamma \left (\phi _0^*T_{\widetilde {X}/k}\right )$
depends only on
![]() $\varphi _0$
and not on the choice of lift
$\varphi _0$
and not on the choice of lift
![]() $\phi _0$
. So the locus of
$\phi _0$
. So the locus of
![]() $\varphi _0\in \lvert \mathcal {X}\rvert $
where
$\varphi _0\in \lvert \mathcal {X}\rvert $
where
![]() $r(\xi _n)$
is constant is the image under
$r(\xi _n)$
is constant is the image under
![]() $\rho $
of the locus of
$\rho $
of the locus of
 $\phi _0\in \left \lvert \widetilde {X}\right \rvert $
where the dimension is constant. By Chevalley’s theorem for Artin stacks [Reference Hall and RydhHR17, Theorem 5.2], it is therefore enough to show that the locus of such
$\phi _0\in \left \lvert \widetilde {X}\right \rvert $
where the dimension is constant. By Chevalley’s theorem for Artin stacks [Reference Hall and RydhHR17, Theorem 5.2], it is therefore enough to show that the locus of such
![]() $\phi _0$
is constructible. This follows by applying [Sta21, Lemma 0BDI] to the
$\phi _0$
is constructible. This follows by applying [Sta21, Lemma 0BDI] to the
![]() $2$
-term complex
$2$
-term complex
![]() $T_{\widetilde {X}/\mathcal {X}}\to T_{\widetilde {X}/k}$
and using the fact that
$T_{\widetilde {X}/\mathcal {X}}\to T_{\widetilde {X}/k}$
and using the fact that
![]() $\left \lvert \widetilde {X}\right \rvert $
is Noetherian, so that all locally constructible sets are constructible.
$\left \lvert \widetilde {X}\right \rvert $
is Noetherian, so that all locally constructible sets are constructible.
Lemma 3.35. Let
![]() $\mathcal {Y}$
,
$\mathcal {Y}$
,
![]() $\mathcal {Z}$
and
$\mathcal {Z}$
and
![]() $\mathcal {F}$
be finite-type Artin stacks over k, let
$\mathcal {F}$
be finite-type Artin stacks over k, let
![]() $\mathcal {Y} \to \mathcal {Z}$
be a k-morphism and assume that for any field extensions
$\mathcal {Y} \to \mathcal {Z}$
be a k-morphism and assume that for any field extensions
![]() $k'$
of k and any k-morphism
$k'$
of k and any k-morphism
![]() $\operatorname {\mathrm {Spec}}(k') \to \mathcal {Z}$
, there exists a
$\operatorname {\mathrm {Spec}}(k') \to \mathcal {Z}$
, there exists a
![]() $k'$
-isomorphism
$k'$
-isomorphism
 $$ \begin{align*} \left(\mathcal{Y} \times_{\mathcal{Z}} \operatorname{\mathrm{Spec}}(k')\right)_{\mathrm{red}} \cong \left(\mathcal{F} \times_{\operatorname{\mathrm{Spec}}(k)} \operatorname{\mathrm{Spec}}(k')\right)_{\mathrm{red}}. \end{align*} $$
$$ \begin{align*} \left(\mathcal{Y} \times_{\mathcal{Z}} \operatorname{\mathrm{Spec}}(k')\right)_{\mathrm{red}} \cong \left(\mathcal{F} \times_{\operatorname{\mathrm{Spec}}(k)} \operatorname{\mathrm{Spec}}(k')\right)_{\mathrm{red}}. \end{align*} $$
Then
Proof. Because
![]() $\mathcal {Z}$
can be stratified by quotient stacks [Reference KreschKre99, Proposition 3.5.9], we may assume that
$\mathcal {Z}$
can be stratified by quotient stacks [Reference KreschKre99, Proposition 3.5.9], we may assume that
![]() $\mathcal {Z} = [Z / G]$
for some finite-type scheme Z over k with an action by a general linear group G over k. Let
$\mathcal {Z} = [Z / G]$
for some finite-type scheme Z over k with an action by a general linear group G over k. Let
![]() $\mathcal {Y}' = \mathcal {Y} \times _{\mathcal {Z}} Z$
. Because
$\mathcal {Y}' = \mathcal {Y} \times _{\mathcal {Z}} Z$
. Because
![]() $Z \to \mathcal {Z}$
and
$Z \to \mathcal {Z}$
and
![]() $\mathcal {Y}' \to \mathcal {Y}$
are G-torsors and G is a special group, [Reference EkedahlEke09, Proposition 1.1(ii)] gives
$\mathcal {Y}' \to \mathcal {Y}$
are G-torsors and G is a special group, [Reference EkedahlEke09, Proposition 1.1(ii)] gives
 $$ \begin{align*} \mathrm{e}(Z) &= \mathrm{e}(G)\mathrm{e}(\mathcal{Z}),\\ \mathrm{e}(\mathcal{Y}') &= \mathrm{e}(G)\mathrm{e}(\mathcal{Y}). \end{align*} $$
$$ \begin{align*} \mathrm{e}(Z) &= \mathrm{e}(G)\mathrm{e}(\mathcal{Z}),\\ \mathrm{e}(\mathcal{Y}') &= \mathrm{e}(G)\mathrm{e}(\mathcal{Y}). \end{align*} $$
By the hypotheses on
![]() $\mathcal {Y} \to \mathcal {Z}$
, Proposition 2.8 implies that
$\mathcal {Y} \to \mathcal {Z}$
, Proposition 2.8 implies that
![]() $\mathcal {Y}' \to Z$
is a piecewise trivial fibration with fibre
$\mathcal {Y}' \to Z$
is a piecewise trivial fibration with fibre
![]() $\mathcal {F}$
, so in particular,
$\mathcal {F}$
, so in particular,
Thus,
Because G is a special group,
![]() $\mathrm {e}(G)^{-1} \in K_0(\mathbf {Stack}_k)$
, so we are done.
$\mathrm {e}(G)^{-1} \in K_0(\mathbf {Stack}_k)$
, so we are done.
We may now prove Theorem 3.33.
Proof of Theorem 3.33
By definition, there exist some
![]() $n_0 \in \mathbb {N}$
and some constructible subset
$n_0 \in \mathbb {N}$
and some constructible subset
 $\mathcal {C}_{n_0} \subset \left \lvert \mathscr {L}_{n_0}(\mathcal {X})\right \rvert $
such that
$\mathcal {C}_{n_0} \subset \left \lvert \mathscr {L}_{n_0}(\mathcal {X})\right \rvert $
such that
 $\mathcal {C} = \left (\theta _{n_0}\right )^{-1}\left (\mathcal {C}_{n_0}\right )$
. Because
$\mathcal {C} = \left (\theta _{n_0}\right )^{-1}\left (\mathcal {C}_{n_0}\right )$
. Because
![]() $\mathcal {X}$
is smooth, infinitesimal lifting implies that the truncation maps
$\mathcal {X}$
is smooth, infinitesimal lifting implies that the truncation maps
![]() $\theta _n: \lvert \mathscr {L}(\mathcal {X})\rvert \to \lvert \mathscr {L}_n(\mathcal {X})\rvert $
are all surjective, so
$\theta _n: \lvert \mathscr {L}(\mathcal {X})\rvert \to \lvert \mathscr {L}_n(\mathcal {X})\rvert $
are all surjective, so
 $$ \begin{align*} \theta_n(\mathcal{C}) = \begin{cases} \left(\theta^n_{n_0}\right)^{-1}\left(\mathcal{C}_{n_0}\right), & n \geq n_0, \\ \theta^{n_0}_n\left(\mathcal{C}_{n_0}\right), & n < n_0. \end{cases} \end{align*} $$
$$ \begin{align*} \theta_n(\mathcal{C}) = \begin{cases} \left(\theta^n_{n_0}\right)^{-1}\left(\mathcal{C}_{n_0}\right), & n \geq n_0, \\ \theta^{n_0}_n\left(\mathcal{C}_{n_0}\right), & n < n_0. \end{cases} \end{align*} $$
Thus all
![]() $\theta _n(\mathcal {C})$
are constructible – immediately for
$\theta _n(\mathcal {C})$
are constructible – immediately for
![]() $n \geq n_0$
, and by Chevalley’s theorem for Artin stacks [Reference Hall and RydhHR17, Theorem 5.2] for
$n \geq n_0$
, and by Chevalley’s theorem for Artin stacks [Reference Hall and RydhHR17, Theorem 5.2] for
![]() $n < n_0$
.
$n < n_0$
.
The remainder of the theorem then follows from the fact that Lemma 3.34 and Lemma 3.35 imply that for any
![]() $n \geq n_0$
,
$n \geq n_0$
,
 $$ \begin{align*} \mathrm{e}(\theta_n(\mathcal{C})) = \left(\theta^n_{n_0}\right)^{-1}\left(\mathcal{C}_{n_0}\right) = \mathrm{e}\left(\mathcal{C}_{n_0}\right)\mathbb{L}^{\left(n-n_0\right)\dim\mathcal{X}}.\\[-39pt] \end{align*} $$
$$ \begin{align*} \mathrm{e}(\theta_n(\mathcal{C})) = \left(\theta^n_{n_0}\right)^{-1}\left(\mathcal{C}_{n_0}\right) = \mathrm{e}\left(\mathcal{C}_{n_0}\right)\mathbb{L}^{\left(n-n_0\right)\dim\mathcal{X}}.\\[-39pt] \end{align*} $$
4 Fibres of the map of arcs
Our goal in this section is to give a combinatorial characterisation of the fibres of
![]() $\mathscr {L}(\pi )\colon \mathscr {L}(\mathcal {X})\to \mathscr {L}(X)$
, where
$\mathscr {L}(\pi )\colon \mathscr {L}(\mathcal {X})\to \mathscr {L}(X)$
, where
![]() $\mathcal {X}$
is a fantastack and
$\mathcal {X}$
is a fantastack and
![]() $\pi \colon \mathcal {X}\to X$
is its good moduli space map (see Theorem 4.9). We accomplish this goal by first defining the tropicalisation of arcs both for toric varieties and for toric stacks.
$\pi \colon \mathcal {X}\to X$
is its good moduli space map (see Theorem 4.9). We accomplish this goal by first defining the tropicalisation of arcs both for toric varieties and for toric stacks.
4.1 Tropicalising arcs of toric stacks
Given a toric variety
![]() $X=\operatorname {\mathrm {Spec}}(k[P])$
, a k-algebra R and an arc
$X=\operatorname {\mathrm {Spec}}(k[P])$
, a k-algebra R and an arc
 $\varphi \in \mathscr {L}\left (\widetilde {X}\right )(R)$
, we denote by
$\varphi \in \mathscr {L}\left (\widetilde {X}\right )(R)$
, we denote by
![]() $\varphi ^*(p)$
the image of p under
$\varphi ^*(p)$
the image of p under
![]() , where the latter map is the pullback corresponding to
, where the latter map is the pullback corresponding to
![]() $\varphi $
.
$\varphi $
.
Definition 4.1. If
![]() $\sigma $
is a pointed rational cone on a finite-rank lattice N and
$\sigma $
is a pointed rational cone on a finite-rank lattice N and
![]() $k'$
is a field extension of k, we define the tropicalisation map
$k'$
is a field extension of k, we define the tropicalisation map
by
![]() $\operatorname {\mathrm {trop}}(\varphi )(p):=\operatorname {\mathrm {ord}}_t\varphi ^*(p)$
, where
$\operatorname {\mathrm {trop}}(\varphi )(p):=\operatorname {\mathrm {ord}}_t\varphi ^*(p)$
, where
![]() $\operatorname {\mathrm {ord}}_t$
denotes the order of vanishing at t.
$\operatorname {\mathrm {ord}}_t$
denotes the order of vanishing at t.
More generally, if
 $\left (\sigma ,\nu \colon \widetilde {N}\to N\right )$
is a stacky fan with
$\left (\sigma ,\nu \colon \widetilde {N}\to N\right )$
is a stacky fan with
![]() $\sigma $
a pointed cone and
$\sigma $
a pointed cone and
![]() $\mathcal {X}:=\mathcal {X}_{\sigma ,\nu }:=[X_\sigma /G_\nu ]$
is the corresponding toric stack, then we define the tropicalisation map on isomorphism classes of arcs
$\mathcal {X}:=\mathcal {X}_{\sigma ,\nu }:=[X_\sigma /G_\nu ]$
is the corresponding toric stack, then we define the tropicalisation map on isomorphism classes of arcs
 $$ \begin{align*} \operatorname{\mathrm{trop}}: \overline{\mathscr{L}(\mathcal{X})}(k') \to \operatorname{\mathrm{Hom}}\left(\sigma^\vee\cap \widetilde{N}^*, \mathbb{N} \cup \{\infty\}\right) \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{trop}}: \overline{\mathscr{L}(\mathcal{X})}(k') \to \operatorname{\mathrm{Hom}}\left(\sigma^\vee\cap \widetilde{N}^*, \mathbb{N} \cup \{\infty\}\right) \end{align*} $$
as follows. If
![]() $\psi \in \mathscr {L}(\mathcal {X})(k')$
, then fix a finite field extension
$\psi \in \mathscr {L}(\mathcal {X})(k')$
, then fix a finite field extension
![]() $k''$
of
$k''$
of
![]() $k'$
and a lift
$k'$
and a lift
![]() $\widetilde {\psi }\in \mathscr {L}(X_\sigma )(k'')$
of
$\widetilde {\psi }\in \mathscr {L}(X_\sigma )(k'')$
of
![]() $\psi $
. We define
$\psi $
. We define
 $\operatorname {\mathrm {trop}}(\psi ):=\operatorname {\mathrm {trop}}\left (\widetilde {\psi }\right )$
. We show in Lemma 4.4 that this is well defined.
$\operatorname {\mathrm {trop}}(\psi ):=\operatorname {\mathrm {trop}}\left (\widetilde {\psi }\right )$
. We show in Lemma 4.4 that this is well defined.
Remark 4.2. Note that we have a natural inclusion
Lemma 4.3. Let
![]() $\Omega $
be any field of characteristic
$\Omega $
be any field of characteristic
![]() $0$
and let
$0$
and let
 $G=\mathbb {G}_m^r\times \prod _{i=1}^N\mu _{n_i}$
. Then every G-torsor over
$G=\mathbb {G}_m^r\times \prod _{i=1}^N\mu _{n_i}$
. Then every G-torsor over
![]() $\operatorname {\mathrm {Spec}}(\Omega [[t]])$
is isomorphic to the pullback of a G-torsor over
$\operatorname {\mathrm {Spec}}(\Omega [[t]])$
is isomorphic to the pullback of a G-torsor over
![]() $\operatorname {\mathrm {Spec}}(\Omega )$
.
$\operatorname {\mathrm {Spec}}(\Omega )$
.
Proof. Let
![]() $q\colon \operatorname {\mathrm {Spec}}(\Omega [[t]])\to \operatorname {\mathrm {Spec}}(\Omega )$
denote the structure map. Since G is an étale group scheme, G-torsors on any
$q\colon \operatorname {\mathrm {Spec}}(\Omega [[t]])\to \operatorname {\mathrm {Spec}}(\Omega )$
denote the structure map. Since G is an étale group scheme, G-torsors on any
![]() $\Omega $
-scheme Y are classified up to isomorphism by
$\Omega $
-scheme Y are classified up to isomorphism by
 $H^1_{et}(Y,G)=H^1_{et}(Y,\mathbb {G}_m)^{\oplus r}\oplus \bigoplus _{i=1}^N H^1_{et}\left (Y,\mu _{n_i}\right )$
. In particular, it suffices to show that the pullback map
$H^1_{et}(Y,G)=H^1_{et}(Y,\mathbb {G}_m)^{\oplus r}\oplus \bigoplus _{i=1}^N H^1_{et}\left (Y,\mu _{n_i}\right )$
. In particular, it suffices to show that the pullback map
![]() $q^*\colon H^1_{et}(\operatorname {\mathrm {Spec}}(\Omega ),G)\to H^1_{et}(\operatorname {\mathrm {Spec}}(\Omega [[t]]),G)$
is an isomorphism when G is either
$q^*\colon H^1_{et}(\operatorname {\mathrm {Spec}}(\Omega ),G)\to H^1_{et}(\operatorname {\mathrm {Spec}}(\Omega [[t]]),G)$
is an isomorphism when G is either
![]() $\mathbb {G}_m$
or
$\mathbb {G}_m$
or
![]() $\mu _n$
.
$\mu _n$
.
We first handle the case
![]() $G=\mathbb {G}_m$
. Since
$G=\mathbb {G}_m$
. Since
![]() $H^1_{et}(Y,\mathbb {G}_m)=\mathrm {Pic}(Y)$
and since both
$H^1_{et}(Y,\mathbb {G}_m)=\mathrm {Pic}(Y)$
and since both
![]() $\mathrm {Pic}(\operatorname {\mathrm {Spec}}(\Omega ))$
and
$\mathrm {Pic}(\operatorname {\mathrm {Spec}}(\Omega ))$
and
![]() $\mathrm {Pic}(\operatorname {\mathrm {Spec}}(\Omega [[t]]))$
are trivial, we see that
$\mathrm {Pic}(\operatorname {\mathrm {Spec}}(\Omega [[t]]))$
are trivial, we see that
![]() $q^*$
is an isomorphism.
$q^*$
is an isomorphism.
We next handle the case
![]() $G=\mu _n$
. From the Kummer sequence
$G=\mu _n$
. From the Kummer sequence
 $$ \begin{align*} 1\to\mu_n\to\mathbb{G}_m\xrightarrow{\times n}\mathbb{G}_m\to1, \end{align*} $$
$$ \begin{align*} 1\to\mu_n\to\mathbb{G}_m\xrightarrow{\times n}\mathbb{G}_m\to1, \end{align*} $$
we see that if Y is any
![]() $\Omega $
-scheme with trivial Picard group, we have
$\Omega $
-scheme with trivial Picard group, we have
 $$ \begin{align*} H^1_{et}(Y,\mu_n)=\mathcal{O}_Y(Y)^*/(\mathcal{O}_Y(Y)^*)^n \end{align*} $$
$$ \begin{align*} H^1_{et}(Y,\mu_n)=\mathcal{O}_Y(Y)^*/(\mathcal{O}_Y(Y)^*)^n \end{align*} $$
(see, for example, [Reference MilneMil80, p. 125]). So it remains to show that
![]() $k^*/(k^*)^n\to k[[t]]^*/(k[[t]]^*)^n$
is an isomorphism. Since every element
$k^*/(k^*)^n\to k[[t]]^*/(k[[t]]^*)^n$
is an isomorphism. Since every element
![]() $f(t)\in k[[t]]^*$
can be written uniquely as
$f(t)\in k[[t]]^*$
can be written uniquely as
![]() $ag(t)$
with
$ag(t)$
with
![]() $a\in k^*$
and
$a\in k^*$
and
![]() $g(t)\in k[[t]]^*$
with
$g(t)\in k[[t]]^*$
with
![]() $g(t)-1\in tk[[t]]$
, it is enough to prove that such
$g(t)-1\in tk[[t]]$
, it is enough to prove that such
![]() $g(t)$
are in
$g(t)$
are in
![]() $(k[[t]]^*)^n$
. This follows immediately from Hensel’s lemma: the polynomial
$(k[[t]]^*)^n$
. This follows immediately from Hensel’s lemma: the polynomial
![]() $P(x)=x^n-g(t)\in k[[t]][x]$
has a root, since
$P(x)=x^n-g(t)\in k[[t]][x]$
has a root, since
![]() $P(1)=0$
mod t and
$P(1)=0$
mod t and
![]() $P'(1)\neq 0$
mod t.
$P'(1)\neq 0$
mod t.
Lemma 4.4. With notation as in Definition 4.1, such a lift
![]() $\widetilde {\psi }$
exists, and
$\widetilde {\psi }$
exists, and
![]() $\operatorname {\mathrm {trop}}(\psi )$
is independent of both
$\operatorname {\mathrm {trop}}(\psi )$
is independent of both
![]() $k''$
and
$k''$
and
![]() $\widetilde {\psi }$
.
$\widetilde {\psi }$
.
Proof. For ease of notation, write
![]() $F:=\sigma ^\vee \cap \widetilde {N}^*$
and
$F:=\sigma ^\vee \cap \widetilde {N}^*$
and
![]() $G:=G_\nu =\operatorname {\mathrm {Spec}}(k[A])$
, where A is a finitely generated abelian group. Note that the G-action on
$G:=G_\nu =\operatorname {\mathrm {Spec}}(k[A])$
, where A is a finitely generated abelian group. Note that the G-action on
![]() $X_\sigma $
corresponds to a monoid map
$X_\sigma $
corresponds to a monoid map
![]() $\eta \colon F\to A$
. The arc
$\eta \colon F\to A$
. The arc
![]() $\psi $
corresponds to a G-torsor
$\psi $
corresponds to a G-torsor
![]() and G-equivariant map
and G-equivariant map
![]() $Q\to X_\sigma $
. By Lemma 4.3, Q is isomorphic to the pullback of a G-torsor over
$Q\to X_\sigma $
. By Lemma 4.3, Q is isomorphic to the pullback of a G-torsor over
![]() $\operatorname {\mathrm {Spec}}(k')$
, which can be itself be trivialised after a finite field extension
$\operatorname {\mathrm {Spec}}(k')$
, which can be itself be trivialised after a finite field extension
![]() $k''$
. Thus, after base change to
$k''$
. Thus, after base change to
![]() , we obtain a trivialisation of Q and hence a lift
, we obtain a trivialisation of Q and hence a lift
![]() $\widetilde {\psi }$
.
$\widetilde {\psi }$
.
Next, it is clear that if
![]() $\widetilde {\psi }\in \mathscr {L}(X_\sigma )(k'')$
is a lift of
$\widetilde {\psi }\in \mathscr {L}(X_\sigma )(k'')$
is a lift of
![]() $\psi $
and
$\psi $
and
![]() $k'''$
is a finite field extension of
$k'''$
is a finite field extension of
![]() $k''$
, then
$k''$
, then
 $\operatorname {\mathrm {trop}}\left (\widetilde {\psi }\right )=\operatorname {\mathrm {trop}}\left (\widetilde {\psi }\otimes _{k''}k'''\right )$
. So it suffices to show that if
$\operatorname {\mathrm {trop}}\left (\widetilde {\psi }\right )=\operatorname {\mathrm {trop}}\left (\widetilde {\psi }\otimes _{k''}k'''\right )$
. So it suffices to show that if
![]() $\widetilde {\psi }_1,\widetilde {\psi }_2\in \mathscr {L}(X_\sigma )(k'')$
are both lifts of
$\widetilde {\psi }_1,\widetilde {\psi }_2\in \mathscr {L}(X_\sigma )(k'')$
are both lifts of
![]() $\psi $
, then
$\psi $
, then
 $\operatorname {\mathrm {trop}}\left (\widetilde {\psi }_1\right )=\operatorname {\mathrm {trop}}\left (\widetilde {\psi }_2\right )$
. In this case, there exists
$\operatorname {\mathrm {trop}}\left (\widetilde {\psi }_1\right )=\operatorname {\mathrm {trop}}\left (\widetilde {\psi }_2\right )$
. In this case, there exists
![]() such that
such that
![]() $g\cdot \widetilde {\psi }_1=\widetilde {\psi }_2$
. Letting
$g\cdot \widetilde {\psi }_1=\widetilde {\psi }_2$
. Letting
![]() $g^*(a)$
denote the pullback of
$g^*(a)$
denote the pullback of
![]() $a\in A$
under the map
$a\in A$
under the map
![]() , we therefore have
, we therefore have
Since
![]() $g^*(\eta (f))$
is a unit, the power series
$g^*(\eta (f))$
is a unit, the power series
![]() $\psi _1^*(f)$
and
$\psi _1^*(f)$
and
![]() $\psi _2^*(f)$
have the same t-order of vanishing – that is,
$\psi _2^*(f)$
have the same t-order of vanishing – that is,
 $\operatorname {\mathrm {trop}}\left (\widetilde {\psi }_1\right )=\operatorname {\mathrm {trop}}\left (\widetilde {\psi }_2\right )$
.
$\operatorname {\mathrm {trop}}\left (\widetilde {\psi }_1\right )=\operatorname {\mathrm {trop}}\left (\widetilde {\psi }_2\right )$
.
We record some basic properties of
![]() $\operatorname {\mathrm {trop}}$
that will be useful later on.
$\operatorname {\mathrm {trop}}$
that will be useful later on.
Definition 4.5. Let
 $\left (\sigma ,\nu \colon \widetilde {N}\to N\right )$
be a stacky fan with
$\left (\sigma ,\nu \colon \widetilde {N}\to N\right )$
be a stacky fan with
![]() $\sigma $
a pointed cone. For any
$\sigma $
a pointed cone. For any
 $w \in \sigma \cap \widetilde {N} \subset \operatorname {\mathrm {Hom}}\left (\sigma ^\vee \cap \widetilde {N}^*, \mathbb {N} \cup \{\infty \}\right )$
, let
$w \in \sigma \cap \widetilde {N} \subset \operatorname {\mathrm {Hom}}\left (\sigma ^\vee \cap \widetilde {N}^*, \mathbb {N} \cup \{\infty \}\right )$
, let
 $$ \begin{align*} \operatorname{\mathrm{trop}}^{-1}(w)=\left\{ \psi\in\overline{\mathscr{L}\left(\mathcal{X}_{\sigma,\nu}\right)}(k') \mid k' \text{is a field extension of } k \text{ and }\operatorname{\mathrm{trop}}(\psi)=w\right\}\subset\left\lvert\mathscr{L}\left(\mathcal{X}_{\sigma,\nu}\right)\right\rvert ,\\[-15pt] \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{trop}}^{-1}(w)=\left\{ \psi\in\overline{\mathscr{L}\left(\mathcal{X}_{\sigma,\nu}\right)}(k') \mid k' \text{is a field extension of } k \text{ and }\operatorname{\mathrm{trop}}(\psi)=w\right\}\subset\left\lvert\mathscr{L}\left(\mathcal{X}_{\sigma,\nu}\right)\right\rvert ,\\[-15pt] \end{align*} $$
where the arcs are taken up to equivalence.
Remark 4.6. Let
![]() $\sigma $
be a pointed rational cone on a finite-rank lattice N and let
$\sigma $
be a pointed rational cone on a finite-rank lattice N and let
![]() $P=\sigma ^\vee \cap N^*$
so that
$P=\sigma ^\vee \cap N^*$
so that
![]() $X_\sigma =\operatorname {\mathrm {Spec}}(k[P])$
. For any
$X_\sigma =\operatorname {\mathrm {Spec}}(k[P])$
. For any
![]() $p\in P$
, let
$p\in P$
, let
![]() $\chi ^p\in k[P]$
be the corresponding monomial. If
$\chi ^p\in k[P]$
be the corresponding monomial. If
![]() $p_1, \dotsc , p_s$
are generators for P, then for every
$p_1, \dotsc , p_s$
are generators for P, then for every
![]() $w \in \sigma \cap N$
, we see
$w \in \sigma \cap N$
, we see
 $$ \begin{align*} \operatorname{\mathrm{trop}}^{-1}(w) = \bigcap_{i = 1}^s \operatorname{\mathrm{ord}}_{\chi^{p_i}}^{-1}(\langle w, p_i \rangle),\\[-15pt] \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{trop}}^{-1}(w) = \bigcap_{i = 1}^s \operatorname{\mathrm{ord}}_{\chi^{p_i}}^{-1}(\langle w, p_i \rangle),\\[-15pt] \end{align*} $$
and hence
![]() $\operatorname {\mathrm {trop}}^{-1}(w) \subset \mathscr {L}(X_\sigma )$
is a cylinder.
$\operatorname {\mathrm {trop}}^{-1}(w) \subset \mathscr {L}(X_\sigma )$
is a cylinder.
Lemma 4.7. Let
![]() $\sigma $
(resp.,
$\sigma $
(resp.,
![]() $\widetilde {\sigma }$
) be a pointed rational cone on a finite-rank lattice N (resp.,
$\widetilde {\sigma }$
) be a pointed rational cone on a finite-rank lattice N (resp.,
![]() $\widetilde {N}$
). If
$\widetilde {N}$
). If
![]() $\rho \colon X_{\widetilde {\sigma }}\to X_{\sigma }$
is a toric morphism and
$\rho \colon X_{\widetilde {\sigma }}\to X_{\sigma }$
is a toric morphism and
![]() $\beta \colon \widetilde {\sigma }\cap \widetilde {N}\to \sigma \cap N$
is the induced map, then
$\beta \colon \widetilde {\sigma }\cap \widetilde {N}\to \sigma \cap N$
is the induced map, then
-
1. for every field extension
 $k'$
of k and every arc
$k'$
of k and every arc
 $\psi \in \mathscr {L}\left (X_{\widetilde {\sigma }}\right )(k')$
, if
$\psi \in \mathscr {L}\left (X_{\widetilde {\sigma }}\right )(k')$
, if
 $\operatorname {\mathrm {trop}}(\psi )\in \widetilde \sigma ^\vee \cap \widetilde {N}^*$
, then
$\operatorname {\mathrm {trop}}(\psi )\in \widetilde \sigma ^\vee \cap \widetilde {N}^*$
, then  $$ \begin{align*} \operatorname{\mathrm{trop}}(\mathscr{L}(\rho)(\psi))=\beta(\operatorname{\mathrm{trop}}(\psi));\\[-15pt] \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{trop}}(\mathscr{L}(\rho)(\psi))=\beta(\operatorname{\mathrm{trop}}(\psi));\\[-15pt] \end{align*} $$
-
2. if for all
 $f\in \widetilde {\sigma }^\vee \cap \widetilde {N}^*$
there exists
$f\in \widetilde {\sigma }^\vee \cap \widetilde {N}^*$
there exists
 $f'\in \widetilde {\sigma }^\vee \cap \widetilde {N}^*$
such that
$f'\in \widetilde {\sigma }^\vee \cap \widetilde {N}^*$
such that
 $f+f'$
lies in the image of
$f+f'$
lies in the image of
 $\sigma ^\vee \cap N^*$
, then
$\sigma ^\vee \cap N^*$
, then  $$ \begin{align*} \mathscr{L}(\rho)^{-1}\left(\operatorname{\mathrm{trop}}^{-1}(w)\right)=\bigcup_{\widetilde{w} \in \beta^{-1}(w)} \operatorname{\mathrm{trop}}^{-1}\left(\widetilde{w}\right). \end{align*} $$
$$ \begin{align*} \mathscr{L}(\rho)^{-1}\left(\operatorname{\mathrm{trop}}^{-1}(w)\right)=\bigcup_{\widetilde{w} \in \beta^{-1}(w)} \operatorname{\mathrm{trop}}^{-1}\left(\widetilde{w}\right). \end{align*} $$
Proof. Let
![]() $\rho ^*\colon \sigma ^\vee \cap N^*\to \widetilde \sigma ^\vee \cap \widetilde {N}^*$
denote the pullback map on monoids. First note that if
$\rho ^*\colon \sigma ^\vee \cap N^*\to \widetilde \sigma ^\vee \cap \widetilde {N}^*$
denote the pullback map on monoids. First note that if
![]() $k'$
is a field extension of k,
$k'$
is a field extension of k,
![]() $\psi \in \mathscr {L}\left (X_{\widetilde {\sigma }}\right )(k')$
and
$\psi \in \mathscr {L}\left (X_{\widetilde {\sigma }}\right )(k')$
and
![]() $p\in \sigma ^\vee \cap N^*$
, then
$p\in \sigma ^\vee \cap N^*$
, then
To prove part (1), let
![]() $\operatorname {\mathrm {trop}}(\psi )=\widetilde {w}\in \widetilde \sigma ^\vee \cap \widetilde {N}^*$
. Then by these equalities, we see
$\operatorname {\mathrm {trop}}(\psi )=\widetilde {w}\in \widetilde \sigma ^\vee \cap \widetilde {N}^*$
. Then by these equalities, we see
so
![]() $\operatorname {\mathrm {trop}}(\mathscr {L}(\rho )(\psi ))=\beta (\widetilde {w})$
.
$\operatorname {\mathrm {trop}}(\mathscr {L}(\rho )(\psi ))=\beta (\widetilde {w})$
.
Part (2) follows immediately from part (1), provided we can show that
![]() $\operatorname {\mathrm {trop}}(\mathscr {L}(\rho )(\psi ))\in \sigma \cap N$
implies
$\operatorname {\mathrm {trop}}(\mathscr {L}(\rho )(\psi ))\in \sigma \cap N$
implies
![]() $\operatorname {\mathrm {trop}}(\psi )\in \widetilde \sigma \cap \widetilde {N}$
. Set
$\operatorname {\mathrm {trop}}(\psi )\in \widetilde \sigma \cap \widetilde {N}$
. Set
![]() $f\in \widetilde {\sigma }^\vee \cap \widetilde {N}^*$
. By hypothesis, there exists
$f\in \widetilde {\sigma }^\vee \cap \widetilde {N}^*$
. By hypothesis, there exists
![]() $f'\in \widetilde {\sigma }^\vee \cap \widetilde {N}^*$
such that
$f'\in \widetilde {\sigma }^\vee \cap \widetilde {N}^*$
such that
![]() $f+f'=\rho ^*(p)$
for some
$f+f'=\rho ^*(p)$
for some
![]() $p\sigma ^\vee \cap N^*$
. Then
$p\sigma ^\vee \cap N^*$
. Then
So
![]() $(\operatorname {\mathrm {trop}}(\psi ))(f)\neq \infty $
for all f, and hence
$(\operatorname {\mathrm {trop}}(\psi ))(f)\neq \infty $
for all f, and hence
![]() $\operatorname {\mathrm {trop}}(\psi )\in \widetilde \sigma \cap \widetilde {N}$
.
$\operatorname {\mathrm {trop}}(\psi )\in \widetilde \sigma \cap \widetilde {N}$
.
Corollary 4.8. Let
![]() $\mathcal {X}=\mathcal {F}_{\sigma ,\nu }$
be a fantastack and suppose the good moduli space map
$\mathcal {X}=\mathcal {F}_{\sigma ,\nu }$
be a fantastack and suppose the good moduli space map
![]() $\pi \colon \mathcal {X}\to X=X_\sigma $
is an isomorphism over the torus
$\pi \colon \mathcal {X}\to X=X_\sigma $
is an isomorphism over the torus
![]() $T\subset X$
. Let
$T\subset X$
. Let
![]() $k'$
be a field extension of k and
$k'$
be a field extension of k and
![]() $\varphi \in \mathscr {L}(X)(k')$
with
$\varphi \in \mathscr {L}(X)(k')$
with
![]() $\operatorname {\mathrm {trop}}(\varphi )=w\in \sigma \cap N$
. If
$\operatorname {\mathrm {trop}}(\varphi )=w\in \sigma \cap N$
. If
![]() $\psi \in \mathscr {L}(\mathcal {X})(k')$
and
$\psi \in \mathscr {L}(\mathcal {X})(k')$
and
![]() $\mathscr {L}(\pi )(\psi )=\varphi $
, then
$\mathscr {L}(\pi )(\psi )=\varphi $
, then
![]() $\operatorname {\mathrm {trop}}(\psi ) \in \beta ^{-1}(w)$
.
$\operatorname {\mathrm {trop}}(\psi ) \in \beta ^{-1}(w)$
.
Proof. We keep the notation listed in Notation 2.19 and let
 $\mathcal {X}=\left [\widetilde {X}/G_\nu \right ]$
. We know there exist a finite field extension
$\mathcal {X}=\left [\widetilde {X}/G_\nu \right ]$
. We know there exist a finite field extension
![]() $k''$
of
$k''$
of
![]() $k'$
and a lift
$k'$
and a lift
 $\widetilde {\psi }\in \mathscr {L}\left (\widetilde {X}\right )(k'')$
of
$\widetilde {\psi }\in \mathscr {L}\left (\widetilde {X}\right )(k'')$
of
![]() $\psi $
. By construction,
$\psi $
. By construction,
 $\operatorname {\mathrm {trop}}(\psi )=\operatorname {\mathrm {trop}}\left (\widetilde {\psi }\right )$
. From Proposition 2.14, we know the hypotheses of Lemma 4.7(2) are satisfied, so
$\operatorname {\mathrm {trop}}(\psi )=\operatorname {\mathrm {trop}}\left (\widetilde {\psi }\right )$
. From Proposition 2.14, we know the hypotheses of Lemma 4.7(2) are satisfied, so
 $\operatorname {\mathrm {trop}}\left (\widetilde {\psi }\right )\in \beta ^{-1}(w)$
.
$\operatorname {\mathrm {trop}}\left (\widetilde {\psi }\right )\in \beta ^{-1}(w)$
.
4.2 Lifting arcs to a fantastack
We can now state the main result of this section, which shows that for the good moduli space map
![]() $\pi \colon \mathcal {X}\to X$
of a fantastack, isomorphism classes of arcs in the fibres of
$\pi \colon \mathcal {X}\to X$
of a fantastack, isomorphism classes of arcs in the fibres of
![]() $\mathscr {L}(\pi )$
are completely determined by their tropicalisations.
$\mathscr {L}(\pi )$
are completely determined by their tropicalisations.
Theorem 4.9. Let
![]() $\mathcal {X}=\mathcal {F}_{\sigma ,\nu }$
be a fantastack and assume the good moduli space map
$\mathcal {X}=\mathcal {F}_{\sigma ,\nu }$
be a fantastack and assume the good moduli space map
![]() $\pi \colon \mathcal {X}\to X:=X_\sigma $
is an isomorphism over the torus
$\pi \colon \mathcal {X}\to X:=X_\sigma $
is an isomorphism over the torus
![]() $T\subset X$
. With the notation listed in Notation 2.19, let
$T\subset X$
. With the notation listed in Notation 2.19, let
![]() $k'$
be a field extension of k and
$k'$
be a field extension of k and
![]() $\varphi \in \mathscr {L}(X)(k')$
with
$\varphi \in \mathscr {L}(X)(k')$
with
![]() $\operatorname {\mathrm {trop}}(\varphi ) = w\in \sigma \cap N$
. Then
$\operatorname {\mathrm {trop}}(\varphi ) = w\in \sigma \cap N$
. Then
induces, by restriction, a bijection
 $$ \begin{align*} \overline{\left(\mathscr{L}(\pi)^{-1}(\varphi)\right)}(k') \to \beta^{-1}(w). \end{align*} $$
$$ \begin{align*} \overline{\left(\mathscr{L}(\pi)^{-1}(\varphi)\right)}(k') \to \beta^{-1}(w). \end{align*} $$
In particular,
 $\overline {\left (\mathscr {L}(\pi )^{-1}(\varphi )\right )}(k')$
is a finite set.
$\overline {\left (\mathscr {L}(\pi )^{-1}(\varphi )\right )}(k')$
is a finite set.
For the rest of this section, we fix the notation as in the statement of Theorem Theorem 4.9. By Corollary 4.8, we know that any
![]() $\psi \in \mathscr {L}(\mathcal {X})(k')$
with
$\psi \in \mathscr {L}(\mathcal {X})(k')$
with
![]() $(\mathscr {L}(\pi ))(\psi ) = \varphi $
must satisfy
$(\mathscr {L}(\pi ))(\psi ) = \varphi $
must satisfy
![]() $\operatorname {\mathrm {trop}}(\psi ) \in \beta ^{-1}(w)$
. We therefore have an induced map
$\operatorname {\mathrm {trop}}(\psi ) \in \beta ^{-1}(w)$
. We therefore have an induced map
 $\overline {\left (\mathscr {L}(\pi )^{-1}(\varphi )\right )}(k') \to \beta ^{-1}(w)$
. We show injectivity and surjectivity in Proposition 4.10 and Proposition 4.11, respectively. Note that the finiteness of
$\overline {\left (\mathscr {L}(\pi )^{-1}(\varphi )\right )}(k') \to \beta ^{-1}(w)$
. We show injectivity and surjectivity in Proposition 4.10 and Proposition 4.11, respectively. Note that the finiteness of
 $\overline {\left (\mathscr {L}(\pi )^{-1}(\varphi )\right )}(k')$
then follows from Proposition 2.15.
$\overline {\left (\mathscr {L}(\pi )^{-1}(\varphi )\right )}(k')$
then follows from Proposition 2.15.
Proposition 4.10. The restriction of the map
to
 $\overline {\left (\mathscr {L}(\pi )^{-1}(\varphi )\right )}(k')$
is injective.
$\overline {\left (\mathscr {L}(\pi )^{-1}(\varphi )\right )}(k')$
is injective.
Proof. Let
![]() $\psi _1, \psi _2 \in \mathscr {L}(\mathcal {X})(k')$
correspond to G-torsors
$\psi _1, \psi _2 \in \mathscr {L}(\mathcal {X})(k')$
correspond to G-torsors
![]() and G-equivariant maps
and G-equivariant maps
![]() $\gamma _1: Q_1 \to \widetilde {X}$
and
$\gamma _1: Q_1 \to \widetilde {X}$
and
![]() $\gamma _2: Q_2 \to \widetilde {X}$
, respectively, and assume that
$\gamma _2: Q_2 \to \widetilde {X}$
, respectively, and assume that
![]() $\mathscr {L}(\pi )(\psi _1) = \mathscr {L}(\pi )(\psi _2) = \varphi $
and
$\mathscr {L}(\pi )(\psi _1) = \mathscr {L}(\pi )(\psi _2) = \varphi $
and
![]() $\operatorname {\mathrm {trop}}(\psi _1) = \operatorname {\mathrm {trop}}(\psi _2)$
. We need to prove that
$\operatorname {\mathrm {trop}}(\psi _1) = \operatorname {\mathrm {trop}}(\psi _2)$
. We need to prove that
![]() $\psi _1$
and
$\psi _1$
and
![]() $\psi _2$
are isomorphic – that is, that there exists an isomorphism of G-torsors
$\psi _2$
are isomorphic – that is, that there exists an isomorphism of G-torsors
![]() $\alpha : Q_1 \to Q_2$
such that
$\alpha : Q_1 \to Q_2$
such that
![]() $\gamma _1 = \gamma _2 \circ \alpha $
. In fact, we prove the stronger statement that there exists a unique such
$\gamma _1 = \gamma _2 \circ \alpha $
. In fact, we prove the stronger statement that there exists a unique such
![]() $\alpha $
.
$\alpha $
.
To prove this stronger statement, by descent, it is enough to show the existence of a unique such
![]() $\alpha $
étale locally on
$\alpha $
étale locally on
![]() . By Lemma 4.3, the
. By Lemma 4.3, the
![]() $Q_i$
are isomorphic to pullbacks of torsors over
$Q_i$
are isomorphic to pullbacks of torsors over
![]() $k'$
, which can themselves be trivialised after base change to a finite field extension
$k'$
, which can themselves be trivialised after base change to a finite field extension
![]() $k''$
of
$k''$
of
![]() $k'$
. Since
$k'$
. Since
![]() , after replacing
, after replacing
![]() $k'$
by
$k'$
by
![]() $k''$
, we may therefore assume that the
$k''$
, we may therefore assume that the
![]() $Q_i$
are trivial G-torsors. Since
$Q_i$
are trivial G-torsors. Since
![]() $\operatorname {\mathrm {trop}}(\psi _i)$
depends only on the isomorphism class of
$\operatorname {\mathrm {trop}}(\psi _i)$
depends only on the isomorphism class of
![]() $\psi _i$
, we may further assume
$\psi _i$
, we may further assume
![]() .
.
Next, the identity section of the G-torsor
![]() $Q_i$
then yields a lift
$Q_i$
then yields a lift
 $\widetilde {\psi }_i\in \mathscr {L}\left (\widetilde {X}\right )(k')$
of
$\widetilde {\psi }_i\in \mathscr {L}\left (\widetilde {X}\right )(k')$
of
![]() $\psi _i$
. Then the map
$\psi _i$
. Then the map
satisfies

where
 $u^{\overline {f}} \in k[A]$
is the monomial indexed by the image
$u^{\overline {f}} \in k[A]$
is the monomial indexed by the image
![]() $\overline {f}$
of f in A. Since
$\overline {f}$
of f in A. Since
 $\operatorname {\mathrm {trop}}\left (\widetilde {\psi }_i\right )=\operatorname {\mathrm {trop}}(\psi _i)$
, we see
$\operatorname {\mathrm {trop}}\left (\widetilde {\psi }_i\right )=\operatorname {\mathrm {trop}}(\psi _i)$
, we see
 $\operatorname {\mathrm {trop}}\left (\widetilde {\psi }_1\right )=\operatorname {\mathrm {trop}}\left (\widetilde {\psi }_2\right )\in \widetilde {\sigma } \cap \widetilde {N}$
. Thus, for all
$\operatorname {\mathrm {trop}}\left (\widetilde {\psi }_1\right )=\operatorname {\mathrm {trop}}\left (\widetilde {\psi }_2\right )\in \widetilde {\sigma } \cap \widetilde {N}$
. Thus, for all
![]() $f \in F$
, the power series
$f \in F$
, the power series
 $\widetilde {\psi }_1^*(f)$
and
$\widetilde {\psi }_1^*(f)$
and
 $\widetilde {\psi }_2^*(f)$
are nonzero and have the same t-order of vanishing. It follows that there is a unique unit
$\widetilde {\psi }_2^*(f)$
are nonzero and have the same t-order of vanishing. It follows that there is a unique unit
such that
 $$ \begin{align*} \psi_1^*(f) = g^{(f)} \psi_2^*(f). \end{align*} $$
$$ \begin{align*} \psi_1^*(f) = g^{(f)} \psi_2^*(f). \end{align*} $$
Since
 $\mathscr {L}(\pi )\left (\widetilde \psi _1\right ) = \mathscr {L}(\pi )\left (\widetilde \psi _2\right )$
, we see that
$\mathscr {L}(\pi )\left (\widetilde \psi _1\right ) = \mathscr {L}(\pi )\left (\widetilde \psi _2\right )$
, we see that
 $\widetilde \psi _1^*(p) = \widetilde \psi _2^*(p)$
, and so
$\widetilde \psi _1^*(p) = \widetilde \psi _2^*(p)$
, and so
![]() $g^{(p)} = 1$
for all
$g^{(p)} = 1$
for all
![]() $p \in P$
.
$p \in P$
.
Thus the semigroup homomorphism
![]() induces a group homomorphism
induces a group homomorphism
![]() , which corresponds to an element
, which corresponds to an element
![]() and hence an automorphism
and hence an automorphism
![]() $\alpha $
of the G-torsor
$\alpha $
of the G-torsor
![]() . By construction,
. By construction,
![]() $\widetilde {\psi _1} = \widetilde {\psi _2} \circ \alpha $
, and so
$\widetilde {\psi _1} = \widetilde {\psi _2} \circ \alpha $
, and so
![]() $\gamma _1 = \gamma _2 \circ \alpha $
. Moreover, the uniqueness of
$\gamma _1 = \gamma _2 \circ \alpha $
. Moreover, the uniqueness of
![]() $\alpha $
follows from the uniqueness of each
$\alpha $
follows from the uniqueness of each
![]() $g^{(f)}$
.
$g^{(f)}$
.
We now complete the proof of Theorem 4.9 by showing the surjectivity of the map
 $\overline {\left (\mathscr {L}(\pi )^{-1}(\varphi )\right )}(k') \to \beta ^{-1}(w)$
.
$\overline {\left (\mathscr {L}(\pi )^{-1}(\varphi )\right )}(k') \to \beta ^{-1}(w)$
.
Proposition 4.11. The image of
 $\overline {\left (\mathscr {L}(\pi )^{-1}(\varphi )\right )}(k')$
under the map
$\overline {\left (\mathscr {L}(\pi )^{-1}(\varphi )\right )}(k')$
under the map
is equal to
![]() $\beta ^{-1}(w)$
.
$\beta ^{-1}(w)$
.
Proof. Recall that in Corollary 4.8, we proved that the image of
 $\overline {\left (\mathscr {L}(\pi )^{-1}(\varphi )\right )}(k')$
under
$\overline {\left (\mathscr {L}(\pi )^{-1}(\varphi )\right )}(k')$
under
![]() $\operatorname {\mathrm {trop}}$
is contained in
$\operatorname {\mathrm {trop}}$
is contained in
![]() $\beta ^{-1}(w)$
.
$\beta ^{-1}(w)$
.
Set
![]() $\widetilde {w} \in \beta ^{-1}(w)$
. We will construct an arc
$\widetilde {w} \in \beta ^{-1}(w)$
. We will construct an arc
![]() $\psi \in \mathscr {L}(\mathcal {X})(k')$
satisfying
$\psi \in \mathscr {L}(\mathcal {X})(k')$
satisfying
![]() $\operatorname {\mathrm {trop}}(\psi ) = \widetilde {w}$
and
$\operatorname {\mathrm {trop}}(\psi ) = \widetilde {w}$
and
![]() $\mathscr {L}(\pi )(\psi ) = \varphi $
. Let
$\mathscr {L}(\pi )(\psi ) = \varphi $
. Let
![]() be the generic point of
be the generic point of
![]() $\varphi $
– that is,
$\varphi $
– that is,
![]() $\eta $
is the composition
$\eta $
is the composition
 . Since
. Since
![]() $w \in \sigma \cap N$
, we see that
$w \in \sigma \cap N$
, we see that
![]() $\eta $
factors through
$\eta $
factors through
![]() $T \hookrightarrow X$
. Thus
$T \hookrightarrow X$
. Thus
![]() $\eta $
is given by a group homomorphism
$\eta $
is given by a group homomorphism
![]() .
.
Given our inclusion
![]() $M\hookrightarrow \widetilde {M}$
, we can choose a
$M\hookrightarrow \widetilde {M}$
, we can choose a
![]() $\mathbb {Z}$
-basis
$\mathbb {Z}$
-basis
![]() $f_1, \dotsc , f_r$
for
$f_1, \dotsc , f_r$
for
![]() $\widetilde {M} = F^{\mathrm {gp}}$
and
$\widetilde {M} = F^{\mathrm {gp}}$
and
![]() $m_1, \dotsc , m_d \in \mathbb {Z}_{>0}$
such that
$m_1, \dotsc , m_d \in \mathbb {Z}_{>0}$
such that
![]() $m_1 f_1, \dotsc , m_d f_d$
is a
$m_1 f_1, \dotsc , m_d f_d$
is a
![]() $\mathbb {Z}$
-basis for M. Since
$\mathbb {Z}$
-basis for M. Since
![]() $\operatorname {\mathrm {trop}}(\varphi ) = w$
, the image of
$\operatorname {\mathrm {trop}}(\varphi ) = w$
, the image of
![]() $m_i f_i$
under
$m_i f_i$
under
![]() has t-order of vanishing
has t-order of vanishing
![]() $\langle w, m_i f_i \rangle $
, so it can be written as
$\langle w, m_i f_i \rangle $
, so it can be written as
![]() $t^{\left \langle w, m_i f_i \right \rangle } g_i$
with
$t^{\left \langle w, m_i f_i \right \rangle } g_i$
with
![]() .
.
Now set R to be the
-algebra

and give
![]() $\operatorname {\mathrm {Spec}}(R)$
the G-action obtained by letting
$\operatorname {\mathrm {Spec}}(R)$
the G-action obtained by letting
![]() $x_i$
have grading
$x_i$
have grading
![]() $\overline {f}_i$
, where
$\overline {f}_i$
, where
![]() $\overline {f}_i$
is the image of
$\overline {f}_i$
is the image of
![]() $f_i$
in A. Since each
$f_i$
in A. Since each
![]() $g_i$
is a unit in
$g_i$
is a unit in
, we see that
is a G-torsor.
Let
![]() $\psi \in \mathscr {L}(\mathcal {X})(k')$
be the arc corresponding to the G-torsor
$\psi \in \mathscr {L}(\mathcal {X})(k')$
be the arc corresponding to the G-torsor
![]() $\operatorname {\mathrm {Spec}}(R)$
and the G-equivariant map
$\operatorname {\mathrm {Spec}}(R)$
and the G-equivariant map
![]() $\operatorname {\mathrm {Spec}}(R) \to \widetilde {X} = \operatorname {\mathrm {Spec}}(k[F])$
defined by
$\operatorname {\mathrm {Spec}}(R) \to \widetilde {X} = \operatorname {\mathrm {Spec}}(k[F])$
defined by
 $$ \begin{align*} F \to R: f \mapsto t^{\left\langle \widetilde{w}, f \right\rangle} \prod_{i=1}^r x_i^{c_i}, \end{align*} $$
$$ \begin{align*} F \to R: f \mapsto t^{\left\langle \widetilde{w}, f \right\rangle} \prod_{i=1}^r x_i^{c_i}, \end{align*} $$
for
![]() $f = \sum _{i=1}^r c_i f_i$
and
$f = \sum _{i=1}^r c_i f_i$
and
![]() $c_1, \dotsc , c_r \in \mathbb {Z}$
. Note that this map is well defined, since
$c_1, \dotsc , c_r \in \mathbb {Z}$
. Note that this map is well defined, since
![]() $\langle \widetilde {w}, f \rangle \geq 0$
when
$\langle \widetilde {w}, f \rangle \geq 0$
when
![]() $f \in F$
, and each
$f \in F$
, and each
![]() $x_i$
is a unit in R as a consequence of the fact that each
$x_i$
is a unit in R as a consequence of the fact that each
![]() $g_i$
is a unit in
$g_i$
is a unit in
![]() . Note further that since the
. Note further that since the
![]() $x_i$
are units, the map sends f to an element whose t-order of vanishing is
$x_i$
are units, the map sends f to an element whose t-order of vanishing is
![]() $\langle \widetilde {w},f\rangle $
. As a result, any lift
$\langle \widetilde {w},f\rangle $
. As a result, any lift
 $\widetilde {\psi }\in \mathscr {L}\left (\widetilde {X}\right )(k'')$
obtained from a trivialisation of the G-torsor after base change to
$\widetilde {\psi }\in \mathscr {L}\left (\widetilde {X}\right )(k'')$
obtained from a trivialisation of the G-torsor after base change to
![]() $k''$
, satisfies
$k''$
, satisfies
 $\operatorname {\mathrm {trop}}(\psi )=\operatorname {\mathrm {trop}}\left (\widetilde {\psi }\right )=\widetilde {w}$
.
$\operatorname {\mathrm {trop}}(\psi )=\operatorname {\mathrm {trop}}\left (\widetilde {\psi }\right )=\widetilde {w}$
.
To finish the proof, we must show
![]() $\mathscr {L}(\pi )(\psi ) = \varphi $
– that is,
$\mathscr {L}(\pi )(\psi ) = \varphi $
– that is,
![]() $\pi \circ \psi =\varphi $
. Since X is separated, it is enough to prove equality after precomposing by the generic point
$\pi \circ \psi =\varphi $
. Since X is separated, it is enough to prove equality after precomposing by the generic point
![]() . But this follows from the facts that
. But this follows from the facts that
![]() $\eta =\varphi \circ \xi $
and that for any
$\eta =\varphi \circ \xi $
and that for any
![]() $i \in \{1, \dotsc , d\}$
, the image of
$i \in \{1, \dotsc , d\}$
, the image of
![]() $m_i f_i$
under the pullback of
$m_i f_i$
under the pullback of
 $\operatorname {\mathrm {Spec}}(R) \to \widetilde {X} \xrightarrow {\widetilde {\pi }} X$
is equal to
$\operatorname {\mathrm {Spec}}(R) \to \widetilde {X} \xrightarrow {\widetilde {\pi }} X$
is equal to
 $$ \begin{align*} t^{\left\langle \widetilde{w}, m_i f_i \right\rangle} x_i^{m_i} = t^{\left\langle w, m_i f_i \right\rangle} g_i.\\[-39pt] \end{align*} $$
$$ \begin{align*} t^{\left\langle \widetilde{w}, m_i f_i \right\rangle} x_i^{m_i} = t^{\left\langle w, m_i f_i \right\rangle} g_i.\\[-39pt] \end{align*} $$
5 Fibres of the maps of jets
Throughout this section set
![]() $d \in \mathbb {N}$
, let
$d \in \mathbb {N}$
, let
![]() $N \cong \mathbb {Z}^d$
be a lattice, let
$N \cong \mathbb {Z}^d$
be a lattice, let
![]() $T = \operatorname {\mathrm {Spec}}(k[N^*])$
be the algebraic torus with cocharacter lattice N, let
$T = \operatorname {\mathrm {Spec}}(k[N^*])$
be the algebraic torus with cocharacter lattice N, let
![]() $\sigma $
be a pointed rational cone in
$\sigma $
be a pointed rational cone in
![]() $N_{\mathbb {R}}$
, let X be the affine T-toric variety associated to
$N_{\mathbb {R}}$
, let X be the affine T-toric variety associated to
![]() $\sigma $
, let
$\sigma $
, let
![]() $\mathcal {X}$
be the canonical stack over X and let
$\mathcal {X}$
be the canonical stack over X and let
![]() $\pi : \mathcal {X} \to X$
be the canonical map.
$\pi : \mathcal {X} \to X$
be the canonical map.
In this section we will control the fibres of the maps
in the case where
![]() $\sigma $
is d-dimensional. In particular, we will prove the following:
$\sigma $
is d-dimensional. In particular, we will prove the following:
Theorem 5.1. Suppose that
![]() $\sigma $
is d-dimensional, and set
$\sigma $
is d-dimensional, and set
![]() $w \in \sigma \cap N$
. Then there exist
$w \in \sigma \cap N$
. Then there exist
![]() $n_w \in \mathbb {N}$
and
$n_w \in \mathbb {N}$
and
![]() $\Theta _w \in K_0(\mathbf {Stack}_k)$
and a sequence of finite-type Artin stacks
$\Theta _w \in K_0(\mathbf {Stack}_k)$
and a sequence of finite-type Artin stacks
![]() $\{\mathcal {F}_n\}_{n \geq n_w}$
over k such that
$\{\mathcal {F}_n\}_{n \geq n_w}$
over k such that
-
1. for each
 $n \geq n_w$
, and
$n \geq n_w$
, and $$ \begin{align*} \mathrm{e}(\mathcal{F}_n) = \Theta_w \in K_0(\mathbf{Stack}_k), \end{align*} $$
$$ \begin{align*} \mathrm{e}(\mathcal{F}_n) = \Theta_w \in K_0(\mathbf{Stack}_k), \end{align*} $$
-
2. for each field extension
 $k'$
of k, each arc
$k'$
of k, each arc
 $\varphi \in \mathscr {L}(X)(k')$
with
$\varphi \in \mathscr {L}(X)(k')$
with
 $\operatorname {\mathrm {trop}}(\varphi ) = w$
and each
$\operatorname {\mathrm {trop}}(\varphi ) = w$
and each
 $n \geq n_w$
, we have
$n \geq n_w$
, we have  $$ \begin{align*} \mathscr{L}_n(\pi)^{-1}(\theta_n(\varphi))_{\mathrm{red}} \cong \mathcal{F}_n \otimes_k k'. \end{align*} $$
$$ \begin{align*} \mathscr{L}_n(\pi)^{-1}(\theta_n(\varphi))_{\mathrm{red}} \cong \mathcal{F}_n \otimes_k k'. \end{align*} $$
For the remainder of this section, we will assume that
![]() $\sigma $
is d-dimensional, and we will use the notation listed in Notation 2.19.
$\sigma $
is d-dimensional, and we will use the notation listed in Notation 2.19.
5.1 Algebraic groups and jets
We begin by introducing some algebraic groups, which in Proposition 5.15 will be used to express the fibres of each
![]() $\mathscr {L}_n(\pi )$
.
$\mathscr {L}_n(\pi )$
.
Remark 5.2. In what follows, for each k-algebra R, each
 $g_n \in \mathscr {L}_n\left (\widetilde {T}\right )(R)$
and each
$g_n \in \mathscr {L}_n\left (\widetilde {T}\right )(R)$
and each
![]() $f \in \widetilde {M}$
, let
$f \in \widetilde {M}$
, let
 $g_n^*(f) \in \left (R[t]/\left (t^{n+1}\right )\right )^\times $
denote the image of f under the pullback map
$g_n^*(f) \in \left (R[t]/\left (t^{n+1}\right )\right )^\times $
denote the image of f under the pullback map
 $ k\left [\widetilde {M}\right ] \to R[t]/\left (t^{n+1}\right )$
corresponding to the jet
$ k\left [\widetilde {M}\right ] \to R[t]/\left (t^{n+1}\right )$
corresponding to the jet
 $g_n: \operatorname {\mathrm {Spec}}\left (R[t]/\left (t^{n+1}\right )\right ) \to \widetilde {T}$
. We also use the analogous notation when T and M are in place of
$g_n: \operatorname {\mathrm {Spec}}\left (R[t]/\left (t^{n+1}\right )\right ) \to \widetilde {T}$
. We also use the analogous notation when T and M are in place of
![]() $\widetilde {T}$
and
$\widetilde {T}$
and
![]() $\widetilde {M}$
.
$\widetilde {M}$
.
For each
![]() $w \in \sigma \cap N$
and
$w \in \sigma \cap N$
and
![]() $n \in \mathbb {N}$
, let
$n \in \mathbb {N}$
, let
![]() $G_n^w$
be the subgroup object of
$G_n^w$
be the subgroup object of
 $\mathscr {L}_n\left (\widetilde {T}\right )$
given by
$\mathscr {L}_n\left (\widetilde {T}\right )$
given by
 $$ \begin{align*} G_n^w(R) = \left\{ g_n \in \mathscr{L}_n\left(\widetilde{T}\right)(R) \mid g_n^*(p)t^{\left\langle w, p \right\rangle} = t^{\left\langle w, p \right\rangle} \in R[t]/\left(t^{n+1}\right)\text{ for all }p \in P\right\}. \end{align*} $$
$$ \begin{align*} G_n^w(R) = \left\{ g_n \in \mathscr{L}_n\left(\widetilde{T}\right)(R) \mid g_n^*(p)t^{\left\langle w, p \right\rangle} = t^{\left\langle w, p \right\rangle} \in R[t]/\left(t^{n+1}\right)\text{ for all }p \in P\right\}. \end{align*} $$
For each
![]() $\widetilde {w} \in \widetilde {\sigma } \cap \widetilde {N}$
and
$\widetilde {w} \in \widetilde {\sigma } \cap \widetilde {N}$
and
![]() $n \in \mathbb {N}$
, let
$n \in \mathbb {N}$
, let
![]() $H_n^{\widetilde {w}}$
be the subgroup object of
$H_n^{\widetilde {w}}$
be the subgroup object of
 $\mathscr {L}_n\left (\widetilde {T}\right )$
given by
$\mathscr {L}_n\left (\widetilde {T}\right )$
given by
 $$ \begin{align*} H_n^{\widetilde{w}}(R) = \left\{ g_n \in \mathscr{L}_n\left(\widetilde{T}\right)(R) \mid g_n^*(f) t^{\left\langle \widetilde{w}, f \right\rangle} = t^{\left\langle \widetilde{w}, f \right\rangle} \in R[t]/\left(t^{n+1}\right)\text{ for all }f \in F\right\}. \end{align*} $$
$$ \begin{align*} H_n^{\widetilde{w}}(R) = \left\{ g_n \in \mathscr{L}_n\left(\widetilde{T}\right)(R) \mid g_n^*(f) t^{\left\langle \widetilde{w}, f \right\rangle} = t^{\left\langle \widetilde{w}, f \right\rangle} \in R[t]/\left(t^{n+1}\right)\text{ for all }f \in F\right\}. \end{align*} $$
By definition,
![]() $H_n^{\widetilde {w}}$
is a subgroup object of
$H_n^{\widetilde {w}}$
is a subgroup object of
 $G_n^{\beta \left (\widetilde {w}\right )}$
. We now show that these group objects are in fact algebraic groups.
$G_n^{\beta \left (\widetilde {w}\right )}$
. We now show that these group objects are in fact algebraic groups.
Proposition 5.3. The subgroup objects
![]() $G_n^w$
and
$G_n^w$
and
![]() $H_n^{\widetilde {w}}$
are represented by closed subgroups of
$H_n^{\widetilde {w}}$
are represented by closed subgroups of
 $\mathscr {L}_n\left (\widetilde {T}\right )$
.
$\mathscr {L}_n\left (\widetilde {T}\right )$
.
Proof. For each
![]() $f \in F$
, let
$f \in F$
, let
 $\mathscr {L}_n(f): \mathscr {L}_n\left (\widetilde {T}\right ) \to \mathscr {L}_n(\mathbb {G}_m)$
be the map induced by the character
$\mathscr {L}_n(f): \mathscr {L}_n\left (\widetilde {T}\right ) \to \mathscr {L}_n(\mathbb {G}_m)$
be the map induced by the character
![]() $\widetilde {T} \to \mathbb {G}_m$
corresponding to f. Then
$\widetilde {T} \to \mathbb {G}_m$
corresponding to f. Then
 $$ \begin{align*} G_n^w = \bigcap_{p \in P} \left(\theta^n_{n-\left\langle w, p \right\rangle} \circ \mathscr{L}_n(p)\right)^{-1}(1) \end{align*} $$
$$ \begin{align*} G_n^w = \bigcap_{p \in P} \left(\theta^n_{n-\left\langle w, p \right\rangle} \circ \mathscr{L}_n(p)\right)^{-1}(1) \end{align*} $$
and
 $$ \begin{align*} H_n^{\widetilde{w}} = \bigcap_{f \in F} \left(\theta^n_{n-\left\langle \widetilde{w}, f \right\rangle} \circ \mathscr{L}_n(f)\right)^{-1}(1), \end{align*} $$
$$ \begin{align*} H_n^{\widetilde{w}} = \bigcap_{f \in F} \left(\theta^n_{n-\left\langle \widetilde{w}, f \right\rangle} \circ \mathscr{L}_n(f)\right)^{-1}(1), \end{align*} $$
where each
![]() $\theta _{n-n'}^n: \mathscr {L}_{n}(\mathbb {G}_m) \to \mathscr {L}_{n-n'}(\mathbb {G}_m)$
is the truncation morphism, each
$\theta _{n-n'}^n: \mathscr {L}_{n}(\mathbb {G}_m) \to \mathscr {L}_{n-n'}(\mathbb {G}_m)$
is the truncation morphism, each
![]() $1 \in \mathscr {L}_{n-n'}(\mathbb {G}_m)$
is the identity element and, by convention, if
$1 \in \mathscr {L}_{n-n'}(\mathbb {G}_m)$
is the identity element and, by convention, if
![]() $n-n' < 0$
, we set
$n-n' < 0$
, we set
![]() $\mathscr {L}_{n-n'}(\mathbb {G}_m)$
to be the single point group
$\mathscr {L}_{n-n'}(\mathbb {G}_m)$
to be the single point group
![]() $\{1\}$
.
$\{1\}$
.
Remark 5.4. Note that
 $$ \begin{align*} \mathscr{L}_n(G)(R) = \left\{g_n \in \mathscr{L}_n\left(\widetilde{T}\right)(R) \mid g_n^*(p) = 1 \in R[t]/\left(t^{n+1}\right)\text{ for all }p \in P\right\}, \end{align*} $$
$$ \begin{align*} \mathscr{L}_n(G)(R) = \left\{g_n \in \mathscr{L}_n\left(\widetilde{T}\right)(R) \mid g_n^*(p) = 1 \in R[t]/\left(t^{n+1}\right)\text{ for all }p \in P\right\}, \end{align*} $$
so for any
![]() $n \in \mathbb {N}$
and
$n \in \mathbb {N}$
and
![]() $w \in \sigma \cap N$
, we have that
$w \in \sigma \cap N$
, we have that
![]() $\mathscr {L}_n(G)$
is a closed subgroup of
$\mathscr {L}_n(G)$
is a closed subgroup of
![]() $G_n^w$
.
$G_n^w$
.
We also prove the following characterisation of the
![]() $H_n^{\widetilde {w}}$
:
$H_n^{\widetilde {w}}$
:
Proposition 5.5. Set
![]() $\widetilde {w} \in \widetilde {\sigma } \cap \widetilde {N}$
and
$\widetilde {w} \in \widetilde {\sigma } \cap \widetilde {N}$
and
![]() $n \in \mathbb {N}$
, and let
$n \in \mathbb {N}$
, and let
![]() $f_1, \dotsc , f_r$
be the minimal generators of F. If
$f_1, \dotsc , f_r$
be the minimal generators of F. If
![]() $n \geq \max _{i=1}^r\left ( 2\left \langle \widetilde {w}, f_i\right \rangle - 1\right )$
, then
$n \geq \max _{i=1}^r\left ( 2\left \langle \widetilde {w}, f_i\right \rangle - 1\right )$
, then
 $$ \begin{align*} H_n^{\widetilde{w}} \cong \mathbb{G}_a^{\sum_{i = 1}^r \left\langle \widetilde{w}, f_i \right\rangle} \end{align*} $$
$$ \begin{align*} H_n^{\widetilde{w}} \cong \mathbb{G}_a^{\sum_{i = 1}^r \left\langle \widetilde{w}, f_i \right\rangle} \end{align*} $$
as algebraic groups.
Proof. Let R be a k-algebra. Then
 $$ \begin{align*} H_n^{\widetilde{w}}(R) &= \left\{ g_n \in \mathscr{L}_n\left(\widetilde{T}\right)(R) \mid g_n^*(f)t^{\left\langle \widetilde{w}, f \right\rangle} = t^{\left\langle \widetilde{w}, f \right\rangle} \in R[t]/\left(t^{n+1}\right)\text{ for all }f \in F\right\} \\ &=\left\{ g_n \in \mathscr{L}_n\left(\widetilde{T}\right)(R) \mid g_n^*(f_i)t^{\left\langle \widetilde{w}, f_i \right\rangle} = t^{\left\langle \widetilde{w}, f_i \right\rangle} \in R[t]/\left(t^{n+1}\right)\text{ for all }i = 1, \dotsc, r\right\}\\ &\cong \left\{ \left(g^{(i)}\right)_i \in \left(\left(R[t]\left(t^{n+1}\right)\right)^\times\right)^r \mid g^{(i)} t^{\left\langle \widetilde{w}, f_i \right\rangle} = t^{\left\langle \widetilde{w}, f_i \right\rangle} \in R[t]/\left(t^{n+1}\right)\text{ for all }i\right\}. \end{align*} $$
$$ \begin{align*} H_n^{\widetilde{w}}(R) &= \left\{ g_n \in \mathscr{L}_n\left(\widetilde{T}\right)(R) \mid g_n^*(f)t^{\left\langle \widetilde{w}, f \right\rangle} = t^{\left\langle \widetilde{w}, f \right\rangle} \in R[t]/\left(t^{n+1}\right)\text{ for all }f \in F\right\} \\ &=\left\{ g_n \in \mathscr{L}_n\left(\widetilde{T}\right)(R) \mid g_n^*(f_i)t^{\left\langle \widetilde{w}, f_i \right\rangle} = t^{\left\langle \widetilde{w}, f_i \right\rangle} \in R[t]/\left(t^{n+1}\right)\text{ for all }i = 1, \dotsc, r\right\}\\ &\cong \left\{ \left(g^{(i)}\right)_i \in \left(\left(R[t]\left(t^{n+1}\right)\right)^\times\right)^r \mid g^{(i)} t^{\left\langle \widetilde{w}, f_i \right\rangle} = t^{\left\langle \widetilde{w}, f_i \right\rangle} \in R[t]/\left(t^{n+1}\right)\text{ for all }i\right\}. \end{align*} $$
Since
![]() $n \geq 0$
, the hypotheses guarantee that
$n \geq 0$
, the hypotheses guarantee that
![]() $n \geq \langle \widetilde {w}, f_i \rangle $
for all
$n \geq \langle \widetilde {w}, f_i \rangle $
for all
![]() $i \in \{1, \dotsc , r\}$
. Thus if
$i \in \{1, \dotsc , r\}$
. Thus if
![]() $i \in \{1, \dotsc , r\}$
and
$i \in \{1, \dotsc , r\}$
and
 $g^{(i)} \in \left (R[t]/\left (t^{n+1}\right )\right )^\times $
, then
$g^{(i)} \in \left (R[t]/\left (t^{n+1}\right )\right )^\times $
, then
 $$ \begin{align*} g^{(i)}t^{\left\langle \widetilde{w}, f_i \right\rangle} = t^{\left\langle \widetilde{w}, f_i \right\rangle} \in R[t]/\left(t^{n+1}\right) \end{align*} $$
$$ \begin{align*} g^{(i)}t^{\left\langle \widetilde{w}, f_i \right\rangle} = t^{\left\langle \widetilde{w}, f_i \right\rangle} \in R[t]/\left(t^{n+1}\right) \end{align*} $$
if and only if
 $$ \begin{align*} g^{(i)} = 1 + a_{n-\left\langle \widetilde{w}, f_i \right\rangle + 1} t^{n-\left\langle \widetilde{w}, f_i \right\rangle+1} + \dotsb + a_{n} t^n \in R[t]/\left(t^{n+1}\right) \end{align*} $$
$$ \begin{align*} g^{(i)} = 1 + a_{n-\left\langle \widetilde{w}, f_i \right\rangle + 1} t^{n-\left\langle \widetilde{w}, f_i \right\rangle+1} + \dotsb + a_{n} t^n \in R[t]/\left(t^{n+1}\right) \end{align*} $$
for some
![]() $a_{n-\left \langle \widetilde {w}, f_i \right \rangle + 1}, \dotsc , a_n \in R$
. The proposition thus follows from the fact that if
$a_{n-\left \langle \widetilde {w}, f_i \right \rangle + 1}, \dotsc , a_n \in R$
. The proposition thus follows from the fact that if
![]() $a_{n-\left \langle \widetilde {w}, f_i \right \rangle +1}, \dotsc , a_n$
,
$a_{n-\left \langle \widetilde {w}, f_i \right \rangle +1}, \dotsc , a_n$
,
![]() $b_{n-\left \langle \widetilde {w}, f_i \right \rangle +1}, \dotsc , b_n \in R$
, then in
$b_{n-\left \langle \widetilde {w}, f_i \right \rangle +1}, \dotsc , b_n \in R$
, then in
![]() $R[t]/\left (t^{n+1}\right )$
,
$R[t]/\left (t^{n+1}\right )$
,
 $$ \begin{align*} &\left(1 + a_{n-\left\langle \widetilde{w}, f_i \right\rangle+1} t^{n-\left\langle \widetilde{w}, f_i \right\rangle+1} + \dotsb + a_n t^n\right) \left(1 + b_{n-\left\langle \widetilde{w}, f_i \right\rangle+1} t^{n-\left\langle \widetilde{w}, f_i \right\rangle+1} + \dotsb + b_n t^n\right) \\ &\qquad\qquad\quad\qquad\qquad\qquad\qquad = 1 + \left(a_{n-\left\langle \widetilde{w}, f_i \right\rangle+1}+b_{n-\left\langle \widetilde{w}, f_i \right\rangle+1}\right) t^{n-\left\langle \widetilde{w}, f_i \right\rangle+1} + \dotsb + (a_n+b_n) t^n, \end{align*} $$
$$ \begin{align*} &\left(1 + a_{n-\left\langle \widetilde{w}, f_i \right\rangle+1} t^{n-\left\langle \widetilde{w}, f_i \right\rangle+1} + \dotsb + a_n t^n\right) \left(1 + b_{n-\left\langle \widetilde{w}, f_i \right\rangle+1} t^{n-\left\langle \widetilde{w}, f_i \right\rangle+1} + \dotsb + b_n t^n\right) \\ &\qquad\qquad\quad\qquad\qquad\qquad\qquad = 1 + \left(a_{n-\left\langle \widetilde{w}, f_i \right\rangle+1}+b_{n-\left\langle \widetilde{w}, f_i \right\rangle+1}\right) t^{n-\left\langle \widetilde{w}, f_i \right\rangle+1} + \dotsb + (a_n+b_n) t^n, \end{align*} $$
because for any
![]() $m_1, m_2 \geq n-\langle \widetilde {w}, f_i \rangle +1$
, we have
$m_1, m_2 \geq n-\langle \widetilde {w}, f_i \rangle +1$
, we have
We finish this subsection with the next two propositions, which characterise the group quotients
![]() $G_n^w / \mathscr {L}_n(G)$
.
$G_n^w / \mathscr {L}_n(G)$
.
Proposition 5.6. Set
![]() $w \in \sigma \cap N$
and
$w \in \sigma \cap N$
and
![]() $n \in \mathbb {N}$
. Then the group quotient
$n \in \mathbb {N}$
. Then the group quotient
![]() $G_n^w / \mathscr {L}_n(G)$
has functor of points given by
$G_n^w / \mathscr {L}_n(G)$
has functor of points given by
 $$ \begin{align*} R \mapsto \left\{h_n \in \mathscr{L}_n(T)(R) \mid h_n^*(p) t^{\left\langle w, p \right\rangle} = t^{\left\langle w, p \right\rangle} \in R[t]/\left(t^{n+1}\right)\text{ for all }p \in P\right\}. \end{align*} $$
$$ \begin{align*} R \mapsto \left\{h_n \in \mathscr{L}_n(T)(R) \mid h_n^*(p) t^{\left\langle w, p \right\rangle} = t^{\left\langle w, p \right\rangle} \in R[t]/\left(t^{n+1}\right)\text{ for all }p \in P\right\}. \end{align*} $$
Proof. First, the subgroup object is represented by a closed subgroup of
![]() $\mathscr {L}_n(T)$
by an identical argument as in Proposition 5.3. Call this closed subgroup
$\mathscr {L}_n(T)$
by an identical argument as in Proposition 5.3. Call this closed subgroup
![]() $H \subset \mathscr {L}_n(T)$
. We will show that
$H \subset \mathscr {L}_n(T)$
. We will show that
![]() $G_n^w / \mathscr {L}_n(G) \cong H$
as schemes.
$G_n^w / \mathscr {L}_n(G) \cong H$
as schemes.
By the definition of H and
![]() $G_n^w$
, the closed subgroup
$G_n^w$
, the closed subgroup
 $G_n^w \subset \mathscr {L}_n\left (\widetilde {T}\right )$
is equal to the preimage of H under the group homomorphism
$G_n^w \subset \mathscr {L}_n\left (\widetilde {T}\right )$
is equal to the preimage of H under the group homomorphism
 $\mathscr {L}_n\left (\widetilde {T}\right ) \to \mathscr {L}_n(T)$
obtained by applying the functor
$\mathscr {L}_n\left (\widetilde {T}\right ) \to \mathscr {L}_n(T)$
obtained by applying the functor
![]() $\mathscr {L}_n$
to the group homomorphism
$\mathscr {L}_n$
to the group homomorphism
 $\widetilde {\pi }\rvert _{\widetilde {T}}: \widetilde {T} \to T$
. Thus we obtain a group homomorphism
$\widetilde {\pi }\rvert _{\widetilde {T}}: \widetilde {T} \to T$
. Thus we obtain a group homomorphism
![]() $G_n^w \to H$
. Endow H with the
$G_n^w \to H$
. Endow H with the
![]() $G_n^w$
-action obtained by left multiplication after
$G_n^w$
-action obtained by left multiplication after
![]() $G_n^w \to H$
.
$G_n^w \to H$
.
For any k-algebra R and
![]() $g_n \in G_n^w(R)$
, we have that
$g_n \in G_n^w(R)$
, we have that
![]() $g_n \in \mathscr {L}_n(G)(R)$
if and only if
$g_n \in \mathscr {L}_n(G)(R)$
if and only if
![]() $g_n^*(p) = 1$
for all
$g_n^*(p) = 1$
for all
![]() $p \in P$
, which is equivalent to
$p \in P$
, which is equivalent to
![]() $g_n$
being in the kernel of
$g_n$
being in the kernel of
![]() $G_n^w \to H$
. Therefore the scheme-theoretic stabiliser of the identity
$G_n^w \to H$
. Therefore the scheme-theoretic stabiliser of the identity
![]() $1 \in H(k)$
is equal to
$1 \in H(k)$
is equal to
![]() $\mathscr {L}_n(G)$
. Thus by [Reference Demazure and GabrielDG70, Chapter III, Section 3, Proposition 5.2], we have a locally closed embedding
$\mathscr {L}_n(G)$
. Thus by [Reference Demazure and GabrielDG70, Chapter III, Section 3, Proposition 5.2], we have a locally closed embedding
whose image, as a set, is equal to the image of the map of underlying sets
![]() $G_n^w \to H$
. Since k has characteristic
$G_n^w \to H$
. Since k has characteristic
![]() $0$
so that H is reduced, we only need to show that
$0$
so that H is reduced, we only need to show that
![]() $G_n^w \to H$
is surjective on underlying sets, which will follow if we can show that
$G_n^w \to H$
is surjective on underlying sets, which will follow if we can show that
 $\mathscr {L}_n\left (\widetilde {T}\right ) \to \mathscr {L}_n(T)$
is surjective on underlying sets. The latter follows immediately from Corollary 3.22, which implies that
$\mathscr {L}_n\left (\widetilde {T}\right ) \to \mathscr {L}_n(T)$
is surjective on underlying sets. The latter follows immediately from Corollary 3.22, which implies that
 $\mathscr {L}_n\left (\widetilde {T}\right ) \to \mathscr {L}_n(T)$
is a
$\mathscr {L}_n\left (\widetilde {T}\right ) \to \mathscr {L}_n(T)$
is a
![]() $\mathscr {L}_n(G)$
-torsor.
$\mathscr {L}_n(G)$
-torsor.
Proposition 5.7. Set
![]() $w \in \sigma \cap N$
. Then there exist
$w \in \sigma \cap N$
. Then there exist
![]() $n^{\prime }_w, j^{\prime }_w \in \mathbb {N}$
such that for all
$n^{\prime }_w, j^{\prime }_w \in \mathbb {N}$
such that for all
![]() $n \geq n^{\prime }_w$
, we have an isomorphism of schemes
$n \geq n^{\prime }_w$
, we have an isomorphism of schemes
 $$ \begin{align*} G_n^w / \mathscr{L}_n(G) \cong \mathbb{A}^{j^{\prime}_w}_k. \end{align*} $$
$$ \begin{align*} G_n^w / \mathscr{L}_n(G) \cong \mathbb{A}^{j^{\prime}_w}_k. \end{align*} $$
Proof. Let
![]() $p_1, \dotsc , p_s$
be a set of generators of the semigroup P and set
$p_1, \dotsc , p_s$
be a set of generators of the semigroup P and set
 $$ \begin{align*} n^{\prime}_w = \max_{1\leq i\leq s}( 2 \langle w, p_i \rangle - 1) \end{align*} $$
$$ \begin{align*} n^{\prime}_w = \max_{1\leq i\leq s}( 2 \langle w, p_i \rangle - 1) \end{align*} $$
and
![]() $m = \max _{1\leq i\leq s} \langle w, p_i \rangle $
. Consider the affine space
$m = \max _{1\leq i\leq s} \langle w, p_i \rangle $
. Consider the affine space
![]() $\mathbb {A}_k^{ms}$
with coordinates
$\mathbb {A}_k^{ms}$
with coordinates
 $\left (x^{(i)}_\ell \right )_{i \in \left \{1, \dotsc , s\right \}, \ell \in \left \{1, \dotsc , m\right \}}$
. Let V be the linear subspace of
$\left (x^{(i)}_\ell \right )_{i \in \left \{1, \dotsc , s\right \}, \ell \in \left \{1, \dotsc , m\right \}}$
. Let V be the linear subspace of
![]() $\mathbb {A}_k^{ms}$
defined by the vanishing of all
$\mathbb {A}_k^{ms}$
defined by the vanishing of all
 $x^{(i)}_\ell $
for
$x^{(i)}_\ell $
for
![]() $\ell> \langle w, p_i \rangle $
and the vanishing of all
$\ell> \langle w, p_i \rangle $
and the vanishing of all
 $\sum _{i =1}^s m_i x^{(i)}_\ell $
for all
$\sum _{i =1}^s m_i x^{(i)}_\ell $
for all
![]() $\ell \in \{1, \dotsc , m\}$
and all
$\ell \in \{1, \dotsc , m\}$
and all
![]() $m_1, \dotsc , m_s \in \mathbb {Z}$
such that
$m_1, \dotsc , m_s \in \mathbb {Z}$
such that
 $$ \begin{align*} \sum_{i =1}^s m_i p_i = 0 \in P^{\mathrm{gp}} = M. \end{align*} $$
$$ \begin{align*} \sum_{i =1}^s m_i p_i = 0 \in P^{\mathrm{gp}} = M. \end{align*} $$
Set
![]() $j^{\prime }_w = \dim V$
. It suffices to show that for all
$j^{\prime }_w = \dim V$
. It suffices to show that for all
![]() $n \geq n^{\prime }_w$
, we have that
$n \geq n^{\prime }_w$
, we have that
![]() $G_n^w / \mathscr {L}_n(G) \cong V$
as schemes.
$G_n^w / \mathscr {L}_n(G) \cong V$
as schemes.
Let
![]() $n \geq n^{\prime }_w$
and let H be the closed subgroup of
$n \geq n^{\prime }_w$
and let H be the closed subgroup of
![]() $\mathscr {L}_n(T)$
representing the subgroup object in the statement of Proposition 5.6. By Proposition 5.6, it is sufficient to prove that
$\mathscr {L}_n(T)$
representing the subgroup object in the statement of Proposition 5.6. By Proposition 5.6, it is sufficient to prove that
![]() $H \cong V$
as schemes.
$H \cong V$
as schemes.
Let
![]() $H \to \mathbb {A}^{ms}_k$
be the morphism that, for each k-algebra R, takes
$H \to \mathbb {A}^{ms}_k$
be the morphism that, for each k-algebra R, takes
![]() $h_n \in H(R)$
to
$h_n \in H(R)$
to
 $\left (a^{(i)}_{n-\ell +1}\right )_{i,\ell } \in R^{ms} = \mathbb {A}^{ms}_k(R)$
, where for all
$\left (a^{(i)}_{n-\ell +1}\right )_{i,\ell } \in R^{ms} = \mathbb {A}^{ms}_k(R)$
, where for all
![]() $i,\ell $
we have that
$i,\ell $
we have that
 $a^{(i)}_{n-\ell +1}$
is the coefficient of
$a^{(i)}_{n-\ell +1}$
is the coefficient of
![]() $t^{n-\ell +1}$
in
$t^{n-\ell +1}$
in
![]() $p_i(h_n) \in R[t]/\left (t^{n+1}\right )$
. This morphism
$p_i(h_n) \in R[t]/\left (t^{n+1}\right )$
. This morphism
![]() $H \to \mathbb {A}_k^{ms}$
factors through an isomorphism
$H \to \mathbb {A}_k^{ms}$
factors through an isomorphism
![]() $H \xrightarrow {\sim } V$
by the definition of H, the construction of V and the fact that
$H \xrightarrow {\sim } V$
by the definition of H, the construction of V and the fact that
![]() $n \geq n^{\prime }_w$
implies that for any k-algebra R, any
$n \geq n^{\prime }_w$
implies that for any k-algebra R, any
![]() $m_1, \dotsc , m_s \in \mathbb {Z}$
and any
$m_1, \dotsc , m_s \in \mathbb {Z}$
and any
 $\left (a^{(i)}_{n-\ell +1}\right )_{i,\ell } \in R^{ms}$
, we have that
$\left (a^{(i)}_{n-\ell +1}\right )_{i,\ell } \in R^{ms}$
, we have that
 $$ \begin{align*} \prod_{i = 1}^s &\left( 1 + a^{(i)}_{n-m+1} t^{n-m+1} + \dotsb + a^{(i)}_n t^n \right)^{m_i} \\ &\qquad\qquad\qquad\qquad = 1 + \left( \sum_{i = 1}^s m_i a^{(i)}_{n-m+1} \right) t^{n-m+1} + \dotsb + \left( \sum_{i = 1}^s m_i a^{(i)}_{n} \right) t^{n} \in R[t]/\left(t^{n+1}\right).\\[-48pt] \end{align*} $$
$$ \begin{align*} \prod_{i = 1}^s &\left( 1 + a^{(i)}_{n-m+1} t^{n-m+1} + \dotsb + a^{(i)}_n t^n \right)^{m_i} \\ &\qquad\qquad\qquad\qquad = 1 + \left( \sum_{i = 1}^s m_i a^{(i)}_{n-m+1} \right) t^{n-m+1} + \dotsb + \left( \sum_{i = 1}^s m_i a^{(i)}_{n} \right) t^{n} \in R[t]/\left(t^{n+1}\right).\\[-48pt] \end{align*} $$
5.2 Components of the fibres
In this subsection, we will control fibres of each
![]() $\mathscr {L}_n(\pi ): \mathcal {X} \to X$
by controlling the connected components of the fibres of each map
$\mathscr {L}_n(\pi ): \mathcal {X} \to X$
by controlling the connected components of the fibres of each map
 $\mathscr {L}_n\left (\widetilde {\pi }\right ): \mathscr {L}_n\left (\widetilde {X}\right ) \to \mathscr {L}_n(X)$
. In particular, we will show that for n sufficiently large and
$\mathscr {L}_n\left (\widetilde {\pi }\right ): \mathscr {L}_n\left (\widetilde {X}\right ) \to \mathscr {L}_n(X)$
. In particular, we will show that for n sufficiently large and
![]() $\varphi \in \mathscr {L}(X)$
with
$\varphi \in \mathscr {L}(X)$
with
![]() $\operatorname {\mathrm {trop}}(\varphi )=w \in \sigma \cap N$
, the connected components of
$\operatorname {\mathrm {trop}}(\varphi )=w \in \sigma \cap N$
, the connected components of
![]() $\mathscr {L}_n\left (\widetilde {\pi }\right )^{-1}(\theta _n(\varphi ))$
are indexed by
$\mathscr {L}_n\left (\widetilde {\pi }\right )^{-1}(\theta _n(\varphi ))$
are indexed by
![]() $\beta ^{-1}(w)$
. To do this, we will define analogues of the map
$\beta ^{-1}(w)$
. To do this, we will define analogues of the map
![]() $\operatorname {\mathrm {trop}}$
for the jet schemes
$\operatorname {\mathrm {trop}}$
for the jet schemes
 $\mathscr {L}_n\left (\widetilde {X}\right )$
.
$\mathscr {L}_n\left (\widetilde {X}\right )$
.
For any
![]() $n \in \mathbb {N}$
, let
$n \in \mathbb {N}$
, let
![]() $\mathbb {N}_n = \{0, 1, \dotsc , n, \infty \}$
with the monoid structure making
$\mathbb {N}_n = \{0, 1, \dotsc , n, \infty \}$
with the monoid structure making
 $$ \begin{align*} \mathbb{N} \cup \{\infty\} \to \mathbb{N}_n: \ell \mapsto \begin{cases} \ell, & \ell \leq n, \\ \infty, &\ell> n \end{cases} \end{align*} $$
$$ \begin{align*} \mathbb{N} \cup \{\infty\} \to \mathbb{N}_n: \ell \mapsto \begin{cases} \ell, & \ell \leq n, \\ \infty, &\ell> n \end{cases} \end{align*} $$
a map of monoids. For any
![]() $\widetilde {w} \in \operatorname {\mathrm {Hom}}(F, \mathbb {N} \cup \{\infty \})$
, let
$\widetilde {w} \in \operatorname {\mathrm {Hom}}(F, \mathbb {N} \cup \{\infty \})$
, let
![]() $\widetilde {w}_n \in \operatorname {\mathrm {Hom}}(F, \mathbb {N}_n)$
be the composition of
$\widetilde {w}_n \in \operatorname {\mathrm {Hom}}(F, \mathbb {N}_n)$
be the composition of
![]() $\widetilde {w}: F \to \mathbb {N} \cup \{\infty \}$
with
$\widetilde {w}: F \to \mathbb {N} \cup \{\infty \}$
with
![]() $\mathbb {N} \cup \{\infty \} \to \mathbb {N}_n$
.
$\mathbb {N} \cup \{\infty \} \to \mathbb {N}_n$
.
Remark 5.8. In what follows, for each k-algebra R, each
 $\widetilde {\psi }_n \in \mathscr {L}_n\left (\widetilde {X}\right )(R)$
and each
$\widetilde {\psi }_n \in \mathscr {L}_n\left (\widetilde {X}\right )(R)$
and each
![]() $f \in F$
, let
$f \in F$
, let
 $\widetilde {\psi }_n^*(f) \in R[t]/\left (t^{n+1}\right )$
denote the image of f under the pullback map
$\widetilde {\psi }_n^*(f) \in R[t]/\left (t^{n+1}\right )$
denote the image of f under the pullback map
![]() $ k[F] \to R[t]/\left (t^{n+1}\right )$
corresponding to the jet
$ k[F] \to R[t]/\left (t^{n+1}\right )$
corresponding to the jet
 $\widetilde {\psi }_n: \operatorname {\mathrm {Spec}}\left (R[t]/\left (t^{n+1}\right )\right ) \to \widetilde {X}$
. We use the analogous notation when X and P are in place of
$\widetilde {\psi }_n: \operatorname {\mathrm {Spec}}\left (R[t]/\left (t^{n+1}\right )\right ) \to \widetilde {X}$
. We use the analogous notation when X and P are in place of
![]() $\widetilde {X}$
and F.
$\widetilde {X}$
and F.
For any field extension
![]() $k'$
of k and
$k'$
of k and
 $\widetilde {\psi }_n \in \mathscr {L}_n\left (\widetilde {X}\right )(k')$
, define
$\widetilde {\psi }_n \in \mathscr {L}_n\left (\widetilde {X}\right )(k')$
, define
 $$ \begin{align*} \operatorname{\mathrm{trop}}_n\left(\widetilde{\psi}_n\right) \in \operatorname{\mathrm{Hom}}(F, \mathbb{N}_n) \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{trop}}_n\left(\widetilde{\psi}_n\right) \in \operatorname{\mathrm{Hom}}(F, \mathbb{N}_n) \end{align*} $$
to be the map taking each
![]() $f \in F$
to the t-order of vanishing of
$f \in F$
to the t-order of vanishing of
 $\widetilde {\psi }_n^*(f) \in k'[t]/\left (t^{n+1}\right )$
. Also define the map
$\widetilde {\psi }_n^*(f) \in k'[t]/\left (t^{n+1}\right )$
. Also define the map
 $$ \begin{align*} \operatorname{\mathrm{trop}}_n: \mathscr{L}_n\left(\widetilde{X}\right) \to \operatorname{\mathrm{Hom}}(F, \mathbb{N}_n) \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{trop}}_n: \mathscr{L}_n\left(\widetilde{X}\right) \to \operatorname{\mathrm{Hom}}(F, \mathbb{N}_n) \end{align*} $$
by considering each
 $\widetilde {\psi }_n \in \mathscr {L}\left (\widetilde {X}\right )$
as a point valued in its residue field.
$\widetilde {\psi }_n \in \mathscr {L}\left (\widetilde {X}\right )$
as a point valued in its residue field.
Remark 5.9. As a direct consequence of the definition,
![]() $\operatorname {\mathrm {trop}}_n$
is compatible with field extensions. In other words, for any field extension
$\operatorname {\mathrm {trop}}_n$
is compatible with field extensions. In other words, for any field extension
![]() $k'$
of k and
$k'$
of k and
 $\widetilde {\psi }_n \in \mathscr {L}_n\left (\widetilde {X}\right )(k')$
, we have that
$\widetilde {\psi }_n \in \mathscr {L}_n\left (\widetilde {X}\right )(k')$
, we have that
 $\operatorname {\mathrm {trop}}_n\left (\widetilde {\psi }_n\right )$
is equal to
$\operatorname {\mathrm {trop}}_n\left (\widetilde {\psi }_n\right )$
is equal to
![]() $\operatorname {\mathrm {trop}}_n$
applied to the image of
$\operatorname {\mathrm {trop}}_n$
applied to the image of
![]() $\widetilde {\psi }_n$
in the underlying set of
$\widetilde {\psi }_n$
in the underlying set of
 $\mathscr {L}_n\left (\widetilde {X}\right )$
.
$\mathscr {L}_n\left (\widetilde {X}\right )$
.
Remark 5.10. For any
 $\widetilde {\psi } \in \mathscr {L}\left (\widetilde {X}\right )(k')$
,
$\widetilde {\psi } \in \mathscr {L}\left (\widetilde {X}\right )(k')$
,
 $$ \begin{align*} \left(\operatorname{\mathrm{trop}}\left(\widetilde{\psi}\right)\right)_n = \operatorname{\mathrm{trop}}_n\left(\theta_n\left(\widetilde{\psi}\right)\right). \end{align*} $$
$$ \begin{align*} \left(\operatorname{\mathrm{trop}}\left(\widetilde{\psi}\right)\right)_n = \operatorname{\mathrm{trop}}_n\left(\theta_n\left(\widetilde{\psi}\right)\right). \end{align*} $$
Note that because
![]() $\widetilde {X}$
is an affine space and thus is smooth, all jets of
$\widetilde {X}$
is an affine space and thus is smooth, all jets of
![]() $\widetilde {X}$
are truncations of arcs of
$\widetilde {X}$
are truncations of arcs of
![]() $\widetilde {X}$
, so this equality in fact determines
$\widetilde {X}$
, so this equality in fact determines
![]() $\operatorname {\mathrm {trop}}_n$
.
$\operatorname {\mathrm {trop}}_n$
.
We next stratify the fibre of
![]() $\mathscr {L}_n\left (\widetilde {\pi }\right )$
according to the value of
$\mathscr {L}_n\left (\widetilde {\pi }\right )$
according to the value of
![]() $\operatorname {\mathrm {trop}}_n$
. We show that for n sufficiently large, each stratum is a union of connected components.
$\operatorname {\mathrm {trop}}_n$
. We show that for n sufficiently large, each stratum is a union of connected components.
Lemma 5.11. For each
![]() $f \in F$
, the map
$f \in F$
, the map
 $$ \begin{align*} \mathscr{L}_n\left(\widetilde{X}\right) \to \mathbb{N}_n: \widetilde{\psi}_n \mapsto \left(\operatorname{\mathrm{trop}}_n\left(\widetilde{\psi}_n\right)\right)(f) \end{align*} $$
$$ \begin{align*} \mathscr{L}_n\left(\widetilde{X}\right) \to \mathbb{N}_n: \widetilde{\psi}_n \mapsto \left(\operatorname{\mathrm{trop}}_n\left(\widetilde{\psi}_n\right)\right)(f) \end{align*} $$
is upper semicontinuous.
Proof. Since
![]() $\widetilde {X}$
is affine,
$\widetilde {X}$
is affine,
 $\mathscr {L}_n\left (\widetilde {X}\right ) = \operatorname {\mathrm {Spec}}(R)$
for some k-algebra R. Let
$\mathscr {L}_n\left (\widetilde {X}\right ) = \operatorname {\mathrm {Spec}}(R)$
for some k-algebra R. Let
![]() $\Psi $
be the universal family of
$\Psi $
be the universal family of
 $\mathscr {L}_n\left (\widetilde {X}\right )$
– that is, let
$\mathscr {L}_n\left (\widetilde {X}\right )$
– that is, let
 $$ \begin{align*} \Psi: \operatorname{\mathrm{Spec}}\left(R[t]/\left(t^{n+1}\right)\right) \to \widetilde{X} \end{align*} $$
$$ \begin{align*} \Psi: \operatorname{\mathrm{Spec}}\left(R[t]/\left(t^{n+1}\right)\right) \to \widetilde{X} \end{align*} $$
be the R-valued jet corresponding to the identity
 $\operatorname {\mathrm {Spec}}(R) = \mathscr {L}_n\left (\widetilde {X}\right )$
, and let
$\operatorname {\mathrm {Spec}}(R) = \mathscr {L}_n\left (\widetilde {X}\right )$
, and let
![]() $\Psi ^*(f) \in R[t]/\left (t^{n+1}\right )$
be the result of pulling back f along
$\Psi ^*(f) \in R[t]/\left (t^{n+1}\right )$
be the result of pulling back f along
![]() $\Psi $
. Write
$\Psi $
. Write
where
![]() $a_0, \dotsc , a_n \in R$
. Then the jets
$a_0, \dotsc , a_n \in R$
. Then the jets
 $\widetilde {\psi }_n \in \mathscr {L}_n\left (\widetilde {X}\right )$
with
$\widetilde {\psi }_n \in \mathscr {L}_n\left (\widetilde {X}\right )$
with
 $\left (\operatorname {\mathrm {trop}}_n\left (\widetilde {\psi }_n\right )\right )(f) \geq \ell $
are exactly the points of
$\left (\operatorname {\mathrm {trop}}_n\left (\widetilde {\psi }_n\right )\right )(f) \geq \ell $
are exactly the points of
![]() $\operatorname {\mathrm {Spec}}(R)$
where
$\operatorname {\mathrm {Spec}}(R)$
where
![]() $a_0, \dotsc , a_{\ell -1}$
vanish.
$a_0, \dotsc , a_{\ell -1}$
vanish.
Proposition 5.12. Set
![]() $w \in \sigma \cap N$
. Then there exists some
$w \in \sigma \cap N$
. Then there exists some
![]() $n_0 \in \mathbb {N}$
such that for any
$n_0 \in \mathbb {N}$
such that for any
![]() $n \geq n_0$
, any field extension
$n \geq n_0$
, any field extension
![]() $k'$
of k and any
$k'$
of k and any
![]() $\varphi \in \mathscr {L}(X)(k')$
with
$\varphi \in \mathscr {L}(X)(k')$
with
![]() $\operatorname {\mathrm {trop}}(\varphi ) =w$
, we have that the restriction of
$\operatorname {\mathrm {trop}}(\varphi ) =w$
, we have that the restriction of
 $\operatorname {\mathrm {trop}}_n: \mathscr {L}_n\left (\widetilde {X}\right ) \to \operatorname {\mathrm {Hom}}(F, \mathbb {N}_n)$
to the fibre
$\operatorname {\mathrm {trop}}_n: \mathscr {L}_n\left (\widetilde {X}\right ) \to \operatorname {\mathrm {Hom}}(F, \mathbb {N}_n)$
to the fibre
![]() $\mathscr {L}_n\left (\widetilde {\pi }\right )^{-1}(\theta _n(\varphi ))$
is locally constant.
$\mathscr {L}_n\left (\widetilde {\pi }\right )^{-1}(\theta _n(\varphi ))$
is locally constant.
Proof. Set
![]() $f \in F$
. We will show that there exists some
$f \in F$
. We will show that there exists some
![]() $n_f \in \mathbb {N}$
such that for any
$n_f \in \mathbb {N}$
such that for any
![]() $n \geq n_f$
, any field extension
$n \geq n_f$
, any field extension
![]() $k'$
of k and any
$k'$
of k and any
![]() $\varphi \in \mathscr {L}(X)(k')$
with
$\varphi \in \mathscr {L}(X)(k')$
with
![]() $\operatorname {\mathrm {trop}}(\varphi ) =w$
, we have that the restriction of
$\operatorname {\mathrm {trop}}(\varphi ) =w$
, we have that the restriction of
 $$ \begin{align*} \mathscr{L}_n\left(\widetilde{X}\right) \to \mathbb{N}_n : \widetilde{\psi}_n \mapsto \left(\operatorname{\mathrm{trop}}_n\left(\widetilde{\psi}_n\right)\right)(f) \end{align*} $$
$$ \begin{align*} \mathscr{L}_n\left(\widetilde{X}\right) \to \mathbb{N}_n : \widetilde{\psi}_n \mapsto \left(\operatorname{\mathrm{trop}}_n\left(\widetilde{\psi}_n\right)\right)(f) \end{align*} $$
to the fibre
![]() $\mathscr {L}_n\left (\widetilde {\pi }\right )^{-1}(\theta _n(\varphi ))$
is locally constant.
$\mathscr {L}_n\left (\widetilde {\pi }\right )^{-1}(\theta _n(\varphi ))$
is locally constant.
By Proposition 2.14, there exists some
![]() $f' \in F$
such that
$f' \in F$
such that
![]() $f + f' \in P$
. Set
$f + f' \in P$
. Set
Let
![]() $n \geq n_f$
, let
$n \geq n_f$
, let
![]() $k'$
be a field extension of k and let
$k'$
be a field extension of k and let
![]() $\varphi \in \mathscr {L}(X)(k')$
with
$\varphi \in \mathscr {L}(X)(k')$
with
![]() $\operatorname {\mathrm {trop}}(\varphi )=w$
. Since
$\operatorname {\mathrm {trop}}(\varphi )=w$
. Since
 $\mathscr {L}_n\left (\widetilde {\pi }\right ): \mathscr {L}_n\left (\widetilde {X}\right ) \to \mathscr {L}_n(X)$
is finite type, it is sufficient to show that on any irreducible component C of the fibre
$\mathscr {L}_n\left (\widetilde {\pi }\right ): \mathscr {L}_n\left (\widetilde {X}\right ) \to \mathscr {L}_n(X)$
is finite type, it is sufficient to show that on any irreducible component C of the fibre
![]() $\mathscr {L}_n\left (\widetilde {\pi }\right )^{-1}(\theta _n(\varphi ))$
, the map
$\mathscr {L}_n\left (\widetilde {\pi }\right )^{-1}(\theta _n(\varphi ))$
, the map
 $$ \begin{align*} \alpha: C \to \mathbb{N}_n : \widetilde{\psi}_n \mapsto \left(\operatorname{\mathrm{trop}}_n\left(\widetilde{\psi}_n\right)\right)(f) \end{align*} $$
$$ \begin{align*} \alpha: C \to \mathbb{N}_n : \widetilde{\psi}_n \mapsto \left(\operatorname{\mathrm{trop}}_n\left(\widetilde{\psi}_n\right)\right)(f) \end{align*} $$
is constant. By Lemma 5.11,
![]() $\alpha $
and the map
$\alpha $
and the map
 $$ \begin{align*} \gamma: C \to \mathbb{N}_n: \widetilde{\psi}_n \mapsto \left(\operatorname{\mathrm{trop}}_n\left(\widetilde{\psi}_n\right)\right)(f') \end{align*} $$
$$ \begin{align*} \gamma: C \to \mathbb{N}_n: \widetilde{\psi}_n \mapsto \left(\operatorname{\mathrm{trop}}_n\left(\widetilde{\psi}_n\right)\right)(f') \end{align*} $$
are upper semicontinuous. Also, for all
![]() $\widetilde {\psi }_n \in C$
,
$\widetilde {\psi }_n \in C$
,
 $$ \begin{align*} \alpha\left(\widetilde{\psi}_n\right) + \gamma\left(\widetilde{\psi}_n\right) = \left(\operatorname{\mathrm{trop}}_n\left(\widetilde{\psi}_n\right)\right)(f + f') = \langle w, f + f'\rangle_n, \end{align*} $$
$$ \begin{align*} \alpha\left(\widetilde{\psi}_n\right) + \gamma\left(\widetilde{\psi}_n\right) = \left(\operatorname{\mathrm{trop}}_n\left(\widetilde{\psi}_n\right)\right)(f + f') = \langle w, f + f'\rangle_n, \end{align*} $$
where
![]() $\langle w, f + f'\rangle _n$
is the image of
$\langle w, f + f'\rangle _n$
is the image of
![]() $\langle w, f+f'\rangle $
in
$\langle w, f+f'\rangle $
in
![]() $\mathbb {N}_n$
. Thus the sum of
$\mathbb {N}_n$
. Thus the sum of
![]() $\alpha $
and
$\alpha $
and
![]() $\gamma $
is a constant function. Furthermore, because
$\gamma $
is a constant function. Furthermore, because
![]() $n \geq \langle w, f + f' \rangle $
, the sum of
$n \geq \langle w, f + f' \rangle $
, the sum of
![]() $\alpha $
and
$\alpha $
and
![]() $\gamma $
is not equal to
$\gamma $
is not equal to
![]() $\infty $
. Therefore,
$\infty $
. Therefore,
![]() $\alpha $
is constant by upper semicontinuity of
$\alpha $
is constant by upper semicontinuity of
![]() $\alpha $
and
$\alpha $
and
![]() $\gamma $
and the fact that C is irreducible.
$\gamma $
and the fact that C is irreducible.
Now the proposition is obtained by taking
![]() $n_0$
to be larger than all
$n_0$
to be larger than all
![]() $n_f$
as f vary over the minimal generators of F.
$n_f$
as f vary over the minimal generators of F.
For any
![]() $n \in \mathbb {N}$
, any
$n \in \mathbb {N}$
, any
![]() $\widetilde {w} \in \widetilde {\sigma } \cap \widetilde {N}$
, any field extension
$\widetilde {w} \in \widetilde {\sigma } \cap \widetilde {N}$
, any field extension
![]() $k'$
of k and any
$k'$
of k and any
![]() $\varphi \in \mathscr {L}(X)(k')$
, let
$\varphi \in \mathscr {L}(X)(k')$
, let
![]() $C_n^{\widetilde {w}}(\varphi )$
denote the locus in
$C_n^{\widetilde {w}}(\varphi )$
denote the locus in
![]() $\mathscr {L}_n\left (\widetilde {\pi }\right )^{-1}(\theta _n(\varphi ))$
where
$\mathscr {L}_n\left (\widetilde {\pi }\right )^{-1}(\theta _n(\varphi ))$
where
![]() $\operatorname {\mathrm {trop}}_n$
is equal to
$\operatorname {\mathrm {trop}}_n$
is equal to
![]() $\widetilde {w}_n$
. We will be interested in the case where
$\widetilde {w}_n$
. We will be interested in the case where
![]() $C_n^{\widetilde {w}}(\varphi )$
is a union of connected components of
$C_n^{\widetilde {w}}(\varphi )$
is a union of connected components of
![]() $\mathscr {L}_n\left (\widetilde {\pi }\right )^{-1}(\theta _n(\varphi ))$
. In that case, we will give
$\mathscr {L}_n\left (\widetilde {\pi }\right )^{-1}(\theta _n(\varphi ))$
. In that case, we will give
![]() $C_n^{\widetilde {w}}(\varphi )$
its reduced scheme structure.
$C_n^{\widetilde {w}}(\varphi )$
its reduced scheme structure.
Proposition 5.13. Set
![]() $w \in \sigma \cap N$
. Then there exists some
$w \in \sigma \cap N$
. Then there exists some
![]() $n_1 \in \mathbb {N}$
such that for any
$n_1 \in \mathbb {N}$
such that for any
![]() $n \geq n_1$
, any field extension
$n \geq n_1$
, any field extension
![]() $k'$
of k, any
$k'$
of k, any
![]() $\varphi \in \mathscr {L}(X)(k')$
with
$\varphi \in \mathscr {L}(X)(k')$
with
![]() $\operatorname {\mathrm {trop}}(\varphi ) = w$
and any
$\operatorname {\mathrm {trop}}(\varphi ) = w$
and any
![]() $\widetilde {w} \in \beta ^{-1}(w)$
,
$\widetilde {w} \in \beta ^{-1}(w)$
,
-
1.
 $C_n^{\widetilde {w}}(\varphi )$
is a union of connected components of
$C_n^{\widetilde {w}}(\varphi )$
is a union of connected components of
 $\mathscr {L}_n\left (\widetilde {\pi }\right )^{-1}(\theta _n(\varphi ))$
, and we have an isomorphism of schemes
$\mathscr {L}_n\left (\widetilde {\pi }\right )^{-1}(\theta _n(\varphi ))$
, and we have an isomorphism of schemes  $$ \begin{align*} \mathscr{L}_n\left(\widetilde{\pi}\right)^{-1}(\theta_n(\varphi))_{\mathrm{red}} \cong \bigsqcup_{\widetilde{w}' \in \beta^{-1}(w)} C_n^{\widetilde{w}'}(\varphi); \end{align*} $$
$$ \begin{align*} \mathscr{L}_n\left(\widetilde{\pi}\right)^{-1}(\theta_n(\varphi))_{\mathrm{red}} \cong \bigsqcup_{\widetilde{w}' \in \beta^{-1}(w)} C_n^{\widetilde{w}'}(\varphi); \end{align*} $$
-
2.
 $C_n^{\widetilde {w}}(\varphi )$
is invariant under the action of
$C_n^{\widetilde {w}}(\varphi )$
is invariant under the action of
 $G_n^w \otimes _k k'$
on
$G_n^w \otimes _k k'$
on
 $\mathscr {L}_n\left (\widetilde {X}\right ) \otimes _k k'$
;
$\mathscr {L}_n\left (\widetilde {X}\right ) \otimes _k k'$
; -
3. for each field extension
 $k''$
of
$k''$
of
 $k'$
, the action of
$k'$
, the action of
 $\left (G_n^w \otimes _k k'\right )(k'')$
on
$\left (G_n^w \otimes _k k'\right )(k'')$
on
 $C_n^{\widetilde {w}}(\varphi )(k'')$
is transitive; and
$C_n^{\widetilde {w}}(\varphi )(k'')$
is transitive; and -
4. for each field extension
 $k''$
of
$k''$
of
 $k'$
, the scheme-theoretic stabiliser of any
$k'$
, the scheme-theoretic stabiliser of any
 $k''$
-point of
$k''$
-point of
 $C_n^{\widetilde {w}}(\varphi )$
under the
$C_n^{\widetilde {w}}(\varphi )$
under the
 $G_n^w \otimes _k k'$
-action is equal to
$G_n^w \otimes _k k'$
-action is equal to
 $H_n^{\widetilde {w}} \otimes _k k''$
.
$H_n^{\widetilde {w}} \otimes _k k''$
.
Remark 5.14. In the statement of Proposition 5.13, the action of
![]() $G_n^w$
on
$G_n^w$
on
 $\mathscr {L}_n\left (\widetilde {X}\right )$
is the one induced by the inclusion
$\mathscr {L}_n\left (\widetilde {X}\right )$
is the one induced by the inclusion
![]() $G_n^w \hookrightarrow \widetilde {T}$
and the functor
$G_n^w \hookrightarrow \widetilde {T}$
and the functor
![]() $\mathscr {L}_n$
applied to the toric action
$\mathscr {L}_n$
applied to the toric action
![]() $\widetilde {T} \times _k \widetilde {X} \to \widetilde {X}$
.
$\widetilde {T} \times _k \widetilde {X} \to \widetilde {X}$
.
Proof. Let
![]() $f_1, \dotsc , f_r$
be the minimal generators of F, and let
$f_1, \dotsc , f_r$
be the minimal generators of F, and let
![]() $p_1, \dotsc , p_s$
be a set of generators for the semigroup P. Let
$p_1, \dotsc , p_s$
be a set of generators for the semigroup P. Let
![]() $n_0 \in \mathbb {N}$
be as in the statement of Proposition 5.12, and let
$n_0 \in \mathbb {N}$
be as in the statement of Proposition 5.12, and let
![]() $n_1 \geq n_0$
be such that
$n_1 \geq n_0$
be such that
![]() $n_1 \geq \langle w, p_i \rangle $
for all
$n_1 \geq \langle w, p_i \rangle $
for all
![]() $i \in \{1, \dotsc , s\}$
and
$i \in \{1, \dotsc , s\}$
and
![]() $n_1 \geq \langle \widetilde {w}, f_i \rangle $
for all
$n_1 \geq \langle \widetilde {w}, f_i \rangle $
for all
![]() $i \in \{1, \dotsc , r\}$
and
$i \in \{1, \dotsc , r\}$
and
![]() $\widetilde {w} \in \beta ^{-1}(w)$
. Note that we can choose such an
$\widetilde {w} \in \beta ^{-1}(w)$
. Note that we can choose such an
![]() $n_1$
by Proposition 2.15.
$n_1$
by Proposition 2.15.
Let
![]() $n \geq n_1$
, let
$n \geq n_1$
, let
![]() $k'$
be a field extension of k and set
$k'$
be a field extension of k and set
![]() $\varphi \in \mathscr {L}(X)(k')$
with
$\varphi \in \mathscr {L}(X)(k')$
with
![]() $\operatorname {\mathrm {trop}}(\varphi )= w$
. We begin by proving the first part of the proposition.
$\operatorname {\mathrm {trop}}(\varphi )= w$
. We begin by proving the first part of the proposition.
-
1. By our choice of
 $n_0$
and Proposition 5.12,
$n_0$
and Proposition 5.12,
 $C_n^{\widetilde {w}}(\varphi )$
is a union of connected components of
$C_n^{\widetilde {w}}(\varphi )$
is a union of connected components of
 $\mathscr {L}_n\left (\widetilde {\pi }\right )^{-1}(\theta _n(\varphi ))$
, so it suffices to prove that
$\mathscr {L}_n\left (\widetilde {\pi }\right )^{-1}(\theta _n(\varphi ))$
, so it suffices to prove that
 $\mathscr {L}_n\left (\widetilde {\pi }\right )^{-1}(\theta _n(\varphi ))$
and
$\mathscr {L}_n\left (\widetilde {\pi }\right )^{-1}(\theta _n(\varphi ))$
and
 $\bigsqcup _{\widetilde {w}' \in \beta ^{-1}(w)} C_n^{\widetilde {w}'}(\varphi )$
are equal as sets.
$\bigsqcup _{\widetilde {w}' \in \beta ^{-1}(w)} C_n^{\widetilde {w}'}(\varphi )$
are equal as sets.Set
 $\widetilde {w} \in \widetilde {\sigma } \cap \widetilde {N}$
. We first show that if
$\widetilde {w} \in \widetilde {\sigma } \cap \widetilde {N}$
. We first show that if
 $C_n^{\widetilde {w}}\neq \emptyset $
, then
$C_n^{\widetilde {w}}\neq \emptyset $
, then
 $\widetilde {w} \in \beta ^{-1}(w)$
. If
$\widetilde {w} \in \beta ^{-1}(w)$
. If
 $\widetilde {\psi }_n \in \mathscr {L}_n\left (\widetilde {\pi }\right )^{-1}(\theta _n(\varphi ))$
, then for all
$\widetilde {\psi }_n \in \mathscr {L}_n\left (\widetilde {\pi }\right )^{-1}(\theta _n(\varphi ))$
, then for all
 $i \in \{1, \dotsc , s\}$
, where
$i \in \{1, \dotsc , s\}$
, where $$ \begin{align*} \left(\operatorname{\mathrm{trop}}_n\left(\widetilde{\psi}_n\right)\right)(p_i) = \langle w, p_i \rangle_n, \end{align*} $$
$$ \begin{align*} \left(\operatorname{\mathrm{trop}}_n\left(\widetilde{\psi}_n\right)\right)(p_i) = \langle w, p_i \rangle_n, \end{align*} $$
 $\langle w, p_i \rangle _n$
is the image of
$\langle w, p_i \rangle _n$
is the image of
 $\langle w, p_i \rangle $
in
$\langle w, p_i \rangle $
in
 $\mathbb {N}_n$
. Since
$\mathbb {N}_n$
. Since
 $n \geq n_1 \geq \langle w, p_i \rangle $
, this implies that if
$n \geq n_1 \geq \langle w, p_i \rangle $
, this implies that if
 $\widetilde {\psi }_n \in C_n^{\widetilde {w}}$
, then
$\widetilde {\psi }_n \in C_n^{\widetilde {w}}$
, then
 $\left \langle \widetilde {w}, p_i \right \rangle = \langle w, p_i \rangle $
for all
$\left \langle \widetilde {w}, p_i \right \rangle = \langle w, p_i \rangle $
for all
 $i \in \{1, \dotsc , s\}$
, and so
$i \in \{1, \dotsc , s\}$
, and so
 $\beta \left (\widetilde {w}\right ) = w$
.
$\beta \left (\widetilde {w}\right ) = w$
.
Having shown
 $C_n^{\widetilde {w}}(\varphi )=\emptyset $
whenever
$C_n^{\widetilde {w}}(\varphi )=\emptyset $
whenever
 $\widetilde {w} \notin \beta ^{-1}(w)$
, we need only show that if
$\widetilde {w} \notin \beta ^{-1}(w)$
, we need only show that if
 $\widetilde {w}_1, \widetilde {w}_2$
are distinct elements of
$\widetilde {w}_1, \widetilde {w}_2$
are distinct elements of
 $\beta ^{-1}(w)$
; then
$\beta ^{-1}(w)$
; then
 $\left (\widetilde {w}_1\right )_n \neq \left (\widetilde {w}_2\right )_n$
. This follows from the fact that for each
$\left (\widetilde {w}_1\right )_n \neq \left (\widetilde {w}_2\right )_n$
. This follows from the fact that for each
 $i \in \{1, \dotsc , r\}$
and
$i \in \{1, \dotsc , r\}$
and
 $\widetilde {w} \in \beta ^{-1}(w)$
,
$\widetilde {w} \in \beta ^{-1}(w)$
,  $$ \begin{align*} \left\langle \widetilde{w}, f_i \right\rangle \leq n_1 \leq n. \end{align*} $$
$$ \begin{align*} \left\langle \widetilde{w}, f_i \right\rangle \leq n_1 \leq n. \end{align*} $$
For the rest of this proof, set
![]() $\widetilde {w} \in \beta ^{-1}(w)$
and set the following notation: for each field extension
$\widetilde {w} \in \beta ^{-1}(w)$
and set the following notation: for each field extension
![]() $k''$
of
$k''$
of
![]() $k'$
, let
$k'$
, let
![]() $\varphi _{n, k''} \in \mathscr {L}_n(X)(k'')$
be the composition
$\varphi _{n, k''} \in \mathscr {L}_n(X)(k'')$
be the composition
 $$ \begin{align*} \operatorname{\mathrm{Spec}}\left(k''[t]/\left(t^{n+1}\right)\right) \to \operatorname{\mathrm{Spec}}\left(k'[t]/\left(t^{n+1}\right)\right) \xrightarrow{\theta_n\left(\varphi\right)} X, \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{Spec}}\left(k''[t]/\left(t^{n+1}\right)\right) \to \operatorname{\mathrm{Spec}}\left(k'[t]/\left(t^{n+1}\right)\right) \xrightarrow{\theta_n\left(\varphi\right)} X, \end{align*} $$
where the map
![]() $\operatorname {\mathrm {Spec}}\left (k''[t]/t^{n+1}\right ) \to \operatorname {\mathrm {Spec}}\left (k'[t]/t^{n+1}\right )$
is given by the
$\operatorname {\mathrm {Spec}}\left (k''[t]/t^{n+1}\right ) \to \operatorname {\mathrm {Spec}}\left (k'[t]/t^{n+1}\right )$
is given by the
![]() $k'$
-algebra map
$k'$
-algebra map
![]() $k'[t]/\left (t^{n+1}\right ) \to k''[t]/\left (t^{n+1}\right ): t \mapsto t$
. Note that the
$k'[t]/\left (t^{n+1}\right ) \to k''[t]/\left (t^{n+1}\right ): t \mapsto t$
. Note that the
![]() $k''$
-points of
$k''$
-points of
![]() $C_n^{\widetilde {w}}(\varphi )$
are precisely those
$C_n^{\widetilde {w}}(\varphi )$
are precisely those
 $\widetilde {\psi }_n: \operatorname {\mathrm {Spec}}\left (k''[t]/\left (t^{n+1}\right )\right ) \to \widetilde {X}$
such that
$\widetilde {\psi }_n: \operatorname {\mathrm {Spec}}\left (k''[t]/\left (t^{n+1}\right )\right ) \to \widetilde {X}$
such that
 $\operatorname {\mathrm {trop}}_n\left (\widetilde {\psi }_n\right ) = \widetilde {w}_n$
and the composition
$\operatorname {\mathrm {trop}}_n\left (\widetilde {\psi }_n\right ) = \widetilde {w}_n$
and the composition
 $ \operatorname {\mathrm {Spec}}\left (k''[t]/\left (t^{n+1}\right )\right ) \xrightarrow {\widetilde {\psi }_n} \widetilde {X} \to X$
is equal to
$ \operatorname {\mathrm {Spec}}\left (k''[t]/\left (t^{n+1}\right )\right ) \xrightarrow {\widetilde {\psi }_n} \widetilde {X} \to X$
is equal to
![]() $\varphi _{n,k''}$
. We now prove the remaining parts of the proposition.
$\varphi _{n,k''}$
. We now prove the remaining parts of the proposition.
-
2. Since
 $C_n^{\widetilde {w}}(\varphi )$
is reduced by definition, it suffices to show that for each field extension
$C_n^{\widetilde {w}}(\varphi )$
is reduced by definition, it suffices to show that for each field extension
 $k''$
of
$k''$
of
 $k'$
, we have that
$k'$
, we have that
 $C_n^{\widetilde {w}}(\varphi )(k'')$
is invariant under the action of
$C_n^{\widetilde {w}}(\varphi )(k'')$
is invariant under the action of
 $G_n^w(k'')$
on
$G_n^w(k'')$
on
 $\mathscr {L}_n\left (\widetilde {X}\right )(k'')$
.
$\mathscr {L}_n\left (\widetilde {X}\right )(k'')$
.Let
 $k''$
be a field extension of
$k''$
be a field extension of
 $k'$
, set
$k'$
, set
 $\widetilde {\psi }_n \in C_n^{\widetilde {w}}(\varphi )(k'')$
and set
$\widetilde {\psi }_n \in C_n^{\widetilde {w}}(\varphi )(k'')$
and set
 $g_n \in G_n^w(k'')$
. Then for all
$g_n \in G_n^w(k'')$
. Then for all
 $f \in F$
, has the same t-order of vanishing as
$f \in F$
, has the same t-order of vanishing as $$ \begin{align*} \left(g_n \cdot \widetilde{\psi}_n\right)^*(f) = g_n^*(f) \widetilde{\psi}_n^*(f) \end{align*} $$
$$ \begin{align*} \left(g_n \cdot \widetilde{\psi}_n\right)^*(f) = g_n^*(f) \widetilde{\psi}_n^*(f) \end{align*} $$
 $\widetilde {\psi }_n^*(f)$
, because
$\widetilde {\psi }_n^*(f)$
, because
 $g_n^*(f) \in k''[t]/\left (t^{n+1}\right )$
is a unit. Thus We also have that for all
$g_n^*(f) \in k''[t]/\left (t^{n+1}\right )$
is a unit. Thus We also have that for all $$ \begin{align*} \operatorname{\mathrm{trop}}_n\left(g_n \cdot \widetilde{\psi}_n\right) = \operatorname{\mathrm{trop}}_n\left(\widetilde{\psi}_n\right) = \widetilde{w}_n. \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{trop}}_n\left(g_n \cdot \widetilde{\psi}_n\right) = \operatorname{\mathrm{trop}}_n\left(\widetilde{\psi}_n\right) = \widetilde{w}_n. \end{align*} $$
 $p \in P$
, where the last equality follows from the definition of
$p \in P$
, where the last equality follows from the definition of $$ \begin{align*} \left(g_n \cdot \widetilde{\psi}_n\right)^*(p) = g_n^*(p) \widetilde{\psi}_n^*(p) = g_n^*(p) \varphi_{n,k''}^*(p) = \varphi_{n,k''}^*(p), \end{align*} $$
$$ \begin{align*} \left(g_n \cdot \widetilde{\psi}_n\right)^*(p) = g_n^*(p) \widetilde{\psi}_n^*(p) = g_n^*(p) \varphi_{n,k''}^*(p) = \varphi_{n,k''}^*(p), \end{align*} $$
 $G_n^w$
and the fact that
$G_n^w$
and the fact that
 $\operatorname {\mathrm {trop}}(\varphi ) = w$
implies that
$\operatorname {\mathrm {trop}}(\varphi ) = w$
implies that
 $\varphi _{n,k''}^*(p)$
is divisible by
$\varphi _{n,k''}^*(p)$
is divisible by
 $t^{\left \langle w, p \right \rangle }$
. Therefore the composition
$t^{\left \langle w, p \right \rangle }$
. Therefore the composition
 $\operatorname {\mathrm {Spec}}\left (k''[t]/\left (t^{n+1}\right )\right ) \xrightarrow {g_n \cdot \widetilde {\psi }_n} \widetilde {X} \to X$
is equal to
$\operatorname {\mathrm {Spec}}\left (k''[t]/\left (t^{n+1}\right )\right ) \xrightarrow {g_n \cdot \widetilde {\psi }_n} \widetilde {X} \to X$
is equal to
 $\varphi _{n,k''}$
. Thus
$\varphi _{n,k''}$
. Thus  $$ \begin{align*} g_n \cdot \widetilde{\psi}_n \in C_n^{\widetilde{w}}(\varphi)(k''). \end{align*} $$
$$ \begin{align*} g_n \cdot \widetilde{\psi}_n \in C_n^{\widetilde{w}}(\varphi)(k''). \end{align*} $$
-
3. Let
 $k''$
be a field extension of
$k''$
be a field extension of
 $k'$
, and set
$k'$
, and set
 $\widetilde {\psi }_n, \widetilde {\psi }^{\prime }_n \in C_n^{\widetilde {w}}(\varphi )(k'')$
. We will first show that there exists some
$\widetilde {\psi }_n, \widetilde {\psi }^{\prime }_n \in C_n^{\widetilde {w}}(\varphi )(k'')$
. We will first show that there exists some
 $g_n \in \mathscr {L}_n\left (\widetilde {T}\right )(k'')$
such that
$g_n \in \mathscr {L}_n\left (\widetilde {T}\right )(k'')$
such that
 $g_n \cdot \widetilde {\psi }_n = \widetilde {\psi }^{\prime }_n$
.
$g_n \cdot \widetilde {\psi }_n = \widetilde {\psi }^{\prime }_n$
.Let
 $f_1, \dotsc , f_r$
be the minimal generators of F. For each
$f_1, \dotsc , f_r$
be the minimal generators of F. For each
 $i \in \{1, \dotsc , r\}$
, we have that
$i \in \{1, \dotsc , r\}$
, we have that
 $\widetilde {\psi }_n^*(f_i)$
and
$\widetilde {\psi }_n^*(f_i)$
and
 $\left (\widetilde {\psi }^{\prime }_n\right )^*(f_i)$
have the same t-order of vanishing because
$\left (\widetilde {\psi }^{\prime }_n\right )^*(f_i)$
have the same t-order of vanishing because
 $\operatorname {\mathrm {trop}}_n\left (\widetilde {\psi }_n\right ) = \widetilde {w} = \operatorname {\mathrm {trop}}_n\left (\widetilde {\psi }^{\prime }_n\right )$
. Thus there exists a unit
$\operatorname {\mathrm {trop}}_n\left (\widetilde {\psi }_n\right ) = \widetilde {w} = \operatorname {\mathrm {trop}}_n\left (\widetilde {\psi }^{\prime }_n\right )$
. Thus there exists a unit
 $g^{(i)} \in k[t]/\left (t^{n+1}\right )$
such that Letting
$g^{(i)} \in k[t]/\left (t^{n+1}\right )$
such that Letting $$ \begin{align*} g^{(i)} \widetilde{\psi}_n^*(f_i) = \left(\widetilde{\psi}^{\prime}_n\right)^*(f_i). \end{align*} $$
$$ \begin{align*} g^{(i)} \widetilde{\psi}_n^*(f_i) = \left(\widetilde{\psi}^{\prime}_n\right)^*(f_i). \end{align*} $$
 $g_n \in \mathscr {L}_n\left (\widetilde {T}\right )(k'')$
be such that
$g_n \in \mathscr {L}_n\left (\widetilde {T}\right )(k'')$
be such that
 $g_n^*(f_i) = g^{(i)}$
for all
$g_n^*(f_i) = g^{(i)}$
for all
 $i \in \{1, \dotsc , r\}$
,
$i \in \{1, \dotsc , r\}$
,  $$ \begin{align*} g_n \cdot \widetilde{\psi}_n = \widetilde{\psi}^{\prime}_n. \end{align*} $$
$$ \begin{align*} g_n \cdot \widetilde{\psi}_n = \widetilde{\psi}^{\prime}_n. \end{align*} $$
Now it suffices to show that if
 $g_n \in \mathscr {L}_n\left (\widetilde {T}\right )(k'')$
and
$g_n \in \mathscr {L}_n\left (\widetilde {T}\right )(k'')$
and
 $\widetilde {\psi }_n$
,
$\widetilde {\psi }_n$
,
 $g_n \cdot \widetilde {\psi }_n \in C_n^{\widetilde {w}}(\varphi )(k'')$
, then
$g_n \cdot \widetilde {\psi }_n \in C_n^{\widetilde {w}}(\varphi )(k'')$
, then
 $g_n \in G_n^w(k'')$
. For all
$g_n \in G_n^w(k'')$
. For all
 $p \in P$
, so because
$p \in P$
, so because $$ \begin{align*} g_n^*(p) \varphi_{n,k''}^*(p) = g_n^*(p) \widetilde{\psi}_n^*(p) = \left(g_n \cdot \widetilde{\psi}_n\right)^*(p) = \varphi_{n,k''}^*(p), \end{align*} $$
$$ \begin{align*} g_n^*(p) \varphi_{n,k''}^*(p) = g_n^*(p) \widetilde{\psi}_n^*(p) = \left(g_n \cdot \widetilde{\psi}_n\right)^*(p) = \varphi_{n,k''}^*(p), \end{align*} $$
 $\varphi _{n,k''}^*(p)$
is a unit multiple of
$\varphi _{n,k''}^*(p)$
is a unit multiple of
 $t^{\left \langle w, p \right \rangle }$
, we have that
$t^{\left \langle w, p \right \rangle }$
, we have that
 $g_n \in G_n^w(k'')$
by definition.
$g_n \in G_n^w(k'')$
by definition.
-
4. Let
 $k''$
be a field extension of
$k''$
be a field extension of
 $k'$
, set
$k'$
, set
 $\widetilde {\psi }_n \in C_n^{\widetilde {w}}(\varphi )(k'')$
, and for any
$\widetilde {\psi }_n \in C_n^{\widetilde {w}}(\varphi )(k'')$
, and for any
 $k''$
-algebra R, let
$k''$
-algebra R, let
 $\widetilde {\psi }_{n,R} \in C_n^{\widetilde {w}}(\varphi )(R)$
be the composition Set
$\widetilde {\psi }_{n,R} \in C_n^{\widetilde {w}}(\varphi )(R)$
be the composition Set $$ \begin{align*} \operatorname{\mathrm{Spec}}\left(R[t]/\left(t^{n+1}\right)\right) \to \operatorname{\mathrm{Spec}}(k''[t]/(t^{n+1})) \xrightarrow{\widetilde{\psi}_n} \widetilde{X}. \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{Spec}}\left(R[t]/\left(t^{n+1}\right)\right) \to \operatorname{\mathrm{Spec}}(k''[t]/(t^{n+1})) \xrightarrow{\widetilde{\psi}_n} \widetilde{X}. \end{align*} $$
 $g_n \in G_n^w(R)$
. Then for each
$g_n \in G_n^w(R)$
. Then for each
 $f \in F$
, we have that
$f \in F$
, we have that
 $\widetilde {\psi }_{n,R}^*(f) \in R[t]/\left (t^{n+1}\right )$
is the product of a unit in
$\widetilde {\psi }_{n,R}^*(f) \in R[t]/\left (t^{n+1}\right )$
is the product of a unit in
 $k''[t]/\left (t^{n+1}\right )$
and
$k''[t]/\left (t^{n+1}\right )$
and
 $t^{\left \langle \widetilde {w}, f\right \rangle }$
, so Therefore
$t^{\left \langle \widetilde {w}, f\right \rangle }$
, so Therefore $$ \begin{align*} g_n^*(f) \widetilde{\psi}_{n,R}^*(f) = \widetilde{\psi}_{n,R}^*(f) \iff g_n^*(f)t^{\left\langle \widetilde{w}, f\right\rangle} = t^{\left\langle \widetilde{w}, f\right\rangle}. \end{align*} $$
$$ \begin{align*} g_n^*(f) \widetilde{\psi}_{n,R}^*(f) = \widetilde{\psi}_{n,R}^*(f) \iff g_n^*(f)t^{\left\langle \widetilde{w}, f\right\rangle} = t^{\left\langle \widetilde{w}, f\right\rangle}. \end{align*} $$
 $g_n$
is in the stabiliser of
$g_n$
is in the stabiliser of
 $\widetilde {\psi }_n$
if and only if
$\widetilde {\psi }_n$
if and only if
 $g_n \in H_n^{\widetilde {w}}(R)$
.
$g_n \in H_n^{\widetilde {w}}(R)$
.
In the next proposition, we use Theorem 4.9 and Proposition 5.13 to control the reduced fibres of each
![]() $\mathscr {L}_n(\pi ): \mathscr {L}_n(\mathcal {X}) \to \mathscr {L}_n(X)$
.
$\mathscr {L}_n(\pi ): \mathscr {L}_n(\mathcal {X}) \to \mathscr {L}_n(X)$
.
Proposition 5.15. Set
![]() $w \in \sigma \cap N$
. Then there exists some
$w \in \sigma \cap N$
. Then there exists some
![]() $n_2 \in \mathbb {N}$
such that for any
$n_2 \in \mathbb {N}$
such that for any
![]() $n \geq n_2$
, any field extension
$n \geq n_2$
, any field extension
![]() $k'$
of k and any
$k'$
of k and any
![]() $\varphi \in \mathscr {L}(X)(k')$
with
$\varphi \in \mathscr {L}(X)(k')$
with
![]() $\operatorname {\mathrm {trop}}(\varphi ) = w$
, we have
$\operatorname {\mathrm {trop}}(\varphi ) = w$
, we have
 $$ \begin{align*} \mathscr{L}_n(\pi)^{-1}(\theta_n(\varphi))_{\mathrm{red}} \cong \left(\bigsqcup_{\widetilde{w} \in \beta^{-1}(w)} \left[\left(G_n^w/\mathscr{L}_n(G)\right) / H_n^{\widetilde{w}}\right]\right) \otimes_k k', \end{align*} $$
$$ \begin{align*} \mathscr{L}_n(\pi)^{-1}(\theta_n(\varphi))_{\mathrm{red}} \cong \left(\bigsqcup_{\widetilde{w} \in \beta^{-1}(w)} \left[\left(G_n^w/\mathscr{L}_n(G)\right) / H_n^{\widetilde{w}}\right]\right) \otimes_k k', \end{align*} $$
where
![]() $H_n^{\widetilde {w}}$
acts on
$H_n^{\widetilde {w}}$
acts on
![]() $G_n^w/\mathscr {L}_n(G)$
via the group homomorphism
$G_n^w/\mathscr {L}_n(G)$
via the group homomorphism
![]() $H_n^{\widetilde {w}} \hookrightarrow G_n^w \to G_n^w/\mathscr {L}_n(G)$
and left multiplication.
$H_n^{\widetilde {w}} \hookrightarrow G_n^w \to G_n^w/\mathscr {L}_n(G)$
and left multiplication.
Proof. Let
![]() $f_1, \dotsc , f_r$
be the minimal generators of F. Let
$f_1, \dotsc , f_r$
be the minimal generators of F. Let
![]() $n_1$
be as in the statement of Proposition 5.13, and let
$n_1$
be as in the statement of Proposition 5.13, and let
![]() $n_2 \geq n_1$
be such that
$n_2 \geq n_1$
be such that
![]() $n_2 \geq \max _{i=1}^r\left ( 2\left \langle \widetilde {w}, f_i\right \rangle - 1\right )$
for all
$n_2 \geq \max _{i=1}^r\left ( 2\left \langle \widetilde {w}, f_i\right \rangle - 1\right )$
for all
![]() $\widetilde {w} \in \beta ^{-1}(w)$
. Note that we can choose such an
$\widetilde {w} \in \beta ^{-1}(w)$
. Note that we can choose such an
![]() $n_2$
by Proposition 2.15.
$n_2$
by Proposition 2.15.
Let
![]() $n \geq n_2$
, let
$n \geq n_2$
, let
![]() $k'$
be a field extension of k and let
$k'$
be a field extension of k and let
![]() $\varphi \in \mathscr {L}(X)(k')$
be such that
$\varphi \in \mathscr {L}(X)(k')$
be such that
![]() $\operatorname {\mathrm {trop}}(\varphi ) = w$
. By Corollary 3.22, there exists an isomorphism
$\operatorname {\mathrm {trop}}(\varphi ) = w$
. By Corollary 3.22, there exists an isomorphism
 $\mathscr {L}_n(\mathcal {X}) \xrightarrow {\sim } \left [\mathscr {L}_n\left (\widetilde {X}\right ) / \mathscr {L}_n(G)\right ]$
such that the following diagram commutes:
$\mathscr {L}_n(\mathcal {X}) \xrightarrow {\sim } \left [\mathscr {L}_n\left (\widetilde {X}\right ) / \mathscr {L}_n(G)\right ]$
such that the following diagram commutes:

Therefore
 $$ \begin{align*} \mathscr{L}_n(\pi)^{-1}(\theta_n(\varphi)) \cong \left[\mathscr{L}_n\left(\widetilde{\pi}\right)^{-1}(\theta_n(\varphi)) / (\mathscr{L}_n(G) \otimes_k k')\right], \end{align*} $$
$$ \begin{align*} \mathscr{L}_n(\pi)^{-1}(\theta_n(\varphi)) \cong \left[\mathscr{L}_n\left(\widetilde{\pi}\right)^{-1}(\theta_n(\varphi)) / (\mathscr{L}_n(G) \otimes_k k')\right], \end{align*} $$
where
![]() $\mathscr {L}_n(G) \otimes _k k'$
acts on
$\mathscr {L}_n(G) \otimes _k k'$
acts on
![]() $\mathscr {L}_n\left (\widetilde {\pi }\right )^{-1}(\theta _n(\varphi ))$
by restriction of its action on
$\mathscr {L}_n\left (\widetilde {\pi }\right )^{-1}(\theta _n(\varphi ))$
by restriction of its action on
 $\mathscr {L}_n\left (\widetilde {X}\right ) \otimes _k k'$
, which itself is the action induced by the inclusion
$\mathscr {L}_n\left (\widetilde {X}\right ) \otimes _k k'$
, which itself is the action induced by the inclusion
 $\mathscr {L}_n(G) \hookrightarrow \mathscr {L}_n\left (\widetilde {T}\right )$
and the functor
$\mathscr {L}_n(G) \hookrightarrow \mathscr {L}_n\left (\widetilde {T}\right )$
and the functor
![]() $\mathscr {L}_n$
applied to the toric action
$\mathscr {L}_n$
applied to the toric action
![]() $\widetilde {T} \times _k \widetilde {X} \to \widetilde {X}$
. Thus by Remark 5.4 and Remark 5.14, the action of
$\widetilde {T} \times _k \widetilde {X} \to \widetilde {X}$
. Thus by Remark 5.4 and Remark 5.14, the action of
![]() $\mathscr {L}_n(G) \otimes _k k'$
on
$\mathscr {L}_n(G) \otimes _k k'$
on
![]() $\mathscr {L}_n\left (\widetilde {\pi }\right )^{-1}(\theta _n(\varphi ))$
is the restriction of the action on
$\mathscr {L}_n\left (\widetilde {\pi }\right )^{-1}(\theta _n(\varphi ))$
is the restriction of the action on
 $\mathscr {L}_n\left (\widetilde {X}\right ) \otimes _k k'$
induced by the inclusion
$\mathscr {L}_n\left (\widetilde {X}\right ) \otimes _k k'$
induced by the inclusion
![]() $\mathscr {L}_n(G) \otimes _k k' \hookrightarrow G_n^w \otimes _k k'$
and the action of
$\mathscr {L}_n(G) \otimes _k k' \hookrightarrow G_n^w \otimes _k k'$
and the action of
![]() $G_n^w \otimes _k k'$
on
$G_n^w \otimes _k k'$
on
 $\mathscr {L}_n\left (\widetilde {X}\right ) \otimes _k k'$
. Thus Proposition 5.13(2) implies that for all
$\mathscr {L}_n\left (\widetilde {X}\right ) \otimes _k k'$
. Thus Proposition 5.13(2) implies that for all
![]() $\widetilde {w} \in \beta ^{-1}(w)$
, we have that
$\widetilde {w} \in \beta ^{-1}(w)$
, we have that
![]() $C_n^{\widetilde {w}}(\varphi )$
is invariant under the
$C_n^{\widetilde {w}}(\varphi )$
is invariant under the
![]() $\mathscr {L}_n(G) \otimes _k k'$
action, so by Proposition 5.13(1),
$\mathscr {L}_n(G) \otimes _k k'$
action, so by Proposition 5.13(1),
 $$ \begin{align*} \mathscr{L}_n(\pi)^{-1}(\theta_n(\varphi))_{\mathrm{red}} \cong \bigsqcup_{\widetilde{w} \in \beta^{-1}(w)} \left[C_n^{\widetilde{w}}(\varphi) / (\mathscr{L}_n(G) \otimes_k k') \right]. \end{align*} $$
$$ \begin{align*} \mathscr{L}_n(\pi)^{-1}(\theta_n(\varphi))_{\mathrm{red}} \cong \bigsqcup_{\widetilde{w} \in \beta^{-1}(w)} \left[C_n^{\widetilde{w}}(\varphi) / (\mathscr{L}_n(G) \otimes_k k') \right]. \end{align*} $$
Set
![]() $\widetilde {w} \in \beta ^{-1}(w)$
. It will be sufficient to prove that
$\widetilde {w} \in \beta ^{-1}(w)$
. It will be sufficient to prove that
 $$ \begin{align*} \left[C_n^{\widetilde{w}}(\varphi) / (\mathscr{L}_n(G) \otimes_k k') \right] \cong \left[\left(G_n^w/\mathscr{L}_n(G)\right) / H_n^{\widetilde{w}}\right] \otimes_k k'. \end{align*} $$
$$ \begin{align*} \left[C_n^{\widetilde{w}}(\varphi) / (\mathscr{L}_n(G) \otimes_k k') \right] \cong \left[\left(G_n^w/\mathscr{L}_n(G)\right) / H_n^{\widetilde{w}}\right] \otimes_k k'. \end{align*} $$
We begin by establishing that
![]() $C_n^{\widetilde {w}}(\varphi ) / (\mathscr {L}_n(G') \otimes _k k')$
is an affine scheme with a
$C_n^{\widetilde {w}}(\varphi ) / (\mathscr {L}_n(G') \otimes _k k')$
is an affine scheme with a
![]() $k'$
-point. Since G is a diagonalisable group scheme, we have
$k'$
-point. Since G is a diagonalisable group scheme, we have
![]() $G\cong T' \times _k G'$
, where
$G\cong T' \times _k G'$
, where
![]() $T'$
is a torus and
$T'$
is a torus and
![]() $G'$
is a finite group. This yields an identification
$G'$
is a finite group. This yields an identification
Note that
![]() $\mathscr {L}_n(G')\cong G'$
, since
$\mathscr {L}_n(G')\cong G'$
, since
![]() $G'$
is a finite group. By Proposition 5.5, our choice of
$G'$
is a finite group. By Proposition 5.5, our choice of
![]() $n_2$
and the fact that k has characteristic
$n_2$
and the fact that k has characteristic
![]() $0$
, we then see
$0$
, we then see
 $$ \begin{align*} \{1\}=\mathscr{L}_n(G') \cap H_n^{\widetilde{w}} \subset G_n^w. \end{align*} $$
$$ \begin{align*} \{1\}=\mathscr{L}_n(G') \cap H_n^{\widetilde{w}} \subset G_n^w. \end{align*} $$
Thus Proposition 5.13(4) implies that
![]() $\mathscr {L}_n(G') \otimes _k k'$
acts freely on
$\mathscr {L}_n(G') \otimes _k k'$
acts freely on
![]() $C_n^{\widetilde {w}}(\varphi )$
. Note that
$C_n^{\widetilde {w}}(\varphi )$
. Note that
![]() $C_n^{\widetilde {w}}(\varphi )$
is affine because
$C_n^{\widetilde {w}}(\varphi )$
is affine because
 $\mathscr {L}_n\left (\widetilde {X}\right )$
and
$\mathscr {L}_n\left (\widetilde {X}\right )$
and
![]() $\mathscr {L}_n(X)$
are affine, so
$\mathscr {L}_n(X)$
are affine, so
 $$ \begin{align*} C_n^{\widetilde{w}}(\varphi) / (\mathscr{L}_n(G') \otimes_k k')\longrightarrow \left[C_n^{\widetilde{w}}(\varphi) / (\mathscr{L}_n(G) \otimes_k k') \right] \end{align*} $$
$$ \begin{align*} C_n^{\widetilde{w}}(\varphi) / (\mathscr{L}_n(G') \otimes_k k')\longrightarrow \left[C_n^{\widetilde{w}}(\varphi) / (\mathscr{L}_n(G) \otimes_k k') \right] \end{align*} $$
is an
![]() $(\mathscr {L}_n(T') \otimes _k k')$
-torsor and the source is an affine scheme. By Theorem 4.9, there exists some
$(\mathscr {L}_n(T') \otimes _k k')$
-torsor and the source is an affine scheme. By Theorem 4.9, there exists some
![]() $\psi \in \left (\mathscr {L}(\pi )^{-1}(\varphi )\right )(k')$
with
$\psi \in \left (\mathscr {L}(\pi )^{-1}(\varphi )\right )(k')$
with
![]() $\operatorname {\mathrm {trop}}(\psi ) = \widetilde {w}$
, so
$\operatorname {\mathrm {trop}}(\psi ) = \widetilde {w}$
, so
 $$ \begin{align*} \theta_n(\psi) \in \left[C_n^{\widetilde{w}}(\varphi) / (\mathscr{L}_n(G) \otimes_k k') \right](k'). \end{align*} $$
$$ \begin{align*} \theta_n(\psi) \in \left[C_n^{\widetilde{w}}(\varphi) / (\mathscr{L}_n(G) \otimes_k k') \right](k'). \end{align*} $$
Since
![]() $\mathscr {L}_n(T')$
is a special group by Remark 2.4,
$\mathscr {L}_n(T')$
is a special group by Remark 2.4,
![]() $\theta _n(\psi )$
lifts to a
$\theta _n(\psi )$
lifts to a
![]() $k'$
-point of
$k'$
-point of
![]() $C_n^{\widetilde {w}}(\varphi ) / (\mathscr {L}_n(G') \otimes _k k')$
.
$C_n^{\widetilde {w}}(\varphi ) / (\mathscr {L}_n(G') \otimes _k k')$
.
Next, by Proposition 5.13(2)–(4), the group
![]() $\left (G_n^w / \mathscr {L}_n(G')\right ) \otimes _k k'$
acts transitively on
$\left (G_n^w / \mathscr {L}_n(G')\right ) \otimes _k k'$
acts transitively on
![]() $C_n^{\widetilde {w}}(\varphi ) / (\mathscr {L}_n(G') \otimes _k k')$
, and each
$C_n^{\widetilde {w}}(\varphi ) / (\mathscr {L}_n(G') \otimes _k k')$
, and each
![]() $k'$
-point has stabiliser
$k'$
-point has stabiliser
 $\left (H_n^{\widetilde {w}} / \left (H_n^{\widetilde {w}} \cap \mathscr {L}_n(G')\right ) \right) \otimes _k k'$
, so [Reference Demazure and GabrielDG70, Chapter III, Section 3, Proposition 5.2] gives an
$\left (H_n^{\widetilde {w}} / \left (H_n^{\widetilde {w}} \cap \mathscr {L}_n(G')\right ) \right) \otimes _k k'$
, so [Reference Demazure and GabrielDG70, Chapter III, Section 3, Proposition 5.2] gives an
![]() $(\mathscr {L}_n(T') \otimes _k k')$
-equivariant isomorphism
$(\mathscr {L}_n(T') \otimes _k k')$
-equivariant isomorphism
 $$ \begin{align*} C_n^{\widetilde{w}}(\varphi) / (\mathscr{L}_n(G') \otimes_k k') &\cong \left( C_n^{\widetilde{w}}(\varphi) / (\mathscr{L}_n(G') \otimes_k k') \right)_{\mathrm{red}} \\ &\cong \left( \left(G_n^w / \mathscr{L}_n(G')\right)/\left( H_n^{\widetilde{w}} / \left(H_n^{\widetilde{w}} \cap \mathscr{L}_n(G')\right)\right) \right)\otimes_k k'\\ &\cong \left[\left(G_n^w / H_n^{\widetilde{w}}\right) / \mathscr{L}_n(G')\right] \otimes_k k', \end{align*} $$
$$ \begin{align*} C_n^{\widetilde{w}}(\varphi) / (\mathscr{L}_n(G') \otimes_k k') &\cong \left( C_n^{\widetilde{w}}(\varphi) / (\mathscr{L}_n(G') \otimes_k k') \right)_{\mathrm{red}} \\ &\cong \left( \left(G_n^w / \mathscr{L}_n(G')\right)/\left( H_n^{\widetilde{w}} / \left(H_n^{\widetilde{w}} \cap \mathscr{L}_n(G')\right)\right) \right)\otimes_k k'\\ &\cong \left[\left(G_n^w / H_n^{\widetilde{w}}\right) / \mathscr{L}_n(G')\right] \otimes_k k', \end{align*} $$
where the last isomorphism holds because
![]() $\mathscr {L}_n(G') \cap H_n^{\widetilde {w}} = \{1\}$
. Taking the quotient by
$\mathscr {L}_n(G') \cap H_n^{\widetilde {w}} = \{1\}$
. Taking the quotient by
![]() $\mathscr {L}_n(T') \otimes _k k'$
, we obtain
$\mathscr {L}_n(T') \otimes _k k'$
, we obtain
 $$ \begin{align*} \left[C_n^{\widetilde{w}}(\varphi) / (\mathscr{L}_n(G) \otimes_k k') \right] \cong \left[\left(G_n^w / H_n^{\widetilde{w}}\right) / \mathscr{L}_n(G)\right] \otimes_k k' \cong \left[\left(G_n^w/\mathscr{L}_n(G)\right) / H_n^{\widetilde{w}}\right] \otimes_k k'.\\[-36pt] \end{align*} $$
$$ \begin{align*} \left[C_n^{\widetilde{w}}(\varphi) / (\mathscr{L}_n(G) \otimes_k k') \right] \cong \left[\left(G_n^w / H_n^{\widetilde{w}}\right) / \mathscr{L}_n(G)\right] \otimes_k k' \cong \left[\left(G_n^w/\mathscr{L}_n(G)\right) / H_n^{\widetilde{w}}\right] \otimes_k k'.\\[-36pt] \end{align*} $$
We may now complete the proof of Theorem 5.1.
Proof of Theorem 5.1
Set
![]() $w \in \sigma \cap N$
, let
$w \in \sigma \cap N$
, let
![]() $f_1, \dotsc , f_r$
be the minimal generators of F, let
$f_1, \dotsc , f_r$
be the minimal generators of F, let
![]() $n^{\prime }_w$
and
$n^{\prime }_w$
and
![]() $j^{\prime }_w$
be as in the statement of Proposition 5.7 and let
$j^{\prime }_w$
be as in the statement of Proposition 5.7 and let
![]() $n_2$
be as in the statement of Proposition 5.15. Recalling that
$n_2$
be as in the statement of Proposition 5.15. Recalling that
![]() $\beta ^{-1}(w)$
is a finite set by Proposition 2.15, set
$\beta ^{-1}(w)$
is a finite set by Proposition 2.15, set
 $$ \begin{align*} n_w = \max \left\{ n^{\prime}_w, n_2, 2 \left\langle \widetilde{w}, f_i \right\rangle - 1 \mid i \in \{1, \dotsc, r\}, \widetilde{w} \in \beta^{-1}(w) \right\} \end{align*} $$
$$ \begin{align*} n_w = \max \left\{ n^{\prime}_w, n_2, 2 \left\langle \widetilde{w}, f_i \right\rangle - 1 \mid i \in \{1, \dotsc, r\}, \widetilde{w} \in \beta^{-1}(w) \right\} \end{align*} $$
and
 $$ \begin{align*} \Theta_w = \sum_{\widetilde{w} \in \beta^{-1}(w)} \mathbb{L}^{j^{\prime}_w - \sum_{i=1}^r \left\langle \widetilde{w}, f_i \right\rangle} \in K_0(\mathbf{Stack}_k), \end{align*} $$
$$ \begin{align*} \Theta_w = \sum_{\widetilde{w} \in \beta^{-1}(w)} \mathbb{L}^{j^{\prime}_w - \sum_{i=1}^r \left\langle \widetilde{w}, f_i \right\rangle} \in K_0(\mathbf{Stack}_k), \end{align*} $$
and for each
![]() $n \geq n_w$
, set
$n \geq n_w$
, set
 $$ \begin{align*} \mathcal{F}_n = \bigsqcup_{\widetilde{w} \in \beta^{-1}(w)} \left[\left(G_n^w/\mathscr{L}_n(G)\right) / H_n^{\widetilde{w}}\right]. \end{align*} $$
$$ \begin{align*} \mathcal{F}_n = \bigsqcup_{\widetilde{w} \in \beta^{-1}(w)} \left[\left(G_n^w/\mathscr{L}_n(G)\right) / H_n^{\widetilde{w}}\right]. \end{align*} $$
We now finish proving each part of Theorem 5.1 separately.
-
1. For all
 $n \geq n_w$
, where the second equality follows from Proposition 5.5 and the fact that
$n \geq n_w$
, where the second equality follows from Proposition 5.5 and the fact that $$ \begin{align*} \mathrm{e}(\mathcal{F}_n) &= \sum_{\widetilde{w} \in \beta^{-1}(w)} \mathrm{e}\left.\left(\left[(G_n^w/\mathscr{L}_n(G)\right) / H_n^{\widetilde{w}}\right]\right)\\ &= \sum_{\widetilde{w} \in \beta^{-1}(w)} \mathrm{e}\left(G_n^w / \mathscr{L}_n(G)\right) \mathbb{L}^{-\sum_{i=1}^r \left\langle \widetilde{w}, f_i \right\rangle} = \sum_{\widetilde{w} \in \beta^{-1}(w)} \mathbb{L}^{j^{\prime}_w - \sum_{i=1}^r \left\langle \widetilde{w}, f_i \right\rangle} = \Theta_w, \end{align*} $$
$$ \begin{align*} \mathrm{e}(\mathcal{F}_n) &= \sum_{\widetilde{w} \in \beta^{-1}(w)} \mathrm{e}\left.\left(\left[(G_n^w/\mathscr{L}_n(G)\right) / H_n^{\widetilde{w}}\right]\right)\\ &= \sum_{\widetilde{w} \in \beta^{-1}(w)} \mathrm{e}\left(G_n^w / \mathscr{L}_n(G)\right) \mathbb{L}^{-\sum_{i=1}^r \left\langle \widetilde{w}, f_i \right\rangle} = \sum_{\widetilde{w} \in \beta^{-1}(w)} \mathbb{L}^{j^{\prime}_w - \sum_{i=1}^r \left\langle \widetilde{w}, f_i \right\rangle} = \Theta_w, \end{align*} $$
 $\mathbb {G}_a$
is a special group, and the third equality follows from Proposition 5.7.
$\mathbb {G}_a$
is a special group, and the third equality follows from Proposition 5.7.
-
2. This is Proposition 5.15 – that is, it follows from our choice of
 $n_2$
and each
$n_2$
and each
 $\mathcal {F}_n$
.
$\mathcal {F}_n$
.
6 Gorenstein measure and toric varieties
Set
![]() $d \in \mathbb {N}$
, let
$d \in \mathbb {N}$
, let
![]() $N \cong \mathbb {Z}^d$
be a lattice, let
$N \cong \mathbb {Z}^d$
be a lattice, let
![]() $T = \operatorname {\mathrm {Spec}}(k[N^*])$
be the algebraic torus with cocharacter lattice N, let
$T = \operatorname {\mathrm {Spec}}(k[N^*])$
be the algebraic torus with cocharacter lattice N, let
![]() $\sigma $
be a pointed rational cone in
$\sigma $
be a pointed rational cone in
![]() $N_{\mathbb {R}}$
and let X be the affine T-toric variety associated to
$N_{\mathbb {R}}$
and let X be the affine T-toric variety associated to
![]() $\sigma $
. We assume that X is
$\sigma $
. We assume that X is
![]() $\mathbb {Q}$
-Gorenstein and let
$\mathbb {Q}$
-Gorenstein and let
![]() $m \in \mathbb {Z}_{>0}$
and
$m \in \mathbb {Z}_{>0}$
and
![]() $q \in N^*$
be such that if v is the first lattice point of any ray of
$q \in N^*$
be such that if v is the first lattice point of any ray of
![]() $\sigma $
,
$\sigma $
,
Then
![]() $mK_X$
is Cartier, so we have the ideal sheaf
$mK_X$
is Cartier, so we have the ideal sheaf
![]() $\mathscr {J}_{X,m}$
on X. Also note that any
$\mathscr {J}_{X,m}$
on X. Also note that any
![]() $\mathbb {Q}$
-Gorenstein toric variety has log-terminal singularities [Reference BatyrevBat98, Corollary 4.2], so the Gorenstein measure
$\mathbb {Q}$
-Gorenstein toric variety has log-terminal singularities [Reference BatyrevBat98, Corollary 4.2], so the Gorenstein measure
 $\mu ^{\mathrm {Gor}}_X$
is well defined.
$\mu ^{\mathrm {Gor}}_X$
is well defined.
In this section, we prove Theorem 6.1 about the Gorenstein measure
 $\mu ^{\mathrm {Gor}}_X$
. In section 8, we will use this theorem and Theorem 7.1 to compare
$\mu ^{\mathrm {Gor}}_X$
. In section 8, we will use this theorem and Theorem 7.1 to compare
 $\mu ^{\mathrm {Gor}}_X$
with the motivic measure
$\mu ^{\mathrm {Gor}}_X$
with the motivic measure
![]() $\mu _{\mathcal {X}}$
of the canonical stack
$\mu _{\mathcal {X}}$
of the canonical stack
![]() $\mathcal {X}$
over X.
$\mathcal {X}$
over X.
Although we will only use Theorem 6.1 in the case where
![]() $\sigma $
is d-dimensional, there is no need to make that assumption on
$\sigma $
is d-dimensional, there is no need to make that assumption on
![]() $\sigma $
in this section.
$\sigma $
in this section.
Theorem 6.1. Set
![]() $w \in \sigma \cap N \subset \operatorname {\mathrm {Hom}}(\sigma ^\vee \cap N^*, \mathbb {N} \cup \{\infty \})$
.
$w \in \sigma \cap N \subset \operatorname {\mathrm {Hom}}(\sigma ^\vee \cap N^*, \mathbb {N} \cup \{\infty \})$
.
-
(a) The restriction of
 $\operatorname {\mathrm {ord}}_{\mathscr {J}_{X,m}}$
to
$\operatorname {\mathrm {ord}}_{\mathscr {J}_{X,m}}$
to
 $\operatorname {\mathrm {trop}}^{-1}(w) \subset \mathscr {L}(X)$
is constant and not equal to infinity. In particular, there exists some
$\operatorname {\mathrm {trop}}^{-1}(w) \subset \mathscr {L}(X)$
is constant and not equal to infinity. In particular, there exists some
 $j_w \in \mathbb {Z}$
such that for any measurable subset
$j_w \in \mathbb {Z}$
such that for any measurable subset
 $C \subset \operatorname {\mathrm {trop}}^{-1}(w) \subset \mathscr {L}(X)$
,
$C \subset \operatorname {\mathrm {trop}}^{-1}(w) \subset \mathscr {L}(X)$
,  $$ \begin{align*} \mu^{\mathrm{Gor}}_X(C) = \left(\mathbb{L}^{1/m}\right)^{j_w} \mu_X(C) \in \widehat{\mathscr{M}}_k\left[\mathbb{L}^{1/m}\right]. \end{align*} $$
$$ \begin{align*} \mu^{\mathrm{Gor}}_X(C) = \left(\mathbb{L}^{1/m}\right)^{j_w} \mu_X(C) \in \widehat{\mathscr{M}}_k\left[\mathbb{L}^{1/m}\right]. \end{align*} $$
-
(b) The set
 $\operatorname {\mathrm {trop}}^{-1}(w) \subset \mathscr {L}(X)$
is measurable and
$\operatorname {\mathrm {trop}}^{-1}(w) \subset \mathscr {L}(X)$
is measurable and  $$ \begin{align*} \mu^{\mathrm{Gor}}_X\left(\operatorname{\mathrm{trop}}^{-1}(w)\right) = \mathbb{L}^{-d}(\mathbb{L}-1)^d \left(\mathbb{L}^{1/m}\right)^{- \left\langle w, q \right\rangle} \in \widehat{\mathscr{M}}_k\left[\mathbb{L}^{1/m}\right]. \end{align*} $$
$$ \begin{align*} \mu^{\mathrm{Gor}}_X\left(\operatorname{\mathrm{trop}}^{-1}(w)\right) = \mathbb{L}^{-d}(\mathbb{L}-1)^d \left(\mathbb{L}^{1/m}\right)^{- \left\langle w, q \right\rangle} \in \widehat{\mathscr{M}}_k\left[\mathbb{L}^{1/m}\right]. \end{align*} $$
Remark 6.2. Summing over
![]() $w \in \sigma \cap N$
, Theorem 6.1(b) gives Batyrev’s formula [Reference BatyrevBat98, Theorem 4.3] for the stringy Hodge–Deligne invariant of a toric variety. Furthermore, Theorem 6.1(b) appears to be a special case of [Reference Batyrev and MoreauBM13, Lemma 4.5]. For the benefit of the reader, we include a short self-contained proof.
$w \in \sigma \cap N$
, Theorem 6.1(b) gives Batyrev’s formula [Reference BatyrevBat98, Theorem 4.3] for the stringy Hodge–Deligne invariant of a toric variety. Furthermore, Theorem 6.1(b) appears to be a special case of [Reference Batyrev and MoreauBM13, Lemma 4.5]. For the benefit of the reader, we include a short self-contained proof.
Remark 6.3. When w is an integer combination of lattice points on the rays of
![]() $\sigma $
, we have that
$\sigma $
, we have that
![]() $\langle w, q \rangle $
is divisible by m, so in that case Theorem 6.1(b) implies
$\langle w, q \rangle $
is divisible by m, so in that case Theorem 6.1(b) implies
 $$ \begin{align*} \mu^{\mathrm{Gor}}_X\left(\operatorname{\mathrm{trop}}^{-1}(w)\right) \in \widehat{\mathscr{M}}_k. \end{align*} $$
$$ \begin{align*} \mu^{\mathrm{Gor}}_X\left(\operatorname{\mathrm{trop}}^{-1}(w)\right) \in \widehat{\mathscr{M}}_k. \end{align*} $$
6.1 Gorenstein measure and monomial ideals
For the remainder of this section, let
![]() $M = N^*$
, let
$M = N^*$
, let
![]() $P = \sigma ^\vee \cap M$
, and for each
$P = \sigma ^\vee \cap M$
, and for each
![]() $p \in P$
, let
$p \in P$
, let
![]() $\chi ^p \in k[P]$
be the monomial indexed by p.
$\chi ^p \in k[P]$
be the monomial indexed by p.
If
![]() $\mathscr {J}$
is a nonzero ideal sheaf on X generated by monomials
$\mathscr {J}$
is a nonzero ideal sheaf on X generated by monomials
![]() $\left \{\chi ^{p_i}\right \}_i$
, then for any
$\left \{\chi ^{p_i}\right \}_i$
, then for any
![]() $\varphi \in \mathscr {L}(X)$
with
$\varphi \in \mathscr {L}(X)$
with
![]() $\operatorname {\mathrm {trop}}(\varphi ) = w$
,
$\operatorname {\mathrm {trop}}(\varphi ) = w$
,
 $$ \begin{align*} \operatorname{\mathrm{ord}}_{\mathscr{J}}(\varphi) = \min_i \langle w, p_i \rangle \in \mathbb{Z}_{\geq 0}. \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{ord}}_{\mathscr{J}}(\varphi) = \min_i \langle w, p_i \rangle \in \mathbb{Z}_{\geq 0}. \end{align*} $$
Therefore, to prove Theorem 6.1(a) it is sufficient to show that the ideal
![]() $\mathscr {J}_{X,m}$
is generated by monomials.
$\mathscr {J}_{X,m}$
is generated by monomials.
For the remainder of this subsection, fix a basis
![]() $e_1, \dotsc , e_d$
for M, and for any
$e_1, \dotsc , e_d$
for M, and for any
![]() $p_1, \dotsc , p_d \in P$
, set
$p_1, \dotsc , p_d \in P$
, set
 $$ \begin{align*} c(p_1, \dotsc, p_d) = \det\left( \left(a_{i, j}\right)_{i, j}\right) \in \mathbb{Z}, \end{align*} $$
$$ \begin{align*} c(p_1, \dotsc, p_d) = \det\left( \left(a_{i, j}\right)_{i, j}\right) \in \mathbb{Z}, \end{align*} $$
where the
![]() $a_{i, j} \in \mathbb {Z}$
are such that
$a_{i, j} \in \mathbb {Z}$
are such that
 $p_j = \sum _{i = 1}^d a_{i, j} e_i$
for all
$p_j = \sum _{i = 1}^d a_{i, j} e_i$
for all
![]() $j \in \{1, \dotsc , d\}$
. For any
$j \in \{1, \dotsc , d\}$
. For any
 $\left (p_{i,j}\right )_{i \in \left \{1, \dotsc , m\right \},j \in \left \{1, \dotsc , d\right \}} \in P^{md}$
, set
$\left (p_{i,j}\right )_{i \in \left \{1, \dotsc , m\right \},j \in \left \{1, \dotsc , d\right \}} \in P^{md}$
, set
 $$ \begin{align*} z\left(\left(p_{i,j}\right)_{i,j}\right) = \chi^{-q} \prod_{i = 1}^m c\left(p_{i,1}, \dotsc, p_{i,d}\right) \chi^{p_{i,1} + \dotsb + p_{i,d}} \in k[M]. \end{align*} $$
$$ \begin{align*} z\left(\left(p_{i,j}\right)_{i,j}\right) = \chi^{-q} \prod_{i = 1}^m c\left(p_{i,1}, \dotsc, p_{i,d}\right) \chi^{p_{i,1} + \dotsb + p_{i,d}} \in k[M]. \end{align*} $$
Lemma 6.4. Set
 $\left (p_{i,j}\right )_{i ,j} \in P^{md}$
. Then
$\left (p_{i,j}\right )_{i ,j} \in P^{md}$
. Then
 $$ \begin{align*} z\left(\left(p_{i,j}\right)_{i,j}\right) \in k[P]. \end{align*} $$
$$ \begin{align*} z\left(\left(p_{i,j}\right)_{i,j}\right) \in k[P]. \end{align*} $$
Proof. If
 $-q + \sum _{ i = 1}^m \sum _{j =1}^d p_{i,j} \in P$
, we are done, so we may assume that there exists some first lattice point v of a ray of
$-q + \sum _{ i = 1}^m \sum _{j =1}^d p_{i,j} \in P$
, we are done, so we may assume that there exists some first lattice point v of a ray of
![]() $\sigma $
such that
$\sigma $
such that
 $\left \langle v, -q + \sum _{ i = 1}^m \sum _{j =1}^d p_{i,j} \right \rangle < 0$
. Then
$\left \langle v, -q + \sum _{ i = 1}^m \sum _{j =1}^d p_{i,j} \right \rangle < 0$
. Then
 $$ \begin{align*} 0> \left\langle v, -q + \sum_{ i = 1}^m \sum_{j =1}^d p_{i,j}\right\rangle = \sum_{i =1}^m \left\langle v, -\frac{1}{m} q + \sum_{j =1}^d p_{i,j} \right\rangle = \sum_{i=1}^m \left(-1 + \sum_{j=1}^d \left\langle v, p_{i,j} \right\rangle \right), \end{align*} $$
$$ \begin{align*} 0> \left\langle v, -q + \sum_{ i = 1}^m \sum_{j =1}^d p_{i,j}\right\rangle = \sum_{i =1}^m \left\langle v, -\frac{1}{m} q + \sum_{j =1}^d p_{i,j} \right\rangle = \sum_{i=1}^m \left(-1 + \sum_{j=1}^d \left\langle v, p_{i,j} \right\rangle \right), \end{align*} $$
so for some
![]() $i \in \{1, \dotsc , m\}$
, we have
$i \in \{1, \dotsc , m\}$
, we have
 $\left \langle v, p_{i,j} \right \rangle = 0$
for all
$\left \langle v, p_{i,j} \right \rangle = 0$
for all
![]() $j \in \{1, \dotsc , d\}$
, so
$j \in \{1, \dotsc , d\}$
, so
which implies that
 $z\left (\left (p_{i,j}\right )_{i,j}\right ) = 0 \in k[P]$
.
$z\left (\left (p_{i,j}\right )_{i,j}\right ) = 0 \in k[P]$
.
We now prove the next proposition, which as discussed, immediately implies Theorem 6.1(a). Note that because
![]() $\sigma $
is pointed,
$\sigma $
is pointed,
![]() $P^{\mathrm {gp}} = M$
, so the
$P^{\mathrm {gp}} = M$
, so the
![]() $c(p_1, \dotsc , p_d)$
are not all equal to
$c(p_1, \dotsc , p_d)$
are not all equal to
![]() $0$
and the
$0$
and the
 $z\left (\left (p_{i,j}\right )_{i,j}\right )$
are not all equal to
$z\left (\left (p_{i,j}\right )_{i,j}\right )$
are not all equal to
![]() $0$
.
$0$
.
Proposition 6.5. The ideal
![]() $\mathscr {J}_{X,m}$
is generated by the set
$\mathscr {J}_{X,m}$
is generated by the set
 $$ \begin{align*} \left\{ z\left(\left(p_{i,j}\right)_{i,j}\right) \mid \left(p_{i,j}\right)_{i ,j} \in P^{md}\right\}. \end{align*} $$
$$ \begin{align*} \left\{ z\left(\left(p_{i,j}\right)_{i,j}\right) \mid \left(p_{i,j}\right)_{i ,j} \in P^{md}\right\}. \end{align*} $$
Proof. Since
![]() $k[P]$
is generated over k by the set
$k[P]$
is generated over k by the set
![]() $\{\chi ^p\mid p\in P\}$
, we see that
$\{\chi ^p\mid p\in P\}$
, we see that
 $\Gamma \left (X,\Omega ^d_X\right )$
is generated by the elements
$\Gamma \left (X,\Omega ^d_X\right )$
is generated by the elements
![]() $\chi ^{p_1}\wedge \dotsb \wedge \chi ^{p_d}$
as
$\chi ^{p_1}\wedge \dotsb \wedge \chi ^{p_d}$
as
![]() $p_1,\dotsc ,p_d$
range over elements of P. So
$p_1,\dotsc ,p_d$
range over elements of P. So
 $\Gamma \left (X,\left (\Omega _X^d\right )^{\otimes m}\right )$
is generated by the set
$\Gamma \left (X,\left (\Omega _X^d\right )^{\otimes m}\right )$
is generated by the set
 $$ \begin{align*} \left\{ \bigotimes_{i=1}^m \mathrm{d} \chi^{p_{i,1}} \wedge \dotsb \wedge \mathrm{d} \chi^{p_{i, d}} \mid \left(p_{i,j}\right)_{i ,j} \in P^{md}\right\}. \end{align*} $$
$$ \begin{align*} \left\{ \bigotimes_{i=1}^m \mathrm{d} \chi^{p_{i,1}} \wedge \dotsb \wedge \mathrm{d} \chi^{p_{i, d}} \mid \left(p_{i,j}\right)_{i ,j} \in P^{md}\right\}. \end{align*} $$
We next show that the global sections of
![]() $\omega _{X,m}$
are generated by
$\omega _{X,m}$
are generated by
this is essentially given by [Reference Cox, Little and SchenckCLS11, Proposition 8.2.9], but they only state the result for
![]() $\omega _X$
instead of
$\omega _X$
instead of
![]() $\omega _{X,m}$
. The proof for all m works identically. To see this, let
$\omega _{X,m}$
. The proof for all m works identically. To see this, let
![]() $\iota : X_{\mathrm {sm}} \hookrightarrow X$
be the inclusion of the smooth locus. By [Reference Cox, Little and SchenckCLS11, Theorem 8.2.3],
$\iota : X_{\mathrm {sm}} \hookrightarrow X$
be the inclusion of the smooth locus. By [Reference Cox, Little and SchenckCLS11, Theorem 8.2.3],
 $$ \begin{align*} \omega_{X,m} = \iota_*\left( \left(\Omega_{X_{\mathrm{sm}}}^{\dim X}\right)^{\otimes m} \right)\cong\iota_*\mathcal{O}_{X_{\mathrm{sm}}}\left(-m\sum_\rho D_\rho\right)=\mathcal{O}_X\left(-m\sum_\rho D_\rho\right), \end{align*} $$
$$ \begin{align*} \omega_{X,m} = \iota_*\left( \left(\Omega_{X_{\mathrm{sm}}}^{\dim X}\right)^{\otimes m} \right)\cong\iota_*\mathcal{O}_{X_{\mathrm{sm}}}\left(-m\sum_\rho D_\rho\right)=\mathcal{O}_X\left(-m\sum_\rho D_\rho\right), \end{align*} $$
where the sum runs over all
![]() $\rho \in \Sigma (1)$
and
$\rho \in \Sigma (1)$
and
![]() $D_\rho $
denotes the corresponding torus-invariant divisor. Implicit in [Reference Cox, Little and SchenckCLS11, Theorem 8.2.3] is an identification of
$D_\rho $
denotes the corresponding torus-invariant divisor. Implicit in [Reference Cox, Little and SchenckCLS11, Theorem 8.2.3] is an identification of
 $\Omega _{X_{\mathrm {sm}}}^{\dim X}$
with a subsheaf of
$\Omega _{X_{\mathrm {sm}}}^{\dim X}$
with a subsheaf of
![]() $\mathcal {O}_{X_{\mathrm {sm}}}$
; this identification comes from [Reference Cox, Little and SchenckCLS11, Maps (8.1.3) and (8.1.5)] and can be described as follows. We have an inclusion of
$\mathcal {O}_{X_{\mathrm {sm}}}$
; this identification comes from [Reference Cox, Little and SchenckCLS11, Maps (8.1.3) and (8.1.5)] and can be described as follows. We have an inclusion of
 $\Omega _{X_{\mathrm {sm}}}^{\dim X}$
into the logarithmic differentials
$\Omega _{X_{\mathrm {sm}}}^{\dim X}$
into the logarithmic differentials
 $\Omega _{X_{\mathrm {sm}}}^{\dim X}(\log D)$
, and the latter is isomorphic to
$\Omega _{X_{\mathrm {sm}}}^{\dim X}(\log D)$
, and the latter is isomorphic to
![]() $\mathcal {O}_{X_{\mathrm {sm}}}$
via the map
$\mathcal {O}_{X_{\mathrm {sm}}}$
via the map
 $$ \begin{gather*} \mathcal{O}_{X_{\mathrm{sm}}}\xrightarrow{\cong}\Omega_{X_{\mathrm{sm}}}^{\dim X}(\log D), \\ f\mapsto f\cdot \mathrm{d}\log \chi^{e_1} \wedge \dotsb \wedge \mathrm{d} \log \chi^{e_d}. \end{gather*} $$
$$ \begin{gather*} \mathcal{O}_{X_{\mathrm{sm}}}\xrightarrow{\cong}\Omega_{X_{\mathrm{sm}}}^{\dim X}(\log D), \\ f\mapsto f\cdot \mathrm{d}\log \chi^{e_1} \wedge \dotsb \wedge \mathrm{d} \log \chi^{e_d}. \end{gather*} $$
For each
![]() $\rho \in \Sigma (1)$
, let
$\rho \in \Sigma (1)$
, let
![]() $v_\rho $
denote the first lattice point on the ray
$v_\rho $
denote the first lattice point on the ray
![]() $\rho $
. Having established that
$\rho $
. Having established that
 $\omega _{X,m}\cong \mathcal {O}_X\left (-m\sum _\rho D_\rho \right )$
, [Reference Cox, Little and SchenckCLS11, Proposition 4.3.2] tells us that
$\omega _{X,m}\cong \mathcal {O}_X\left (-m\sum _\rho D_\rho \right )$
, [Reference Cox, Little and SchenckCLS11, Proposition 4.3.2] tells us that
![]() $\Gamma \left (X,\omega _{X,m}\right )$
is generated over k by the sections of the form
$\Gamma \left (X,\omega _{X,m}\right )$
is generated over k by the sections of the form
![]() $\chi ^p \cdot \left ( \mathrm {d}\log \chi ^{e_1} \wedge \dotsb \wedge \mathrm {d} \log \chi ^{e_d} \right )^{\otimes m}$
for
$\chi ^p \cdot \left ( \mathrm {d}\log \chi ^{e_1} \wedge \dotsb \wedge \mathrm {d} \log \chi ^{e_d} \right )^{\otimes m}$
for
![]() $p\in M$
such that
$p\in M$
such that
 $\left \langle p,v_\rho \right \rangle \geq m$
for all
$\left \langle p,v_\rho \right \rangle \geq m$
for all
![]() $\rho \in \Sigma (1)$
. This condition on the inner product implies
$\rho \in \Sigma (1)$
. This condition on the inner product implies
![]() $p-q\in P$
, and so
$p-q\in P$
, and so
![]() $\Gamma \left (X,\omega _{X,m}\right )$
is generated over
$\Gamma \left (X,\omega _{X,m}\right )$
is generated over
![]() $k[P]$
by
$k[P]$
by
Lastly, for any
![]() $p_1, \dotsc , p_d \in P$
,
$p_1, \dotsc , p_d \in P$
,
 $$ \begin{align*} \mathrm{d} \chi^{p_1} \wedge \dotsb \wedge \mathrm{d} \chi^{p_d} &= \chi^{p_1+\dotsb + p_d } \cdot \mathrm{d}\log \chi^{p_1} \wedge \dotsb \wedge \mathrm{d} \log \chi^{p_d}\\ &= c(p_1, \dotsc, p_d) \chi^{p_1+\dotsb + p_d } \cdot \mathrm{d}\log \chi^{e_1} \wedge \dotsb \wedge \mathrm{d} \log \chi^{e_d}. \end{align*} $$
$$ \begin{align*} \mathrm{d} \chi^{p_1} \wedge \dotsb \wedge \mathrm{d} \chi^{p_d} &= \chi^{p_1+\dotsb + p_d } \cdot \mathrm{d}\log \chi^{p_1} \wedge \dotsb \wedge \mathrm{d} \log \chi^{p_d}\\ &= c(p_1, \dotsc, p_d) \chi^{p_1+\dotsb + p_d } \cdot \mathrm{d}\log \chi^{e_1} \wedge \dotsb \wedge \mathrm{d} \log \chi^{e_d}. \end{align*} $$
Thus for any
 $\left (p_{i,j}\right )_{i ,j} \in P^{md}$
,
$\left (p_{i,j}\right )_{i ,j} \in P^{md}$
,
 $$ \begin{align*} \bigotimes_{i=1}^m \mathrm{d} \chi^{p_{i,1}} \wedge \dotsb \wedge \mathrm{d} \chi^{p_{i, d}} = z\left(\left(p_{i,j}\right)_{i,j}\right) \cdot \chi^q \cdot \left( \mathrm{d}\log \chi^{e_1} \wedge \dotsb \wedge \mathrm{d} \log \chi^{e_d} \right)^{\otimes m}. \end{align*} $$
$$ \begin{align*} \bigotimes_{i=1}^m \mathrm{d} \chi^{p_{i,1}} \wedge \dotsb \wedge \mathrm{d} \chi^{p_{i, d}} = z\left(\left(p_{i,j}\right)_{i,j}\right) \cdot \chi^q \cdot \left( \mathrm{d}\log \chi^{e_1} \wedge \dotsb \wedge \mathrm{d} \log \chi^{e_d} \right)^{\otimes m}. \end{align*} $$
The proposition then follows from the definition of
![]() $\mathscr {J}_{X,m}$
.
$\mathscr {J}_{X,m}$
.
Remark 6.6. Proposition 6.5 implies that if
![]() $\varphi \in \mathscr {L}(X)$
with
$\varphi \in \mathscr {L}(X)$
with
![]() $\operatorname {\mathrm {trop}}(\varphi )=w$
, then
$\operatorname {\mathrm {trop}}(\varphi )=w$
, then
 $$ \begin{align*} \operatorname{\mathrm{ord}}_{\mathscr{J}_{X,m}}(\varphi) = - \langle w, q \rangle + \min_{\substack{p_1, \dotsc, p_d \in P\\ c\left(p_1, \dotsc, p_d\right) \neq 0}} m \langle w, p_1 + \dotsb + p_d \rangle, \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{ord}}_{\mathscr{J}_{X,m}}(\varphi) = - \langle w, q \rangle + \min_{\substack{p_1, \dotsc, p_d \in P\\ c\left(p_1, \dotsc, p_d\right) \neq 0}} m \langle w, p_1 + \dotsb + p_d \rangle, \end{align*} $$
so if w is an integer combination of lattice points on the rays of
![]() $\sigma $
, then
$\sigma $
, then
![]() $\operatorname {\mathrm {ord}}_{\mathscr {J}_{X,m}}(\varphi )$
is divisible by m and
$\operatorname {\mathrm {ord}}_{\mathscr {J}_{X,m}}(\varphi )$
is divisible by m and
 $\mu ^{\mathrm {Gor}}_X(C) \in \widehat {\mathscr {M}}_k$
for any measurable subset
$\mu ^{\mathrm {Gor}}_X(C) \in \widehat {\mathscr {M}}_k$
for any measurable subset
![]() $C \subset \operatorname {\mathrm {trop}}^{-1}(w)$
.
$C \subset \operatorname {\mathrm {trop}}^{-1}(w)$
.
6.2 Gorenstein measure and toric modifications
In this subsection, we complete the proof of Theorem 6.1(b). We first handle the case where
![]() $w = 0$
.
$w = 0$
.
Proposition 6.7. We have
 $$ \begin{align*} \mu^{\mathrm{Gor}}_X\left(\operatorname{\mathrm{trop}}^{-1}(0)\right) = \mathbb{L}^{-d}(\mathbb{L} - 1)^d. \end{align*} $$
$$ \begin{align*} \mu^{\mathrm{Gor}}_X\left(\operatorname{\mathrm{trop}}^{-1}(0)\right) = \mathbb{L}^{-d}(\mathbb{L} - 1)^d. \end{align*} $$
Proof. If
![]() $\varphi \in \mathscr {L}(X)$
, then
$\varphi \in \mathscr {L}(X)$
, then
![]() $\operatorname {\mathrm {trop}}(\varphi ) = 0$
if and only if
$\operatorname {\mathrm {trop}}(\varphi ) = 0$
if and only if
![]() $\varphi ^*(p)$
is a unit for all
$\varphi ^*(p)$
is a unit for all
![]() $p \in P$
, which occurs if and only if
$p \in P$
, which occurs if and only if
![]() $\varphi \in \mathscr {L}(T)$
. Thus
$\varphi \in \mathscr {L}(T)$
. Thus
and because T is smooth, we have
 $$ \begin{align*} \mu^{\mathrm{Gor}}_X\left(\operatorname{\mathrm{trop}}^{-1}(0)\right) = \mu_T(\mathscr{L}(T)) = \mathbb{L}^{-\dim T} \mathrm{e}(T) = \mathbb{L}^{-d}(\mathbb{L}-1)^d, \end{align*} $$
$$ \begin{align*} \mu^{\mathrm{Gor}}_X\left(\operatorname{\mathrm{trop}}^{-1}(0)\right) = \mu_T(\mathscr{L}(T)) = \mathbb{L}^{-\dim T} \mathrm{e}(T) = \mathbb{L}^{-d}(\mathbb{L}-1)^d, \end{align*} $$
We now only need to prove Theorem 6.1(b) in the case where
![]() $w \neq 0$
. For the remainder of this section, fix
$w \neq 0$
. For the remainder of this section, fix
![]() $w \in \sigma \cap N$
, assume that
$w \in \sigma \cap N$
, assume that
![]() $w \neq 0$
, and let
$w \neq 0$
, and let
![]() $\ell \in \mathbb {Z}_{>0}$
be such that
$\ell \in \mathbb {Z}_{>0}$
be such that
![]() $(1/\ell )w$
is the first lattice point of the ray
$(1/\ell )w$
is the first lattice point of the ray
![]() $\tau :=\mathbb {R}_{\geq 0} w$
. We will compute
$\tau :=\mathbb {R}_{\geq 0} w$
. We will compute
![]() $\mu _X\left (\operatorname {\mathrm {trop}}^{-1}(w)\right )$
by applying the change-of-variables formula to a certain toric modification of X. Let
$\mu _X\left (\operatorname {\mathrm {trop}}^{-1}(w)\right )$
by applying the change-of-variables formula to a certain toric modification of X. Let
![]() $Y\cong \mathbb {A}^1\times \mathbb {G}_m^{d-1}$
be the affine T-toric variety whose fan is given by
$Y\cong \mathbb {A}^1\times \mathbb {G}_m^{d-1}$
be the affine T-toric variety whose fan is given by
![]() $\tau $
, let D be the (irreducible) boundary divisor of Y and let
$\tau $
, let D be the (irreducible) boundary divisor of Y and let
![]() $\rho : Y \to X$
be the toric morphism induced by the identity map
$\rho : Y \to X$
be the toric morphism induced by the identity map
![]() $N \to N$
. It is standard to compute the relative canonical divisor of such a birational toric morphism. In this case,
$N \to N$
. It is standard to compute the relative canonical divisor of such a birational toric morphism. In this case,
 $$ \begin{align*} mK_{Y} - \rho^* (mK_X) = \left(\frac{1}{\ell}\langle w, q \rangle - m\right)D. \end{align*} $$
$$ \begin{align*} mK_{Y} - \rho^* (mK_X) = \left(\frac{1}{\ell}\langle w, q \rangle - m\right)D. \end{align*} $$
For the remainder of this section, let
![]() $\mathcal {O}(-D)$
be the ideal sheaf of D in Y.
$\mathcal {O}(-D)$
be the ideal sheaf of D in Y.
Proposition 6.8. The map
![]() $\mathscr {L}(\rho ): \mathscr {L}(Y) \to \mathscr {L}(X)$
induces a bijection
$\mathscr {L}(\rho ): \mathscr {L}(Y) \to \mathscr {L}(X)$
induces a bijection
 $$ \begin{align*} \left(\operatorname{\mathrm{ord}}_{\mathcal{O}(-D)}^{-1}(\ell)\right)(k') \to \left(\operatorname{\mathrm{trop}}^{-1}(w)\right)(k') \end{align*} $$
$$ \begin{align*} \left(\operatorname{\mathrm{ord}}_{\mathcal{O}(-D)}^{-1}(\ell)\right)(k') \to \left(\operatorname{\mathrm{trop}}^{-1}(w)\right)(k') \end{align*} $$
for every field extension
![]() $k'$
of k.
$k'$
of k.
Proof. Let
![]() $k'$
be a field extension of k. By construction,
$k'$
be a field extension of k. By construction,
![]() $\mathscr {L}(\rho )$
induces a bijection
$\mathscr {L}(\rho )$
induces a bijection
![]() $(\mathscr {L}(Y) \setminus \mathscr {L}(Y \setminus T))(k') \to \left (\operatorname {\mathrm {trop}}^{-1}\left (N \cap \mathbb {R}_{\geq 0} w\right )\right )(k')$
. Therefore it is sufficient to show that
$(\mathscr {L}(Y) \setminus \mathscr {L}(Y \setminus T))(k') \to \left (\operatorname {\mathrm {trop}}^{-1}\left (N \cap \mathbb {R}_{\geq 0} w\right )\right )(k')$
. Therefore it is sufficient to show that
 $$ \begin{align*} \mathscr{L}(\rho)^{-1}\left(\left(\operatorname{\mathrm{trop}}^{-1}(w)\right)(k')\right) = \left(\operatorname{\mathrm{ord}}_{\mathcal{O}(-D)}^{-1}(\ell)\right)(k'). \end{align*} $$
$$ \begin{align*} \mathscr{L}(\rho)^{-1}\left(\left(\operatorname{\mathrm{trop}}^{-1}(w)\right)(k')\right) = \left(\operatorname{\mathrm{ord}}_{\mathcal{O}(-D)}^{-1}(\ell)\right)(k'). \end{align*} $$
By Lemma 4.7(2), it is enough to show that if
![]() $u\in \tau ^\vee \cap M$
, there exists
$u\in \tau ^\vee \cap M$
, there exists
![]() $u'\in \tau ^\vee \cap M$
with
$u'\in \tau ^\vee \cap M$
with
![]() $u+u'\in \sigma ^\vee \cap M$
. Consider the quotient map
$u+u'\in \sigma ^\vee \cap M$
. Consider the quotient map
![]() $\eta \colon M\to M/\left (w^\perp \cap M\right )\cong \mathbb {Z}$
. Since
$\eta \colon M\to M/\left (w^\perp \cap M\right )\cong \mathbb {Z}$
. Since
![]() $\sigma ^\vee \subset \tau ^\vee $
, we see that
$\sigma ^\vee \subset \tau ^\vee $
, we see that
![]() $\eta (\sigma ^\vee \cap M)\subset \eta (\tau ^\vee \cap M)=\mathbb {N}$
. So for any
$\eta (\sigma ^\vee \cap M)\subset \eta (\tau ^\vee \cap M)=\mathbb {N}$
. So for any
![]() $u\in \tau ^\vee \cap M$
, there exists
$u\in \tau ^\vee \cap M$
, there exists
![]() $n\in \mathbb {Z}_{>0}$
such that
$n\in \mathbb {Z}_{>0}$
such that
![]() $n\eta (u)\in \eta (\sigma ^\vee \cap M)$
– that is, for some choice of
$n\eta (u)\in \eta (\sigma ^\vee \cap M)$
– that is, for some choice of
![]() $u''\in w^\perp \cap M$
, letting
$u''\in w^\perp \cap M$
, letting
![]() $u'=u''+(n-1)u$
, we have
$u'=u''+(n-1)u$
, we have
![]() $u+u'\in \sigma ^\vee \cap M$
.
$u+u'\in \sigma ^\vee \cap M$
.
The next proposition completes the proof of Theorem 6.1(b).
Proposition 6.9. We have
 $$ \begin{align*} \mu^{\mathrm{Gor}}_X\left(\operatorname{\mathrm{trop}}^{-1}(w)\right) = \mathbb{L}^{-d}(\mathbb{L}-1)^d \left(\mathbb{L}^{1/m}\right)^{- \left\langle w, q \right\rangle}. \end{align*} $$
$$ \begin{align*} \mu^{\mathrm{Gor}}_X\left(\operatorname{\mathrm{trop}}^{-1}(w)\right) = \mathbb{L}^{-d}(\mathbb{L}-1)^d \left(\mathbb{L}^{1/m}\right)^{- \left\langle w, q \right\rangle}. \end{align*} $$
Proof. By Theorem 6.1(a), there exists some
![]() $j_w \in \mathbb {Z}$
such that
$j_w \in \mathbb {Z}$
such that
![]() $\operatorname {\mathrm {ord}}_{\mathscr {J}_{X,m}}$
is equal to
$\operatorname {\mathrm {ord}}_{\mathscr {J}_{X,m}}$
is equal to
![]() $j_w$
on
$j_w$
on
![]() $\operatorname {\mathrm {trop}}^{-1}(w)$
. By Proposition 6.8, we also have that
$\operatorname {\mathrm {trop}}^{-1}(w)$
. By Proposition 6.8, we also have that
![]() $\operatorname {\mathrm {ord}}_{\mathscr {J}_{X,m}} \circ \mathscr {L}(\rho )$
is equal to
$\operatorname {\mathrm {ord}}_{\mathscr {J}_{X,m}} \circ \mathscr {L}(\rho )$
is equal to
![]() $j_w$
on
$j_w$
on
 $\operatorname {\mathrm {ord}}_{\mathcal {O}(-D)}^{-1}(\ell )$
. Thus [Reference Chambert-Loir, Nicaise and SebagCLNS18, Chapter 7, Proposition 3.2.5] implies that on
$\operatorname {\mathrm {ord}}_{\mathcal {O}(-D)}^{-1}(\ell )$
. Thus [Reference Chambert-Loir, Nicaise and SebagCLNS18, Chapter 7, Proposition 3.2.5] implies that on
 $\operatorname {\mathrm {ord}}_{\mathcal {O}(-D)}^{-1}(\ell )$
,
$\operatorname {\mathrm {ord}}_{\mathcal {O}(-D)}^{-1}(\ell )$
,
 $$ \begin{align*} - \operatorname{\mathrm{ordjac}}_\rho\ =\ -\frac{1}{m}\operatorname{\mathrm{ord}}_{\mathscr{J}_{X,m}} \circ \mathscr{L}(\rho) -\frac{1}{m}\left(\frac{1}{\ell}\langle w, q \rangle - m\right) \operatorname{\mathrm{ord}}_{\mathcal{O}(-D)}\ =\ -\frac{j_w}{m} - \frac{1}{m}\langle w, q \rangle + \ell, \end{align*} $$
$$ \begin{align*} - \operatorname{\mathrm{ordjac}}_\rho\ =\ -\frac{1}{m}\operatorname{\mathrm{ord}}_{\mathscr{J}_{X,m}} \circ \mathscr{L}(\rho) -\frac{1}{m}\left(\frac{1}{\ell}\langle w, q \rangle - m\right) \operatorname{\mathrm{ord}}_{\mathcal{O}(-D)}\ =\ -\frac{j_w}{m} - \frac{1}{m}\langle w, q \rangle + \ell, \end{align*} $$
where
![]() $\operatorname {\mathrm {ordjac}}_\rho : \mathscr {L}(Y) \to \mathbb {N} \cup \{\infty \}$
denotes the order function of the Jacobian ideal of
$\operatorname {\mathrm {ordjac}}_\rho : \mathscr {L}(Y) \to \mathbb {N} \cup \{\infty \}$
denotes the order function of the Jacobian ideal of
![]() $\rho $
. Therefore,
$\rho $
. Therefore,
 $$ \begin{align*} \mu^{\mathrm{Gor}}_X\left(\operatorname{\mathrm{trop}}^{-1}(w)\right) & = \int_{\operatorname{\mathrm{trop}}^{-1}(w)} \left(\mathbb{L}^{1/m}\right)^{\operatorname{\mathrm{ord}}_{\mathscr{J}_{X,m}}} \mathrm{d}\mu_X = \left(\mathbb{L}^{1/m}\right)^{j_w} \mu_X\left(\operatorname{\mathrm{trop}}^{-1}(w)\right)\\ & = \left(\mathbb{L}^{1/m}\right)^{j_w}\int_{\operatorname{\mathrm{ord}}_{\mathcal{O}(-D)}^{-1}(\ell)} \mathbb{L}^{-\operatorname{\mathrm{ordjac}}_\rho}\mathrm{d}\mu_Y = \left(\mathbb{L}^{1/m}\right)^{j_w}\int_{\operatorname{\mathrm{ord}}_{\mathcal{O}(-D)}^{-1}(\ell)} \mathbb{L}^{-j_w/m - \left\langle w, q \right\rangle/m + \ell}\mathrm{d}\mu_Y\\ &= \left(\mathbb{L}^{1/m}\right)^{-\left\langle w, q \right\rangle} \mathbb{L}^\ell \mu_Y\left(\operatorname{\mathrm{ord}}_{\mathcal{O}(-D)}^{-1}(\ell)\right) \ =\ \mathbb{L}^{-d}(\mathbb{L}-1)^d \left(\mathbb{L}^{1/m}\right)^{- \left\langle w, q \right\rangle}, \end{align*} $$
$$ \begin{align*} \mu^{\mathrm{Gor}}_X\left(\operatorname{\mathrm{trop}}^{-1}(w)\right) & = \int_{\operatorname{\mathrm{trop}}^{-1}(w)} \left(\mathbb{L}^{1/m}\right)^{\operatorname{\mathrm{ord}}_{\mathscr{J}_{X,m}}} \mathrm{d}\mu_X = \left(\mathbb{L}^{1/m}\right)^{j_w} \mu_X\left(\operatorname{\mathrm{trop}}^{-1}(w)\right)\\ & = \left(\mathbb{L}^{1/m}\right)^{j_w}\int_{\operatorname{\mathrm{ord}}_{\mathcal{O}(-D)}^{-1}(\ell)} \mathbb{L}^{-\operatorname{\mathrm{ordjac}}_\rho}\mathrm{d}\mu_Y = \left(\mathbb{L}^{1/m}\right)^{j_w}\int_{\operatorname{\mathrm{ord}}_{\mathcal{O}(-D)}^{-1}(\ell)} \mathbb{L}^{-j_w/m - \left\langle w, q \right\rangle/m + \ell}\mathrm{d}\mu_Y\\ &= \left(\mathbb{L}^{1/m}\right)^{-\left\langle w, q \right\rangle} \mathbb{L}^\ell \mu_Y\left(\operatorname{\mathrm{ord}}_{\mathcal{O}(-D)}^{-1}(\ell)\right) \ =\ \mathbb{L}^{-d}(\mathbb{L}-1)^d \left(\mathbb{L}^{1/m}\right)^{- \left\langle w, q \right\rangle}, \end{align*} $$
where the third equality is due to Proposition 6.8 and the motivic change-of-variables formula (see, for example, [Reference Chambert-Loir, Nicaise and SebagCLNS18, Chapter 6, Theorem 4.3.1]), and the final equality follows from
 $$ \begin{align*} \mu_Y\left(\operatorname{\mathrm{ord}}_{\mathcal{O}(-D)}^{-1}(\ell)\right) = \mathrm{e}(D)(\mathbb{L}-1)\mathbb{L}^{-d-\ell} = (\mathbb{L}-1)^d\mathbb{L}^{-d-\ell}, \end{align*} $$
$$ \begin{align*} \mu_Y\left(\operatorname{\mathrm{ord}}_{\mathcal{O}(-D)}^{-1}(\ell)\right) = \mathrm{e}(D)(\mathbb{L}-1)\mathbb{L}^{-d-\ell} = (\mathbb{L}-1)^d\mathbb{L}^{-d-\ell}, \end{align*} $$
which is a consequence of [Reference Chambert-Loir, Nicaise and SebagCLNS18, Chapter 7, Lemma 3.3.3].
7 Motivic measure and canonical stacks
Set
![]() $d \in \mathbb {N}$
, let
$d \in \mathbb {N}$
, let
![]() $N \cong \mathbb {Z}^d$
be a lattice, let
$N \cong \mathbb {Z}^d$
be a lattice, let
![]() $T = \operatorname {\mathrm {Spec}}(k[N^*])$
be the algebraic torus with cocharacter lattice N, let
$T = \operatorname {\mathrm {Spec}}(k[N^*])$
be the algebraic torus with cocharacter lattice N, let
![]() $\sigma $
be a pointed rational cone in
$\sigma $
be a pointed rational cone in
![]() $N_{\mathbb {R}}$
, let X be the affine T-toric variety associated to
$N_{\mathbb {R}}$
, let X be the affine T-toric variety associated to
![]() $\sigma $
, let
$\sigma $
, let
![]() $\mathcal {X}$
be the canonical stack over X and let
$\mathcal {X}$
be the canonical stack over X and let
![]() $\pi : \mathcal {X} \to X$
be the canonical map. We assume that
$\pi : \mathcal {X} \to X$
be the canonical map. We assume that
![]() $\sigma $
is d-dimensional and use the notation listed in Notation 2.19. We assume that X is
$\sigma $
is d-dimensional and use the notation listed in Notation 2.19. We assume that X is
![]() $\mathbb {Q}$
-Gorenstein and let
$\mathbb {Q}$
-Gorenstein and let
![]() $m \in \mathbb {Z}_{>0}$
and
$m \in \mathbb {Z}_{>0}$
and
![]() $q \in P$
be such that if v is the first lattice point of any ray of
$q \in P$
be such that if v is the first lattice point of any ray of
![]() $\sigma $
,
$\sigma $
,
In this section, we prove the following theorem about the motivic measure
![]() $\mu _{\mathcal {X}}$
, which mirrors Theorem 6.1 for
$\mu _{\mathcal {X}}$
, which mirrors Theorem 6.1 for
 $\mu ^{\mathrm {Gor}}_X$
. In section 8, we will combine these two theorems to compare the measures
$\mu ^{\mathrm {Gor}}_X$
. In section 8, we will combine these two theorems to compare the measures
![]() $\mu _{\mathcal {X}}$
and
$\mu _{\mathcal {X}}$
and
 $\mu ^{\mathrm {Gor}}_X$
.
$\mu ^{\mathrm {Gor}}_X$
.
Theorem 7.1. Set
![]() $w \in \sigma \cap N \subset \operatorname {\mathrm {Hom}}(P, \mathbb {N} \cup \{\infty \})$
.
$w \in \sigma \cap N \subset \operatorname {\mathrm {Hom}}(P, \mathbb {N} \cup \{\infty \})$
.
-
(a) If
 $C \subset \operatorname {\mathrm {trop}}^{-1}(w) \subset \mathscr {L}(X)$
is measurable, then
$C \subset \operatorname {\mathrm {trop}}^{-1}(w) \subset \mathscr {L}(X)$
is measurable, then
 $\mathscr {L}(\pi )^{-1}(C)$
is a measurable subset of
$\mathscr {L}(\pi )^{-1}(C)$
is a measurable subset of
 $\lvert \mathscr {L}(\mathcal {X})\rvert $
. Furthermore, there exists
$\lvert \mathscr {L}(\mathcal {X})\rvert $
. Furthermore, there exists
 $\Theta _w \in \widehat {\mathscr {M}}_k$
such that for any measurable subset
$\Theta _w \in \widehat {\mathscr {M}}_k$
such that for any measurable subset
 $C \subset \operatorname {\mathrm {trop}}^{-1}(w) \subset \mathscr {L}(X)$
,
$C \subset \operatorname {\mathrm {trop}}^{-1}(w) \subset \mathscr {L}(X)$
,  $$ \begin{align*} \mu_{\mathcal{X}}\left(\mathscr{L}(\pi)^{-1}(C)\right) = \Theta_w \mu_X(C). \end{align*} $$
$$ \begin{align*} \mu_{\mathcal{X}}\left(\mathscr{L}(\pi)^{-1}(C)\right) = \Theta_w \mu_X(C). \end{align*} $$
-
(b) The set
 $\mathscr {L}(\pi )^{-1}\left (\operatorname {\mathrm {trop}}^{-1}(w)\right ) \subset \lvert \mathscr {L}(\mathcal {X})\rvert $
is measurable and
$\mathscr {L}(\pi )^{-1}\left (\operatorname {\mathrm {trop}}^{-1}(w)\right ) \subset \lvert \mathscr {L}(\mathcal {X})\rvert $
is measurable and  $$ \begin{align*} \mu_{\mathcal{X}}\left(\mathscr{L}(\pi)^{-1}\left(\operatorname{\mathrm{trop}}^{-1}(w)\right)\right) = \left(\# \beta^{-1}(w)\right) \mathbb{L}^{-d}(\mathbb{L}-1)^d \left(\mathbb{L}^{1/m}\right)^{- \left\langle w, q \right\rangle}. \end{align*} $$
$$ \begin{align*} \mu_{\mathcal{X}}\left(\mathscr{L}(\pi)^{-1}\left(\operatorname{\mathrm{trop}}^{-1}(w)\right)\right) = \left(\# \beta^{-1}(w)\right) \mathbb{L}^{-d}(\mathbb{L}-1)^d \left(\mathbb{L}^{1/m}\right)^{- \left\langle w, q \right\rangle}. \end{align*} $$
Remark 7.2. A priori, we only have that
 $$ \begin{align*} \left(\# \beta^{-1}(w)\right) \mathbb{L}^{-d}(\mathbb{L}-1)^d \left(\mathbb{L}^{1/m}\right)^{- \left\langle w, q \right\rangle} \in \widehat{\mathscr{M}}_k\left[\mathbb{L}^{1/m}\right] \supset \widehat{\mathscr{M}_k}; \end{align*} $$
$$ \begin{align*} \left(\# \beta^{-1}(w)\right) \mathbb{L}^{-d}(\mathbb{L}-1)^d \left(\mathbb{L}^{1/m}\right)^{- \left\langle w, q \right\rangle} \in \widehat{\mathscr{M}}_k\left[\mathbb{L}^{1/m}\right] \supset \widehat{\mathscr{M}_k}; \end{align*} $$
but by Lemma 7.9 we have either that
![]() $\beta ^{-1}(w) = \emptyset $
or that
$\beta ^{-1}(w) = \emptyset $
or that
![]() $\langle w, q \rangle $
is divisible by m, so
$\langle w, q \rangle $
is divisible by m, so
 $$ \begin{align*} \left(\# \beta^{-1}(w)\right) \mathbb{L}^{-d}(\mathbb{L}-1)^d \left(\mathbb{L}^{1/m}\right)^{- \left\langle w, q \right\rangle} \in \widehat{\mathscr{M}}_k. \end{align*} $$
$$ \begin{align*} \left(\# \beta^{-1}(w)\right) \mathbb{L}^{-d}(\mathbb{L}-1)^d \left(\mathbb{L}^{1/m}\right)^{- \left\langle w, q \right\rangle} \in \widehat{\mathscr{M}}_k. \end{align*} $$
Before we prove Theorem 7.1, we show that it implies the next proposition.
Proposition 7.3. Let
![]() $C \subset \mathscr {L}(X)$
be a measurable subset. Then
$C \subset \mathscr {L}(X)$
be a measurable subset. Then
![]() $\mathscr {L}(\pi )^{-1}(C)$
is a measurable subset of
$\mathscr {L}(\pi )^{-1}(C)$
is a measurable subset of
![]() $\lvert \mathscr {L}(\mathcal {X})\rvert $
and
$\lvert \mathscr {L}(\mathcal {X})\rvert $
and
 $$ \begin{align*} \mu_{\mathcal{X}}\left(\mathscr{L}(\pi)^{-1}(C)\right) = \sum_{w \in \sigma \cap N} \mu_{\mathcal{X}}\left(\mathscr{L}(\pi)^{-1}\left(\operatorname{\mathrm{trop}}^{-1}(w) \cap C\right)\right). \end{align*} $$
$$ \begin{align*} \mu_{\mathcal{X}}\left(\mathscr{L}(\pi)^{-1}(C)\right) = \sum_{w \in \sigma \cap N} \mu_{\mathcal{X}}\left(\mathscr{L}(\pi)^{-1}\left(\operatorname{\mathrm{trop}}^{-1}(w) \cap C\right)\right). \end{align*} $$
Remark 7.4. By Remark 4.6 and Theorem 7.1(a), each
![]() $\mathscr {L}(\pi )^{-1}\left (\operatorname {\mathrm {trop}}^{-1}(w) \cap C\right )$
in the statement of Proposition 7.3 is a measurable subset of
$\mathscr {L}(\pi )^{-1}\left (\operatorname {\mathrm {trop}}^{-1}(w) \cap C\right )$
in the statement of Proposition 7.3 is a measurable subset of
![]() $\lvert \mathscr {L}(\mathcal {X})\rvert $
.
$\lvert \mathscr {L}(\mathcal {X})\rvert $
.
Proof. Set
 $$ \begin{align*} \mathcal{C} &= \mathscr{L}(\pi)^{-1}(C),\\ \mathcal{C}^{(0)} &= \bigcup_{w \in \sigma \cap N} \mathscr{L}(\pi)^{-1}\left(\operatorname{\mathrm{trop}}^{-1}(w) \cap C\right),\\ \mathcal{C}^{(\infty)} &= \mathcal{C} \setminus \mathcal{C}^{(0)}. \end{align*} $$
$$ \begin{align*} \mathcal{C} &= \mathscr{L}(\pi)^{-1}(C),\\ \mathcal{C}^{(0)} &= \bigcup_{w \in \sigma \cap N} \mathscr{L}(\pi)^{-1}\left(\operatorname{\mathrm{trop}}^{-1}(w) \cap C\right),\\ \mathcal{C}^{(\infty)} &= \mathcal{C} \setminus \mathcal{C}^{(0)}. \end{align*} $$
For each
![]() $w \in \sigma \cap N$
,
$w \in \sigma \cap N$
,
 $$ \begin{align*} \left\lVert \mu_{\mathcal{X}}\left(\mathscr{L}(\pi)^{-1}\left(\operatorname{\mathrm{trop}}^{-1}(w) \cap C\right)\right) \right\rVert &\leq \left\lVert \mu_{\mathcal{X}}\left(\mathscr{L}(\pi)^{-1}\left(\operatorname{\mathrm{trop}}^{-1}(w)\right)\right) \right\rVert\\ &\leq \left\lVert \mathbb{L}^{-d}(\mathbb{L}-1)^d \right\rVert \exp(-\langle w, q \rangle/m), \end{align*} $$
$$ \begin{align*} \left\lVert \mu_{\mathcal{X}}\left(\mathscr{L}(\pi)^{-1}\left(\operatorname{\mathrm{trop}}^{-1}(w) \cap C\right)\right) \right\rVert &\leq \left\lVert \mu_{\mathcal{X}}\left(\mathscr{L}(\pi)^{-1}\left(\operatorname{\mathrm{trop}}^{-1}(w)\right)\right) \right\rVert\\ &\leq \left\lVert \mathbb{L}^{-d}(\mathbb{L}-1)^d \right\rVert \exp(-\langle w, q \rangle/m), \end{align*} $$
where the first inequality is by Proposition 3.29 and the second is by Theorem 7.1(b). For each
![]() $\varepsilon \in \mathbb {R}_{>0}$
there are only finitely many
$\varepsilon \in \mathbb {R}_{>0}$
there are only finitely many
![]() $w \in \sigma \cap N$
with
$w \in \sigma \cap N$
with
![]() $\exp (-\langle w, q \rangle / m) \geq \varepsilon $
, so Proposition 3.27 implies that
$\exp (-\langle w, q \rangle / m) \geq \varepsilon $
, so Proposition 3.27 implies that
![]() $\mathcal {C}^{(0)}$
is measurable and
$\mathcal {C}^{(0)}$
is measurable and
 $$ \begin{align*} \mu_{\mathcal{X}}\left(\mathcal{C}^{(0)}\right) = \sum_{w \in \sigma \cap N} \mu_{\mathcal{X}}\left(\mathscr{L}(\pi)^{-1}\left(\operatorname{\mathrm{trop}}^{-1}(w) \cap C\right)\right). \end{align*} $$
$$ \begin{align*} \mu_{\mathcal{X}}\left(\mathcal{C}^{(0)}\right) = \sum_{w \in \sigma \cap N} \mu_{\mathcal{X}}\left(\mathscr{L}(\pi)^{-1}\left(\operatorname{\mathrm{trop}}^{-1}(w) \cap C\right)\right). \end{align*} $$
By Proposition 3.28 and Proposition 3.30, the set
![]() $\mathcal {C}^{(\infty )}$
is measurable and
$\mathcal {C}^{(\infty )}$
is measurable and
 $$ \begin{align*} \mu_{\mathcal{X}}\left(\mathcal{C}^{(\infty)}\right) = 0. \end{align*} $$
$$ \begin{align*} \mu_{\mathcal{X}}\left(\mathcal{C}^{(\infty)}\right) = 0. \end{align*} $$
Therefore by Proposition 3.27, the set
![]() $\mathcal {C} = \mathcal {C}^{(0)} \sqcup \mathcal {C}^{(\infty )}$
is measurable and
$\mathcal {C} = \mathcal {C}^{(0)} \sqcup \mathcal {C}^{(\infty )}$
is measurable and
 $$ \begin{align*} \mu_{\mathcal{X}}(\mathcal{C}) = \mu_{\mathcal{X}}\left(\mathcal{C}^{(0)}\right) = \sum_{w \in \sigma \cap N} \mu_{\mathcal{X}}\left(\mathscr{L}(\pi)^{-1}\left(\operatorname{\mathrm{trop}}^{-1}(w) \cap C\right)\right).\\[-40pt] \end{align*} $$
$$ \begin{align*} \mu_{\mathcal{X}}(\mathcal{C}) = \mu_{\mathcal{X}}\left(\mathcal{C}^{(0)}\right) = \sum_{w \in \sigma \cap N} \mu_{\mathcal{X}}\left(\mathscr{L}(\pi)^{-1}\left(\operatorname{\mathrm{trop}}^{-1}(w) \cap C\right)\right).\\[-40pt] \end{align*} $$
We will use the remainder of this section to prove Theorem 7.1.
7.1 Canonical stacks and preimages of measurable subsets
In this subsection, we will prove Theorem 7.1(a). We begin with a couple lemmas.
Lemma 7.5. Let Y be an irreducible finite-type scheme over k with smooth locus
![]() $Y_{\mathrm {sm}} \subset Y$
, and let
$Y_{\mathrm {sm}} \subset Y$
, and let
![]() $C \subset \mathscr {L}(Y)$
be a cylinder such that
$C \subset \mathscr {L}(Y)$
be a cylinder such that
![]() $C \cap \mathscr {L}(Y \setminus Y_{\mathrm {sm}}) = \emptyset $
.
$C \cap \mathscr {L}(Y \setminus Y_{\mathrm {sm}}) = \emptyset $
.
Then there exists some
![]() $n_C \in \mathbb {N}$
that satisfies the following: For any field extension
$n_C \in \mathbb {N}$
that satisfies the following: For any field extension
![]() $k'$
of k, any
$k'$
of k, any
![]() $n \geq n_C$
and any
$n \geq n_C$
and any
![]() $\varphi _n \in \mathscr {L}_n(Y)(k')$
with image in
$\varphi _n \in \mathscr {L}_n(Y)(k')$
with image in
![]() $\theta _n(C)$
, there exists some
$\theta _n(C)$
, there exists some
![]() $\varphi \in \mathscr {L}(Y)(k')$
with image in C such that
$\varphi \in \mathscr {L}(Y)(k')$
with image in C such that
![]() $\theta _n(\varphi ) = \varphi _n$
.
$\theta _n(\varphi ) = \varphi _n$
.
Proof. By [Reference Chambert-Loir, Nicaise and SebagCLNS18, Chapter 5, Propositions 1.3.2(a) and 2.3.4], there exists a function
![]() $\operatorname {\mathrm {ordjac}}_Y: \mathscr {L}(Y) \to \mathbb {N} \cup \{\infty \}$
and some
$\operatorname {\mathrm {ordjac}}_Y: \mathscr {L}(Y) \to \mathbb {N} \cup \{\infty \}$
and some
![]() $c \in \mathbb {Z}_{>0}$
such that
$c \in \mathbb {Z}_{>0}$
such that
-
• for every
 $n \in \mathbb {N}$
, the set
$n \in \mathbb {N}$
, the set
 $\operatorname {\mathrm {ordjac}}_Y^{-1}(n) \subset \mathscr {L}(Y)$
is a cylinder;
$\operatorname {\mathrm {ordjac}}_Y^{-1}(n) \subset \mathscr {L}(Y)$
is a cylinder; -
• the image of
 $\mathscr {L}(Y) \setminus \mathscr {L}(Y \setminus Y_{\mathrm {sm}})$
under
$\mathscr {L}(Y) \setminus \mathscr {L}(Y \setminus Y_{\mathrm {sm}})$
under
 $\operatorname {\mathrm {ordjac}}_Y$
is contained in
$\operatorname {\mathrm {ordjac}}_Y$
is contained in
 $\mathbb {N}$
; and
$\mathbb {N}$
; and -
• for every
 $n \in \mathbb {N}$
, field extension
$n \in \mathbb {N}$
, field extension
 $k'$
of k and
$k'$
of k and
 $\varphi _n \in \mathscr {L}_n(Y)(k')$
whose image in
$\varphi _n \in \mathscr {L}_n(Y)(k')$
whose image in
 $\mathscr {L}_n(Y)$
is contained in
$\mathscr {L}_n(Y)$
is contained in
 $\theta _{n}\left ( \operatorname {\mathrm {ordjac}}_Y^{-1}(n') \right )$
for some
$\theta _{n}\left ( \operatorname {\mathrm {ordjac}}_Y^{-1}(n') \right )$
for some
 $n' \leq n/c$
, there exists some
$n' \leq n/c$
, there exists some
 $\varphi \in \mathscr {L}(Y)(k')$
with
$\varphi \in \mathscr {L}(Y)(k')$
with
 $\theta _n(\varphi ) = \varphi _n$
.
$\theta _n(\varphi ) = \varphi _n$
.
Because
![]() $C \cap \mathscr {L}(Y \setminus Y_{\mathrm {sm}}) = \emptyset $
, the collection
$C \cap \mathscr {L}(Y \setminus Y_{\mathrm {sm}}) = \emptyset $
, the collection
 $\left \{\operatorname {\mathrm {ordjac}}_Y^{-1}(n)\right \}_{n \in \mathbb {N}}$
is a cover of the cylinder C by cylinders. Thus by the quasicompactness of the constructible topology of
$\left \{\operatorname {\mathrm {ordjac}}_Y^{-1}(n)\right \}_{n \in \mathbb {N}}$
is a cover of the cylinder C by cylinders. Thus by the quasicompactness of the constructible topology of
![]() $\mathscr {L}(Y)$
(see, for example, [Reference Chambert-Loir, Nicaise and SebagCLNS18, Appendix, Theorem 1.2.4(a)]), there exists some
$\mathscr {L}(Y)$
(see, for example, [Reference Chambert-Loir, Nicaise and SebagCLNS18, Appendix, Theorem 1.2.4(a)]), there exists some
![]() $n^{\prime }_C \in \mathbb {N}$
such that
$n^{\prime }_C \in \mathbb {N}$
such that
 $C \subset \bigcup _{n = 0}^{n^{\prime }_C} \operatorname {\mathrm {ordjac}}_Y^{-1}(n)$
. Let
$C \subset \bigcup _{n = 0}^{n^{\prime }_C} \operatorname {\mathrm {ordjac}}_Y^{-1}(n)$
. Let
![]() $n_C \in \mathbb {N}$
be such that
$n_C \in \mathbb {N}$
be such that
![]() $n_C \geq cn^{\prime }_C$
and such that C is the preimage under
$n_C \geq cn^{\prime }_C$
and such that C is the preimage under
![]() $\theta _{n_C}$
of a constructible subset of
$\theta _{n_C}$
of a constructible subset of
![]() $\mathscr {L}_{n_C}(Y)$
.
$\mathscr {L}_{n_C}(Y)$
.
Now let
![]() $k'$
be a field extension of k, let
$k'$
be a field extension of k, let
![]() $n \geq n_C$
and let
$n \geq n_C$
and let
![]() $\varphi _n \in \mathscr {L}_n(Y)(k')$
have image in
$\varphi _n \in \mathscr {L}_n(Y)(k')$
have image in
![]() $\theta _n(C)$
. Then the image of
$\theta _n(C)$
. Then the image of
![]() $\varphi _n$
is contained in
$\varphi _n$
is contained in
 $\theta _n\left (\operatorname {\mathrm {ordjac}}_Y^{-1}(n')\right )$
for some
$\theta _n\left (\operatorname {\mathrm {ordjac}}_Y^{-1}(n')\right )$
for some
![]() $n' \leq n^{\prime }_C \leq n_C/c \leq n/c$
, so there exists some
$n' \leq n^{\prime }_C \leq n_C/c \leq n/c$
, so there exists some
![]() $\varphi \in \mathscr {L}(Y)(k')$
with
$\varphi \in \mathscr {L}(Y)(k')$
with
![]() $\theta _n(\varphi ) = \varphi _n$
. Because C is the preimage of a subset of
$\theta _n(\varphi ) = \varphi _n$
. Because C is the preimage of a subset of
![]() $\mathscr {L}_n(Y)$
, the arc
$\mathscr {L}_n(Y)$
, the arc
![]() $\varphi $
has image in C.
$\varphi $
has image in C.
Lemma 7.6. Let Y be a finite-type scheme over k, let
![]() $\mathcal {Y}$
be a smooth Artin stack over k, let
$\mathcal {Y}$
be a smooth Artin stack over k, let
![]() $\xi : \mathcal {Y} \to Y$
be a morphism, let
$\xi : \mathcal {Y} \to Y$
be a morphism, let
![]() $C \subset \mathscr {L}(Y)$
be a cylinder and set
$C \subset \mathscr {L}(Y)$
be a cylinder and set
![]() $\mathcal {C} = \mathscr {L}(\xi )^{-1}(C) \subset \lvert \mathscr {L}(\mathcal {Y}) \rvert $
.
$\mathcal {C} = \mathscr {L}(\xi )^{-1}(C) \subset \lvert \mathscr {L}(\mathcal {Y}) \rvert $
.
Then
![]() $\mathcal {C}$
is a cylinder and there exists some
$\mathcal {C}$
is a cylinder and there exists some
![]() $n_0 \in \mathbb {N}$
such that for all
$n_0 \in \mathbb {N}$
such that for all
![]() $n \geq n_0$
,
$n \geq n_0$
,
Proof. We first note that for all
![]() $n \in \mathbb {N}$
, we have an obvious inclusion
$n \in \mathbb {N}$
, we have an obvious inclusion
Because C is a cylinder, there exists some
![]() $n_0 \in \mathbb {N}$
and some constructible subset
$n_0 \in \mathbb {N}$
and some constructible subset
![]() $C_{n_0} \subset \mathscr {L}_{n_0}(Y)$
such that
$C_{n_0} \subset \mathscr {L}_{n_0}(Y)$
such that
 $C = \left (\theta _{n_0}\right )^{-1}\left (C_{n_0}\right )$
. Then
$C = \left (\theta _{n_0}\right )^{-1}\left (C_{n_0}\right )$
. Then
 $$ \begin{align*} \mathcal{C} = \mathscr{L}(\xi)^{-1}\left( \left(\theta_{n_0}\right)^{-1}\left(C_{n_0}\right) \right) = \left(\theta_{n_0}\right)^{-1}\left( \mathscr{L}_n(\xi)^{-1}\left(C_{n_0}\right) \right) \end{align*} $$
$$ \begin{align*} \mathcal{C} = \mathscr{L}(\xi)^{-1}\left( \left(\theta_{n_0}\right)^{-1}\left(C_{n_0}\right) \right) = \left(\theta_{n_0}\right)^{-1}\left( \mathscr{L}_n(\xi)^{-1}\left(C_{n_0}\right) \right) \end{align*} $$
is a cylinder because
![]() $\mathscr {L}_n(\xi )^{-1}\left (C_{n_0}\right )$
is a constructible subset of
$\mathscr {L}_n(\xi )^{-1}\left (C_{n_0}\right )$
is a constructible subset of
![]() $\lvert \mathscr {L}_n(\mathcal {Y})\rvert $
. We will finish this proof by showing that for any
$\lvert \mathscr {L}_n(\mathcal {Y})\rvert $
. We will finish this proof by showing that for any
![]() $n \geq n_0$
, we have
$n \geq n_0$
, we have
![]() $\theta _n(\mathcal {C}) \supset \mathscr {L}_n(\xi )^{-1}(\theta _n(C))$
.
$\theta _n(\mathcal {C}) \supset \mathscr {L}_n(\xi )^{-1}(\theta _n(C))$
.
Set
![]() $n \geq n_0$
and
$n \geq n_0$
and
![]() $\varphi _n \in \mathscr {L}_n(\xi )^{-1}(\theta _n(C))$
. Because
$\varphi _n \in \mathscr {L}_n(\xi )^{-1}(\theta _n(C))$
. Because
![]() $\mathcal {Y}$
is smooth, there exists some
$\mathcal {Y}$
is smooth, there exists some
![]() $\varphi \in \lvert \mathscr {L}(\mathcal {Y})\rvert $
such that
$\varphi \in \lvert \mathscr {L}(\mathcal {Y})\rvert $
such that
![]() $\theta _n(\varphi ) = \varphi _n$
. Then
$\theta _n(\varphi ) = \varphi _n$
. Then
![]() $\theta _n(\mathscr {L}(\xi )(\varphi )) = \mathscr {L}_n(\xi )( \varphi _n ) \in \theta _n(C)$
, so
$\theta _n(\mathscr {L}(\xi )(\varphi )) = \mathscr {L}_n(\xi )( \varphi _n ) \in \theta _n(C)$
, so
![]() $\mathscr {L}(\xi )(\varphi ) \in (\theta _n)^{-1}(\theta _n(C))$
. But
$\mathscr {L}(\xi )(\varphi ) \in (\theta _n)^{-1}(\theta _n(C))$
. But
![]() $(\theta _n)^{-1}(\theta _n(C)) = C$
, because
$(\theta _n)^{-1}(\theta _n(C)) = C$
, because
 $C = (\theta _n)^{-1}\left ( \left (\theta ^n_{n_0}\right )^{-1}\left (C_{n_0}\right ) \right )$
is the preimage of a subset of
$C = (\theta _n)^{-1}\left ( \left (\theta ^n_{n_0}\right )^{-1}\left (C_{n_0}\right ) \right )$
is the preimage of a subset of
![]() $\mathscr {L}_n(Y)$
. Thus
$\mathscr {L}_n(Y)$
. Thus
![]() $\mathscr {L}(\xi )(\varphi ) \in C$
, which implies
$\mathscr {L}(\xi )(\varphi ) \in C$
, which implies
![]() $\varphi \in \mathcal {C}$
and
$\varphi \in \mathcal {C}$
and
![]() $\varphi _n \in \theta _n(\mathcal {C})$
.
$\varphi _n \in \theta _n(\mathcal {C})$
.
We may now prove the special case of Theorem 7.1(a) where C is a cylinder.
Proposition 7.7. Set
![]() $w \in \sigma \cap N$
. If
$w \in \sigma \cap N$
. If
![]() $C \subset \operatorname {\mathrm {trop}}^{-1}(w) \subset \mathscr {L}(X)$
is a cylinder, then
$C \subset \operatorname {\mathrm {trop}}^{-1}(w) \subset \mathscr {L}(X)$
is a cylinder, then
![]() $\mathscr {L}(\pi )^{-1}(C)\subset \lvert \mathscr {L}(\mathcal {X})\rvert $
is a cylinder. Furthermore, there exists some
$\mathscr {L}(\pi )^{-1}(C)\subset \lvert \mathscr {L}(\mathcal {X})\rvert $
is a cylinder. Furthermore, there exists some
![]() $\Theta _w \in \widehat {\mathscr {M}}_k$
such that for any cylinder
$\Theta _w \in \widehat {\mathscr {M}}_k$
such that for any cylinder
![]() $C \subset \operatorname {\mathrm {trop}}^{-1}(w) \subset \mathscr {L}(X)$
,
$C \subset \operatorname {\mathrm {trop}}^{-1}(w) \subset \mathscr {L}(X)$
,
 $$ \begin{align*} \mu_{\mathcal{X}}\left(\mathscr{L}(\pi)^{-1}(C)\right) = \Theta_w \mu_X(C). \end{align*} $$
$$ \begin{align*} \mu_{\mathcal{X}}\left(\mathscr{L}(\pi)^{-1}(C)\right) = \Theta_w \mu_X(C). \end{align*} $$
Proof. Let
![]() $n_w, \Theta _w, \{\mathcal {F}_n\}_{n \geq n_w}$
be as in the statement of Theorem 5.1, and let
$n_w, \Theta _w, \{\mathcal {F}_n\}_{n \geq n_w}$
be as in the statement of Theorem 5.1, and let
![]() $n_{\operatorname {\mathrm {trop}}^{-1}(w)}$
be as in the statement of Lemma 7.5 (with
$n_{\operatorname {\mathrm {trop}}^{-1}(w)}$
be as in the statement of Lemma 7.5 (with
![]() $Y = X$
and
$Y = X$
and
![]() $C = \operatorname {\mathrm {trop}}^{-1}(w)$
). We show that if
$C = \operatorname {\mathrm {trop}}^{-1}(w)$
). We show that if
 $n \geq \max \left \{n_w, n_{\operatorname {\mathrm {trop}}^{-1}(w)}\right \}$
and
$n \geq \max \left \{n_w, n_{\operatorname {\mathrm {trop}}^{-1}(w)}\right \}$
and
![]() $C_n \subset \theta _n\left (\operatorname {\mathrm {trop}}^{-1}(w)\right )$
is constructible, then
$C_n \subset \theta _n\left (\operatorname {\mathrm {trop}}^{-1}(w)\right )$
is constructible, then
 $$ \begin{align*} \mathrm{e}\left(\mathscr{L}_n(\pi)^{-1}(C_n)\right) = \Theta_w \mathrm{e}(C_n). \end{align*} $$
$$ \begin{align*} \mathrm{e}\left(\mathscr{L}_n(\pi)^{-1}(C_n)\right) = \Theta_w \mathrm{e}(C_n). \end{align*} $$
Let
 $n \geq \max \left \{n_w, n_{\operatorname {\mathrm {trop}}^{-1}(w)}\right \}$
, let
$n \geq \max \left \{n_w, n_{\operatorname {\mathrm {trop}}^{-1}(w)}\right \}$
, let
![]() $k'$
be a field extension of k and set
$k'$
be a field extension of k and set
![]() $\varphi _n \in \mathscr {L}_n(X)(k')$
with image in
$\varphi _n \in \mathscr {L}_n(X)(k')$
with image in
![]() $\theta _n\left (\operatorname {\mathrm {trop}}^{-1}(w)\right )$
. Then by our choice of
$\theta _n\left (\operatorname {\mathrm {trop}}^{-1}(w)\right )$
. Then by our choice of
![]() $n_{\operatorname {\mathrm {trop}}^{-1}(w)}$
, there exists some
$n_{\operatorname {\mathrm {trop}}^{-1}(w)}$
, there exists some
![]() $\varphi \in \mathscr {L}(X)(k')$
such that
$\varphi \in \mathscr {L}(X)(k')$
such that
![]() $\operatorname {\mathrm {trop}}(\varphi ) = w$
and
$\operatorname {\mathrm {trop}}(\varphi ) = w$
and
![]() $\theta _n(\varphi ) = \varphi _n$
. Then by our choice of
$\theta _n(\varphi ) = \varphi _n$
. Then by our choice of
![]() $n_w$
and
$n_w$
and
![]() $\mathcal {F}_n$
,
$\mathcal {F}_n$
,
Therefore Proposition 2.5, Remark 2.7, and Proposition 2.8 imply that for any constructible subset
![]() $C_n \subset \theta _n\left (\operatorname {\mathrm {trop}}^{-1}(w)\right )$
,
$C_n \subset \theta _n\left (\operatorname {\mathrm {trop}}^{-1}(w)\right )$
,
 $$ \begin{align*} \mathrm{e}\left(\mathscr{L}_n(\pi)^{-1}(C_n)\right) = \mathrm{e}(\mathcal{F}_n)\mathrm{e}(C_n) = \Theta_w \mathrm{e}(C_n), \end{align*} $$
$$ \begin{align*} \mathrm{e}\left(\mathscr{L}_n(\pi)^{-1}(C_n)\right) = \mathrm{e}(\mathcal{F}_n)\mathrm{e}(C_n) = \Theta_w \mathrm{e}(C_n), \end{align*} $$
where the second equality holds by our choice of
![]() $n_w, \Theta _w, \mathcal {F}_n$
.
$n_w, \Theta _w, \mathcal {F}_n$
.
Now let
![]() $C \subset \operatorname {\mathrm {trop}}^{-1}(w)$
be a cylinder, and let
$C \subset \operatorname {\mathrm {trop}}^{-1}(w)$
be a cylinder, and let
![]() $\mathcal {C} = \mathscr {L}(\pi )^{-1}(C) \subset \lvert \mathscr {L}(\mathcal {X})\rvert $
. Then
$\mathcal {C} = \mathscr {L}(\pi )^{-1}(C) \subset \lvert \mathscr {L}(\mathcal {X})\rvert $
. Then
![]() $\mathcal {C}$
is a cylinder by Lemma 7.6. Let
$\mathcal {C}$
is a cylinder by Lemma 7.6. Let
![]() $n_0$
be as in the statement of Lemma 7.6 (with
$n_0$
be as in the statement of Lemma 7.6 (with
![]() $\xi = \pi $
). Then for any
$\xi = \pi $
). Then for any
 $n \geq \max \left \{n_w, n_{\operatorname {\mathrm {trop}}^{-1}(w)}, n_0\right \}$
,
$n \geq \max \left \{n_w, n_{\operatorname {\mathrm {trop}}^{-1}(w)}, n_0\right \}$
,
 $$ \begin{align*} \mathrm{e}(\theta_n( \mathcal{C} )) = \mathrm{e}\left(\mathscr{L}_n(\pi)^{-1}(\theta_n(C))\right) = \Theta_w \mathrm{e}(\theta_n(C)), \end{align*} $$
$$ \begin{align*} \mathrm{e}(\theta_n( \mathcal{C} )) = \mathrm{e}\left(\mathscr{L}_n(\pi)^{-1}(\theta_n(C))\right) = \Theta_w \mathrm{e}(\theta_n(C)), \end{align*} $$
where the first equality holds by our choice of
![]() $n_0$
. Therefore
$n_0$
. Therefore
 $$ \begin{align*} \mu_{\mathcal{X}}( \mathcal{C} ) &= \lim_{n \to \infty} \mathrm{e}(\theta_n(\mathcal{C}))\mathbb{L}^{-(n+1)\dim\mathcal{X}}\\ &= \Theta_w \lim_{n \to \infty} \mathrm{e}(\theta_n(C))\mathbb{L}^{-(n+1)\dim X}\\ &= \Theta_w \mu_X(C).\\[-36pt] \end{align*} $$
$$ \begin{align*} \mu_{\mathcal{X}}( \mathcal{C} ) &= \lim_{n \to \infty} \mathrm{e}(\theta_n(\mathcal{C}))\mathbb{L}^{-(n+1)\dim\mathcal{X}}\\ &= \Theta_w \lim_{n \to \infty} \mathrm{e}(\theta_n(C))\mathbb{L}^{-(n+1)\dim X}\\ &= \Theta_w \mu_X(C).\\[-36pt] \end{align*} $$
Now we may complete the proof of Theorem 7.1(a) in general.
Proof of Theorem 7.1(a)
Set
![]() $w \in \sigma \cap N$
, let
$w \in \sigma \cap N$
, let
![]() $\Theta _w$
be as in the statement of Proposition 7.7 and let
$\Theta _w$
be as in the statement of Proposition 7.7 and let
![]() $C \subset \operatorname {\mathrm {trop}}^{-1}(w)$
be a measurable subset of
$C \subset \operatorname {\mathrm {trop}}^{-1}(w)$
be a measurable subset of
![]() $\mathscr {L}(X)$
.
$\mathscr {L}(X)$
.
For any
![]() $\varepsilon \in \mathbb {R}_{>0}$
and any cylindrical
$\varepsilon \in \mathbb {R}_{>0}$
and any cylindrical
![]() $\varepsilon $
-approximation
$\varepsilon $
-approximation
 $\left (C^{(0)}, \left (C^{(i)}\right )_{i \in I}\right )$
of C, Proposition 7.7 implies that
$\left (C^{(0)}, \left (C^{(i)}\right )_{i \in I}\right )$
of C, Proposition 7.7 implies that
 $\left (\mathscr {L}(\pi )^{-1}\left (C^{(0)}\right ),\left (\mathscr {L}(\pi )^{-1}\left (C^{(i)}\right )\right )_{i \in I}\right )$
is a cylindrical
$\left (\mathscr {L}(\pi )^{-1}\left (C^{(0)}\right ),\left (\mathscr {L}(\pi )^{-1}\left (C^{(i)}\right )\right )_{i \in I}\right )$
is a cylindrical
![]() $\varepsilon \lVert \Theta _w \rVert $
-approximation of
$\varepsilon \lVert \Theta _w \rVert $
-approximation of
![]() $\mathscr {L}(\pi )^{-1}(C)$
. Therefore
$\mathscr {L}(\pi )^{-1}(C)$
. Therefore
![]() $\mathscr {L}(\pi )^{-1}(C)$
is measurable, and by another application of Proposition 7.7,
$\mathscr {L}(\pi )^{-1}(C)$
is measurable, and by another application of Proposition 7.7,
 $$ \begin{align*} \mu_{\mathcal{X}}\left(\mathscr{L}(\pi)^{-1}(C)\right) = \Theta_w \mu_X(C).\\[-38pt] \end{align*} $$
$$ \begin{align*} \mu_{\mathcal{X}}\left(\mathscr{L}(\pi)^{-1}(C)\right) = \Theta_w \mu_X(C).\\[-38pt] \end{align*} $$
7.2 Quotient by an algebraic torus
In order to apply Theorem 3.9 to prove Theorem 7.1(b), we must rewrite our fantastack as the quotient by a torus. The following result provides an explicit way to do so:
Proposition 7.8. Define
![]() $\widehat {N} := \widetilde {N} \oplus N$
and let
$\widehat {N} := \widetilde {N} \oplus N$
and let
![]() $\widehat {\sigma } = \widetilde {\sigma } \times \{0\}$
. Letting
$\widehat {\sigma } = \widetilde {\sigma } \times \{0\}$
. Letting
![]() $\widehat {X}$
be the toric variety associated to
$\widehat {X}$
be the toric variety associated to
![]() $\widehat {\sigma }$
, there is a
$\widehat {\sigma }$
, there is a
![]() $\widetilde {T}$
-action on
$\widetilde {T}$
-action on
![]() $\widehat {X}$
and an isomorphism
$\widehat {X}$
and an isomorphism
 $\left [\widehat {X} / \widetilde {T}\right ] \xrightarrow {\sim } \mathcal {X}$
such that
$\left [\widehat {X} / \widetilde {T}\right ] \xrightarrow {\sim } \mathcal {X}$
such that
 $\widehat {X} \to \left [\widehat {X} / \widetilde {T}\right ] \xrightarrow {\sim } \mathcal {X} \xrightarrow {\pi } X$
is the toric morphism induced by
$\widehat {X} \to \left [\widehat {X} / \widetilde {T}\right ] \xrightarrow {\sim } \mathcal {X} \xrightarrow {\pi } X$
is the toric morphism induced by
![]() $\nu \oplus \operatorname {\mathrm {id}}\colon \widehat {N} \to N$
.
$\nu \oplus \operatorname {\mathrm {id}}\colon \widehat {N} \to N$
.
Proof. For ease of notation, let
![]() $\widehat {\nu }=\nu \oplus \operatorname {\mathrm {id}}$
and consider the stacky fan
$\widehat {\nu }=\nu \oplus \operatorname {\mathrm {id}}$
and consider the stacky fan
![]() $\left (\widehat {\sigma },\widehat {\nu }\right )$
. One computes that
$\left (\widehat {\sigma },\widehat {\nu }\right )$
. One computes that
![]() $\operatorname {\mathrm {cok}}\left (\widehat {\nu }^*\right )=\widetilde {M}$
and hence
$\operatorname {\mathrm {cok}}\left (\widehat {\nu }^*\right )=\widetilde {M}$
and hence
![]() $G_{\widehat {\nu }}=\widetilde {T}$
. As a result,
$G_{\widehat {\nu }}=\widetilde {T}$
. As a result,
 $\mathcal {X}_{\widehat {\sigma },\widehat {\nu }}=\left [\widehat {X} / \widetilde {T}\right ]$
for an appropriate
$\mathcal {X}_{\widehat {\sigma },\widehat {\nu }}=\left [\widehat {X} / \widetilde {T}\right ]$
for an appropriate
![]() $\widetilde {T}$
-action on
$\widetilde {T}$
-action on
![]() $\widehat {X}$
.
$\widehat {X}$
.
Next note that
![]() $\mathcal {X}$
is, by definition, the toric stack
$\mathcal {X}$
is, by definition, the toric stack
![]() $\mathcal {X}_{\widetilde {\sigma },\nu }$
, and consider the following commutative diagram, where the vertical maps are stacky fans and the horizontal maps are morphisms between the stacky fans:
$\mathcal {X}_{\widetilde {\sigma },\nu }$
, and consider the following commutative diagram, where the vertical maps are stacky fans and the horizontal maps are morphisms between the stacky fans:

This induces morphisms
 $\mathcal {X}\to \left [\widehat {X} / \widetilde {T}\right ]\to X$
of toric stacks, and the composite is the morphism
$\mathcal {X}\to \left [\widehat {X} / \widetilde {T}\right ]\to X$
of toric stacks, and the composite is the morphism
![]() $\pi $
. By [Reference Geraschenko and SatrianoGS15a, Lemma B.17], the former map is an isomorphism of toric stacks; this is the inverse of our desired isomorphism
$\pi $
. By [Reference Geraschenko and SatrianoGS15a, Lemma B.17], the former map is an isomorphism of toric stacks; this is the inverse of our desired isomorphism
 $\left [\widehat {X} / \widetilde {T}\right ] \xrightarrow {\sim } \mathcal {X}$
. Lastly, we see that the toric morphism
$\left [\widehat {X} / \widetilde {T}\right ] \xrightarrow {\sim } \mathcal {X}$
. Lastly, we see that the toric morphism
 $\widehat {X}\to \left [\widehat {X} / \widetilde {T}\right ]\to X$
is induced by the rightmost map in the top row of the diagram, namely
$\widehat {X}\to \left [\widehat {X} / \widetilde {T}\right ]\to X$
is induced by the rightmost map in the top row of the diagram, namely
![]() $\widehat {\nu }\colon \widehat {N} \to N$
.
$\widehat {\nu }\colon \widehat {N} \to N$
.
7.3 Canonical stacks and preimages of cocharacters
We end this section by proving Theorem 7.1(b).
For the remainder of this section, let
![]() $r = \operatorname {\mathrm {rk}} \widetilde {N}$
, let
$r = \operatorname {\mathrm {rk}} \widetilde {N}$
, let
![]() $v_1, \dotsc , v_r$
be the first lattice points of the rays of
$v_1, \dotsc , v_r$
be the first lattice points of the rays of
![]() $\sigma $
, let
$\sigma $
, let
![]() $e_1, \dotsc , e_r$
be the generators of
$e_1, \dotsc , e_r$
be the generators of
![]() $\widetilde {N}$
indexed by the rays
$\widetilde {N}$
indexed by the rays
![]() $\mathbb {R}_{\geq 0} v_1, \dotsc , \mathbb {R}_{\geq 0} v_r$
, so
$\mathbb {R}_{\geq 0} v_1, \dotsc , \mathbb {R}_{\geq 0} v_r$
, so
for all
![]() $i \in \{1, \dotsc , r\}$
, and let
$i \in \{1, \dotsc , r\}$
, and let
![]() $f_1, \dotsc , f_r$
be the basis of
$f_1, \dotsc , f_r$
be the basis of
![]() $\widetilde {M}$
dual to
$\widetilde {M}$
dual to
![]() $e_1, \dotsc , e_r$
. Thus
$e_1, \dotsc , e_r$
. Thus
![]() $f_1, \dotsc , f_r$
are the minimal generators of the monoid F.
$f_1, \dotsc , f_r$
are the minimal generators of the monoid F.
Lemma 7.9. We have the equality
Proof. Because the inclusion
![]() $P \hookrightarrow F$
is dual to
$P \hookrightarrow F$
is dual to
![]() $\beta $
,
$\beta $
,
for all
![]() $i \in \{1, \dotsc , r\}$
. Then
$i \in \{1, \dotsc , r\}$
. Then
For the remainder of this section, let
![]() $\widehat {N}$
,
$\widehat {N}$
,
![]() $\widehat {\sigma }$
and
$\widehat {\sigma }$
and
![]() $\widehat {X}$
be as in Proposition 7.8. Let
$\widehat {X}$
be as in Proposition 7.8. Let
![]() $\rho : \widehat {X} \to \mathcal {X}$
be the composition
$\rho : \widehat {X} \to \mathcal {X}$
be the composition
 $\widehat {X} \to \left [ \widehat {X} / \widetilde {T} \right ] \xrightarrow {\sim } \mathcal {X}$
, where the
$\widehat {X} \to \left [ \widehat {X} / \widetilde {T} \right ] \xrightarrow {\sim } \mathcal {X}$
, where the
![]() $\widetilde {T}$
-action on
$\widetilde {T}$
-action on
![]() $\widehat {X}$
and the isomorphism
$\widehat {X}$
and the isomorphism
 $\left [ \widehat {X} / \widetilde {T} \right ] \xrightarrow {\sim } \mathcal {X}$
are as in the statement of Proposition 7.8; let
$\left [ \widehat {X} / \widetilde {T} \right ] \xrightarrow {\sim } \mathcal {X}$
are as in the statement of Proposition 7.8; let
![]() $D_1, \dotsc , D_r$
be the divisors of
$D_1, \dotsc , D_r$
be the divisors of
![]() $\widehat {X}$
indexed by
$\widehat {X}$
indexed by
![]() $e_1 \oplus 0, \dotsc , e_r\oplus 0 \in \widetilde {N} \oplus N = \widehat {N}$
, respectively; and let
$e_1 \oplus 0, \dotsc , e_r\oplus 0 \in \widetilde {N} \oplus N = \widehat {N}$
, respectively; and let
![]() $\mathcal {O}(-D_1), \dotsc , \mathcal {O}(-D_r)$
be the ideal sheaves on
$\mathcal {O}(-D_1), \dotsc , \mathcal {O}(-D_r)$
be the ideal sheaves on
![]() $\widehat {X}$
of
$\widehat {X}$
of
![]() $D_1, \dotsc , D_r$
, respectively. Note that for all
$D_1, \dotsc , D_r$
, respectively. Note that for all
![]() $i \in \{1, \dotsc , r\}$
, the ideal
$i \in \{1, \dotsc , r\}$
, the ideal
![]() $\mathcal {O}(-D_i)$
is generated by the monomial in
$\mathcal {O}(-D_i)$
is generated by the monomial in
![]() $k[F \oplus M]$
indexed by
$k[F \oplus M]$
indexed by
![]() $f_i \oplus 0$
.
$f_i \oplus 0$
.
Proposition 7.10. Set
![]() $w \in \sigma \cap N$
. Then
$w \in \sigma \cap N$
. Then
 $$ \begin{align*} \mathscr{L}(\rho)^{-1} \left( \mathscr{L}(\pi)^{-1}\left(\operatorname{\mathrm{trop}}^{-1}(w)\right) \right) = \bigcup_{\widetilde{w} \in \beta^{-1}(w)} \left( \bigcap_{i =1}^r \operatorname{\mathrm{ord}}_{\mathcal{O}\left(-D_i\right)}^{-1}\left( \left\langle \widetilde{w}, f_i \right\rangle \right) \right).\\[-15pt] \end{align*} $$
$$ \begin{align*} \mathscr{L}(\rho)^{-1} \left( \mathscr{L}(\pi)^{-1}\left(\operatorname{\mathrm{trop}}^{-1}(w)\right) \right) = \bigcup_{\widetilde{w} \in \beta^{-1}(w)} \left( \bigcap_{i =1}^r \operatorname{\mathrm{ord}}_{\mathcal{O}\left(-D_i\right)}^{-1}\left( \left\langle \widetilde{w}, f_i \right\rangle \right) \right).\\[-15pt] \end{align*} $$
Proof. By Remark 4.6 and Lemma 4.7(2), it is enough to show that for any
![]() $\widehat {f}\in \widehat {\sigma }^\vee \cap \widehat {N}^*$
, there exists
$\widehat {f}\in \widehat {\sigma }^\vee \cap \widehat {N}^*$
, there exists
![]() $\widehat {f}'\in \widehat {\sigma }^\vee \cap \widehat {N}^*$
such that
$\widehat {f}'\in \widehat {\sigma }^\vee \cap \widehat {N}^*$
such that
![]() $\widehat {f}+\widehat {f}'$
is in the image of
$\widehat {f}+\widehat {f}'$
is in the image of
![]() $\sigma ^\vee \cap M$
. By the definition of
$\sigma ^\vee \cap M$
. By the definition of
![]() $\widehat {\nu }$
, the map
$\widehat {\nu }$
, the map
 $$ \begin{align*} P=\sigma^\vee\cap M\to\widehat{\sigma}^\vee\cap\widehat{N}^*=\left(\widetilde{\sigma}^\vee\cap\widetilde{M}\right)\oplus 0=F\oplus 0\\[-15pt] \end{align*} $$
$$ \begin{align*} P=\sigma^\vee\cap M\to\widehat{\sigma}^\vee\cap\widehat{N}^*=\left(\widetilde{\sigma}^\vee\cap\widetilde{M}\right)\oplus 0=F\oplus 0\\[-15pt] \end{align*} $$
is precisely
![]() $p\mapsto (p,0)$
. The result then follows from Proposition 2.14.
$p\mapsto (p,0)$
. The result then follows from Proposition 2.14.
We may now complete the proof of Theorem 7.1(b).
Proof of Theorem 7.1(b)
Set
![]() $w \in \sigma \cap N$
, and set
$w \in \sigma \cap N$
, and set
 $$ \begin{align*} \widehat{C} = \mathscr{L}(\rho)^{-1} \left( \mathscr{L}(\pi)^{-1}\left(\operatorname{\mathrm{trop}}^{-1}(w)\right) \right) \subset \mathscr{L}\left(\widehat{X}\right). \\[-15pt]\end{align*} $$
$$ \begin{align*} \widehat{C} = \mathscr{L}(\rho)^{-1} \left( \mathscr{L}(\pi)^{-1}\left(\operatorname{\mathrm{trop}}^{-1}(w)\right) \right) \subset \mathscr{L}\left(\widehat{X}\right). \\[-15pt]\end{align*} $$
Then
 $$ \begin{align*} \mu_{\widehat{X}} \left(\widehat{C}\right) &= \mu_{\widehat{X}}\left( \bigcup_{\widetilde{w} \in \beta^{-1}(w)} \left( \bigcap_{i =1}^r \operatorname{\mathrm{ord}}_{\mathcal{O}\left(-D_i\right)}^{-1}\left( \left\langle \widetilde{w}, f_i \right\rangle \right) \right) \right)\\ &= \sum_{\widetilde{w} \in \beta^{-1}(w)} \mu_{\widehat{X}} \left( \bigcap_{i =1}^r \operatorname{\mathrm{ord}}_{\mathcal{O}\left(-D_i\right)}^{-1}\left( \left\langle \widetilde{w}, f_i \right\rangle \right) \right)\\ &= \sum_{\widetilde{w} \in \beta^{-1}(w)} (\mathbb{L}-1)^{r+d} \mathbb{L}^{-(r+d)-\sum_{i =1}^r \left\langle \widetilde{w}, f_i\right\rangle}\\ &=\sum_{\widetilde{w} \in \beta^{-1}(w)} (\mathbb{L}-1)^{r+d} \mathbb{L}^{-(r+d) - \left\langle w, q \right\rangle/m}\\ &= \left(\#\beta^{-1}(w)\right)(\mathbb{L}-1)^{r+d} \mathbb{L}^{-(r+d) - \left\langle w, q \right\rangle/m}, \end{align*} $$
$$ \begin{align*} \mu_{\widehat{X}} \left(\widehat{C}\right) &= \mu_{\widehat{X}}\left( \bigcup_{\widetilde{w} \in \beta^{-1}(w)} \left( \bigcap_{i =1}^r \operatorname{\mathrm{ord}}_{\mathcal{O}\left(-D_i\right)}^{-1}\left( \left\langle \widetilde{w}, f_i \right\rangle \right) \right) \right)\\ &= \sum_{\widetilde{w} \in \beta^{-1}(w)} \mu_{\widehat{X}} \left( \bigcap_{i =1}^r \operatorname{\mathrm{ord}}_{\mathcal{O}\left(-D_i\right)}^{-1}\left( \left\langle \widetilde{w}, f_i \right\rangle \right) \right)\\ &= \sum_{\widetilde{w} \in \beta^{-1}(w)} (\mathbb{L}-1)^{r+d} \mathbb{L}^{-(r+d)-\sum_{i =1}^r \left\langle \widetilde{w}, f_i\right\rangle}\\ &=\sum_{\widetilde{w} \in \beta^{-1}(w)} (\mathbb{L}-1)^{r+d} \mathbb{L}^{-(r+d) - \left\langle w, q \right\rangle/m}\\ &= \left(\#\beta^{-1}(w)\right)(\mathbb{L}-1)^{r+d} \mathbb{L}^{-(r+d) - \left\langle w, q \right\rangle/m}, \end{align*} $$
where the first equality is by Proposition 7.10, the second is by Proposition 2.15 and the fact that the union in the first line is disjoint, the third equality is by [Reference Chambert-Loir, Nicaise and SebagCLNS18, Chapter 7, Lemma 3.3.3] and the definition of
![]() $\widehat {X}$
and
$\widehat {X}$
and
![]() $D_1, \dotsc , D_r$
and the fourth equality is by Lemma 7.9.
$D_1, \dotsc , D_r$
and the fourth equality is by Lemma 7.9.
The set
![]() $\mathscr {L}(\pi )^{-1}\left (\operatorname {\mathrm {trop}}^{-1}(w)\right ) \subset \lvert \mathscr {L}(\mathcal {X})\rvert $
is a cylinder, by Remark 4.6 and Proposition 7.7. Then by Theorem 3.9,
$\mathscr {L}(\pi )^{-1}\left (\operatorname {\mathrm {trop}}^{-1}(w)\right ) \subset \lvert \mathscr {L}(\mathcal {X})\rvert $
is a cylinder, by Remark 4.6 and Proposition 7.7. Then by Theorem 3.9,
 $$ \begin{align*} \mu_{\mathcal{X}}\left( \mathscr{L}(\pi)^{-1}\left(\operatorname{\mathrm{trop}}^{-1}(w)\right)\right) &= \mu_{\widehat{X}} \left(\widehat{C}\right) \mathrm{e}\left(\widetilde{T}\right)^{-1} \mathbb{L}^{\dim \widetilde{T}}\\ &= \left(\#\beta^{-1}(w)\right)(\mathbb{L}-1)^{d} \mathbb{L}^{-d - \left\langle w, q \right\rangle/m}.\\[-36pt] \end{align*} $$
$$ \begin{align*} \mu_{\mathcal{X}}\left( \mathscr{L}(\pi)^{-1}\left(\operatorname{\mathrm{trop}}^{-1}(w)\right)\right) &= \mu_{\widehat{X}} \left(\widehat{C}\right) \mathrm{e}\left(\widetilde{T}\right)^{-1} \mathbb{L}^{\dim \widetilde{T}}\\ &= \left(\#\beta^{-1}(w)\right)(\mathbb{L}-1)^{d} \mathbb{L}^{-d - \left\langle w, q \right\rangle/m}.\\[-36pt] \end{align*} $$
8 Stringy invariants and toric Artin stacks: Proof of Theorem 1.7
We complete the proof of Theorem 1.7 in this section. Set
![]() $d \in \mathbb {N}$
, let
$d \in \mathbb {N}$
, let
![]() $N \cong \mathbb {Z}^d$
be a lattice and let
$N \cong \mathbb {Z}^d$
be a lattice and let
![]() $T = \operatorname {\mathrm {Spec}}(k[N^*])$
be the algebraic torus with cocharacter lattice N. We recall the following lemma, whose proof is standard:
$T = \operatorname {\mathrm {Spec}}(k[N^*])$
be the algebraic torus with cocharacter lattice N. We recall the following lemma, whose proof is standard:
Lemma 8.1. Let
![]() $\sigma $
be a pointed rational cone in
$\sigma $
be a pointed rational cone in
![]() $N_{\mathbb {R}}$
, and assume that the affine T-toric variety associated to it is
$N_{\mathbb {R}}$
, and assume that the affine T-toric variety associated to it is
![]() $\mathbb {Q}$
-Gorenstein. Then there exists a d-dimensional pointed rational cone
$\mathbb {Q}$
-Gorenstein. Then there exists a d-dimensional pointed rational cone
![]() $\overline {\sigma }$
in
$\overline {\sigma }$
in
![]() $N_{\mathbb {R}}$
such that
$N_{\mathbb {R}}$
such that
![]() $\sigma $
is a face of
$\sigma $
is a face of
![]() $\overline {\sigma }$
and the T-toric variety associeted to
$\overline {\sigma }$
and the T-toric variety associeted to
![]() $\overline {\sigma }$
is
$\overline {\sigma }$
is
![]() $\mathbb {Q}$
-Gorenstein.
$\mathbb {Q}$
-Gorenstein.
Remark 8.2. By Remark 1.8, Proposition 2.18, Proposition 3.27, Proposition 3.31, Proposition 3.32 and Lemma 8.1, to prove Theorem 1.7 it is sufficient to prove the special case where
![]() $\mathcal {X}$
is the canonical stack over an affine T-toric variety defined by a d-dimensional cone in
$\mathcal {X}$
is the canonical stack over an affine T-toric variety defined by a d-dimensional cone in
![]() $N_{\mathbb {R}}$
.
$N_{\mathbb {R}}$
.
Set
![]() $\sigma $
be a d-dimensional pointed rational cone in
$\sigma $
be a d-dimensional pointed rational cone in
![]() $N_{\mathbb {R}}$
, let X be the affine T-toric variety associated to
$N_{\mathbb {R}}$
, let X be the affine T-toric variety associated to
![]() $\sigma $
, let
$\sigma $
, let
![]() $\mathcal {X}$
be the canonical stack over X, let
$\mathcal {X}$
be the canonical stack over X, let
![]() $\pi : \mathcal {X} \to X$
be the canonical map and assume that X is
$\pi : \mathcal {X} \to X$
be the canonical map and assume that X is
![]() $\mathbb {Q}$
-Gorenstein. We will use the notation listed in Notation 2.19.
$\mathbb {Q}$
-Gorenstein. We will use the notation listed in Notation 2.19.
Proposition 8.3. Set
![]() $W \subset \sigma \cap N$
. Then
$W \subset \sigma \cap N$
. Then
 $$ \begin{align*} \bigcup_{w \in W} \operatorname{\mathrm{trop}}^{-1}(w) \end{align*} $$
$$ \begin{align*} \bigcup_{w \in W} \operatorname{\mathrm{trop}}^{-1}(w) \end{align*} $$
is a measurable subset of
![]() $\mathscr {L}(X)$
.
$\mathscr {L}(X)$
.
Proof. We have that
![]() $\mathscr {L}(X \setminus T)$
is a measurable subset of
$\mathscr {L}(X \setminus T)$
is a measurable subset of
![]() $\mathscr {L}(X)$
, because
$\mathscr {L}(X)$
, because
![]() $X \setminus T$
is a closed subscheme of X. For each
$X \setminus T$
is a closed subscheme of X. For each
![]() $w \in \sigma \cap N$
, the set
$w \in \sigma \cap N$
, the set
![]() $\operatorname {\mathrm {trop}}^{-1}(w)$
is a measurable subset of
$\operatorname {\mathrm {trop}}^{-1}(w)$
is a measurable subset of
![]() $\mathscr {L}(X)$
by Remark 4.6. Also,
$\mathscr {L}(X)$
by Remark 4.6. Also,
 $$ \begin{align*} \mathscr{L}(X \setminus T) \cup \bigcup_{w \in \sigma \cap N} \operatorname{\mathrm{trop}}^{-1}(w) = \mathscr{L}(X) \end{align*} $$
$$ \begin{align*} \mathscr{L}(X \setminus T) \cup \bigcup_{w \in \sigma \cap N} \operatorname{\mathrm{trop}}^{-1}(w) = \mathscr{L}(X) \end{align*} $$
is measurable and disjoint, so for any
![]() $\varepsilon \in \mathbb {R}_{>0}$
, there are only finitely many
$\varepsilon \in \mathbb {R}_{>0}$
, there are only finitely many
![]() $w \in \sigma \cap N$
such that
$w \in \sigma \cap N$
such that
 $\left \lVert \mu _X\left (\operatorname {\mathrm {trop}}^{-1}(w)\right )\right \rVert \geq \varepsilon $
. Thus
$\left \lVert \mu _X\left (\operatorname {\mathrm {trop}}^{-1}(w)\right )\right \rVert \geq \varepsilon $
. Thus
![]() $\bigcup _{w \in W} \operatorname {\mathrm {trop}}^{-1}(w)$
is a measurable subset of
$\bigcup _{w \in W} \operatorname {\mathrm {trop}}^{-1}(w)$
is a measurable subset of
![]() $\mathscr {L}(X)$
.
$\mathscr {L}(X)$
.
Proposition 8.4. The function
![]() $\operatorname {\mathrm {sep}}_\pi : \mathscr {L}(X) \to \mathbb {N}$
has measurable fibres.
$\operatorname {\mathrm {sep}}_\pi : \mathscr {L}(X) \to \mathbb {N}$
has measurable fibres.
Proof. Theorem 4.9 implies that for any
![]() $\varphi \in \mathscr {L}(X)$
with
$\varphi \in \mathscr {L}(X)$
with
![]() $\operatorname {\mathrm {trop}}(\varphi ) \in \sigma \cap N$
,
$\operatorname {\mathrm {trop}}(\varphi ) \in \sigma \cap N$
,
 $$ \begin{align*} \operatorname{\mathrm{sep}}_\pi(\varphi) = \#\beta^{-1}(\operatorname{\mathrm{trop}}(\varphi)). \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{sep}}_\pi(\varphi) = \#\beta^{-1}(\operatorname{\mathrm{trop}}(\varphi)). \end{align*} $$
Thus, noting that each
![]() $\beta ^{-1}(w)$
is finite, we have that for any
$\beta ^{-1}(w)$
is finite, we have that for any
![]() $n \in \mathbb {N}$
,
$n \in \mathbb {N}$
,
 $$ \begin{align*} \operatorname{\mathrm{sep}}_\pi^{-1}(n) = \left( \operatorname{\mathrm{sep}}_\pi^{-1}(n) \cap \mathscr{L}(X \setminus T) \right) \cup \bigcup_{\substack{w \in \sigma \cap N\\ \#\beta^{-1}(w) = n}} \operatorname{\mathrm{trop}}^{-1}(w) \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{sep}}_\pi^{-1}(n) = \left( \operatorname{\mathrm{sep}}_\pi^{-1}(n) \cap \mathscr{L}(X \setminus T) \right) \cup \bigcup_{\substack{w \in \sigma \cap N\\ \#\beta^{-1}(w) = n}} \operatorname{\mathrm{trop}}^{-1}(w) \end{align*} $$
is measurable by Proposition 8.3 and the fact that
![]() $\mu _X(\mathscr {L}(X \setminus T)) = 0$
, which implies that any subset of
$\mu _X(\mathscr {L}(X \setminus T)) = 0$
, which implies that any subset of
![]() $\mathscr {L}(X \setminus T)$
is a measurable subset of
$\mathscr {L}(X \setminus T)$
is a measurable subset of
![]() $\mathscr {L}(X)$
.
$\mathscr {L}(X)$
.
For the remainder of this section, we will use the fact that by Proposition 8.4, the integral
 $\int _C \operatorname {\mathrm {sep}}_\pi \mathrm {d}\mu ^{\mathrm {Gor}}_X$
is well defined for any measurable subset
$\int _C \operatorname {\mathrm {sep}}_\pi \mathrm {d}\mu ^{\mathrm {Gor}}_X$
is well defined for any measurable subset
![]() $C \subset \mathscr {L}(X)$
.
$C \subset \mathscr {L}(X)$
.
We end this section with the next proposition, which along with Remark 8.2 and Proposition 8.4 implies Theorem 1.7.
Proposition 8.5. Let C be a measurable subset of
![]() $\mathscr {L}(X)$
. Then
$\mathscr {L}(X)$
. Then
![]() $\mathscr {L}(\pi )^{-1}(C)$
is a measurable subset of
$\mathscr {L}(\pi )^{-1}(C)$
is a measurable subset of
![]() $\lvert \mathscr {L}(\mathcal {X})\rvert $
and
$\lvert \mathscr {L}(\mathcal {X})\rvert $
and
 $$ \begin{align*} \mu_{\mathcal{X}}\left(\mathscr{L}(\pi)^{-1}(C)\right) = \int_C \operatorname{\mathrm{sep}}_\pi \mathrm{d}\mu^{\mathrm{Gor}}_X. \end{align*} $$
$$ \begin{align*} \mu_{\mathcal{X}}\left(\mathscr{L}(\pi)^{-1}(C)\right) = \int_C \operatorname{\mathrm{sep}}_\pi \mathrm{d}\mu^{\mathrm{Gor}}_X. \end{align*} $$
Proof. By Proposition 2.3, Proposition 7.3 and the fact that
 $$ \begin{align*} \mu_X\left(\mathscr{L}(X) \setminus \bigcup_{w \in \sigma \cap N} \operatorname{\mathrm{trop}}^{-1}(w) \right) = \mu_X \left(\mathscr{L}(X \setminus T)\right) = 0, \end{align*} $$
$$ \begin{align*} \mu_X\left(\mathscr{L}(X) \setminus \bigcup_{w \in \sigma \cap N} \operatorname{\mathrm{trop}}^{-1}(w) \right) = \mu_X \left(\mathscr{L}(X \setminus T)\right) = 0, \end{align*} $$
it is enough to prove the statement for each
![]() $\operatorname {\mathrm {trop}}^{-1}(w)\cap C$
. In other words, we may fix w and assume
$\operatorname {\mathrm {trop}}^{-1}(w)\cap C$
. In other words, we may fix w and assume
![]() $C\subset \operatorname {\mathrm {trop}}^{-1}(w)$
.
$C\subset \operatorname {\mathrm {trop}}^{-1}(w)$
.
We first note that
![]() $\mathscr {L}(\pi )^{-1}(C) \subset \lvert \mathscr {L}(\mathcal {X})\rvert $
is measurable, by Theorem 7.1(a). Let
$\mathscr {L}(\pi )^{-1}(C) \subset \lvert \mathscr {L}(\mathcal {X})\rvert $
is measurable, by Theorem 7.1(a). Let
![]() $m \in \mathbb {Z}_{>0}$
and
$m \in \mathbb {Z}_{>0}$
and
![]() $q \in P$
be such that
$q \in P$
be such that
![]() $\langle v, q \rangle = m$
for any first lattice point v of a ray of
$\langle v, q \rangle = m$
for any first lattice point v of a ray of
![]() $\sigma $
. Let
$\sigma $
. Let
![]() $j_w$
be as in the statement of Theorem 6.1(a), and let
$j_w$
be as in the statement of Theorem 6.1(a), and let
![]() $\Theta _w$
be as in the statement of Theorem 7.1(a). By Theorem 6.1(b) and our choice of
$\Theta _w$
be as in the statement of Theorem 7.1(a). By Theorem 6.1(b) and our choice of
![]() $j_w$
,
$j_w$
,
 $$ \begin{align*} \left(\mathbb{L}^{1/m}\right)^{j_w} \mu_X\left(\operatorname{\mathrm{trop}}^{-1}(w)\right) = \mu^{\mathrm{Gor}}_X\left(\operatorname{\mathrm{trop}}^{-1}(w)\right) = \mathbb{L}^{-d}(\mathbb{L}-1)^d \left(\mathbb{L}^{1/m}\right)^{- \left\langle w, q \right\rangle}. \end{align*} $$
$$ \begin{align*} \left(\mathbb{L}^{1/m}\right)^{j_w} \mu_X\left(\operatorname{\mathrm{trop}}^{-1}(w)\right) = \mu^{\mathrm{Gor}}_X\left(\operatorname{\mathrm{trop}}^{-1}(w)\right) = \mathbb{L}^{-d}(\mathbb{L}-1)^d \left(\mathbb{L}^{1/m}\right)^{- \left\langle w, q \right\rangle}. \end{align*} $$
In particular,
![]() $\mu _X\left (\operatorname {\mathrm {trop}}^{-1}(w)\right )$
is a unit in
$\mu _X\left (\operatorname {\mathrm {trop}}^{-1}(w)\right )$
is a unit in
 $\widehat {\mathscr {M}_k}\left [\mathbb {L}^{1/m}\right ]$
. Then by the foregoing equality, Theorem 7.1(b) and our choice of
$\widehat {\mathscr {M}_k}\left [\mathbb {L}^{1/m}\right ]$
. Then by the foregoing equality, Theorem 7.1(b) and our choice of
![]() $\Theta _w$
,
$\Theta _w$
,
 $$ \begin{align*} \left(\#\beta^{-1}(w)\right)\left(\mathbb{L}^{1/m}\right)^{j_w} \mu_X\left(\operatorname{\mathrm{trop}}^{-1}(w)\right) &= \left(\#\beta^{-1}(w)\right)\mathbb{L}^{-d}(\mathbb{L}-1)^d \left(\mathbb{L}^{1/m}\right)^{- \left\langle w, q \right\rangle}\\ &= \mu_{\mathcal{X}}\left(\mathscr{L}(\pi)^{-1}\left(\operatorname{\mathrm{trop}}^{-1}(w)\right)\right)\\ &= \Theta_w \mu_X\left(\operatorname{\mathrm{trop}}^{-1}(w)\right), \end{align*} $$
$$ \begin{align*} \left(\#\beta^{-1}(w)\right)\left(\mathbb{L}^{1/m}\right)^{j_w} \mu_X\left(\operatorname{\mathrm{trop}}^{-1}(w)\right) &= \left(\#\beta^{-1}(w)\right)\mathbb{L}^{-d}(\mathbb{L}-1)^d \left(\mathbb{L}^{1/m}\right)^{- \left\langle w, q \right\rangle}\\ &= \mu_{\mathcal{X}}\left(\mathscr{L}(\pi)^{-1}\left(\operatorname{\mathrm{trop}}^{-1}(w)\right)\right)\\ &= \Theta_w \mu_X\left(\operatorname{\mathrm{trop}}^{-1}(w)\right), \end{align*} $$
so
 $$ \begin{align*} \Theta_w = \left(\#\beta^{-1}(w)\right)\left(\mathbb{L}^{1/m}\right)^{j_w}. \end{align*} $$
$$ \begin{align*} \Theta_w = \left(\#\beta^{-1}(w)\right)\left(\mathbb{L}^{1/m}\right)^{j_w}. \end{align*} $$
Therefore, by our choice of
![]() $\Theta _w$
and
$\Theta _w$
and
![]() $j_w$
,
$j_w$
,
 $$ \begin{align*} \mu_{\mathcal{X}}\left(\mathscr{L}(\pi)^{-1}(C)\right) &= \Theta_w\mu_X(C)\\ &= \left(\#\beta^{-1}(w)\right)\left(\mathbb{L}^{1/m}\right)^{j_w} \mu_X(C)\\ &= \left(\#\beta^{-1}(w)\right) \mu^{\mathrm{Gor}}_X(C)\\ &= \int_C \operatorname{\mathrm{sep}}_\pi \mathrm{d}\mu^{\mathrm{Gor}}_X, \end{align*} $$
$$ \begin{align*} \mu_{\mathcal{X}}\left(\mathscr{L}(\pi)^{-1}(C)\right) &= \Theta_w\mu_X(C)\\ &= \left(\#\beta^{-1}(w)\right)\left(\mathbb{L}^{1/m}\right)^{j_w} \mu_X(C)\\ &= \left(\#\beta^{-1}(w)\right) \mu^{\mathrm{Gor}}_X(C)\\ &= \int_C \operatorname{\mathrm{sep}}_\pi \mathrm{d}\mu^{\mathrm{Gor}}_X, \end{align*} $$
where the last equality is by Theorem 4.9.
9 Fantastacks with special stabilisers: Proof of Theorem 1.11
The goal of this section is to prove Theorem 9.1, which characterises when a fantastack has only special stabilisers, and then to use this characterisation to prove Theorem 1.11. For simplicity, we state the criterion Theorem 9.1 only in the case where the good moduli space is affine (and defined by a full-dimensional cone).
Throughout this section, set
![]() $d \in \mathbb {N}$
, let
$d \in \mathbb {N}$
, let
![]() $N \cong \mathbb {Z}^d$
be a lattice and let
$N \cong \mathbb {Z}^d$
be a lattice and let
![]() $T = \operatorname {\mathrm {Spec}}(k[N^*])$
be the algebraic torus with cocharacter lattice N.
$T = \operatorname {\mathrm {Spec}}(k[N^*])$
be the algebraic torus with cocharacter lattice N.
Theorem 9.1. Let
![]() $\mathcal {X}=\mathcal {F}_{\sigma ,\nu }$
be a fantastack with dense torus T and keep the notation listed in Definition 2.12. Then the following are equivalent:
$\mathcal {X}=\mathcal {F}_{\sigma ,\nu }$
be a fantastack with dense torus T and keep the notation listed in Definition 2.12. Then the following are equivalent:
-
(i) The stabilisers of
 $\mathcal {X}$
are all special groups.
$\mathcal {X}$
are all special groups. -
(ii) For all
 $I \subset \{1, \dotsc , r\}$
, the set
$I \subset \{1, \dotsc , r\}$
, the set
 $\{\nu (e_i) \mid i \in I\}$
is linearly independent if and only if it can be extended to a basis for N.
$\{\nu (e_i) \mid i \in I\}$
is linearly independent if and only if it can be extended to a basis for N. -
(iii) For some
 $n \in \mathbb {N}$
, we have
$n \in \mathbb {N}$
, we have
 $\mathcal {X}\cong \left [\mathbb {A}^r_k/\mathbb {G}_m^n\right ]$
, where
$\mathcal {X}\cong \left [\mathbb {A}^r_k/\mathbb {G}_m^n\right ]$
, where
 $\mathbb {G}_m^n$
acts on
$\mathbb {G}_m^n$
acts on
 $\mathbb {A}^r_k$
with weights
$\mathbb {A}^r_k$
with weights
 $w_1,\dotsc ,w_r\in \mathbb {Z}^n$
such that for all
$w_1,\dotsc ,w_r\in \mathbb {Z}^n$
such that for all
 $I \subset \{1, \dotsc , r\}$
, the set
$I \subset \{1, \dotsc , r\}$
, the set
 $\{w_i \mid i \in I\}$
is linearly independent if and only if it can be extended to a basis for
$\{w_i \mid i \in I\}$
is linearly independent if and only if it can be extended to a basis for
 $\mathbb {Z}^n$
.
$\mathbb {Z}^n$
.
The following is an immediate consequence of Theorem 9.1, noting that taking a canonical stack is compatible with taking products of toric varieties:
Corollary 9.2. Let
![]() $\sigma $
be a pointed rational cone in
$\sigma $
be a pointed rational cone in
![]() $N_{\mathbb {R}}$
, and let
$N_{\mathbb {R}}$
, and let
![]() $\mathcal {X}$
be the canonical stack over
$\mathcal {X}$
be the canonical stack over
![]() $X_\sigma $
. If
$X_\sigma $
. If
![]() $v_1, \dotsc , v_r \in N$
are the first lattice points of the rays of
$v_1, \dotsc , v_r \in N$
are the first lattice points of the rays of
![]() $\sigma $
, then the following are equivalent:
$\sigma $
, then the following are equivalent:
-
(i) The stabilisers of
 $\mathcal {X}$
are all special groups.
$\mathcal {X}$
are all special groups. -
(ii) For all
 $I \subset \{1, \dotsc , r \}$
, the set
$I \subset \{1, \dotsc , r \}$
, the set
 $\{v_i \mid i \in I\}$
is linearly independent if and only if it can be extended to a basis for N.
$\{v_i \mid i \in I\}$
is linearly independent if and only if it can be extended to a basis for N.
Before proving Theorem 9.1, we use Corollary 9.2 to prove Theorem 1.11.
Proof of Theorem 1.11
Let X be a toric variety over k, let
![]() $\pi : \mathcal {X} \to X$
be its canonical stack (see Remark 2.21) and assume that the stabilisers of
$\pi : \mathcal {X} \to X$
be its canonical stack (see Remark 2.21) and assume that the stabilisers of
![]() $\mathcal {X}$
are all special groups. By Proposition 2.18 and the definition of
$\mathcal {X}$
are all special groups. By Proposition 2.18 and the definition of
![]() $\operatorname {\mathrm {sep}}_\pi $
, we may assume that X is the affine T-toric variety defined by a pointed rational cone
$\operatorname {\mathrm {sep}}_\pi $
, we may assume that X is the affine T-toric variety defined by a pointed rational cone
![]() $\sigma $
in
$\sigma $
in
![]() $N_{\mathbb {R}}$
. It is easy to check, for example by using Corollary 9.2, that because the stabilisers of
$N_{\mathbb {R}}$
. It is easy to check, for example by using Corollary 9.2, that because the stabilisers of
![]() $\mathcal {X}$
are all special groups, the cone
$\mathcal {X}$
are all special groups, the cone
![]() $\sigma $
is a face of a d-dimensional pointed rational cone in
$\sigma $
is a face of a d-dimensional pointed rational cone in
![]() $N_{\mathbb {R}}$
whose associated toric variety has a canonical stack with only special stabilisers. Therefore we may assume that
$N_{\mathbb {R}}$
whose associated toric variety has a canonical stack with only special stabilisers. Therefore we may assume that
![]() $\sigma $
is d-dimensional and use the notation listed in Notation 2.19. Then by Proposition 2.15, Theorem 4.9 and the fact that
$\sigma $
is d-dimensional and use the notation listed in Notation 2.19. Then by Proposition 2.15, Theorem 4.9 and the fact that
 $$ \begin{align*} \mu_X\left( \mathscr{L}(X) \setminus \bigcup_{w \in \sigma \cap N} \operatorname{\mathrm{trop}}^{-1}(w) \right) = \mu_X\left( \mathscr{L}(X \setminus T) \right) = 0, \end{align*} $$
$$ \begin{align*} \mu_X\left( \mathscr{L}(X) \setminus \bigcup_{w \in \sigma \cap N} \operatorname{\mathrm{trop}}^{-1}(w) \right) = \mu_X\left( \mathscr{L}(X \setminus T) \right) = 0, \end{align*} $$
it is sufficient to show that
![]() $\beta $
is surjective.
$\beta $
is surjective.
Set
![]() $w \in \sigma \cap N$
. We will use Corollary 9.2 to show that w is in the image of
$w \in \sigma \cap N$
. We will use Corollary 9.2 to show that w is in the image of
![]() $\beta $
. Let
$\beta $
. Let
![]() $\Sigma $
be a simplicial subdivision of
$\Sigma $
be a simplicial subdivision of
![]() $\sigma $
whose rays are all rays of
$\sigma $
whose rays are all rays of
![]() $\sigma $
, and let
$\sigma $
, and let
![]() $\sigma _w \in \Sigma $
be a cone containing w. By Corollary 9.2, the cone
$\sigma _w \in \Sigma $
be a cone containing w. By Corollary 9.2, the cone
![]() $\sigma _w$
is unimodular, so w is a positive integer combination of first lattice points of rays of
$\sigma _w$
is unimodular, so w is a positive integer combination of first lattice points of rays of
![]() $\sigma $
. Therefore w is in the image of
$\sigma $
. Therefore w is in the image of
![]() $\beta $
by the definition of
$\beta $
by the definition of
![]() $\beta $
, and we are done.
$\beta $
, and we are done.
The remainder of this paper will be used to prove Theorem 9.1.
9.1 A combinatorial criterion for special stabilisers
We start with some preliminary results, the first of which is a standard fact.
Lemma 9.3. If A and B are finite-rank lattices and
 $$ \begin{align*} 0\to A\xrightarrow{f} B\to C\to 0 \end{align*} $$
$$ \begin{align*} 0\to A\xrightarrow{f} B\to C\to 0 \end{align*} $$
is a short exact sequence, then
![]() $\operatorname {\mathrm {cok}}(f^*)$
is finite. Moreover, C is torsion-free if and only if
$\operatorname {\mathrm {cok}}(f^*)$
is finite. Moreover, C is torsion-free if and only if
![]() $f^*$
is surjective.
$f^*$
is surjective.
Proof. Letting
![]() $C_{\operatorname {\mathrm {tor}}}$
be the torsion part of C, applying
$C_{\operatorname {\mathrm {tor}}}$
be the torsion part of C, applying
![]() $\operatorname {\mathrm {Hom}}(-,\mathbb {Z})$
to the short exact sequence
$\operatorname {\mathrm {Hom}}(-,\mathbb {Z})$
to the short exact sequence
we see that
![]() $\operatorname {\mathrm {Ext}}^1(C,\mathbb {Z})\cong \operatorname {\mathrm {Ext}}^1(C_{\operatorname {\mathrm {tor}}},\mathbb {Z})$
, which is finite. Then from the exact sequence
$\operatorname {\mathrm {Ext}}^1(C,\mathbb {Z})\cong \operatorname {\mathrm {Ext}}^1(C_{\operatorname {\mathrm {tor}}},\mathbb {Z})$
, which is finite. Then from the exact sequence
 $$ \begin{align*} 0\to C^*\to B^*\xrightarrow{f^*} A^*\to \operatorname{\mathrm{Ext}}^1(C,\mathbb{Z})\to 0, \end{align*} $$
$$ \begin{align*} 0\to C^*\to B^*\xrightarrow{f^*} A^*\to \operatorname{\mathrm{Ext}}^1(C,\mathbb{Z})\to 0, \end{align*} $$
we see that
![]() $\operatorname {\mathrm {cok}}(f^*)$
is finite and that
$\operatorname {\mathrm {cok}}(f^*)$
is finite and that
![]() $f^*$
is surjective if and only if
$f^*$
is surjective if and only if
![]() $\operatorname {\mathrm {Ext}}^1(C,\mathbb {Z})=0$
if and only if C is a lattice.
$\operatorname {\mathrm {Ext}}^1(C,\mathbb {Z})=0$
if and only if C is a lattice.
Lemma 9.4. Let A be a lattice and suppose
![]() $v_1,\dotsc ,v_r\in A$
span
$v_1,\dotsc ,v_r\in A$
span
![]() $A_{\mathbb {Q}}$
. Then the following conditions are equivalent:
$A_{\mathbb {Q}}$
. Then the following conditions are equivalent:
-
1.
 $A/\sum _{i\in S}\mathbb {Z} v_i$
is torsion-free for all
$A/\sum _{i\in S}\mathbb {Z} v_i$
is torsion-free for all
 $S\subseteq \{1,\dotsc ,r\}$
.
$S\subseteq \{1,\dotsc ,r\}$
. -
2. For every
 $S\subseteq \{1,\dotsc ,r\}$
, if
$S\subseteq \{1,\dotsc ,r\}$
, if
 $\{v_i\mid i\in S\}$
is a
$\{v_i\mid i\in S\}$
is a
 $\mathbb {Q}$
-basis for
$\mathbb {Q}$
-basis for
 $A_{\mathbb {Q}}$
, then it is a
$A_{\mathbb {Q}}$
, then it is a
 $\mathbb {Z}$
-basis for A.
$\mathbb {Z}$
-basis for A.
Proof. To ease notation, define
![]() $L_S:=\sum _{i\in S}\mathbb {Z} v_i$
and
$L_S:=\sum _{i\in S}\mathbb {Z} v_i$
and
![]() $L^{\operatorname {\mathrm {sat}}}_S:=A\cap (L_S)_{\mathbb {Q}}$
for all
$L^{\operatorname {\mathrm {sat}}}_S:=A\cap (L_S)_{\mathbb {Q}}$
for all
![]() $S\subseteq \{1,\dotsc ,r\}$
. Note that
$S\subseteq \{1,\dotsc ,r\}$
. Note that
![]() $A/L^{\operatorname {\mathrm {sat}}}_S$
is torsion-free, so
$A/L^{\operatorname {\mathrm {sat}}}_S$
is torsion-free, so
![]() $L^{\operatorname {\mathrm {sat}}}_S$
is a direct summand of A. It follows that
$L^{\operatorname {\mathrm {sat}}}_S$
is a direct summand of A. It follows that
![]() $A/L_S$
is torsion-free if and only if
$A/L_S$
is torsion-free if and only if
![]() $L^{\operatorname {\mathrm {sat}}}_S/L_S$
is torsion-free, and since
$L^{\operatorname {\mathrm {sat}}}_S/L_S$
is torsion-free, and since
![]() $L^{\operatorname {\mathrm {sat}}}_S/L_S$
is finite, we see that condition (1) is equivalent to
$L^{\operatorname {\mathrm {sat}}}_S/L_S$
is finite, we see that condition (1) is equivalent to
![]() $L_S=L^{\operatorname {\mathrm {sat}}}_S$
.
$L_S=L^{\operatorname {\mathrm {sat}}}_S$
.
Now suppose that condition (1) holds and set
![]() $S\subseteq \{1,\dotsc ,r\}$
such that
$S\subseteq \{1,\dotsc ,r\}$
such that
![]() $\{v_i\mid i\in S\}$
is a
$\{v_i\mid i\in S\}$
is a
![]() $\mathbb {Q}$
-basis for
$\mathbb {Q}$
-basis for
![]() $A_{\mathbb {Q}}$
. Then
$A_{\mathbb {Q}}$
. Then
![]() $L_S=L^{\operatorname {\mathrm {sat}}}_S=A$
, so
$L_S=L^{\operatorname {\mathrm {sat}}}_S=A$
, so
![]() $\{v_i\mid i\in S\}$
is a
$\{v_i\mid i\in S\}$
is a
![]() $\mathbb {Z}$
-basis for A.
$\mathbb {Z}$
-basis for A.
Conversely, suppose condition (2) holds, and let
![]() $S\subseteq \{1,\dotsc ,r\}$
be any subset. Choose
$S\subseteq \{1,\dotsc ,r\}$
be any subset. Choose
![]() $S'\subseteq S$
such that
$S'\subseteq S$
such that
![]() $\{v_i\mid i\in S'\}$
form a
$\{v_i\mid i\in S'\}$
form a
![]() $\mathbb {Q}$
-basis for
$\mathbb {Q}$
-basis for
![]() $(L_S)_{\mathbb {Q}}$
. Since the
$(L_S)_{\mathbb {Q}}$
. Since the
![]() $\mathbb {Q}$
-span of
$\mathbb {Q}$
-span of
![]() $v_1,\dotsc ,v_r$
is
$v_1,\dotsc ,v_r$
is
![]() $A_{\mathbb {Q}}$
, we can choose
$A_{\mathbb {Q}}$
, we can choose
![]() $S''\subseteq \{1,\dotsc ,r\}\setminus S$
such that
$S''\subseteq \{1,\dotsc ,r\}\setminus S$
such that
![]() $\{v_i\mid i\in S'\cup S''\}$
form a
$\{v_i\mid i\in S'\cup S''\}$
form a
![]() $\mathbb {Q}$
-basis for
$\mathbb {Q}$
-basis for
![]() $A_{\mathbb {Q}}$
. It follows that
$A_{\mathbb {Q}}$
. It follows that
![]() $\{v_i\mid i\in S'\cup S''\}$
is a
$\{v_i\mid i\in S'\cup S''\}$
is a
![]() $\mathbb {Z}$
-basis for A, and hence
$\mathbb {Z}$
-basis for A, and hence
![]() $A\cong L_{S'}\oplus L_{S''}$
.
$A\cong L_{S'}\oplus L_{S''}$
.
To show that condition (1) holds – that is,
![]() $A/L_S$
is torsion-free – it thus suffices to show
$A/L_S$
is torsion-free – it thus suffices to show
![]() $L_{S'}=L_S$
. To see why this equality holds, set
$L_{S'}=L_S$
. To see why this equality holds, set
![]() $j\in S$
and write
$j\in S$
and write
![]() $v_j=\sum _{i\in S'}a^{\prime }_iv_i+\sum _{i\in S''}a^{\prime \prime }_iv_i$
, with
$v_j=\sum _{i\in S'}a^{\prime }_iv_i+\sum _{i\in S''}a^{\prime \prime }_iv_i$
, with
![]() $a^{\prime }_i,a^{\prime \prime }_i\in \mathbb {Z}$
. On the other hand, by the definition of
$a^{\prime }_i,a^{\prime \prime }_i\in \mathbb {Z}$
. On the other hand, by the definition of
![]() $S'$
, we can write
$S'$
, we can write
![]() $v_j=\sum _{i\in S'}b^{\prime }_iv_i$
, with
$v_j=\sum _{i\in S'}b^{\prime }_iv_i$
, with
![]() $b^{\prime }_i\in \mathbb {Q}$
. Equating our two expressions and using the fact that
$b^{\prime }_i\in \mathbb {Q}$
. Equating our two expressions and using the fact that
![]() $\{v_i\mid i\in S'\cup S''\}$
is a
$\{v_i\mid i\in S'\cup S''\}$
is a
![]() $\mathbb {Q}$
-basis for
$\mathbb {Q}$
-basis for
![]() $A_{\mathbb {Q}}$
, we see that
$A_{\mathbb {Q}}$
, we see that
![]() $a^{\prime \prime }_i=0$
for all
$a^{\prime \prime }_i=0$
for all
![]() $i\in S''$
. So
$i\in S''$
. So
![]() $v_j\in L_{S'}$
.
$v_j\in L_{S'}$
.
Lemma 9.5. Let
 $\mathcal {X}=\left [\mathbb {A}^r_k/\mathbb {G}_m^n\right ]$
, where
$\mathcal {X}=\left [\mathbb {A}^r_k/\mathbb {G}_m^n\right ]$
, where
![]() $\mathbb {G}_m^n$
acts with weights
$\mathbb {G}_m^n$
acts with weights
![]() $w_1,\dotsc ,w_r\in \mathbb {Z}^n$
which span
$w_1,\dotsc ,w_r\in \mathbb {Z}^n$
which span
![]() $\mathbb {Q}^n$
.Footnote
2
Then
$\mathbb {Q}^n$
.Footnote
2
Then
![]() $\mathcal {X}$
has special stabilisers if and only if for every
$\mathcal {X}$
has special stabilisers if and only if for every
![]() $S\subseteq \{1,\dotsc ,r\}$
, if
$S\subseteq \{1,\dotsc ,r\}$
, if
![]() $\{w_i\mid i\in S\}$
is a
$\{w_i\mid i\in S\}$
is a
![]() $\mathbb {Q}$
-basis for
$\mathbb {Q}$
-basis for
![]() $\mathbb {Q}^n$
, then it is a
$\mathbb {Q}^n$
, then it is a
![]() $\mathbb {Z}$
-basis for
$\mathbb {Z}$
-basis for
![]() $\mathbb {Z}^n$
.
$\mathbb {Z}^n$
.
Proof. Since the stabilisers of
![]() $\mathcal {X}$
are subgroups of
$\mathcal {X}$
are subgroups of
![]() $\mathbb {G}_m^n$
, they are special if and only if they are connected. Let
$\mathbb {G}_m^n$
, they are special if and only if they are connected. Let
![]() $w_i=(a_{i1},\dotsc ,a_{in})\in \mathbb {Z}^n$
. Given a point
$w_i=(a_{i1},\dotsc ,a_{in})\in \mathbb {Z}^n$
. Given a point
![]() $x=(x_1,\dotsc ,x_r)\in \mathbb {A}^r_k$
, let
$x=(x_1,\dotsc ,x_r)\in \mathbb {A}^r_k$
, let
![]() $S_x=\{i\mid x_i\neq 0\}$
. Then the stabiliser
$S_x=\{i\mid x_i\neq 0\}$
. Then the stabiliser
![]() $G_x$
of x is the set of
$G_x$
of x is the set of
![]() $(\lambda _1,\dotsc ,\lambda _n)\in \mathbb {G}_m^n$
such that
$(\lambda _1,\dotsc ,\lambda _n)\in \mathbb {G}_m^n$
such that
 $\prod _{j=1}^n\lambda _j^{a_{ij}}=1$
for all
$\prod _{j=1}^n\lambda _j^{a_{ij}}=1$
for all
![]() $i\in S_x$
. In other words, we have a short exact sequence
$i\in S_x$
. In other words, we have a short exact sequence
 $$ \begin{align*} 1\to G_x\to \mathbb{G}_m^n\xrightarrow{\varphi} \mathbb{G}_m^{S_x}\to1, \end{align*} $$
$$ \begin{align*} 1\to G_x\to \mathbb{G}_m^n\xrightarrow{\varphi} \mathbb{G}_m^{S_x}\to1, \end{align*} $$
where for
![]() $i\in S_x$
, the ith coordinate of
$i\in S_x$
, the ith coordinate of
![]() $\varphi (\lambda _1,\dotsc ,\lambda _n)$
is given by
$\varphi (\lambda _1,\dotsc ,\lambda _n)$
is given by
 $\prod _{j=1}^n\lambda _j^{a_{ij}}$
. Taking Cartier duals
$\prod _{j=1}^n\lambda _j^{a_{ij}}$
. Taking Cartier duals
![]() $D(-):=\operatorname {\mathrm {Hom}}(-,\mathbb {G}_m)$
, we see that
$D(-):=\operatorname {\mathrm {Hom}}(-,\mathbb {G}_m)$
, we see that
![]() $D(G_x)$
is the cokernel of the map
$D(G_x)$
is the cokernel of the map
![]() $\mathbb {Z}^{S_x}\to \mathbb {Z}^n$
sending the ith standard basis vector to
$\mathbb {Z}^{S_x}\to \mathbb {Z}^n$
sending the ith standard basis vector to
![]() $w_i$
. By Cartier duality,
$w_i$
. By Cartier duality,
![]() $G_x$
is connected if and only if
$G_x$
is connected if and only if
![]() $D(G_x)$
is torsion-free. We have thus shown that
$D(G_x)$
is torsion-free. We have thus shown that
![]() $\mathcal {X}$
has connected stabilisers if and only if
$\mathcal {X}$
has connected stabilisers if and only if
![]() $\mathbb {Z}^n/\sum _{i\in S}\mathbb {Z} w_i$
is torsion-free for all subsets
$\mathbb {Z}^n/\sum _{i\in S}\mathbb {Z} w_i$
is torsion-free for all subsets
![]() $S\subseteq \{1,\dotsc ,r\}$
. Lemma 9.4 then finishes the proof.
$S\subseteq \{1,\dotsc ,r\}$
. Lemma 9.4 then finishes the proof.
We now turn to Theorem 9.1.
Proof of Theorem 9.1
The map
![]() $\nu \colon \mathbb {Z}^r\to N$
has finite cokernel, or equivalently,
$\nu \colon \mathbb {Z}^r\to N$
has finite cokernel, or equivalently,
![]() $\nu ^*$
is injective. So we have a short exact sequence
$\nu ^*$
is injective. So we have a short exact sequence

By the construction of fantastacks, we have
 $\mathcal {X}=\left [\mathbb {A}^r_k/G\right ]$
, where G is the Cartier dual of A. Note that G is the stabiliser of the origin, and it is connected if and only if A is torsion-free. By Lemma 9.3, this is equivalent to surjectivity of
$\mathcal {X}=\left [\mathbb {A}^r_k/G\right ]$
, where G is the Cartier dual of A. Note that G is the stabiliser of the origin, and it is connected if and only if A is torsion-free. By Lemma 9.3, this is equivalent to surjectivity of
![]() $\nu $
.
$\nu $
.
So we may now assume
![]() $\nu $
is surjective, and in light of Lemma 9.5, we need only establish the equivalence of conditions (ii) and (iii). By Lemma 9.4, condition (ii) holds if and only if
$\nu $
is surjective, and in light of Lemma 9.5, we need only establish the equivalence of conditions (ii) and (iii). By Lemma 9.4, condition (ii) holds if and only if
![]() $\operatorname {\mathrm {cok}}\left (\nu \rvert _{\mathbb {Z}^S}\right )$
is torsion-free for all subsets
$\operatorname {\mathrm {cok}}\left (\nu \rvert _{\mathbb {Z}^S}\right )$
is torsion-free for all subsets
![]() $S\subseteq \{1,\dotsc ,r\}$
. Letting
$S\subseteq \{1,\dotsc ,r\}$
. Letting
![]() $e_i^*\in (\mathbb {Z}^r)^*$
denote the dual linear functional, notice that
$e_i^*\in (\mathbb {Z}^r)^*$
denote the dual linear functional, notice that
 $\alpha \left (e_i^*\right )$
is the ith weight for the G-action on
$\alpha \left (e_i^*\right )$
is the ith weight for the G-action on
![]() $\mathbb {A}^r_k$
. Given any subset
$\mathbb {A}^r_k$
. Given any subset
![]() $S\subseteq \{1,\dotsc ,r\}$
, we let
$S\subseteq \{1,\dotsc ,r\}$
, we let
![]() $S'$
denote the complement of S. We have a natural inclusion
$S'$
denote the complement of S. We have a natural inclusion
 $\left (\mathbb {Z}^{S'}\right )^*\subseteq (\mathbb {Z}^r)^*$
with cokernel
$\left (\mathbb {Z}^{S'}\right )^*\subseteq (\mathbb {Z}^r)^*$
with cokernel
 $\left (\mathbb {Z}^S\right )^*$
. Another application of Lemma 9.4 shows that condition (iii) holds if and only if
$\left (\mathbb {Z}^S\right )^*$
. Another application of Lemma 9.4 shows that condition (iii) holds if and only if
 $Q_S:=A/\alpha \left (\left (\mathbb {Z}^{S'}\right )^*\right )$
is torsion-free for all S. We show that this latter condition is equivalent to
$Q_S:=A/\alpha \left (\left (\mathbb {Z}^{S'}\right )^*\right )$
is torsion-free for all S. We show that this latter condition is equivalent to
![]() $\operatorname {\mathrm {cok}}\left (\nu \rvert _{\mathbb {Z}^S}\right )$
being torsion-free for all subsets
$\operatorname {\mathrm {cok}}\left (\nu \rvert _{\mathbb {Z}^S}\right )$
being torsion-free for all subsets
![]() $S\subseteq \{1,\dotsc ,r\}$
.
$S\subseteq \{1,\dotsc ,r\}$
.
Consider the diagram

where B is the image of
![]() $\pi \circ \nu ^*$
and
$\pi \circ \nu ^*$
and
 $C=\left (\mathbb {Z}^{S'}\right )^*\cap \ker \alpha $
; in particular, all rows and columns are exact. Note that all
$C=\left (\mathbb {Z}^{S'}\right )^*\cap \ker \alpha $
; in particular, all rows and columns are exact. Note that all
![]() $\mathbb {Z}$
-modules in this diagram are torsion-free, with the possible exception of
$\mathbb {Z}$
-modules in this diagram are torsion-free, with the possible exception of
![]() $Q_S$
. Applying
$Q_S$
. Applying
![]() $\operatorname {\mathrm {Hom}}(-,\mathbb {Z})$
, we have the diagram
$\operatorname {\mathrm {Hom}}(-,\mathbb {Z})$
, we have the diagram

where all rows are exact and all vertical maps are injective. We see then that
Letting
![]() $Q_{S,\operatorname {\mathrm {tor}}}\subseteq Q_S$
denote the torsion part, we have
$Q_{S,\operatorname {\mathrm {tor}}}\subseteq Q_S$
denote the torsion part, we have
 $\operatorname {\mathrm {Ext}}^1(Q_S,\mathbb {Z})=\operatorname {\mathrm {Ext}}^1\left (Q_{S,\operatorname {\mathrm {tor}}},\mathbb {Z}\right )$
, which is finite, so
$\operatorname {\mathrm {Ext}}^1(Q_S,\mathbb {Z})=\operatorname {\mathrm {Ext}}^1\left (Q_{S,\operatorname {\mathrm {tor}}},\mathbb {Z}\right )$
, which is finite, so
![]() $\operatorname {\mathrm {cok}}\left (\nu \rvert _{\mathbb {Z}^S}\right )$
is torsion-free if and only if
$\operatorname {\mathrm {cok}}\left (\nu \rvert _{\mathbb {Z}^S}\right )$
is torsion-free if and only if
![]() $\operatorname {\mathrm {Ext}}^1(Q_S,\mathbb {Z})=0$
if and only if
$\operatorname {\mathrm {Ext}}^1(Q_S,\mathbb {Z})=0$
if and only if
![]() $Q_S$
is torsion-free.
$Q_S$
is torsion-free.
10 Quotients by
 $\mathrm {SL}_2$
and cones over Grassmannians
$\mathrm {SL}_2$
and cones over Grassmannians
Until now, we have only considered stacks with abelian stabilisers. In this section, we verify Conjecture 1.1 and Conjecture 1.2 for nontrivial examples where the stabilisers are nonabelian. Our primary running example in this section is a stack
 $\mathcal {X}=\left [\mathbb {A}^8/\mathrm {SL}_2\right ]$
whose good moduli space is the affine cone over the Grassmannian
$\mathcal {X}=\left [\mathbb {A}^8/\mathrm {SL}_2\right ]$
whose good moduli space is the affine cone over the Grassmannian
![]() $\operatorname {\mathrm {Gr}}(2,4)$
with respect to the Plücker embedding; we will additionally verify Conjecture 1.2 and answer Question 1.4 for a stack
$\operatorname {\mathrm {Gr}}(2,4)$
with respect to the Plücker embedding; we will additionally verify Conjecture 1.2 and answer Question 1.4 for a stack
 $\mathcal {X}=\left [\mathbb {A}^{2r}/\mathrm {SL}_2\right ]$
whose good moduli space is the affine cone over the Grassmannian
$\mathcal {X}=\left [\mathbb {A}^{2r}/\mathrm {SL}_2\right ]$
whose good moduli space is the affine cone over the Grassmannian
![]() $\operatorname {\mathrm {Gr}}(2,r)$
. The cases we consider are particularly interesting because, unlike fantastacks, we show here that
$\operatorname {\mathrm {Gr}}(2,r)$
. The cases we consider are particularly interesting because, unlike fantastacks, we show here that
![]() $\mu _X\left (\operatorname {\mathrm {sep}}_\pi ^{-1}(\infty )\right ) \neq 0$
.
$\mu _X\left (\operatorname {\mathrm {sep}}_\pi ^{-1}(\infty )\right ) \neq 0$
.
We begin by setting up some notation. Throughout this section, fix some
![]() $r \in \mathbb {Z}_{>1}$
and let
$r \in \mathbb {Z}_{>1}$
and let
![]() $[r]=\{1,\dotsc ,r\}$
. Let
$[r]=\{1,\dotsc ,r\}$
. Let
![]() $\widetilde {X}=\mathbb {A}^{2\times r}$
, which we think of as
$\widetilde {X}=\mathbb {A}^{2\times r}$
, which we think of as
![]() $2\times r$
matrices with coordinates
$2\times r$
matrices with coordinates
 $$ \begin{align*} \begin{pmatrix} y_{1,1} & \dotsb & y_{1,r} \\ y_{2,1} & \dotsb & y_{2,r} \end{pmatrix}. \end{align*} $$
$$ \begin{align*} \begin{pmatrix} y_{1,1} & \dotsb & y_{1,r} \\ y_{2,1} & \dotsb & y_{2,r} \end{pmatrix}. \end{align*} $$
There is an
![]() $\mathrm {SL}_2$
-action on
$\mathrm {SL}_2$
-action on
![]() $\widetilde {X}$
given by left multiplication. The invariant functions are generated by the
$\widetilde {X}$
given by left multiplication. The invariant functions are generated by the
![]() $2\times 2$
minors, and so the quotient
$2\times 2$
minors, and so the quotient
 $X=\widetilde {X}/\mathrm {SL}_2\subset \mathbb {A}^{[r] \choose 2}_k$
is the affine cone over the Grassmannian
$X=\widetilde {X}/\mathrm {SL}_2\subset \mathbb {A}^{[r] \choose 2}_k$
is the affine cone over the Grassmannian
![]() $\operatorname {\mathrm {Gr}}(2, r)$
with respect to the Plücker embedding of
$\operatorname {\mathrm {Gr}}(2, r)$
with respect to the Plücker embedding of
![]() $\operatorname {\mathrm {Gr}}(2,r)$
. Letting
$\operatorname {\mathrm {Gr}}(2,r)$
. Letting
 $\left \{x_{\ell ,m}\mid 1\leq \ell < m\leq r\right \}$
be the coordinates on
$\left \{x_{\ell ,m}\mid 1\leq \ell < m\leq r\right \}$
be the coordinates on
 $\mathbb {A}^{[r] \choose 2}_k$
, the quotient map
$\mathbb {A}^{[r] \choose 2}_k$
, the quotient map
![]() $\widetilde {X}\to X$
sends each
$\widetilde {X}\to X$
sends each
![]() $x_{\ell ,m}\rvert _X$
to the
$x_{\ell ,m}\rvert _X$
to the
![]() $(\ell , m)$
th minor of the matrix. Set
$(\ell , m)$
th minor of the matrix. Set
 $\mathcal {X} = \left [ \widetilde {X} / \mathrm {SL}_2 \right ]$
, let
$\mathcal {X} = \left [ \widetilde {X} / \mathrm {SL}_2 \right ]$
, let
![]() $\rho : \widetilde {X} \to \mathcal {X}$
be the quotient map and let
$\rho : \widetilde {X} \to \mathcal {X}$
be the quotient map and let
![]() $\pi \colon \mathcal {X}\to X$
be the good moduli space map. Note that all stabilisers of
$\pi \colon \mathcal {X}\to X$
be the good moduli space map. Note that all stabilisers of
![]() $\mathcal {X}$
are special: the zero matrix has stabiliser
$\mathcal {X}$
are special: the zero matrix has stabiliser
![]() $\mathrm {SL}_2$
, a full-rank matrix has trivial stabiliser and a rank
$\mathrm {SL}_2$
, a full-rank matrix has trivial stabiliser and a rank
![]() $1$
matrix has stabiliser
$1$
matrix has stabiliser
![]() $\mathbb {G}_a$
.
$\mathbb {G}_a$
.
Remark 10.1. When
![]() $r \geq 3$
, the exceptional locus of
$r \geq 3$
, the exceptional locus of
![]() $\pi $
has codimension at least
$\pi $
has codimension at least
![]() $2$
: it is straightforward to check that if
$2$
: it is straightforward to check that if
![]() $U \subset X$
is the intersection of X with the complement
$U \subset X$
is the intersection of X with the complement
 $\mathbb {G}_m^{[n] \choose 2}$
of the coordinate axes of
$\mathbb {G}_m^{[n] \choose 2}$
of the coordinate axes of
 $\mathbb {A}_k^{[n] \choose 2}$
, then
$\mathbb {A}_k^{[n] \choose 2}$
, then
 $\pi \rvert _{\pi ^{-1}(U)}: \pi ^{-1}(U) \to U$
is an isomorphism; and when
$\pi \rvert _{\pi ^{-1}(U)}: \pi ^{-1}(U) \to U$
is an isomorphism; and when
![]() $r \geq 3$
, the complement of
$r \geq 3$
, the complement of
![]() $\pi ^{-1}(U)$
in
$\pi ^{-1}(U)$
in
![]() $\mathcal {X}$
has codimension at least
$\mathcal {X}$
has codimension at least
![]() $2$
.
$2$
.
The next two propositions verify Conjecture 1.2 and answer Question 1.4.
Proposition 10.2. For
![]() $r\geq 2$
, Conjecture 1.2 holds for
$r\geq 2$
, Conjecture 1.2 holds for
![]() $\pi \colon \mathcal {X}\to X$
.
$\pi \colon \mathcal {X}\to X$
.
Proposition 10.3. For
![]() $r\geq 2$
, we have
$r\geq 2$
, we have
![]() $\mu _X\left (\operatorname {\mathrm {sep}}_\pi ^{-1}(\infty )\right ) \neq 0$
, answering Question 1.4 for
$\mu _X\left (\operatorname {\mathrm {sep}}_\pi ^{-1}(\infty )\right ) \neq 0$
, answering Question 1.4 for
![]() $\pi \colon \mathcal {X}\to X$
.
$\pi \colon \mathcal {X}\to X$
.
For any
 $\mathbf {w} \in (\mathbb {N} \cup \{\infty \})^{[r] \choose 2}$
, let
$\mathbf {w} \in (\mathbb {N} \cup \{\infty \})^{[r] \choose 2}$
, let
![]() $C^{(\mathbf {w})} \subset \mathscr {L}(X)$
denote the subset of arcs whose prescribed vanishing orders with respect to the Plücker coordinate are given by
$C^{(\mathbf {w})} \subset \mathscr {L}(X)$
denote the subset of arcs whose prescribed vanishing orders with respect to the Plücker coordinate are given by
![]() $\mathbf {w}$
. More precisely,
$\mathbf {w}$
. More precisely,
 $$ \begin{align*} C^{(\mathbf{w})} = \bigcap_{\ell< m \in [r]} \operatorname{\mathrm{ord}}_{x_{\ell,m} \rvert_X}^{-1}\left(w_{\ell,m}\right) \subset \mathscr{L}(X). \end{align*} $$
$$ \begin{align*} C^{(\mathbf{w})} = \bigcap_{\ell< m \in [r]} \operatorname{\mathrm{ord}}_{x_{\ell,m} \rvert_X}^{-1}\left(w_{\ell,m}\right) \subset \mathscr{L}(X). \end{align*} $$
Note that if
![]() $\mathbf {w} \in \mathbb {N}^{[r] \choose 2}$
, then
$\mathbf {w} \in \mathbb {N}^{[r] \choose 2}$
, then
![]() $C^{(\mathbf {w})}$
is a cylinder.
$C^{(\mathbf {w})}$
is a cylinder.
Remark 10.4. If
 $\mathbf {w} \in \left ( (\mathbb {N} \cup \{\infty \})^{[r] \choose 2} \setminus \mathbb {N}^{[r] \choose 2}\right )$
, then
$\mathbf {w} \in \left ( (\mathbb {N} \cup \{\infty \})^{[r] \choose 2} \setminus \mathbb {N}^{[r] \choose 2}\right )$
, then
![]() $C^{(\mathbf {w})}$
is a measurable set with
$C^{(\mathbf {w})}$
is a measurable set with
 $\mu _X\left (C^{(\mathbf {w})}\right ) = 0$
.
$\mu _X\left (C^{(\mathbf {w})}\right ) = 0$
.
With this notation, we now prove Proposition 10.2 and Proposition 10.3.
Proof of Proposition 10.2
It suffices to show that away from a set of measure
![]() $0$
, every arc
$0$
, every arc
![]() $\varphi \in \mathscr {L}(X)(k')$
lifts to an arc in
$\varphi \in \mathscr {L}(X)(k')$
lifts to an arc in
![]() $\mathscr {L}(\mathcal {X})(k')$
, where
$\mathscr {L}(\mathcal {X})(k')$
, where
![]() $k'$
is an extension field of k. By Remark 10.4, we may assume
$k'$
is an extension field of k. By Remark 10.4, we may assume
![]() $\varphi \in C^{(\mathbf {w})}$
with
$\varphi \in C^{(\mathbf {w})}$
with
 $\mathbf {w} =\left (w_{i,j}\right ) \in \mathbb {N}^{[r] \choose 2}$
. Without loss of generality, we may additionally assume
$\mathbf {w} =\left (w_{i,j}\right ) \in \mathbb {N}^{[r] \choose 2}$
. Without loss of generality, we may additionally assume
![]() $w_{1,2}=\min \left (w_{i,j}\right )$
. Let the map on coordinate rings induced by
$w_{1,2}=\min \left (w_{i,j}\right )$
. Let the map on coordinate rings induced by
![]() send
send
![]() $x_{i,j}\rvert _X$
to
$x_{i,j}\rvert _X$
to
![]() . Let
. Let
 $\widetilde \psi \in \mathscr {L}\left (\widetilde {X}\right )$
be the arc given by the matrix
$\widetilde \psi \in \mathscr {L}\left (\widetilde {X}\right )$
be the arc given by the matrix
 $$ \begin{align} \begin{pmatrix} g_{1,2} & 0 & -g_{2,3} & -g_{2,4} & \dotsb & -g_{2,r} \\ 0 & 1 & g_{1,3}g_{1,2}^{-1} & g_{1,4}g_{1,2}^{-1} & \dotsb & g_{1,r}g_{1,2}^{-1} \end{pmatrix}. \end{align} $$
$$ \begin{align} \begin{pmatrix} g_{1,2} & 0 & -g_{2,3} & -g_{2,4} & \dotsb & -g_{2,r} \\ 0 & 1 & g_{1,3}g_{1,2}^{-1} & g_{1,4}g_{1,2}^{-1} & \dotsb & g_{1,r}g_{1,2}^{-1} \end{pmatrix}. \end{align} $$
Note that all
![]() $g_{i,j}$
are nonzero, since
$g_{i,j}$
are nonzero, since
![]() $\mathbf {w} \in \mathbb {N}^{[r] \choose 2}$
, and all entries of the matrix are in
$\mathbf {w} \in \mathbb {N}^{[r] \choose 2}$
, and all entries of the matrix are in
![]() , since
, since
![]() $w_{1,2}=\min \left (w_{i,j}\right )$
. Note further that the
$w_{1,2}=\min \left (w_{i,j}\right )$
. Note further that the
![]() $(i,j)$
th minor of the matrix is precisely
$(i,j)$
th minor of the matrix is precisely
![]() $g_{i,j}$
; this is clear when
$g_{i,j}$
; this is clear when
![]() $i\in \{1,2\}$
, so the Plücker relations ensure that it remains true for all
$i\in \{1,2\}$
, so the Plücker relations ensure that it remains true for all
![]() $(i,j)$
. As a result,
$(i,j)$
. As a result,
![]() $\widetilde \psi $
is a lift of
$\widetilde \psi $
is a lift of
![]() $\varphi $
, and hence
$\varphi $
, and hence
 $\psi =\mathscr {L}(\rho )\left (\widetilde \psi \right )\in \mathscr {L}(\mathcal {X})$
is a lift of
$\psi =\mathscr {L}(\rho )\left (\widetilde \psi \right )\in \mathscr {L}(\mathcal {X})$
is a lift of
![]() $\varphi $
.
$\varphi $
.
Proof of Proposition 10.3
As in the proof of Proposition 10.2, it suffices to show that
![]() $\operatorname {\mathrm {sep}}_\pi $
is infinite on
$\operatorname {\mathrm {sep}}_\pi $
is infinite on
![]() $C^{(\mathbf {w})}$
under the assumption that
$C^{(\mathbf {w})}$
under the assumption that
 $\mathbf {w} =\left (w_{i,j}\right ) \in \mathbb {N}^{[r] \choose 2}$
and
$\mathbf {w} =\left (w_{i,j}\right ) \in \mathbb {N}^{[r] \choose 2}$
and
![]() $1\leq w_{1,2}=\min \left (w_{i,j}\right )$
. Again, set
$1\leq w_{1,2}=\min \left (w_{i,j}\right )$
. Again, set
![]() $\varphi \in C^{(\mathbf {w})}$
and let
$\varphi \in C^{(\mathbf {w})}$
and let
![]() send
send
![]() $x_{i,j}\rvert _X$
to
$x_{i,j}\rvert _X$
to
![]() . Then for any
. Then for any
![]() , we obtain a lift
, we obtain a lift
 $\widetilde \psi _h\in \mathscr {L}\left (\widetilde {X}\right )$
of
$\widetilde \psi _h\in \mathscr {L}\left (\widetilde {X}\right )$
of
![]() $\varphi $
, where
$\varphi $
, where
![]() $\widetilde \psi _h$
is the arc given by the matrix
$\widetilde \psi _h$
is the arc given by the matrix
 $$ \begin{align*} \begin{pmatrix} g_{1,2} & 0 & -g_{2,3} & -g_{2,4} & \dotsb & -g_{2,r} \\ h & 1 & \left(g_{1,3}-hg_{2,3}\right)g_{1,2}^{-1} & \left(g_{1,4}-hg_{2,4}\right)g_{1,2}^{-1} & \dotsb & \left(g_{1,r}-hg_{2,r}\right)g_{1,2}^{-1} \end{pmatrix}. \end{align*} $$
$$ \begin{align*} \begin{pmatrix} g_{1,2} & 0 & -g_{2,3} & -g_{2,4} & \dotsb & -g_{2,r} \\ h & 1 & \left(g_{1,3}-hg_{2,3}\right)g_{1,2}^{-1} & \left(g_{1,4}-hg_{2,4}\right)g_{1,2}^{-1} & \dotsb & \left(g_{1,r}-hg_{2,r}\right)g_{1,2}^{-1} \end{pmatrix}. \end{align*} $$
Notice that for any
![]() for which
for which
![]() $h'-h$
is not divisible by
$h'-h$
is not divisible by
![]() $t^{w_{1,2}}$
, there is no
$t^{w_{1,2}}$
, there is no
![]() for which
for which
![]() $A\widetilde \psi _h=\widetilde \psi _{h'}$
. Indeed, the unique
$A\widetilde \psi _h=\widetilde \psi _{h'}$
. Indeed, the unique
![]() with
with
 $$ \begin{align*} A\begin{pmatrix} g_{1,2} & 0 \\ h & 1\end{pmatrix}=\begin{pmatrix} g_{1,2} & 0 \\ h' & 1\end{pmatrix} \end{align*} $$
$$ \begin{align*} A\begin{pmatrix} g_{1,2} & 0 \\ h & 1\end{pmatrix}=\begin{pmatrix} g_{1,2} & 0 \\ h' & 1\end{pmatrix} \end{align*} $$
is given by
 $$ \begin{align*} A=\begin{pmatrix} 1 & 0 \\ (h'-h)g_{1,2}^{-1} & 1\end{pmatrix}, \end{align*} $$
$$ \begin{align*} A=\begin{pmatrix} 1 & 0 \\ (h'-h)g_{1,2}^{-1} & 1\end{pmatrix}, \end{align*} $$
which is not in
![]() , by the assumption on
, by the assumption on
![]() $h'-h$
. Noting that
$h'-h$
. Noting that
![]() $w_{1,2} \geq 1$
, it follows that
$w_{1,2} \geq 1$
, it follows that
![]() $\operatorname {\mathrm {sep}}_\pi $
is infinite on
$\operatorname {\mathrm {sep}}_\pi $
is infinite on
![]() $C^{(\mathbf {w})}$
.
$C^{(\mathbf {w})}$
.
There are two features of the proof of Proposition 10.2 that we wish to highlight. First, for the matrices in expression (3) to define arcs of
![]() $\mathscr {L}(\mathcal {X})$
, we needed not
$\mathscr {L}(\mathcal {X})$
, we needed not
![]() $w_{1,2}=\min \left (w_{i,j}\right )$
but rather
$w_{1,2}=\min \left (w_{i,j}\right )$
but rather
![]() $w_{1,2} \leq w_{1,3}, \dotsc , w_{1, r}, w_{2,3}, \dotsc , w_{2,r}$
. Second, for any
$w_{1,2} \leq w_{1,3}, \dotsc , w_{1, r}, w_{2,3}, \dotsc , w_{2,r}$
. Second, for any
![]() $i\leq w_{1,2}$
we have many more lifts of
$i\leq w_{1,2}$
we have many more lifts of
![]() $\varphi $
given by matrices of the form
$\varphi $
given by matrices of the form
 $$ \begin{align*} \begin{pmatrix} g_{1,2}t^{-i} & 0 & -g_{2,3}t^{-i} & -g_{2,4}t^{-i} & \dotsb & -g_{2,r}t^{-i} \\ 0 & t^i & g_{1,3}g_{1,2}^{-1}t^i & g_{1,4}g_{1,2}^{-1}t^i & \dotsb & g_{1,r}g_{1,2}^{-1}t^i \end{pmatrix}. \end{align*} $$
$$ \begin{align*} \begin{pmatrix} g_{1,2}t^{-i} & 0 & -g_{2,3}t^{-i} & -g_{2,4}t^{-i} & \dotsb & -g_{2,r}t^{-i} \\ 0 & t^i & g_{1,3}g_{1,2}^{-1}t^i & g_{1,4}g_{1,2}^{-1}t^i & \dotsb & g_{1,r}g_{1,2}^{-1}t^i \end{pmatrix}. \end{align*} $$
With this as motivation, we introduce the following sets. For any
![]() $i, w_{1,2} \in \mathbb {N}$
and
$i, w_{1,2} \in \mathbb {N}$
and
![]() $\mathbf {w}_1 = \left (w_{1,3}, \dotsc , w_{1,r}\right ), \mathbf {w}_2 = \left (w_{2,3}, \dotsc , w_{2, r}\right ) \in \mathbb {N}^{r-2}$
satisfying
$\mathbf {w}_1 = \left (w_{1,3}, \dotsc , w_{1,r}\right ), \mathbf {w}_2 = \left (w_{2,3}, \dotsc , w_{2, r}\right ) \in \mathbb {N}^{r-2}$
satisfying
let
![]() $Z^{\left (i, w_{1,2}, \mathbf {w}_1, \mathbf {w}_2\right )}$
be the subset of
$Z^{\left (i, w_{1,2}, \mathbf {w}_1, \mathbf {w}_2\right )}$
be the subset of
 $\mathscr {L}\left (\widetilde {X}\right )$
whose
$\mathscr {L}\left (\widetilde {X}\right )$
whose
![]() $k'$
-valued points, for any extension
$k'$
-valued points, for any extension
![]() $k'$
of k, are the
$k'$
of k, are the
![]() $2 \times r$
matrices of the form
$2 \times r$
matrices of the form
 $$ \begin{align*} \begin{pmatrix} f_{1,1} & 0 & f_{1,3} & f_{1,4} & \dotsb & f_{1,r} \\ 0 & t^i & f_{2,3} & f_{2,4} & \dotsb & f_{2,r} \end{pmatrix}, \end{align*} $$
$$ \begin{align*} \begin{pmatrix} f_{1,1} & 0 & f_{1,3} & f_{1,4} & \dotsb & f_{1,r} \\ 0 & t^i & f_{2,3} & f_{2,4} & \dotsb & f_{2,r} \end{pmatrix}, \end{align*} $$
where
![]() satisfies
satisfies
 $$ \begin{align*} \operatorname{\mathrm{ord}}_t\left(f_{1,1}\right) &= w_{1,2} - i,\\ \operatorname{\mathrm{ord}}_t\left(f_{1,j}\right) &= w_{2,j} - i, & \text{for all }j = 3, \dotsc, r,\\ \operatorname{\mathrm{ord}}_t\left(f_{2,j}\right) &= w_{1,j} - w_{1,2} + i, & \text{for all }j = 3, \dotsc, r. \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{ord}}_t\left(f_{1,1}\right) &= w_{1,2} - i,\\ \operatorname{\mathrm{ord}}_t\left(f_{1,j}\right) &= w_{2,j} - i, & \text{for all }j = 3, \dotsc, r,\\ \operatorname{\mathrm{ord}}_t\left(f_{2,j}\right) &= w_{1,j} - w_{1,2} + i, & \text{for all }j = 3, \dotsc, r. \end{align*} $$
Note that the condition (⋆) guarantees that these vanishing orders are nonnegative. For any
![]() $i, w_{1,2} \in \mathbb {N}$
and
$i, w_{1,2} \in \mathbb {N}$
and
![]() $\mathbf {w}_1, \mathbf {w}_2 \in \mathbb {N}^{r-2}$
satisfying (⋆), set
$\mathbf {w}_1, \mathbf {w}_2 \in \mathbb {N}^{r-2}$
satisfying (⋆), set
 $$ \begin{align*} \mathcal{C}^{\left(i, w_{1,2}, \mathbf{w}_1, \mathbf{w}_2\right)} = \mathscr{L}(\rho)\left(Z^{\left(i, w_{1,2}, \mathbf{w}_1, \mathbf{w}_2\right)}\right) \subset \lvert\mathscr{L}(\mathcal{X})\rvert \end{align*} $$
$$ \begin{align*} \mathcal{C}^{\left(i, w_{1,2}, \mathbf{w}_1, \mathbf{w}_2\right)} = \mathscr{L}(\rho)\left(Z^{\left(i, w_{1,2}, \mathbf{w}_1, \mathbf{w}_2\right)}\right) \subset \lvert\mathscr{L}(\mathcal{X})\rvert \end{align*} $$
and set
 $$ \begin{align*} C^{\left(w_{1,2}, \mathbf{w}_1, \mathbf{w}_2\right)} = \bigcup_{\mathbf{w}} C^{(\mathbf{w})}, \end{align*} $$
$$ \begin{align*} C^{\left(w_{1,2}, \mathbf{w}_1, \mathbf{w}_2\right)} = \bigcup_{\mathbf{w}} C^{(\mathbf{w})}, \end{align*} $$
where
![]() $\mathbf {w}$
varies over all elements of
$\mathbf {w}$
varies over all elements of
 $(\mathbb {N} \cup \{\infty \})^{[r] \choose 2}$
whose
$(\mathbb {N} \cup \{\infty \})^{[r] \choose 2}$
whose
![]() $(\ell , m)$
th entry is equal to
$(\ell , m)$
th entry is equal to
![]() $w_{\ell , m}$
for all
$w_{\ell , m}$
for all
![]() $(\ell , m) = (1,2), (1,3), \dotsc , (1,r), (2,3), \dotsc , (2,r)$
.
$(\ell , m) = (1,2), (1,3), \dotsc , (1,r), (2,3), \dotsc , (2,r)$
.
Last, although (for ease of notation) we have chosen to define all of these sets with
![]() $w_{1,2}$
playing a special role, by symmetry of the Plücker coordinates, we obtain many analogous sets as follows. Note that there is a natural
$w_{1,2}$
playing a special role, by symmetry of the Plücker coordinates, we obtain many analogous sets as follows. Note that there is a natural
![]() $S_r$
-action on
$S_r$
-action on
![]() $\mathcal {X}$
given by permuting columns of the matrices in
$\mathcal {X}$
given by permuting columns of the matrices in
![]() $\widetilde {X}$
; by functoriality, this descends to an
$\widetilde {X}$
; by functoriality, this descends to an
![]() $S_r$
-action on the good moduli space X. Let
$S_r$
-action on the good moduli space X. Let
 $$ \begin{align*} \mathcal{C}^{\left(i, w_{1,2}, \mathbf{w}_1, \mathbf{w}_2\right)}_\sigma = \sigma\left(\mathcal{C}^{\left(i, w_{1,2}, \mathbf{w}_1, \mathbf{w}_2\right)}\right) \subset \lvert\mathscr{L}(\mathcal{X})\rvert\qquad\textrm{and}\qquad C^{\left(w_{1,2}, \mathbf{w}_1, \mathbf{w}_2\right)}_\sigma=\sigma\left(C^{\left(w_{1,2}, \mathbf{w}_1, \mathbf{w}_2\right)}\right)\subset\mathscr{L}(X). \end{align*} $$
$$ \begin{align*} \mathcal{C}^{\left(i, w_{1,2}, \mathbf{w}_1, \mathbf{w}_2\right)}_\sigma = \sigma\left(\mathcal{C}^{\left(i, w_{1,2}, \mathbf{w}_1, \mathbf{w}_2\right)}\right) \subset \lvert\mathscr{L}(\mathcal{X})\rvert\qquad\textrm{and}\qquad C^{\left(w_{1,2}, \mathbf{w}_1, \mathbf{w}_2\right)}_\sigma=\sigma\left(C^{\left(w_{1,2}, \mathbf{w}_1, \mathbf{w}_2\right)}\right)\subset\mathscr{L}(X). \end{align*} $$
Definition 10.5. Let
![]() $\mathcal {S}'$
be the collection of pairs
$\mathcal {S}'$
be the collection of pairs
 $$ \begin{align*} \left(\mathcal{C}^{\left(i, w_{1,2}, \mathbf{w}_1, \mathbf{w}_2\right)}_\sigma,C^{\left(w_{1,2}, \mathbf{w}_1, \mathbf{w}_2\right)}_\sigma\right) \end{align*} $$
$$ \begin{align*} \left(\mathcal{C}^{\left(i, w_{1,2}, \mathbf{w}_1, \mathbf{w}_2\right)}_\sigma,C^{\left(w_{1,2}, \mathbf{w}_1, \mathbf{w}_2\right)}_\sigma\right) \end{align*} $$
with
![]() $i, w_{1,2} \in \mathbb {N}$
and
$i, w_{1,2} \in \mathbb {N}$
and
![]() $\mathbf {w}_1, \mathbf {w}_2 \in \mathbb {N}^{r-2}$
satisfying (⋆), and
$\mathbf {w}_1, \mathbf {w}_2 \in \mathbb {N}^{r-2}$
satisfying (⋆), and
![]() $\sigma \in S_r$
. Let
$\sigma \in S_r$
. Let
![]() $\mathcal {S}\subset \mathcal {S}'$
be the subset consisting of pairs where
$\mathcal {S}\subset \mathcal {S}'$
be the subset consisting of pairs where
![]() $i>0$
.
$i>0$
.
Remark 10.6. Since the
![]() $S_r$
-actions on
$S_r$
-actions on
![]() $\mathscr {L}(\mathcal {X})$
and
$\mathscr {L}(\mathcal {X})$
and
![]() $\mathscr {L}(X)$
are measure-preserving, to prove Conjecture 1.1 for
$\mathscr {L}(X)$
are measure-preserving, to prove Conjecture 1.1 for
 $\left (\mathcal {C}^{\left (i, w_{1,2}, \mathbf {w}_1, \mathbf {w}_2\right )}_\sigma ,C^{\left (w_{1,2}, \mathbf {w}_1, \mathbf {w}_2\right )}_\sigma \right )$
it is enough to prove the conjecture for
$\left (\mathcal {C}^{\left (i, w_{1,2}, \mathbf {w}_1, \mathbf {w}_2\right )}_\sigma ,C^{\left (w_{1,2}, \mathbf {w}_1, \mathbf {w}_2\right )}_\sigma \right )$
it is enough to prove the conjecture for
 $\left (\mathcal {C}^{\left (i, w_{1,2}, \mathbf {w}_1, \mathbf {w}_2\right )},C^{\left (w_{1,2}, \mathbf {w}_1, \mathbf {w}_2\right )}\right )$
.
$\left (\mathcal {C}^{\left (i, w_{1,2}, \mathbf {w}_1, \mathbf {w}_2\right )},C^{\left (w_{1,2}, \mathbf {w}_1, \mathbf {w}_2\right )}\right )$
.
The next proposition verifies Conjecture 1.1 for an infinite collection of pairs
![]() $(\mathcal {C}, C)$
such that the C cover
$(\mathcal {C}, C)$
such that the C cover
![]() $\mathscr {L}(X)$
up to measure
$\mathscr {L}(X)$
up to measure
![]() $0$
. Our collection of
$0$
. Our collection of
![]() $(\mathcal {C},C)$
involves nonabelian stabilisers in a nontrivial way by the fourth bullet point in the proposition. Furthermore, for every C we prove Conjecture 1.1 for multiple different choices of
$(\mathcal {C},C)$
involves nonabelian stabilisers in a nontrivial way by the fourth bullet point in the proposition. Furthermore, for every C we prove Conjecture 1.1 for multiple different choices of
![]() $\mathcal {C}$
, thereby illustrating the flexibility of the conjecture in choosing
$\mathcal {C}$
, thereby illustrating the flexibility of the conjecture in choosing
![]() $\mathcal {C}$
.
$\mathcal {C}$
.
Proposition 10.7. Set
![]() $r\in \{3,4\}$
and let
$r\in \{3,4\}$
and let
![]() $\mathcal {S} \subset \mathcal {S}'$
be the collections of measurable subsets of
$\mathcal {S} \subset \mathcal {S}'$
be the collections of measurable subsets of
![]() $\lvert \mathscr {L}(\mathcal {X})\rvert \times \mathscr {L}(X)$
given in Definition 10.5. Then
$\lvert \mathscr {L}(\mathcal {X})\rvert \times \mathscr {L}(X)$
given in Definition 10.5. Then
-
•
 $\mathcal {S}$
is an infinite set;
$\mathcal {S}$
is an infinite set; -
• for all
 $(\mathcal {C}, C) \in \mathcal {S}'$
, the measurable sets
$(\mathcal {C}, C) \in \mathcal {S}'$
, the measurable sets
 $\mathcal {C}$
and C both have nonzero measure;
$\mathcal {C}$
and C both have nonzero measure; -
• the complement of
 $\bigcup _{\left (\mathcal {C},C\right )\in \mathcal {S}'}C$
has measure
$\bigcup _{\left (\mathcal {C},C\right )\in \mathcal {S}'}C$
has measure
 $0$
;
$0$
; -
• for all
 $(\mathcal {C},C)\in \mathcal {S}$
, every
$(\mathcal {C},C)\in \mathcal {S}$
, every
 $\psi \in \mathcal {C}$
has special point mapping to the point with
$\psi \in \mathcal {C}$
has special point mapping to the point with
 $\mathrm {SL}_2$
stabiliser;
$\mathrm {SL}_2$
stabiliser; -
•
 $C= \mathscr {L}(\pi )(\mathcal {C})$
for all
$C= \mathscr {L}(\pi )(\mathcal {C})$
for all
 $(\mathcal {C},C)\in \mathcal {S}'$
; and
$(\mathcal {C},C)\in \mathcal {S}'$
; and -
• Conjecture 1.1 holds for all
 $(\mathcal {C},C)\in \mathcal {S}'$
– that is,
$(\mathcal {C},C)\in \mathcal {S}'$
– that is,  $$ \begin{align*} \mu_{\mathcal{X}}(\mathcal{C}) = \mu_{\mathcal{X}}\left(\mathcal{C} \cap \mathscr{L}(\pi)^{-1}(C)\right) = \int_C \operatorname{\mathrm{sep}}_{\pi, \mathcal{C}} \mathrm{d}\mu^{\mathrm{Gor}}_X. \end{align*} $$
$$ \begin{align*} \mu_{\mathcal{X}}(\mathcal{C}) = \mu_{\mathcal{X}}\left(\mathcal{C} \cap \mathscr{L}(\pi)^{-1}(C)\right) = \int_C \operatorname{\mathrm{sep}}_{\pi, \mathcal{C}} \mathrm{d}\mu^{\mathrm{Gor}}_X. \end{align*} $$
Remark 10.8. By definition, for every
![]() $(\mathcal {C},C)\in \mathcal {S}$
and
$(\mathcal {C},C)\in \mathcal {S}$
and
![]() $\psi \in \mathcal {C}$
the matrix corresponding to
$\psi \in \mathcal {C}$
the matrix corresponding to
![]() $\psi $
specialises to the
$\psi $
specialises to the
![]() $0$
matrix. As a result, the special point of
$0$
matrix. As a result, the special point of
![]() $\psi $
maps to the point in
$\psi $
maps to the point in
![]() $\mathcal {X}$
with
$\mathcal {X}$
with
![]() $\mathrm {SL}_2$
stabiliser, justifying the fourth bullet point of Proposition 10.7.
$\mathrm {SL}_2$
stabiliser, justifying the fourth bullet point of Proposition 10.7.
The remainder of this section is concerned with the proof of Proposition 10.7. To compute
 $\mu ^{\mathrm {Gor}}_X\left (C^{\left (w_{1,2}, \mathbf {w}_1, \mathbf {w}_2\right )}\right )$
, it is enough to compute
$\mu ^{\mathrm {Gor}}_X\left (C^{\left (w_{1,2}, \mathbf {w}_1, \mathbf {w}_2\right )}\right )$
, it is enough to compute
 $\mu ^{\mathrm {Gor}}_X\left (C^{(\mathbf {w})}\right )$
, which is done in Proposition 10.9 (the only result in this section where we impose
$\mu ^{\mathrm {Gor}}_X\left (C^{(\mathbf {w})}\right )$
, which is done in Proposition 10.9 (the only result in this section where we impose
![]() $r\in \{3,4\}$
as opposed to
$r\in \{3,4\}$
as opposed to
![]() $r\geq 2$
).
$r\geq 2$
).
Proposition 10.9.
-
(a) Suppose
 $r = 3$
, and set
$r = 3$
, and set
 $\mathbf {w} = \left (w_{1,2}, w_{1,3}, w_{2,3}\right ) \in \mathbb {N}^{[r] \choose 2}$
. Then X is smooth, and
$\mathbf {w} = \left (w_{1,2}, w_{1,3}, w_{2,3}\right ) \in \mathbb {N}^{[r] \choose 2}$
. Then X is smooth, and  $$ \begin{align*} \mu^{\mathrm{Gor}}_X\left(C^{(\mathbf{w})}\right) = (\mathbb{L}-1)^3\mathbb{L}^{-3-w_{1,2} - w_{1,3} - w_{2,3}}. \end{align*} $$
$$ \begin{align*} \mu^{\mathrm{Gor}}_X\left(C^{(\mathbf{w})}\right) = (\mathbb{L}-1)^3\mathbb{L}^{-3-w_{1,2} - w_{1,3} - w_{2,3}}. \end{align*} $$
-
(b) Suppose
 $r = 4$
, set
$r = 4$
, set
 $\mathbf {w} = \left (w_{1,2}, w_{3,4}, w_{1,3}, w_{2,4}, w_{1,4}, w_{2,3}\right ) \in \mathbb {N}^{[r] \choose 2}$
and set Then X has log-terminal singularities, and
$\mathbf {w} = \left (w_{1,2}, w_{3,4}, w_{1,3}, w_{2,4}, w_{1,4}, w_{2,3}\right ) \in \mathbb {N}^{[r] \choose 2}$
and set Then X has log-terminal singularities, and $$ \begin{align*} m &= \min\left(w_{1,2} + w_{3,4}, w_{1,3} + w_{2,4}, w_{1,4} + w_{2,3}\right),\\ j &= -5+ m - w_{1,2} - w_{3,4} - w_{1,3} - w_{2,4} - w_{1,4} - w_{2,3}. \end{align*} $$
$$ \begin{align*} m &= \min\left(w_{1,2} + w_{3,4}, w_{1,3} + w_{2,4}, w_{1,4} + w_{2,3}\right),\\ j &= -5+ m - w_{1,2} - w_{3,4} - w_{1,3} - w_{2,4} - w_{1,4} - w_{2,3}. \end{align*} $$

Proof.
-
(a) This is immediate from the fact that
 $X = \mathbb {A}_k^{[3] \choose 2}$
.
$X = \mathbb {A}_k^{[3] \choose 2}$
. -
(b) We only sketch the proof, as the details are somewhat extensive but do not involve any novel ideas. We have that X is defined in
 $\mathbb {A}_k^{[4] \choose 2}$
by the vanishing of a single polynomial
$\mathbb {A}_k^{[4] \choose 2}$
by the vanishing of a single polynomial
 $x_{1,2}x_{3,4} - x_{1,3}x_{2,4} + x_{1,4}x_{2,3}$
. This polynomial is nondegenerate with respect to its Newton polyhedron, so the claim follows from standard techniques: a certain toric modification of
$x_{1,2}x_{3,4} - x_{1,3}x_{2,4} + x_{1,4}x_{2,3}$
. This polynomial is nondegenerate with respect to its Newton polyhedron, so the claim follows from standard techniques: a certain toric modification of
 $\mathbb {A}_k^{[4] \choose 2}$
gives a resolution of X (see, for example, [Reference Schepers and VeysSV09], especially the discrepancy computation in the proof of [Reference Schepers and VeysSV09, Proposition 2.3]). Note that to get our claim from these techniques, one needs to verify that
$\mathbb {A}_k^{[4] \choose 2}$
gives a resolution of X (see, for example, [Reference Schepers and VeysSV09], especially the discrepancy computation in the proof of [Reference Schepers and VeysSV09, Proposition 2.3]). Note that to get our claim from these techniques, one needs to verify that
 $\mathrm {e}\left (X \cap \mathbb {G}_m^{[4] \choose 2}\right ) = (\mathbb {L}-1)^3(\mathbb {L}-2)$
, which, for example, follows from the relationship between
$\mathrm {e}\left (X \cap \mathbb {G}_m^{[4] \choose 2}\right ) = (\mathbb {L}-1)^3(\mathbb {L}-2)$
, which, for example, follows from the relationship between
 $X \cap \mathbb {G}_m^{[4] \choose 2}$
and the realisation space of the rank
$X \cap \mathbb {G}_m^{[4] \choose 2}$
and the realisation space of the rank
 $2$
uniform matroid on four elements (see, for example, [Reference KatzKat16, Proposition 9.7]), which has class
$2$
uniform matroid on four elements (see, for example, [Reference KatzKat16, Proposition 9.7]), which has class
 $\mathbb {L}-2$
.
$\mathbb {L}-2$
.
We next turn to the computation of
 $\mu _{\mathcal {X}}\left (\mathcal {C}^{\left (i, w_{1,2}, \mathbf {w}_1, \mathbf {w}_2\right )}\right )$
. This is the technical heart of this section.
$\mu _{\mathcal {X}}\left (\mathcal {C}^{\left (i, w_{1,2}, \mathbf {w}_1, \mathbf {w}_2\right )}\right )$
. This is the technical heart of this section.
Proposition 10.10. Let
![]() $i, w_{1,2} \in \mathbb {N}$
and
$i, w_{1,2} \in \mathbb {N}$
and
![]() $\mathbf {w}_1 = \left (w_{1,3}, \dotsc , w_{1,r}\right )$
,
$\mathbf {w}_1 = \left (w_{1,3}, \dotsc , w_{1,r}\right )$
,
![]() $\mathbf {w}_2 = \left (w_{2,3}, \dotsc , w_{2, r}\right )$
satisfy (⋆). Then
$\mathbf {w}_2 = \left (w_{2,3}, \dotsc , w_{2, r}\right )$
satisfy (⋆). Then
![]() $\mathcal {C}^{\left (i, w_{1,2}, \mathbf {w}_1, \mathbf {w}_2\right )}$
is a cylinder in
$\mathcal {C}^{\left (i, w_{1,2}, \mathbf {w}_1, \mathbf {w}_2\right )}$
is a cylinder in
![]() $\lvert \mathscr {L}_n(\mathcal {X})\rvert $
and
$\lvert \mathscr {L}_n(\mathcal {X})\rvert $
and
 $$ \begin{align*} \mu_{\mathcal{X}}\left(\mathcal{C}^{\left(i, w_{1,2}, \mathbf{w}_1, \mathbf{w}_2\right)}\right) = (\mathbb{L}-1)^{2r-3} \mathbb{L}^{-(2r-3)+(r-4)w_{1,2}-\left(w_{1,3} + \dotsb + w_{1,r} + w_{2,3} + \dotsb + w_{2,r}\right)}. \end{align*} $$
$$ \begin{align*} \mu_{\mathcal{X}}\left(\mathcal{C}^{\left(i, w_{1,2}, \mathbf{w}_1, \mathbf{w}_2\right)}\right) = (\mathbb{L}-1)^{2r-3} \mathbb{L}^{-(2r-3)+(r-4)w_{1,2}-\left(w_{1,3} + \dotsb + w_{1,r} + w_{2,3} + \dotsb + w_{2,r}\right)}. \end{align*} $$
Proof. To ease notation, set
![]() $Z = Z^{\left (i, w_{1,2}, \mathbf {w}_1, \mathbf {w}_2\right )}$
and
$Z = Z^{\left (i, w_{1,2}, \mathbf {w}_1, \mathbf {w}_2\right )}$
and
![]() $\mathcal {C} = \mathcal {C}^{\left (i, w_{1,2}, \mathbf {w}_1, \mathbf {w}_2\right )}$
. For any
$\mathcal {C} = \mathcal {C}^{\left (i, w_{1,2}, \mathbf {w}_1, \mathbf {w}_2\right )}$
. For any
![]() $n \in \mathbb {N}$
, let
$n \in \mathbb {N}$
, let
![]() $Z_n$
be the locally closed subscheme of
$Z_n$
be the locally closed subscheme of
 $\mathscr {L}_n\left (\widetilde {X}\right )$
whose A-valued points, for any k-algebra A, are the
$\mathscr {L}_n\left (\widetilde {X}\right )$
whose A-valued points, for any k-algebra A, are the
![]() $2 \times r$
matrices of the form
$2 \times r$
matrices of the form
 $$ \begin{align*} \begin{pmatrix} u_{1,1} t^{w_{1,2} - i} & 0 & u_{1,3} t^{w_{2,3} - i} & u_{1,4} t^{w_{2,4} - i} & \dotsb & u_{1,r} t^{w_{2,r} - i} \\ 0 & t^i & u_{2,3}t^{w_{1,3} - w_{1,2} + i} & u_{2,4}t^{w_{1,4} - w_{1,2} + i} & \dotsb & u_{2,r}t^{w_{1,r} - w_{1,2} + i} \end{pmatrix}, \end{align*} $$
$$ \begin{align*} \begin{pmatrix} u_{1,1} t^{w_{1,2} - i} & 0 & u_{1,3} t^{w_{2,3} - i} & u_{1,4} t^{w_{2,4} - i} & \dotsb & u_{1,r} t^{w_{2,r} - i} \\ 0 & t^i & u_{2,3}t^{w_{1,3} - w_{1,2} + i} & u_{2,4}t^{w_{1,4} - w_{1,2} + i} & \dotsb & u_{2,r}t^{w_{1,r} - w_{1,2} + i} \end{pmatrix}, \end{align*} $$
where
![]() $u_{1,1}, u_{1,3}, \dotsc , u_{1, r}, u_{2,3}, \dotsc , u_{2, r}$
are all units in
$u_{1,1}, u_{1,3}, \dotsc , u_{1, r}, u_{2,3}, \dotsc , u_{2, r}$
are all units in
![]() $A[t]/\left (t^{n+1}\right )$
; so by construction,
$A[t]/\left (t^{n+1}\right )$
; so by construction,
Thus for any
![]() $n \in \mathbb {N}$
,
$n \in \mathbb {N}$
,
Now set
![]() $n_0 = \max \left (w_{1,2}, i, w_{2,3}, \dotsc , w_{2, r}, w_{1,3} + i, \dotsc , w_{1,r} + i\right )$
. We will show that
$n_0 = \max \left (w_{1,2}, i, w_{2,3}, \dotsc , w_{2, r}, w_{1,3} + i, \dotsc , w_{1,r} + i\right )$
. We will show that
 $$ \begin{align*} \mathcal{C} = \theta_{n_0}^{-1}\left( \mathscr{L}_{n_0}(\rho)\left(Z_{n_0}\right) \right). \end{align*} $$
$$ \begin{align*} \mathcal{C} = \theta_{n_0}^{-1}\left( \mathscr{L}_{n_0}(\rho)\left(Z_{n_0}\right) \right). \end{align*} $$
One inclusion is clear from equation (4). To show the other inclusion, let
![]() $k'$
be a field extension of k and
$k'$
be a field extension of k and
![]() $\psi $
be a
$\psi $
be a
![]() $k'$
-point of
$k'$
-point of
 $\theta _{n_0}^{-1}\left ( \mathscr {L}_{n_0}(\rho )\left (Z_{n_0}\right ) \right )$
. For the sake of showing the desired inclusion, we may extend
$\theta _{n_0}^{-1}\left ( \mathscr {L}_{n_0}(\rho )\left (Z_{n_0}\right ) \right )$
. For the sake of showing the desired inclusion, we may extend
![]() $k'$
, so we may assume there exists a
$k'$
, so we may assume there exists a
![]() $k'$
-point
$k'$
-point
![]() $\widetilde {\psi }_{n_0}$
of
$\widetilde {\psi }_{n_0}$
of
![]() $Z_{n_0}$
such that
$Z_{n_0}$
such that
 $\mathscr {L}_n(\rho )\left (\widetilde {\psi }_{n_0}\right ) \cong \theta _{n_0}(\psi )$
. Because
$\mathscr {L}_n(\rho )\left (\widetilde {\psi }_{n_0}\right ) \cong \theta _{n_0}(\psi )$
. Because
![]() $\rho : \widetilde {X} \to \mathcal {X}$
is smooth, there exists a
$\rho : \widetilde {X} \to \mathcal {X}$
is smooth, there exists a
![]() $k'$
-point
$k'$
-point
![]() $\widetilde {\psi }$
of
$\widetilde {\psi }$
of
 $\mathscr {L}\left (\widetilde {X}\right )$
such that
$\mathscr {L}\left (\widetilde {X}\right )$
such that
 $\theta _{n_0}\left (\widetilde {\psi }\right ) = \widetilde {\psi }_{n_0}$
and
$\theta _{n_0}\left (\widetilde {\psi }\right ) = \widetilde {\psi }_{n_0}$
and
 $\mathscr {L}(\rho )\left (\widetilde {\psi }\right ) \cong \psi $
. We want to show that there exists some
$\mathscr {L}(\rho )\left (\widetilde {\psi }\right ) \cong \psi $
. We want to show that there exists some
![]() such that
such that
![]() $g \cdot \widetilde {\psi } \in Z$
, as this would imply that
$g \cdot \widetilde {\psi } \in Z$
, as this would imply that
 $\psi \cong \mathscr {L}(\rho )\left (\widetilde {\psi }\right ) \cong \mathscr {L}(\rho )\left (g \cdot \widetilde {\psi }\right ) \in \mathscr {L}(\rho )(Z) = \mathcal {C}$
. By our choice of
$\psi \cong \mathscr {L}(\rho )\left (\widetilde {\psi }\right ) \cong \mathscr {L}(\rho )\left (g \cdot \widetilde {\psi }\right ) \in \mathscr {L}(\rho )(Z) = \mathcal {C}$
. By our choice of
![]() $n_0$
and the fact that
$n_0$
and the fact that
 $\theta _{n_0}\left (\widetilde {\psi }\right ) \in Z_{n_0}$
, the arc
$\theta _{n_0}\left (\widetilde {\psi }\right ) \in Z_{n_0}$
, the arc
![]() $\tilde {\psi }$
is equal to
$\tilde {\psi }$
is equal to
 $$ \begin{align*} \begin{pmatrix} f_{1,1} & h_{1,2}t^{n_0+1} & f_{1,3} & f_{1,4} & \dotsb & f_{1,r} \\ h_{2,1}t^{n_0+1} & t^i + h_{2,2}t^{n_0+1} & f_{2,3} & f_{2,4} & \dotsb & f_{2,r} \end{pmatrix}, \end{align*} $$
$$ \begin{align*} \begin{pmatrix} f_{1,1} & h_{1,2}t^{n_0+1} & f_{1,3} & f_{1,4} & \dotsb & f_{1,r} \\ h_{2,1}t^{n_0+1} & t^i + h_{2,2}t^{n_0+1} & f_{2,3} & f_{2,4} & \dotsb & f_{2,r} \end{pmatrix}, \end{align*} $$
for some
![]() and some
and some
![]() satisfying
satisfying
 $$ \begin{align*} \operatorname{\mathrm{ord}}_t\left(f_{1,1}\right) &= w_{1,2} - i,\\ \operatorname{\mathrm{ord}}_t\left(f_{1,j}\right) &= w_{2,j} - i, &\text{for all } j = 3, \dotsc, r,\\ \operatorname{\mathrm{ord}}_t\left(f_{2,j}\right) &= w_{1,j} - w_{1,2} + i, &\text{for all } j = 3, \dotsc, r. \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{ord}}_t\left(f_{1,1}\right) &= w_{1,2} - i,\\ \operatorname{\mathrm{ord}}_t\left(f_{1,j}\right) &= w_{2,j} - i, &\text{for all } j = 3, \dotsc, r,\\ \operatorname{\mathrm{ord}}_t\left(f_{2,j}\right) &= w_{1,j} - w_{1,2} + i, &\text{for all } j = 3, \dotsc, r. \end{align*} $$
Let
![]() be the
be the
![]() $(1,2)$
th minor of
$(1,2)$
th minor of
![]() $\widetilde {\psi }$
. We have
$\widetilde {\psi }$
. We have
![]() $h \neq 0$
, because h and
$h \neq 0$
, because h and
![]() $f_{1,1}t^i$
have the same image in
$f_{1,1}t^i$
have the same image in
![]() $k'[t]/\left (t^{n_0+1}\right )$
, and the latter image is nonzero by
$k'[t]/\left (t^{n_0+1}\right )$
, and the latter image is nonzero by
![]() $n_0 \geq w_{1,2}$
. Thus there exists some
$n_0 \geq w_{1,2}$
. Thus there exists some
![]() such that
such that
 $$ \begin{align*} g \cdot \begin{pmatrix} f_{1,1} & h_{1,2}t^{n_0+1} \\ h_{2,1}t^{n_0+1} & t^i + h_{2,2}t^{n_0+1} \end{pmatrix} = \begin{pmatrix} ht^{-i} & 0 \\ 0 & t^i \end{pmatrix}. \end{align*} $$
$$ \begin{align*} g \cdot \begin{pmatrix} f_{1,1} & h_{1,2}t^{n_0+1} \\ h_{2,1}t^{n_0+1} & t^i + h_{2,2}t^{n_0+1} \end{pmatrix} = \begin{pmatrix} ht^{-i} & 0 \\ 0 & t^i \end{pmatrix}. \end{align*} $$
Then
 $$ \begin{align*} g^{-1} = \begin{pmatrix} f_{1,1} & h_{1,2}t^{n_0+1} \\ h_{2,1}t^{n_0+1} & t^i + h_{2,2}t^{n_0+1} \end{pmatrix} \begin{pmatrix} ht^{-i} & 0 \\ 0 & t^i \end{pmatrix}^{-1} = \begin{pmatrix} f_{1,1}t^ih^{-1} & h_{1,2}t^{n_0+1-i} \\ h_{2,1}t^{n_0+1+i}h^{-1} & t^i + h_{2,2}t^{n_0+1-i} \end{pmatrix}. \end{align*} $$
$$ \begin{align*} g^{-1} = \begin{pmatrix} f_{1,1} & h_{1,2}t^{n_0+1} \\ h_{2,1}t^{n_0+1} & t^i + h_{2,2}t^{n_0+1} \end{pmatrix} \begin{pmatrix} ht^{-i} & 0 \\ 0 & t^i \end{pmatrix}^{-1} = \begin{pmatrix} f_{1,1}t^ih^{-1} & h_{1,2}t^{n_0+1-i} \\ h_{2,1}t^{n_0+1+i}h^{-1} & t^i + h_{2,2}t^{n_0+1-i} \end{pmatrix}. \end{align*} $$
Because h and
![]() $f_{1,1}t^i$
have the same image in
$f_{1,1}t^i$
have the same image in
![]() $k'[t]/\left (t^{n_0+1}\right )$
and
$k'[t]/\left (t^{n_0+1}\right )$
and
![]() $n_0 \geq w_{1,2} =\operatorname {\mathrm {ord}}_t\left (f_{1,1}t^i\right )$
, we have that
$n_0 \geq w_{1,2} =\operatorname {\mathrm {ord}}_t\left (f_{1,1}t^i\right )$
, we have that
![]() $\operatorname {\mathrm {ord}}_t(h) = w_{1,2}$
. Together with the fact that
$\operatorname {\mathrm {ord}}_t(h) = w_{1,2}$
. Together with the fact that
![]() $n_0 \geq i$
, this implies that the entries of
$n_0 \geq i$
, this implies that the entries of
![]() $g^{-1}$
are all elements of
$g^{-1}$
are all elements of
![]() , so
, so
![]() . We will now show that
. We will now show that
![]() $g \cdot \widetilde {\psi } \in Z$
. We see that
$g \cdot \widetilde {\psi } \in Z$
. We see that
![]() $g \cdot \widetilde {\psi }$
is equal to
$g \cdot \widetilde {\psi }$
is equal to
 $$ \begin{align*} \begin{pmatrix} ht^{-i} & 0 & h_{1,3} & h_{1,4} & \dotsb & h_{1,r} \\ 0 & t^i & h_{2,3} & h_{2,4} & \dotsb & h_{2,r} \end{pmatrix} \end{align*} $$
$$ \begin{align*} \begin{pmatrix} ht^{-i} & 0 & h_{1,3} & h_{1,4} & \dotsb & h_{1,r} \\ 0 & t^i & h_{2,3} & h_{2,4} & \dotsb & h_{2,r} \end{pmatrix} \end{align*} $$
for some
![]() , and we have already shown that
, and we have already shown that
![]() $\operatorname {\mathrm {ord}}_t\left (ht^{-i}\right ) = w_{1,2} - i$
. For any
$\operatorname {\mathrm {ord}}_t\left (ht^{-i}\right ) = w_{1,2} - i$
. For any
![]() $j = 3, \dotsc , r$
, let
$j = 3, \dotsc , r$
, let
![]() (resp.,
(resp.,
![]() ) be the
) be the
![]() $(1,j)$
th (resp.,
$(1,j)$
th (resp.,
![]() $(2,j)$
th) minor of
$(2,j)$
th) minor of
![]() $\psi $
. Then for any
$\psi $
. Then for any
![]() $j = 3, \dotsc , r$
, we have that
$j = 3, \dotsc , r$
, we have that
![]() $-f_{1,j}t^{i}$
and
$-f_{1,j}t^{i}$
and
![]() $q_{2,j}$
(resp.,
$q_{2,j}$
(resp.,
![]() $f_{1,1}f_{2,j}$
and
$f_{1,1}f_{2,j}$
and
![]() $q_{1,j}$
) have the same image in
$q_{1,j}$
) have the same image in
![]() $k'[t]/\left (t^{n_0+1}\right )$
, so because
$k'[t]/\left (t^{n_0+1}\right )$
, so because
![]() $n_0 \geq w_{2,j} = \operatorname {\mathrm {ord}}_t\left (-f_{1,j}t^i\right )$
(resp.,
$n_0 \geq w_{2,j} = \operatorname {\mathrm {ord}}_t\left (-f_{1,j}t^i\right )$
(resp.,
![]() $n_0 \geq w_{1,j} = \operatorname {\mathrm {ord}}_t(f_{1,1}f_{2,j})$
), we have
$n_0 \geq w_{1,j} = \operatorname {\mathrm {ord}}_t(f_{1,1}f_{2,j})$
), we have
![]() $\operatorname {\mathrm {ord}}_t\left (q_{2,j}\right ) = w_{2,j}$
(resp.,
$\operatorname {\mathrm {ord}}_t\left (q_{2,j}\right ) = w_{2,j}$
(resp.,
![]() $\operatorname {\mathrm {ord}}_t(q_{1,j}) = w_{1,j}$
). Because
$\operatorname {\mathrm {ord}}_t(q_{1,j}) = w_{1,j}$
). Because
![]() , the matrices
, the matrices
![]() $\widetilde {\psi }$
and
$\widetilde {\psi }$
and
![]() $g \cdot \widetilde {\psi }$
have the same minors, so
$g \cdot \widetilde {\psi }$
have the same minors, so
 $$ \begin{align*} \operatorname{\mathrm{ord}}_t\left(h_{1,j}\right) &= \operatorname{\mathrm{ord}}_t\left(-q_{2,j}t^{-i}\right) = w_{2,j} - i, &\text{for all } j = 3, \dotsc, r,\\ \operatorname{\mathrm{ord}}_t\left(h_{2,j}\right) &= \operatorname{\mathrm{ord}}_t\left(q_{1,j}h^{-1}t^i\right) =w_{1,j} - w_{1,2} + i, &\text{for all } j = 3, \dotsc, r. \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{ord}}_t\left(h_{1,j}\right) &= \operatorname{\mathrm{ord}}_t\left(-q_{2,j}t^{-i}\right) = w_{2,j} - i, &\text{for all } j = 3, \dotsc, r,\\ \operatorname{\mathrm{ord}}_t\left(h_{2,j}\right) &= \operatorname{\mathrm{ord}}_t\left(q_{1,j}h^{-1}t^i\right) =w_{1,j} - w_{1,2} + i, &\text{for all } j = 3, \dotsc, r. \end{align*} $$
We have thus verified that
![]() $g \cdot \widetilde {\psi } \in Z$
, so
$g \cdot \widetilde {\psi } \in Z$
, so
![]() $\psi \in \mathcal {C}$
, and thus we have finished showing
$\psi \in \mathcal {C}$
, and thus we have finished showing
 $$ \begin{align*} \mathcal{C}= \theta_{n_0}^{-1}\left( \mathscr{L}_{n_0}(\rho)\left(Z_{n_0}\right) \right). \end{align*} $$
$$ \begin{align*} \mathcal{C}= \theta_{n_0}^{-1}\left( \mathscr{L}_{n_0}(\rho)\left(Z_{n_0}\right) \right). \end{align*} $$
Because
![]() $\mathscr {L}_{n_0}(\rho )\left (Z_{n_0}\right )$
is a constructible subset of
$\mathscr {L}_{n_0}(\rho )\left (Z_{n_0}\right )$
is a constructible subset of
![]() $\mathscr {L}_n(\mathcal {X})$
by Chevalley’s theorem for Artin stacks [Reference Hall and RydhHR17, Theorem 5.2], this implies that
$\mathscr {L}_n(\mathcal {X})$
by Chevalley’s theorem for Artin stacks [Reference Hall and RydhHR17, Theorem 5.2], this implies that
![]() $\mathcal {C}$
is a cylinder. We will use the remainder of this proof to compute
$\mathcal {C}$
is a cylinder. We will use the remainder of this proof to compute
![]() $\mu _{\mathcal {X}}(\mathcal {C})$
.
$\mu _{\mathcal {X}}(\mathcal {C})$
.
Set
![]() $n_1 = \max (n_0, 2i-1)$
. For any
$n_1 = \max (n_0, 2i-1)$
. For any
![]() $n \geq n_1$
, let
$n \geq n_1$
, let
![]() $H_n$
be the closed subscheme of
$H_n$
be the closed subscheme of
 $\mathscr {L}_n\left (\mathbb {A}^{2 \times 2}_k\right )$
whose A-valued points, for any k-algebra A, are the
$\mathscr {L}_n\left (\mathbb {A}^{2 \times 2}_k\right )$
whose A-valued points, for any k-algebra A, are the
![]() $2 \times 2$
matrices of the form
$2 \times 2$
matrices of the form
 $$ \begin{align*} \begin{pmatrix} 1+g_{1,1}t^{n+1-i} & g_{1,2}t^{n+1-i} \\ g_{2,1}t^{n+1-w_{1,2}+i} & 1-g_{1,1}t^{n+1-i} \\ \end{pmatrix} \end{align*} $$
$$ \begin{align*} \begin{pmatrix} 1+g_{1,1}t^{n+1-i} & g_{1,2}t^{n+1-i} \\ g_{2,1}t^{n+1-w_{1,2}+i} & 1-g_{1,1}t^{n+1-i} \\ \end{pmatrix} \end{align*} $$
for some
![]() $g_{1,2}, g_{2,1}, g_{2,2} \in A[t]/\left (t^{n+1}\right )$
. By our choice of
$g_{1,2}, g_{2,1}, g_{2,2} \in A[t]/\left (t^{n+1}\right )$
. By our choice of
![]() $n_1$
,
$n_1$
,
 $$ \begin{align*} \det \begin{pmatrix} 1+g_{1,1}t^{n+1-i} & g_{1,2}t^{n+1-i} \\ g_{2,1}t^{n+1-w_{1,2}+i} & 1-g_{1,1}t^{n+1-i} \\ \end{pmatrix} = 1 \end{align*} $$
$$ \begin{align*} \det \begin{pmatrix} 1+g_{1,1}t^{n+1-i} & g_{1,2}t^{n+1-i} \\ g_{2,1}t^{n+1-w_{1,2}+i} & 1-g_{1,1}t^{n+1-i} \\ \end{pmatrix} = 1 \end{align*} $$
and
 $$ \begin{align*} \begin{pmatrix} 1+g_{1,1}t^{n+1-i} & g_{1,2}t^{n+1-i} \\ g_{2,1}t^{n+1-w_{1,2}+i} & 1-g_{1,1}t^{n+1-i} \\ \end{pmatrix}& \begin{pmatrix} 1+g^{\prime}_{1,1}t^{n+1-i} & g^{\prime}_{1,2}t^{n+1-i} \\ g^{\prime}_{2,1}t^{n+1-w_{1,2}+i} & 1-g^{\prime}_{1,1}t^{n+1-i} \\ \end{pmatrix} \\ &= \begin{pmatrix} 1+\left(g_{1,1}+g^{\prime}_{1,1}\right)t^{n+1-i} & \left(g_{1,2}+g^{\prime}_{1,2}\right)t^{n+1-i} \\ \left(g_{2,1}+g^{\prime}_{2,1}\right)t^{n+1-w_{1,2}+i} & 1-\left(g_{1,1}+g^{\prime}_{1,1}\right)t^{n+1-i} \\ \end{pmatrix}, \end{align*} $$
$$ \begin{align*} \begin{pmatrix} 1+g_{1,1}t^{n+1-i} & g_{1,2}t^{n+1-i} \\ g_{2,1}t^{n+1-w_{1,2}+i} & 1-g_{1,1}t^{n+1-i} \\ \end{pmatrix}& \begin{pmatrix} 1+g^{\prime}_{1,1}t^{n+1-i} & g^{\prime}_{1,2}t^{n+1-i} \\ g^{\prime}_{2,1}t^{n+1-w_{1,2}+i} & 1-g^{\prime}_{1,1}t^{n+1-i} \\ \end{pmatrix} \\ &= \begin{pmatrix} 1+\left(g_{1,1}+g^{\prime}_{1,1}\right)t^{n+1-i} & \left(g_{1,2}+g^{\prime}_{1,2}\right)t^{n+1-i} \\ \left(g_{2,1}+g^{\prime}_{2,1}\right)t^{n+1-w_{1,2}+i} & 1-\left(g_{1,1}+g^{\prime}_{1,1}\right)t^{n+1-i} \\ \end{pmatrix}, \end{align*} $$
so the inclusion
 $H_n \hookrightarrow \mathscr {L}_n\left (\mathbb {A}^{2 \times 2}_k\right )$
factors through a closed immersion
$H_n \hookrightarrow \mathscr {L}_n\left (\mathbb {A}^{2 \times 2}_k\right )$
factors through a closed immersion
![]() $H_n \hookrightarrow \mathscr {L}_n(\mathrm {SL}_2)$
that gives
$H_n \hookrightarrow \mathscr {L}_n(\mathrm {SL}_2)$
that gives
![]() $H_n$
the structure of a closed subgroup of
$H_n$
the structure of a closed subgroup of
![]() $\mathscr {L}_n(\mathrm {SL}_2)$
, and
$\mathscr {L}_n(\mathrm {SL}_2)$
, and
 $H_n \cong \mathbb {G}_a^{w_{1,2} + i}$
as algebraic groups.
$H_n \cong \mathbb {G}_a^{w_{1,2} + i}$
as algebraic groups.
For any
![]() $n \in \mathbb {N}$
, set
$n \in \mathbb {N}$
, set
 $\widetilde {C}_n = \mathscr {L}_n(\rho )^{-1}\left (\theta _n(\mathcal {C})\right ) \subset \mathscr {L}_n\left (\widetilde {X}\right )$
. We will show that for
$\widetilde {C}_n = \mathscr {L}_n(\rho )^{-1}\left (\theta _n(\mathcal {C})\right ) \subset \mathscr {L}_n\left (\widetilde {X}\right )$
. We will show that for
![]() $n \geq n_1$
,
$n \geq n_1$
,
 $$ \begin{align} \mathrm{e}\left(\widetilde{C}_n\right) = \mathrm{e}(Z_n)\mathrm{e}(\mathscr{L}_n(\mathrm{SL}_2))\mathrm{e}(H_n)^{-1} = \mathrm{e}(Z_n)\mathrm{e}(\mathscr{L}_n(\mathrm{SL}_2))\mathbb{L}^{-w_{1,2}-i} \in K_0(\mathbf{Stack}_k). \end{align} $$
$$ \begin{align} \mathrm{e}\left(\widetilde{C}_n\right) = \mathrm{e}(Z_n)\mathrm{e}(\mathscr{L}_n(\mathrm{SL}_2))\mathrm{e}(H_n)^{-1} = \mathrm{e}(Z_n)\mathrm{e}(\mathscr{L}_n(\mathrm{SL}_2))\mathbb{L}^{-w_{1,2}-i} \in K_0(\mathbf{Stack}_k). \end{align} $$
By equation (4) and Corollary 3.22,
![]() $\widetilde {C}_n$
is equal to the image of the morphism
$\widetilde {C}_n$
is equal to the image of the morphism
 $$ \begin{align*} \mathscr{L}_n(\mathrm{SL}_2) \times_k Z_n \to \mathscr{L}_n\left(\widetilde{X}\right) \end{align*} $$
$$ \begin{align*} \mathscr{L}_n(\mathrm{SL}_2) \times_k Z_n \to \mathscr{L}_n\left(\widetilde{X}\right) \end{align*} $$
induced by the action of
![]() $\mathscr {L}_n(\mathrm {SL}_2)$
on
$\mathscr {L}_n(\mathrm {SL}_2)$
on
 $\mathscr {L}_n\left (\widetilde {X}\right )$
. Thus to show equation (5), it is sufficient to show that for any field extension
$\mathscr {L}_n\left (\widetilde {X}\right )$
. Thus to show equation (5), it is sufficient to show that for any field extension
![]() $k'$
of k and any
$k'$
of k and any
![]() $\widetilde {\psi }_n \in \widetilde {C}_n(k')$
, the fibre of
$\widetilde {\psi }_n \in \widetilde {C}_n(k')$
, the fibre of
 $\mathscr {L}_n(\mathrm {SL}_2) \times _k Z_n \to \mathscr {L}_n\left (\widetilde {X}\right )$
over
$\mathscr {L}_n(\mathrm {SL}_2) \times _k Z_n \to \mathscr {L}_n\left (\widetilde {X}\right )$
over
![]() $\widetilde {\psi }_n$
is isomorphic to
$\widetilde {\psi }_n$
is isomorphic to
![]() $H_n \otimes _k k'$
. Because
$H_n \otimes _k k'$
. Because
![]() $H_n$
is special and thus
$H_n$
is special and thus
![]() $H_n$
-torsors over
$H_n$
-torsors over
![]() $k'$
are trivial, it is sufficient to show that for any field extension
$k'$
are trivial, it is sufficient to show that for any field extension
![]() $k'$
of k and
$k'$
of k and
![]() $\widetilde {\psi }_n \in Z_n(k')$
,
$\widetilde {\psi }_n \in Z_n(k')$
,
-
• the stabiliser of
 $\widetilde {\psi }_n$
under the
$\widetilde {\psi }_n$
under the
 $\mathscr {L}_n(\mathrm {SL}_2)$
action is
$\mathscr {L}_n(\mathrm {SL}_2)$
action is
 $H_n \otimes _k k'$
, and
$H_n \otimes _k k'$
, and -
• if
 $g_n \in \mathscr {L}_n(\mathrm {SL}_2)(k')$
is such that
$g_n \in \mathscr {L}_n(\mathrm {SL}_2)(k')$
is such that
 $g_n \cdot \widetilde {\psi }_n \in Z_n(k')$
, then
$g_n \cdot \widetilde {\psi }_n \in Z_n(k')$
, then
 $g_n \cdot \widetilde {\psi }_n = \widetilde {\psi }_n$
.
$g_n \cdot \widetilde {\psi }_n = \widetilde {\psi }_n$
.
To show both of these items, it is sufficient to show that for any
![]() $g_n \in \mathscr {L}_n(\mathrm {SL}_2)(k')$
,
$g_n \in \mathscr {L}_n(\mathrm {SL}_2)(k')$
,
where we note that because k has characteristic
![]() $0$
, we only need to show that
$0$
, we only need to show that
![]() $H_n \otimes _k k'$
and the stabiliser of
$H_n \otimes _k k'$
and the stabiliser of
![]() $\widetilde {\psi }_n$
have the same underlying subset of
$\widetilde {\psi }_n$
have the same underlying subset of
![]() $\mathscr {L}_n(\mathrm {SL}_2) \otimes _k k'$
. Write
$\mathscr {L}_n(\mathrm {SL}_2) \otimes _k k'$
. Write
 $$ \begin{align*} \widetilde{\psi}_n = \begin{pmatrix} u_{1,1} t^{w_{1,2} - i} & 0 & \dotsb & u_{1,j} t^{w_{2,j} - i} & \dotsb \\ 0 & t^i & \dotsb & u_{2,j}t^{w_{1,j} - w_{1,2} + i} & \dotsb \end{pmatrix}, \end{align*} $$
$$ \begin{align*} \widetilde{\psi}_n = \begin{pmatrix} u_{1,1} t^{w_{1,2} - i} & 0 & \dotsb & u_{1,j} t^{w_{2,j} - i} & \dotsb \\ 0 & t^i & \dotsb & u_{2,j}t^{w_{1,j} - w_{1,2} + i} & \dotsb \end{pmatrix}, \end{align*} $$
and write
 $$ \begin{align*} g_n = \begin{pmatrix} a & b \\ c & d \\ \end{pmatrix}, \end{align*} $$
$$ \begin{align*} g_n = \begin{pmatrix} a & b \\ c & d \\ \end{pmatrix}, \end{align*} $$
with
![]() $a,b,c,d \in k'[t]/\left (t^{n+1}\right )$
. Then
$a,b,c,d \in k'[t]/\left (t^{n+1}\right )$
. Then
 $$ \begin{align} g_n \cdot \widetilde{\psi}_n = \begin{pmatrix} au_{1,1} t^{w_{1,2} - i} & bt^i & \dotsb & au_{1,j}t^{w_{2,j}-i} + bu_{2,j}t^{w_{1,j}-w_{1,2}+i} & \dotsb \\ cu_{1,1}t^{w_{1,2}-i} & dt^i & \dotsb & cu_{1,j}t^{w_{2,j}-i} + du_{2,j}t^{w_{1,j}-w_{1,2}+i} & \dotsb \end{pmatrix}. \end{align} $$
$$ \begin{align} g_n \cdot \widetilde{\psi}_n = \begin{pmatrix} au_{1,1} t^{w_{1,2} - i} & bt^i & \dotsb & au_{1,j}t^{w_{2,j}-i} + bu_{2,j}t^{w_{1,j}-w_{1,2}+i} & \dotsb \\ cu_{1,1}t^{w_{1,2}-i} & dt^i & \dotsb & cu_{1,j}t^{w_{2,j}-i} + du_{2,j}t^{w_{1,j}-w_{1,2}+i} & \dotsb \end{pmatrix}. \end{align} $$
We start with the first implication, so suppose
![]() $g_n \cdot \widetilde {\psi }_n \in Z_n(k')$
. Then
$g_n \cdot \widetilde {\psi }_n \in Z_n(k')$
. Then
![]() $bt^i = cu_{1,1}t^{w_{1,2}-i} = 0$
and
$bt^i = cu_{1,1}t^{w_{1,2}-i} = 0$
and
![]() $dt^i = t^i$
, so
$dt^i = t^i$
, so
![]() $b = g_{1,2}t^{n+1-i}$
,
$b = g_{1,2}t^{n+1-i}$
,
![]() $c = g_{2,1}t^{n+1 - w_{1,2}+i}$
,
$c = g_{2,1}t^{n+1 - w_{1,2}+i}$
,
![]() $d = 1 - g_{1,1}t^{n+1-i}$
for some units
$d = 1 - g_{1,1}t^{n+1-i}$
for some units
![]() $g_{1,2}, g_{2,1}, g_{1,1}$
in
$g_{1,2}, g_{2,1}, g_{1,1}$
in
![]() $k'[t]/\left (t^{n+1}\right )$
. By our choice of
$k'[t]/\left (t^{n+1}\right )$
. By our choice of
![]() $n_1$
,
$n_1$
,
 $$ \begin{align*} 1 = \det g_n = a\left(1 - g_{1,1}t^{n+1-i}\right) - g_{1,2}t^{n+1-i}g_{2,1}t^{n+1 - w_{1,2}+i} = a\left(1 - g_{1,1}t^{n+1-i}\right), \end{align*} $$
$$ \begin{align*} 1 = \det g_n = a\left(1 - g_{1,1}t^{n+1-i}\right) - g_{1,2}t^{n+1-i}g_{2,1}t^{n+1 - w_{1,2}+i} = a\left(1 - g_{1,1}t^{n+1-i}\right), \end{align*} $$
so
 $$ \begin{align*} a = \left(1 - g_{1,1}t^{n+1-i}\right)^{-1} = 1 + g_{1,1}t^{n+1-i}, \end{align*} $$
$$ \begin{align*} a = \left(1 - g_{1,1}t^{n+1-i}\right)^{-1} = 1 + g_{1,1}t^{n+1-i}, \end{align*} $$
and we have
![]() $g_n \in H_n(k')$
. The second implication is a straightforward application of equation (6) and condition (⋆). We have therefore finished showing that
$g_n \in H_n(k')$
. The second implication is a straightforward application of equation (6) and condition (⋆). We have therefore finished showing that
 $\mathrm {e}\left (\widetilde {C}_n\right ) = \mathrm {e}(Z_n)\mathrm {e}(\mathscr {L}_n(\mathrm {SL}_2))\mathbb {L}^{-w_{1,2}-i}$
.
$\mathrm {e}\left (\widetilde {C}_n\right ) = \mathrm {e}(Z_n)\mathrm {e}(\mathscr {L}_n(\mathrm {SL}_2))\mathbb {L}^{-w_{1,2}-i}$
.
Now we can complete the computation of
![]() $\mu _{\mathcal {X}}(\mathcal {C})$
. Set
$\mu _{\mathcal {X}}(\mathcal {C})$
. Set
By Corollary 3.22 and the fact that
![]() $\mathscr {L}_n(\mathrm {SL}_2)$
is a special group, for any
$\mathscr {L}_n(\mathrm {SL}_2)$
is a special group, for any
![]() $n \geq n_1$
,
$n \geq n_1$
,
 $$ \begin{align*} \mathrm{e}(\theta_n(\mathcal{C})) = \mathrm{e}\left(\widetilde{C}_n\right) \mathrm{e}(\mathscr{L}_n(\mathrm{SL}_2))^{-1} = \mathrm{e}(Z_n)\mathbb{L}^{-w_{1,2}-i} = (\mathbb{L}-1)^{2r-3}\mathbb{L}^{n(2r-3) + (r-4)w_{1,2} - s}, \end{align*} $$
$$ \begin{align*} \mathrm{e}(\theta_n(\mathcal{C})) = \mathrm{e}\left(\widetilde{C}_n\right) \mathrm{e}(\mathscr{L}_n(\mathrm{SL}_2))^{-1} = \mathrm{e}(Z_n)\mathbb{L}^{-w_{1,2}-i} = (\mathbb{L}-1)^{2r-3}\mathbb{L}^{n(2r-3) + (r-4)w_{1,2} - s}, \end{align*} $$
where the last equality is by the construction of
![]() $Z_n$
. Therefore, noting that
$Z_n$
. Therefore, noting that
 $\dim \mathcal {X} = \dim \left (\mathbb {A}^{2 \times r}_k\right ) - \dim \mathrm {SL}_2 = 2r-3$
,
$\dim \mathcal {X} = \dim \left (\mathbb {A}^{2 \times r}_k\right ) - \dim \mathrm {SL}_2 = 2r-3$
,
 $$ \begin{align*} \mu_{\mathcal{X}}(\mathcal{C}) = \lim_{n \to \infty} \mathrm{e}(\theta_n(\mathcal{C})) \mathbb{L}^{-(n+1)\dim\mathcal{X}} = (\mathbb{L}-1)^{2r-3} \mathbb{L}^{-(2r-3)+(r-4)w_{1,2}-s}.\\[-36pt] \end{align*} $$
$$ \begin{align*} \mu_{\mathcal{X}}(\mathcal{C}) = \lim_{n \to \infty} \mathrm{e}(\theta_n(\mathcal{C})) \mathbb{L}^{-(n+1)\dim\mathcal{X}} = (\mathbb{L}-1)^{2r-3} \mathbb{L}^{-(2r-3)+(r-4)w_{1,2}-s}.\\[-36pt] \end{align*} $$
We next compute the value of
![]() $\operatorname {\mathrm {sep}}_\pi $
on our sets of interest.
$\operatorname {\mathrm {sep}}_\pi $
on our sets of interest.
Proposition 10.11. Let
![]() $i, w_{1,2} \in \mathbb {N}$
and
$i, w_{1,2} \in \mathbb {N}$
and
![]() $\mathbf {w}_1, \mathbf {w}_2 \in \mathbb {N}^{r-2}$
satisfy (⋆). Then the image of
$\mathbf {w}_1, \mathbf {w}_2 \in \mathbb {N}^{r-2}$
satisfy (⋆). Then the image of
![]() $\mathcal {C}^{\left (i, w_{1,2}, \mathbf {w}_1, \mathbf {w}_2\right )}$
under
$\mathcal {C}^{\left (i, w_{1,2}, \mathbf {w}_1, \mathbf {w}_2\right )}$
under
![]() $\mathscr {L}(\pi )$
is equal to
$\mathscr {L}(\pi )$
is equal to
![]() $C^{\left (w_{1,2}, \mathbf {w}_1, \mathbf {w}_2\right )}$
, and
$C^{\left (w_{1,2}, \mathbf {w}_1, \mathbf {w}_2\right )}$
, and
 $\operatorname {\mathrm {sep}}_{\pi , \mathcal {C}^{\left (i, w_{1,2}, \mathbf {w}_1, \mathbf {w}_2\right )}}$
is equal to
$\operatorname {\mathrm {sep}}_{\pi , \mathcal {C}^{\left (i, w_{1,2}, \mathbf {w}_1, \mathbf {w}_2\right )}}$
is equal to
![]() $1$
on all of
$1$
on all of
![]() $C^{\left (w_{1,2}, \mathbf {w}_1, \mathbf {w}_2\right )}$
.
$C^{\left (w_{1,2}, \mathbf {w}_1, \mathbf {w}_2\right )}$
.
Proof. The image of
![]() $\mathcal {C}^{\left (i, w_{1,2}, \mathbf {w}_1, \mathbf {w}_2\right )}$
is contained in
$\mathcal {C}^{\left (i, w_{1,2}, \mathbf {w}_1, \mathbf {w}_2\right )}$
is contained in
![]() $C^{\left (w_{1,2}, \mathbf {w}_1, \mathbf {w}_2\right )}$
by the construction of
$C^{\left (w_{1,2}, \mathbf {w}_1, \mathbf {w}_2\right )}$
by the construction of
![]() $Z^{\left (i, w_{1,2}, \mathbf {w}_1, \mathbf {w}_2\right )}$
. We now only need to show that
$Z^{\left (i, w_{1,2}, \mathbf {w}_1, \mathbf {w}_2\right )}$
. We now only need to show that
 $\operatorname {\mathrm {sep}}_{\pi , \mathcal {C}^{\left (i, w_{1,2}, \mathbf {w}_1, \mathbf {w}_2\right )}}$
is equal to
$\operatorname {\mathrm {sep}}_{\pi , \mathcal {C}^{\left (i, w_{1,2}, \mathbf {w}_1, \mathbf {w}_2\right )}}$
is equal to
![]() $1$
on all of
$1$
on all of
![]() $C^{\left (w_{1,2}, \mathbf {w}_1, \mathbf {w}_2\right )}$
. Let
$C^{\left (w_{1,2}, \mathbf {w}_1, \mathbf {w}_2\right )}$
. Let
![]() $k'$
be a field extension of k and set
$k'$
be a field extension of k and set
 $\varphi \in C^{\left (w_{1,2}, \mathbf {w}_1, \mathbf {w}_2\right )}(k')$
. Then for any
$\varphi \in C^{\left (w_{1,2}, \mathbf {w}_1, \mathbf {w}_2\right )}(k')$
. Then for any
 $\{\ell , m\} \in {[r] \choose 2}$
, let
$\{\ell , m\} \in {[r] \choose 2}$
, let
![]() be such that
be such that
![]() pulls back
pulls back
![]() $x_{\ell ,m}\rvert _X$
to
$x_{\ell ,m}\rvert _X$
to
![]() $h_{\ell ,m}$
. Then
$h_{\ell ,m}$
. Then
![]() $\varphi $
is the image of the element
$\varphi $
is the image of the element
![]() $\widetilde {\psi }$
of
$\widetilde {\psi }$
of
 $Z^{\left (i, w_{1,2}, \mathbf {w}_1, \mathbf {w}_2\right )}(k')$
given by the matrix
$Z^{\left (i, w_{1,2}, \mathbf {w}_1, \mathbf {w}_2\right )}(k')$
given by the matrix
 $$ \begin{align*} \begin{pmatrix} h_{1,2}t^{-i} & 0 & -h_{2,3}t^{-i} & -h_{2, 4}t^{-i} & \dotsb & -h_{2, r}t^{-i} \\ 0 & t^i & h_{1,3} h_{1,2}^{-1} t^i & h_{1,4} h_{1,2}^{-1} t^i & \dotsb & h_{1,r} h_{1,2}^{-1} t^i\end{pmatrix}, \end{align*} $$
$$ \begin{align*} \begin{pmatrix} h_{1,2}t^{-i} & 0 & -h_{2,3}t^{-i} & -h_{2, 4}t^{-i} & \dotsb & -h_{2, r}t^{-i} \\ 0 & t^i & h_{1,3} h_{1,2}^{-1} t^i & h_{1,4} h_{1,2}^{-1} t^i & \dotsb & h_{1,r} h_{1,2}^{-1} t^i\end{pmatrix}, \end{align*} $$
so
 $\operatorname {\mathrm {sep}}_{\pi , \mathcal {C}^{\left (i, w_{1,2}, \mathbf {w}_1, \mathbf {w}_2\right )}} \geq 1$
on all of
$\operatorname {\mathrm {sep}}_{\pi , \mathcal {C}^{\left (i, w_{1,2}, \mathbf {w}_1, \mathbf {w}_2\right )}} \geq 1$
on all of
![]() $C^{\left (w_{1,2}, \mathbf {w}_1, \mathbf {w}_2\right )}$
. Let
$C^{\left (w_{1,2}, \mathbf {w}_1, \mathbf {w}_2\right )}$
. Let
![]() $\psi \in \mathscr {L}(\mathcal {X})(k')$
be the image of
$\psi \in \mathscr {L}(\mathcal {X})(k')$
be the image of
![]() $\widetilde {\psi }$
. To finish this proof, we only need to show that if
$\widetilde {\psi }$
. To finish this proof, we only need to show that if
![]() $\psi ' \in \mathscr {L}(\mathcal {X})(k')$
has class in
$\psi ' \in \mathscr {L}(\mathcal {X})(k')$
has class in
![]() $\lvert \mathscr {L}(\mathcal {X})\rvert $
contained in
$\lvert \mathscr {L}(\mathcal {X})\rvert $
contained in
![]() $\mathcal {C}^{\left (i, w_{1,2}, \mathbf {w}_1, \mathbf {w}_2\right )}$
and satisfies
$\mathcal {C}^{\left (i, w_{1,2}, \mathbf {w}_1, \mathbf {w}_2\right )}$
and satisfies
![]() $\mathscr {L}(\pi )(\psi ') = \varphi $
, then
$\mathscr {L}(\pi )(\psi ') = \varphi $
, then
![]() $\psi ' \cong \psi $
. Because
$\psi ' \cong \psi $
. Because
![]() $\mathrm {SL}_2$
is a special group and thus has only trivial torsors over
$\mathrm {SL}_2$
is a special group and thus has only trivial torsors over
![]() , there exists
, there exists
 $\widetilde {\psi }' \in \mathscr {L}\left (\widetilde {X}\right )(k')$
whose image is isomorphic to
$\widetilde {\psi }' \in \mathscr {L}\left (\widetilde {X}\right )(k')$
whose image is isomorphic to
![]() $\psi '$
. By construction, there exist some field extension
$\psi '$
. By construction, there exist some field extension
![]() $k''$
of
$k''$
of
![]() $k'$
and
$k'$
and
![]() such that
such that
 $g \cdot \widetilde {\psi }^{\prime }_{k''} \in Z^{\left (i, w_{1,2}, \mathbf {w}_1, \mathbf {w}_2\right )}(k'')$
, where
$g \cdot \widetilde {\psi }^{\prime }_{k''} \in Z^{\left (i, w_{1,2}, \mathbf {w}_1, \mathbf {w}_2\right )}(k'')$
, where
 $\widetilde {\psi }^{\prime }_{k''}$
is the composition of
$\widetilde {\psi }^{\prime }_{k''}$
is the composition of
![]() with
with
![]() . By the construction of
. By the construction of
![]() $Z^{\left (i, w_{1,2}, \mathbf {w}_1, \mathbf {w}_2\right )}$
, the entries of
$Z^{\left (i, w_{1,2}, \mathbf {w}_1, \mathbf {w}_2\right )}$
, the entries of
 $g \cdot \widetilde {\psi }^{\prime }_{k''}$
are all determined by its minors and thus
$g \cdot \widetilde {\psi }^{\prime }_{k''}$
are all determined by its minors and thus
 $g \cdot \widetilde {\psi }^{\prime }_{k''}$
is equal to the composition of
$g \cdot \widetilde {\psi }^{\prime }_{k''}$
is equal to the composition of
![]() with
with
![]() . Because
. Because
![]() $\widetilde {\psi }$
has nonzero
$\widetilde {\psi }$
has nonzero
![]() $(1,2)$
-minor, this implies
$(1,2)$
-minor, this implies
![]() , so
, so
![]() $g \cdot \widetilde {\psi '} = \widetilde {\psi }$
and
$g \cdot \widetilde {\psi '} = \widetilde {\psi }$
and
![]() $\psi ' \cong \psi $
, as desired.
$\psi ' \cong \psi $
, as desired.
Remark 10.1 and Proposition 10.11 tell us that if
![]() $r \geq 3$
, X has log-terminal singularities and
$r \geq 3$
, X has log-terminal singularities and
![]() $i, w_{1,2} \in \mathbb {N}$
and
$i, w_{1,2} \in \mathbb {N}$
and
![]() $\mathbf {w}_1, \mathbf {w}_2 \in \mathbb {N}^{r-2}$
satisfy (⋆), then Conjecture 1.1 implies that
$\mathbf {w}_1, \mathbf {w}_2 \in \mathbb {N}^{r-2}$
satisfy (⋆), then Conjecture 1.1 implies that
 $\mu _{\mathcal {X}}\left (\mathcal {C}^{\left (i, w_{1,2}, \mathbf {w}_1, \mathbf {w}_2\right )}\right ) = \mu ^{\mathrm {Gor}}_X\left (C^{\left (w_{1,2}, \mathbf {w}_1, \mathbf {w}_2\right )}\right )$
. For
$\mu _{\mathcal {X}}\left (\mathcal {C}^{\left (i, w_{1,2}, \mathbf {w}_1, \mathbf {w}_2\right )}\right ) = \mu ^{\mathrm {Gor}}_X\left (C^{\left (w_{1,2}, \mathbf {w}_1, \mathbf {w}_2\right )}\right )$
. For
![]() $r \in \{3,4\}$
, we verify this unconditionally by combining the foregoing results, thereby proving Proposition 10.7.
$r \in \{3,4\}$
, we verify this unconditionally by combining the foregoing results, thereby proving Proposition 10.7.
Proof of Proposition 10.7
Set
![]() $r \in \{3,4\}$
. It is clear that
$r \in \{3,4\}$
. It is clear that
![]() $\mathcal {S}$
is an infinite set. The third and fourth bullet points are justified by Remark 10.4 and Remark 10.8. Next, a straightforward computation using Remark 10.4, Proposition 10.9 and Proposition 10.10 shows
$\mathcal {S}$
is an infinite set. The third and fourth bullet points are justified by Remark 10.4 and Remark 10.8. Next, a straightforward computation using Remark 10.4, Proposition 10.9 and Proposition 10.10 shows
 $$ \begin{align*} 0 \neq \mu_{\mathcal{X}}\left(\mathcal{C}^{\left(i, w_{1,2}, \mathbf{w}_1, \mathbf{w}_2\right)}\right) = \mu^{\mathrm{Gor}}_X\left(C^{\left(w_{1,2}, \mathbf{w}_1, \mathbf{w}_2\right)}\right). \end{align*} $$
$$ \begin{align*} 0 \neq \mu_{\mathcal{X}}\left(\mathcal{C}^{\left(i, w_{1,2}, \mathbf{w}_1, \mathbf{w}_2\right)}\right) = \mu^{\mathrm{Gor}}_X\left(C^{\left(w_{1,2}, \mathbf{w}_1, \mathbf{w}_2\right)}\right). \end{align*} $$
By Remark 10.6 and Proposition 10.11, this implies
 $$ \begin{align*} 0 \neq \mu_{\mathcal{X}}(\mathcal{C}) = \mu_{\mathcal{X}}\left(\mathcal{C} \cap \mathscr{L}(\pi)^{-1}(C)\right) = \int_C \operatorname{\mathrm{sep}}_{\pi, \mathcal{C}} \mathrm{d}\mu^{\mathrm{Gor}}_X \end{align*} $$
$$ \begin{align*} 0 \neq \mu_{\mathcal{X}}(\mathcal{C}) = \mu_{\mathcal{X}}\left(\mathcal{C} \cap \mathscr{L}(\pi)^{-1}(C)\right) = \int_C \operatorname{\mathrm{sep}}_{\pi, \mathcal{C}} \mathrm{d}\mu^{\mathrm{Gor}}_X \end{align*} $$
for all
![]() $(\mathcal {C},C)\in \mathcal {S}'$
.
$(\mathcal {C},C)\in \mathcal {S}'$
.
Acknowledgments
We thank Dan Abramovich, Dan Edidin, Jack Hall, Martin Olsson and Karl Schwede for helpful conversations. We are also grateful to the anonymous referee for a thorough reading of our paper and many suggestions which improved the paper.
The first author’s research was partially supported by a Discovery Grant (RGPIN-2015-05631) from the National Science and Engineering Research Council of Canada.
Conflicts of Interest
None.