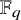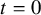1. Introduction
In [Reference Griffin, Levinson and Woo10], Levinson, Woo and the author introduced the
![]() $\Delta $
-Springer varieties
$\Delta $
-Springer varieties
![]() $Y_{n,\lambda ,s}$
as a generalization of Springer fibers that give a compact geometric realization of the Delta Conjecture at
$Y_{n,\lambda ,s}$
as a generalization of Springer fibers that give a compact geometric realization of the Delta Conjecture at
![]() $t=0$
. Precisely, they showed that the symmetric function
$t=0$
. Precisely, they showed that the symmetric function
![]() $\Delta ^{\prime }_{e_{k-1}}e_n|_{t=0}$
corresponds under the graded Frobenius characteristic map to the cohomology ring of a certain
$\Delta ^{\prime }_{e_{k-1}}e_n|_{t=0}$
corresponds under the graded Frobenius characteristic map to the cohomology ring of a certain
![]() $\Delta $
-Springer variety, up to a minor twist. In this article, we give a proof of the expansion, originally announced in [Reference Griffin9], of the graded Frobenius characteristic of the cohomology ring of a
$\Delta $
-Springer variety, up to a minor twist. In this article, we give a proof of the expansion, originally announced in [Reference Griffin9], of the graded Frobenius characteristic of the cohomology ring of a
![]() $\Delta $
-Springer variety as a positive sum of modified Hall–Littlewood symmetric functions. As a special case, our proof gives a geometric explanation of the Hall–Littlewood expansion for
$\Delta $
-Springer variety as a positive sum of modified Hall–Littlewood symmetric functions. As a special case, our proof gives a geometric explanation of the Hall–Littlewood expansion for
![]() $\Delta ^{\prime }_{e_{k-1}}e_n|_{t=0}$
given by Haglund, Rhoades and Shimozono [Reference Haglund, Rhoades and Shimozono12].
$\Delta ^{\prime }_{e_{k-1}}e_n|_{t=0}$
given by Haglund, Rhoades and Shimozono [Reference Haglund, Rhoades and Shimozono12].
1.1. Background and context
Springer fibers
![]() $\mathcal {B}_{\lambda }$
are a family of subvarieties of the complete flag variety indexed by partitions
$\mathcal {B}_{\lambda }$
are a family of subvarieties of the complete flag variety indexed by partitions
![]() $\lambda $
that have remarkable connections to representation theory. Notably, Springer [Reference Springer22, Reference Springer23] constructed an action of the symmetric group
$\lambda $
that have remarkable connections to representation theory. Notably, Springer [Reference Springer22, Reference Springer23] constructed an action of the symmetric group
![]() $S_n$
on the cohomology ring of a Springer fiber and showed that the top nonzero cohomology group is an irreducible representation of
$S_n$
on the cohomology ring of a Springer fiber and showed that the top nonzero cohomology group is an irreducible representation of
![]() $S_n$
and that all finite-dimensional irreducible representations of
$S_n$
and that all finite-dimensional irreducible representations of
![]() $S_n$
appear this way. Furthermore, the graded
$S_n$
appear this way. Furthermore, the graded
![]() $S_n$
-module structure of the cohomology ring is well studied. Under the Frobenius characteristic map that sends an
$S_n$
-module structure of the cohomology ring is well studied. Under the Frobenius characteristic map that sends an
![]() $S_n$
-module to a symmetric function, the cohomology ring of a Springer fiber corresponds to the Hall–Littlewood symmetric function [Reference Hotta and Springer15],
$S_n$
-module to a symmetric function, the cohomology ring of a Springer fiber corresponds to the Hall–Littlewood symmetric function [Reference Hotta and Springer15],
Alternatively, the modified Hall–Littlewood symmetric functions can be obtained by counting
![]() $\mathbb {F}_q$
-points. Letting
$\mathbb {F}_q$
-points. Letting
![]() $\mathrm {Stein}_{\lambda }^{\mu }$
be the Steinberg variety of partial flags of type
$\mathrm {Stein}_{\lambda }^{\mu }$
be the Steinberg variety of partial flags of type
![]() $\mu $
that are preserved by a fixed nilpotent matrix of Jordan type
$\mu $
that are preserved by a fixed nilpotent matrix of Jordan type
![]() $\lambda $
, it is well known that for all prime powers q,
$\lambda $
, it is well known that for all prime powers q,
where
![]() $m_{\mu }$
is the monomial symmetric function and
$m_{\mu }$
is the monomial symmetric function and
![]() $\mathrm {Stein}_{\lambda }^{\mu }(\mathbb {F}_q)$
stands for the set of
$\mathrm {Stein}_{\lambda }^{\mu }(\mathbb {F}_q)$
stands for the set of
![]() $\mathbb {F}_q$
points of
$\mathbb {F}_q$
points of
![]() $\mathrm {Stein}_{\lambda }^{\mu }$
.
$\mathrm {Stein}_{\lambda }^{\mu }$
.
Similar interpretations have been given for the modified Macdonald polynomials
![]() $\widetilde H_{\lambda }(\mathbf {x};q,t)$
, which are a generalization of modified Hall-Littlewood symmetric functions with coefficients in two parameters q and t. Haiman proved that
$\widetilde H_{\lambda }(\mathbf {x};q,t)$
, which are a generalization of modified Hall-Littlewood symmetric functions with coefficients in two parameters q and t. Haiman proved that
![]() $\widetilde H_{\lambda }(\mathbf {x};q,t)$
is the bi-graded Frobenius characteristic of the fiber of a certain tautological bundle on the Hilbert scheme of points in the plane [Reference Haiman13, Reference Haiman14]. Mellit realized
$\widetilde H_{\lambda }(\mathbf {x};q,t)$
is the bi-graded Frobenius characteristic of the fiber of a certain tautological bundle on the Hilbert scheme of points in the plane [Reference Haiman13, Reference Haiman14]. Mellit realized
![]() $\widetilde H_{\lambda }(\mathbf {x};q,t)$
as a weighted count of points in an affine Springer fiber [Reference Mellit18].
$\widetilde H_{\lambda }(\mathbf {x};q,t)$
as a weighted count of points in an affine Springer fiber [Reference Mellit18].
In a related line of work, the Delta Conjecture of Haglund, Remmel and Wilson [Reference Haglund, Remmel and Wilson11] gives two combinatorial formulas for a symmetric function
![]() $\Delta ^{\prime }_{e_{k-1}}e_n$
, where
$\Delta ^{\prime }_{e_{k-1}}e_n$
, where
![]() $\Delta ^{\prime }_{e_{k-1}}$
is a certain eigenoperator that diagonalizes the modified Macdonald polynomial basis. There has been recent progress on realizing this symmetric function naturally as the Frobenius characteristic of an
$\Delta ^{\prime }_{e_{k-1}}$
is a certain eigenoperator that diagonalizes the modified Macdonald polynomial basis. There has been recent progress on realizing this symmetric function naturally as the Frobenius characteristic of an
![]() $S_n$
-module. Haglund, Rhoades and Shimozono [Reference Haglund, Rhoades and Shimozono12] found a graded ring
$S_n$
-module. Haglund, Rhoades and Shimozono [Reference Haglund, Rhoades and Shimozono12] found a graded ring
![]() $R_{n,k}$
whose graded Frobenius characteristic is
$R_{n,k}$
whose graded Frobenius characteristic is
![]() $\mathrm {rev}_q\circ \omega (\Delta ^{\prime }_{e_{k-1}}e_n|_{t=0})$
, where
$\mathrm {rev}_q\circ \omega (\Delta ^{\prime }_{e_{k-1}}e_n|_{t=0})$
, where
![]() $\omega $
is the involution that swaps elementary symmetric functions
$\omega $
is the involution that swaps elementary symmetric functions
![]() $e_n$
with complete homogeneous symmetric functions
$e_n$
with complete homogeneous symmetric functions
![]() $h_n$
, and
$h_n$
, and
![]() $\mathrm {rev}_q$
reverses the coefficients as a polynomial in q. Pawlowski and Rhoades subsequently defined the space of spanning line configurations, which is a smooth noncompact variety whose cohomology is
$\mathrm {rev}_q$
reverses the coefficients as a polynomial in q. Pawlowski and Rhoades subsequently defined the space of spanning line configurations, which is a smooth noncompact variety whose cohomology is
![]() $R_{n,k}$
. Additionally, Zabrocki [Reference Zabrocki24] has conjectured that the graded Frobenius characteristic of the superspace coinvariant ring in the
$R_{n,k}$
. Additionally, Zabrocki [Reference Zabrocki24] has conjectured that the graded Frobenius characteristic of the superspace coinvariant ring in the
![]() $n-k$
fermionic degree is
$n-k$
fermionic degree is
![]() $\Delta ^{\prime }_{e_{k-1}}e_n$
, and Bergeron [Reference Bergeron1] has conjectured that
$\Delta ^{\prime }_{e_{k-1}}e_n$
, and Bergeron [Reference Bergeron1] has conjectured that
![]() $\Delta ^{\prime }_{e_{k-1}}e_n$
can be obtained via skewing operators. See [Reference Rhoades20] for a survey of these and related results.
$\Delta ^{\prime }_{e_{k-1}}e_n$
can be obtained via skewing operators. See [Reference Rhoades20] for a survey of these and related results.
In [Reference Griffin9], the author generalized the ring
![]() $R_{n,k}$
to a family of quotient rings
$R_{n,k}$
to a family of quotient rings
![]() $R_{n,\lambda ,s}$
that also include Tanisaki’s presentation of the cohomology ring of a Springer fiber as a special case. Each ring
$R_{n,\lambda ,s}$
that also include Tanisaki’s presentation of the cohomology ring of a Springer fiber as a special case. Each ring
![]() $R_{n,\lambda ,s}$
has the structure of a graded
$R_{n,\lambda ,s}$
has the structure of a graded
![]() $S_n$
-module whose graded Frobenius characteristic has several combinatorial formulas that extend previously known formulas for
$S_n$
-module whose graded Frobenius characteristic has several combinatorial formulas that extend previously known formulas for
![]() $\Delta _{e_{k-1}}^{\prime }e_n|_{t=0}$
and
$\Delta _{e_{k-1}}^{\prime }e_n|_{t=0}$
and
![]() $\widetilde H_{\lambda }(\mathbf {x};q)$
. In particular, there are two monomial symmetric function expansions in terms of inversions and diagonal inversions, respectively, of labeled diagrams called partial row-decreasing fillings. We recall the relevant notation and statistics in Section 2.
$\widetilde H_{\lambda }(\mathbf {x};q)$
. In particular, there are two monomial symmetric function expansions in terms of inversions and diagonal inversions, respectively, of labeled diagrams called partial row-decreasing fillings. We recall the relevant notation and statistics in Section 2.
Theorem 1.1 [Reference Griffin9]
We have
 $$\begin{align*}\mathrm{Frob}(R_{n,\lambda,s} ;q) = \sum_{\mu\vdash n}\sum_{\varphi\in \operatorname{\mathrm{PRD}}^{\mu}_{n,\lambda,s}} q^{\operatorname{{\mathrm{inv}}}(\varphi)} m_{\mu}(\mathbf{x}) = \sum_{\mu\vdash n}\sum_{\varphi\in\operatorname{\mathrm{PRD}}^{\mu}_{n,\lambda,s}} q^{\operatorname{{\mathrm{dinv}}}(\varphi)} m_{\mu}(\mathbf{x}). \end{align*}$$
$$\begin{align*}\mathrm{Frob}(R_{n,\lambda,s} ;q) = \sum_{\mu\vdash n}\sum_{\varphi\in \operatorname{\mathrm{PRD}}^{\mu}_{n,\lambda,s}} q^{\operatorname{{\mathrm{inv}}}(\varphi)} m_{\mu}(\mathbf{x}) = \sum_{\mu\vdash n}\sum_{\varphi\in\operatorname{\mathrm{PRD}}^{\mu}_{n,\lambda,s}} q^{\operatorname{{\mathrm{dinv}}}(\varphi)} m_{\mu}(\mathbf{x}). \end{align*}$$
Levinson, Woo and the author [Reference Griffin, Levinson and Woo10] then constructed a compact variety
![]() $Y_{n,\lambda ,s}$
, the
$Y_{n,\lambda ,s}$
, the
![]() $\Delta $
-Springer variety, whose cohomology ring is
$\Delta $
-Springer variety, whose cohomology ring is
![]() $R_{n,\lambda ,s}$
. In the special case of
$R_{n,\lambda ,s}$
. In the special case of
![]() $\lambda = (1^k)$
and
$\lambda = (1^k)$
and
![]() $s=k$
, the variety
$s=k$
, the variety
![]() $Y_{n,(1^k),k}$
gives a compact geometric realization of the Delta Conjecture symmetric function at
$Y_{n,(1^k),k}$
gives a compact geometric realization of the Delta Conjecture symmetric function at
![]() $t=0$
, since
$t=0$
, since
![]() $H^{*}(Y_{n,(1^k),k}) \cong R_{n,k}$
. It was also shown that
$H^{*}(Y_{n,(1^k),k}) \cong R_{n,k}$
. It was also shown that
![]() $Y_{n,\lambda ,s}$
has many of the same geometric and representation-theoretic properties as Springer fibers, including a characterization of the
$Y_{n,\lambda ,s}$
has many of the same geometric and representation-theoretic properties as Springer fibers, including a characterization of the
![]() $S_n$
-module structure of the top cohomology group.
$S_n$
-module structure of the top cohomology group.
Theorem 1.2 [Reference Griffin, Levinson and Woo10]
The variety
![]() $Y_{n,\lambda ,s}$
is equidimensional of complex dimension
$Y_{n,\lambda ,s}$
is equidimensional of complex dimension
where
![]() $n(\lambda ) = \sum _i \binom {\lambda _i^{\prime }}{2}$
. For
$n(\lambda ) = \sum _i \binom {\lambda _i^{\prime }}{2}$
. For
![]() $s>\ell (\lambda )$
, we have an isomorphism of
$s>\ell (\lambda )$
, we have an isomorphism of
![]() $S_n$
-modules
$S_n$
-modules
where
![]() $S^\lambda $
is considered as a
$S^\lambda $
is considered as a
![]() $S_k\times S_{n-k}$
-module in which
$S_k\times S_{n-k}$
-module in which
![]() $S_{n-k}$
acts trivially.
$S_{n-k}$
acts trivially.
1.2. Results of this paper
Our main theorem is a positive expansion of the graded Frobenius characteristic of
![]() $H^{*}(Y_{n,\lambda ,s};\mathbb {Q})$
(equivalently of
$H^{*}(Y_{n,\lambda ,s};\mathbb {Q})$
(equivalently of
![]() $R_{n,\lambda ,s}$
) into modified Hall–Littlewood symmetric functions, a result that was announced in [Reference Griffin9].
$R_{n,\lambda ,s}$
) into modified Hall–Littlewood symmetric functions, a result that was announced in [Reference Griffin9].
Theorem 1.3. We have
 $$ \begin{align} \mathrm{Frob}(H^{*}(Y_{n,\lambda,s};\mathbb{Q});q) &= \mathrm{rev}_q\left[ \sum_{\substack{\nu\in \mathrm{Par}(n,s),\\ \nu\supseteq \lambda}} q^{n(\nu/\lambda)} \prod_{i\geq 0} \genfrac{[}{]}{0pt}{}{\nu_i^{\prime}-\lambda_{i+1}^{\prime}}{\nu_i^{\prime}-\nu_{i+1}^{\prime}}_q H_\nu(\mathbf{x};q)\right] \end{align} $$
$$ \begin{align} \mathrm{Frob}(H^{*}(Y_{n,\lambda,s};\mathbb{Q});q) &= \mathrm{rev}_q\left[ \sum_{\substack{\nu\in \mathrm{Par}(n,s),\\ \nu\supseteq \lambda}} q^{n(\nu/\lambda)} \prod_{i\geq 0} \genfrac{[}{]}{0pt}{}{\nu_i^{\prime}-\lambda_{i+1}^{\prime}}{\nu_i^{\prime}-\nu_{i+1}^{\prime}}_q H_\nu(\mathbf{x};q)\right] \end{align} $$
 $$ \begin{align} & = \sum_{\substack{\nu\in \mathrm{Par}(n,s),\\ \nu\supseteq \lambda}} q^{\sum_i (s-\nu_i^{\prime})(\nu_{i+1}^{\prime}-\lambda_{i+1}^{\prime})}\prod_{i\geq 0} \genfrac{[}{]}{0pt}{}{\nu_i^{\prime}-\lambda_{i+1}^{\prime}}{\nu_i^{\prime}-\nu_{i+1}'}_q \widetilde{H}_\nu(\mathbf{x};q), \end{align} $$
$$ \begin{align} & = \sum_{\substack{\nu\in \mathrm{Par}(n,s),\\ \nu\supseteq \lambda}} q^{\sum_i (s-\nu_i^{\prime})(\nu_{i+1}^{\prime}-\lambda_{i+1}^{\prime})}\prod_{i\geq 0} \genfrac{[}{]}{0pt}{}{\nu_i^{\prime}-\lambda_{i+1}^{\prime}}{\nu_i^{\prime}-\nu_{i+1}'}_q \widetilde{H}_\nu(\mathbf{x};q), \end{align} $$
where ![]() .
.
A special case of this formula has been used to verify the construction of higher Specht bases for some infinite subfamilies of the rings
![]() $R_{n,\lambda ,s}$
[Reference Gillespie and Rhoades8].
$R_{n,\lambda ,s}$
[Reference Gillespie and Rhoades8].
The outline of the proof of Theorem 1.3 is as follows. We start with the fact that the left-hand side of (1.2) is given by the inversion formula in Theorem 1.1. We then show that
![]() $Y^{\mu }_{n,\lambda ,s}$
, the projection of
$Y^{\mu }_{n,\lambda ,s}$
, the projection of
![]() $Y_{n,\lambda ,s}$
down to a partial flag variety, has an affine paving such that the dimension of a cell is computed by the inversion statistic
$Y_{n,\lambda ,s}$
down to a partial flag variety, has an affine paving such that the dimension of a cell is computed by the inversion statistic
![]() $\operatorname {{\mathrm {inv}}}$
. We use this to show that the
$\operatorname {{\mathrm {inv}}}$
. We use this to show that the
![]() $m_{\mu }(\mathbf {x})$
coefficient of the inversion formula in Theorem 1.1 can be computed by counting
$m_{\mu }(\mathbf {x})$
coefficient of the inversion formula in Theorem 1.1 can be computed by counting
![]() $\mathbb {F}_q$
points of
$\mathbb {F}_q$
points of
![]() $Y_{n,\lambda ,s}^{\mu }$
. We then show that the
$Y_{n,\lambda ,s}^{\mu }$
. We then show that the
![]() $\mathbb {F}_q$
points of
$\mathbb {F}_q$
points of
![]() $Y_{n,\lambda ,s}^{\mu }$
can alternatively be computed by partitioning
$Y_{n,\lambda ,s}^{\mu }$
can alternatively be computed by partitioning
![]() $Y_{n,\lambda ,s}^{\mu }$
into a disjoint union of copies of affine spaces crossed with Steinberg varieties.
$Y_{n,\lambda ,s}^{\mu }$
into a disjoint union of copies of affine spaces crossed with Steinberg varieties.
When
![]() $\lambda = (1^k)$
and
$\lambda = (1^k)$
and
![]() $s=k$
, the right-hand side of (1.2) is the right-hand side of [Reference Haglund, Rhoades and Shimozono12, Theorem 6.14], the formula for
$s=k$
, the right-hand side of (1.2) is the right-hand side of [Reference Haglund, Rhoades and Shimozono12, Theorem 6.14], the formula for
![]() $\mathrm {Frob}(R_{n,k};q)$
proven by Haglund, Rhoades and Shimozono. Since
$\mathrm {Frob}(R_{n,k};q)$
proven by Haglund, Rhoades and Shimozono. Since
![]() $R_{n,k} \cong H^{*}(Y_{n,(1^k),k};\mathbb {Q})$
(up to doubling the degree), this can be seen as a solution to Problem 9.9 in [Reference Pawlowski and Rhoades19], but with the space of spanning line configurations
$R_{n,k} \cong H^{*}(Y_{n,(1^k),k};\mathbb {Q})$
(up to doubling the degree), this can be seen as a solution to Problem 9.9 in [Reference Pawlowski and Rhoades19], but with the space of spanning line configurations
![]() $X_{n,k}$
replaced by the
$X_{n,k}$
replaced by the
![]() $\Delta $
-Springer variety
$\Delta $
-Springer variety
![]() $Y_{n,(1^k),k}$
.
$Y_{n,(1^k),k}$
.
2. Background
2.1. Compositions and partitions
Let us recall basic notions about symmetric functions and their connections to
![]() $S_n$
-modules. A composition
$S_n$
-modules. A composition
![]() $\alpha $
of n of length s is a tuple
$\alpha $
of n of length s is a tuple
![]() $\alpha =(\alpha _1,\alpha _2,\dots , \alpha _s)$
of nonnegative integers such that
$\alpha =(\alpha _1,\alpha _2,\dots , \alpha _s)$
of nonnegative integers such that
![]() $\alpha _1+\cdots +\alpha _s = n$
. We write
$\alpha _1+\cdots +\alpha _s = n$
. We write
![]() $|\alpha |=n$
for the size of
$|\alpha |=n$
for the size of
![]() $\alpha $
. Let
$\alpha $
. Let
![]() $\mathrm {Comp}(n,s)$
be the set of compositions of n with length s. We say
$\mathrm {Comp}(n,s)$
be the set of compositions of n with length s. We say
![]() $\alpha $
is a strong composition if
$\alpha $
is a strong composition if
![]() $\alpha _i>0$
for all
$\alpha _i>0$
for all
![]() $i\leq s$
. Given
$i\leq s$
. Given
![]() $\alpha $
a strong composition of n, let
$\alpha $
a strong composition of n, let
be the i
th block of
![]() $\alpha $
.
$\alpha $
.
A partition is a composition
![]() $\lambda $
such that
$\lambda $
such that
![]() $\lambda _1\geq \lambda _2\geq \cdots \geq \lambda _s\geq 0$
. The length of
$\lambda _1\geq \lambda _2\geq \cdots \geq \lambda _s\geq 0$
. The length of
![]() $\lambda $
, written
$\lambda $
, written
![]() $\ell (\lambda )$
, is the number of positive parts of
$\ell (\lambda )$
, is the number of positive parts of
![]() $\lambda $
. We sometimes write
$\lambda $
. We sometimes write
![]() $\lambda \vdash n$
to mean that
$\lambda \vdash n$
to mean that
![]() $\lambda $
is a partition of n. The conjugate partition
$\lambda $
is a partition of n. The conjugate partition
![]() $\lambda '$
is the partition of n whose ith entry
$\lambda '$
is the partition of n whose ith entry
![]() $\lambda _i^{\prime }$
is the number of indices j such that
$\lambda _i^{\prime }$
is the number of indices j such that
![]() $\lambda _j\geq i$
. Occasionally, we write
$\lambda _j\geq i$
. Occasionally, we write
![]() $(a^b)$
to mean the partition
$(a^b)$
to mean the partition
![]() $(a,a,\dots ,a)$
with b many a’s. We write
$(a,a,\dots ,a)$
with b many a’s. We write
![]() $(\lambda ,a)$
to mean the partition obtained by appending a to the end of
$(\lambda ,a)$
to mean the partition obtained by appending a to the end of
![]() $\lambda $
. Let
$\lambda $
. Let
![]() $\mathrm {Par}(n,s)$
be the set of partitions
$\mathrm {Par}(n,s)$
be the set of partitions
![]() $\lambda $
of n such that
$\lambda $
of n such that
![]() $\ell (\lambda )\leq s$
, where we identify partitions up to adding trailing
$\ell (\lambda )\leq s$
, where we identify partitions up to adding trailing
![]() $0$
s.
$0$
s.
Given
![]() $\alpha \in \mathrm {Comp}(n,s)$
and
$\alpha \in \mathrm {Comp}(n,s)$
and
![]() $\lambda \in \mathrm {Par}(k,s)$
for some
$\lambda \in \mathrm {Par}(k,s)$
for some
![]() $k\leq n$
, we write
$k\leq n$
, we write
![]() $\lambda \subseteq \alpha $
if
$\lambda \subseteq \alpha $
if
![]() $\lambda _i\leq \alpha _i$
for all
$\lambda _i\leq \alpha _i$
for all
![]() $i\leq s$
. A coinversion of
$i\leq s$
. A coinversion of
![]() $\alpha $
is a pair
$\alpha $
is a pair
![]() $(i,j)$
such that
$(i,j)$
such that
![]() $1\leq i<j\leq s$
and
$1\leq i<j\leq s$
and
![]() $\alpha _i<\alpha _j$
. Let
$\alpha _i<\alpha _j$
. Let
![]() $\operatorname {\mathrm {coinv}}(\alpha )$
be the number of coinversions of
$\operatorname {\mathrm {coinv}}(\alpha )$
be the number of coinversions of
![]() $\alpha $
. For example, for
$\alpha $
. For example, for
![]() $n=10$
,
$n=10$
,
![]() $k=4$
and
$k=4$
and
![]() $s=5$
, we have
$s=5$
, we have
![]() $\lambda = (2,1,1,0,0)\in \mathrm {Par}(4,5)$
, and
$\lambda = (2,1,1,0,0)\in \mathrm {Par}(4,5)$
, and
![]() $\alpha = (2,3,1,0,4) \in \mathrm {Comp}(10,5)$
such that
$\alpha = (2,3,1,0,4) \in \mathrm {Comp}(10,5)$
such that
![]() $\lambda \subseteq \alpha $
. It can be checked that
$\lambda \subseteq \alpha $
. It can be checked that
![]() $\operatorname {\mathrm {coinv}}(\alpha ) = 5$
.
$\operatorname {\mathrm {coinv}}(\alpha ) = 5$
.
2.2. Symmetric functions and q-analogues
A symmetric function f is a formal power series in the variables ![]() that is invariant under any permutation of the variables. Let
that is invariant under any permutation of the variables. Let
![]() $m_{\lambda }(\mathbf {x})$
,
$m_{\lambda }(\mathbf {x})$
,
![]() $h_{\lambda }(\mathbf {x})$
and
$h_{\lambda }(\mathbf {x})$
and
![]() $s_{\lambda }(\mathbf {x})$
be the usual monomial, complete homogeneous and Schur symmetric functions, each of which forms a basis of the ring of symmetric functions as
$s_{\lambda }(\mathbf {x})$
be the usual monomial, complete homogeneous and Schur symmetric functions, each of which forms a basis of the ring of symmetric functions as
![]() $\lambda $
ranges over all partitions of n. See [Reference Macdonald17] for their definitions.
$\lambda $
ranges over all partitions of n. See [Reference Macdonald17] for their definitions.
To each finite-dimensional representation of
![]() $S_n$
over
$S_n$
over
![]() $\mathbb {Q}$
, we associate a symmetric function via the Frobenius characteristic map as follows. For
$\mathbb {Q}$
, we associate a symmetric function via the Frobenius characteristic map as follows. For
![]() $\lambda \vdash n$
, let
$\lambda \vdash n$
, let
![]() $S^\lambda $
be the Specht module, which is the irreducible representation of
$S^\lambda $
be the Specht module, which is the irreducible representation of
![]() $S_n$
indexed by
$S_n$
indexed by
![]() $\lambda $
. Given a finite-dimensional vector space V over
$\lambda $
. Given a finite-dimensional vector space V over
![]() $\mathbb {Q}$
that has the structure of an
$\mathbb {Q}$
that has the structure of an
![]() $S_n$
-module, it decomposes as a direct sum of Specht modules,
$S_n$
-module, it decomposes as a direct sum of Specht modules,
![]() $V \cong \bigoplus _{\lambda \vdash n} (S^\lambda )^{\oplus a_{\lambda }}$
, where
$V \cong \bigoplus _{\lambda \vdash n} (S^\lambda )^{\oplus a_{\lambda }}$
, where
![]() $a_{\lambda }$
is the multiplicity of
$a_{\lambda }$
is the multiplicity of
![]() $S^\lambda $
in V. The Frobenius characteristic of V is then defined to be
$S^\lambda $
in V. The Frobenius characteristic of V is then defined to be
Given a graded vector space
![]() $V = \bigoplus _{i\geq 0} V^{(i)}$
where
$V = \bigoplus _{i\geq 0} V^{(i)}$
where
![]() $V^{(i)}$
is finite dimensional, its Hilbert series is the generating function
$V^{(i)}$
is finite dimensional, its Hilbert series is the generating function
If each
![]() $V^{(i)}$
also has the structure of a finite-dimensional
$V^{(i)}$
also has the structure of a finite-dimensional
![]() $S_n$
-module, its graded Frobenius characteristic is
$S_n$
-module, its graded Frobenius characteristic is
The ring
![]() $\Lambda _{\mathbb {Q}(q)}$
has a basis given by the Hall–Littlewood symmetric functions
$\Lambda _{\mathbb {Q}(q)}$
has a basis given by the Hall–Littlewood symmetric functions
![]() $P_{\mu }(\mathbf {x};q)$
, which have the property that
$P_{\mu }(\mathbf {x};q)$
, which have the property that
where
![]() $K_{\lambda ,\mu }(q)$
is the Kostka–Foulkes polynomial; see [Reference Macdonald17] for more details. The dual Hall–Littlewood symmetric functions are defined by
$K_{\lambda ,\mu }(q)$
is the Kostka–Foulkes polynomial; see [Reference Macdonald17] for more details. The dual Hall–Littlewood symmetric functions are defined by
These symmetric functions are sometimes alternatively denoted by
![]() $Q^{\prime }_{\mu }(\mathbf {x};q) = H_{\mu }(\mathbf {x};q)$
. Given a polynomial
$Q^{\prime }_{\mu }(\mathbf {x};q) = H_{\mu }(\mathbf {x};q)$
. Given a polynomial
![]() $f(q) = a_0 + a_1q + \cdots +a_mq^m$
with symmetric function coefficients such that
$f(q) = a_0 + a_1q + \cdots +a_mq^m$
with symmetric function coefficients such that
![]() $a_m\neq 0$
, the q
-reversal of f is
$a_m\neq 0$
, the q
-reversal of f is
![]() $\mathrm {rev}_q(f) = a_m + a_{m-1}q + \cdots + a_1 q^{m-1} + a_0q^m$
. In the case of Hall-Littlewood symmetric functions, the degree of
$\mathrm {rev}_q(f) = a_m + a_{m-1}q + \cdots + a_1 q^{m-1} + a_0q^m$
. In the case of Hall-Littlewood symmetric functions, the degree of
![]() $H_{\mu }(\mathbf {x};q)$
as a polynomial in q is
$H_{\mu }(\mathbf {x};q)$
as a polynomial in q is ![]() . The reversal of
. The reversal of
![]() $H_{\mu }(\mathbf {x};q)$
is the modified (dual) Hall–Littlewood symmetric function, written
$H_{\mu }(\mathbf {x};q)$
is the modified (dual) Hall–Littlewood symmetric function, written
We use the following standard q-analogues of integers, factorials and binomial coefficients.

2.3. Flag varieties and Schubert cells
Given a field
![]() $\mathbb {F}$
, a partial flag in
$\mathbb {F}$
, a partial flag in
![]() $\mathbb {F}^K$
is a nested sequence of vector subspaces of
$\mathbb {F}^K$
is a nested sequence of vector subspaces of
![]() $\mathbb {F}^K$
,
$\mathbb {F}^K$
,
Given a strong composition
![]() $\mu = (\mu _1,\dots , \mu _m)$
such that
$\mu = (\mu _1,\dots , \mu _m)$
such that
![]() $|\mu |=\mu _1+\cdots +\mu _m \leq K$
, define the partial flag variety to be the set of partial flags of
$|\mu |=\mu _1+\cdots +\mu _m \leq K$
, define the partial flag variety to be the set of partial flags of
![]() $\mathbb {F}^K$
such that the dimensions of the successive quotients
$\mathbb {F}^K$
such that the dimensions of the successive quotients
![]() $V_i/V_{i-1}$
are recorded by the parts of
$V_i/V_{i-1}$
are recorded by the parts of
![]() $\mu $
,
$\mu $
,
Here, by convention, we define ![]() . (Note that we have switched to using
. (Note that we have switched to using
![]() $\mu $
as a strong composition here, since the symbol
$\mu $
as a strong composition here, since the symbol
![]() $\alpha $
will be reserved later to denote a different composition.) We occasionally write
$\alpha $
will be reserved later to denote a different composition.) We occasionally write ![]() when
when
![]() $|\mu | = K$
and the field
$|\mu | = K$
and the field
![]() $\mathbb {F}$
is clear from context.
$\mathbb {F}$
is clear from context.
The partial flag variety is realized as a projective algebraic variety as
![]() $G/P^{\mu }$
, where
$G/P^{\mu }$
, where
![]() $G=GL_K$
and
$G=GL_K$
and
![]() $P^{\mu }$
is the parabolic subgroup of block upper triangular matrices with blocks of sizes
$P^{\mu }$
is the parabolic subgroup of block upper triangular matrices with blocks of sizes
![]() $\mu _1,\mu _2,\dots , \mu _m,K-|\mu |$
. We remark that although
$\mu _1,\mu _2,\dots , \mu _m,K-|\mu |$
. We remark that although
![]() $\mathcal {B}^{\mu }(\mathbb {F}^K)$
is isomorphic to
$\mathcal {B}^{\mu }(\mathbb {F}^K)$
is isomorphic to
![]() $\mathcal {B}^{\mu ,K-|\mu |}$
, it will be notationally convenient for us to distinguish the two spaces. In the case when
$\mathcal {B}^{\mu ,K-|\mu |}$
, it will be notationally convenient for us to distinguish the two spaces. In the case when
![]() $K=n$
and
$K=n$
and
![]() $\mu = (1^n)$
,
$\mu = (1^n)$
,
![]() $\mathcal {B}^{(1^n)}$
is the complete flag variety.
$\mathcal {B}^{(1^n)}$
is the complete flag variety.
Returning to the general case when
![]() $|\mu |\leq K$
, let
$|\mu |\leq K$
, let ![]() and let
and let ![]() . Given an injective map
. Given an injective map
![]() $w : [n]\rightarrow [K]$
, we say that w is
$w : [n]\rightarrow [K]$
, we say that w is
![]() $\mu $
-increasing if for each
$\mu $
-increasing if for each
![]() $i\leq \ell (\mu )$
, w is increasing on the ith block of
$i\leq \ell (\mu )$
, w is increasing on the ith block of
![]() $\mu $
; that is,
$\mu $
; that is,
![]() $w_j<w_k$
for all elements
$w_j<w_k$
for all elements
![]() $j<k$
of
$j<k$
of
![]() $\mu [i]$
. Given any w, let
$\mu [i]$
. Given any w, let
![]() $\mathrm {sort}_{\mu }(w)$
be the unique injective
$\mathrm {sort}_{\mu }(w)$
be the unique injective
![]() $\mu $
-increasing function such that the images of the set
$\mu $
-increasing function such that the images of the set
![]() $\mu [i]$
under w and
$\mu [i]$
under w and
![]() $\mathrm {sort}_{\mu }(w)$
are the same for each i.
$\mathrm {sort}_{\mu }(w)$
are the same for each i.
Define
![]() $f_1,f_2,\dots ,f_K$
to be the standard ordered basis of
$f_1,f_2,\dots ,f_K$
to be the standard ordered basis of
![]() $\mathbb {F}^K$
. Given a
$\mathbb {F}^K$
. Given a
![]() $\mu $
-increasing injective map
$\mu $
-increasing injective map
![]() $w:[n]\rightarrow [K]$
, let the coordinate flag
$w:[n]\rightarrow [K]$
, let the coordinate flag
![]() $F_{\bullet }^{(w)}\in \mathcal {B}^{\mu }(\mathbb {F}^K)$
be defined by setting
$F_{\bullet }^{(w)}\in \mathcal {B}^{\mu }(\mathbb {F}^K)$
be defined by setting
![]() $F^{(w)}_p=\mathrm {span}\{f_{w(1)},\ldots , f_{w(\mu _1+\cdots +\mu _p)}\}$
for all p such that
$F^{(w)}_p=\mathrm {span}\{f_{w(1)},\ldots , f_{w(\mu _1+\cdots +\mu _p)}\}$
for all p such that
![]() $1\leq p\leq \ell (\mu )$
. Now define the Schubert cell
$1\leq p\leq \ell (\mu )$
. Now define the Schubert cell
![]() $C_w$
to be the
$C_w$
to be the
![]() $P^{\mu }$
orbit of
$P^{\mu }$
orbit of
![]() $F^{(w)}_{\bullet }$
. When
$F^{(w)}_{\bullet }$
. When
![]() $\mathbb {F} = \mathbb {C}$
, the Schubert cells are the cells of an affine paving (in fact, a CW-complex) of the partial flag variety.
$\mathbb {F} = \mathbb {C}$
, the Schubert cells are the cells of an affine paving (in fact, a CW-complex) of the partial flag variety.
There is another description of the Schubert cells that will be useful for us. Given a vector
![]() $v = \sum _i a_if_i\in \mathbb {F}^K$
, we say its leading term is the term
$v = \sum _i a_if_i\in \mathbb {F}^K$
, we say its leading term is the term
![]() $a_if_i$
with i maximal such that
$a_if_i$
with i maximal such that
![]() $a_i\neq 0$
. Given any
$a_i\neq 0$
. Given any
![]() $V_{\bullet }\in C_w\subseteq \mathcal {B}^{\mu }(\mathbb {F}^K)$
, for each i such that
$V_{\bullet }\in C_w\subseteq \mathcal {B}^{\mu }(\mathbb {F}^K)$
, for each i such that
![]() $1\leq i\leq \ell (\mu )$
, there exist unique vectors
$1\leq i\leq \ell (\mu )$
, there exist unique vectors
![]() $v_1,\dots ,v_n\in \mathbb {F}^K$
such that for
$v_1,\dots ,v_n\in \mathbb {F}^K$
such that for
![]() $p\in \mu [i]$
, we have
$p\in \mu [i]$
, we have
![]() $v_p\in V_i\setminus V_{i-1}$
,
$v_p\in V_i\setminus V_{i-1}$
,
![]() $v_p$
has leading term
$v_p$
has leading term
![]() $f_{w(p)}$
, and
$f_{w(p)}$
, and
 $$ \begin{align} v_{p} =f_{w(p)}+\sum_{h=1}^{w(p)-1} \beta_{w(p),h}\, f_h, \end{align} $$
$$ \begin{align} v_{p} =f_{w(p)}+\sum_{h=1}^{w(p)-1} \beta_{w(p),h}\, f_h, \end{align} $$
for some
![]() $\beta _{w(p),h}$
such that
$\beta _{w(p),h}$
such that
![]() $\beta _{w(p),h}=0$
if
$\beta _{w(p),h}=0$
if
![]() $h\in \{w(1),\ldots ,w(p-1)\}$
. Note
$h\in \{w(1),\ldots ,w(p-1)\}$
. Note
![]() $V_i=\mathrm {span}\{v_1,\ldots ,v_{\mu _1+\cdots +\mu _i}\}$
. The
$V_i=\mathrm {span}\{v_1,\ldots ,v_{\mu _1+\cdots +\mu _i}\}$
. The
![]() $\beta _{w(p),h}$
that are not required to be 0 can be taken as algebraically independent coordinates on
$\beta _{w(p),h}$
that are not required to be 0 can be taken as algebraically independent coordinates on
![]() $C_w$
. We will say that (2.6) is the standard coordinate representation of
$C_w$
. We will say that (2.6) is the standard coordinate representation of
![]() $V_{\bullet }$
and that the
$V_{\bullet }$
and that the
![]() $\beta _{w(p),h}$
are the standard coordinates of the Schubert cell. Equivalently, if
$\beta _{w(p),h}$
are the standard coordinates of the Schubert cell. Equivalently, if
![]() $V_{\bullet }$
is represented as a matrix whose first
$V_{\bullet }$
is represented as a matrix whose first
![]() $\mu _1+\cdots +\mu _i$
many columns span
$\mu _1+\cdots +\mu _i$
many columns span
![]() $V_i$
, then the
$V_i$
, then the
![]() $\beta _{w(p),h}$
are the matrix entries after column reducing.
$\beta _{w(p),h}$
are the matrix entries after column reducing.
Note that we have a projection map
defined by sending
![]() $V_{\bullet }$
to
$V_{\bullet }$
to
![]() $(V_{\mu _1},V_{\mu _1+\mu _2},\dots ,V_n)$
. Given w a
$(V_{\mu _1},V_{\mu _1+\mu _2},\dots ,V_n)$
. Given w a
![]() $\mu $
-increasing injective function, it is evident from the coordinate description of the Schubert cell
$\mu $
-increasing injective function, it is evident from the coordinate description of the Schubert cell
![]() $C_w\subseteq \mathcal {B}^{(1^n)}(\mathbb {F}^K)$
that
$C_w\subseteq \mathcal {B}^{(1^n)}(\mathbb {F}^K)$
that
![]() $C_w$
is mapped isomorphically under
$C_w$
is mapped isomorphically under
![]() $\pi ^{\mu }$
onto the corresponding Schubert cell
$\pi ^{\mu }$
onto the corresponding Schubert cell
![]() $C_w\subseteq \mathcal {B}^{\mu }(\mathbb {F}^K)$
(which justifies our abuse of notation by not decorating
$C_w\subseteq \mathcal {B}^{\mu }(\mathbb {F}^K)$
(which justifies our abuse of notation by not decorating
![]() $C_w$
with
$C_w$
with
![]() $\mu $
).
$\mu $
).
2.4. Springer fibers and Steinberg varieties
Springer fibers are subvarieties of the complete flag variety studied by Springer [Reference Springer22, Reference Springer23]. Given a nilpotent
![]() $n\times n$
matrix N over
$n\times n$
matrix N over
![]() $\mathbb {F}$
, the Springer fiber associated to it is
$\mathbb {F}$
, the Springer fiber associated to it is
with the reduced induced scheme structure. Given two nilpotent matrices whose Jordan block sizes are recorded by the partition
![]() $\lambda \vdash n$
, their associated Springer fibers are isomorphic, so we simply denote the Springer fiber by
$\lambda \vdash n$
, their associated Springer fibers are isomorphic, so we simply denote the Springer fiber by ![]() , where
, where
![]() $\lambda $
is the Jordan type of N. Springer showed that although the symmetric group
$\lambda $
is the Jordan type of N. Springer showed that although the symmetric group
![]() $S_n$
does not act directly on
$S_n$
does not act directly on
![]() $\mathcal {B}_{\lambda }$
, it does act on the cohomology ring
$\mathcal {B}_{\lambda }$
, it does act on the cohomology ring
![]() $H^{*}(\mathcal {B}_{\lambda }(\mathbb {C});\mathbb {Q})$
, and used this action to geometrically construct the irreducible representations of
$H^{*}(\mathcal {B}_{\lambda }(\mathbb {C});\mathbb {Q})$
, and used this action to geometrically construct the irreducible representations of
![]() $S_n$
. The connection between Springer fibers and symmetric functions is summed up in the following elegant formula [Reference Garsia and Procesi6, Reference Hotta and Springer15]:
$S_n$
. The connection between Springer fibers and symmetric functions is summed up in the following elegant formula [Reference Garsia and Procesi6, Reference Hotta and Springer15]:
Here, and throughout the paper, we define the grading on cohomology so that
![]() $H^{2k}$
is in degree k. This is possible since the odd degree cohomology groups of all of the varieties mentioned in this paper are
$H^{2k}$
is in degree k. This is possible since the odd degree cohomology groups of all of the varieties mentioned in this paper are
![]() $0$
.
$0$
.
It can be shown by induction that the Springer fiber has an alternative definition as a variety where the conditions
![]() $NV_i\subseteq V_i$
are replaced with the conditions
$NV_i\subseteq V_i$
are replaced with the conditions
![]() $NV_i\subseteq V_{i-1}$
for all i, since N is nilpotent and we are considering complete flags. For partial flags of type
$NV_i\subseteq V_{i-1}$
for all i, since N is nilpotent and we are considering complete flags. For partial flags of type
![]() $\mu $
a composition of K, these conditions give rise to two different varieties, which we refer to as the Steinberg and the Spaltenstein varieties, defined respectively as
$\mu $
a composition of K, these conditions give rise to two different varieties, which we refer to as the Steinberg and the Spaltenstein varieties, defined respectively as

We note that
![]() $\mathrm {Spalt}_{\lambda }^{\mu }$
is denoted by
$\mathrm {Spalt}_{\lambda }^{\mu }$
is denoted by
![]() $\mathcal {B}^\lambda _{\mu }$
in [Reference Griffin, Levinson and Woo10]. By the construction of the Springer action, there is an isomorphism of graded vector spaces [Reference Borho and MacPherson2, Reference Brundan and Ostrik4]
$\mathcal {B}^\lambda _{\mu }$
in [Reference Griffin, Levinson and Woo10]. By the construction of the Springer action, there is an isomorphism of graded vector spaces [Reference Borho and MacPherson2, Reference Brundan and Ostrik4]
where the superscript
![]() $S_{\mu }$
denotes taking the fixed subspace under the action of the Young subgroup
$S_{\mu }$
denotes taking the fixed subspace under the action of the Young subgroup ![]() permuting the elements in the sets
permuting the elements in the sets
![]() $\mu [1],\dots ,\mu [\ell (\mu )]$
independently. Similarly, there is an identification of the cohomology of
$\mu [1],\dots ,\mu [\ell (\mu )]$
independently. Similarly, there is an identification of the cohomology of
![]() $\mathrm {Spalt}_{\lambda }^{\mu }(\mathbb {C})$
with the
$\mathrm {Spalt}_{\lambda }^{\mu }(\mathbb {C})$
with the
![]() $S_{\mu }$
-anti-invariants of the cohomology of the Springer fiber, up to a grading shift.
$S_{\mu }$
-anti-invariants of the cohomology of the Springer fiber, up to a grading shift.
For X a complex variety, an affine paving of X is a filtration of X by closed subvarieties
such that for all i,
![]() $X_i\setminus X_{i-1}\cong \bigsqcup _{j} C_{i,j}$
, a disjoint union where
$X_i\setminus X_{i-1}\cong \bigsqcup _{j} C_{i,j}$
, a disjoint union where
![]() $C_{i,j}\cong \mathbb {C}^{a_{i,j}}$
for some
$C_{i,j}\cong \mathbb {C}^{a_{i,j}}$
for some
![]() $a_{i,j}$
. If a compact complex variety X has an affine paving, then the dimensions of the even degree cohomology groups can be computed by counting dimensions of cells,
$a_{i,j}$
. If a compact complex variety X has an affine paving, then the dimensions of the even degree cohomology groups can be computed by counting dimensions of cells,
and the odd degree cohomology groups are
![]() $0$
.
$0$
.
It is well known [Reference Brundan and Ostrik4, Reference Fresse5, Reference Spaltenstein21] that both
![]() $\mathrm {Stein}_{\lambda }^{\mu }(\mathbb {C})$
and
$\mathrm {Stein}_{\lambda }^{\mu }(\mathbb {C})$
and
![]() $\mathrm {Spalt}_{\lambda }^{\mu }(\mathbb {C})$
have affine pavings. Hence, their odd degree cohomology groups are
$\mathrm {Spalt}_{\lambda }^{\mu }(\mathbb {C})$
have affine pavings. Hence, their odd degree cohomology groups are
![]() $0$
.
$0$
.
2.5.
 $\Delta $
-Springer varieties and affine pavings
$\Delta $
-Springer varieties and affine pavings
We now recall the definition of the
![]() $\Delta $
-Springer variety
$\Delta $
-Springer variety
![]() $Y_{n,\lambda ,s}$
and the affine pavings of
$Y_{n,\lambda ,s}$
and the affine pavings of
![]() $Y_{n,\lambda ,s}$
constructed in [Reference Griffin, Levinson and Woo10].
$Y_{n,\lambda ,s}$
constructed in [Reference Griffin, Levinson and Woo10].
Fix an integer
![]() $n\geq 0$
, a partition
$n\geq 0$
, a partition
![]() $\lambda $
of size
$\lambda $
of size
![]() $|\lambda |=k\leq n$
and an integer
$|\lambda |=k\leq n$
and an integer
![]() $s\geq \ell (\lambda )$
. Define
$s\geq \ell (\lambda )$
. Define ![]() , where
, where ![]() for
for
![]() $i>\ell (\lambda )$
, and define
$i>\ell (\lambda )$
, and define ![]() . Given
. Given
![]() $\mathbb {F}$
a field and a nilpotent matrix
$\mathbb {F}$
a field and a nilpotent matrix
![]() $N_\Lambda $
over
$N_\Lambda $
over
![]() $\mathbb {F}$
of Jordan type
$\mathbb {F}$
of Jordan type
![]() $\Lambda $
, the
$\Lambda $
, the
![]() $\Delta $
-Springer variety over
$\Delta $
-Springer variety over
![]() $\mathbb {F}$
is defined to be
$\mathbb {F}$
is defined to be
When
![]() $n=|\lambda | = k$
and s is arbitrary, the
$n=|\lambda | = k$
and s is arbitrary, the
![]() $\Delta $
-Springer variety specializes to
$\Delta $
-Springer variety specializes to
![]() $\mathcal {B}_{\lambda }$
, the usual Springer fiber.
$\mathcal {B}_{\lambda }$
, the usual Springer fiber.
The
![]() $\Delta $
-Springer variety can equivalently be defined as the projection of a certain Spaltenstein variety. Letting
$\Delta $
-Springer variety can equivalently be defined as the projection of a certain Spaltenstein variety. Letting
![]() $(1^n,(s-1)^{n-k}) = (1^n,s-1,s-1,\dots ,s-1)$
, where
$(1^n,(s-1)^{n-k}) = (1^n,s-1,s-1,\dots ,s-1)$
, where
![]() $s-1$
is repeated
$s-1$
is repeated
![]() $n-k$
many times, and
$n-k$
many times, and
![]() $\pi : \mathcal {B}^{(1^n,(s-1)^{n-k})}\to \mathcal {B}^{(1^n)}(\mathbb {F}^K)$
be the projection map that forgets all but the first n parts of the flag, we have [Reference Griffin, Levinson and Woo10, Lemma 5.8]
$\pi : \mathcal {B}^{(1^n,(s-1)^{n-k})}\to \mathcal {B}^{(1^n)}(\mathbb {F}^K)$
be the projection map that forgets all but the first n parts of the flag, we have [Reference Griffin, Levinson and Woo10, Lemma 5.8]
To briefly illustrate why (2.9) holds, given
![]() $V_{\bullet } \in \mathrm {Spalt}^{(1^n,(s-1)^{n-k})}_\Lambda $
, then by definition
$V_{\bullet } \in \mathrm {Spalt}^{(1^n,(s-1)^{n-k})}_\Lambda $
, then by definition
![]() $N_\Lambda V_i\subseteq V_{i-1}$
for all i and
$N_\Lambda V_i\subseteq V_{i-1}$
for all i and
![]() $V_{2n-k} = \mathbb {C}^K$
. Combining these conditions for the
$V_{2n-k} = \mathbb {C}^K$
. Combining these conditions for the
![]() $n-k$
many indices
$n-k$
many indices
![]() $i=n+1,\dots , 2n-k$
gives
$i=n+1,\dots , 2n-k$
gives
![]() $N_\Lambda ^{n-k} \mathbb {C}^K = N_\Lambda ^{n-k} V_{2n-k} \subseteq V_n$
, which is the same condition as in
$N_\Lambda ^{n-k} \mathbb {C}^K = N_\Lambda ^{n-k} V_{2n-k} \subseteq V_n$
, which is the same condition as in
![]() $Y_{n,\lambda ,s}$
. Additionally, the conditions
$Y_{n,\lambda ,s}$
. Additionally, the conditions
![]() $N_\Lambda V_i \subseteq V_{i-1}$
for
$N_\Lambda V_i \subseteq V_{i-1}$
for
![]() $i=1,\dots , n$
are equivalent to the conditions
$i=1,\dots , n$
are equivalent to the conditions
![]() $N_\Lambda V_i\subseteq V_i$
for
$N_\Lambda V_i\subseteq V_i$
for
![]() $i=1,\dots , n$
since
$i=1,\dots , n$
since
![]() $N_\Lambda $
is nilpotent so the action of
$N_\Lambda $
is nilpotent so the action of
![]() $N_\Lambda $
on the
$N_\Lambda $
on the
![]() $1$
-dimensional space
$1$
-dimensional space
![]() $V_i/V_{i-1}$
must be
$V_i/V_{i-1}$
must be
![]() $0$
.
$0$
.
We denote by
![]() $[\Lambda ]$
the Young diagram of
$[\Lambda ]$
the Young diagram of
![]() $\Lambda $
according to English convention, which formally is the set
$\Lambda $
according to English convention, which formally is the set
where
![]() $(i,j)$
is the cell in the ith row from the top and the jth column from the left. There are two copies of
$(i,j)$
is the cell in the ith row from the top and the jth column from the left. There are two copies of
![]() $[\lambda ]$
inside of
$[\lambda ]$
inside of
![]() $[\Lambda ]$
that we will consider, which are respectively left justified and right justified inside of
$[\Lambda ]$
that we will consider, which are respectively left justified and right justified inside of
![]() $[\Lambda ]$
,
$[\Lambda ]$
,


Figure 1. An example of
![]() $[\Lambda ]$
for
$[\Lambda ]$
for
![]() $n=7$
,
$n=7$
,
![]() $\lambda =(2,1)$
,
$\lambda =(2,1)$
,
![]() $s=3$
, with the two copies of the Young diagram of
$s=3$
, with the two copies of the Young diagram of
![]() $\lambda $
shaded.
$\lambda $
shaded.
The affine pavings of
![]() $Y_{n,\lambda ,s} = Y_{n,\lambda ,s}(\mathbb {C})$
are defined in terms of specific choices of the nilpotent matrix
$Y_{n,\lambda ,s} = Y_{n,\lambda ,s}(\mathbb {C})$
are defined in terms of specific choices of the nilpotent matrix
![]() $N_\Lambda $
. Recall
$N_\Lambda $
. Recall
![]() $f_1,\dots , f_K\in \mathbb {C}^K$
is the standard basis, and let
$f_1,\dots , f_K\in \mathbb {C}^K$
is the standard basis, and let ![]() . Given a bijection
. Given a bijection
![]() $T : [\Lambda ] \to [K]$
, define two nilpotent matrices
$T : [\Lambda ] \to [K]$
, define two nilpotent matrices
![]() $N_T$
and
$N_T$
and
![]() $N_T^t$
by
$N_T^t$
by


For example, for T as in Figure 2, we have
![]() $N_T f_5 = f_3$
and
$N_T f_5 = f_3$
and
![]() $N_T f_1 = 0$
, whereas
$N_T f_1 = 0$
, whereas
![]() $N_{T}^t f_3 = f_5$
and
$N_{T}^t f_3 = f_5$
and
![]() $N_T^t f_{16} = 0$
. Observe that both
$N_T^t f_{16} = 0$
. Observe that both
![]() $N_T$
and
$N_T$
and
![]() $N_T^t$
have Jordan type
$N_T^t$
have Jordan type
![]() $\Lambda $
by construction and that
$\Lambda $
by construction and that
![]() $N_T^t$
is simply the transpose of the matrix
$N_T^t$
is simply the transpose of the matrix
![]() $N_T$
. We define
$N_T$
. We define
![]() $Y_{N_T}$
and
$Y_{N_T}$
and
![]() $Y_{N_T^t}$
to be the
$Y_{N_T^t}$
to be the
![]() $\Delta $
-Springer varieties for
$\Delta $
-Springer varieties for
![]() $N_T$
and
$N_T$
and
![]() $N_T^t$
, respectively, where we are abusing notation by suppressing the data of n,
$N_T^t$
, respectively, where we are abusing notation by suppressing the data of n,
![]() $\lambda $
and s.
$\lambda $
and s.

Figure 2. The reading order filling T of
![]() $[\Lambda (7,(2,2),4)]$
, and the associated labelings
$[\Lambda (7,(2,2),4)]$
, and the associated labelings
![]() $T^{(i)}$
.
$T^{(i)}$
.
Definition 2.1. We say that T is
![]() $(n,\lambda ,s)$
-Schubert compatible if
$(n,\lambda ,s)$
-Schubert compatible if
-
○ T restricts to a bijection between
 $[\lambda ]^r$
and
$[\lambda ]^r$
and
 $[k]$
.
$[k]$
. -
○ T is decreasing along each row from left to right.
-
○ For all
 $(i,j)\in [\lambda ]^r$
, the label
$(i,j)\in [\lambda ]^r$
, the label
 $T(i,j)$
is greater than all labels in column
$T(i,j)$
is greater than all labels in column
 $j+1$
.
$j+1$
. -
○ For
 $i'<i$
, we have
$i'<i$
, we have
 $T(i',\Lambda _{i'}) < T(i,\Lambda _{i})$
.
$T(i',\Lambda _{i'}) < T(i,\Lambda _{i})$
. -
○ Whenever
 $T(a,b)> T(c,d)$
for
$T(a,b)> T(c,d)$
for
 $b,d>1$
, then
$b,d>1$
, then
 $T(a,b-1)> T(c,d-1)$
.
$T(a,b-1)> T(c,d-1)$
.
When n,
![]() $\lambda $
and s are clear from context, we simply say T is Schubert compatible.
$\lambda $
and s are clear from context, we simply say T is Schubert compatible.
Definition 2.2. The reading order of
![]() $[\Lambda ]$
is the sequence of cells obtained by reading down each column of
$[\Lambda ]$
is the sequence of cells obtained by reading down each column of
![]() $[\Lambda ]$
, ordering the columns from right to left. The reading order filling of
$[\Lambda ]$
, ordering the columns from right to left. The reading order filling of
![]() $[\Lambda ]$
is the unique bijection
$[\Lambda ]$
is the unique bijection
![]() $T:[\Lambda ]\to [K]$
such that
$T:[\Lambda ]\to [K]$
such that
![]() $T(i,j) = \ell $
if and only if
$T(i,j) = \ell $
if and only if
![]() $(i,j)$
is the
$(i,j)$
is the
![]() $\ell $
th cell in reading order.
$\ell $
th cell in reading order.
It is noted in [Reference Griffin, Levinson and Woo10] that the reading order filling is Schubert compatible. See the filling T in Figure 2 for an example of the reading order filling.
When T is Schubert compatible, the intersection of a Schubert cell with
![]() $Y_{N_T}$
is either empty or a copy of affine space, and the nonempty intersections are the cells of an affine paving of
$Y_{N_T}$
is either empty or a copy of affine space, and the nonempty intersections are the cells of an affine paving of
![]() $Y_{N_T}$
. In fact, these cells have a recursive structure which we state next.
$Y_{N_T}$
. In fact, these cells have a recursive structure which we state next.
Let T be Schubert compatible. For
![]() $1\leq i \leq s$
, define the flattening function
$1\leq i \leq s$
, define the flattening function
![]() $\mathrm {f\hspace {0.25pt}l}_T^{(i)}$
and filling
$\mathrm {f\hspace {0.25pt}l}_T^{(i)}$
and filling
![]() $T^{(i)}$
as follows. If
$T^{(i)}$
as follows. If
![]() $i\leq \ell (\lambda )$
, then
$i\leq \ell (\lambda )$
, then
![]() $\mathrm {f\hspace {0.25pt}l}_T^{(i)}$
is the unique order-preserving function with the following domain and codomain:
$\mathrm {f\hspace {0.25pt}l}_T^{(i)}$
is the unique order-preserving function with the following domain and codomain:
Let
![]() $T^{(i)}$
be the filling obtained by deleting the cell
$T^{(i)}$
be the filling obtained by deleting the cell
![]() $(i,\Lambda _i)$
, applying
$(i,\Lambda _i)$
, applying
![]() $\mathrm {f\hspace {0.25pt}l}_T^{(i)}$
to the label in each remaining cell and reordering the rows so that the labels in the right-most cells increase from top to bottom. If
$\mathrm {f\hspace {0.25pt}l}_T^{(i)}$
to the label in each remaining cell and reordering the rows so that the labels in the right-most cells increase from top to bottom. If
![]() $i> \ell (\lambda )$
, then
$i> \ell (\lambda )$
, then
![]() $\mathrm {f\hspace {0.25pt}l}_T^{(i)}$
is the unique order-preserving function
$\mathrm {f\hspace {0.25pt}l}_T^{(i)}$
is the unique order-preserving function
We define
![]() $T^{(i)}$
in the same way as the previous case, except we also delete the cells
$T^{(i)}$
in the same way as the previous case, except we also delete the cells
![]() $(i',1)$
for
$(i',1)$
for
![]() $i'\neq i$
and shift those rows to the left by one unit before applying
$i'\neq i$
and shift those rows to the left by one unit before applying
![]() $\mathrm {f\hspace {0.25pt}l}_T^{(i)}$
and reordering the rows. See Figure 2 for examples.
$\mathrm {f\hspace {0.25pt}l}_T^{(i)}$
and reordering the rows. See Figure 2 for examples.
Given an injective map
![]() $w: [n]\to [K]$
, we say w is admissible with respect to T if the image of w contains
$w: [n]\to [K]$
, we say w is admissible with respect to T if the image of w contains
![]() $[k]$
, and whenever
$[k]$
, and whenever
![]() $T(a,b) = w(i)$
for some i, then either
$T(a,b) = w(i)$
for some i, then either
![]() $b=\Lambda _a$
or
$b=\Lambda _a$
or
![]() $T(a,b+1) = w(i')$
for some
$T(a,b+1) = w(i')$
for some
![]() $i'<i$
. It is proven in [Reference Griffin, Levinson and Woo10].
$i'<i$
. It is proven in [Reference Griffin, Levinson and Woo10].
We have the following recursion for the cells
![]() $C_w\cap Y_{N_T}$
.
$C_w\cap Y_{N_T}$
.
Lemma 2.3 [Reference Griffin, Levinson and Woo10]
Let T be Schubert compatible. The intersection
![]() $C_w\cap Y_{N_T}$
is nonempty if and only if w is admissible with respect to T. If
$C_w\cap Y_{N_T}$
is nonempty if and only if w is admissible with respect to T. If
![]() $C_w\cap Y_{N_T}$
is nonempty, then there is an isomorphism
$C_w\cap Y_{N_T}$
is nonempty, then there is an isomorphism
where i is such that
![]() $w(1) = T(i,\Lambda _i)$
.
$w(1) = T(i,\Lambda _i)$
.
Remark 2.4. The proof of Lemma 2.3 given in [Reference Griffin, Levinson and Woo10] can be used without change to show that for any field
![]() $\mathbb {F}$
, there is a bijection
$\mathbb {F}$
, there is a bijection
We use the symbol
![]() $\cong $
throughout the paper to mean a bijection between sets, but all bijections below are easily seen to be isomorphisms of complex algebraic varieties in the case when
$\cong $
throughout the paper to mean a bijection between sets, but all bijections below are easily seen to be isomorphisms of complex algebraic varieties in the case when
![]() $\mathbb {F}=\mathbb {C}$
. Furthermore, the term ‘isomorphism’ should be translated as ‘bijection’ in the general setting and as ‘isomorphism of complex algebraic varieties’ in the case
$\mathbb {F}=\mathbb {C}$
. Furthermore, the term ‘isomorphism’ should be translated as ‘bijection’ in the general setting and as ‘isomorphism of complex algebraic varieties’ in the case
![]() $\mathbb {F}=\mathbb {C}$
.
$\mathbb {F}=\mathbb {C}$
.
A partial row-decreasing filling (PRD) of
![]() $[\Lambda ]$
is a filling of a subset of size n of the cells of
$[\Lambda ]$
is a filling of a subset of size n of the cells of
![]() $[\Lambda ] = [\Lambda (n,\lambda ,s)]$
with positive integers such that the filled cells are right justified in each row, the labeling weakly decreases along each row, and each cell of
$[\Lambda ] = [\Lambda (n,\lambda ,s)]$
with positive integers such that the filled cells are right justified in each row, the labeling weakly decreases along each row, and each cell of
![]() $[\lambda ]^r$
is filled. A PRD is standard if the filling uses the labels
$[\lambda ]^r$
is filled. A PRD is standard if the filling uses the labels
![]() $1,2,\dots , n$
without repeats.
$1,2,\dots , n$
without repeats.
Given w admissible with respect to T, let
![]() $\operatorname {\mathrm {PRD}}_T(w)$
be the standard partial row-decreasing filling of
$\operatorname {\mathrm {PRD}}_T(w)$
be the standard partial row-decreasing filling of
![]() $[\Lambda ]$
such that, for
$[\Lambda ]$
such that, for
![]() $1\leq i\leq n$
, if
$1\leq i\leq n$
, if
![]() $w(i) = T(a,b)$
, then the cell
$w(i) = T(a,b)$
, then the cell
![]() $(a,b)$
of
$(a,b)$
of
![]() $[\Lambda ]$
is labeled by i. It can be checked that the map
$[\Lambda ]$
is labeled by i. It can be checked that the map
![]() $\operatorname {\mathrm {PRD}}_T$
gives a bijection between admissible w and standard partial row-decreasing fillings. Hence, standard partial row-decreasing fillings of
$\operatorname {\mathrm {PRD}}_T$
gives a bijection between admissible w and standard partial row-decreasing fillings. Hence, standard partial row-decreasing fillings of
![]() $[\Lambda ]$
also index the cells of
$[\Lambda ]$
also index the cells of
![]() $Y_{N_T}$
. See Figure 3 for an example of
$Y_{N_T}$
. See Figure 3 for an example of
![]() $\operatorname {\mathrm {PRD}}_T(w)$
for T the reading order filling of
$\operatorname {\mathrm {PRD}}_T(w)$
for T the reading order filling of
![]() $[\Lambda (7,(2,2),4)]$
and
$[\Lambda (7,(2,2),4)]$
and
![]() $w = 2713594$
(where we have listed out the images of
$w = 2713594$
(where we have listed out the images of
![]() $1,2,\dots ,7$
in order).
$1,2,\dots ,7$
in order).

Figure 3. For T as in Figure 2, the partial row-decreasing filling
![]() $\operatorname {\mathrm {PRD}}_T(w)$
associated to the admissible function
$\operatorname {\mathrm {PRD}}_T(w)$
associated to the admissible function
![]() $w=2713594$
.
$w=2713594$
.
2.6. Monomial symmetric function formulas
In [Reference Griffin, Levinson and Woo10], it is shown that the map on cohomology induced by inclusion of varieties
is surjective. There is a well-defined
![]() $S_n$
action on
$S_n$
action on
![]() $H^{*}(Y_{n,\lambda ,s}(\mathbb {C});\mathbb {Q})$
which is the unique one that makes the above map
$H^{*}(Y_{n,\lambda ,s}(\mathbb {C});\mathbb {Q})$
which is the unique one that makes the above map
![]() $S_n$
-equivariant. Thus,
$S_n$
-equivariant. Thus,
![]() $H^{*}(Y_{n,\lambda ,s}(\mathbb {C});\mathbb {Q})$
has the structure of a graded
$H^{*}(Y_{n,\lambda ,s}(\mathbb {C});\mathbb {Q})$
has the structure of a graded
![]() $S_n$
-module. In [Reference Griffin9], several formulas for the graded Frobenius characteristic of
$S_n$
-module. In [Reference Griffin9], several formulas for the graded Frobenius characteristic of
![]() $H^{*}(Y_{n,\lambda ,s}(\mathbb {C});\mathbb {Q})$
are given, which we recall next.
$H^{*}(Y_{n,\lambda ,s}(\mathbb {C});\mathbb {Q})$
are given, which we recall next.
For
![]() $\mu \vdash n$
, let
$\mu \vdash n$
, let
![]() $\operatorname {\mathrm {PRD}}_{n,\lambda ,s}^{\mu }$
be the set of partial row-decreasing fillings of
$\operatorname {\mathrm {PRD}}_{n,\lambda ,s}^{\mu }$
be the set of partial row-decreasing fillings of
![]() $\Lambda = \Lambda (n,\lambda ,s)$
with
$\Lambda = \Lambda (n,\lambda ,s)$
with
![]() $\mu _i$
many i’s. Given such a labeling
$\mu _i$
many i’s. Given such a labeling
![]() $\varphi \in \operatorname {\mathrm {PRD}}_{n,\lambda ,s}^{\mu }$
, let
$\varphi \in \operatorname {\mathrm {PRD}}_{n,\lambda ,s}^{\mu }$
, let
![]() $\varphi _{i,j}$
be the label in cell
$\varphi _{i,j}$
be the label in cell
![]() $(i,j)$
. Given a pair of cells
$(i,j)$
. Given a pair of cells
![]() $((i,j)$
,
$((i,j)$
,
![]() $(p,q))$
of
$(p,q))$
of
![]() $[\Lambda ]$
, we say they are an attacking pair if either
$[\Lambda ]$
, we say they are an attacking pair if either
![]() $j=q$
and
$j=q$
and
![]() $i<p$
, or if
$i<p$
, or if
![]() $j = q+1$
and
$j = q+1$
and
![]() $i> p$
.
$i> p$
.
Definition 2.5. Given
![]() $\varphi \in \operatorname {\mathrm {PRD}}_{n,\lambda ,s}^{\mu }$
, a diagonal inversion of
$\varphi \in \operatorname {\mathrm {PRD}}_{n,\lambda ,s}^{\mu }$
, a diagonal inversion of
![]() $\varphi $
is an attacking pair
$\varphi $
is an attacking pair
![]() $((i,j),(p,q))$
of cells of
$((i,j),(p,q))$
of cells of
![]() $[\Lambda ]$
such that one of the following hold:
$[\Lambda ]$
such that one of the following hold:
-
(D1)
 $(i,j)$
and
$(i,j)$
and
 $(p,q)$
are filled such that
$(p,q)$
are filled such that
 $\varphi _{i,j}> \varphi _{p,q}$
,
$\varphi _{i,j}> \varphi _{p,q}$
, -
(D2)
 $(i,j)$
is not filled and
$(i,j)$
is not filled and
 $(p,q)$
is filled.
$(p,q)$
is filled.
Let
![]() $\operatorname {{\mathrm {dinv}}}(\varphi )$
be the number of diagonal inversions of
$\operatorname {{\mathrm {dinv}}}(\varphi )$
be the number of diagonal inversions of
![]() $\varphi $
.
$\varphi $
.
For
![]() $\varphi = \operatorname {\mathrm {PRD}}_T(2713594)$
as in Figure 3,
$\varphi = \operatorname {\mathrm {PRD}}_T(2713594)$
as in Figure 3,
![]() $\varphi $
has three diagonal inversions of type (D1);
$\varphi $
has three diagonal inversions of type (D1);
![]() $((1,5),(2,5))$
,
$((1,5),(2,5))$
,
![]() $((2,4),(1,3))$
, and
$((2,4),(1,3))$
, and
![]() $((1,3),(3,3))$
; and three of type (D2);
$((1,3),(3,3))$
; and three of type (D2);
![]() $((2,3),(3,3))$
,
$((2,3),(3,3))$
,
![]() $((4,3),(1,2))$
, and
$((4,3),(1,2))$
, and
![]() $((2,3),(1,2))$
, so
$((2,3),(1,2))$
, so
![]() $\operatorname {{\mathrm {dinv}}}(\varphi ) = 6$
.
$\operatorname {{\mathrm {dinv}}}(\varphi ) = 6$
.
We have the following restatement of Theorem 1.1.
Theorem 2.6 [Reference Griffin, Levinson and Woo10]
We have
 $$\begin{align*}\mathrm{Frob}(H^{*}(Y_{n,\lambda,s}(\mathbb{C});\mathbb{Q}) ;q) = \sum_{\mu\vdash n} \sum_{\varphi\in \operatorname{\mathrm{PRD}}_{n,\lambda,s}^{\mu}} q^{\operatorname{{\mathrm{dinv}}}(\varphi)} m_{\mu}(\mathbf{x}). \end{align*}$$
$$\begin{align*}\mathrm{Frob}(H^{*}(Y_{n,\lambda,s}(\mathbb{C});\mathbb{Q}) ;q) = \sum_{\mu\vdash n} \sum_{\varphi\in \operatorname{\mathrm{PRD}}_{n,\lambda,s}^{\mu}} q^{\operatorname{{\mathrm{dinv}}}(\varphi)} m_{\mu}(\mathbf{x}). \end{align*}$$
Remark 2.7. In Corollary 3.7, we show that the statistic
![]() $\operatorname {{\mathrm {dinv}}}$
counts the dimensions of the cells of
$\operatorname {{\mathrm {dinv}}}$
counts the dimensions of the cells of
![]() $Y_{N_T}$
when T is the reading order of
$Y_{N_T}$
when T is the reading order of
![]() $[\Lambda ]$
. There is another inversion statistic
$[\Lambda ]$
. There is another inversion statistic
![]() $\operatorname {{\mathrm {inv}}}$
defined in [Reference Griffin9, Reference Griffin, Levinson and Woo10] that also gives a monomial expansion of the graded Frobenius characteristic of
$\operatorname {{\mathrm {inv}}}$
defined in [Reference Griffin9, Reference Griffin, Levinson and Woo10] that also gives a monomial expansion of the graded Frobenius characteristic of
![]() $H^{*}(Y_{n,\lambda ,s}(\mathbb {C});\mathbb {Q})$
. We do not define it here because it does not immediately come from a Schubert compatible filling of the cells of
$H^{*}(Y_{n,\lambda ,s}(\mathbb {C});\mathbb {Q})$
. We do not define it here because it does not immediately come from a Schubert compatible filling of the cells of
![]() $[\Lambda ]$
. However, it may still be possible to show it counts dimensions of cells of
$[\Lambda ]$
. However, it may still be possible to show it counts dimensions of cells of
![]() $Y_{N_T}$
for some choice of filling T.
$Y_{N_T}$
for some choice of filling T.
3. Counting
 $\mathbb {F}_q$
-points of projected
$\mathbb {F}_q$
-points of projected
 $\Delta $
-Springer varieties
$\Delta $
-Springer varieties
In this section, we analyze the projections of the
![]() $\Delta $
-Springer variety to other partial flag varieties. We then show that the graded Frobenius characteristic of
$\Delta $
-Springer variety to other partial flag varieties. We then show that the graded Frobenius characteristic of
![]() $H^{*}(Y_{n,\lambda ,s}(\mathbb {C});\mathbb {Q})$
can be written in terms of counting
$H^{*}(Y_{n,\lambda ,s}(\mathbb {C});\mathbb {Q})$
can be written in terms of counting
![]() $\mathbb {F}_q$
points of these projected varieties.
$\mathbb {F}_q$
points of these projected varieties.
Fix
![]() $n,\lambda ,s,$
and
$n,\lambda ,s,$
and
![]() $k=|\lambda |$
as in Subsection 2.5, let
$k=|\lambda |$
as in Subsection 2.5, let ![]() and let
and let ![]() .
.
Definition 3.1. Let
![]() $\mu $
be a strong composition of n and let
$\mu $
be a strong composition of n and let
![]() $N_\Lambda $
is a nilpotent matrix of type
$N_\Lambda $
is a nilpotent matrix of type
![]() $\Lambda $
. Define the projected
$\Lambda $
. Define the projected
![]() $\Delta $
-Springer variety to be
$\Delta $
-Springer variety to be
Lemma 3.2. We have
where
![]() $\pi ^{\mu } : \mathcal {B}^{(1^n,(s-1)^{n-k})}\to \mathcal {B}^{\mu }(\mathbb {F}^K)$
is the usual projection map of partial flag varieties.
$\pi ^{\mu } : \mathcal {B}^{(1^n,(s-1)^{n-k})}\to \mathcal {B}^{\mu }(\mathbb {F}^K)$
is the usual projection map of partial flag varieties.
Proof. Let
![]() $\rho ^{\mu } : \mathcal {B}^{(1^n)}(\mathbb {F}^K)\to \mathcal {B}^{\mu }(\mathbb {F}^K)$
be the usual projection map, which factors through
$\rho ^{\mu } : \mathcal {B}^{(1^n)}(\mathbb {F}^K)\to \mathcal {B}^{\mu }(\mathbb {F}^K)$
be the usual projection map, which factors through
![]() $\pi ^{\mu }$
(i.e.,
$\pi ^{\mu }$
(i.e.,
![]() $\pi ^{\mu } = \rho ^{\mu }\circ \pi $
), where
$\pi ^{\mu } = \rho ^{\mu }\circ \pi $
), where
![]() $\pi $
is the projection in (2.9). By (2.9), it is immediate that
$\pi $
is the projection in (2.9). By (2.9), it is immediate that
![]() $\pi ^{\mu }(\mathrm {Spalt}_\Lambda ^{(1^n,(s-1)^{n-k})}) = \rho ^{\mu }(Y_{n,\lambda ,s})$
, which is contained in the right-hand side of (3.1). For the other containment, it is necessary to show that any
$\pi ^{\mu }(\mathrm {Spalt}_\Lambda ^{(1^n,(s-1)^{n-k})}) = \rho ^{\mu }(Y_{n,\lambda ,s})$
, which is contained in the right-hand side of (3.1). For the other containment, it is necessary to show that any
![]() $V_{\bullet }\in \mathcal {B}^{\mu }(\mathbb {F}^K)$
on the right-hand side can be extended to an element of
$V_{\bullet }\in \mathcal {B}^{\mu }(\mathbb {F}^K)$
on the right-hand side can be extended to an element of
![]() $Y_{n,\lambda ,s}$
. This follows from the fact that
$Y_{n,\lambda ,s}$
. This follows from the fact that
where
![]() $N_i$
is the nilpotent operator induced by
$N_i$
is the nilpotent operator induced by
![]() $N_\Lambda $
on
$N_\Lambda $
on
![]() $V_i/V_{i-1}$
. Indeed, since each of the Springer fibers in the product is nonempty, then
$V_i/V_{i-1}$
. Indeed, since each of the Springer fibers in the product is nonempty, then
![]() $V_{\bullet }$
can be extended to an element
$V_{\bullet }$
can be extended to an element
![]() $W_{\bullet }\in Y_{n,\lambda ,s}$
so that
$W_{\bullet }\in Y_{n,\lambda ,s}$
so that
![]() $\rho ^{\mu } (W_{\bullet }) = V_{\bullet }$
. Thus, we have equality of the two sets.
$\rho ^{\mu } (W_{\bullet }) = V_{\bullet }$
. Thus, we have equality of the two sets.
For
![]() $T:[\Lambda ]\to [K]$
a bijection, we denote by
$T:[\Lambda ]\to [K]$
a bijection, we denote by
![]() $Y_{N_T}^{\mu }$
the projected
$Y_{N_T}^{\mu }$
the projected
![]() $\Delta $
-Springer variety
$\Delta $
-Springer variety
![]() $Y_{n,\lambda ,s}^{\mu }$
for the specific choice of nilpotent
$Y_{n,\lambda ,s}^{\mu }$
for the specific choice of nilpotent
![]() $N_T$
, and similarly for
$N_T$
, and similarly for
![]() $N_T^t$
.
$N_T^t$
.
Lemma 3.3. Let T be Schubert compatible and w admissible with respect to T. The projection
![]() $\rho ^{\mu } : Y_{N_T} \to Y_{N_T}^{\mu }$
maps
$\rho ^{\mu } : Y_{N_T} \to Y_{N_T}^{\mu }$
maps
![]() $C_w\cap Y_{N_T}$
to
$C_w\cap Y_{N_T}$
to
![]() $C_{\mathrm {sort}_{\mu }(w)}\cap Y_{N_T}^{\mu }$
. When w is
$C_{\mathrm {sort}_{\mu }(w)}\cap Y_{N_T}^{\mu }$
. When w is
![]() $\mu $
-increasing,
$\mu $
-increasing,
![]() $C_w\cap Y_{N_T}$
maps isomorphically onto
$C_w\cap Y_{N_T}$
maps isomorphically onto
![]() $C_w\cap Y_{N_T}^{\mu }$
. Thus, when
$C_w\cap Y_{N_T}^{\mu }$
. Thus, when
![]() $\mathbb {F}=\mathbb {C}$
, the subspaces
$\mathbb {F}=\mathbb {C}$
, the subspaces
![]() $C_w \cap Y_{n,\lambda ,s}^{\mu }(\mathbb {C})$
for w admissible and
$C_w \cap Y_{n,\lambda ,s}^{\mu }(\mathbb {C})$
for w admissible and
![]() $\mu $
-increasing are the cells of an affine paving of
$\mu $
-increasing are the cells of an affine paving of
![]() $Y_{n,\lambda ,s}^{\mu }(\mathbb {C})$
.
$Y_{n,\lambda ,s}^{\mu }(\mathbb {C})$
.
Proof. The first part of the lemma is immediate from the fact that
![]() $\rho ^{\mu }$
maps
$\rho ^{\mu }$
maps
![]() $C_w$
to
$C_w$
to
![]() $C_{\mathrm {sort}_{\mu }(w)}$
and the definition of
$C_{\mathrm {sort}_{\mu }(w)}$
and the definition of
![]() $Y_{N_T}^{\mu }$
. Let w be
$Y_{N_T}^{\mu }$
. Let w be
![]() $\mu $
-increasing. Since
$\mu $
-increasing. Since
![]() $\rho ^{\mu }:\mathcal {B}^{(1^n)}(\mathbb {F}^K)\to \mathcal {B}^{\mu }(\mathbb {F}^K)$
maps
$\rho ^{\mu }:\mathcal {B}^{(1^n)}(\mathbb {F}^K)\to \mathcal {B}^{\mu }(\mathbb {F}^K)$
maps
![]() $C_w$
isomorphically onto
$C_w$
isomorphically onto
![]() $C_w\subseteq \mathcal {B}^{\mu }(\mathbb {F}^K)$
, then the restriction of
$C_w\subseteq \mathcal {B}^{\mu }(\mathbb {F}^K)$
, then the restriction of
![]() $\rho ^{\mu }$
to
$\rho ^{\mu }$
to
![]() $C_w\cap Y_{N_T}$
maps
$C_w\cap Y_{N_T}$
maps
![]() $C_w\cap Y_{N_T}$
isomorphically onto its image, so it suffices to show that
$C_w\cap Y_{N_T}$
isomorphically onto its image, so it suffices to show that
![]() $C_w\cap Y_{N_T}$
maps surjectively onto
$C_w\cap Y_{N_T}$
maps surjectively onto
![]() $C_w\cap Y_{N_T}^{\mu }$
.
$C_w\cap Y_{N_T}^{\mu }$
.
Let
![]() $V_{\bullet }\in C_w\cap Y_{N_T}^{\mu }$
. For each i, let
$V_{\bullet }\in C_w\cap Y_{N_T}^{\mu }$
. For each i, let
![]() $v_1,\dots ,v_n$
be the vectors such that for
$v_1,\dots ,v_n$
be the vectors such that for
![]() $p\in \mu [i]$
, we have
$p\in \mu [i]$
, we have
![]() $v_p\in V_i\setminus V_{i-1}$
,
$v_p\in V_i\setminus V_{i-1}$
,
![]() $v_p$
has leading term
$v_p$
has leading term
![]() $f_{w(p)}$
, and
$f_{w(p)}$
, and
 $$ \begin{align} v_{p} =f_{w(p)}+\sum_{h=1}^{w(p)-1} \beta_{w(p),h}\, f_h \end{align} $$
$$ \begin{align} v_{p} =f_{w(p)}+\sum_{h=1}^{w(p)-1} \beta_{w(p),h}\, f_h \end{align} $$
for some
![]() $\beta _{w(p),h}$
such that
$\beta _{w(p),h}$
such that
![]() $\beta _{w(p),h}=0$
if
$\beta _{w(p),h}=0$
if
![]() $h\in \{w(1),\ldots ,w(p-1)\}$
. We claim that the partial flag
$h\in \{w(1),\ldots ,w(p-1)\}$
. We claim that the partial flag
![]() $W_{\bullet }\in \mathcal {B}^{(1^n)}(\mathbb {F}^K)$
defined by
$W_{\bullet }\in \mathcal {B}^{(1^n)}(\mathbb {F}^K)$
defined by
![]() $W_i = \mathrm {span}\{v_1,\dots , v_i\}$
for
$W_i = \mathrm {span}\{v_1,\dots , v_i\}$
for
![]() $i\leq n$
is in
$i\leq n$
is in
![]() $Y_{N_T}$
. Indeed, since
$Y_{N_T}$
. Indeed, since
![]() $N_T V_i\subseteq V_i$
, then
$N_T V_i\subseteq V_i$
, then
![]() $N_TW_{\mu _i}\subseteq W_{\mu _i}$
for all i. For
$N_TW_{\mu _i}\subseteq W_{\mu _i}$
for all i. For
![]() $\mu _1+\cdots +\mu _{i-1}+1 \leq p\leq \mu _1+\cdots +\mu _i$
, then
$\mu _1+\cdots +\mu _{i-1}+1 \leq p\leq \mu _1+\cdots +\mu _i$
, then
![]() $N_Tv_p\in W_{\mu _i}$
. Let
$N_Tv_p\in W_{\mu _i}$
. Let
![]() $(a,b)$
be the coordinates of the label
$(a,b)$
be the coordinates of the label
![]() $w(p)$
in T, so
$w(p)$
in T, so
![]() $w(p) = T(a,b)$
. Since T is Schubert compatible, either
$w(p) = T(a,b)$
. Since T is Schubert compatible, either
![]() $N_Tv_p=0$
or the leading term of
$N_Tv_p=0$
or the leading term of
![]() $N_Tv_p$
is
$N_Tv_p$
is
![]() $N_Tf_{w(p)}=f_{T(a,b+1)}$
. In the latter case, since w is admissible with respect to T, then
$N_Tf_{w(p)}=f_{T(a,b+1)}$
. In the latter case, since w is admissible with respect to T, then
![]() $T(a,b+1)=w(p')$
for some
$T(a,b+1)=w(p')$
for some
![]() $p'<p$
. Since w is
$p'<p$
. Since w is
![]() $\mu $
-increasing, we have
$\mu $
-increasing, we have
![]() $w(p')\notin \{p+1,\dots , \mu _i\}$
, so the expansion of
$w(p')\notin \{p+1,\dots , \mu _i\}$
, so the expansion of
![]() $N_Tv_p$
into the
$N_Tv_p$
into the
![]() $v_i$
vectors cannot have any terms with nonzero coefficient on
$v_i$
vectors cannot have any terms with nonzero coefficient on
![]() $v_{p+1},\dots , v_{\mu _i}$
(otherwise the leading term would not be
$v_{p+1},\dots , v_{\mu _i}$
(otherwise the leading term would not be
![]() $f_{w(p')}$
); hence,
$f_{w(p')}$
); hence,
![]() $N_Tv_p\in W_p$
. Therefore, we have the containment
$N_Tv_p\in W_p$
. Therefore, we have the containment
![]() $N_TW_p\subseteq W_p$
for all p.
$N_TW_p\subseteq W_p$
for all p.
Since
![]() $N_T^{n-k}\mathbb {F}^{|\Lambda |} \subseteq V_{\ell (\mu )} = W_n$
, then we have
$N_T^{n-k}\mathbb {F}^{|\Lambda |} \subseteq V_{\ell (\mu )} = W_n$
, then we have
![]() $W_{\bullet }\in Y_{n,\lambda ,s}$
and by construction,
$W_{\bullet }\in Y_{n,\lambda ,s}$
and by construction,
![]() $\rho ^{\mu }(W_{\bullet }) = V_{\bullet }$
, so
$\rho ^{\mu }(W_{\bullet }) = V_{\bullet }$
, so
![]() $\rho ^{\mu }$
maps
$\rho ^{\mu }$
maps
![]() $C_w\cap Y_{n,\lambda ,s}$
surjectively, hence isomorphically, onto
$C_w\cap Y_{n,\lambda ,s}$
surjectively, hence isomorphically, onto
![]() $C_w\cap Y_{n,\lambda ,s}^{\mu }$
.
$C_w\cap Y_{n,\lambda ,s}^{\mu }$
.
When
![]() $\mathbb {F}=\mathbb {C}$
, since
$\mathbb {F}=\mathbb {C}$
, since
![]() $C_w\cap Y_{n,\lambda ,s}$
is isomorphic to an affine space, then
$C_w\cap Y_{n,\lambda ,s}$
is isomorphic to an affine space, then
![]() $C_w\cap Y_{n,\lambda ,s}^{\mu }$
is as well. Since the
$C_w\cap Y_{n,\lambda ,s}^{\mu }$
is as well. Since the
![]() $C_w$
are cells of an affine paving of
$C_w$
are cells of an affine paving of
![]() $\mathcal {B}^{\mu }(\mathbb {C}^K)$
, then the intersections
$\mathcal {B}^{\mu }(\mathbb {C}^K)$
, then the intersections
![]() $C_w\cap Y_{n,\lambda ,s}^{\mu }(\mathbb {C})$
for
$C_w\cap Y_{n,\lambda ,s}^{\mu }(\mathbb {C})$
for
![]() $\mu $
-increasing w are the cells of an affine paving of
$\mu $
-increasing w are the cells of an affine paving of
![]() $Y_{n,\lambda ,s}^{\mu }(\mathbb {C})$
.
$Y_{n,\lambda ,s}^{\mu }(\mathbb {C})$
.
Recall that for T Schubert compatible and w admissible with respect to T,
![]() $\operatorname {\mathrm {PRD}}_T(w)$
is defined to be the row-decreasing filling of
$\operatorname {\mathrm {PRD}}_T(w)$
is defined to be the row-decreasing filling of
![]() $[\Lambda ]$
such that if
$[\Lambda ]$
such that if
![]() $w(i) = T(p,q)$
, then the cell
$w(i) = T(p,q)$
, then the cell
![]() $(p,q)$
is labeled by i. Equivalently, if we let
$(p,q)$
is labeled by i. Equivalently, if we let
![]() $\operatorname {\mathrm {PRD}}_T(w)^{-1}(a)$
be the position of the label a in
$\operatorname {\mathrm {PRD}}_T(w)^{-1}(a)$
be the position of the label a in
![]() $\operatorname {\mathrm {PRD}}_T(w)$
, we have
$\operatorname {\mathrm {PRD}}_T(w)$
, we have
Definition 3.4. For T Schubert compatible and w admissible with respect to T, an inversion of w with respect to T is a pair
![]() $(c,i)$
with
$(c,i)$
with
![]() $1\leq c\leq n$
,
$1\leq c\leq n$
,
![]() $1\leq i\leq s$
such that one of the following conditions holds:
$1\leq i\leq s$
such that one of the following conditions holds:
-
(IT1) There exists a label
 $\ell>c$
of
$\ell>c$
of
 $\operatorname {\mathrm {PRD}}_T(w)$
in row i such that
$\operatorname {\mathrm {PRD}}_T(w)$
in row i such that
 $w(\ell ) < w(c)$
,
$w(\ell ) < w(c)$
, -
(IT2) The condition (IT1) does not hold, and there exists an empty cell
 $(i,j)$
of
$(i,j)$
of
 $\operatorname {\mathrm {PRD}}_T(w)$
in row i such that
$\operatorname {\mathrm {PRD}}_T(w)$
in row i such that
 $T(i,j) < w(c)$
.
$T(i,j) < w(c)$
.
Define
![]() $\operatorname {{\mathrm {inv}}}_T(w)$
to be the number of such pairs.
$\operatorname {{\mathrm {inv}}}_T(w)$
to be the number of such pairs.
For example, letting T be as in Figure 2 (reading order for
![]() $\Lambda (7,(2,2),4)$
) and
$\Lambda (7,(2,2),4)$
) and
![]() $w=2713594$
as in Figure 3, then the inversions of w with respect to T of type (IT1) are
$w=2713594$
as in Figure 3, then the inversions of w with respect to T of type (IT1) are
![]() $(c,i) = (1,1), (2,1)$
and
$(c,i) = (1,1), (2,1)$
and
![]() $(5,2)$
, and those of type (IT2) are
$(5,2)$
, and those of type (IT2) are
![]() $(c,i) = (2,2), (6,2)$
and
$(c,i) = (2,2), (6,2)$
and
![]() $(6,4)$
. Thus,
$(6,4)$
. Thus,
![]() $\operatorname {{\mathrm {inv}}}_T(w) = 6$
.
$\operatorname {{\mathrm {inv}}}_T(w) = 6$
.
Lemma 3.5. Let T be a Schubert-compatible filling of
![]() $[\Lambda ]$
. If w is admissible with respect to T and
$[\Lambda ]$
. If w is admissible with respect to T and
![]() $\mu $
-increasing, then
$\mu $
-increasing, then
Proof. By Lemma 3.3, it suffices to prove the result for the case
![]() $\mu = (1^n)$
. We proceed by induction on n. In the base case when
$\mu = (1^n)$
. We proceed by induction on n. In the base case when
![]() $n=0$
(and s is arbitrary), then
$n=0$
(and s is arbitrary), then
![]() $\lambda = \emptyset $
, and the unique admissible w is the empty function
$\lambda = \emptyset $
, and the unique admissible w is the empty function
![]() $w=\emptyset $
. Furthermore,
$w=\emptyset $
. Furthermore,
![]() $C_\emptyset \cap Y_{N_T} = Y_{N_T}$
is a single point and
$C_\emptyset \cap Y_{N_T} = Y_{N_T}$
is a single point and
![]() $\operatorname {{\mathrm {inv}}}_T(w) = 0$
. Thus, the base case holds.
$\operatorname {{\mathrm {inv}}}_T(w) = 0$
. Thus, the base case holds.
Let
![]() $n\geq 1$
and T and w be arbitrary with
$n\geq 1$
and T and w be arbitrary with
![]() $w(1) = T(i,\Lambda _i)$
. To complete the induction, by Lemma 2.3, it suffices to show
$w(1) = T(i,\Lambda _i)$
. To complete the induction, by Lemma 2.3, it suffices to show
First, we claim that the left-hand side of (3.4) is the number of inversions of w with respect to T that are of the form
![]() $(1,i')$
. Indeed, there is an injective map from the inversions of
$(1,i')$
. Indeed, there is an injective map from the inversions of
![]() $\mathrm {f\hspace {0.25pt}l}_T^{(i)}(w)$
with respect to
$\mathrm {f\hspace {0.25pt}l}_T^{(i)}(w)$
with respect to
![]() $T^{(i)}$
to the inversions of w with respect to T by sending
$T^{(i)}$
to the inversions of w with respect to T by sending
![]() $(c,r)$
to
$(c,r)$
to
![]() $(c+1,r')$
, where
$(c+1,r')$
, where
![]() $r'$
is the row of T corresponding to row r of
$r'$
is the row of T corresponding to row r of
![]() $T^{(i)}$
in the row-sorting step of forming
$T^{(i)}$
in the row-sorting step of forming
![]() $T^{(i)}$
. The inversions of w that are not in the image of this map are those of the form
$T^{(i)}$
. The inversions of w that are not in the image of this map are those of the form
![]() $(1,i')$
, together with inversions of w of the form
$(1,i')$
, together with inversions of w of the form
![]() $(c,r)$
with
$(c,r)$
with
![]() $c>1$
of type (IT2) that involve an empty cell
$c>1$
of type (IT2) that involve an empty cell
![]() $(p,1)$
that was deleted from T to form
$(p,1)$
that was deleted from T to form
![]() $T^{(i)}$
in the case when
$T^{(i)}$
in the case when
![]() $i>\ell (\lambda )$
. However, observe that
$i>\ell (\lambda )$
. However, observe that
![]() $[\Lambda ]/[\lambda ]^r$
has
$[\Lambda ]/[\lambda ]^r$
has
![]() $n-k$
cells in each row, and the number of labels in
$n-k$
cells in each row, and the number of labels in
![]() $[\Lambda ]/[\lambda ]^r$
is
$[\Lambda ]/[\lambda ]^r$
is
![]() $n-k$
. Therefore, since both
$n-k$
. Therefore, since both
![]() $1$
and c are not in row p, both entries
$1$
and c are not in row p, both entries
![]() $(p,1)$
and
$(p,1)$
and
![]() $(p,2)$
are empty, and
$(p,2)$
are empty, and
![]() $T(p,2) < T(p,1) < w(c)$
, so
$T(p,2) < T(p,1) < w(c)$
, so
![]() $(c,p)$
is in the image of the injective map described above. Thus, the left-hand side of (3.4) only counts inversions of w of the form
$(c,p)$
is in the image of the injective map described above. Thus, the left-hand side of (3.4) only counts inversions of w of the form
![]() $(1,i')$
.
$(1,i')$
.
Second, we claim that
![]() $(1,i')$
is an inversion if and only if
$(1,i')$
is an inversion if and only if
![]() $i'<i$
. Indeed, if
$i'<i$
. Indeed, if
![]() $i'<i$
, then
$i'<i$
, then
![]() $T(i',\Lambda _{i'}) < T(i,\Lambda _i)=w(1)$
since T is Schubert compatible. If
$T(i',\Lambda _{i'}) < T(i,\Lambda _i)=w(1)$
since T is Schubert compatible. If
![]() $(i',\Lambda _{i'})$
is filled in
$(i',\Lambda _{i'})$
is filled in
![]() $\operatorname {\mathrm {PRD}}_T(w)$
, let its label be
$\operatorname {\mathrm {PRD}}_T(w)$
, let its label be
![]() $\ell $
. Since w is injective, then
$\ell $
. Since w is injective, then
![]() $\ell>1$
. Furthermore,
$\ell>1$
. Furthermore,
![]() $w(\ell ) = T(\operatorname {\mathrm {PRD}}_T(w)^{-1}(\ell )) = T(i',\Lambda _{i'}) < w(1)$
; thus,
$w(\ell ) = T(\operatorname {\mathrm {PRD}}_T(w)^{-1}(\ell )) = T(i',\Lambda _{i'}) < w(1)$
; thus,
![]() $(1,i')$
is an inversion of type (IT1). Otherwise,
$(1,i')$
is an inversion of type (IT1). Otherwise,
![]() $(i',\Lambda _{i'})$
is not filled in
$(i',\Lambda _{i'})$
is not filled in
![]() $\operatorname {\mathrm {PRD}}_T(w)$
, so since
$\operatorname {\mathrm {PRD}}_T(w)$
, so since
![]() $T(i',\Lambda _{i'}) < w(1)$
, then
$T(i',\Lambda _{i'}) < w(1)$
, then
![]() $(1,i')$
is an inversion of type (IT2).
$(1,i')$
is an inversion of type (IT2).
Suppose
![]() $(1,i')$
is an inversion for some
$(1,i')$
is an inversion for some
![]() $i'\geq i$
. Then in either of the cases (IT1) or (IT2), there exists a cell
$i'\geq i$
. Then in either of the cases (IT1) or (IT2), there exists a cell
![]() $(i',j')$
in row
$(i',j')$
in row
![]() $i'$
such that
$i'$
such that
![]() $T(i',j') < w(1) = T(i,\Lambda _i)$
(where
$T(i',j') < w(1) = T(i,\Lambda _i)$
(where
![]() $T(i',j') = w(\ell )$
in the (IT1) case). By Schubert compatibility, we have
$T(i',j') = w(\ell )$
in the (IT1) case). By Schubert compatibility, we have
![]() $T(i,\Lambda _i) \leq T(i',\Lambda _{i'}) \leq T(i',j')$
, a contradiction. Therefore,
$T(i,\Lambda _i) \leq T(i',\Lambda _{i'}) \leq T(i',j')$
, a contradiction. Therefore,
![]() $(1,i')$
is an inversion if and only if
$(1,i')$
is an inversion if and only if
![]() $i'<i$
, so the number of inversions counted by the left-hand side of (3.4) is
$i'<i$
, so the number of inversions counted by the left-hand side of (3.4) is
![]() $i-1$
. The inductive step is thus complete.
$i-1$
. The inductive step is thus complete.
Lemma 3.6. Let T be the reading order filling of
![]() $[\Lambda ]$
. For all w admissible with respect to T, we have
$[\Lambda ]$
. For all w admissible with respect to T, we have
![]() $\operatorname {{\mathrm {inv}}}_T(w) = \operatorname {{\mathrm {dinv}}}(\operatorname {\mathrm {PRD}}_T(w))$
.
$\operatorname {{\mathrm {inv}}}_T(w) = \operatorname {{\mathrm {dinv}}}(\operatorname {\mathrm {PRD}}_T(w))$
.
Proof. Let
![]() $\varphi = \operatorname {\mathrm {PRD}}_T(w)$
. We define a map from diagonal inversions of
$\varphi = \operatorname {\mathrm {PRD}}_T(w)$
. We define a map from diagonal inversions of
![]() $\varphi $
to inversions of w with respect to T as follows. For each diagonal inversion
$\varphi $
to inversions of w with respect to T as follows. For each diagonal inversion
![]() $((i,j),(p,q))$
, let its corresponding inversion of w be
$((i,j),(p,q))$
, let its corresponding inversion of w be
![]() $(\varphi _{p,q},i)$
. The pair
$(\varphi _{p,q},i)$
. The pair
![]() $(\varphi _{p,q},i)$
is indeed an inversion. If
$(\varphi _{p,q},i)$
is indeed an inversion. If
![]() $((i,j),(p,q))$
is a type (D1) inversion, then
$((i,j),(p,q))$
is a type (D1) inversion, then
![]() $(\varphi _{p,q},i)$
is a type (IT1) inversion, where
$(\varphi _{p,q},i)$
is a type (IT1) inversion, where
![]() $\ell =\varphi _{i,j}$
. If
$\ell =\varphi _{i,j}$
. If
![]() $((i,j),(p,q))$
is type (D2), then
$((i,j),(p,q))$
is type (D2), then
![]() $(\varphi _{p,q},i)$
is type (IT1) or type (IT2) depending on whether there exists a label
$(\varphi _{p,q},i)$
is type (IT1) or type (IT2) depending on whether there exists a label
![]() $\ell>\varphi _{p,q}$
in row i of
$\ell>\varphi _{p,q}$
in row i of
![]() $\varphi $
or not, respectively. We claim that the map defined above is a bijection between diagonal inversions of
$\varphi $
or not, respectively. We claim that the map defined above is a bijection between diagonal inversions of
![]() $\varphi $
and inversions of w with respect to T.
$\varphi $
and inversions of w with respect to T.
To show bijectivity, we give the inverse bijection, as follows. Given
![]() $(c,i)$
an inversion of w, let
$(c,i)$
an inversion of w, let
![]() $(p,q)$
be the coordinates of the label c in
$(p,q)$
be the coordinates of the label c in
![]() $\varphi $
. If
$\varphi $
. If
![]() $(c,i)$
is of type (IT1), then there exists a label
$(c,i)$
is of type (IT1), then there exists a label
![]() $\ell>c$
in row i of
$\ell>c$
in row i of
![]() $\varphi $
such that
$\varphi $
such that
![]() $w(\ell ) < w(c)$
. Since
$w(\ell ) < w(c)$
. Since
![]() $w(\ell ) < w(c)$
, then either
$w(\ell ) < w(c)$
, then either
![]() $i<p$
and
$i<p$
and
![]() $\ell $
is in a cell above and weakly to the right of c, or
$\ell $
is in a cell above and weakly to the right of c, or
![]() $i>p$
and
$i>p$
and
![]() $\ell $
is in a cell below and strictly to the right of c. In the first case,
$\ell $
is in a cell below and strictly to the right of c. In the first case,
![]() $(c,i)$
corresponds to the diagonal inversion
$(c,i)$
corresponds to the diagonal inversion
![]() $((i,q),(p,q))$
. Indeed, the cell
$((i,q),(p,q))$
. Indeed, the cell
![]() $(i,q)$
is either empty in
$(i,q)$
is either empty in
![]() $\varphi $
, so
$\varphi $
, so
![]() $((i,q),(p,q))$
is a type (D2) diagonal inversion, or the cell
$((i,q),(p,q))$
is a type (D2) diagonal inversion, or the cell
![]() $(i,q)$
is labeled and
$(i,q)$
is labeled and
![]() $\varphi _{i,q} \geq \ell> c$
by the row-decreasing property of
$\varphi _{i,q} \geq \ell> c$
by the row-decreasing property of
![]() $\varphi $
so
$\varphi $
so
![]() $((i,q),(p,q))$
is a type (D1) diagonal inversion. In the second case when
$((i,q),(p,q))$
is a type (D1) diagonal inversion. In the second case when
![]() $i>p$
, then
$i>p$
, then
![]() $(c,i)$
corresponds to the diagonal inversion
$(c,i)$
corresponds to the diagonal inversion
![]() $((i,q+1),(p,q))$
. Indeed, the cell
$((i,q+1),(p,q))$
. Indeed, the cell
![]() $(i,q+1)$
is either empty in
$(i,q+1)$
is either empty in
![]() $\varphi $
, so
$\varphi $
, so
![]() $((i,q+1),(p,q))$
is a type (D2) diagonal inversion, or the cell
$((i,q+1),(p,q))$
is a type (D2) diagonal inversion, or the cell
![]() $(i,q+1)$
is labeled and
$(i,q+1)$
is labeled and
![]() $\varphi _{i,q+1}\geq \ell> c$
so
$\varphi _{i,q+1}\geq \ell> c$
so
![]() $((i,q+1),(p,q))$
is a type (D1) diagonal inversion.
$((i,q+1),(p,q))$
is a type (D1) diagonal inversion.
Finally, if
![]() $(c,i)$
is of type (IT2), then there exists an empty cell
$(c,i)$
is of type (IT2), then there exists an empty cell
![]() $(i,j)$
in
$(i,j)$
in
![]() $\varphi $
such that
$\varphi $
such that
![]() $T(i,j) < w(c)$
. Then either
$T(i,j) < w(c)$
. Then either
![]() $i<p$
and
$i<p$
and
![]() $((i,q),(p,q))$
is a diagonal inversion of type (D2), or
$((i,q),(p,q))$
is a diagonal inversion of type (D2), or
![]() $i>p$
and
$i>p$
and
![]() $((i,q+1),(p,q))$
is a diagonal inversion of type (D2). It can then be checked that this is the inverse map, and hence, the number of inversions of w with respect to T is equal to the number of diagonal inversions of
$((i,q+1),(p,q))$
is a diagonal inversion of type (D2). It can then be checked that this is the inverse map, and hence, the number of inversions of w with respect to T is equal to the number of diagonal inversions of
![]() $\varphi $
.
$\varphi $
.
Combining Lemma 3.6 with Lemma 3.5, we see that
![]() $\operatorname {{\mathrm {dinv}}}$
has geometric meaning: it counts the dimensions of cells in
$\operatorname {{\mathrm {dinv}}}$
has geometric meaning: it counts the dimensions of cells in
![]() $Y_{N_T}$
.
$Y_{N_T}$
.
Corollary 3.7. For T the reading order filling of
![]() $[\Lambda ]$
and w that is
$[\Lambda ]$
and w that is
![]() $\mu $
-increasing and admissible with respect to T, we have
$\mu $
-increasing and admissible with respect to T, we have
We are now able to prove the main theorem of this section.
Theorem 3.8. For all prime powers q, we have
Proof. Let T be the reading order filling of
![]() $[\Lambda ]$
and let
$[\Lambda ]$
and let
![]() $\mu \vdash n$
. We claim that
$\mu \vdash n$
. We claim that
 $$ \begin{align} \sum_{\varphi \in \operatorname{\mathrm{PRD}}_{n,\lambda,s}^{\mu}} q^{\operatorname{{\mathrm{dinv}}}(\varphi)} = \sum_{\substack{w \text{ admissible wrt }T,\\ \mu\text{-increasing}}} q^{\operatorname{{\mathrm{dinv}}}(\operatorname{\mathrm{PRD}}_T(w))}. \end{align} $$
$$ \begin{align} \sum_{\varphi \in \operatorname{\mathrm{PRD}}_{n,\lambda,s}^{\mu}} q^{\operatorname{{\mathrm{dinv}}}(\varphi)} = \sum_{\substack{w \text{ admissible wrt }T,\\ \mu\text{-increasing}}} q^{\operatorname{{\mathrm{dinv}}}(\operatorname{\mathrm{PRD}}_T(w))}. \end{align} $$
Indeed, given w admissible with respect to T that is
![]() $\mu $
-increasing, define
$\mu $
-increasing, define
![]() $\varphi \in \operatorname {\mathrm {PRD}}_{n,\lambda ,s}^{\mu }$
by replacing the labels
$\varphi \in \operatorname {\mathrm {PRD}}_{n,\lambda ,s}^{\mu }$
by replacing the labels
![]() $\mu _1+\cdots +\mu _{i-1}+1, \mu _1+\cdots +\mu _{i-1}+2,\dots , \mu _1+\cdots +\mu _{i}$
in
$\mu _1+\cdots +\mu _{i-1}+1, \mu _1+\cdots +\mu _{i-1}+2,\dots , \mu _1+\cdots +\mu _{i}$
in
![]() $\operatorname {\mathrm {PRD}}_T(w)$
with i for each
$\operatorname {\mathrm {PRD}}_T(w)$
with i for each
![]() $i\leq \ell (\mu )$
. Since w is
$i\leq \ell (\mu )$
. Since w is
![]() $\mu $
-increasing, then the labels
$\mu $
-increasing, then the labels
![]() $\mu _1+\cdots +\mu _{i-1}+1, \mu _1+\cdots +\mu _{i-1}+2,\dots , \mu _1+\cdots +\mu _{i}$
in
$\mu _1+\cdots +\mu _{i-1}+1, \mu _1+\cdots +\mu _{i-1}+2,\dots , \mu _1+\cdots +\mu _{i}$
in
![]() $\operatorname {\mathrm {PRD}}_T(w)$
are increasing in reading order, so there are no diagonal inversions among these labels. Therefore, it follows from the definition of
$\operatorname {\mathrm {PRD}}_T(w)$
are increasing in reading order, so there are no diagonal inversions among these labels. Therefore, it follows from the definition of
![]() $\operatorname {{\mathrm {dinv}}}$
that
$\operatorname {{\mathrm {dinv}}}$
that
![]() $\operatorname {{\mathrm {dinv}}}(\varphi ) = \operatorname {{\mathrm {dinv}}}(\operatorname {\mathrm {PRD}}_T(w))$
.
$\operatorname {{\mathrm {dinv}}}(\varphi ) = \operatorname {{\mathrm {dinv}}}(\operatorname {\mathrm {PRD}}_T(w))$
.
Using (3.6), we have
 $$ \begin{align} \mathrm{Frob}(H^{*}(Y_{n,\lambda,s}(\mathbb{C});\mathbb{Q});q) &= \sum_{\mu\vdash n} \sum_{\varphi \in \operatorname{\mathrm{PRD}}_{n,\lambda,s}^{\mu}} q^{\operatorname{{\mathrm{dinv}}}(\varphi)} m_{\mu}(\mathbf{x}) \end{align} $$
$$ \begin{align} \mathrm{Frob}(H^{*}(Y_{n,\lambda,s}(\mathbb{C});\mathbb{Q});q) &= \sum_{\mu\vdash n} \sum_{\varphi \in \operatorname{\mathrm{PRD}}_{n,\lambda,s}^{\mu}} q^{\operatorname{{\mathrm{dinv}}}(\varphi)} m_{\mu}(\mathbf{x}) \end{align} $$
 $$ \begin{align} &= \sum_{\mu\vdash n} \,\,\sum_{\substack{w \text{ admissible wrt }T,\\ \mu\text{-increasing}}} |C_w \cap Y_{N_T}^{\mu}(\mathbb{F}_q)| m_{\mu}(\mathbf{x}) \end{align} $$
$$ \begin{align} &= \sum_{\mu\vdash n} \,\,\sum_{\substack{w \text{ admissible wrt }T,\\ \mu\text{-increasing}}} |C_w \cap Y_{N_T}^{\mu}(\mathbb{F}_q)| m_{\mu}(\mathbf{x}) \end{align} $$
The first equality is Theorem 2.6, the second follows from Corollary 3.7 and the fact that
![]() $\operatorname {\mathrm {PRD}}_T$
restricts to a bijection between the set of w that are admissible and
$\operatorname {\mathrm {PRD}}_T$
restricts to a bijection between the set of w that are admissible and
![]() $\mu $
-increasing and
$\mu $
-increasing and
![]() $\operatorname {\mathrm {PRD}}_{n,\lambda ,s}^{\mu }$
, and the third equality follows from the fact that the intersections
$\operatorname {\mathrm {PRD}}_{n,\lambda ,s}^{\mu }$
, and the third equality follows from the fact that the intersections
![]() $C_w\cap Y_{N_T}^{\mu }$
for w that are admissible with respect to T and
$C_w\cap Y_{N_T}^{\mu }$
for w that are admissible with respect to T and
![]() $\mu $
-increasing partition the space
$\mu $
-increasing partition the space
![]() $Y_{N_T}^{\mu }$
by Lemma 3.3.
$Y_{N_T}^{\mu }$
by Lemma 3.3.
As a corollary, we obtain the following generalization of Borho and Macpherson’s result (2.8).
Corollary 3.9. For all
![]() $\mu \vdash n$
, we have an isomorphism of graded vector spaces
$\mu \vdash n$
, we have an isomorphism of graded vector spaces
Proof. By Frobenius reciprocity (see, for example, [Reference Brosnan and Chow3]), the
![]() $m_{\mu }(\mathbf {x})$
coefficient of the graded Frobenius characteristic of a graded
$m_{\mu }(\mathbf {x})$
coefficient of the graded Frobenius characteristic of a graded
![]() $S_n$
-module is the Hilbert series of the
$S_n$
-module is the Hilbert series of the
![]() $S_{\mu }$
-invariant subspace. By Theorem 3.8, applying this fact to the cohomology of
$S_{\mu }$
-invariant subspace. By Theorem 3.8, applying this fact to the cohomology of
![]() $Y_{n,\lambda ,s}(\mathbb {C})$
yields
$Y_{n,\lambda ,s}(\mathbb {C})$
yields
for all prime powers q. By the last part of Lemma 3.3,
 $$\begin{align*}\mathrm{Hilb}(H^{*}(Y_{n,\lambda,s}^{\mu}(\mathbb{C});\mathbb{Q});q) = \sum_{\substack{w \text{ admissible wrt }T,\\ \mu\text{-increasing}}} q^{\dim_{\mathbb{C}}(C_w \cap Y_{N_T}^{\mu}(\mathbb{C}))}. \end{align*}$$
$$\begin{align*}\mathrm{Hilb}(H^{*}(Y_{n,\lambda,s}^{\mu}(\mathbb{C});\mathbb{Q});q) = \sum_{\substack{w \text{ admissible wrt }T,\\ \mu\text{-increasing}}} q^{\dim_{\mathbb{C}}(C_w \cap Y_{N_T}^{\mu}(\mathbb{C}))}. \end{align*}$$
By (2.13), it can be checked by induction that
![]() $|C_w\cap Y_{N_T}^{\mu }(\mathbb {F}_q)| = q^{\dim _{\mathbb {C}}(C_w \cap Y_{N_T}^{\mu }(\mathbb {C}))}$
for each w admissible and
$|C_w\cap Y_{N_T}^{\mu }(\mathbb {F}_q)| = q^{\dim _{\mathbb {C}}(C_w \cap Y_{N_T}^{\mu }(\mathbb {C}))}$
for each w admissible and
![]() $\mu $
-increasing. Since the
$\mu $
-increasing. Since the
![]() $C_w\cap Y_{N_T}^{\mu }(\mathbb {F}_q)$
partition
$C_w\cap Y_{N_T}^{\mu }(\mathbb {F}_q)$
partition
![]() $\mathbb {F}_q$
, we have
$\mathbb {F}_q$
, we have
Combining (3.11) and (3.12), the two spaces have the same Hilbert series and are hence isomorphic as graded vector spaces.
Remark 3.10. We note that a second proof of Corollary 3.9 has been given by Gillespie and the author [Reference Gillespie and Griffin7] by realizing
![]() $Y_{n,\lambda ,s}$
as a special case of a variety studied by Borho and MacPherson in their study of partial resolutions of nilpotent orbit closures [Reference Borho and MacPherson2].
$Y_{n,\lambda ,s}$
as a special case of a variety studied by Borho and MacPherson in their study of partial resolutions of nilpotent orbit closures [Reference Borho and MacPherson2].
4. A Springer fiber decomposition of
 $Y_{n,\lambda ,s}$
$Y_{n,\lambda ,s}$
In this section, we decompose the
![]() $\Delta $
-Springer variety
$\Delta $
-Springer variety
![]() $Y_{n,\lambda ,s}^{\mu }$
into subspaces that are isomorphic to Steinberg varieties crossed with affine spaces, so, in particular,
$Y_{n,\lambda ,s}^{\mu }$
into subspaces that are isomorphic to Steinberg varieties crossed with affine spaces, so, in particular,
![]() $Y_{n,\lambda ,s}$
decomposes into copies of Springer fibers crossed with affine spaces. We then use this to prove our expansion of the graded Frobenius characteristic of the cohomology ring in terms of Hall-Littlewood polynomials in Section 5.
$Y_{n,\lambda ,s}$
decomposes into copies of Springer fibers crossed with affine spaces. We then use this to prove our expansion of the graded Frobenius characteristic of the cohomology ring in terms of Hall-Littlewood polynomials in Section 5.
Definition 4.1. The reverse reading order of
![]() $[\Lambda ]$
is the sequence of cells obtained by reading down each column of
$[\Lambda ]$
is the sequence of cells obtained by reading down each column of
![]() $[\Lambda ]$
, ordering the columns from left to right. The reverse reading order filling of
$[\Lambda ]$
, ordering the columns from left to right. The reverse reading order filling of
![]() $[\Lambda ]$
is the unique bijection
$[\Lambda ]$
is the unique bijection
![]() $T:[\Lambda ]\to [K]$
such that
$T:[\Lambda ]\to [K]$
such that
![]() $T(i,j) = \ell $
if and only if
$T(i,j) = \ell $
if and only if
![]() $(i,j)$
is the
$(i,j)$
is the
![]() $\ell $
th cell in reverse reading order.
$\ell $
th cell in reverse reading order.
Note that in reverse reading order, only the order of the columns are reversed (not the order of the rows). See Figure 4 for the reverse reading order filling of
![]() $[\Lambda (7,(2,2),4]$
.
$[\Lambda (7,(2,2),4]$
.

Figure 4. The reverse reading order filling T for
![]() $[\Lambda (7,(2,2),4)]$
, with
$[\Lambda (7,(2,2),4)]$
, with
![]() $[\lambda ] = [(2,2)]$
shaded in orange. The diagram of
$[\lambda ] = [(2,2)]$
shaded in orange. The diagram of
![]() $\alpha = (2,4,0,1)\in \mathrm {Comp}(7,4)$
is the union of the orange and blue cells.
$\alpha = (2,4,0,1)\in \mathrm {Comp}(7,4)$
is the union of the orange and blue cells.
Throughout this section, we let T be the reverse reading order filling of
![]() $[\Lambda ]$
. For notational convenience, we use the simplified notation
$[\Lambda ]$
. For notational convenience, we use the simplified notation ![]() and
and ![]() .
.
Given
![]() $\alpha \in \mathrm {Comp}(n,s)$
such that
$\alpha \in \mathrm {Comp}(n,s)$
such that
![]() $\lambda \subseteq \alpha $
, let
$\lambda \subseteq \alpha $
, let
![]() $[\alpha ]$
be the subdiagram of
$[\alpha ]$
be the subdiagram of
![]() $[\Lambda ]$
defined by
$[\Lambda ]$
defined by
Note that the inequality
![]() $\alpha _i\leq \Lambda _i = (n-k)+\lambda _i$
is guaranteed for all i by the fact that
$\alpha _i\leq \Lambda _i = (n-k)+\lambda _i$
is guaranteed for all i by the fact that
![]() $\alpha $
has size n and contains
$\alpha $
has size n and contains
![]() $\lambda $
(which has size k), so
$\lambda $
(which has size k), so
![]() $[\alpha ]$
is indeed a subdiagram of
$[\alpha ]$
is indeed a subdiagram of
![]() $[\Lambda ]$
.
$[\Lambda ]$
.
Let
![]() $\mathbb {F}^\alpha \subseteq \mathbb {F}^K$
, which is the subspace spanned by
$\mathbb {F}^\alpha \subseteq \mathbb {F}^K$
, which is the subspace spanned by
![]() $f_{i}$
for i a label of T contained in
$f_{i}$
for i a label of T contained in
![]() $[\alpha ]$
. Similarly, let
$[\alpha ]$
. Similarly, let ![]() be the subspace spanned by
be the subspace spanned by
![]() $f_i$
for i a label of T contained in
$f_i$
for i a label of T contained in
![]() $[\lambda ]$
.
$[\lambda ]$
.
Let
![]() $w: [n]\to [K]$
be the unique
$w: [n]\to [K]$
be the unique
![]() $(n)$
-increasing injective function whose image is the set of labels of T in
$(n)$
-increasing injective function whose image is the set of labels of T in
![]() $[\alpha ]$
, and let
$[\alpha ]$
, and let
![]() $C_{w}$
be the corresponding Schubert cell in the Grassmannian
$C_{w}$
be the corresponding Schubert cell in the Grassmannian
![]() $\mathcal {B}^{(n,K-n)} = \mathrm {Gr}(n,\mathbb {F}^K)$
. Define
$\mathcal {B}^{(n,K-n)} = \mathrm {Gr}(n,\mathbb {F}^K)$
. Define
Note that since
![]() $N^t$
restricts to a nilpotent matrix on the subspace
$N^t$
restricts to a nilpotent matrix on the subspace
![]() $\mathbb {F}^\alpha $
with Jordan type
$\mathbb {F}^\alpha $
with Jordan type
![]() $\mathrm {sort}(\alpha )$
, then
$\mathrm {sort}(\alpha )$
, then
![]() $Z_\alpha ^{\mu }\cong \mathrm {Stein}_{\mathrm {sort}(\alpha )}^{\mu }$
.
$Z_\alpha ^{\mu }\cong \mathrm {Stein}_{\mathrm {sort}(\alpha )}^{\mu }$
.
The following is the main theorem of this section. In the case
![]() $\mu = (1^n)$
, it says that the subspaces
$\mu = (1^n)$
, it says that the subspaces
![]() $\widehat {Z}_{\alpha }$
, which partition
$\widehat {Z}_{\alpha }$
, which partition
![]() $Y_{n,\lambda ,s}$
, are isomorphic to a Springer fiber crossed with an affine space.
$Y_{n,\lambda ,s}$
, are isomorphic to a Springer fiber crossed with an affine space.
Theorem 4.2. We have
where
![]() $\ell = \sum _i (s-\alpha _i^{\prime })(\alpha _{i+1}^{\prime }-\lambda _{i+1}^{\prime }) + \operatorname {\mathrm {coinv}}(\alpha )$
(where
$\ell = \sum _i (s-\alpha _i^{\prime })(\alpha _{i+1}^{\prime }-\lambda _{i+1}^{\prime }) + \operatorname {\mathrm {coinv}}(\alpha )$
(where
![]() $\operatorname {\mathrm {coinv}}$
was defined at the end of Subsection 2.1) and
$\operatorname {\mathrm {coinv}}$
was defined at the end of Subsection 2.1) and
![]() $\alpha _i^{\prime }$
is the number of cells of
$\alpha _i^{\prime }$
is the number of cells of
![]() $[\alpha ]$
in the ith column where
$[\alpha ]$
in the ith column where ![]() .
.
In order to prove Theorem 4.2, we need several definitions and lemmata.
Definition 4.3. A pair
![]() $(i,j)$
with
$(i,j)$
with
![]() $i>j$
is a free pair for
$i>j$
is a free pair for
![]() $\alpha $
if the cell with label i of T is in
$\alpha $
if the cell with label i of T is in
![]() $[\alpha ]/[\lambda ]$
and the cell with label j of T is the leftmost cell of
$[\alpha ]/[\lambda ]$
and the cell with label j of T is the leftmost cell of
![]() $[\Lambda ]\setminus [\alpha ]$
in j’s own row.
$[\Lambda ]\setminus [\alpha ]$
in j’s own row.
Remark 4.4. Let w be the unique admissible
![]() $(n)$
-increasing injective function whose image is the set of labels of T in
$(n)$
-increasing injective function whose image is the set of labels of T in
![]() $[\alpha ]$
, as above. Free pairs
$[\alpha ]$
, as above. Free pairs
![]() $(i,j)$
are defined to correspond to a subset of standard coordinates
$(i,j)$
are defined to correspond to a subset of standard coordinates
![]() $\beta _{i,j}$
of
$\beta _{i,j}$
of
![]() $C_w$
. Note that
$C_w$
. Note that
![]() $\beta _{i,j}$
is undefined unless i is in the image of w, and that if i is in the image of w, then
$\beta _{i,j}$
is undefined unless i is in the image of w, and that if i is in the image of w, then
![]() $\beta _{i,j}=0$
if j is a label in
$\beta _{i,j}=0$
if j is a label in
![]() $[\alpha ]$
.
$[\alpha ]$
.
Example 4.5. For
![]() $n=7$
,
$n=7$
,
![]() $\lambda = (2,2)$
,
$\lambda = (2,2)$
,
![]() $s=4$
and
$s=4$
and
![]() $\alpha = (2,4,0,1)$
as depicted in Figure 4, the free pairs are
$\alpha = (2,4,0,1)$
as depicted in Figure 4, the free pairs are
![]() $(14,9)$
,
$(14,9)$
,
![]() $(14,8)$
,
$(14,8)$
,
![]() $(14,3)$
,
$(14,3)$
,
![]() $(10,9)$
,
$(10,9)$
,
![]() $(10,8)$
,
$(10,8)$
,
![]() $(10,3)$
and
$(10,3)$
and
![]() $(4,3)$
.
$(4,3)$
.
Lemma 4.6. The number of free pairs of
![]() $\alpha $
is
$\alpha $
is
Proof. Let
![]() $(i,j)$
be a free pair for
$(i,j)$
be a free pair for
![]() $\alpha $
. If i and j are not in the same column, in which case j must be in a column to the left of i, then associate
$\alpha $
. If i and j are not in the same column, in which case j must be in a column to the left of i, then associate
![]() $(i,j)$
to the pair
$(i,j)$
to the pair
![]() $(i,j')$
, where
$(i,j')$
, where
![]() $j'$
is the label in the same row as j and in the column immediately to the left of the column of i. This correspondence sets up a bijection between free pairs in which i and j are not in the same column and pairs
$j'$
is the label in the same row as j and in the column immediately to the left of the column of i. This correspondence sets up a bijection between free pairs in which i and j are not in the same column and pairs
![]() $(i,j')$
where i is a label in
$(i,j')$
where i is a label in
![]() $[\alpha ]\setminus [\lambda ]$
and
$[\alpha ]\setminus [\lambda ]$
and
![]() $j'$
is a label in
$j'$
is a label in
![]() $[\Lambda ]\setminus [\alpha ]$
in the column immediately to the left of i. Counting these latter pairs by the column containing i, we have the sum
$[\Lambda ]\setminus [\alpha ]$
in the column immediately to the left of i. Counting these latter pairs by the column containing i, we have the sum
If i and j are in the same column, then associate the free pair
![]() $(i,j)$
to the coinversion
$(i,j)$
to the coinversion
![]() $(r,r')$
of
$(r,r')$
of
![]() $\alpha $
, where r is the row of j and
$\alpha $
, where r is the row of j and
![]() $r'$
is the row of i. Indeed,
$r'$
is the row of i. Indeed,
![]() $(r,r')$
is a coinversion since
$(r,r')$
is a coinversion since
![]() $r<r'$
by the fact that
$r<r'$
by the fact that
![]() $i>j$
and the definition of reverse reading order, and
$i>j$
and the definition of reverse reading order, and
![]() $\alpha _r<\alpha _{r'}$
since i is in
$\alpha _r<\alpha _{r'}$
since i is in
![]() $[\alpha ]$
and j is not. This correspondence is a bijection between free pairs with i and j in the same column and coinversions of
$[\alpha ]$
and j is not. This correspondence is a bijection between free pairs with i and j in the same column and coinversions of
![]() $\alpha $
. Thus, the total number of free pairs is given by (4.3).
$\alpha $
. Thus, the total number of free pairs is given by (4.3).
Example 4.7. For
![]() $\alpha $
as in Example 4.5, the free pairs
$\alpha $
as in Example 4.5, the free pairs
![]() $(10,9)$
and
$(10,9)$
and
![]() $(4,3)$
contribute to
$(4,3)$
contribute to
![]() $\operatorname {\mathrm {coinv}}(\alpha )$
in (4.3). The terms of (4.4) are:
$\operatorname {\mathrm {coinv}}(\alpha )$
in (4.3). The terms of (4.4) are:
![]() $1\cdot 0$
for
$1\cdot 0$
for
![]() $p=1$
,
$p=1$
,
![]() $2\cdot 1$
for
$2\cdot 1$
for
![]() $p=2$
corresponding to pairs
$p=2$
corresponding to pairs
![]() $(10,3)$
and
$(10,3)$
and
![]() $(10,8)$
,
$(10,8)$
,
![]() $3\cdot 1$
for
$3\cdot 1$
for
![]() $p=3$
corresponding to pairs
$p=3$
corresponding to pairs
![]() $(14,9)$
,
$(14,9)$
,
![]() $(14, 3)$
and
$(14, 3)$
and
![]() $(14,8)$
, and
$(14,8)$
, and
![]() $1\cdot 0$
for
$1\cdot 0$
for
![]() $p=4$
.
$p=4$
.
Definition 4.8. For
![]() $(i,j)$
a free pair with
$(i,j)$
a free pair with
![]() $i>j$
, let
$i>j$
, let
![]() $U_{i,j}(t)$
be the
$U_{i,j}(t)$
be the
![]() $K\times K$
matrix such that
$K\times K$
matrix such that
and
![]() $U_{i,j}(t)f_\ell =f_\ell $
for all labels
$U_{i,j}(t)f_\ell =f_\ell $
for all labels
![]() $\ell $
of T that are not in the same row as i.
$\ell $
of T that are not in the same row as i.
Similarly, let
![]() $\widehat {U}_{i,j}(t)$
be the matrix such that
$\widehat {U}_{i,j}(t)$
be the matrix such that
and
![]() $\widehat {U}_{i,j}(t) f_\ell =f_\ell $
for all labels
$\widehat {U}_{i,j}(t) f_\ell =f_\ell $
for all labels
![]() $\ell $
of T that are either not in the same row as i or not weakly to the right of i.
$\ell $
of T that are either not in the same row as i or not weakly to the right of i.
Example 4.9. Continuing our running Example 4.5, the operator
![]() $U_{14,9}(t)$
is defined by
$U_{14,9}(t)$
is defined by
-
○
 $U_{14,9}(t)f_{14} = f_{14} + tf_9$
,
$U_{14,9}(t)f_{14} = f_{14} + tf_9$
, -
○
 $U_{14,9}(t)f_{16} = f_{16} + tf_{13}$
,
$U_{14,9}(t)f_{16} = f_{16} + tf_{13}$
, -
○
 $U_{14,9}(t)f_{10} = f_{10} + tf_5$
,
$U_{14,9}(t)f_{10} = f_{10} + tf_5$
, -
○
 $U_{14,9}(t)f_{6} = f_{6} + tf_1$
,
$U_{14,9}(t)f_{6} = f_{6} + tf_1$
, -
○
 $U_{14,9}(t)f_{2} = f_{2} + 0$
,
$U_{14,9}(t)f_{2} = f_{2} + 0$
,
and
![]() $U_{14,9}(t)f_{\ell } = f_{\ell }$
for all
$U_{14,9}(t)f_{\ell } = f_{\ell }$
for all
![]() $\ell \notin \{2,6,10,14,16\}$
. However,
$\ell \notin \{2,6,10,14,16\}$
. However,
-
○
 $\widehat {U}_{14,9}(t) f_{14} = f_{14} + tf_9$
,
$\widehat {U}_{14,9}(t) f_{14} = f_{14} + tf_9$
, -
○
 $\widehat {U}_{14,9}(t) f_{16} = f_{16} + tf_{13}$
,
$\widehat {U}_{14,9}(t) f_{16} = f_{16} + tf_{13}$
,
and
![]() $\widehat {U}_{14,9}(t)f_\ell = f_\ell $
for all
$\widehat {U}_{14,9}(t)f_\ell = f_\ell $
for all
![]() $\ell \notin \{14,16\}$
.
$\ell \notin \{14,16\}$
.
Lemma 4.10. The matrices
![]() $U_{i,j}(t)$
and
$U_{i,j}(t)$
and
![]() $\widehat {U}_{i,j}(t)$
are unipotent upper triangular.
$\widehat {U}_{i,j}(t)$
are unipotent upper triangular.
Proof. By construction,
![]() $U_{i,j}(t)$
has
$U_{i,j}(t)$
has
![]() $1$
s along the diagonal, so it suffices to check it is upper triangular. Thus, it suffices to check that for all m, the vector
$1$
s along the diagonal, so it suffices to check it is upper triangular. Thus, it suffices to check that for all m, the vector
![]() $N^mf_i$
has index greater than the vector
$N^mf_i$
has index greater than the vector
![]() $N^m f_j$
(if both are nonzero), and the vector
$N^m f_j$
(if both are nonzero), and the vector
![]() $(N^t)^mf_i$
has index greater than the vector
$(N^t)^mf_i$
has index greater than the vector
![]() $(N^t)^mf_j$
(if both are nonzero). Both of these claims follow immediately from the definition of free pairs and reverse reading order. The same reasoning applies to
$(N^t)^mf_j$
(if both are nonzero). Both of these claims follow immediately from the definition of free pairs and reverse reading order. The same reasoning applies to
![]() $\widehat {U}_{i,j}(t)$
.
$\widehat {U}_{i,j}(t)$
.
Lemma 4.11. Let
![]() $(i_1,j_1),(i_2,j_2),\dots ,(i_\ell ,j_\ell )$
be the free pairs for
$(i_1,j_1),(i_2,j_2),\dots ,(i_\ell ,j_\ell )$
be the free pairs for
![]() $\alpha $
listed so that
$\alpha $
listed so that
![]() $i_1\geq i_2\geq \cdots \geq i_\ell $
. Then for all
$i_1\geq i_2\geq \cdots \geq i_\ell $
. Then for all
![]() $p\leq \ell $
,
$p\leq \ell $
,
Proof. We proceed by induction on p. The base case
![]() $p=0$
is trivial, so suppose that for some
$p=0$
is trivial, so suppose that for some
![]() $p\geq 0$
, (4.8) holds. It suffices to show that
$p\geq 0$
, (4.8) holds. It suffices to show that
Let
![]() $v\in \widehat {U}_{i_{p},j_{p}}(t_{p})\cdots \widehat {U}_{i_1,j_1}(t_1)\mathbb {F}^\alpha $
. Since the image of the operator
$v\in \widehat {U}_{i_{p},j_{p}}(t_{p})\cdots \widehat {U}_{i_1,j_1}(t_1)\mathbb {F}^\alpha $
. Since the image of the operator
![]() $U_{i_{p+1},j_{p+1}}(t_{p+1})-\widehat {U}_{i_{p+1},j_{p+1}}(t_{p+1})$
is contained in the span of the vectors
$U_{i_{p+1},j_{p+1}}(t_{p+1})-\widehat {U}_{i_{p+1},j_{p+1}}(t_{p+1})$
is contained in the span of the vectors
![]() $(N^t)^m f_{j_{p+1}}$
for
$(N^t)^m f_{j_{p+1}}$
for
![]() $m>0$
(in fact, they are equal when
$m>0$
(in fact, they are equal when
![]() $t_{p+1}\neq 0$
), then
$t_{p+1}\neq 0$
), then
is a linear combination of the vectors
![]() $(N^t)^mf_{j_{p+1}}$
for
$(N^t)^mf_{j_{p+1}}$
for
![]() $m>0$
. For a fixed
$m>0$
. For a fixed
![]() $m>0$
, let
$m>0$
, let
![]() $f_{j'} = (N^t)^mf_{j_{p+1}}$
. Then
$f_{j'} = (N^t)^mf_{j_{p+1}}$
. Then
![]() $j'$
is in a column strictly to the left of
$j'$
is in a column strictly to the left of
![]() $i_q$
for all
$i_q$
for all
![]() $q\leq p+1$
. Since the operators
$q\leq p+1$
. Since the operators
![]() $\widehat {U}_{i_q,j_q}(t_q)$
for
$\widehat {U}_{i_q,j_q}(t_q)$
for
![]() $q\leq p+1$
fix
$q\leq p+1$
fix
![]() $f_{j'}$
, and since
$f_{j'}$
, and since
![]() $f_{j'}\in \mathbb {F}^\alpha $
, then
$f_{j'}\in \mathbb {F}^\alpha $
, then
Furthermore, since
![]() $j'$
is not in the same row as
$j'$
is not in the same row as
![]() $i_{p+1}$
, then
$i_{p+1}$
, then
![]() $U_{i_{p+1},j_{p+1}}(t_{p+1})$
and
$U_{i_{p+1},j_{p+1}}(t_{p+1})$
and
![]() $\widehat {U}_{i_{p+1},j_{p+1}}(t_{p+1})$
fix
$\widehat {U}_{i_{p+1},j_{p+1}}(t_{p+1})$
fix
![]() $f_{j'}$
, so
$f_{j'}$
, so
![]() $f_{j'}$
is in both sides of (4.9). Therefore, (4.10) is in the intersection of the left-hand side and right-hand side of (4.9). Since
$f_{j'}$
is in both sides of (4.9). Therefore, (4.10) is in the intersection of the left-hand side and right-hand side of (4.9). Since
![]() $U_{i_{p+1},j_{p+1}}(t_{p+1})v$
and
$U_{i_{p+1},j_{p+1}}(t_{p+1})v$
and
![]() $\widehat {U}_{i_{p+1},j_{p+1}}(t_{p+1})v$
are arbitrary elements of the left- and right-hand sides of (4.9), respectively, then the two sets are equal. The induction is thus complete.
$\widehat {U}_{i_{p+1},j_{p+1}}(t_{p+1})v$
are arbitrary elements of the left- and right-hand sides of (4.9), respectively, then the two sets are equal. The induction is thus complete.
Example 4.12. For our running example and
![]() $(i_1,j_1) = (14,9)$
, then
$(i_1,j_1) = (14,9)$
, then
![]() $U_{14,9}(t) - \widehat {U}_{14,9}(t)$
sends
$U_{14,9}(t) - \widehat {U}_{14,9}(t)$
sends
![]() $f_{10}$
to
$f_{10}$
to
![]() $tf_5$
and
$tf_5$
and
![]() $f_6$
to
$f_6$
to
![]() $tf_1$
(and everything else to
$tf_1$
(and everything else to
![]() $0$
) but both
$0$
) but both
![]() $tf_5$
and
$tf_5$
and
![]() $tf_1$
are in
$tf_1$
are in
![]() $\mathbb {F}^\alpha $
and fixed by both
$\mathbb {F}^\alpha $
and fixed by both
![]() $U_{14,9}(t)$
and
$U_{14,9}(t)$
and
![]() $\widehat {U}_{14,9}(t)$
, so
$\widehat {U}_{14,9}(t)$
, so
![]() $U_{14,9}(t)\mathbb {F}^\alpha = \widehat {U}_{14,9}(t)\mathbb {F}^\alpha = \mathrm {span}\{f_{14} + tf_9, f_{10},f_6,f_5,f_4,f_2,f_1\}$
.
$U_{14,9}(t)\mathbb {F}^\alpha = \widehat {U}_{14,9}(t)\mathbb {F}^\alpha = \mathrm {span}\{f_{14} + tf_9, f_{10},f_6,f_5,f_4,f_2,f_1\}$
.
Lemma 4.13. Let
![]() $(i_1,j_1),(i_2,j_2),\dots , (i_\ell ,j_\ell )$
be the free pairs for
$(i_1,j_1),(i_2,j_2),\dots , (i_\ell ,j_\ell )$
be the free pairs for
![]() $\alpha $
, listed so that
$\alpha $
, listed so that
![]() $i_1\geq i_2\geq \cdots \geq i_\ell $
. Then we have a well-defined map
$i_1\geq i_2\geq \cdots \geq i_\ell $
. Then we have a well-defined map
defined by sending
![]() $(\vec {t},V_{\bullet })$
to
$(\vec {t},V_{\bullet })$
to
![]() ${U}_{i_\ell ,j_\ell }(t_\ell )\cdots {U}_{i_2,j_2}(t_2) {U}_{i_1,j_1}(t_1)V_{\bullet }$
.
${U}_{i_\ell ,j_\ell }(t_\ell )\cdots {U}_{i_2,j_2}(t_2) {U}_{i_1,j_1}(t_1)V_{\bullet }$
.
Proof. Letting
![]() $V_{\bullet }\in Z^{\mu }_\alpha $
, it suffices to show that
$V_{\bullet }\in Z^{\mu }_\alpha $
, it suffices to show that
![]() ${U}_{i_\ell ,j_\ell }(t_\ell )\cdots {U}_{i_2,j_2}(t_2) {U}_{i_1,j_1}(t_1)V_{\bullet } \in \widehat {Z}^{\mu }_\alpha $
. Since each
${U}_{i_\ell ,j_\ell }(t_\ell )\cdots {U}_{i_2,j_2}(t_2) {U}_{i_1,j_1}(t_1)V_{\bullet } \in \widehat {Z}^{\mu }_\alpha $
. Since each
![]() ${U}_{i_p,j_p}(t_p)$
is unipotent upper triangular by Lemma 4.10 and
${U}_{i_p,j_p}(t_p)$
is unipotent upper triangular by Lemma 4.10 and
![]() $V_n=\mathbb {F}^\alpha \in C_{w}$
, then
$V_n=\mathbb {F}^\alpha \in C_{w}$
, then
By construction, we have
![]() $U_{i_p,j_p}(t_p) N^t = N^t U_{i_p,j_p}(t_p)$
for all
$U_{i_p,j_p}(t_p) N^t = N^t U_{i_p,j_p}(t_p)$
for all
![]() $p\leq \ell $
, so
$p\leq \ell $
, so
![]() $N^t$
preserves each part of the partial flag
$N^t$
preserves each part of the partial flag
![]() $U_{i_\ell ,j_\ell }(t_\ell )\cdots U_{i_2,j_2}(t_2) U_{i_1,j_1}(t_1)V_{\bullet }$
.
$U_{i_\ell ,j_\ell }(t_\ell )\cdots U_{i_2,j_2}(t_2) U_{i_1,j_1}(t_1)V_{\bullet }$
.
Finally, we must check that
![]() ${U}_{i_\ell ,j_\ell }(t_\ell )\cdots {U}_{i_2,j_2}(t_2) {U}_{i_1,j_1}(t_1)V_n \supseteq \mathbb {F}^\lambda $
. Indeed, this follows from the fact that
${U}_{i_\ell ,j_\ell }(t_\ell )\cdots {U}_{i_2,j_2}(t_2) {U}_{i_1,j_1}(t_1)V_n \supseteq \mathbb {F}^\lambda $
. Indeed, this follows from the fact that
![]() $V_n = \mathbb {F}^\alpha \supseteq \mathbb {F}^\lambda $
, Lemma 4.11, and the fact that each
$V_n = \mathbb {F}^\alpha \supseteq \mathbb {F}^\lambda $
, Lemma 4.11, and the fact that each
![]() $\widehat {U}_{i_p,j_p}(t_p)$
fixes
$\widehat {U}_{i_p,j_p}(t_p)$
fixes
![]() $\mathbb {F}^\lambda $
. Thus, the map is well defined.
$\mathbb {F}^\lambda $
. Thus, the map is well defined.
Example 4.14. For our running example with
![]() $n=7$
,
$n=7$
,
![]() $\lambda = (2,2)$
,
$\lambda = (2,2)$
,
![]() $s=4$
and
$s=4$
and
![]() $\alpha = (2,4,0,1)$
, one (of many) partial flags in
$\alpha = (2,4,0,1)$
, one (of many) partial flags in
![]() $Z_\alpha ^{(1^7)}$
is the one represented by the
$Z_\alpha ^{(1^7)}$
is the one represented by the
![]() $K\times n$
matrix A below (we do not need the full
$K\times n$
matrix A below (we do not need the full
![]() $K\times K$
matrix because the span of the first n columns completely determines the type
$K\times K$
matrix because the span of the first n columns completely determines the type
![]() $(1^n,K-n)$
partial flag). The reader can check that the matrix representative of the partial flag
$(1^n,K-n)$
partial flag). The reader can check that the matrix representative of the partial flag
is the matrix B below.
 $$\begin{align*}A = \begin{bmatrix} 0 & 0 & 3 & 0 & 1 & 0 & 0\\ 1 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 6 & 1\\ 0 & 0 & 0 & 3 & 0 & 1 & 0\\ 0 & 1 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \end{bmatrix} \qquad B = \begin{bmatrix} t_4 & t_1 & 3 & 0 & 1 & 0 & 0\\ 1 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & t_6 & t_3 & 0 & 0 & t_7\\ 0 & t_5 & t_2 & 0 & 0 & 6 & 1\\ 0 & t_4 & t_1 & 3 & 0 & 1 & 0\\ 0 & 1 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & t_6 & 0 & 0 & 0\\ 0 & 0 & t_5 & t_2 & 0 & 0 & 0\\ 0 & 0 & t_4 & t_1 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & t_5 & 0 & 0 & 0\\ 0 & 0 & 0 & t_4 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \end{bmatrix} \end{align*}$$
$$\begin{align*}A = \begin{bmatrix} 0 & 0 & 3 & 0 & 1 & 0 & 0\\ 1 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 6 & 1\\ 0 & 0 & 0 & 3 & 0 & 1 & 0\\ 0 & 1 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \end{bmatrix} \qquad B = \begin{bmatrix} t_4 & t_1 & 3 & 0 & 1 & 0 & 0\\ 1 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & t_6 & t_3 & 0 & 0 & t_7\\ 0 & t_5 & t_2 & 0 & 0 & 6 & 1\\ 0 & t_4 & t_1 & 3 & 0 & 1 & 0\\ 0 & 1 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & t_6 & 0 & 0 & 0\\ 0 & 0 & t_5 & t_2 & 0 & 0 & 0\\ 0 & 0 & t_4 & t_1 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & t_5 & 0 & 0 & 0\\ 0 & 0 & 0 & t_4 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \end{bmatrix} \end{align*}$$
We leave it to the reader to check that B represents a partial flag
![]() $\widehat {Z}_\alpha ^{(1^7)}$
.
$\widehat {Z}_\alpha ^{(1^7)}$
.
Lemma 4.15. Let
![]() $V_{\bullet }\in Z^{\mu }_\alpha $
and let
$V_{\bullet }\in Z^{\mu }_\alpha $
and let
![]() $(i_1,j_1),(i_2,j_2),\dots ,(i_\ell ,j_\ell )$
be the free pairs for
$(i_1,j_1),(i_2,j_2),\dots ,(i_\ell ,j_\ell )$
be the free pairs for
![]() $\alpha $
listed so that
$\alpha $
listed so that
![]() $i_1\geq i_2\geq \cdots \geq i_\ell $
. For all
$i_1\geq i_2\geq \cdots \geq i_\ell $
. For all
![]() $p\leq \ell $
, the standard coordinate
$p\leq \ell $
, the standard coordinate
![]() $\beta _{i_p,j_p}$
of
$\beta _{i_p,j_p}$
of
![]() ${U}_{i_\ell ,j_\ell }(t_\ell )\cdots {U}_{i_1,j_1}(t_1)V_n\in C_w$
is
${U}_{i_\ell ,j_\ell }(t_\ell )\cdots {U}_{i_1,j_1}(t_1)V_n\in C_w$
is
![]() $t_p$
.
$t_p$
.
Proof. By construction of
![]() $\widehat {U}_{i,j}(t)$
, the standard coordinates of
$\widehat {U}_{i,j}(t)$
, the standard coordinates of
![]() $\widehat {U}_{i,j}(t)V$
are obtained by applying
$\widehat {U}_{i,j}(t)V$
are obtained by applying
![]() $\widehat {U}_{i,j}(t)$
directly to each
$\widehat {U}_{i,j}(t)$
directly to each
![]() $v_p$
and collecting terms (in terms of matrix representatives,
$v_p$
and collecting terms (in terms of matrix representatives,
![]() $\widehat {U}_{i,j}(t)$
sends column-reduced matrices to column-reduced matrices); hence, the standard coordinates of
$\widehat {U}_{i,j}(t)$
sends column-reduced matrices to column-reduced matrices); hence, the standard coordinates of
![]() ${U}_{i_\ell ,j_\ell }(t_\ell )\cdots {U}_{i_1,j_1}(t_1)V_n = \widehat {U}_{i_\ell ,j_\ell }(t_\ell )\cdots \widehat {U}_{i_1,j_1}(t_1)V_n$
are obtained by applying these operators to the standard coordinates of
${U}_{i_\ell ,j_\ell }(t_\ell )\cdots {U}_{i_1,j_1}(t_1)V_n = \widehat {U}_{i_\ell ,j_\ell }(t_\ell )\cdots \widehat {U}_{i_1,j_1}(t_1)V_n$
are obtained by applying these operators to the standard coordinates of
![]() $V_n$
. Observe the following:
$V_n$
. Observe the following:
-
1. The
 $\beta _{i_p,j_p}$
coordinate of
$\beta _{i_p,j_p}$
coordinate of
 $V_n$
is
$V_n$
is
 $0$
since
$0$
since
 $V_n = \mathbb {F}^\alpha $
.
$V_n = \mathbb {F}^\alpha $
. -
2. The operator
 $\widehat {U}_{i_p,j_p}(t_p)$
is the only
$\widehat {U}_{i_p,j_p}(t_p)$
is the only
 $\widehat {U}_{i_q,j_q}(t_q)$
operator that changes the
$\widehat {U}_{i_q,j_q}(t_q)$
operator that changes the
 $\beta _{i_p,j_p}$
coordinate. Otherwise, there must exist some q and
$\beta _{i_p,j_p}$
coordinate. Otherwise, there must exist some q and
 $m>0$
such that
$m>0$
such that
 $N^m f_{i_q} = f_{i_p}$
and
$N^m f_{i_q} = f_{i_p}$
and
 $N^m f_{j_q} = f_{j_p}$
. But this would imply that the label
$N^m f_{j_q} = f_{j_p}$
. But this would imply that the label
 $j_p$
is strictly to the right of the label
$j_p$
is strictly to the right of the label
 $j_q$
in T, contradicting the fact that
$j_q$
in T, contradicting the fact that
 $j_p$
is the leftmost label in
$j_p$
is the leftmost label in
 $[\Lambda ]/[\lambda ]$
in
$[\Lambda ]/[\lambda ]$
in
 $j_p$
’s row.
$j_p$
’s row. -
3.
 $\widehat {U}_{i_p,j_p}(t_p) f_{i_p} = f_{i_p} + t_pf_{j_p}$
.
$\widehat {U}_{i_p,j_p}(t_p) f_{i_p} = f_{i_p} + t_pf_{j_p}$
.
Combining 1–3 above, the
![]() $\beta _{i_p,j_p}$
coordinate after applying all of these operators is
$\beta _{i_p,j_p}$
coordinate after applying all of these operators is
![]() $t_p$
.
$t_p$
.
Lemma 4.16. Let
![]() $V\in C_{w}$
such that
$V\in C_{w}$
such that
![]() $N^tV\subseteq V$
and let
$N^tV\subseteq V$
and let
![]() $(i,j)$
be a pair of labels of T such that
$(i,j)$
be a pair of labels of T such that
![]() $i>j$
, i is in
$i>j$
, i is in
![]() $[\alpha ]$
, and j is in
$[\alpha ]$
, and j is in
![]() $[\Lambda ]/[\alpha ]$
(for example,
$[\Lambda ]/[\alpha ]$
(for example,
![]() $(i,j)$
is a free pair of
$(i,j)$
is a free pair of
![]() $\alpha $
). Suppose that for all labels
$\alpha $
). Suppose that for all labels
![]() $r<i$
of T in
$r<i$
of T in
![]() $[\alpha ]$
, we have
$[\alpha ]$
, we have
![]() $f_{r}\in V$
. Then for any
$f_{r}\in V$
. Then for any
![]() $m>0$
, if
$m>0$
, if
![]() $N^mf_i = f_{i'}$
and
$N^mf_i = f_{i'}$
and
![]() $N^mf_j = f_{j'}$
, then the
$N^mf_j = f_{j'}$
, then the
![]() $\beta _{i,j}$
and
$\beta _{i,j}$
and
![]() $\beta _{i',j'}$
coordinates of V are equal.
$\beta _{i',j'}$
coordinates of V are equal.
Proof. Letting
![]() $v_q$
be the vectors for the standard coordinate representation of V and letting
$v_q$
be the vectors for the standard coordinate representation of V and letting
![]() $a_\ell = \beta _{i,\ell }$
and
$a_\ell = \beta _{i,\ell }$
and
![]() $b_{\ell '} = \beta _{i',\ell '}$
for notational convenience, we have
$b_{\ell '} = \beta _{i',\ell '}$
for notational convenience, we have
 $$ \begin{align*} v_{w^{-1}(i)} &= f_i + a_j f_{j} + \sum_{j\neq \ell<i} a_\ell f_\ell,\\ v_{w^{-1}(i')} &= f_{i'} + b_{j'} f_{j'} + \sum_{j'\neq \ell'<i'} b_{\ell'} f_{\ell'},\\ (N^t)^m v_{w^{-1}(i')} &= f_i + b_{j'} f_j + \sum_{j'\neq \ell' < i'} b_{\ell'} ((N^t)^m f_{\ell'}). \end{align*} $$
$$ \begin{align*} v_{w^{-1}(i)} &= f_i + a_j f_{j} + \sum_{j\neq \ell<i} a_\ell f_\ell,\\ v_{w^{-1}(i')} &= f_{i'} + b_{j'} f_{j'} + \sum_{j'\neq \ell'<i'} b_{\ell'} f_{\ell'},\\ (N^t)^m v_{w^{-1}(i')} &= f_i + b_{j'} f_j + \sum_{j'\neq \ell' < i'} b_{\ell'} ((N^t)^m f_{\ell'}). \end{align*} $$
Since all of the above vectors are in V, then
 $$ \begin{align} v_{w^{-1}(i)} - (N^t)^m v_{w^{-1}(i')} = (a_j-b_{j'}) f_j + \sum_{j\neq \ell<i} a_\ell f_\ell - \sum_{j'\neq \ell' < i'} b_{\ell'} ((N^t)^m f_{\ell'})\in V. \end{align} $$
$$ \begin{align} v_{w^{-1}(i)} - (N^t)^m v_{w^{-1}(i')} = (a_j-b_{j'}) f_j + \sum_{j\neq \ell<i} a_\ell f_\ell - \sum_{j'\neq \ell' < i'} b_{\ell'} ((N^t)^m f_{\ell'})\in V. \end{align} $$
Observe that the
![]() $f_j$
coefficient of this vector is exactly
$f_j$
coefficient of this vector is exactly
![]() $a_j-b_{j'}$
, since the two sums contain no
$a_j-b_{j'}$
, since the two sums contain no
![]() $f_j$
terms.
$f_j$
terms.
Suppose by way of contradiction that
![]() $a_j\neq b_{j'}$
. Then the vector (4.11) is nonzero, and since it is in V, its leading term must be a scalar multiple of
$a_j\neq b_{j'}$
. Then the vector (4.11) is nonzero, and since it is in V, its leading term must be a scalar multiple of
![]() $f_p$
for some p a label in
$f_p$
for some p a label in
![]() $[\alpha ]$
. Since
$[\alpha ]$
. Since
![]() $a_\ell = \beta _{i,\ell } = 0$
for all
$a_\ell = \beta _{i,\ell } = 0$
for all
![]() $\ell \in \{w(1),w(2),\dots , i\}$
, then no nonzero terms in the first sum correspond to
$\ell \in \{w(1),w(2),\dots , i\}$
, then no nonzero terms in the first sum correspond to
![]() $\ell $
a label in
$\ell $
a label in
![]() $[\alpha ]$
. Therefore, the leading term must be
$[\alpha ]$
. Therefore, the leading term must be
![]() $b_{\ell '}((N^t)^mf_{\ell '})$
for some
$b_{\ell '}((N^t)^mf_{\ell '})$
for some
![]() $\ell '$
in the second sum. Let
$\ell '$
in the second sum. Let
![]() $\ell $
be such that
$\ell $
be such that
![]() $(N^t)^mf_{\ell '} = f_\ell $
, and note that
$(N^t)^mf_{\ell '} = f_\ell $
, and note that
![]() $\ell>j$
since it is the leading term. However, since
$\ell>j$
since it is the leading term. However, since
![]() $\ell '<i'$
by assumption, then
$\ell '<i'$
by assumption, then
![]() $\ell <i$
(a property of reverse reading order). Since we necessarily have that
$\ell <i$
(a property of reverse reading order). Since we necessarily have that
![]() $\ell $
is a label in
$\ell $
is a label in
![]() $[\alpha ]$
, then by the hypothesis in the statement of the lemma, we have
$[\alpha ]$
, then by the hypothesis in the statement of the lemma, we have
![]() $f_\ell \in V$
. Therefore, we can eliminate the
$f_\ell \in V$
. Therefore, we can eliminate the
![]() $b_{\ell '}f_\ell = b_{\ell '}((N^t)^mf_{\ell '})$
term from (4.11). After repeating this process of eliminating terms from (4.11), we get a nonzero vector in V whose leading term does not correspond to a label in
$b_{\ell '}f_\ell = b_{\ell '}((N^t)^mf_{\ell '})$
term from (4.11). After repeating this process of eliminating terms from (4.11), we get a nonzero vector in V whose leading term does not correspond to a label in
![]() $[\alpha ]$
, a contradiction. Therefore, we must have
$[\alpha ]$
, a contradiction. Therefore, we must have
![]() $a_j=b_{j'}$
, which completes the proof.
$a_j=b_{j'}$
, which completes the proof.
Lemma 4.17. Let
![]() $(i_1,j_1),(i_2,j_2),\dots , (i_\ell ,j_\ell )$
be the free pairs for
$(i_1,j_1),(i_2,j_2),\dots , (i_\ell ,j_\ell )$
be the free pairs for
![]() $\alpha $
, listed so that
$\alpha $
, listed so that
![]() $i_1\geq i_2\geq \cdots \geq i_\ell $
. Then the map
$i_1\geq i_2\geq \cdots \geq i_\ell $
. Then the map
defined by sending
![]() $(\vec {t},V_{\bullet })$
to
$(\vec {t},V_{\bullet })$
to
![]() $U_{i_\ell ,j_\ell }(t_\ell )\cdots U_{i_2,j_2}(t_2) U_{i_1,j_1}(t_1)V_{\bullet }$
is an isomorphism.
$U_{i_\ell ,j_\ell }(t_\ell )\cdots U_{i_2,j_2}(t_2) U_{i_1,j_1}(t_1)V_{\bullet }$
is an isomorphism.
Proof. First, observe that the map is well defined by Lemma 4.13. Second, by Lemma 4.15, the
![]() $\beta _{i_m,j_m}$
coordinate of
$\beta _{i_m,j_m}$
coordinate of
![]() $U_{i_\ell ,j_\ell }(t_\ell )\cdots U_{i_2,j_2}(t_2) U_{i_1,j_1}(t_1)V_{\bullet }$
is
$U_{i_\ell ,j_\ell }(t_\ell )\cdots U_{i_2,j_2}(t_2) U_{i_1,j_1}(t_1)V_{\bullet }$
is
![]() $t_m$
for each m. Therefore, any two pairs that map to the same partial flag must have the same
$t_m$
for each m. Therefore, any two pairs that map to the same partial flag must have the same
![]() $\vec {t}$
vector, and since the operators
$\vec {t}$
vector, and since the operators
![]() $U_{i,j}(t)$
are invertible, the map is injective.
$U_{i,j}(t)$
are invertible, the map is injective.
Finally, we show that the map is surjective. Let
![]() $V_{\bullet }\in \widehat {Z}^{\mu }_\alpha $
and let
$V_{\bullet }\in \widehat {Z}^{\mu }_\alpha $
and let
![]() $t_m = \beta _{i_m,j_m}$
be the standard coordinate of
$t_m = \beta _{i_m,j_m}$
be the standard coordinate of
![]() $V_n$
. We claim that
$V_n$
. We claim that
![]() $U_{i_1,j_1}^{-1}(t_1) U_{i_2,j_2}^{-1}(t_2)\cdots U_{i_\ell ,j_\ell }^{-1}(t_\ell )V_{\bullet } \in Z^{\mu }_\alpha $
. Observe that
$U_{i_1,j_1}^{-1}(t_1) U_{i_2,j_2}^{-1}(t_2)\cdots U_{i_\ell ,j_\ell }^{-1}(t_\ell )V_{\bullet } \in Z^{\mu }_\alpha $
. Observe that
![]() $U_{i,j}^{-1}(t) = U_{i,j}(-t)$
. Thus, it is clear that this flag is in
$U_{i,j}^{-1}(t) = U_{i,j}(-t)$
. Thus, it is clear that this flag is in
![]() $\widehat {Z}^{\mu }_\alpha $
, so it suffices to prove that
$\widehat {Z}^{\mu }_\alpha $
, so it suffices to prove that
This follows from the next claim.
Claim: Letting
![]() $\beta _{*,*}$
be the standard coordinates of
$\beta _{*,*}$
be the standard coordinates of
![]() $U_{i_p,j_p}(-t_p)\cdots U_{i_\ell ,j_\ell }(-t_\ell )V_n$
, for all
$U_{i_p,j_p}(-t_p)\cdots U_{i_\ell ,j_\ell }(-t_\ell )V_n$
, for all
![]() $1\leq p\leq q\leq \ell $
, we have
$1\leq p\leq q\leq \ell $
, we have
![]() $\beta _{i_q,j_q}=0$
, and for all pairs
$\beta _{i_q,j_q}=0$
, and for all pairs
![]() $(i_q,j)$
with
$(i_q,j)$
with
![]() $j<i_q$
that are not free pairs, we have
$j<i_q$
that are not free pairs, we have
![]() $\beta _{i_q,j}=0$
.
$\beta _{i_q,j}=0$
.
We prove the claim by reverse induction on p. In the base case when
![]() $p=q=\ell $
, then for all
$p=q=\ell $
, then for all
![]() $r<i_\ell $
such that r is a label of T in
$r<i_\ell $
such that r is a label of T in
![]() $[\alpha ]$
, then
$[\alpha ]$
, then
![]() $f_r\in V_n$
, so we have
$f_r\in V_n$
, so we have
![]() $U_{i_\ell ,j_\ell }(-t_\ell ) V_n = \widehat {U}_{i_\ell ,j_\ell }(-t_\ell )V_n$
. Since the standard coordinates of
$U_{i_\ell ,j_\ell }(-t_\ell ) V_n = \widehat {U}_{i_\ell ,j_\ell }(-t_\ell )V_n$
. Since the standard coordinates of
![]() $\widehat {U}_{i_\ell ,j_\ell }(-t_\ell )V_n$
are obtained by applying
$\widehat {U}_{i_\ell ,j_\ell }(-t_\ell )V_n$
are obtained by applying
![]() $\widehat {U}_{i_\ell ,j_\ell }(-t_\ell )$
to the standard coordinate representation of
$\widehat {U}_{i_\ell ,j_\ell }(-t_\ell )$
to the standard coordinate representation of
![]() $V_n$
, then
$V_n$
, then
![]() $\widehat {U}_{i_\ell ,j_\ell }(-t_\ell )$
eliminates the
$\widehat {U}_{i_\ell ,j_\ell }(-t_\ell )$
eliminates the
![]() $\beta _{i_\ell ,j_\ell }$
coordinate by construction, so the first part of the claim holds in the base case.
$\beta _{i_\ell ,j_\ell }$
coordinate by construction, so the first part of the claim holds in the base case.
Let
![]() $(i_\ell ,j)$
be a pair with
$(i_\ell ,j)$
be a pair with
![]() $j < i_\ell $
that is not a free pair. If j is a label in
$j < i_\ell $
that is not a free pair. If j is a label in
![]() $[\alpha ]$
, then
$[\alpha ]$
, then
![]() $\beta _{i_\ell ,j} = 0$
by definition, so assume j is a label of T in
$\beta _{i_\ell ,j} = 0$
by definition, so assume j is a label of T in
![]() $[\Lambda ]/[\alpha ]$
. Let
$[\Lambda ]/[\alpha ]$
. Let
![]() $i'$
be the label in the cell immediately to the left of
$i'$
be the label in the cell immediately to the left of
![]() $i_\ell $
and let
$i_\ell $
and let
![]() $j'$
be the label of the cell immediately to the left of j (both of which must exist since
$j'$
be the label of the cell immediately to the left of j (both of which must exist since
![]() $(i_\ell ,j)$
is not a free pair. Notice that if
$(i_\ell ,j)$
is not a free pair. Notice that if
![]() $i_\ell $
were in the first column, then j would also have to be in the first column). Since, as we mentioned above,
$i_\ell $
were in the first column, then j would also have to be in the first column). Since, as we mentioned above,
![]() $f_r \in V_n$
for all
$f_r \in V_n$
for all
![]() $r < i_\ell $
such that r is in
$r < i_\ell $
such that r is in
![]() $[\alpha ]$
, then
$[\alpha ]$
, then
![]() $f_r\in \widehat {U}_{i_\ell ,j_\ell }(-t_\ell )V_n = U_{i_\ell ,j_\ell }(-t_\ell )V_n$
for
$f_r\in \widehat {U}_{i_\ell ,j_\ell }(-t_\ell )V_n = U_{i_\ell ,j_\ell }(-t_\ell )V_n$
for
![]() $r< i'$
. By Lemma 4.16, we have
$r< i'$
. By Lemma 4.16, we have
![]() $\beta _{i_\ell ,j} = \beta _{i',j'}$
. Furthermore, by the minimality of
$\beta _{i_\ell ,j} = \beta _{i',j'}$
. Furthermore, by the minimality of
![]() $i_\ell $
, we have that
$i_\ell $
, we have that
![]() $i'$
is in
$i'$
is in
![]() $[\lambda ]$
(otherwise,
$[\lambda ]$
(otherwise,
![]() $(i',j')$
would be a free pair, contradicting the minimality of
$(i',j')$
would be a free pair, contradicting the minimality of
![]() $i_\ell $
). Thus,
$i_\ell $
). Thus,
![]() $\beta _{i',j'}=0$
and so also
$\beta _{i',j'}=0$
and so also
![]() $\beta _{i_\ell ,j} = 0$
, which completes the base case.
$\beta _{i_\ell ,j} = 0$
, which completes the base case.
In the inductive step, suppose the statement of the claim holds for p. Then by the inductive hypothesis, for all
![]() $r<i_{p-1}$
such that r is a label of T in
$r<i_{p-1}$
such that r is a label of T in
![]() $[\alpha ]$
(note, this may exclude
$[\alpha ]$
(note, this may exclude
![]() $i_p$
if
$i_p$
if
![]() $i_p=i_{p-1}$
), then all
$i_p=i_{p-1}$
), then all
![]() $\beta _{r,j}$
coordinates of
$\beta _{r,j}$
coordinates of
![]() $U_{i_p,j_p}(-t_p)\cdots U_{i_\ell ,j_\ell }(-t_\ell )V_n$
are
$U_{i_p,j_p}(-t_p)\cdots U_{i_\ell ,j_\ell }(-t_\ell )V_n$
are
![]() $0$
, so
$0$
, so
![]() $f_r \in U_{i_p,j_p}(-t_p)\cdots U_{i_\ell ,j_\ell }(-t_\ell )V_n$
. Therefore,
$f_r \in U_{i_p,j_p}(-t_p)\cdots U_{i_\ell ,j_\ell }(-t_\ell )V_n$
. Therefore,
 $$ \begin{align*} U_{i_{p-1},j_{p-1}}(-t_{p-1})U_{i_p,j_p}(-t_p) \cdots U_{i_\ell,j_\ell}(-t_\ell) &V_n \\ &= \widehat{U}_{i_{p-1},j_{p-1}}(-t_{p-1})U_{i_p,j_p}(-t_p) \cdots U_{i_\ell,j_\ell}(-t_\ell)V_n. \end{align*} $$
$$ \begin{align*} U_{i_{p-1},j_{p-1}}(-t_{p-1})U_{i_p,j_p}(-t_p) \cdots U_{i_\ell,j_\ell}(-t_\ell) &V_n \\ &= \widehat{U}_{i_{p-1},j_{p-1}}(-t_{p-1})U_{i_p,j_p}(-t_p) \cdots U_{i_\ell,j_\ell}(-t_\ell)V_n. \end{align*} $$
By construction,
![]() $\widehat {U}_{i_{p-1},j_{p-1}}(-t_{p-1})$
eliminates the
$\widehat {U}_{i_{p-1},j_{p-1}}(-t_{p-1})$
eliminates the
![]() $\beta _{i_{p-1},j_{p-1}}$
coordinate and does not change the coordinates guaranteed to be
$\beta _{i_{p-1},j_{p-1}}$
coordinate and does not change the coordinates guaranteed to be
![]() $0$
in the inductive hypothesis. Given a pair
$0$
in the inductive hypothesis. Given a pair
![]() $(i_{p-1},j)$
such that j is a label of T not in
$(i_{p-1},j)$
such that j is a label of T not in
![]() $[\alpha ]$
, then there exist m and
$[\alpha ]$
, then there exist m and
![]() $q>p-1$
such that
$q>p-1$
such that
![]() $(N^t)^mf_{i_{p-1}} = f_{i_q}$
and
$(N^t)^mf_{i_{p-1}} = f_{i_q}$
and
![]() $(N^t)^m f_{j_{p-1}} = f_{j_q}$
. Note this implies
$(N^t)^m f_{j_{p-1}} = f_{j_q}$
. Note this implies
![]() $N^m f_{i_q} = f_{i_{p-1}}$
and
$N^m f_{i_q} = f_{i_{p-1}}$
and
![]() $N^m f_{j_q} = f_{j_{p-1}}$
. Since
$N^m f_{j_q} = f_{j_{p-1}}$
. Since
for all
![]() $r\leq i_q$
such that r is a label in
$r\leq i_q$
such that r is a label in
![]() $[\alpha ]$
, then by Lemma 4.16, the
$[\alpha ]$
, then by Lemma 4.16, the
![]() $\beta _{i_q,j_q}$
and
$\beta _{i_q,j_q}$
and
![]() $\beta _{i_{p-1},j}$
coordinates of this subspace are equal and thus are both
$\beta _{i_{p-1},j}$
coordinates of this subspace are equal and thus are both
![]() $0$
. This completes the induction and the proof of the claim.
$0$
. This completes the induction and the proof of the claim.
By the claim, we have for
![]() $p=1$
that
$p=1$
that
![]() $U_{i_1,j_1}(-t_1)U_{i_2,j_2}(-t_2)\cdots U_{i_\ell ,j_\ell }(-t_\ell )V_{\bullet }\in Z^{\mu }_\alpha $
, so the map in the statement of the lemma is surjective. In the case when
$U_{i_1,j_1}(-t_1)U_{i_2,j_2}(-t_2)\cdots U_{i_\ell ,j_\ell }(-t_\ell )V_{\bullet }\in Z^{\mu }_\alpha $
, so the map in the statement of the lemma is surjective. In the case when
![]() $\mathbb {F} = \mathbb {C}$
, since the inverse is a regular map, it is an isomorphism of varieties.
$\mathbb {F} = \mathbb {C}$
, since the inverse is a regular map, it is an isomorphism of varieties.
5. Proof of Theorem 1.3
In this section, we use the results from Sections 3 and 4 to prove the main theorem, Theorem 1.3. Throughout this section, we utilize the notation ![]() for
for
![]() $\nu \in \mathrm {Par}(n,s)$
. Recall our convention that we consider
$\nu \in \mathrm {Par}(n,s)$
. Recall our convention that we consider
![]() $H^{2k}(Y_{n,\lambda ,s};\mathbb {Q})$
to be the degree k component of the cohomology ring.
$H^{2k}(Y_{n,\lambda ,s};\mathbb {Q})$
to be the degree k component of the cohomology ring.
Lemma 5.1. Let
![]() $\nu \in \mathrm {Par}(n,s)$
such that
$\nu \in \mathrm {Par}(n,s)$
such that
![]() $\lambda \subseteq \nu $
. Then
$\lambda \subseteq \nu $
. Then
 $$ \begin{align} \sum_{\substack{\alpha\in \mathrm{Comp}(n,s),\\ \mathrm{sort}(\alpha)=\nu, \\ \alpha\supseteq \lambda}} q^{\operatorname{\mathrm{coinv}}(\alpha)} = \prod_{i\geq 0} \genfrac{[}{]}{0pt}{}{\nu_i^{\prime} - \lambda_{i+1}^{\prime}}{\nu_i^{\prime} - \nu_{i+1}^{\prime}}_q. \end{align} $$
$$ \begin{align} \sum_{\substack{\alpha\in \mathrm{Comp}(n,s),\\ \mathrm{sort}(\alpha)=\nu, \\ \alpha\supseteq \lambda}} q^{\operatorname{\mathrm{coinv}}(\alpha)} = \prod_{i\geq 0} \genfrac{[}{]}{0pt}{}{\nu_i^{\prime} - \lambda_{i+1}^{\prime}}{\nu_i^{\prime} - \nu_{i+1}^{\prime}}_q. \end{align} $$
Proof. We proceed by induction on
![]() $m=\nu _1$
. In the base case
$m=\nu _1$
. In the base case
![]() $m=\nu _1=1$
, then
$m=\nu _1=1$
, then
![]() $\lambda = (1^k)$
and
$\lambda = (1^k)$
and
![]() $\nu = (1^n)$
. In this case, each
$\nu = (1^n)$
. In this case, each
![]() $\alpha $
in the summation has parts
$\alpha $
in the summation has parts
![]() $0$
and
$0$
and
![]() $1$
such that
$1$
such that
![]() $\alpha _1=\cdots =\alpha _k = 1$
. Deleting the first k parts from
$\alpha _1=\cdots =\alpha _k = 1$
. Deleting the first k parts from
![]() $\alpha $
, we get a weak composition consisting of
$\alpha $
, we get a weak composition consisting of
![]() $0$
s and
$0$
s and
![]() $1$
s of size
$1$
s of size
![]() $n-k$
and length
$n-k$
and length
![]() $s-k$
(and the same number of coinversions as
$s-k$
(and the same number of coinversions as
![]() $\alpha $
). Thus, the left-hand side of (5.1) can be rewritten as
$\alpha $
). Thus, the left-hand side of (5.1) can be rewritten as
 $$\begin{align*}\sum_{\alpha \in \mathrm{Comp}(n-k,s-k)} q^{\operatorname{\mathrm{coinv}}(\alpha)}=\genfrac{[}{]}{0pt}{}{s-k}{n-k}_q = \genfrac{[}{]}{0pt}{}{s-k}{s-n}_q = \genfrac{[}{]}{0pt}{}{\nu_0^{\prime}-\lambda_1^{\prime}}{\nu_0^{\prime}-\nu_1^{\prime}}_q, \end{align*}$$
$$\begin{align*}\sum_{\alpha \in \mathrm{Comp}(n-k,s-k)} q^{\operatorname{\mathrm{coinv}}(\alpha)}=\genfrac{[}{]}{0pt}{}{s-k}{n-k}_q = \genfrac{[}{]}{0pt}{}{s-k}{s-n}_q = \genfrac{[}{]}{0pt}{}{\nu_0^{\prime}-\lambda_1^{\prime}}{\nu_0^{\prime}-\nu_1^{\prime}}_q, \end{align*}$$
which equals the right-hand side, so the base case holds.
Let
![]() $m>1$
and assume by way of induction that the identity holds for all
$m>1$
and assume by way of induction that the identity holds for all
![]() $\nu $
with
$\nu $
with
![]() $\nu _1=m-1$
, and let
$\nu _1=m-1$
, and let
![]() $\nu \in \mathrm {Par}(n,s)$
such that
$\nu \in \mathrm {Par}(n,s)$
such that
![]() $\lambda \subseteq \nu $
. Define
$\lambda \subseteq \nu $
. Define
![]() $\overline {\nu }$
and
$\overline {\nu }$
and
![]() $\overline {\lambda }$
by removing all cells in column m of the Young diagrams of
$\overline {\lambda }$
by removing all cells in column m of the Young diagrams of
![]() $\nu $
and
$\nu $
and
![]() $\lambda $
, respectively. Then
$\lambda $
, respectively. Then
![]() $\alpha \in \mathrm {Comp}(n,s)$
such that
$\alpha \in \mathrm {Comp}(n,s)$
such that
![]() $\lambda \subseteq \alpha $
and
$\lambda \subseteq \alpha $
and
![]() $\mathrm {sort}(\alpha ) = \nu $
is obtained uniquely by the following process:
$\mathrm {sort}(\alpha ) = \nu $
is obtained uniquely by the following process:
-
○ Start with
 $\overline {\alpha } \in \mathrm {Comp}(n-\nu _m^{\prime },s)$
such that
$\overline {\alpha } \in \mathrm {Comp}(n-\nu _m^{\prime },s)$
such that
 $\overline {\lambda }\subseteq \overline {\alpha }$
and
$\overline {\lambda }\subseteq \overline {\alpha }$
and
 $\mathrm {sort}(\overline {\alpha }) = \overline {\nu }$
,
$\mathrm {sort}(\overline {\alpha }) = \overline {\nu }$
, -
○ Append one cell to the first
 $\lambda _m^{\prime }$
rows of
$\lambda _m^{\prime }$
rows of
 $[\overline {\alpha }]$
,
$[\overline {\alpha }]$
, -
○ Append one cell to
 $(\nu _m^{\prime }-\lambda _m^{\prime })$
many of the remaining rows of
$(\nu _m^{\prime }-\lambda _m^{\prime })$
many of the remaining rows of
 $[\overline {\alpha }]$
that have length
$[\overline {\alpha }]$
that have length
 $m-1$
.
$m-1$
.
There are
![]() $(\nu _{m-1}^{\prime }-\lambda _m^{\prime })$
many rows of
$(\nu _{m-1}^{\prime }-\lambda _m^{\prime })$
many rows of
![]() $[\overline {\alpha }]$
with length
$[\overline {\alpha }]$
with length
![]() $m-1$
(apart from the first
$m-1$
(apart from the first
![]() $\lambda _m^{\prime }$
rows). Furthermore, the difference
$\lambda _m^{\prime }$
rows). Furthermore, the difference
![]() $\operatorname {\mathrm {coinv}}(\alpha )-\operatorname {\mathrm {coinv}}(\overline {\alpha })$
is the number of pairs
$\operatorname {\mathrm {coinv}}(\alpha )-\operatorname {\mathrm {coinv}}(\overline {\alpha })$
is the number of pairs
![]() $i<j$
such that
$i<j$
such that
![]() $\alpha _i= m-1$
and
$\alpha _i= m-1$
and
![]() $\alpha _j=m$
. For a fixed
$\alpha _j=m$
. For a fixed
![]() $\overline {\alpha }$
, the total contribution to the left-hand side of (5.1) is thus
$\overline {\alpha }$
, the total contribution to the left-hand side of (5.1) is thus
 $$\begin{align*}q^{\operatorname{\mathrm{coinv}}(\overline{\alpha})} \genfrac{[}{]}{0pt}{}{\nu_{m-1}^{\prime}-\lambda_m^{\prime}}{\nu_m^{\prime}-\lambda_m^{\prime}}_q = q^{\operatorname{\mathrm{coinv}}(\overline{\alpha})} \genfrac{[}{]}{0pt}{}{\nu_{m-1}^{\prime}-\lambda_m^{\prime}}{\nu_{m-1}^{\prime}-\nu_m^{\prime}}_q, \end{align*}$$
$$\begin{align*}q^{\operatorname{\mathrm{coinv}}(\overline{\alpha})} \genfrac{[}{]}{0pt}{}{\nu_{m-1}^{\prime}-\lambda_m^{\prime}}{\nu_m^{\prime}-\lambda_m^{\prime}}_q = q^{\operatorname{\mathrm{coinv}}(\overline{\alpha})} \genfrac{[}{]}{0pt}{}{\nu_{m-1}^{\prime}-\lambda_m^{\prime}}{\nu_{m-1}^{\prime}-\nu_m^{\prime}}_q, \end{align*}$$
which is
![]() $q^{\operatorname {\mathrm {coinv}}(\overline {\alpha })}$
times the
$q^{\operatorname {\mathrm {coinv}}(\overline {\alpha })}$
times the
![]() $i=m-1$
factor on the right-hand side of (5.1). An application of the inductive hypothesis then completes the proof.
$i=m-1$
factor on the right-hand side of (5.1). An application of the inductive hypothesis then completes the proof.
Theorem 5.2. We have
 $$ \begin{align} \mathrm{Frob}(H^{*}(Y_{n,\lambda,s};\mathbb{Q});q) = \sum_{\substack{\nu\in \mathrm{Par}(n,s),\\ \nu\supseteq \lambda}} q^{\sum_i (s-\nu_i^{\prime})(\nu_{i+1}^{\prime}-\lambda_{i+1}^{\prime})}\prod_{i\geq 0} \genfrac{[}{]}{0pt}{}{\nu_i^{\prime}-\lambda_{i+1}^{\prime}}{\nu_i^{\prime}-\nu_{i+1}^{\prime}}_q \widetilde{H}_\nu(\mathbf{x};q). \end{align} $$
$$ \begin{align} \mathrm{Frob}(H^{*}(Y_{n,\lambda,s};\mathbb{Q});q) = \sum_{\substack{\nu\in \mathrm{Par}(n,s),\\ \nu\supseteq \lambda}} q^{\sum_i (s-\nu_i^{\prime})(\nu_{i+1}^{\prime}-\lambda_{i+1}^{\prime})}\prod_{i\geq 0} \genfrac{[}{]}{0pt}{}{\nu_i^{\prime}-\lambda_{i+1}^{\prime}}{\nu_i^{\prime}-\nu_{i+1}^{\prime}}_q \widetilde{H}_\nu(\mathbf{x};q). \end{align} $$
Proof. Combining (1.1), Theorem 3.8, Theorem 4.2 and Lemma 5.1, we have for all prime powers q the following string of identities.
 $$ \begin{align} &= \sum_{\mu\vdash n} \sum_{\substack{\alpha\in \mathrm{Comp}(n,s),\\ \alpha\supseteq \lambda}} |\widehat{Z}^{\mu}_\alpha (\mathbb{F}_q)| m_{\mu}(\mathbf{x}) \end{align} $$
$$ \begin{align} &= \sum_{\mu\vdash n} \sum_{\substack{\alpha\in \mathrm{Comp}(n,s),\\ \alpha\supseteq \lambda}} |\widehat{Z}^{\mu}_\alpha (\mathbb{F}_q)| m_{\mu}(\mathbf{x}) \end{align} $$
 $$ \begin{align} &= \sum_{\mu\vdash n} \sum_{\substack{\alpha\in \mathrm{Comp}(n,s),\\ \alpha\supseteq \lambda}} q^{\sum_i (s-\alpha_i^{\prime})(\alpha_{i+1}^{\prime} - \lambda_{i+1}^{\prime}) + \operatorname{\mathrm{coinv}}(\alpha)} |Z^{\mu}_\alpha(\mathbb{F}_q)| m_{\mu}(\mathbf{x}) \end{align} $$
$$ \begin{align} &= \sum_{\mu\vdash n} \sum_{\substack{\alpha\in \mathrm{Comp}(n,s),\\ \alpha\supseteq \lambda}} q^{\sum_i (s-\alpha_i^{\prime})(\alpha_{i+1}^{\prime} - \lambda_{i+1}^{\prime}) + \operatorname{\mathrm{coinv}}(\alpha)} |Z^{\mu}_\alpha(\mathbb{F}_q)| m_{\mu}(\mathbf{x}) \end{align} $$
 $$ \begin{align} &= \sum_{\substack{\alpha\in \mathrm{Comp}(n,s),\\ \alpha\supseteq \lambda}} q^{\sum_i (s-\alpha_i^{\prime})(\alpha_{i+1}^{\prime} - \lambda_{i+1}^{\prime}) + \operatorname{\mathrm{coinv}}(\alpha)} \left(\sum_{\mu\vdash n} |Z^{\mu}_\alpha (\mathbb{F}_q)| m_{\mu}(\mathbf{x})\right) \end{align} $$
$$ \begin{align} &= \sum_{\substack{\alpha\in \mathrm{Comp}(n,s),\\ \alpha\supseteq \lambda}} q^{\sum_i (s-\alpha_i^{\prime})(\alpha_{i+1}^{\prime} - \lambda_{i+1}^{\prime}) + \operatorname{\mathrm{coinv}}(\alpha)} \left(\sum_{\mu\vdash n} |Z^{\mu}_\alpha (\mathbb{F}_q)| m_{\mu}(\mathbf{x})\right) \end{align} $$
 $$ \begin{align} &= \sum_{\substack{\alpha\in \mathrm{Comp}(n,s),\\ \alpha\supseteq \lambda}} q^{\sum_i (s-\alpha_i^{\prime})(\alpha_{i+1}^{\prime} - \lambda_{i+1}^{\prime}) + \operatorname{\mathrm{coinv}}(\alpha)} \widetilde{H}_{\mathrm{sort}(\alpha)}(\mathbf{x};q) \end{align} $$
$$ \begin{align} &= \sum_{\substack{\alpha\in \mathrm{Comp}(n,s),\\ \alpha\supseteq \lambda}} q^{\sum_i (s-\alpha_i^{\prime})(\alpha_{i+1}^{\prime} - \lambda_{i+1}^{\prime}) + \operatorname{\mathrm{coinv}}(\alpha)} \widetilde{H}_{\mathrm{sort}(\alpha)}(\mathbf{x};q) \end{align} $$
 $$ \begin{align} &= \sum_{\substack{\nu\in \mathrm{Par}(n,s),\\ \nu\supseteq \lambda}} q^{\sum_i (s-\nu_i^{\prime})(\nu_{i+1}^{\prime} - \lambda_{i+1}^{\prime})} \sum_{\substack{\alpha\in \mathrm{Comp}(n,s),\\ \mathrm{sort}(\alpha) = \nu,\\ \alpha\supseteq \lambda}} q^{\operatorname{\mathrm{coinv}}(\alpha)} \widetilde{H}_{\nu}(\mathbf{x};q) \end{align} $$
$$ \begin{align} &= \sum_{\substack{\nu\in \mathrm{Par}(n,s),\\ \nu\supseteq \lambda}} q^{\sum_i (s-\nu_i^{\prime})(\nu_{i+1}^{\prime} - \lambda_{i+1}^{\prime})} \sum_{\substack{\alpha\in \mathrm{Comp}(n,s),\\ \mathrm{sort}(\alpha) = \nu,\\ \alpha\supseteq \lambda}} q^{\operatorname{\mathrm{coinv}}(\alpha)} \widetilde{H}_{\nu}(\mathbf{x};q) \end{align} $$
 $$ \begin{align} &= \sum_{\substack{\nu\in \mathrm{Par}(n,s),\\ \nu\supseteq \lambda}} q^{\sum_i (s-\nu_i^{\prime})(\nu_{i+1}^{\prime} - \lambda_{i+1}^{\prime})} \prod_{i\geq 0} \genfrac{[}{]}{0pt}{}{\nu_i^{\prime}-\lambda_{i+1}^{\prime}}{\nu_i^{\prime}-\nu_{i+1}^{\prime}}_q \widetilde{H}_{\nu}(\mathbf{x};q). \end{align} $$
$$ \begin{align} &= \sum_{\substack{\nu\in \mathrm{Par}(n,s),\\ \nu\supseteq \lambda}} q^{\sum_i (s-\nu_i^{\prime})(\nu_{i+1}^{\prime} - \lambda_{i+1}^{\prime})} \prod_{i\geq 0} \genfrac{[}{]}{0pt}{}{\nu_i^{\prime}-\lambda_{i+1}^{\prime}}{\nu_i^{\prime}-\nu_{i+1}^{\prime}}_q \widetilde{H}_{\nu}(\mathbf{x};q). \end{align} $$
In (5.9), we have used the fact that if
![]() $\mathrm {sort}(\alpha ) = \nu $
, then
$\mathrm {sort}(\alpha ) = \nu $
, then
![]() $\alpha _i^{\prime } = \nu _i^{\prime }$
for all i. Since the identities hold for infinitely many values of q, the final identity holds for q a formal parameter.
$\alpha _i^{\prime } = \nu _i^{\prime }$
for all i. Since the identities hold for infinitely many values of q, the final identity holds for q a formal parameter.
Corollary 5.3. We have
 $$ \begin{align} \mathrm{Frob}(H^{*}(Y_{n,\lambda,s};\mathbb{Q});q) = \mathrm{rev}_q\left[ \sum_{\substack{\nu\in \mathrm{Par}(n,s),\\ \nu\supseteq \lambda}} q^{n(\nu/\lambda)} \prod_{i\geq 0} \genfrac{[}{]}{0pt}{}{\nu_i^{\prime}-\lambda_{i+1}^{\prime}}{\nu_i^{\prime}-\nu_{i+1}^{\prime}}_q H_\nu(\mathbf{x};q)\right], \end{align} $$
$$ \begin{align} \mathrm{Frob}(H^{*}(Y_{n,\lambda,s};\mathbb{Q});q) = \mathrm{rev}_q\left[ \sum_{\substack{\nu\in \mathrm{Par}(n,s),\\ \nu\supseteq \lambda}} q^{n(\nu/\lambda)} \prod_{i\geq 0} \genfrac{[}{]}{0pt}{}{\nu_i^{\prime}-\lambda_{i+1}^{\prime}}{\nu_i^{\prime}-\nu_{i+1}^{\prime}}_q H_\nu(\mathbf{x};q)\right], \end{align} $$
where ![]() ,
, ![]() , and
, and ![]() .
.
Proof. By [Reference Griffin, Levinson and Woo10, Theorem 1.2], the degree of
![]() $\mathrm {Frob}(H^{*}(Y_{n,\lambda ,s};\mathbb {Q});q)$
is
$\mathrm {Frob}(H^{*}(Y_{n,\lambda ,s};\mathbb {Q});q)$
is
![]() $n(\lambda )+(s-1)(n-k)$
. By Theorem 5.2, it suffices to show that
$n(\lambda )+(s-1)(n-k)$
. By Theorem 5.2, it suffices to show that
![]() $\mathrm {rev}_q$
applied to the right-hand side of (5.2) is equal to the expression in the right-hand side of (5.11) inside of
$\mathrm {rev}_q$
applied to the right-hand side of (5.2) is equal to the expression in the right-hand side of (5.11) inside of
![]() $\mathrm {rev}_q$
. In other words, it suffices to prove that
$\mathrm {rev}_q$
. In other words, it suffices to prove that
 $$ \begin{align} q^{n(\lambda)+(s-1)(n-k)}\sum_{\substack{\nu\in \mathrm{Par}(n,s),\\ \nu\supseteq \lambda}} q^{-\sum_i (s-\nu_i^{\prime})(\nu_{i+1}^{\prime}-\lambda_{i+1}^{\prime})}\prod_{i\geq 0} \genfrac{[}{]}{0pt}{}{\nu_i^{\prime}-\lambda_{i+1}^{\prime}}{\nu_i^{\prime}-\nu_{i+1}^{\prime}}_{q^{-1}} \widetilde{H}_\nu(\mathbf{x};q^{-1}) = \end{align} $$
$$ \begin{align} q^{n(\lambda)+(s-1)(n-k)}\sum_{\substack{\nu\in \mathrm{Par}(n,s),\\ \nu\supseteq \lambda}} q^{-\sum_i (s-\nu_i^{\prime})(\nu_{i+1}^{\prime}-\lambda_{i+1}^{\prime})}\prod_{i\geq 0} \genfrac{[}{]}{0pt}{}{\nu_i^{\prime}-\lambda_{i+1}^{\prime}}{\nu_i^{\prime}-\nu_{i+1}^{\prime}}_{q^{-1}} \widetilde{H}_\nu(\mathbf{x};q^{-1}) = \end{align} $$
 $$ \begin{align} \sum_{\substack{\nu\in \mathrm{Par(n,s)},\\ \nu\supseteq \lambda}} q^{n(\nu/\lambda)} \prod_{i\geq 0} \genfrac{[}{]}{0pt}{}{\nu_i^{\prime}-\lambda_{i+1}^{\prime}}{\nu_i^{\prime}-\nu_{i+1}^{\prime}}_q H_\nu(\mathbf{x};q). \end{align} $$
$$ \begin{align} \sum_{\substack{\nu\in \mathrm{Par(n,s)},\\ \nu\supseteq \lambda}} q^{n(\nu/\lambda)} \prod_{i\geq 0} \genfrac{[}{]}{0pt}{}{\nu_i^{\prime}-\lambda_{i+1}^{\prime}}{\nu_i^{\prime}-\nu_{i+1}^{\prime}}_q H_\nu(\mathbf{x};q). \end{align} $$
Since
![]() $\widetilde {H}_\nu (\mathbf {x};q^{-1}) =q^{-n(\nu )}H_\nu (\mathbf {x};q)$
and
$\widetilde {H}_\nu (\mathbf {x};q^{-1}) =q^{-n(\nu )}H_\nu (\mathbf {x};q)$
and
![]() $\genfrac {[}{]}{0pt}{}{a}{b}_{q^{-1}} = q^{-b(a-b)}\genfrac {[}{]}{0pt}{}{a}{b}_q$
, we are reduced to proving that
$\genfrac {[}{]}{0pt}{}{a}{b}_{q^{-1}} = q^{-b(a-b)}\genfrac {[}{]}{0pt}{}{a}{b}_q$
, we are reduced to proving that
which follows by a straightforward calculation using the facts that
![]() $\sum _i \nu _i^{\prime } = n$
and
$\sum _i \nu _i^{\prime } = n$
and
![]() $\sum _i\lambda _i^{\prime } = k$
. Indeed, combining terms in the right-hand side of (5.14), we have
$\sum _i\lambda _i^{\prime } = k$
. Indeed, combining terms in the right-hand side of (5.14), we have
 $$ \begin{align*} &\frac{1}{2}\left(\sum_i \lambda_i^{\prime}(\lambda_i^{\prime}-1) - 2(s-1)(n-k) - \sum_i 2(s-\nu_{i+1}^{\prime})(\nu_{i+1}^{\prime}-\lambda_{i+1}^{\prime}) -\sum_i \nu_i^{\prime}(\nu_i^{\prime}-1)\right)\\ &= \frac{1}{2}\left(-2(s-1)(n-k) + \sum_i\left( 2s(\nu_{i+1}^{\prime}-\lambda_{i+1}^{\prime}) + \nu_i^{\prime} -\lambda_i^{\prime} + (\lambda_i^{\prime})^2 + (\nu_i^{\prime})^2 - 2\nu_{i+1}^{\prime}\lambda_{i+1}^{\prime}\right)\right)\\ &=\frac{1}{2} \left(-2(s-1)(n-k) + 2sn - 2sk + 2\sum_i(\nu_i^{\prime}-\lambda_i^{\prime}) + \sum_i ((\lambda_i^{\prime})^2 + (\nu_i^{\prime})^2 - 2\nu_i^{\prime}\lambda_i^{\prime} - \nu_i^{\prime} - \lambda_i^{\prime})\right)\\ &=\frac{1}{2} \left(0 + \sum_i (\nu_i^{\prime} - \lambda_i^{\prime})(\nu_i^{\prime} - \lambda_i^{\prime} - 1)\right) = n(\nu/\lambda). \end{align*} $$
$$ \begin{align*} &\frac{1}{2}\left(\sum_i \lambda_i^{\prime}(\lambda_i^{\prime}-1) - 2(s-1)(n-k) - \sum_i 2(s-\nu_{i+1}^{\prime})(\nu_{i+1}^{\prime}-\lambda_{i+1}^{\prime}) -\sum_i \nu_i^{\prime}(\nu_i^{\prime}-1)\right)\\ &= \frac{1}{2}\left(-2(s-1)(n-k) + \sum_i\left( 2s(\nu_{i+1}^{\prime}-\lambda_{i+1}^{\prime}) + \nu_i^{\prime} -\lambda_i^{\prime} + (\lambda_i^{\prime})^2 + (\nu_i^{\prime})^2 - 2\nu_{i+1}^{\prime}\lambda_{i+1}^{\prime}\right)\right)\\ &=\frac{1}{2} \left(-2(s-1)(n-k) + 2sn - 2sk + 2\sum_i(\nu_i^{\prime}-\lambda_i^{\prime}) + \sum_i ((\lambda_i^{\prime})^2 + (\nu_i^{\prime})^2 - 2\nu_i^{\prime}\lambda_i^{\prime} - \nu_i^{\prime} - \lambda_i^{\prime})\right)\\ &=\frac{1}{2} \left(0 + \sum_i (\nu_i^{\prime} - \lambda_i^{\prime})(\nu_i^{\prime} - \lambda_i^{\prime} - 1)\right) = n(\nu/\lambda). \end{align*} $$
The proof is thus complete.
6. Further directions
We list a few open problems and possible further connections with geometry and combinatorics:
-
○ Counting partial flags also has connections with the q-Burge correspondence by work of Karp and Thomas [Reference Karp and Thomas16]. Is there a generalization of the q-Burge correspondence that corresponds to counting pairs of points of the
 $\Delta $
-Springer varieties?
$\Delta $
-Springer varieties? -
○ The proof of Theorem 1.3 given in this article is geometric, relying on counting the points of the
 $\Delta $
-Springer variety over
$\Delta $
-Springer variety over
 $\mathbb {F}_q$
using different ways to partition the space. A more direct combinatorial proof should be possible starting from Theorem 1.1. Such a combinatorial proof would find a weight-preserving bijection that collects terms of this formula into sums that can be identified as monomial expansions of Hall-Littlewood symmetric functions.
$\mathbb {F}_q$
using different ways to partition the space. A more direct combinatorial proof should be possible starting from Theorem 1.1. Such a combinatorial proof would find a weight-preserving bijection that collects terms of this formula into sums that can be identified as monomial expansions of Hall-Littlewood symmetric functions. -
○ Formulas for Macdonald polynomials, which are two-parameter generalizations of Hall-Littlewood symmetric functions, have been obtained by Mellit [Reference Mellit18] as weighted sums over points of affine Springer fibers. It may be possible to define generalizations of
 $\Delta $
-Springer varieties in the setting of affine flag varieties. One can then ask whether weighted point counts over these varieties yield symmetric functions that can simultaneously be defined using Macdonald eigenoperators. In particular, since
$\Delta $
-Springer varieties in the setting of affine flag varieties. One can then ask whether weighted point counts over these varieties yield symmetric functions that can simultaneously be defined using Macdonald eigenoperators. In particular, since
 $\Delta ^{\prime }_{e_{k-1}}e_n|_{t=0}$
is, up to a minor twist, the graded Frobenius characteristic of the cohomology of
$\Delta ^{\prime }_{e_{k-1}}e_n|_{t=0}$
is, up to a minor twist, the graded Frobenius characteristic of the cohomology of
 $Y_{n,(1^k),k}$
, one might hope that extending the definition of
$Y_{n,(1^k),k}$
, one might hope that extending the definition of
 $Y_{n,(1^k),k}$
to the affine setting and taking a weighted point count can recover the full symmetric function
$Y_{n,(1^k),k}$
to the affine setting and taking a weighted point count can recover the full symmetric function
 $\Delta ^{\prime }_{e_{k-1}}e_n$
.
$\Delta ^{\prime }_{e_{k-1}}e_n$
.
Acknowledgements
The author would like to thank Jake Levinson and Alexander Woo for many helpful discussions and the anonymous referees for many helpful comments that improved the article and for pointing out an error in the proof of Lemma 4.12 in an earlier version of this article.
Competing interest
The authors have no competing interest to declare.