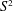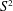Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Kim, Hee Jung
and
Ruberman, Daniel
2020.
Topological spines of 4–manifolds.
Algebraic & Geometric Topology,
Vol. 20,
Issue. 7,
p.
3589.
Hom, Jennifer
Levine, Adam Simon
and
Lidman, Tye
2022.
Knot concordance in homology cobordisms.
Duke Mathematical Journal,
Vol. 171,
Issue. 15,