Article contents
A REFINED WARING PROBLEM FOR FINITE SIMPLE GROUPS
Published online by Cambridge University Press: 17 March 2015
Abstract
Let 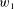 $w_{1}$ and
$w_{1}$ and 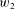 $w_{2}$ be nontrivial words in free groups
$w_{2}$ be nontrivial words in free groups 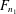 $F_{n_{1}}$ and
$F_{n_{1}}$ and 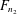 $F_{n_{2}}$, respectively. We prove that, for all sufficiently large finite nonabelian simple groups
$F_{n_{2}}$, respectively. We prove that, for all sufficiently large finite nonabelian simple groups 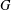 $G$, there exist subsets
$G$, there exist subsets 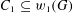 $C_{1}\subseteq w_{1}(G)$ and
$C_{1}\subseteq w_{1}(G)$ and 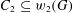 $C_{2}\subseteq w_{2}(G)$ such that
$C_{2}\subseteq w_{2}(G)$ such that 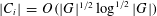 $|C_{i}|=O(|G|^{1/2}\log ^{1/2}|G|)$ and
$|C_{i}|=O(|G|^{1/2}\log ^{1/2}|G|)$ and 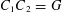 $C_{1}C_{2}=G$. In particular, if
$C_{1}C_{2}=G$. In particular, if  $w$ is any nontrivial word and
$w$ is any nontrivial word and 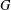 $G$ is a sufficiently large finite nonabelian simple group, then
$G$ is a sufficiently large finite nonabelian simple group, then 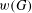 $w(G)$ contains a thin base of order
$w(G)$ contains a thin base of order 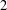 $2$. This is a nonabelian analog of a result of Van Vu [‘On a refinement of Waring’s problem’, Duke Math. J. 105(1) (2000), 107–134.] for the classical Waring problem. Further results concerning thin bases of
$2$. This is a nonabelian analog of a result of Van Vu [‘On a refinement of Waring’s problem’, Duke Math. J. 105(1) (2000), 107–134.] for the classical Waring problem. Further results concerning thin bases of 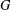 $G$ of order
$G$ of order 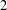 $2$ are established for any finite group and for any compact Lie group
$2$ are established for any finite group and for any compact Lie group 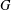 $G$.
$G$.
MSC classification
- Type
- Research Article
- Information
- Creative Commons
- This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/3.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
- Copyright
- © The Author(s) 2015
References
- 1
- Cited by


