Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-26T16:01:09.851Z Has data issue: false hasContentIssue false
  • English
  • Français

REDUCED POWERS OF SOUSLIN TREES

Part of: Graph theory Set theory

Published online by Cambridge University Press:  16 January 2017

ARI MEIR BRODSKY  and
ASSAF RINOT
ARI MEIR BRODSKY
Affiliation:
Department of Mathematics, Bar-Ilan University, Ramat-Gan 5290002, Israel; [email protected]
ASSAF RINOT
Affiliation:
Department of Mathematics, Bar-Ilan University, Ramat-Gan 5290002, Israel; [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study the relationship between a $\unicode[STIX]{x1D705}$-Souslin tree 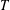$T$ and its reduced powers 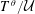$T^{\unicode[STIX]{x1D703}}/{\mathcal{U}}$.

Previous works addressed this problem from the viewpoint of a single power 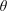$\unicode[STIX]{x1D703}$, whereas here, tools are developed for controlling different powers simultaneously. As a sample corollary, we obtain the consistency of an 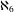$\aleph _{6}$-Souslin tree 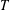$T$ and a sequence of uniform ultrafilters 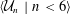$\langle {\mathcal{U}}_{n}\mid n<6\rangle$ such that 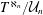$T^{\aleph _{n}}/{\mathcal{U}}_{n}$ is 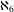$\aleph _{6}$-Aronszajn if and only if 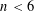$n<6$ is not a prime number.

This paper is the first application of the microscopic approach to Souslin-tree construction, recently introduced by the authors. A major component here is devising a method for constructing trees with a prescribed combination of freeness degree and ascent-path characteristics.

MSC classification

Primary: 03E05: Other combinatorial set theory
Secondary: 03E65: Other hypotheses and axioms 03E35: Consistency and independence results 05C05: Trees
Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 5 , 2017 , e2
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2017

References

Baumgartner, J., Malitz, J. and Reinhardt, W., ‘Embedding trees in the rationals’, Proc. Natl Acad. Sci. USA 67 (1970), 1748–1753.Google Scholar
Ben-David, S. and Shelah, S., ‘Souslin trees and successors of singular cardinals’, Ann. Pure Appl. Logic 30(3) (1986), 207–217.CrossRefGoogle Scholar
Brodsky, A. M. and Rinot, A., ‘A microscopic approach to Souslin-tree constructions. Part I’, Preprint, 2015, arXiv:1601.01821, http://www.assafrinot.com/paper/22.Google Scholar
Brodsky, A. M. and Rinot, A., ‘More notions of forcing add a Souslin tree’, Preprint, 2016, arXiv:1607.07033, http://www.assafrinot.com/paper/26.Google Scholar
Brodsky, A. M. and Rinot, A., ‘A microscopic approach to Souslin-tree constructions. Part II’, in preparation, 2017, http://www.assafrinot.com/paper/23.Google Scholar
Chang, C. C. and Keisler, H. J., Model Theory, 3rd edn, Studies in Logic and the Foundations of Mathematics, 73 (North-Holland Publishing Co., Amsterdam, 1990).Google Scholar
Cummings, J., ‘Souslin trees which are hard to specialise’, Proc. Amer. Math. Soc. 125(8) (1997), 2435–2441.Google Scholar
Cummings, J. and Magidor, M., ‘Martin’s maximum and weak square’, Proc. Amer. Math. Soc. 139(9) (2011), 3339–3348.Google Scholar
Devlin, K. J., ‘Morass-like constructions of ℵ 2 -trees in L ’, inSet Theory and Model Theory (Bonn, 1979), Lecture Notes in Mathematics, 872 (Springer, Berlin–New York, 1981), 1–36.Google Scholar
Devlin, K. J., ‘Reduced powers of ℵ 2 -trees’, Fund. Math. 118(2) (1983), 129–134.Google Scholar
Devlin, K. J. and Johnsbrȧten, H., The Souslin Problem, Lecture Notes in Mathematics, 405 (Springer, Berlin, 1974).Google Scholar
Fremlin, D. H., Consequences of Martin’s Axiom, Cambridge Tracts in Mathematics, 84 (Cambridge University Press, Cambridge, 1984).Google Scholar
Jensen, R. B., ‘The fine structure of the constructible hierarchy’, Ann. Math. Logic 4 229–308. erratum, ibid. 4 (1972), 443, 1972. With a section by Jack Silver.Google Scholar
Kanamori, A., ‘Large cardinals in set theory from their beginnings’, inThe Higher Infinite, 2nd edn, Springer Monographs in Mathematics (Springer, Berlin, 2003).Google Scholar
Kurepa, D., ‘Sur une propriété caractéristique du continu linéaire et le problème de Suslin’, Acad. Serbe Sci. Publ. Inst. Math. 4 (1952), 97–108.Google Scholar
Lambie-Hanson, C., ‘Aronszajn trees, square principles, and stationary reflection’, MLQ Math. Log. Q., to appear.Google Scholar
Laver, R. and Shelah, S., ‘The ℵ 2 -Souslin hypothesis’, Trans. Amer. Math. Soc. 264(2) (1981), 411–417.Google Scholar
Lücke, P., ‘Ascending paths and forcings that specialize higher Aronszajn trees’, Fund. Math. (2017), to appear.CrossRefGoogle Scholar
Rinot, A., ‘On guessing generalized clubs at the successors of regulars’, Ann. Pure Appl. Logic 162(7) (2011), 566–577.Google Scholar
Rinot, A., ‘Chromatic numbers of graphs—large gaps’, Combinatorica 35(2) (2015), 215–233.Google Scholar
Rinot, A., ‘Putting a diamond inside the square’, Bull. Lond. Math. Soc. 47(3) (2015), 436–442.Google Scholar
Rinot, A. and Schindler, R., ‘Square with built-in diamond-plus’, J. Symbolic Logic (2017), to appear, http://www.assafrinot.com/paper/21.Google Scholar
Shani, A., ‘Fresh subsets of ultrapowers’, Arch. Math. Logic 55(5) (2016), 835–845.CrossRefGoogle Scholar
Shelah, S., Proper Forcing, Lecture Notes in Mathematics, 940 (Springer, Berlin–New York, 1982).Google Scholar
Shelah, S. and Stanley, L., ‘Weakly compact cardinals and nonspecial Aronszajn trees’, Proc. Amer. Math. Soc. 104(3) (1988), 887–897.CrossRefGoogle Scholar
Todorčević, S., ‘Partitioning pairs of countable ordinals’, Acta Math. 159(3–4) (1987), 261–294.Google Scholar
Todorčević, S. and Torres Pérez, V., ‘Conjectures of Rado and Chang and special Aronszajn trees’, MLQ Math. Log. Q. 58(4–5) (2012), 342–347.CrossRefGoogle Scholar