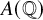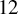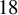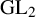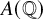1 Introduction
1.1 Motivation
Let E be an elliptic curve over
![]() ${\mathbb {Q}}$
. In [Reference MazurMaz77], Mazur famously showed that if a prime
${\mathbb {Q}}$
. In [Reference MazurMaz77], Mazur famously showed that if a prime
![]() $\ell $
divides the order of the torsion subgroup
$\ell $
divides the order of the torsion subgroup
![]() $E({\mathbb {Q}})_{ {\mathrm{tors}}}$
of
$E({\mathbb {Q}})_{ {\mathrm{tors}}}$
of
![]() $E({\mathbb {Q}})$
, then
$E({\mathbb {Q}})$
, then
![]() $\ell \leq 7$
. Combining with previous work of Kubert [Reference KubertKub76], Mazur deduced that
$\ell \leq 7$
. Combining with previous work of Kubert [Reference KubertKub76], Mazur deduced that
![]() $\#E({\mathbb {Q}})_{ {\mathrm{tors}}} \leq 16$
and that
$\#E({\mathbb {Q}})_{ {\mathrm{tors}}} \leq 16$
and that
![]() $E({\mathbb {Q}})_{\mathrm {tors}}$
is isomorphic to one of fifteen finite abelian groups, each of which gives rise to a genus
$E({\mathbb {Q}})_{\mathrm {tors}}$
is isomorphic to one of fifteen finite abelian groups, each of which gives rise to a genus
![]() $0$
modular curve with a well-known rational parametrization.
$0$
modular curve with a well-known rational parametrization.
It is not known whether there is a uniform bound on the size of the rational torsion subgroup of abelian varieties of fixed dimension
![]() $g\geq 2$
over a fixed number field. In fact, there is not even a single integer N for which it is known that there is no abelian surface over
$g\geq 2$
over a fixed number field. In fact, there is not even a single integer N for which it is known that there is no abelian surface over
![]() ${\mathbb {Q}}$
with a torsion point of order N. Indeed, determining rational points on Siegel modular threefolds with level structure seems out of reach in general.
${\mathbb {Q}}$
with a torsion point of order N. Indeed, determining rational points on Siegel modular threefolds with level structure seems out of reach in general.
1.2 Results
In this paper, we study the torsion subgroup of abelian surfaces A over
![]() ${\mathbb {Q}}$
whose geometric endomorphism ring is large. Namely, we suppose that the geometric endomorphism ring
${\mathbb {Q}}$
whose geometric endomorphism ring is large. Namely, we suppose that the geometric endomorphism ring
![]() $ {\mathrm{End}}(A_{\overline {{\mathbb {Q}}}})$
is a maximal order
$ {\mathrm{End}}(A_{\overline {{\mathbb {Q}}}})$
is a maximal order
![]() ${\mathcal {O}}$
in a division quaternion algebra over
${\mathcal {O}}$
in a division quaternion algebra over
![]() ${\mathbb {Q}}$
; we refer to these as
${\mathbb {Q}}$
; we refer to these as
![]() ${\mathcal {O}}$
-
${\mathcal {O}}$
-
![]() ${{\mathrm {PQM}}}$
surfaces (‘potential quaternionic multiplication’). Such abelian surfaces are geometrically simple, so their torsion subgroup cannot be studied using torsion subgroups of elliptic curves. However, they give rise to rational points on certain Shimura curves, much as elliptic curves over
${{\mathrm {PQM}}}$
surfaces (‘potential quaternionic multiplication’). Such abelian surfaces are geometrically simple, so their torsion subgroup cannot be studied using torsion subgroups of elliptic curves. However, they give rise to rational points on certain Shimura curves, much as elliptic curves over
![]() ${\mathbb {Q}}$
give rise to rational points on modular curves. Thus,
${\mathbb {Q}}$
give rise to rational points on modular curves. Thus,
![]() ${\mathcal {O}}$
-
${\mathcal {O}}$
-
![]() ${{\mathrm {PQM}}}$
surfaces are a natural place to explore torsion questions in higher dimension.
${{\mathrm {PQM}}}$
surfaces are a natural place to explore torsion questions in higher dimension.
Our main results show that the torsion behaviour of
![]() ${\mathcal {O}}$
-PQM surfaces is rather constrained.
${\mathcal {O}}$
-PQM surfaces is rather constrained.
Theorem 1.1. Let A be an
![]() ${\mathcal {O}}$
-
${\mathcal {O}}$
-
![]() ${\mathrm {PQM}}$
abelian surface over
${\mathrm {PQM}}$
abelian surface over
![]() ${\mathbb {Q}}$
with a rational point of order
${\mathbb {Q}}$
with a rational point of order
![]() $\ell $
, where
$\ell $
, where
![]() $\ell $
is a prime number. Then
$\ell $
is a prime number. Then
![]() $\ell =2$
or
$\ell =2$
or
![]() $\ell =3$
.
$\ell =3$
.
Theorem 1.2. Each
![]() ${\mathcal {O}}$
-
${\mathcal {O}}$
-
![]() ${\mathrm {PQM}}$
abelian surface A over
${\mathrm {PQM}}$
abelian surface A over
![]() ${\mathbb {Q}}$
has
${\mathbb {Q}}$
has
![]() $\#A({\mathbb {Q}})_{ {\mathrm{tors}}} \leq 18$
.
$\#A({\mathbb {Q}})_{ {\mathrm{tors}}} \leq 18$
.
The fact that the rational torsion on
![]() ${\mathcal {O}}$
-PQM surfaces is uniformly bounded is not new nor is it difficult to prove. Indeed, since
${\mathcal {O}}$
-PQM surfaces is uniformly bounded is not new nor is it difficult to prove. Indeed, since
![]() ${\mathcal {O}}$
-
${\mathcal {O}}$
-
![]() ${\mathrm {PQM}}$
surfaces have everywhere potentially good reduction (Lemma 4.1), local methods quickly show that
${\mathrm {PQM}}$
surfaces have everywhere potentially good reduction (Lemma 4.1), local methods quickly show that
![]() $\ell \mid \#A({\mathbb {Q}})_{ {\mathrm{tors}}}$
implies
$\ell \mid \#A({\mathbb {Q}})_{ {\mathrm{tors}}}$
implies
![]() $\ell \leq 19$
and that
$\ell \leq 19$
and that
![]() $\#A({\mathbb {Q}})_{ {\mathrm{tors}}} \leq 72$
[Reference Clark and XarlesCX08, Theorem 1.4]. The goal of this paper is instead to prove results which are as precise as possible.
$\#A({\mathbb {Q}})_{ {\mathrm{tors}}} \leq 72$
[Reference Clark and XarlesCX08, Theorem 1.4]. The goal of this paper is instead to prove results which are as precise as possible.
Theorems 1.1 and 1.2 are optimal since it is known that each of the seven groups
 $$ \begin{align} & \{1\}, \, {\mathbb{Z}}/2{\mathbb{Z}}, \, {\mathbb{Z}}/3{\mathbb{Z}}, \, ({\mathbb{Z}}/2{\mathbb{Z}})^2 \nonumber\\ & {\mathbb{Z}}/6{\mathbb{Z}}, \, ({\mathbb{Z}}/3{\mathbb{Z}})^2,\, {\mathbb{Z}}/2{\mathbb{Z}} \times ({\mathbb{Z}}/3{\mathbb{Z}})^2 \end{align} $$
$$ \begin{align} & \{1\}, \, {\mathbb{Z}}/2{\mathbb{Z}}, \, {\mathbb{Z}}/3{\mathbb{Z}}, \, ({\mathbb{Z}}/2{\mathbb{Z}})^2 \nonumber\\ & {\mathbb{Z}}/6{\mathbb{Z}}, \, ({\mathbb{Z}}/3{\mathbb{Z}})^2,\, {\mathbb{Z}}/2{\mathbb{Z}} \times ({\mathbb{Z}}/3{\mathbb{Z}})^2 \end{align} $$
is isomorphic to
![]() $A({\mathbb {Q}})_{ {\mathrm{tors}}}$
for some
$A({\mathbb {Q}})_{ {\mathrm{tors}}}$
for some
![]() ${\mathcal {O}}$
-
${\mathcal {O}}$
-
![]() $\mathrm {PQM}$
surface
$\mathrm {PQM}$
surface
![]() $A/{\mathbb {Q}}$
, with the largest group having order
$A/{\mathbb {Q}}$
, with the largest group having order
![]() $18$
. Indeed, each of these groups arises as
$18$
. Indeed, each of these groups arises as
![]() $A({\mathbb {Q}})_{\mathrm {tors}}$
for infinitely many
$A({\mathbb {Q}})_{\mathrm {tors}}$
for infinitely many
![]() $\overline {\mathbb {Q}}$
-isomorphism classes of such surfaces by [Reference Laga and ShnidmanLS23, Theorem 1.1].
$\overline {\mathbb {Q}}$
-isomorphism classes of such surfaces by [Reference Laga and ShnidmanLS23, Theorem 1.1].
Our methods give the following more precise constraints on the group structure of
![]() $A({\mathbb {Q}})_{ {\mathrm{tors}}}$
.
$A({\mathbb {Q}})_{ {\mathrm{tors}}}$
.
Theorem 1.3. Let A be an
![]() ${\mathcal {O}}$
-
${\mathcal {O}}$
-
![]() $\mathrm {PQM}$
abelian surface over
$\mathrm {PQM}$
abelian surface over
![]() ${\mathbb {Q}}$
. Then
${\mathbb {Q}}$
. Then
![]() $A({\mathbb {Q}})_{ {\mathrm{tors}}}$
is isomorphic either to one of the groups in (1.1) or to one of the following groups:
$A({\mathbb {Q}})_{ {\mathrm{tors}}}$
is isomorphic either to one of the groups in (1.1) or to one of the following groups:
 $$ \begin{align} & {\mathbb{Z}}/4{\mathbb{Z}}, {\mathbb{Z}}/2{\mathbb{Z}} \times {\mathbb{Z}}/4{\mathbb{Z}}, ({\mathbb{Z}}/2{\mathbb{Z}})^3, ({\mathbb{Z}}/2{\mathbb{Z}})^2 \times {\mathbb{Z}}/3{\mathbb{Z}}, \nonumber\\ & {\mathbb{Z}}/4{\mathbb{Z}} \times {\mathbb{Z}}/3{\mathbb{Z}}, ({\mathbb{Z}}/2{\mathbb{Z}})^2 \times {\mathbb{Z}}/4{\mathbb{Z}}, ({\mathbb{Z}}/4{\mathbb{Z}})^2. \end{align} $$
$$ \begin{align} & {\mathbb{Z}}/4{\mathbb{Z}}, {\mathbb{Z}}/2{\mathbb{Z}} \times {\mathbb{Z}}/4{\mathbb{Z}}, ({\mathbb{Z}}/2{\mathbb{Z}})^3, ({\mathbb{Z}}/2{\mathbb{Z}})^2 \times {\mathbb{Z}}/3{\mathbb{Z}}, \nonumber\\ & {\mathbb{Z}}/4{\mathbb{Z}} \times {\mathbb{Z}}/3{\mathbb{Z}}, ({\mathbb{Z}}/2{\mathbb{Z}})^2 \times {\mathbb{Z}}/4{\mathbb{Z}}, ({\mathbb{Z}}/4{\mathbb{Z}})^2. \end{align} $$
We leave open the question of whether any of the groups of (1.2) arise as
![]() $A({\mathbb {Q}})_{\mathrm {tors}}$
for some
$A({\mathbb {Q}})_{\mathrm {tors}}$
for some
![]() ${\mathcal {O}}$
-
${\mathcal {O}}$
-
![]() $\mathrm {PQM}$
surface or not.
$\mathrm {PQM}$
surface or not.
Theorem 1.3 can be interpreted as a non-existence result for non-special rational points on certain types of Shimura curves with level structure. Since the discriminant of
![]() $ {\mathrm{End}}(A_{\overline {\mathbb {Q}}})$
and level are unconstrained, the result covers infinitely many distinct such curves. However, as we explain below, our proof of Theorem 1.3 does not make direct use of the arithmetic of Shimura curves.
$ {\mathrm{End}}(A_{\overline {\mathbb {Q}}})$
and level are unconstrained, the result covers infinitely many distinct such curves. However, as we explain below, our proof of Theorem 1.3 does not make direct use of the arithmetic of Shimura curves.
Whereas the theorems above consider general
![]() ${\mathcal {O}}$
-
${\mathcal {O}}$
-
![]() $\mathrm {PQM}$
abelian surfaces, one is sometimes interested in surfaces with additional structure. For example, recall that A is of
$\mathrm {PQM}$
abelian surfaces, one is sometimes interested in surfaces with additional structure. For example, recall that A is of
![]() $ {\mathrm{GL}}_2$
-type if the endomorphism ring
$ {\mathrm{GL}}_2$
-type if the endomorphism ring
![]() $ {\mathrm{End}}(A)$
is a quadratic ring. Modularity results (see Theorem 5.1) imply that an abelian variety A of
$ {\mathrm{End}}(A)$
is a quadratic ring. Modularity results (see Theorem 5.1) imply that an abelian variety A of
![]() $ {\mathrm{GL}}_2$
-type over
$ {\mathrm{GL}}_2$
-type over
![]() ${\mathbb {Q}}$
is a quotient of the modular Jacobian
${\mathbb {Q}}$
is a quotient of the modular Jacobian
![]() $J_1(N)$
for some N. More precisely, the isogeny class of A arises from a cuspidal newform of weight
$J_1(N)$
for some N. More precisely, the isogeny class of A arises from a cuspidal newform of weight
![]() $2$
and level N, where A has conductor
$2$
and level N, where A has conductor
![]() $N^2$
. Specializing our methods to this setting, we obtain the following complete classification.
$N^2$
. Specializing our methods to this setting, we obtain the following complete classification.
Theorem 1.4. Let A be an
![]() ${\mathcal {O}}$
-
${\mathcal {O}}$
-
![]() $\mathrm {PQM}$
surface over
$\mathrm {PQM}$
surface over
![]() ${\mathbb {Q}}$
of
${\mathbb {Q}}$
of
![]() $ {\mathrm{GL}}_2$
-type. Then
$ {\mathrm{GL}}_2$
-type. Then
![]() $A({\mathbb {Q}})_{ {\mathrm{tors}}}$
is isomorphic to one of the following groups:
$A({\mathbb {Q}})_{ {\mathrm{tors}}}$
is isomorphic to one of the following groups:
Every one of these groups arises as
![]() $A({\mathbb {Q}})_{ {\mathrm{tors}}}$
for infinitely many
$A({\mathbb {Q}})_{ {\mathrm{tors}}}$
for infinitely many
![]() $\overline {{\mathbb {Q}}}$
-isomorphism classes of
$\overline {{\mathbb {Q}}}$
-isomorphism classes of
![]() ${\mathcal {O}}$
-
${\mathcal {O}}$
-
![]() $\mathrm {PQM}$
surfaces A over
$\mathrm {PQM}$
surfaces A over
![]() ${\mathbb {Q}}$
of
${\mathbb {Q}}$
of
![]() $ {\mathrm{GL}}_2$
-type.
$ {\mathrm{GL}}_2$
-type.
Remark 1.5. The proof shows that if the maximality assumption on
![]() ${\mathcal {O}}$
is omitted, then a similar classification holds, except we do not know whether the group
${\mathcal {O}}$
is omitted, then a similar classification holds, except we do not know whether the group
![]() $({\mathbb {Z}}/2{\mathbb {Z}})^3$
arises or not.
$({\mathbb {Z}}/2{\mathbb {Z}})^3$
arises or not.
Another natural class of abelian surfaces is Jacobians of genus two curves. Recall that for geometrically simple abelian surfaces, being a Jacobian is equivalent to carrying a principal polarization. Thus, the following result gives a near-classification for rational torsion subgroups of genus two Jacobians over
![]() ${\mathbb {Q}}$
in the
${\mathbb {Q}}$
in the
![]() ${\mathcal {O}}$
-
${\mathcal {O}}$
-
![]() $\mathrm {PQM}$
locus of the Siegel modular 3-fold
$\mathrm {PQM}$
locus of the Siegel modular 3-fold
![]() $\mathcal {A}_2$
parameterizing principally polarized abelian surfaces.
$\mathcal {A}_2$
parameterizing principally polarized abelian surfaces.
Theorem 1.6. Let J be an
![]() ${\mathcal {O}}$
-
${\mathcal {O}}$
-
![]() $\mathrm {PQM}$
surface over
$\mathrm {PQM}$
surface over
![]() ${\mathbb {Q}}$
which is the Jacobian of a genus two curve over
${\mathbb {Q}}$
which is the Jacobian of a genus two curve over
![]() ${\mathbb {Q}}$
. Then
${\mathbb {Q}}$
. Then
![]() $J({\mathbb {Q}})_{ {\mathrm{tors}}}$
is isomorphic to one of the following groups:
$J({\mathbb {Q}})_{ {\mathrm{tors}}}$
is isomorphic to one of the following groups:
 $$ \begin{align*} & \{1\}, {\mathbb{Z}}/2{\mathbb{Z}}, {\mathbb{Z}}/3{\mathbb{Z}}, ({\mathbb{Z}}/2{\mathbb{Z}})^2,{\mathbb{Z}}/6{\mathbb{Z}}, ({\mathbb{Z}}/3{\mathbb{Z}})^2, \\ & {\mathbb{Z}}/4{\mathbb{Z}}, {\mathbb{Z}}/2{\mathbb{Z}} \times {\mathbb{Z}}/4{\mathbb{Z}}, ({\mathbb{Z}}/2{\mathbb{Z}})^2 \times {\mathbb{Z}}/3{\mathbb{Z}}, {\mathbb{Z}}/4{\mathbb{Z}} \times {\mathbb{Z}}/3{\mathbb{Z}}, ({\mathbb{Z}}/4{\mathbb{Z}})^2. \end{align*} $$
$$ \begin{align*} & \{1\}, {\mathbb{Z}}/2{\mathbb{Z}}, {\mathbb{Z}}/3{\mathbb{Z}}, ({\mathbb{Z}}/2{\mathbb{Z}})^2,{\mathbb{Z}}/6{\mathbb{Z}}, ({\mathbb{Z}}/3{\mathbb{Z}})^2, \\ & {\mathbb{Z}}/4{\mathbb{Z}}, {\mathbb{Z}}/2{\mathbb{Z}} \times {\mathbb{Z}}/4{\mathbb{Z}}, ({\mathbb{Z}}/2{\mathbb{Z}})^2 \times {\mathbb{Z}}/3{\mathbb{Z}}, {\mathbb{Z}}/4{\mathbb{Z}} \times {\mathbb{Z}}/3{\mathbb{Z}}, ({\mathbb{Z}}/4{\mathbb{Z}})^2. \end{align*} $$
In particular,
![]() $\# J({\mathbb {Q}})_{ {\mathrm{tors}}} \leq 16$
.
$\# J({\mathbb {Q}})_{ {\mathrm{tors}}} \leq 16$
.
The first six groups in the list above can be realized as
![]() $J({\mathbb {Q}})_{ {\mathrm{tors}}}$
; see Table 2. We do not know whether they can be realized infinitely often by
$J({\mathbb {Q}})_{ {\mathrm{tors}}}$
; see Table 2. We do not know whether they can be realized infinitely often by
![]() ${\mathcal {O}}$
-
${\mathcal {O}}$
-
![]() $\mathrm {PQM}$
Jacobians over
$\mathrm {PQM}$
Jacobians over
![]() ${\mathbb {Q}}$
.
${\mathbb {Q}}$
.
1.3 Methods
We first describe the proof of Theorem 1.4, which is almost entirely local in nature. Let A be an
![]() ${\mathcal {O}}$
-
${\mathcal {O}}$
-
![]() $\mathrm {PQM}$
surface over
$\mathrm {PQM}$
surface over
![]() ${\mathbb {Q}}$
of
${\mathbb {Q}}$
of
![]() $ {\mathrm{GL}}_2$
-type. We show that A has totally additive reduction at every prime p of bad reduction, meaning that the identity component of the special fiber of the Néron model at p is unipotent. It is well known that, in this case, the prime-to-p torsion subgroup of
$ {\mathrm{GL}}_2$
-type. We show that A has totally additive reduction at every prime p of bad reduction, meaning that the identity component of the special fiber of the Néron model at p is unipotent. It is well known that, in this case, the prime-to-p torsion subgroup of
![]() $A({\mathbb {Q}}_p)$
embeds in the Néron component group of A at p and that this component group is controlled by the smallest field over which A acquires good reduction. Our proof of Theorem 1.4 therefore involves an analysis of this field extension. In particular, we show that its degree is coprime to
$A({\mathbb {Q}}_p)$
embeds in the Néron component group of A at p and that this component group is controlled by the smallest field over which A acquires good reduction. Our proof of Theorem 1.4 therefore involves an analysis of this field extension. In particular, we show that its degree is coprime to
![]() $\ell $
for any prime
$\ell $
for any prime
![]() $\ell \geq 5$
. Applying these local arguments requires the existence of suitable primes of bad reduction and breaks down when A has conductor dividing
$\ell \geq 5$
. Applying these local arguments requires the existence of suitable primes of bad reduction and breaks down when A has conductor dividing
![]() $2^n$
,
$2^n$
,
![]() $3^n$
, or
$3^n$
, or
![]() $6^4$
. We handle these cases seperately by invoking the modularity theorem and using modular forms computations contained in the LMFDB [LMF23]. It turns out there is a single isogeny class whose conductor is of this form – namely, the isogeny class of conductor
$6^4$
. We handle these cases seperately by invoking the modularity theorem and using modular forms computations contained in the LMFDB [LMF23]. It turns out there is a single isogeny class whose conductor is of this form – namely, the isogeny class of conductor
![]() $3^{10}$
– corresponding to a Galois orbit of newforms of level
$3^{10}$
– corresponding to a Galois orbit of newforms of level
![]() $3^5=243$
, with LMFDB label 243.2.a.d.
$3^5=243$
, with LMFDB label 243.2.a.d.
To prove Theorem 1.1, we need to exclude the existence of an
![]() ${\mathcal {O}}$
-
${\mathcal {O}}$
-
![]() $\mathrm {PQM}$
surface A over
$\mathrm {PQM}$
surface A over
![]() ${\mathbb {Q}}$
such that
${\mathbb {Q}}$
such that
![]() $A[\ell ]({\mathbb {Q}})$
is nontrivial for some prime
$A[\ell ]({\mathbb {Q}})$
is nontrivial for some prime
![]() $\ell \geq 5$
. By studying the interaction between the Galois action on the torsion points of A and the Galois action on
$\ell \geq 5$
. By studying the interaction between the Galois action on the torsion points of A and the Galois action on
![]() $ {\mathrm{End}}(A_{\overline {\mathbb {Q}}})$
, we show that such an A must necessarily be of
$ {\mathrm{End}}(A_{\overline {\mathbb {Q}}})$
, we show that such an A must necessarily be of
![]() $ {\mathrm{GL}}_2$
-type, so we may conclude using Theorem 1.4. The methods of this ‘reduction to
$ {\mathrm{GL}}_2$
-type, so we may conclude using Theorem 1.4. The methods of this ‘reduction to
![]() $ {\mathrm{GL}}_2$
-type’ argument are surprisingly elementary. Aside from some calculations in the quaternion order
$ {\mathrm{GL}}_2$
-type’ argument are surprisingly elementary. Aside from some calculations in the quaternion order
![]() ${\mathcal {O}}$
, the key observation is that in the non-
${\mathcal {O}}$
, the key observation is that in the non-
![]() $ {\mathrm{GL}}_2$
-type case, the geometric endomorphism algebra
$ {\mathrm{GL}}_2$
-type case, the geometric endomorphism algebra
![]() $ {\mathrm{End}}^0(A_{\overline {\mathbb {Q}}})$
contains a (unique) Galois-stable imaginary quadratic subfield, which is naturally determined by the (unique) polarization defined over
$ {\mathrm{End}}^0(A_{\overline {\mathbb {Q}}})$
contains a (unique) Galois-stable imaginary quadratic subfield, which is naturally determined by the (unique) polarization defined over
![]() ${\mathbb {Q}}$
.
${\mathbb {Q}}$
.
To prove Theorems 1.2 and 1.3, we must constrain the remaining possibilities for
![]() $A({\mathbb {Q}})_{ {\mathrm{tors}}}$
, which is a group of order
$A({\mathbb {Q}})_{ {\mathrm{tors}}}$
, which is a group of order
![]() $2^i3^j$
by Theorem 1.1. Our arguments here are ad hoc, relying on a careful analysis of the reduction of A modulo various primes via Honda–Tate theory (with the aid of the LMFDB) to constrain the possible torsion groups, reduction types and Galois action on the endomorphism ring. The proof of Theorem 1.6 is similar, but using the relationship between endomorphisms, polarizations and level structures.
$2^i3^j$
by Theorem 1.1. Our arguments here are ad hoc, relying on a careful analysis of the reduction of A modulo various primes via Honda–Tate theory (with the aid of the LMFDB) to constrain the possible torsion groups, reduction types and Galois action on the endomorphism ring. The proof of Theorem 1.6 is similar, but using the relationship between endomorphisms, polarizations and level structures.
1.4 Previous work
Rational torsion on
![]() ${\mathcal {O}}$
-
${\mathcal {O}}$
-
![]() $\mathrm {PQM}$
surfaces was previously considered in the PhD thesis of Clark [Reference ClarkCla03, Chapter 5], but see the author’s caveat emptor, indicating that the proofs of the main results of that chapter are incomplete.
$\mathrm {PQM}$
surfaces was previously considered in the PhD thesis of Clark [Reference ClarkCla03, Chapter 5], but see the author’s caveat emptor, indicating that the proofs of the main results of that chapter are incomplete.
1.5 Future directions
Our methods use the maximality assumption on
![]() $ {\mathrm{End}}(A_{\overline {\mathbb {Q}}})$
in various places. It would be interesting and desirable to relax this condition, especially since groups of order 12 and 18 can indeed arise in genus two Jacobians with non-maximal PQM; see, for example, the curve
$ {\mathrm{End}}(A_{\overline {\mathbb {Q}}})$
in various places. It would be interesting and desirable to relax this condition, especially since groups of order 12 and 18 can indeed arise in genus two Jacobians with non-maximal PQM; see, for example, the curve
![]() $y^2 = 24x^5 + 36x^4- 4x^3-12x^2+1$
and [Reference Laga and ShnidmanLS23, Remark 7.17]. It would also be interesting to systematically analyze rational points on (Atkin–Lehner quotients of) Shimura curves with level structure – for example, to determine whether the remaining groups (1.2) arise or not.
$y^2 = 24x^5 + 36x^4- 4x^3-12x^2+1$
and [Reference Laga and ShnidmanLS23, Remark 7.17]. It would also be interesting to systematically analyze rational points on (Atkin–Lehner quotients of) Shimura curves with level structure – for example, to determine whether the remaining groups (1.2) arise or not.
1.6 Organization
Sections 2-4 are preliminary, and the remaining sections are devoted to proving the main theorems of the introduction. As explained in §1.3, we start by proving Theorem 1.4 because the other theorems depend on it.
Those who wish to take the shortest route to Theorem 1.4 (minus eliminating
![]() $({\mathbb {Z}}/2{\mathbb {Z}})^3$
) only need to read Sections 3.2, 4 and 5. Eliminating the last group
$({\mathbb {Z}}/2{\mathbb {Z}})^3$
) only need to read Sections 3.2, 4 and 5. Eliminating the last group
![]() $({\mathbb {Z}}/2{\mathbb {Z}})^3$
in Proposition 5.16 requires more algebraic preliminaries from Section 2 and 3.
$({\mathbb {Z}}/2{\mathbb {Z}})^3$
in Proposition 5.16 requires more algebraic preliminaries from Section 2 and 3.
1.7 Notation
We fix the following notation for the remainder of this paper:
-
• B: an indefinite (so
 $B\otimes \mathbb {R} \simeq {\mathrm{Mat}}_2(\mathbb {R})$
) quaternion algebra over
$B\otimes \mathbb {R} \simeq {\mathrm{Mat}}_2(\mathbb {R})$
) quaternion algebra over
 ${\mathbb {Q}}$
of discriminant
${\mathbb {Q}}$
of discriminant
 $ {\mathrm{disc}}(B)\neq 1$
;
$ {\mathrm{disc}}(B)\neq 1$
; -
•
 $ {\mathrm{trd}}(b)$
,
$ {\mathrm{trd}}(b)$
,
 $ {\mathrm{nrd}}(b)$
and
$ {\mathrm{nrd}}(b)$
and
 $\bar {b}$
: reduced trace, reduced norm and canonical involution of an element
$\bar {b}$
: reduced trace, reduced norm and canonical involution of an element
 $b\in B$
, respectively;
$b\in B$
, respectively; -
•
 ${\mathcal {O}}$
: a choice of maximal order of B;
${\mathcal {O}}$
: a choice of maximal order of B; -
•
 $\bar F$
: a choice of algebraic closure of a field F;
$\bar F$
: a choice of algebraic closure of a field F; -
•
 $ {\mathrm{Gal}}_F$
: the absolute Galois group of F;
$ {\mathrm{Gal}}_F$
: the absolute Galois group of F; -
•
 $ {\mathrm{End}}(A)$
: the endomorphism ring of an abelian variety A defined over F;
$ {\mathrm{End}}(A)$
: the endomorphism ring of an abelian variety A defined over F; -
•
 $ {\mathrm{End}}^0(A)= {\mathrm{End}}(A) \otimes {\mathbb {Q}}$
: the endomorphism algebra of A;
$ {\mathrm{End}}^0(A)= {\mathrm{End}}(A) \otimes {\mathbb {Q}}$
: the endomorphism algebra of A; -
•
 $ {\mathrm{NS}}(A)$
: the Néron–Severi group of A;
$ {\mathrm{NS}}(A)$
: the Néron–Severi group of A; -
•
 $A_{K}$
: base change of
$A_{K}$
: base change of
 $A/F$
along a field extension
$A/F$
along a field extension
 $K/F$
;
$K/F$
; -
•
 $\left (\frac {m,n}{F}\right )$
: the quaternion algebra over F with basis
$\left (\frac {m,n}{F}\right )$
: the quaternion algebra over F with basis
 $\{1,i,j,ij\}$
such that
$\{1,i,j,ij\}$
such that
 $i^2= m, j^2=n$
and
$i^2= m, j^2=n$
and
 $ij = -ji$
;
$ij = -ji$
; -
•
 $D_n:$
the dihedral group of order
$D_n:$
the dihedral group of order
 $2n$
.
$2n$
.
We say an abelian surface A over a field F is an
![]() ${\mathcal {O}}$
-
${\mathcal {O}}$
-
![]() $\mathrm {PQM}$
surface if there is an isomorphism
$\mathrm {PQM}$
surface if there is an isomorphism
![]() $ {\mathrm{End}}(A_{\bar {F}})\simeq {\mathcal {O}}$
.
$ {\mathrm{End}}(A_{\bar {F}})\simeq {\mathcal {O}}$
.
![]() ${\mathcal {O}}$
-
${\mathcal {O}}$
-
![]() $\mathrm {PQM}$
surfaces over
$\mathrm {PQM}$
surfaces over
![]() ${\mathbb {Q}}$
are the central object of interest in this paper, but some of our results apply to abelian surfaces whose geometric endomorphism ring is a possibly non-maximal order in a non-split quaternion algebra. We call such surfaces simply PQM surfaces.
${\mathbb {Q}}$
are the central object of interest in this paper, but some of our results apply to abelian surfaces whose geometric endomorphism ring is a possibly non-maximal order in a non-split quaternion algebra. We call such surfaces simply PQM surfaces.
We emphasize that this is a restrictive definition of ‘PQM’: we require that
![]() $ {\mathrm{End}}(A_{\bar {F}})$
does not merely contain such a quaternion order, but is equal to it. In particular, under our terminology, a
$ {\mathrm{End}}(A_{\bar {F}})$
does not merely contain such a quaternion order, but is equal to it. In particular, under our terminology, a
![]() $\mathrm {PQM}$
surface A is geometrically simple.
$\mathrm {PQM}$
surface A is geometrically simple.
Concerning actions: we will view Galois actions as right actions. We will view
![]() $ {\mathrm{End}}(A)$
as acting on A on the left. If a group G acts on a set X on the right, we write
$ {\mathrm{End}}(A)$
as acting on A on the left. If a group G acts on a set X on the right, we write
![]() $X^G$
for the set of G-fixed points.
$X^G$
for the set of G-fixed points.
2 Quaternionic arithmetic
This section collects some algebraic calculations in the quaternion order
![]() ${\mathcal {O}}$
. It can be safely skipped on a first pass; the reader can return back to it when these calculations are used.
${\mathcal {O}}$
. It can be safely skipped on a first pass; the reader can return back to it when these calculations are used.
2.1 The normalizer of a maximal order
We recall the following characterization of the normalizer
![]() $N_{B^{\times }}({\mathcal {O}})$
of
$N_{B^{\times }}({\mathcal {O}})$
of
![]() ${\mathcal {O}}$
in
${\mathcal {O}}$
in
![]() $B^{\times }$
(with respect to the conjugation action).
$B^{\times }$
(with respect to the conjugation action).
Lemma 2.1. An element of
![]() $B^{\times }/{\mathbb {Q}}^{\times }$
lies in
$B^{\times }/{\mathbb {Q}}^{\times }$
lies in
![]() $N_{B^{\times }}({\mathcal {O}})/{\mathbb {Q}}^{\times }$
if and only if it can be represented by an element of
$N_{B^{\times }}({\mathcal {O}})/{\mathbb {Q}}^{\times }$
if and only if it can be represented by an element of
![]() ${\mathcal {O}}$
of reduced norm dividing
${\mathcal {O}}$
of reduced norm dividing
![]() $ {\mathrm{disc}}(B)$
.
$ {\mathrm{disc}}(B)$
.
Proof. An element
![]() $b\in B^{\times }$
lies in
$b\in B^{\times }$
lies in
![]() $N_{B^{\times }}({\mathcal {O}})$
if and only if it lies in the local normalizer
$N_{B^{\times }}({\mathcal {O}})$
if and only if it lies in the local normalizer
![]() $N_{(B\otimes {\mathbb {Q}}_p)^{\times }}({\mathcal {O}}\otimes {\mathbb {Z}}_p)$
for all primes p. If p does not divide
$N_{(B\otimes {\mathbb {Q}}_p)^{\times }}({\mathcal {O}}\otimes {\mathbb {Z}}_p)$
for all primes p. If p does not divide
![]() $ {\mathrm{disc}}(B)$
, then this normalizer group equals
$ {\mathrm{disc}}(B)$
, then this normalizer group equals
![]() ${\mathbb {Q}}_p^{\times }({\mathcal {O}}\otimes {\mathbb {Z}}_p)^{\times }$
[Reference VoightVoi21, (23.2.4)]. If p divides
${\mathbb {Q}}_p^{\times }({\mathcal {O}}\otimes {\mathbb {Z}}_p)^{\times }$
[Reference VoightVoi21, (23.2.4)]. If p divides
![]() $ {\mathrm{disc}}(B)$
, this group equals
$ {\mathrm{disc}}(B)$
, this group equals
![]() $(B\otimes {\mathbb {Q}}_p)^{\times }$
((23.2.8) in op. cit.). If
$(B\otimes {\mathbb {Q}}_p)^{\times }$
((23.2.8) in op. cit.). If
![]() $b\in {\mathcal {O}}$
has norm dividing
$b\in {\mathcal {O}}$
has norm dividing
![]() $ {\mathrm{disc}}(B)$
, then this description shows that b lies in all local normalizer groups. Conversely, if
$ {\mathrm{disc}}(B)$
, then this description shows that b lies in all local normalizer groups. Conversely, if
![]() $b\in B^{\times }$
normalizes
$b\in B^{\times }$
normalizes
![]() ${\mathcal {O}}$
, then this description shows that there exists a finite adele
${\mathcal {O}}$
, then this description shows that there exists a finite adele
![]() $(\lambda _p)_p$
such that
$(\lambda _p)_p$
such that
![]() $\lambda _p b \in ({\mathcal {O}}\otimes {\mathbb {Z}}_p)^{\times }$
for all
$\lambda _p b \in ({\mathcal {O}}\otimes {\mathbb {Z}}_p)^{\times }$
for all
![]() $p\nmid {\mathrm{disc}}(B)$
and such that
$p\nmid {\mathrm{disc}}(B)$
and such that
![]() $ {\mathrm{nrd}}(\lambda _p b)$
has p-adic valuation
$ {\mathrm{nrd}}(\lambda _p b)$
has p-adic valuation
![]() $\leq 1$
for all
$\leq 1$
for all
![]() $p\mid {\mathrm{disc}}(B)$
. Since
$p\mid {\mathrm{disc}}(B)$
. Since
![]() ${\mathbb {Z}}$
has class number one, there exists
${\mathbb {Z}}$
has class number one, there exists
![]() $\lambda \in {\mathbb {Q}}^{\times }$
such that
$\lambda \in {\mathbb {Q}}^{\times }$
such that
![]() $\lambda \lambda _p^{-1}\in {\mathbb {Z}}_p^{\times }$
for all p and so
$\lambda \lambda _p^{-1}\in {\mathbb {Z}}_p^{\times }$
for all p and so
![]() $\lambda b \in {\mathcal {O}}$
has norm dividing
$\lambda b \in {\mathcal {O}}$
has norm dividing
![]() $ {\mathrm{disc}}(B)$
, as desired.
$ {\mathrm{disc}}(B)$
, as desired.
We recall for future reference that the quotient of
![]() $N_{B^{\times }}({\mathcal {O}})/{\mathbb {Q}}^{\times }$
by the subgroup
$N_{B^{\times }}({\mathcal {O}})/{\mathbb {Q}}^{\times }$
by the subgroup
![]() ${\mathcal {O}}^{\times }/\{\pm 1\}$
is by definition the Atkin–Lehner group W of
${\mathcal {O}}^{\times }/\{\pm 1\}$
is by definition the Atkin–Lehner group W of
![]() ${\mathcal {O}}$
, an elementary abelian
${\mathcal {O}}$
, an elementary abelian
![]() $2$
-group whose elements can be identified with positive divisors of
$2$
-group whose elements can be identified with positive divisors of
![]() $ {\mathrm{disc}}(B)$
.
$ {\mathrm{disc}}(B)$
.
2.2 Dihedral actions on
 ${\mathcal {O}}$
${\mathcal {O}}$
For reasons that will become clear in §3.2, we are interested in subgroups
![]() $G\subset {\mathrm{Aut}}({\mathcal {O}})$
isomorphic to
$G\subset {\mathrm{Aut}}({\mathcal {O}})$
isomorphic to
![]() $D_n$
for some
$D_n$
for some
![]() $n\in \{1,2,3,4,6\}$
. In this section, we describe these subgroups very explicitly.
$n\in \{1,2,3,4,6\}$
. In this section, we describe these subgroups very explicitly.
By the Skolem–Noether theorem, every ring automorphism of
![]() ${\mathcal {O}}$
is of the form
${\mathcal {O}}$
is of the form
![]() $x\mapsto b^{-1}xb$
for some
$x\mapsto b^{-1}xb$
for some
![]() $b\in B^{\times }$
normalising
$b\in B^{\times }$
normalising
![]() ${\mathcal {O}}$
, and b is uniquely determined up to
${\mathcal {O}}$
, and b is uniquely determined up to
![]() ${\mathbb {Q}}^{\times }$
-multiples. Therefore,
${\mathbb {Q}}^{\times }$
-multiples. Therefore,
![]() $ {\mathrm{Aut}}({\mathcal {O}}) \simeq N_{B^{\times }}({\mathcal {O}})/{\mathbb {Q}}^{\times }$
.
$ {\mathrm{Aut}}({\mathcal {O}}) \simeq N_{B^{\times }}({\mathcal {O}})/{\mathbb {Q}}^{\times }$
.
If
![]() $b\in B^{\times }$
, write
$b\in B^{\times }$
, write
![]() $[b]$
for its class in
$[b]$
for its class in
![]() $B^{\times }/{\mathbb {Q}}^{\times }$
.
$B^{\times }/{\mathbb {Q}}^{\times }$
.
Lemma 2.2. Every element of
![]() $N_{B^{\times }}({\mathcal {O}})/{\mathbb {Q}}^{\times }$
of order
$N_{B^{\times }}({\mathcal {O}})/{\mathbb {Q}}^{\times }$
of order
![]() $2$
is represented by an element
$2$
is represented by an element
![]() $b\in {\mathcal {O}}$
such that
$b\in {\mathcal {O}}$
such that
![]() $b^2=m\neq 1$
is an integer dividing
$b^2=m\neq 1$
is an integer dividing
![]() $ {\mathrm{disc}}(B)$
. Moreover,
$ {\mathrm{disc}}(B)$
. Moreover,
![]() ${\mathcal {O}}^{\langle b\rangle } = \{x\in {\mathcal {O}} \mid b^{-1}xb = x \}$
is isomorphic to an order in
${\mathcal {O}}^{\langle b\rangle } = \{x\in {\mathcal {O}} \mid b^{-1}xb = x \}$
is isomorphic to an order in
![]() ${\mathbb {Q}}(\sqrt {m})$
containing
${\mathbb {Q}}(\sqrt {m})$
containing
![]() ${\mathbb {Z}}[\sqrt {m}]$
.
${\mathbb {Z}}[\sqrt {m}]$
.
Proof. By Lemma 2.1, we may choose a representative
![]() $b\in N_{B^{\times }}({\mathcal {O}})$
lying in
$b\in N_{B^{\times }}({\mathcal {O}})$
lying in
![]() ${\mathcal {O}}$
whose norm
${\mathcal {O}}$
whose norm
![]() $ {\mathrm{nrd}}(b)$
divides
$ {\mathrm{nrd}}(b)$
divides
![]() $ {\mathrm{disc}}(B)$
. Since the element has order
$ {\mathrm{disc}}(B)$
. Since the element has order
![]() $2$
,
$2$
,
![]() $m := b^2 = - {\mathrm{nrd}}(b)$
is an integer. We have
$m := b^2 = - {\mathrm{nrd}}(b)$
is an integer. We have
![]() $m\neq 1$
since otherwise
$m\neq 1$
since otherwise
![]() $b^2=1$
; hence,
$b^2=1$
; hence,
![]() $b =\pm 1\in {\mathbb {Q}}^{\times }$
, which is trivial in
$b =\pm 1\in {\mathbb {Q}}^{\times }$
, which is trivial in
![]() $N_{B^{\times }}({\mathcal {O}})/{\mathbb {Q}}^{\times }$
. This implies
$N_{B^{\times }}({\mathcal {O}})/{\mathbb {Q}}^{\times }$
. This implies
![]() ${\mathcal {O}}^{\langle b\rangle } = \{x\in B\mid b^{-1}xb = x\}$
is an order in
${\mathcal {O}}^{\langle b\rangle } = \{x\in B\mid b^{-1}xb = x\}$
is an order in
![]() $B^{\langle b\rangle } = {\mathbb {Q}}(b)$
containing
$B^{\langle b\rangle } = {\mathbb {Q}}(b)$
containing
![]() ${\mathbb {Z}}[b]\simeq {\mathbb {Z}}[\sqrt {m}]$
, as claimed.
${\mathbb {Z}}[b]\simeq {\mathbb {Z}}[\sqrt {m}]$
, as claimed.
Lemma 2.3. Let
![]() $G\subset N_{B^{\times }}({\mathcal {O}})/{\mathbb {Q}}^{\times }$
be a subgroup isomorphic to
$G\subset N_{B^{\times }}({\mathcal {O}})/{\mathbb {Q}}^{\times }$
be a subgroup isomorphic to
![]() $D_2 = C_2\times C_2$
. Then there exist elements
$D_2 = C_2\times C_2$
. Then there exist elements
![]() $i,j,k\in {\mathcal {O}}$
such that B has basis
$i,j,k\in {\mathcal {O}}$
such that B has basis
![]() $\{1,i,j,k\}$
, such that
$\{1,i,j,k\}$
, such that
![]() $i^2 = m$
,
$i^2 = m$
,
![]() $j^2 =n$
and
$j^2 =n$
and
![]() $k^2 = t$
all divide
$k^2 = t$
all divide
![]() $ {\mathrm{disc}}(B)$
, such that
$ {\mathrm{disc}}(B)$
, such that
![]() $ij = -ji$
and
$ij = -ji$
and
![]() $ij \in {\mathbb {Q}}^{\times } k$
, and such that
$ij \in {\mathbb {Q}}^{\times } k$
, and such that
![]() $G = \{1,[i],[j],[k]\}$
. Moreover, t equals
$G = \{1,[i],[j],[k]\}$
. Moreover, t equals
![]() $-mn$
up to squares.
$-mn$
up to squares.
Proof. By Lemma 2.2, we can pick representatives
![]() $i,j,k \in {\mathcal {O}}$
of the nontrivial elements of G that each square to an integer dividing
$i,j,k \in {\mathcal {O}}$
of the nontrivial elements of G that each square to an integer dividing
![]() $ {\mathrm{disc}}(B)$
. Since G is commutative,
$ {\mathrm{disc}}(B)$
. Since G is commutative,
![]() $ji = \lambda ij$
for some
$ji = \lambda ij$
for some
![]() $\lambda \in {\mathbb {Q}}^{\times }$
. Comparing norms shows that
$\lambda \in {\mathbb {Q}}^{\times }$
. Comparing norms shows that
![]() $\lambda =\pm 1$
. If
$\lambda =\pm 1$
. If
![]() $\lambda =1$
, then
$\lambda =1$
, then
![]() $ij = ji$
, but this would imply that B is commutative: a contradiction. Therefore,
$ij = ji$
, but this would imply that B is commutative: a contradiction. Therefore,
![]() $ij = -ji$
. Finally, since
$ij = -ji$
. Finally, since
![]() $[i][j] = [k]$
,
$[i][j] = [k]$
,
![]() $k \in {\mathbb {Q}}^{\times } ij$
. Taking norms, we see that t equals
$k \in {\mathbb {Q}}^{\times } ij$
. Taking norms, we see that t equals
![]() $-mn$
up to squares.
$-mn$
up to squares.
Lemma 2.4. Let
![]() $G\subset N_{B^{\times }}({\mathcal {O}})/{\mathbb {Q}}^{\times }$
be a subgroup isomorphic to
$G\subset N_{B^{\times }}({\mathcal {O}})/{\mathbb {Q}}^{\times }$
be a subgroup isomorphic to
![]() $D_4$
. Then there exists elements
$D_4$
. Then there exists elements
![]() $i,j\in {\mathcal {O}}$
such that B has basis
$i,j\in {\mathcal {O}}$
such that B has basis
![]() $\{1,i,j,ij\}$
, such that
$\{1,i,j,ij\}$
, such that
![]() $i^2= -1$
,
$i^2= -1$
,
![]() $j^2= m$
divides
$j^2= m$
divides
![]() $ {\mathrm{disc}}(B)$
and
$ {\mathrm{disc}}(B)$
and
![]() $ij=-ji$
, and such that
$ij=-ji$
, and such that
![]() $G = \langle [1+i],[j]\rangle $
. Moreover,
$G = \langle [1+i],[j]\rangle $
. Moreover,
![]() $2\mid {\mathrm{disc}}(B)$
.
$2\mid {\mathrm{disc}}(B)$
.
Proof. The fact that such
![]() $i,j\in B$
exist follows from [Reference VoightVoi21, §32.5 and §32.6] (itself based on results of [Reference Chinburg and FriedmanCF00]). By
$i,j\in B$
exist follows from [Reference VoightVoi21, §32.5 and §32.6] (itself based on results of [Reference Chinburg and FriedmanCF00]). By
![]() ${\mathbb {Q}}^{\times }$
-scaling j, we may assume that
${\mathbb {Q}}^{\times }$
-scaling j, we may assume that
![]() $j^2 = m$
is a squarefree integer. Since
$j^2 = m$
is a squarefree integer. Since
![]() $1+i,j \in N_{B^{\times }}({\mathcal {O}})$
, Lemma 2.1 shows that
$1+i,j \in N_{B^{\times }}({\mathcal {O}})$
, Lemma 2.1 shows that
![]() $i,j\in {\mathcal {O}}$
and
$i,j\in {\mathcal {O}}$
and
![]() $m\mid {\mathrm{disc}}(B)$
and
$m\mid {\mathrm{disc}}(B)$
and
![]() $ {\mathrm{nrd}}(1+i) = 2\mid {\mathrm{disc}}(B)$
.
$ {\mathrm{nrd}}(1+i) = 2\mid {\mathrm{disc}}(B)$
.
Lemma 2.5. Let
![]() $G\subset N_{B^{\times }}({\mathcal {O}})/{\mathbb {Q}}^{\times }$
be a subgroup isomorphic to
$G\subset N_{B^{\times }}({\mathcal {O}})/{\mathbb {Q}}^{\times }$
be a subgroup isomorphic to
![]() $D_3$
or
$D_3$
or
![]() $D_6$
. Then there exist elements
$D_6$
. Then there exist elements
![]() $\omega , j \in {\mathcal {O}}$
such that B has basis
$\omega , j \in {\mathcal {O}}$
such that B has basis
![]() $\{1,\omega ,j,\omega j\}$
, such that
$\{1,\omega ,j,\omega j\}$
, such that
![]() $\omega ^3=1$
,
$\omega ^3=1$
,
![]() $j^2= m \mid {\mathrm{disc}}(B)$
and
$j^2= m \mid {\mathrm{disc}}(B)$
and
![]() $\omega j = j\bar {\omega }= j(-1-\omega )$
, and such that
$\omega j = j\bar {\omega }= j(-1-\omega )$
, and such that
![]() $G = \langle [1+\omega ],[j]\rangle $
if
$G = \langle [1+\omega ],[j]\rangle $
if
![]() $G \simeq D_3$
and
$G \simeq D_3$
and
![]() $G = \langle [1-\omega ], [j]\rangle $
if
$G = \langle [1-\omega ], [j]\rangle $
if
![]() $G\simeq D_6$
. Moroever, if
$G\simeq D_6$
. Moroever, if
![]() $G \simeq D_6$
, then
$G \simeq D_6$
, then
![]() $3\mid {\mathrm{disc}}(B)$
.
$3\mid {\mathrm{disc}}(B)$
.
Proof. Identical to that of Lemma 2.4, again using [Reference VoightVoi21, §32.5 and §32.6] and Lemma 2.1.
2.3 Fixed point subgroups modulo N
For reasons similar to those of §2.2, we study the fixed points of G-actions on
![]() ${\mathcal {O}}/N{\mathcal {O}}$
for subgroups
${\mathcal {O}}/N{\mathcal {O}}$
for subgroups
![]() $G\subset {\mathrm{Aut}}({\mathcal {O}})$
isomorphic to
$G\subset {\mathrm{Aut}}({\mathcal {O}})$
isomorphic to
![]() $D_n$
for some
$D_n$
for some
![]() $n\in \{1,2,3,4,6\}$
and integers
$n\in \{1,2,3,4,6\}$
and integers
![]() $N\geq 1$
of interest.
$N\geq 1$
of interest.
Theorem 2.6. Let G be a subgroup of
![]() $ {\mathrm{Aut}}({\mathcal {O}})$
isomorphic to
$ {\mathrm{Aut}}({\mathcal {O}})$
isomorphic to
![]() $D_n$
for some
$D_n$
for some
![]() $n\in \{1,2,3,4,6\}$
.
$n\in \{1,2,3,4,6\}$
.
-
(a) Suppose that N is coprime to
 $2$
and
$2$
and
 $3$
. Then
$3$
. Then
 $({\mathcal {O}}/N{\mathcal {O}})^G$
is isomorphic to
$({\mathcal {O}}/N{\mathcal {O}})^G$
is isomorphic to
 $({\mathbb {Z}}/N{\mathbb {Z}})^2$
if
$({\mathbb {Z}}/N{\mathbb {Z}})^2$
if
 $G=D_1$
and isomorphic to
$G=D_1$
and isomorphic to
 ${\mathbb {Z}}/N{\mathbb {Z}}$
if
${\mathbb {Z}}/N{\mathbb {Z}}$
if
 $G=D_2,D_3,D_4$
or
$G=D_2,D_3,D_4$
or
 $D_6$
.
$D_6$
. -
(b) The group
 $({\mathcal {O}}/3{\mathcal {O}})^G$
is isomorphic to
$({\mathcal {O}}/3{\mathcal {O}})^G$
is isomorphic to
 $({\mathbb {Z}}/3{\mathbb {Z}})^2$
if
$({\mathbb {Z}}/3{\mathbb {Z}})^2$
if
 $G=D_1$
; isomorphic to
$G=D_1$
; isomorphic to
 ${\mathbb {Z}}/3{\mathbb {Z}}$
if
${\mathbb {Z}}/3{\mathbb {Z}}$
if
 $G=D_2,D_4,D_6$
; and isomorphic to
$G=D_2,D_4,D_6$
; and isomorphic to
 ${\mathbb {Z}}/3{\mathbb {Z}}$
or
${\mathbb {Z}}/3{\mathbb {Z}}$
or
 $({\mathbb {Z}}/3{\mathbb {Z}})^2$
if
$({\mathbb {Z}}/3{\mathbb {Z}})^2$
if
 $G = D_3$
.
$G = D_3$
. -
(c) We have
 $$ \begin{align*} ({\mathcal{O}}/2{\mathcal{O}})^G \simeq \begin{cases} ({\mathbb{Z}}/2{\mathbb{Z}})^2,({\mathbb{Z}}/2{\mathbb{Z}})^3\text{ or }({\mathbb{Z}}/2{\mathbb{Z}})^4 & \text{ if } G = D_1,\\ ({\mathbb{Z}}/2{\mathbb{Z}})^2 \text{ or }({\mathbb{Z}}/2{\mathbb{Z}})^3 & \text{ if } G = D_2,\\ ({\mathbb{Z}}/2{\mathbb{Z}})^2 & \text{ if } G = D_4,\\ {\mathbb{Z}}/2{\mathbb{Z}} & \text{ if } G =D_3\text{ or }D_6. \end{cases} \end{align*} $$
$$ \begin{align*} ({\mathcal{O}}/2{\mathcal{O}})^G \simeq \begin{cases} ({\mathbb{Z}}/2{\mathbb{Z}})^2,({\mathbb{Z}}/2{\mathbb{Z}})^3\text{ or }({\mathbb{Z}}/2{\mathbb{Z}})^4 & \text{ if } G = D_1,\\ ({\mathbb{Z}}/2{\mathbb{Z}})^2 \text{ or }({\mathbb{Z}}/2{\mathbb{Z}})^3 & \text{ if } G = D_2,\\ ({\mathbb{Z}}/2{\mathbb{Z}})^2 & \text{ if } G = D_4,\\ {\mathbb{Z}}/2{\mathbb{Z}} & \text{ if } G =D_3\text{ or }D_6. \end{cases} \end{align*} $$
Proof. The reduction map
![]() $r_N\colon {\mathcal {O}}^G\otimes {\mathbb {Z}}/N{\mathbb {Z}} \rightarrow ({\mathcal {O}}/N{\mathcal {O}})^G$
is injective, and its cokernel is isomorphic to the N-torsion of the group cohomology
$r_N\colon {\mathcal {O}}^G\otimes {\mathbb {Z}}/N{\mathbb {Z}} \rightarrow ({\mathcal {O}}/N{\mathcal {O}})^G$
is injective, and its cokernel is isomorphic to the N-torsion of the group cohomology
![]() $H^1(G,{\mathcal {O}})$
. Indeed, this can be seen by taking G-fixed points of the exact sequence
$H^1(G,{\mathcal {O}})$
. Indeed, this can be seen by taking G-fixed points of the exact sequence
![]() $0\rightarrow {\mathcal {O}} \rightarrow {\mathcal {O}} \rightarrow {\mathcal {O}}/N \rightarrow 0$
. The group
$0\rightarrow {\mathcal {O}} \rightarrow {\mathcal {O}} \rightarrow {\mathcal {O}}/N \rightarrow 0$
. The group
![]() ${\mathcal {O}}^G$
is isomorphic to
${\mathcal {O}}^G$
is isomorphic to
![]() ${\mathbb {Z}}^2$
if
${\mathbb {Z}}^2$
if
![]() $G = D_1$
and to
$G = D_1$
and to
![]() ${\mathbb {Z}}$
if
${\mathbb {Z}}$
if
![]() $G = D_2,D_3,D_4$
or
$G = D_2,D_3,D_4$
or
![]() $D_6$
. Since the finite abelian group
$D_6$
. Since the finite abelian group
![]() $H^1(G,{\mathcal {O}})$
is killed by the order of G, Part (a) immediately follows. To prove (b) and (c), it therefore suffices to prove that
$H^1(G,{\mathcal {O}})$
is killed by the order of G, Part (a) immediately follows. To prove (b) and (c), it therefore suffices to prove that
![]() $H^1(G,{\mathcal {O}})[6]$
is a subgroup of
$H^1(G,{\mathcal {O}})[6]$
is a subgroup of
![]() $({\mathbb {Z}}/2{\mathbb {Z}})^2$
if
$({\mathbb {Z}}/2{\mathbb {Z}})^2$
if
![]() $G=D_1$
; isomorphic to
$G=D_1$
; isomorphic to
![]() $({\mathbb {Z}}/2{\mathbb {Z}})$
or
$({\mathbb {Z}}/2{\mathbb {Z}})$
or
![]() $({\mathbb {Z}}/2{\mathbb {Z}})^2$
if
$({\mathbb {Z}}/2{\mathbb {Z}})^2$
if
![]() $G=D_2$
; a subgroup of
$G=D_2$
; a subgroup of
![]() ${\mathbb {Z}}/3{\mathbb {Z}}$
if
${\mathbb {Z}}/3{\mathbb {Z}}$
if
![]() $G=D_3$
; isomorphic to
$G=D_3$
; isomorphic to
![]() $({\mathbb {Z}}/2{\mathbb {Z}})$
if
$({\mathbb {Z}}/2{\mathbb {Z}})$
if
![]() $G=D_4$
; and trivial if
$G=D_4$
; and trivial if
![]() $G=D_6$
. Since
$G=D_6$
. Since
![]() $H^1(G,{\mathcal {O}}\otimes {\mathbb {Z}}_p)\simeq H^1(G,{\mathcal {O}})\otimes {\mathbb {Z}}_p$
for all primes p and since
$H^1(G,{\mathcal {O}}\otimes {\mathbb {Z}}_p)\simeq H^1(G,{\mathcal {O}})\otimes {\mathbb {Z}}_p$
for all primes p and since
![]() $ {\mathrm{Aut}}({\mathcal {O}}\otimes {\mathbb {Z}}_p)$
has only finitely many subgroups isomorphic to G up to conjugacy, this is in principle a finite computation; we give a more detailed proof below.
$ {\mathrm{Aut}}({\mathcal {O}}\otimes {\mathbb {Z}}_p)$
has only finitely many subgroups isomorphic to G up to conjugacy, this is in principle a finite computation; we give a more detailed proof below.
Case G = D
1. Since
![]() $G=D_1=C_2$
has order
$G=D_1=C_2$
has order
![]() $2$
,
$2$
,
![]() $H^1(G,{\mathcal {O}})$
is
$H^1(G,{\mathcal {O}})$
is
![]() $2$
-torsion and is isomorphic to the cokernel of
$2$
-torsion and is isomorphic to the cokernel of
![]() $r_2\colon {\mathcal {O}}^G\otimes {\mathbb {Z}}/2{\mathbb {Z}}\rightarrow ({\mathcal {O}}/2{\mathcal {O}})^G$
. By Lemma 2.2,
$r_2\colon {\mathcal {O}}^G\otimes {\mathbb {Z}}/2{\mathbb {Z}}\rightarrow ({\mathcal {O}}/2{\mathcal {O}})^G$
. By Lemma 2.2,
![]() ${\mathcal {O}}^G\simeq {\mathbb {Z}}^2$
, and so this cokernel is either
${\mathcal {O}}^G\simeq {\mathbb {Z}}^2$
, and so this cokernel is either
![]() $0, {\mathbb {Z}}/2{\mathbb {Z}}$
or
$0, {\mathbb {Z}}/2{\mathbb {Z}}$
or
![]() $({\mathbb {Z}}/2{\mathbb {Z}})^2$
. It follows that
$({\mathbb {Z}}/2{\mathbb {Z}})^2$
. It follows that
![]() $H^1(G,{\mathcal {O}})\simeq 0, {\mathbb {Z}}/2{\mathbb {Z}}$
or
$H^1(G,{\mathcal {O}})\simeq 0, {\mathbb {Z}}/2{\mathbb {Z}}$
or
![]() $({\mathbb {Z}}/2{\mathbb {Z}})^2$
.
$({\mathbb {Z}}/2{\mathbb {Z}})^2$
.
Case G = D
2. By Lemma 2.3, there exist
![]() $i,j,k\in {\mathcal {O}}$
such that
$i,j,k\in {\mathcal {O}}$
such that
![]() $i^2=m$
,
$i^2=m$
,
![]() $j^2=n$
and
$j^2=n$
and
![]() $k^2=t$
are all integers dividing
$k^2=t$
are all integers dividing
![]() $ {\mathrm{disc}}(B)$
, such that
$ {\mathrm{disc}}(B)$
, such that
![]() $ij=-ji$
and
$ij=-ji$
and
![]() $k \in {\mathbb {Q}}^{\times }ij$
and such that
$k \in {\mathbb {Q}}^{\times }ij$
and such that
![]() $G = \{1,[i],[j],[k]\}$
. Let
$G = \{1,[i],[j],[k]\}$
. Let
![]() $S_i = {\mathcal {O}} \cap {\mathbb {Q}}(i)$
,
$S_i = {\mathcal {O}} \cap {\mathbb {Q}}(i)$
,
![]() $S_j = {\mathcal {O}}\cap {\mathbb {Q}}(j)$
,
$S_j = {\mathcal {O}}\cap {\mathbb {Q}}(j)$
,
![]() $S_k = {\mathcal {O}} \cap {\mathbb {Q}}(k)$
. Then
$S_k = {\mathcal {O}} \cap {\mathbb {Q}}(k)$
. Then
![]() $S_i$
is an order in
$S_i$
is an order in
![]() ${\mathbb {Q}}(i)$
containing
${\mathbb {Q}}(i)$
containing
![]() ${\mathbb {Z}}[i]$
, and similarly for
${\mathbb {Z}}[i]$
, and similarly for
![]() $S_j$
and
$S_j$
and
![]() $S_k$
. Since
$S_k$
. Since
![]() $-mn$
equals t up to squares, upon reordering
$-mn$
equals t up to squares, upon reordering
![]() $\{i,j,k\}$
, we may assume that
$\{i,j,k\}$
, we may assume that
![]() ${\mathbb {Z}}[i]$
is maximal at
${\mathbb {Z}}[i]$
is maximal at
![]() $2$
. Therefore,
$2$
. Therefore,
![]() ${\mathbb {Z}}[\sqrt {m}]\otimes ({\mathbb {Z}}/2{\mathbb {Z}}) = S_i\otimes ({\mathbb {Z}}/2{\mathbb {Z}})\subset ({\mathcal {O}}/2{\mathcal {O}})$
is a subring on which G acts trivially. It follows that
${\mathbb {Z}}[\sqrt {m}]\otimes ({\mathbb {Z}}/2{\mathbb {Z}}) = S_i\otimes ({\mathbb {Z}}/2{\mathbb {Z}})\subset ({\mathcal {O}}/2{\mathcal {O}})$
is a subring on which G acts trivially. It follows that
![]() $({\mathbb {Z}}/2{\mathbb {Z}})^2\subset ({\mathcal {O}}/2{\mathcal {O}})^G$
. We will now show that G acts nontrivially on
$({\mathbb {Z}}/2{\mathbb {Z}})^2\subset ({\mathcal {O}}/2{\mathcal {O}})^G$
. We will now show that G acts nontrivially on
![]() $({\mathcal {O}}/2{\mathcal {O}})$
, so assume by contradiction that this action is trivial. By the classification of involutions on finite free
$({\mathcal {O}}/2{\mathcal {O}})$
, so assume by contradiction that this action is trivial. By the classification of involutions on finite free
![]() ${\mathbb {Z}}$
-modules, every such involution is a direct sum of involutions of the form
${\mathbb {Z}}$
-modules, every such involution is a direct sum of involutions of the form
![]() $x\mapsto x$
,
$x\mapsto x$
,
![]() $x\mapsto -x$
and
$x\mapsto -x$
and
![]() $(x,y)\mapsto (y,x)$
. If
$(x,y)\mapsto (y,x)$
. If
![]() $G = \langle [i],[j]\rangle $
acts trivially on
$G = \langle [i],[j]\rangle $
acts trivially on
![]() ${\mathcal {O}}/2{\mathcal {O}}$
, then both
${\mathcal {O}}/2{\mathcal {O}}$
, then both
![]() $[i],[j]\in {\mathrm{Aut}}({\mathcal {O}})$
are direct sums of involutions of the first two kinds. It follows that
$[i],[j]\in {\mathrm{Aut}}({\mathcal {O}})$
are direct sums of involutions of the first two kinds. It follows that
![]() ${\mathcal {O}}$
is a direct sum of the eigenspaces corresponding to the eigenvalues of
${\mathcal {O}}$
is a direct sum of the eigenspaces corresponding to the eigenvalues of
![]() $[i]$
and
$[i]$
and
![]() $[j]$
. It follows that
$[j]$
. It follows that
![]() ${\mathcal {O}} = {\mathbb {Z}}1\oplus {\mathbb {Z}} i \oplus {\mathbb {Z}} j \oplus {\mathbb {Z}} k$
. This implies that the discriminant of
${\mathcal {O}} = {\mathbb {Z}}1\oplus {\mathbb {Z}} i \oplus {\mathbb {Z}} j \oplus {\mathbb {Z}} k$
. This implies that the discriminant of
![]() ${\mathcal {O}}$
is
${\mathcal {O}}$
is
![]() $\pm 4u$
, contradicting the fact that
$\pm 4u$
, contradicting the fact that
![]() ${\mathcal {O}}$
is maximal at
${\mathcal {O}}$
is maximal at
![]() $2$
. We conclude that
$2$
. We conclude that
![]() $({\mathcal {O}}/2{\mathcal {O}})^G$
is
$({\mathcal {O}}/2{\mathcal {O}})^G$
is
![]() $({\mathbb {Z}}/2{\mathbb {Z}})^2$
or
$({\mathbb {Z}}/2{\mathbb {Z}})^2$
or
![]() $({\mathbb {Z}}/2{\mathbb {Z}})^3$
and since G is coprime to
$({\mathbb {Z}}/2{\mathbb {Z}})^3$
and since G is coprime to
![]() $3$
, this proves that
$3$
, this proves that
![]() $H^1(G,{\mathcal {O}})[6]$
is isomorphic to
$H^1(G,{\mathcal {O}})[6]$
is isomorphic to
![]() ${\mathbb {Z}}/2{\mathbb {Z}}$
or
${\mathbb {Z}}/2{\mathbb {Z}}$
or
![]() $({\mathbb {Z}}/2{\mathbb {Z}})^2$
.
$({\mathbb {Z}}/2{\mathbb {Z}})^2$
.
Case G = D
4. Let
![]() $i,j\in {\mathcal {O}}$
be elements satisfying the conclusion of Lemma 2.4, so
$i,j\in {\mathcal {O}}$
be elements satisfying the conclusion of Lemma 2.4, so
![]() $G = \langle [1+i],[j]\rangle $
. Since
$G = \langle [1+i],[j]\rangle $
. Since
![]() ${\mathbb {Z}}[i]$
is maximal at
${\mathbb {Z}}[i]$
is maximal at
![]() $2$
, the map
$2$
, the map
![]() ${\mathbb {Z}}[i]\otimes {\mathbb {Z}}/2{\mathbb {Z}}\rightarrow {\mathcal {O}}/2{\mathcal {O}}$
is injective. Since G acts trivially on the image of this map,
${\mathbb {Z}}[i]\otimes {\mathbb {Z}}/2{\mathbb {Z}}\rightarrow {\mathcal {O}}/2{\mathcal {O}}$
is injective. Since G acts trivially on the image of this map,
![]() $({\mathcal {O}}/2{\mathcal {O}})^G$
contains
$({\mathcal {O}}/2{\mathcal {O}})^G$
contains
![]() $({\mathbb {Z}}/2{\mathbb {Z}})^2$
. We need to show that
$({\mathbb {Z}}/2{\mathbb {Z}})^2$
. We need to show that
![]() $({\mathcal {O}}/2{\mathcal {O}})^G = ({\mathbb {Z}}/2{\mathbb {Z}})^2$
. To prove this, it is enough to show that
$({\mathcal {O}}/2{\mathcal {O}})^G = ({\mathbb {Z}}/2{\mathbb {Z}})^2$
. To prove this, it is enough to show that
![]() $({\mathcal {O}}/2{\mathcal {O}})^{\langle 1+i \rangle } = ({\mathbb {Z}}/2{\mathbb {Z}})^2$
. Since
$({\mathcal {O}}/2{\mathcal {O}})^{\langle 1+i \rangle } = ({\mathbb {Z}}/2{\mathbb {Z}})^2$
. Since
![]() ${\mathcal {O}}$
is ramified at
${\mathcal {O}}$
is ramified at
![]() $2$
, there exists a unique conjugacy class of embeddings
$2$
, there exists a unique conjugacy class of embeddings
![]() ${\mathbb {Z}}_2[i]\hookrightarrow {\mathcal {O}}_{{\mathbb {Z}}_2}$
[Reference VoightVoi21, Proposition 30.5.3]. Therefore, it is enough to verify that
${\mathbb {Z}}_2[i]\hookrightarrow {\mathcal {O}}_{{\mathbb {Z}}_2}$
[Reference VoightVoi21, Proposition 30.5.3]. Therefore, it is enough to verify that
![]() $({\mathcal {O}}/2{\mathcal {O}})^{\langle 1+i \rangle } = ({\mathbb {Z}}/2{\mathbb {Z}})^2$
in a single example, for which this can be checked explicitly. Indeed, one may take
$({\mathcal {O}}/2{\mathcal {O}})^{\langle 1+i \rangle } = ({\mathbb {Z}}/2{\mathbb {Z}})^2$
in a single example, for which this can be checked explicitly. Indeed, one may take
![]() $B = \left (\frac {-1,6}{{\mathbb {Q}}}\right )$
, which has maximal order with
$B = \left (\frac {-1,6}{{\mathbb {Q}}}\right )$
, which has maximal order with
![]() ${\mathbb {Z}}$
-basis
${\mathbb {Z}}$
-basis
![]() $\{1,(1+i+ij)/2,(1-i+ij)/2,(j+ij)/2\}$
. Since
$\{1,(1+i+ij)/2,(1-i+ij)/2,(j+ij)/2\}$
. Since
![]() $\# G$
is coprime to
$\# G$
is coprime to
![]() $3$
, we conclude that
$3$
, we conclude that
![]() $H^1(G,{\mathcal {O}})[6] = {\mathbb {Z}}/2{\mathbb {Z}}$
.
$H^1(G,{\mathcal {O}})[6] = {\mathbb {Z}}/2{\mathbb {Z}}$
.
Case: G = D
3, D
6. Let
![]() $\omega ,j\in {\mathcal {O}}$
be elements satisfying the conclusion of Lemma 2.5. Let
$\omega ,j\in {\mathcal {O}}$
be elements satisfying the conclusion of Lemma 2.5. Let
![]() $C_n\leq D_n$
be the cyclic normal subgroup of order n for
$C_n\leq D_n$
be the cyclic normal subgroup of order n for
![]() $n\in \{3,6\}$
. The low terms of the Lyndon–Hochschild–Serre spectral sequence give rise to the exact sequence
$n\in \{3,6\}$
. The low terms of the Lyndon–Hochschild–Serre spectral sequence give rise to the exact sequence
The subring
![]() ${\mathcal {O}}^{C_n}$
equals
${\mathcal {O}}^{C_n}$
equals
![]() ${\mathcal {O}}^{\langle 1\pm \omega \rangle } = {\mathbb {Z}}[\omega ]$
, and
${\mathcal {O}}^{\langle 1\pm \omega \rangle } = {\mathbb {Z}}[\omega ]$
, and
![]() $C_2=D_n/C_n$
acts on
$C_2=D_n/C_n$
acts on
![]() ${\mathcal {O}}^{C_n}$
via conjugation
${\mathcal {O}}^{C_n}$
via conjugation
![]() $\omega \mapsto \bar {\omega }$
. A cyclic group cohomology calculation shows that
$\omega \mapsto \bar {\omega }$
. A cyclic group cohomology calculation shows that
![]() $H^i(C_2,{\mathbb {Z}}[\omega ])$
is trivial for all
$H^i(C_2,{\mathbb {Z}}[\omega ])$
is trivial for all
![]() $i\geq 1$
. Therefore,
$i\geq 1$
. Therefore,
![]() $H^1(G,{\mathcal {O}})\simeq H^1(C_n,{\mathcal {O}})^{C_2}$
. Assume
$H^1(G,{\mathcal {O}})\simeq H^1(C_n,{\mathcal {O}})^{C_2}$
. Assume
![]() $G=D_6$
. Using the analogous exact sequence to (2.1) for the subgroup
$G=D_6$
. Using the analogous exact sequence to (2.1) for the subgroup
![]() $C_3\leq C_6$
, we get
$C_3\leq C_6$
, we get
![]() $H^1(C_6,{\mathcal {O}})\simeq H^1(C_3,{\mathcal {O}})^{C_2}$
. Since
$H^1(C_6,{\mathcal {O}})\simeq H^1(C_3,{\mathcal {O}})^{C_2}$
. Since
![]() $C_2$
acts trivially on
$C_2$
acts trivially on
![]() $C_3=\{1,g,g^2\}$
and acts as
$C_3=\{1,g,g^2\}$
and acts as
![]() $-1$
on
$-1$
on
![]() $\{x\in {\mathcal {O}} \mid x+gx+g^2x=0\}$
, it will act as
$\{x\in {\mathcal {O}} \mid x+gx+g^2x=0\}$
, it will act as
![]() $-1$
on
$-1$
on
![]() $H^1(C_3,{\mathcal {O}})\simeq ({\mathbb {Z}}/3{\mathbb {Z}})^r$
, so
$H^1(C_3,{\mathcal {O}})\simeq ({\mathbb {Z}}/3{\mathbb {Z}})^r$
, so
![]() $H^1(C_3,{\mathcal {O}})^{C_2}=0$
and so
$H^1(C_3,{\mathcal {O}})^{C_2}=0$
and so
![]() $H^1(G,{\mathcal {O}})\simeq H^1(C_6,{\mathcal {O}})^{C_2}\subset H^1(C_6,{\mathcal {O}}) \simeq H^1(C_3,{\mathcal {O}})^{C_2}$
is zero too in this case. It remains to consider the case
$H^1(G,{\mathcal {O}})\simeq H^1(C_6,{\mathcal {O}})^{C_2}\subset H^1(C_6,{\mathcal {O}}) \simeq H^1(C_3,{\mathcal {O}})^{C_2}$
is zero too in this case. It remains to consider the case
![]() $G=D_3$
. Then
$G=D_3$
. Then
![]() $H^1(G,{\mathcal {O}})\simeq H^1(C_3,{\mathcal {O}})^{C_2}$
. Let
$H^1(G,{\mathcal {O}})\simeq H^1(C_3,{\mathcal {O}})^{C_2}$
. Let
![]() $g\in C_3$
be a generator, given by conjugating by
$g\in C_3$
be a generator, given by conjugating by
![]() $1+\omega $
. Let
$1+\omega $
. Let
![]() $L =\{x\in {\mathcal {O}} \mid x+gx+g^2x=0\}$
. Using the basis
$L =\{x\in {\mathcal {O}} \mid x+gx+g^2x=0\}$
. Using the basis
![]() $\{1,\omega ,j,\omega \}$
of B, we see that
$\{1,\omega ,j,\omega \}$
of B, we see that
![]() $L={\mathcal {O}} \cap {\mathbb {Q}}(\omega )\cdot j$
. Using the explicit description of group cohomology of cyclic groups,
$L={\mathcal {O}} \cap {\mathbb {Q}}(\omega )\cdot j$
. Using the explicit description of group cohomology of cyclic groups,
![]() $H^1(C_3,{\mathcal {O}})$
is isomorphic to
$H^1(C_3,{\mathcal {O}})$
is isomorphic to
![]() $L/(1-g) {\mathcal {O}}$
. Since
$L/(1-g) {\mathcal {O}}$
. Since
![]() $(1-g){\mathcal {O}}$
contains
$(1-g){\mathcal {O}}$
contains
![]() $(1-g)L = (1-\omega )L$
,
$(1-g)L = (1-\omega )L$
,
![]() $H^1(C_3,{\mathcal {O}})$
is a quotient of
$H^1(C_3,{\mathcal {O}})$
is a quotient of
![]() $L/(1-\omega )L$
. Since
$L/(1-\omega )L$
. Since
![]() $(1-\omega )^2 L = 3L$
and
$(1-\omega )^2 L = 3L$
and
![]() $L/3L\simeq ({\mathbb {Z}}/3{\mathbb {Z}})^2$
,
$L/3L\simeq ({\mathbb {Z}}/3{\mathbb {Z}})^2$
,
![]() $L/(1-\omega )L$
is of order
$L/(1-\omega )L$
is of order
![]() $3$
. This shows that
$3$
. This shows that
![]() $H^1(C_3,{\mathcal {O}})=0$
or
$H^1(C_3,{\mathcal {O}})=0$
or
![]() ${\mathbb {Z}}/3{\mathbb {Z}}$
, so
${\mathbb {Z}}/3{\mathbb {Z}}$
, so
![]() $H^1(D_3,{\mathcal {O}}) = 0$
or
$H^1(D_3,{\mathcal {O}}) = 0$
or
![]() ${\mathbb {Z}}/3{\mathbb {Z}}$
, as claimed.
${\mathbb {Z}}/3{\mathbb {Z}}$
, as claimed.
Remark 2.7. All the possibilities of Theorem 2.6 do occur: whenever the group G and the integer N do not uniquely determine
![]() $({\mathcal {O}}/N{\mathcal {O}})^G$
, we give an example for each possibility.
$({\mathcal {O}}/N{\mathcal {O}})^G$
, we give an example for each possibility.
-
• Case
 $(G,N) = (D_1,2)$
. The action of
$(G,N) = (D_1,2)$
. The action of
 $G=\langle [i]\rangle $
on a maximal order
$G=\langle [i]\rangle $
on a maximal order
 ${\mathcal {O}}$
in
${\mathcal {O}}$
in
 $\left (\frac {m,n}{{\mathbb {Q}}}\right )$
, for
$\left (\frac {m,n}{{\mathbb {Q}}}\right )$
, for
 $(m,n) = (10,3), (-1,3),(5,7)$
has
$(m,n) = (10,3), (-1,3),(5,7)$
has
 $({\mathcal {O}}/2{\mathcal {O}})^G\simeq ({\mathbb {Z}}/2{\mathbb {Z}})^2, ({\mathbb {Z}}/2{\mathbb {Z}})^3, ({\mathbb {Z}}/2{\mathbb {Z}})^4$
, respectively.
$({\mathcal {O}}/2{\mathcal {O}})^G\simeq ({\mathbb {Z}}/2{\mathbb {Z}})^2, ({\mathbb {Z}}/2{\mathbb {Z}})^3, ({\mathbb {Z}}/2{\mathbb {Z}})^4$
, respectively. -
• Case
 $(G,N) = (D_2,2)$
. The action of
$(G,N) = (D_2,2)$
. The action of
 $G = \langle [i],[j]\rangle $
on a maximal order
$G = \langle [i],[j]\rangle $
on a maximal order
 ${\mathcal {O}}$
in
${\mathcal {O}}$
in
 $\left (\frac {m,n}{{\mathbb {Q}}}\right )$
, for
$\left (\frac {m,n}{{\mathbb {Q}}}\right )$
, for
 $(m,n) = (5,7), (-1,3)$
has
$(m,n) = (5,7), (-1,3)$
has
 $({\mathcal {O}}/2{\mathcal {O}})^G\simeq ({\mathbb {Z}}/2{\mathbb {Z}})^2, ({\mathbb {Z}}/2{\mathbb {Z}})^3$
, respectively.
$({\mathcal {O}}/2{\mathcal {O}})^G\simeq ({\mathbb {Z}}/2{\mathbb {Z}})^2, ({\mathbb {Z}}/2{\mathbb {Z}})^3$
, respectively. -
• Case
 $(G,N) = (D_3,3)$
. The action of
$(G,N) = (D_3,3)$
. The action of
 $G = \langle [1+\omega ],[j]\rangle $
on a maximal order
$G = \langle [1+\omega ],[j]\rangle $
on a maximal order
 ${\mathcal {O}}$
in
${\mathcal {O}}$
in
 $\left (\frac {m,n}{{\mathbb {Q}}}\right )$
, for
$\left (\frac {m,n}{{\mathbb {Q}}}\right )$
, for
 $(m,n) = (-3,2),(-3,15)$
has
$(m,n) = (-3,2),(-3,15)$
has
 $({\mathcal {O}}/3{\mathcal {O}})^G\simeq ({\mathbb {Z}}/3{\mathbb {Z}}), ({\mathbb {Z}}/3{\mathbb {Z}})^2$
, respectively.
$({\mathcal {O}}/3{\mathcal {O}})^G\simeq ({\mathbb {Z}}/3{\mathbb {Z}}), ({\mathbb {Z}}/3{\mathbb {Z}})^2$
, respectively.
Here we use the standard forms of dihedral action on
![]() ${\mathcal {O}}$
from §2.2. See our associated GitHub repositoryFootnote
1
for a (short) Magma script that verifies these calculations.
${\mathcal {O}}$
from §2.2. See our associated GitHub repositoryFootnote
1
for a (short) Magma script that verifies these calculations.
The next three lemmas give some more precise information about subgroups
![]() $G\subset {\mathrm{Aut}}({\mathcal {O}})$
for which
$G\subset {\mathrm{Aut}}({\mathcal {O}})$
for which
![]() $({\mathcal {O}}/2{\mathcal {O}})^G \simeq ({\mathbb {Z}}/2{\mathbb {Z}})^3$
. In these lemmas, we will use the fact that if
$({\mathcal {O}}/2{\mathcal {O}})^G \simeq ({\mathbb {Z}}/2{\mathbb {Z}})^3$
. In these lemmas, we will use the fact that if
![]() $2\mid {\mathrm{disc}}(B)$
, there exists a unique ring homomorphism
$2\mid {\mathrm{disc}}(B)$
, there exists a unique ring homomorphism
![]() ${\mathcal {O}}/2{\mathcal {O}}\rightarrow \mathbb F_4$
; see [Reference VoightVoi21, Theorem 13.3.11].
${\mathcal {O}}/2{\mathcal {O}}\rightarrow \mathbb F_4$
; see [Reference VoightVoi21, Theorem 13.3.11].
Lemma 2.8. Let
![]() $b\in {\mathcal {O}} \cap N_{B^{\times }}({\mathcal {O}})$
be an element with
$b\in {\mathcal {O}} \cap N_{B^{\times }}({\mathcal {O}})$
be an element with
![]() $b^2 = m \mid {\mathrm{disc}}(B)$
and
$b^2 = m \mid {\mathrm{disc}}(B)$
and
![]() $m\neq 1$
. Write
$m\neq 1$
. Write
![]() $F \subset {\mathcal {O}}/2{\mathcal {O}}$
for the subset centralized by the reduction of b in
$F \subset {\mathcal {O}}/2{\mathcal {O}}$
for the subset centralized by the reduction of b in
![]() ${\mathcal {O}}/2{\mathcal {O}}$
. Then
${\mathcal {O}}/2{\mathcal {O}}$
. Then
![]() $F \simeq ({\mathbb {Z}}/2{\mathbb {Z}})^3$
if and only if
$F \simeq ({\mathbb {Z}}/2{\mathbb {Z}})^3$
if and only if
![]() $2\mid {\mathrm{disc}}(B)$
and
$2\mid {\mathrm{disc}}(B)$
and
![]() $m\equiv 3\ \mod 4$
. In that case, F equals the subset of elements of
$m\equiv 3\ \mod 4$
. In that case, F equals the subset of elements of
![]() ${\mathcal {O}}/2{\mathcal {O}}$
whose image under the ring homomorphism
${\mathcal {O}}/2{\mathcal {O}}$
whose image under the ring homomorphism
![]() ${\mathcal {O}}/2{\mathcal {O}} \rightarrow \mathbb F_4$
lands in
${\mathcal {O}}/2{\mathcal {O}} \rightarrow \mathbb F_4$
lands in
![]() $\mathbb F_2$
.
$\mathbb F_2$
.
Proof. Suppose
![]() $F\simeq ({\mathbb {Z}}/2{\mathbb {Z}})^3$
. We first show that
$F\simeq ({\mathbb {Z}}/2{\mathbb {Z}})^3$
. We first show that
![]() $2\mid {\mathrm{disc}}(B)$
. If not, then m is odd by Lemma 2.2,
$2\mid {\mathrm{disc}}(B)$
. If not, then m is odd by Lemma 2.2,
![]() ${\mathcal {O}}/2{\mathcal {O}} \simeq {\mathrm{Mat}}_2(\mathbb F_2)$
and F is the fixed points of conjugating by an element of order dividing
${\mathcal {O}}/2{\mathcal {O}} \simeq {\mathrm{Mat}}_2(\mathbb F_2)$
and F is the fixed points of conjugating by an element of order dividing
![]() $2$
in
$2$
in
![]() $ {\mathrm{GL}}_2(\mathbb F_2)$
. Since there is only one involution in
$ {\mathrm{GL}}_2(\mathbb F_2)$
. Since there is only one involution in
![]() $ {\mathrm{GL}}_2(\mathbb F_2)$
up to conjugacy, which we may calculate has centralizer
$ {\mathrm{GL}}_2(\mathbb F_2)$
up to conjugacy, which we may calculate has centralizer
![]() $({\mathbb {Z}}/2{\mathbb {Z}})^2$
, this shows that
$({\mathbb {Z}}/2{\mathbb {Z}})^2$
, this shows that
![]() $2\mid {\mathrm{disc}}(B)$
. We now show that
$2\mid {\mathrm{disc}}(B)$
. We now show that
![]() $2\nmid m$
. If
$2\nmid m$
. If
![]() $2\mid m$
, then since m is squarefree, b is a
$2\mid m$
, then since m is squarefree, b is a
![]() $2$
-adic uniformizer of
$2$
-adic uniformizer of
![]() ${\mathcal {O}} \otimes {\mathbb {Z}}_2$
. Then there exists an unramified quadratic subring
${\mathcal {O}} \otimes {\mathbb {Z}}_2$
. Then there exists an unramified quadratic subring
![]() $S\subset {\mathcal {O}}\otimes {\mathbb {Z}}_2$
isomorphic to
$S\subset {\mathcal {O}}\otimes {\mathbb {Z}}_2$
isomorphic to
![]() ${\mathbb {Z}}_2\left [\frac {-1+\sqrt {-3}}{2}\right ]$
such that
${\mathbb {Z}}_2\left [\frac {-1+\sqrt {-3}}{2}\right ]$
such that
![]() ${\mathcal {O}} \otimes {\mathbb {Z}}_2 = S + S\cdot b$
[Reference VoightVoi21, Theorem 13.3.11]. This shows that conjugation by b acts via
${\mathcal {O}} \otimes {\mathbb {Z}}_2 = S + S\cdot b$
[Reference VoightVoi21, Theorem 13.3.11]. This shows that conjugation by b acts via
![]() $x+yb\mapsto \bar {x}+\bar {y}b$
. This map has
$x+yb\mapsto \bar {x}+\bar {y}b$
. This map has
![]() $4$
fixed points; hence, we obtain a contradiction and m is odd. It follows that F is given by the fixed points of conjugating by an element of
$4$
fixed points; hence, we obtain a contradiction and m is odd. It follows that F is given by the fixed points of conjugating by an element of
![]() $({\mathcal {O}}/2{\mathcal {O}})^{\times }$
. This element is trivial if and only if
$({\mathcal {O}}/2{\mathcal {O}})^{\times }$
. This element is trivial if and only if
![]() $b\in 1+2{\mathcal {O}}$
. Since
$b\in 1+2{\mathcal {O}}$
. Since
![]() ${\mathcal {O}}\otimes {\mathbb {Z}}_2$
consists of all integral elements of
${\mathcal {O}}\otimes {\mathbb {Z}}_2$
consists of all integral elements of
![]() $B\otimes {\mathbb {Q}}_2$
[Reference VoightVoi21, Proposition 13.3.4] and since
$B\otimes {\mathbb {Q}}_2$
[Reference VoightVoi21, Proposition 13.3.4] and since
![]() $b\in {\mathcal {O}}$
, this is equivalent to
$b\in {\mathcal {O}}$
, this is equivalent to
![]() $(b-1)/2$
being integral at
$(b-1)/2$
being integral at
![]() $2$
, that is to say to
$2$
, that is to say to
![]() $m \equiv 1\ \mod 4$
. This proves the forward direction of the lemma. For the other direction, note that
$m \equiv 1\ \mod 4$
. This proves the forward direction of the lemma. For the other direction, note that
![]() $({\mathcal {O}}/2{\mathcal {O}})^{\times }$
(where
$({\mathcal {O}}/2{\mathcal {O}})^{\times }$
(where
![]() ${\mathcal {O}}$
is ramified at
${\mathcal {O}}$
is ramified at
![]() $2$
) has a unique involution up to conjugacy, which can be checked to have
$2$
) has a unique involution up to conjugacy, which can be checked to have
![]() $({\mathbb {Z}}/2{\mathbb {Z}})^3$
fixed points in the presentation (6.1).
$({\mathbb {Z}}/2{\mathbb {Z}})^3$
fixed points in the presentation (6.1).
Lemma 2.9. Let
![]() $b\in {\mathcal {O}} \cap N_{B^{\times }}({\mathcal {O}})$
be an element with
$b\in {\mathcal {O}} \cap N_{B^{\times }}({\mathcal {O}})$
be an element with
![]() $b^2 = m \mid {\mathrm{disc}}(B)$
and
$b^2 = m \mid {\mathrm{disc}}(B)$
and
![]() $m\neq 1$
. Suppose that the conjugation action of b on
$m\neq 1$
. Suppose that the conjugation action of b on
![]() ${\mathcal {O}}/2{\mathcal {O}}$
has fixed points
${\mathcal {O}}/2{\mathcal {O}}$
has fixed points
![]() $\simeq ({\mathbb {Z}}/2{\mathbb {Z}})^3$
. Then there exists no
$\simeq ({\mathbb {Z}}/2{\mathbb {Z}})^3$
. Then there exists no
![]() $x\in {\mathcal {O}}/4{\mathcal {O}}$
with
$x\in {\mathcal {O}}/4{\mathcal {O}}$
with
![]() $x \equiv 1\ \mod 2{\mathcal {O}}$
and
$x \equiv 1\ \mod 2{\mathcal {O}}$
and
![]() $b^{-1}xbx = -1$
.
$b^{-1}xbx = -1$
.
Proof. Suppose that
![]() $x\in {\mathcal {O}}/4{\mathcal {O}}$
is such an element. Let
$x\in {\mathcal {O}}/4{\mathcal {O}}$
is such an element. Let
![]() $y = bx$
. Since
$y = bx$
. Since
![]() $m b^{-1} = b$
, multiplying the equation
$m b^{-1} = b$
, multiplying the equation
![]() $b^{-1}xbx = -1$
by m shows that
$b^{-1}xbx = -1$
by m shows that
![]() $y^2 = -m$
in
$y^2 = -m$
in
![]() ${\mathcal {O}}/4{\mathcal {O}}$
. By Lemma 2.8,
${\mathcal {O}}/4{\mathcal {O}}$
. By Lemma 2.8,
![]() $2\mid {\mathrm{disc}}(B)$
and
$2\mid {\mathrm{disc}}(B)$
and
![]() $m \equiv 3 \mod {4}$
, so
$m \equiv 3 \mod {4}$
, so
![]() $y^2=1$
in
$y^2=1$
in
![]() ${\mathcal {O}}/4{\mathcal {O}}$
. Since
${\mathcal {O}}/4{\mathcal {O}}$
. Since
![]() $x \equiv 1\ \mod 2{\mathcal {O}}$
,
$x \equiv 1\ \mod 2{\mathcal {O}}$
,
![]() $y = bx \equiv b\ \mod 2{\mathcal {O}}$
. We may therefore write
$y = bx \equiv b\ \mod 2{\mathcal {O}}$
. We may therefore write
![]() $y = b + 2z$
for some
$y = b + 2z$
for some
![]() $z\in {\mathcal {O}}/4{\mathcal {O}}$
. We compute, in
$z\in {\mathcal {O}}/4{\mathcal {O}}$
. We compute, in
![]() ${\mathcal {O}}/4{\mathcal {O}}$
, that
${\mathcal {O}}/4{\mathcal {O}}$
, that
Since
![]() $y^2=1$
, this shows that
$y^2=1$
, this shows that
![]() $2(bz+zb) = 2$
. Write
$2(bz+zb) = 2$
. Write
![]() $\bar {b}$
and
$\bar {b}$
and
![]() $\bar {z}$
for the mod
$\bar {z}$
for the mod
![]() $2$
reductions of b and z. Then the above identity implies that
$2$
reductions of b and z. Then the above identity implies that
Since
![]() $2$
is ramified in B and
$2$
is ramified in B and
![]() ${\mathcal {O}}$
is maximal, there exists a surjective ring homomorphism
${\mathcal {O}}$
is maximal, there exists a surjective ring homomorphism
![]() $\lambda \colon {\mathcal {O}}/2{\mathcal {O}}\rightarrow \mathbb F_4$
. Applying
$\lambda \colon {\mathcal {O}}/2{\mathcal {O}}\rightarrow \mathbb F_4$
. Applying
![]() $\lambda $
to (2.2) shows that
$\lambda $
to (2.2) shows that
![]() $\lambda (\bar {b})\lambda (\bar {z})+ \lambda (\bar {z})\lambda (\bar {b}) = \lambda (1) = 1$
. Since
$\lambda (\bar {b})\lambda (\bar {z})+ \lambda (\bar {z})\lambda (\bar {b}) = \lambda (1) = 1$
. Since
![]() $\mathbb F_4$
is commutative, the left-hand side of this equation also equals
$\mathbb F_4$
is commutative, the left-hand side of this equation also equals
![]() $2\lambda (\bar {b})\lambda (\bar {z})= 0$
, which is a contradiction.
$2\lambda (\bar {b})\lambda (\bar {z})= 0$
, which is a contradiction.
Recall from Lemma 2.3 that a subgroup
![]() $G\leq N_{B^{\times }}({\mathcal {O}})$
isomorphic to
$G\leq N_{B^{\times }}({\mathcal {O}})$
isomorphic to
![]() $C_2\times C_2$
can be generated by elements
$C_2\times C_2$
can be generated by elements
![]() $i,j\in {\mathcal {O}}$
with
$i,j\in {\mathcal {O}}$
with
![]() $ij = -ji$
,
$ij = -ji$
,
![]() $i^2 = m$
,
$i^2 = m$
,
![]() $j^2=n$
and
$j^2=n$
and
![]() $m,n\mid {\mathrm{disc}}(B)$
.
$m,n\mid {\mathrm{disc}}(B)$
.
Lemma 2.10. Let
![]() $G\subset N_{B^{\times }}({\mathcal {O}})$
be a subgroup isomorphic to
$G\subset N_{B^{\times }}({\mathcal {O}})$
be a subgroup isomorphic to
![]() $C_2\times C_2$
. Then
$C_2\times C_2$
. Then
![]() $({\mathcal {O}}/2{\mathcal {O}})^G \simeq ({\mathbb {Z}}/2{\mathbb {Z}})^3$
if and only if (in the above notation)
$({\mathcal {O}}/2{\mathcal {O}})^G \simeq ({\mathbb {Z}}/2{\mathbb {Z}})^3$
if and only if (in the above notation)
![]() $2\mid {\mathrm{disc}}(B)$
and
$2\mid {\mathrm{disc}}(B)$
and
![]() $m,n \equiv 3\ \mod 4$
.
$m,n \equiv 3\ \mod 4$
.
Proof. Suppose first that
![]() $({\mathcal {O}}/2{\mathcal {O}})^G \simeq ({\mathbb {Z}}/2{\mathbb {Z}})^3$
. Then the conjugation involutions
$({\mathcal {O}}/2{\mathcal {O}})^G \simeq ({\mathbb {Z}}/2{\mathbb {Z}})^3$
. Then the conjugation involutions
![]() $[i]$
and
$[i]$
and
![]() $[j]$
have both
$[j]$
have both
![]() $2^3$
or
$2^3$
or
![]() $2^4$
fixed points on
$2^4$
fixed points on
![]() ${\mathcal {O}}/2{\mathcal {O}}$
. At least one of them, say j, has
${\mathcal {O}}/2{\mathcal {O}}$
. At least one of them, say j, has
![]() $2^3$
fixed points. By Lemma 2.8,
$2^3$
fixed points. By Lemma 2.8,
![]() $2\mid {\mathrm{disc}}(B)$
and
$2\mid {\mathrm{disc}}(B)$
and
![]() $n\equiv 3\ \mod 4$
. If
$n\equiv 3\ \mod 4$
. If
![]() $2\mid m$
, then i is a
$2\mid m$
, then i is a
![]() $2$
-adic uniformizer and the action of i on
$2$
-adic uniformizer and the action of i on
![]() ${\mathcal {O}}/2{\mathcal {O}}$
would have
${\mathcal {O}}/2{\mathcal {O}}$
would have
![]() $2^2$
fixed points (by an argument similar to the proof of Lemma 2.8). So m is odd. If
$2^2$
fixed points (by an argument similar to the proof of Lemma 2.8). So m is odd. If
![]() $m\equiv 1\ \mod 4$
, then the
$m\equiv 1\ \mod 4$
, then the
![]() $2$
-adic Hilbert symbol of
$2$
-adic Hilbert symbol of
![]() $(m,n)$
is trivial, contradicting the fact that
$(m,n)$
is trivial, contradicting the fact that
![]() $2\mid {\mathrm{disc}}(B)$
and
$2\mid {\mathrm{disc}}(B)$
and
![]() $B \simeq \left (\frac {m,n}{{\mathbb {Q}}}\right )$
. We conclude that
$B \simeq \left (\frac {m,n}{{\mathbb {Q}}}\right )$
. We conclude that
![]() $m\equiv 3\ \mod 4$
. The converse follows from Lemma 2.8.
$m\equiv 3\ \mod 4$
. The converse follows from Lemma 2.8.
3 Galois actions, polarizations and endomorphisms
This section collects some preliminaries concerning the arithmetic of
![]() $\mathrm {PQM}$
surfaces. In particular, we study the Galois action on the endomorphism algebra, the set of polarizations, the torsion points and the interaction between these. The most important subsection is §3.2, where the endomorphism field of a
$\mathrm {PQM}$
surfaces. In particular, we study the Galois action on the endomorphism algebra, the set of polarizations, the torsion points and the interaction between these. The most important subsection is §3.2, where the endomorphism field of a
![]() $\mathrm {PQM}$
surface is introduced.
$\mathrm {PQM}$
surface is introduced.
3.1 Abelian surfaces of
 $ {\mathrm{GL}}_2$
-type
$ {\mathrm{GL}}_2$
-type
Recall that an abelian surface A over a number field F is said to be of
![]() $ {\mathrm{GL}}_2$
-type if
$ {\mathrm{GL}}_2$
-type if
![]() $ {\mathrm{End}}^0(A)$
is a quadratic field extension of
$ {\mathrm{End}}^0(A)$
is a quadratic field extension of
![]() ${\mathbb {Q}}$
. We will show that if A is geometrically simple and F admits a real place, then this field must be real quadratic. (The geometrically simple hypothesis is necessary; for example, the simple modular abelian surface
${\mathbb {Q}}$
. We will show that if A is geometrically simple and F admits a real place, then this field must be real quadratic. (The geometrically simple hypothesis is necessary; for example, the simple modular abelian surface
![]() $J_1(13)$
satisfies
$J_1(13)$
satisfies
![]() $ {\mathrm{End}}^0(J_1(13)) \simeq {\mathbb {Q}}(\sqrt {-3})$
.) This is well known over
$ {\mathrm{End}}^0(J_1(13)) \simeq {\mathbb {Q}}(\sqrt {-3})$
.) This is well known over
![]() ${\mathbb {Q}}$
(see [Reference RotgerRot08, Lemma 2.3]), which suffices for our purposes – but we also give an argument that works over any field contained in
${\mathbb {Q}}$
(see [Reference RotgerRot08, Lemma 2.3]), which suffices for our purposes – but we also give an argument that works over any field contained in
![]() $\mathbb R$
that might be of independent interest. (We thank Davide Lombardo for suggesting it.)
$\mathbb R$
that might be of independent interest. (We thank Davide Lombardo for suggesting it.)
Lemma 3.1. Let
![]() $A/\mathbb R$
be an abelian surface. Then
$A/\mathbb R$
be an abelian surface. Then
![]() $ {\mathrm{rk}} \, {\mathrm{NS}}(A) \geq {\mathrm{rk}} \, {\mathrm{NS}}(A_{\mathbb C})-1$
.
$ {\mathrm{rk}} \, {\mathrm{NS}}(A) \geq {\mathrm{rk}} \, {\mathrm{NS}}(A_{\mathbb C})-1$
.
Proof. There exists a two-dimensional
![]() $\mathbb {R}$
-vector space W, a lattice
$\mathbb {R}$
-vector space W, a lattice
![]() $\Lambda \subset W_{\mathbb C} := W\otimes \mathbb C$
stable under the automorphism
$\Lambda \subset W_{\mathbb C} := W\otimes \mathbb C$
stable under the automorphism
![]() $\sigma $
induced by complex conjugation on the second factor, and a complex analytic isomorphism
$\sigma $
induced by complex conjugation on the second factor, and a complex analytic isomorphism
![]() $A(\mathbb C) \simeq (W_{\mathbb C})/\Lambda $
that intertwines complex conjugation on
$A(\mathbb C) \simeq (W_{\mathbb C})/\Lambda $
that intertwines complex conjugation on
![]() $A(\mathbb C)$
with
$A(\mathbb C)$
with
![]() $\sigma $
. Under this isomorphism,
$\sigma $
. Under this isomorphism,
![]() $ {\mathrm{NS}}(A_{\mathbb C})$
can be identified with the set of
$ {\mathrm{NS}}(A_{\mathbb C})$
can be identified with the set of
![]() ${\mathbb {Z}}$
-bilinear alternating forms
${\mathbb {Z}}$
-bilinear alternating forms
![]() $E\colon \Lambda \times \Lambda \rightarrow {\mathbb {Z}}$
with the property that the
$E\colon \Lambda \times \Lambda \rightarrow {\mathbb {Z}}$
with the property that the
![]() $\mathbb {R}$
-linear extension
$\mathbb {R}$
-linear extension
![]() $E_{\mathbb {R}}$
of E to
$E_{\mathbb {R}}$
of E to
![]() $W_{\mathbb C}$
satisfies
$W_{\mathbb C}$
satisfies
![]() $E_{\mathbb {R}}(iv,iw) = E_{\mathbb {R}}(v,w)$
for all
$E_{\mathbb {R}}(iv,iw) = E_{\mathbb {R}}(v,w)$
for all
![]() $v,w\in \Lambda \otimes \mathbb {R} = W_{\mathbb C}$
. By [Reference SilholSil89, Chapter IV, Theorem (3.4)], such an E lies in
$v,w\in \Lambda \otimes \mathbb {R} = W_{\mathbb C}$
. By [Reference SilholSil89, Chapter IV, Theorem (3.4)], such an E lies in
![]() $ {\mathrm{NS}}(A)$
if and only if the associated Hermitian form
$ {\mathrm{NS}}(A)$
if and only if the associated Hermitian form
![]() $E_{\mathbb {R}}(iv,w)+iE_{\mathbb {R}}(v,w)$
is
$E_{\mathbb {R}}(iv,w)+iE_{\mathbb {R}}(v,w)$
is
![]() $\mathbb {R}$
-valued on
$\mathbb {R}$
-valued on
![]() $W\times W$
, that is to say
$W\times W$
, that is to say
![]() $E_{\mathbb {R}}(W,W) = 0$
. Since the intersection
$E_{\mathbb {R}}(W,W) = 0$
. Since the intersection
![]() $\Lambda ' = \Lambda \cap W$
is a lattice in W, the condition
$\Lambda ' = \Lambda \cap W$
is a lattice in W, the condition
![]() $E_{\mathbb {R}}(W,W) = 0$
is equivalent to
$E_{\mathbb {R}}(W,W) = 0$
is equivalent to
![]() $E(\Lambda ',\Lambda ') = 0$
. In conclusion,
$E(\Lambda ',\Lambda ') = 0$
. In conclusion,
![]() $ {\mathrm{NS}}(A) = \ker ( {\mathrm{NS}}(A_{\mathbb C}) \rightarrow {\mathrm{Hom}}(\wedge ^2(\Lambda '),{\mathbb {Z}}))$
, where the map sends E to its restriction to
$ {\mathrm{NS}}(A) = \ker ( {\mathrm{NS}}(A_{\mathbb C}) \rightarrow {\mathrm{Hom}}(\wedge ^2(\Lambda '),{\mathbb {Z}}))$
, where the map sends E to its restriction to
![]() $\Lambda '\times \Lambda '$
. Since the target of this map is isomorphic to
$\Lambda '\times \Lambda '$
. Since the target of this map is isomorphic to
![]() ${\mathbb {Z}}$
, the lemma is proved.
${\mathbb {Z}}$
, the lemma is proved.
Proposition 3.2. Let
![]() $A/\mathbb R$
be a geometrically simple abelian surface. Then
$A/\mathbb R$
be a geometrically simple abelian surface. Then
![]() $ {\mathrm{End}}(A)$
is isomorphic to
$ {\mathrm{End}}(A)$
is isomorphic to
![]() ${\mathbb {Z}}$
or an order in a real quadratic field.
${\mathbb {Z}}$
or an order in a real quadratic field.
Proof. By the classification of endomorphism algebras of simple complex abelian surfaces [Reference Birkenhake and LangeBL04, Proposition 5.5.7, Exercise 9.10(1) and Exercise 9.10(4)],
![]() $ {\mathrm{End}}^0(A_{\mathbb C})$
is isomorphic to either
$ {\mathrm{End}}^0(A_{\mathbb C})$
is isomorphic to either
![]() ${\mathbb {Q}}$
, a real quadratic field, a non-split indefinite quaternion algebra or a quartic CM field. The proposition is clear in the first two cases, so we may assume that we are in one of the latter two cases.
${\mathbb {Q}}$
, a real quadratic field, a non-split indefinite quaternion algebra or a quartic CM field. The proposition is clear in the first two cases, so we may assume that we are in one of the latter two cases.
Since
![]() $ {\mathrm{End}}^0(A)$
acts on the
$ {\mathrm{End}}^0(A)$
acts on the
![]() ${\mathbb {Q}}$
-homology of
${\mathbb {Q}}$
-homology of
![]() $A(\mathbb R)^{\circ } \simeq S^1\times S^1$
, there is a (nonzero, hence injective) map
$A(\mathbb R)^{\circ } \simeq S^1\times S^1$
, there is a (nonzero, hence injective) map
![]() $ {\mathrm{End}}^0(A) \hookrightarrow {\mathrm{Mat}}_2({\mathbb {Q}})$
. Since
$ {\mathrm{End}}^0(A) \hookrightarrow {\mathrm{Mat}}_2({\mathbb {Q}})$
. Since
![]() $ {\mathrm{End}}^0(A_{\mathbb C})$
does not embed in
$ {\mathrm{End}}^0(A_{\mathbb C})$
does not embed in
![]() $ {\mathrm{Mat}}_2({\mathbb {Q}})$
,
$ {\mathrm{Mat}}_2({\mathbb {Q}})$
,
![]() $ {\mathrm{End}}^0(A)\neq {\mathrm{End}}^0(A_{\mathbb C})$
and so
$ {\mathrm{End}}^0(A)\neq {\mathrm{End}}^0(A_{\mathbb C})$
and so
![]() $ {\mathrm{End}}^0(A)$
is at most two-dimensional. It remains to exclude that
$ {\mathrm{End}}^0(A)$
is at most two-dimensional. It remains to exclude that
![]() $ {\mathrm{End}}^0(A)$
is an imaginary quadratic field, so assume for contradiction that this is the case. If
$ {\mathrm{End}}^0(A)$
is an imaginary quadratic field, so assume for contradiction that this is the case. If
![]() $ {\mathrm{End}}^0(A_{\mathbb C})$
is a quaternion algebra, Lemma 3.1 shows that
$ {\mathrm{End}}^0(A_{\mathbb C})$
is a quaternion algebra, Lemma 3.1 shows that
![]() $ {\mathrm{rk}}( {\mathrm{NS}}(A))\geq 3-1 = 2$
, contradicting the fact that
$ {\mathrm{rk}}( {\mathrm{NS}}(A))\geq 3-1 = 2$
, contradicting the fact that
![]() $ {\mathrm{End}}^0(A)$
is imaginary quadratic [Reference Dieulefait and RotgerDR04, p. 9]. If
$ {\mathrm{End}}^0(A)$
is imaginary quadratic [Reference Dieulefait and RotgerDR04, p. 9]. If
![]() $ {\mathrm{End}}(A_{\mathbb C})$
is a quartic CM field F, this CM field has at least two quadratic subfields (namely, its unique real quadratic subfield and
$ {\mathrm{End}}(A_{\mathbb C})$
is a quartic CM field F, this CM field has at least two quadratic subfields (namely, its unique real quadratic subfield and
![]() $ {\mathrm{End}}^0(A)$
), so it must be a biquadratic extension of
$ {\mathrm{End}}^0(A)$
), so it must be a biquadratic extension of
![]() ${\mathbb {Q}}$
. A counting argument then shows that every CM type of F is imprimitive. This implies [Reference LangLan83, Theorem 3.5] that
${\mathbb {Q}}$
. A counting argument then shows that every CM type of F is imprimitive. This implies [Reference LangLan83, Theorem 3.5] that
![]() $A_{\mathbb C}$
is not simple. We again obtain a contradiction and have completed all cases of the proof.
$A_{\mathbb C}$
is not simple. We again obtain a contradiction and have completed all cases of the proof.
3.2 The endomorphism field of a
 $\mathrm {PQM}$
surface
$\mathrm {PQM}$
surface
Let F be a field of characteristic zero and
![]() $A/F$
a
$A/F$
a
![]() $\mathrm {PQM}$
surface. The absolute Galois group
$\mathrm {PQM}$
surface. The absolute Galois group
![]() $ {\mathrm{Gal}}_{F}$
acts on
$ {\mathrm{Gal}}_{F}$
acts on
![]() $ {\mathrm{End}}(A_{\bar {F}})$
on the right by ring automorphisms via
$ {\mathrm{End}}(A_{\bar {F}})$
on the right by ring automorphisms via
![]() $\phi ^{\sigma }(a) = \phi \left (a^{\sigma ^{-1}}\right )^{\sigma }$
for
$\phi ^{\sigma }(a) = \phi \left (a^{\sigma ^{-1}}\right )^{\sigma }$
for
![]() $\sigma \in {\mathrm{Gal}}_F$
,
$\sigma \in {\mathrm{Gal}}_F$
,
![]() $\phi \in {\mathrm{End}}(A_{\bar {F}})$
and
$\phi \in {\mathrm{End}}(A_{\bar {F}})$
and
![]() $a\in A(\bar {F})$
. The kernel of this action cuts out a Galois extension
$a\in A(\bar {F})$
. The kernel of this action cuts out a Galois extension
![]() $L/F$
over which all the endomorphisms of
$L/F$
over which all the endomorphisms of
![]() $A_{\bar {F}}$
are defined. Following [Reference Guralnick and KedlayaGK17], we call L the endomorphism field of A. This determines an injective map
$A_{\bar {F}}$
are defined. Following [Reference Guralnick and KedlayaGK17], we call L the endomorphism field of A. This determines an injective map
![]() $\rho _{ {\mathrm{End}}}\colon {\mathrm{Gal}}(L/F) \rightarrow {\mathrm{Aut}}( {\mathrm{End}}(A_{\bar {F}}))$
. We recall the results of [Reference Dieulefait and RotgerDR04] studying this map which are relevant for our purposes. Write
$\rho _{ {\mathrm{End}}}\colon {\mathrm{Gal}}(L/F) \rightarrow {\mathrm{Aut}}( {\mathrm{End}}(A_{\bar {F}}))$
. We recall the results of [Reference Dieulefait and RotgerDR04] studying this map which are relevant for our purposes. Write
![]() $C_n$
(resp.
$C_n$
(resp.
![]() $D_n$
) for the cyclic (resp. dihedral) group of order n (resp.
$D_n$
) for the cyclic (resp. dihedral) group of order n (resp.
![]() $2n$
). Note the isomorphisms
$2n$
). Note the isomorphisms
![]() $D_1 \simeq C_2$
and
$D_1 \simeq C_2$
and
![]() $D_2 \simeq C_2\times C_2$
.
$D_2 \simeq C_2\times C_2$
.
Proposition 3.3. Let
![]() $A/F$
be a
$A/F$
be a
![]() $\mathrm {PQM}$
surface with endomorphism field L and let
$\mathrm {PQM}$
surface with endomorphism field L and let
![]() $G = {\mathrm{Gal}}(L/F)$
. Then
$G = {\mathrm{Gal}}(L/F)$
. Then
![]() $G \simeq C_n$
or
$G \simeq C_n$
or
![]() $D_n$
for some
$D_n$
for some
![]() $n\in \{1,2,3,4,6\}$
. If F admits an embedding into
$n\in \{1,2,3,4,6\}$
. If F admits an embedding into
![]() $\mathbb {R}$
, then
$\mathbb {R}$
, then
![]() $G\simeq D_n$
for some
$G\simeq D_n$
for some
![]() $n\in \{1,2,3,4,6\}$
.
$n\in \{1,2,3,4,6\}$
.
Proof. The classification of finite subgroups of
![]() $B^{\times }/{\mathbb {Q}}^{\times }$
shows that G is isomorphic to
$B^{\times }/{\mathbb {Q}}^{\times }$
shows that G is isomorphic to
![]() $C_n$
or
$C_n$
or
![]() $D_n$
for some
$D_n$
for some
![]() $n\in \{1,2,3,4,6\}$
[Reference Dieulefait and RotgerDR04, Proposition 2.1]. It therefore suffices to exclude that G is isomorphic to
$n\in \{1,2,3,4,6\}$
[Reference Dieulefait and RotgerDR04, Proposition 2.1]. It therefore suffices to exclude that G is isomorphic to
![]() $C_1, C_3,C_4$
or
$C_1, C_3,C_4$
or
![]() $C_6$
if there exists an embedding
$C_6$
if there exists an embedding
![]() $\iota \colon F\hookrightarrow \mathbb {R}$
. If G is isomorphic to one of these groups, then
$\iota \colon F\hookrightarrow \mathbb {R}$
. If G is isomorphic to one of these groups, then
![]() $ {\mathrm{End}}^0(A)$
is isomorphic to B (if G is trivial) or an imaginary quadratic field [Reference Dieulefait and RotgerDR04, Theorem 3.4(C)]. This contradicts Proposition 3.2.
$ {\mathrm{End}}^0(A)$
is isomorphic to B (if G is trivial) or an imaginary quadratic field [Reference Dieulefait and RotgerDR04, Theorem 3.4(C)]. This contradicts Proposition 3.2.
Lemma 3.4. Let A be a
![]() $\mathrm {PQM}$
surface over a number field F admitting a real place. Then A is of
$\mathrm {PQM}$
surface over a number field F admitting a real place. Then A is of
![]() $ {\mathrm{GL}}_2$
-type if and only if the endomorphism field
$ {\mathrm{GL}}_2$
-type if and only if the endomorphism field
![]() $L/F$
is a quadratic extension.
$L/F$
is a quadratic extension.
Proof. By Proposition 3.2, A is of
![]() $ {\mathrm{GL}}_2$
-type if and only if
$ {\mathrm{GL}}_2$
-type if and only if
![]() $ {\mathrm{End}}(A) \neq {\mathbb {Z}}$
. By [Reference Dieulefait and RotgerDR04, Theorem 3.4(C)],
$ {\mathrm{End}}(A) \neq {\mathbb {Z}}$
. By [Reference Dieulefait and RotgerDR04, Theorem 3.4(C)],
![]() $ {\mathrm{End}}(A) \neq {\mathbb {Z}}$
if and only if L is a cyclic extension of F. By Proposition 3.3,
$ {\mathrm{End}}(A) \neq {\mathbb {Z}}$
if and only if L is a cyclic extension of F. By Proposition 3.3,
![]() $L/F$
is cyclic if and only if it is a quadratic extension.
$L/F$
is cyclic if and only if it is a quadratic extension.
Assume now that A is an
![]() ${\mathcal {O}}$
-
${\mathcal {O}}$
-
![]() $\mathrm {PQM}$
surface and fix an isomorphism
$\mathrm {PQM}$
surface and fix an isomorphism
![]() $ {\mathrm{End}}(A_{\bar {F}})\simeq {\mathcal {O}}$
. By the Skolem–Noether theorem, every ring automorphism of
$ {\mathrm{End}}(A_{\bar {F}})\simeq {\mathcal {O}}$
. By the Skolem–Noether theorem, every ring automorphism of
![]() ${\mathcal {O}}$
is of the form
${\mathcal {O}}$
is of the form
![]() $x\mapsto b^{-1}xb$
for some
$x\mapsto b^{-1}xb$
for some
![]() $b\in B^{\times }$
normalising
$b\in B^{\times }$
normalising
![]() ${\mathcal {O}}$
, and b is uniquely determined up to
${\mathcal {O}}$
, and b is uniquely determined up to
![]() ${\mathbb {Q}}^{\times }$
-multiples. Therefore,
${\mathbb {Q}}^{\times }$
-multiples. Therefore,
![]() $ {\mathrm{Aut}}({\mathcal {O}}) \simeq N_{B^{\times }}({\mathcal {O}})/{\mathbb {Q}}^{\times } \subset B^{\times }/{\mathbb {Q}}^{\times }$
; hence, the map
$ {\mathrm{Aut}}({\mathcal {O}}) \simeq N_{B^{\times }}({\mathcal {O}})/{\mathbb {Q}}^{\times } \subset B^{\times }/{\mathbb {Q}}^{\times }$
; hence, the map
![]() $ {\mathrm{Gal}}(L/F) \rightarrow {\mathrm{Aut}}( {\mathrm{End}}(A_{\bar {F}}))$
can be viewed as an injective homomorphism
$ {\mathrm{Gal}}(L/F) \rightarrow {\mathrm{Aut}}( {\mathrm{End}}(A_{\bar {F}}))$
can be viewed as an injective homomorphism
whose image is isomorphic to
![]() $C_n$
or
$C_n$
or
![]() $D_n$
for some
$D_n$
for some
![]() $n\in \{1,2,3,4,6\}$
by Proposition 3.3.
$n\in \{1,2,3,4,6\}$
by Proposition 3.3.
Remark 3.5. The existence of a polarization of a certain type puts restrictions on the Galois group of the endomorphism field; see [Reference Dieulefait and RotgerDR04, Theorem 3.4]. In particular, that theorem shows that if an
![]() ${\mathcal {O}}$
-
${\mathcal {O}}$
-
![]() $\mathrm {PQM}$
surface A is principally polarized over F, then this Galois group is
$\mathrm {PQM}$
surface A is principally polarized over F, then this Galois group is
![]() $\{1\}$
,
$\{1\}$
,
![]() $C_2$
or
$C_2$
or
![]() $C_2\times C_2$
.
$C_2\times C_2$
.
For future reference, we record the following result of Silverberg [Reference SilverbergSil92, Proposition 2.2].
Proposition 3.6 (Silverberg).
Let
![]() $N\geq 3$
be an integer and suppose that the
$N\geq 3$
be an integer and suppose that the
![]() $ {\mathrm{Gal}}_F$
-action on
$ {\mathrm{Gal}}_F$
-action on
![]() $A[N]$
is trivial. Then
$A[N]$
is trivial. Then
![]() $L = F$
.
$L = F$
.
We also record the useful fact that the endomorphism field is preserved by quadratic twist.
Lemma 3.7. Let
![]() $A/F$
be a
$A/F$
be a
![]() $\mathrm {PQM}$
surface and
$\mathrm {PQM}$
surface and
![]() $M/F$
a quadratic extension. Let
$M/F$
a quadratic extension. Let
![]() $A^M$
be the quadratic twist of A along
$A^M$
be the quadratic twist of A along
![]() $M/F$
. Then under the identification
$M/F$
. Then under the identification
![]() $ {\mathrm{End}}(A_{\bar {F}}) = {\mathrm{End}}((A^M)_{\bar {F}})$
,
$ {\mathrm{End}}(A_{\bar {F}}) = {\mathrm{End}}((A^M)_{\bar {F}})$
,
![]() $\rho _{ {\mathrm{End}},A} = \rho _{ {\mathrm{End}}, A^M}$
.
$\rho _{ {\mathrm{End}},A} = \rho _{ {\mathrm{End}}, A^M}$
.
Proof. This follows from the fact that
![]() $-1$
is central in
$-1$
is central in
![]() $ {\mathrm{End}}(A_{\bar {F}})$
.
$ {\mathrm{End}}(A_{\bar {F}})$
.
3.3 Polarizations and positive involutions
Let A be an abelian surface over a field F of characteristic zero. Recall that a polarization is an ample class L in
![]() $ {\mathrm{NS}}(A)$
. Such a class gives rise to an isogeny
$ {\mathrm{NS}}(A)$
. Such a class gives rise to an isogeny
![]() $\lambda _L\colon A\rightarrow A^{\vee }$
, and we frequently identify L with this isogeny. There exists unique positive integers
$\lambda _L\colon A\rightarrow A^{\vee }$
, and we frequently identify L with this isogeny. There exists unique positive integers
![]() $d_1\mid d_2$
such that
$d_1\mid d_2$
such that
![]() $\ker (\lambda _L)(\bar {F})\simeq ({\mathbb {Z}}/d_1)^2\times ({\mathbb {Z}}/d_2)^2$
; the pair
$\ker (\lambda _L)(\bar {F})\simeq ({\mathbb {Z}}/d_1)^2\times ({\mathbb {Z}}/d_2)^2$
; the pair
![]() $(d_1,d_2)$
is called the type of the polarization, and the integer
$(d_1,d_2)$
is called the type of the polarization, and the integer
![]() $\deg (L) = d_1d_2$
is called its degree. We say two polarizations L and
$\deg (L) = d_1d_2$
is called its degree. We say two polarizations L and
![]() $L'$
are
$L'$
are
![]() ${\mathbb {Q}}^{\times }$
-equivalent if there exist nonzero integers
${\mathbb {Q}}^{\times }$
-equivalent if there exist nonzero integers
![]() $m,n$
such that
$m,n$
such that
![]() $mL = nL'$
, and we call a
$mL = nL'$
, and we call a
![]() ${\mathbb {Q}}^{\times }$
-equivalence class of polarizations a
${\mathbb {Q}}^{\times }$
-equivalence class of polarizations a
![]() ${\mathbb {Q}}^{\times }$
-polarization. Every
${\mathbb {Q}}^{\times }$
-polarization. Every
![]() ${\mathbb {Q}}^{\times }$
-polarization contains a unique polarization of type
${\mathbb {Q}}^{\times }$
-polarization contains a unique polarization of type
![]() $(1,d)$
for some
$(1,d)$
for some
![]() $d\geq 1$
, called a primitive polarization.
$d\geq 1$
, called a primitive polarization.
Recall that a positive involution of B is a
![]() ${\mathbb {Q}}$
-linear involution
${\mathbb {Q}}$
-linear involution
![]() $\iota \colon B\rightarrow B$
satisfying
$\iota \colon B\rightarrow B$
satisfying
![]() $\iota (ab) = \iota (b)\iota (a)$
and
$\iota (ab) = \iota (b)\iota (a)$
and
![]() $ {\mathrm{trd}}(a\iota (a)) \in {\mathbb {Q}}_{\geq 0}$
for all
$ {\mathrm{trd}}(a\iota (a)) \in {\mathbb {Q}}_{\geq 0}$
for all
![]() $a,b\in B$
. By the Skolem–Noether theorem, every such involution is of the form
$a,b\in B$
. By the Skolem–Noether theorem, every such involution is of the form
![]() $b\mapsto \mu ^{-1} \bar {b}\mu $
, where
$b\mapsto \mu ^{-1} \bar {b}\mu $
, where
![]() $\bar {b}= {\mathrm{trd}}(b)-b$
denotes the canonical involution and
$\bar {b}= {\mathrm{trd}}(b)-b$
denotes the canonical involution and
![]() $\mu \in B^{\times }$
is an element with
$\mu \in B^{\times }$
is an element with
![]() $\mu ^2 \in {\mathbb {Q}}_{<0}$
. Two such elements
$\mu ^2 \in {\mathbb {Q}}_{<0}$
. Two such elements
![]() $\mu ,\mu '\in B^{\times }$
give rise to the same involution if and only if
$\mu ,\mu '\in B^{\times }$
give rise to the same involution if and only if
![]() $\mu $
is a
$\mu $
is a
![]() ${\mathbb {Q}}^{\times }$
-multiple of
${\mathbb {Q}}^{\times }$
-multiple of
![]() $\mu '$
.
$\mu '$
.
To combine these two notions, suppose that
![]() $ {\mathrm{End}}(A) = {\mathrm{End}}(A_{\bar {F}})\simeq {\mathcal {O}}$
; let us fix such an isomorphism to identify
$ {\mathrm{End}}(A) = {\mathrm{End}}(A_{\bar {F}})\simeq {\mathcal {O}}$
; let us fix such an isomorphism to identify
![]() $ {\mathrm{End}}(A)$
with
$ {\mathrm{End}}(A)$
with
![]() ${\mathcal {O}}$
. Given a polarization L of A, the Rosati involution on
${\mathcal {O}}$
. Given a polarization L of A, the Rosati involution on
![]() $ {\mathrm{End}}^0(A)$
, defined by
$ {\mathrm{End}}^0(A)$
, defined by
![]() $f \mapsto \lambda _L^{-1}\circ f^{\vee } \circ \lambda _L$
, corresponds to a positive involution
$f \mapsto \lambda _L^{-1}\circ f^{\vee } \circ \lambda _L$
, corresponds to a positive involution
![]() $\iota _L$
of B.
$\iota _L$
of B.
Proposition 3.8. The assignment
![]() $L\mapsto \iota _L$
induces a bijection between the set of
$L\mapsto \iota _L$
induces a bijection between the set of
![]() ${\mathbb {Q}}^{\times }$
-polarizations of A and the set of positive involutions of B. In addition, if L is a polarization and
${\mathbb {Q}}^{\times }$
-polarizations of A and the set of positive involutions of B. In addition, if L is a polarization and
![]() $\mu \in B^{\times }$
is an element such that
$\mu \in B^{\times }$
is an element such that
![]() $\iota _L$
is of the form
$\iota _L$
is of the form
![]() $b\mapsto \mu ^{-1}\bar {b}\mu $
, then
$b\mapsto \mu ^{-1}\bar {b}\mu $
, then
Proof. This can be deduced from [Reference Dieulefait and RotgerDR04, Theorem 3.1] but can also be proved purely algebraically as follows. Choose an element
![]() $\nu \in {\mathcal {O}}$
with
$\nu \in {\mathcal {O}}$
with
![]() $\nu ^2 = - {\mathrm{disc}}(B)$
. Then it is well known [Reference VoightVoi21, Lemma 43.6.23] that A has a unique principal polarization M such that
$\nu ^2 = - {\mathrm{disc}}(B)$
. Then it is well known [Reference VoightVoi21, Lemma 43.6.23] that A has a unique principal polarization M such that
![]() $\iota _M(b) = \nu ^{-1} \bar {b} \nu $
for all
$\iota _M(b) = \nu ^{-1} \bar {b} \nu $
for all
![]() $b\in B$
. To determine all polarizations of A, consider the maps
$b\in B$
. To determine all polarizations of A, consider the maps
where
![]() $\alpha (L)=\lambda _M^{-1}\circ \lambda _L $
and
$\alpha (L)=\lambda _M^{-1}\circ \lambda _L $
and
![]() $\beta (x) = \nu x$
. Since
$\beta (x) = \nu x$
. Since
![]() $L\mapsto \lambda _L$
induces a bijection
$L\mapsto \lambda _L$
induces a bijection
![]() $ {\mathrm{NS}}(A)\otimes {\mathbb {Q}} \rightarrow \{f\in {\mathrm{Hom}}(A,A^{\vee })\mid f^{\vee }=f\}$
,
$ {\mathrm{NS}}(A)\otimes {\mathbb {Q}} \rightarrow \{f\in {\mathrm{Hom}}(A,A^{\vee })\mid f^{\vee }=f\}$
,
![]() $\alpha $
is a bijection. Moreover,
$\alpha $
is a bijection. Moreover,
![]() $\beta $
is a bijection by a direct computation. In addition, one can also compute that the Rosati involution associated to a Neron–Severi class L is given by conjugation by
$\beta $
is a bijection by a direct computation. In addition, one can also compute that the Rosati involution associated to a Neron–Severi class L is given by conjugation by
![]() $\beta (\alpha (L))$
. Both
$\beta (\alpha (L))$
. Both
![]() $( {\mathrm{NS}}(A)\otimes {\mathbb {Q}})\setminus \{0\}$
and
$( {\mathrm{NS}}(A)\otimes {\mathbb {Q}})\setminus \{0\}$
and
![]() $\{\mu \in B^{\times } \mid \bar {\mu } = -\mu \}$
have evident
$\{\mu \in B^{\times } \mid \bar {\mu } = -\mu \}$
have evident
![]() ${\mathbb {Q}}^{\times }$
-actions, and their quotients are given by the set of
${\mathbb {Q}}^{\times }$
-actions, and their quotients are given by the set of
![]() ${\mathbb {Q}}^{\times }$
-polarizations and the set of positive involutions on B, respectively. Combining these observations shows that
${\mathbb {Q}}^{\times }$
-polarizations and the set of positive involutions on B, respectively. Combining these observations shows that
![]() $L\mapsto \iota _L$
is indeed a bijection between the set of
$L\mapsto \iota _L$
is indeed a bijection between the set of
![]() ${\mathbb {Q}}^{\times }$
-polarizations and the set of positive involutions. To check (3.2), we compute that for
${\mathbb {Q}}^{\times }$
-polarizations and the set of positive involutions. To check (3.2), we compute that for
![]() $\alpha (L) = x$
and
$\alpha (L) = x$
and
![]() $\mu = \nu x$
:
$\mu = \nu x$
:
![]() $\deg (L) = {\mathrm{nrd}}(x) = {\mathrm{nrd}}(\mu )/ {\mathrm{nrd}}(\nu ) \equiv {\mathrm{disc}}(B) \cdot {\mathrm{nrd}}(\mu )\ \mod {\mathbb {Q}}^{\times 2}$
.
$\deg (L) = {\mathrm{nrd}}(x) = {\mathrm{nrd}}(\mu )/ {\mathrm{nrd}}(\nu ) \equiv {\mathrm{disc}}(B) \cdot {\mathrm{nrd}}(\mu )\ \mod {\mathbb {Q}}^{\times 2}$
.
Remark 3.9. If we want to avoid choosing an isomorphism
![]() $ {\mathrm{End}}(A)\simeq {\mathcal {O}}$
, we may rephrase Proposition 3.8 as saying that there is a bijection between
$ {\mathrm{End}}(A)\simeq {\mathcal {O}}$
, we may rephrase Proposition 3.8 as saying that there is a bijection between
![]() ${\mathbb {Q}}^{\times }$
-polarizations on A and positive involutions on the quaternion algebra
${\mathbb {Q}}^{\times }$
-polarizations on A and positive involutions on the quaternion algebra
![]() $ {\mathrm{End}}^0(A)$
.
$ {\mathrm{End}}^0(A)$
.
Now suppose that
![]() $A/F$
is an abelian surface with
$A/F$
is an abelian surface with
![]() $ {\mathrm{End}}(A_{\bar {F}})\simeq {\mathcal {O}}$
. Recall from §3.2 that
$ {\mathrm{End}}(A_{\bar {F}})\simeq {\mathcal {O}}$
. Recall from §3.2 that
![]() $ {\mathrm{Gal}}_F$
acts on
$ {\mathrm{Gal}}_F$
acts on
![]() $ {\mathrm{End}}(A_{\bar {F}})$
by ring automorphisms. If L is a polarization on
$ {\mathrm{End}}(A_{\bar {F}})$
by ring automorphisms. If L is a polarization on
![]() $A_{\bar {F}}$
, the Rosati involution associated to L is of the form
$A_{\bar {F}}$
, the Rosati involution associated to L is of the form
![]() $b\mapsto \mu ^{-1}b\mu $
for some
$b\mapsto \mu ^{-1}b\mu $
for some
![]() $\mu \in {\mathrm{End}}^0(A_{\bar {F}})$
, uniquely determined up to
$\mu \in {\mathrm{End}}^0(A_{\bar {F}})$
, uniquely determined up to
![]() ${\mathbb {Q}}^{\times }$
-multiple. Therefore, the imaginary quadratic field
${\mathbb {Q}}^{\times }$
-multiple. Therefore, the imaginary quadratic field
![]() ${\mathbb {Q}}(\mu )\subset {\mathrm{End}}^0(A_{\bar {F}})$
is independent of the choice of
${\mathbb {Q}}(\mu )\subset {\mathrm{End}}^0(A_{\bar {F}})$
is independent of the choice of
![]() $\mu $
.
$\mu $
.
Corollary 3.10. The map
![]() $L\mapsto {\mathbb {Q}}(\mu )$
constructed above induces a bijection between
$L\mapsto {\mathbb {Q}}(\mu )$
constructed above induces a bijection between
![]() ${\mathbb {Q}}^{\times }$
-polarizations of
${\mathbb {Q}}^{\times }$
-polarizations of
![]() $A_{\bar {F}}$
and imaginary quadratic fields contained in
$A_{\bar {F}}$
and imaginary quadratic fields contained in
![]() $ {\mathrm{End}}^0(A_{\bar {F}})$
. A polarization descends to A if and only if the imaginary quadratic field is
$ {\mathrm{End}}^0(A_{\bar {F}})$
. A polarization descends to A if and only if the imaginary quadratic field is
![]() $ {\mathrm{Gal}}_F$
-normalized.
$ {\mathrm{Gal}}_F$
-normalized.
Proof. The bijection part immediately follows from Proposition 3.8, together with the fact that the set of positive involutions on
![]() $ {\mathrm{End}}^0(A_{\bar {F}})$
is in bijection with the set of imaginary quadratic subfields of
$ {\mathrm{End}}^0(A_{\bar {F}})$
is in bijection with the set of imaginary quadratic subfields of
![]() $ {\mathrm{End}}^0(A_{\bar {F}})$
.
$ {\mathrm{End}}^0(A_{\bar {F}})$
.
Since taking the Rosati involution is
![]() $ {\mathrm{Gal}}_F$
-equivariant, this bijection preserves the Galois action on both sides. This induces a bijection on the
$ {\mathrm{Gal}}_F$
-equivariant, this bijection preserves the Galois action on both sides. This induces a bijection on the
![]() $ {\mathrm{Gal}}_F$
-fixed points on both sides, justifying the last sentence of the corollary.
$ {\mathrm{Gal}}_F$
-fixed points on both sides, justifying the last sentence of the corollary.
3.4 The distinguished quadratic subring
If
![]() $A/{\mathbb {Q}}$
is an
$A/{\mathbb {Q}}$
is an
![]() ${\mathcal {O}}$
-
${\mathcal {O}}$
-
![]() $\mathrm {PQM}$
surface of
$\mathrm {PQM}$
surface of
![]() $ {\mathrm{GL}}_2$
-type, then the torsion groups
$ {\mathrm{GL}}_2$
-type, then the torsion groups
![]() $A[n]$
are modules over
$A[n]$
are modules over
![]() $S/nS$
, where S is the real quadratic ring
$S/nS$
, where S is the real quadratic ring
![]() $ {\mathrm{End}}(A)$
. If A is not of
$ {\mathrm{End}}(A)$
. If A is not of
![]() $ {\mathrm{GL}}_2$
-type, then
$ {\mathrm{GL}}_2$
-type, then
![]() $ {\mathrm{End}}(A) = {\mathbb {Z}}$
, and so it may seem that there is no structure to exploit. However, we have seen in Corollary 3.10 that any polarization of A determines a
$ {\mathrm{End}}(A) = {\mathbb {Z}}$
, and so it may seem that there is no structure to exploit. However, we have seen in Corollary 3.10 that any polarization of A determines a
![]() $ {\mathrm{Gal}}_{{\mathbb {Q}}}$
-stable imaginary quadratic subring
$ {\mathrm{Gal}}_{{\mathbb {Q}}}$
-stable imaginary quadratic subring
![]() $S \subset {\mathrm{End}}(A_{\overline {\mathbb {Q}}})$
.
$S \subset {\mathrm{End}}(A_{\overline {\mathbb {Q}}})$
.
Definition 3.3. Let
![]() $A/{\mathbb {Q}}$
be an
$A/{\mathbb {Q}}$
be an
![]() ${\mathcal {O}}$
-
${\mathcal {O}}$
-
![]() $\mathrm {PQM}$
surface. If A is of
$\mathrm {PQM}$
surface. If A is of
![]() $ {\mathrm{GL}}_2$
-type, let
$ {\mathrm{GL}}_2$
-type, let
![]() $M = {\mathrm{End}}^0(A)$
. Otherwise, let
$M = {\mathrm{End}}^0(A)$
. Otherwise, let
![]() $M\subset {\mathrm{End}}^0(A_{\overline {\mathbb {Q}}})$
be the imaginary quadratic field corresponding to the unique primitive polarization on A via Corollary 3.10. We call
$M\subset {\mathrm{End}}^0(A_{\overline {\mathbb {Q}}})$
be the imaginary quadratic field corresponding to the unique primitive polarization on A via Corollary 3.10. We call
![]() $M\subset {\mathrm{End}}^0(A_{\overline {\mathbb {Q}}})$
the distinguished quadratic subfield and
$M\subset {\mathrm{End}}^0(A_{\overline {\mathbb {Q}}})$
the distinguished quadratic subfield and
![]() $S = M \cap {\mathrm{End}}(A_{\overline {\mathbb {Q}}})$
the distinguished quadratic subring of A.
$S = M \cap {\mathrm{End}}(A_{\overline {\mathbb {Q}}})$
the distinguished quadratic subring of A.
The next proposition describes the distinguished quadratic subring more explicitly.
Proposition 3.11. Let
![]() $A/{\mathbb {Q}}$
be an
$A/{\mathbb {Q}}$
be an
![]() ${\mathcal {O}}$
-
${\mathcal {O}}$
-
![]() $\mathrm {PQM}$
surface and let S be its distinguished quadratic subring, seen as a subring of
$\mathrm {PQM}$
surface and let S be its distinguished quadratic subring, seen as a subring of
![]() ${\mathcal {O}}$
using an isomorphism
${\mathcal {O}}$
using an isomorphism
![]() ${\mathcal {O}} \simeq {\mathrm{End}}(A_{\overline {\mathbb {Q}}})$
. Let G be the Galois group of the endomorphism field of A (as in §3.2).
${\mathcal {O}} \simeq {\mathrm{End}}(A_{\overline {\mathbb {Q}}})$
. Let G be the Galois group of the endomorphism field of A (as in §3.2).
-
(a) S is isomorphic to an order of
 ${\mathbb {Q}}(\sqrt {m})$
containing
${\mathbb {Q}}(\sqrt {m})$
containing
 ${\mathbb {Z}}[\sqrt {m}]$
for some
${\mathbb {Z}}[\sqrt {m}]$
for some
 $m\in {\mathbb {Z}}_{\geq 2}$
dividing
$m\in {\mathbb {Z}}_{\geq 2}$
dividing
 $ {\mathrm{disc}}(B)$
if
$ {\mathrm{disc}}(B)$
if
 $G=C_2$
; to an order of
$G=C_2$
; to an order of
 ${\mathbb {Q}}(\sqrt {-m})$
containing
${\mathbb {Q}}(\sqrt {-m})$
containing
 ${\mathbb {Z}}[\sqrt {-m}]$
for some
${\mathbb {Z}}[\sqrt {-m}]$
for some
 $m\in {\mathbb {Z}}_{\geq 2}$
dividing
$m\in {\mathbb {Z}}_{\geq 2}$
dividing
 $ {\mathrm{disc}}(B)$
if
$ {\mathrm{disc}}(B)$
if
 $G = D_2$
; to
$G = D_2$
; to
 ${\mathbb {Z}}[i]$
with
${\mathbb {Z}}[i]$
with
 $i^2=-1$
if
$i^2=-1$
if
 $G= D_4$
; and to
$G= D_4$
; and to
 ${\mathbb {Z}}[\omega ]$
with
${\mathbb {Z}}[\omega ]$
with
 $\omega ^3 = 1$
if
$\omega ^3 = 1$
if
 $G = D_3$
or
$G = D_3$
or
 $D_6$
.
$D_6$
. -
(b) S is an order in a quadratic field, maximal away from
 $2$
and unramified away from
$2$
and unramified away from
 $6 {\mathrm{disc}}(B)$
.
$6 {\mathrm{disc}}(B)$
.
Proof. The description of S in the
![]() $C_2$
case follows from Lemma 2.2. If
$C_2$
case follows from Lemma 2.2. If
![]() $G\not \simeq C_2$
(in other words, if A is not of
$G\not \simeq C_2$
(in other words, if A is not of
![]() $ {\mathrm{GL}}_2$
-type by Lemma 3.4), then Corollary 3.10 shows that S is the unique imaginary quadratic subring of
$ {\mathrm{GL}}_2$
-type by Lemma 3.4), then Corollary 3.10 shows that S is the unique imaginary quadratic subring of
![]() $ {\mathrm{End}}(A_{\overline {\mathbb {Q}}})$
that is
$ {\mathrm{End}}(A_{\overline {\mathbb {Q}}})$
that is
![]() $ {\mathrm{Gal}}_{{\mathbb {Q}}}$
-stable and that is optimally embedded (i.e.,
$ {\mathrm{Gal}}_{{\mathbb {Q}}}$
-stable and that is optimally embedded (i.e.,
![]() $(S\otimes {\mathbb {Q}}) \cap {\mathcal {O}} = S$
). So to prove (a), it suffices to find a subring of
$(S\otimes {\mathbb {Q}}) \cap {\mathcal {O}} = S$
). So to prove (a), it suffices to find a subring of
![]() ${\mathcal {O}}$
satisfying the stated conditions. This follows from the explicit description of the G-action given in §2.2. Part (b) immediately follows from the first part.
${\mathcal {O}}$
satisfying the stated conditions. This follows from the explicit description of the G-action given in §2.2. Part (b) immediately follows from the first part.
3.5 The enhanced Galois representation
Let A be an
![]() ${\mathcal {O}}$
-
${\mathcal {O}}$
-
![]() $\mathrm {PQM}$
surface over a field F of characteristic zero and fix an isomorphism
$\mathrm {PQM}$
surface over a field F of characteristic zero and fix an isomorphism
![]() ${\mathcal {O}}\simeq {\mathrm{End}}(A_{\bar {F}})$
so that
${\mathcal {O}}\simeq {\mathrm{End}}(A_{\bar {F}})$
so that
![]() ${\mathcal {O}}$
acts on
${\mathcal {O}}$
acts on
![]() $A_{\bar {F}}$
on the left. In §3.2, we have described how
$A_{\bar {F}}$
on the left. In §3.2, we have described how
![]() $ {\mathrm{Gal}}_F$
acts on the endomorphism ring
$ {\mathrm{Gal}}_F$
acts on the endomorphism ring
![]() ${\mathcal {O}}$
; this action is encoded by the homomorphism
${\mathcal {O}}$
; this action is encoded by the homomorphism
![]() $\rho _{ {\mathrm{End}}}\colon {\mathrm{Gal}}_F\rightarrow {\mathrm{Aut}}({\mathcal {O}})$
of Equation 3.1. However,
$\rho _{ {\mathrm{End}}}\colon {\mathrm{Gal}}_F\rightarrow {\mathrm{Aut}}({\mathcal {O}})$
of Equation 3.1. However,
![]() $ {\mathrm{Gal}}_F$
acts on the torsion points of
$ {\mathrm{Gal}}_F$
acts on the torsion points of
![]() $A_{\bar {F}}$
. In this section, we formalize the interaction of these two
$A_{\bar {F}}$
. In this section, we formalize the interaction of these two
![]() $ {\mathrm{Gal}}_F$
-actions using a homomorphism that we call the enhanced Galois representation. This basic definition might be of independent interest and will be used in the proof of Theorem 1.4, more specifically to exclude
$ {\mathrm{Gal}}_F$
-actions using a homomorphism that we call the enhanced Galois representation. This basic definition might be of independent interest and will be used in the proof of Theorem 1.4, more specifically to exclude
![]() $({\mathbb {Z}}/2{\mathbb {Z}})^3$
in the
$({\mathbb {Z}}/2{\mathbb {Z}})^3$
in the
![]() $ {\mathrm{GL}}_2$
-type case in Proposition 5.16.
$ {\mathrm{GL}}_2$
-type case in Proposition 5.16.
Let
![]() $I\subset {\mathcal {O}}$
be a
$I\subset {\mathcal {O}}$
be a
![]() $ {\mathrm{Gal}}_F$
-stable two-sided ideal – for example,
$ {\mathrm{Gal}}_F$
-stable two-sided ideal – for example,
![]() $I = N\cdot {\mathcal {O}}$
for some integer
$I = N\cdot {\mathcal {O}}$
for some integer
![]() $N\geq 1$
. The subgroup
$N\geq 1$
. The subgroup
![]() $A[I](\bar {F})\subset A(\bar {F})$
of points killed by I is a
$A[I](\bar {F})\subset A(\bar {F})$
of points killed by I is a
![]() $ {\mathrm{Gal}}_F$
-module. Let
$ {\mathrm{Gal}}_F$
-module. Let
![]() $ {\mathrm{GL}}(A[I])$
be the group of
$ {\mathrm{GL}}(A[I])$
be the group of
![]() ${\mathbb {Z}}$
-module automorphisms of
${\mathbb {Z}}$
-module automorphisms of
![]() $A[I](\bar {F})$
, seen as acting on
$A[I](\bar {F})$
, seen as acting on
![]() $A[I](\bar {F})$
on the right. The
$A[I](\bar {F})$
on the right. The
![]() $ {\mathrm{Gal}}_F$
-action on
$ {\mathrm{Gal}}_F$
-action on
![]() $A[I]$
is encoded in a homomorphism
$A[I]$
is encoded in a homomorphism
![]() $\rho _I\colon {\mathrm{Gal}}_F\rightarrow {\mathrm{GL}}(A[I])$
. The left
$\rho _I\colon {\mathrm{Gal}}_F\rightarrow {\mathrm{GL}}(A[I])$
. The left
![]() ${\mathcal {O}}$
-action on
${\mathcal {O}}$
-action on
![]() $A_{\bar {F}}$
induces an
$A_{\bar {F}}$
induces an
![]() ${\mathcal {O}}/I$
-action on
${\mathcal {O}}/I$
-action on
![]() $A[I](\bar {F})$
such that
$A[I](\bar {F})$
such that
for all
![]() $P \in A[I](\bar {F}), \ a \in {\mathcal {O}}$
and
$P \in A[I](\bar {F}), \ a \in {\mathcal {O}}$
and
![]() $\sigma \in {\mathrm{Gal}}_F.$
Let
$\sigma \in {\mathrm{Gal}}_F.$
Let
![]() $ {\mathrm{Aut}}^{\circ }(A[I])$
be the subgroup of pairs
$ {\mathrm{Aut}}^{\circ }(A[I])$
be the subgroup of pairs
![]() $(\gamma , \varphi ) \in {\mathrm{Aut}}({\mathcal {O}}) \times {\mathrm{GL}}(A[I])$
such that
$(\gamma , \varphi ) \in {\mathrm{Aut}}({\mathcal {O}}) \times {\mathrm{GL}}(A[I])$
such that
![]() $(a\cdot P)^{\varphi } = a^{\gamma } \cdot P^{\varphi }$
for all
$(a\cdot P)^{\varphi } = a^{\gamma } \cdot P^{\varphi }$
for all
![]() $a\in {\mathcal {O}}$
and
$a\in {\mathcal {O}}$
and
![]() $P \in A[I](\bar {F})$
. The compatibility (3.4) implies that the product homomorphism
$P \in A[I](\bar {F})$
. The compatibility (3.4) implies that the product homomorphism
![]() $\rho _{ {\mathrm{End}}}\times \rho _I\colon {\mathrm{Gal}}_F \rightarrow {\mathrm{Aut}}({\mathcal {O}})\times {\mathrm{GL}}(A[I])$
lands in
$\rho _{ {\mathrm{End}}}\times \rho _I\colon {\mathrm{Gal}}_F \rightarrow {\mathrm{Aut}}({\mathcal {O}})\times {\mathrm{GL}}(A[I])$
lands in
![]() $ {\mathrm{Aut}}^{\circ }(A[I])$
, so we obtain a homomorphism
$ {\mathrm{Aut}}^{\circ }(A[I])$
, so we obtain a homomorphism
We now identity
![]() $ {\mathrm{Aut}}^{\circ }(A[I])$
with an explicit semidirect product. Consider the group
$ {\mathrm{Aut}}^{\circ }(A[I])$
with an explicit semidirect product. Consider the group
![]() $ {\mathrm{Aut}}({\mathcal {O}})\ltimes ({\mathcal {O}}/I)^{\times }$
, where
$ {\mathrm{Aut}}({\mathcal {O}})\ltimes ({\mathcal {O}}/I)^{\times }$
, where
![]() $ {\mathrm{Aut}}({\mathcal {O}})$
acts on
$ {\mathrm{Aut}}({\mathcal {O}})$
acts on
![]() $({\mathcal {O}}/I)^{\times }$
via restricting the standard right
$({\mathcal {O}}/I)^{\times }$
via restricting the standard right
![]() $ {\mathrm{Aut}}({\mathcal {O}})$
-action on
$ {\mathrm{Aut}}({\mathcal {O}})$
-action on
![]() ${\mathcal {O}}/I$
to
${\mathcal {O}}/I$
to
![]() $({\mathcal {O}}/I)^{\times }$
. Multiplication in this group is given by
$({\mathcal {O}}/I)^{\times }$
. Multiplication in this group is given by
![]() $(\gamma _1,x_1) \cdot (\gamma _2,x_2) = (\gamma _1\gamma _2, x_1^{\gamma _2}x_2)$
. The
$(\gamma _1,x_1) \cdot (\gamma _2,x_2) = (\gamma _1\gamma _2, x_1^{\gamma _2}x_2)$
. The
![]() ${\mathcal {O}}/I$
-module
${\mathcal {O}}/I$
-module
![]() $A[I](\bar {F})$
is free of rank
$A[I](\bar {F})$
is free of rank
![]() $1$
[Reference OhtaOht74]. Let
$1$
[Reference OhtaOht74]. Let
![]() $Q \in A[I](\bar {F})$
be an
$Q \in A[I](\bar {F})$
be an
![]() ${\mathcal {O}}/I$
-module generator. For every
${\mathcal {O}}/I$
-module generator. For every
![]() $(\gamma ,x) \in {\mathrm{Aut}}({\mathcal {O}})\ltimes ({\mathcal {O}}/I)^{\times }$
, let
$(\gamma ,x) \in {\mathrm{Aut}}({\mathcal {O}})\ltimes ({\mathcal {O}}/I)^{\times }$
, let
![]() $\varphi _{(\gamma ,x)}$
be the element of
$\varphi _{(\gamma ,x)}$
be the element of
![]() $ {\mathrm{GL}}(A[I])$
sending
$ {\mathrm{GL}}(A[I])$
sending
![]() $a\cdot Q$
to
$a\cdot Q$
to
![]() $a^{\gamma } x\cdot Q$
for all
$a^{\gamma } x\cdot Q$
for all
![]() $a\in {\mathcal {O}}/I$
.
$a\in {\mathcal {O}}/I$
.
Lemma 3.12. The map
![]() $(\gamma , x)\mapsto (\gamma , \varphi _{(\gamma ,x)})$
induces an isomorphism
$(\gamma , x)\mapsto (\gamma , \varphi _{(\gamma ,x)})$
induces an isomorphism
![]() $ {\mathrm{Aut}}({\mathcal {O}})\ltimes ({\mathcal {O}}/I)^{\times }\xrightarrow {\sim } {\mathrm{Aut}}^{\circ }(A[I])$
.
$ {\mathrm{Aut}}({\mathcal {O}})\ltimes ({\mathcal {O}}/I)^{\times }\xrightarrow {\sim } {\mathrm{Aut}}^{\circ }(A[I])$
.
Proof. This is a formal verification. The inverse of this isomorphism is given by sending
![]() $(\gamma , \varphi )$
to
$(\gamma , \varphi )$
to
![]() $(\gamma , x)$
, where
$(\gamma , x)$
, where
![]() $x\in ({\mathcal {O}}/I)^{\times }$
is the unique element with
$x\in ({\mathcal {O}}/I)^{\times }$
is the unique element with
![]() $Q^{\varphi } = x\cdot Q$
.
$Q^{\varphi } = x\cdot Q$
.
Using Lemma 3.12, we may view the homomorphism (3.5) as a homomorphism
Definition 3.7. The homomorphism (3.5) – or, after a choice of
![]() ${\mathcal {O}}/I$
-module generator of
${\mathcal {O}}/I$
-module generator of
![]() $A[I](\bar {F})$
, the homomorphism (3.6) – is called the enhanced Galois representation associated to A and I.
$A[I](\bar {F})$
, the homomorphism (3.6) – is called the enhanced Galois representation associated to A and I.
Since
![]() $ {\mathrm{Aut}}^{\circ }(A[I])$
is a subgroup of
$ {\mathrm{Aut}}^{\circ }(A[I])$
is a subgroup of
![]() $ {\mathrm{Aut}}({\mathcal {O}})\times {\mathrm{GL}}(A[I])$
, it comes equipped with projection homomorphisms
$ {\mathrm{Aut}}({\mathcal {O}})\times {\mathrm{GL}}(A[I])$
, it comes equipped with projection homomorphisms
![]() $\pi _1\colon {\mathrm{Aut}}^{\circ }(A[I])\rightarrow {\mathrm{Aut}}({\mathcal {O}})$
and
$\pi _1\colon {\mathrm{Aut}}^{\circ }(A[I])\rightarrow {\mathrm{Aut}}({\mathcal {O}})$
and
![]() $\pi _2\colon {\mathrm{Aut}}^{\circ }(A[I])\rightarrow {\mathrm{GL}}(A[I])$
satisfying
$\pi _2\colon {\mathrm{Aut}}^{\circ }(A[I])\rightarrow {\mathrm{GL}}(A[I])$
satisfying
![]() $\rho _{ {\mathrm{End}}} = \pi _1 \circ \rho ^{\circ }_I$
and
$\rho _{ {\mathrm{End}}} = \pi _1 \circ \rho ^{\circ }_I$
and
![]() $\rho _I = \pi _2 \circ \rho _{I}^{\circ }$
.
$\rho _I = \pi _2 \circ \rho _{I}^{\circ }$
.
Remark 3.13. Suppose that
![]() $\rho _{ {\mathrm{End}}}$
is trivial; in other words,
$\rho _{ {\mathrm{End}}}$
is trivial; in other words,
![]() $ {\mathrm{End}}(A) = {\mathrm{End}}(A_{\bar {F}}) \simeq {\mathcal {O}}$
. Then the homomorphism (3.6) lands in the subgroup
$ {\mathrm{End}}(A) = {\mathrm{End}}(A_{\bar {F}}) \simeq {\mathcal {O}}$
. Then the homomorphism (3.6) lands in the subgroup
![]() $\{1\} \ltimes ({\mathcal {O}}/I)^{\times }$
and hence simplifies to a homomorphism
$\{1\} \ltimes ({\mathcal {O}}/I)^{\times }$
and hence simplifies to a homomorphism
![]() $ {\mathrm{Gal}}_F\rightarrow ({\mathcal {O}}/I)^{\times }$
. This recovers the well-known description [Reference OhtaOht74] of the Galois representation
$ {\mathrm{Gal}}_F\rightarrow ({\mathcal {O}}/I)^{\times }$
. This recovers the well-known description [Reference OhtaOht74] of the Galois representation
![]() $\rho _I$
in this case.
$\rho _I$
in this case.
We show that, usually, the image of
![]() $\rho ^{\circ }_I$
is isomorphic to the image of
$\rho ^{\circ }_I$
is isomorphic to the image of
![]() $\rho _I$
, using the following well-known lemma.
$\rho _I$
, using the following well-known lemma.
Lemma 3.14. Let G be a finite subgroup of
![]() $ {\mathrm{GL}}_n({\mathbb {Z}})$
for some
$ {\mathrm{GL}}_n({\mathbb {Z}})$
for some
![]() $n\geq 1$
and let
$n\geq 1$
and let
![]() $ {\mathrm{red}}_N\colon G\rightarrow {\mathrm{GL}}_n({\mathbb {Z}}/N{\mathbb {Z}})$
be the restriction of the reduction map. Then
$ {\mathrm{red}}_N\colon G\rightarrow {\mathrm{GL}}_n({\mathbb {Z}}/N{\mathbb {Z}})$
be the restriction of the reduction map. Then
![]() $ {\mathrm{red}}_N$
is injective if
$ {\mathrm{red}}_N$
is injective if
![]() $N \geq 3$
, and every element of the kernel of
$N \geq 3$
, and every element of the kernel of
![]() $ {\mathrm{red}}_2$
has order
$ {\mathrm{red}}_2$
has order
![]() $1$
or
$1$
or
![]() $2$
.
$2$
.
Proof. This is a classical result of Minkowski [Reference MinkowskiMin87]; see [Reference Silverberg and ZarhinSZ95, Theorem 4.1] for an accessible reference.
Proposition 3.15. Supppose that
![]() $I = N\cdot {\mathcal {O}}$
for some integer
$I = N\cdot {\mathcal {O}}$
for some integer
![]() $N\geq 3$
. Then
$N\geq 3$
. Then
![]() $\pi _2$
is injective on the image
$\pi _2$
is injective on the image
![]() $\rho _I^{\circ }$
. Consequently, the image of
$\rho _I^{\circ }$
. Consequently, the image of
![]() $\rho _I^{\circ }$
is isomorphic to the image of
$\rho _I^{\circ }$
is isomorphic to the image of
![]() $\rho _I$
.
$\rho _I$
.
Proof. Choose a
![]() ${\mathcal {O}}/N$
-module generator
${\mathcal {O}}/N$
-module generator
![]() $Q\in A[N](\bar {F})$
. If
$Q\in A[N](\bar {F})$
. If
![]() $(\gamma , \varphi )\in \ker (\pi _2)$
, then
$(\gamma , \varphi )\in \ker (\pi _2)$
, then
![]() $\varphi = \text {Id}$
and
$\varphi = \text {Id}$
and
![]() $a\cdot Q = a^{\gamma }\cdot Q$
for all
$a\cdot Q = a^{\gamma }\cdot Q$
for all
![]() $a\in {\mathcal {O}}/N$
. So
$a\in {\mathcal {O}}/N$
. So
![]() $a = a^{\gamma }$
for all
$a = a^{\gamma }$
for all
![]() $a\in {\mathcal {O}}/N$
. Therefore,
$a\in {\mathcal {O}}/N$
. Therefore,
![]() $\gamma \in \ker ( {\mathrm{Aut}}({\mathcal {O}})\rightarrow {\mathrm{Aut}}({\mathcal {O}}/N))$
. By Lemma 3.14, this kernel does not contain any nontrivial element of finite order. However, the image of
$\gamma \in \ker ( {\mathrm{Aut}}({\mathcal {O}})\rightarrow {\mathrm{Aut}}({\mathcal {O}}/N))$
. By Lemma 3.14, this kernel does not contain any nontrivial element of finite order. However, the image of
![]() $\rho _{ {\mathrm{End}}}$
is finite (Proposition 3.3). We conclude that
$\rho _{ {\mathrm{End}}}$
is finite (Proposition 3.3). We conclude that
![]() $\ker (\pi _2) \cap \text {image}(\rho _I^{\circ }) = \{1\}$
.
$\ker (\pi _2) \cap \text {image}(\rho _I^{\circ }) = \{1\}$
.
Remark 3.16. We can also define
![]() $\ell $
-adic versions of the enhanced Galois representation: for every prime
$\ell $
-adic versions of the enhanced Galois representation: for every prime
![]() $\ell $
, this is a group homomorphism
$\ell $
, this is a group homomorphism
![]() $ {\mathrm{Gal}}_F\rightarrow {\mathrm{Aut}}({\mathcal {O}})\ltimes ({\mathcal {O}}\otimes {\mathbb {Z}}_{\ell })^{\times }$
encoding both the
$ {\mathrm{Gal}}_F\rightarrow {\mathrm{Aut}}({\mathcal {O}})\ltimes ({\mathcal {O}}\otimes {\mathbb {Z}}_{\ell })^{\times }$
encoding both the
![]() $ {\mathrm{Gal}}_F$
-action on
$ {\mathrm{Gal}}_F$
-action on
![]() ${\mathcal {O}}$
and on the
${\mathcal {O}}$
and on the
![]() $\ell $
-adic Tate module of A.
$\ell $
-adic Tate module of A.
4 PQM surfaces over local and finite fields
We collect some results about
![]() $\mathrm {PQM}$
surfaces A over local and finite fields, especially the possible reduction types. The most important facts for our purposes are as follows: a
$\mathrm {PQM}$
surfaces A over local and finite fields, especially the possible reduction types. The most important facts for our purposes are as follows: a
![]() $\mathrm {PQM}$
surface
$\mathrm {PQM}$
surface
![]() $A/{\mathbb {Q}}$
of
$A/{\mathbb {Q}}$
of
![]() $ {\mathrm{GL}}_2$
-type has totally additive reduction at every bad prime (Corollary 4.3); the prime-to-p torsion in the totally additive case is controlled by the Néron component group (Lemma 4.10); and the latter, in turn, is controlled by the smallest field extension over which A acquires good reduction (Proposition 4.6).
$ {\mathrm{GL}}_2$
-type has totally additive reduction at every bad prime (Corollary 4.3); the prime-to-p torsion in the totally additive case is controlled by the Néron component group (Lemma 4.10); and the latter, in turn, is controlled by the smallest field extension over which A acquires good reduction (Proposition 4.6).
For the remainder of this section, let R be a henselian discrete valuation ring with fraction field F of characteristic zero and perfect residue field k of characteristic
![]() $p\geq 0$
.
$p\geq 0$
.
4.1 Néron models of PQM surfaces
We first recall some notions in the theory of Néron models. Let
![]() $A/F$
be an abelian variety with Néron model
$A/F$
be an abelian variety with Néron model
![]() $\mathcal A/R$
. The special fiber
$\mathcal A/R$
. The special fiber
![]() $\mathcal A_k$
fits into an exact sequence
$\mathcal A_k$
fits into an exact sequence
where
![]() $\Phi $
is the component group of
$\Phi $
is the component group of
![]() $\mathcal A_k$
, a finite étale k-group scheme. The identity component
$\mathcal A_k$
, a finite étale k-group scheme. The identity component
![]() $\mathcal A_k^0$
fits into an exact sequence
$\mathcal A_k^0$
fits into an exact sequence
where U is a unipotent group, T is a torus and B is an abelian variety over k. The dimensions of
![]() $U,T$
and B, which we denote by
$U,T$
and B, which we denote by
![]() $u,t$
and b, are called the unipotent, toric and abelian ranks of A, respectively. We have
$u,t$
and b, are called the unipotent, toric and abelian ranks of A, respectively. We have
![]() $ u + t + b = \dim A$
, and A has bad reduction if and only if
$ u + t + b = \dim A$
, and A has bad reduction if and only if
![]() $b < \dim A$
. Similarly, A has potentially good reduction over F if and only if its toric rank is 0 over every finite extension of F.
$b < \dim A$
. Similarly, A has potentially good reduction over F if and only if its toric rank is 0 over every finite extension of F.
Lemma 4.1. Suppose that
![]() $A/F$
is an abelian surface such that
$A/F$
is an abelian surface such that
![]() $ {\mathrm{End}}^0(A_{\bar {F}})$
contains a non-split quaternion algebra. Then there exists a finite extension
$ {\mathrm{End}}^0(A_{\bar {F}})$
contains a non-split quaternion algebra. Then there exists a finite extension
![]() $F'/F$
such that
$F'/F$
such that
![]() $A_{F'}$
has good reduction. If k is finite, we may take
$A_{F'}$
has good reduction. If k is finite, we may take
![]() $F'$
to be a totally ramified extension of F.
$F'$
to be a totally ramified extension of F.
Proof. The fact that A has potentially good reduction is well known; see, for example, [Reference Clark and XarlesCX08, p. 536]. It follows from the fact that a non-split quaternion algebra does not embed in
![]() $\mathrm {Mat}_2({\mathbb {Q}})$
and hence does not embed in
$\mathrm {Mat}_2({\mathbb {Q}})$
and hence does not embed in
![]() $ {\mathrm{End}}(T)\otimes {\mathbb {Q}}$
for any torus
$ {\mathrm{End}}(T)\otimes {\mathbb {Q}}$
for any torus
![]() $T/k$
of dimension
$T/k$
of dimension
![]() $1$
or
$1$
or
![]() $2$
.
$2$
.
If k is finite, the last sentence of the lemma can be justified by taking a lift in
![]() $ {\mathrm{Gal}}_{F}$
of the Frobenius in
$ {\mathrm{Gal}}_{F}$
of the Frobenius in
![]() $ {\mathrm{Gal}}_{k}$
, in a manner analogous to [Reference Serre and TateST68, p. 498].
$ {\mathrm{Gal}}_{k}$
, in a manner analogous to [Reference Serre and TateST68, p. 498].
Proposition 4.2. Suppose that
![]() $A/F$
is an abelian surface such that
$A/F$
is an abelian surface such that
![]() $ {\mathrm{End}}^0(A_{\bar {F}})$
contains a non-split quaternion algebra. Suppose that A has bad reduction. Then,
$ {\mathrm{End}}^0(A_{\bar {F}})$
contains a non-split quaternion algebra. Suppose that A has bad reduction. Then,
-
(a)
 $t = 0$
.
$t = 0$
. -
(b) If
 $ {\mathrm{End}}^0(A)$
contains a real quadratic field, then
$ {\mathrm{End}}^0(A)$
contains a real quadratic field, then
 $u = \dim A = 2$
.
$u = \dim A = 2$
. -
(c) If
 $u = 1$
, then
$u = 1$
, then
 $A_K$
has good reduction over any field extension
$A_K$
has good reduction over any field extension
 $K/F$
such that
$K/F$
such that
 $ {\mathrm{End}}^0(A_K)$
contains a real quadratic field.
$ {\mathrm{End}}^0(A_K)$
contains a real quadratic field.
Proof.
![]() $(a)$
follows from the fact that A has potentially good reduction and the fact that the toric rank cannot decrease under extension of the base field [Reference Clark and XarlesCX08, Proposition 2.4]. For
$(a)$
follows from the fact that A has potentially good reduction and the fact that the toric rank cannot decrease under extension of the base field [Reference Clark and XarlesCX08, Proposition 2.4]. For
![]() $(b)$
, we only need to exclude the possibility that
$(b)$
, we only need to exclude the possibility that
![]() $u=b=1$
, so suppose by contradiction that it holds. Let
$u=b=1$
, so suppose by contradiction that it holds. Let
![]() $E\subset {\mathrm{End}}^0(A)$
be a real quadratic subfield. Reducing endomorphisms in (4.1) gives a (nonzero, hence injective) map
$E\subset {\mathrm{End}}^0(A)$
be a real quadratic subfield. Reducing endomorphisms in (4.1) gives a (nonzero, hence injective) map
![]() $E \hookrightarrow {\mathrm{End}}^0(B)$
. By assumption, B is an elliptic curve. However, this contradicts the fact that the endomorphism algebra of an elliptic curve (over any field) does not contain a real quadratic field. Finally,
$E \hookrightarrow {\mathrm{End}}^0(B)$
. By assumption, B is an elliptic curve. However, this contradicts the fact that the endomorphism algebra of an elliptic curve (over any field) does not contain a real quadratic field. Finally,
![]() $(c)$
follows from
$(c)$
follows from
![]() $(b)$
, since the abelian rank cannot decrease after base change [Reference Clark and XarlesCX08, Proposition 2.4].
$(b)$
, since the abelian rank cannot decrease after base change [Reference Clark and XarlesCX08, Proposition 2.4].
When
![]() $u = \dim A$
, one says that A has totally additive reduction.
$u = \dim A$
, one says that A has totally additive reduction.
Corollary 4.3. Let
![]() $A/{\mathbb {Q}}$
be a
$A/{\mathbb {Q}}$
be a
![]() $\mathrm {PQM}$
surface and p a prime of bad reduction. Suppose that A is of
$\mathrm {PQM}$
surface and p a prime of bad reduction. Suppose that A is of
![]() $ {\mathrm{GL}}_2$
-type. Then A has totally additive reduction at p.
$ {\mathrm{GL}}_2$
-type. Then A has totally additive reduction at p.
Proof. This follows from Proposition 4.2(b) and the fact that
![]() $ {\mathrm{End}}(A)$
is real quadratic by Proposition 3.2.
$ {\mathrm{End}}(A)$
is real quadratic by Proposition 3.2.
Remark 4.4. One can show that if
![]() $p\geq 5$
, then the Prym variety of
$p\geq 5$
, then the Prym variety of
![]() $y^3 = x^4+x^2+p$
(which has
$y^3 = x^4+x^2+p$
(which has
![]() $\mathrm {PQM}$
by [Reference Laga and ShnidmanLS23]) has unipotent rank
$\mathrm {PQM}$
by [Reference Laga and ShnidmanLS23]) has unipotent rank
![]() $1$
over
$1$
over
![]() ${\mathbb {Q}}_p$
. So the
${\mathbb {Q}}_p$
. So the
![]() $ {\mathrm{GL}}_2$
-type hypothesis cannot be dropped in general in Corollary 4.3.
$ {\mathrm{GL}}_2$
-type hypothesis cannot be dropped in general in Corollary 4.3.
Finally, we state Raynaud’s criterion for
![]() $A/F$
to have semistable reduction, which in the case of a
$A/F$
to have semistable reduction, which in the case of a
![]() $\mathrm {PQM}$
surface is necessarily good by Proposition 4.2.
$\mathrm {PQM}$
surface is necessarily good by Proposition 4.2.
Lemma 4.5. Let
![]() $A/F$
be a
$A/F$
be a
![]() $\mathrm {PQM}$
surface and n an integer not divisible by the residue characteristic p, and suppose that all points in
$\mathrm {PQM}$
surface and n an integer not divisible by the residue characteristic p, and suppose that all points in
![]() $A[n]$
are defined over an unramified extension of F. Then
$A[n]$
are defined over an unramified extension of F. Then
-
(a) if
 $n=2$
, then A has good reduction over every ramified quadratic extension of F;
$n=2$
, then A has good reduction over every ramified quadratic extension of F; -
(b) if
 $n \geq 3$
, then A has good reduction over F.
$n \geq 3$
, then A has good reduction over F.
Proof. See [Reference Silverberg and ZarhinSZ95, §7].
4.2 The good reduction field and component group of a PQM surface
Let
![]() $A/F$
be an abelian variety with potentially good reduction. If k is algebraically closed, there exists a smallest field extension
$A/F$
be an abelian variety with potentially good reduction. If k is algebraically closed, there exists a smallest field extension
![]() $M/F$
such that
$M/F$
such that
![]() $A_M$
has good reduction, called the good reduction field of A. This is a Galois extension, equal to
$A_M$
has good reduction, called the good reduction field of A. This is a Galois extension, equal to
![]() $F(A[N])$
for every
$F(A[N])$
for every
![]() $N\geq 3$
coprime to p [Reference Serre and TateST68, §2, Corollary 3]. It is relevant for us because it controls the size of the component group by the following result [Reference Edixhoven, Liu and LorenziniELL96, Theorem 1].
$N\geq 3$
coprime to p [Reference Serre and TateST68, §2, Corollary 3]. It is relevant for us because it controls the size of the component group by the following result [Reference Edixhoven, Liu and LorenziniELL96, Theorem 1].
Proposition 4.6. Suppose that k is algebraically closed. Let
![]() $A/F$
be an abelian variety with potentially good reduction and good reduction field
$A/F$
be an abelian variety with potentially good reduction and good reduction field
![]() $M/F$
. Then the Néron component group
$M/F$
. Then the Néron component group
![]() $\Phi $
is killed by
$\Phi $
is killed by
![]() $[M:F]$
.
$[M:F]$
.
The next lemma constrains the good reduction field of a
![]() $\mathrm {PQM}$
surface.
$\mathrm {PQM}$
surface.
Lemma 4.7. Suppose that k is algebraically closed. Let
![]() $A/F$
be a
$A/F$
be a
![]() $\mathrm {PQM}$
surface with good reduction field
$\mathrm {PQM}$
surface with good reduction field
![]() $M/F$
. Then
$M/F$
. Then
![]() $[M:F]$
divides
$[M:F]$
divides
![]() $24^2$
. In particular,
$24^2$
. In particular,
![]() $[M:F]$
is coprime to any prime
$[M:F]$
is coprime to any prime
![]() $\ell> 3$
.
$\ell> 3$
.
Proof. Let L be the endomorphism field of
![]() $A/F$
(Section 3.2). By the Néron–Ogg–Shafarevich criterion, all prime-to-p torsion is defined over M; hence,
$A/F$
(Section 3.2). By the Néron–Ogg–Shafarevich criterion, all prime-to-p torsion is defined over M; hence,
![]() $L\subset M$
by a result of Silverberg (Proposition 3.6). By Proposition 3.3,
$L\subset M$
by a result of Silverberg (Proposition 3.6). By Proposition 3.3,
![]() $[L:F]$
divides
$[L:F]$
divides
![]() $24$
. By [Reference Jordan and MorrisonJM94, Proposition 4.2] and its proof (whose notation does not agree with ours), we have
$24$
. By [Reference Jordan and MorrisonJM94, Proposition 4.2] and its proof (whose notation does not agree with ours), we have
![]() $[M:L] \mid 24$
. We conclude that
$[M:L] \mid 24$
. We conclude that
![]() $[M:F] = [M:L][L:F]$
divides
$[M:F] = [M:L][L:F]$
divides
![]() $24^2$
.
$24^2$
.
Lemma 4.8. Let
![]() $A/F$
be a
$A/F$
be a
![]() $\mathrm {PQM}$
surface and let
$\mathrm {PQM}$
surface and let
![]() $\ell \geq 5$
. Then the order of
$\ell \geq 5$
. Then the order of
![]() $\Phi $
is not divisible by
$\Phi $
is not divisible by
![]() $\ell $
.
$\ell $
.
Proof. Since formation of Néron models commutes with unramified base change, it is enough to prove the lemma in the case where F has algebraically closed residue field. This then follows from Proposition 4.6 and Lemma 4.7.
We record the following technical lemma that will allow us to sometimes ‘quadratic twist away’ bad primes. This will be useful in the proof of Proposition 5.8.
Lemma 4.9. Suppose that
![]() $p\neq 2$
. Let
$p\neq 2$
. Let
![]() $A/F$
be an abelian variety with totally additive reduction. Suppose that
$A/F$
be an abelian variety with totally additive reduction. Suppose that
![]() $A_M$
has good reduction for some quadratic extension
$A_M$
has good reduction for some quadratic extension
![]() $M/F$
. Then the quadratic twist
$M/F$
. Then the quadratic twist
![]() $A^M$
of A by M has good reduction.
$A^M$
of A by M has good reduction.
Proof. Let
![]() $I_F$
and
$I_F$
and
![]() $I_M$
denote the inertia group of
$I_M$
denote the inertia group of
![]() $ {\mathrm{Gal}}_F$
and
$ {\mathrm{Gal}}_F$
and
![]() $ {\mathrm{Gal}}_M$
, respectively. Fix a prime
$ {\mathrm{Gal}}_M$
, respectively. Fix a prime
![]() $\ell \neq p$
. By the Néron–Ogg–Shafarevich criterion, the
$\ell \neq p$
. By the Néron–Ogg–Shafarevich criterion, the
![]() $I_F$
-action on the
$I_F$
-action on the
![]() $\ell $
-adic Tate module
$\ell $
-adic Tate module
![]() $T_{\ell }A$
factors through a faithful
$T_{\ell }A$
factors through a faithful
![]() $I_F/I_M$
-action and so acts via an element
$I_F/I_M$
-action and so acts via an element
![]() $\sigma \in {\mathrm{GL}}(T_{\ell }A)$
of order
$\sigma \in {\mathrm{GL}}(T_{\ell }A)$
of order
![]() $2$
. Since A has totally additive reduction,
$2$
. Since A has totally additive reduction,
![]() $(T_{\ell }A)^{I_F} = 0$
and so
$(T_{\ell }A)^{I_F} = 0$
and so
![]() $\sigma =-1$
. Let
$\sigma =-1$
. Let
![]() $\chi _M\colon {\mathrm{Gal}}_F\rightarrow \{\pm 1\}$
be the character corresponding to the extension
$\chi _M\colon {\mathrm{Gal}}_F\rightarrow \{\pm 1\}$
be the character corresponding to the extension
![]() $M/F$
. Then
$M/F$
. Then
![]() $T_{\ell }( A^M) \simeq T_{\ell }A \otimes \chi _M$
as
$T_{\ell }( A^M) \simeq T_{\ell }A \otimes \chi _M$
as
![]() $ {\mathrm{Gal}}_F$
-modules. Therefore,
$ {\mathrm{Gal}}_F$
-modules. Therefore,
![]() $I_F$
acts trivially on
$I_F$
acts trivially on
![]() $T_{\ell } (A^M)$
and
$T_{\ell } (A^M)$
and
![]() $A^M$
has good reduction.
$A^M$
has good reduction.
4.3 Component groups and torsion
The relevance of the component group is the following well-known fact; see, for example, [Reference LorenziniLor93, Remark 1.3]. If G is an abelian group, write
![]() $G^{(p)}$
for its subgroup of elements of finite order prime to p.
$G^{(p)}$
for its subgroup of elements of finite order prime to p.
Lemma 4.10. If
![]() $A/F$
is an abelian variety with totally additive reduction
$A/F$
is an abelian variety with totally additive reduction
![]() $($
i.e.,
$($
i.e.,
![]() $u = \dim A)$
, then
$u = \dim A)$
, then
![]() $A(F)^{(p)}_{\mathrm {tors}}$
is isomorphic to a subgroup of
$A(F)^{(p)}_{\mathrm {tors}}$
is isomorphic to a subgroup of
![]() $\Phi (k)^{(p)}$
, where
$\Phi (k)^{(p)}$
, where
![]() $\Phi $
denotes the component group of
$\Phi $
denotes the component group of
![]() $\mathcal {A}_k$
.
$\mathcal {A}_k$
.
Lorenzini has studied the component groups of general abelian surfaces with potentially good reduction and totally additive reduction, which leads to the following severe constraint on their torsion subgroups [Reference LorenziniLor93, Corollary 3.25].
Theorem 4.11 (Lorenzini).
Let
![]() $A/F$
be an abelian surface with totally additive and potentially good reduction. Then
$A/F$
be an abelian surface with totally additive and potentially good reduction. Then
![]() $A(F)^{(p)}_{\mathrm {tors}}$
is a subgroup of one of the following groups:
$A(F)^{(p)}_{\mathrm {tors}}$
is a subgroup of one of the following groups:
We can say more if A has totally additive reduction over any proper subextension of the good reduction field. The following slight variant of [Reference LorenziniLor93, Corollary 3.24] will be very useful in classifying torsion in the
![]() $ {\mathrm{GL}}_2$
-type case.
$ {\mathrm{GL}}_2$
-type case.
Proposition 4.12. Suppose that the residue field of F is algebraically closed. Let
![]() $A/F$
be an abelian variety with bad and potentially good reduction. Let
$A/F$
be an abelian variety with bad and potentially good reduction. Let
![]() $M/F$
be the good reduction field of A. Suppose that
$M/F$
be the good reduction field of A. Suppose that
![]() $A_{F'}$
has totally additive reduction for every
$A_{F'}$
has totally additive reduction for every
![]() $F\subset F' \subsetneq M$
. Suppose that the prime-to-p torsion subgroup
$F\subset F' \subsetneq M$
. Suppose that the prime-to-p torsion subgroup
![]() $A(F)^{(p)}_{\mathrm {tors}}$
of
$A(F)^{(p)}_{\mathrm {tors}}$
of
![]() $A(F)$
is nontrivial. Then there exists a prime number
$A(F)$
is nontrivial. Then there exists a prime number
![]() $\ell \neq p$
such that
$\ell \neq p$
such that
![]() $[M:F]$
is a power of
$[M:F]$
is a power of
![]() $\ell $
and
$\ell $
and
![]() $A(F)^{(p)}_{\mathrm {tors}} \simeq ({\mathbb {Z}}/\ell {\mathbb {Z}})^k$
for some
$A(F)^{(p)}_{\mathrm {tors}} \simeq ({\mathbb {Z}}/\ell {\mathbb {Z}})^k$
for some
![]() $k\geq 1$
.
$k\geq 1$
.
Proof. Let
![]() $G := {\mathrm{Gal}}(M/F)$
. For every
$G := {\mathrm{Gal}}(M/F)$
. For every
![]() $F \subset F' \subsetneq M$
,
$F \subset F' \subsetneq M$
,
![]() $A(F)^{(p)}_{\mathrm {tors}}\subset A(F')^{(p)}_{\mathrm {tors}}$
is isomorphic to a subgroup of the component group of
$A(F)^{(p)}_{\mathrm {tors}}\subset A(F')^{(p)}_{\mathrm {tors}}$
is isomorphic to a subgroup of the component group of
![]() $A_{F'}$
by Lemma 4.10, which is killed by
$A_{F'}$
by Lemma 4.10, which is killed by
![]() $[F:F']$
by Proposition 4.6. By Galois theory,
$[F:F']$
by Proposition 4.6. By Galois theory,
![]() $A(F)^{(p)}_{\mathrm {tors}}$
is therefore killed by
$A(F)^{(p)}_{\mathrm {tors}}$
is therefore killed by
![]() $\#H$
for every nontrivial subgroup
$\#H$
for every nontrivial subgroup
![]() $H \leq G$
. The group
$H \leq G$
. The group
![]() $A(F)^{(p)}_{\mathrm {tors}}$
is nontrivial by assumption; let
$A(F)^{(p)}_{\mathrm {tors}}$
is nontrivial by assumption; let
![]() $\ell $
be a prime dividing its order. We claim that this
$\ell $
be a prime dividing its order. We claim that this
![]() $\ell $
satisfies the conclusions of the proposition. Indeed, by definition of
$\ell $
satisfies the conclusions of the proposition. Indeed, by definition of
![]() $A(F)^{(p)}_{\mathrm {tors}}$
, we have
$A(F)^{(p)}_{\mathrm {tors}}$
, we have
![]() $\ell \neq p$
. Moreover, if
$\ell \neq p$
. Moreover, if
![]() $\#G$
is divisible by another prime
$\#G$
is divisible by another prime
![]() $\ell '$
, then by taking H a Sylow-
$\ell '$
, then by taking H a Sylow-
![]() $\ell '$
subgroup of G, we get a contradiction, so
$\ell '$
subgroup of G, we get a contradiction, so
![]() $\#G = [M:F]$
is a power of
$\#G = [M:F]$
is a power of
![]() $\ell $
. By taking H to be an order
$\ell $
. By taking H to be an order
![]() $\ell $
subgroup of G, we see that
$\ell $
subgroup of G, we see that
![]() $A(F)^{(p)}_{\mathrm {tors}}$
is killed by
$A(F)^{(p)}_{\mathrm {tors}}$
is killed by
![]() $\ell $
, as desired.
$\ell $
, as desired.
In the general case (not necessarily totally additive reduction), we have the following well-known result when F is a finite extension of
![]() ${\mathbb {Q}}_p$
, which follows from formal group law considerations [Reference Clark and XarlesCX08, §2.5 and Proposition 3.1].
${\mathbb {Q}}_p$
, which follows from formal group law considerations [Reference Clark and XarlesCX08, §2.5 and Proposition 3.1].
Lemma 4.13. Suppose that
![]() $F/{\mathbb {Q}}_p$
is a finite extension of ramification degree e. Let
$F/{\mathbb {Q}}_p$
is a finite extension of ramification degree e. Let
![]() $A/F$
be an abelian variety with Néron model
$A/F$
be an abelian variety with Néron model
![]() $\mathcal A/R$
. Let
$\mathcal A/R$
. Let
![]() $ {\mathrm{red}}\colon A(F) =\mathcal A(R)\rightarrow \mathcal A(k)$
be the reduction map.
$ {\mathrm{red}}\colon A(F) =\mathcal A(R)\rightarrow \mathcal A(k)$
be the reduction map.
-
(a) The restriction of
 $ {\mathrm{red}}$
to prime-to-p part of
$ {\mathrm{red}}$
to prime-to-p part of
 $A(F)_{ {\mathrm{tors}}}$
is injective.
$A(F)_{ {\mathrm{tors}}}$
is injective. -
(b) If in addition
 $e<p-1$
, then
$e<p-1$
, then
 $ {\mathrm{red}}$
is injective on
$ {\mathrm{red}}$
is injective on
 $A(F)_{ {\mathrm{tors}}}$
.
$A(F)_{ {\mathrm{tors}}}$
.
4.4 The conductor of a PQM surface
Recall that the conductor
![]() $\mathfrak {f}(A)$
of an abelian variety
$\mathfrak {f}(A)$
of an abelian variety
![]() $A/{\mathbb {Q}}$
is a positive integer divisible exactly by the primes of bad reduction of A; see [Reference Brumer and KramerBK94] for a precise definition and more information. We may write
$A/{\mathbb {Q}}$
is a positive integer divisible exactly by the primes of bad reduction of A; see [Reference Brumer and KramerBK94] for a precise definition and more information. We may write
![]() $\mathfrak {f}(A) = \prod _p p^{\mathfrak {f}_p(A)}$
, where
$\mathfrak {f}(A) = \prod _p p^{\mathfrak {f}_p(A)}$
, where
![]() $\mathfrak {f}_p(A)$
denotes the conductor exponent at a prime p.
$\mathfrak {f}_p(A)$
denotes the conductor exponent at a prime p.
Lemma 4.14. Let
![]() $A/{\mathbb {Q}}$
be a
$A/{\mathbb {Q}}$
be a
![]() $\mathrm {PQM}$
surface of
$\mathrm {PQM}$
surface of
![]() $ {\mathrm{GL}}_2$
-type. Let p be a prime such that A has bad reduction at p but acquires good reduction over a tame extension of
$ {\mathrm{GL}}_2$
-type. Let p be a prime such that A has bad reduction at p but acquires good reduction over a tame extension of
![]() ${\mathbb {Q}}_p$
. Then
${\mathbb {Q}}_p$
. Then
![]() $\mathfrak {f}_p(A) = 4$
.
$\mathfrak {f}_p(A) = 4$
.
Proof. In that case,
![]() $\mathfrak {f}_p(A)$
equals the tame conductor exponent at p, which is
$\mathfrak {f}_p(A)$
equals the tame conductor exponent at p, which is
![]() $2\times (\text {unipotent rank})+(\text {toric rank})$
. This equals
$2\times (\text {unipotent rank})+(\text {toric rank})$
. This equals
![]() $2\times 2+0 =4$
by Proposition 4.2.
$2\times 2+0 =4$
by Proposition 4.2.
Proposition 4.15. Let
![]() $A/{\mathbb {Q}}$
be a
$A/{\mathbb {Q}}$
be a
![]() $\mathrm {PQM}$
surface of
$\mathrm {PQM}$
surface of
![]() $ {\mathrm{GL}}_2$
-type. Then the conductor of A is of the form
$ {\mathrm{GL}}_2$
-type. Then the conductor of A is of the form
![]() $2^{2i}3^{2j}N^4$
, where
$2^{2i}3^{2j}N^4$
, where
![]() $0\leq i\leq 10$
,
$0\leq i\leq 10$
,
![]() $0\leq j \leq 5$
, and N is squarefree and coprime to
$0\leq j \leq 5$
, and N is squarefree and coprime to
![]() $6$
.
$6$
.
Proof. By Lemmas 4.7 and 4.14,
![]() $\mathfrak {f}_p(A)=4$
for every bad prime
$\mathfrak {f}_p(A)=4$
for every bad prime
![]() $p\geq 5$
. The bounds
$p\geq 5$
. The bounds
![]() $\mathfrak {f}_2(A)\leq 20$
and
$\mathfrak {f}_2(A)\leq 20$
and
![]() $\mathfrak {f}_3(A)\leq 10$
follow from a general result of Brumer–Kramer [Reference Brumer and KramerBK94, Theorem 6.2]. The fact that
$\mathfrak {f}_3(A)\leq 10$
follow from a general result of Brumer–Kramer [Reference Brumer and KramerBK94, Theorem 6.2]. The fact that
![]() $\mathfrak {f}_2(A)$
and
$\mathfrak {f}_2(A)$
and
![]() $\mathfrak {f}_3(A)$
are even follows from the fact that
$\mathfrak {f}_3(A)$
are even follows from the fact that
![]() $ {\mathrm{End}}^0(A)$
is a real quadratic field (Proposition 3.2) and [Reference SerreSer87, (4.7.2)].
$ {\mathrm{End}}^0(A)$
is a real quadratic field (Proposition 3.2) and [Reference SerreSer87, (4.7.2)].
4.5 Finite fields
Let
![]() $k = \mathbb F_q$
be a finite field of order
$k = \mathbb F_q$
be a finite field of order
![]() $p^r$
. We will use the following two statements, whose proof can be found in [Reference JordanJor86, §2].
$p^r$
. We will use the following two statements, whose proof can be found in [Reference JordanJor86, §2].
Lemma 4.16. Let
![]() $A/k$
be an abelian surface such that
$A/k$
be an abelian surface such that
![]() $ {\mathrm{End}}^0(A)$
contains the quaternion algebra B. Then the characteristic polynomial of Frobenius is of the form
$ {\mathrm{End}}^0(A)$
contains the quaternion algebra B. Then the characteristic polynomial of Frobenius is of the form
![]() $(T^2+aT+q)^2$
for some integer
$(T^2+aT+q)^2$
for some integer
![]() $a\in {\mathbb {Z}}$
satisfying
$a\in {\mathbb {Z}}$
satisfying
![]() $|a|\leq 2\sqrt {q}$
.
$|a|\leq 2\sqrt {q}$
.
Proposition 4.17. Let
![]() $A/k$
be an abelian surface such that
$A/k$
be an abelian surface such that
![]() $ {\mathrm{End}}^0(A)$
contains the quaternion algebra B. If r is odd or
$ {\mathrm{End}}^0(A)$
contains the quaternion algebra B. If r is odd or
![]() $p \nmid {\mathrm{disc}}(B)$
, then A is isogenous to the square of an elliptic curve over k. If r is even and
$p \nmid {\mathrm{disc}}(B)$
, then A is isogenous to the square of an elliptic curve over k. If r is even and
![]() $p\mid {\mathrm{disc}}(B)$
,
$p\mid {\mathrm{disc}}(B)$
,
![]() $A_{\bar {k}}$
is isogenous to the square of a supersingular elliptic curve over
$A_{\bar {k}}$
is isogenous to the square of a supersingular elliptic curve over
![]() $\bar {k}$
.
$\bar {k}$
.
5 Proof of Theorem 1.4: PQM surfaces of
 $ {\mathrm{GL}}_2$
-type
$ {\mathrm{GL}}_2$
-type
Before proving Theorems 1.1–1.3, it is useful to first prove Theorem 1.4, which classifies torsion subgroups of
![]() $\mathcal {O}$
-PQM abelian surfaces A over
$\mathcal {O}$
-PQM abelian surfaces A over
![]() ${\mathbb {Q}}$
which are of
${\mathbb {Q}}$
which are of
![]() $ {\mathrm{GL}}_2$
-type. At a certain point in the argument, we make use of the modularity of abelian surfaces of
$ {\mathrm{GL}}_2$
-type. At a certain point in the argument, we make use of the modularity of abelian surfaces of
![]() $ {\mathrm{GL}}_2$
-type, which we recall in §5.1 and classify
$ {\mathrm{GL}}_2$
-type, which we recall in §5.1 and classify
![]() $\mathrm {PQM}$
surfaces of
$\mathrm {PQM}$
surfaces of
![]() $ {\mathrm{GL}}_2$
-type with good reduction outside
$ {\mathrm{GL}}_2$
-type with good reduction outside
![]() $2$
or
$2$
or
![]() $3$
. In §5.2, we deduce that a general
$3$
. In §5.2, we deduce that a general
![]() ${\mathcal {O}}$
-
${\mathcal {O}}$
-
![]() $\mathrm {PQM}$
surface cannot have a full level
$\mathrm {PQM}$
surface cannot have a full level
![]() $2$
-structure over
$2$
-structure over
![]() ${\mathbb {Q}}$
. In §5.3, we prove Theorem 1.4.
${\mathbb {Q}}$
. In §5.3, we prove Theorem 1.4.
5.1 Abelian surfaces of
 $ {\mathrm{GL}}_2$
-type and modular forms
$ {\mathrm{GL}}_2$
-type and modular forms
Theorem 5.1. Let A be an abelian surface such that
![]() $ {\mathrm{End}}^0(A)$
is a real quadratic field. Then the conductor of A is of the form
$ {\mathrm{End}}^0(A)$
is a real quadratic field. Then the conductor of A is of the form
![]() $N^2$
for some positive integer N, and there exists a unique Galois orbit
$N^2$
for some positive integer N, and there exists a unique Galois orbit
![]() $[f_A] \subset S_2(\Gamma _0(N))$
having coefficient field
$[f_A] \subset S_2(\Gamma _0(N))$
having coefficient field
![]() $K \simeq {\mathrm{End}}^0(A)$
whose local L-factors agree for each prime p:
$K \simeq {\mathrm{End}}^0(A)$
whose local L-factors agree for each prime p:
Moreover, we have
![]() $[f_A] = [f_{A'}]$
if and only if A is isogenous to
$[f_A] = [f_{A'}]$
if and only if A is isogenous to
![]() $A'$
(over
$A'$
(over
![]() ${\mathbb {Q}}$
).
${\mathbb {Q}}$
).
Proof. As explained by Ribet [Reference RibetRib04, Theorem (4.4)], the fact that A is of
![]() $ {\mathrm{GL}}_2$
-type over
$ {\mathrm{GL}}_2$
-type over
![]() ${\mathbb {Q}}$
implies that A is modular assuming Serre’s modularity conjecture [Reference SerreSer87, §4.7, Theorem 5], which was proven by Khare–Wintenberger [Reference Khare and WintenbergerKW09]. Thus, the equality of L-series (5.1) holds for some newform
${\mathbb {Q}}$
implies that A is modular assuming Serre’s modularity conjecture [Reference SerreSer87, §4.7, Theorem 5], which was proven by Khare–Wintenberger [Reference Khare and WintenbergerKW09]. Thus, the equality of L-series (5.1) holds for some newform
![]() $f_A$
. Since
$f_A$
. Since
![]() $ {\mathrm{End}}^0(A)$
is real, the character of
$ {\mathrm{End}}^0(A)$
is real, the character of
![]() $f_A$
is trivial [Reference RibetRib76, Lemma (4.5.1)]. It follows from a theorem of Carayol [Reference CarayolCar86, Theoreme (A)] (local-global compatibility) that A has conductor equal to
$f_A$
is trivial [Reference RibetRib76, Lemma (4.5.1)]. It follows from a theorem of Carayol [Reference CarayolCar86, Theoreme (A)] (local-global compatibility) that A has conductor equal to
![]() $N^2$
, where N is the level of
$N^2$
, where N is the level of
![]() $f_A$
. Finally, the fact that the Galois orbit of
$f_A$
. Finally, the fact that the Galois orbit of
![]() $f_A$
characterizes A up to isogeny follows from the theorem of Faltings.
$f_A$
characterizes A up to isogeny follows from the theorem of Faltings.
Recall that if
![]() $f\in S_2(\Gamma _0(N))$
is a newform and
$f\in S_2(\Gamma _0(N))$
is a newform and
![]() $\psi $
a primitive Dirichlet character, there exists a unique newform
$\psi $
a primitive Dirichlet character, there exists a unique newform
![]() $g = f\otimes \psi $
, the twist of f by
$g = f\otimes \psi $
, the twist of f by
![]() $\psi $
, whose q-expansion satisfies
$\psi $
, whose q-expansion satisfies
![]() $a_n(g) = a_n(f) \psi (n)$
for all n coprime to N and the conductor of
$a_n(g) = a_n(f) \psi (n)$
for all n coprime to N and the conductor of
![]() $\psi $
. If
$\psi $
. If
![]() $f =g$
, then g is called a self-twist. If f and g are Galois conjugate, g is called an inner twist.
$f =g$
, then g is called a self-twist. If f and g are Galois conjugate, g is called an inner twist.
Proposition 5.2. Let A be an abelian surface over
![]() ${\mathbb {Q}}$
such that
${\mathbb {Q}}$
such that
![]() $ {\mathrm{End}}^0(A) \simeq {\mathbb {Q}}(\sqrt {m})$
with
$ {\mathrm{End}}^0(A) \simeq {\mathbb {Q}}(\sqrt {m})$
with
![]() $m\geq 2$
. Then A has
$m\geq 2$
. Then A has
![]() $\mathrm {PQM}$
if and only if all of the following conditions hold:
$\mathrm {PQM}$
if and only if all of the following conditions hold:
-
(i)
 $f_A$
has no self-twists; equivalently,
$f_A$
has no self-twists; equivalently,
 $f_A$
is not CM;
$f_A$
is not CM; -
(ii)
 $f_A$
has a nontrivial inner twist by a Dirichlet character associated to a quadratic field
$f_A$
has a nontrivial inner twist by a Dirichlet character associated to a quadratic field
 ${\mathbb {Q}}(\sqrt {d})$
; and
${\mathbb {Q}}(\sqrt {d})$
; and -
(iii) The quaternion algebra
 $B_{d,m} := \displaystyle {\biggl (\frac {d,m}{{\mathbb {Q}}}\biggr )}$
is a division algebra.
$B_{d,m} := \displaystyle {\biggl (\frac {d,m}{{\mathbb {Q}}}\biggr )}$
is a division algebra.
If all conditions (i)–(iii) hold, then, in fact,
![]() $ {\mathrm{End}}^0(A_{\overline {\mathbb {Q}}}) \simeq B_{d,m}$
.
$ {\mathrm{End}}^0(A_{\overline {\mathbb {Q}}}) \simeq B_{d,m}$
.
Proof. See Cremona [Reference CremonaCre92, §2].
This reduces the enumeration of isogeny classes of
![]() $ {\mathrm{GL}}_2$
-type
$ {\mathrm{GL}}_2$
-type
![]() $\mathrm {PQM}$
surfaces A over
$\mathrm {PQM}$
surfaces A over
![]() ${\mathbb {Q}}$
with fixed conductor to a computation in a space of modular forms.
${\mathbb {Q}}$
with fixed conductor to a computation in a space of modular forms.
Corollary 5.3. There are no
![]() $\mathrm {PQM}$
surfaces A over
$\mathrm {PQM}$
surfaces A over
![]() ${\mathbb {Q}}$
of
${\mathbb {Q}}$
of
![]() $ {\mathrm{GL}}_2$
-type with good reduction outside
$ {\mathrm{GL}}_2$
-type with good reduction outside
![]() $\{2\}$
.
$\{2\}$
.
Proof. By Proposition 4.15, it is enough to check that there is no eigenform corresponding to a
![]() $\mathrm {PQM}$
surface of level
$\mathrm {PQM}$
surface of level
![]() $2^k$
for any
$2^k$
for any
![]() $k \leq 10$
. This information is contained in the LMFDB [LMF23] or [Reference González and GuàrdiaGG09, Table 1].
$k \leq 10$
. This information is contained in the LMFDB [LMF23] or [Reference González and GuàrdiaGG09, Table 1].
Corollary 5.4. There is exactly one isogeny class of
![]() $\mathrm {PQM}$
surfaces A over
$\mathrm {PQM}$
surfaces A over
![]() ${\mathbb {Q}}$
of
${\mathbb {Q}}$
of
![]() $ {\mathrm{GL}}_2$
-type with good reduction outside
$ {\mathrm{GL}}_2$
-type with good reduction outside
![]() $\{3\}$
: it has conductor
$\{3\}$
: it has conductor
![]() $3^{10}$
, any abelian surface A in the isogeny class satisfies
$3^{10}$
, any abelian surface A in the isogeny class satisfies
![]() $A({\mathbb {Q}})_{\mathrm {tors}} \leq {\mathbb {Z}}/3{\mathbb {Z}}$
.
$A({\mathbb {Q}})_{\mathrm {tors}} \leq {\mathbb {Z}}/3{\mathbb {Z}}$
.
Proof. The fact that there is exactly one such isogeny class again follows from Proposition 4.15 and information in the LMFDB or [Reference González and GuàrdiaGG09, Table 1]. The corresponding Galois orbit of weight two newforms has LMFDB label 243.2.a.d. From
![]() $L_2(1)=3$
and
$L_2(1)=3$
and
![]() $L_{13}(1)=225$
, we conclude that
$L_{13}(1)=225$
, we conclude that
![]() $\#A({\mathbb {Q}})_{\mathrm {tors}} \mid 3$
for every A in this isogeny class. (In fact, the corresponding optimal quotient of
$\#A({\mathbb {Q}})_{\mathrm {tors}} \mid 3$
for every A in this isogeny class. (In fact, the corresponding optimal quotient of
![]() $J_0(243)$
has
$J_0(243)$
has
![]() ${\mathbb {Z}}/3{\mathbb {Z}}$
torsion subgroup by considering the image of the cuspidal subgroup of
${\mathbb {Z}}/3{\mathbb {Z}}$
torsion subgroup by considering the image of the cuspidal subgroup of
![]() $J_0(243)$
.)
$J_0(243)$
.)
Remark 5.5. The isogeny class of Corollary 5.4 has minimal conductor among all
![]() $\mathrm {PQM}$
surfaces A of
$\mathrm {PQM}$
surfaces A of
![]() $ {\mathrm{GL}}_2$
-type. It would be interesting to produce an explicit model over
$ {\mathrm{GL}}_2$
-type. It would be interesting to produce an explicit model over
![]() ${\mathbb {Q}}$
; see also [Reference Laga and ShnidmanLS23, Question 2].
${\mathbb {Q}}$
; see also [Reference Laga and ShnidmanLS23, Question 2].
For the purposes of proving Theorem 1.4, the modular form computations contained in Corollaries 5.3 and 5.4 will suffice. However, the next proposition, which might be of independent interest, goes further than these corollaries by computing modular forms of higher level.
Proposition 5.6. There are exactly
![]() $44$
isogeny classes of
$44$
isogeny classes of
![]() $\mathrm {PQM}$
surfaces over
$\mathrm {PQM}$
surfaces over
![]() ${\mathbb {Q}}$
of
${\mathbb {Q}}$
of
![]() $ {\mathrm{GL}}_2$
-type with good reduction outside
$ {\mathrm{GL}}_2$
-type with good reduction outside
![]() $\{2,3\}$
.
$\{2,3\}$
.
Proof. Again, we use Propositions 4.15 and 5.2 to reduce the question to computing the number of Galois orbits of newforms in
![]() $S_2(\Gamma _0(N))$
, where
$S_2(\Gamma _0(N))$
, where
![]() $N \mid 2^{10} 3^5$
, with quadratic Hecke coefficient field, having an inner twist but no self-twist. However, here we need to do a new computation in a large dimensional space. The code is available at https://github.com/ciaran-schembri/QM-Mazur; we provide a few details to explain how we proceeded, referring to the book by Stein [Reference SteinSte07] on modular symbols and, more broadly, [Reference Best, Bober, Booker, Costa, Cremona, Derickx, Lee, Lowry-Duda, Roe, Sutherland and VoightBBB21] for a survey of methods to compute modular forms.
$N \mid 2^{10} 3^5$
, with quadratic Hecke coefficient field, having an inner twist but no self-twist. However, here we need to do a new computation in a large dimensional space. The code is available at https://github.com/ciaran-schembri/QM-Mazur; we provide a few details to explain how we proceeded, referring to the book by Stein [Reference SteinSte07] on modular symbols and, more broadly, [Reference Best, Bober, Booker, Costa, Cremona, Derickx, Lee, Lowry-Duda, Roe, Sutherland and VoightBBB21] for a survey of methods to compute modular forms.
We work with modular symbols, and we loop over all possible (imaginary) quadratic characters
![]() $\psi $
supported at
$\psi $
supported at
![]() $2,3$
, corresponding to the inner twist. For each character
$2,3$
, corresponding to the inner twist. For each character
![]() $\psi $
, of conductor d:
$\psi $
, of conductor d:
-
• For a list of split primes
 $p \geq 5$
, we inductively compute the kernels of
$p \geq 5$
, we inductively compute the kernels of
 $T_p-a$
where
$T_p-a$
where
 $|a| \leq 2\sqrt {p}$
.
$|a| \leq 2\sqrt {p}$
. -
• For a list of inert primes
 $p \geq 5$
, we further inductively compute the kernels of
$p \geq 5$
, we further inductively compute the kernels of
 $T_p^2-db^2$
, where
$T_p^2-db^2$
, where
 $db^2 \leq 4p$
.
$db^2 \leq 4p$
.
The first bound holds since
![]() $\psi (p)=1$
so
$\psi (p)=1$
so
![]() $a_p(f)\psi (p)=\tau (a_p(f)) = a_p(f)$
so
$a_p(f)\psi (p)=\tau (a_p(f)) = a_p(f)$
so
![]() $a_p(f) \in {\mathbb {Z}}$
, and the Ramanujan–Petersson bound holds; the second bound holds since
$a_p(f) \in {\mathbb {Z}}$
, and the Ramanujan–Petersson bound holds; the second bound holds since
![]() $\psi (p)=-1$
now gives
$\psi (p)=-1$
now gives
![]() $\tau (a_p(f))=-a_p(f)$
so
$\tau (a_p(f))=-a_p(f)$
so
![]() $a_p(f)=\sqrt {d} b$
with again
$a_p(f)=\sqrt {d} b$
with again
![]() $\sqrt {d}|b| \leq 2\sqrt {p}$
. It is essential to compute the split primes first, and only compute the induced action of
$\sqrt {d}|b| \leq 2\sqrt {p}$
. It is essential to compute the split primes first, and only compute the induced action of
![]() $T_p$
on the kernels computed in the first step.
$T_p$
on the kernels computed in the first step.
To simplify the linear algebra, we work modulo a large prime number q, checking that each Hecke matrix
![]() $T_p$
(having entries in
$T_p$
(having entries in
![]() ${\mathbb {Q}}$
) has no denominator divisible by q. The corresponding decomposition gives us an ‘upper bound’: if we had the desired eigenspace for
${\mathbb {Q}}$
) has no denominator divisible by q. The corresponding decomposition gives us an ‘upper bound’: if we had the desired eigenspace for
![]() $T_p$
, it reduces modulo q, but a priori some of these spaces could accidentally coincide or the dimension could go down (corresponding to a prime of norm q in the Hecke field). To certify the ‘lower bound’, we compute a small linear combination of Hecke operators supported at split primes and use the computed eigenvalues to recompute the kernel over
$T_p$
, it reduces modulo q, but a priori some of these spaces could accidentally coincide or the dimension could go down (corresponding to a prime of norm q in the Hecke field). To certify the ‘lower bound’, we compute a small linear combination of Hecke operators supported at split primes and use the computed eigenvalues to recompute the kernel over
![]() ${\mathbb {Q}}$
working with divisors
${\mathbb {Q}}$
working with divisors
![]() $N' \mid N$
, and when we find it, we compute the dimension of the oldspace for the form at level
$N' \mid N$
, and when we find it, we compute the dimension of the oldspace for the form at level
![]() $N'$
inside level N and confirm that it matches the dimension computed modulo q.
$N'$
inside level N and confirm that it matches the dimension computed modulo q.
In fact, we find that
![]() $N \mid 2^8 3^5$
or
$N \mid 2^8 3^5$
or
![]() $N \mid 2^{10} 3^4$
. (Indeed, a careful analysis of the possible endomorphism algebra can be used to show this a priori.)
$N \mid 2^{10} 3^4$
. (Indeed, a careful analysis of the possible endomorphism algebra can be used to show this a priori.)
To certify that the form is not PCM, we find a coefficient for an inert prime that is nonzero. To certify that the form has inner twist by
![]() $\psi $
, we apply the bound [Reference Best, Bober, Booker, Costa, Cremona, Derickx, Lee, Lowry-Duda, Roe, Sutherland and VoightBBB21, Lemma 11.2.1(a)] on the level of the twist: in particular, we find that the twist has the same level whenever
$\psi $
, we apply the bound [Reference Best, Bober, Booker, Costa, Cremona, Derickx, Lee, Lowry-Duda, Roe, Sutherland and VoightBBB21, Lemma 11.2.1(a)] on the level of the twist: in particular, we find that the twist has the same level whenever
![]() $ {\mathrm{ord}}_p( {\mathrm{cond}}(\psi ))^2 \neq {\mathrm{ord}}_p(N)$
for
$ {\mathrm{ord}}_p( {\mathrm{cond}}(\psi ))^2 \neq {\mathrm{ord}}_p(N)$
for
![]() $p=2,3$
, and this condition happened to hold in all cases that arose for certification. (In general, we could also check up to the Sturm bound as in [Reference Best, Bober, Booker, Costa, Cremona, Derickx, Lee, Lowry-Duda, Roe, Sutherland and VoightBBB21, Theorem 11.2.4].) We similarly certify and discard the forms with PCM, using the LMFDB for this certification for a handful of cases when the level of the twist was different.
$p=2,3$
, and this condition happened to hold in all cases that arose for certification. (In general, we could also check up to the Sturm bound as in [Reference Best, Bober, Booker, Costa, Cremona, Derickx, Lee, Lowry-Duda, Roe, Sutherland and VoightBBB21, Theorem 11.2.4].) We similarly certify and discard the forms with PCM, using the LMFDB for this certification for a handful of cases when the level of the twist was different.
Finally, we compute the split
![]() $\mathrm {PQM}$
forms by identifying the quaternion algebra above using Proposition 5.2.
$\mathrm {PQM}$
forms by identifying the quaternion algebra above using Proposition 5.2.
The complete data is available online (https://github.com/ciaran-schembri/QM-Mazur); we give a summary in Table 1, listing forms in a fixed level, up to (quadratic) twist.
Table 1 Twist classes of modular forms corresponding to PQM abelian surfaces over
![]() ${\mathbb {Q}}$
of
${\mathbb {Q}}$
of
![]() $ {\mathrm{GL}}_2$
-type with good reduction outside
$ {\mathrm{GL}}_2$
-type with good reduction outside
![]() $\{2,3\}$
$\{2,3\}$

For example, Table 1 says that up to twist, there are
![]() $3$
newforms of level
$3$
newforms of level
![]() $N=20736=2^8 3^4$
, each having
$N=20736=2^8 3^4$
, each having
![]() $4$
Galois newform orbits for a total of
$4$
Galois newform orbits for a total of
![]() $12$
newform orbits.
$12$
newform orbits.
Corollary 5.7. If A is a
![]() $\mathrm {PQM}$
abelian surface of
$\mathrm {PQM}$
abelian surface of
![]() $ {\mathrm{GL}}_2$
-type over
$ {\mathrm{GL}}_2$
-type over
![]() ${\mathbb {Q}}$
with good reduction outside
${\mathbb {Q}}$
with good reduction outside
![]() $\{2,3\}$
and
$\{2,3\}$
and
![]() $\#A({\mathbb {Q}})_{\text {tors}}$
nontrivial, then A corresponds to either 243.2.a.d or 972.2.a.e. In particular,
$\#A({\mathbb {Q}})_{\text {tors}}$
nontrivial, then A corresponds to either 243.2.a.d or 972.2.a.e. In particular,
![]() $\#A({\mathbb {Q}})_{\text {tors}} \leq 9$
.
$\#A({\mathbb {Q}})_{\text {tors}} \leq 9$
.
Proof. Direct calculation as in Corollary 5.4.
5.2 Full level
 $2$
-structure
$2$
-structure
Before imposing the
![]() $ {\mathrm{GL}}_2$
-type assumption in the next subsection, we show that
$ {\mathrm{GL}}_2$
-type assumption in the next subsection, we show that
![]() ${\mathcal {O}}$
-
${\mathcal {O}}$
-
![]() $\mathrm {PQM}$
surfaces cannot have full level
$\mathrm {PQM}$
surfaces cannot have full level
![]() $2$
-structure over
$2$
-structure over
![]() ${\mathbb {Q}}$
.
${\mathbb {Q}}$
.
Proposition 5.8. Let
![]() $A/{\mathbb {Q}}$
be an
$A/{\mathbb {Q}}$
be an
![]() ${\mathcal {O}}$
-
${\mathcal {O}}$
-
![]() $\mathrm {PQM}$
surface. Then
$\mathrm {PQM}$
surface. Then
![]() $A({\mathbb {Q}})[2] \not \simeq ({\mathbb {Z}}/2{\mathbb {Z}})^4$
.
$A({\mathbb {Q}})[2] \not \simeq ({\mathbb {Z}}/2{\mathbb {Z}})^4$
.
Proof. Suppose
![]() $A({\mathbb {Q}})[2] \simeq ({\mathbb {Z}}/2{\mathbb {Z}})^4$
. Since
$A({\mathbb {Q}})[2] \simeq ({\mathbb {Z}}/2{\mathbb {Z}})^4$
. Since
![]() $A[2]$
is free of rank one as an
$A[2]$
is free of rank one as an
![]() ${\mathcal {O}}/2{\mathcal {O}}$
-module and contains a
${\mathcal {O}}/2{\mathcal {O}}$
-module and contains a
![]() ${\mathbb {Q}}$
-rational generator, we have
${\mathbb {Q}}$
-rational generator, we have
![]() $A[2] \simeq {\mathcal {O}}/2{\mathcal {O}}$
as
$A[2] \simeq {\mathcal {O}}/2{\mathcal {O}}$
as
![]() $ {\mathrm{Gal}}_{\mathbb {Q}}$
-modules. By Theorem 2.6 and Proposition 3.3, this implies that the endomorphism field
$ {\mathrm{Gal}}_{\mathbb {Q}}$
-modules. By Theorem 2.6 and Proposition 3.3, this implies that the endomorphism field
![]() $L/{\mathbb {Q}}$
is quadratic, so that A has
$L/{\mathbb {Q}}$
is quadratic, so that A has
![]() $ {\mathrm{GL}}_2$
-type by Lemma 3.4.
$ {\mathrm{GL}}_2$
-type by Lemma 3.4.
Let K be a quadratic field ramified at all primes
![]() $p\geq 3$
of bad reduction of A and unramified at all primes
$p\geq 3$
of bad reduction of A and unramified at all primes
![]() $p\geq 3$
of good reduction. Corollary 4.3 and Lemmas 4.5(a), 4.9 and 3.7 show that the quadratic twist of A by K is an
$p\geq 3$
of good reduction. Corollary 4.3 and Lemmas 4.5(a), 4.9 and 3.7 show that the quadratic twist of A by K is an
![]() ${\mathcal {O}}$
-
${\mathcal {O}}$
-
![]() ${\mathrm {PQM}}$
surface of
${\mathrm {PQM}}$
surface of
![]() $ {\mathrm{GL}}_2$
-type with good reduction outside
$ {\mathrm{GL}}_2$
-type with good reduction outside
![]() $\{2\}$
. But by Corollary 5.3, no such surface exists.
$\{2\}$
. But by Corollary 5.3, no such surface exists.
5.3 Torsion classification in the
 $ {\mathrm{GL}}_2$
-type case
$ {\mathrm{GL}}_2$
-type case
Now we assume
![]() $A/{\mathbb {Q}}$
is a
$A/{\mathbb {Q}}$
is a
![]() $\mathrm {PQM}$
surface of
$\mathrm {PQM}$
surface of
![]() $ {\mathrm{GL}}_2$
-type. By Lemma 3.4, there exists a quadratic extension
$ {\mathrm{GL}}_2$
-type. By Lemma 3.4, there exists a quadratic extension
![]() $L/{\mathbb {Q}}$
(the endomorphism field) such that
$L/{\mathbb {Q}}$
(the endomorphism field) such that
![]() $ {\mathrm{End}}(A_L) = {\mathrm{End}}(A_{\overline {\mathbb {Q}}})$
.
$ {\mathrm{End}}(A_L) = {\mathrm{End}}(A_{\overline {\mathbb {Q}}})$
.
Lemma 5.9. If
![]() $\ell $
is a prime such that
$\ell $
is a prime such that
![]() $A[\ell ]({\mathbb {Q}}) \neq 0$
, then
$A[\ell ]({\mathbb {Q}}) \neq 0$
, then
![]() $\ell \leq 7$
.
$\ell \leq 7$
.
Proof. By Lemma 4.1, there exists a finite extension
![]() $L'/L$
that is totally ramified at
$L'/L$
that is totally ramified at
![]() $2$
and such that
$2$
and such that
![]() $A_{L'}$
has good reduction. Let
$A_{L'}$
has good reduction. Let
![]() $\mathfrak {q}$
be a prime in
$\mathfrak {q}$
be a prime in
![]() $L'$
above
$L'$
above
![]() $2$
and let k be its residue field. Since
$2$
and let k be its residue field. Since
![]() $L/{\mathbb {Q}}$
is quadratic, k is isomorphic to
$L/{\mathbb {Q}}$
is quadratic, k is isomorphic to
![]() $\mathbb F_2$
or
$\mathbb F_2$
or
![]() $\mathbb F_4$
. Therefore, the reduction of
$\mathbb F_4$
. Therefore, the reduction of
![]() $A_{L'}$
at
$A_{L'}$
at
![]() $\mathfrak {q}$
is an abelian surface B over k such that
$\mathfrak {q}$
is an abelian surface B over k such that
![]() $ {\mathrm{End}}^0(B)$
contains
$ {\mathrm{End}}^0(B)$
contains
![]() $ {\mathrm{End}}^0(A_L)$
. By Lemma 4.13,
$ {\mathrm{End}}^0(A_L)$
. By Lemma 4.13,
![]() $B[\ell ](k)\neq 0$
and so
$B[\ell ](k)\neq 0$
and so
![]() $\ell $
divides
$\ell $
divides
![]() $\#B(\mathbb F_4)$
. However, Lemma 4.16 shows that the L-polynomial of
$\#B(\mathbb F_4)$
. However, Lemma 4.16 shows that the L-polynomial of
![]() $B_{\mathbb F_4}$
is of the form
$B_{\mathbb F_4}$
is of the form
![]() $(T^2+aT+4)^2$
with
$(T^2+aT+4)^2$
with
![]() $a\in {\mathbb {Z}}$
satisfying
$a\in {\mathbb {Z}}$
satisfying
![]() $|a|\leq 2\sqrt {4} = 4$
. Therefore,
$|a|\leq 2\sqrt {4} = 4$
. Therefore,
![]() $\ell $
divides
$\ell $
divides
![]() $(1+a+4)^2$
; hence,
$(1+a+4)^2$
; hence,
![]() $\ell $
divides
$\ell $
divides
![]() $(1+a+4)\leq 9$
, hence
$(1+a+4)\leq 9$
, hence
![]() $\ell \leq 9$
.
$\ell \leq 9$
.
Lemma 5.10. If
![]() $\ell \geq 5$
is a prime such that
$\ell \geq 5$
is a prime such that
![]() $A[\ell ]({\mathbb {Q}}) \neq 0$
, then
$A[\ell ]({\mathbb {Q}}) \neq 0$
, then
![]() $A/{\mathbb {Q}}$
has good reduction away from
$A/{\mathbb {Q}}$
has good reduction away from
![]() $\ell $
.
$\ell $
.
Proof. Let p be a prime of bad reduction of A. Since A is of
![]() $ {\mathrm{GL}}_2$
-type, the algebra
$ {\mathrm{GL}}_2$
-type, the algebra
![]() $ {\mathrm{End}}^0(A)$
is a quadratic field; it is real quadratic by Proposition 3.2. Proposition 4.2(c) implies that A has totally additive reduction at p. By Lemmas 4.8 and 4.10, we must have
$ {\mathrm{End}}^0(A)$
is a quadratic field; it is real quadratic by Proposition 3.2. Proposition 4.2(c) implies that A has totally additive reduction at p. By Lemmas 4.8 and 4.10, we must have
![]() $p=\ell $
. We conclude that A has good reduction outside
$p=\ell $
. We conclude that A has good reduction outside
![]() $\{\ell \}$
.
$\{\ell \}$
.
Proposition 5.11. If
![]() $\ell $
is a prime such that
$\ell $
is a prime such that
![]() $A[\ell ]({\mathbb {Q}}) \neq 0$
, then
$A[\ell ]({\mathbb {Q}}) \neq 0$
, then
![]() $\ell \in \{2,3\}$
.
$\ell \in \{2,3\}$
.
Proof. Suppose that
![]() $\ell \geq 5$
. By Proposition 3.2, the quadratic extension
$\ell \geq 5$
. By Proposition 3.2, the quadratic extension
![]() $L/{\mathbb {Q}}$
is imaginary quadratic. Moreover, by a result of Silverberg [Reference SilverbergSil92, Theorem 4.2], the surface A has bad reduction at all primes ramifying in L. By Lemma 5.10, L is therefore only ramified at
$L/{\mathbb {Q}}$
is imaginary quadratic. Moreover, by a result of Silverberg [Reference SilverbergSil92, Theorem 4.2], the surface A has bad reduction at all primes ramifying in L. By Lemma 5.10, L is therefore only ramified at
![]() $\ell $
. If
$\ell $
. If
![]() $\ell = 5$
, this is already a contradiction since there are no imaginary quadratic fields ramified only at
$\ell = 5$
, this is already a contradiction since there are no imaginary quadratic fields ramified only at
![]() $5$
. If
$5$
. If
![]() $\ell = 7$
, then we conclude that
$\ell = 7$
, then we conclude that
![]() $L = {\mathbb {Q}}(\sqrt {-7})$
. Since
$L = {\mathbb {Q}}(\sqrt {-7})$
. Since
![]() $2$
splits in L, this means that the residue field in the proof of Lemma 5.9 is equal to
$2$
splits in L, this means that the residue field in the proof of Lemma 5.9 is equal to
![]() $\mathbb F_2$
. Continuing with the proof there, we deduce the stronger inequality
$\mathbb F_2$
. Continuing with the proof there, we deduce the stronger inequality
![]() $|a| \leq 2\sqrt {2}$
, and we find that
$|a| \leq 2\sqrt {2}$
, and we find that
![]() $\ell $
divides
$\ell $
divides
![]() $1 + a + 2 < 6$
, which is a contradiction.
$1 + a + 2 < 6$
, which is a contradiction.
Remark 5.12. We can also deduce Proposition 5.11 from Lemma 5.10 by invoking modularity (Proposition 5.2), the fact that such an abelian surface must have conductor
![]() $\ell ^4$
(Proposition 4.15) and the fact that there are no
$\ell ^4$
(Proposition 4.15) and the fact that there are no
![]() $\mathrm {PQM}$
eigenforms in
$\mathrm {PQM}$
eigenforms in
![]() $S_2(\Gamma _0(25))$
or
$S_2(\Gamma _0(25))$
or
![]() $S_2(\Gamma _0(49))$
. We also note that Schoof has proven that there are no abelian varieties with everywhere good reduction over
$S_2(\Gamma _0(49))$
. We also note that Schoof has proven that there are no abelian varieties with everywhere good reduction over
![]() ${\mathbb {Q}}(\zeta _\ell )$
for various small
${\mathbb {Q}}(\zeta _\ell )$
for various small
![]() $\ell $
, including
$\ell $
, including
![]() $5$
and
$5$
and
![]() $7$
[Reference SchoofSch03].
$7$
[Reference SchoofSch03].
Proposition 5.13. Either
![]() $A({\mathbb {Q}})_{ {\mathrm{tors}}}\subset ({\mathbb {Z}}/2{\mathbb {Z}})^3$
or
$A({\mathbb {Q}})_{ {\mathrm{tors}}}\subset ({\mathbb {Z}}/2{\mathbb {Z}})^3$
or
![]() $A({\mathbb {Q}})_{ {\mathrm{tors}}}\subset ({\mathbb {Z}}/3{\mathbb {Z}})^2$
.
$A({\mathbb {Q}})_{ {\mathrm{tors}}}\subset ({\mathbb {Z}}/3{\mathbb {Z}})^2$
.
Proof. By Proposition 5.11,
![]() $A({\mathbb {Q}})_{ {\mathrm{tors}}}$
is a group of order
$A({\mathbb {Q}})_{ {\mathrm{tors}}}$
is a group of order
![]() $2^i3^j$
. We may assume that
$2^i3^j$
. We may assume that
![]() $A({\mathbb {Q}})_{\mathrm {tors}}\neq 0$
; let
$A({\mathbb {Q}})_{\mathrm {tors}}\neq 0$
; let
![]() $\ell \in \{2,3\}$
be such that
$\ell \in \{2,3\}$
be such that
![]() $A[\ell ]({\mathbb {Q}}) \neq 0$
.
$A[\ell ]({\mathbb {Q}}) \neq 0$
.
Suppose there exists a prime
![]() $p\geq 5$
of bad reduction. Then A has totally additive reduction over every finite extension
$p\geq 5$
of bad reduction. Then A has totally additive reduction over every finite extension
![]() $F/{\mathbb {Q}}_p$
over which it has bad reduction by Proposition 4.2. Therefore, the assumptions of Proposition 4.12 apply for
$F/{\mathbb {Q}}_p$
over which it has bad reduction by Proposition 4.2. Therefore, the assumptions of Proposition 4.12 apply for
![]() $F= {\mathbb {Q}}_p^{\mathrm {nr}}$
(the maximal unramified extension of
$F= {\mathbb {Q}}_p^{\mathrm {nr}}$
(the maximal unramified extension of
![]() ${\mathbb {Q}}_p$
), and so
${\mathbb {Q}}_p$
), and so
![]() $A({\mathbb {Q}})_{\mathrm {tors}} = A({\mathbb {Q}})_{\mathrm {tors}}^{(p)} \subset A({\mathbb {Q}}_p^{\mathrm {nr}})_{\mathrm {tors}}^{(p)}\simeq ({\mathbb {Z}}/\ell {\mathbb {Z}})^k$
for some
$A({\mathbb {Q}})_{\mathrm {tors}} = A({\mathbb {Q}})_{\mathrm {tors}}^{(p)} \subset A({\mathbb {Q}}_p^{\mathrm {nr}})_{\mathrm {tors}}^{(p)}\simeq ({\mathbb {Z}}/\ell {\mathbb {Z}})^k$
for some
![]() $1 \leq k\leq 4$
. If
$1 \leq k\leq 4$
. If
![]() $\ell = 2$
, then
$\ell = 2$
, then
![]() $k \leq 3$
by Proposition 5.8. If
$k \leq 3$
by Proposition 5.8. If
![]() $\ell = 3$
, then
$\ell = 3$
, then
![]() $k \leq 2$
, since
$k \leq 2$
, since
![]() $A({\mathbb {Q}})^{(2)}_{\mathrm {tors}} \hookrightarrow A_2(\mathbb F_2)$
for some abelian surface
$A({\mathbb {Q}})^{(2)}_{\mathrm {tors}} \hookrightarrow A_2(\mathbb F_2)$
for some abelian surface
![]() $A_2/\mathbb F_2$
(using Lemmas 4.1 and 4.13) and
$A_2/\mathbb F_2$
(using Lemmas 4.1 and 4.13) and
![]() $\#A_2(\mathbb F_2) \leq 25$
for all such surfaces. We conclude
$\#A_2(\mathbb F_2) \leq 25$
for all such surfaces. We conclude
![]() $A({\mathbb {Q}})_{ {\mathrm{tors}}}\subset ({\mathbb {Z}}/2{\mathbb {Z}})^3$
or
$A({\mathbb {Q}})_{ {\mathrm{tors}}}\subset ({\mathbb {Z}}/2{\mathbb {Z}})^3$
or
![]() $A({\mathbb {Q}})_{ {\mathrm{tors}}}\subset ({\mathbb {Z}}/3{\mathbb {Z}})^2$
, as desired.
$A({\mathbb {Q}})_{ {\mathrm{tors}}}\subset ({\mathbb {Z}}/3{\mathbb {Z}})^2$
, as desired.
It remains to consider the case that A has good reduction outside
![]() $\{2,3\}$
. A computation with modular forms of level dividing
$\{2,3\}$
. A computation with modular forms of level dividing
![]() $2^{10}\cdot 3^5$
shows that
$2^{10}\cdot 3^5$
shows that
![]() $\# A({\mathbb {Q}})_{ {\mathrm{tors}}} \mid 9$
for such surfaces by Corollary 5.7, but we give an argument that only involves computing modular forms of much smaller level. We may assume A has bad reduction at both of these primes by Corollaries 5.3 and 5.4. If
$\# A({\mathbb {Q}})_{ {\mathrm{tors}}} \mid 9$
for such surfaces by Corollary 5.7, but we give an argument that only involves computing modular forms of much smaller level. We may assume A has bad reduction at both of these primes by Corollaries 5.3 and 5.4. If
![]() $A[2]({\mathbb {Q}}) = 0$
, then Proposition 4.12 shows again that
$A[2]({\mathbb {Q}}) = 0$
, then Proposition 4.12 shows again that
![]() $A({\mathbb {Q}})_{\mathrm {tors}}=A({\mathbb {Q}})_{\mathrm {tors}}^{(2)} \subset A({\mathbb {Q}}_2^{\mathrm {nr}})_{\mathrm {tors}}^{(2)}\subset ({\mathbb {Z}}/3{\mathbb {Z}})^2$
. Similarly,
$A({\mathbb {Q}})_{\mathrm {tors}}=A({\mathbb {Q}})_{\mathrm {tors}}^{(2)} \subset A({\mathbb {Q}}_2^{\mathrm {nr}})_{\mathrm {tors}}^{(2)}\subset ({\mathbb {Z}}/3{\mathbb {Z}})^2$
. Similarly,
![]() $A({\mathbb {Q}})_{\mathrm {tors}}\subset ({\mathbb {Z}}/2{\mathbb {Z}})^3$
if
$A({\mathbb {Q}})_{\mathrm {tors}}\subset ({\mathbb {Z}}/2{\mathbb {Z}})^3$
if
![]() $A[3]({\mathbb {Q}})=0$
. Thus, it remains to rule out the possibility that
$A[3]({\mathbb {Q}})=0$
. Thus, it remains to rule out the possibility that
![]() $A({\mathbb {Q}})$
contains a point of order
$A({\mathbb {Q}})$
contains a point of order
![]() $6$
. In that case, Proposition 4.12 shows that the extensions
$6$
. In that case, Proposition 4.12 shows that the extensions
![]() $M_2/{\mathbb {Q}}^{\mathrm {nr}}_2$
and
$M_2/{\mathbb {Q}}^{\mathrm {nr}}_2$
and
![]() $M_3/{\mathbb {Q}}^{\mathrm {nr}}_3$
over which A attains good reduction have degrees that are powers of
$M_3/{\mathbb {Q}}^{\mathrm {nr}}_3$
over which A attains good reduction have degrees that are powers of
![]() $3$
and
$3$
and
![]() $2$
, respectively, and hence are tamely ramified. Hence, A has conductor
$2$
, respectively, and hence are tamely ramified. Hence, A has conductor
![]() $2^43^4$
by Lemma 4.14 and corresponds to an eigenform of level
$2^43^4$
by Lemma 4.14 and corresponds to an eigenform of level
![]() $2^23^2 = 36$
, by Theorem 5.1. However, there are no
$2^23^2 = 36$
, by Theorem 5.1. However, there are no
![]() $\mathrm {PQM}$
eigenforms of level
$\mathrm {PQM}$
eigenforms of level
![]() $36$
[Reference González and GuàrdiaGG09, Table 1].
$36$
[Reference González and GuàrdiaGG09, Table 1].
Next we constrain the torsion even further and show that
![]() $({\mathbb {Z}}/2{\mathbb {Z}})^3$
does not occur. For this, we combine a cute fact from linear algebra with a purely local proposition that makes use of the enhanced Galois representation of §3.5.
$({\mathbb {Z}}/2{\mathbb {Z}})^3$
does not occur. For this, we combine a cute fact from linear algebra with a purely local proposition that makes use of the enhanced Galois representation of §3.5.
Lemma 5.14. Let k be a field and
![]() $V\subset {\mathcal {O}}_k := {\mathcal {O}} \otimes _{{\mathbb {Z}}} k$
a
$V\subset {\mathcal {O}}_k := {\mathcal {O}} \otimes _{{\mathbb {Z}}} k$
a
![]() $3$
-dimensional k-subspace. Then V contains an
$3$
-dimensional k-subspace. Then V contains an
![]() ${\mathcal {O}}_k$
-module generator of
${\mathcal {O}}_k$
-module generator of
![]() ${\mathcal {O}}_k$
.
${\mathcal {O}}_k$
.
Proof. If
![]() ${\mathcal {O}}_k$
is a division algebra, every nonzero element of V is an
${\mathcal {O}}_k$
is a division algebra, every nonzero element of V is an
![]() ${\mathcal {O}}_k$
-generator. If the characteristic of k divides
${\mathcal {O}}_k$
-generator. If the characteristic of k divides
![]() $ {\mathrm{disc}}(B)$
, the lemma follows from Lemma 6.3 and the fact that the ideal J described there is
$ {\mathrm{disc}}(B)$
, the lemma follows from Lemma 6.3 and the fact that the ideal J described there is
![]() $2$
-dimensional. It suffices to consider the case when
$2$
-dimensional. It suffices to consider the case when
![]() ${\mathcal {O}}_k\simeq {\mathrm{Mat}}_2(k)$
and to prove that in this case, V contains an invertible matrix. (This is well known; we give a quick proof here.) Suppose otherwise. If k admits a quadratic field extension
${\mathcal {O}}_k\simeq {\mathrm{Mat}}_2(k)$
and to prove that in this case, V contains an invertible matrix. (This is well known; we give a quick proof here.) Suppose otherwise. If k admits a quadratic field extension
![]() $k'$
, then embedding
$k'$
, then embedding
![]() $k' \subset \mathrm {Mat}_2(k)$
, we compute
$k' \subset \mathrm {Mat}_2(k)$
, we compute
![]() $\dim (V + k') = \dim V + \dim k' - \dim (V \cap k') = 3 + 2 - 0 = 5$
, which is a contradiction. In general, the subspace V is defined over a subfield
$\dim (V + k') = \dim V + \dim k' - \dim (V \cap k') = 3 + 2 - 0 = 5$
, which is a contradiction. In general, the subspace V is defined over a subfield
![]() $k"$
of k which is finitely generated over its prime field. The previous argument then applies over
$k"$
of k which is finitely generated over its prime field. The previous argument then applies over
![]() $k"$
.
$k"$
.
Recall that
![]() ${\mathbb {Q}}_p^{\mathrm {nr}}$
denotes the maximal unramified extension of
${\mathbb {Q}}_p^{\mathrm {nr}}$
denotes the maximal unramified extension of
![]() ${\mathbb {Q}}_p$
.
${\mathbb {Q}}_p$
.
Proposition 5.15. Let p be an odd prime, F a finite extension of
![]() ${\mathbb {Q}}_p^{\mathrm {nr}}$
and
${\mathbb {Q}}_p^{\mathrm {nr}}$
and
![]() $A/F$
an
$A/F$
an
![]() ${\mathcal {O}}$
-
${\mathcal {O}}$
-
![]() $\mathrm {PQM}$
surface with
$\mathrm {PQM}$
surface with
![]() $({\mathbb {Z}}/2{\mathbb {Z}})^3\subset A[2](F)$
. Then A acquires good reduction over every quadratic extension of F.
$({\mathbb {Z}}/2{\mathbb {Z}})^3\subset A[2](F)$
. Then A acquires good reduction over every quadratic extension of F.
Proof. If
![]() $A[2](F)\simeq ({\mathbb {Z}}/2{\mathbb {Z}})^4$
, this immediately follows from Raynaud’s criterion (Lemma 4.5(a)), so assume that
$A[2](F)\simeq ({\mathbb {Z}}/2{\mathbb {Z}})^4$
, this immediately follows from Raynaud’s criterion (Lemma 4.5(a)), so assume that
![]() $A[2](F)\simeq ({\mathbb {Z}}/2{\mathbb {Z}})^3$
. By Lemma 5.14, there exists an F-rational
$A[2](F)\simeq ({\mathbb {Z}}/2{\mathbb {Z}})^3$
. By Lemma 5.14, there exists an F-rational
![]() ${\mathcal {O}}/2{\mathcal {O}}$
-generator
${\mathcal {O}}/2{\mathcal {O}}$
-generator
![]() $P\in A[2](F)$
, and hence,
$P\in A[2](F)$
, and hence,
![]() $A[2]\simeq {\mathcal {O}}/2{\mathcal {O}}$
as
$A[2]\simeq {\mathcal {O}}/2{\mathcal {O}}$
as
![]() $ {\mathrm{Gal}}_F$
-modules.
$ {\mathrm{Gal}}_F$
-modules.
Let
![]() $L/F$
be the endomorphism field of
$L/F$
be the endomorphism field of
![]() $A_F$
and let
$A_F$
and let
![]() $M/F$
be the smallest field over which
$M/F$
be the smallest field over which
![]() $A_F$
acquires good reduction. By the Néron-Ogg-Shafarevich criterion,
$A_F$
acquires good reduction. By the Néron-Ogg-Shafarevich criterion,
![]() $M = F(A[4])$
. By Proposition 3.6,
$M = F(A[4])$
. By Proposition 3.6,
![]() $L\subset M$
. Since
$L\subset M$
. Since
![]() $A[2]\simeq {\mathcal {O}}/2{\mathcal {O}}$
as
$A[2]\simeq {\mathcal {O}}/2{\mathcal {O}}$
as
![]() $ {\mathrm{Gal}}_{{\mathbb {Q}}}$
-modules,
$ {\mathrm{Gal}}_{{\mathbb {Q}}}$
-modules,
![]() $F(A[2]) \subset L$
. We therefore have a chain of inclusions
$F(A[2]) \subset L$
. We therefore have a chain of inclusions
![]() $F \subset F(A[2]) \subset L\subset M = F(A[4])$
. Since
$F \subset F(A[2]) \subset L\subset M = F(A[4])$
. Since
![]() $A[2]({\mathbb {Q}}) \simeq ({\mathbb {Z}}/2{\mathbb {Z}})^3$
,
$A[2]({\mathbb {Q}}) \simeq ({\mathbb {Z}}/2{\mathbb {Z}})^3$
,
![]() $F(A[2])/F$
is a
$F(A[2])/F$
is a
![]() $(2,2,\dots ,2)$
-extension. The same is true for
$(2,2,\dots ,2)$
-extension. The same is true for
![]() $F(A[4])/F(A[2])$
. Since p is odd and the residue field is algebraically closed, both these extensions are cyclic, so at most quadratic. Therefore,
$F(A[4])/F(A[2])$
. Since p is odd and the residue field is algebraically closed, both these extensions are cyclic, so at most quadratic. Therefore,
![]() $F(A[2])/F$
is a quadratic extension. If
$F(A[2])/F$
is a quadratic extension. If
![]() $L \neq F(A[2])$
, then
$L \neq F(A[2])$
, then
![]() $L/F$
would be cyclic of order
$L/F$
would be cyclic of order
![]() $4$
, and there would be an order
$4$
, and there would be an order
![]() $4$
element
$4$
element
![]() $g\in {\mathrm{Aut}}({\mathcal {O}})$
whose fixed points on
$g\in {\mathrm{Aut}}({\mathcal {O}})$
whose fixed points on
![]() ${\mathcal {O}}/2{\mathcal {O}}$
is
${\mathcal {O}}/2{\mathcal {O}}$
is
![]() $({\mathbb {Z}}/2{\mathbb {Z}})^3$
. A calculation similar to the proof of the
$({\mathbb {Z}}/2{\mathbb {Z}})^3$
. A calculation similar to the proof of the
![]() $D_4$
case in Theorem 2.6 shows that this is not possible. We conclude that
$D_4$
case in Theorem 2.6 shows that this is not possible. We conclude that
![]() $L = F(A[2])$
and that
$L = F(A[2])$
and that
![]() $M / L$
is at most quadratic.
$M / L$
is at most quadratic.
To prove the proposition, it suffices to prove that
![]() $M/F$
is quadratic, so assume by contradiction that this is not the case. Then
$M/F$
is quadratic, so assume by contradiction that this is not the case. Then
![]() $M/L$
and
$M/L$
and
![]() $L/F$
are both quadratic, and
$L/F$
are both quadratic, and
![]() $ {\mathrm{Gal}}(M/F)= \{1,g,g^2,g^3\}$
is cyclic of order
$ {\mathrm{Gal}}(M/F)= \{1,g,g^2,g^3\}$
is cyclic of order
![]() $4$
.
$4$
.
Consider the mod
![]() $4$
Galois representation
$4$
Galois representation
![]() $\rho \colon {\mathrm{Gal}}_F\rightarrow {\mathrm{GL}}(A[4])$
, which factors through
$\rho \colon {\mathrm{Gal}}_F\rightarrow {\mathrm{GL}}(A[4])$
, which factors through
![]() $ {\mathrm{Gal}}_F \rightarrow {\mathrm{Gal}}(M/F)$
. Let
$ {\mathrm{Gal}}_F \rightarrow {\mathrm{Gal}}(M/F)$
. Let
![]() $Q\in A[4](M)$
be a lift of the
$Q\in A[4](M)$
be a lift of the
![]() ${\mathcal {O}}/2{\mathcal {O}}$
-generator
${\mathcal {O}}/2{\mathcal {O}}$
-generator
![]() $P\in A[2](F)$
. Then Q is an
$P\in A[2](F)$
. Then Q is an
![]() ${\mathcal {O}}/4{\mathcal {O}}$
-generator for
${\mathcal {O}}/4{\mathcal {O}}$
-generator for
![]() $A[4]$
, and hence, by the enhanced Galois representation construction, we know that
$A[4]$
, and hence, by the enhanced Galois representation construction, we know that
![]() $\rho \simeq \rho _4^\circ $
lands in
$\rho \simeq \rho _4^\circ $
lands in
![]() $ {\mathrm{Gal}}(L/F) \ltimes ({\mathcal {O}}/4{\mathcal {O}})^{\times } $
(see §3.5 and Proposition 3.15). The situation can be summarized as follows:
$ {\mathrm{Gal}}(L/F) \ltimes ({\mathcal {O}}/4{\mathcal {O}})^{\times } $
(see §3.5 and Proposition 3.15). The situation can be summarized as follows:

The horizontal maps are the enhanced Galois representations for L mod
![]() $4$
, F mod
$4$
, F mod
![]() $4$
and F mod
$4$
and F mod
![]() $2$
, respectively. Write
$2$
, respectively. Write
![]() $ {\mathrm{Gal}}(L/F) = \{1,\sigma \}$
. Since P is F-rational, the bottom map sends
$ {\mathrm{Gal}}(L/F) = \{1,\sigma \}$
. Since P is F-rational, the bottom map sends
![]() $\sigma $
to
$\sigma $
to
![]() $(\sigma ,1)$
. By commutativity of the bottom square,
$(\sigma ,1)$
. By commutativity of the bottom square,
![]() $\rho _4^\circ (g) = (\sigma ,x)$
, where
$\rho _4^\circ (g) = (\sigma ,x)$
, where
![]() $x\in ({\mathcal {O}}/4{\mathcal {O}})$
satisfies
$x\in ({\mathcal {O}}/4{\mathcal {O}})$
satisfies
![]() $x\equiv 1\ \mod 2{\mathcal {O}}$
. Since
$x\equiv 1\ \mod 2{\mathcal {O}}$
. Since
![]() $A_L$
has bad and hence totally additive reduction by Proposition 4.2, the nontrivial element of
$A_L$
has bad and hence totally additive reduction by Proposition 4.2, the nontrivial element of
![]() $ {\mathrm{Gal}}(M/L)$
maps to
$ {\mathrm{Gal}}(M/L)$
maps to
![]() $-1$
in
$-1$
in
![]() $({\mathcal {O}}/4{\mathcal {O}})^{\times }$
. (In fact, the generator of
$({\mathcal {O}}/4{\mathcal {O}})^{\times }$
. (In fact, the generator of
![]() $ {\mathrm{Gal}}(M/L)$
even maps to
$ {\mathrm{Gal}}(M/L)$
even maps to
![]() $-1$
in
$-1$
in
![]() $ {\mathrm{GL}}(T_2A)$
by an argument identical to the proof of Lemma 4.9.) By the commutativity of the top diagram,
$ {\mathrm{GL}}(T_2A)$
by an argument identical to the proof of Lemma 4.9.) By the commutativity of the top diagram,
![]() $(\sigma ,x)^2 = (1,-1)$
. The involution
$(\sigma ,x)^2 = (1,-1)$
. The involution
![]() $\sigma $
acts on
$\sigma $
acts on
![]() $({\mathcal {O}}/4{\mathcal {O}})^{\times }$
by conjugating by an element
$({\mathcal {O}}/4{\mathcal {O}})^{\times }$
by conjugating by an element
![]() $b\in {\mathcal {O}} \cap N_{B^{\times }}({\mathcal {O}})$
whose fixed points on
$b\in {\mathcal {O}} \cap N_{B^{\times }}({\mathcal {O}})$
whose fixed points on
![]() ${\mathcal {O}}/2{\mathcal {O}}$
are
${\mathcal {O}}/2{\mathcal {O}}$
are
![]() $({\mathbb {Z}}/2 {\mathbb {Z}})^3$
. Therefore,
$({\mathbb {Z}}/2 {\mathbb {Z}})^3$
. Therefore,
![]() $(\sigma ,x)^2 = (1,-1)$
is equivalent to
$(\sigma ,x)^2 = (1,-1)$
is equivalent to
![]() $b^{-1}xbx = -1$
. By Lemma 2.9, no such x exists, obtaining the desired contradiction.
$b^{-1}xbx = -1$
. By Lemma 2.9, no such x exists, obtaining the desired contradiction.
Proposition 5.16. Let
![]() $A/{\mathbb {Q}}$
be an
$A/{\mathbb {Q}}$
be an
![]() ${\mathcal {O}}$
-
${\mathcal {O}}$
-
![]() $\mathrm {PQM}$
surface of
$\mathrm {PQM}$
surface of
![]() $ {\mathrm{GL}}_2$
-type. Then
$ {\mathrm{GL}}_2$
-type. Then
![]() $({\mathbb {Z}}/2{\mathbb {Z}})^3\not \subset A({\mathbb {Q}})[2]$
.
$({\mathbb {Z}}/2{\mathbb {Z}})^3\not \subset A({\mathbb {Q}})[2]$
.
Proof. Let K be a quadratic field ramified at all primes
![]() $p\geq 3$
of bad reduction of A and unramified at all primes
$p\geq 3$
of bad reduction of A and unramified at all primes
![]() $p\geq 3$
of good reduction. Corollary 4.3, Proposition 5.15 and Lemmas 4.9 and 3.7 show that the quadratic twist of A by K is an
$p\geq 3$
of good reduction. Corollary 4.3, Proposition 5.15 and Lemmas 4.9 and 3.7 show that the quadratic twist of A by K is an
![]() ${\mathcal {O}}$
-
${\mathcal {O}}$
-
![]() $\mathrm {PQM}$
surface of
$\mathrm {PQM}$
surface of
![]() $ {\mathrm{GL}}_2$
-type with good reduction outside
$ {\mathrm{GL}}_2$
-type with good reduction outside
![]() $\{2\}$
. But no such
$\{2\}$
. But no such
![]() ${\mathcal {O}}$
-
${\mathcal {O}}$
-
![]() $\mathrm {PQM}$
surface exists by Corollary 5.3.
$\mathrm {PQM}$
surface exists by Corollary 5.3.
We are finally ready to prove our classification result for torsion subgroups of
![]() ${\mathcal {O}}$
-
${\mathcal {O}}$
-
![]() $\mathrm {PQM}$
surfaces of
$\mathrm {PQM}$
surfaces of
![]() $ {\mathrm{GL}}_2$
-type.
$ {\mathrm{GL}}_2$
-type.
Proof of Theorem 1.4.
By Propositions 5.13 and 5.16, we have ruled out all groups aside from those listed in the theorem. It remains to exhibit infinitely many abelian surfaces
![]() $A/{\mathbb {Q}}$
of
$A/{\mathbb {Q}}$
of
![]() $ {\mathrm{GL}}_2$
-type with torsion subgroups isomorphic to each of the groups
$ {\mathrm{GL}}_2$
-type with torsion subgroups isomorphic to each of the groups
Let
![]() ${\mathcal {O}}_6$
be the maximal quaternion order of discriminant
${\mathcal {O}}_6$
be the maximal quaternion order of discriminant
![]() $6$
(unique up to isomorphism). In [Reference Laga and ShnidmanLS23, §9], one-parameter families of
$6$
(unique up to isomorphism). In [Reference Laga and ShnidmanLS23, §9], one-parameter families of
![]() $ {\mathrm{GL}}_2$
-type
$ {\mathrm{GL}}_2$
-type
![]() ${\mathcal {O}}_6$
-PQM surfaces with generic torsion subgroups
${\mathcal {O}}_6$
-PQM surfaces with generic torsion subgroups
![]() $\{0\}, {\mathbb {Z}}/2{\mathbb {Z}}$
,
$\{0\}, {\mathbb {Z}}/2{\mathbb {Z}}$
,
![]() ${\mathbb {Z}}/3{\mathbb {Z}}$
and
${\mathbb {Z}}/3{\mathbb {Z}}$
and
![]() $({\mathbb {Z}}/3{\mathbb {Z}})^2$
are given among Prym surfaces of bielliptic Picard curves. In Proposition 5.17 below, we give a one-parameter family of
$({\mathbb {Z}}/3{\mathbb {Z}})^2$
are given among Prym surfaces of bielliptic Picard curves. In Proposition 5.17 below, we give a one-parameter family of
![]() $ {\mathrm{GL}}_2$
-type
$ {\mathrm{GL}}_2$
-type
![]() ${\mathcal {O}}_6$
-PQM Jacobians J with
${\mathcal {O}}_6$
-PQM Jacobians J with
![]() $({\mathbb {Z}}/2{\mathbb {Z}})^2 \subset J({\mathbb {Q}})_{ {\mathrm{tors}}}$
.
$({\mathbb {Z}}/2{\mathbb {Z}})^2 \subset J({\mathbb {Q}})_{ {\mathrm{tors}}}$
.
To state the next result, we define the rational functions
 $$ \begin{align*} j(T) &=\frac{(-64T^{20} + 256T^{16} - 384T^{12} + 256T^8 - 64T^4)}{(T^{24} + 42T^{20} + 591T^{16} + 2828T^{12} + 591T^8 + 42T^4 + 1)}; \\ J_2(T) &=12(j+1); \\ J_4(T) &=6(j^2+j+1); \\ J_6(T) &=4(j^3-2j^2+1); \\ J_8(T) &=(J_2J_6-J_4^2)/4; \\ J_{10}(T) &=j^3. \end{align*} $$
$$ \begin{align*} j(T) &=\frac{(-64T^{20} + 256T^{16} - 384T^{12} + 256T^8 - 64T^4)}{(T^{24} + 42T^{20} + 591T^{16} + 2828T^{12} + 591T^8 + 42T^4 + 1)}; \\ J_2(T) &=12(j+1); \\ J_4(T) &=6(j^2+j+1); \\ J_6(T) &=4(j^3-2j^2+1); \\ J_8(T) &=(J_2J_6-J_4^2)/4; \\ J_{10}(T) &=j^3. \end{align*} $$
Proposition 5.17. For all but finitely many
![]() $t \in {\mathbb {Q}}$
, there exists a genus two curve
$t \in {\mathbb {Q}}$
, there exists a genus two curve
![]() $C_t/{\mathbb {Q}}$
with Igusa invariants
$C_t/{\mathbb {Q}}$
with Igusa invariants
![]() $(J_2(t): J_4(t) : J_6(t) : J_8(t) : J_{10}(t))$
, whose Jacobian
$(J_2(t): J_4(t) : J_6(t) : J_8(t) : J_{10}(t))$
, whose Jacobian
![]() $J_t/{\mathbb {Q}}$
is an
$J_t/{\mathbb {Q}}$
is an
![]() ${\mathcal {O}}_6$
-
${\mathcal {O}}_6$
-
![]() $\mathrm {PQM}$
surface of
$\mathrm {PQM}$
surface of
![]() $ {\mathrm{GL}}_2$
-type and satisfies
$ {\mathrm{GL}}_2$
-type and satisfies
![]() $J_t({\mathbb {Q}})_{ {\mathrm{tors}}} \supset ({\mathbb {Z}}/2{\mathbb {Z}})^2$
.
$J_t({\mathbb {Q}})_{ {\mathrm{tors}}} \supset ({\mathbb {Z}}/2{\mathbb {Z}})^2$
.
Proof. In [Reference Baba and GranathBG08, p.742], the authors have an expression for Igusa-Clebsch invariants (which we have translated to Igusa invariants) of genus 2 curves defining
![]() ${\mathcal {O}}$
-
${\mathcal {O}}$
-
![]() $\mathrm {PQM}$
surfaces for every value of a parameter j (which is a coordinate on the full Atkin-Lehner quotient of the discriminant 6 Shimura curve). The field of moduli for
$\mathrm {PQM}$
surfaces for every value of a parameter j (which is a coordinate on the full Atkin-Lehner quotient of the discriminant 6 Shimura curve). The field of moduli for
![]() $k_{R_3}$
, in their notation, is
$k_{R_3}$
, in their notation, is
![]() ${\mathbb {Q}}(\sqrt {-27 - 16j^{-1}})$
, and the obstruction for these genus 2 curves to be defined over
${\mathbb {Q}}(\sqrt {-27 - 16j^{-1}})$
, and the obstruction for these genus 2 curves to be defined over
![]() ${\mathbb {Q}}$
is given by the Mestre obstruction
${\mathbb {Q}}$
is given by the Mestre obstruction
![]() $\Big (\frac {-6j, -2(27j+16)}{{\mathbb {Q}}}\Big ).$
A short computation for the family
$\Big (\frac {-6j, -2(27j+16)}{{\mathbb {Q}}}\Big ).$
A short computation for the family
![]() $j(T)$
shows that
$j(T)$
shows that
![]() $-27-16j^{-1}$
is a square in
$-27-16j^{-1}$
is a square in
![]() ${\mathbb {Q}}(T)^\times $
, and hence,
${\mathbb {Q}}(T)^\times $
, and hence,
![]() $k_{R_3} = {\mathbb {Q}}$
for all non-singular specializations. Furthermore, one checks that the Mestre obstruction also vanishes for all such t. Thus, the Igusa invariants in the statement of the proposition give an infinite family of
$k_{R_3} = {\mathbb {Q}}$
for all non-singular specializations. Furthermore, one checks that the Mestre obstruction also vanishes for all such t. Thus, the Igusa invariants in the statement of the proposition give an infinite family of
![]() ${\mathcal {O}}$
-
${\mathcal {O}}$
-
![]() $\mathrm {PQM}$
Jacobians
$\mathrm {PQM}$
Jacobians
![]() $J/{\mathbb {Q}}$
of
$J/{\mathbb {Q}}$
of
![]() $ {\mathrm{GL}}_2$
-type with
$ {\mathrm{GL}}_2$
-type with
![]() $ {\mathrm{End}}^0(J) \simeq {\mathbb {Q}}(\sqrt {3}).$
(Only finitely many
$ {\mathrm{End}}^0(J) \simeq {\mathbb {Q}}(\sqrt {3}).$
(Only finitely many
![]() $j\in {\mathbb {Q}}$
correspond to CM points [Reference Baba and GranathBG08, §5, Table 1], so J is geometrically simple for all but finitely many
$j\in {\mathbb {Q}}$
correspond to CM points [Reference Baba and GranathBG08, §5, Table 1], so J is geometrically simple for all but finitely many
![]() $t\in {\mathbb {Q}}$
.)
$t\in {\mathbb {Q}}$
.)
Using Magma, one can write down an explicit sextic polynomial
![]() $f_T(x)$
such that
$f_T(x)$
such that
![]() $C_t$
has model
$C_t$
has model
![]() $y^2 = f_t(x)$
. The coefficients of
$y^2 = f_t(x)$
. The coefficients of
![]() $f_T(x)$
are too large to include here, but they can be found on our associated GitHub repository.Footnote
2
We find that there is a factoriztion
$f_T(x)$
are too large to include here, but they can be found on our associated GitHub repository.Footnote
2
We find that there is a factoriztion
where each
![]() $q_{i,T}$
is a quadratic polynomial in
$q_{i,T}$
is a quadratic polynomial in
![]() ${\mathbb {Q}}(T)[x]$
. From this, we see that for all but finitely many t, the group
${\mathbb {Q}}(T)[x]$
. From this, we see that for all but finitely many t, the group
![]() $({\mathbb {Z}}/2{\mathbb {Z}})^2$
is a subgroup of
$({\mathbb {Z}}/2{\mathbb {Z}})^2$
is a subgroup of
![]() $J_t({\mathbb {Q}})_{ {\mathrm{tors}}}.$
Indeed,
$J_t({\mathbb {Q}})_{ {\mathrm{tors}}}.$
Indeed,
![]() $J_t = {\mathrm{Pic}}_0(C_t)$
, and for each
$J_t = {\mathrm{Pic}}_0(C_t)$
, and for each
![]() $i \in \{1,2,3\}$
, the divisor class
$i \in \{1,2,3\}$
, the divisor class
![]() $(\alpha ,0) - (\alpha ',0)$
, where
$(\alpha ,0) - (\alpha ',0)$
, where
![]() $q_{i,t}(x) = (x-\alpha )(x - \alpha ')$
, is defined over
$q_{i,t}(x) = (x-\alpha )(x - \alpha ')$
, is defined over
![]() ${\mathbb {Q}}$
and has order
${\mathbb {Q}}$
and has order
![]() $2$
. In future work, we will explain how the special family
$2$
. In future work, we will explain how the special family
![]() $j(T)$
was found using the arithmetic of Shimura curves.
$j(T)$
was found using the arithmetic of Shimura curves.
6 Proof of Theorem 1.1: Reduction to
 $ {\mathrm{GL}}_2$
-type
$ {\mathrm{GL}}_2$
-type
In this section, we prove Theorem 1.1. By Theorem 1.4, it is enough to prove the following:
Theorem 6.1. Let
![]() $A/{\mathbb {Q}}$
be an
$A/{\mathbb {Q}}$
be an
![]() ${\mathcal {O}}$
-
${\mathcal {O}}$
-
![]() $\mathrm {PQM}$
surface and let
$\mathrm {PQM}$
surface and let
![]() $\ell \geq 5$
be a prime number such that
$\ell \geq 5$
be a prime number such that
![]() $A[\ell ]({\mathbb {Q}})\neq 0$
. Then A is of
$A[\ell ]({\mathbb {Q}})\neq 0$
. Then A is of
![]() $ {\mathrm{GL}}_2$
-type.
$ {\mathrm{GL}}_2$
-type.
Theorem 6.1 follows from combining Propositions 6.8 and 6.10 below. The proofs consist mostly of careful semi-linear algebra over noncommutative rings, combined with a small drop of global arithmetic input.
6.1 Linear algebra
Let
![]() $\ell $
be a prime and
$\ell $
be a prime and
![]() ${\mathcal {O}}_{\ell } := {\mathcal {O}}\otimes \mathbb F_{\ell }$
. If
${\mathcal {O}}_{\ell } := {\mathcal {O}}\otimes \mathbb F_{\ell }$
. If
![]() $\ell \nmid {\mathrm{disc}}(B)$
, then
$\ell \nmid {\mathrm{disc}}(B)$
, then
![]() ${\mathcal {O}}_{\ell } \simeq {\mathrm{Mat}}_2(\mathbb F_{\ell })$
, since
${\mathcal {O}}_{\ell } \simeq {\mathrm{Mat}}_2(\mathbb F_{\ell })$
, since
![]() ${\mathcal {O}}$
is maximal. If
${\mathcal {O}}$
is maximal. If
![]() $\ell \mid {\mathrm{disc}}(B)$
, then
$\ell \mid {\mathrm{disc}}(B)$
, then
![]() ${\mathcal {O}}_{\ell }$
is isomorphic to the nonsemisimple algebra [Reference JordanJor86, §4]
${\mathcal {O}}_{\ell }$
is isomorphic to the nonsemisimple algebra [Reference JordanJor86, §4]
 $$ \begin{align} \left\{\begin{pmatrix} \alpha & \beta \\ 0 & \alpha^{\ell} \end{pmatrix} \mid \alpha,\beta\in \mathbb F_{{\ell}^2} \right\}\subset {\mathrm{Mat}}_2(\mathbb F_{\ell^2}). \end{align} $$
$$ \begin{align} \left\{\begin{pmatrix} \alpha & \beta \\ 0 & \alpha^{\ell} \end{pmatrix} \mid \alpha,\beta\in \mathbb F_{{\ell}^2} \right\}\subset {\mathrm{Mat}}_2(\mathbb F_{\ell^2}). \end{align} $$
In both cases, we will describe all left ideals of
![]() ${\mathcal {O}}_{\ell }$
. Equivalently, given a left
${\mathcal {O}}_{\ell }$
. Equivalently, given a left
![]() ${\mathcal {O}}_{\ell }$
-module M, free of rank one, we will describe all its (left)
${\mathcal {O}}_{\ell }$
-module M, free of rank one, we will describe all its (left)
![]() ${\mathcal {O}}_{\ell }$
-submodules.
${\mathcal {O}}_{\ell }$
-submodules.
First, we suppose that
![]() $\ell \nmid {\mathrm{disc}}(B)$
; fix an isomorphism
$\ell \nmid {\mathrm{disc}}(B)$
; fix an isomorphism
![]() ${\mathcal {O}}_{\ell }\simeq {\mathrm{Mat}}_2(\mathbb F_{\ell })$
and a free rank one left
${\mathcal {O}}_{\ell }\simeq {\mathrm{Mat}}_2(\mathbb F_{\ell })$
and a free rank one left
![]() ${\mathcal {O}}_{\ell }$
-module M. Let
${\mathcal {O}}_{\ell }$
-module M. Let
![]() $e_1,e_2,w$
be the elements of
$e_1,e_2,w$
be the elements of
![]() ${\mathcal {O}}_{\ell }$
corresponding to the matrices
${\mathcal {O}}_{\ell }$
corresponding to the matrices
 $$ \begin{align*} \begin{pmatrix} 1 & 0 \\ 0 & 0 \end{pmatrix}, \begin{pmatrix} 0 & 0 \\ 0 & 1 \end{pmatrix}, \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix}, \end{align*} $$
$$ \begin{align*} \begin{pmatrix} 1 & 0 \\ 0 & 0 \end{pmatrix}, \begin{pmatrix} 0 & 0 \\ 0 & 1 \end{pmatrix}, \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix}, \end{align*} $$
respectively. Then
![]() $e_1$
,
$e_1$
,
![]() $e_2$
are idempotents satisfying
$e_2$
are idempotents satisfying
![]() $e_1e_2=0$
,
$e_1e_2=0$
,
![]() $e_1+e_2=1$
and
$e_1+e_2=1$
and
![]() $e_1w = we_2$
. Set
$e_1w = we_2$
. Set
![]() $M_i = \ker (e_i \colon M\rightarrow M)\subset M$
. Then
$M_i = \ker (e_i \colon M\rightarrow M)\subset M$
. Then
![]() $M = M_1\oplus M_2$
, and w induces mutually inverse bijections
$M = M_1\oplus M_2$
, and w induces mutually inverse bijections
![]() $M_1\rightarrow M_2$
and
$M_1\rightarrow M_2$
and
![]() $M_2\rightarrow M_1$
. Given an
$M_2\rightarrow M_1$
. Given an
![]() ${\mathcal {O}}_{\ell }$
-submodule
${\mathcal {O}}_{\ell }$
-submodule
![]() $N\subset M$
, define
$N\subset M$
, define
![]() $N_i := N\cap M_i$
. Since N is
$N_i := N\cap M_i$
. Since N is
![]() ${\mathcal {O}}_{\ell }$
-stable,
${\mathcal {O}}_{\ell }$
-stable,
![]() $N = N_1\oplus N_2$
and
$N = N_1\oplus N_2$
and
![]() $w(N_1) = N_2$
.
$w(N_1) = N_2$
.
Lemma 6.2 (Unramified case).
The map
![]() $N\mapsto (N_1,N_2)$
induces a bijection between left
$N\mapsto (N_1,N_2)$
induces a bijection between left
![]() ${\mathcal {O}}_{\ell }$
-submodules of M and pairs of
${\mathcal {O}}_{\ell }$
-submodules of M and pairs of
![]() $\mathbb F_{\ell }$
-subspaces
$\mathbb F_{\ell }$
-subspaces
![]() $(N_1\subset M_1,N_2\subset M_2)$
satisfying
$(N_1\subset M_1,N_2\subset M_2)$
satisfying
![]() $w(N_1) = N_2$
.
$w(N_1) = N_2$
.
Proof. This is elementary, using the fact that
![]() ${\mathcal {O}}_{\ell }$
is generated (as a ring) by
${\mathcal {O}}_{\ell }$
is generated (as a ring) by
![]() $e_1,e_2$
and w.
$e_1,e_2$
and w.
Next, suppose that
![]() $\ell $
divides
$\ell $
divides
![]() $ {\mathrm{disc}}(B)$
and fix an isomorphism between
$ {\mathrm{disc}}(B)$
and fix an isomorphism between
![]() ${\mathcal {O}}_{\ell }$
and the ring described in (6.1). The set of strictly upper triangular matrices is a two-sided ideal
${\mathcal {O}}_{\ell }$
and the ring described in (6.1). The set of strictly upper triangular matrices is a two-sided ideal
![]() $J\subset {\mathcal {O}}_{\ell }$
that satisfies
$J\subset {\mathcal {O}}_{\ell }$
that satisfies
![]() ${\mathcal {O}}_{\ell }/J\simeq \mathbb F_{\ell ^2}$
. The following lemma is easily verified [Reference JordanJor86, §4].
${\mathcal {O}}_{\ell }/J\simeq \mathbb F_{\ell ^2}$
. The following lemma is easily verified [Reference JordanJor86, §4].
Lemma 6.3 (Ramified case).
The only proper left ideal of
![]() ${\mathcal {O}}_{\ell }$
is J. Consequently, the only proper
${\mathcal {O}}_{\ell }$
is J. Consequently, the only proper
![]() ${\mathcal {O}}_{\ell }$
-submodule of M is
${\mathcal {O}}_{\ell }$
-submodule of M is
![]() $M[J] = \{m\in M\mid j\cdot m=0 \text { for all }j\in J\}$
.
$M[J] = \{m\in M\mid j\cdot m=0 \text { for all }j\in J\}$
.
6.2 The subgroup generated by a torsion point
Let
![]() $A/{\mathbb {Q}}$
be an
$A/{\mathbb {Q}}$
be an
![]() ${\mathcal {O}}$
-
${\mathcal {O}}$
-
![]() $\mathrm {PQM}$
surface and
$\mathrm {PQM}$
surface and
![]() $\ell $
be a prime number. Let
$\ell $
be a prime number. Let
![]() ${\mathcal {O}}_{\ell } := {\mathcal {O}}\otimes \mathbb F_{\ell }$
and
${\mathcal {O}}_{\ell } := {\mathcal {O}}\otimes \mathbb F_{\ell }$
and
![]() $M := A[\ell ](\bar {{\mathbb {Q}}})$
. Then M is a free
$M := A[\ell ](\bar {{\mathbb {Q}}})$
. Then M is a free
![]() ${\mathcal {O}}_{\ell }$
-module of rank one, and
${\mathcal {O}}_{\ell }$
-module of rank one, and
![]() $ {\mathrm{Gal}}_{{\mathbb {Q}}}$
acts on
$ {\mathrm{Gal}}_{{\mathbb {Q}}}$
acts on
![]() ${\mathcal {O}}_{\ell }$
by ring automorphisms (as studied in §3.2) and on M by
${\mathcal {O}}_{\ell }$
by ring automorphisms (as studied in §3.2) and on M by
![]() $\mathbb F_{\ell }$
-linear automorphisms. These actions satisfy
$\mathbb F_{\ell }$
-linear automorphisms. These actions satisfy
![]() $(a\cdot m)^\sigma = a^\sigma \cdot m^\sigma $
for all
$(a\cdot m)^\sigma = a^\sigma \cdot m^\sigma $
for all
![]() $\sigma \in {\mathrm{Gal}}_{{\mathbb {Q}}}, a\in {\mathcal {O}}_{\ell }$
and
$\sigma \in {\mathrm{Gal}}_{{\mathbb {Q}}}, a\in {\mathcal {O}}_{\ell }$
and
![]() $m\in M$
.
$m\in M$
.
Lemma 6.4. Suppose that the
![]() $ {\mathrm{Gal}}_{{\mathbb {Q}}}$
-modules
$ {\mathrm{Gal}}_{{\mathbb {Q}}}$
-modules
![]() ${\mathcal {O}}_{\ell }$
and M are isomorphic. Then
${\mathcal {O}}_{\ell }$
and M are isomorphic. Then
![]() $\ell \leq 3$
.
$\ell \leq 3$
.
Proof. This follows by comparing determinants. On one hand, the
![]() $ {\mathrm{Gal}}_{{\mathbb {Q}}}$
-action on
$ {\mathrm{Gal}}_{{\mathbb {Q}}}$
-action on
![]() ${\mathcal {O}}_{\ell }$
has determinant
${\mathcal {O}}_{\ell }$
has determinant
![]() $1$
. Indeed, the determinant of left/right multiplication by
$1$
. Indeed, the determinant of left/right multiplication by
![]() $b \in B$
acting on B is the square of the reduced norm, so conjugation has determinant 1. On the other hand, the determinant of the
$b \in B$
acting on B is the square of the reduced norm, so conjugation has determinant 1. On the other hand, the determinant of the
![]() $ {\mathrm{Gal}}_{{\mathbb {Q}}}$
-action on M is the square of the mod
$ {\mathrm{Gal}}_{{\mathbb {Q}}}$
-action on M is the square of the mod
![]() $\ell $
cyclotomic character
$\ell $
cyclotomic character
![]() $\bar {\chi }_{\ell }$
. This implies that
$\bar {\chi }_{\ell }$
. This implies that
![]() $\bar {\chi }_{\ell }^2=1$
, so
$\bar {\chi }_{\ell }^2=1$
, so
![]() ${\mathbb {Q}}(\zeta _{\ell }+\zeta _{\ell }^{-1}) = {\mathbb {Q}}$
, so
${\mathbb {Q}}(\zeta _{\ell }+\zeta _{\ell }^{-1}) = {\mathbb {Q}}$
, so
![]() $\ell \leq 3$
.
$\ell \leq 3$
.
Remark 6.5. When
![]() $\ell = 3$
, we know of no examples of
$\ell = 3$
, we know of no examples of
![]() ${\mathcal {O}}$
-
${\mathcal {O}}$
-
![]() $\mathrm {PQM}$
surfaces over
$\mathrm {PQM}$
surfaces over
![]() ${\mathbb {Q}}$
with
${\mathbb {Q}}$
with
![]() ${\mathcal {O}}_\ell \simeq M$
as
${\mathcal {O}}_\ell \simeq M$
as
![]() $ {\mathrm{Gal}}_{{\mathbb {Q}}}$
-modules. Such examples do exist for
$ {\mathrm{Gal}}_{{\mathbb {Q}}}$
-modules. Such examples do exist for
![]() $\ell = 2$
; see [Reference Laga and ShnidmanLS23, Corollary 7.5].
$\ell = 2$
; see [Reference Laga and ShnidmanLS23, Corollary 7.5].
Lemma 6.6. If
![]() $m\in M^{ {\mathrm{Gal}}_{{\mathbb {Q}}}}$
is nonzero and
$m\in M^{ {\mathrm{Gal}}_{{\mathbb {Q}}}}$
is nonzero and
![]() $\ell \geq 5$
, then
$\ell \geq 5$
, then
![]() ${\mathcal {O}}_{\ell }\cdot m\subset M$
has order
${\mathcal {O}}_{\ell }\cdot m\subset M$
has order
![]() $\ell ^2$
.
$\ell ^2$
.
Proof. By Lemmas 6.2 and 6.3, it suffices to show that
![]() ${\mathcal {O}}_{\ell }\cdot m\neq M$
. But if
${\mathcal {O}}_{\ell }\cdot m\neq M$
. But if
![]() ${\mathcal {O}}_{\ell } \cdot m = M$
, then
${\mathcal {O}}_{\ell } \cdot m = M$
, then
![]() ${\mathcal {O}}_{\ell }\rightarrow M, x\mapsto x\cdot m$
is an isomorphism, contradicting Lemma 6.4.
${\mathcal {O}}_{\ell }\rightarrow M, x\mapsto x\cdot m$
is an isomorphism, contradicting Lemma 6.4.
To analyze the case
![]() $\ell \mid {\mathrm{disc}}(B)$
, we use the following theorem attributed to Ohta.
$\ell \mid {\mathrm{disc}}(B)$
, we use the following theorem attributed to Ohta.
Theorem 6.7. Let F be a number field and let
![]() $A/F$
be an abelian variety with
$A/F$
be an abelian variety with
![]() $ {\mathrm{End}}(A) \simeq {\mathcal {O}}$
. Suppose
$ {\mathrm{End}}(A) \simeq {\mathcal {O}}$
. Suppose
![]() ${\mathcal {O}}$
is ramified at a prime
${\mathcal {O}}$
is ramified at a prime
![]() $\ell $
and let
$\ell $
and let
![]() $J \subset {\mathcal {O}}$
be the maximal ideal above
$J \subset {\mathcal {O}}$
be the maximal ideal above
![]() $\ell $
. Then the composition of the Galois representation
$\ell $
. Then the composition of the Galois representation
![]() $ {\mathrm{Gal}}_F \to {\mathrm{Aut}}_{\mathbb F_{\ell ^2}}A[J] \simeq \mathbb F_{\ell ^2}^\times $
with the norm
$ {\mathrm{Gal}}_F \to {\mathrm{Aut}}_{\mathbb F_{\ell ^2}}A[J] \simeq \mathbb F_{\ell ^2}^\times $
with the norm
![]() $\mathbb F_{\ell ^2}^\times \to \mathbb F_\ell ^\times $
is equal to the mod
$\mathbb F_{\ell ^2}^\times \to \mathbb F_\ell ^\times $
is equal to the mod
![]() $\ell $
cyclotomic character
$\ell $
cyclotomic character
![]() $ {\mathrm{Gal}}_F \to {\mathrm{Aut}}(\mu _\ell ) \simeq \mathbb F_\ell ^\times $
.
$ {\mathrm{Gal}}_F \to {\mathrm{Aut}}(\mu _\ell ) \simeq \mathbb F_\ell ^\times $
.
Proof. See [Reference JordanJor86, Proposition 4.6].
Proposition 6.8. If
![]() $\ell \mid {\mathrm{disc}}(B)$
and
$\ell \mid {\mathrm{disc}}(B)$
and
![]() $M^{ {\mathrm{Gal}}_{{\mathbb {Q}}}}\neq 0$
, then
$M^{ {\mathrm{Gal}}_{{\mathbb {Q}}}}\neq 0$
, then
![]() $\ell \leq 3$
.
$\ell \leq 3$
.
Proof. Choose a nonzero
![]() $m\in M^{ {\mathrm{Gal}}_{{\mathbb {Q}}}}$
and suppose that
$m\in M^{ {\mathrm{Gal}}_{{\mathbb {Q}}}}$
and suppose that
![]() $\ell \geq 5$
. By the previous lemma,
$\ell \geq 5$
. By the previous lemma,
![]() ${\mathcal {O}}_{\ell }\cdot m$
is a proper submodule of M. Therefore,
${\mathcal {O}}_{\ell }\cdot m$
is a proper submodule of M. Therefore,
![]() ${\mathcal {O}}_{\ell }\cdot m = M[J]$
by Lemma 6.3. Let
${\mathcal {O}}_{\ell }\cdot m = M[J]$
by Lemma 6.3. Let
![]() $L/{\mathbb {Q}}$
be the endomorphism field of A. Then the
$L/{\mathbb {Q}}$
be the endomorphism field of A. Then the
![]() $ {\mathrm{Gal}}_{{\mathbb {Q}}}$
-action on M restricts to a
$ {\mathrm{Gal}}_{{\mathbb {Q}}}$
-action on M restricts to a
![]() $ {\mathrm{Gal}}_L$
-action on
$ {\mathrm{Gal}}_L$
-action on
![]() $M[J]$
through elements of
$M[J]$
through elements of
![]() $\mathbb F_{\ell ^2}^{\times }$
(after choosing an isomorphism
$\mathbb F_{\ell ^2}^{\times }$
(after choosing an isomorphism
![]() ${\mathcal {O}}_{\ell }/J \simeq \mathbb F_{\ell ^2}$
), giving a homomorphism
${\mathcal {O}}_{\ell }/J \simeq \mathbb F_{\ell ^2}$
), giving a homomorphism
![]() $\epsilon \colon {\mathrm{Gal}}_L \rightarrow \mathbb F_{\ell ^2}^{\times }$
. Since m is
$\epsilon \colon {\mathrm{Gal}}_L \rightarrow \mathbb F_{\ell ^2}^{\times }$
. Since m is
![]() $ {\mathrm{Gal}}_{{\mathbb {Q}}}$
-invariant, the
$ {\mathrm{Gal}}_{{\mathbb {Q}}}$
-invariant, the
![]() $ {\mathrm{Gal}}_L$
-action on
$ {\mathrm{Gal}}_L$
-action on
![]() $M[J]$
is trivial, so
$M[J]$
is trivial, so
![]() $\epsilon $
is trivial. However, the composition
$\epsilon $
is trivial. However, the composition
![]() $N_{\mathbb F_{\ell ^2}/\mathbb F_{\ell }}\circ \epsilon \colon {\mathrm{Gal}}_L \rightarrow \mathbb F_{\ell }^{\times }$
equals the mod
$N_{\mathbb F_{\ell ^2}/\mathbb F_{\ell }}\circ \epsilon \colon {\mathrm{Gal}}_L \rightarrow \mathbb F_{\ell }^{\times }$
equals the mod
![]() $\ell $
cyclotomic character
$\ell $
cyclotomic character
![]() $\bar {\chi }_{\ell }$
, by Theorem 6.7. It follows that
$\bar {\chi }_{\ell }$
, by Theorem 6.7. It follows that
![]() $\bar {\chi }_{\ell }|_{ {\mathrm{Gal}}_L} = 1$
, or in other words,
$\bar {\chi }_{\ell }|_{ {\mathrm{Gal}}_L} = 1$
, or in other words,
![]() ${\mathbb {Q}}(\zeta _{\ell })\subset L$
. Thus,
${\mathbb {Q}}(\zeta _{\ell })\subset L$
. Thus,
![]() $ {\mathrm{Gal}}(L/{\mathbb {Q}})$
surjects onto
$ {\mathrm{Gal}}(L/{\mathbb {Q}})$
surjects onto
![]() $ {\mathrm{Gal}}({\mathbb {Q}}(\zeta _{\ell })/{\mathbb {Q}})\simeq ({\mathbb {Z}}/\ell {\mathbb {Z}})^{\times } \simeq {\mathbb {Z}}/(\ell -1){\mathbb {Z}}$
. Since
$ {\mathrm{Gal}}({\mathbb {Q}}(\zeta _{\ell })/{\mathbb {Q}})\simeq ({\mathbb {Z}}/\ell {\mathbb {Z}})^{\times } \simeq {\mathbb {Z}}/(\ell -1){\mathbb {Z}}$
. Since
![]() $ {\mathrm{Gal}}(L/{\mathbb {Q}})$
is dihedral (Proposition 3.3), every nontrivial cyclic quotient of
$ {\mathrm{Gal}}(L/{\mathbb {Q}})$
is dihedral (Proposition 3.3), every nontrivial cyclic quotient of
![]() $ {\mathrm{Gal}}(L/{\mathbb {Q}})$
has order
$ {\mathrm{Gal}}(L/{\mathbb {Q}})$
has order
![]() $2$
, and we conclude that
$2$
, and we conclude that
![]() $\ell \leq 3$
.
$\ell \leq 3$
.
We now treat the unramified case, using the following key linear-algebraic lemma, which we call the ‘torus trick’.
Lemma 6.9. Suppose that
![]() $\ell \nmid {\mathrm{disc}}(B)$
. Let
$\ell \nmid {\mathrm{disc}}(B)$
. Let
![]() $S\subset {\mathcal {O}}_{\ell }$
be a
$S\subset {\mathcal {O}}_{\ell }$
be a
![]() $2$
-dimensional semisimple commutative
$2$
-dimensional semisimple commutative
![]() $ {\mathrm{Gal}}_{{\mathbb {Q}}}$
-stable subalgebra such that
$ {\mathrm{Gal}}_{{\mathbb {Q}}}$
-stable subalgebra such that
![]() $S\cdot m = {\mathcal {O}}_{\ell }\cdot m$
for some nonzero
$S\cdot m = {\mathcal {O}}_{\ell }\cdot m$
for some nonzero
![]() $m\in M^{ {\mathrm{Gal}}_{{\mathbb {Q}}}}$
. Then every
$m\in M^{ {\mathrm{Gal}}_{{\mathbb {Q}}}}$
. Then every
![]() $\sigma \in {\mathrm{Gal}}_{{\mathbb {Q}}}$
acting trivially on S also acts trivially on
$\sigma \in {\mathrm{Gal}}_{{\mathbb {Q}}}$
acting trivially on S also acts trivially on
![]() ${\mathcal {O}}_{\ell }$
.
${\mathcal {O}}_{\ell }$
.
Proof. Let
![]() $\sigma \in {\mathrm{Gal}}_{{\mathbb {Q}}}$
be an element acting trivially on S and let
$\sigma \in {\mathrm{Gal}}_{{\mathbb {Q}}}$
be an element acting trivially on S and let
![]() $m \in M^{ {\mathrm{Gal}}_{{\mathbb {Q}}}}\setminus \{0\}$
be an element such that
$m \in M^{ {\mathrm{Gal}}_{{\mathbb {Q}}}}\setminus \{0\}$
be an element such that
![]() $S\cdot m = {\mathcal {O}}_{\ell }\cdot m$
. Let
$S\cdot m = {\mathcal {O}}_{\ell }\cdot m$
. Let
![]() $k = \bar {\mathbb F}_{\ell }$
. It suffices to prove that
$k = \bar {\mathbb F}_{\ell }$
. It suffices to prove that
![]() $\sigma $
acts trivially on
$\sigma $
acts trivially on
![]() ${\mathcal {O}}_k := {\mathcal {O}}_{\ell } \otimes _{\mathbb F_{\ell }} k$
. The assumptions imply that
${\mathcal {O}}_k := {\mathcal {O}}_{\ell } \otimes _{\mathbb F_{\ell }} k$
. The assumptions imply that
![]() $S_k \simeq k\times k$
, and we may fix an isomorphism
$S_k \simeq k\times k$
, and we may fix an isomorphism
![]() ${\mathcal {O}}_k\simeq {\mathrm{Mat}}_2(k)$
of k-algebras such that
${\mathcal {O}}_k\simeq {\mathrm{Mat}}_2(k)$
of k-algebras such that
![]() $S_k$
is identified with the subalgebra of diagonal matrices of
$S_k$
is identified with the subalgebra of diagonal matrices of
![]() $ {\mathrm{Mat}}_2(k)$
. Lemma 6.2 and the fact that
$ {\mathrm{Mat}}_2(k)$
. Lemma 6.2 and the fact that
![]() $S_k$
is
$S_k$
is
![]() $2$
-dimensional shows that
$2$
-dimensional shows that
![]() $\dim _k (S_k \cdot m) = \dim _k({\mathcal {O}}_k\cdot m) = 2$
. Let
$\dim _k (S_k \cdot m) = \dim _k({\mathcal {O}}_k\cdot m) = 2$
. Let
![]() $I = \{x\in {\mathcal {O}}_k \mid x\cdot m=0\}$
be the annihilator of m, an ideal of
$I = \{x\in {\mathcal {O}}_k \mid x\cdot m=0\}$
be the annihilator of m, an ideal of
![]() ${\mathcal {O}}_k$
of dimension
${\mathcal {O}}_k$
of dimension
![]() $2$
. Using the analogue of Lemma 6.2 over k, such an ideal is necessarily of the form
$2$
. Using the analogue of Lemma 6.2 over k, such an ideal is necessarily of the form
 $$ \begin{align*} \left\{\begin{pmatrix} ax & bx \\ ay & by \end{pmatrix} \mid x,y\in k \right\} \end{align*} $$
$$ \begin{align*} \left\{\begin{pmatrix} ax & bx \\ ay & by \end{pmatrix} \mid x,y\in k \right\} \end{align*} $$
for some
![]() $a,b\in k$
which are not both zero. The assumption that
$a,b\in k$
which are not both zero. The assumption that
![]() $S\cdot m = {\mathcal {O}}_{\ell } \cdot m$
implies that
$S\cdot m = {\mathcal {O}}_{\ell } \cdot m$
implies that
![]() $S_k \cap I =0$
. It follows that a and b must be nonzero and
$S_k \cap I =0$
. It follows that a and b must be nonzero and
![]() ${\mathcal {O}}_k = S_k \oplus I$
as
${\mathcal {O}}_k = S_k \oplus I$
as
![]() $ {\mathrm{Gal}}_{{\mathbb {Q}}}$
-modules. Let
$ {\mathrm{Gal}}_{{\mathbb {Q}}}$
-modules. Let
![]() $N\subset {\mathcal {O}}_k$
be the subspace normalising but not centralising
$N\subset {\mathcal {O}}_k$
be the subspace normalising but not centralising
![]() $S_k$
. Then the above calculation also shows that
$S_k$
. Then the above calculation also shows that
![]() $N\cap I = 0$
. Moreover, N is
$N\cap I = 0$
. Moreover, N is
![]() $ {\mathrm{Gal}}_{{\mathbb {Q}}}$
-stable since S is. The relation
$ {\mathrm{Gal}}_{{\mathbb {Q}}}$
-stable since S is. The relation
![]() ${\mathcal {O}}_k = S_k \oplus I$
shows that
${\mathcal {O}}_k = S_k \oplus I$
shows that
![]() $\sigma (x)-x\in I$
for all
$\sigma (x)-x\in I$
for all
![]() $x\in {\mathcal {O}}_k$
. It follows that
$x\in {\mathcal {O}}_k$
. It follows that
![]() $\sigma (x)-x\in I \cap N = 0$
for all
$\sigma (x)-x\in I \cap N = 0$
for all
![]() $x\in N$
. Since
$x\in N$
. Since
![]() ${\mathcal {O}}_k$
is spanned by
${\mathcal {O}}_k$
is spanned by
![]() $S_k$
and N, the claim follows.
$S_k$
and N, the claim follows.
Proposition 6.10. Suppose that
![]() $\ell \nmid {\mathrm{disc}}(B)$
and
$\ell \nmid {\mathrm{disc}}(B)$
and
![]() $M^{ {\mathrm{Gal}}_{{\mathbb {Q}}}}\neq 0$
and
$M^{ {\mathrm{Gal}}_{{\mathbb {Q}}}}\neq 0$
and
![]() $\ell \geq 5$
. Then A is of
$\ell \geq 5$
. Then A is of
![]() $ {\mathrm{GL}}_2$
-type.
$ {\mathrm{GL}}_2$
-type.
Proof. We apply the torus trick using the distinguished quadratic subring
![]() $S \subset {\mathcal {O}}$
of A (Definition 3.3). Write
$S \subset {\mathcal {O}}$
of A (Definition 3.3). Write
![]() $S_{\ell } = S \otimes _{\mathbb {Z}} \mathbb F_{\ell }$
. Then
$S_{\ell } = S \otimes _{\mathbb {Z}} \mathbb F_{\ell }$
. Then
![]() $S_{\ell }\subset {\mathcal {O}}_{\ell }$
is a commutative semisimple subalgebra since S is unramified at
$S_{\ell }\subset {\mathcal {O}}_{\ell }$
is a commutative semisimple subalgebra since S is unramified at
![]() $\ell $
by Proposition 3.11. Suppose that A is not of
$\ell $
by Proposition 3.11. Suppose that A is not of
![]() $ {\mathrm{GL}}_2$
-type. Then
$ {\mathrm{GL}}_2$
-type. Then
![]() $ {\mathrm{Gal}}_{{\mathbb {Q}}}$
acts nontrivially on S since
$ {\mathrm{Gal}}_{{\mathbb {Q}}}$
acts nontrivially on S since
![]() $ {\mathrm{End}}(A) = {\mathbb {Z}}$
; let
$ {\mathrm{End}}(A) = {\mathbb {Z}}$
; let
![]() $K/{\mathbb {Q}}$
be the quadratic extension splitting this action. We claim that the
$K/{\mathbb {Q}}$
be the quadratic extension splitting this action. We claim that the
![]() $ {\mathrm{Gal}}_{K}$
-action on
$ {\mathrm{Gal}}_{K}$
-action on
![]() ${\mathcal {O}}_{\ell }$
is trivial. Indeed, let
${\mathcal {O}}_{\ell }$
is trivial. Indeed, let
![]() $m\in M^{ {\mathrm{Gal}}_{{\mathbb {Q}}}}$
be a nonzero element. By Lemma 6.9, it suffices to prove that
$m\in M^{ {\mathrm{Gal}}_{{\mathbb {Q}}}}$
be a nonzero element. By Lemma 6.9, it suffices to prove that
![]() $S_{\ell }\cdot m = {\mathcal {O}}_{\ell }\cdot m$
. But the set
$S_{\ell }\cdot m = {\mathcal {O}}_{\ell }\cdot m$
. But the set
![]() $\{x\in S_{\ell } \mid x\cdot m=0\}$
is a proper
$\{x\in S_{\ell } \mid x\cdot m=0\}$
is a proper
![]() $ {\mathrm{Gal}}_{{\mathbb {Q}}}$
-invariant ideal of
$ {\mathrm{Gal}}_{{\mathbb {Q}}}$
-invariant ideal of
![]() $S_{\ell }$
. Since the only such ideal is
$S_{\ell }$
. Since the only such ideal is
![]() $0$
(using the fact that the
$0$
(using the fact that the
![]() $ {\mathrm{Gal}}_{{\mathbb {Q}}}$
-action on S is nontrivial and
$ {\mathrm{Gal}}_{{\mathbb {Q}}}$
-action on S is nontrivial and
![]() $\ell \neq 2$
), the map
$\ell \neq 2$
), the map
![]() $S \cdot m\rightarrow {\mathcal {O}}\cdot m$
is injective and hence by dimension reasons (and Lemma 6.6) it must be surjective. This proves that the
$S \cdot m\rightarrow {\mathcal {O}}\cdot m$
is injective and hence by dimension reasons (and Lemma 6.6) it must be surjective. This proves that the
![]() $ {\mathrm{Gal}}_{K}$
-action on
$ {\mathrm{Gal}}_{K}$
-action on
![]() ${\mathcal {O}}_{\ell }$
is trivial. By Lemma 3.14, this even implies that that
${\mathcal {O}}_{\ell }$
is trivial. By Lemma 3.14, this even implies that that
![]() $ {\mathrm{Gal}}_{K}$
-action on
$ {\mathrm{Gal}}_{K}$
-action on
![]() ${\mathcal {O}}$
is trivial. We conclude that the quadratic field K is the endomorphism field of A; hence, A is of
${\mathcal {O}}$
is trivial. We conclude that the quadratic field K is the endomorphism field of A; hence, A is of
![]() $ {\mathrm{GL}}_2$
-type by Lemma 3.4, contradiction.
$ {\mathrm{GL}}_2$
-type by Lemma 3.4, contradiction.
7 Proof of Theorems 1.2 and 1.3: Eliminating groups of order
 $2^i3^j$
$2^i3^j$
Let
![]() $A/{\mathbb {Q}}$
be an
$A/{\mathbb {Q}}$
be an
![]() ${\mathcal {O}}$
-
${\mathcal {O}}$
-
![]() $\mathrm {PQM}$
surface. By Theorem 1.1, we have
$\mathrm {PQM}$
surface. By Theorem 1.1, we have
![]() $\#A({\mathbb {Q}})_{ {\mathrm{tors}}} = 2^i3^j$
for some
$\#A({\mathbb {Q}})_{ {\mathrm{tors}}} = 2^i3^j$
for some
![]() $i,j\geq 0$
. Since A has potentially good reduction, local methods show that
$i,j\geq 0$
. Since A has potentially good reduction, local methods show that
![]() $2^i3^j\leq 72$
[Reference Clark and XarlesCX08, Theorem 1.4]. In this section, we will improve this bound and constrain the group structure of
$2^i3^j\leq 72$
[Reference Clark and XarlesCX08, Theorem 1.4]. In this section, we will improve this bound and constrain the group structure of
![]() $A({\mathbb {Q}})_{\mathrm {tors}}$
as much as possible using the
$A({\mathbb {Q}})_{\mathrm {tors}}$
as much as possible using the
![]() ${\mathcal {O}}$
-action on
${\mathcal {O}}$
-action on
![]() $A_{\overline {\mathbb {Q}}}$
. We may assume A is not of
$A_{\overline {\mathbb {Q}}}$
. We may assume A is not of
![]() $ {\mathrm{GL}}_2$
-type since we have already proven Theorem 1.4.
$ {\mathrm{GL}}_2$
-type since we have already proven Theorem 1.4.
For each prime p, there exists a totally ramified extension
![]() $K/{\mathbb {Q}}_p$
such that
$K/{\mathbb {Q}}_p$
such that
![]() $A_K$
has good reduction (Lemma 4.1). The special fiber of the Néron model of
$A_K$
has good reduction (Lemma 4.1). The special fiber of the Néron model of
![]() $A_K$
is an abelian surface over
$A_K$
is an abelian surface over
![]() $\mathbb F_p$
which we denote by
$\mathbb F_p$
which we denote by
![]() $A_p$
. We call
$A_p$
. We call
![]() $A_p$
the good reduction of A at p, though it is only uniquely determined up to twists (since a different choice of totally ramified extension
$A_p$
the good reduction of A at p, though it is only uniquely determined up to twists (since a different choice of totally ramified extension
![]() $K'$
would give rise to a possibly non-isomorphic twist of
$K'$
would give rise to a possibly non-isomorphic twist of
![]() $A_p$
).
$A_p$
).
Lemma 4.13 shows that the prime-to-p subgroup of
![]() $A({\mathbb {Q}})_{\mathrm {tors}}$
injects into
$A({\mathbb {Q}})_{\mathrm {tors}}$
injects into
![]() $A_p(\mathbb F_p)$
. Moreover,
$A_p(\mathbb F_p)$
. Moreover,
![]() $ {\mathrm{End}}(A_{\overline {\mathbb {Q}}})\subset {\mathrm{End}}(A_{\bar {\mathbb {F}}_p})$
; hence,
$ {\mathrm{End}}(A_{\overline {\mathbb {Q}}})\subset {\mathrm{End}}(A_{\bar {\mathbb {F}}_p})$
; hence,
![]() $A_p$
is
$A_p$
is
![]() $\bar {\mathbb {F}}_p$
-isogenous to the square of an elliptic curve
$\bar {\mathbb {F}}_p$
-isogenous to the square of an elliptic curve
![]() $E/\bar {\mathbb {F}}_p$
by Proposition 4.17, so its isogeny class is rather constrained. This leads to the following slight strengthening of [Reference Clark and XarlesCX08, Theorem 1.4] in our case:
$E/\bar {\mathbb {F}}_p$
by Proposition 4.17, so its isogeny class is rather constrained. This leads to the following slight strengthening of [Reference Clark and XarlesCX08, Theorem 1.4] in our case:
Proposition 7.1. We have
![]() $\#A({\mathbb {Q}})_{ {\mathrm{tors}}}= 2^i3^j$
for some
$\#A({\mathbb {Q}})_{ {\mathrm{tors}}}= 2^i3^j$
for some
![]() $i \in \{0,1,2,3,4\}$
and
$i \in \{0,1,2,3,4\}$
and
![]() $j \in \{0,1,2\}$
. Moreover,
$j \in \{0,1,2\}$
. Moreover,
![]() $\#A({\mathbb {Q}})_{ {\mathrm{tors}}} \leq 48$
.
$\#A({\mathbb {Q}})_{ {\mathrm{tors}}} \leq 48$
.
Proof. By the above remarks, to bound the prime-to-
![]() $2$
(resp. prime-to-3) torsion, it is enough to bound
$2$
(resp. prime-to-3) torsion, it is enough to bound
![]() $X(\mathbb F_2)[3^\infty ]$
(resp.
$X(\mathbb F_2)[3^\infty ]$
(resp.
![]() $X(\mathbb F_3)[2^\infty ]$
), as X varies over all abelian surfaces over
$X(\mathbb F_3)[2^\infty ]$
), as X varies over all abelian surfaces over
![]() $\mathbb F_2$
(resp.
$\mathbb F_2$
(resp.
![]() $\mathbb F_3$
) that are geometrically isogenous to the square of an elliptic curve. For this, it is enough to compute
$\mathbb F_3$
) that are geometrically isogenous to the square of an elliptic curve. For this, it is enough to compute
![]() $\max _X\gcd (f_X(1),3^{100})$
(resp.
$\max _X\gcd (f_X(1),3^{100})$
(resp.
![]() $\max _X\gcd (f_X(1),2^{100})$
), where
$\max _X\gcd (f_X(1),2^{100})$
), where
![]() $f_X$
is the L-polynomial of X and the maximum is over all the aforementioned isogeny classes. This computation is easily done with the help of the LMFDB’s database of isogeny classes of abelian varieties over finite fields [LMF23], and the conclusion is the first sentence of the proposition.
$f_X$
is the L-polynomial of X and the maximum is over all the aforementioned isogeny classes. This computation is easily done with the help of the LMFDB’s database of isogeny classes of abelian varieties over finite fields [LMF23], and the conclusion is the first sentence of the proposition.
The second sentence is equivalent to the claim that
![]() $\#A({\mathbb {Q}})_{ {\mathrm{tors}}}$
cannot equal
$\#A({\mathbb {Q}})_{ {\mathrm{tors}}}$
cannot equal
![]() $144$
nor
$144$
nor
![]() $72$
. We cannot have
$72$
. We cannot have
![]() $144$
since
$144$
since
![]() $\#A_5(\mathbb F_5) \leq 100$
, and we cannot have
$\#A_5(\mathbb F_5) \leq 100$
, and we cannot have
![]() $72$
since the only isogeny class of abelian surfaces
$72$
since the only isogeny class of abelian surfaces
![]() $X/\mathbb F_5$
with
$X/\mathbb F_5$
with
![]() $72 \mid \#X(\mathbb F_5)$
(which has LMFDB label 2.5.f q) is not geometrically isogenous to a square of an elliptic curve.
$72 \mid \#X(\mathbb F_5)$
(which has LMFDB label 2.5.f q) is not geometrically isogenous to a square of an elliptic curve.
The remainder of the proof of Theorems 1.2 and 1.3 will be similar (but more difficult) to that of Proposition 7.1, using the good reduction model
![]() $A_p$
at various primes p and the
$A_p$
at various primes p and the
![]() ${\mathcal {O}}$
-action. In what follows, we will freely use the Honda-Tate computations conveniently recorded in the LMFDB [LMF23], so the careful reader will want to follow along in a web browser. We use the LMFDB’s method of labeling isogeny classes (e.g., 2.5.d e is an isogeny class of abelian surfaces over
${\mathcal {O}}$
-action. In what follows, we will freely use the Honda-Tate computations conveniently recorded in the LMFDB [LMF23], so the careful reader will want to follow along in a web browser. We use the LMFDB’s method of labeling isogeny classes (e.g., 2.5.d e is an isogeny class of abelian surfaces over
![]() $\mathbb F_5$
with label
$\mathbb F_5$
with label
![]() $d_e$
).
$d_e$
).
7.1 Torsion constraints arising from the endomorphism field
Before analyzing specific groups, we state the following useful proposition, which uses techniques similar to the proof of Theorem 6.1, including the torus trick.
Proposition 7.2. Let G be the Galois group of the endomorphism field
![]() $L/{\mathbb {Q}}$
.
$L/{\mathbb {Q}}$
.
-
(a) If
 $G \simeq D_3$
or
$G \simeq D_3$
or
 $D_6$
, then
$D_6$
, then
 $A[2]({\mathbb {Q}})\subset {\mathbb {Z}}/2{\mathbb {Z}}$
. If in addition
$A[2]({\mathbb {Q}})\subset {\mathbb {Z}}/2{\mathbb {Z}}$
. If in addition
 $A[2]({\mathbb {Q}}) = {\mathbb {Z}}/2{\mathbb {Z}}$
, then
$A[2]({\mathbb {Q}}) = {\mathbb {Z}}/2{\mathbb {Z}}$
, then
 $A[2]\simeq {\mathcal {O}}/2{\mathcal {O}}$
as
$A[2]\simeq {\mathcal {O}}/2{\mathcal {O}}$
as
 $ {\mathrm{Gal}}_{{\mathbb {Q}}}$
-modules or
$ {\mathrm{Gal}}_{{\mathbb {Q}}}$
-modules or
 $2\mid {\mathrm{disc}}(B)$
.
$2\mid {\mathrm{disc}}(B)$
. -
(b) If
 $G \simeq D_2$
or
$G \simeq D_2$
or
 $D_4$
, then
$D_4$
, then
 $A[3]({\mathbb {Q}})\subset {\mathbb {Z}}/3{\mathbb {Z}}$
. If in addition
$A[3]({\mathbb {Q}})\subset {\mathbb {Z}}/3{\mathbb {Z}}$
. If in addition
 $A[3]({\mathbb {Q}}) = {\mathbb {Z}}/3{\mathbb {Z}}$
, then
$A[3]({\mathbb {Q}}) = {\mathbb {Z}}/3{\mathbb {Z}}$
, then
 $A[3]\simeq {\mathcal {O}}/3{\mathcal {O}}$
as
$A[3]\simeq {\mathcal {O}}/3{\mathcal {O}}$
as
 $ {\mathrm{Gal}}_{{\mathbb {Q}}}$
-modules or
$ {\mathrm{Gal}}_{{\mathbb {Q}}}$
-modules or
 $3\mid {\mathrm{disc}}(B)$
.
$3\mid {\mathrm{disc}}(B)$
.
Proof.
-
(a) Let
 $S\subset {\mathcal {O}}$
be the distinguished quadratic subring of A (Definition 3.3). By Proposition 3.11,
$S\subset {\mathcal {O}}$
be the distinguished quadratic subring of A (Definition 3.3). By Proposition 3.11,
 $S \simeq {\mathbb {Z}}[\omega ]$
, where
$S \simeq {\mathbb {Z}}[\omega ]$
, where
 $\omega ^2+ \omega +1=0$
. Let
$\omega ^2+ \omega +1=0$
. Let
 $K/{\mathbb {Q}}$
be the quadratic field trivializing the Galois action on S, so
$K/{\mathbb {Q}}$
be the quadratic field trivializing the Galois action on S, so
 $ {\mathrm{End}}(A_K) = S$
. Let
$ {\mathrm{End}}(A_K) = S$
. Let
 $S_2 := S\otimes \mathbb F_2$
and
$S_2 := S\otimes \mathbb F_2$
and
 ${\mathcal {O}}_2 := {\mathcal {O}}\otimes \mathbb F_2$
. If
${\mathcal {O}}_2 := {\mathcal {O}}\otimes \mathbb F_2$
. If
 $A[2]\simeq {\mathcal {O}}_2$
as
$A[2]\simeq {\mathcal {O}}_2$
as
 $ {\mathrm{Gal}}_{{\mathbb {Q}}}$
-modules, then
$ {\mathrm{Gal}}_{{\mathbb {Q}}}$
-modules, then
 $A[2]({\mathbb {Q}}) \simeq ({\mathcal {O}}/2{\mathcal {O}})^{ {\mathrm{Gal}}_{{\mathbb {Q}}}}$
is isomorphic to
$A[2]({\mathbb {Q}}) \simeq ({\mathcal {O}}/2{\mathcal {O}})^{ {\mathrm{Gal}}_{{\mathbb {Q}}}}$
is isomorphic to
 ${\mathbb {Z}}/2{\mathbb {Z}}$
by Theorem 2.6, so indeed,
${\mathbb {Z}}/2{\mathbb {Z}}$
by Theorem 2.6, so indeed,
 $A[2]({\mathbb {Q}}) \subset {\mathbb {Z}}/2{\mathbb {Z}}$
in this case. We may therefore assume that
$A[2]({\mathbb {Q}}) \subset {\mathbb {Z}}/2{\mathbb {Z}}$
in this case. We may therefore assume that
 $A[2]({\mathbb {Q}}) \not \simeq {\mathcal {O}}_2$
in what follows.
$A[2]({\mathbb {Q}}) \not \simeq {\mathcal {O}}_2$
in what follows.It suffices to show that if there exists a nonzero
 $m \in A[2]({\mathbb {Q}})$
, then
$m \in A[2]({\mathbb {Q}})$
, then
 $A[2]({\mathbb {Q}})$
has order
$A[2]({\mathbb {Q}})$
has order
 $2$
. By the classification of
$2$
. By the classification of
 ${\mathcal {O}}_2$
-submodules of
${\mathcal {O}}_2$
-submodules of
 $A[2]$
of §6.1 and the fact that
$A[2]$
of §6.1 and the fact that
 ${\mathcal {O}}_2$
is not isomorphic to
${\mathcal {O}}_2$
is not isomorphic to
 $A[2]$
, the submodule
$A[2]$
, the submodule
 ${\mathcal {O}}_2 \cdot m \subset A[2]$
has order
${\mathcal {O}}_2 \cdot m \subset A[2]$
has order
 $4$
. Since
$4$
. Since
 $S_2 \simeq \mathbb F_4$
has no
$S_2 \simeq \mathbb F_4$
has no
 $ {\mathrm{Gal}}_{{\mathbb {Q}}}$
-stable nonzero proper ideals, the map
$ {\mathrm{Gal}}_{{\mathbb {Q}}}$
-stable nonzero proper ideals, the map
 $S_2\rightarrow A[2], x\mapsto x\cdot m$
is injective; hence,
$S_2\rightarrow A[2], x\mapsto x\cdot m$
is injective; hence,
 $S_2\cdot m \subset {\mathcal {O}}_2\cdot m$
has order
$S_2\cdot m \subset {\mathcal {O}}_2\cdot m$
has order
 $4$
too. Therefore,
$4$
too. Therefore,
 $S_2\cdot m ={\mathcal {O}}_2 \cdot m$
. Suppose first that
$S_2\cdot m ={\mathcal {O}}_2 \cdot m$
. Suppose first that
 $2 \nmid {\mathrm{disc}}(B)$
. We can then apply Lemma 6.9 to conclude that
$2 \nmid {\mathrm{disc}}(B)$
. We can then apply Lemma 6.9 to conclude that
 $ {\mathrm{Gal}}_K$
acts trivially on
$ {\mathrm{Gal}}_K$
acts trivially on
 ${\mathcal {O}}_2$
. Since
${\mathcal {O}}_2$
. Since
 $ {\mathrm{Gal}}_K$
acts on
$ {\mathrm{Gal}}_K$
acts on
 ${\mathcal {O}}_2$
through
${\mathcal {O}}_2$
through
 $ {\mathrm{Gal}}(L/K)\simeq C_3$
or
$ {\mathrm{Gal}}(L/K)\simeq C_3$
or
 $C_6$
, this contradicts Lemma 3.14 and proves the second claim of (a). It remains to consider the case
$C_6$
, this contradicts Lemma 3.14 and proves the second claim of (a). It remains to consider the case
 $2\mid {\mathrm{disc}}(B)$
. In that case, there exists a unique proper nonzero left ideal J of
$2\mid {\mathrm{disc}}(B)$
. In that case, there exists a unique proper nonzero left ideal J of
 ${\mathcal {O}}_2$
, and
${\mathcal {O}}_2$
, and
 $A[J]$
is the unique nonzero proper
$A[J]$
is the unique nonzero proper
 ${\mathcal {O}}_2$
-submodule of
${\mathcal {O}}_2$
-submodule of
 $A[2]$
(Lemma 6.3). It follows that
$A[2]$
(Lemma 6.3). It follows that
 $S_2\cdot m = {\mathcal {O}}_2\cdot m = A[J]$
. Since
$S_2\cdot m = {\mathcal {O}}_2\cdot m = A[J]$
. Since
 $A[2]\not \simeq {\mathcal {O}}_2$
as
$A[2]\not \simeq {\mathcal {O}}_2$
as
 $ {\mathrm{Gal}}_{{\mathbb {Q}}}$
-modules, no element of
$ {\mathrm{Gal}}_{{\mathbb {Q}}}$
-modules, no element of
 $A[2]({\mathbb {Q}})$
is an
$A[2]({\mathbb {Q}})$
is an
 ${\mathcal {O}}_2$
-generator, so
${\mathcal {O}}_2$
-generator, so
 $A[2]({\mathbb {Q}})= A[J]({\mathbb {Q}})$
. However, the equality
$A[2]({\mathbb {Q}})= A[J]({\mathbb {Q}})$
. However, the equality
 $S_2\cdot m = A[J]$
shows that
$S_2\cdot m = A[J]$
shows that
 $S_2\simeq A[J]$
as
$S_2\simeq A[J]$
as
 $ {\mathrm{Gal}}_{{\mathbb {Q}}}$
-modules. Since
$ {\mathrm{Gal}}_{{\mathbb {Q}}}$
-modules. Since
 $ {\mathrm{Gal}}_{{\mathbb {Q}}}$
acts nontrivially on
$ {\mathrm{Gal}}_{{\mathbb {Q}}}$
acts nontrivially on
 $S_2 = \mathbb F_4$
,
$S_2 = \mathbb F_4$
,
 $A[J]({\mathbb {Q}}) = A[2]({\mathbb {Q}})$
has order
$A[J]({\mathbb {Q}}) = A[2]({\mathbb {Q}})$
has order
 $2$
.
$2$
. -
(b) The argument is very similar to the proof of (a), using that in the
 $D_4$
case, the distinguished quadratic subring
$D_4$
case, the distinguished quadratic subring
 ${\mathbb {Z}}[i]$
is unramified at
${\mathbb {Z}}[i]$
is unramified at
 $3$
. In the
$3$
. In the
 $D_2$
case, the distinguished quadratic subring might be ramified at
$D_2$
case, the distinguished quadratic subring might be ramified at
 $3$
, but by Lemma 2.3, there exist three squarefree integers
$3$
, but by Lemma 2.3, there exist three squarefree integers
 $m,n,t$
and embeddings of
$m,n,t$
and embeddings of
 ${\mathbb {Z}}[\sqrt {m}]$
,
${\mathbb {Z}}[\sqrt {m}]$
,
 ${\mathbb {Z}}[\sqrt {n}]$
and
${\mathbb {Z}}[\sqrt {n}]$
and
 ${\mathbb {Z}}[\sqrt {t}]$
into
${\mathbb {Z}}[\sqrt {t}]$
into
 $ {\mathrm{Gal}}_{{\mathbb {Q}}}$
whose image is
$ {\mathrm{Gal}}_{{\mathbb {Q}}}$
whose image is
 $ {\mathrm{Gal}}_{{\mathbb {Q}}}$
-stable. Since
$ {\mathrm{Gal}}_{{\mathbb {Q}}}$
-stable. Since
 $t = -mn$
up to squares, at least one of these three subrings is unramified at
$t = -mn$
up to squares, at least one of these three subrings is unramified at
 $3$
, and the argument of (a) can be carried out using this subring.
$3$
, and the argument of (a) can be carried out using this subring.
7.2 Groups of order
 $48$
$48$
Lemma 7.3. Let E be an elliptic curve over the finite field
![]() $\mathbb F_{p^n}$
, and assume either that E is ordinary or that
$\mathbb F_{p^n}$
, and assume either that E is ordinary or that
![]() $n = 1$
. Then any abelian surface
$n = 1$
. Then any abelian surface
![]() $X/\mathbb F_{p^n}$
isogenous to
$X/\mathbb F_{p^n}$
isogenous to
![]() $E^2$
is isomorphic to a product of elliptic curves over
$E^2$
is isomorphic to a product of elliptic curves over
![]() $\mathbb F_{p^n}$
.
$\mathbb F_{p^n}$
.
Proof. Let
![]() $\pi \in {\mathrm{End}}(E)$
be the Frobenius. Replacing E by an isogenous elliptic curve, we may assume that
$\pi \in {\mathrm{End}}(E)$
be the Frobenius. Replacing E by an isogenous elliptic curve, we may assume that
![]() $ {\mathrm{End}}(E) = {\mathbb {Z}}[\pi ]$
[Reference Jordan, Keeton, Poonen, Rains, Shepherd-Barron and TateJKP18, §7.2-7.3]. By [Reference Jordan, Keeton, Poonen, Rains, Shepherd-Barron and TateJKP18, Theorem 1.1], the functor
$ {\mathrm{End}}(E) = {\mathbb {Z}}[\pi ]$
[Reference Jordan, Keeton, Poonen, Rains, Shepherd-Barron and TateJKP18, §7.2-7.3]. By [Reference Jordan, Keeton, Poonen, Rains, Shepherd-Barron and TateJKP18, Theorem 1.1], the functor
![]() $X \mapsto {\mathrm{Hom}}(X,E)$
is an equivalence between the category of abelian varieties isogenous to a power of E and isomorphism classes of finitely generated torsion-free
$X \mapsto {\mathrm{Hom}}(X,E)$
is an equivalence between the category of abelian varieties isogenous to a power of E and isomorphism classes of finitely generated torsion-free
![]() $ {\mathrm{End}}(E)$
-modules. Since
$ {\mathrm{End}}(E)$
-modules. Since
![]() $ {\mathrm{End}}(E)$
is an order in a quadratic field, any finitely generated torsion-free
$ {\mathrm{End}}(E)$
is an order in a quadratic field, any finitely generated torsion-free
![]() $ {\mathrm{End}}(E)$
-module is a direct sum of rank
$ {\mathrm{End}}(E)$
-module is a direct sum of rank
![]() $1$
modules [Reference Jordan, Keeton, Poonen, Rains, Shepherd-Barron and TateJKP18, Theorem 3.2], so the lemma follows.
$1$
modules [Reference Jordan, Keeton, Poonen, Rains, Shepherd-Barron and TateJKP18, Theorem 3.2], so the lemma follows.
Lemma 7.4. If
![]() $G\subset A({\mathbb {Q}})_{ {\mathrm{tors}}}$
is a subgroup of order
$G\subset A({\mathbb {Q}})_{ {\mathrm{tors}}}$
is a subgroup of order
![]() $16$
, then G is isomorphic to
$16$
, then G is isomorphic to
![]() $({\mathbb {Z}}/4{\mathbb {Z}})^2$
or
$({\mathbb {Z}}/4{\mathbb {Z}})^2$
or
![]() $({\mathbb {Z}}/2{\mathbb {Z}})^2 \times {\mathbb {Z}}/4{\mathbb {Z}}$
.
$({\mathbb {Z}}/2{\mathbb {Z}})^2 \times {\mathbb {Z}}/4{\mathbb {Z}}$
.
Proof. There is a unique isogeny class of abelian surfaces X over
![]() $\mathbb F_3$
with
$\mathbb F_3$
with
![]() $16\mid \#X(\mathbb F_3)$
– namely, the square of the elliptic curve
$16\mid \#X(\mathbb F_3)$
– namely, the square of the elliptic curve
![]() $E/\mathbb F_3$
with
$E/\mathbb F_3$
with
![]() $ {\mathrm{End}}_{\mathbb F_p}(E) \simeq {\mathbb {Z}}[\sqrt {-3}]$
and
$ {\mathrm{End}}_{\mathbb F_p}(E) \simeq {\mathbb {Z}}[\sqrt {-3}]$
and
![]() $\#E(\mathbb F_3) = 4$
. By Lemma 7.3,
$\#E(\mathbb F_3) = 4$
. By Lemma 7.3,
![]() $A_p$
is isomorphic to a product of two elliptic curves both of which have four
$A_p$
is isomorphic to a product of two elliptic curves both of which have four
![]() $\mathbb F_3$
-rational points. Since such an elliptic curve has its group of
$\mathbb F_3$
-rational points. Since such an elliptic curve has its group of
![]() $\mathbb F_3$
-points isomorphic to either
$\mathbb F_3$
-points isomorphic to either
![]() ${\mathbb {Z}}/4{\mathbb {Z}}$
or
${\mathbb {Z}}/4{\mathbb {Z}}$
or
![]() $({\mathbb {Z}}/2{\mathbb {Z}})^2$
,
$({\mathbb {Z}}/2{\mathbb {Z}})^2$
,
![]() $A_p(\mathbb F_3)$
is isomorphic to
$A_p(\mathbb F_3)$
is isomorphic to
![]() $({\mathbb {Z}}/4{\mathbb {Z}})^2$
or
$({\mathbb {Z}}/4{\mathbb {Z}})^2$
or
![]() $({\mathbb {Z}}/4{\mathbb {Z}})\times ({\mathbb {Z}}/2{\mathbb {Z}})^2$
or
$({\mathbb {Z}}/4{\mathbb {Z}})\times ({\mathbb {Z}}/2{\mathbb {Z}})^2$
or
![]() $({\mathbb {Z}}/2{\mathbb {Z}})^4$
. By Proposition 5.8, the latter cannot happen. The lemma now follows since
$({\mathbb {Z}}/2{\mathbb {Z}})^4$
. By Proposition 5.8, the latter cannot happen. The lemma now follows since
![]() $A({\mathbb {Q}})[16] \hookrightarrow A_p(\mathbb F_3)$
.
$A({\mathbb {Q}})[16] \hookrightarrow A_p(\mathbb F_3)$
.
Proposition 7.5.
![]() $\#A({\mathbb {Q}})_{ {\mathrm{tors}}} < 48$
.
$\#A({\mathbb {Q}})_{ {\mathrm{tors}}} < 48$
.
Proof. By Proposition 7.1, it is enough to show that
![]() $A({\mathbb {Q}})_{ {\mathrm{tors}}} \neq 48$
. Assume for the sake of contradiction that
$A({\mathbb {Q}})_{ {\mathrm{tors}}} \neq 48$
. Assume for the sake of contradiction that
![]() $\#A({\mathbb {Q}})_{\mathrm {tors}} = 48$
. The reduction
$\#A({\mathbb {Q}})_{\mathrm {tors}} = 48$
. The reduction
![]() $A_5/\mathbb F_5$
must then be in the isogeny class 2.5.d e. We see that
$A_5/\mathbb F_5$
must then be in the isogeny class 2.5.d e. We see that
![]() $ {\mathrm{End}}^0((A_p)_{\mathbb F_{5^n}})$
contains a quaternion algebra if and only if
$ {\mathrm{End}}^0((A_p)_{\mathbb F_{5^n}})$
contains a quaternion algebra if and only if
![]() $3$
divides n. Therefore, the Galois group of the endomorphism field of A has order divisible by
$3$
divides n. Therefore, the Galois group of the endomorphism field of A has order divisible by
![]() $3$
, and so by Proposition 3.3 must be
$3$
, and so by Proposition 3.3 must be
![]() $D_3$
or
$D_3$
or
![]() $D_6$
. Proposition 7.2 then implies
$D_6$
. Proposition 7.2 then implies
![]() $A[2]({\mathbb {Q}})\subset {\mathbb {Z}}/2{\mathbb {Z}}$
, contradicting the fact that
$A[2]({\mathbb {Q}})\subset {\mathbb {Z}}/2{\mathbb {Z}}$
, contradicting the fact that
![]() $A[2]({\mathbb {Q}})$
has size
$A[2]({\mathbb {Q}})$
has size
![]() $\geq 4$
(Lemma 7.4).
$\geq 4$
(Lemma 7.4).
7.3 Groups of order
 $36$
$36$
Lemma 7.6. If
![]() $36 \mid \#A({\mathbb {Q}})_{\mathrm {tors}}$
, then
$36 \mid \#A({\mathbb {Q}})_{\mathrm {tors}}$
, then
![]() $A({\mathbb {Q}})_{\mathrm {tors}} \simeq ({\mathbb {Z}}/6{\mathbb {Z}})^2$
.
$A({\mathbb {Q}})_{\mathrm {tors}} \simeq ({\mathbb {Z}}/6{\mathbb {Z}})^2$
.
Proof. Over
![]() $\mathbb F_5$
there is exactly one isogeny class of abelian surface X with
$\mathbb F_5$
there is exactly one isogeny class of abelian surface X with
![]() $36 \mid \#X(\mathbb F_5)$
and whose geometric endomorphism algebra contains a quaternion algebra – namely, 2.5.a k – which is isogenous to the square of an elliptic curve. Thus, the reduction
$36 \mid \#X(\mathbb F_5)$
and whose geometric endomorphism algebra contains a quaternion algebra – namely, 2.5.a k – which is isogenous to the square of an elliptic curve. Thus, the reduction
![]() $A_5$
is isomorphic to a product of two elliptic curves (Lemma 7.3). Every elliptic curve in this isogeny class has
$A_5$
is isomorphic to a product of two elliptic curves (Lemma 7.3). Every elliptic curve in this isogeny class has
![]() $E(\mathbb F_5) \simeq {\mathbb {Z}}/6{\mathbb {Z}}$
; hence,
$E(\mathbb F_5) \simeq {\mathbb {Z}}/6{\mathbb {Z}}$
; hence,
![]() $A_5(\mathbb F_5) \simeq ({\mathbb {Z}}/6{\mathbb {Z}})^2$
.
$A_5(\mathbb F_5) \simeq ({\mathbb {Z}}/6{\mathbb {Z}})^2$
.
Proposition 7.7.
![]() $\#A({\mathbb {Q}})_{ {\mathrm{tors}}} < 36$
.
$\#A({\mathbb {Q}})_{ {\mathrm{tors}}} < 36$
.
Proof. By Proposition 7.5 and Proposition 7.1, it is enough to show that
![]() $A({\mathbb {Q}})_{ {\mathrm{tors}}}$
does not have order
$A({\mathbb {Q}})_{ {\mathrm{tors}}}$
does not have order
![]() $36$
. By Lemma 7.6, such an A would have
$36$
. By Lemma 7.6, such an A would have
![]() $A({\mathbb {Q}})_{ {\mathrm{tors}}} \simeq ({\mathbb {Z}}/6{\mathbb {Z}})^2$
. By Proposition 7.2, A cannot have endomorphism field
$A({\mathbb {Q}})_{ {\mathrm{tors}}} \simeq ({\mathbb {Z}}/6{\mathbb {Z}})^2$
. By Proposition 7.2, A cannot have endomorphism field
![]() $D_n$
for every
$D_n$
for every
![]() $n\in \{2,3,4,6\}$
, so A has
$n\in \{2,3,4,6\}$
, so A has
![]() $ {\mathrm{GL}}_2$
-type, which we have also already ruled out.
$ {\mathrm{GL}}_2$
-type, which we have also already ruled out.
It follows that
![]() $\#A({\mathbb {Q}})_{ {\mathrm{tors}}} \leq 24$
. Before we show that this inequality is strict, we rule out the existence of rational points of order
$\#A({\mathbb {Q}})_{ {\mathrm{tors}}} \leq 24$
. Before we show that this inequality is strict, we rule out the existence of rational points of order
![]() $9$
and
$9$
and
![]() $8$
.
$8$
.
7.4 Rational points of order
 $9$
$9$
Proposition 7.8.
![]() $A({\mathbb {Q}})_{ {\mathrm{tors}}}$
contains no elements of order
$A({\mathbb {Q}})_{ {\mathrm{tors}}}$
contains no elements of order
![]() $9$
.
$9$
.
Proof. Suppose
![]() $A({\mathbb {Q}})$
has a point of order
$A({\mathbb {Q}})$
has a point of order
![]() $9$
. Then the reduction
$9$
. Then the reduction
![]() $A_2/\mathbb F_2$
must live in the isogeny class 2.2.a e or 2.2.b b. The latter has commutative geometric endomorphism algebra and so cannot be the reduction of a
$A_2/\mathbb F_2$
must live in the isogeny class 2.2.a e or 2.2.b b. The latter has commutative geometric endomorphism algebra and so cannot be the reduction of a
![]() ${\mathcal {O}}$
-
${\mathcal {O}}$
-
![]() $\mathrm {PQM}$
surface by Proposition 4.17. The former is the isogeny class of the square of an elliptic curve E over
$\mathrm {PQM}$
surface by Proposition 4.17. The former is the isogeny class of the square of an elliptic curve E over
![]() $\mathbb F_2$
with
$\mathbb F_2$
with
![]() $\#E(\mathbb F_2) = 3$
, so by Lemma 7.3, we have
$\#E(\mathbb F_2) = 3$
, so by Lemma 7.3, we have
![]() $A_2(\mathbb F_2) \simeq ({\mathbb {Z}}/3{\mathbb {Z}})^2$
.
$A_2(\mathbb F_2) \simeq ({\mathbb {Z}}/3{\mathbb {Z}})^2$
.
7.5 Rational points of order
 $8$
$8$
Proposition 7.9.
![]() $A({\mathbb {Q}})_{ {\mathrm{tors}}}$
contains no elements of order
$A({\mathbb {Q}})_{ {\mathrm{tors}}}$
contains no elements of order
![]() $8$
.
$8$
.
Proof. Suppose otherwise. The reduction
![]() $A_3/\mathbb F_3$
must be in the isogeny class 2.3.a ac, which is simple with endomorphism algebra
$A_3/\mathbb F_3$
must be in the isogeny class 2.3.a ac, which is simple with endomorphism algebra
![]() ${\mathbb {Q}}(\zeta _8) = {\mathbb {Q}}(\sqrt {2}, \sqrt {-2})$
. (It cannot be in the isogeny class 2.3.a g by the proof of Lemma 7.4.) Since
${\mathbb {Q}}(\zeta _8) = {\mathbb {Q}}(\sqrt {2}, \sqrt {-2})$
. (It cannot be in the isogeny class 2.3.a g by the proof of Lemma 7.4.) Since
![]() $\#A_3(\mathbb F_3) = 8$
, we must have
$\#A_3(\mathbb F_3) = 8$
, we must have
![]() $A_3(\mathbb F_3) = {\mathbb {Z}}/8{\mathbb {Z}}$
. This eliminates the possibility that
$A_3(\mathbb F_3) = {\mathbb {Z}}/8{\mathbb {Z}}$
. This eliminates the possibility that
![]() $A({\mathbb {Q}})$
contains a prime-to-3 subgroup any larger than
$A({\mathbb {Q}})$
contains a prime-to-3 subgroup any larger than
![]() ${\mathbb {Z}}/8{\mathbb {Z}}$
. Note also that
${\mathbb {Z}}/8{\mathbb {Z}}$
. Note also that
![]() $\#A_3(\mathbb F_9) = 64$
and A is isomorphic to a product of ordinary elliptic curves over
$\#A_3(\mathbb F_9) = 64$
and A is isomorphic to a product of ordinary elliptic curves over
![]() $\mathbb F_9$
by Lemma 7.3, at least one of which has
$\mathbb F_9$
by Lemma 7.3, at least one of which has
![]() $E(\mathbb F_9) \simeq {\mathbb {Z}}/8{\mathbb {Z}}$
. It follows that the
$E(\mathbb F_9) \simeq {\mathbb {Z}}/8{\mathbb {Z}}$
. It follows that the
![]() $\mathbb F_2$
-dimension of
$\mathbb F_2$
-dimension of
![]() $A_3[2](\mathbb F_9)$
is at most
$A_3[2](\mathbb F_9)$
is at most
![]() $3$
, and in particular, not all
$3$
, and in particular, not all
![]() $2$
-torsion points are defined over
$2$
-torsion points are defined over
![]() $\mathbb F_9$
. However, all endomorphisms of
$\mathbb F_9$
. However, all endomorphisms of
![]() $(A_3)_{\bar {\mathbb {F}}_3}$
are defined over
$(A_3)_{\bar {\mathbb {F}}_3}$
are defined over
![]() $\mathbb F_9$
, so we conclude by Lemmas 6.2 and 6.3 that the
$\mathbb F_9$
, so we conclude by Lemmas 6.2 and 6.3 that the
![]() ${\mathcal {O}}/2{\mathcal {O}}$
-module generated by any
${\mathcal {O}}/2{\mathcal {O}}$
-module generated by any
![]() $\mathbb F_9$
-rational point of order
$\mathbb F_9$
-rational point of order
![]() $2$
has order
$2$
has order
![]() $4$
.
$4$
.
Suppose first that
![]() $2$
divides
$2$
divides
![]() $ {\mathrm{disc}}(B)$
. Then the aforementioned
$ {\mathrm{disc}}(B)$
. Then the aforementioned
![]() ${\mathcal {O}}$
-module must be
${\mathcal {O}}$
-module must be
![]() $A[J]$
, where J is the ideal in
$A[J]$
, where J is the ideal in
![]() ${\mathcal {O}}$
such that
${\mathcal {O}}$
such that
![]() $J^2 = 2{\mathcal {O}}$
(see §6.1). Let
$J^2 = 2{\mathcal {O}}$
(see §6.1). Let
![]() $t \in J$
be any element not in
$t \in J$
be any element not in
![]() $2{\mathcal {O}}$
. Then over
$2{\mathcal {O}}$
. Then over
![]() $\mathbb F_9$
, we have an exact sequence
$\mathbb F_9$
, we have an exact sequence
with the last map being multiplication by t. Let
![]() $P \in A_3[4](\mathbb F_9)$
be a point of order
$P \in A_3[4](\mathbb F_9)$
be a point of order
![]() $4$
. Without loss of generality, we may assume
$4$
. Without loss of generality, we may assume
![]() $Q = tP$
has order
$Q = tP$
has order
![]() $2$
(if not, just replace P by
$2$
(if not, just replace P by
![]() $tP$
) and
$tP$
) and
![]() $Q \notin A_3[J]$
. Then we have seen that
$Q \notin A_3[J]$
. Then we have seen that
![]() ${\mathcal {O}} \cdot Q \neq A_3[2]$
, so
${\mathcal {O}} \cdot Q \neq A_3[2]$
, so
![]() ${\mathcal {O}}\cdot Q = A_3[J]$
, but this contradicts
${\mathcal {O}}\cdot Q = A_3[J]$
, but this contradicts
![]() $Q \notin A_3[J]$
.
$Q \notin A_3[J]$
.
Now suppose that
![]() $2$
does not divide
$2$
does not divide
![]() $ {\mathrm{disc}}(B)$
so that
$ {\mathrm{disc}}(B)$
so that
![]() ${\mathcal {O}} \simeq \mathrm {Mat}_2(\mathbb F_2)$
. Let
${\mathcal {O}} \simeq \mathrm {Mat}_2(\mathbb F_2)$
. Let
![]() $L/{\mathbb {Q}}$
be the endomorphism field. If
$L/{\mathbb {Q}}$
be the endomorphism field. If
![]() $ {\mathrm{Gal}}(L/{\mathbb {Q}}) \simeq D_2$
, then at least one of the quadratic subfields of L is not inert at
$ {\mathrm{Gal}}(L/{\mathbb {Q}}) \simeq D_2$
, then at least one of the quadratic subfields of L is not inert at
![]() $3$
. So
$3$
. So
![]() $ {\mathrm{End}}_{\mathbb F_3}(A_3)$
must contain a quadratic order S in
$ {\mathrm{End}}_{\mathbb F_3}(A_3)$
must contain a quadratic order S in
![]() ${\mathbb {Z}}[i]$
or
${\mathbb {Z}}[i]$
or
![]() ${\mathbb {Z}}[\sqrt {2}]$
or in
${\mathbb {Z}}[\sqrt {2}]$
or in
![]() ${\mathbb {Z}}[\sqrt {-2}]$
. But we saw in Lemma 2.2 that S contains
${\mathbb {Z}}[\sqrt {-2}]$
. But we saw in Lemma 2.2 that S contains
![]() ${\mathbb {Z}}[\sqrt {m}]$
with m squarefree. So S is
${\mathbb {Z}}[\sqrt {m}]$
with m squarefree. So S is
![]() ${\mathbb {Z}}[i]$
or
${\mathbb {Z}}[i]$
or
![]() ${\mathbb {Z}}[\sqrt {2}]$
or
${\mathbb {Z}}[\sqrt {2}]$
or
![]() ${\mathbb {Z}}[\sqrt {-2}]$
. In all cases, there exists
${\mathbb {Z}}[\sqrt {-2}]$
. In all cases, there exists
![]() $t \in S$
such that
$t \in S$
such that
![]() $t^2S = 2S$
, and so we have an endomorphism (defined over
$t^2S = 2S$
, and so we have an endomorphism (defined over
![]() $\mathbb F_3$
) which behaves like
$\mathbb F_3$
) which behaves like
![]() $\sqrt 2$
on
$\sqrt 2$
on
![]() $A_3[2]$
. But we also have a rational point P of order 4. Without loss of generality, the orders of
$A_3[2]$
. But we also have a rational point P of order 4. Without loss of generality, the orders of
![]() $tP$
and
$tP$
and
![]() $t^2P$
are both
$t^2P$
are both
![]() $2$
. But
$2$
. But
![]() $t^2P \neq tP$
, so
$t^2P \neq tP$
, so
![]() $\dim _{\mathbb F_2} A_3[2](\mathbb F_3)> 1$
, which contradicts
$\dim _{\mathbb F_2} A_3[2](\mathbb F_3)> 1$
, which contradicts
![]() $A_3(\mathbb F_3) \simeq {\mathbb {Z}}/8{\mathbb {Z}}$
. The case
$A_3(\mathbb F_3) \simeq {\mathbb {Z}}/8{\mathbb {Z}}$
. The case
![]() $ {\mathrm{Gal}}(L/{\mathbb {Q}}) = D_4$
does not happen when
$ {\mathrm{Gal}}(L/{\mathbb {Q}}) = D_4$
does not happen when
![]() $ {\mathrm{disc}}(B)$
is odd by Lemma 2.4, so we consider the case where
$ {\mathrm{disc}}(B)$
is odd by Lemma 2.4, so we consider the case where
![]() $ {\mathrm{Gal}}(L/{\mathbb {Q}})$
is
$ {\mathrm{Gal}}(L/{\mathbb {Q}})$
is
![]() $D_3$
or
$D_3$
or
![]() $D_6$
. By Proposition 7.2(a),
$D_6$
. By Proposition 7.2(a),
![]() $A[2] \simeq {\mathcal {O}}/2{\mathcal {O}}$
as
$A[2] \simeq {\mathcal {O}}/2{\mathcal {O}}$
as
![]() $ {\mathrm{Gal}}_{{\mathbb {Q}}}$
-modules. But then
$ {\mathrm{Gal}}_{{\mathbb {Q}}}$
-modules. But then
![]() $A_3[2] \simeq {\mathcal {O}}/2{\mathcal {O}}$
as
$A_3[2] \simeq {\mathcal {O}}/2{\mathcal {O}}$
as
![]() $ {\mathrm{Gal}}_{\mathbb F_3}$
-modules, contradicting the fact that
$ {\mathrm{Gal}}_{\mathbb F_3}$
-modules, contradicting the fact that
![]() $A_3[2](\mathbb F_3)$
contains no
$A_3[2](\mathbb F_3)$
contains no
![]() ${\mathcal {O}}/2{\mathcal {O}}$
-generator.
${\mathcal {O}}/2{\mathcal {O}}$
-generator.
We are left to consider the case
![]() $ {\mathrm{Gal}}(L/{\mathbb {Q}}) = D_1 = C_2$
(i.e., the
$ {\mathrm{Gal}}(L/{\mathbb {Q}}) = D_1 = C_2$
(i.e., the
![]() $ {\mathrm{GL}}_2$
-type case), which we have already treated in Proposition 5.13.
$ {\mathrm{GL}}_2$
-type case), which we have already treated in Proposition 5.13.
7.6 Groups of order
 $24$
$24$
If
![]() $A({\mathbb {Q}})_{ {\mathrm{tors}}}$
has order
$A({\mathbb {Q}})_{ {\mathrm{tors}}}$
has order
![]() $24$
, then by Proposition 7.9, the group structure is either
$24$
, then by Proposition 7.9, the group structure is either
![]() $({\mathbb {Z}}/2{\mathbb {Z}})^3 \times {\mathbb {Z}}/3{\mathbb {Z}}$
or
$({\mathbb {Z}}/2{\mathbb {Z}})^3 \times {\mathbb {Z}}/3{\mathbb {Z}}$
or
![]() ${\mathbb {Z}}/2{\mathbb {Z}} \times {\mathbb {Z}}/4{\mathbb {Z}} \times {\mathbb {Z}}/3{\mathbb {Z}}$
. We show below that in fact neither can occur. First, we gather some facts common to both cases.
${\mathbb {Z}}/2{\mathbb {Z}} \times {\mathbb {Z}}/4{\mathbb {Z}} \times {\mathbb {Z}}/3{\mathbb {Z}}$
. We show below that in fact neither can occur. First, we gather some facts common to both cases.
Lemma 7.10. Suppose
![]() $\#A({\mathbb {Q}})_{\mathrm {tors}} = 24$
, and let
$\#A({\mathbb {Q}})_{\mathrm {tors}} = 24$
, and let
![]() $L/{\mathbb {Q}}$
be the endomorphism field of A. Then
$L/{\mathbb {Q}}$
be the endomorphism field of A. Then
-
(a)
 $ {\mathrm{Gal}}(L/{\mathbb {Q}})$
is isomorphic to
$ {\mathrm{Gal}}(L/{\mathbb {Q}})$
is isomorphic to
 $D_2$
or
$D_2$
or
 $D_4$
,
$D_4$
, -
(b)
 ${\mathbb {Q}}(\zeta _3) \subset L$
, and
${\mathbb {Q}}(\zeta _3) \subset L$
, and -
(c) if
 $ {\mathrm{Gal}}(L/{\mathbb {Q}}) \not \simeq D_4$
then A has unipotent rank
$ {\mathrm{Gal}}(L/{\mathbb {Q}}) \not \simeq D_4$
then A has unipotent rank
 $1$
over
$1$
over
 ${\mathbb {Q}}_3 (\text{in the terminology of}\ \, \S 4.1)$
.
${\mathbb {Q}}_3 (\text{in the terminology of}\ \, \S 4.1)$
.
Proof. Since A is not of
![]() $ {\mathrm{GL}}_2$
-type, Proposition 7.2 implies that
$ {\mathrm{GL}}_2$
-type, Proposition 7.2 implies that
![]() $ {\mathrm{Gal}}(L/{\mathbb {Q}})$
is isomorphic to
$ {\mathrm{Gal}}(L/{\mathbb {Q}})$
is isomorphic to
![]() $D_2$
or
$D_2$
or
![]() $D_4$
, proving
$D_4$
, proving
![]() $(a)$
.
$(a)$
.
Checking isogeny classes over
![]() $\mathbb F_5$
, we see that the reduction
$\mathbb F_5$
, we see that the reduction
![]() $A_5$
is in the isogeny class 2.5a ac; the isogeny class 2.5d e is ruled out since it only acquires QM over
$A_5$
is in the isogeny class 2.5a ac; the isogeny class 2.5d e is ruled out since it only acquires QM over
![]() $\mathbb F_{5^3}$
, which is not compatible with
$\mathbb F_{5^3}$
, which is not compatible with
![]() $(a)$
. The fact that
$(a)$
. The fact that
![]() $\#A_5(\mathbb F_{25})[3^\infty ] = 9$
shows that the point of order
$\#A_5(\mathbb F_{25})[3^\infty ] = 9$
shows that the point of order
![]() $3$
in
$3$
in
![]() $A({\mathbb {Q}})$
is not an
$A({\mathbb {Q}})$
is not an
![]() ${\mathcal {O}}$
-module generator of
${\mathcal {O}}$
-module generator of
![]() $A[3]$
(since the
$A[3]$
(since the
![]() ${\mathcal {O}}$
-action on
${\mathcal {O}}$
-action on
![]() $A_5$
is defined over
$A_5$
is defined over
![]() $\mathbb F_{25}$
). By Proposition 7.2, we deduce that the quaternion algebra B is ramified at
$\mathbb F_{25}$
). By Proposition 7.2, we deduce that the quaternion algebra B is ramified at
![]() $3$
. Since
$3$
. Since
![]() $A[3]({\mathbb {Q}})$
has a rational point, it follows from Theorem 6.7 that
$A[3]({\mathbb {Q}})$
has a rational point, it follows from Theorem 6.7 that
![]() ${\mathbb {Q}}(\sqrt {-3}) = {\mathbb {Q}}(\zeta _3) \subset L$
, proving
${\mathbb {Q}}(\sqrt {-3}) = {\mathbb {Q}}(\zeta _3) \subset L$
, proving
![]() $(b)$
.
$(b)$
.
Since
![]() $3$
ramifies in L, A has bad reduction over
$3$
ramifies in L, A has bad reduction over
![]() ${\mathbb {Q}}_3$
by Proposition 3.6. If
${\mathbb {Q}}_3$
by Proposition 3.6. If
![]() $A[2]({\mathbb {Q}}) \simeq ({\mathbb {Z}}/2{\mathbb {Z}})^3$
, then A achieves good reduction over every ramified quadratic extension of
$A[2]({\mathbb {Q}}) \simeq ({\mathbb {Z}}/2{\mathbb {Z}})^3$
, then A achieves good reduction over every ramified quadratic extension of
![]() ${\mathbb {Q}}_3$
by Proposition 5.15. If
${\mathbb {Q}}_3$
by Proposition 5.15. If
![]() $A/{\mathbb {Q}}_3$
has totally additive reduction, then the quadratic twist of A by
$A/{\mathbb {Q}}_3$
has totally additive reduction, then the quadratic twist of A by
![]() ${\mathbb {Q}}(\sqrt {3})$
, say, will have good reduction at
${\mathbb {Q}}(\sqrt {3})$
, say, will have good reduction at
![]() $3$
by Lemma 4.9. But quadratic twisting does not change the endomorphism field by Lemma 3.7, so any quadratic twist of A must have endomorphism field which contains
$3$
by Lemma 4.9. But quadratic twisting does not change the endomorphism field by Lemma 3.7, so any quadratic twist of A must have endomorphism field which contains
![]() ${\mathbb {Q}}(\sqrt {-3})$
and hence must have bad reduction at
${\mathbb {Q}}(\sqrt {-3})$
and hence must have bad reduction at
![]() $3$
. We conclude that A must have unipotent rank
$3$
. We conclude that A must have unipotent rank
![]() $1$
over
$1$
over
![]() ${\mathbb {Q}}_3$
by Proposition 4.2.
${\mathbb {Q}}_3$
by Proposition 4.2.
If
![]() $A[2]({\mathbb {Q}}) \simeq ({\mathbb {Z}}/2{\mathbb {Z}})^2$
and
$A[2]({\mathbb {Q}}) \simeq ({\mathbb {Z}}/2{\mathbb {Z}})^2$
and
![]() $ {\mathrm{Gal}}(L/{\mathbb {Q}}) \not \simeq D_4$
, then
$ {\mathrm{Gal}}(L/{\mathbb {Q}}) \not \simeq D_4$
, then
![]() $ {\mathrm{Gal}}(L/{\mathbb {Q}}) \simeq D_2$
and so
$ {\mathrm{Gal}}(L/{\mathbb {Q}}) \simeq D_2$
and so
![]() $L/{\mathbb {Q}}$
is a biquadratic field containing
$L/{\mathbb {Q}}$
is a biquadratic field containing
![]() ${\mathbb {Q}}(\zeta _3)$
. It follows that A has all of its endomorphisms defined over
${\mathbb {Q}}(\zeta _3)$
. It follows that A has all of its endomorphisms defined over
![]() ${\mathbb {Q}}_3^{\mathrm {nr}}(\zeta _3)$
. If A still has bad reduction over
${\mathbb {Q}}_3^{\mathrm {nr}}(\zeta _3)$
. If A still has bad reduction over
![]() ${\mathbb {Q}}_3(\zeta _3)$
, then it must have totally additive bad reduction (since it has QM after enlarging the residue field) by Proposition 4.2, and we obtain a contradiction with Proposition 4.12 and the fact that A has a point of order
${\mathbb {Q}}_3(\zeta _3)$
, then it must have totally additive bad reduction (since it has QM after enlarging the residue field) by Proposition 4.2, and we obtain a contradiction with Proposition 4.12 and the fact that A has a point of order
![]() $4$
. Thus, A attains good reduction over
$4$
. Thus, A attains good reduction over
![]() ${\mathbb {Q}}_3(\zeta _3)$
, and arguing as above, we conclude that A has unipotent rank
${\mathbb {Q}}_3(\zeta _3)$
, and arguing as above, we conclude that A has unipotent rank
![]() $1$
over
$1$
over
![]() ${\mathbb {Q}}_3$
.
${\mathbb {Q}}_3$
.
Proposition 7.11.
![]() $A({\mathbb {Q}})_{ {\mathrm{tors}}} \not \simeq ({\mathbb {Z}}/2{\mathbb {Z}})^3 \times {\mathbb {Z}}/3{\mathbb {Z}}$
.
$A({\mathbb {Q}})_{ {\mathrm{tors}}} \not \simeq ({\mathbb {Z}}/2{\mathbb {Z}})^3 \times {\mathbb {Z}}/3{\mathbb {Z}}$
.
Proof. Assume otherwise, for the sake of contradiction. Theorem 2.6 and Lemma 5.14 show that the endomorphism field
![]() $L/{\mathbb {Q}}$
has Galois group
$L/{\mathbb {Q}}$
has Galois group
![]() $ {\mathrm{Gal}}(L/{\mathbb {Q}}) \simeq D_2$
.
$ {\mathrm{Gal}}(L/{\mathbb {Q}}) \simeq D_2$
.
First, assume there exists a prime
![]() $p> 3$
of bad reduction for A. By Theorem 4.11, A must have unipotent rank 1 over
$p> 3$
of bad reduction for A. By Theorem 4.11, A must have unipotent rank 1 over
![]() ${\mathbb {Q}}_p$
, and hence, p must ramify in L by Proposition 4.2. Next, recall that there are three
${\mathbb {Q}}_p$
, and hence, p must ramify in L by Proposition 4.2. Next, recall that there are three
![]() $ {\mathrm{Gal}}_{\mathbb {Q}}$
-stable quadratic subfields of B, one of which is imaginary. Let
$ {\mathrm{Gal}}_{\mathbb {Q}}$
-stable quadratic subfields of B, one of which is imaginary. Let
![]() $L_1$
,
$L_1$
,
![]() $L_2$
and
$L_2$
and
![]() $L_3$
be the corresponding quadratic subfields of L, labeled so that
$L_3$
be the corresponding quadratic subfields of L, labeled so that
![]() $B^{ {\mathrm{Gal}}_{L_1}}$
is imaginary quadratic. Since L is biquadratic, exactly one of the
$B^{ {\mathrm{Gal}}_{L_1}}$
is imaginary quadratic. Since L is biquadratic, exactly one of the
![]() $L_i$
must be unramified over
$L_i$
must be unramified over
![]() ${\mathbb {Q}}_p$
. Since A has unipotent rank 1, it must be
${\mathbb {Q}}_p$
. Since A has unipotent rank 1, it must be
![]() $L_1$
(by Proposition 4.2). But by Lemma 7.10(b), we have
$L_1$
(by Proposition 4.2). But by Lemma 7.10(b), we have
![]() ${\mathbb {Q}}(\zeta _3) \subset L$
, and
${\mathbb {Q}}(\zeta _3) \subset L$
, and
![]() ${\mathbb {Q}}(\zeta _3)$
is also unramified at p, so
${\mathbb {Q}}(\zeta _3)$
is also unramified at p, so
![]() $L_1 = {\mathbb {Q}}(\sqrt {-3})$
. Now,
$L_1 = {\mathbb {Q}}(\sqrt {-3})$
. Now,
![]() $A/{\mathbb {Q}}_3$
has unipotent rank 1 by Lemma 7.10(c). As above, Proposition 4.2 implies that the unique sub-extension
$A/{\mathbb {Q}}_3$
has unipotent rank 1 by Lemma 7.10(c). As above, Proposition 4.2 implies that the unique sub-extension
![]() $L_i$
unramified at
$L_i$
unramified at
![]() $3$
must be
$3$
must be
![]() $L_1$
. This contradicts
$L_1$
. This contradicts
![]() $L_1 = {\mathbb {Q}}(\sqrt {-3})$
.
$L_1 = {\mathbb {Q}}(\sqrt {-3})$
.
Thus, it remains to consider the possibility that A has good reduction outside
![]() $\{2,3\}$
. This forces the endomorphism field to be unramified outside
$\{2,3\}$
. This forces the endomorphism field to be unramified outside
![]() $\{2,3\}$
. Moreover, A has unipotent rank
$\{2,3\}$
. Moreover, A has unipotent rank
![]() $1$
reduction over
$1$
reduction over
![]() ${\mathbb {Q}}_3$
, so L must contain an imaginary quadratic subfield that is unramified at
${\mathbb {Q}}_3$
, so L must contain an imaginary quadratic subfield that is unramified at
![]() $3$
. Hence, L is isomorphic to
$3$
. Hence, L is isomorphic to
![]() ${\mathbb {Q}}(\sqrt {-3},i)$
or
${\mathbb {Q}}(\sqrt {-3},i)$
or
![]() ${\mathbb {Q}}(\sqrt {-3}, \sqrt {-2})$
. We also know that
${\mathbb {Q}}(\sqrt {-3}, \sqrt {-2})$
. We also know that
![]() $B^{ {\mathrm{Gal}}_{{\mathbb {Q}}(\sqrt {-3})}}$
is a real quadratic field, and
$B^{ {\mathrm{Gal}}_{{\mathbb {Q}}(\sqrt {-3})}}$
is a real quadratic field, and
![]() $L_1$
is either
$L_1$
is either
![]() ${\mathbb {Q}}(i)$
or
${\mathbb {Q}}(i)$
or
![]() ${\mathbb {Q}}(\sqrt {-2})$
.
${\mathbb {Q}}(\sqrt {-2})$
.
Over
![]() $\mathbb F_7$
, there are two possible isogeny classes: 2.7a ac and 2.7i be. Since
$\mathbb F_7$
, there are two possible isogeny classes: 2.7a ac and 2.7i be. Since
![]() $7$
is inert in
$7$
is inert in
![]() $L_1$
, L does not split completely at
$L_1$
, L does not split completely at
![]() $7$
. The isogeny class is therefore not
$7$
. The isogeny class is therefore not
![]() $2.7i_{be}$
since all its endomorphisms are defined over
$2.7i_{be}$
since all its endomorphisms are defined over
![]() $\mathbb F_7$
; hence, the isogeny class is
$\mathbb F_7$
; hence, the isogeny class is
![]() $2.7a_{ac}$
. Thus,
$2.7a_{ac}$
. Thus,
![]() $ {\mathrm{End}}^0(A_7) \simeq {\mathbb {Q}}(\sqrt {-3}) \times {\mathbb {Q}}(\sqrt {-3})$
. Since
$ {\mathrm{End}}^0(A_7) \simeq {\mathbb {Q}}(\sqrt {-3}) \times {\mathbb {Q}}(\sqrt {-3})$
. Since
![]() $7$
splits in
$7$
splits in
![]() ${\mathbb {Q}}(\sqrt {-3})$
, we see that
${\mathbb {Q}}(\sqrt {-3})$
, we see that
![]() $B^{ {\mathrm{Gal}}_{{\mathbb {Q}}(\sqrt {-3})}} = {\mathbb {Q}}(\sqrt {-3})$
, which shows that
$B^{ {\mathrm{Gal}}_{{\mathbb {Q}}(\sqrt {-3})}} = {\mathbb {Q}}(\sqrt {-3})$
, which shows that
![]() $L_1 = {\mathbb {Q}}(\sqrt {-3})$
, contradicting what was said above.
$L_1 = {\mathbb {Q}}(\sqrt {-3})$
, contradicting what was said above.
Proposition 7.12.
![]() $A({\mathbb {Q}})_{ {\mathrm{tors}}} \not \simeq ({\mathbb {Z}}/2{\mathbb {Z}}) \times ({\mathbb {Z}}/4{\mathbb {Z}}) \times ({\mathbb {Z}}/3{\mathbb {Z}})$
.
$A({\mathbb {Q}})_{ {\mathrm{tors}}} \not \simeq ({\mathbb {Z}}/2{\mathbb {Z}}) \times ({\mathbb {Z}}/4{\mathbb {Z}}) \times ({\mathbb {Z}}/3{\mathbb {Z}})$
.
Proof. Assume otherwise, for the sake of contradiction. We separate cases according to the size of
![]() $G = {\mathrm{Gal}}(L/{\mathbb {Q}})$
. First suppose
$G = {\mathrm{Gal}}(L/{\mathbb {Q}})$
. First suppose
![]() $G \simeq D_4$
, so that the distinguished subring S of Definition §3.3 is isomorphic to
$G \simeq D_4$
, so that the distinguished subring S of Definition §3.3 is isomorphic to
![]() ${\mathbb {Z}}[i]$
. Then
${\mathbb {Z}}[i]$
. Then
![]() $2\mid {\mathrm{disc}}(B)$
by Lemma 2.4. Since B is ramified at
$2\mid {\mathrm{disc}}(B)$
by Lemma 2.4. Since B is ramified at
![]() $2$
and
$2$
and
![]() $3$
and
$3$
and
![]() $A({\mathbb {Q}})$
contains points of order
$A({\mathbb {Q}})$
contains points of order
![]() $4$
and
$4$
and
![]() $3$
, we see that L contains both
$3$
, we see that L contains both
![]() ${\mathbb {Q}}(i)$
and
${\mathbb {Q}}(i)$
and
![]() ${\mathbb {Q}}(\zeta _3)$
, by Theorem 6.7. Over one of these two quadratic subfields, the
${\mathbb {Q}}(\zeta _3)$
, by Theorem 6.7. Over one of these two quadratic subfields, the
![]() $ {\mathrm{Gal}}_{\mathbb {Q}}$
-action on
$ {\mathrm{Gal}}_{\mathbb {Q}}$
-action on
![]() $S = {\mathbb {Z}}[i]$
trivializes. Indeed, the
$S = {\mathbb {Z}}[i]$
trivializes. Indeed, the
![]() $ {\mathrm{Gal}}_{\mathbb {Q}}$
-action on
$ {\mathrm{Gal}}_{\mathbb {Q}}$
-action on
![]() ${\mathbb {Z}}[i]$
cannot be trivialized by the third quadratic subfield
${\mathbb {Z}}[i]$
cannot be trivialized by the third quadratic subfield
![]() ${\mathbb {Q}}(\sqrt {3})$
of L, by Proposition 3.2. Looking over
${\mathbb {Q}}(\sqrt {3})$
of L, by Proposition 3.2. Looking over
![]() $\mathbb F_5$
, we see that
$\mathbb F_5$
, we see that
![]() ${\mathbb {Q}}(i)$
could only trivialize a ring isomorphic to
${\mathbb {Q}}(i)$
could only trivialize a ring isomorphic to
![]() ${\mathbb {Z}}[\sqrt {3}]$
. Looking over
${\mathbb {Z}}[\sqrt {3}]$
. Looking over
![]() $\mathbb F_7$
, we see that
$\mathbb F_7$
, we see that
![]() ${\mathbb {Q}}(\zeta _3)$
could only trivialize a ring isomorphic to
${\mathbb {Q}}(\zeta _3)$
could only trivialize a ring isomorphic to
![]() ${\mathbb {Z}}[\sqrt {-3}]$
. So neither trivialize
${\mathbb {Z}}[\sqrt {-3}]$
. So neither trivialize
![]() ${\mathbb {Z}}[i]$
, and we have a contradiction.
${\mathbb {Z}}[i]$
, and we have a contradiction.
So we may now assume that
![]() $G \simeq D_2$
. Arguing as above, we may also assume that L does not contain
$G \simeq D_2$
. Arguing as above, we may also assume that L does not contain
![]() ${\mathbb {Q}}(i)$
. We know A has unipotent rank 1 reduction over
${\mathbb {Q}}(i)$
. We know A has unipotent rank 1 reduction over
![]() ${\mathbb {Q}}_3$
by Lemma 7.10(c). It also has unipotent rank 1 reduction at all bad primes
${\mathbb {Q}}_3$
by Lemma 7.10(c). It also has unipotent rank 1 reduction at all bad primes
![]() $p> 3$
, by Theorem 4.11. By Proposition 4.2, the imaginary quadratic subfield
$p> 3$
, by Theorem 4.11. By Proposition 4.2, the imaginary quadratic subfield
![]() $L_1 \subset L$
that trivializes the distinguished imaginary quadratic subring of
$L_1 \subset L$
that trivializes the distinguished imaginary quadratic subring of
![]() ${\mathcal {O}}$
is unramified outside
${\mathcal {O}}$
is unramified outside
![]() $\{2\}$
. Since
$\{2\}$
. Since
![]() $L_1 \neq {\mathbb {Q}}(i)$
, we must have
$L_1 \neq {\mathbb {Q}}(i)$
, we must have
![]() $L_1 = {\mathbb {Q}}(\sqrt {-2})$
, but this field does not embed in B (which is ramified at
$L_1 = {\mathbb {Q}}(\sqrt {-2})$
, but this field does not embed in B (which is ramified at
![]() $3$
), giving a contradiction.
$3$
), giving a contradiction.
As a corollary, we are now able to finish the proofs of Theorems 1.2 and 1.3.
Proof of Theorem 1.2.
Propositions 7.9, 7.11 and 7.12 show that
![]() $\#A({\mathbb {Q}})_{ {\mathrm{tors}}} {\kern-1.5pt}<{\kern-1.5pt} 24$
. Hence,
$\#A({\mathbb {Q}})_{ {\mathrm{tors}}} {\kern-1.5pt}<{\kern-1.5pt} 24$
. Hence,
![]() $\#A({\mathbb {Q}})_{ {\mathrm{tors}}} {\kern-1.5pt}\leq{\kern-1.5pt} 18$
.
$\#A({\mathbb {Q}})_{ {\mathrm{tors}}} {\kern-1.5pt}\leq{\kern-1.5pt} 18$
.
By the results of this section and the previous one, the group
![]() $A({\mathbb {Q}})_{ {\mathrm{tors}}}$
has order
$A({\mathbb {Q}})_{ {\mathrm{tors}}}$
has order
![]() $2^i3^j \leq 18$
and does not contain any subgroup of the form
$2^i3^j \leq 18$
and does not contain any subgroup of the form
![]() ${\mathbb {Z}}/8{\mathbb {Z}}$
,
${\mathbb {Z}}/8{\mathbb {Z}}$
,
![]() ${\mathbb {Z}}/9{\mathbb {Z}}$
, or
${\mathbb {Z}}/9{\mathbb {Z}}$
, or
![]() $({\mathbb {Z}}/2{\mathbb {Z}})^4$
. We deduce the following result, which is equivalent to Theorem 1.3.
$({\mathbb {Z}}/2{\mathbb {Z}})^4$
. We deduce the following result, which is equivalent to Theorem 1.3.
Theorem 7.13. Let
![]() $A/{\mathbb {Q}}$
be an abelian surface such that
$A/{\mathbb {Q}}$
be an abelian surface such that
![]() $ {\mathrm{End}}(A_{\overline {\mathbb {Q}}})$
is a maximal order in a non-split quaternion algebra. Then
$ {\mathrm{End}}(A_{\overline {\mathbb {Q}}})$
is a maximal order in a non-split quaternion algebra. Then
![]() $A({\mathbb {Q}})_{ {\mathrm{tors}}} = A[12]({\mathbb {Q}})$
and
$A({\mathbb {Q}})_{ {\mathrm{tors}}} = A[12]({\mathbb {Q}})$
and
![]() $\#A({\mathbb {Q}})_{ {\mathrm{tors}}}\leq 18$
. Moreover,
$\#A({\mathbb {Q}})_{ {\mathrm{tors}}}\leq 18$
. Moreover,
![]() $A({\mathbb {Q}})_{ {\mathrm{tors}}}$
does not contain a subgroup isomorphic to
$A({\mathbb {Q}})_{ {\mathrm{tors}}}$
does not contain a subgroup isomorphic to
![]() $({\mathbb {Z}}/2{\mathbb {Z}})^4$
. In other words,
$({\mathbb {Z}}/2{\mathbb {Z}})^4$
. In other words,
![]() $A({\mathbb {Q}})_{ {\mathrm{tors}}}$
is isomorphic to one of the groups
$A({\mathbb {Q}})_{ {\mathrm{tors}}}$
is isomorphic to one of the groups
 $$ \begin{align*} \{1\},{\mathbb{Z}}/2,{\mathbb{Z}}/3,{\mathbb{Z}}/4, ({\mathbb{Z}}/2{\mathbb{Z}})^2, {\mathbb{Z}}/6, ({\mathbb{Z}}/2{\mathbb{Z}})^3, {\mathbb{Z}}/2{\mathbb{Z}} \times {\mathbb{Z}}/4{\mathbb{Z}},({\mathbb{Z}}/3{\mathbb{Z}})^2,\\ {\mathbb{Z}}/12, {\mathbb{Z}}/2{\mathbb{Z}}\times {\mathbb{Z}}/6{\mathbb{Z}}, ({\mathbb{Z}}/2{\mathbb{Z}})^2 \times {\mathbb{Z}}/4{\mathbb{Z}}, ({\mathbb{Z}}/4{\mathbb{Z}})^2,{\mathbb{Z}}/3{\mathbb{Z}}\times {\mathbb{Z}}/6{\mathbb{Z}}. \end{align*} $$
$$ \begin{align*} \{1\},{\mathbb{Z}}/2,{\mathbb{Z}}/3,{\mathbb{Z}}/4, ({\mathbb{Z}}/2{\mathbb{Z}})^2, {\mathbb{Z}}/6, ({\mathbb{Z}}/2{\mathbb{Z}})^3, {\mathbb{Z}}/2{\mathbb{Z}} \times {\mathbb{Z}}/4{\mathbb{Z}},({\mathbb{Z}}/3{\mathbb{Z}})^2,\\ {\mathbb{Z}}/12, {\mathbb{Z}}/2{\mathbb{Z}}\times {\mathbb{Z}}/6{\mathbb{Z}}, ({\mathbb{Z}}/2{\mathbb{Z}})^2 \times {\mathbb{Z}}/4{\mathbb{Z}}, ({\mathbb{Z}}/4{\mathbb{Z}})^2,{\mathbb{Z}}/3{\mathbb{Z}}\times {\mathbb{Z}}/6{\mathbb{Z}}. \end{align*} $$
Not all of the groups above are known to be realized as
![]() $A({\mathbb {Q}})_{ {\mathrm{tors}}}$
for some
$A({\mathbb {Q}})_{ {\mathrm{tors}}}$
for some
![]() ${\mathcal {O}}$
-
${\mathcal {O}}$
-
![]() $\mathrm {PQM}$
surface
$\mathrm {PQM}$
surface
![]() $A/{\mathbb {Q}}$
. However, all groups that have been realized (including the largest one of order 18) have been realized in the family of bielliptic Picard Prym surfaces [Reference Laga and ShnidmanLS23]. It would be interesting to systematically analyze rational points on Shimura curves of small discriminant and with small level structure, to try to find more examples. It would also be interesting to see which groups can be realized by Jacobians, which is the topic we turn to next.
$A/{\mathbb {Q}}$
. However, all groups that have been realized (including the largest one of order 18) have been realized in the family of bielliptic Picard Prym surfaces [Reference Laga and ShnidmanLS23]. It would be interesting to systematically analyze rational points on Shimura curves of small discriminant and with small level structure, to try to find more examples. It would also be interesting to see which groups can be realized by Jacobians, which is the topic we turn to next.
8 Proof of Theorem 1.6: PQM Jacobians
In this section, we consider
![]() ${\mathcal {O}}$
-
${\mathcal {O}}$
-
![]() $\mathrm {PQM}$
surfaces
$\mathrm {PQM}$
surfaces
![]() $A/{\mathbb {Q}}$
equipped with a principal polarization. Since A is geometrically simple, there exists an isomorphism of polarized surfaces
$A/{\mathbb {Q}}$
equipped with a principal polarization. Since A is geometrically simple, there exists an isomorphism of polarized surfaces
![]() $A \simeq {\mathrm{Jac}}(C)$
, where C is a smooth projective genus two curve over
$A \simeq {\mathrm{Jac}}(C)$
, where C is a smooth projective genus two curve over
![]() ${\mathbb {Q}}$
[Reference SekiguchiSek82, Theorem 3.1]. To emphasize this, we use the letter J instead of A. The goal of this section to prove some additional constraints on the torsion group
${\mathbb {Q}}$
[Reference SekiguchiSek82, Theorem 3.1]. To emphasize this, we use the letter J instead of A. The goal of this section to prove some additional constraints on the torsion group
![]() $J({\mathbb {Q}})_{ {\mathrm{tors}}}$
(i.e., we prove Theorem 1.6).
$J({\mathbb {Q}})_{ {\mathrm{tors}}}$
(i.e., we prove Theorem 1.6).
Lemma 8.1. Let M be the imaginary quadratic subfield of
![]() $ {\mathrm{End}}^0(J_{\bar {{\mathbb {Q}}}})$
corresponding to a principal polarization on J under Corollary 3.10. Then
$ {\mathrm{End}}^0(J_{\bar {{\mathbb {Q}}}})$
corresponding to a principal polarization on J under Corollary 3.10. Then
![]() $M\simeq {\mathbb {Q}}(\sqrt {-D})$
, where
$M\simeq {\mathbb {Q}}(\sqrt {-D})$
, where
![]() $D = {\mathrm{disc}}(B)$
.
$D = {\mathrm{disc}}(B)$
.
Lemma 8.2. The endomorphism field
![]() $L/{\mathbb {Q}}$
has Galois group
$L/{\mathbb {Q}}$
has Galois group
![]() $D_1 = C_2$
or
$D_1 = C_2$
or
![]() $D_2 = C_2 \times C_2$
.
$D_2 = C_2 \times C_2$
.
Proof. See [Reference Dieulefait and RotgerDR04, Theorem 3.4 A(1)].
Proposition 8.3.
![]() $\#J({\mathbb {Q}})_{ {\mathrm{tors}}} < 18$
.
$\#J({\mathbb {Q}})_{ {\mathrm{tors}}} < 18$
.
Proof. By Theorem 1.3, we need only exclude
![]() $({\mathbb {Z}}/2{\mathbb {Z}}) \times ({\mathbb {Z}}/3{\mathbb {Z}})^2$
. By Proposition 7.2(b) and Lemma 8.2, the endomorphism field of J would be a
$({\mathbb {Z}}/2{\mathbb {Z}}) \times ({\mathbb {Z}}/3{\mathbb {Z}})^2$
. By Proposition 7.2(b) and Lemma 8.2, the endomorphism field of J would be a
![]() $C_2$
-extension. In other words, J is of
$C_2$
-extension. In other words, J is of
![]() $ {\mathrm{GL}}_2$
-type, but this contradicts Theorem 1.4.
$ {\mathrm{GL}}_2$
-type, but this contradicts Theorem 1.4.
Finally, we rule out the group
![]() $({\mathbb {Z}}/2{\mathbb {Z}})^3$
from appearing in
$({\mathbb {Z}}/2{\mathbb {Z}})^3$
from appearing in
![]() $J[2]({\mathbb {Q}})$
. We have already proven this when J is of
$J[2]({\mathbb {Q}})$
. We have already proven this when J is of
![]() $ {\mathrm{GL}}_2$
-type (Proposition 5.16), so it remains to consider the case
$ {\mathrm{GL}}_2$
-type (Proposition 5.16), so it remains to consider the case
![]() $ {\mathrm{Gal}}(L/{\mathbb {Q}}) \simeq C_2 \times C_2$
. We deduce this from the following more general result.
$ {\mathrm{Gal}}(L/{\mathbb {Q}}) \simeq C_2 \times C_2$
. We deduce this from the following more general result.
Proposition 8.4. Suppose that
![]() $A/{\mathbb {Q}}$
is
$A/{\mathbb {Q}}$
is
![]() ${\mathcal {O}}$
-
${\mathcal {O}}$
-
![]() $\mathrm {PQM}$
, has
$\mathrm {PQM}$
, has
![]() $C_2\times C_2$
endomorphism field and has
$C_2\times C_2$
endomorphism field and has
![]() $A[2]({\mathbb {Q}})\simeq ({\mathbb {Z}}/2{\mathbb {Z}})^3$
. Let d be the degree of the unique primitive polarization of A. Then
$A[2]({\mathbb {Q}})\simeq ({\mathbb {Z}}/2{\mathbb {Z}})^3$
. Let d be the degree of the unique primitive polarization of A. Then
![]() $2\mid {\mathrm{disc}}(B)$
, and there exists an integer
$2\mid {\mathrm{disc}}(B)$
, and there exists an integer
![]() $m \equiv 1\ \mod 4$
such that
$m \equiv 1\ \mod 4$
such that
![]() $ {\mathrm{disc}}(B)$
and
$ {\mathrm{disc}}(B)$
and
![]() $d m$
agree up to squares. In particular, d is even and A is not a Jacobian.
$d m$
agree up to squares. In particular, d is even and A is not a Jacobian.
Proof. Let
![]() $L/{\mathbb {Q}}$
be the endomorphism field of A with Galois group G. By Lemma 5.14, there exists a
$L/{\mathbb {Q}}$
be the endomorphism field of A with Galois group G. By Lemma 5.14, there exists a
![]() ${\mathbb {Q}}$
-rational
${\mathbb {Q}}$
-rational
![]() ${\mathcal {O}}/2{\mathcal {O}}$
-generator
${\mathcal {O}}/2{\mathcal {O}}$
-generator
![]() $P\in A[2]({\mathbb {Q}})$
; hence,
$P\in A[2]({\mathbb {Q}})$
; hence,
![]() $A[2]\simeq {\mathcal {O}}/2{\mathcal {O}}$
as
$A[2]\simeq {\mathcal {O}}/2{\mathcal {O}}$
as
![]() $ {\mathrm{Gal}}_{{\mathbb {Q}}}$
-modules. Therefore, the G-action on
$ {\mathrm{Gal}}_{{\mathbb {Q}}}$
-modules. Therefore, the G-action on
![]() ${\mathcal {O}}/2{\mathcal {O}}$
has
${\mathcal {O}}/2{\mathcal {O}}$
has
![]() $({\mathbb {Z}}/2{\mathbb {Z}})^3$
fixed points. By Lemma 2.10,
$({\mathbb {Z}}/2{\mathbb {Z}})^3$
fixed points. By Lemma 2.10,
![]() $2\mid {\mathrm{disc}}(B)$
and there exist positive integers
$2\mid {\mathrm{disc}}(B)$
and there exist positive integers
![]() $m,n$
with
$m,n$
with
![]() $m\equiv 1\ \mod 4$
and
$m\equiv 1\ \mod 4$
and
![]() $n \equiv 3\ \mod 4$
such that the three
$n \equiv 3\ \mod 4$
such that the three
![]() $ {\mathrm{Gal}}_{{\mathbb {Q}}}$
-stable quadratic subfields of B are
$ {\mathrm{Gal}}_{{\mathbb {Q}}}$
-stable quadratic subfields of B are
![]() ${\mathbb {Q}}(\sqrt {-m}), {\mathbb {Q}}(\sqrt {n})$
and
${\mathbb {Q}}(\sqrt {-m}), {\mathbb {Q}}(\sqrt {n})$
and
![]() ${\mathbb {Q}}(\sqrt {mn})$
. Under Corollary 3.10, the unique primitive polarization of A corresponds to the subfield
${\mathbb {Q}}(\sqrt {mn})$
. Under Corollary 3.10, the unique primitive polarization of A corresponds to the subfield
![]() ${\mathbb {Q}}(\sqrt {-m})$
, and the relation (3.2) of Proposition 3.8 shows that
${\mathbb {Q}}(\sqrt {-m})$
, and the relation (3.2) of Proposition 3.8 shows that
![]() $d {\mathrm{disc}}(B)$
and m agree up to squares. In other words,
$d {\mathrm{disc}}(B)$
and m agree up to squares. In other words,
![]() $ {\mathrm{disc}}(B)$
and
$ {\mathrm{disc}}(B)$
and
![]() $dm$
agree up to squares. Since
$dm$
agree up to squares. Since
![]() $ {\mathrm{disc}}(B)$
is even and squarefree and m is odd, d must be even too.
$ {\mathrm{disc}}(B)$
is even and squarefree and m is odd, d must be even too.
In Table 2, we give some examples of Jacobians with nontrivial torsion subgroups and
![]() ${\mathcal {O}}_D$
-PQM, where
${\mathcal {O}}_D$
-PQM, where
![]() ${\mathcal {O}}_D$
is a maximal quaternion order of discriminant D. These were found by computing the relevant covers of Shimura curves of level 1 and their full Atkin-Lehner quotients and then substituting into the Igusa-Clebsch invariants in [Reference Lin and YangLY20, Appendix B]. The torsion and endomorphism data can be independently verified using MAGMA.Footnote
3
${\mathcal {O}}_D$
is a maximal quaternion order of discriminant D. These were found by computing the relevant covers of Shimura curves of level 1 and their full Atkin-Lehner quotients and then substituting into the Igusa-Clebsch invariants in [Reference Lin and YangLY20, Appendix B]. The torsion and endomorphism data can be independently verified using MAGMA.Footnote
3
Table 2
![]() ${\mathcal {O}}$
-
${\mathcal {O}}$
-
![]() ${\mathrm {PQM}}$
Jacobians
${\mathrm {PQM}}$
Jacobians
![]() $J/{\mathbb {Q}}$
with torsion
$J/{\mathbb {Q}}$
with torsion

Acknowledgements
We would like to thank Davide Lombardo for interesting discussions related to this project and the anonymous referee for their careful reading of the paper.
Competing interests
The authors have no competing interest to declare.
Funding Statement
Schembri and Voight were supported by a Simons Collaboration Grant (550029, to JV). Shnidman was funded by the European Research Council (ERC, CurveArithmetic, 101078157).
Data Availability Statement
Code can be found in the GitHub repository: https://github.com/ciaran-schembri/QM-Mazur.