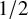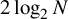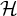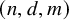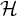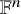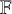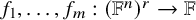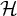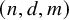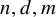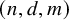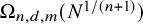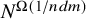1 Introduction
The quantitative version of Ramsey’s theorem, proved by Erdős and Szekeres [Reference Erdős and Szekeres23], tells us that every graph on N vertices contains a clique or an independent set of size at least
![]() $\frac {1}{2}\log _2 N$
. In 1947, Erdős [Reference Erdős17] proved that this bound is best possible up to the constant factor, as the random graph on N vertices with edge probability
$\frac {1}{2}\log _2 N$
. In 1947, Erdős [Reference Erdős17] proved that this bound is best possible up to the constant factor, as the random graph on N vertices with edge probability
![]() $1/2$
contains no clique or independent set of size larger than
$1/2$
contains no clique or independent set of size larger than
![]() $2\log _2 N$
, with high probability. Since then, it has become a central problem in graph theory to find explicit constructions of graphs having only logarithmic-sized cliques and independent sets. One natural approach to constructing such graphs is to use algebraic tools.
$2\log _2 N$
, with high probability. Since then, it has become a central problem in graph theory to find explicit constructions of graphs having only logarithmic-sized cliques and independent sets. One natural approach to constructing such graphs is to use algebraic tools.
Let
![]() $r,n,d,m$
be positive integers. Say that an r-uniform hypergraph
$r,n,d,m$
be positive integers. Say that an r-uniform hypergraph
![]() $\mathcal {H}$
is algebraic of complexity
$\mathcal {H}$
is algebraic of complexity
![]() $(n,d,m)$
if the following holds. The vertex set of
$(n,d,m)$
if the following holds. The vertex set of
![]() $\mathcal {H}$
is a subset of
$\mathcal {H}$
is a subset of
![]() $\mathbb {F}^{n}$
, where
$\mathbb {F}^{n}$
, where
![]() $\mathbb {F}$
is some field, and there exist m polynomials
$\mathbb {F}$
is some field, and there exist m polynomials
![]() $f_1,\ldots ,f_m:(\mathbb {F}^{n})^{r}\rightarrow \mathbb {F}$
of degree at most d and a Boolean formula
$f_1,\ldots ,f_m:(\mathbb {F}^{n})^{r}\rightarrow \mathbb {F}$
of degree at most d and a Boolean formula
![]() $\phi :\{\mbox {false},\mbox {true}\}^{m}\rightarrow \{\mbox {false},\mbox {true}\}$
such that
$\phi :\{\mbox {false},\mbox {true}\}^{m}\rightarrow \{\mbox {false},\mbox {true}\}$
such that
![]() $\{\mathbf {v}_1,\dots ,\mathbf {v}_r\}\in V(\mathcal {H})^{(r)}$
is an edge if and only if
$\{\mathbf {v}_1,\dots ,\mathbf {v}_r\}\in V(\mathcal {H})^{(r)}$
is an edge if and only if
That is, the edges of
![]() $\mathcal {H}$
are determined by zero patterns of polynomials
$\mathcal {H}$
are determined by zero patterns of polynomials
![]() $f_1,\ldots ,f_m$
. We assume that for
$f_1,\ldots ,f_m$
. We assume that for
![]() $\{\mathbf {v}_1,\dots ,\mathbf {v}_r\}\in V(\mathcal {H})^{(r)}$
, the left-hand side of (1.1) is invariant under the permutation of
$\{\mathbf {v}_1,\dots ,\mathbf {v}_r\}\in V(\mathcal {H})^{(r)}$
, the left-hand side of (1.1) is invariant under the permutation of
![]() $\{\mathbf {v}_1,\dots ,\mathbf {v}_r\}$
, so the edges of
$\{\mathbf {v}_1,\dots ,\mathbf {v}_r\}$
, so the edges of
![]() $\mathcal {H}$
are well defined. Also, say that an r-uniform hypergraph
$\mathcal {H}$
are well defined. Also, say that an r-uniform hypergraph
![]() $\mathcal {H}$
is strongly algebraic of complexity
$\mathcal {H}$
is strongly algebraic of complexity
![]() $(n,d)$
if there exists a single polynomial
$(n,d)$
if there exists a single polynomial
![]() $f:(\mathbb {F}^{n})^{r}\rightarrow \mathbb {F}$
of degree at most d such that
$f:(\mathbb {F}^{n})^{r}\rightarrow \mathbb {F}$
of degree at most d such that
![]() $\{\mathbf {v}_1,\dots ,\mathbf {v}_r\}\in V(\mathcal {H})^{(r)}$
is an edge if and only if
$\{\mathbf {v}_1,\dots ,\mathbf {v}_r\}\in V(\mathcal {H})^{(r)}$
is an edge if and only if
![]() $f(\mathbf {v}_1,\dots ,\mathbf {v}_r)\neq 0$
. We assume that the statement
$f(\mathbf {v}_1,\dots ,\mathbf {v}_r)\neq 0$
. We assume that the statement
![]() $f(\mathbf {v}_1,\dots ,\mathbf {v}_r)=0$
is invariant under the permutation of
$f(\mathbf {v}_1,\dots ,\mathbf {v}_r)=0$
is invariant under the permutation of
![]() $\mathbf {v}_1,\dots ,\mathbf {v}_r$
. (We could have also defined edges by
$\mathbf {v}_1,\dots ,\mathbf {v}_r$
. (We could have also defined edges by
![]() $f(\mathbf {v}_1,\dots ,\mathbf {v}_r)= 0$
, but later it will be more convenient to work with this definition.)
$f(\mathbf {v}_1,\dots ,\mathbf {v}_r)= 0$
, but later it will be more convenient to work with this definition.)
1.1 Ramsey properties of algebraic graphs
One of the best-known explicit constructions of graphs having small cliques and independent sets is due to Frankl and Wilson [Reference Frankl and Wilson24]. For a prime p, they consider the graph G whose vertex set is the
![]() $p^2-1$
element subsets of
$p^2-1$
element subsets of
![]() $[n]$
, and the sets A and B are joined by an edge if
$[n]$
, and the sets A and B are joined by an edge if
![]() $|A\cap B|\equiv -1 \pmod p$
. This graph is strongly algebraic of complexity
$|A\cap B|\equiv -1 \pmod p$
. This graph is strongly algebraic of complexity
![]() $(n,2)$
, as we can identify each set with its characteristic vector over
$(n,2)$
, as we can identify each set with its characteristic vector over
![]() $\mathbb {F}_p^{n}$
, and two such vectors
$\mathbb {F}_p^{n}$
, and two such vectors
![]() $\mathbf {v}$
and
$\mathbf {v}$
and
![]() $\mathbf {w}$
are joined by an edge if
$\mathbf {w}$
are joined by an edge if
![]() $\langle \mathbf {v},\mathbf {w}\rangle \neq -1$
. Note that G is also algebraic of complexity
$\langle \mathbf {v},\mathbf {w}\rangle \neq -1$
. Note that G is also algebraic of complexity
![]() $(p^2-1,1,(p^2-1)^2)$
over
$(p^2-1,1,(p^2-1)^2)$
over
![]() $\mathbb {R}$
, as we can identify each set of size
$\mathbb {R}$
, as we can identify each set of size
![]() $p^2-1$
with a vector listing its elements, and whether the vectors
$p^2-1$
with a vector listing its elements, and whether the vectors
![]() $\mathbf {u},\mathbf {v}\in \mathbb {R}^{p^2-1}$
are joined by an edge can be decided by the
$\mathbf {u},\mathbf {v}\in \mathbb {R}^{p^2-1}$
are joined by an edge can be decided by the
![]() $(p^2-1)^2$
linear equations
$(p^2-1)^2$
linear equations
![]() $\mathbf {u}(i)=\mathbf {v}(j)$
. The number of vertices of G is
$\mathbf {u}(i)=\mathbf {v}(j)$
. The number of vertices of G is
![]() $N=\binom {n}{p^2-1}$
, and the celebrated Frankl-Wilson theorem on restricted intersections implies that G has no clique or independent set of size larger than
$N=\binom {n}{p^2-1}$
, and the celebrated Frankl-Wilson theorem on restricted intersections implies that G has no clique or independent set of size larger than
![]() $\binom {n}{p-1}=O_p(N^{1/(p+1)})$
. Choosing
$\binom {n}{p-1}=O_p(N^{1/(p+1)})$
. Choosing
![]() $n=p^3$
, the largest clique and independent set in G has size
$n=p^3$
, the largest clique and independent set in G has size
![]() $2^{O(\sqrt {\log N\log \log N})}$
. Another candidate for a graph with good Ramsey properties is the Paley-graph. If
$2^{O(\sqrt {\log N\log \log N})}$
. Another candidate for a graph with good Ramsey properties is the Paley-graph. If
![]() $p=1\,(\mod 4)$
is a prime, the Paley-graph of order p is the graph whose vertex set is
$p=1\,(\mod 4)$
is a prime, the Paley-graph of order p is the graph whose vertex set is
![]() $\mathbb {F}_p$
, and x and y are joined by an edge if
$\mathbb {F}_p$
, and x and y are joined by an edge if
![]() $x+y$
is a quadratic residue: that is,
$x+y$
is a quadratic residue: that is,
![]() $(x+y)^{(p-1)/2}\neq -1$
. Such graphs are strongly algebraic of complexity
$(x+y)^{(p-1)/2}\neq -1$
. Such graphs are strongly algebraic of complexity
![]() $(1,(p-1)/2)$
, and it is widely believed that Paley-graphs have only polylogarithmic-sized cliques or independent sets. For the best-known explicit constructions of Ramsey graphs, see the recent works of Chattopadhyay, Zuckerman [Reference Chattopadhyay and Zuckerman7] and Cohen [Reference Cohen11].
$(1,(p-1)/2)$
, and it is widely believed that Paley-graphs have only polylogarithmic-sized cliques or independent sets. For the best-known explicit constructions of Ramsey graphs, see the recent works of Chattopadhyay, Zuckerman [Reference Chattopadhyay and Zuckerman7] and Cohen [Reference Cohen11].
The above two constructions of algebraic graphs have at least one large parameter in their complexity. In this paper, we show that this is not a coincidence, and if an algebraic graph of complexity
![]() $(n,d,m)$
has good Ramsey properties, then at least one of the parameters
$(n,d,m)$
has good Ramsey properties, then at least one of the parameters
![]() $n,d,m$
must be large. In 2001, Rónyai, Babai and Ganapathy [Reference Rónyai, Babai and Ganapathy35] considered a bipartite version of this problem. A bi-clique in a graph G is two disjoint sets
$n,d,m$
must be large. In 2001, Rónyai, Babai and Ganapathy [Reference Rónyai, Babai and Ganapathy35] considered a bipartite version of this problem. A bi-clique in a graph G is two disjoint sets
![]() $A,B\subset V(G)$
such that
$A,B\subset V(G)$
such that
![]() $|A|=|B|$
and every vertex in A is joined to every vertex in B by an edge. Note that if G is the random N-vertex graph with edge probability
$|A|=|B|$
and every vertex in A is joined to every vertex in B by an edge. Note that if G is the random N-vertex graph with edge probability
![]() $1/2$
, then the size of the largest bi-clique in both G and its complement is
$1/2$
, then the size of the largest bi-clique in both G and its complement is
![]() $O(\log N)$
, with high probability. In contrast, Rónyai, Babai and Ganapathy [Reference Rónyai, Babai and Ganapathy35] proved that if G is an algebraic graph on N vertices of complexity
$O(\log N)$
, with high probability. In contrast, Rónyai, Babai and Ganapathy [Reference Rónyai, Babai and Ganapathy35] proved that if G is an algebraic graph on N vertices of complexity
![]() $(n,d,m)$
, then either G or its complement contains a bi-clique of size at least
$(n,d,m)$
, then either G or its complement contains a bi-clique of size at least
![]() $cN^{1/(n+1)}$
, where
$cN^{1/(n+1)}$
, where
![]() $c=c(n,d,m)>0$
. However, the existence of large bi-cliques or their complements does not imply the existence of large cliques or independent sets. Our first theorem extends the result of Rónyai, Babai and Ganapathy as follows.
$c=c(n,d,m)>0$
. However, the existence of large bi-cliques or their complements does not imply the existence of large cliques or independent sets. Our first theorem extends the result of Rónyai, Babai and Ganapathy as follows.
Theorem 1.1. There exists a constant
![]() $c>0$
such that the following holds. Let
$c>0$
such that the following holds. Let
![]() $n,d,m,N$
be positive integers. Let G be an algebraic graph of complexity
$n,d,m,N$
be positive integers. Let G be an algebraic graph of complexity
![]() $(n,d,m)$
on N vertices. Then G contains either a clique or an independent set of size at least
$(n,d,m)$
on N vertices. Then G contains either a clique or an independent set of size at least
![]() $c'N^{1/\gamma }$
, where
$c'N^{1/\gamma }$
, where
![]() $c'=c'(n,d,m)>0$
and
$c'=c'(n,d,m)>0$
and
 $$ \begin{align*} \gamma=c n m\min\left\{d,\frac{n\log d}{\log n}\right\}. \end{align*} $$
$$ \begin{align*} \gamma=c n m\min\left\{d,\frac{n\log d}{\log n}\right\}. \end{align*} $$
That is, the growth of exponent
![]() $\gamma $
as a function of n is linear, while as a function of d, it is at most logarithmic.
$\gamma $
as a function of n is linear, while as a function of d, it is at most logarithmic.
The more general multicolour Ramsey problem considers edge-colourings of the complete graph
![]() $K_{N}$
with t colours and asks how small the size of the largest monochromatic clique can be. A colouring
$K_{N}$
with t colours and asks how small the size of the largest monochromatic clique can be. A colouring
![]() $c:E(K_{N})\rightarrow [t]$
of the complete graph
$c:E(K_{N})\rightarrow [t]$
of the complete graph
![]() $K_{N}$
with t colours is algebraic of complexity
$K_{N}$
with t colours is algebraic of complexity
![]() $(n,d,m)$
, if there exist m polynomials
$(n,d,m)$
, if there exist m polynomials
![]() $f_1,\dots ,f_{m}:(\mathbb {F}^{n})^{2}\rightarrow \mathbb {F}$
of degree at most d and a function
$f_1,\dots ,f_{m}:(\mathbb {F}^{n})^{2}\rightarrow \mathbb {F}$
of degree at most d and a function
![]() $\phi :\{\mbox {false},\mbox {true}\}^{m}\rightarrow [t]$
such that
$\phi :\{\mbox {false},\mbox {true}\}^{m}\rightarrow [t]$
such that
![]() $c(\mathbf {u},\mathbf {v})=\phi (\{f_{i}(\mathbf {u},\mathbf {v})=0\}_{i\in [m]})$
.
$c(\mathbf {u},\mathbf {v})=\phi (\{f_{i}(\mathbf {u},\mathbf {v})=0\}_{i\in [m]})$
.
In case
![]() $t=p+1$
, where p is prime, the best-known construction (not necessarily explicit) of a colouring of
$t=p+1$
, where p is prime, the best-known construction (not necessarily explicit) of a colouring of
![]() $K_N$
with t colours having small monochromatic cliques is a recent result of Conlon and Ferber [Reference Conlon and Ferber12], which was further improved for
$K_N$
with t colours having small monochromatic cliques is a recent result of Conlon and Ferber [Reference Conlon and Ferber12], which was further improved for
![]() $t>3$
by Wigderson [Reference Wigderson41]. In [Reference Conlon and Ferber12], it is proved that if n is a positive integer and
$t>3$
by Wigderson [Reference Wigderson41]. In [Reference Conlon and Ferber12], it is proved that if n is a positive integer and
![]() $N=2^{n/2}p^{3n/8+o(n)}$
, then
$N=2^{n/2}p^{3n/8+o(n)}$
, then
![]() $K_{N}$
has a colouring with t colours containing no monochromatic clique of size n. Surprisingly, the colouring they provide is almost algebraic. More precisely, first they consider an algebraic
$K_{N}$
has a colouring with t colours containing no monochromatic clique of size n. Surprisingly, the colouring they provide is almost algebraic. More precisely, first they consider an algebraic
![]() $(t-1)$
-colouring of complexity
$(t-1)$
-colouring of complexity
![]() $(n,2,t-1)$
, and then they recolour the last colour class with two new colours randomly.
$(n,2,t-1)$
, and then they recolour the last colour class with two new colours randomly.
We prove the extension of Theorem 1.1, which shows that in an algebraic colouring of complexity
![]() $(n,d,m)$
, at least one of the parameters
$(n,d,m)$
, at least one of the parameters
![]() $n,d,m$
must be large if we want to avoid large monochromatic cliques.
$n,d,m$
must be large if we want to avoid large monochromatic cliques.
Theorem 1.2. There exists a constant
![]() $c>0$
such that the following holds. Let
$c>0$
such that the following holds. Let
![]() $n,d,m,t,N$
be positive integers. Every algebraic colouring of
$n,d,m,t,N$
be positive integers. Every algebraic colouring of
![]() $K_{N}$
of complexity
$K_{N}$
of complexity
![]() $(n,d,m)$
with t colours contains a monochromatic clique of size at least
$(n,d,m)$
with t colours contains a monochromatic clique of size at least
![]() $c'N^{1/\gamma }$
, where
$c'N^{1/\gamma }$
, where
![]() $c'=c'(n,d,m)$
and
$c'=c'(n,d,m)$
and
 $$ \begin{align*} \gamma=c n m\min\left\{d,\frac{n\log d}{\log n}\right\}. \end{align*} $$
$$ \begin{align*} \gamma=c n m\min\left\{d,\frac{n\log d}{\log n}\right\}. \end{align*} $$
1.2 Ramsey properties of algebraic hypergraphs
The Ramsey problem for hypergraphs is also the subject of extensive study. For positive integers r and t, let
![]() $R_{r}(t)$
denote the smallest N such that any r-uniform hypergraph on N vertices contains either a clique or an independent set of size t. Erdős, Hajnal and Rado [Reference Erdős, Hajnal and Rado20] and Erdős and Rado [Reference Erdős and Rado21] proved that there exist constants
$R_{r}(t)$
denote the smallest N such that any r-uniform hypergraph on N vertices contains either a clique or an independent set of size t. Erdős, Hajnal and Rado [Reference Erdős, Hajnal and Rado20] and Erdős and Rado [Reference Erdős and Rado21] proved that there exist constants
![]() $c,C>0$
such that
$c,C>0$
such that
where the tower function
![]() $\mbox {tw}_{k}(x)$
is defined as
$\mbox {tw}_{k}(x)$
is defined as
![]() $\mbox {tw}_{1}(x)=x$
and
$\mbox {tw}_{1}(x)=x$
and
![]() $\mbox {tw}_{k}(x)=2^{\mbox {tw}_{k-1}(x)}$
. For recent developments on the topic, see also the works of Conlon, Fox and Sudakov [Reference Conlon, Fox and Sudakov14, Reference Conlon, Fox and Sudakov15].
$\mbox {tw}_{k}(x)=2^{\mbox {tw}_{k-1}(x)}$
. For recent developments on the topic, see also the works of Conlon, Fox and Sudakov [Reference Conlon, Fox and Sudakov14, Reference Conlon, Fox and Sudakov15].
Semi-algebraic graphs and hypergraphs are closely related to algebraic ones and were first studied by Alon, Pach, Pinchasi, Radoičić and Sharir [Reference Alon, Pach, Pinchasi, Radoičić and Sharir2]. An r-uniform hypergraph
![]() $\mathcal {H}$
is semi-algebraic of complexity
$\mathcal {H}$
is semi-algebraic of complexity
![]() $(n,d,m)$
if
$(n,d,m)$
if
![]() $V(\mathcal {H})\subset \mathbb {R}^{n}$
, and there exist m polynomials
$V(\mathcal {H})\subset \mathbb {R}^{n}$
, and there exist m polynomials
![]() $f_1,\dots ,f_{m}:(\mathbb {R}^{n})^{r}\rightarrow \mathbb {R}$
and a Boolean formula
$f_1,\dots ,f_{m}:(\mathbb {R}^{n})^{r}\rightarrow \mathbb {R}$
and a Boolean formula
![]() $\phi $
such that
$\phi $
such that
![]() $\{\mathbf {v}_1,\dots ,\mathbf {v}_r\}\in V(\mathcal {H})^{(r)}$
is an edge if and only if
$\{\mathbf {v}_1,\dots ,\mathbf {v}_r\}\in V(\mathcal {H})^{(r)}$
is an edge if and only if
![]() $\phi (\{f_{i}(\mathbf {v}_1,\dots ,\mathbf {v}_r)\geq 0\}_{i\in [m]})$
is true.
$\phi (\{f_{i}(\mathbf {v}_1,\dots ,\mathbf {v}_r)\geq 0\}_{i\in [m]})$
is true.
Let
![]() $R^{n,d,m}_{r}(t)$
denote the smallest N such that any r-uniform semi-algebraic hypergraph of complexity
$R^{n,d,m}_{r}(t)$
denote the smallest N such that any r-uniform semi-algebraic hypergraph of complexity
![]() $(n,d,m)$
contains either a clique or an independent set of size t. Conlon et al. [Reference Conlon, Fox, Pach, Sudakov and Suk13] studied the Ramsey problem for semi-algebraic hypergraphs and proved that there exist
$(n,d,m)$
contains either a clique or an independent set of size t. Conlon et al. [Reference Conlon, Fox, Pach, Sudakov and Suk13] studied the Ramsey problem for semi-algebraic hypergraphs and proved that there exist
![]() $c=c(r,n,m,d)>0$
and
$c=c(r,n,m,d)>0$
and
![]() $C=C(r,n,m,d)>0$
such that
$C=C(r,n,m,d)>0$
such that
In the special case of
![]() $n=1$
, Bukh and Matoušek [Reference Bukh and Matoušek6] proved that if
$n=1$
, Bukh and Matoušek [Reference Bukh and Matoušek6] proved that if
![]() $\mathcal {H}$
is an r-uniform semi-algebraic hypergraph of complexity
$\mathcal {H}$
is an r-uniform semi-algebraic hypergraph of complexity
![]() $(n,d,m)$
on N vertices, then one can always find a clique or independent set of size at least
$(n,d,m)$
on N vertices, then one can always find a clique or independent set of size at least
![]() $c'\log \log N$
, where
$c'\log \log N$
, where
![]() $c'$
may depend not only on complexity but also on the defining polynomials
$c'$
may depend not only on complexity but also on the defining polynomials
![]() $f_1,\dots ,f_m$
.
$f_1,\dots ,f_m$
.
Quite surprisingly, algebraic hypergraphs behave very differently. We show that such hypergraphs of constant complexity contain polynomial-sized cliques or independent sets.
Theorem 1.3. Let
![]() $r,n,d,m$
be positive integers. Then there exist
$r,n,d,m$
be positive integers. Then there exist
![]() $\gamma =\gamma (r,n,d,m)>0$
and
$\gamma =\gamma (r,n,d,m)>0$
and
![]() $c=c(r,n,d,m)>0$
such that the following holds. If
$c=c(r,n,d,m)>0$
such that the following holds. If
![]() $\mathcal {H}$
is an r-uniform algebraic hypergraph of complexity
$\mathcal {H}$
is an r-uniform algebraic hypergraph of complexity
![]() $(n,d,m)$
on N vertices, then
$(n,d,m)$
on N vertices, then
![]() $\mathcal {H}$
contains either a clique or an independent set of size at least
$\mathcal {H}$
contains either a clique or an independent set of size at least
![]() $cN^{1/\gamma }$
. One can choose
$cN^{1/\gamma }$
. One can choose
 $$ \begin{align*} \gamma=2r^2m\left(\binom{n+d}{d}+1\right). \end{align*} $$
$$ \begin{align*} \gamma=2r^2m\left(\binom{n+d}{d}+1\right). \end{align*} $$
Let us remark that the existence of
![]() $\gamma $
(whose dependence on
$\gamma $
(whose dependence on
![]() $n,d,m$
is not quite explicit) also follows from a model theoretic argument of Malliaris and Shelah, Theorem 3.5 in [Reference Malliaris and Shelah33] (see also [Reference Chernikov and Starchenko9] for a shorter proof). They show that if
$n,d,m$
is not quite explicit) also follows from a model theoretic argument of Malliaris and Shelah, Theorem 3.5 in [Reference Malliaris and Shelah33] (see also [Reference Chernikov and Starchenko9] for a shorter proof). They show that if
![]() $\mathcal {H}$
is a p-stable r-uniform hypergraph on N vertices (see [Reference Chernikov and Starchenko9] for definitions), then
$\mathcal {H}$
is a p-stable r-uniform hypergraph on N vertices (see [Reference Chernikov and Starchenko9] for definitions), then
![]() $\mathcal {H}$
contains either a clique or an independent set of size
$\mathcal {H}$
contains either a clique or an independent set of size
![]() $N^{\gamma }$
, where
$N^{\gamma }$
, where
![]() $\gamma =\gamma (r,p)>0$
. They also remark that r-uniform algebraic hypergraphs of complexity
$\gamma =\gamma (r,p)>0$
. They also remark that r-uniform algebraic hypergraphs of complexity
![]() $(n,d,m)$
are p-stable for some
$(n,d,m)$
are p-stable for some
![]() $p=p(r,n,d,m)$
.
$p=p(r,n,d,m)$
.
Theorem 1.3 might give the feeling that semi-algebraic graphs and hypergraphs always have stronger Ramsey-type properties than algebraic ones. In the concluding remarks, we will show that this is not always true.
1.3 Erdős-Hajnal conjecture and graphs of bounded VC-dimension
Our results are also closely related to the celebrated Erdős-Hajnal conjecture. It was proved by Erdős and Hajnal [Reference Erdős and Hajnal18] that if G is a graph on N vertices that contains no induced copy of some fixed graph H, then G contains a clique or an independent set of size at least
![]() $e^{c\sqrt {\log N}}$
, where
$e^{c\sqrt {\log N}}$
, where
![]() $c=c(H)>0$
only depends on H. They also proposed the conjecture that G contains a clique or an independent set of size at least
$c=c(H)>0$
only depends on H. They also proposed the conjecture that G contains a clique or an independent set of size at least
![]() $N^{c}$
for some
$N^{c}$
for some
![]() $c=c(H)>0$
. This conjecture, referred to as the Erdős-Hajnal conjecture, is one of the central open problems in graph theory. Say that a family of graphs
$c=c(H)>0$
. This conjecture, referred to as the Erdős-Hajnal conjecture, is one of the central open problems in graph theory. Say that a family of graphs
![]() $\mathcal {G}$
has the Erdős-Hajnal property if there exists a constant
$\mathcal {G}$
has the Erdős-Hajnal property if there exists a constant
![]() $c=c(\mathcal {G})>0$
such that every
$c=c(\mathcal {G})>0$
such that every
![]() $G\in \mathcal {G}$
contains a clique or an independent set of size at least
$G\in \mathcal {G}$
contains a clique or an independent set of size at least
![]() $|V(G)|^{c}$
. The Erdős-Hajnal conjecture is equivalent to the statement that every hereditary family of graphs has the Erdős-Hajnal property unless it is the family of all graphs. Here, we say that a family
$|V(G)|^{c}$
. The Erdős-Hajnal conjecture is equivalent to the statement that every hereditary family of graphs has the Erdős-Hajnal property unless it is the family of all graphs. Here, we say that a family
![]() $\mathcal {F}$
of r-uniform hypergraphs is hereditary if
$\mathcal {F}$
of r-uniform hypergraphs is hereditary if
![]() $\mathcal {F}$
is closed under taking induced subhypergraphs.
$\mathcal {F}$
is closed under taking induced subhypergraphs.
Although the Erdős-Hajnal conjecture is still wide open, its bipartite analogue was solved twenty years ago by Erdős, Hajnal and Pach [Reference Erdős, Hajnal and Pach19]. They proved that if an N-vertex graph G contains no induced copy of H, then either G or its complement has a bi-clique of size at least
![]() $N^{c}$
for some
$N^{c}$
for some
![]() $c=c(H)>0$
. Fox and Sudakov [Reference Fox and Sudakov28] improved this by showing that either G contains a bi-clique of size
$c=c(H)>0$
. Fox and Sudakov [Reference Fox and Sudakov28] improved this by showing that either G contains a bi-clique of size
![]() $N^{c}$
or it contains an independent set of size at least
$N^{c}$
or it contains an independent set of size at least
![]() $N^{c}$
. This suggests that finding polynomial-sized cliques or independent sets is considerably harder than finding bi-cliques or their complements.
$N^{c}$
. This suggests that finding polynomial-sized cliques or independent sets is considerably harder than finding bi-cliques or their complements.
The aforementioned bound of Erdős and Hajnal was recently improved for graphs of bounded VC-dimension. The concept of graphs of bounded VC-dimension extends both algebraic and semi-algebraic graphs of bounded complexity (as we shall see later). Let
![]() $\mathcal {F}$
be a family of subsets of a base set X. If
$\mathcal {F}$
be a family of subsets of a base set X. If
![]() $U\subset X$
, then
$U\subset X$
, then
![]() $\mathcal {F}\mid _{U}=\{A\cap U:A\in \mathcal {F}\}$
is the projection of
$\mathcal {F}\mid _{U}=\{A\cap U:A\in \mathcal {F}\}$
is the projection of
![]() $\mathcal {F}$
to U. Also, for every positive integer z, the shatter function of
$\mathcal {F}$
to U. Also, for every positive integer z, the shatter function of
![]() $\mathcal {F}$
is defined as
$\mathcal {F}$
is defined as
The VC-dimension (Vapnik-Chervonenkis dimension) of the family
![]() $\mathcal {F}$
is the largest integer n such that
$\mathcal {F}$
is the largest integer n such that
![]() $\pi _{\mathcal {F}}(n)=2^n$
: that is, there exists a set
$\pi _{\mathcal {F}}(n)=2^n$
: that is, there exists a set
![]() $U\subset X$
of size n such that
$U\subset X$
of size n such that
![]() $\mathcal {F}\mid _{U}=2^{U}$
. In this case, we say that U is shattered by
$\mathcal {F}\mid _{U}=2^{U}$
. In this case, we say that U is shattered by
![]() $\mathcal {F}$
. The VC-dimension, introduced by Vapnik and Chervonenkis [Reference Vapnik and Chervonenkis40], is one of the most widely used measures of complexity of set systems in computer science and computational geometry. We say that a graph G has VC-dimension n if the family
$\mathcal {F}$
. The VC-dimension, introduced by Vapnik and Chervonenkis [Reference Vapnik and Chervonenkis40], is one of the most widely used measures of complexity of set systems in computer science and computational geometry. We say that a graph G has VC-dimension n if the family
![]() $\{N(v):v\in V(G)\}$
has VC-dimension n. Ramsey properties of graphs of bounded VC-dimension were recently studied by Fox, Pach and Suk [Reference Fox, Pach and Suk27]. They proved that if G is a graph on N vertices of VC-dimension n, then G contains either a clique or an independent set of size
$\{N(v):v\in V(G)\}$
has VC-dimension n. Ramsey properties of graphs of bounded VC-dimension were recently studied by Fox, Pach and Suk [Reference Fox, Pach and Suk27]. They proved that if G is a graph on N vertices of VC-dimension n, then G contains either a clique or an independent set of size
![]() $e^{(\log N)^{1-o(1)}}$
, where
$e^{(\log N)^{1-o(1)}}$
, where
![]() $o(1)\rightarrow 0$
as
$o(1)\rightarrow 0$
as
![]() $N\rightarrow \infty $
while n is fixed. It is open whether this bound can be improved to
$N\rightarrow \infty $
while n is fixed. It is open whether this bound can be improved to
![]() $N^{c}$
, where
$N^{c}$
, where
![]() $c=c(n)>0$
: that is, whether the family of graphs of VC-dimension at most n has the Erdős-Hajnal property. Theorem 1.1 shows that this holds for the family of algebraic graphs of constant complexity.
$c=c(n)>0$
: that is, whether the family of graphs of VC-dimension at most n has the Erdős-Hajnal property. Theorem 1.1 shows that this holds for the family of algebraic graphs of constant complexity.
Corollary 1.4. Let
![]() $n,d,m$
be positive integers. The family of algebraic graphs of complexity
$n,d,m$
be positive integers. The family of algebraic graphs of complexity
![]() $(n,d,m)$
has the Erdős-Hajnal property.
$(n,d,m)$
has the Erdős-Hajnal property.
1.4 Regularity lemma for algebraic hypergraphs
Graph and hypergraph regularity lemmas are among the most powerful tools in combinatorics. Let
![]() $\mathcal {H}$
be an r-uniform hypergraph, and let
$\mathcal {H}$
be an r-uniform hypergraph, and let
![]() $V_{1},\dots ,V_{r}$
be disjoint subsets of
$V_{1},\dots ,V_{r}$
be disjoint subsets of
![]() $V(\mathcal {H})$
. The density of
$V(\mathcal {H})$
. The density of
![]() $(V_{1},\dots ,V_{r})$
is
$(V_{1},\dots ,V_{r})$
is
![]() $d(V_{1},\dots ,V_{r})=\frac {|E(V_{1},\dots ,V_{r})|}{|V_{1}|\dots |V_{r}|}$
, where
$d(V_{1},\dots ,V_{r})=\frac {|E(V_{1},\dots ,V_{r})|}{|V_{1}|\dots |V_{r}|}$
, where
![]() $E(V_1,\dots ,V_{r})$
is the set of edges containing exactly one vertex from each of
$E(V_1,\dots ,V_{r})$
is the set of edges containing exactly one vertex from each of
![]() $V_{1},\dots ,V_{r}$
. A partition of
$V_{1},\dots ,V_{r}$
. A partition of
![]() $V(\mathcal {H})$
into parts
$V(\mathcal {H})$
into parts
![]() $V_1,\dots ,V_{K}$
is equitable if the sizes of
$V_1,\dots ,V_{K}$
is equitable if the sizes of
![]() $V_1,\dots ,V_K$
differ by at most 1.
$V_1,\dots ,V_K$
differ by at most 1.
If G is a graph and
![]() $(U,V)$
is a pair of disjoint subsets of the vertex set, then
$(U,V)$
is a pair of disjoint subsets of the vertex set, then
![]() $(U,V)$
is
$(U,V)$
is
![]() $\epsilon $
-regular if
$\epsilon $
-regular if
![]() $|d(U,V)-d(U',V')|<\epsilon $
for every
$|d(U,V)-d(U',V')|<\epsilon $
for every
![]() $U'\subset U$
,
$U'\subset U$
,
![]() $V'\subset V$
satisfying
$V'\subset V$
satisfying
![]() $|U'|\geq \epsilon |U|$
and
$|U'|\geq \epsilon |U|$
and
![]() $|V'|\geq \epsilon |V|$
. The regularity lemma of Szemerédi [Reference Szemerédi38] states that if G is a graph and
$|V'|\geq \epsilon |V|$
. The regularity lemma of Szemerédi [Reference Szemerédi38] states that if G is a graph and
![]() $\epsilon>0$
, then G has an equitable partition into K parts with
$\epsilon>0$
, then G has an equitable partition into K parts with
![]() $1/\epsilon <K<m(\epsilon )$
, where
$1/\epsilon <K<m(\epsilon )$
, where
![]() $m(\epsilon )$
depends only on
$m(\epsilon )$
depends only on
![]() $\epsilon $
, such that all but
$\epsilon $
, such that all but
![]() $\epsilon $
fraction of the pairs of parts are
$\epsilon $
fraction of the pairs of parts are
![]() $\epsilon $
-regular. Unfortunately, the dependence of
$\epsilon $
-regular. Unfortunately, the dependence of
![]() $m(\epsilon )$
on
$m(\epsilon )$
on
![]() $1/\epsilon $
is Ackermann-type, so often, this regularity lemma is quite inefficient.
$1/\epsilon $
is Ackermann-type, so often, this regularity lemma is quite inefficient.
For certain special families of hypergraphs, one can obtain stronger results. Say that the r-tuple of sets
![]() $(V_{1},\dots ,V_{r})$
in the r-uniform hypergraph
$(V_{1},\dots ,V_{r})$
in the r-uniform hypergraph
![]() $\mathcal {H}$
is
$\mathcal {H}$
is
![]() $\epsilon $
-homogeneous if
$\epsilon $
-homogeneous if
![]() $d(V_{1},\dots ,V_{r})\leq \epsilon $
or
$d(V_{1},\dots ,V_{r})\leq \epsilon $
or
![]() $d(V_{1},\dots ,V_{r})\geq 1-\epsilon $
. Also, say that
$d(V_{1},\dots ,V_{r})\geq 1-\epsilon $
. Also, say that
![]() $(V_{1},\dots ,V_{r})$
is homogeneous if it is
$(V_{1},\dots ,V_{r})$
is homogeneous if it is
![]() $0$
-homogeneous. It was proved in the aforementioned paper of Fox, Pach and Suk [Reference Fox, Pach and Suk27] that if
$0$
-homogeneous. It was proved in the aforementioned paper of Fox, Pach and Suk [Reference Fox, Pach and Suk27] that if
![]() $\mathcal {H}$
has VC-dimension n, then
$\mathcal {H}$
has VC-dimension n, then
![]() $\mathcal {H}$
has an equitable partition into K parts with
$\mathcal {H}$
has an equitable partition into K parts with
![]() $1/\epsilon <K<O_{r,n}((1/\epsilon )^{2n+1})$
such that all but at most
$1/\epsilon <K<O_{r,n}((1/\epsilon )^{2n+1})$
such that all but at most
![]() $\epsilon $
fraction of the r-tuples of parts are
$\epsilon $
fraction of the r-tuples of parts are
![]() $\epsilon $
-homogeneous. The authors refer to this as the ‘ultra-strong regularity lemma’, and their bound on the number of parts has an exponent that is optimal up to an absolute constant factor. This result improves on a sequence of earlier regularity lemmas for this class of hypergraphs [Reference Alon, Fischer and Newman1, Reference Chernikov and Starchenko8, Reference Lovász and Szegedy31]. One can do even better for semi-algebraic graphs. Fox, Pach and Suk [Reference Fox, Pach and Suk26] also proved that if
$\epsilon $
-homogeneous. The authors refer to this as the ‘ultra-strong regularity lemma’, and their bound on the number of parts has an exponent that is optimal up to an absolute constant factor. This result improves on a sequence of earlier regularity lemmas for this class of hypergraphs [Reference Alon, Fischer and Newman1, Reference Chernikov and Starchenko8, Reference Lovász and Szegedy31]. One can do even better for semi-algebraic graphs. Fox, Pach and Suk [Reference Fox, Pach and Suk26] also proved that if
![]() $\mathcal {H}$
is semi-algebraic of constant complexity, then
$\mathcal {H}$
is semi-algebraic of constant complexity, then
![]() $\mathcal {H}$
has an equitable partition into K parts, where K is bounded by a polynomial of
$\mathcal {H}$
has an equitable partition into K parts, where K is bounded by a polynomial of
![]() $\epsilon $
depending only on the complexity, such that all but at most
$\epsilon $
depending only on the complexity, such that all but at most
![]() $\epsilon $
fraction of the r-tuples of parts are homogeneous.
$\epsilon $
fraction of the r-tuples of parts are homogeneous.
But what can we say about algebraic hypergraphs? It turns out that it is too much to ask for a partition in which all but a small fraction of r-tuples of parts are homogeneous. Indeed, if this were true, it would imply that if G is an algebraic graph of complexity
![]() $(n,d,m)$
, then either G or its complement contains a bi-clique of linear size. In the concluding remarks, we present an example showing that this does not hold in general. On the other hand, Chernikov and Starchenko [Reference Chernikov and Starchenko8] showed (see Theorem 4.13) that if a hypergraph
$(n,d,m)$
, then either G or its complement contains a bi-clique of linear size. In the concluding remarks, we present an example showing that this does not hold in general. On the other hand, Chernikov and Starchenko [Reference Chernikov and Starchenko8] showed (see Theorem 4.13) that if a hypergraph
![]() $\mathcal {H}$
is p-stable, then
$\mathcal {H}$
is p-stable, then
![]() $\mathcal {H}$
has an equitable partition into K parts with
$\mathcal {H}$
has an equitable partition into K parts with
![]() $1/\epsilon <K<O_{p}((1/\epsilon )^{p+1})$
such that all r-tuples of parts are
$1/\epsilon <K<O_{p}((1/\epsilon )^{p+1})$
such that all r-tuples of parts are
![]() $\epsilon $
-homogeneous. Here, we will prove the following interesting regularity type lemma for strongly algebraic hypergraphs, which shows that strongly algebraic hypergraphs are halfway between semi-algebraic hypergraphs and hypergraphs of bounded VC-dimension.
$\epsilon $
-homogeneous. Here, we will prove the following interesting regularity type lemma for strongly algebraic hypergraphs, which shows that strongly algebraic hypergraphs are halfway between semi-algebraic hypergraphs and hypergraphs of bounded VC-dimension.
Theorem 1.5. Let
![]() $r,n,d$
be positive integers. Then there exists
$r,n,d$
be positive integers. Then there exists
![]() $c=c(r,n,d)$
such that the following holds. Let
$c=c(r,n,d)$
such that the following holds. Let
![]() $\mathcal {H}$
be a strongly algebraic r-uniform hypergraph of complexity
$\mathcal {H}$
be a strongly algebraic r-uniform hypergraph of complexity
![]() $(n,d)$
. Then
$(n,d)$
. Then
![]() $V(\mathcal {H})$
has an equitable partition
$V(\mathcal {H})$
has an equitable partition
![]() $V_1,\dots ,V_{K}$
with
$V_1,\dots ,V_{K}$
with
![]() $8/\epsilon <K<c(1/\epsilon )^{r!(2n+1)}$
parts such that all but at most
$8/\epsilon <K<c(1/\epsilon )^{r!(2n+1)}$
parts such that all but at most
![]() $\epsilon $
-fraction of the r-tuples of parts are either empty or have density at least
$\epsilon $
-fraction of the r-tuples of parts are either empty or have density at least
![]() $1-\epsilon $
.
$1-\epsilon $
.
Another regularity lemma in an algebraic setting was proved by Tao [Reference Tao39]. This lemma applies to graphs and hypergraphs whose vertices and edges are both defined by algebraic varieties of bounded complexity over some field
![]() $\mathbb {F}$
and, more generally, are definable sets of bounded complexity (see [Reference Tao39] for details). For example, the above-mentioned Paley-graph falls into this category. Tao’s lemma shows that, remarkably, one can find an
$\mathbb {F}$
and, more generally, are definable sets of bounded complexity (see [Reference Tao39] for details). For example, the above-mentioned Paley-graph falls into this category. Tao’s lemma shows that, remarkably, one can find an
![]() $\epsilon $
-regular partition of the vertices of the graph or hypergraph in question into a constant number of (definable) parts, where
$\epsilon $
-regular partition of the vertices of the graph or hypergraph in question into a constant number of (definable) parts, where
![]() $\epsilon \approx |\mathbb {F}|^{-1/4}$
. Interestingly, this seems quite different from our regularity lemma for strongly algebraic hypergraphs.
$\epsilon \approx |\mathbb {F}|^{-1/4}$
. Interestingly, this seems quite different from our regularity lemma for strongly algebraic hypergraphs.
Let us present an application of Theorem 1.5 to the Ramsey problem for strongly algebraic hypergraphs. The following theorem roughly tells us that finding an independent set of size s for some constant
![]() $s=s(r,n,d)$
in a strongly algebraic r-uniform hypergraph of complexity
$s=s(r,n,d)$
in a strongly algebraic r-uniform hypergraph of complexity
![]() $(n,d)$
is almost as ‘costly’ as finding a very large independent set. This suggests that the exponent in Theorem 1.3 can be improved, and in order to do so, it is enough to show that every such hypergraph contains either an independent set of size s or a large clique.
$(n,d)$
is almost as ‘costly’ as finding a very large independent set. This suggests that the exponent in Theorem 1.3 can be improved, and in order to do so, it is enough to show that every such hypergraph contains either an independent set of size s or a large clique.
Theorem 1.6. Let
![]() $r,n,d$
be positive integers,
$r,n,d$
be positive integers,
![]() $s=(r-1)\binom {n+d}{d}+1$
and
$s=(r-1)\binom {n+d}{d}+1$
and
![]() $c,\alpha ,\beta>0$
. Let
$c,\alpha ,\beta>0$
. Let
![]() $\mathcal {F}$
be a hereditary family of strongly algebraic r-uniform hypergraphs of complexity
$\mathcal {F}$
be a hereditary family of strongly algebraic r-uniform hypergraphs of complexity
![]() $(n,d)$
. Suppose that each
$(n,d)$
. Suppose that each
![]() $\mathcal {H}\in \mathcal {F}$
on N vertices contains either a clique of size at least
$\mathcal {H}\in \mathcal {F}$
on N vertices contains either a clique of size at least
![]() $cN^{\alpha }$
or an independent set of size s. Then every
$cN^{\alpha }$
or an independent set of size s. Then every
![]() $\mathcal {H}\in \mathcal {F}$
on N vertices contains either a clique of size
$\mathcal {H}\in \mathcal {F}$
on N vertices contains either a clique of size
![]() $c_1N^{d\alpha \beta /n}$
or an independent set of size at least
$c_1N^{d\alpha \beta /n}$
or an independent set of size at least
![]() $c_2N^{1-\beta }$
, where
$c_2N^{1-\beta }$
, where
![]() $c_1,c_2>0$
depend only on the parameters
$c_1,c_2>0$
depend only on the parameters
![]() $r,n,d,c,\alpha ,\beta $
and
$r,n,d,c,\alpha ,\beta $
and
![]() $d=d(r)>0$
depends only on r.
$d=d(r)>0$
depends only on r.
Our paper is organised as follows. In the next section, we introduce our notation and prepare several tools to prove our theorems. We also present the proof of Theorem 1.3 in this section. Then, in Section 3, we present the proof of Theorems 1.1 and 1.2. We continue with the proof of Theorem 1.5 in Section 4 and present the proof of Theorem 1.6 in Section 5. Finally, we provide some discussion in the concluding remarks.
2 Properties of algebraic hypergraphs
In this section, we prepare some tools for the proofs of our main results, and we prove Theorem 1.3. First, let us introduce the notation we use throughout the paper, which is mostly conventional.
2.1 Notation and preliminaries
If V is some set and s is a positive integer,
![]() $V^{(s)}$
denotes the family of s element subsets of V. Let
$V^{(s)}$
denotes the family of s element subsets of V. Let
![]() $\mathcal {H}$
be an r-uniform hypergraph. The density of
$\mathcal {H}$
be an r-uniform hypergraph. The density of
![]() $\mathcal {H}$
is
$\mathcal {H}$
is
![]() $d(\mathcal {H})=|E(\mathcal {H})|/\binom {|V(\mathcal {H})|}{r}$
. If
$d(\mathcal {H})=|E(\mathcal {H})|/\binom {|V(\mathcal {H})|}{r}$
. If
![]() $X\in V(\mathcal {H})^{(s)}$
for some
$X\in V(\mathcal {H})^{(s)}$
for some
![]() $1\leq s\leq r-1$
, then
$1\leq s\leq r-1$
, then
is the neighbourhood of X.
The following is a well-known result that tells us hypergraphs of density very close to 1 contain large cliques.
Lemma 2.1. Let N be a positive integer,
![]() $\frac {1}{N^{r-1}}<\alpha <\frac {1}{2}$
, and let
$\frac {1}{N^{r-1}}<\alpha <\frac {1}{2}$
, and let
![]() $\mathcal {H}$
be an r-uniform hypergraph on N vertices of density at least
$\mathcal {H}$
be an r-uniform hypergraph on N vertices of density at least
![]() $1-\alpha $
. Then
$1-\alpha $
. Then
![]() $\mathcal {H}$
contains a clique of size at least
$\mathcal {H}$
contains a clique of size at least
![]() $\frac {1}{4}(1/\alpha )^{1/(r-1)}$
.
$\frac {1}{4}(1/\alpha )^{1/(r-1)}$
.
Proof. Select each vertex of
![]() $\mathcal {H}$
with probability
$\mathcal {H}$
with probability
![]() $p=(2N\alpha ^{1/(r-1)})^{-1}<1$
, and let U be the set of selected vertices. Let X be the number of non-edges spanned by U. Then
$p=(2N\alpha ^{1/(r-1)})^{-1}<1$
, and let U be the set of selected vertices. Let X be the number of non-edges spanned by U. Then
![]() $\mathbb {E}(X)\leq \alpha p^{r}\binom {N}{r}$
. Delete a vertex of each non-edge in
$\mathbb {E}(X)\leq \alpha p^{r}\binom {N}{r}$
. Delete a vertex of each non-edge in
![]() $\mathcal {H}[U]$
, and let V be the resulting set; then V is a clique. We have
$\mathcal {H}[U]$
, and let V be the resulting set; then V is a clique. We have
 $$ \begin{align*}\mathbb{E}(|V|)\geq \mathbb{E}(|U|-X)=pN-\alpha p^{r}\binom{N}{r}\geq \frac{pN}{2}\geq \frac{1}{4}\left(\frac{1}{\alpha}\right)^{1/(r-1)}, \end{align*} $$
$$ \begin{align*}\mathbb{E}(|V|)\geq \mathbb{E}(|U|-X)=pN-\alpha p^{r}\binom{N}{r}\geq \frac{pN}{2}\geq \frac{1}{4}\left(\frac{1}{\alpha}\right)^{1/(r-1)}, \end{align*} $$
where the last two inequalities hold by the choice of p. Hence, there exists a choice for U such that
![]() $|V|\geq \frac {1}{4}(1/\alpha )^{1/(r-1)}$
.
$|V|\geq \frac {1}{4}(1/\alpha )^{1/(r-1)}$
.
To describe hypergraphs defined by a single polynomial, let us introduce directed hypergraphs. A directed r-uniform hypergraph (or r-uniform dihypergraph) is a pair
![]() $\mathcal {H}=(V,E)$
, where V is the set of vertices and E is a set of (ordered) r-tuples of distinct elements of V, called edges. Given an r-element subset f of V, an orientation of f is an r-tuple containing the elements of f. In a directed r-uniform hypergraph, we allow multiple orientations of the same r-element set. Say that an r-element set X of a dihypergraph
$\mathcal {H}=(V,E)$
, where V is the set of vertices and E is a set of (ordered) r-tuples of distinct elements of V, called edges. Given an r-element subset f of V, an orientation of f is an r-tuple containing the elements of f. In a directed r-uniform hypergraph, we allow multiple orientations of the same r-element set. Say that an r-element set X of a dihypergraph
![]() $\mathcal {H}$
is complete if all
$\mathcal {H}$
is complete if all
![]() $r!$
orientations of X are edges. Let
$r!$
orientations of X are edges. Let
![]() $[\mathcal {H}]$
be the hypergraph formed by the complete edges of
$[\mathcal {H}]$
be the hypergraph formed by the complete edges of
![]() $\mathcal {H}$
. A clique in an r-uniform directed hypergraph
$\mathcal {H}$
. A clique in an r-uniform directed hypergraph
![]() $\mathcal {H}$
is a clique in
$\mathcal {H}$
is a clique in
![]() $[\mathcal {H}]$
. Also, an independent set of
$[\mathcal {H}]$
. Also, an independent set of
![]() $\mathcal {H}$
is a set of vertices in which no r-tuple forms an edge.
$\mathcal {H}$
is a set of vertices in which no r-tuple forms an edge.
Given
![]() $I\subset [r]$
and an
$I\subset [r]$
and an
![]() $|I|$
-tuple of vertices
$|I|$
-tuple of vertices
![]() $X=(v_i)_{i\in I}$
, the I-neighbourhood of X is
$X=(v_i)_{i\in I}$
, the I-neighbourhood of X is
![]() $N_{I}(X)=N_{\mathcal {H},I}(X)=\{(v_j)_{j\in [r]\setminus I}\in V^{r-|I|}:(v_1,\dots ,v_r)\in E\}$
. Note that the vertices of X appear in the corresponding directed edges in the order given by I. In the case of directed graphs, we write simply
$N_{I}(X)=N_{\mathcal {H},I}(X)=\{(v_j)_{j\in [r]\setminus I}\in V^{r-|I|}:(v_1,\dots ,v_r)\in E\}$
. Note that the vertices of X appear in the corresponding directed edges in the order given by I. In the case of directed graphs, we write simply
![]() $N^{+}(v)$
and
$N^{+}(v)$
and
![]() $N^{-}(v)$
for the out- and in-neighbourhood of v, respectively. If X is an r-tuple and
$N^{-}(v)$
for the out- and in-neighbourhood of v, respectively. If X is an r-tuple and
![]() $k\in [r]$
, then
$k\in [r]$
, then
![]() $X(k)$
is the kth element of X and
$X(k)$
is the kth element of X and
![]() $\hat {X}(k)=(X(1),\dots ,X(k-1),X(k+1),\dots ,X(r)).$
$\hat {X}(k)=(X(1),\dots ,X(k-1),X(k+1),\dots ,X(r)).$
2.2 Linear algebra
In this section, we collect some facts from linear algebra and introduce the flattening rank of tensors. Let
![]() $T:A_1\times \dots \times A_r\rightarrow \mathbb {F}$
be an r-dimensional tensor, where
$T:A_1\times \dots \times A_r\rightarrow \mathbb {F}$
be an r-dimensional tensor, where
![]() $A_1,\dots ,A_r$
are finite sets and
$A_1,\dots ,A_r$
are finite sets and
![]() $\mathbb {F}$
is a field. For
$\mathbb {F}$
is a field. For
![]() $i\in [r]$
, the i-flattening rank of T, denoted by
$i\in [r]$
, the i-flattening rank of T, denoted by
![]() $\operatorname {\mathrm {frank}}_{i}(T)$
, is defined as follows. Let
$\operatorname {\mathrm {frank}}_{i}(T)$
, is defined as follows. Let
![]() $B_{i}=A_1\times \dots \times A_{i-1}\times A_{i+1}\times \dots \times A_{r}$
; then T can be viewed as a matrix M with rows indexed by
$B_{i}=A_1\times \dots \times A_{i-1}\times A_{i+1}\times \dots \times A_{r}$
; then T can be viewed as a matrix M with rows indexed by
![]() $A_{i}$
and columns indexed by
$A_{i}$
and columns indexed by
![]() $B_{i}$
. Then
$B_{i}$
. Then
![]() $\operatorname {\mathrm {frank}}_{i}(T):=\mbox {rank}(M)$
. Note that
$\operatorname {\mathrm {frank}}_{i}(T):=\mbox {rank}(M)$
. Note that
![]() $\operatorname {\mathrm {frank}}_{i}(T)=1$
if and only if
$\operatorname {\mathrm {frank}}_{i}(T)=1$
if and only if
![]() $T\neq 0$
, and there exist two functions
$T\neq 0$
, and there exist two functions
![]() $f:A_{i}\rightarrow \mathbb {F}$
and
$f:A_{i}\rightarrow \mathbb {F}$
and
![]() $g:B_i\rightarrow \mathbb {F}$
such that
$g:B_i\rightarrow \mathbb {F}$
such that
![]() $T(a_1,\dots ,a_r)=f(a_i)g(a_1,\dots ,a_{i-1},a_{i+1},\dots ,a_{r})$
. Also, the i-flattening rank of T is the minimum t such that T is the sum of t tensors of i-flattening rank 1. Equivalently,
$T(a_1,\dots ,a_r)=f(a_i)g(a_1,\dots ,a_{i-1},a_{i+1},\dots ,a_{r})$
. Also, the i-flattening rank of T is the minimum t such that T is the sum of t tensors of i-flattening rank 1. Equivalently,
![]() $\operatorname {\mathrm {frank}}_{i}(T)$
is the dimension of the vector space generated by the rows of T in the ith dimension.
$\operatorname {\mathrm {frank}}_{i}(T)$
is the dimension of the vector space generated by the rows of T in the ith dimension.
It is easy to see that the i-flattening rank satisfies the usual properties of rank. It is subadditive, and if
![]() $T'$
is a subtensor of T, then
$T'$
is a subtensor of T, then
![]() $\operatorname {\mathrm {frank}}_i(T')\leq \operatorname {\mathrm {frank}}_i(T)$
. Here,
$\operatorname {\mathrm {frank}}_i(T')\leq \operatorname {\mathrm {frank}}_i(T)$
. Here,
![]() $T':A_1'\times \dots \times A_{r}'\rightarrow \mathbb {F}$
is a subtensor of
$T':A_1'\times \dots \times A_{r}'\rightarrow \mathbb {F}$
is a subtensor of
![]() $T:A_1\times \dots \times A_{r}\rightarrow \mathbb {F}$
if
$T:A_1\times \dots \times A_{r}\rightarrow \mathbb {F}$
if
![]() $A_{i}'\subset A_{i}$
for
$A_{i}'\subset A_{i}$
for
![]() $i\in [r]$
and
$i\in [r]$
and
![]() $T'(a_1,\dots ,a_r)=T(a_1,\dots ,a_r)$
for
$T'(a_1,\dots ,a_r)=T(a_1,\dots ,a_r)$
for
![]() $(a_1,\dots ,a_{r})\in A_{1}'\times \dots \times A_{r}'$
. A detailed discussion of i-flattening rank and its combinatorial applications can be found in [Reference Munhá Correia, Sudakov and Tomon34]. In this paper, we use the following property of the i-flattening rank of tensors defined by polynomials.
$(a_1,\dots ,a_{r})\in A_{1}'\times \dots \times A_{r}'$
. A detailed discussion of i-flattening rank and its combinatorial applications can be found in [Reference Munhá Correia, Sudakov and Tomon34]. In this paper, we use the following property of the i-flattening rank of tensors defined by polynomials.
Lemma 2.2. Let
![]() $f:(\mathbb {F}^{n})^{r}\rightarrow \mathbb {F}$
be a polynomial of degree at most d, and let
$f:(\mathbb {F}^{n})^{r}\rightarrow \mathbb {F}$
be a polynomial of degree at most d, and let
![]() $V\subset \mathbb {F}^{n}$
. Define the r-dimensional tensor
$V\subset \mathbb {F}^{n}$
. Define the r-dimensional tensor
![]() $T:V^{r}\rightarrow \mathbb {F}$
such that
$T:V^{r}\rightarrow \mathbb {F}$
such that
![]() $T(X):=f(X)$
for
$T(X):=f(X)$
for
![]() $X\in V^{r}$
. Then
$X\in V^{r}$
. Then
![]() $\operatorname {\mathrm {frank}}_{i}(T)\leq \binom {n+d}{d}$
for
$\operatorname {\mathrm {frank}}_{i}(T)\leq \binom {n+d}{d}$
for
![]() $i\in [r]$
.
$i\in [r]$
.
Proof. Let
![]() $\Lambda =\{\mathbf {\alpha }\in \mathbb {N}^{n}:\sum _{i=1}^{n}\mathbf {\alpha }(i)\leq d\}$
. For
$\Lambda =\{\mathbf {\alpha }\in \mathbb {N}^{n}:\sum _{i=1}^{n}\mathbf {\alpha }(i)\leq d\}$
. For
![]() $\mathbf {x}\in \mathbb {F}^{n}$
and
$\mathbf {x}\in \mathbb {F}^{n}$
and
![]() $\alpha \in \mathbb {N}^{n}$
, let
$\alpha \in \mathbb {N}^{n}$
, let
![]() $h_{\alpha }(\mathbf {x})=\mathbf {x}(1)^{\mathbf {\alpha }(1)}\dots \mathbf {x}(n)^{\mathbf {\alpha }(n)}$
. Then the polynomial f can be written as
$h_{\alpha }(\mathbf {x})=\mathbf {x}(1)^{\mathbf {\alpha }(1)}\dots \mathbf {x}(n)^{\mathbf {\alpha }(n)}$
. Then the polynomial f can be written as
where
![]() $X\in V^{r}$
is considered as an r-tuple of elements of V, and
$X\in V^{r}$
is considered as an r-tuple of elements of V, and
![]() $g_{\mathbf {\alpha }}:\mathbb {F}^{(r-1)n}\rightarrow \mathbb {F}$
is some polynomial for
$g_{\mathbf {\alpha }}:\mathbb {F}^{(r-1)n}\rightarrow \mathbb {F}$
is some polynomial for
![]() $\alpha \in \Lambda $
. But then T is the sum of
$\alpha \in \Lambda $
. But then T is the sum of
![]() $|\Lambda |\leq \binom {n+d}{d}$
tensors of i-flattening rank 1, so
$|\Lambda |\leq \binom {n+d}{d}$
tensors of i-flattening rank 1, so
![]() $\operatorname {\mathrm {frank}}_i(T)\leq \binom {n+d}{d}$
.
$\operatorname {\mathrm {frank}}_i(T)\leq \binom {n+d}{d}$
.
We use this lemma in the next section to define a family of forbidden directed subhypergraphs in dihypergraphs defined by a single polynomial. Working with the flattening rank (versus matrix rank) is not necessary for this application, but later (see Section 5) we will exploit more of its properties.
2.3 Forbidden subhypergraphs
In this section, we show that algebraic dihypergraphs defined by a single polynomial avoid the following simple family of dihypergraphs.
Definition 1. For positive integers
![]() $r,s,k$
with
$r,s,k$
with
![]() $k\in [r]$
, let
$k\in [r]$
, let
![]() $\mathcal {M}(r,s,k)$
be the family of r-uniform dihypergraphs
$\mathcal {M}(r,s,k)$
be the family of r-uniform dihypergraphs
![]() $\mathcal {M}$
having the following form. There are given, not all necessarily distinct, vertices
$\mathcal {M}$
having the following form. There are given, not all necessarily distinct, vertices
![]() $u_{i,j}$
for
$u_{i,j}$
for
![]() $(i,j)\in [s]\times [r]$
forming the vertex set of
$(i,j)\in [s]\times [r]$
forming the vertex set of
![]() $\mathcal {M}$
. For
$\mathcal {M}$
. For
![]() $(i,i')\in [s]\times [s]$
, let
$(i,i')\in [s]\times [s]$
, let
![]() $X_{i,i'}$
be the r-tuple (of distinct) vertices satisfying
$X_{i,i'}$
be the r-tuple (of distinct) vertices satisfying
![]() $X_{i,i'}(j)=u_{i,j}$
for
$X_{i,i'}(j)=u_{i,j}$
for
![]() $j\in [r]\setminus \{k\}$
and
$j\in [r]\setminus \{k\}$
and
![]() $X_{i,i'}(k)=u_{i',k}$
. Then
$X_{i,i'}(k)=u_{i',k}$
. Then
![]() $X_{i,i}$
is an edge of
$X_{i,i}$
is an edge of
![]() $\mathcal {M}$
for
$\mathcal {M}$
for
![]() $i\in [s]$
, and
$i\in [s]$
, and
![]() $X_{i,i'}$
is not an edge for
$X_{i,i'}$
is not an edge for
![]() $1\leq i<i'\leq s$
. The rest of the r-tuples can be either edges or non-edges. Also, let
$1\leq i<i'\leq s$
. The rest of the r-tuples can be either edges or non-edges. Also, let
![]() $\mathcal {M}(r,s)$
be the union of the families
$\mathcal {M}(r,s)$
be the union of the families
![]() $\mathcal {M}(r,s,k)$
for
$\mathcal {M}(r,s,k)$
for
![]() $k\in [r]$
.
$k\in [r]$
.
Lemma 2.3. Let
![]() $\mathcal {H}$
be a strongly algebraic r-uniform dihypergraph of complexity
$\mathcal {H}$
be a strongly algebraic r-uniform dihypergraph of complexity
![]() $(n,d)$
. Then
$(n,d)$
. Then
![]() $\mathcal {H}$
contains no member of
$\mathcal {H}$
contains no member of
![]() $\mathcal {M}(r,s)$
for
$\mathcal {M}(r,s)$
for
![]() $s>\binom {n+d}{d}$
.
$s>\binom {n+d}{d}$
.
Proof. Let
![]() $V=V(\mathcal {H})$
, and let f be the polynomial defining
$V=V(\mathcal {H})$
, and let f be the polynomial defining
![]() $\mathcal {H}$
. Define the tensor
$\mathcal {H}$
. Define the tensor
![]() $T:V^{r}\rightarrow \mathbb {F}$
such that for
$T:V^{r}\rightarrow \mathbb {F}$
such that for
![]() $X\in V^{r}$
,
$X\in V^{r}$
,
![]() $T(X):=f(X)$
. For
$T(X):=f(X)$
. For
![]() $k\in [r]$
, let
$k\in [r]$
, let
![]() $M_{k}:V\times V^{r-1}\rightarrow \mathbb {F}$
be the matrix defined as
$M_{k}:V\times V^{r-1}\rightarrow \mathbb {F}$
be the matrix defined as
![]() $M_{k}(X(k),\hat {X}(k)):=T(X)$
for
$M_{k}(X(k),\hat {X}(k)):=T(X)$
for
![]() $X\in V^{r}$
. Then by Lemma 2.2, we have
$X\in V^{r}$
. Then by Lemma 2.2, we have
![]() $\mbox {rank}(M_{k})=\operatorname {\mathrm {frank}}_{k}(T)\leq \binom {n+d}{d}$
.
$\mbox {rank}(M_{k})=\operatorname {\mathrm {frank}}_{k}(T)\leq \binom {n+d}{d}$
.
Let
![]() $s>\binom {n+d}{n}$
, and suppose that
$s>\binom {n+d}{n}$
, and suppose that
![]() $\mathcal {H}$
contains a copy of a member of
$\mathcal {H}$
contains a copy of a member of
![]() $\mathcal {M}(r,s,k)$
for some
$\mathcal {M}(r,s,k)$
for some
![]() $k\in [r]$
. Then there exist
$k\in [r]$
. Then there exist
![]() $\mathbf {u}_{i,j}\in V$
for
$\mathbf {u}_{i,j}\in V$
for
![]() $(i,j)\in [s]\times [r]$
such that the following holds. For
$(i,j)\in [s]\times [r]$
such that the following holds. For
![]() $(i,i')\in [s]\times [s]$
, define
$(i,i')\in [s]\times [s]$
, define
![]() $U_{i,i'}\in V^{r}$
such that
$U_{i,i'}\in V^{r}$
such that
![]() $U_{i,i'}(j)=\mathbf {u}_{i,j}$
for
$U_{i,i'}(j)=\mathbf {u}_{i,j}$
for
![]() $j\neq k$
, and
$j\neq k$
, and
![]() $U_{i,i'}(k)=\mathbf {u}_{i',k}$
. Then
$U_{i,i'}(k)=\mathbf {u}_{i',k}$
. Then
![]() $f(U_{i,i})\neq 0$
for
$f(U_{i,i})\neq 0$
for
![]() $i\in [s]$
and
$i\in [s]$
and
![]() $f(U_{i,i'})=0$
if
$f(U_{i,i'})=0$
if
![]() $1\leq i< i'\leq s$
. But then the submatrix of
$1\leq i< i'\leq s$
. But then the submatrix of
![]() $M_{k}$
induced by the rows
$M_{k}$
induced by the rows
![]() $\mathbf {u}_{1,k},\dots ,\mathbf {u}_{s,k}$
and columns
$\mathbf {u}_{1,k},\dots ,\mathbf {u}_{s,k}$
and columns
![]() $\hat {U}_{1,1}(k),\dots ,\hat {U}_{s,s}(k)$
is an upper-triangular matrix, which has full rank. Therefore,
$\hat {U}_{1,1}(k),\dots ,\hat {U}_{s,s}(k)$
is an upper-triangular matrix, which has full rank. Therefore,
![]() $\mbox {rank}(A)\geq s$
, which is a contradiction.
$\mbox {rank}(A)\geq s$
, which is a contradiction.
Lemma 2.4. Let
![]() $\mathcal {H}_1,\dots ,\mathcal {H}_m$
be r-uniform dihypergraphs on an N element vertex set V. If
$\mathcal {H}_1,\dots ,\mathcal {H}_m$
be r-uniform dihypergraphs on an N element vertex set V. If
![]() $\mathcal {H}_{i}$
contains no member of
$\mathcal {H}_{i}$
contains no member of
![]() $\mathcal {M}(r,s)$
for
$\mathcal {M}(r,s)$
for
![]() $i\in [m]$
, then there exists
$i\in [m]$
, then there exists
![]() $U\subset V$
such that
$U\subset V$
such that
![]() $\mathcal {H}_{i}[U]$
is either a clique or an independent set for
$\mathcal {H}_{i}[U]$
is either a clique or an independent set for
![]() $i\in [m]$
, and
$i\in [m]$
, and
![]() $|U|\geq cN^{1/2r^2ms}$
, where
$|U|\geq cN^{1/2r^2ms}$
, where
![]() $c=c(r,s,m)>0$
depends only on
$c=c(r,s,m)>0$
depends only on
![]() $r,s,m$
.
$r,s,m$
.
Proof. We prepare the proof with the following claims.
Claim 2.5. Let
![]() $\mathcal {G}$
be a nonempty r-uniform hypergraph on
$\mathcal {G}$
be a nonempty r-uniform hypergraph on
![]() $M\geq 100r$
vertices, and suppose that the density of
$M\geq 100r$
vertices, and suppose that the density of
![]() $\mathcal {G}$
is at most
$\mathcal {G}$
is at most
![]() $1-\alpha $
. Then there exists
$1-\alpha $
. Then there exists
![]() $X\in V(\mathcal {G})^{(r-1)}$
such that
$X\in V(\mathcal {G})^{(r-1)}$
such that
![]() $1\leq |N(X)|\leq (1-\alpha /2r)M$
.
$1\leq |N(X)|\leq (1-\alpha /2r)M$
.
Proof. Let
![]() $\alpha '$
be the unique real number such that
$\alpha '$
be the unique real number such that
![]() $|E(\mathcal {G})|=\binom {(1-\alpha ')M}{r} \leq (1-\alpha )\binom {M}{r}$
. Then one can check that
$|E(\mathcal {G})|=\binom {(1-\alpha ')M}{r} \leq (1-\alpha )\binom {M}{r}$
. Then one can check that
![]() $\alpha '\geq \alpha /2r$
. We prove by induction on r that
$\alpha '\geq \alpha /2r$
. We prove by induction on r that
![]() $\mathcal {G}$
contains an
$\mathcal {G}$
contains an
![]() $(r-1)$
-element set X such that
$(r-1)$
-element set X such that
![]() $1\leq |N(X)|\leq (1-\alpha ')M$
. This is certainly true if
$1\leq |N(X)|\leq (1-\alpha ')M$
. This is certainly true if
![]() $r=1$
, so suppose that
$r=1$
, so suppose that
![]() $r\geq 2$
.
$r\geq 2$
.
Let
![]() $U\subset V(\mathcal {G})$
be the set of vertices with at least 1 neighbour. Then there exists
$U\subset V(\mathcal {G})$
be the set of vertices with at least 1 neighbour. Then there exists
![]() $u\in U$
such that
$u\in U$
such that
Note that
![]() $\binom {|U|}{r}\geq |E(\mathcal {G})|$
, as every edge is contained in U, so
$\binom {|U|}{r}\geq |E(\mathcal {G})|$
, as every edge is contained in U, so
![]() $|U|\geq (1-\alpha ')M$
. But then
$|U|\geq (1-\alpha ')M$
. But then
 $$ \begin{align*} |N(u)|\leq \frac{r\binom{(1-\alpha')M}{r}}{(1-\alpha')M}=\binom{(1-\alpha')M-1}{r-1}<\binom{(1-\alpha')M}{r-1}. \end{align*} $$
$$ \begin{align*} |N(u)|\leq \frac{r\binom{(1-\alpha')M}{r}}{(1-\alpha')M}=\binom{(1-\alpha')M-1}{r-1}<\binom{(1-\alpha')M}{r-1}. \end{align*} $$
Let
![]() $\mathcal {G}'$
be the link graph of u. Then
$\mathcal {G}'$
be the link graph of u. Then
![]() $\mathcal {G}'$
is a nonempty
$\mathcal {G}'$
is a nonempty
![]() $(r-1)$
-uniform hypergraph such that
$(r-1)$
-uniform hypergraph such that
![]() $|E(\mathcal {G}')|\leq \binom {(1-\alpha ')M}{r-1}$
. Therefore, by our induction hypothesis, there exists an
$|E(\mathcal {G}')|\leq \binom {(1-\alpha ')M}{r-1}$
. Therefore, by our induction hypothesis, there exists an
![]() $(r-2)$
-element set
$(r-2)$
-element set
![]() $X'$
such that
$X'$
such that
![]() $1\leq |N_{\mathcal {G}'}(X')|\leq (1-\alpha ')M$
. But then
$1\leq |N_{\mathcal {G}'}(X')|\leq (1-\alpha ')M$
. But then
![]() $X=X'\cup \{u\}$
satisfies
$X=X'\cup \{u\}$
satisfies
![]() $1\leq |N_{\mathcal {G}}(X)|\leq (1-\alpha ')M$
as well, finishing the proof.
$1\leq |N_{\mathcal {G}}(X)|\leq (1-\alpha ')M$
as well, finishing the proof.
Claim 2.6. Let
![]() $\mathcal {G}$
be a nonempty r-uniform dihypergraph on
$\mathcal {G}$
be a nonempty r-uniform dihypergraph on
![]() $M\geq 100r$
vertices, and suppose that the density of
$M\geq 100r$
vertices, and suppose that the density of
![]() $[\mathcal {G}]$
is at most
$[\mathcal {G}]$
is at most
![]() $1-\alpha $
. Then there exist
$1-\alpha $
. Then there exist
![]() $\ell \in [r]$
and
$\ell \in [r]$
and
![]() $Y\in V(\mathcal {G})^{r-1}$
such that
$Y\in V(\mathcal {G})^{r-1}$
such that
Proof. First, consider the case that
![]() $[\mathcal {G}]$
is nonempty. Then by the previous claim, there exists
$[\mathcal {G}]$
is nonempty. Then by the previous claim, there exists
![]() $X\in V(\mathcal {G})^{(r-1)}$
such that
$X\in V(\mathcal {G})^{(r-1)}$
such that
![]() $1\leq |N_{[\mathcal {G}]}(X)|\leq (1-\alpha /2r)M$
. Let
$1\leq |N_{[\mathcal {G}]}(X)|\leq (1-\alpha /2r)M$
. Let
![]() $U=V(\mathcal {G})\setminus N_{[\mathcal {G}]}(X)$
, and note that
$U=V(\mathcal {G})\setminus N_{[\mathcal {G}]}(X)$
, and note that
![]() $|U|\leq \frac {\alpha }{2r}M$
. For every
$|U|\leq \frac {\alpha }{2r}M$
. For every
![]() $u\in U$
, the set
$u\in U$
, the set
![]() $X\cup \{u\}$
has an orientation not present in
$X\cup \{u\}$
has an orientation not present in
![]() $\mathcal {G}$
. Hence, there exist
$\mathcal {G}$
. Hence, there exist
![]() $U'\subset U$
,
$U'\subset U$
,
![]() $\ell \in [r]$
and an orientation Y of X such that
$\ell \in [r]$
and an orientation Y of X such that
![]() $|U'|\geq |U|/r!$
and
$|U'|\geq |U|/r!$
and
![]() $U'$
is disjoint from
$U'$
is disjoint from
![]() $N_{[r]\setminus \{\ell \}}(Y)$
. But then
$N_{[r]\setminus \{\ell \}}(Y)$
. But then
![]() $|N_{[r]\setminus \{\ell \}}(Y)|\leq (1-\frac {\alpha }{2r\cdot r!})M$
. Also,
$|N_{[r]\setminus \{\ell \}}(Y)|\leq (1-\frac {\alpha }{2r\cdot r!})M$
. Also,
![]() $ N_{[\mathcal {G}]}(Y)\subset N_{[r]\setminus \{\ell \}}(Y)$
, so
$ N_{[\mathcal {G}]}(Y)\subset N_{[r]\setminus \{\ell \}}(Y)$
, so
![]() $|N_{[r]\setminus \{\ell \}}(Y)|\geq 1$
as well.
$|N_{[r]\setminus \{\ell \}}(Y)|\geq 1$
as well.
Now consider the case when
![]() $[\mathcal {G}]$
is empty. Let
$[\mathcal {G}]$
is empty. Let
![]() $\beta =1/r!$
. In this case, we show that there exist
$\beta =1/r!$
. In this case, we show that there exist
![]() $\ell \in [r]$
and
$\ell \in [r]$
and
![]() $Y\in V(\mathcal {G})^{r-1}$
such that
$Y\in V(\mathcal {G})^{r-1}$
such that
![]() $1\leq |N_{[r]\setminus \{\ell \}}(Y)|\leq (1-\beta )M$
. Suppose this is not the case: that is, for each
$1\leq |N_{[r]\setminus \{\ell \}}(Y)|\leq (1-\beta )M$
. Suppose this is not the case: that is, for each
![]() $W\in E(\mathcal {G})$
and
$W\in E(\mathcal {G})$
and
![]() $\ell \in [r]$
, we have
$\ell \in [r]$
, we have
![]() $|N_{[r]\setminus \{\ell \}}(\hat {W}(\ell ))|> (1-\beta )M$
. We define the sets of edges
$|N_{[r]\setminus \{\ell \}}(\hat {W}(\ell ))|> (1-\beta )M$
. We define the sets of edges
![]() $F_0,\dots ,F_r$
of
$F_0,\dots ,F_r$
of
![]() $\mathcal {G}$
as follows. Let
$\mathcal {G}$
as follows. Let
![]() $F_0$
contain a single edge
$F_0$
contain a single edge
![]() $W_0$
of
$W_0$
of
![]() $\mathcal {G}$
. For
$\mathcal {G}$
. For
![]() $i\in [r]$
,
$i\in [r]$
,
![]() $F_i$
will have the following form. There exist
$F_i$
will have the following form. There exist
![]() $x_1,\dots ,x_i\in V(\mathcal {G})$
such that
$x_1,\dots ,x_i\in V(\mathcal {G})$
such that
![]() $F_i$
contains all r-tuples W for which W agrees with
$F_i$
contains all r-tuples W for which W agrees with
![]() $W_0$
in exactly
$W_0$
in exactly
![]() $(r-i)$
coordinates, and the rest of the coordinates are a permutation of
$(r-i)$
coordinates, and the rest of the coordinates are a permutation of
![]() $x_1,\dots ,x_i$
. Note that then
$x_1,\dots ,x_i$
. Note that then
![]() $|F_i|=r(r-1)\dots (r-i+1)$
. If
$|F_i|=r(r-1)\dots (r-i+1)$
. If
![]() $F_i$
is already defined satisfying this property, we define
$F_i$
is already defined satisfying this property, we define
![]() $F_{i+1}$
as follows. For each
$F_{i+1}$
as follows. For each
![]() $W\in F_i$
, let
$W\in F_i$
, let
![]() $I_W$
be the set of coordinates
$I_W$
be the set of coordinates
![]() $\ell \in [r]$
for which
$\ell \in [r]$
for which
![]() $W(\ell )=W_0(\ell )$
. Consider the set
$W(\ell )=W_0(\ell )$
. Consider the set
Then U is the intersection of
![]() $(r-i)|F_i|\leq r!$
subsets of
$(r-i)|F_i|\leq r!$
subsets of
![]() $V(\mathcal {G})$
of size at least
$V(\mathcal {G})$
of size at least
![]() $(1-\beta )M$
; hence, U is nonempty. Therefore, there exists
$(1-\beta )M$
; hence, U is nonempty. Therefore, there exists
![]() $x_{i+1}\in U$
. Let
$x_{i+1}\in U$
. Let
![]() $F_{i+1}$
be the set of all edges
$F_{i+1}$
be the set of all edges
![]() $W'$
for which
$W'$
for which
![]() $\hat {W}'(\ell )=\hat {W}(\ell )$
and
$\hat {W}'(\ell )=\hat {W}(\ell )$
and
![]() $W'(\ell )=x_{i+1}$
for some
$W'(\ell )=x_{i+1}$
for some
![]() $W\in F_i$
and
$W\in F_i$
and
![]() $\ell \in I_W$
. Then
$\ell \in I_W$
. Then
![]() $F_{i+1}$
has the desired properties. In particular,
$F_{i+1}$
has the desired properties. In particular,
![]() $F_{r}$
contains every orientation of
$F_{r}$
contains every orientation of
![]() $\{x_1,\dots ,x_r\}$
contradicting that
$\{x_1,\dots ,x_r\}$
contradicting that
![]() $[\mathcal {G}]$
is nonempty. This finishes the proof.
$[\mathcal {G}]$
is nonempty. This finishes the proof.
Let us illustrate the previous argument in the case
![]() $r=3$
. Here,
$r=3$
. Here,
![]() $F_0$
contains some edge
$F_0$
contains some edge
![]() $abc$
. Then we can find
$abc$
. Then we can find
![]() $x=x_1$
such that
$x=x_1$
such that
![]() $abx,axc,xbc$
are all edges: they form
$abx,axc,xbc$
are all edges: they form
![]() $F_1$
. Then we can find some
$F_1$
. Then we can find some
![]() $y=x_2$
such that
$y=x_2$
such that
![]() $ayx,ybx,axy,yxc,xby,xyc$
are all edges: they form
$ayx,ybx,axy,yxc,xby,xyc$
are all edges: they form
![]() $F_2$
. Finally, we can find some
$F_2$
. Finally, we can find some
![]() $z=x_3$
such that
$z=x_3$
such that
![]() $zyx,yzx,zxy,yxz,xzy,xyz$
are all edges, forming
$zyx,yzx,zxy,yxz,xzy,xyz$
are all edges, forming
![]() $F_3$
.
$F_3$
.
Let
![]() $\alpha =2r\cdot r! N^{-1/2rms}$
. Let
$\alpha =2r\cdot r! N^{-1/2rms}$
. Let
![]() $U_{0}=V(\mathcal {H})$
,
$U_{0}=V(\mathcal {H})$
,
![]() $s_{0,i,k}=s$
for
$s_{0,i,k}=s$
for
![]() $(i,k)\in [m]\times [r]$
, and define the nested sequence of vertex sets
$(i,k)\in [m]\times [r]$
, and define the nested sequence of vertex sets
![]() $U_{0}\supset U_{1}\supset \dots $
and sequence of integers
$U_{0}\supset U_{1}\supset \dots $
and sequence of integers
![]() $s_{\ell ,i,k}$
for
$s_{\ell ,i,k}$
for
![]() $\ell =1,\dots $
and
$\ell =1,\dots $
and
![]() $(i,k)\in [m]\times [r]$
as follows. Suppose that
$(i,k)\in [m]\times [r]$
as follows. Suppose that
![]() $U_{\ell }$
and
$U_{\ell }$
and
![]() $s_{\ell ,i,k}$
are already defined for some
$s_{\ell ,i,k}$
are already defined for some
![]() $\ell \geq 0$
such that
$\ell \geq 0$
such that
![]() $\mathcal {H}_{i}[U_{\ell }]$
contains no member of
$\mathcal {H}_{i}[U_{\ell }]$
contains no member of
![]() $\mathcal {M}(r,s_{\ell ,i,k},k)$
for
$\mathcal {M}(r,s_{\ell ,i,k},k)$
for
![]() $(i,k)\in [m]\times [r]$
. Let
$(i,k)\in [m]\times [r]$
. Let
![]() $I\subset [m]$
be the set of indices i such that
$I\subset [m]$
be the set of indices i such that
![]() $\mathcal {H}_{i}[U_{\ell }]$
is nonempty. For such indices i, we must have
$\mathcal {H}_{i}[U_{\ell }]$
is nonempty. For such indices i, we must have
![]() $s_{\ell ,i}>1$
, as the family
$s_{\ell ,i}>1$
, as the family
![]() $\mathcal {M}(r,1)$
is composed of a single dihypergraph containing a single edge. Consider three cases.
$\mathcal {M}(r,1)$
is composed of a single dihypergraph containing a single edge. Consider three cases.
-
Case 1.
 $I=\emptyset $
.
$I=\emptyset $
.In this case, we stop and set
 $U=U_{\ell }$
.
$U=U_{\ell }$
. -
Case 2. For every
 $i\in I$
, the density of
$i\in I$
, the density of
 $[\mathcal {H}_{i}][U_{\ell }]$
is at least
$[\mathcal {H}_{i}][U_{\ell }]$
is at least
 $1-\alpha $
.
$1-\alpha $
.Let
 $\mathcal {H}_{I}=\bigcap _{i\in I} [\mathcal {H}_{i}]$
; then
$\mathcal {H}_{I}=\bigcap _{i\in I} [\mathcal {H}_{i}]$
; then
 $d(\mathcal {H}_{I}[U_{\ell }])\geq 1-\alpha |I|\geq 1-\alpha m$
. Therefore, by Lemma 2.1,
$d(\mathcal {H}_{I}[U_{\ell }])\geq 1-\alpha |I|\geq 1-\alpha m$
. Therefore, by Lemma 2.1,
 $\mathcal {H}_{I}[U_{\ell }]$
contains a clique U of size at least
$\mathcal {H}_{I}[U_{\ell }]$
contains a clique U of size at least
 $\frac {1}{4}(1/\alpha m)^{1/(r-1)}$
. Note that
$\frac {1}{4}(1/\alpha m)^{1/(r-1)}$
. Note that
 $\mathcal {H}_{i}[U]$
is a clique for every
$\mathcal {H}_{i}[U]$
is a clique for every
 $i\in I$
, and
$i\in I$
, and
 $\mathcal {H}_{i}[U]$
is an independent set for every
$\mathcal {H}_{i}[U]$
is an independent set for every
 $i\in [m]\setminus I$
.
$i\in [m]\setminus I$
. -
Case 3. There exists
 $i\in I$
such that the density of
$i\in I$
such that the density of
 $[\mathcal {H}_{i}][U_{\ell }]$
is less than
$[\mathcal {H}_{i}][U_{\ell }]$
is less than
 $1-\alpha $
.
$1-\alpha $
.As
 $\mathcal {H}_{i}[U_{\ell }]$
is not empty, we get by Claim 2.6 that there exist
$\mathcal {H}_{i}[U_{\ell }]$
is not empty, we get by Claim 2.6 that there exist
 $X\subset U_{\ell }^{r-1}$
and
$X\subset U_{\ell }^{r-1}$
and
 $k\in [r]$
such that Let
$k\in [r]$
such that Let $$ \begin{align*} 1\leq |N_{\mathcal{H}_{i}[U_{\ell}],[r]\setminus\{k\}}(X)|\leq \left(1-\frac{\alpha}{2r\cdot r!}\right)|U_{\ell}|. \end{align*} $$
$$ \begin{align*} 1\leq |N_{\mathcal{H}_{i}[U_{\ell}],[r]\setminus\{k\}}(X)|\leq \left(1-\frac{\alpha}{2r\cdot r!}\right)|U_{\ell}|. \end{align*} $$
 $U_{\ell +1}=U_{\ell }\setminus N_{\mathcal {H}_{i}[U_{\ell }],[r]\setminus \{k\}}(X)$
. Also set
$U_{\ell +1}=U_{\ell }\setminus N_{\mathcal {H}_{i}[U_{\ell }],[r]\setminus \{k\}}(X)$
. Also set
 $s_{\ell ,i',k'}=s_{\ell +1,i',k'}$
if
$s_{\ell ,i',k'}=s_{\ell +1,i',k'}$
if
 $(i',k')\neq (i,k)$
, and let
$(i',k')\neq (i,k)$
, and let
 $s_{\ell +1,i,k}=s_{\ell ,i,k}-1$
. Note that
$s_{\ell +1,i,k}=s_{\ell ,i,k}-1$
. Note that
 $|U_{\ell +1}|\geq \frac {\alpha }{2r\cdot r!}|U_{\ell }|$
, and
$|U_{\ell +1}|\geq \frac {\alpha }{2r\cdot r!}|U_{\ell }|$
, and
 $\mathcal {H}_{j}[U_{\ell }]$
contains no member of
$\mathcal {H}_{j}[U_{\ell }]$
contains no member of
 $\mathcal {M}(r,s_{\ell +1,i',k'},k)$
for
$\mathcal {M}(r,s_{\ell +1,i',k'},k)$
for
 $(i',k')\in [m]\times [r]$
. The latter is clear if
$(i',k')\in [m]\times [r]$
. The latter is clear if
 $(i',k')\neq (i,k)$
. If
$(i',k')\neq (i,k)$
. If
 $(i',k')=(i,k)$
, let f be any edge in
$(i',k')=(i,k)$
, let f be any edge in
 $\mathcal {H}_{i}[U_{\ell }]$
with
$\mathcal {H}_{i}[U_{\ell }]$
with
 $\hat {f}(k)=X$
. If
$\hat {f}(k)=X$
. If
 $\mathcal {H}_{i}[U_{\ell +1}]$
contains a member of
$\mathcal {H}_{i}[U_{\ell +1}]$
contains a member of
 $\mathcal {M}(r,s_{\ell +1,i,k},k)$
, then together with f, this forms a member of
$\mathcal {M}(r,s_{\ell +1,i,k},k)$
, then together with f, this forms a member of
 $\mathcal {M}(r,s_{\ell ,i,k},k)$
in
$\mathcal {M}(r,s_{\ell ,i,k},k)$
in
 $\mathcal {H}_{i}[U_{\ell }]$
, a contradiction.
$\mathcal {H}_{i}[U_{\ell }]$
, a contradiction.
Let L be the index
![]() $\ell $
for which we stop. For
$\ell $
for which we stop. For
![]() $\ell =1,\dots ,L$
, let
$\ell =1,\dots ,L$
, let
![]() $s_{\ell }=\sum _{i=1}^{m}\sum _{k=1}^{r}s_{\ell ,i,k}$
. Then
$s_{\ell }=\sum _{i=1}^{m}\sum _{k=1}^{r}s_{\ell ,i,k}$
. Then
![]() $s_{0}=rms$
,
$s_{0}=rms$
,
![]() $s_{L}\geq rm$
, and
$s_{L}\geq rm$
, and
![]() $s_{\ell +1}=s_{\ell }-1$
, so we get
$s_{\ell +1}=s_{\ell }-1$
, so we get
![]() $L\leq rm(s-1)$
. Also,
$L\leq rm(s-1)$
. Also,
![]() $|U_{\ell +1}|\geq \frac {\alpha }{2r\cdot r!}|U_{\ell }|$
, so
$|U_{\ell +1}|\geq \frac {\alpha }{2r\cdot r!}|U_{\ell }|$
, so
![]() $|U_{L}|\geq (\alpha /2r\cdot r!)^{L}N\geq (\alpha /2r\cdot r!)^{rms}N\geq N^{1/2}$
.
$|U_{L}|\geq (\alpha /2r\cdot r!)^{L}N\geq (\alpha /2r\cdot r!)^{rms}N\geq N^{1/2}$
.
If we stop in Case 1, then
![]() $U=U_{\ell }$
, so
$U=U_{\ell }$
, so
![]() $|U|\geq N^{1/2}$
. If we stop in Case 2, then
$|U|\geq N^{1/2}$
. If we stop in Case 2, then
![]() $|U|\geq \frac {1}{4}(1/\alpha m)^{1/(r-1)}\geq c N^{1/2msr(r-1)}$
, where
$|U|\geq \frac {1}{4}(1/\alpha m)^{1/(r-1)}\geq c N^{1/2msr(r-1)}$
, where
![]() $c=c(r,s,m)>0$
depends only on
$c=c(r,s,m)>0$
depends only on
![]() $r,s,m$
. This finishes the proof.
$r,s,m$
. This finishes the proof.
From this, we can immediately deduce Theorem 1.3.
Proof of Theorem 1.3
Let
![]() $f_1,\dots ,f_m:(\mathbb {F}^{n})^r$
be polynomials of degree at most d and
$f_1,\dots ,f_m:(\mathbb {F}^{n})^r$
be polynomials of degree at most d and
![]() $\phi $
be a Boolean formula defining
$\phi $
be a Boolean formula defining
![]() $\mathcal {H}$
, and let
$\mathcal {H}$
, and let
![]() $\mathcal {H}_i$
be the algebraic dihypergraph defined by
$\mathcal {H}_i$
be the algebraic dihypergraph defined by
![]() $f_i$
on
$f_i$
on
![]() $V(\mathcal {H})$
for
$V(\mathcal {H})$
for
![]() $i\in [m]$
. By Lemma 2.3,
$i\in [m]$
. By Lemma 2.3,
![]() $\mathcal {H}_{i}$
contains no member of
$\mathcal {H}_{i}$
contains no member of
![]() $\mathcal {M}(r,s)$
for
$\mathcal {M}(r,s)$
for
![]() $s=\binom {n+d}{n}+1$
. But then by Lemma 2.4, there exists
$s=\binom {n+d}{n}+1$
. But then by Lemma 2.4, there exists
![]() $U\subset V(\mathcal {H})$
such that
$U\subset V(\mathcal {H})$
such that
![]() $|U|\geq cN^{1/2r^2ms}$
and
$|U|\geq cN^{1/2r^2ms}$
and
![]() $\mathcal {H}_{i}[U]$
is either a clique or an independent set for
$\mathcal {H}_{i}[U]$
is either a clique or an independent set for
![]() $i\in [m]$
.
$i\in [m]$
.
If
![]() $X\in V(\mathcal {H})^{(r)}$
and Y is an orientation of X, then X is an edge of
$X\in V(\mathcal {H})^{(r)}$
and Y is an orientation of X, then X is an edge of
![]() $\mathcal {H}$
if and only if
$\mathcal {H}$
if and only if
By the definition of U, the left-hand side is the same for every
![]() $Y\in U^{r}$
, so
$Y\in U^{r}$
, so
![]() $\mathcal {H}[U]$
is either a clique or an independent set.
$\mathcal {H}[U]$
is either a clique or an independent set.
Let us remark that the bound in Lemma 2.4 is optimal in the following sense. Let G be a graph, which we view as a digraph in which each edge is oriented both ways. Note that if G contains no two sets of size
![]() $\lfloor s/2\rfloor $
with no edges between them, then G contains no member of
$\lfloor s/2\rfloor $
with no edges between them, then G contains no member of
![]() $\mathcal {M}(2,s)$
as well. But standard probabilistic arguments show that there are graphs G on N vertices containing no two such sets, and every clique and independent set in G is of size
$\mathcal {M}(2,s)$
as well. But standard probabilistic arguments show that there are graphs G on N vertices containing no two such sets, and every clique and independent set in G is of size
![]() $N^{O(1/s)}$
. In the next section, we show that this bound can be significantly improved if we exploit some other properties of algebraic graphs as well.
$N^{O(1/s)}$
. In the next section, we show that this bound can be significantly improved if we exploit some other properties of algebraic graphs as well.
2.4 Zero-patterns
One of the key results in our proof is the following lemma of Rónyai, Babai and Ganapathy [Reference Rónyai, Babai and Ganapathy35] on the number of zero-patterns of polynomials.
Given a sequence of m polynomials
![]() $\mathbf {f}=(f_1,\dots ,f_{m})$
in n variables over the field
$\mathbf {f}=(f_1,\dots ,f_{m})$
in n variables over the field
![]() $\mathbb {F}$
, a zero-pattern of
$\mathbb {F}$
, a zero-pattern of
![]() $\mathbf {f}$
is a sequence
$\mathbf {f}$
is a sequence
![]() $\epsilon \in \{0,*\}^{m}$
for which there exists
$\epsilon \in \{0,*\}^{m}$
for which there exists
![]() $x\in \mathbb {F}^{n}$
such that
$x\in \mathbb {F}^{n}$
such that
![]() $f_{i}(x)=0$
if and only if
$f_{i}(x)=0$
if and only if
![]() $\epsilon (i)=0$
. Let
$\epsilon (i)=0$
. Let
![]() $Z(\mathbf {f})$
denote the number of zero-patterns of
$Z(\mathbf {f})$
denote the number of zero-patterns of
![]() $\mathbf {f}$
. Using elegant algebraic tools, Rónyai, Babai and Ganapathy [Reference Rónyai, Babai and Ganapathy35] proved the following.
$\mathbf {f}$
. Using elegant algebraic tools, Rónyai, Babai and Ganapathy [Reference Rónyai, Babai and Ganapathy35] proved the following.
Lemma 2.7. Let
![]() $f_1,\dots ,f_m:\mathbb {F}^{n}\rightarrow \mathbb {F}$
be a sequence of polynomials of degree at most d. Then the number of zero-patterns of
$f_1,\dots ,f_m:\mathbb {F}^{n}\rightarrow \mathbb {F}$
be a sequence of polynomials of degree at most d. Then the number of zero-patterns of
![]() $\mathbf {f}=(f_1,\dots ,f_m)$
is at most
$\mathbf {f}=(f_1,\dots ,f_m)$
is at most
![]() $\binom {md+n}{n}$
. In particular,
$\binom {md+n}{n}$
. In particular,
![]() $Z(\mathbf {f})\leq cm^{n}$
, where
$Z(\mathbf {f})\leq cm^{n}$
, where
![]() $c=c(n,d)$
depends only on n and d.
$c=c(n,d)$
depends only on n and d.
2.5 Weak-VC-dimension
In this section, we show that algebraic graphs of complexity
![]() $(n,d,m)$
behave similarly to graphs of VC-dimension n. By the celebrated Sauer-Shelah lemma [Reference Sauer36, Reference Shelah37], if a family of sets
$(n,d,m)$
behave similarly to graphs of VC-dimension n. By the celebrated Sauer-Shelah lemma [Reference Sauer36, Reference Shelah37], if a family of sets
![]() $\mathcal {F}$
has VC-dimension n, then
$\mathcal {F}$
has VC-dimension n, then
 $$ \begin{align*} \pi_{\mathcal{F}}(z)\leq\sum_{i=0}^{n}\binom{z}{i}\leq cz^{n}, \end{align*} $$
$$ \begin{align*} \pi_{\mathcal{F}}(z)\leq\sum_{i=0}^{n}\binom{z}{i}\leq cz^{n}, \end{align*} $$
where
![]() $c=c(n)$
depends only on n.
$c=c(n)$
depends only on n.
Let us relax the notion of a VC-dimension as follows, and note that we now work with undirected hypergraphs. Say that the family
![]() $\mathcal {F}$
has weak-VC-dimension
$\mathcal {F}$
has weak-VC-dimension
![]() $(c,n)$
if
$(c,n)$
if
![]() $\pi _{\mathcal {F}}(z)\leq cz^{n}$
for every positive integer z. Also, an r-uniform hypergraph
$\pi _{\mathcal {F}}(z)\leq cz^{n}$
for every positive integer z. Also, an r-uniform hypergraph
![]() $\mathcal {H}$
has weak-VC-dimension
$\mathcal {H}$
has weak-VC-dimension
![]() $(c,n)$
if the family
$(c,n)$
if the family
![]() $\{N(v):v\in V(\mathcal {H})\}\subset 2^{V(\mathcal {H})^{(r-1)}}$
has weak-VC-dimension
$\{N(v):v\in V(\mathcal {H})\}\subset 2^{V(\mathcal {H})^{(r-1)}}$
has weak-VC-dimension
![]() $(c,n)$
(that is,
$(c,n)$
(that is,
![]() $\{N(v):v\in V(\mathcal {H})\}$
is viewed as a family of subsets of the base set
$\{N(v):v\in V(\mathcal {H})\}$
is viewed as a family of subsets of the base set
![]() $\mathcal {V}=V(\mathcal {H})^{(r-1)}$
). Also, say that a family of hypergraphs
$\mathcal {V}=V(\mathcal {H})^{(r-1)}$
). Also, say that a family of hypergraphs
![]() $\mathcal {F}$
has weak-VC-dimension n if there exists a constant
$\mathcal {F}$
has weak-VC-dimension n if there exists a constant
![]() $c=c(\mathcal {F})$
such that every
$c=c(\mathcal {F})$
such that every
![]() $\mathcal {H}\in \mathcal {F}$
has weak-VC-dimension
$\mathcal {H}\in \mathcal {F}$
has weak-VC-dimension
![]() $(c,n)$
.
$(c,n)$
.
Lemma 2.8. Let
![]() $\mathcal {H}$
be an r-uniform algebraic hypergraph of complexity
$\mathcal {H}$
be an r-uniform algebraic hypergraph of complexity
![]() $(n,d,m)$
, and let
$(n,d,m)$
, and let
![]() $\mathcal {F}=\{N(v):v\in V(\mathcal {H})\}$
. Then
$\mathcal {F}=\{N(v):v\in V(\mathcal {H})\}$
. Then
 $$ \begin{align*} \pi_{\mathcal{F}}(z)\leq \binom{zmd+n}{n}\leq cz^{n}, \end{align*} $$
$$ \begin{align*} \pi_{\mathcal{F}}(z)\leq \binom{zmd+n}{n}\leq cz^{n}, \end{align*} $$
where
![]() $c=c(n,d,m)$
depends only on
$c=c(n,d,m)$
depends only on
![]() $n,d,m$
.
$n,d,m$
.
Proof. Let
![]() $f_1,\dots ,f_m:(\mathbb {F}^{n})^{r}\rightarrow \mathbb {F}$
be polynomials of degree at most d whose zero-patterns determine the edges of
$f_1,\dots ,f_m:(\mathbb {F}^{n})^{r}\rightarrow \mathbb {F}$
be polynomials of degree at most d whose zero-patterns determine the edges of
![]() $\mathcal {H}$
.
$\mathcal {H}$
.
Let
![]() $\mathcal {V}=V(\mathcal {H})^{(r-1)}$
: that is, the base set of
$\mathcal {V}=V(\mathcal {H})^{(r-1)}$
: that is, the base set of
![]() $\mathcal {F}$
. For
$\mathcal {F}$
. For
![]() $U\in \mathcal {V}$
and
$U\in \mathcal {V}$
and
![]() $i\in [m]$
, define the polynomial
$i\in [m]$
, define the polynomial
![]() $f_{i,U}:\mathbb {F}^{n}\rightarrow \mathbb {F}$
as
$f_{i,U}:\mathbb {F}^{n}\rightarrow \mathbb {F}$
as
![]() $f_{i,U}(\mathbf {x})=f_{i}(U',\mathbf {x})$
, where
$f_{i,U}(\mathbf {x})=f_{i}(U',\mathbf {x})$
, where
![]() $U'\in (\mathbb {F}^{n})^{r-1}$
is a fixed orientation of U. If
$U'\in (\mathbb {F}^{n})^{r-1}$
is a fixed orientation of U. If
![]() $\mathcal {U}\subset \mathcal {V}$
such that
$\mathcal {U}\subset \mathcal {V}$
such that
![]() $|\mathcal {U}|=z$
, then each element of the family
$|\mathcal {U}|=z$
, then each element of the family
![]() $\{N(v)\cap \mathcal {U}:v\in V(\mathcal {H})\}$
is determined by a zero-pattern of the
$\{N(v)\cap \mathcal {U}:v\in V(\mathcal {H})\}$
is determined by a zero-pattern of the
![]() $zm$
polynomials
$zm$
polynomials
![]() $f_{i,U}$
for
$f_{i,U}$
for
![]() $i\in [m]$
and
$i\in [m]$
and
![]() $U\in \mathcal {U}$
. Therefore, by Lemma 2.7, we have
$U\in \mathcal {U}$
. Therefore, by Lemma 2.7, we have
 $$ \begin{align*} \pi_{\mathcal{F}}(z)\leq \binom{zmd+n}{n}.\\[-43pt] \end{align*} $$
$$ \begin{align*} \pi_{\mathcal{F}}(z)\leq \binom{zmd+n}{n}.\\[-43pt] \end{align*} $$
Solving the inequality
![]() $\binom {zmd+n}{n}<2^z$
, Lemma 2.8 shows that an algebraic graph of complexity
$\binom {zmd+n}{n}<2^z$
, Lemma 2.8 shows that an algebraic graph of complexity
![]() $(n,d,m)$
has VC-dimension at most
$(n,d,m)$
has VC-dimension at most
![]() $n\log (ndm)$
. Also, the VC-dimension of such graphs cannot be bounded by a function of n alone: every graph is an algebraic graph of complexity
$n\log (ndm)$
. Also, the VC-dimension of such graphs cannot be bounded by a function of n alone: every graph is an algebraic graph of complexity
![]() $(1,d,1)$
and
$(1,d,1)$
and
![]() $(1,1,m)$
for some positive integers d and m. However, Lemma 2.8 also tells us that the family of algebraic graphs of complexity
$(1,1,m)$
for some positive integers d and m. However, Lemma 2.8 also tells us that the family of algebraic graphs of complexity
![]() $(n,d,m)$
has weak-VC-dimension at most n.
$(n,d,m)$
has weak-VC-dimension at most n.
Let
![]() $\delta>0$
. Say that the family
$\delta>0$
. Say that the family
![]() $\mathcal {F}$
of subsets of the base set X is
$\mathcal {F}$
of subsets of the base set X is
![]() $\delta $
-separated if
$\delta $
-separated if
![]() $|A\Delta B|\geq \delta |X|$
holds for any two distinct
$|A\Delta B|\geq \delta |X|$
holds for any two distinct
![]() $A,B\in \mathcal {F}$
. The following packing lemma is due to Haussler [Reference Haussler29]. While it is originally stated for families of bounded VC-dimension, the same proof implies the following result as well.
$A,B\in \mathcal {F}$
. The following packing lemma is due to Haussler [Reference Haussler29]. While it is originally stated for families of bounded VC-dimension, the same proof implies the following result as well.
Lemma 2.9. Let n be a positive integer and
![]() $c>0$
; then there exists
$c>0$
; then there exists
![]() $c'=c'(c,n)$
such that the following holds. Let
$c'=c'(c,n)$
such that the following holds. Let
![]() $\mathcal {F}$
be a
$\mathcal {F}$
be a
![]() $\delta $
-separated family of weak-VC-dimension
$\delta $
-separated family of weak-VC-dimension
![]() $(c,n)$
. Then
$(c,n)$
. Then
![]() $|\mathcal {F}|\leq c'(1/\delta )^{n}$
.
$|\mathcal {F}|\leq c'(1/\delta )^{n}$
.
Next, we show that Lemma 2.8 and Lemma 2.9 can be combined to prove that if G is a graph of bounded weak-VC-dimension whose density is not too close to 1, then G contains two large subsets with few edges between them. This lemma is inspired by Theorem 1.3 in the paper of Fox, Pach and Suk [Reference Fox, Pach and Suk27], which is a regularity-type result for hypergraphs of bounded VC-dimension. Later, we will also use this theorem; see Lemma 4.1 for the precise statement.
Lemma 2.10. Let n be a positive integer and
![]() $c>0$
; then there exists
$c>0$
; then there exists
![]() $c_{0}=c_{0}(c,n)>0$
such that the following holds. Let
$c_{0}=c_{0}(c,n)>0$
such that the following holds. Let
![]() $\alpha ,\beta>0$
, and let G be a graph of weak-VC-dimension
$\alpha ,\beta>0$
, and let G be a graph of weak-VC-dimension
![]() $(c,n)$
on N vertices such that
$(c,n)$
on N vertices such that
![]() $d(G)\leq 1-\alpha $
. Then G contains two disjoint sets A and B such that
$d(G)\leq 1-\alpha $
. Then G contains two disjoint sets A and B such that
![]() $|A|\geq \frac {\alpha }{4}N $
,
$|A|\geq \frac {\alpha }{4}N $
,
![]() $|B|\geq c_0\alpha (\alpha \beta )^{n} N$
, and every vertex in B has at most
$|B|\geq c_0\alpha (\alpha \beta )^{n} N$
, and every vertex in B has at most
![]() $\beta |A|$
neighbors in A.
$\beta |A|$
neighbors in A.
Proof. Let
![]() $U\subset V(G)$
be the set of vertices v such that
$U\subset V(G)$
be the set of vertices v such that
![]() $|N(v)|\leq (1-\alpha /2)N$
. Then
$|N(v)|\leq (1-\alpha /2)N$
. Then
 $$ \begin{align*} (1-\alpha)\binom{N}{2}\geq |E(G)|\geq \frac{(N-|U|)}{2}\left(1-\frac{\alpha}{2}\right)N, \end{align*} $$
$$ \begin{align*} (1-\alpha)\binom{N}{2}\geq |E(G)|\geq \frac{(N-|U|)}{2}\left(1-\frac{\alpha}{2}\right)N, \end{align*} $$
from which we get
Let
![]() $\gamma =\alpha \beta /4$
, and let
$\gamma =\alpha \beta /4$
, and let
![]() $Z\subset U$
be maximal such that the family
$Z\subset U$
be maximal such that the family
![]() $\{N(v):v\in Z\}$
is
$\{N(v):v\in Z\}$
is
![]() $\gamma $
separated. Then by Lemma 2.9, we have
$\gamma $
separated. Then by Lemma 2.9, we have
![]() $|Z|\leq c'(1/\gamma )^{n}$
, where
$|Z|\leq c'(1/\gamma )^{n}$
, where
![]() $c'=c'(c,n)$
depends only on the parameters c and n. By the maximality of Z, for every
$c'=c'(c,n)$
depends only on the parameters c and n. By the maximality of Z, for every
![]() $v\in U$
, there exists
$v\in U$
, there exists
![]() $z\in Z$
such that
$z\in Z$
such that
![]() $|N(v)\Delta N(z)|\leq \gamma N$
. Hence, we can find
$|N(v)\Delta N(z)|\leq \gamma N$
. Hence, we can find
![]() $z_{0}\in Z$
such that the set B is formed by the vertices v such that
$z_{0}\in Z$
such that the set B is formed by the vertices v such that
![]() $|N(v)\Delta N(z_0)|\leq \gamma N$
satisfies
$|N(v)\Delta N(z_0)|\leq \gamma N$
satisfies
By deleting some elements of B, we can assume that
![]() $|B|\leq \frac {\alpha }{4}$
and that
$|B|\leq \frac {\alpha }{4}$
and that
![]() $|B|$
still satisfies the previous inequality. Set
$|B|$
still satisfies the previous inequality. Set
![]() $A=V(G)\setminus (B\cup N(z_{0}))$
; then we show that A and B suffice.
$A=V(G)\setminus (B\cup N(z_{0}))$
; then we show that A and B suffice.
Indeed,
Also, every
![]() $v\in B$
satisfies
$v\in B$
satisfies
![]() $|N(v)\Delta N(z_{0})|\leq \gamma N$
, and
$|N(v)\Delta N(z_{0})|\leq \gamma N$
, and
![]() $z_{0}$
has no neighbor in A, so
$z_{0}$
has no neighbor in A, so
![]() $|N(v)\cap A|\leq \gamma N\leq \beta |A|$
.
$|N(v)\cap A|\leq \gamma N\leq \beta |A|$
.
3 A Ramsey-type result for algebraic graphs
In this section, we prove Theorems 1.1 and 1.2. If G is a directed graph and
![]() $(A,B)$
is a pair of disjoint subsets of
$(A,B)$
is a pair of disjoint subsets of
![]() $V(G)$
, say that
$V(G)$
, say that
![]() $(A,B)$
is well-directed if either every edge of G between A and B goes from A to B, or every edge between A and B goes from B to A. We show that if G is an algebraic digraph defined by a single polynomial and A and B are two sets of vertices such that
$(A,B)$
is well-directed if either every edge of G between A and B goes from A to B, or every edge between A and B goes from B to A. We show that if G is an algebraic digraph defined by a single polynomial and A and B are two sets of vertices such that
![]() $[G]$
has few edges between A and B, then we can find a large subset
$[G]$
has few edges between A and B, then we can find a large subset
![]() $A'\subset A$
and
$A'\subset A$
and
![]() $B'\subset B$
such that
$B'\subset B$
such that
![]() $(A',B')$
is well-directed. This is the consequence of the fact that G contains no member of
$(A',B')$
is well-directed. This is the consequence of the fact that G contains no member of
![]() $\mathcal {M}(2,s)$
for some constant s. For simplicity, write
$\mathcal {M}(2,s)$
for some constant s. For simplicity, write
![]() $\mathcal {M}^{-}(s)$
and
$\mathcal {M}^{-}(s)$
and
![]() $\mathcal {M}^{+}(s)$
instead of
$\mathcal {M}^{+}(s)$
instead of
![]() $\mathcal {M}(2,s,1)$
and
$\mathcal {M}(2,s,1)$
and
![]() $\mathcal {M}(2,s,2)$
, respectively. Note that each member of
$\mathcal {M}(2,s,2)$
, respectively. Note that each member of
![]() $\mathcal {M}^{-}(s)$
(and
$\mathcal {M}^{-}(s)$
(and
![]() $\mathcal {M}^{+}(s)$
) is composed of s directed edges
$\mathcal {M}^{+}(s)$
) is composed of s directed edges
![]() $(u_1,v_1),\dots ,(u_s,v_s)$
such that
$(u_1,v_1),\dots ,(u_s,v_s)$
such that
![]() $(u_{i},v_j)$
is not an edge for
$(u_{i},v_j)$
is not an edge for
![]() $i>j$
(
$i>j$
(
![]() $j>i$
, respectively).
$j>i$
, respectively).
Lemma 3.1. Let
![]() $n,d$
be positive integers. Then there exist
$n,d$
be positive integers. Then there exist
![]() $c_{1}=c_{1}(n,d)>0$
and
$c_{1}=c_{1}(n,d)>0$
and
![]() $c_2=c_2(n,d)>0$
such that the following holds. Let G be a strongly algebraic digraph of complexity
$c_2=c_2(n,d)>0$
such that the following holds. Let G be a strongly algebraic digraph of complexity
![]() $(n,d)$
on N vertices such that
$(n,d)$
on N vertices such that
![]() $d([G])\leq 1-\alpha $
. Then
$d([G])\leq 1-\alpha $
. Then
![]() $V(G)$
contains two disjoint subsets A and B such that
$V(G)$
contains two disjoint subsets A and B such that
![]() $|A|\geq c_1\alpha N$
,
$|A|\geq c_1\alpha N$
,
![]() $|B|\geq c_2 \alpha ^{n+1}N$
, and
$|B|\geq c_2 \alpha ^{n+1}N$
, and
![]() $(A,B)$
is well-directed.
$(A,B)$
is well-directed.
Proof. Let
![]() $s=\binom {n+2d}{n}+1$
and
$s=\binom {n+2d}{n}+1$
and
![]() $\beta =\frac {1}{6\cdot 3^{2s}}$
. Note that
$\beta =\frac {1}{6\cdot 3^{2s}}$
. Note that
![]() $[G]$
is a strongly algebraic graph of complexity
$[G]$
is a strongly algebraic graph of complexity
![]() $(n,2d)$
. Indeed, if G is defined by the polynomial
$(n,2d)$
. Indeed, if G is defined by the polynomial
![]() $f:(\mathbb {F}^{n})^{2}\rightarrow \mathbb {F}$
of degree at most d, then the polynomial
$f:(\mathbb {F}^{n})^{2}\rightarrow \mathbb {F}$
of degree at most d, then the polynomial
![]() $f'(\mathbf {x},\mathbf {y})=f(\mathbf {x},\mathbf {y})\cdot f(\mathbf {y},\mathbf {x})$
defines
$f'(\mathbf {x},\mathbf {y})=f(\mathbf {x},\mathbf {y})\cdot f(\mathbf {y},\mathbf {x})$
defines
![]() $[G]$
and has degree at most
$[G]$
and has degree at most
![]() $2d$
. Therefore, by Lemma 2.8,
$2d$
. Therefore, by Lemma 2.8,
![]() $[G]$
has weak-VC-dimension
$[G]$
has weak-VC-dimension
![]() $(c,n)$
for some
$(c,n)$
for some
![]() $c=c(n,d)$
. Hence, by Lemma 2.10, there exist two subsets
$c=c(n,d)$
. Hence, by Lemma 2.10, there exist two subsets
![]() $A_0$
and
$A_0$
and
![]() $B_0$
of
$B_0$
of
![]() $V(G)$
such that
$V(G)$
such that
![]() $|A_0|\geq \frac {\alpha }{4}N$
,
$|A_0|\geq \frac {\alpha }{4}N$
,
![]() $|B_0|\geq c_0\alpha (\alpha \beta )^{n}N=c_2' \alpha ^{n+1}N$
(where
$|B_0|\geq c_0\alpha (\alpha \beta )^{n}N=c_2' \alpha ^{n+1}N$
(where
![]() $c_2'=c_2'(n,d)$
depends only on n and d), and in
$c_2'=c_2'(n,d)$
depends only on n and d), and in
![]() $[G]$
, every vertex in
$[G]$
, every vertex in
![]() $B_0$
has at most
$B_0$
has at most
![]() $\beta |A_0|$
neighbours in
$\beta |A_0|$
neighbours in
![]() $A_0$
. We show that
$A_0$
. We show that
![]() $c_1=\frac {1}{4\cdot 3^{2s}}$
and
$c_1=\frac {1}{4\cdot 3^{2s}}$
and
![]() $c_2=c_2'/2$
suffices.
$c_2=c_2'/2$
suffices.
We define the sequence of sets
![]() $A_0\supset A_1\supset \dots $
and sequence of edges
$A_0\supset A_1\supset \dots $
and sequence of edges
![]() $f_1,f_2,\dots \in E(G)$
as follows. For
$f_1,f_2,\dots \in E(G)$
as follows. For
![]() $i=1,2,\dots $
,
$i=1,2,\dots $
,
-
•
 $|A_i|\geq |A_0|3^{-i}$
.
$|A_i|\geq |A_0|3^{-i}$
. -
•
 $f_i=(u_i,v_i)$
has one vertex in
$f_i=(u_i,v_i)$
has one vertex in
 $A_{i-1}$
and one vertex in B.
$A_{i-1}$
and one vertex in B. -
• If
 $v_i\in B_0$
, then
$v_i\in B_0$
, then
 $v_i$
has no in-neighbor in
$v_i$
has no in-neighbor in
 $A_{i}$
, and if
$A_{i}$
, and if
 $u_i\in B_0$
, then
$u_i\in B_0$
, then
 $u_i$
has no out-neighbor in
$u_i$
has no out-neighbor in
 $A_{i}$
.
$A_{i}$
.
Suppose that
![]() $A_{i-1}$
is already defined for some
$A_{i-1}$
is already defined for some
![]() $1\leq i<2s$
. Consider two cases. First, consider the case that for every
$1\leq i<2s$
. Consider two cases. First, consider the case that for every
![]() $b\in B_0$
, either
$b\in B_0$
, either
![]() $N^{+}(b)\cap A_{i-1}=\emptyset $
or
$N^{+}(b)\cap A_{i-1}=\emptyset $
or
![]() $N^{-}(b)\cap A_{i-1}=\emptyset $
. Then there exists
$N^{-}(b)\cap A_{i-1}=\emptyset $
. Then there exists
![]() $B\subset B_0$
such that
$B\subset B_0$
such that
![]() $|B|\geq |B_0|/2$
and either every
$|B|\geq |B_0|/2$
and either every
![]() $b\in B$
satisfies
$b\in B$
satisfies
![]() $N^{+}(b)\cap A_{i-1}=\emptyset $
, or every
$N^{+}(b)\cap A_{i-1}=\emptyset $
, or every
![]() $b\in B$
satisfies
$b\in B$
satisfies
![]() $N^{-}(b)\cap A_{i-1}=\emptyset $
. Set
$N^{-}(b)\cap A_{i-1}=\emptyset $
. Set
![]() $A=A_{i-1}$
; then
$A=A_{i-1}$
; then
![]() $(A,B)$
is well-directed. As
$(A,B)$
is well-directed. As
![]() $|A_{i-1}|> |A_0|3^{-2s}\geq c_1 \alpha N$
and
$|A_{i-1}|> |A_0|3^{-2s}\geq c_1 \alpha N$
and
![]() $|B|\geq c_2 N$
, the sets A and B satisfy our conditions. In this case, we stop.
$|B|\geq c_2 N$
, the sets A and B satisfy our conditions. In this case, we stop.
Now consider the case when there exists
![]() $b\in B_0$
such that both
$b\in B_0$
such that both
![]() $N^{+}(b)\cap A_{i-1}$
and
$N^{+}(b)\cap A_{i-1}$
and
![]() $N^{-}(b)\cap A_{i-1}$
are nonempty. If
$N^{-}(b)\cap A_{i-1}$
are nonempty. If
![]() $a\in N^{+}(b)\cap N^{-}(b)\cap A_{i-1}$
, then
$a\in N^{+}(b)\cap N^{-}(b)\cap A_{i-1}$
, then
![]() $\{a,b\}\in E([G])$
, so
$\{a,b\}\in E([G])$
, so
![]() $|N^{+}(b)\cap N^{-}(b)\cap A_{i-1}|\leq \beta |A_0|<\frac {1}{6}|A_{i-1}|$
. But then, either
$|N^{+}(b)\cap N^{-}(b)\cap A_{i-1}|\leq \beta |A_0|<\frac {1}{6}|A_{i-1}|$
. But then, either
![]() $|N^{+}(b)\cap A_{i-1}|\leq \frac {2}{3}|A_{i-1}|$
or
$|N^{+}(b)\cap A_{i-1}|\leq \frac {2}{3}|A_{i-1}|$
or
![]() $|N^{-}(b)\cap A_{i-1}|\leq \frac {2}{3}|A_{i-1}|$
. In the first case, set
$|N^{-}(b)\cap A_{i-1}|\leq \frac {2}{3}|A_{i-1}|$
. In the first case, set
![]() $A_i=A_{i-1}\setminus N^{+}(b)$
and
$A_i=A_{i-1}\setminus N^{+}(b)$
and
![]() $f_{i}=(b,a)$
for some
$f_{i}=(b,a)$
for some
![]() $a\in N^{+}(b)$
; in the second case,
$a\in N^{+}(b)$
; in the second case,
![]() $A_i=A_{i-1}\setminus N^{-}(b)$
and
$A_i=A_{i-1}\setminus N^{-}(b)$
and
![]() $f_{i}=(a,b)$
for some
$f_{i}=(a,b)$
for some
![]() $a\in N^{-}(b)$
. Then
$a\in N^{-}(b)$
. Then
![]() $A_i$
and
$A_i$
and
![]() $f_i$
satisfy the desired properties.
$f_i$
satisfy the desired properties.
Note that we must have stopped for some
![]() $i\leq 2s$
. Indeed, either at least half of the edges
$i\leq 2s$
. Indeed, either at least half of the edges
![]() $f_1,\dots ,f_i$
go from
$f_1,\dots ,f_i$
go from
![]() $A_0$
to
$A_0$
to
![]() $B_0$
, or at least half of the edges go from
$B_0$
, or at least half of the edges go from
![]() $B_0$
to
$B_0$
to
![]() $A_0$
. In the first case, G contains a member of
$A_0$
. In the first case, G contains a member of
![]() $\mathcal {M}^{-}(\lceil i/2\rceil )$
; in the second case, G contains a member of
$\mathcal {M}^{-}(\lceil i/2\rceil )$
; in the second case, G contains a member of
![]() $\mathcal {M}^{+}(\lceil i/2\rceil )$
.
$\mathcal {M}^{+}(\lceil i/2\rceil )$
.
The following theorem will immediately imply Theorem 1.2, which in turn implies Theorem 1.1.
Theorem 3.2. There exists
![]() $c>0$
such that the following holds. Let
$c>0$
such that the following holds. Let
![]() $n,d,m,N$
be positive integers,
$n,d,m,N$
be positive integers,
![]() $\mathbb {F}$
be a field and
$\mathbb {F}$
be a field and
![]() $0<\beta <1$
. Let
$0<\beta <1$
. Let
![]() $f_1,\dots ,f_m: (\mathbb {F}^{n})^{2}\rightarrow \mathbb {F}$
be polynomials of degree at most d, and let
$f_1,\dots ,f_m: (\mathbb {F}^{n})^{2}\rightarrow \mathbb {F}$
be polynomials of degree at most d, and let
![]() $V\subset \mathbb {F}^{n}$
such that
$V\subset \mathbb {F}^{n}$
such that
![]() $|V|=N$
. For
$|V|=N$
. For
![]() $I\subset [m]$
, let
$I\subset [m]$
, let
![]() $G_{I}$
be the digraph defined on V such that
$G_{I}$
be the digraph defined on V such that
![]() $(\mathbf {x},\mathbf {y})$
is an edge if
$(\mathbf {x},\mathbf {y})$
is an edge if
![]() $f_{i}(\mathbf {x},\mathbf {y})\neq 0$
for
$f_{i}(\mathbf {x},\mathbf {y})\neq 0$
for
![]() $i\in I$
and
$i\in I$
and
![]() $f_{i}(\mathbf {x},\mathbf {y})= 0$
for
$f_{i}(\mathbf {x},\mathbf {y})= 0$
for
![]() $i\not \in I$
. If N is sufficiently large, then either
$i\not \in I$
. If N is sufficiently large, then either
![]() $G_{\emptyset }$
contains a clique of size at least
$G_{\emptyset }$
contains a clique of size at least
![]() $N^{1-\beta }$
or there exists
$N^{1-\beta }$
or there exists
![]() $I\subset [m]$
,
$I\subset [m]$
,
![]() $I\neq \emptyset $
such that
$I\neq \emptyset $
such that
![]() $G_{I}$
contains a clique of size at least
$G_{I}$
contains a clique of size at least
![]() $\frac {1}{4m}N^{\beta /\gamma }$
, where
$\frac {1}{4m}N^{\beta /\gamma }$
, where
 $$ \begin{align*} \gamma=c n m\min\left\{d,\frac{n\log d}{\log n}\right\}. \end{align*} $$
$$ \begin{align*} \gamma=c n m\min\left\{d,\frac{n\log d}{\log n}\right\}. \end{align*} $$
Proof. For
![]() $i=1,\dots ,m$
, let
$i=1,\dots ,m$
, let
![]() $G_{i}$
be the algebraic digraph on V defined by
$G_{i}$
be the algebraic digraph on V defined by
![]() $f_{i}$
. Then
$f_{i}$
. Then
![]() $G_{I}=(\bigcap _{i\in I}G_{i})\cap (\bigcap _{i\in [m]\setminus I}\overline {G}_{i})$
. Here,
$G_{I}=(\bigcap _{i\in I}G_{i})\cap (\bigcap _{i\in [m]\setminus I}\overline {G}_{i})$
. Here,
![]() $\overline {G}_i$
is the digraph in which every directed edge is included that is not present in
$\overline {G}_i$
is the digraph in which every directed edge is included that is not present in
![]() $G_i$
.
$G_i$
.
Let
![]() $0<\alpha <1$
,
$0<\alpha <1$
,
![]() $s_{0,1}=\dots =s_{0,m}=\binom {n+d}{d}+1$
and
$s_{0,1}=\dots =s_{0,m}=\binom {n+d}{d}+1$
and
![]() $U_{0}=V$
. In what comes, we define the nested sequence of sets
$U_{0}=V$
. In what comes, we define the nested sequence of sets
![]() $U_{0}\supset U_{1}\supset \dots $
and sequence of positive integers
$U_{0}\supset U_{1}\supset \dots $
and sequence of positive integers
![]() $s_{\ell ,i}$
for
$s_{\ell ,i}$
for
![]() $\ell =0,1,\dots $
and
$\ell =0,1,\dots $
and
![]() $i\in [m]$
such that
$i\in [m]$
such that
![]() $G_{i}[U_{\ell }]$
contains no member of
$G_{i}[U_{\ell }]$
contains no member of
![]() $\mathcal {M}^{+}(s_{\ell ,i})$
. By Lemma 2.3, this is satisfied for
$\mathcal {M}^{+}(s_{\ell ,i})$
. By Lemma 2.3, this is satisfied for
![]() $\ell =0$
. Suppose that
$\ell =0$
. Suppose that
![]() $U_{\ell }$
and
$U_{\ell }$
and
![]() $s_{\ell ,i}$
has been already defined for some
$s_{\ell ,i}$
has been already defined for some
![]() $\ell \geq 0$
.
$\ell \geq 0$
.
Let
![]() $I\subset [m]$
be the set of indices i such that
$I\subset [m]$
be the set of indices i such that
![]() $s_{\ell ,i}>1$
. Consider three cases.
$s_{\ell ,i}>1$
. Consider three cases.
-
Case 1.
 $I=\emptyset $
.
$I=\emptyset $
.In this case, we stop and set
 $U=U_{\ell }$
. Note that
$U=U_{\ell }$
. Note that
 $G_{i}[U]$
is empty for
$G_{i}[U]$
is empty for
 $i=1,\dots ,m$
, so
$i=1,\dots ,m$
, so
 $G_{\emptyset }[U]$
is a clique.
$G_{\emptyset }[U]$
is a clique. -
Case 2. For every
 $i\in I$
, we have
$i\in I$
, we have
 $d([G_{i}][U_{\ell }])\geq 1-\alpha $
.
$d([G_{i}][U_{\ell }])\geq 1-\alpha $
.Let
 $G^{*}_{I}=\bigcap _{i\in I} [G_{i}]$
; then
$G^{*}_{I}=\bigcap _{i\in I} [G_{i}]$
; then
 $d(G^{*}_{I}[U_{\ell }])\geq 1-\alpha |I|\geq 1-\alpha m$
. Therefore, by Lemma 2.1,
$d(G^{*}_{I}[U_{\ell }])\geq 1-\alpha |I|\geq 1-\alpha m$
. Therefore, by Lemma 2.1,
 $G^{*}_{I}[U_{\ell }]$
contains a clique U of size at least
$G^{*}_{I}[U_{\ell }]$
contains a clique U of size at least
 $\frac {1}{4\alpha m}$
. Note that
$\frac {1}{4\alpha m}$
. Note that
 $G_{i}[U]$
is a clique for every
$G_{i}[U]$
is a clique for every
 $i\in I$
, and
$i\in I$
, and
 $G_{i}[U]$
is an independent set for every
$G_{i}[U]$
is an independent set for every
 $i\in [m]\setminus I$
, so
$i\in [m]\setminus I$
, so
 $G_{I}[U]$
is a clique. In this case, we stop as well.
$G_{I}[U]$
is a clique. In this case, we stop as well. -
Case 3. There exists
 $i\in I$
such that
$i\in I$
such that
 $d([G_{i}][U_{\ell }])< 1-\alpha $
.
$d([G_{i}][U_{\ell }])< 1-\alpha $
.Then by Lemma 3.1, there exist two disjoint sets A and B in
 $U_{\ell }$
such that
$U_{\ell }$
such that
 $|A|\geq c_1\alpha |U_{\ell }|$
,
$|A|\geq c_1\alpha |U_{\ell }|$
,
 $|B|\geq c_2 \alpha ^{n+1}|U_{\ell }|$
and
$|B|\geq c_2 \alpha ^{n+1}|U_{\ell }|$
and
 $(A,B)$
is well-directed in
$(A,B)$
is well-directed in
 $G_i$
. Let
$G_i$
. Let
 $t=\max \{1,\lfloor s_{\ell ,i}/n^{1/2}\rfloor \}$
and
$t=\max \{1,\lfloor s_{\ell ,i}/n^{1/2}\rfloor \}$
and
 $u=s_{\ell ,i}-t$
. Note that if
$u=s_{\ell ,i}-t$
. Note that if
 $G_{i}[A]$
contains a member of
$G_{i}[A]$
contains a member of
 $\mathcal {M}^{+}(u)$
and
$\mathcal {M}^{+}(u)$
and
 $G_{i}[B]$
contains a member of
$G_{i}[B]$
contains a member of
 $\mathcal {M}^{+}(t)$
, then
$\mathcal {M}^{+}(t)$
, then
 $G_{i}[U_{\ell }]$
contains a member of
$G_{i}[U_{\ell }]$
contains a member of
 $\mathcal {M}^{+}(s_{l,i})$
. Indeed, suppose that the directed edges
$\mathcal {M}^{+}(s_{l,i})$
. Indeed, suppose that the directed edges
 $(x_1,y_1),\dots ,(x_u,y_u)$
form a copy of a member of
$(x_1,y_1),\dots ,(x_u,y_u)$
form a copy of a member of
 $\mathcal {M}^{+}(u)$
in
$\mathcal {M}^{+}(u)$
in
 $G_{i}[A]$
and
$G_{i}[A]$
and
 $(x^{\prime }_1,y^{\prime }_1),\dots ,(x^{\prime }_t,y^{\prime }_t)$
form a copy of a member of
$(x^{\prime }_1,y^{\prime }_1),\dots ,(x^{\prime }_t,y^{\prime }_t)$
form a copy of a member of
 $\mathcal {M}^{+}(t)$
in
$\mathcal {M}^{+}(t)$
in
 $G_{i}[B]$
. If every edge between A and B goes from A to B, then setting
$G_{i}[B]$
. If every edge between A and B goes from A to B, then setting
 $x^{\prime }_{i+t}=x_i$
and
$x^{\prime }_{i+t}=x_i$
and
 $y^{\prime }_{i+t}=y_{i}$
for
$y^{\prime }_{i+t}=y_{i}$
for
 $i\in [u]$
, the edges
$i\in [u]$
, the edges
 $(x^{\prime }_1,y^{\prime }_1),\dots ,(x^{\prime }_{u+t},y^{\prime }_{u+t})$
form a copy of a member of
$(x^{\prime }_1,y^{\prime }_1),\dots ,(x^{\prime }_{u+t},y^{\prime }_{u+t})$
form a copy of a member of
 $\mathcal {M}^{+}(s_{l,i})$
. On the other hand, if every edge between A and B goes from B to A, then setting
$\mathcal {M}^{+}(s_{l,i})$
. On the other hand, if every edge between A and B goes from B to A, then setting
 $x_{i+u}=x^{\prime }_i$
and
$x_{i+u}=x^{\prime }_i$
and
 $y_{i+u}=y^{\prime }_{i}$
for
$y_{i+u}=y^{\prime }_{i}$
for
 $i\in [t]$
, the edges
$i\in [t]$
, the edges
 $(x_1,y_1),\dots ,(x_{u+t},y_{u+t})$
form a copy of a member of
$(x_1,y_1),\dots ,(x_{u+t},y_{u+t})$
form a copy of a member of
 $\mathcal {M}^{+}(s_{l,i})$
.
$\mathcal {M}^{+}(s_{l,i})$
.Therefore, either
 $G_{i}[A]$
contains no member of
$G_{i}[A]$
contains no member of
 $\mathcal {M}^{+}(u)$
, in which case set
$\mathcal {M}^{+}(u)$
, in which case set
 $U_{\ell +1}=A$
and
$U_{\ell +1}=A$
and
 $s_{\ell +1,i}=u$
and say that
$s_{\ell +1,i}=u$
and say that
 $\ell $
is a small-jump, or
$\ell $
is a small-jump, or
 $G_{i}[B]$
contains no member of
$G_{i}[B]$
contains no member of
 $\mathcal {M}(t)$
, in which case set
$\mathcal {M}(t)$
, in which case set
 $U_{\ell +1}=B$
,
$U_{\ell +1}=B$
,
 $s_{\ell +1,i}=t$
and say that
$s_{\ell +1,i}=t$
and say that
 $\ell $
is a big-jump. For
$\ell $
is a big-jump. For
 $j\in [m]\setminus \{i\}$
, set
$j\in [m]\setminus \{i\}$
, set
 $s_{\ell +1,j}=s_{\ell ,j}$
.
$s_{\ell +1,j}=s_{\ell ,j}$
.
Let
![]() $s_{\ell }=s_{\ell ,1}\dots s_{\ell ,m}\cdot n^{-z/2}$
, where z is the number of 1s among
$s_{\ell }=s_{\ell ,1}\dots s_{\ell ,m}\cdot n^{-z/2}$
, where z is the number of 1s among
![]() $s_{\ell ,1},\dots ,s_{\ell ,m}$
. Let L be the index
$s_{\ell ,1},\dots ,s_{\ell ,m}$
. Let L be the index
![]() $\ell $
at which we stop, let a be the number of big jumps, and let b be the number of small jumps. Note that if
$\ell $
at which we stop, let a be the number of big jumps, and let b be the number of small jumps. Note that if
![]() $\ell $
is a small jump, then
$\ell $
is a small jump, then
![]() $s_{\ell +1}\leq s_{\ell }(1-n^{-1/2}/2)$
and
$s_{\ell +1}\leq s_{\ell }(1-n^{-1/2}/2)$
and
![]() $|U_{\ell +1}|\geq c_1\alpha |U_{\ell }|$
. Also, if
$|U_{\ell +1}|\geq c_1\alpha |U_{\ell }|$
. Also, if
![]() $\ell $
is a big jump, then
$\ell $
is a big jump, then
![]() $s_{\ell +1}\leq s_{\ell }n^{-1/2}$
and
$s_{\ell +1}\leq s_{\ell }n^{-1/2}$
and
![]() $|U_{\ell +1}|\geq c_2\alpha ^{n+1}|U_{\ell }|$
. Therefore,
$|U_{\ell +1}|\geq c_2\alpha ^{n+1}|U_{\ell }|$
. Therefore,
As
![]() $s_{L}\geq n^{-m/2}$
and
$s_{L}\geq n^{-m/2}$
and
![]() $s_{0}=(\binom {n+d}{d}+1)^{m}\leq \min \{n^{dm},d^{nm}\}$
, we get
$s_{0}=(\binom {n+d}{d}+1)^{m}\leq \min \{n^{dm},d^{nm}\}$
, we get
 $$ \begin{align*} a\leq \frac{2\log (s_0/s_L)}{\log n}\leq 4m\min\left\{d,\frac{n\log d}{\log n}\right\} \end{align*} $$
$$ \begin{align*} a\leq \frac{2\log (s_0/s_L)}{\log n}\leq 4m\min\left\{d,\frac{n\log d}{\log n}\right\} \end{align*} $$
and
Also, we get
where
![]() $c_3=c_3(n,m,d)>0$
. Choosing
$c_3=c_3(n,m,d)>0$
. Choosing
![]() $\alpha =N^{-\beta /\gamma '}$
, where
$\alpha =N^{-\beta /\gamma '}$
, where
![]() $\gamma '=32mn\min \{d,n\log d/\log n\}$
, the left-hand side is at least
$\gamma '=32mn\min \{d,n\log d/\log n\}$
, the left-hand side is at least
![]() $N^{1-\beta }$
for sufficiently large N. Therefore, if we stopped in Case 1, then we found a set U such that
$N^{1-\beta }$
for sufficiently large N. Therefore, if we stopped in Case 1, then we found a set U such that
![]() $G_{\emptyset }[U]$
is a clique of size
$G_{\emptyset }[U]$
is a clique of size
![]() $|U_{L}|\geq N^{1-\beta }$
. On the other hand, if we stopped at Case 2, then we found
$|U_{L}|\geq N^{1-\beta }$
. On the other hand, if we stopped at Case 2, then we found
![]() $I\subset [m]$
,
$I\subset [m]$
,
![]() $I\neq [m]$
and a set U such that
$I\neq [m]$
and a set U such that
![]() $G_{I}[U]$
is a clique of size at least
$G_{I}[U]$
is a clique of size at least
![]() $\frac {1}{4m\alpha }\geq \frac {1}{4m}N^{\beta /\gamma '}$
. This finishes the proof.
$\frac {1}{4m\alpha }\geq \frac {1}{4m}N^{\beta /\gamma '}$
. This finishes the proof.
Proof of Theorem 1.2
Consider an algebraic colouring of
![]() $K_{N}$
of complexity
$K_{N}$
of complexity
![]() $(n,d,m)$
with t colours. Let the polynomials
$(n,d,m)$
with t colours. Let the polynomials
![]() $f_1,\dots ,f_{m}$
define the colouring of
$f_1,\dots ,f_{m}$
define the colouring of
![]() $K_{N}$
. Apply Theorem 3.2 with
$K_{N}$
. Apply Theorem 3.2 with
![]() $\beta =1/2$
. Then there exists
$\beta =1/2$
. Then there exists
![]() $I\subset [m]$
such that
$I\subset [m]$
such that
![]() $G_{I}$
contains a clique of size at least
$G_{I}$
contains a clique of size at least
![]() $\frac {1}{4m}N^{1/2\gamma }$
, where
$\frac {1}{4m}N^{1/2\gamma }$
, where
 $$ \begin{align*} \gamma=c n m\min\left\{d,\frac{n\log d}{\log n}\right\}. \end{align*} $$
$$ \begin{align*} \gamma=c n m\min\left\{d,\frac{n\log d}{\log n}\right\}. \end{align*} $$
Note that for every
![]() $I\subset [m]$
, the graph
$I\subset [m]$
, the graph
![]() $G_{I}$
is monochromatic; hence,
$G_{I}$
is monochromatic; hence,
![]() $K_{N}$
contains a monochromatic clique of size at least
$K_{N}$
contains a monochromatic clique of size at least
![]() $\frac {1}{4m}N^{1/2\gamma }$
.
$\frac {1}{4m}N^{1/2\gamma }$
.
4 Regularity lemma for algebraic hypergraphs
In this section, we prove Theorem 1.5. We remark that in the rest of the paper, we shall only work with undirected hypergraphs. We prepare the proof of Theorem 1.5 with several lemmas. The following regularity lemma is proved in [Reference Fox, Pach and Suk27] for hypergraphs of bounded VC-dimension; however, the same proof works almost word for word for hypergraphs of bounded weak-VC-dimension as well.
Lemma 4.1. Let r be a positive integer and
![]() $c,n>0$
. Then there exists
$c,n>0$
. Then there exists
![]() $c'=c'(r,c,n)>0$
such that the following holds. Let
$c'=c'(r,c,n)>0$
such that the following holds. Let
![]() $0<\epsilon <1/4$
. Let
$0<\epsilon <1/4$
. Let
![]() $\mathcal {H}$
be an r-uniform hypergraph of weak-VC-dimension
$\mathcal {H}$
be an r-uniform hypergraph of weak-VC-dimension
![]() $(c,n)$
. Then
$(c,n)$
. Then
![]() $V(\mathcal {H})$
has an equitable partition
$V(\mathcal {H})$
has an equitable partition
![]() $V_1,\dots ,V_K$
with
$V_1,\dots ,V_K$
with
![]() $8/\epsilon <K<c'(1/\epsilon )^{2n+1}$
parts such that all but at most
$8/\epsilon <K<c'(1/\epsilon )^{2n+1}$
parts such that all but at most
![]() $\epsilon $
-fraction of the r-tuples of parts are
$\epsilon $
-fraction of the r-tuples of parts are
![]() $\epsilon $
-homogeneous.
$\epsilon $
-homogeneous.
Let us restate the definition of
![]() $\mathcal {M}(r,s)$
for undirected hypergraphs. The hypergraph
$\mathcal {M}(r,s)$
for undirected hypergraphs. The hypergraph
![]() $\mathcal {M}$
is a member of
$\mathcal {M}$
is a member of
![]() $\mathcal {M}(r,s)$
if the vertex set of
$\mathcal {M}(r,s)$
if the vertex set of
![]() $\mathcal {M}$
is the union of (not necessarily disjoint)
$\mathcal {M}$
is the union of (not necessarily disjoint)
![]() $(r-1)$
-element sets
$(r-1)$
-element sets
![]() $Z_{1},\dots ,Z_{s}$
and s vertices
$Z_{1},\dots ,Z_{s}$
and s vertices
![]() $z_{1},\dots ,z_{s}$
,
$z_{1},\dots ,z_{s}$
,
![]() $Z_{i}\cup \{z_{i}\}$
is an edge of
$Z_{i}\cup \{z_{i}\}$
is an edge of
![]() $\mathcal {M}$
for
$\mathcal {M}$
for
![]() $i\in [s]$
, and
$i\in [s]$
, and
![]() $Z_{i}\cup \{z_{j}\}$
is not an edge for
$Z_{i}\cup \{z_{j}\}$
is not an edge for
![]() $1\leq i<j\leq s$
. The rest of the r-tuples can be either edges or non-edges. If
$1\leq i<j\leq s$
. The rest of the r-tuples can be either edges or non-edges. If
![]() $Z_1,\dots ,Z_{s}$
and
$Z_1,\dots ,Z_{s}$
and
![]() $z_1,\dots ,z_s$
satisfy these properties, say that they define a member of
$z_1,\dots ,z_s$
satisfy these properties, say that they define a member of
![]() $\mathcal {M}(r,s)$
.
$\mathcal {M}(r,s)$
.
In what follows, we show that if we also assume that
![]() $\mathcal {H}$
contains no member of
$\mathcal {H}$
contains no member of
![]() $\mathcal {M}(r,s)$
, then those r-tuples of parts that have density at most
$\mathcal {M}(r,s)$
, then those r-tuples of parts that have density at most
![]() $\epsilon $
can be made empty by removing a few vertices. We first need the following technical lemma, which can be viewed as a variant of Claim 2.5 for sparse hypergraphs.
$\epsilon $
can be made empty by removing a few vertices. We first need the following technical lemma, which can be viewed as a variant of Claim 2.5 for sparse hypergraphs.
Lemma 4.2. Let
![]() $\mathcal {G}$
be a nonempty r-partite r-uniform hypergraph with vertex classes
$\mathcal {G}$
be a nonempty r-partite r-uniform hypergraph with vertex classes
![]() $W_1,\dots ,W_r$
such that
$W_1,\dots ,W_r$
such that
![]() $d(W_1,\dots ,W_r)\leq \epsilon $
. Then there exist
$d(W_1,\dots ,W_r)\leq \epsilon $
. Then there exist
![]() $\ell \in [r]$
and
$\ell \in [r]$
and
![]() $X\in \bigcup _{i\in [r]\setminus \{\ell \}}W_{i}$
such that
$X\in \bigcup _{i\in [r]\setminus \{\ell \}}W_{i}$
such that
![]() $|X|=r-1$
and
$|X|=r-1$
and
![]() $1\leq |N(X)|\leq \epsilon ^{1/r}|W_{\ell }|$
.
$1\leq |N(X)|\leq \epsilon ^{1/r}|W_{\ell }|$
.
Proof. We proceed by induction on r. In case
![]() $r=1$
, the statement is trivial, so assume
$r=1$
, the statement is trivial, so assume
![]() $r\geq 2$
.
$r\geq 2$
.
Let
![]() $U\subset V(\mathcal {G})$
be the set of vertices with positive degree, and let
$U\subset V(\mathcal {G})$
be the set of vertices with positive degree, and let
![]() $U_i=W_i\cap U$
for
$U_i=W_i\cap U$
for
![]() $i\in [r]$
. Then
$i\in [r]$
. Then
![]() $|U_1|\cdots |U_r|\geq \epsilon |W_1|\cdots |W_{r}|$
, so there exists
$|U_1|\cdots |U_r|\geq \epsilon |W_1|\cdots |W_{r}|$
, so there exists
![]() $j\in [r]$
such that
$j\in [r]$
such that
![]() $|U_j|\geq \epsilon ^{1/r}|W_j|$
. Without loss of generality, assume that
$|U_j|\geq \epsilon ^{1/r}|W_j|$
. Without loss of generality, assume that
![]() $j=r$
. Then by simple averaging, there exists
$j=r$
. Then by simple averaging, there exists
![]() $x\in U_r$
such that
$x\in U_r$
such that
Let
![]() $\mathcal {G}'$
be the
$\mathcal {G}'$
be the
![]() $(r-1)$
-partite
$(r-1)$
-partite
![]() $(r-1)$
-uniform hypergraph with vertex classes
$(r-1)$
-uniform hypergraph with vertex classes
![]() $W_1,\dots ,W_{r-1}$
formed by the neighbourhood of x. By our induction hypothesis, there exist
$W_1,\dots ,W_{r-1}$
formed by the neighbourhood of x. By our induction hypothesis, there exist
![]() $\ell \in [r-1]$
and
$\ell \in [r-1]$
and
![]() $X'\in \bigcup _{i\in [r-1]\setminus \{\ell \}}W_{i}$
such that
$X'\in \bigcup _{i\in [r-1]\setminus \{\ell \}}W_{i}$
such that
![]() $|X'|=r-2$
and
$|X'|=r-2$
and
![]() $1\leq |N(X')|\leq \epsilon ^{1/r}|W_{\ell }|$
. But then
$1\leq |N(X')|\leq \epsilon ^{1/r}|W_{\ell }|$
. But then
![]() $\ell $
and
$\ell $
and
![]() $X=X'\cup \{x\}$
satisfy our desired properties.
$X=X'\cup \{x\}$
satisfy our desired properties.
The next lemma will be the heart of the proof of Theorem 1.5. Before we state it, let us introduce a definition. Let
![]() $\mathcal {H}$
be an r-uniform hypergraph, and let
$\mathcal {H}$
be an r-uniform hypergraph, and let
![]() $(V_{1},\dots ,V_{K})$
be disjoint subsets of its vertex set. Suppose that
$(V_{1},\dots ,V_{K})$
be disjoint subsets of its vertex set. Suppose that
![]() $Z_{1},\dots ,Z_{s}\in V(\mathcal {H})^{(r-1)}$
and
$Z_{1},\dots ,Z_{s}\in V(\mathcal {H})^{(r-1)}$
and
![]() $z_{1},\dots ,z_{s}\in V(\mathcal {H})$
define a member of
$z_{1},\dots ,z_{s}\in V(\mathcal {H})$
define a member of
![]() $\mathcal {M}(r,s)$
in
$\mathcal {M}(r,s)$
in
![]() $\mathcal {H}$
. If
$\mathcal {H}$
. If
![]() $z_{1},\dots ,z_{s}$
belong to the same part
$z_{1},\dots ,z_{s}$
belong to the same part
![]() $V_{j}$
, and no two vertices of
$V_{j}$
, and no two vertices of
![]() $Z_{i}\cup \{z_{i}\}$
belong to the same part for
$Z_{i}\cup \{z_{i}\}$
belong to the same part for
![]() $i\in [s]$
, then say that
$i\in [s]$
, then say that
![]() $\bigcup _{i=1}^{s} Z_{i}\cup \{z_1,\dots ,z_{s}\}$
induces a focused copy of a member of
$\bigcup _{i=1}^{s} Z_{i}\cup \{z_1,\dots ,z_{s}\}$
induces a focused copy of a member of
![]() $\mathcal {M}(r,s)$
and
$\mathcal {M}(r,s)$
and
![]() $Z_{1},\dots ,Z_{s}$
and
$Z_{1},\dots ,Z_{s}$
and
![]() $z_{1},\dots ,z_{s}$
defines a focused member of
$z_{1},\dots ,z_{s}$
defines a focused member of
![]() $\mathcal {M}(r,s)$
.
$\mathcal {M}(r,s)$
.
Lemma 4.3. Let
![]() $r,s$
be positive integers. Then there exists
$r,s$
be positive integers. Then there exists
![]() $c=c(r,s)>0$
such that the following holds. Let
$c=c(r,s)>0$
such that the following holds. Let
![]() $\epsilon _0>0$
, let
$\epsilon _0>0$
, let
![]() $\mathcal {H}$
be an r-uniform hypergraph, and let
$\mathcal {H}$
be an r-uniform hypergraph, and let
![]() $U_{1},\dots ,U_{L}$
be disjoint subsets of
$U_{1},\dots ,U_{L}$
be disjoint subsets of
![]() $V(\mathcal {H})$
. Suppose that
$V(\mathcal {H})$
. Suppose that
![]() $\mathcal {H}$
contains no focused copy of a member of
$\mathcal {H}$
contains no focused copy of a member of
![]() $\mathcal {M}(r,s)$
. Let
$\mathcal {M}(r,s)$
. Let
![]() $\mathcal {G}$
be an r-uniform hypergraph on
$\mathcal {G}$
be an r-uniform hypergraph on
![]() $[L]$
such that if
$[L]$
such that if
![]() $\{i_1,\dots ,i_r\}$
is an edge of
$\{i_1,\dots ,i_r\}$
is an edge of
![]() $\mathcal {G}$
; then
$\mathcal {G}$
; then
![]() $d_{\mathcal {H}}(U_{i_1},\dots ,U_{i_r})\leq \epsilon _0$
. Then for
$d_{\mathcal {H}}(U_{i_1},\dots ,U_{i_r})\leq \epsilon _0$
. Then for
![]() $i\in [L]$
, there exists
$i\in [L]$
, there exists
![]() $V_{i}\subset U_{i}$
such that
$V_{i}\subset U_{i}$
such that
![]() $|V_{i}|\geq (1-c\epsilon _0^{1/r!})|U_i|$
, and
$|V_{i}|\geq (1-c\epsilon _0^{1/r!})|U_i|$
, and
![]() $(V_{i_1},\dots ,V_{i_r})$
is empty for every
$(V_{i_1},\dots ,V_{i_r})$
is empty for every
![]() $\{i_1,\dots ,i_r\}\in E(\mathcal {G})$
.
$\{i_1,\dots ,i_r\}\in E(\mathcal {G})$
.
Proof. We prove this by induction on r. We proceed with the base case
![]() $r=2$
and the general case
$r=2$
and the general case
![]() $r\geq 3$
simultaneously. Let
$r\geq 3$
simultaneously. Let
![]() $T:=\emptyset $
, and let
$T:=\emptyset $
, and let
![]() $\epsilon _1=\epsilon _0^{1/r}$
. Let
$\epsilon _1=\epsilon _0^{1/r}$
. Let
![]() $X\in [L]^{(r-1)}$
and
$X\in [L]^{(r-1)}$
and
![]() $k\in [L]\setminus X$
. If
$k\in [L]\setminus X$
. If
![]() $X\cup \{k\}\not \in E(\mathcal {G})$
, set
$X\cup \{k\}\not \in E(\mathcal {G})$
, set
![]() $F_{X,k}=\emptyset $
. Otherwise, let
$F_{X,k}=\emptyset $
. Otherwise, let
![]() $F_{X,k}$
be the
$F_{X,k}$
be the
![]() $(r-1)$
-partite
$(r-1)$
-partite
![]() $(r-1)$
-uniform hypergraph on
$(r-1)$
-uniform hypergraph on
![]() $\bigcup _{x\in X}U_{x}$
whose edges are the
$\bigcup _{x\in X}U_{x}$
whose edges are the
![]() $(r-1)$
-tuples
$(r-1)$
-tuples
![]() $Z\in V(\mathcal {H})^{(r-1)}$
such that Z has one vertex in
$Z\in V(\mathcal {H})^{(r-1)}$
such that Z has one vertex in
![]() $U_{x}$
for
$U_{x}$
for
![]() $x\in X$
and
$x\in X$
and
![]() $|N_{\mathcal {H}}(Z)\cap U_{k}|\geq \epsilon _{1} |U_{k}|$
. As
$|N_{\mathcal {H}}(Z)\cap U_{k}|\geq \epsilon _{1} |U_{k}|$
. As
![]() $d_{\mathcal {H}}(\{U_{x}\}_{x\in X},U_{k})\leq \epsilon _{0}$
, we have
$d_{\mathcal {H}}(\{U_{x}\}_{x\in X},U_{k})\leq \epsilon _{0}$
, we have
Also, define
![]() $T_{k}\subset U_{k}$
as the union of the sets
$T_{k}\subset U_{k}$
as the union of the sets
![]() $U_{k}\cap N_{\mathcal {H}}(Z')$
, where
$U_{k}\cap N_{\mathcal {H}}(Z')$
, where
![]() $Z'\in (V(\mathcal {H})\setminus U_{k})^{(r-1)}$
has all its vertices in different parts and
$Z'\in (V(\mathcal {H})\setminus U_{k})^{(r-1)}$
has all its vertices in different parts and
![]() $|U_{k}\cap N_{\mathcal {H}}(Z')|\leq \epsilon _{1}|U_{k}|$
.
$|U_{k}\cap N_{\mathcal {H}}(Z')|\leq \epsilon _{1}|U_{k}|$
.
Claim 4.4.
Proof. Suppose that
![]() $|T_{k}|>s\epsilon _{1}|U_{k}|$
. Then we can find greedily
$|T_{k}|>s\epsilon _{1}|U_{k}|$
. Then we can find greedily
![]() $Z_{1},\dots ,Z_{s}\in (V(\mathcal {H})\setminus U_{k})^{(r-1)}$
and
$Z_{1},\dots ,Z_{s}\in (V(\mathcal {H})\setminus U_{k})^{(r-1)}$
and
![]() $z_{1},\dots ,z_{s}\in T_{k}$
such that
$z_{1},\dots ,z_{s}\in T_{k}$
such that
![]() $z_{i}\in N(Z_{i})$
for
$z_{i}\in N(Z_{i})$
for
![]() $i\in [s]$
and
$i\in [s]$
and
![]() $z_{i}\not \in N(Z_{j})$
for
$z_{i}\not \in N(Z_{j})$
for
![]() $i>j$
. But then
$i>j$
. But then
![]() $Z_{1},\dots ,Z_{s}$
and
$Z_{1},\dots ,Z_{s}$
and
![]() $z_1\dots ,z_s$
induces a focused copy of a member of
$z_1\dots ,z_s$
induces a focused copy of a member of
![]() $\mathcal {M}(r,s)$
, a contradiction.
$\mathcal {M}(r,s)$
, a contradiction.
For
![]() $k\in [L]$
, let
$k\in [L]$
, let
![]() $U^{\prime }_{k}=U_{k}\setminus T_{k}$
. Note that if
$U^{\prime }_{k}=U_{k}\setminus T_{k}$
. Note that if
![]() $X\cup \{k\}\in E(\mathcal {G})$
and
$X\cup \{k\}\in E(\mathcal {G})$
and
![]() $Z\cup \{z\}$
is an edge of
$Z\cup \{z\}$
is an edge of
![]() $\mathcal {H}$
for some Z having one vertex in every
$\mathcal {H}$
for some Z having one vertex in every
![]() $U^{\prime }_{x}, x\in X$
and
$U^{\prime }_{x}, x\in X$
and
![]() $z\in U^{\prime }_{k}$
, then
$z\in U^{\prime }_{k}$
, then
![]() $Z\in E(F_{X,k})$
. Remove every edge Z from
$Z\in E(F_{X,k})$
. Remove every edge Z from
![]() $F_{X,k}$
that has no neighbor in
$F_{X,k}$
that has no neighbor in
![]() $U^{\prime }_{k}$
. Let
$U^{\prime }_{k}$
. Let
![]() $F_{X}=\bigcup _{k\in [L]\setminus X}F_{X,k}$
.
$F_{X}=\bigcup _{k\in [L]\setminus X}F_{X,k}$
.
Now let us consider the base case
![]() $r=2$
. Then every
$r=2$
. Then every
![]() $F_{X,k}$
is a just a subset of
$F_{X,k}$
is a just a subset of
![]() $U_X$
, which by (4.1) has size at most
$U_X$
, which by (4.1) has size at most
![]() $\epsilon _1|U_X|$
. This implies that
$\epsilon _1|U_X|$
. This implies that
![]() $|F_{X}|\leq s\epsilon _1 |U_{X}|$
for
$|F_{X}|\leq s\epsilon _1 |U_{X}|$
for
![]() $X\in [L]$
. Indeed, otherwise, by a simple greedy argument, we can find
$X\in [L]$
. Indeed, otherwise, by a simple greedy argument, we can find
![]() $z_1,\dots ,z_{s}\in F_{X}$
and
$z_1,\dots ,z_{s}\in F_{X}$
and
![]() $k_1,\dots ,k_s$
such that
$k_1,\dots ,k_s$
such that
![]() $z_{i}\in F_{X,k_i}$
and
$z_{i}\in F_{X,k_i}$
and
![]() $z_{i}\not \in F_{X,k_j}$
for
$z_{i}\not \in F_{X,k_j}$
for
![]() $i>j$
. Choose an arbitrary vertex
$i>j$
. Choose an arbitrary vertex
![]() $w_{i}\in N(z_{i})\cap U^{\prime }_{k_i}$
. Then
$w_{i}\in N(z_{i})\cap U^{\prime }_{k_i}$
. Then
![]() $w_1,\dots ,w_{s}$
and
$w_1,\dots ,w_{s}$
and
![]() $z_1,\dots ,z_n$
define a focused copy of a member of
$z_1,\dots ,z_n$
define a focused copy of a member of
![]() $\mathcal {M}(2,s)$
, a contradiction. For
$\mathcal {M}(2,s)$
, a contradiction. For
![]() $i\in [L]$
, set
$i\in [L]$
, set
![]() $V_{i}=U^{\prime }_{i}\setminus F_{i}$
. Then
$V_{i}=U^{\prime }_{i}\setminus F_{i}$
. Then
![]() $|V_{i}|\geq |U_{i}|(1-2s\epsilon _1)$
, and there are no edges between
$|V_{i}|\geq |U_{i}|(1-2s\epsilon _1)$
, and there are no edges between
![]() $V_{i}$
and
$V_{i}$
and
![]() $V_j$
for
$V_j$
for
![]() $\{i,j\}\in E(\mathcal {G})$
. Therefore, choosing
$\{i,j\}\in E(\mathcal {G})$
. Therefore, choosing
![]() $c(2,s)=2s$
proves this case. Now consider the general case
$c(2,s)=2s$
proves this case. Now consider the general case
![]() $r\geq 3$
.
$r\geq 3$
.
Claim 4.5.
Proof. Let
![]() $F:=F_{X}$
, let
$F:=F_{X}$
, let
![]() $W_{x}:=U^{\prime }_{x}$
for
$W_{x}:=U^{\prime }_{x}$
for
![]() $x\in X$
. In what follows, step by step, we define
$x\in X$
. In what follows, step by step, we define
![]() $|X|$
sequences of pairs
$|X|$
sequences of pairs
![]() $(Z_{i,x},z_{i,x})\in (\bigcup _{y\in X\setminus \{x\}} U^{\prime }_{y})^{(r-1)}\times U^{\prime }_{x}$
for
$(Z_{i,x},z_{i,x})\in (\bigcup _{y\in X\setminus \{x\}} U^{\prime }_{y})^{(r-1)}\times U^{\prime }_{x}$
for
![]() $x\in X$
and
$x\in X$
and
![]() $i=0,1,\dots $
, while removing elements from
$i=0,1,\dots $
, while removing elements from
![]() $W_{x}$
and edges from F. Suppose that
$W_{x}$
and edges from F. Suppose that
![]() $j_x$
is the largest index i for which
$j_x$
is the largest index i for which
![]() $(Z_{i,x},z_{i,x})$
is already defined. If
$(Z_{i,x},z_{i,x})$
is already defined. If
![]() $(\{W_{x}\}_{x\in X})$
spans no edge in F, then stop. Otherwise, there exists
$(\{W_{x}\}_{x\in X})$
spans no edge in F, then stop. Otherwise, there exists
![]() $k\in [L]$
such that
$k\in [L]$
such that
![]() $F_{X,k}$
is not empty on
$F_{X,k}$
is not empty on
![]() $(\{W_{x}\}_{x\in X})$
. By applying Lemma 4.2 to the
$(\{W_{x}\}_{x\in X})$
. By applying Lemma 4.2 to the
![]() $(r-1)$
-tuple
$(r-1)$
-tuple
![]() $(\{U_x\}_{x\in X})$
and hypergraph
$(\{U_x\}_{x\in X})$
and hypergraph
![]() $F_{X,k}\cap F$
(which by (4.1) has density at most
$F_{X,k}\cap F$
(which by (4.1) has density at most
![]() $\epsilon _1^{r-1}$
), there exist
$\epsilon _1^{r-1}$
), there exist
![]() $x\in X$
and
$x\in X$
and
![]() $Z\in \bigcup _{y\in X\setminus \{x\}} W_{y}$
such that
$Z\in \bigcup _{y\in X\setminus \{x\}} W_{y}$
such that
![]() $1\leq |N_{F_{X,k}\cap F}(Z)\cap W_{x}|\leq \epsilon _1|U_{x}|$
. Let
$1\leq |N_{F_{X,k}\cap F}(Z)\cap W_{x}|\leq \epsilon _1|U_{x}|$
. Let
![]() $z_{j_{x}+1,x}$
be an arbitrary element of
$z_{j_{x}+1,x}$
be an arbitrary element of
![]() $N_{F_{X,k}\cap F}(Z)\cap W_{x}$
. Furthermore, remove the elements of
$N_{F_{X,k}\cap F}(Z)\cap W_{x}$
. Furthermore, remove the elements of
![]() $N_{F_{X,k}\cap F}(Z)$
from
$N_{F_{X,k}\cap F}(Z)$
from
![]() $W_{x}$
, and remove the edges of
$W_{x}$
, and remove the edges of
![]() $F_{X,k}$
from F. Also, let
$F_{X,k}$
from F. Also, let
![]() $Z_{j_{x}+1,x}:=Z$
and define
$Z_{j_{x}+1,x}:=Z$
and define
![]() $k_{j_x+1,x}:=k$
.
$k_{j_x+1,x}:=k$
.
After we stop, let
![]() $s_x$
be the largest index i such that
$s_x$
be the largest index i such that
![]() $(Z_{i,x},z_{i,x})$
is defined. Note that for every
$(Z_{i,x},z_{i,x})$
is defined. Note that for every
![]() $x\in X$
and
$x\in X$
and
![]() $i\leq s_x$
,
$i\leq s_x$
,
![]() $Z_{1,x},\dots ,Z_{i,x}$
and
$Z_{1,x},\dots ,Z_{i,x}$
and
![]() $z_{1,x},\dots ,z_{i,x}$
define a focused copy of a member of
$z_{1,x},\dots ,z_{i,x}$
define a focused copy of a member of
![]() $\mathcal {M}(r-1,i)$
. Let
$\mathcal {M}(r-1,i)$
. Let
![]() $u_{i,x}$
be an arbitrary element of
$u_{i,x}$
be an arbitrary element of
![]() $U^{\prime }_{k_{i,x}}\cap N_{\mathcal {H}}(Z_{i,x}\cup \{z_{i,x}\})$
. Then
$U^{\prime }_{k_{i,x}}\cap N_{\mathcal {H}}(Z_{i,x}\cup \{z_{i,x}\})$
. Then
![]() $Z_{1,x}\cup \{u_{1,x}\},\dots ,Z_{i,x}\cup \{u_{i,x}\}$
and
$Z_{1,x}\cup \{u_{1,x}\},\dots ,Z_{i,x}\cup \{u_{i,x}\}$
and
![]() $z_{1,x},\dots ,z_{i,x}$
define a focused copy of a member of
$z_{1,x},\dots ,z_{i,x}$
define a focused copy of a member of
![]() $\mathcal {M}(r,i)$
in
$\mathcal {M}(r,i)$
in
![]() $\mathcal {H}$
. Therefore, we have
$\mathcal {H}$
. Therefore, we have
![]() $s_x<s$
. Also, at each step, when we modify
$s_x<s$
. Also, at each step, when we modify
![]() $W_x$
, we remove at most
$W_x$
, we remove at most
![]() $\epsilon _1|U_{x}|$
elements; so after we stop, we have
$\epsilon _1|U_{x}|$
elements; so after we stop, we have
![]() $|W_x|\geq |U^{\prime }_{x}|-s_{x}\epsilon _1|U_{x}|$
.
$|W_x|\geq |U^{\prime }_{x}|-s_{x}\epsilon _1|U_{x}|$
.
Let us bound
![]() $d_{F_{X}}(\{U_{x}\}_{x\in X})$
. Recall that
$d_{F_{X}}(\{U_{x}\}_{x\in X})$
. Recall that
![]() $d_{F_{X,k_{i,x}}}(\{U_{x}\}_{x\in X}) \leq \epsilon _1^{r-1}$
by (4.1). Let
$d_{F_{X,k_{i,x}}}(\{U_{x}\}_{x\in X}) \leq \epsilon _1^{r-1}$
by (4.1). Let
![]() $F^{*}=\bigcup _{x\in X}\bigcup _{i\in [s_x]} F_{X,k_{i,x}}$
. Then
$F^{*}=\bigcup _{x\in X}\bigcup _{i\in [s_x]} F_{X,k_{i,x}}$
. Then
If
![]() $k\neq k_{i,x}$
for every
$k\neq k_{i,x}$
for every
![]() $x\in X$
and
$x\in X$
and
![]() $i\in [s_x]$
, then every edge of
$i\in [s_x]$
, then every edge of
![]() $F_{k,X}$
touches
$F_{k,X}$
touches
![]() $U_{x}\setminus W_{x}$
for some
$U_{x}\setminus W_{x}$
for some
![]() $x\in X$
. Note that
$x\in X$
. Note that
![]() $|U_{x}\setminus W_{x}|=|U_{x}\setminus U^{\prime }_{x}|+|U^{\prime }_{x}\setminus W_{x}| \leq 2s\epsilon _1|U_x|$
. Hence
$|U_{x}\setminus W_{x}|=|U_{x}\setminus U^{\prime }_{x}|+|U^{\prime }_{x}\setminus W_{x}| \leq 2s\epsilon _1|U_x|$
. Hence
![]() $\frac {|U_{x}\setminus W_{x}|}{|U_{x}|}< 2s\epsilon _1$
. Therefore, we have
$\frac {|U_{x}\setminus W_{x}|}{|U_{x}|}< 2s\epsilon _1$
. Therefore, we have
Finally, by our construction,
![]() $(\{W_{x}\}_{x\in X})$
spans no edges. Thus,
$(\{W_{x}\}_{x\in X})$
spans no edges. Thus,
![]() $d_{F_{X}}(\{U_{x}\}_{x\in X})<3rs\epsilon _1.$
$d_{F_{X}}(\{U_{x}\}_{x\in X})<3rs\epsilon _1.$
Since
![]() $|U^{\prime }_x| \geq (1-s\epsilon _1)|U_x|$
, we can write
$|U^{\prime }_x| \geq (1-s\epsilon _1)|U_x|$
, we can write
![]() $\prod _{x \in X} |U^{\prime }_x| \geq (1-s\epsilon _1)^{r-1}\prod _{x \in X} |U_x| \geq \frac {1}{2} \prod _{x \in X} |U_x|$
, assuming
$\prod _{x \in X} |U^{\prime }_x| \geq (1-s\epsilon _1)^{r-1}\prod _{x \in X} |U_x| \geq \frac {1}{2} \prod _{x \in X} |U_x|$
, assuming
![]() $s\epsilon _1<1/10r$
. Therefore, from the last claim, we have that
$s\epsilon _1<1/10r$
. Therefore, from the last claim, we have that
![]() $d_{F_{X}}(\{U^{\prime }_{x}\}_{x\in X})\leq 6rs\epsilon _1$
.
$d_{F_{X}}(\{U^{\prime }_{x}\}_{x\in X})\leq 6rs\epsilon _1$
.
Let
![]() $\mathcal {H}'=\bigcup _{X\in [L]^{(r-1)}}F_{X}$
. We show that
$\mathcal {H}'=\bigcup _{X\in [L]^{(r-1)}}F_{X}$
. We show that
![]() $\mathcal {H}'$
contains no focused copy of a member of
$\mathcal {H}'$
contains no focused copy of a member of
![]() $\mathcal {M}(r-1,s)$
with respect to the disjoint sets
$\mathcal {M}(r-1,s)$
with respect to the disjoint sets
![]() $U^{\prime }_1,\dots ,U^{\prime }_{L}$
. Otherwise, there exist
$U^{\prime }_1,\dots ,U^{\prime }_{L}$
. Otherwise, there exist
![]() $W_{1},\dots ,W_{s}\in V(\mathcal {H}')^{(r-2)}$
and
$W_{1},\dots ,W_{s}\in V(\mathcal {H}')^{(r-2)}$
and
![]() $w_{1},\dots ,w_{s}\in U^{\prime }_j$
for some
$w_{1},\dots ,w_{s}\in U^{\prime }_j$
for some
![]() $j\in [L]$
defining a focused member of
$j\in [L]$
defining a focused member of
![]() $\mathcal {M}(r-1,s)$
. Let
$\mathcal {M}(r-1,s)$
. Let
![]() $Z_{i}=W_{i}\cup \{w_i\}$
. But then for
$Z_{i}=W_{i}\cup \{w_i\}$
. But then for
![]() $i\in [s]$
, there exist
$i\in [s]$
, there exist
![]() $k_i\in [L]$
and
$k_i\in [L]$
and
![]() $X_{i}\in [L]^{(r-1)}$
such that
$X_{i}\in [L]^{(r-1)}$
such that
![]() $Z_{i}\in F_{X_{i},k_i}$
. Picking
$Z_{i}\in F_{X_{i},k_i}$
. Picking
![]() $z_{i}\in N_{\mathcal {H}}(Z_{i})\cap U_{i}'$
arbitrarily,
$z_{i}\in N_{\mathcal {H}}(Z_{i})\cap U_{i}'$
arbitrarily,
![]() $\{W_{i}\cup \{z_i\}\}_{i\in [s]}$
and
$\{W_{i}\cup \{z_i\}\}_{i\in [s]}$
and
![]() $\{w_{i}\}_{i\in [s]}$
define a focused member of
$\{w_{i}\}_{i\in [s]}$
define a focused member of
![]() $\mathcal {M}(r,s)$
in
$\mathcal {M}(r,s)$
in
![]() $\mathcal {H}$
, a contradiction.
$\mathcal {H}$
, a contradiction.
But then we can apply our induction hypothesis with the following parameters: the
![]() $(r-1)$
-uniform hypergraph
$(r-1)$
-uniform hypergraph
![]() $\mathcal {H}'$
instead of
$\mathcal {H}'$
instead of
![]() $\mathcal {H}$
, the disjoint sets
$\mathcal {H}$
, the disjoint sets
![]() $U_1',\dots ,U_{L}'$
instead of
$U_1',\dots ,U_{L}'$
instead of
![]() $U_1,\dots ,U_L$
,
$U_1,\dots ,U_L$
,
![]() $6rs\epsilon _1$
instead of
$6rs\epsilon _1$
instead of
![]() $\epsilon _0$
and the complete
$\epsilon _0$
and the complete
![]() $(r-1)$
-uniform hypergraph on
$(r-1)$
-uniform hypergraph on
![]() $[L]$
instead of
$[L]$
instead of
![]() $\mathcal {G}$
. Recalling that
$\mathcal {G}$
. Recalling that
![]() $|U^{\prime }_i| \geq (1-s\epsilon _1)|U_i|$
and
$|U^{\prime }_i| \geq (1-s\epsilon _1)|U_i|$
and
![]() $\epsilon _1=\epsilon _0^{1/r}$
, we conclude that for
$\epsilon _1=\epsilon _0^{1/r}$
, we conclude that for
![]() $i\in [L]$
, there exists
$i\in [L]$
, there exists
![]() $V_{i}\subset U_{i}'$
such that
$V_{i}\subset U_{i}'$
such that
for some suitable
![]() $c(r,s)>0$
, and
$c(r,s)>0$
, and
![]() $(V_{i_1},V_{i_2},\dots ,V_{i_{r-1}})$
is empty for
$(V_{i_1},V_{i_2},\dots ,V_{i_{r-1}})$
is empty for
![]() $(i_1,\dots ,i_{r-1})\in [L]^{(r-1)}$
. But note that then
$(i_1,\dots ,i_{r-1})\in [L]^{(r-1)}$
. But note that then
![]() $(V_{i_1},\dots ,V_{i_r})$
is also empty in
$(V_{i_1},\dots ,V_{i_r})$
is also empty in
![]() $\mathcal {H}$
if
$\mathcal {H}$
if
![]() $\{i_1,\dots ,i_r\}\in E(\mathcal {G})$
. This finishes the proof.
$\{i_1,\dots ,i_r\}\in E(\mathcal {G})$
. This finishes the proof.
Now everything is set to prove the main theorem of this section.
Proof of Theorem 1.5
Let
![]() $\epsilon _0>0$
, which we shall specify later as a function of
$\epsilon _0>0$
, which we shall specify later as a function of
![]() $\epsilon $
. By Lemma 2.8 and Lemma 4.1, there exists an equitable partition of
$\epsilon $
. By Lemma 2.8 and Lemma 4.1, there exists an equitable partition of
![]() $V(\mathcal {H})$
into L parts
$V(\mathcal {H})$
into L parts
![]() $U_1,\dots ,U_L$
such that
$U_1,\dots ,U_L$
such that
![]() $8/\epsilon _{0}<L<c'(1/\epsilon _{0})^{2n+1}$
and all but at most
$8/\epsilon _{0}<L<c'(1/\epsilon _{0})^{2n+1}$
and all but at most
![]() $\epsilon _{0}$
-fraction of the r-tuples of parts are
$\epsilon _{0}$
-fraction of the r-tuples of parts are
![]() $\epsilon _{0}$
-homogeneous.
$\epsilon _{0}$
-homogeneous.
Let
![]() $s=\binom {n+d}{d}+1$
; then
$s=\binom {n+d}{d}+1$
; then
![]() $\mathcal {H}$
contains no member of
$\mathcal {H}$
contains no member of
![]() $\mathcal {M}(r,s)$
by Lemma 2.3. In particular,
$\mathcal {M}(r,s)$
by Lemma 2.3. In particular,
![]() $\mathcal {H}$
contains no focused copy of a member of
$\mathcal {H}$
contains no focused copy of a member of
![]() $\mathcal {M}(r,s)$
with respect to the partition
$\mathcal {M}(r,s)$
with respect to the partition
![]() $U_1,\dots ,U_L$
. Let
$U_1,\dots ,U_L$
. Let
![]() $c_0=c(r,s)$
be the constant given by Lemma 4.3. Then for every
$c_0=c(r,s)$
be the constant given by Lemma 4.3. Then for every
![]() $i\in [L]$
, there exists
$i\in [L]$
, there exists
![]() $V^{\prime }_{i}\subset U_{i}$
such that
$V^{\prime }_{i}\subset U_{i}$
such that
 $$ \begin{align*} |V^{\prime}_{i}|\geq (1-c_0 \epsilon_0^{1/r!})|U_{i}|\geq (1-c_0 \epsilon_0^{1/r!})\left\lfloor \frac{N}{L}\right\rfloor, \end{align*} $$
$$ \begin{align*} |V^{\prime}_{i}|\geq (1-c_0 \epsilon_0^{1/r!})|U_{i}|\geq (1-c_0 \epsilon_0^{1/r!})\left\lfloor \frac{N}{L}\right\rfloor, \end{align*} $$
and
![]() $(V^{\prime }_{i_1},\dots ,V^{\prime }_{i_r})$
is empty if
$(V^{\prime }_{i_1},\dots ,V^{\prime }_{i_r})$
is empty if
![]() $d(U_{i_1},\dots ,U_{i_r})<\epsilon _0$
. Let K be a minimal positive integer such that
$d(U_{i_1},\dots ,U_{i_r})<\epsilon _0$
. Let K be a minimal positive integer such that
![]() $N/K<\min _{i\in [L]}|V_{i}'|$
; then
$N/K<\min _{i\in [L]}|V_{i}'|$
; then
![]() $K<L+2c_{0}\epsilon _{0}^{1/r!}L<2L$
. In particular, when we choose
$K<L+2c_{0}\epsilon _{0}^{1/r!}L<2L$
. In particular, when we choose
![]() $\epsilon _0$
, it will satisfy
$\epsilon _0$
, it will satisfy
![]() $c_{0}\epsilon _{0}^{1/r!}<1/2$
. Let
$c_{0}\epsilon _{0}^{1/r!}<1/2$
. Let
![]() $V_1,\dots ,V_{K}$
be any equitable partition of
$V_1,\dots ,V_{K}$
be any equitable partition of
![]() $V(\mathcal {H})$
such that
$V(\mathcal {H})$
such that
![]() $V_{i}\subset V_{i}'$
for
$V_{i}\subset V_{i}'$
for
![]() $i\in [L]$
: this clearly exists by the definition of K.
$i\in [L]$
: this clearly exists by the definition of K.
Say that an r-tuple
![]() $\{i_1,\dots ,i_r\}\in [K]^{(r)}$
is good if
$\{i_1,\dots ,i_r\}\in [K]^{(r)}$
is good if
![]() $d(V_{i_1},\dots ,V_{i_r})>1-2^{r}\epsilon _0$
or
$d(V_{i_1},\dots ,V_{i_r})>1-2^{r}\epsilon _0$
or
![]() $(V_{i_1},\dots ,V_{i_r})$
is empty. Otherwise, say that
$(V_{i_1},\dots ,V_{i_r})$
is empty. Otherwise, say that
![]() $\{i_1,\dots ,i_r\}$
is bad. Note that if
$\{i_1,\dots ,i_r\}$
is bad. Note that if
![]() $\{i_1,\dots ,i_r\}\in [L]^{r}$
, then
$\{i_1,\dots ,i_r\}\in [L]^{r}$
, then
![]() $\{i_1,\dots ,i_r\}$
is good if
$\{i_1,\dots ,i_r\}$
is good if
![]() $(U_{i_1},\dots ,U_{i_r})$
is
$(U_{i_1},\dots ,U_{i_r})$
is
![]() $\epsilon $
-homogeneous. Indeed, if
$\epsilon $
-homogeneous. Indeed, if
![]() $d(U_{i_1},\dots ,U_{i_r})>1-\epsilon _0$
, then
$d(U_{i_1},\dots ,U_{i_r})>1-\epsilon _0$
, then
and if
![]() $d(U_{i_1},\dots ,U_{i_r})<\epsilon _0$
, then
$d(U_{i_1},\dots ,U_{i_r})<\epsilon _0$
, then
![]() $(V_{i_1},\dots ,V_{i_r})$
is empty by definition. The number of r-tuples
$(V_{i_1},\dots ,V_{i_r})$
is empty by definition. The number of r-tuples
![]() $\{i_1,\dots ,i_r\}\in [K]^{(r)}$
having a nonempty intersection with
$\{i_1,\dots ,i_r\}\in [K]^{(r)}$
having a nonempty intersection with
![]() $\{L+1,\dots ,K\}$
is fewer than
$\{L+1,\dots ,K\}$
is fewer than
![]() $(K-L)K^{r-1}$
. Hence, the total number of bad r-tuples is at most
$(K-L)K^{r-1}$
. Hence, the total number of bad r-tuples is at most
 $$ \begin{align*} \epsilon_0\binom{L}{r}+(K-L)K^{r-1}< \epsilon_0 \binom{K}{r}+2c_0\epsilon_{0}^{1/r!} K^{r}\leq c_{1}\epsilon_{0}^{1/r!}\binom{K}{r}, \end{align*} $$
$$ \begin{align*} \epsilon_0\binom{L}{r}+(K-L)K^{r-1}< \epsilon_0 \binom{K}{r}+2c_0\epsilon_{0}^{1/r!} K^{r}\leq c_{1}\epsilon_{0}^{1/r!}\binom{K}{r}, \end{align*} $$
where
![]() $c_{1}=c_1(r,s)>c_0$
depends only on r and s. Choose
$c_{1}=c_1(r,s)>c_0$
depends only on r and s. Choose
![]() $\epsilon _0$
such that both
$\epsilon _0$
such that both
![]() $c_1\epsilon _0^{1/r!}, 2^{r}\epsilon _0 \leq \epsilon <1/4$
. Then
$c_1\epsilon _0^{1/r!}, 2^{r}\epsilon _0 \leq \epsilon <1/4$
. Then
![]() $V_1,\dots ,V_K$
is an equitable partition of
$V_1,\dots ,V_K$
is an equitable partition of
![]() $\mathcal {H}$
such that
$\mathcal {H}$
such that
![]() $8/\epsilon <8/\epsilon _0<K\leq 2c'(1/\epsilon _0)^{2n+1}<c(1/\epsilon )^{r!(2n+1)}$
for some
$8/\epsilon <8/\epsilon _0<K\leq 2c'(1/\epsilon _0)^{2n+1}<c(1/\epsilon )^{r!(2n+1)}$
for some
![]() $c=c(r,s)>0$
, and all but at most an
$c=c(r,s)>0$
, and all but at most an
![]() $\epsilon $
-fraction of the r-tuples of parts
$\epsilon $
-fraction of the r-tuples of parts
![]() $(V_{i_1},\dots ,V_{i_r})$
satisfy that either
$(V_{i_1},\dots ,V_{i_r})$
satisfy that either
![]() $d(V_{i_1},\dots ,V_{i_r})>1-2^{r}\epsilon _0>1-\epsilon $
, or
$d(V_{i_1},\dots ,V_{i_r})>1-2^{r}\epsilon _0>1-\epsilon $
, or
![]() $(V_{i_1},\dots ,V_{i_r})$
is empty.
$(V_{i_1},\dots ,V_{i_r})$
is empty.
5 A Ramsey-type result for algebraic hypergraphs
In this section, we prove Theorem 1.6. First, let us extend the list of forbidden hypergraphs in algebraic hypergraphs of constant complexity. To do this, we use a result about the maximum flattening rank of tensors that are almost diagonal. Let
![]() $T:A_1\times \dots \times A_{r}\rightarrow \mathbb {F}$
be an r-dimensional tensor. Let the max-flattening rank of T, denoted by
$T:A_1\times \dots \times A_{r}\rightarrow \mathbb {F}$
be an r-dimensional tensor. Let the max-flattening rank of T, denoted by
![]() $\operatorname {\mathrm {mfrank}}(T)$
, be the maximum of
$\operatorname {\mathrm {mfrank}}(T)$
, be the maximum of
![]() $\operatorname {\mathrm {frank}}_i(T)$
for
$\operatorname {\mathrm {frank}}_i(T)$
for
![]() $i\in [r]$
. Say that an r-dimensional tensor
$i\in [r]$
. Say that an r-dimensional tensor
![]() $T:A^{r}\rightarrow \mathbb {F}$
is semi-diagonal if the following holds. Let
$T:A^{r}\rightarrow \mathbb {F}$
is semi-diagonal if the following holds. Let
![]() $a_1,\dots ,a_r\in A$
. Then
$a_1,\dots ,a_r\in A$
. Then
![]() $T(a_1,\dots ,a_{r})=0$
if
$T(a_1,\dots ,a_{r})=0$
if
![]() $a_1,\dots ,a_r$
are pairwise distinct, and
$a_1,\dots ,a_r$
are pairwise distinct, and
![]() $T(a_1,\dots ,a_r)\neq 0$
if
$T(a_1,\dots ,a_r)\neq 0$
if
![]() $a_1=\dots =a_d$
. If
$a_1=\dots =a_d$
. If
![]() $a_1,\dots ,a_r$
are neither all equal or all distinct, there is no restriction on
$a_1,\dots ,a_r$
are neither all equal or all distinct, there is no restriction on
![]() $T(a_1,\dots ,a_r)$
. We prove the following result in the companion note [Reference Munhá Correia, Sudakov and Tomon34].
$T(a_1,\dots ,a_r)$
. We prove the following result in the companion note [Reference Munhá Correia, Sudakov and Tomon34].
Theorem 5.1. Let
![]() $T:A^{r}\rightarrow \mathbb {F}$
be an r-dimensional semi-diagonal tensor. Then
$T:A^{r}\rightarrow \mathbb {F}$
be an r-dimensional semi-diagonal tensor. Then
Let
![]() $\mathcal {N}_{r,s}$
be the family of r-uniform hypergraphs
$\mathcal {N}_{r,s}$
be the family of r-uniform hypergraphs
![]() $\mathcal {N}$
having the following form. There are s disjoint edges
$\mathcal {N}$
having the following form. There are s disjoint edges
![]() $f_{i}=\{u_{i,1},\dots ,u_{i,r}\}$
for
$f_{i}=\{u_{i,1},\dots ,u_{i,r}\}$
for
![]() $i\in [s]$
, whose union is the vertex set of
$i\in [s]$
, whose union is the vertex set of
![]() $\mathcal {N}$
, and the r element set
$\mathcal {N}$
, and the r element set
![]() $\{u_{i_1,1},\dots ,u_{i_r,r}\}$
is not an edge for any r-tuple
$\{u_{i_1,1},\dots ,u_{i_r,r}\}$
is not an edge for any r-tuple
![]() $(i_1,\dots ,i_r)\in [s]^{r}$
, where
$(i_1,\dots ,i_r)\in [s]^{r}$
, where
![]() $i_1,\dots ,i_r$
are pairwise distinct. The rest of the r element subsets of the vertex set can be either edges or non-edges.
$i_1,\dots ,i_r$
are pairwise distinct. The rest of the r element subsets of the vertex set can be either edges or non-edges.
Lemma 5.2. Let
![]() $\mathcal {H}$
be a strongly algebraic r-uniform hypergraph of complexity
$\mathcal {H}$
be a strongly algebraic r-uniform hypergraph of complexity
![]() $(n,d)$
. Then
$(n,d)$
. Then
![]() $\mathcal {H}$
contains no member of
$\mathcal {H}$
contains no member of
![]() $\mathcal {N}_{r,s}$
for
$\mathcal {N}_{r,s}$
for
![]() $s>(r-1)\binom {n+d}{d}$
.
$s>(r-1)\binom {n+d}{d}$
.
Proof. Let
![]() $V=V(\mathcal {H})\subset \mathbb {F}^{n}$
, and let
$V=V(\mathcal {H})\subset \mathbb {F}^{n}$
, and let
![]() $f:(\mathbb {F}^{n})^r\rightarrow \mathbb {F}$
be the polynomial defining
$f:(\mathbb {F}^{n})^r\rightarrow \mathbb {F}$
be the polynomial defining
![]() $\mathcal {H}$
. Define tensor
$\mathcal {H}$
. Define tensor
![]() $T:V^{r}\rightarrow \mathbb {F}$
to be
$T:V^{r}\rightarrow \mathbb {F}$
to be
![]() $T(\mathbf {x}_1,\dots ,\mathbf {x}_r)=f(\mathbf {x}_1,\dots ,\mathbf {x}_r)$
. Then by Lemma 2.2
$T(\mathbf {x}_1,\dots ,\mathbf {x}_r)=f(\mathbf {x}_1,\dots ,\mathbf {x}_r)$
. Then by Lemma 2.2
![]() $\operatorname {\mathrm {mfrank}}(T)\leq \binom {n+d}{d}$
.
$\operatorname {\mathrm {mfrank}}(T)\leq \binom {n+d}{d}$
.
Suppose that
![]() $\mathcal {H}$
contains a member of
$\mathcal {H}$
contains a member of
![]() $\mathcal {N}_{r,s}$
for some
$\mathcal {N}_{r,s}$
for some
![]() $s>(r-1)\binom {n+d}{n}$
. Then there exists
$s>(r-1)\binom {n+d}{n}$
. Then there exists
![]() $\mathbf {u}_{i,j}\in \mathbb {F}^{n}$
for
$\mathbf {u}_{i,j}\in \mathbb {F}^{n}$
for
![]() $(i,j)\in [s]\times [r]$
such that
$(i,j)\in [s]\times [r]$
such that
![]() $f(\mathbf {u}_{i,1},\dots ,\mathbf {u}_{i,r})\neq 0$
for
$f(\mathbf {u}_{i,1},\dots ,\mathbf {u}_{i,r})\neq 0$
for
![]() $i\in [s]$
and
$i\in [s]$
and
![]() $f(\mathbf {u}_{i_1,1},\dots ,\mathbf {u}_{i_r,r})=0$
for
$f(\mathbf {u}_{i_1,1},\dots ,\mathbf {u}_{i_r,r})=0$
for
![]() $(i_1,\dots ,i_r)\in [s]^{r}$
for which
$(i_1,\dots ,i_r)\in [s]^{r}$
for which
![]() $i_1,\dots ,i_r$
are pairwise distinct. Let
$i_1,\dots ,i_r$
are pairwise distinct. Let
![]() $T'$
be the subtensor of T induced on
$T'$
be the subtensor of T induced on
![]() $\{\mathbf {u}_{1,1},\dots ,\mathbf {u}_{s,1}\}\times \dots \times \{\mathbf {u}_{1,r},\dots ,\mathbf {u}_{s,r}\}$
. Identifying
$\{\mathbf {u}_{1,1},\dots ,\mathbf {u}_{s,1}\}\times \dots \times \{\mathbf {u}_{1,r},\dots ,\mathbf {u}_{s,r}\}$
. Identifying
![]() $\mathbf {u}_{i,j}$
by i, the tensor
$\mathbf {u}_{i,j}$
by i, the tensor
![]() $T':[s]^{r}\rightarrow \mathbb {F}$
is semi-diagonal, so
$T':[s]^{r}\rightarrow \mathbb {F}$
is semi-diagonal, so
by Theorem 5.1. This is a contradiction, finishing the proof.
Now everything is set to prove the main theorem of this section.
Proof of Theorem 1.6
Let
![]() $\mathcal {H}\in \mathcal {F}$
, and let
$\mathcal {H}\in \mathcal {F}$
, and let
![]() $N=|V(\mathcal {H})|$
. Then
$N=|V(\mathcal {H})|$
. Then
![]() $\mathcal {H}$
is an r-uniform strongly algebraic hypergraph of complexity
$\mathcal {H}$
is an r-uniform strongly algebraic hypergraph of complexity
![]() $(n,d)$
. Let
$(n,d)$
. Let
![]() $\epsilon =N^{-\beta /r!(2n+1)}$
. Then by Theorem 1.5, there is an equitable partition of
$\epsilon =N^{-\beta /r!(2n+1)}$
. Then by Theorem 1.5, there is an equitable partition of
![]() $V(\mathcal {H})$
into parts
$V(\mathcal {H})$
into parts
![]() $V_1,\dots ,V_{K}$
for some
$V_1,\dots ,V_{K}$
for some
![]() $8/\epsilon <K<c'(1/\epsilon )^{r!(2n+1)}$
such that all but at most
$8/\epsilon <K<c'(1/\epsilon )^{r!(2n+1)}$
such that all but at most
![]() $\epsilon $
-fraction of the r-tuples of parts either are empty or have density at least
$\epsilon $
-fraction of the r-tuples of parts either are empty or have density at least
![]() $1-\epsilon $
. Here,
$1-\epsilon $
. Here,
![]() ${c'=c'(r,n,d)>0}$
.
${c'=c'(r,n,d)>0}$
.
For
![]() $i\in [K]$
, pick a vertex
$i\in [K]$
, pick a vertex
![]() $v_i\in V_i$
randomly with uniform distribution. Let
$v_i\in V_i$
randomly with uniform distribution. Let
![]() $\mathcal {H}'$
be the hypergraph induced on the vertex set
$\mathcal {H}'$
be the hypergraph induced on the vertex set
![]() $\{v_1,\dots ,v_{K}\}$
; then
$\{v_1,\dots ,v_{K}\}$
; then
![]() $\mathcal {H}'\in \mathcal {F}$
as well. Define the r-uniform hypergraph
$\mathcal {H}'\in \mathcal {F}$
as well. Define the r-uniform hypergraph
![]() $\mathcal {G}$
on vertex set
$\mathcal {G}$
on vertex set
![]() $[K]$
as follows. The r-element set
$[K]$
as follows. The r-element set
![]() $\{i_1,\dots ,i_r\}\in [K]^{(r)}$
is an edge of
$\{i_1,\dots ,i_r\}\in [K]^{(r)}$
is an edge of
![]() $\mathcal {G}$
if and only if either
$\mathcal {G}$
if and only if either
![]() $\{v_{i_1},\dots ,v_{i_r}\}\in E(\mathcal {H})$
and
$\{v_{i_1},\dots ,v_{i_r}\}\in E(\mathcal {H})$
and
![]() $d(V_{i_1},\dots ,V_{i_r})\geq 1-\epsilon $
, or
$d(V_{i_1},\dots ,V_{i_r})\geq 1-\epsilon $
, or
![]() $\{v_{i_1},\dots ,v_{i_r}\}\not \in E(\mathcal {H})$
and
$\{v_{i_1},\dots ,v_{i_r}\}\not \in E(\mathcal {H})$
and
![]() $(V_{i_1},\dots ,V_{i_r})$
is empty. Note that if
$(V_{i_1},\dots ,V_{i_r})$
is empty. Note that if
![]() $(V_{i_1},\dots ,V_{i_r})$
either is empty or has density at least
$(V_{i_1},\dots ,V_{i_r})$
either is empty or has density at least
![]() $1-\epsilon $
, then
$1-\epsilon $
, then
![]() $\{i_1,\dots ,i_r\}$
is an edge with probability at least
$\{i_1,\dots ,i_r\}$
is an edge with probability at least
![]() $1-\epsilon $
. Therefore,
$1-\epsilon $
. Therefore,
![]() $\mathbb {E}(d(\mathcal {G}))\geq 1-2\epsilon $
, so there is a choice for
$\mathbb {E}(d(\mathcal {G}))\geq 1-2\epsilon $
, so there is a choice for
![]() $v_1,\dots ,v_{K}$
such that
$v_1,\dots ,v_{K}$
such that
![]() $d(\mathcal {G})\geq 1-2\epsilon $
. Fix such a choice. By Lemma 2.1,
$d(\mathcal {G})\geq 1-2\epsilon $
. Fix such a choice. By Lemma 2.1,
![]() $\mathcal {G}$
contains a clique J of size at least
$\mathcal {G}$
contains a clique J of size at least
![]() $\frac {1}{8}\epsilon ^{-1/(r-1)}$
. Let
$\frac {1}{8}\epsilon ^{-1/(r-1)}$
. Let
![]() $\mathcal {H}^{*}$
be the subhypergraph of
$\mathcal {H}^{*}$
be the subhypergraph of
![]() $\mathcal {H}$
induced on the vertex set
$\mathcal {H}$
induced on the vertex set
![]() $\{v_j:j\in J\}$
. As
$\{v_j:j\in J\}$
. As
![]() $\mathcal {H}^{*}\in \mathcal {F}$
,
$\mathcal {H}^{*}\in \mathcal {F}$
,
![]() $\mathcal {H}^{*}$
contains either an independent set of size s or a clique of size
$\mathcal {H}^{*}$
contains either an independent set of size s or a clique of size
![]() $c|J|^{\alpha }=c_1N^{\alpha \beta /r!(r-1)(2n+1)}$
for some
$c|J|^{\alpha }=c_1N^{\alpha \beta /r!(r-1)(2n+1)}$
for some
![]() $c_1=c_1(r,n,d,c,\alpha ,\beta )>0$
. In the latter case, we are done, so assume that
$c_1=c_1(r,n,d,c,\alpha ,\beta )>0$
. In the latter case, we are done, so assume that
![]() $\mathcal {H}^{*}$
contains an independent set
$\mathcal {H}^{*}$
contains an independent set
![]() $\{v_i:i\in I\}$
of size s.
$\{v_i:i\in I\}$
of size s.
We finish the proof by noting that at least one of
![]() $U_{i}$
,
$U_{i}$
,
![]() $i\in I$
is an independent set in
$i\in I$
is an independent set in
![]() $\mathcal {H}$
. Otherwise, if
$\mathcal {H}$
. Otherwise, if
![]() $U_{i}$
contains an edge
$U_{i}$
contains an edge
![]() $f_i$
for every
$f_i$
for every
![]() $i\in I$
, then
$i\in I$
, then
![]() $\bigcup _{i\in I}f_i$
spans a member of
$\bigcup _{i\in I}f_i$
spans a member of
![]() $\mathcal {N}_{r,s}$
in
$\mathcal {N}_{r,s}$
in
![]() $\mathcal {H}$
, contradicting Lemma 5.2. Therefore,
$\mathcal {H}$
, contradicting Lemma 5.2. Therefore,
![]() $\mathcal {H}$
contains an independent set of size at least
$\mathcal {H}$
contains an independent set of size at least
![]() $\frac {1}{2}\lfloor N/K\rfloor>c_2N^{1-\beta }$
, where
$\frac {1}{2}\lfloor N/K\rfloor>c_2N^{1-\beta }$
, where
![]() $c_2=c_2(r,n,d,c,\alpha ,\beta )>0$
.
$c_2=c_2(r,n,d,c,\alpha ,\beta )>0$
.
6 Concluding remarks
Following Fox and Pach [Reference Fox and Pach25], we say that a family of graphs
![]() $\mathcal {G}$
has the strong-Erdős-Hajnal property if there exists a constant
$\mathcal {G}$
has the strong-Erdős-Hajnal property if there exists a constant
![]() $c=c(\mathcal {G})>0$
such that for every
$c=c(\mathcal {G})>0$
such that for every
![]() $G\in \mathcal {G}$
, either G or its complement contains a bi-clique of size at least
$G\in \mathcal {G}$
, either G or its complement contains a bi-clique of size at least
![]() $c|V(G)|$
. In [Reference Alon, Pach, Pinchasi, Radoičić and Sharir2], it is proved that the strong-Erdős-Hajnal property implies the Erdős-Hajnal property in hereditary graph families and that the family of semi-algebraic graphs of complexity
$c|V(G)|$
. In [Reference Alon, Pach, Pinchasi, Radoičić and Sharir2], it is proved that the strong-Erdős-Hajnal property implies the Erdős-Hajnal property in hereditary graph families and that the family of semi-algebraic graphs of complexity
![]() $(n,d,m)$
has the strong-Erdős-Hajnal property. On the other hand, it is known that this is not the case for algebraic graphs. For infinitely many N, one describes a strongly algebraic graph G of complexity
$(n,d,m)$
has the strong-Erdős-Hajnal property. On the other hand, it is known that this is not the case for algebraic graphs. For infinitely many N, one describes a strongly algebraic graph G of complexity
![]() $(3,2)$
such that the size of the largest bi-clique in both G and its complement is
$(3,2)$
such that the size of the largest bi-clique in both G and its complement is
![]() $O(N^{3/4})$
.
$O(N^{3/4})$
.
If q is a prime power, the Erdős-Rényi graph
![]() $ER_{q}$
is defined as follows. The vertices of
$ER_{q}$
is defined as follows. The vertices of
![]() $ER_{q}$
are the elements of the projective plane over
$ER_{q}$
are the elements of the projective plane over
![]() $\mathbb {F}_{q}$
, and
$\mathbb {F}_{q}$
, and
![]() $(x_0,x_1,x_2)$
and
$(x_0,x_1,x_2)$
and
![]() $(y_0,y_1,y_2)$
are joined by an edge if
$(y_0,y_1,y_2)$
are joined by an edge if
![]() $x_0y_0+x_1y_1+x_2y_2=0$
. The graph
$x_0y_0+x_1y_1+x_2y_2=0$
. The graph
![]() $ER_{q}$
has
$ER_{q}$
has
![]() $N=q^{2}+q+1$
vertices, is
$N=q^{2}+q+1$
vertices, is
![]() $(q+1)$
-regular and has at most
$(q+1)$
-regular and has at most
![]() $2(q+1)$
vertices with loops. This graph contains no copy of
$2(q+1)$
vertices with loops. This graph contains no copy of
![]() $K_{2,2}$
and has eigenvalues
$K_{2,2}$
and has eigenvalues
![]() $\pm \sqrt {q}$
and
$\pm \sqrt {q}$
and
![]() $q+1$
, where the multiplicity of
$q+1$
, where the multiplicity of
![]() $q+1$
is
$q+1$
is
![]() $1$
; see, for example, [Reference Krivelevich and Sudakov30]. By the expander mixing lemma (see, for example, Theorem 2.11 in [Reference Krivelevich and Sudakov30]), one can bound the number of the edges/non-edges of
$1$
; see, for example, [Reference Krivelevich and Sudakov30]. By the expander mixing lemma (see, for example, Theorem 2.11 in [Reference Krivelevich and Sudakov30]), one can bound the number of the edges/non-edges of
![]() $ER_{q}$
between two disjoint subsets of vertices using its eigenvalues. This lemma implies that both
$ER_{q}$
between two disjoint subsets of vertices using its eigenvalues. This lemma implies that both
![]() $ER_{q}$
and its complement contains no bi-clique of size larger than
$ER_{q}$
and its complement contains no bi-clique of size larger than
 $$ \begin{align*} \frac{N\sqrt{q}}{q+1}=O(N^{3/4}). \end{align*} $$
$$ \begin{align*} \frac{N\sqrt{q}}{q+1}=O(N^{3/4}). \end{align*} $$
Note that the complement of
![]() $ER_{q}$
is strongly algebraic of complexity
$ER_{q}$
is strongly algebraic of complexity
![]() $(3,2)$
. Indeed, we can view the vertices of
$(3,2)$
. Indeed, we can view the vertices of
![]() $ER_{q}$
as elements of
$ER_{q}$
as elements of
![]() $\mathbb {F}_{q}^{3}$
by replacing each
$\mathbb {F}_{q}^{3}$
by replacing each
![]() $(x_0,x_1,x_2)\in \mathbb {PF}_{q}^{2}$
with one element of the equivalence class
$(x_0,x_1,x_2)\in \mathbb {PF}_{q}^{2}$
with one element of the equivalence class
![]() $C_{(x_{0},x_{1},x_{2})}=\{(\lambda x_{0},\lambda x_{1},\lambda x_{2}):\lambda \in \mathbb {F}_{q}\setminus \{0\}\}\subset \mathbb {F}_{q}^3$
. For a variant of this construction, see, for example, [Reference Chernikov and Starchenko10], Section 6.1.
$C_{(x_{0},x_{1},x_{2})}=\{(\lambda x_{0},\lambda x_{1},\lambda x_{2}):\lambda \in \mathbb {F}_{q}\setminus \{0\}\}\subset \mathbb {F}_{q}^3$
. For a variant of this construction, see, for example, [Reference Chernikov and Starchenko10], Section 6.1.
Finally, let us mention that although algebraic graphs of bounded complexity do not have strong Ramsey properties (as we proved in this paper), they are one of the main sources of best examples for so-called Turán-type questions. Given an r-uniform hypergraph
![]() $\mathcal {H}$
, the extremal number (or Turán number) of
$\mathcal {H}$
, the extremal number (or Turán number) of
![]() $\mathcal {H}$
denoted by
$\mathcal {H}$
denoted by
![]() $\mbox {ex}(N,\mathcal {H})$
is the maximum number of edges in an r-uniform hypergraph on N vertices that contains no copy of
$\mbox {ex}(N,\mathcal {H})$
is the maximum number of edges in an r-uniform hypergraph on N vertices that contains no copy of
![]() $\mathcal {H}$
as a subhypergraph. If H is a graph, the asymptotic value of the extremal number of H is known by the Erdős-Stone theorem, unless H is bipartite. The case of bipartite graphs is notoriously hard. In many cases, when the order of
$\mathcal {H}$
as a subhypergraph. If H is a graph, the asymptotic value of the extremal number of H is known by the Erdős-Stone theorem, unless H is bipartite. The case of bipartite graphs is notoriously hard. In many cases, when the order of
![]() $\mbox {ex}(N,H)$
is known for some bipartite graph H, the construction achieving the right order of magnitude is an algebraic graph of bounded complexity; see, for example, [Reference Brown3, Reference Bukh4, Reference Bukh and Conlon5, Reference Erdős, Rényi and Sós22]. Algebraic hypergraphs of bounded complexity also appear in connection to Turán type results; see, for example, [Reference Ma, Yuan and Zhang32, Reference Conlon, Pohoata and Zakharov16].
$\mbox {ex}(N,H)$
is known for some bipartite graph H, the construction achieving the right order of magnitude is an algebraic graph of bounded complexity; see, for example, [Reference Brown3, Reference Bukh4, Reference Bukh and Conlon5, Reference Erdős, Rényi and Sós22]. Algebraic hypergraphs of bounded complexity also appear in connection to Turán type results; see, for example, [Reference Ma, Yuan and Zhang32, Reference Conlon, Pohoata and Zakharov16].
Acknowledgements
We would like to thank the anonymous referee for their useful comments and suggestions. Moreover, we would like to thank Jacob Fox, János Pach and Artem Chernikov for pointing out the related references and results.
Conflicts of Interest
The authors have no conflicts of interest to declare.
Financial support
Both authors were supported by the SNSF grant 200021_196965. István Tomon also acknowledges the support of the Russian Government in the framework of MegaGrant no 075-15-2019-1926.