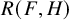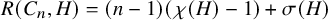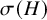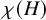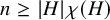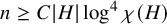1 Introduction
For any pair of graphs F and H, Ramsey [Reference Ramsey26] famously proved in 1930 that there exists a number
![]() $R(F,H)$
such that given any graph G on at least
$R(F,H)$
such that given any graph G on at least
![]() $R(F,H)$
vertices either
$R(F,H)$
vertices either
![]() $F \subseteq G$
or
$F \subseteq G$
or
![]() $H \subseteq \overline {G}$
. Determining
$H \subseteq \overline {G}$
. Determining
![]() $R(F,H)$
exactly for every pair of graphs
$R(F,H)$
exactly for every pair of graphs
![]() $F,H$
is a notoriously difficult problem in combinatorics. Indeed,
$F,H$
is a notoriously difficult problem in combinatorics. Indeed,
![]() $R(K_n, K_n)$
is not even known exactly for
$R(K_n, K_n)$
is not even known exactly for
![]() $n = 5$
. However, for some pairs of graphs, particularly when F and/or H are certain sparse graphs,
$n = 5$
. However, for some pairs of graphs, particularly when F and/or H are certain sparse graphs,
![]() $R(F,H)$
is known. We require some notation. For a graph H, define the chromatic number
$R(F,H)$
is known. We require some notation. For a graph H, define the chromatic number
![]() $\chi (H)$
of H to be the smallest number of colours in a proper colouring of H, that is, a colouring where no two adjacent vertices have the same colour. Further, let
$\chi (H)$
of H to be the smallest number of colours in a proper colouring of H, that is, a colouring where no two adjacent vertices have the same colour. Further, let
![]() $\sigma (H)$
be the minimum possible size of a colour class in a
$\sigma (H)$
be the minimum possible size of a colour class in a
![]() $\chi (H)$
-colouring of H.
$\chi (H)$
-colouring of H.
Building on observations of Erdős [Reference Erdős10] and Chvátal and Harary [Reference Chvátal and Harary8], Burr [Reference Burr4] constructed the following lower bound for
![]() $R(F,H)$
when F is a connected graph with
$R(F,H)$
when F is a connected graph with
![]() $\lvert F\rvert \geq \sigma (H)$
:
$\lvert F\rvert \geq \sigma (H)$
:
The construction proving this bound is the graph G on
![]() $(\lvert F\rvert - 1)(\chi (H) - 1) + \sigma (H) - 1$
vertices consisting of
$(\lvert F\rvert - 1)(\chi (H) - 1) + \sigma (H) - 1$
vertices consisting of
![]() $\chi (H) - 1$
disjoint cliques of size
$\chi (H) - 1$
disjoint cliques of size
![]() $\lvert F\rvert -1$
and an additional disjoint clique of size
$\lvert F\rvert -1$
and an additional disjoint clique of size
![]() $\sigma (H) - 1$
. Clearly, since F is connected,
$\sigma (H) - 1$
. Clearly, since F is connected,
![]() $F \nsubseteq G$
. Since
$F \nsubseteq G$
. Since
![]() $\overline {G}$
is the complete
$\overline {G}$
is the complete
![]() $\chi (H)$
-partite graph with
$\chi (H)$
-partite graph with
![]() $\chi (H)-1$
vertex sets of size
$\chi (H)-1$
vertex sets of size
![]() $\lvert F\rvert - 1$
and one vertex set of size
$\lvert F\rvert - 1$
and one vertex set of size
![]() $\sigma (H) - 1$
and the vertex set of size
$\sigma (H) - 1$
and the vertex set of size
![]() $\sigma (H) - 1$
cannot completely contain any colour class of H, we have
$\sigma (H) - 1$
cannot completely contain any colour class of H, we have
![]() $H \nsubseteq \overline {G}$
. In what follows, we will often say a graph G is H-free to mean
$H \nsubseteq \overline {G}$
. In what follows, we will often say a graph G is H-free to mean
![]() $H \nsubseteq G$
.
$H \nsubseteq G$
.
Although the bound in inequality (1) is very general, for some pairs of graphs it is extremely far from the truth. Indeed, Erdős [Reference Erdős10] proved that
![]() $R(K_k, K_k) \geq \Omega (2^{k/2})$
, whereas inequality (1) only gives the much smaller lower bound of
$R(K_k, K_k) \geq \Omega (2^{k/2})$
, whereas inequality (1) only gives the much smaller lower bound of
![]() $(k-1)^2 + 1$
. For some pairs of graphs, however, the bound in inequality (1) is tight. For graphs F and H satisfying this lower bound
$(k-1)^2 + 1$
. For some pairs of graphs, however, the bound in inequality (1) is tight. For graphs F and H satisfying this lower bound
![]() $R(F,H)=(\chi (H)-1)(\lvert F\rvert -1)+\sigma (H)$
, Burr and Erdős [Reference Burr and Erdős5] coined the expression ‘F is H-good’. The study of so-called Ramsey goodness, after being initiated by Burr and Erdős in 1983 [Reference Burr and Erdős5], has attracted considerable interest. Prior to Burr’s observation [Reference Burr4], already Erdős [Reference Erdős10] had proved that the path on n vertices
$R(F,H)=(\chi (H)-1)(\lvert F\rvert -1)+\sigma (H)$
, Burr and Erdős [Reference Burr and Erdős5] coined the expression ‘F is H-good’. The study of so-called Ramsey goodness, after being initiated by Burr and Erdős in 1983 [Reference Burr and Erdős5], has attracted considerable interest. Prior to Burr’s observation [Reference Burr4], already Erdős [Reference Erdős10] had proved that the path on n vertices
![]() $P_n$
was
$P_n$
was
![]() $K_k$
-good; Gerenscér and Gyárfás [Reference Gerencsér and Gyárfás14] proved that for
$K_k$
-good; Gerenscér and Gyárfás [Reference Gerencsér and Gyárfás14] proved that for
![]() $n \geq k$
the path
$n \geq k$
the path
![]() $P_n$
is
$P_n$
is
![]() $P_k$
-good; and Chvátal [Reference Chvátal7] proved every tree T is
$P_k$
-good; and Chvátal [Reference Chvátal7] proved every tree T is
![]() $K_k$
-good. The result of Chvatal can be in fact viewed as a generalisation of Turán’s theorem, which states that the complete balanced
$K_k$
-good. The result of Chvatal can be in fact viewed as a generalisation of Turán’s theorem, which states that the complete balanced
![]() $(k-1)$
-partite graph on N vertices, the so-called Turán graph, has the maximum number of edges amongst
$(k-1)$
-partite graph on N vertices, the so-called Turán graph, has the maximum number of edges amongst
![]() $K_k$
-free graphs. Indeed, Turán’s theorem is equivalent to the statement ‘
$K_k$
-free graphs. Indeed, Turán’s theorem is equivalent to the statement ‘
![]() $S_n$
is
$S_n$
is
![]() $K_k$
-good’, where
$K_k$
-good’, where
![]() $S_n$
is the n-vertex star with
$S_n$
is the n-vertex star with
![]() $n-1$
leaves. To see this, let
$n-1$
leaves. To see this, let
![]() $N = (n-1)(k-1)$
and T be the complement of this Turán graph. Then T is precisely the construction in inequality (1) when
$N = (n-1)(k-1)$
and T be the complement of this Turán graph. Then T is precisely the construction in inequality (1) when
![]() $(F,H) = (S_n, K_k)$
. Moreover, T is the unique graph on
$(F,H) = (S_n, K_k)$
. Moreover, T is the unique graph on
![]() $(n-1)(k-1)$
vertices without
$(n-1)(k-1)$
vertices without
![]() $S_n \subseteq T$
or
$S_n \subseteq T$
or
![]() $K_k \subseteq \overline {T}$
. Add a vertex to T, and denote the resulting graph by
$K_k \subseteq \overline {T}$
. Add a vertex to T, and denote the resulting graph by
![]() $T + v$
. If v neighbours any vertex in T, then
$T + v$
. If v neighbours any vertex in T, then
![]() $S_n \subseteq T + v$
. Otherwise,
$S_n \subseteq T + v$
. Otherwise,
![]() $K_k \subseteq \overline {T + v}$
. That is,
$K_k \subseteq \overline {T + v}$
. That is,
![]() $R(S_n, K_k) = (n-1)(k-1) + \sigma (K_k) = (n-1)(k-1) + 1$
. This connection to Turán’s theorem highlights how Ramsey goodness results can generalise other results in graph theory. See [Reference Fox, He and Wigderson13, Reference Lin and Liu19, Reference Moreira22, Reference Pokrovskiy and Sudakov24, Reference Pokrovskiy and Sudakov25] and their references for more recent progress in the area of Ramsey goodness, as well as the survey of Conlon, Fox and Sudakov [Reference Conlon, Fox and Sudakov9, Section 2.5].
$R(S_n, K_k) = (n-1)(k-1) + \sigma (K_k) = (n-1)(k-1) + 1$
. This connection to Turán’s theorem highlights how Ramsey goodness results can generalise other results in graph theory. See [Reference Fox, He and Wigderson13, Reference Lin and Liu19, Reference Moreira22, Reference Pokrovskiy and Sudakov24, Reference Pokrovskiy and Sudakov25] and their references for more recent progress in the area of Ramsey goodness, as well as the survey of Conlon, Fox and Sudakov [Reference Conlon, Fox and Sudakov9, Section 2.5].
In this paper, we are specifically interested in when
![]() $C_n$
, the n-vertex cycle, is H-good for general graphs H. This study can be traced back to Bondy and Erdős [Reference Bondy and Erdős3], who proved that
$C_n$
, the n-vertex cycle, is H-good for general graphs H. This study can be traced back to Bondy and Erdős [Reference Bondy and Erdős3], who proved that
![]() $C_n$
is
$C_n$
is
![]() $K_k$
-good whenever
$K_k$
-good whenever
![]() $n \geq k^2-2$
, which led Erdős, Faudree, Rousseau and Schelp [Reference Erdős, Faudree, Rousseau and Schelp11] to conjecture that
$n \geq k^2-2$
, which led Erdős, Faudree, Rousseau and Schelp [Reference Erdős, Faudree, Rousseau and Schelp11] to conjecture that
![]() $C_n$
is
$C_n$
is
![]() $K_k$
-good whenever
$K_k$
-good whenever
![]() $n \geq k \geq 3$
. Keevash, Long and Skokan [Reference Keevash, Long and Skokan17] recently proved a strengthening of this conjecture for large k, showing that
$n \geq k \geq 3$
. Keevash, Long and Skokan [Reference Keevash, Long and Skokan17] recently proved a strengthening of this conjecture for large k, showing that
![]() $n\ge C\frac {\log k}{\log \log k}$
suffices for some constant
$n\ge C\frac {\log k}{\log \log k}$
suffices for some constant
![]() $C \geq 1$
. For smaller k, Nikiforov [Reference Nikiforov23] proved
$C \geq 1$
. For smaller k, Nikiforov [Reference Nikiforov23] proved
![]() $n \geq 4k+2$
is sufficient and several authors have proved the conjecture for certain small values of k (see [Reference Chen, Cheng and Zhang6] and its references).
$n \geq 4k+2$
is sufficient and several authors have proved the conjecture for certain small values of k (see [Reference Chen, Cheng and Zhang6] and its references).
For Ramsey numbers of cycles versus general graphs H, Burr [Reference Burr4], in 1981, proved a satisfying result that
![]() $C_n$
is H-good when n is sufficiently large as a function of
$C_n$
is H-good when n is sufficiently large as a function of
![]() $\lvert H\rvert $
. It remains an intriguing open question to determine the threshold of n below which the Ramsey number
$\lvert H\rvert $
. It remains an intriguing open question to determine the threshold of n below which the Ramsey number
![]() $R(C_n,H)$
behaves differently from the natural construction of Burr yielding inequality (1). In particular, Allen, Brightwell and Skokan [Reference Allen, Brightwell and Skokan1] conjectured the following explicit bound.
$R(C_n,H)$
behaves differently from the natural construction of Burr yielding inequality (1). In particular, Allen, Brightwell and Skokan [Reference Allen, Brightwell and Skokan1] conjectured the following explicit bound.
Conjecture 1.1. For any graph H and
![]() $n\geq \chi (H)\lvert H\rvert $
, the cycle
$n\geq \chi (H)\lvert H\rvert $
, the cycle
![]() $C_n$
is H-good, that is,
$C_n$
is H-good, that is,
![]() $R(C_n, H) = (\chi (H)-1)(n-1)+\sigma (H)$
.
$R(C_n, H) = (\chi (H)-1)(n-1)+\sigma (H)$
.
Note that we may assume H to be a complete multipartite graph, as every H is a subgraph of some complete
![]() $\chi (H)$
-partite graph
$\chi (H)$
-partite graph
![]() $H'$
with
$H'$
with
![]() $\sigma (H')=\sigma (H)$
, and clearly
$\sigma (H')=\sigma (H)$
, and clearly
![]() $R(C_n, H)\leq R(C_n,H')$
.
$R(C_n, H)\leq R(C_n,H')$
.
Towards Conjecture 1.1, Pokrovskiy and Sudakov [Reference Pokrovskiy and Sudakov25] very recently proved an important case when the graph H has a polynomially small chromatic number:
![]() $\lvert H\rvert \ge \chi (H)^{23}$
. More precisely, they showed that for
$\lvert H\rvert \ge \chi (H)^{23}$
. More precisely, they showed that for
![]() $n\geq 10^{60} m_k$
and
$n\geq 10^{60} m_k$
and
![]() $m_1 \leq m_2 \leq \cdots \leq m_k$
satisfying
$m_1 \leq m_2 \leq \cdots \leq m_k$
satisfying
![]() $m_i\geq i^{22}$
for each i,
$m_i\geq i^{22}$
for each i,
![]() $R(C_n ,K_{m_1,\ldots ,m_k} ) = (n - 1)(k - 1) + m_1$
. Note, however, that it is well known from random graph theory (e.g., [Reference Bollobás2]) that, for almost all graphs H, the chromatic number is much larger:
$R(C_n ,K_{m_1,\ldots ,m_k} ) = (n - 1)(k - 1) + m_1$
. Note, however, that it is well known from random graph theory (e.g., [Reference Bollobás2]) that, for almost all graphs H, the chromatic number is much larger:
![]() $\chi (H)=\Theta \big (\frac {\lvert H\rvert }{\log \lvert H\rvert }\big )$
.
$\chi (H)=\Theta \big (\frac {\lvert H\rvert }{\log \lvert H\rvert }\big )$
.
Our main result below is an almost optimal quantitative version of Burr’s result [Reference Burr4]. In particular, this theorem holds for all graphs H. Moreover, as
![]() $x> C\log ^4 x$
for all large x, it proves a strengthening of Conjecture 1.1 for all graphs H with large (constant) chromatic number.
$x> C\log ^4 x$
for all large x, it proves a strengthening of Conjecture 1.1 for all graphs H with large (constant) chromatic number.
Theorem 1.2. There exists a constant
![]() $C> 0$
such that for any graph H and any
$C> 0$
such that for any graph H and any
![]() $n\geq C\lvert H\rvert \log ^4\chi (H)$
we have that
$n\geq C\lvert H\rvert \log ^4\chi (H)$
we have that
![]() $C_n$
is H-good, that is,
$C_n$
is H-good, that is,
![]() $R(C_n, H) = (\chi (H)-1)(n-1)+\sigma (H)$
.
$R(C_n, H) = (\chi (H)-1)(n-1)+\sigma (H)$
.
The bound on n in Theorem 1.2 is best possible up to the logarithmic factor
![]() $\log ^4\chi (H)$
. The following construction shows that the cycle length n has to be at least
$\log ^4\chi (H)$
. The following construction shows that the cycle length n has to be at least
![]() $(1-o(1))\lvert H\rvert $
in order to be H-good.
$(1-o(1))\lvert H\rvert $
in order to be H-good.
Lower bound construction. Fix arbitrary
![]() $m,k\in \mathbb {N}$
with
$m,k\in \mathbb {N}$
with
![]() $k\ge 2$
and
$k\ge 2$
and
![]() $0<\varepsilon <\frac {1}{4}$
. Set
$0<\varepsilon <\frac {1}{4}$
. Set
![]() $n=(1-\varepsilon )mk$
. Consider the complete k-partite graph H on partite set
$n=(1-\varepsilon )mk$
. Consider the complete k-partite graph H on partite set
![]() $V_1,\ldots ,V_k$
with
$V_1,\ldots ,V_k$
with
![]() $\lvert V_1\rvert =(1-\varepsilon )mk$
and
$\lvert V_1\rvert =(1-\varepsilon )mk$
and
![]() $\lvert V_2\rvert =\cdots =\lvert V_k\rvert =\frac {\varepsilon mk}{k-1}$
; so
$\lvert V_2\rvert =\cdots =\lvert V_k\rvert =\frac {\varepsilon mk}{k-1}$
; so
![]() $\lvert H\rvert =mk$
and
$\lvert H\rvert =mk$
and
![]() $\sigma (H)=\frac {\varepsilon mk}{k-1}$
. Let G be the N-vertex graph, with
$\sigma (H)=\frac {\varepsilon mk}{k-1}$
. Let G be the N-vertex graph, with
![]() $N=k(n-1)$
, consisting of k vertex disjoint cliques
$N=k(n-1)$
, consisting of k vertex disjoint cliques
![]() $K_{n-1}$
. It is easy to see that G is
$K_{n-1}$
. It is easy to see that G is
![]() $C_n$
-free with H-free complement. Therefore, for these choices of
$C_n$
-free with H-free complement. Therefore, for these choices of
![]() $C_n$
and H, we have
$C_n$
and H, we have
Our proof takes a similar approach to the work of Pokrovskiy and Sudakov [Reference Pokrovskiy and Sudakov25] and Keevash, Long and Skokan [Reference Keevash, Long and Skokan17]. The bulk of the work is to prove a stability type result showing that
![]() $C_n$
-free graphs G with H-free complement whose order is around the lower bound in inequality (1) must be structurally close to Burr’s construction. The two novel ingredients at the heart of our proof are (i) certain sublinear expansion properties and (ii) an ‘adjuster’ structure, both of which are inspired by recent work of Liu and Montgomery [Reference Liu and Montgomery21] on cycle embeddings in sublinear expanders. The theory of sublinear expanders has played a pivotal role in the resolutions of several old conjectures; see, for example, [Reference Gil Fernández, Kim, Kim and Liu15, Reference Haslegrave, Kim and Liu16, Reference Kim, Liu, Sharifzadeh and Staden18, Reference Liu and Montgomery20, Reference Liu and Montgomery21].
$C_n$
-free graphs G with H-free complement whose order is around the lower bound in inequality (1) must be structurally close to Burr’s construction. The two novel ingredients at the heart of our proof are (i) certain sublinear expansion properties and (ii) an ‘adjuster’ structure, both of which are inspired by recent work of Liu and Montgomery [Reference Liu and Montgomery21] on cycle embeddings in sublinear expanders. The theory of sublinear expanders has played a pivotal role in the resolutions of several old conjectures; see, for example, [Reference Gil Fernández, Kim, Kim and Liu15, Reference Haslegrave, Kim and Liu16, Reference Kim, Liu, Sharifzadeh and Staden18, Reference Liu and Montgomery20, Reference Liu and Montgomery21].
The logarithmic factor in our bound is an artifact of the use of sublinear expansion. Considering the above construction, it is not inconceivable that already when
![]() $n\ge (1+o(1))\lvert H\rvert $
, the cycle
$n\ge (1+o(1))\lvert H\rvert $
, the cycle
![]() $C_n$
is H-good. It would be interesting to at least get rid of the logarithmic factor and obtain a bound linear in
$C_n$
is H-good. It would be interesting to at least get rid of the logarithmic factor and obtain a bound linear in
![]() $\lvert H\rvert $
.
$\lvert H\rvert $
.
Organisation. The rest of the paper is organised as follows. We give an outline in Section 1. Preliminaries are given in Section 2. The two main ingredients, the sublinear expansion and the adjuster structure (and related lemmas), are given in Sections 3 and 4, respectively. The stability result and the proof of the main theorem are in Section 5.
2 Outline
Suppose that G has order at least
![]() $(\chi (H)-1)(n-1)+\sigma (H)$
but
$(\chi (H)-1)(n-1)+\sigma (H)$
but
![]() $\overline G$
is H-free. With the given condition on n, it is not too hard to find a cycle of length at least n in G; the difficulty lies in obtaining a cycle of the precise desired length n. A natural approach to deal with this is to create a sufficiently large structure which has inbuilt flexibility about the length of cycles it can produce. Pokrovskiy and Sudakov [Reference Pokrovskiy and Sudakov25] use expansion properties to create some complex gadgets, which can be joined together to produce structures capable of producing paths of a wide range of lengths, up to almost all of their total size. However, the connectivity properties needed to link up these structures require n to be very large compared to
$\overline G$
is H-free. With the given condition on n, it is not too hard to find a cycle of length at least n in G; the difficulty lies in obtaining a cycle of the precise desired length n. A natural approach to deal with this is to create a sufficiently large structure which has inbuilt flexibility about the length of cycles it can produce. Pokrovskiy and Sudakov [Reference Pokrovskiy and Sudakov25] use expansion properties to create some complex gadgets, which can be joined together to produce structures capable of producing paths of a wide range of lengths, up to almost all of their total size. However, the connectivity properties needed to link up these structures require n to be very large compared to
![]() $\chi (H)$
, and in particular only produce a good bound on n if
$\chi (H)$
, and in particular only produce a good bound on n if
![]() $\lvert H\rvert $
is at least a large power of
$\lvert H\rvert $
is at least a large power of
![]() $\chi (H)$
.
$\chi (H)$
.
To deal with the missing regime where
![]() $\lvert H\rvert $
is bounded by a polynomial in
$\lvert H\rvert $
is bounded by a polynomial in
![]() $\chi (H)$
, we use an orthogonal approach. Instead of the complex gadgets featured in [Reference Pokrovskiy and Sudakov25], we borrow ideas from recent work of Liu and Montgomery [Reference Liu and Montgomery21] to use certain sublinear expansion properties (Definition 4.1) to find simpler gadgets which we call adjusters (Definition 3.5). However, these adjusters are less flexible in terms of how much we can vary the length of the final cycle, relative to its total length. We circumvent this potential difficulty by creating a cycle which has enough adjusters to permit slightly more than
$\chi (H)$
, we use an orthogonal approach. Instead of the complex gadgets featured in [Reference Pokrovskiy and Sudakov25], we borrow ideas from recent work of Liu and Montgomery [Reference Liu and Montgomery21] to use certain sublinear expansion properties (Definition 4.1) to find simpler gadgets which we call adjusters (Definition 3.5). However, these adjusters are less flexible in terms of how much we can vary the length of the final cycle, relative to its total length. We circumvent this potential difficulty by creating a cycle which has enough adjusters to permit slightly more than
![]() $\lvert H\rvert $
different lengths, and also has a long adjuster-free section. The complement being H-free means that we may shorten this section until the cycle is close enough to the desired length, and use the flexibility from the adjusters to deliver the final blow.
$\lvert H\rvert $
different lengths, and also has a long adjuster-free section. The complement being H-free means that we may shorten this section until the cycle is close enough to the desired length, and use the flexibility from the adjusters to deliver the final blow.
One of the main technical difficulties in our proof is showing that a suitable expanding subgraph may be found in a graph with H-free complement under our definition of sublinear expansion. Additionally, we need to work directly with the specific graph H, rather than passing to a balanced multipartite graph, and the possibility that the parts of H are very unbalanced creates additional difficulties when one tries to use induction and it is necessary to reduce the number of parts first. We prove this, together with some useful consequences of expansion, in Section 3.
We then leverage these expansion properties to find the adjusters that we need in Section 4 and show how these may be combined together to give a suitable long cycle in a sufficiently well-connected subgraph. As a consequence of sublinear expansion and the fact that we do not need as much flexibility in length adjustment, we require only a very weak connectivity condition.
Finally, in Section 5 we establish a stability result on graphs G which have close to
![]() $(\chi (H)-1)(n-1)$
vertices, no copy of
$(\chi (H)-1)(n-1)$
vertices, no copy of
![]() $C_n$
, no copy of H in the complement and which cannot be reduced to a smaller example by removing a part from H. That is, we show that a small number of vertices may be removed from such a graph G to leave
$C_n$
, no copy of H in the complement and which cannot be reduced to a smaller example by removing a part from H. That is, we show that a small number of vertices may be removed from such a graph G to leave
![]() $\chi (H)-1$
reasonably well-connected subgraphs of order close to n, whose complements exclude a complete bipartite graph
$\chi (H)-1$
reasonably well-connected subgraphs of order close to n, whose complements exclude a complete bipartite graph
![]() $H'$
; here, our low connectivity requirements will obviate the need for a lower bound on the class sizes of H. The Ramsey goodness of the cycle then follows quickly from this stability result by considering how
$H'$
; here, our low connectivity requirements will obviate the need for a lower bound on the class sizes of H. The Ramsey goodness of the cycle then follows quickly from this stability result by considering how
![]() $2$
-connected blocks in G are linked.
$2$
-connected blocks in G are linked.
3 Preliminaries
Our aim is to use induction on the number of partite sets k. We therefore define how we order possible graphs H. For a complete multipartite graph H, we write
![]() $H'\sqsubset H$
if there exists a graph
$H'\sqsubset H$
if there exists a graph
![]() $H"$
such that
$H"$
such that
![]() $H\cong H'\vee H"$
, where
$H\cong H'\vee H"$
, where
![]() $\vee $
denotes graph join, that is, H is obtained by taking disjoint copies of
$\vee $
denotes graph join, that is, H is obtained by taking disjoint copies of
![]() $H'$
and
$H'$
and
![]() $H"$
and then adding all edges between
$H"$
and then adding all edges between
![]() $V(H')$
and
$V(H')$
and
![]() $V(H")$
. Informally,
$V(H")$
. Informally,
![]() $H'$
consists of the subgraph induced by a proper subcollection of the parts of H. We will sometimes use
$H'$
consists of the subgraph induced by a proper subcollection of the parts of H. We will sometimes use
![]() $H'\sqsubseteq H$
to mean ‘
$H'\sqsubseteq H$
to mean ‘
![]() $H'\sqsubset H$
or
$H'\sqsubset H$
or
![]() $H'=H$
’, that is,
$H'=H$
’, that is,
![]() $H'$
is induced by a (not necessarily proper) subcollection of parts of H. For the main step of the induction, we will require both
$H'$
is induced by a (not necessarily proper) subcollection of parts of H. For the main step of the induction, we will require both
![]() $H'\sqsubset H$
and
$H'\sqsubset H$
and
![]() $\sigma (H')=\sigma (H)$
, but in some intermediate steps, this latter condition is not needed. For a graph H with
$\sigma (H')=\sigma (H)$
, but in some intermediate steps, this latter condition is not needed. For a graph H with
![]() $\chi (H)=k$
, we write
$\chi (H)=k$
, we write
![]() $m=m(H)=\frac {\lvert H\rvert }{k}$
for the average part size of H, that is,
$m=m(H)=\frac {\lvert H\rvert }{k}$
for the average part size of H, that is,
![]() $\lvert H\rvert =km$
.
$\lvert H\rvert =km$
.
For a graph G and vertex set
![]() $A\subset V(G)$
, we define the external neighbourhood
$A\subset V(G)$
, we define the external neighbourhood
![]() $N_G(A)$
to be the set
$N_G(A)$
to be the set
![]() $\{w\in V(G)\setminus A:vw\in E(G)\}$
; note that this is disjoint from A. We omit the subscript if the graph is clear from context. The subgraph induced on A will be denoted by
$\{w\in V(G)\setminus A:vw\in E(G)\}$
; note that this is disjoint from A. We omit the subscript if the graph is clear from context. The subgraph induced on A will be denoted by
![]() $G[A]$
. We write
$G[A]$
. We write
![]() $G-A=G[V(G)\setminus A]$
for the subgraph obtained by removing vertices in A. For disjoint subsets
$G-A=G[V(G)\setminus A]$
for the subgraph obtained by removing vertices in A. For disjoint subsets
![]() $A,B\subset V(G)$
, an A-B path is a path between a vertex of A and a vertex of B. For two vertices
$A,B\subset V(G)$
, an A-B path is a path between a vertex of A and a vertex of B. For two vertices
![]() $u,v\in V(G)$
, the graph distance
$u,v\in V(G)$
, the graph distance
![]() $\operatorname {dist}_G(u,v)$
is the length of a shortest u-v path in G.
$\operatorname {dist}_G(u,v)$
is the length of a shortest u-v path in G.
Logarithms with no specified base are always taken to the base e throughout. For an integer t, we write
![]() $[t]$
for the set
$[t]$
for the set
![]() $\{1,2,\ldots ,t\}$
.
$\{1,2,\ldots ,t\}$
.
We will need the following result of Erdős and Szekeres [Reference Erdős and Szekeres12].
Theorem 3.1. Any sequence of at least
![]() $(r-1)^2+1$
integers contains a monotonic subsequence of length r.
$(r-1)^2+1$
integers contains a monotonic subsequence of length r.
We use the following results of Pokrovskiy and Sudakov [Reference Pokrovskiy and Sudakov25].
Corollary 3.2. For
![]() $n\geq 10^{60} m_k$
and
$n\geq 10^{60} m_k$
and
![]() $m_1 \leq m_2 \leq \cdots \leq m_k$
satisfying
$m_1 \leq m_2 \leq \cdots \leq m_k$
satisfying
![]() $m_k\geq k^{22}$
, we have
$m_k\geq k^{22}$
, we have
![]() $R(C_n ,K_{m_1,\ldots ,m_k} ) = (n - 1)(k - 1) + m_1$
.
$R(C_n ,K_{m_1,\ldots ,m_k} ) = (n - 1)(k - 1) + m_1$
.
Proof. Apply the aforementioned result [Reference Pokrovskiy and Sudakov25] for
![]() $K_{m_1,\ldots ,m_k}$
with
$K_{m_1,\ldots ,m_k}$
with
![]() $m_i\geq i^{22}$
for each i to
$m_i\geq i^{22}$
for each i to
![]() $K_{m^{\prime }_1,\ldots , m^{\prime }_k}$
where
$K_{m^{\prime }_1,\ldots , m^{\prime }_k}$
where
![]() $m^{\prime }_1=m_1$
and
$m^{\prime }_1=m_1$
and
![]() $m^{\prime }_i=m_k$
if
$m^{\prime }_i=m_k$
if
![]() $i>1$
. For each
$i>1$
. For each
![]() $i>1$
, we have
$i>1$
, we have
![]() $m^{\prime }_i=m_k\geq k^{22}\geq i^{22}$
, and clearly
$m^{\prime }_i=m_k\geq k^{22}\geq i^{22}$
, and clearly
![]() $m^{\prime }_1\geq 1^{22}$
. Thus, if G is a
$m^{\prime }_1\geq 1^{22}$
. Thus, if G is a
![]() $C_n$
-free graph on
$C_n$
-free graph on
![]() $(n - 1)(k - 1) + m_1$
vertices, then
$(n - 1)(k - 1) + m_1$
vertices, then
![]() $\overline {G}$
contains a copy of
$\overline {G}$
contains a copy of
![]() $K_{m^{\prime }_1,\ldots , m^{\prime }_k}$
, which in turn contains
$K_{m^{\prime }_1,\ldots , m^{\prime }_k}$
, which in turn contains
![]() $K_{m_1,\ldots , m_k}$
.
$K_{m_1,\ldots , m_k}$
.
Our induction may reduce to the case when H is a complete bipartite graph.
Corollary 3.3 [Reference Pokrovskiy and Sudakov25, Corollary 3.8].
Let
![]() $n, m_1, m_2$
be integers with
$n, m_1, m_2$
be integers with
![]() $m_2 \geq m_1$
,
$m_2 \geq m_1$
,
![]() $m_2 \geq 8$
and
$m_2 \geq 8$
and
![]() $n \geq 2\times 10^{49}m_2$
. Then we have
$n \geq 2\times 10^{49}m_2$
. Then we have
![]() $R(C_n, K_{m_1 ,m_2}) = n + m_1 - 1$
.
$R(C_n, K_{m_1 ,m_2}) = n + m_1 - 1$
.
The last one we need is an intermediate result on path embeddings.
Lemma 3.4 [Reference Pokrovskiy and Sudakov25, Lemma 3.7].
Let n and m be integers with
![]() $n \geq 2\times 10^{49}m$
and
$n \geq 2\times 10^{49}m$
and
![]() $m \geq 8$
. Let G be a graph with
$m \geq 8$
. Let G be a graph with
![]() $\overline G$
being
$\overline G$
being
![]() $K_{m,m}$
-free and
$K_{m,m}$
-free and
![]() $\lvert N_G (A) \cup A\rvert \geq n$
for every
$\lvert N_G (A) \cup A\rvert \geq n$
for every
![]() $A\subseteq V (G)$
with
$A\subseteq V (G)$
with
![]() $\lvert A\rvert \geq m$
. Let x and y be two vertices in G such that there exists an x-y path with order at least
$\lvert A\rvert \geq m$
. Let x and y be two vertices in G such that there exists an x-y path with order at least
![]() $8m$
. Then there is an x-y path of order exactly n in G.
$8m$
. Then there is an x-y path of order exactly n in G.
3.1 Adjusters
In order to construct cycles covering a range of lengths, we will use the following graphs called adjusters. In the following definition, m and k are fixed numbers. When constructing adjusters, the relevant values of m and k will be clear from context.
Definition 3.5. For
![]() $r\geq 1$
, an r-adjuster consists of r disjoint odd cycles
$r\geq 1$
, an r-adjuster consists of r disjoint odd cycles
![]() $C_1,\ldots ,C_r$
, with
$C_1,\ldots ,C_r$
, with
![]() $C_i$
having distinguished vertices
$C_i$
having distinguished vertices
![]() $v_i,w_i$
which are almost-antipodal (i.e.,
$v_i,w_i$
which are almost-antipodal (i.e.,
![]() $\operatorname {dist}_{C_i}(v_i,w_i)=(\lvert C_i\rvert -1)/2$
), together with paths
$\operatorname {dist}_{C_i}(v_i,w_i)=(\lvert C_i\rvert -1)/2$
), together with paths
![]() $P_1,\ldots ,P_r$
, where the endpoints of
$P_1,\ldots ,P_r$
, where the endpoints of
![]() $P_i$
are
$P_i$
are
![]() $w_i$
and
$w_i$
and
![]() $v_{i+1}$
(subscripts taken modulo r), such that the paths are internally disjoint from each other and from the cycles, and
$v_{i+1}$
(subscripts taken modulo r), such that the paths are internally disjoint from each other and from the cycles, and
![]() $\lvert C_i\rvert \leq 2,000\log k\log (km)$
. For the special case
$\lvert C_i\rvert \leq 2,000\log k\log (km)$
. For the special case
![]() $r=0$
, a
$r=0$
, a
![]() $0$
-adjuster is simply a cycle.
$0$
-adjuster is simply a cycle.
We refer to the cycles
![]() $C_i$
as the short cycles of the adjuster. There are also cycles which use all the paths
$C_i$
as the short cycles of the adjuster. There are also cycles which use all the paths
![]() $P_i$
and part of each short cycle; we refer to these as the routes of the adjuster. An r-adjuster contains
$P_i$
and part of each short cycle; we refer to these as the routes of the adjuster. An r-adjuster contains
![]() $2^r$
routes, whose lengths are
$2^r$
routes, whose lengths are
![]() $r+1$
consecutive integers. We define the length of an adjuster to be the length of its longest route.
$r+1$
consecutive integers. We define the length of an adjuster to be the length of its longest route.

Figure 1 An r-adjuster. An example of a route in this r-adjuster is given by the red dashed line.
4 Sublinear expansions
Given a large graph whose complement is H-free, we will pass to a subgraph which is not too large and has sublinear expansion properties, in which we can find an r-adjuster for some suitable r. After removing this r-adjuster, we repeat the process with the remaining graph. We then join many adjusters together to create a very large adjuster with greater flexibility in the length of a route and where this length can exceed n. We will shrink the structure, if necessary, to ensure that the maximum length of a cycle is not much more than n, without impairing this flexibility. We then show this structure contains
![]() $C_n$
.
$C_n$
.
In this section, we define the expansion properties we need, and show that any sufficiently large graph whose complement is F-free, for some graph F, contains an expanding subgraph of suitable size.
Definition 4.1. A graph
![]() $G \ (\Delta ,\beta ,d,k)$
-expands into a set
$G \ (\Delta ,\beta ,d,k)$
-expands into a set
![]() $W \subseteq V(G)$
if the following holds.
$W \subseteq V(G)$
if the following holds.
-
•
 $\lvert N_G(S) \cap W\rvert \geq \Delta \lvert S\rvert $
, for every
$\lvert N_G(S) \cap W\rvert \geq \Delta \lvert S\rvert $
, for every
 $S\subseteq V(G)$
with
$S\subseteq V(G)$
with
 $\lvert S\rvert \leq \beta d$
.
$\lvert S\rvert \leq \beta d$
. -
•
 $\lvert N_G(S)\rvert \geq \frac {\lvert S\rvert }{10\log k}$
, for every
$\lvert N_G(S)\rvert \geq \frac {\lvert S\rvert }{10\log k}$
, for every
 $S\subseteq V(G)$
with
$S\subseteq V(G)$
with
 $\beta d \leq \lvert S\rvert \leq \lvert G\rvert /2$
.
$\beta d \leq \lvert S\rvert \leq \lvert G\rvert /2$
.
Note that, whenever we say that
![]() $G \ (\Delta , \beta , d, k)$
-expands and do not specify the set G expands into, we mean that
$G \ (\Delta , \beta , d, k)$
-expands and do not specify the set G expands into, we mean that
![]() $G \ (\Delta , \beta , d, k)$
-expands into
$G \ (\Delta , \beta , d, k)$
-expands into
![]() $W = V(G)$
.
$W = V(G)$
.
Lemma 4.2. Fix a complete k-partite graph H of order
![]() $mk$
, where
$mk$
, where
![]() $k\geq 2$
, then for all
$k\geq 2$
, then for all
![]() $\beta , M, \Delta \geq 1$
with
$\beta , M, \Delta \geq 1$
with
![]() $M \geq 60 \beta \geq 240 \Delta $
,
$M \geq 60 \beta \geq 240 \Delta $
,
![]() $M \geq 10\beta \Delta $
,
$M \geq 10\beta \Delta $
,
![]() $M \geq 4k$
and
$M \geq 4k$
and
![]() $\beta \geq 10\log k$
, the following holds. Let G be a graph with
$\beta \geq 10\log k$
, the following holds. Let G be a graph with
![]() $\overline {G}$
being H-free and
$\overline {G}$
being H-free and
![]() $\lvert G\rvert \geq Mmk\log k$
. Then there exists a subgraph
$\lvert G\rvert \geq Mmk\log k$
. Then there exists a subgraph
![]() $H'\sqsubseteq H$
induced by some collection of at least two parts and an induced subgraph
$H'\sqsubseteq H$
induced by some collection of at least two parts and an induced subgraph
![]() $F \subseteq G$
such that the following holds:
$F \subseteq G$
such that the following holds:
-
•
 $\overline {F}$
is
$\overline {F}$
is
 $H'$
-free.
$H'$
-free. -
•
 $M\lvert H'\rvert \log \chi (H') - m(H') \leq \lvert F\rvert \leq M\lvert H'\rvert \log \chi (H')$
.
$M\lvert H'\rvert \log \chi (H') - m(H') \leq \lvert F\rvert \leq M\lvert H'\rvert \log \chi (H')$
. -
• F is
 $(\Delta ,\beta ,m(H'),\chi (H'))$
-expanding.
$(\Delta ,\beta ,m(H'),\chi (H'))$
-expanding.
Proof. We proceed by induction on k, considering two cases. The base case
![]() $k=2$
will be covered by the inductive argument since we argue that we may either (i) construct a suitable subgraph directly for
$k=2$
will be covered by the inductive argument since we argue that we may either (i) construct a suitable subgraph directly for
![]() $H'=H$
, (ii) reduce to some smaller
$H'=H$
, (ii) reduce to some smaller
![]() $H'\sqsubset H$
with at least two parts or (iii) obtain a contradiction; in the base case only, the first and third possibilities arise. Note that, by removing vertices if necessary, we may assume
$H'\sqsubset H$
with at least two parts or (iii) obtain a contradiction; in the base case only, the first and third possibilities arise. Note that, by removing vertices if necessary, we may assume
![]() $\lvert G\rvert =Mmk \log k$
for
$\lvert G\rvert =Mmk \log k$
for
![]() $k\geq 2$
. We write
$k\geq 2$
. We write
![]() $m_1\leq \cdots \leq m_k$
for the orders of the vertex classes of H.
$m_1\leq \cdots \leq m_k$
for the orders of the vertex classes of H.
The first case is if there exists a set
![]() $S\subset V(G)$
such that
$S\subset V(G)$
such that
![]() $m \leq \lvert S\rvert \leq \lvert G\rvert /2$
and
$m \leq \lvert S\rvert \leq \lvert G\rvert /2$
and
![]() $\lvert N_G(S)\rvert \leq \lvert S\rvert /(10\log k) + m\Delta \beta $
. Let
$\lvert N_G(S)\rvert \leq \lvert S\rvert /(10\log k) + m\Delta \beta $
. Let
![]() $T = V(G)\setminus (N_G(S) \cup S)$
. Since
$T = V(G)\setminus (N_G(S) \cup S)$
. Since
![]() $M \geq 10\Delta \beta $
, we have that
$M \geq 10\Delta \beta $
, we have that
 $$ \begin{align*} \lvert T\rvert\geq \lvert G\rvert-\lvert N_G(S)\cup S\rvert & \geq \left(1-1/(10\log k)\right)\lvert G\rvert/2 - m\Delta\beta \\ & = m\left(\tfrac{Mk}{2}(\log k-1/10) - \Delta\beta\right) \\ & \geq km. \end{align*} $$
$$ \begin{align*} \lvert T\rvert\geq \lvert G\rvert-\lvert N_G(S)\cup S\rvert & \geq \left(1-1/(10\log k)\right)\lvert G\rvert/2 - m\Delta\beta \\ & = m\left(\tfrac{Mk}{2}(\log k-1/10) - \Delta\beta\right) \\ & \geq km. \end{align*} $$
We distinguish two subcases depending on whether
![]() $\lvert S\rvert \geq mk$
or
$\lvert S\rvert \geq mk$
or
![]() $\lvert S\rvert <mk$
.
$\lvert S\rvert <mk$
.
First, suppose
![]() $\lvert S\rvert \geq mk$
. We choose
$\lvert S\rvert \geq mk$
. We choose
![]() $t \in \mathbb {N}$
as large as possible such that
$t \in \mathbb {N}$
as large as possible such that
![]() $\lvert T\rvert \geq M\lvert H_t\rvert \log t$
, where
$\lvert T\rvert \geq M\lvert H_t\rvert \log t$
, where
![]() $H_t$
is the graph induced by the t smallest parts of H. We then choose
$H_t$
is the graph induced by the t smallest parts of H. We then choose
![]() $s \in \mathbb {N}$
as large as possible so that
$s \in \mathbb {N}$
as large as possible so that
![]() $\lvert S\rvert \geq M\lvert H_{s,t}\rvert \log s$
, where
$\lvert S\rvert \geq M\lvert H_{s,t}\rvert \log s$
, where
![]() $H_{s,t}$
is the graph induced by the s smallest parts of H not contained in
$H_{s,t}$
is the graph induced by the s smallest parts of H not contained in
![]() $H_t$
; observe that
$H_t$
; observe that
![]() $s,t\geq 1$
and
$s,t\geq 1$
and
![]() $s,t\leq k-1$
.
$s,t\leq k-1$
.
We will quickly be able to resolve our first subcase after proving the following claim.
Claim 4.3.
![]() $s + t = k$
.
$s + t = k$
.
Proof of claim. The claim is trivial for
![]() $k=2$
since
$k=2$
since
![]() $s,t\geq 1$
. For all
$s,t\geq 1$
. For all
![]() $k\geq 3$
, we have
$k\geq 3$
, we have
which implies
![]() $t\geq \lceil k/2\rceil $
; in particular, this proves the claim when
$t\geq \lceil k/2\rceil $
; in particular, this proves the claim when
![]() $k=3$
.
$k=3$
.
Assume for a contradiction that
![]() $s + t < k$
, where
$s + t < k$
, where
![]() $k\geq 4$
is fixed; as
$k\geq 4$
is fixed; as
![]() $t \geq \lceil k/2\rceil $
, we have
$t \geq \lceil k/2\rceil $
, we have
![]() $s\leq (k-1)/2$
. Maximalities of s and t ensure that
$s\leq (k-1)/2$
. Maximalities of s and t ensure that
and
Observe that
![]() $H_{t+1}$
and
$H_{t+1}$
and
![]() $H_{s+1, t}$
both contain the
$H_{s+1, t}$
both contain the
![]() $(t+1)$
th smallest part of H.
$(t+1)$
th smallest part of H.
Also,
![]() $\lvert S\rvert +\lvert T\rvert = \lvert G\rvert - \lvert N_G(S)\rvert> Mmk\log k - \frac {\lvert S\rvert }{10\log k} - m\Delta \beta $
; hence by inequality (2), inequality (3) and the fact that
$\lvert S\rvert +\lvert T\rvert = \lvert G\rvert - \lvert N_G(S)\rvert> Mmk\log k - \frac {\lvert S\rvert }{10\log k} - m\Delta \beta $
; hence by inequality (2), inequality (3) and the fact that
![]() $M\geq 10\beta \Delta $
, we have
$M\geq 10\beta \Delta $
, we have
where
![]() $c(k)=\left (1 + \frac {1}{10\log k}\right )$
. We want to show that inequality (4) is in fact false, which provides the contradiction we need to prove Claim 4.3. To this end, we may assume
$c(k)=\left (1 + \frac {1}{10\log k}\right )$
. We want to show that inequality (4) is in fact false, which provides the contradiction we need to prove Claim 4.3. To this end, we may assume
![]() $s+t = k-1$
. It follows that
$s+t = k-1$
. It follows that
recall that
![]() $m_{t+1}$
is the size of the
$m_{t+1}$
is the size of the
![]() $(t+1)$
th smallest part of H. Consequently, the left-hand side of inequality (4) is at most
$(t+1)$
th smallest part of H. Consequently, the left-hand side of inequality (4) is at most
Note that
![]() $m(s+1)\leq \lvert H_{s+1, t}\rvert \leq mk$
. For fixed s, expression (5) is linear in
$m(s+1)\leq \lvert H_{s+1, t}\rvert \leq mk$
. For fixed s, expression (5) is linear in
![]() $|H_{s+1, t}|$
, and consequently, within this range it is maximised either at
$|H_{s+1, t}|$
, and consequently, within this range it is maximised either at
![]() $\lvert H_{s+1, t}\rvert =m(s+1)$
or at
$\lvert H_{s+1, t}\rvert =m(s+1)$
or at
![]() $\lvert H_{s+1, t}\rvert =mk$
.
$\lvert H_{s+1, t}\rvert =mk$
.
We first consider the case
![]() $\lvert H_{s+1, t}\rvert =m(s+1)$
when expression (5) becomes
$\lvert H_{s+1, t}\rvert =m(s+1)$
when expression (5) becomes
This is a convex function of s and so for
![]() $1\leq s\leq (k-1)/2$
is maximised when
$1\leq s\leq (k-1)/2$
is maximised when
![]() $s=1$
or when
$s=1$
or when
![]() $s=(k-1)/2$
. When
$s=(k-1)/2$
. When
![]() $s=1$
, we have
$s=1$
, we have
for all
![]() $k\geq 4$
. When
$k\geq 4$
. When
![]() $s=(k-1)/2$
, we likewise have
$s=(k-1)/2$
, we likewise have
 $$ \begin{align} (1+c(k))\frac{k+1}{2}\log\left(\frac{k+1}{2}\right)<k\log k-0.1 \end{align} $$
$$ \begin{align} (1+c(k))\frac{k+1}{2}\log\left(\frac{k+1}{2}\right)<k\log k-0.1 \end{align} $$
for all
![]() $k\geq 4$
.
$k\geq 4$
.
Finally, we consider the case
![]() $\lvert H_{s+1, t}\rvert =mk$
when expression (5) becomes
$\lvert H_{s+1, t}\rvert =mk$
when expression (5) becomes
Suppose
![]() $2\leq s\leq \log (k-s)$
. Then
$2\leq s\leq \log (k-s)$
. Then
![]() $\frac {s}{s+1}\log (k-s)\geq \frac {s^2}{s+1}\geq c(k)\log (s+1)+0.1$
, and so expression (5) is decreasing in
$\frac {s}{s+1}\log (k-s)\geq \frac {s^2}{s+1}\geq c(k)\log (s+1)+0.1$
, and so expression (5) is decreasing in
![]() $\lvert H_{s+1, t}\rvert $
and maximised when
$\lvert H_{s+1, t}\rvert $
and maximised when
![]() $\lvert H_{s+1, t}\rvert =m(s+1)$
. Similarly, if
$\lvert H_{s+1, t}\rvert =m(s+1)$
. Similarly, if
![]() $s=1$
and
$s=1$
and
![]() $k\geq 7$
, expression (5) is decreasing. For
$k\geq 7$
, expression (5) is decreasing. For
![]() $s=1$
and
$s=1$
and
![]() $4\leq k\leq 6$
, by direct calculation expression (5) contradicts inequality (4). Thus, we may assume that
$4\leq k\leq 6$
, by direct calculation expression (5) contradicts inequality (4). Thus, we may assume that
![]() $s\geq \log (k-s)$
. Since
$s\geq \log (k-s)$
. Since
![]() $s\leq (k-1)/2$
, we have
$s\leq (k-1)/2$
, we have
![]() $s+1\leq k-s$
. Thus,
$s+1\leq k-s$
. Thus,
 $$\begin{align*}\frac{\mathrm{d}}{\mathrm{d}s}\left(\log(s+1)c(k)+ \frac{\log(k-s)}{s+1}\right)=\frac{c(k)(s+1)-\frac{s+1}{k-s}-\log(k-s)}{(s+1)^2}>0, \end{align*}$$
$$\begin{align*}\frac{\mathrm{d}}{\mathrm{d}s}\left(\log(s+1)c(k)+ \frac{\log(k-s)}{s+1}\right)=\frac{c(k)(s+1)-\frac{s+1}{k-s}-\log(k-s)}{(s+1)^2}>0, \end{align*}$$
and so
![]() $\log (s+1)c(k)+\log (k-s)/(s+1)$
is increasing in s for
$\log (s+1)c(k)+\log (k-s)/(s+1)$
is increasing in s for
![]() $\log (k-s)\leq s\leq (k-1)/2$
. Hence, within this range
$\log (k-s)\leq s\leq (k-1)/2$
. Hence, within this range
![]() $mk(\log (s+1)c(k)+\log (k-s)/(s+1))$
is maximised when
$mk(\log (s+1)c(k)+\log (k-s)/(s+1))$
is maximised when
![]() $s=(k-1)/2$
, and we obtain
$s=(k-1)/2$
, and we obtain
 $$ \begin{align} k\left(c(k)+\frac{2}{k+1}\right)\log\left(\frac{k+1}{2}\right)<k\log k - 0.1 \end{align} $$
$$ \begin{align} k\left(c(k)+\frac{2}{k+1}\right)\log\left(\frac{k+1}{2}\right)<k\log k - 0.1 \end{align} $$
for all
![]() $k\geq 4$
. Then inequalities (6), (7) and (8) together show that expression (5) is less than
$k\geq 4$
. Then inequalities (6), (7) and (8) together show that expression (5) is less than
![]() $mk\log k - \frac {m}{10}$
, contradicting inequality (4).
$mk\log k - \frac {m}{10}$
, contradicting inequality (4).
Hence,
![]() $s+t= k$
. Now, either
$s+t= k$
. Now, either
![]() $\overline {G[T]}$
is
$\overline {G[T]}$
is
![]() $H_t$
-free or
$H_t$
-free or
![]() $\overline {G[S]}$
is
$\overline {G[S]}$
is
![]() $H_{s,t}$
-free since otherwise disjointness of T and
$H_{s,t}$
-free since otherwise disjointness of T and
![]() $N_G(S)\cup S$
ensures we have a copy of H in
$N_G(S)\cup S$
ensures we have a copy of H in
![]() $\overline {G[S\cup T]}$
. However, since
$\overline {G[S\cup T]}$
. However, since
![]() $\lvert S\rvert ,\lvert T\rvert \geq mk$
,
$\lvert S\rvert ,\lvert T\rvert \geq mk$
,
![]() $\overline {G[T]}$
is not
$\overline {G[T]}$
is not
![]() $H_1$
-free and
$H_1$
-free and
![]() $\overline {G[S]}$
is not
$\overline {G[S]}$
is not
![]() $H_{1,k-1}$
-free. Thus, in the former case we have
$H_{1,k-1}$
-free. Thus, in the former case we have
![]() $2\leq t\leq k-1$
so we may apply the induction hypothesis to
$2\leq t\leq k-1$
so we may apply the induction hypothesis to
![]() $G[T]$
with k replaced by t and H by
$G[T]$
with k replaced by t and H by
![]() $H_t$
, and in the latter
$H_t$
, and in the latter
![]() $2\leq s\leq k-1$
so we may apply the induction hypothesis to
$2\leq s\leq k-1$
so we may apply the induction hypothesis to
![]() $G[S]$
with k replaced by s and H by
$G[S]$
with k replaced by s and H by
![]() $H_{s,t}$
. Here, such applications of the induction hypothesis are possible by the definition of s and t.
$H_{s,t}$
. Here, such applications of the induction hypothesis are possible by the definition of s and t.
Secondly, suppose
![]() $m\leq \lvert S\rvert <mk$
. Note that, since
$m\leq \lvert S\rvert <mk$
. Note that, since
![]() $M \geq 10\Delta \beta $
and
$M \geq 10\Delta \beta $
and
![]() $M \geq 4k$
, in this case
$M \geq 4k$
, in this case
Indeed,
![]() $Mmk\log \frac {k}{k-1} \geq Mm \geq 2mk + m\Delta \beta $
where we have used
$Mmk\log \frac {k}{k-1} \geq Mm \geq 2mk + m\Delta \beta $
where we have used
![]() $\log (1+x) \geq \frac {x}{1+x}$
with
$\log (1+x) \geq \frac {x}{1+x}$
with
![]() $x = \frac {1}{k-1}$
. Thus,
$x = \frac {1}{k-1}$
. Thus,
![]() $\lvert T\rvert \geq M\lvert H_{k-1, 1}\rvert \log (k-1)$
and
$\lvert T\rvert \geq M\lvert H_{k-1, 1}\rvert \log (k-1)$
and
![]() $\lvert S\rvert \geq m \geq \lvert H_1\rvert $
. Since
$\lvert S\rvert \geq m \geq \lvert H_1\rvert $
. Since
![]() $H_1$
is an independent set of size at most m,
$H_1$
is an independent set of size at most m,
![]() $\overline {G[S]}$
contains
$\overline {G[S]}$
contains
![]() $H_1$
. Thus,
$H_1$
. Thus,
![]() $\overline {G[T]}$
must be
$\overline {G[T]}$
must be
![]() $H_{k-1, 1}$
-free, as otherwise
$H_{k-1, 1}$
-free, as otherwise
![]() $\overline {G[S\cup T]}$
contains H, as before. Since
$\overline {G[S\cup T]}$
contains H, as before. Since
![]() $\lvert T\rvert \geq mk$
, it is not
$\lvert T\rvert \geq mk$
, it is not
![]() $H_{1,1}$
-free and so
$H_{1,1}$
-free and so
![]() $k-1\geq 2$
. We may therefore apply the induction hypothesis to
$k-1\geq 2$
. We may therefore apply the induction hypothesis to
![]() $G[T]$
with
$G[T]$
with
![]() $k-1$
replacing k and
$k-1$
replacing k and
![]() $H_{k-1,1}$
replacing H.
$H_{k-1,1}$
replacing H.
The final case is where we have
![]() $\lvert N_G(S)\cup S\rvert \geq \left (1+1/(10\log {k})\right )\lvert S\rvert + m\Delta \beta $
for every set
$\lvert N_G(S)\cup S\rvert \geq \left (1+1/(10\log {k})\right )\lvert S\rvert + m\Delta \beta $
for every set
![]() $S \subseteq V(G)$
with
$S \subseteq V(G)$
with
![]() $m \leq \lvert S\rvert \leq \lvert G\rvert /2$
. Consider the largest set
$m \leq \lvert S\rvert \leq \lvert G\rvert /2$
. Consider the largest set
![]() $X \subseteq V(G)$
with
$X \subseteq V(G)$
with
![]() $\lvert X\rvert \leq 2m$
such that
$\lvert X\rvert \leq 2m$
such that
![]() $\lvert N_G(X)\rvert \leq \Delta \lvert X\rvert $
. Since
$\lvert N_G(X)\rvert \leq \Delta \lvert X\rvert $
. Since
![]() $\beta \geq 4\Delta $
, we have that
$\beta \geq 4\Delta $
, we have that
![]() $\lvert N_G(X) \cup X\rvert \leq (\Delta + 1)\lvert X\rvert \leq m\Delta \beta $
. Thus, we must have
$\lvert N_G(X) \cup X\rvert \leq (\Delta + 1)\lvert X\rvert \leq m\Delta \beta $
. Thus, we must have
![]() $\lvert X\rvert < m$
. Now, consider
$\lvert X\rvert < m$
. Now, consider
![]() $F = G- X$
. If there is some
$F = G- X$
. If there is some
![]() $Y\subset V(F)$
with
$Y\subset V(F)$
with
![]() $\lvert Y\rvert \leq m$
and
$\lvert Y\rvert \leq m$
and
![]() $N_F(Y) < \Delta \lvert Y\rvert $
, then
$N_F(Y) < \Delta \lvert Y\rvert $
, then
contradicting our choice of X.
For
![]() $\lvert Y\rvert \geq m$
, we have
$\lvert Y\rvert \geq m$
, we have
 $$\begin{align*}\lvert N_F(Y) \cup Y\rvert \geq \lvert N_G(Y) \cup Y\rvert - \lvert X\rvert\geq \left(1 + \frac{1}{10\log{k}}\right)\lvert Y\rvert + m\Delta\beta - m. \end{align*}$$
$$\begin{align*}\lvert N_F(Y) \cup Y\rvert \geq \lvert N_G(Y) \cup Y\rvert - \lvert X\rvert\geq \left(1 + \frac{1}{10\log{k}}\right)\lvert Y\rvert + m\Delta\beta - m. \end{align*}$$
If
![]() $\lvert Y\rvert \leq \beta m$
, then utilising
$\lvert Y\rvert \leq \beta m$
, then utilising
![]() $\beta \geq 10\log k$
we have that
$\beta \geq 10\log k$
we have that
![]() $\lvert N_F(Y) \cup Y\rvert \geq \lvert Y\rvert +\Delta \lvert Y\rvert $
, whereas if
$\lvert N_F(Y) \cup Y\rvert \geq \lvert Y\rvert +\Delta \lvert Y\rvert $
, whereas if
![]() $\beta m \leq \lvert Y\rvert \leq \lvert F\rvert /2$
, then
$\beta m \leq \lvert Y\rvert \leq \lvert F\rvert /2$
, then
![]() $\lvert N_F(Y) \cup Y\rvert \geq \left (1 + 1/10\log {k}\right )\lvert Y\rvert $
. Thus, F fulfils the requirements of Lemma 4.2 for
$\lvert N_F(Y) \cup Y\rvert \geq \left (1 + 1/10\log {k}\right )\lvert Y\rvert $
. Thus, F fulfils the requirements of Lemma 4.2 for
![]() $H'=H$
.
$H'=H$
.
These expansion properties give us three abilities we will need to construct adjusters. The first is the ability to link together large sets, while avoiding a smaller set, via a path which is not too long. The main advantage of our stronger definition of expansion (compared to that in [Reference Pokrovskiy and Sudakov25]) is that the length of path required is much shorter, being only of order
![]() $\log k\log \lvert G\rvert $
, and the control we have over the size of the expanding subgraph means that we can ensure
$\log k\log \lvert G\rvert $
, and the control we have over the size of the expanding subgraph means that we can ensure
![]() $\log \lvert G\rvert =O(\log k)$
.
$\log \lvert G\rvert =O(\log k)$
.
Lemma 4.4. Suppose that
![]() $G \ (\Delta ,\beta ,d,k)$
-expands into a set
$G \ (\Delta ,\beta ,d,k)$
-expands into a set
![]() $W\subseteq V(G)$
, for
$W\subseteq V(G)$
, for
![]() $\Delta \geq 2$
and
$\Delta \geq 2$
and
![]() $k \geq 2$
. If
$k \geq 2$
. If
![]() $A,B,C\subseteq V(G)$
are disjoint sets with
$A,B,C\subseteq V(G)$
are disjoint sets with
![]() $A,B\neq \varnothing $
such that
$A,B\neq \varnothing $
such that
![]() $\lvert C\cap W\rvert \leq (\Delta -2) \min \{\lvert A\rvert ,\lvert B\rvert \}$
and
$\lvert C\cap W\rvert \leq (\Delta -2) \min \{\lvert A\rvert ,\lvert B\rvert \}$
and
![]() $\lvert C\rvert \leq \beta d/(20\log k)$
, then there is an A-B path P in G avoiding C and with
$\lvert C\rvert \leq \beta d/(20\log k)$
, then there is an A-B path P in G avoiding C and with
![]() $\lvert P\rvert \leq 44\log k\log \lvert G\rvert $
.
$\lvert P\rvert \leq 44\log k\log \lvert G\rvert $
.
Proof. Set
![]() $A_0=A$
and
$A_0=A$
and
![]() $A_{i+1}=(N(A_i)\cup A_i)\setminus C$
for each i. Since we have that
$A_{i+1}=(N(A_i)\cup A_i)\setminus C$
for each i. Since we have that
![]() $\lvert A_{i+1}\rvert \geq 2\lvert A_i\rvert $
for
$\lvert A_{i+1}\rvert \geq 2\lvert A_i\rvert $
for
![]() $\lvert A_i\rvert <\beta d$
, and thus
$\lvert A_i\rvert <\beta d$
, and thus
![]() $\lvert A_a\rvert \geq \beta d$
, where
$\lvert A_a\rvert \geq \beta d$
, where
![]() $a=\log _2(\beta d)$
. For
$a=\log _2(\beta d)$
. For
![]() $i\geq a$
, we have
$i\geq a$
, we have
![]() $\lvert N(A_i)\rvert \geq \frac {1}{10\log k}\lvert A_i\rvert \geq 2\lvert C\rvert $
, and so
$\lvert N(A_i)\rvert \geq \frac {1}{10\log k}\lvert A_i\rvert \geq 2\lvert C\rvert $
, and so
![]() $\lvert A_{i+1}\rvert \geq (1+1/20\log k)\lvert A_i\rvert $
. Consequently,
$\lvert A_{i+1}\rvert \geq (1+1/20\log k)\lvert A_i\rvert $
. Consequently,
![]() $\lvert A_b\rvert \geq \lvert G\rvert /2$
, where
$\lvert A_b\rvert \geq \lvert G\rvert /2$
, where
![]() $b=a+\log _{1+1/20\log k}(\lvert G\rvert /2\beta d)$
. Applying
$b=a+\log _{1+1/20\log k}(\lvert G\rvert /2\beta d)$
. Applying
![]() $\log (1+x)=-\log (1-\frac {x}{1+x})\geq (1+1/x)^{-1}$
for
$\log (1+x)=-\log (1-\frac {x}{1+x})\geq (1+1/x)^{-1}$
for
![]() $x=1/20\log k$
and noting that
$x=1/20\log k$
and noting that
![]() $1+20\log k\leq 22\log k$
, we get
$1+20\log k\leq 22\log k$
, we get
Since the same argument applies to B, we have that
![]() $A_b\cap B_b\neq \varnothing $
, and so there is a path of length at most
$A_b\cap B_b\neq \varnothing $
, and so there is a path of length at most
![]() $2b\leq 44\log k \log \lvert G\rvert $
avoiding C, as desired.
$2b\leq 44\log k \log \lvert G\rvert $
avoiding C, as desired.
The next ingredient follows from Lemma 4.4 and allows us to find a short odd cycle while retaining expansion into the rest of the graph.
Lemma 4.5. Suppose G is not bipartite and
![]() $(\Delta ,\beta ,d,k)$
-expands into
$(\Delta ,\beta ,d,k)$
-expands into
![]() $W\subseteq V(G)$
for
$W\subseteq V(G)$
for
![]() $\Delta \geq 4$
,
$\Delta \geq 4$
,
![]() $k \geq 2$
and
$k \geq 2$
and
![]() $\beta \geq 8\Delta $
. Then G contains an odd cycle C with length at most
$\beta \geq 8\Delta $
. Then G contains an odd cycle C with length at most
![]() $88\log k\log \lvert G\rvert $
such that G also
$88\log k\log \lvert G\rvert $
such that G also
![]() $(\Delta -3,\beta ,d,k)$
-expands into
$(\Delta -3,\beta ,d,k)$
-expands into
![]() $W\setminus V(C)$
.
$W\setminus V(C)$
.
Proof. Since G is not bipartite, it contains an odd cycle. Let C be a shortest odd cycle; it follows that if
![]() $x,y\in V(C)$
, then
$x,y\in V(C)$
, then
![]() $\operatorname {dist}_G(x,y)=\operatorname {dist}_C(x,y)$
. Indeed, if not, choosing
$\operatorname {dist}_G(x,y)=\operatorname {dist}_C(x,y)$
. Indeed, if not, choosing
![]() $x,y$
to violate this condition with minimal distance, the shortest path between x and y is internally disjoint from the cycle, and adding this path to whichever path around the cycle has the appropriate parity gives a shorter odd cycle. Consequently,
$x,y$
to violate this condition with minimal distance, the shortest path between x and y is internally disjoint from the cycle, and adding this path to whichever path around the cycle has the appropriate parity gives a shorter odd cycle. Consequently,
![]() $\lvert C\rvert $
is at most twice the diameter of G. Using Lemma 4.4 with
$\lvert C\rvert $
is at most twice the diameter of G. Using Lemma 4.4 with
![]() $A_{3.4},B_{3.4}$
being any singletons and
$A_{3.4},B_{3.4}$
being any singletons and
![]() $C_{3.4}=\varnothing $
implies the desired bound
$C_{3.4}=\varnothing $
implies the desired bound
![]() $\lvert C\rvert \leq 88\log k\log \lvert G\rvert $
.
$\lvert C\rvert \leq 88\log k\log \lvert G\rvert $
.
Now, if C is a triangle then any vertex v can have at most three neighbours on C (trivially). Otherwise, v can have at most two neighbours on C; indeed, if v has at least three neighbours on C, then either v has two neighbours
![]() $x,y$
with
$x,y$
with
![]() $\operatorname {dist}_C(x,y)\geq 3>\operatorname {dist}_G(x,y)$
, contradicting the earlier observation, or v has two neighbours
$\operatorname {dist}_C(x,y)\geq 3>\operatorname {dist}_G(x,y)$
, contradicting the earlier observation, or v has two neighbours
![]() $x,y$
which are adjacent, giving a shorter odd cycle
$x,y$
which are adjacent, giving a shorter odd cycle
![]() $vxy$
. Thus, for any set S we have
$vxy$
. Thus, for any set S we have
![]() $\lvert N_G(S)\cap (W\setminus V(C))\rvert \geq \lvert N_G(S)\cap W\rvert -3\lvert S\rvert $
, and, since
$\lvert N_G(S)\cap (W\setminus V(C))\rvert \geq \lvert N_G(S)\cap W\rvert -3\lvert S\rvert $
, and, since
![]() $G \ (\Delta ,\beta ,d,k)$
-expands into W, G also
$G \ (\Delta ,\beta ,d,k)$
-expands into W, G also
![]() $(\Delta -3,\beta ,d,k)$
-expands into
$(\Delta -3,\beta ,d,k)$
-expands into
![]() $W\setminus V(C)$
.
$W\setminus V(C)$
.
Finally, we show that we can construct two large, well-connected disjoint sets centred around any two given vertices.
Lemma 4.6. Suppose G is a graph which
![]() $(\Delta ,\beta ,d,k)$
-expands into
$(\Delta ,\beta ,d,k)$
-expands into
![]() $W\subseteq V(G)$
, and let
$W\subseteq V(G)$
, and let
![]() $x,y$
be distinct vertices. Then there exist disjoint sets
$x,y$
be distinct vertices. Then there exist disjoint sets
![]() $A,B\subset W\cup \{x,y\}$
of size
$A,B\subset W\cup \{x,y\}$
of size
![]() $\beta d/2$
such that
$\beta d/2$
such that
![]() $x\in A$
, and every vertex of A is connected to x by a path in A of length at most
$x\in A$
, and every vertex of A is connected to x by a path in A of length at most
![]() $\log _{\Delta }(\beta d/2)$
and similarly for B and y.
$\log _{\Delta }(\beta d/2)$
and similarly for B and y.
Proof. We iteratively build up sets
![]() $A_i,B_i$
with
$A_i,B_i$
with
![]() $\lvert A_i\rvert =\lvert B_i\rvert =\Delta ^i$
such that any vertex in
$\lvert A_i\rvert =\lvert B_i\rvert =\Delta ^i$
such that any vertex in
![]() $A_i$
is connected to x by a path in
$A_i$
is connected to x by a path in
![]() $A_i$
of length at most i until i is large enough that
$A_i$
of length at most i until i is large enough that
![]() $\lvert A_i\rvert \geq \beta d/2$
. We start from
$\lvert A_i\rvert \geq \beta d/2$
. We start from
![]() $A_0=\{x\},B_0=\{y\}$
. Given disjoint sets
$A_0=\{x\},B_0=\{y\}$
. Given disjoint sets
![]() $A_i,B_i$
with
$A_i,B_i$
with
![]() $\lvert A_i\rvert =\lvert B_i\rvert <\beta d/2$
, we aim to choose disjoint sets
$\lvert A_i\rvert =\lvert B_i\rvert <\beta d/2$
, we aim to choose disjoint sets
![]() $A'\subset N_G(A_i)\cap W$
and
$A'\subset N_G(A_i)\cap W$
and
![]() $B'\subset N_G(B_i)\cap W$
of size at least
$B'\subset N_G(B_i)\cap W$
of size at least
![]() $\Delta \lvert A_i\rvert $
. Then we can pick
$\Delta \lvert A_i\rvert $
. Then we can pick
![]() $A_{i+1}\subseteq A_i\cup (A'\setminus B_i)$
and
$A_{i+1}\subseteq A_i\cup (A'\setminus B_i)$
and
![]() $B_{i+1} \subseteq B_i \cup (B'\setminus A_i)$
with the required disjointness, connectivity and size properties.
$B_{i+1} \subseteq B_i \cup (B'\setminus A_i)$
with the required disjointness, connectivity and size properties.
First, take
![]() $A"=(N(A_i) \cap W)\setminus N(B_i)$
and
$A"=(N(A_i) \cap W)\setminus N(B_i)$
and
![]() $B"=(N(B_i) \cap W)\setminus N(A_i)$
. If either of these, say
$B"=(N(B_i) \cap W)\setminus N(A_i)$
. If either of these, say
![]() $A"$
has size at least
$A"$
has size at least
![]() $\Delta \lvert A_i\rvert $
, then we may choose
$\Delta \lvert A_i\rvert $
, then we may choose
![]() $A'\subseteq A"$
and
$A'\subseteq A"$
and
![]() $B'\subseteq N(B_i) \cap W$
both of size
$B'\subseteq N(B_i) \cap W$
both of size
![]() $\Delta \lvert A_i\rvert $
(using the expansion property for the latter); by definition of
$\Delta \lvert A_i\rvert $
(using the expansion property for the latter); by definition of
![]() $A"$
these sets are disjoint.
$A"$
these sets are disjoint.
Consequently, we may assume
![]() $\lvert A"\rvert ,\lvert B"\rvert <\Delta \lvert A_i\rvert $
. Since
$\lvert A"\rvert ,\lvert B"\rvert <\Delta \lvert A_i\rvert $
. Since
![]() $\lvert A_i\cup B_i\rvert <\beta d$
, the expansion property gives
$\lvert A_i\cup B_i\rvert <\beta d$
, the expansion property gives
![]() $\lvert N(A_i)\cap N(B_i) \cap W\rvert \geq 2\Delta \lvert A_i\rvert -\lvert A"\rvert -\lvert B"\rvert $
, and so we can add disjoint subsets of
$\lvert N(A_i)\cap N(B_i) \cap W\rvert \geq 2\Delta \lvert A_i\rvert -\lvert A"\rvert -\lvert B"\rvert $
, and so we can add disjoint subsets of
![]() $\lvert N(A_i)\cap N(B_i) \cap W\rvert $
to
$\lvert N(A_i)\cap N(B_i) \cap W\rvert $
to
![]() $A"$
and
$A"$
and
![]() $B"$
to form sets
$B"$
to form sets
![]() $A',B'$
as required.
$A',B'$
as required.
5 Constructing adjusters
In this section, we prove the following result for some suitable constant C.
Lemma 5.1. There exists a constant
![]() $C>0$
satisfying the following. Fix integers
$C>0$
satisfying the following. Fix integers
![]() $m,k$
with
$m,k$
with
![]() $C\leq m\leq k^{22}$
and
$C\leq m\leq k^{22}$
and
![]() $n\geq 8\times 10^{18}mk\log ^4k$
. Let H be a complete k-partite graph on
$n\geq 8\times 10^{18}mk\log ^4k$
. Let H be a complete k-partite graph on
![]() $mk$
vertices,
$mk$
vertices,
![]() $H' \sqsubseteq H$
be
$H' \sqsubseteq H$
be
![]() $(s+1)$
-partite for some
$(s+1)$
-partite for some
![]() $1\leq s\leq k-1$
and
$1\leq s\leq k-1$
and
![]() $m_2$
be the size of the second smallest part of H. Let G be a graph of order at least
$m_2$
be the size of the second smallest part of H. Let G be a graph of order at least
![]() $sn-n/10$
with
$sn-n/10$
with
![]() $\overline {G}$
being
$\overline {G}$
being
![]() $H'$
-free, and such that any two sets of size at least
$H'$
-free, and such that any two sets of size at least
![]() $m_2+4.1\times 10^{18}\log ^4 k$
have at least
$m_2+4.1\times 10^{18}\log ^4 k$
have at least
![]() $4.1\times 10^{18}\log ^4 k$
disjoint paths between them.
$4.1\times 10^{18}\log ^4 k$
disjoint paths between them.
-
• If
 $s\geq 2$
, then G contains a cycle of length exactly n.
$s\geq 2$
, then G contains a cycle of length exactly n. -
• If
 $s=1$
, then G contains an r-adjuster for some
$s=1$
, then G contains an r-adjuster for some
 $r\geq 9mk/8$
having length between
$r\geq 9mk/8$
having length between
 $0.6n$
and
$0.6n$
and
 $0.7n$
.
$0.7n$
.
We first show how the expansion properties established in Section 3 can be used to construct adjusters.
Lemma 5.2. Fix
![]() $k \geq 2$
,
$k \geq 2$
,
![]() $10^6 \leq m\leq k^{22}$
and
$10^6 \leq m\leq k^{22}$
and
![]() $n\geq 8\times 10^{5}mk\log ^2 k$
. Let H be a complete
$n\geq 8\times 10^{5}mk\log ^2 k$
. Let H be a complete
![]() $(s+1)$
-partite graph of order
$(s+1)$
-partite graph of order
![]() $m'(s+1)$
, where
$m'(s+1)$
, where
![]() $m' \in \mathbb {R}$
,
$m' \in \mathbb {R}$
,
![]() $1\leq s\leq k-1$
and
$1\leq s\leq k-1$
and
![]() $\lvert H\rvert \leq mk$
. Let G be a graph with
$\lvert H\rvert \leq mk$
. Let G be a graph with
![]() $\overline {G}$
being H-free and
$\overline {G}$
being H-free and
![]() $\lvert G\rvert \geq sn/10$
. Then G contains an r-adjuster for some
$\lvert G\rvert \geq sn/10$
. Then G contains an r-adjuster for some
![]() $r\geq \frac {mk}{2\times 10^4\log ^2 k}$
, which has between
$r\geq \frac {mk}{2\times 10^4\log ^2 k}$
, which has between
![]() $mk$
and
$mk$
and
![]() $mk + (3\times 10^4\log ^2) k$
vertices.
$mk + (3\times 10^4\log ^2) k$
vertices.
Proof. First, note that we may assume, at the cost of replacing the upper bound with
![]() $\lvert H\rvert \leq 2mk$
, that every part of H has order at least
$\lvert H\rvert \leq 2mk$
, that every part of H has order at least
![]() $m'$
. Indeed, we may replace each part of H with order below
$m'$
. Indeed, we may replace each part of H with order below
![]() $m'$
with a part of order
$m'$
with a part of order
![]() $\lceil m'\rceil $
; this adds at most
$\lceil m'\rceil $
; this adds at most
![]() $sm'$
vertices, and the new graph has average part size at most
$sm'$
vertices, and the new graph has average part size at most
![]() $2m'$
. In particular, this means that if
$2m'$
. In particular, this means that if
![]() $H'\sqsubseteq H$
is a-partite of order
$H'\sqsubseteq H$
is a-partite of order
![]() $ab$
, then
$ab$
, then
![]() $b\geq m'$
and
$b\geq m'$
and
![]() $ab\leq 2m'(s+1)\leq 2mk$
. Clearly, replacing H with a supergraph preserves the property that
$ab\leq 2m'(s+1)\leq 2mk$
. Clearly, replacing H with a supergraph preserves the property that
![]() $\overline {G}$
is H-free.
$\overline {G}$
is H-free.
Set
Then, as
![]() $1 \leq s \leq k-1$
, we get
$1 \leq s \leq k-1$
, we get
Further, note that
![]() $M \geq 4(s+1)$
and
$M \geq 4(s+1)$
and
![]() $\beta \geq 10 \log k$
. We use Lemma 4.2 with
$\beta \geq 10 \log k$
. We use Lemma 4.2 with
![]() $(M, \beta , \Delta , m, k)_{3.2} = (M, \beta , 10, m', s+1)$
to pass to a subgraph
$(M, \beta , \Delta , m, k)_{3.2} = (M, \beta , 10, m', s+1)$
to pass to a subgraph
![]() $G'$
, where
$G'$
, where
![]() $\overline {G'}$
is
$\overline {G'}$
is
![]() $H'$
-free for some
$H'$
-free for some
![]() $H'\sqsubseteq H$
and which
$H'\sqsubseteq H$
and which
![]() $(10,\beta ,m",s')$
-expands into
$(10,\beta ,m",s')$
-expands into
![]() $V(G')$
, where
$V(G')$
, where
![]() $\lvert H'\rvert =s'm"$
and
$\lvert H'\rvert =s'm"$
and
![]() $\chi (H')=s'$
with
$\chi (H')=s'$
with
![]() $2 \leq s' \leq s+1$
, such that
$2 \leq s' \leq s+1$
, such that
In particular, since
![]() $m"\geq m'$
, we have that
$m"\geq m'$
, we have that
![]() $G' \ (10,\beta ,m',s')$
-expands.
$G' \ (10,\beta ,m',s')$
-expands.
As
![]() $\overline {G'}$
is
$\overline {G'}$
is
![]() $H'$
-free,
$H'$
-free,
![]() $G'$
has no independent set of order
$G'$
has no independent set of order
![]() $\lvert H'\rvert = s'm"$
, and it follows that
$\lvert H'\rvert = s'm"$
, and it follows that
![]() $\chi (G')\geq \lvert G'\rvert /(s'm")>2$
. Note that as
$\chi (G')\geq \lvert G'\rvert /(s'm")>2$
. Note that as
![]() $m \leq k^{22}$
, from inequality (9) we have that
$m \leq k^{22}$
, from inequality (9) we have that
![]() $\lvert G'\rvert \leq M (2m'(s+1)) \log k \leq 10^{5}mk^2 \log ^2 k \leq 10^{5}k^{26}$
. Thus, by Lemma 4.5 we may find an odd cycle
$\lvert G'\rvert \leq M (2m'(s+1)) \log k \leq 10^{5}mk^2 \log ^2 k \leq 10^{5}k^{26}$
. Thus, by Lemma 4.5 we may find an odd cycle
![]() $C_1$
of length at most
$C_1$
of length at most
![]() $88\log k \log \lvert G'\rvert \leq 10^4\log ^2 k$
, such that we retain
$88\log k \log \lvert G'\rvert \leq 10^4\log ^2 k$
, such that we retain
![]() $(7,\beta ,m',s')$
-expansion into
$(7,\beta ,m',s')$
-expansion into
![]() $V(G')\setminus V(C_1)$
. Choosing almost-antipodal points
$V(G')\setminus V(C_1)$
. Choosing almost-antipodal points
![]() $v_1,w_1$
on
$v_1,w_1$
on
![]() $C_1$
(i.e.,
$C_1$
(i.e.,
![]() $\operatorname {dist}_{C_1}(v_1,w_1) = (\lvert C_1\rvert - 1)/2$
), we use Lemma 4.6 to find sets
$\operatorname {dist}_{C_1}(v_1,w_1) = (\lvert C_1\rvert - 1)/2$
), we use Lemma 4.6 to find sets
![]() $A_1$
and
$A_1$
and
![]() $B_1$
of size
$B_1$
of size
![]() $\beta m'/2$
with
$\beta m'/2$
with
![]() $A_1\cap B_1=\varnothing $
,
$A_1\cap B_1=\varnothing $
,
![]() $A_1\cap V(C_1)=\{v_1\}$
and
$A_1\cap V(C_1)=\{v_1\}$
and
![]() $B_1\cap V(C_1)=\{w_1\}$
, with each vertex in
$B_1\cap V(C_1)=\{w_1\}$
, with each vertex in
![]() $A_1$
(resp.
$A_1$
(resp.
![]() $B_1$
) having a path in
$B_1$
) having a path in
![]() $A_1$
to
$A_1$
to
![]() $v_1$
(resp. in
$v_1$
(resp. in
![]() $B_1$
to
$B_1$
to
![]() $w_1$
) of length at most
$w_1$
) of length at most
![]() $\log _{7}(\beta m'/2)<40\log ^2 k$
.
$\log _{7}(\beta m'/2)<40\log ^2 k$
.
Next, we set
![]() $X=A_1\cup V(C_1)\cup B_1$
and
$X=A_1\cup V(C_1)\cup B_1$
and
![]() $Y=V(C_1)$
. Note that, by inequality (9) and that
$Y=V(C_1)$
. Note that, by inequality (9) and that
![]() $\lvert X\rvert \leq \beta m' + 10^4 \log ^2 k$
, we have
$\lvert X\rvert \leq \beta m' + 10^4 \log ^2 k$
, we have
![]() $\lvert G' - X\rvert \geq \frac {1}{2}Mm"s'\log s'$
. We apply Lemma 4.2 with
$\lvert G' - X\rvert \geq \frac {1}{2}Mm"s'\log s'$
. We apply Lemma 4.2 with
![]() $(M, \beta , \Delta , m, k)_{3.2} = (M/2, \beta , 10, m", s')$
again to find a subgraph
$(M, \beta , \Delta , m, k)_{3.2} = (M/2, \beta , 10, m", s')$
again to find a subgraph
![]() $G"$
with
$G"$
with
![]() $V(G")\subset V(G')\setminus X$
which
$V(G")\subset V(G')\setminus X$
which
![]() $(10,\beta , m"',s")$
-expands and has order at most
$(10,\beta , m"',s")$
-expands and has order at most
![]() $\frac {1}{2}Mm"'s"\log s"$
, for some
$\frac {1}{2}Mm"'s"\log s"$
, for some
![]() $2 \leq s"\leq s'$
and
$2 \leq s"\leq s'$
and
![]() $m"'\geq m'$
. Within
$m"'\geq m'$
. Within
![]() $G"$
, we find another similar structure
$G"$
, we find another similar structure
![]() $A_2\cup C_2\cup B_2$
, and since
$A_2\cup C_2\cup B_2$
, and since
![]() $G' \ (10, \beta , m', s')$
-expands we can use Lemma 4.4, with parameters
$G' \ (10, \beta , m', s')$
-expands we can use Lemma 4.4, with parameters
![]() $(\Delta , \beta , d, k, A, B, C, W)_{3.4} = (10, \beta , m', s', A_2, B_1, V(C_1 \cup C_2), G')$
to find a path
$(\Delta , \beta , d, k, A, B, C, W)_{3.4} = (10, \beta , m', s', A_2, B_1, V(C_1 \cup C_2), G')$
to find a path
![]() $Q_1$
between
$Q_1$
between
![]() $A_2$
and
$A_2$
and
![]() $B_1$
that avoids
$B_1$
that avoids
![]() $V(C_1\cup C_2)$
and is of length at most
$V(C_1\cup C_2)$
and is of length at most
![]() $5,000\log ^2 k$
. We may assume
$5,000\log ^2 k$
. We may assume
![]() $Q_1$
is disjoint from
$Q_1$
is disjoint from
![]() $A_1\cup B_2$
since otherwise we may find a shorter path between (say)
$A_1\cup B_2$
since otherwise we may find a shorter path between (say)
![]() $A_1$
and
$A_1$
and
![]() $A_2$
then relabel appropriately. We then extend
$A_2$
then relabel appropriately. We then extend
![]() $Q_1$
by paths within
$Q_1$
by paths within
![]() $A_2$
to
$A_2$
to
![]() $v_2$
and within
$v_2$
and within
![]() $B_1$
to
$B_1$
to
![]() $w_1$
to obtain a
$w_1$
to obtain a
![]() $w_1$
-
$w_1$
-
![]() $v_2$
path
$v_2$
path
![]() $P_1$
of length at most
$P_1$
of length at most
![]() $10^4\log ^2 k$
.
$10^4\log ^2 k$
.
Now, we update X to
![]() $A_1\cup V(C_1\cup P_1\cup C_2)\cup B_2$
(note that the unused parts of
$A_1\cup V(C_1\cup P_1\cup C_2)\cup B_2$
(note that the unused parts of
![]() $A_2\cup B_1$
are released) and Y to
$A_2\cup B_1$
are released) and Y to
![]() $V(C_1\cup P_1\cup C_2)$
. As before, we choose
$V(C_1\cup P_1\cup C_2)$
. As before, we choose
![]() $G"'$
with
$G"'$
with
![]() $V(G"')\subset V(G')\setminus X$
such that
$V(G"')\subset V(G')\setminus X$
such that
![]() $G"' \ (10,\beta , m^{(4)},s"')$
-expands for some
$G"' \ (10,\beta , m^{(4)},s"')$
-expands for some
![]() $2 \leq s"'\leq s'$
and
$2 \leq s"'\leq s'$
and
![]() $m^{(4)}\geq m'$
and continue as before, updating X and Y. Observe that we can continue this process as long as
$m^{(4)}\geq m'$
and continue as before, updating X and Y. Observe that we can continue this process as long as
![]() $\lvert G' - X\rvert \geq \frac {1}{2}Mm"s'\log s'$
. Thus, since
$\lvert G' - X\rvert \geq \frac {1}{2}Mm"s'\log s'$
. Thus, since
![]() $\lvert G'\rvert \geq Mm"s'\log s' - m"$
, we can continue whenever
$\lvert G'\rvert \geq Mm"s'\log s' - m"$
, we can continue whenever
![]() $\lvert X\rvert \leq \frac {1}{4}Mm"s'\log s'$
. Since
$\lvert X\rvert \leq \frac {1}{4}Mm"s'\log s'$
. Since
![]() $mk + \beta m' \leq \frac {1}{4}Mm"s'\log s'$
, we can continue the process until
$mk + \beta m' \leq \frac {1}{4}Mm"s'\log s'$
, we can continue the process until
![]() $\lvert Y\rvert>mk$
, as
$\lvert Y\rvert>mk$
, as
![]() $\lvert A_i\rvert , \lvert B_i\rvert \leq \beta m'/2$
for all i. Moreover, at each stage of this process
$\lvert A_i\rvert , \lvert B_i\rvert \leq \beta m'/2$
for all i. Moreover, at each stage of this process
![]() $\lvert Y\rvert $
increases by at most
$\lvert Y\rvert $
increases by at most
![]() $2\times 10^4\log ^2 k$
. Thus, as soon as
$2\times 10^4\log ^2 k$
. Thus, as soon as
![]() $\lvert Y\rvert>mk$
we can stop the process and ensure
$\lvert Y\rvert>mk$
we can stop the process and ensure
![]() $\lvert Y\rvert \leq mk + (2\times 10^4)\log ^2 k$
at this point. Since
$\lvert Y\rvert \leq mk + (2\times 10^4)\log ^2 k$
at this point. Since
![]() $mk + 2\times 10^4\log ^2 k \leq \beta m'/20\log (s+1) \leq \beta m'/20\log s'$
, we can then apply Lemma 4.4 with
$mk + 2\times 10^4\log ^2 k \leq \beta m'/20\log (s+1) \leq \beta m'/20\log s'$
, we can then apply Lemma 4.4 with
![]() $(\Delta , \beta , d, k, A, B, C, W)_{3.4} = (10, \beta , m', s', A_1, B_r, Y, G')$
to find a path of length at most
$(\Delta , \beta , d, k, A, B, C, W)_{3.4} = (10, \beta , m', s', A_1, B_r, Y, G')$
to find a path of length at most
![]() $10^4\log ^2 k$
connecting the two remaining large sets
$10^4\log ^2 k$
connecting the two remaining large sets
![]() $A_1,B_r$
avoiding Y, which closes up the structure into an r-adjuster; since each cycle
$A_1,B_r$
avoiding Y, which closes up the structure into an r-adjuster; since each cycle
![]() $C_i$
and each path
$C_i$
and each path
![]() $P_i$
built in this whole process has length at most
$P_i$
built in this whole process has length at most
![]() $10^4\log ^2 k$
, we have
$10^4\log ^2 k$
, we have
![]() $r \geq \frac {mk}{2 \times 10^4\log ^2 k}$
, and the adjuster contains all of Y, giving the required bounds.
$r \geq \frac {mk}{2 \times 10^4\log ^2 k}$
, and the adjuster contains all of Y, giving the required bounds.
We will also need some long cycles to extend the adjusters we construct.
Lemma 5.3. Fix
![]() $k \geq 2$
,
$k \geq 2$
,
![]() $10^6 \leq m\leq k^{22}$
and
$10^6 \leq m\leq k^{22}$
and
![]() $n\geq 8\times 10^{5}mk\log ^2 k$
. Let H be a complete
$n\geq 8\times 10^{5}mk\log ^2 k$
. Let H be a complete
![]() $(s+1)$
-partite graph of order
$(s+1)$
-partite graph of order
![]() $m'(s+1)$
, where
$m'(s+1)$
, where
![]() $m' \in \mathbb {R}$
,
$m' \in \mathbb {R}$
,
![]() $1\leq s\leq k-1$
and
$1\leq s\leq k-1$
and
![]() $\lvert H\rvert \leq mk$
. Let G be a graph with
$\lvert H\rvert \leq mk$
. Let G be a graph with
![]() $\overline {G}$
being H-free and
$\overline {G}$
being H-free and
![]() $\lvert G\rvert \geq sn/10$
. Then G contains a cycle of length between
$\lvert G\rvert \geq sn/10$
. Then G contains a cycle of length between
![]() $n/((8\times 10^5)\log ^2 k)$
and
$n/((8\times 10^5)\log ^2 k)$
and
![]() $n/((8\times 10^5)\log ^2 k) + 2mk$
.
$n/((8\times 10^5)\log ^2 k) + 2mk$
.
Proof. We proceed as in Lemma 5.2, with the following differences. First, set
Secondly, at each stage rather than finding a cycle with two large sets, each of size
![]() $\beta m'/2$
, attached we find a single edge with two large sets. This ensures that after each joining step we have a path with two large sets attached. Again, we continue until the total size of the path exceeds
$\beta m'/2$
, attached we find a single edge with two large sets. This ensures that after each joining step we have a path with two large sets attached. Again, we continue until the total size of the path exceeds
![]() $\beta m'/40\log k$
and then join the two large sets, using Lemma 4.4, to obtain a desired long cycle. If this cycle is longer than our desired upper bound, we truncate it using that
$\beta m'/40\log k$
and then join the two large sets, using Lemma 4.4, to obtain a desired long cycle. If this cycle is longer than our desired upper bound, we truncate it using that
![]() $\overline {G}$
is H-free (choose
$\overline {G}$
is H-free (choose
![]() $mk$
vertices that are nonadjacent on the cycle).
$mk$
vertices that are nonadjacent on the cycle).
In order to complete the proof of Lemma 5.1, we need to be able to join adjusters together while simultaneously retaining most of the flexibility of each adjuster and most of the length. This resembles Lemma 2.19 of [Reference Pokrovskiy and Sudakov25], but the fact that in our case the length of an adjuster and the number of vertices are only loosely related creates extra difficulties.
Lemma 5.4. Let
![]() $F_i$
be an
$F_i$
be an
![]() $r_i$
-adjuster of length
$r_i$
-adjuster of length
![]() $\ell _i$
for
$\ell _i$
for
![]() $i\in \{1,2\}$
, with
$i\in \{1,2\}$
, with
![]() $F_1$
and
$F_1$
and
![]() $F_2$
disjoint. Suppose there are
$F_2$
disjoint. Suppose there are
![]() $s>16$
vertex-disjoint paths
$s>16$
vertex-disjoint paths
![]() $P_1,\ldots ,P_s$
between
$P_1,\ldots ,P_s$
between
![]() $F_1$
and
$F_1$
and
![]() $F_2$
, each of length at most t. Then for some
$F_2$
, each of length at most t. Then for some
![]() $i\neq j$
there is an r-adjuster of length
$i\neq j$
there is an r-adjuster of length
![]() $\ell $
contained in
$\ell $
contained in
![]() $F_1\cup F_2\cup P_i\cup P_j$
, where
$F_1\cup F_2\cup P_i\cup P_j$
, where
and
Furthermore, if
![]() $r_2=0$
, then the adjuster obtained contains a section of length
$r_2=0$
, then the adjuster obtained contains a section of length
![]() $\ell -\ell _1$
with no short cycles.
$\ell -\ell _1$
with no short cycles.
Proof. We may assume each
![]() $P_i$
is internally disjoint from
$P_i$
is internally disjoint from
![]() $F_1\cup F_2$
since otherwise we can replace it by a shorter path with this property. Write
$F_1\cup F_2$
since otherwise we can replace it by a shorter path with this property. Write
![]() $x_i$
for the endpoint of
$x_i$
for the endpoint of
![]() $P_i$
in
$P_i$
in
![]() $F_1$
, and
$F_1$
, and
![]() $y_i$
for the endpoint in
$y_i$
for the endpoint in
![]() $F_2$
.
$F_2$
.
We will progressively reduce the number of paths to focus our attention on at least
![]() $s^{1/2}/4$
paths which relate to one another in a useful way. First, we give each path
$s^{1/2}/4$
paths which relate to one another in a useful way. First, we give each path
![]() $P_i$
an ordered pair of labels from
$P_i$
an ordered pair of labels from
![]() $\{+,-\}$
as follows. If
$\{+,-\}$
as follows. If
![]() $x_i$
lies on one of the
$x_i$
lies on one of the
![]() $r_1$
short cycles of
$r_1$
short cycles of
![]() $F_1$
, choose the first label to be
$F_1$
, choose the first label to be
![]() $+$
if it is on the longer section of that cycle (that is, the longer section between the two vertices of that short cycle that have degree
$+$
if it is on the longer section of that cycle (that is, the longer section between the two vertices of that short cycle that have degree
![]() $3$
in
$3$
in
![]() $F_1$
) and
$F_1$
) and
![]() $-$
if it is on the shorter section. If
$-$
if it is on the shorter section. If
![]() $x_i$
lies on a path between cycles, choose the first label arbitrarily. Choose the second label similarly with respect to
$x_i$
lies on a path between cycles, choose the first label arbitrarily. Choose the second label similarly with respect to
![]() $y_i$
. Now, we may find a set of at least
$y_i$
. Now, we may find a set of at least
![]() $s/4$
paths with identical label pairs. Note that this ensures there are routes
$s/4$
paths with identical label pairs. Note that this ensures there are routes
![]() $C_1$
around
$C_1$
around
![]() $F_1$
and
$F_1$
and
![]() $C_2$
around
$C_2$
around
![]() $F_2$
which cover all the
$F_2$
which cover all the
![]() $x_i$
and
$x_i$
and
![]() $y_i$
for
$y_i$
for
![]() $P_i$
in this set of paths, with
$P_i$
in this set of paths, with
![]() $\lvert C_i\rvert \in [\ell _i-r_i,\ell _i]$
. In what follows, we consider
$\lvert C_i\rvert \in [\ell _i-r_i,\ell _i]$
. In what follows, we consider
![]() $C_1$
and
$C_1$
and
![]() $C_2$
to be oriented in a particular direction around
$C_2$
to be oriented in a particular direction around
![]() $F_1$
and
$F_1$
and
![]() $F_2$
, respectively. Renumbering, if necessary, we may assume these paths are
$F_2$
, respectively. Renumbering, if necessary, we may assume these paths are
![]() $P_1,\ldots ,P_{\lceil s/4\rceil }$
, and that
$P_1,\ldots ,P_{\lceil s/4\rceil }$
, and that
![]() $x_1,\ldots ,x_{\lceil s/4\rceil }$
are in order of their appearance in
$x_1,\ldots ,x_{\lceil s/4\rceil }$
are in order of their appearance in
![]() $C_1$
. By the Erdős–Szekeres theorem (Theorem 3.1), there is a subset of at least
$C_1$
. By the Erdős–Szekeres theorem (Theorem 3.1), there is a subset of at least
![]() $t\geq \left \lceil \sqrt {s/4}\right \rceil \geq 2$
paths with endvertices
$t\geq \left \lceil \sqrt {s/4}\right \rceil \geq 2$
paths with endvertices
![]() $y_i$
either in order of their appearance in
$y_i$
either in order of their appearance in
![]() $C_2$
or in reverse order. Again, by renumbering and reversing
$C_2$
or in reverse order. Again, by renumbering and reversing
![]() $C_2$
if necessary we may assume these are
$C_2$
if necessary we may assume these are
![]() $P_1,\ldots ,P_{t}$
and the
$P_1,\ldots ,P_{t}$
and the
![]() $y_i$
appear in reverse order.
$y_i$
appear in reverse order.
Let
![]() $C^{\prime }_1$
be the longest route in
$C^{\prime }_1$
be the longest route in
![]() $F_1$
, and associate each vertex
$F_1$
, and associate each vertex
![]() $x_i$
for
$x_i$
for
![]() $i\in [t]$
with a vertex
$i\in [t]$
with a vertex
![]() $x^{\prime }_i$
, chosen as follows. If
$x^{\prime }_i$
, chosen as follows. If
![]() $x_i$
is internal to a shorter side of a short cycle, let
$x_i$
is internal to a shorter side of a short cycle, let
![]() $x^{\prime }_i$
be the vertex on the longer side which is the same distance from the start vertex of the cycle (consequently,
$x^{\prime }_i$
be the vertex on the longer side which is the same distance from the start vertex of the cycle (consequently,
![]() $x^{\prime }_i$
is one step further from the end of the cycle than
$x^{\prime }_i$
is one step further from the end of the cycle than
![]() $x_i$
). If
$x_i$
). If
![]() $x_i$
is on one of the paths or is internal to the longer side of a short cycle, set
$x_i$
is on one of the paths or is internal to the longer side of a short cycle, set
![]() $x^{\prime }_i=x_i$
. Define
$x^{\prime }_i=x_i$
. Define
![]() $C^{\prime }_2$
and each
$C^{\prime }_2$
and each
![]() $y_i'$
similarly.
$y_i'$
similarly.
Now, we show that some consecutive pair of paths work. Consider making a new adjuster from
![]() $F_1$
,
$F_1$
,
![]() $F_2$
,
$F_2$
,
![]() $P_i$
and
$P_i$
and
![]() $P_{i+1}$
for
$P_{i+1}$
for
![]() $i\in [t]$
(we take subscripts modulo t) as follows: Starting from
$i\in [t]$
(we take subscripts modulo t) as follows: Starting from
![]() $x_i$
, traverse
$x_i$
, traverse
![]() $P_i$
to
$P_i$
to
![]() $y_i$
, then follow a route around
$y_i$
, then follow a route around
![]() $F_2$
to
$F_2$
to
![]() $y_{i+1}$
, including both sections of any short cycle traversed in this route (apart from any short cycle containing
$y_{i+1}$
, including both sections of any short cycle traversed in this route (apart from any short cycle containing
![]() $y_i$
or
$y_i$
or
![]() $y_{i+1}$
), traverse
$y_{i+1}$
), traverse
![]() $P_{i+1}$
to
$P_{i+1}$
to
![]() $x_{i+1}$
, then follow a route around
$x_{i+1}$
, then follow a route around
![]() $F_1$
to
$F_1$
to
![]() $x_i$
similarly. See Figure 2 for an example.
$x_i$
similarly. See Figure 2 for an example.

Figure 2 Creating a new adjuster using paths
![]() $P_i$
and
$P_i$
and
![]() $P_{i+1}$
with label
$P_{i+1}$
with label
![]() $(-,+)$
. Dashed sections are not part of the new adjuster, which has five fewer short cycles. The red section shows how much length is lost from
$(-,+)$
. Dashed sections are not part of the new adjuster, which has five fewer short cycles. The red section shows how much length is lost from
![]() $F_1$
and
$F_1$
and
![]() $F_2$
; in the former case, this includes one extra edge since
$F_2$
; in the former case, this includes one extra edge since
![]() $x_{i+1}$
is on the short side of a cycle.
$x_{i+1}$
is on the short side of a cycle.
Write
![]() $S_1$
for the edges of
$S_1$
for the edges of
![]() $C^{\prime }_1$
between
$C^{\prime }_1$
between
![]() $x^{\prime }_i$
and
$x^{\prime }_i$
and
![]() $x^{\prime }_{i+1}$
and
$x^{\prime }_{i+1}$
and
![]() $S_2$
for the edges of
$S_2$
for the edges of
![]() $C^{\prime }_2$
between
$C^{\prime }_2$
between
![]() $y^{\prime }_{i+1}$
and
$y^{\prime }_{i+1}$
and
![]() $y^{\prime }_{i}$
. The short cycles of the new adjuster are those of the original two adjusters except for any which intersect
$y^{\prime }_{i}$
. The short cycles of the new adjuster are those of the original two adjusters except for any which intersect
![]() $S_1$
or
$S_1$
or
![]() $S_2$
. The longest route through the new adjuster uses all of
$S_2$
. The longest route through the new adjuster uses all of
![]() $C^{\prime }_1$
except for at most
$C^{\prime }_1$
except for at most
![]() $\lvert S_1\rvert + 1$
edges (the
$\lvert S_1\rvert + 1$
edges (the
![]() $+1$
added if
$+1$
added if
![]() $x^{\prime }_{i+1}\neq x_{i+1}$
), and all of
$x^{\prime }_{i+1}\neq x_{i+1}$
), and all of
![]() $C^{\prime }_2$
except for at most
$C^{\prime }_2$
except for at most
![]() $\lvert S_2\rvert + 1$
edges (the
$\lvert S_2\rvert + 1$
edges (the
![]() $+1$
added if
$+1$
added if
![]() $y^{\prime }_{i+1}\neq y_{i+1}$
). It also uses all of the two paths
$y^{\prime }_{i+1}\neq y_{i+1}$
). It also uses all of the two paths
![]() $P_i$
and
$P_i$
and
![]() $P_{i+1}$
, which contain at least one edge each, so its length is at least
$P_{i+1}$
, which contain at least one edge each, so its length is at least
![]() $\ell _1+\ell _2-\lvert S_1\rvert -\lvert S_2\rvert $
. Note that the sets
$\ell _1+\ell _2-\lvert S_1\rvert -\lvert S_2\rvert $
. Note that the sets
![]() $S_1\cup S_2$
obtained for different choices of
$S_1\cup S_2$
obtained for different choices of
![]() $i\in [t]$
are disjoint.
$i\in [t]$
are disjoint.
Now, we claim that for some pair
![]() $P_i,P_{i+1}$
the adjuster constructed has the required properties. Note that, since each path
$P_i,P_{i+1}$
the adjuster constructed has the required properties. Note that, since each path
![]() $P_i$
has length at most t, the upper bound on length is satisfied for all adjusters constructed in this way, so it suffices to prove the lower bounds on
$P_i$
has length at most t, the upper bound on length is satisfied for all adjusters constructed in this way, so it suffices to prove the lower bounds on
![]() $\ell $
and r. Suppose not, then for each i either more than
$\ell $
and r. Suppose not, then for each i either more than
![]() $(r_1+r_2)4s^{-1/2}+4$
short cycles are lost, or
$(r_1+r_2)4s^{-1/2}+4$
short cycles are lost, or
![]() $\lvert S_1\rvert +\lvert S_2\rvert>4s^{-1/2}(\ell _1+\ell _2)$
. In the former case, this means more than
$\lvert S_1\rvert +\lvert S_2\rvert>4s^{-1/2}(\ell _1+\ell _2)$
. In the former case, this means more than
![]() $(r_1+r_2)4s^{-1/2}$
short cycles lie entirely in the section between
$(r_1+r_2)4s^{-1/2}$
short cycles lie entirely in the section between
![]() $x_i$
and
$x_i$
and
![]() $x_{i+1}$
or the section between
$x_{i+1}$
or the section between
![]() $y_{i+1}$
and
$y_{i+1}$
and
![]() $y_i$
since only
$y_i$
since only
![]() $4$
can lie partially in these sections. Since these sections are disjoint, the former case occurs for fewer than
$4$
can lie partially in these sections. Since these sections are disjoint, the former case occurs for fewer than
![]() $s^{1/2}/4$
choices of i. Similarly, the latter case occurs for fewer than
$s^{1/2}/4$
choices of i. Similarly, the latter case occurs for fewer than
![]() $s^{1/2}/4$
choices of i. Since there are at least
$s^{1/2}/4$
choices of i. Since there are at least
![]() $s^{1/2}/2$
choices for i, some choice gives an adjuster with the required properties.
$s^{1/2}/2$
choices for i, some choice gives an adjuster with the required properties.
Finally, note that the section of the adjuster obtained consisting of vertices not in
![]() $F_1$
is contiguous and contributes at least
$F_1$
is contiguous and contributes at least
![]() $\ell -\ell _1$
to the overall length. If
$\ell -\ell _1$
to the overall length. If
![]() $r_2=0$
, this section has no short cycles, as required.
$r_2=0$
, this section has no short cycles, as required.
We are now ready to prove the main result of this section.
Proof of Lemma 5.1.
Let
![]() $C= 10^{30}$
. We will prove both parts of the statement simultaneously by finding an r-adjuster of suitable length for some
$C= 10^{30}$
. We will prove both parts of the statement simultaneously by finding an r-adjuster of suitable length for some
![]() $r\geq 9mk/8$
. If
$r\geq 9mk/8$
. If
![]() $s\geq 2$
, this adjuster can be taken to have length slightly larger than n such that one of the routes has length exactly n. However, for
$s\geq 2$
, this adjuster can be taken to have length slightly larger than n such that one of the routes has length exactly n. However, for
![]() $s=1$
this is not possible since G itself could have order less than n. In this case, we show that the length of the adjuster can be made significantly larger than
$s=1$
this is not possible since G itself could have order less than n. In this case, we show that the length of the adjuster can be made significantly larger than
![]() $n/2$
.
$n/2$
.
We repeatedly apply Lemma 5.2, with
![]() $H_{4.2}=H'$
and
$H_{4.2}=H'$
and
![]() $G_{4.2}=G-X_{i-1}$
, where
$G_{4.2}=G-X_{i-1}$
, where
![]() $X_0=\varnothing $
and
$X_0=\varnothing $
and
![]() $X_i=V(F^{\prime }_{i})$
for
$X_i=V(F^{\prime }_{i})$
for
![]() $i\geq 1$
is the set of vertices used up from G (see the construction of
$i\geq 1$
is the set of vertices used up from G (see the construction of
![]() $F_i'$
, for each i, below), in order to find
$F_i'$
, for each i, below), in order to find
![]() $f \leq 4\times 10^4\log ^2 k$
adjusters
$f \leq 4\times 10^4\log ^2 k$
adjusters
![]() $F_i$
for
$F_i$
for
![]() $i\in [f]$
, such that
$i\in [f]$
, such that
![]() $F_i$
is an
$F_i$
is an
![]() $r_i$
-adjuster and
$r_i$
-adjuster and
![]() $r_{\mathrm {total}}:=\sum ^{f}_{i=1}r_i\geq 2mk$
. Note that, since
$r_{\mathrm {total}}:=\sum ^{f}_{i=1}r_i\geq 2mk$
. Note that, since
![]() $k^{22}\geq m\geq C= 10^{30}$
and
$k^{22}\geq m\geq C= 10^{30}$
and
![]() $k\geq 10\log ^4 k$
for any
$k\geq 10\log ^4 k$
for any
![]() $k\geq 2$
, each
$k\geq 2$
, each
![]() $F_i$
satisfies
$F_i$
satisfies
Also, the total size of all these adjusters (using the fact that every adjuster found has size at most
![]() $mk+3\times 10^4\log ^4 k\leq 1.1mk$
) is at most
$mk+3\times 10^4\log ^4 k\leq 1.1mk$
) is at most
![]() $5\times 10^4mk\log ^2k$
.
$5\times 10^4mk\log ^2k$
.
Set
![]() $F^{\prime }_1=F_1$
and
$F^{\prime }_1=F_1$
and
![]() $r^{\prime }_1=r_1$
. After finding each
$r^{\prime }_1=r_1$
. After finding each
![]() $F_i$
(for
$F_i$
(for
![]() $i\geq 2$
), we merge it with the adjuster
$i\geq 2$
), we merge it with the adjuster
![]() $F^{\prime }_{i-1}$
using Lemma 5.4. There are at least
$F^{\prime }_{i-1}$
using Lemma 5.4. There are at least
![]() $q=4.1\times 10^{18}\log ^4k$
vertex-disjoint paths between the two adjusters, by inequality (10) and the hypothesis, and we may choose these to have length at most
$q=4.1\times 10^{18}\log ^4k$
vertex-disjoint paths between the two adjusters, by inequality (10) and the hypothesis, and we may choose these to have length at most
![]() $\lvert H'\rvert +s\leq mk+k$
since the fact that
$\lvert H'\rvert +s\leq mk+k$
since the fact that
![]() $\overline G$
is
$\overline G$
is
![]() $H'$
-free implies that any longer path contains a shortcut. Thus, we obtain a merged adjuster
$H'$
-free implies that any longer path contains a shortcut. Thus, we obtain a merged adjuster
![]() $F^{\prime }_i$
, which is an
$F^{\prime }_i$
, which is an
![]() $r^{\prime }_i$
-adjuster with
$r^{\prime }_i$
-adjuster with
and
It follows from inequality (12) that for each
![]() $i \in [f]$
,
$i \in [f]$
,
and so, setting
![]() $X_i=V(F^{\prime }_i)$
, we have
$X_i=V(F^{\prime }_i)$
, we have
![]() $\lvert G-X_{i-1}\rvert \geq (sn - n/10) - n/10 \geq sn/10$
. Consequently, we can indeed repeatedly apply Lemma 5.2 with
$\lvert G-X_{i-1}\rvert \geq (sn - n/10) - n/10 \geq sn/10$
. Consequently, we can indeed repeatedly apply Lemma 5.2 with
![]() $G_{4.2} = G-X_{i-1}$
for all
$G_{4.2} = G-X_{i-1}$
for all
![]() $i \in [f]$
.
$i \in [f]$
.
Using inequality (11), by induction we have
![]() $r^{\prime }_{i-1}\leq \sum _{j<i}r_j$
for each
$r^{\prime }_{i-1}\leq \sum _{j<i}r_j$
for each
![]() $i\geq 2$
, and so
$i\geq 2$
, and so
Summing inequality (13), we obtain
![]() $r^{\prime }_{f}\geq r_{\mathrm {total}}(1-((16\times 10^4)q^{-1/2}\log ^2 k))-4f\geq 3r_{\mathrm {total}}/4$
.
$r^{\prime }_{f}\geq r_{\mathrm {total}}(1-((16\times 10^4)q^{-1/2}\log ^2 k))-4f\geq 3r_{\mathrm {total}}/4$
.
We repeatedly apply Lemma 5.3 with
![]() $H_{4.3} = H'$
and
$H_{4.3} = H'$
and
![]() $G_{4.3} = G - Y_j$
, where
$G_{4.3} = G - Y_j$
, where
![]() $Y_1 = V(F_{f}')$
and
$Y_1 = V(F_{f}')$
and
![]() $Y_j =Y_1\cup V(C_j')$
for
$Y_j =Y_1\cup V(C_j')$
for
![]() $j \geq 2$
is the set of vertices used up from G so far (see the construction of
$j \geq 2$
is the set of vertices used up from G so far (see the construction of
![]() $C_i'$
below), in order to find
$C_i'$
below), in order to find
![]() $c \leq 1.6 \times 10^6\log ^2 k$
cycles
$c \leq 1.6 \times 10^6\log ^2 k$
cycles
![]() $C_i$
each of length at least
$C_i$
each of length at least
![]() $n/(8\times 10^5\log ^2k) \geq m_2 + 4.1 \times 10^{18}\log ^4k$
(which we regard as
$n/(8\times 10^5\log ^2k) \geq m_2 + 4.1 \times 10^{18}\log ^4k$
(which we regard as
![]() $0$
-adjusters) satisfying the following bound on their total length:
$0$
-adjusters) satisfying the following bound on their total length:
-
• if
 $s\geq 2$
then
$s\geq 2$
then
 $3n/2 \geq \sum _{i=1}^c\lvert C_i\rvert \geq 4n/3$
, whereas
$3n/2 \geq \sum _{i=1}^c\lvert C_i\rvert \geq 4n/3$
, whereas -
• if
 $s=1$
, then
$s=1$
, then
 $3n/4 \geq \sum _{i=1}^c\lvert C_i\rvert \geq 2n/3$
.
$3n/4 \geq \sum _{i=1}^c\lvert C_i\rvert \geq 2n/3$
.
Set
![]() $C_1' = C_1$
. After finding each
$C_1' = C_1$
. After finding each
![]() $C_i$
(for
$C_i$
(for
![]() $i \geq 2$
), we merge it with the cycle
$i \geq 2$
), we merge it with the cycle
![]() $C_{i-1}'$
using Lemma 5.4. As before, there are at least
$C_{i-1}'$
using Lemma 5.4. As before, there are at least
![]() $q = 4.1 \times 10^{18}\log ^4 k$
vertex-disjoint paths between the two cycles, by the hypothesis, and we may choose these to have length at most
$q = 4.1 \times 10^{18}\log ^4 k$
vertex-disjoint paths between the two cycles, by the hypothesis, and we may choose these to have length at most
![]() $\lvert H'\rvert + s \leq mk + k$
. Thus, we obtain a merged cycle
$\lvert H'\rvert + s \leq mk + k$
. Thus, we obtain a merged cycle
![]() $C_i'$
with
$C_i'$
with
 $$ \begin{align*} (\lvert C_{i-1}'\rvert + \lvert C_i\rvert)(1 - 4q^{-1/2})\leq \lvert C_i'\rvert \leq \lvert C_{i-1}'\rvert + \lvert C_i\rvert +2mk + 2k. \end{align*} $$
$$ \begin{align*} (\lvert C_{i-1}'\rvert + \lvert C_i\rvert)(1 - 4q^{-1/2})\leq \lvert C_i'\rvert \leq \lvert C_{i-1}'\rvert + \lvert C_i\rvert +2mk + 2k. \end{align*} $$
By induction, and that after each merging of cycles we can truncate the length of the new cycle (just as we did with the paths), we have
![]() $\lvert C_{i-1}'\rvert \leq \left (\sum _{j<i}\lvert C_j\rvert \right ) + 2mk+2m$
for each
$\lvert C_{i-1}'\rvert \leq \left (\sum _{j<i}\lvert C_j\rvert \right ) + 2mk+2m$
for each
![]() $i \geq 2$
, and so
$i \geq 2$
, and so
 $$ \begin{align} \lvert C_i'\rvert \geq \lvert C_{i-1}'\rvert + \lvert C_i\rvert - 4q^{-1/2}\left(\left(\sum_{j=1}^{c}\lvert C_j\rvert\right) + 2mk + 2m\right). \end{align} $$
$$ \begin{align} \lvert C_i'\rvert \geq \lvert C_{i-1}'\rvert + \lvert C_i\rvert - 4q^{-1/2}\left(\left(\sum_{j=1}^{c}\lvert C_j\rvert\right) + 2mk + 2m\right). \end{align} $$
Summing inequality (14), we obtain
 $$\begin{align*}\lvert C_c'\rvert \geq \sum_{j=1}^{c}\lvert C_j\rvert(1 - (6.4 \times 10^6)q^{-1/2}\log^2 k) - ((6.4 \times 10^6)q^{-1/2}\log^2 k)(2mk + 2m),\end{align*}$$
$$\begin{align*}\lvert C_c'\rvert \geq \sum_{j=1}^{c}\lvert C_j\rvert(1 - (6.4 \times 10^6)q^{-1/2}\log^2 k) - ((6.4 \times 10^6)q^{-1/2}\log^2 k)(2mk + 2m),\end{align*}$$
hence for
![]() $s\geq 2$
,
$s\geq 2$
,
![]() $\lvert C_c'\rvert \geq 5n/4$
and for
$\lvert C_c'\rvert \geq 5n/4$
and for
![]() $s=1$
,
$s=1$
,
![]() $\lvert C_c'\rvert \geq 0.62n$
.
$\lvert C_c'\rvert \geq 0.62n$
.
Now, merge
![]() $C_c'$
with
$C_c'$
with
![]() $F_{f}'$
using Lemma 5.4 to produce our desired r-adjuster. One can see that
$F_{f}'$
using Lemma 5.4 to produce our desired r-adjuster. One can see that
![]() $r \geq (3/4)^2r_{\mathrm {total}}\geq 9mk/8\geq (m+1)k$
.
$r \geq (3/4)^2r_{\mathrm {total}}\geq 9mk/8\geq (m+1)k$
.
Suppose
![]() $s\geq 2$
. Note that the final use of Lemma 5.4 merges a adjuster of length less than n with a
$s\geq 2$
. Note that the final use of Lemma 5.4 merges a adjuster of length less than n with a
![]() $0$
-adjuster of length at least
$0$
-adjuster of length at least
![]() $5n/4$
, and thus, our r-adjuster of length
$5n/4$
, and thus, our r-adjuster of length
![]() $\ell>n$
contains a section of length at least
$\ell>n$
contains a section of length at least
![]() $\ell -n$
in which there are no short cycles. Using the fact that
$\ell -n$
in which there are no short cycles. Using the fact that
![]() $\overline G$
is
$\overline G$
is
![]() $H'$
-free, we can shortcut parts of this section, if necessary, without reducing r, until
$H'$
-free, we can shortcut parts of this section, if necessary, without reducing r, until
![]() $0\leq \ell -n\leq mk+k$
. Now, using the fact that it is an r-adjuster for some
$0\leq \ell -n\leq mk+k$
. Now, using the fact that it is an r-adjuster for some
![]() $r\geq (m+1)k$
, we may find a route of length exactly n.
$r\geq (m+1)k$
, we may find a route of length exactly n.
Finally, if
![]() $s=1$
the final adjuster similarly has length
$s=1$
the final adjuster similarly has length
![]() $\ell \geq 0.6 n$
and contains a section of length
$\ell \geq 0.6 n$
and contains a section of length
![]() $\ell -0.6n$
with no short cycles. We can shorten this section, if necessary, as before to obtain an r-adjuster of length between
$\ell -0.6n$
with no short cycles. We can shorten this section, if necessary, as before to obtain an r-adjuster of length between
![]() $0.6n$
and
$0.6n$
and
![]() $0.7n$
.
$0.7n$
.
6 Stability and exactness
In this section, we prove our main result via the following statement.
Theorem 6.1. There exists a constant
![]() $C'> 0$
such that, for any complete k-partite graph H on
$C'> 0$
such that, for any complete k-partite graph H on
![]() $mk$
vertices where
$mk$
vertices where
![]() $C' \leq m \leq k^{22}$
and
$C' \leq m \leq k^{22}$
and
![]() $n \geq 10^{60}mk\log ^4 k$
, we have that
$n \geq 10^{60}mk\log ^4 k$
, we have that
![]() $C_n$
is H-good, that is,
$C_n$
is H-good, that is,
![]() $R(C_n, H) = (\chi (H)-1)(n-1)+\sigma (H)$
.
$R(C_n, H) = (\chi (H)-1)(n-1)+\sigma (H)$
.
Proof of Theorem 1.2.
Set
![]() $k=\chi (H)$
and
$k=\chi (H)$
and
![]() $m=\lvert H\rvert /k$
. By adding edges to H, if necessary, without changing
$m=\lvert H\rvert /k$
. By adding edges to H, if necessary, without changing
![]() $\sigma (H)$
, we may assume it is a complete k-partite graph for
$\sigma (H)$
, we may assume it is a complete k-partite graph for
![]() $k=\chi (H)$
. If
$k=\chi (H)$
. If
![]() $m>k^{22}$
, then the same is true of the size of the largest part, and so Corollary 3.2 gives the required bound for some constant
$m>k^{22}$
, then the same is true of the size of the largest part, and so Corollary 3.2 gives the required bound for some constant
![]() $C"$
(and in fact the logarithmic term is not needed). If
$C"$
(and in fact the logarithmic term is not needed). If
![]() $C'\leq m\leq k^{22}$
, then Theorem 6.1 gives the required bound with constant
$C'\leq m\leq k^{22}$
, then Theorem 6.1 gives the required bound with constant
![]() $10^{60}$
. Finally, if
$10^{60}$
. Finally, if
![]() $m<C'$
, then by increasing the size of the largest part we may replace H with a graph
$m<C'$
, then by increasing the size of the largest part we may replace H with a graph
![]() $H'$
of order at most
$H'$
of order at most
![]() $C'\lvert H\rvert $
and
$C'\lvert H\rvert $
and
![]() $\sigma (H')=\sigma (H)$
which satisfies the conditions of Theorem 6.1, giving that
$\sigma (H')=\sigma (H)$
which satisfies the conditions of Theorem 6.1, giving that
![]() $C_n$
is
$C_n$
is
![]() $H'$
-good (and hence H-good) for
$H'$
-good (and hence H-good) for
![]() $n\geq 10^{60}C'\lvert H\rvert \log ^4\chi (H)$
.
$n\geq 10^{60}C'\lvert H\rvert \log ^4\chi (H)$
.
To prove Theorem 6.1, we first establish the following stability result.
Lemma 6.2. There exists a constant
![]() $C>0$
satisfying the following. Fix
$C>0$
satisfying the following. Fix
![]() $k\geq 2$
and
$k\geq 2$
and
![]() $C\leq m\leq k^{22}$
and
$C\leq m\leq k^{22}$
and
![]() $z\geq 0$
and
$z\geq 0$
and
![]() $n\geq 10^{49}km\log ^4 k$
. Let H be a complete k-partite graph with
$n\geq 10^{49}km\log ^4 k$
. Let H be a complete k-partite graph with
![]() $mk$
vertices, and write
$mk$
vertices, and write
![]() $m_1\leq \cdots \leq m_k$
for the sizes of the parts. Define
$m_1\leq \cdots \leq m_k$
for the sizes of the parts. Define
![]() $\hat {H}\sqsubset H$
to be the graph obtained by removing a part of size
$\hat {H}\sqsubset H$
to be the graph obtained by removing a part of size
![]() $m_2$
. Suppose G is a
$m_2$
. Suppose G is a
![]() $C_n$
-free graph with
$C_n$
-free graph with
![]() $\lvert G\rvert \geq (k-1)(n-1)+z$
such that
$\lvert G\rvert \geq (k-1)(n-1)+z$
such that
![]() $\overline {G}$
is H-free. Then at least one of the following holds.
$\overline {G}$
is H-free. Then at least one of the following holds.
-
(i) There exists
 $G'\subset G$
such that
$G'\subset G$
such that
 $\overline {G'}$
is
$\overline {G'}$
is
 $\hat H$
-free and
$\hat H$
-free and
 $\lvert G'\rvert \geq (k-2)(n-1)+z$
.
$\lvert G'\rvert \geq (k-2)(n-1)+z$
. -
(ii) There exist disjoint sets
 $A_1,\ldots ,A_{k-1}$
, with no edges between them, such that for each i we have
$A_1,\ldots ,A_{k-1}$
, with no edges between them, such that for each i we have-
•
 $\lvert A_i\rvert \geq 0.95n$
,
$\lvert A_i\rvert \geq 0.95n$
, -
•
 $\overline {G[A_i]}$
is
$\overline {G[A_i]}$
is
 $K_{m_1,m_2}$
-free, and
$K_{m_1,m_2}$
-free, and -
• within
 $G[A_i]$
, any two disjoint sets of size at least
$G[A_i]$
, any two disjoint sets of size at least
 $m_2+4.1\times 10^{18}\log ^4 k$
have at least
$m_2+4.1\times 10^{18}\log ^4 k$
have at least
 $4.1\times 10^{18}\log ^4 k$
disjoint paths between them.
$4.1\times 10^{18}\log ^4 k$
disjoint paths between them.
-
Proof. Let C be a constant given in Lemma 5.1. Suppose not. Start with
![]() $A=V(G)$
and
$A=V(G)$
and
![]() $S=\varnothing $
. If there exists a set X of order at most
$S=\varnothing $
. If there exists a set X of order at most
![]() $4.1\times 10^{18}\log ^4k$
such that removing X from
$4.1\times 10^{18}\log ^4k$
such that removing X from
![]() $G[A]$
increases the number of components of
$G[A]$
increases the number of components of
![]() $G[A]$
of order at least
$G[A]$
of order at least
![]() $m_2$
, remove X from A and add it to S. Do this for k iterations or until no such set exists. At the end of the process, we have
$m_2$
, remove X from A and add it to S. Do this for k iterations or until no such set exists. At the end of the process, we have
![]() $\lvert S\rvert \leq 4.1\times 10^{18}k\log ^4k$
.
$\lvert S\rvert \leq 4.1\times 10^{18}k\log ^4k$
.
Note that any set B of order at least
![]() $m_2$
satisfies
$m_2$
satisfies
![]() $\lvert B\cup N(B)\rvert \geq n$
, else
$\lvert B\cup N(B)\rvert \geq n$
, else
![]() $G[V(G)\setminus (B\cup N(B))]$
satisfies (i). In particular, if
$G[V(G)\setminus (B\cup N(B))]$
satisfies (i). In particular, if
![]() $B\subset A$
with
$B\subset A$
with
![]() $\lvert B\rvert \geq m_2$
, then
$\lvert B\rvert \geq m_2$
, then
It follows that the total size of all components of
![]() $G[A]$
of size less than
$G[A]$
of size less than
![]() $m_2$
is less than
$m_2$
is less than
![]() $m_2$
, since otherwise there is a union of some of these components of size between
$m_2$
, since otherwise there is a union of some of these components of size between
![]() $m_2$
and
$m_2$
and
![]() $2m_2$
, contradicting the fact that sets of this size expand well. It also follows that any other component has order at least
$2m_2$
, contradicting the fact that sets of this size expand well. It also follows that any other component has order at least
![]() $n-4.1\times 10^{18}k\log ^4 k$
; let these components of
$n-4.1\times 10^{18}k\log ^4 k$
; let these components of
![]() $G[A]$
be
$G[A]$
be
![]() $A_1,\ldots A_t$
, where
$A_1,\ldots A_t$
, where
![]() $t\geq 1$
and
$t\geq 1$
and
We must have
![]() $t\leq k-1$
since otherwise
$t\leq k-1$
since otherwise
![]() $\overline G$
contains a copy of H obtained by choosing a suitable number of vertices from
$\overline G$
contains a copy of H obtained by choosing a suitable number of vertices from
![]() $A_1,\ldots ,A_k$
.
$A_1,\ldots ,A_k$
.
In particular, we added vertices to S fewer than k times, and so the process described above stopped because no more removals were possible. This will give the required connectivity properties. Indeed, if
![]() $B_1,B_2$
are disjoint sets in
$B_1,B_2$
are disjoint sets in
![]() $A_i$
of size at least
$A_i$
of size at least
![]() $m_2+4.1\times 10^{18}\log ^4 k$
, then no set X of order
$m_2+4.1\times 10^{18}\log ^4 k$
, then no set X of order
![]() $4.1\times 10^{18}\log ^4 k$
separates
$4.1\times 10^{18}\log ^4 k$
separates
![]() $B_1\setminus X$
from
$B_1\setminus X$
from
![]() $B_2\setminus X$
within
$B_2\setminus X$
within
![]() $G[A_i]$
(since both these sets have size at least
$G[A_i]$
(since both these sets have size at least
![]() $m_2$
and by the construction of A). Thus, by Menger’s theorem there are at least
$m_2$
and by the construction of A). Thus, by Menger’s theorem there are at least
![]() $4.1\times 10^{18}\log ^4 k$
disjoint paths between them in
$4.1\times 10^{18}\log ^4 k$
disjoint paths between them in
![]() $G[A_i]$
.
$G[A_i]$
.
For each
![]() $i\leq t$
, we define
$i\leq t$
, we define
![]() $k-t+1$
subgraphs
$k-t+1$
subgraphs
![]() $H^{(1)}_i\sqsubset \cdots \sqsubset H^{(k-t+1)}_i\sqsubset H$
as follows. Set
$H^{(1)}_i\sqsubset \cdots \sqsubset H^{(k-t+1)}_i\sqsubset H$
as follows. Set
![]() $H_i^{(1)}$
to be an independent set of
$H_i^{(1)}$
to be an independent set of
![]() $m_{k+1-i}$
vertices, and for
$m_{k+1-i}$
vertices, and for
![]() $2\leq j\leq k-t+1$
set
$2\leq j\leq k-t+1$
set
![]() $H_i^{(j)}=K_{m_{k+1-i},m_{k-t},m_{k-t-1},\ldots ,m_{k-t-j+2}}$
, that is,
$H_i^{(j)}=K_{m_{k+1-i},m_{k-t},m_{k-t-1},\ldots ,m_{k-t-j+2}}$
, that is,
![]() $H_i^{(j)}$
is a complete j-partite subgraph consisting of the ith largest class of H together with
$H_i^{(j)}$
is a complete j-partite subgraph consisting of the ith largest class of H together with
![]() $j-1$
of the
$j-1$
of the
![]() $k-t$
smallest classes taken in decreasing order.
$k-t$
smallest classes taken in decreasing order.
For each
![]() $i\leq t$
, let
$i\leq t$
, let
![]() $s_i\geq 1$
be the largest value such that
$s_i\geq 1$
be the largest value such that
![]() $\overline {G[A_i]}$
contains
$\overline {G[A_i]}$
contains
![]() $H_i^{(s_i)}$
. Suppose that
$H_i^{(s_i)}$
. Suppose that
![]() $\sum _{i\in [t]} s_i\geq k$
, and consider the graph induced in
$\sum _{i\in [t]} s_i\geq k$
, and consider the graph induced in
![]() $\overline {G}$
by the vertices of a copy of
$\overline {G}$
by the vertices of a copy of
![]() $H_i^{(s_i)}$
in
$H_i^{(s_i)}$
in
![]() $\overline {G[A_i]}$
for each i. Taking the largest class from each copy creates a copy of
$\overline {G[A_i]}$
for each i. Taking the largest class from each copy creates a copy of
![]() $K_{m_k,\ldots ,m_{k-t+1}}$
, and the other classes give a complete
$K_{m_k,\ldots ,m_{k-t+1}}$
, and the other classes give a complete
![]() $(k-t)$
-partite graph with jth largest part having size at least
$(k-t)$
-partite graph with jth largest part having size at least
![]() $m_{k-t+1-j}$
for each
$m_{k-t+1-j}$
for each
![]() $j\in [k-t]$
, which contains
$j\in [k-t]$
, which contains
![]() $K_{m_{k-t},\ldots ,m_1}$
. Thus,
$K_{m_{k-t},\ldots ,m_1}$
. Thus,
![]() $\overline G\supset H$
, a contradiction.
$\overline G\supset H$
, a contradiction.
Consequently, we have
![]() $\sum _{i\in [t]} s_i\leq k-1$
, and in particular
$\sum _{i\in [t]} s_i\leq k-1$
, and in particular
![]() $s_i\leq k-t$
for each i. By definition of
$s_i\leq k-t$
for each i. By definition of
![]() $s_i$
,
$s_i$
,
![]() $\overline {G[A_i]}$
is
$\overline {G[A_i]}$
is
![]() $H^{(s_i+1)}_i$
-free for each i. If
$H^{(s_i+1)}_i$
-free for each i. If
![]() $s_i>1$
, we have
$s_i>1$
, we have
![]() $\lvert A_i\rvert <s_in-n/10$
, since otherwise Lemma 5.1, taking
$\lvert A_i\rvert <s_in-n/10$
, since otherwise Lemma 5.1, taking
![]() $H^{\prime }_{4.1}=H_i^{(s_i+1)}$
, gives a copy of
$H^{\prime }_{4.1}=H_i^{(s_i+1)}$
, gives a copy of
![]() $C_n$
inside
$C_n$
inside
![]() $G[A_i]$
. Contrariwise, if
$G[A_i]$
. Contrariwise, if
![]() $s_i=1$
we have
$s_i=1$
we have
![]() $\lvert A_i\rvert <n+m_{k-t}$
by Corollary 3.3. In either case, for each
$\lvert A_i\rvert <n+m_{k-t}$
by Corollary 3.3. In either case, for each
![]() $i\in [t]$
we have
$i\in [t]$
we have
![]() $\lvert A_i\rvert <s_in+m_{k-t}$
. Note that
$\lvert A_i\rvert <s_in+m_{k-t}$
. Note that
![]() $(t-1)m_{k-t}\leq \lvert H\rvert =mk$
. Thus, if for any i we have
$(t-1)m_{k-t}\leq \lvert H\rvert =mk$
. Thus, if for any i we have
![]() $s_i>1$
, then
$s_i>1$
, then
 $$\begin{align*}\sum_{j\in [t]}\lvert A_j\rvert<s_in-n/10+\sum_{\substack{j\in[t]\\ j\neq i}}(s_in+m_{k-t})\leq (k-1)n-n/10+(t-1)m_{k-t}, \end{align*}$$
$$\begin{align*}\sum_{j\in [t]}\lvert A_j\rvert<s_in-n/10+\sum_{\substack{j\in[t]\\ j\neq i}}(s_in+m_{k-t})\leq (k-1)n-n/10+(t-1)m_{k-t}, \end{align*}$$
contradicting inequality (15). We may therefore assume each
![]() $s_i=1$
. Similarly, if
$s_i=1$
. Similarly, if
![]() $\sum _{i\in [t]} s_i<k-1$
, and so
$\sum _{i\in [t]} s_i<k-1$
, and so
![]() $t<k-1$
, we obtain a contradiction to inequality (15). Thus,
$t<k-1$
, we obtain a contradiction to inequality (15). Thus,
![]() $t=k-1$
, and each of
$t=k-1$
, and each of
![]() $A_1,\ldots ,A_{k-1}$
has size at least
$A_1,\ldots ,A_{k-1}$
has size at least
![]() $n-4.1\times 10^{18}k\log ^4k\geq 0.95n$
. If for some i we have
$n-4.1\times 10^{18}k\log ^4k\geq 0.95n$
. If for some i we have
![]() $K_{m_1,m_2}\subset \overline {G[A_i]}$
, then taking the copy of
$K_{m_1,m_2}\subset \overline {G[A_i]}$
, then taking the copy of
![]() $K_{m_1,m_2}$
together with
$K_{m_1,m_2}$
together with
![]() $m_k$
vertices from each other part gives a copy of
$m_k$
vertices from each other part gives a copy of
![]() $K_{m_k,\ldots ,m_k,m_2,m_1}$
(with k parts in total) in
$K_{m_k,\ldots ,m_k,m_2,m_1}$
(with k parts in total) in
![]() $\overline {G}$
, and so
$\overline {G}$
, and so
![]() $\overline G\supset H$
, a contradiction. Together with the connectivity properties heretofore established, this completes the proof.
$\overline G\supset H$
, a contradiction. Together with the connectivity properties heretofore established, this completes the proof.
We now proceed from the stability result above to exactness. We need the following result which says that when the complement is
![]() $K_{m_1,m_2}$
-free we can do much better than Lemma 5.4.
$K_{m_1,m_2}$
-free we can do much better than Lemma 5.4.
Lemma 6.3. Let
![]() $F_i$
be an
$F_i$
be an
![]() $r_i$
-adjuster of length
$r_i$
-adjuster of length
![]() $\ell _i$
for
$\ell _i$
for
![]() $i\in \{1,2\}$
, with
$i\in \{1,2\}$
, with
![]() $F_1$
and
$F_1$
and
![]() $F_2$
disjoint, and suppose
$F_2$
disjoint, and suppose
![]() $\overline {G[V(F_i)]}$
is
$\overline {G[V(F_i)]}$
is
![]() $K_{m_1,m_2}$
-free for each i, where
$K_{m_1,m_2}$
-free for each i, where
![]() $m_2\geq m_1$
. Suppose further that there are two vertex-disjoint paths
$m_2\geq m_1$
. Suppose further that there are two vertex-disjoint paths
![]() $P_1,P_2$
between
$P_1,P_2$
between
![]() $F_1$
and
$F_1$
and
![]() $F_2$
, each of length at most t. Then there is an r-adjuster of length
$F_2$
, each of length at most t. Then there is an r-adjuster of length
![]() $\ell $
all of whose vertices are contained in
$\ell $
all of whose vertices are contained in
![]() $F_1\cup F_2\cup P_1\cup P_2$
, where
$F_1\cup F_2\cup P_1\cup P_2$
, where
![]() $r\geq r_1+r_2-2(m_1+m_2)$
and
$r\geq r_1+r_2-2(m_1+m_2)$
and
![]() $\ell _1+\ell _2-2(m_1+m_2)\leq \ell \leq \ell _1+\ell _2+2t$
. Furthermore, if
$\ell _1+\ell _2-2(m_1+m_2)\leq \ell \leq \ell _1+\ell _2+2t$
. Furthermore, if
![]() $r_2=0$
, then the adjuster contains a section of length at least
$r_2=0$
, then the adjuster contains a section of length at least
![]() $\ell -\ell _1$
with no short cycles.
$\ell -\ell _1$
with no short cycles.
Proof. Let
![]() $P_i$
have ends
$P_i$
have ends
![]() $x_i$
in
$x_i$
in
![]() $F_1$
and
$F_1$
and
![]() $y_i$
in
$y_i$
in
![]() $F_2$
. We claim that there is a path
$F_2$
. We claim that there is a path
![]() $Q_1$
of length at least
$Q_1$
of length at least
![]() $\ell _1-m_1-m_2-1$
in
$\ell _1-m_1-m_2-1$
in
![]() $F_1$
between
$F_1$
between
![]() $x_1$
and
$x_1$
and
![]() $x_2$
. To see this, first note that, unless
$x_2$
. To see this, first note that, unless
![]() $x_1$
and
$x_1$
and
![]() $x_2$
are on opposite sides of the same short cycle, there is a route in
$x_2$
are on opposite sides of the same short cycle, there is a route in
![]() $F_1$
which includes both
$F_1$
which includes both
![]() $x_1$
and
$x_1$
and
![]() $x_2$
and has length at least
$x_2$
and has length at least
![]() $\ell _1-2$
. If
$\ell _1-2$
. If
![]() $x_1$
and
$x_1$
and
![]() $x_2$
are at distance at most
$x_2$
are at distance at most
![]() $m_2$
in this route, then by taking the whole route except for a path of length at most
$m_2$
in this route, then by taking the whole route except for a path of length at most
![]() $m_2$
between the two vertices, we are done. If not, then the
$m_2$
between the two vertices, we are done. If not, then the
![]() $m_1$
vertices immediately before
$m_1$
vertices immediately before
![]() $x_1$
on the route do not include
$x_1$
on the route do not include
![]() $x_2$
, and the
$x_2$
, and the
![]() $m_2$
vertices immediately before
$m_2$
vertices immediately before
![]() $x_2$
do not include
$x_2$
do not include
![]() $x_1$
. There is an edge
$x_1$
. There is an edge
![]() $z_1z_2$
between these two sets of vertices in
$z_1z_2$
between these two sets of vertices in
![]() $G[V(F_1)]$
, since
$G[V(F_1)]$
, since
![]() $\overline {G[V(F_1)]}$
is
$\overline {G[V(F_1)]}$
is
![]() $K_{m_{1},m_{2}}$
-free, and so there is a path which starts at
$K_{m_{1},m_{2}}$
-free, and so there is a path which starts at
![]() $x_1$
, goes around the route to
$x_1$
, goes around the route to
![]() $z_2$
, via the extra edge to
$z_2$
, via the extra edge to
![]() $z_1$
and then around the route in the opposite direction to
$z_1$
and then around the route in the opposite direction to
![]() $x_2$
. This path misses out at most
$x_2$
. This path misses out at most
![]() $m_1+m_2-1$
vertices from the route so has at least the required length. See Figure 3. Finally, if
$m_1+m_2-1$
vertices from the route so has at least the required length. See Figure 3. Finally, if
![]() $x_1$
and
$x_1$
and
![]() $x_2$
are on opposite sides of the same short cycle, there is a path around the adjuster from
$x_2$
are on opposite sides of the same short cycle, there is a path around the adjuster from
![]() $x_1$
to
$x_1$
to
![]() $x_2$
using the vertices on that short cycle after
$x_2$
using the vertices on that short cycle after
![]() $x_1$
and before
$x_1$
and before
![]() $x_2$
and the longer side of every other short cycle. Similarly, there is another path which uses the vertices on that short cycle after
$x_2$
and the longer side of every other short cycle. Similarly, there is another path which uses the vertices on that short cycle after
![]() $x_2$
and before
$x_2$
and before
![]() $x_1$
. At least one of these uses at least half of every short cycle, so has length at least
$x_1$
. At least one of these uses at least half of every short cycle, so has length at least
![]() $\ell _1$
.
$\ell _1$
.

Figure 3 A long
![]() $x_1$
-
$x_1$
-
![]() $x_2$
path using the extra edge
$x_2$
path using the extra edge
![]() $z_1z_2$
(shown in bold and highlighted if colour is available). Dashed lines indicate parts of the adjuster not in the relevant route.
$z_1z_2$
(shown in bold and highlighted if colour is available). Dashed lines indicate parts of the adjuster not in the relevant route.
Now, taking this path together with a corresponding path for
![]() $F_2$
and the two paths
$F_2$
and the two paths
![]() $P_1,P_2$
between them gives a cycle C of length between
$P_1,P_2$
between them gives a cycle C of length between
![]() $\ell _1+\ell _2-2(m_1+m_2)$
and
$\ell _1+\ell _2-2(m_1+m_2)$
and
![]() $\ell _1+\ell _2+2t$
. We extend this to an adjuster by including all short cycles from
$\ell _1+\ell _2+2t$
. We extend this to an adjuster by including all short cycles from
![]() $F_1$
and
$F_1$
and
![]() $F_2$
such that one of the routes round that short cycle is entirely contained in C. Since all but at most
$F_2$
such that one of the routes round that short cycle is entirely contained in C. Since all but at most
![]() $m_1+m_2$
edges of a route of
$m_1+m_2$
edges of a route of
![]() $F_i$
are included in the cycle, this means at most
$F_i$
are included in the cycle, this means at most
![]() $2(m_1+m_2)$
short cycles of
$2(m_1+m_2)$
short cycles of
![]() $F_1$
or
$F_1$
or
![]() $F_2$
are not included, giving
$F_2$
are not included, giving
![]() $r\geq r_1+r_2-2(m_1+m_2)$
. Finally, note that the section of the adjuster obtained consisting of vertices not in
$r\geq r_1+r_2-2(m_1+m_2)$
. Finally, note that the section of the adjuster obtained consisting of vertices not in
![]() $F_1$
is contiguous, and contributes at least
$F_1$
is contiguous, and contributes at least
![]() $\ell -\ell _1$
to the overall length. If
$\ell -\ell _1$
to the overall length. If
![]() $r_2=0$
, this section has no short cycles, as required.
$r_2=0$
, this section has no short cycles, as required.
This enables us to effectively deal with the case where two of the
![]() $A_i$
(or, more precisely, the expanding subgraphs within them) are connected by two disjoint paths.
$A_i$
(or, more precisely, the expanding subgraphs within them) are connected by two disjoint paths.
Proof of Theorem 6.1.
It suffices to prove, via induction on k, the conclusion for
![]() $2C\frac {k-1}{k}\le m\le k^{22}$
, where C is at least the constants in Lemma 5.1 and Lemma 6.2. Since we have
$2C\frac {k-1}{k}\le m\le k^{22}$
, where C is at least the constants in Lemma 5.1 and Lemma 6.2. Since we have
![]() $C\leq 2C\frac {k-1}{k}\leq 2C$
, we can then take
$C\leq 2C\frac {k-1}{k}\leq 2C$
, we can then take
![]() $C'=2C$
to conclude.
$C'=2C$
to conclude.
Suppose it is not true, and take a counterexample, that is, a graph G of order
![]() $(k-1)(n-1)+\sigma (H)$
that is
$(k-1)(n-1)+\sigma (H)$
that is
![]() $C_n$
-free and with H-free complement. We apply Lemma 6.2. If statement (i) applies, then we have a graph
$C_n$
-free and with H-free complement. We apply Lemma 6.2. If statement (i) applies, then we have a graph
![]() $G'\subset G$
of order
$G'\subset G$
of order
![]() $(k-2)(n-1)+\sigma (H)$
, with
$(k-2)(n-1)+\sigma (H)$
, with
![]() $\hat H$
-free complement. Note that by definition of
$\hat H$
-free complement. Note that by definition of
![]() $\hat H$
we have
$\hat H$
we have
![]() $\sigma (H)=\sigma (\hat H)$
. Also, since
$\sigma (H)=\sigma (\hat H)$
. Also, since
![]() $m_2\leq \frac {mk}{k-1}$
, we have
$m_2\leq \frac {mk}{k-1}$
, we have
Thus, if
![]() $\lvert \hat H\rvert \leq (k-1)^{23}$
we have
$\lvert \hat H\rvert \leq (k-1)^{23}$
we have
![]() $G'\supset C_n$
by the induction hypothesis, whereas otherwise we have
$G'\supset C_n$
by the induction hypothesis, whereas otherwise we have
![]() $G'\supset C_n$
by Corollary 3.2. Consequently, we must have statement (ii).
$G'\supset C_n$
by Corollary 3.2. Consequently, we must have statement (ii).
Within each set
![]() $A_i$
, we apply Lemma 4.2 with
$A_i$
, we apply Lemma 4.2 with
![]() $G_{3.2}=G[A_i]$
,
$G_{3.2}=G[A_i]$
,
![]() $H_{3.2}=K_{m_1,m_2}$
,
$H_{3.2}=K_{m_1,m_2}$
,
![]() $M_{3.2}=\lvert A_i\rvert /((m_1+m_2)\log 2)$
and
$M_{3.2}=\lvert A_i\rvert /((m_1+m_2)\log 2)$
and
![]() $\beta _{3.2}=M_{3.2}/100>40$
(note that also
$\beta _{3.2}=M_{3.2}/100>40$
(note that also
![]() $\beta _{3.2} \geq 10 \log k$
) to find a
$\beta _{3.2} \geq 10 \log k$
) to find a
![]() $(10,M_{3.2}/100,(m_1+m_2)/2,2)$
-expander
$(10,M_{3.2}/100,(m_1+m_2)/2,2)$
-expander
![]() $H_i$
of order at least
$H_i$
of order at least
![]() $\lvert A_i\rvert -(m_1+m_2)/2\geq \lvert A_i\rvert -m$
.
$\lvert A_i\rvert -(m_1+m_2)/2\geq \lvert A_i\rvert -m$
.
Suppose that
![]() $H_i$
and
$H_i$
and
![]() $H_j$
are linked (in G) by two disjoint paths for some distinct
$H_j$
are linked (in G) by two disjoint paths for some distinct
![]() $i,j\in [k-1]$
. Recall that
$i,j\in [k-1]$
. Recall that
![]() $\lvert A_i\rvert \geq 0.95n$
. Applying Lemma 5.1 to
$\lvert A_i\rvert \geq 0.95n$
. Applying Lemma 5.1 to
![]() $G[A_i]$
, we find an r-adjuster
$G[A_i]$
, we find an r-adjuster
![]() $F_i$
for
$F_i$
for
![]() $r\geq 9mk/8$
with length between
$r\geq 9mk/8$
with length between
![]() $0.6n$
and
$0.6n$
and
![]() $0.7n$
. Similarly, we may find an adjuster in
$0.7n$
. Similarly, we may find an adjuster in
![]() $A_j$
of length between
$A_j$
of length between
![]() $0.6n$
and
$0.6n$
and
![]() $0.7n$
; however, instead of using it as an adjuster we simply take the longest route to find a cycle
$0.7n$
; however, instead of using it as an adjuster we simply take the longest route to find a cycle
![]() $C_j$
of that length.
$C_j$
of that length.
Note that the size of the adjuster and cycle ensures that they intersect
![]() $H_i$
and
$H_i$
and
![]() $H_j$
, respectively, in at least
$H_j$
, respectively, in at least
![]() $\lvert H_i\rvert +0.6n-\lvert A_i\rvert \geq 0.5n$
vertices. Suppose that the disjoint paths between
$\lvert H_i\rvert +0.6n-\lvert A_i\rvert \geq 0.5n$
vertices. Suppose that the disjoint paths between
![]() $H_i$
and
$H_i$
and
![]() $H_j$
have endpoints
$H_j$
have endpoints
![]() $x_1$
and
$x_1$
and
![]() $x_2$
in
$x_2$
in
![]() $H_i$
and endpoints
$H_i$
and endpoints
![]() $y_1$
and
$y_1$
and
![]() $y_2$
in
$y_2$
in
![]() $H_j$
. By Lemma 4.6, we may find disjoint sets
$H_j$
. By Lemma 4.6, we may find disjoint sets
![]() $B_1\ni x_1$
and
$B_1\ni x_1$
and
![]() $B_2\ni x_2$
in
$B_2\ni x_2$
in
![]() $V(H_i)$
of size
$V(H_i)$
of size
![]() $\lvert A_i\rvert /200$
such that every vertex in
$\lvert A_i\rvert /200$
such that every vertex in
![]() $B_1$
is connected to
$B_1$
is connected to
![]() $x_1$
by a path and likewise for
$x_1$
by a path and likewise for
![]() $B_2$
and
$B_2$
and
![]() $x_2$
. We may therefore use Lemma 4.4 with
$x_2$
. We may therefore use Lemma 4.4 with
![]() $A_{3.4}=V(F_i)\cap V(H_i),B_{3.4}=B_1\cup B_2,C_{3.4}=\varnothing $
to give a path from
$A_{3.4}=V(F_i)\cap V(H_i),B_{3.4}=B_1\cup B_2,C_{3.4}=\varnothing $
to give a path from
![]() $V(F_i)$
to
$V(F_i)$
to
![]() $B_1$
or
$B_1$
or
![]() $B_2$
, without loss of generality the former. Extend it to a path from
$B_2$
, without loss of generality the former. Extend it to a path from
![]() $V(F_1)$
to
$V(F_1)$
to
![]() $x_1$
using vertices from
$x_1$
using vertices from
![]() $B_1$
, and remove vertices from this path, if necessary, to obtain a shortest path
$B_1$
, and remove vertices from this path, if necessary, to obtain a shortest path
![]() $P_1$
. This ensures that
$P_1$
. This ensures that
![]() $\lvert V(P_1)\rvert \leq m_1+m_2+1$
since
$\lvert V(P_1)\rvert \leq m_1+m_2+1$
since
![]() $\overline {G[A_i]}$
is
$\overline {G[A_i]}$
is
![]() $K_{m_1,m_2}$
-free; note also that
$K_{m_1,m_2}$
-free; note also that
![]() $P_1$
is disjoint from
$P_1$
is disjoint from
![]() $B_2$
. Next, apply Lemma 4.4 with
$B_2$
. Next, apply Lemma 4.4 with
![]() $A_{3.4}=(V(F_i) \cap V(H_i)) \setminus V(P_1),B_{3.4}=B_2,C_{3.4}=V(P_1)$
to give a disjoint
$A_{3.4}=(V(F_i) \cap V(H_i)) \setminus V(P_1),B_{3.4}=B_2,C_{3.4}=V(P_1)$
to give a disjoint
![]() $x_{2}$
-
$x_{2}$
-
![]() $V(F_{i})$
path
$V(F_{i})$
path
![]() $P_{2}$
. We can similarly find two disjoint paths from
$P_{2}$
. We can similarly find two disjoint paths from
![]() $y_1$
,
$y_1$
,
![]() $y_2$
to
$y_2$
to
![]() $F_j$
in
$F_j$
in
![]() $H_j$
, and the union of these with the existing paths between
$H_j$
, and the union of these with the existing paths between
![]() $H_i$
and
$H_i$
and
![]() $H_j$
give two disjoint paths between the adjuster and the cycle. Since
$H_j$
give two disjoint paths between the adjuster and the cycle. Since
![]() $\overline {G}$
is H-free, each of these paths contains a shortest path of length at most
$\overline {G}$
is H-free, each of these paths contains a shortest path of length at most
![]() $mk+k$
. We apply Lemma 6.3 to merge the adjuster and cycle using these shortest paths, obtaining an adjuster with at least
$mk+k$
. We apply Lemma 6.3 to merge the adjuster and cycle using these shortest paths, obtaining an adjuster with at least
![]() $9mk/8-2(m_1+m_2)\geq mk+k$
short cycles, of total length
$9mk/8-2(m_1+m_2)\geq mk+k$
short cycles, of total length
![]() $\ell $
between
$\ell $
between
![]() $1.2n-2(m_1+m_2)> 1.19n$
and
$1.2n-2(m_1+m_2)> 1.19n$
and
![]() $1.4n+2(mk+k)<1.41n$
. Recall that
$1.4n+2(mk+k)<1.41n$
. Recall that
![]() $F_i$
has length at most
$F_i$
has length at most
![]() $0.7n$
, so the adjuster obtained from merging
$0.7n$
, so the adjuster obtained from merging
![]() $F_i$
and
$F_i$
and
![]() $C_j$
contains a section of length at least
$C_j$
contains a section of length at least
![]() $\ell -0.7n\ge 0.49n>\ell -n$
without short cycles (the part corresponding to
$\ell -0.7n\ge 0.49n>\ell -n$
without short cycles (the part corresponding to
![]() $C_j$
). We may reduce this section until the total length is between n and
$C_j$
). We may reduce this section until the total length is between n and
![]() $n+mk+k$
, since
$n+mk+k$
, since
![]() $\overline G$
is H-free, and then use the reducing power of the adjuster to obtain a cycle of length exactly n.
$\overline G$
is H-free, and then use the reducing power of the adjuster to obtain a cycle of length exactly n.
Thus, we may assume that no pair
![]() $H_i,H_j$
is linked by two disjoint paths. It follows that for some index i there is a vertex v which separates
$H_i,H_j$
is linked by two disjoint paths. It follows that for some index i there is a vertex v which separates
![]() $H_i$
from all other
$H_i$
from all other
![]() $H_j$
. Let A be the component of
$H_j$
. Let A be the component of
![]() $G-v$
containing
$G-v$
containing
![]() $H_i-v$
, and let
$H_i-v$
, and let
![]() $G'=G[A\cup \{v\}]$
. Note that
$G'=G[A\cup \{v\}]$
. Note that
![]() $\overline {G'}$
is
$\overline {G'}$
is
![]() $K_{m_1+1,m_2+1}$
-free, since otherwise we may choose
$K_{m_1+1,m_2+1}$
-free, since otherwise we may choose
![]() $m_k$
vertices from
$m_k$
vertices from
![]() $H_j-v$
for each
$H_j-v$
for each
![]() $j\neq i$
together with the vertices of a
$j\neq i$
together with the vertices of a
![]() $K_{m_1,m_2}$
in
$K_{m_1,m_2}$
in
![]() $\overline {G'-v}$
to give a graph containing H in
$\overline {G'-v}$
to give a graph containing H in
![]() $\overline {G}$
. Recall that statement (i) of Lemma 6.2 does not apply. It follows that any set
$\overline {G}$
. Recall that statement (i) of Lemma 6.2 does not apply. It follows that any set
![]() $B\subset A$
of size
$B\subset A$
of size
![]() $m_2$
has
$m_2$
has
![]() $\lvert N_G(B)\cup B\rvert \geq n$
, since otherwise
$\lvert N_G(B)\cup B\rvert \geq n$
, since otherwise
![]() $\overline {G-(N_G(B)\cup B)}$
is not
$\overline {G-(N_G(B)\cup B)}$
is not
![]() $\hat {H}$
-free, implying that
$\hat {H}$
-free, implying that
![]() $\overline G$
is not H-free. Since also
$\overline G$
is not H-free. Since also
![]() $N_{G'}(B)\cup B=N_G(B)\cup B$
, we have
$N_{G'}(B)\cup B=N_G(B)\cup B$
, we have
![]() $\lvert N_{G'}(B)\cup B\rvert \geq n$
. Thus, for any set
$\lvert N_{G'}(B)\cup B\rvert \geq n$
. Thus, for any set
![]() $B'\subset V(G')$
of order at least
$B'\subset V(G')$
of order at least
![]() $m_2+1$
, we have
$m_2+1$
, we have
![]() $\lvert N_{G'}(B')\cup B'\rvert \geq n$
(since
$\lvert N_{G'}(B')\cup B'\rvert \geq n$
(since
![]() $B'$
contains a set of order
$B'$
contains a set of order
![]() $m_2$
not including v). Now, using Lemma 5.3 with
$m_2$
not including v). Now, using Lemma 5.3 with
![]() $G_{4.3}=H_i$
and
$G_{4.3}=H_i$
and
![]() $H_{4.3}=K_{m_2,m_2}$
, we may find a cycle of length at least
$H_{4.3}=K_{m_2,m_2}$
, we may find a cycle of length at least
![]() $10m_2$
in
$10m_2$
in
![]() $H_i$
. Taking
$H_i$
. Taking
![]() $x,y$
to be two consecutive vertices on this cycle, Lemma 3.4 applies to
$x,y$
to be two consecutive vertices on this cycle, Lemma 3.4 applies to
![]() $G_{2.4}=G'$
with
$G_{2.4}=G'$
with
![]() $m_{2.4}=m_2+1$
, and we may find a path of order exactly n between x and y, giving a copy of
$m_{2.4}=m_2+1$
, and we may find a path of order exactly n between x and y, giving a copy of
![]() $C_n$
.
$C_n$
.
Acknowledgements
John Haslegrave is supported by the UK Research and Innovation Future Leaders Fellowship MR/S016325/1. Joseph Hyde is supported by the UK Research and Innovation Future Leaders Fellowship MR/S016325/1 and ERC Advanced Grant 101020255. Jaehoon Kim is supported by the POSCO Science Fellowship of POSCO TJ Park Foundation and by the KAIX Challenge program of KAIST Advanced Institute for Science-X. Hong Liu is supported by the Institute for Basic Science (IBS-R029-C4) and the UK Research and Innovation Future Leaders Fellowship MR/S016325/1. The authors are grateful to the referee for their careful review.
Conflict of Interest
The authors have no conflict of interest to declare.