Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-24T13:04:55.693Z Has data issue: false hasContentIssue false
  • English
  • Français

Profinite invariants of arithmetic groups

Part of: Structure and classification of infinite or finite groups Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  13 November 2020

Holger Kammeyer Open the ORCID record for Holger Kammeyer [Opens in a new window] ,
Steffen Kionke Open the ORCID record for Steffen Kionke [Opens in a new window] ,
Jean Raimbault Open the ORCID record for Jean Raimbault [Opens in a new window]  and
Roman Sauer Open the ORCID record for Roman Sauer [Opens in a new window]
Holger Kammeyer
Affiliation:
Institute for Algebra and Geometry, Karlsruhe Institute of Technology, 76131Karlsruhe, Germany; E-mail: [email protected], [email protected]
Steffen Kionke
Affiliation:
Faculty of Mathematics and Computer Science, FernUniversität in Hagen, 58097Hagen, Germany; E-mail: [email protected]
Jean Raimbault
Affiliation:
Institut de Mathématiques de Toulouse; UMR5219 Université de Toulouse; CNRS UPS IMT, F-31062 Toulouse Cedex 9, France; E-mail: [email protected]
Roman Sauer
Affiliation:
Institute for Algebra and Geometry, Karlsruhe Institute of Technology, 76131Karlsruhe, Germany; E-mail: [email protected], [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We prove that the sign of the Euler characteristic of arithmetic groups with the congruence subgroup property is determined by the profinite completion. In contrast, we construct examples showing that this is not true for the Euler characteristic itself and that the sign of the Euler characteristic is not profinite among general residually finite groups of type F. Our methods imply similar results for 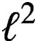$\ell^2$ -torsion as well as a strong profiniteness statement for Novikov–Shubin invariants.

Keywords

profinite rigidityarithmetic groupsl2-invariants

MSC classification

Primary: 20E18: Limits, profinite groups
Secondary: 11F75: Cohomology of arithmetic groups
Type
Algebra
Information
Forum of Mathematics, Sigma , Volume 8 , 2020 , e54
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s), 2020. Published by Cambridge University Press

References

Agol, I., ‘The virtual Haken conjecture’, Doc. Math. 18 (2013), 1045–1087, with an appendix by Agol, I., Groves, D., and Manning, J..Google Scholar
Aka, M., ‘Arithmetic groups with isomorphic finite quotients’, J. Algebra 352 (2012), 322–340.CrossRefGoogle Scholar
Aka, M., ‘Profinite completions and Kazhdan’s property (T)’, Groups Geom. Dyn. 6(2), 221–229, 2012.CrossRefGoogle Scholar
Artin, E., Geometric Algebra (Interscience Publishers, Inc., New York-London, 1957).Google Scholar
Baumslag, G., ‘Residually finite groups with the same finite images’, Compositio Math. 29 (1974), 249–252.Google Scholar
Bergeron, N., Haglund, F., and Wise, D. T., ‘Hyperplane sections in arithmetic hyperbolic manifolds’, J. Lond. Math. Soc. 83(2) (2011), 431–448.CrossRefGoogle Scholar
Boileau, M. and Friedl, S., ‘The profinite completion of $3$ -manifold groups, fiberedness and the thurston norm’ (2015).Google Scholar
Borel, A., Introduction aux groupes arithmétiques (Publications de l’Institut de Mathématique de l’Université de Strasbourg, XV, Actualités Scientifiques et Industrielles, No. 1341, Hermann, Paris, 1969).Google Scholar
Borel, A., ‘The ${L}^2$ -cohomology of negatively curved Riemannian symmetric spaces’, Ann. Acad. Sci. Fenn. Ser. A I Math. 10 (1985), 95–105.CrossRefGoogle Scholar
Borel, A. and Serre, J.-P., ‘Corners and arithmetic groups’, Comment. Math. Helv. 48 (1973), 436–491, avec un appendice: ‘Arrondissement des variétés à coins’, par A. Douady et L. Hérault.CrossRefGoogle Scholar
Bridson, M. R., Conder, M. D. E., and Reid, A. W., ‘Determining Fuchsian groups by their finite quotients’, Israel J. Math. 214(1) (2016), 1–41.CrossRefGoogle Scholar
Bridson, M. R., McReynolds, D. B., Reid, A. W., and Spitler, R., ‘Absolute profinite rigidity and hyperbolic geometry’, 2018.Google Scholar
Bridson, M. R. and Reid, A. W., ‘Profinite rigidity, fibering, and the figure-eight knot’, arXiv e-print, 2015.Google Scholar
Burghelea, D., Friedlander, L., Kappeler, T., and McDonald, P., ‘Analytic and Reidemeister torsion for representations in finite type Hilbert modules’, Geom. Funct. Anal. 6(5) (1996), 751–859.CrossRefGoogle Scholar
Cassels, J. W. S., Rational quadratic forms , vol. 13 of London Mathematical Society Monographs (Academic Press, Inc. [Harcourt Brace Jovanovich, Publishers], London-New York, 1978).Google Scholar
Cheeger, J. and Gromov, M., ‘ ${L}_2$ -cohomology and group cohomology’, Topology 25(2) (1986), 189–215.CrossRefGoogle Scholar
Demazure, M. and Gabriel, P., ‘Groupes algébriques, Tome I: Géométrie algébrique, généralités, groupes commutatifs, Masson, and Cie, , eds. (Paris; North-Holland Publishing Co., Amsterdam, 1970), avec un appendice ıt Corps de classes local par Hazewinkel, M..Google Scholar
Dixon, J., du Sautoy, M., Mann, A., and Segal, D., Analytic pro-p Groups , Cambridge Studies in Advanced Mathematics, vol. 61 (Cambridge University Press, Cambridge, 2003).Google Scholar
Dixon, J. D., Formanek, E. W., Poland, J. C., and Ribes, L., ‘Profinite completions and isomorphic finite quotients’, J. Pure Appl. Algebra 23(3) (1982) 227–231.CrossRefGoogle Scholar
Edwards, H. M., Riemann’s Zeta Function , Pure and Applied Mathematics, vol. 58 (Academic Press, New York-London, 1974).Google Scholar
Efremov, A. V., ‘Cell decompositions and the Novikov-Shubin invariants’, Uspekhi Mat. Nauk 46(3(279)) (1991), 189–190.Google Scholar
Furman, A., ‘A survey of measured group theory’, in: Geometry, Rigidity, and Group Actions, Chicago Lectures in Math. (Univ. Chicago Press, Chicago, IL, 2011), 296–374.Google Scholar
Gaboriau, D., ‘Invariants ${l}^2$ de relations d’équivalence et de groupes’, Publ. Math. Inst. Hautes Études Sci. (95) (2002), 93–150.CrossRefGoogle Scholar
Gille, P. and Polo, P., editors, Schémas en groupes (SGA 3), Tome III Structure des schémas en groupes réductifs, Documents Mathématiques (Paris), vol. 8 (Société Mathématique de France, Paris, 2011), Séminaire de Géométrie Algébrique du Bois Marie, 1962–64.Google Scholar
Harder, G., ‘A Gauss-Bonnet formula for discrete arithmetically defined groups’, Ann. Sci. École Norm. Sup. 4 (1971), 409–455.CrossRefGoogle Scholar
Hilgert, J. and Neeb, K.-H., Structure and Geometry of Lie Groups, Springer Monographs in Mathematics (Springer, New York, 2012).CrossRefGoogle Scholar
Humphreys, J. E., Introduction to Lie algebras and Representation Theory, Graduate Texts in Mathematics, vol. 9 (Springer-Verlag, New York-Berlin, 1972).CrossRefGoogle Scholar
Kammeyer, H., ‘ ${L}^2$ -invariants of nonuniform lattices in semisimple Lie groups’, PhD thesis, Universität Göttingen (2013).CrossRefGoogle Scholar
Kammeyer, H., ‘ ${L}^2$ -invariants of nonuniform lattices in semisimple Lie groups’, Algebr. Geom. Topol. 14(4) (2014) 2475–2509.CrossRefGoogle Scholar
Kammeyer, H., ‘Profinite commensurability of $S$ -arithmetic groups’, Acta Arith., to appear (2018).Google Scholar
Kammeyer, H., Introduction to ${\ell}^2$ -invariants, Lecture Notes in Mathematics, vol. 2247 (Springer, Cham, 2019).CrossRefGoogle Scholar
Kammeyer, H. and Sauer, R., ‘ $S$ -arithmetic spinor groups with the same finite quotients and distinct ${\ell}^2$ -cohomology’, Groups Geom. Dyn., to appear (2018).Google Scholar
Kionke, S., ‘Lefschetz numbers of involutions on arithmetic subgroups of inner forms of the special linear group’, PhD thesis, Universität Wien (2012).Google Scholar
Kionke, S., ‘Lefschetz numbers of symplectic involutions on arithmetic groups’, Pacific J. Math. 271(2) (2014), 369–414.CrossRefGoogle Scholar
Kionke, S., ‘On lower bounds for cohomology growth in p-adic analytic towers’, Math. Z. 277 (2014), 709–723.CrossRefGoogle Scholar
Knapp, A. W., Lie Groups Beyond an Introduction , 2nd ed, Progress in Mathematics, vol. 140 (Birkhäuser, Boston, 2002).Google Scholar
Kneser, M., ‘Normalteiler ganzzahliger Spingruppen’, J. Reine Angew. Math. 311/312 (1979), 191–214.Google Scholar
Knus, M.-A., Quadratic and Hermitian forms over rings , Grundlehren der Mathematischen Wissenschaften, vol. 294 (Springer-Verlag, Berlin, 1991), with a foreword by Bertuccioni, I..Google Scholar
Knus, M.-A., Merkurjev, A., Rost, M., and Tignol, J.-P., The Book of Involutions, American Mathematical Society Colloquium Publications, vol. 44 (American Mathematical Society, Providence, RI, 1998), with a preface in French by Tits, J..Google Scholar
Kottwitz, R. E., ‘Tamagawa numbers’, Ann. of Math. (2) 127(3) (1988) 629–646.CrossRefGoogle Scholar
Lubotzky, A. and Segal, D., Subgroup Growth, Progress in Mathematics , vol. 22 (Birkhäuser Verlag, Basel, 2003).CrossRefGoogle Scholar
Lück, W., ${L}^2$ -Invariants: Theory and Applications to Geometry and $K$ -Theory, Results in Mathematics and Related Areas (3) (Springer-Verlag, Berlin, 2002).Google Scholar
Lück, W., Sauer, R., and Wegner, C., ‘ ${L}^2$ -torsion, the measure-theoretic determinant conjecture, and uniform measure equivalence’, J. Topol. Anal. 2(2) (2010), 145–171.CrossRefGoogle Scholar
Margulis, G. A., Discrete Subgroups of Semisimple Lie Groups , Results in Mathematics and Related Areas (3), vol. 17 (Springer-Verlag, Berlin, 1991).Google Scholar
Milne, J. S., Algebraic Groups, Cambridge Studies in Advanced Mathematics , vol. 170 (Cambridge University Press, Cambridge, 2017).CrossRefGoogle Scholar
Minasyan, A. and Zalesskii, P., ‘Virtually compact special hyperbolic groups are conjugacy separable’, Comment. Math. Helv. 91(4) (2016) 609–627.CrossRefGoogle Scholar
Neukirch, J., Algebraic Number Theory, Grundlehren der Mathematischen Wissenschaften , vol. 322 (Springer-Verlag, Berlin, 1999).Google Scholar
Olbrich, M., ‘ ${L}^2$ -invariants of locally symmetric spaces’, Doc. Math. 7 (2002), 219–237.Google Scholar
Platonov, V. and Rapinchuk, A., Algebraic Groups and Number Theory, Pure and Applied Mathematics , vol. 139 (Academic Press, Inc., Boston, 1994).Google Scholar
Raghunathan, M. S., ‘The congruence subgroup problem’, Proc. Indian Acad. Sci. Math. Sci. 114(4), 299–308, 2004.CrossRefGoogle Scholar
Rapinchuk, A., ‘The congruence subgroup problem for algebraic groups’, in: Topics in Algebra, Part 2 (Warsaw, 1988), vol. 26 (PWN, Warsaw, 1990), 399–410.Google Scholar
Rapinchuk, A. S., Segev, Y., and Seitz, G. M., ‘Finite quotients of the multiplicative group of a finite dimensional division algebra are solvable’, J. Amer. Math. Soc. 15(4) (2002), 929–978.CrossRefGoogle Scholar
Ribes, L. and Zalesskii, P., Profinite Groups, Results in Mathematics and Related Areas (3) , vol. 40, 2nd ed. (Springer-Verlag, Berlin, 2010).Google Scholar
Rohlfs, J. and Speh, B., ‘Automorphic representations and Lefschetz numbers’, Ann. Sci. Éc. Norm. Supér. 22(3) (1989), 473–499.CrossRefGoogle Scholar
Scharlau, W., Quadratic and Hermitian Forms, Grundlehren der math. Wiss. 270 (Springer-Verlag, Berlin, 1985).CrossRefGoogle Scholar
Serre, J.-P., ‘Cohomologie des groupes discrets’, Ann. of Math. Studies 70 (1971), 77–169.Google Scholar
Serre, J.-P., ‘Groupes de congruence’ (Bass, d’après H., Matsumoto, H., Mennicke, J, Milnor, J., Moore, C.) in: Séminaire Bourbaki, vol. 10 (Soc. Math. France, Paris, 1995), Exp. No. 330, 275–291.Google Scholar
Stover, M., ‘Lattices in $\mathrm{PU}\left(n,1\right)$ that are not profinitely rigid’, Proc. Amer. Math. Soc. 147(12) (2019), 5055–5062.CrossRefGoogle Scholar