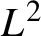1. Introduction and main results
It is a major open problem to classify knots in 3-space modulo concordance. Our understanding is far from complete, for both topological and smooth knot concordance groups. The sophistication of the smooth case beyond topological concordance is measured by the smooth concordance group of topologically slice knots, which has been actively investigated using modern smooth techniques.
In the study of knot concordance, the notion of primary decomposition first appeared in Jerome Levine’s foundational work [Reference Levine35, Reference Levine34]. Briefly, he constructed an algebraic concordance group of Seifert matrices and proved that it is isomorphic to the knot concordance group in high odd dimensions, whereas it gives algebraic invariants in the classical dimension [Reference Levine35]. He proved that a rational coefficient version of the algebraic concordance group decomposes into a direct sum of certain ‘primary parts’ indexed by irreducible factors of Alexander polynomials. This plays a crucial role in his well-known classification result that the algebraic concordance group and high odd-dimensional knot concordance groups are isomorphic to
![]() $\mathbb {Z}^{\infty }\oplus (\mathbb {Z}_2)^{\infty } \oplus (\mathbb {Z}_4)^{\infty }$
[Reference Levine34].
$\mathbb {Z}^{\infty }\oplus (\mathbb {Z}_2)^{\infty } \oplus (\mathbb {Z}_4)^{\infty }$
[Reference Levine34].
For the low-dimensional case, it is natural to ask whether the classical knot concordance groups and related objects admit analogous primary decomposition and to study the structures via primary parts. In an appendix, we formulate a general notion of primary decomposition, which specialises to several specific cases including concordance and rational homology cobordism, and discuss related questions. We hope this is useful for future study as well. The appendix also discusses known earlier results from the viewpoint of the general formulation. In particular, for topological knot concordance, there were remarkable results related to primary decomposition [Reference Livingston36, Reference Kim28, Reference Kim and Kim29, Reference Cochran, Harvey and Leidy14, Reference Cochran, Harvey and Leidy13, Reference Kim and Kim30].
In this article, we begin a detailed study of the smooth concordance group of topologically slice knots
![]() ${\mathcal T}$
, via primary decomposition. Precise statements of our results are given in Subsections 1.1 and 1.2. Briefly, the conjectural primary decompositions (see Question 1.1) are direct sum decompositions, along irreducible factors of Alexander polynomials, of the quotient
${\mathcal T}$
, via primary decomposition. Precise statements of our results are given in Subsections 1.1 and 1.2. Briefly, the conjectural primary decompositions (see Question 1.1) are direct sum decompositions, along irreducible factors of Alexander polynomials, of the quotient
![]() ${\mathcal T}/\Delta $
where
${\mathcal T}/\Delta $
where
![]() $\Delta $
is the subgroup generated by knots with unit Alexander polynomials. (Taking the quotient by
$\Delta $
is the subgroup generated by knots with unit Alexander polynomials. (Taking the quotient by
![]() $\Delta $
is along the same lines of ignoring units for factorisations in a ring.) We show that the conjectures hold for a large subgroup of
$\Delta $
is along the same lines of ignoring units for factorisations in a ring.) We show that the conjectures hold for a large subgroup of
![]() ${\mathcal T}$
and that there are infinitely many primary parts, each of which has infinite rank (see Theorems A and B). This provides evidence supporting primary decomposition conjectures and reveals a rich structure in
${\mathcal T}$
and that there are infinitely many primary parts, each of which has infinite rank (see Theorems A and B). This provides evidence supporting primary decomposition conjectures and reveals a rich structure in
![]() ${\mathcal T}/\Delta $
, generalising a result of Hedden, Livingston and Ruberman [Reference Hedden, Livingston and Ruberman25] that
${\mathcal T}/\Delta $
, generalising a result of Hedden, Livingston and Ruberman [Reference Hedden, Livingston and Ruberman25] that
![]() ${\mathcal T}/\Delta $
has infinite rank.
${\mathcal T}/\Delta $
has infinite rank.
In proving this, the essential challenge is to find irreducible polynomials
![]() $\lambda (t)$
and topologically slice knots (whose nontrivial linear combinations are) not concordant to any knot whose Alexander polynomial is relatively prime to
$\lambda (t)$
and topologically slice knots (whose nontrivial linear combinations are) not concordant to any knot whose Alexander polynomial is relatively prime to
![]() $\lambda (t)$
. It appears to be hard, if possible at all, to do this using known smooth invariants such as those from gauge theory, Heegaard Floer homology and Khovanov homology. Our proof combines amenable
$\lambda (t)$
. It appears to be hard, if possible at all, to do this using known smooth invariants such as those from gauge theory, Heegaard Floer homology and Khovanov homology. Our proof combines amenable
![]() $L^2$
-signatures, which are key ingredients of recent studies of topological concordance, with smooth information from Heegaard Floer homology of infinitely many branched covers of a knot. It seems intriguing to study whether more recent smooth invariants are useful in understanding primary decomposition, motivated from the results and approaches of this article.
$L^2$
-signatures, which are key ingredients of recent studies of topological concordance, with smooth information from Heegaard Floer homology of infinitely many branched covers of a knot. It seems intriguing to study whether more recent smooth invariants are useful in understanding primary decomposition, motivated from the results and approaches of this article.
We also prove results that support primary decomposition conjectures for the bipolar filtration of topologically slice knots (see Theorems C and D).
1.1. Primary decomposition for topologically slice knots
In what follows, we state primary decomposition conjectures and main results for
![]() ${\mathcal T}$
.
${\mathcal T}$
.
For a knot K in
![]() $S^3$
, denote the Alexander polynomial by
$S^3$
, denote the Alexander polynomial by
![]() $\Delta _K$
and regard it as an element in the Laurent polynomial ring
$\Delta _K$
and regard it as an element in the Laurent polynomial ring
![]() $\mathbb {Q}[t^{\pm 1}]$
. Then
$\mathbb {Q}[t^{\pm 1}]$
. Then
![]() $\Delta _K$
is well defined up to associates. Recall that
$\Delta _K$
is well defined up to associates. Recall that
![]() $\lambda $
and
$\lambda $
and
![]() $\mu \in \mathbb {Q}[t^{\pm 1}]$
are associates if
$\mu \in \mathbb {Q}[t^{\pm 1}]$
are associates if
![]() $\lambda = at^k \mu $
for some
$\lambda = at^k \mu $
for some
![]() $a\in \mathbb {Q}\smallsetminus \{0\}$
and
$a\in \mathbb {Q}\smallsetminus \{0\}$
and
![]() $k\in \mathbb {Z}$
. The standard involution on
$k\in \mathbb {Z}$
. The standard involution on
![]() $\mathbb {Q}[t^{\pm 1}]$
is defined by
$\mathbb {Q}[t^{\pm 1}]$
is defined by
![]() $\bigl (\sum a_i t^i\bigr )^* = \sum a_i t^{-i}$
. We say that
$\bigl (\sum a_i t^i\bigr )^* = \sum a_i t^{-i}$
. We say that
![]() $\lambda $
and
$\lambda $
and
![]() $\mu \in \mathbb {Q}[t^{\pm 1}]$
are
$\mu \in \mathbb {Q}[t^{\pm 1}]$
are
![]() $*$
-associates if
$*$
-associates if
![]() $\lambda $
is an associate of either
$\lambda $
is an associate of either
![]() $\mu $
or
$\mu $
or
![]() $\mu ^*$
.
$\mu ^*$
.
Denote the smooth concordance class of a knot K by
![]() $[K]$
. Recall that
$[K]$
. Recall that
![]() $\Delta = \{[K] \in {\mathcal T} \mid \Delta _K$
is trivial
$\Delta = \{[K] \in {\mathcal T} \mid \Delta _K$
is trivial
![]() $\}$
. For an irreducible
$\}$
. For an irreducible
![]() $\lambda $
in
$\lambda $
in
![]() $\mathbb {Q}[t^{\pm 1}]$
, let
$\mathbb {Q}[t^{\pm 1}]$
, let
 $$ \begin{align*} {\mathcal T}_{\lambda} &=\{[K] \in {\mathcal T} \mid \Delta_K \text{ is an associate of } (\lambda\lambda^*)^k\text{ for some }k\ge 0\}, \\ {\mathcal T}^{\kern3pt\lambda} &= \{[K] \in {\mathcal T} \mid \Delta_K \text{ is relatively prime to }\lambda\}. \end{align*} $$
$$ \begin{align*} {\mathcal T}_{\lambda} &=\{[K] \in {\mathcal T} \mid \Delta_K \text{ is an associate of } (\lambda\lambda^*)^k\text{ for some }k\ge 0\}, \\ {\mathcal T}^{\kern3pt\lambda} &= \{[K] \in {\mathcal T} \mid \Delta_K \text{ is relatively prime to }\lambda\}. \end{align*} $$
We remark that the product
![]() $\lambda \lambda ^*$
in the definition of
$\lambda \lambda ^*$
in the definition of
![]() ${\mathcal T}_{\lambda }$
reflects the Fox-Milnor condition that
${\mathcal T}_{\lambda }$
reflects the Fox-Milnor condition that
![]() $\Delta _K$
is an associate of
$\Delta _K$
is an associate of
![]() $ff^*$
for some
$ff^*$
for some
![]() $f\in \mathbb {Q}[t^{\pm 1}]$
when K is topologically slice. Note that
$f\in \mathbb {Q}[t^{\pm 1}]$
when K is topologically slice. Note that
![]() ${\mathcal T}_{\lambda }$
and
${\mathcal T}_{\lambda }$
and
![]() ${\mathcal T}^{\kern3pt\lambda }$
are subgroups containing
${\mathcal T}^{\kern3pt\lambda }$
are subgroups containing
![]() $\Delta $
for every irreducible
$\Delta $
for every irreducible
![]() $\lambda $
. Also,
$\lambda $
. Also,
![]() ${\mathcal T}_{\lambda }={\mathcal T}_{\mu }$
and
${\mathcal T}_{\lambda }={\mathcal T}_{\mu }$
and
![]() ${\mathcal T}^{\kern3pt\lambda }={\mathcal T}^{\kern3pt\mu }$
if
${\mathcal T}^{\kern3pt\lambda }={\mathcal T}^{\kern3pt\mu }$
if
![]() $\lambda $
and
$\lambda $
and
![]() $\mu $
are
$\mu $
are
![]() $*$
-associates.
$*$
-associates.
Primary decomposition for topologically slice knots concerns natural homomorphisms
 $$ \begin{align*} \Phi_L\colon \bigoplus_{[\lambda]} {\mathcal T}_{\lambda}/\Delta {\longrightarrow} {\mathcal T}/\Delta \quad\text{and}\quad \Phi_R\colon {\mathcal T}/\Delta {\longrightarrow} \bigoplus_{[\lambda]} {\mathcal T}/{\mathcal T}^{\kern3pt\lambda}. \end{align*} $$
$$ \begin{align*} \Phi_L\colon \bigoplus_{[\lambda]} {\mathcal T}_{\lambda}/\Delta {\longrightarrow} {\mathcal T}/\Delta \quad\text{and}\quad \Phi_R\colon {\mathcal T}/\Delta {\longrightarrow} \bigoplus_{[\lambda]} {\mathcal T}/{\mathcal T}^{\kern3pt\lambda}. \end{align*} $$
Here the index
![]() $[\lambda ]$
of the direct sums varies over the
$[\lambda ]$
of the direct sums varies over the
![]() $*$
-associate classes of irreducibles
$*$
-associate classes of irreducibles
![]() $\lambda $
that arise as the factor of an Alexander polynomial of a knot. The homomorphism
$\lambda $
that arise as the factor of an Alexander polynomial of a knot. The homomorphism
![]() $\Phi _L$
is defined to be the sum of the inclusions
$\Phi _L$
is defined to be the sum of the inclusions
![]() ${\mathcal T}_{\lambda }/\Delta \hookrightarrow {\mathcal T}/\Delta $
. Because
${\mathcal T}_{\lambda }/\Delta \hookrightarrow {\mathcal T}/\Delta $
. Because
![]() $\Delta _K$
is a product of finitely many irreducibles, the quotient epimorphisms
$\Delta _K$
is a product of finitely many irreducibles, the quotient epimorphisms
![]() ${\mathcal T}/\Delta \twoheadrightarrow {\mathcal T}/{\mathcal T}^{\kern3pt\lambda }$
induce a homomorphism into the direct sum, which is our
${\mathcal T}/\Delta \twoheadrightarrow {\mathcal T}/{\mathcal T}^{\kern3pt\lambda }$
induce a homomorphism into the direct sum, which is our
![]() $\Phi _R$
above. This formulation is influenced by earlier work in the literature, particularly Levine [Reference Levine35, Reference Levine34] and Cochran, Harvey and Leidy [Reference Cochran, Harvey and Leidy14, Reference Cochran, Harvey and Leidy13].
$\Phi _R$
above. This formulation is influenced by earlier work in the literature, particularly Levine [Reference Levine35, Reference Levine34] and Cochran, Harvey and Leidy [Reference Cochran, Harvey and Leidy14, Reference Cochran, Harvey and Leidy13].
An informal remark. One might regard elements in
![]() ${\mathcal T}_{\lambda }/\Delta \subset {\mathcal T}/\Delta $
as ‘
${\mathcal T}_{\lambda }/\Delta \subset {\mathcal T}/\Delta $
as ‘
![]() $\lambda $
-primary’ and
$\lambda $
-primary’ and
![]() ${\mathcal T}/\Delta \to {\mathcal T}/{\mathcal T}^{\kern3pt\lambda }$
as ‘forgetting those coprime to
${\mathcal T}/\Delta \to {\mathcal T}/{\mathcal T}^{\kern3pt\lambda }$
as ‘forgetting those coprime to
![]() $\lambda $
’ or ‘extracting the
$\lambda $
’ or ‘extracting the
![]() $\lambda $
-primary component’ of an element. Then, the surjectivity of
$\lambda $
-primary component’ of an element. Then, the surjectivity of
![]() $\Phi _L$
means the existence of a ‘decomposition into a sum of primary elements’, and the injectivity of
$\Phi _L$
means the existence of a ‘decomposition into a sum of primary elements’, and the injectivity of
![]() $\Phi _L$
means the uniqueness of such a decomposition. Also, the injectivity of
$\Phi _L$
means the uniqueness of such a decomposition. Also, the injectivity of
![]() $\Phi _R$
means that ‘primary components determine an element uniquely’, and the surjectivity of
$\Phi _R$
means that ‘primary components determine an element uniquely’, and the surjectivity of
![]() $\Phi _R$
means that ‘every combination of primary components is realisable’.
$\Phi _R$
means that ‘every combination of primary components is realisable’.
Question 1.1 Primary decomposition for topologically slice knots
-
(1) Left primary decomposability: is
 $\Phi _L$
an isomorphism?
$\Phi _L$
an isomorphism? -
(2) Right primary decomposability: is
 $\Phi _R$
an isomorphism?
$\Phi _R$
an isomorphism?
More generally (if they are not isomorphisms), what are their kernel and cokernel?
We conjecture an affirmative answer to (2) and that
![]() $\Phi _L$
is injective at the least. In any case, it appears to be interesting to study
$\Phi _L$
is injective at the least. In any case, it appears to be interesting to study
![]() ${\mathcal T}_{\lambda }/\Delta $
and
${\mathcal T}_{\lambda }/\Delta $
and
![]() ${\mathcal T}/{\mathcal T}^{\kern3pt\lambda }$
, which we call left and right primary parts (or primary factors). This leads us particularly to the following.
${\mathcal T}/{\mathcal T}^{\kern3pt\lambda }$
, which we call left and right primary parts (or primary factors). This leads us particularly to the following.
-
(3) Nontriviality of primary parts: are
 ${\mathcal T}_{\lambda }/\Delta $
and
${\mathcal T}_{\lambda }/\Delta $
and
 ${\mathcal T}/{\mathcal T}^{\kern3pt\lambda }$
nonzero for each irreducible
${\mathcal T}/{\mathcal T}^{\kern3pt\lambda }$
nonzero for each irreducible
 $\lambda $
that arises as the factor of an Alexander polynomial of a knot?
$\lambda $
that arises as the factor of an Alexander polynomial of a knot?
More generally (if they are nontrivial), what are the isomorphism types of the primary parts
![]() ${\mathcal T}_{\lambda }/\Delta $
and
${\mathcal T}_{\lambda }/\Delta $
and
![]() ${\mathcal T}/{\mathcal T}^{\kern3pt\lambda }$
?
${\mathcal T}/{\mathcal T}^{\kern3pt\lambda }$
?
-
(4) Relationship of left and right primary parts: is the composition
an isomorphism? $$ \begin{align*} {\mathcal T}_{\lambda}/\Delta \hookrightarrow {\mathcal T}/\Delta \twoheadrightarrow {\mathcal T}/{\mathcal T}^{\kern3pt\lambda} \end{align*} $$
$$ \begin{align*} {\mathcal T}_{\lambda}/\Delta \hookrightarrow {\mathcal T}/\Delta \twoheadrightarrow {\mathcal T}/{\mathcal T}^{\kern3pt\lambda} \end{align*} $$
We remark that Definition A.1 in the appendix generalises the notion of left and right primary decomposition to a broader context. Also, regarding the relationship of Question 1.1(1) and (2), see Lemma A.4 in the appendix.
The first main result of this article, which is given as Theorem A, says that there is a large subgroup of
![]() ${\mathcal T}$
for which the answers to the above questions are affirmative and many primary parts of
${\mathcal T}$
for which the answers to the above questions are affirmative and many primary parts of
![]() ${\mathcal T}$
are highly nontrivial. To state the result, we use the following notation. For a subgroup
${\mathcal T}$
are highly nontrivial. To state the result, we use the following notation. For a subgroup
![]() ${\mathcal S}$
of
${\mathcal S}$
of
![]() ${\mathcal T}$
and an irreducible
${\mathcal T}$
and an irreducible
![]() $\lambda \in \mathbb {Q}[t^{\pm 1}]$
, let
$\lambda \in \mathbb {Q}[t^{\pm 1}]$
, let
![]() ${\mathcal S}_{\lambda }$
be the subgroup of
${\mathcal S}_{\lambda }$
be the subgroup of
![]() $[K]\in {\mathcal S}$
with
$[K]\in {\mathcal S}$
with
![]() $\Delta _K$
a power of
$\Delta _K$
a power of
![]() $\lambda \lambda ^*$
and
$\lambda \lambda ^*$
and
![]() ${\mathcal S}^{\lambda }$
be the subgroup of
${\mathcal S}^{\lambda }$
be the subgroup of
![]() $[K]\in {\mathcal S}$
with
$[K]\in {\mathcal S}$
with
![]() $\gcd (\Delta _K,\lambda )=1$
. That is,
$\gcd (\Delta _K,\lambda )=1$
. That is,
![]() ${\mathcal S}_{\lambda } = {\mathcal S}\cap {\mathcal T}_{\lambda }$
and
${\mathcal S}_{\lambda } = {\mathcal S}\cap {\mathcal T}_{\lambda }$
and
![]() ${\mathcal S}^{\lambda } = {\mathcal S}\cap {\mathcal T}^{\kern3pt\lambda }$
. Then one can ask Question 1.1 for
${\mathcal S}^{\lambda } = {\mathcal S}\cap {\mathcal T}^{\kern3pt\lambda }$
. Then one can ask Question 1.1 for
![]() ${\mathcal S}$
in place of
${\mathcal S}$
in place of
![]() ${\mathcal T}$
. Let
${\mathcal T}$
. Let
Note that
![]() $\Lambda $
is an infinite collection of pairwise non-
$\Lambda $
is an infinite collection of pairwise non-
![]() $*$
-associate irreducibles
$*$
-associate irreducibles
![]() $\lambda $
such that
$\lambda $
such that
![]() $\lambda \lambda ^*$
is an Alexander polynomial of a knot.
$\lambda \lambda ^*$
is an Alexander polynomial of a knot.
Theorem A. There is a subgroup
![]() ${\mathcal S}$
in
${\mathcal S}$
in
![]() ${\mathcal T}$
containing
${\mathcal T}$
containing
![]() $\Delta $
that satisfies the following:
$\Delta $
that satisfies the following:
-
(1) For every
 $\lambda \in \Lambda $
,
$\lambda \in \Lambda $
,
 ${\mathcal S}_{\lambda }/\Delta \cong \mathbb {Z}^{\infty }$
,
${\mathcal S}_{\lambda }/\Delta \cong \mathbb {Z}^{\infty }$
,
 ${\mathcal S}/{\mathcal S}^{\lambda } \cong \mathbb {Z}^{\infty }$
and the composition
${\mathcal S}/{\mathcal S}^{\lambda } \cong \mathbb {Z}^{\infty }$
and the composition
 ${\mathcal S}_{\lambda }/\Delta \hookrightarrow {\mathcal S}/\Delta \twoheadrightarrow {\mathcal S}/{\mathcal S}^{\lambda }$
is an isomorphism.
${\mathcal S}_{\lambda }/\Delta \hookrightarrow {\mathcal S}/\Delta \twoheadrightarrow {\mathcal S}/{\mathcal S}^{\lambda }$
is an isomorphism. -
(2) The inclusions
 ${\mathcal S}_{\lambda }/\Delta \to {\mathcal S}/\Delta $
induce an isomorphism
${\mathcal S}_{\lambda }/\Delta \to {\mathcal S}/\Delta $
induce an isomorphism
 $\bigoplus _{\lambda \in \Lambda } {\mathcal S}_{\lambda }/\Delta \to {\mathcal S}/\Delta $
.
$\bigoplus _{\lambda \in \Lambda } {\mathcal S}_{\lambda }/\Delta \to {\mathcal S}/\Delta $
. -
(3) The surjections
 ${\mathcal S}/\Delta \to {\mathcal S}/{\mathcal S}^{\lambda }$
induce an isomorphism
${\mathcal S}/\Delta \to {\mathcal S}/{\mathcal S}^{\lambda }$
induce an isomorphism
 ${\mathcal S}/\Delta \to \bigoplus _{\lambda \in \Lambda } {\mathcal S}/{\mathcal S}^{\lambda }$
.
${\mathcal S}/\Delta \to \bigoplus _{\lambda \in \Lambda } {\mathcal S}/{\mathcal S}^{\lambda }$
.

From Theorem A it follows that each of the primary parts
![]() ${\mathcal T}_{\lambda } /\Delta $
and
${\mathcal T}_{\lambda } /\Delta $
and
![]() ${\mathcal T}/{\mathcal T}^{\kern3pt\lambda }$
has a subgroup isomorphic to
${\mathcal T}/{\mathcal T}^{\kern3pt\lambda }$
has a subgroup isomorphic to
![]() $\mathbb {Z}^{\infty }$
for all
$\mathbb {Z}^{\infty }$
for all
![]() $\lambda \in \Lambda $
. An immediate consequence is the main result of [Reference Hedden, Livingston and Ruberman25] that
$\lambda \in \Lambda $
. An immediate consequence is the main result of [Reference Hedden, Livingston and Ruberman25] that
![]() ${\mathcal T}/\Delta $
has a subgroup isomorphic to
${\mathcal T}/\Delta $
has a subgroup isomorphic to
![]() $\mathbb {Z}^{\infty }$
.
$\mathbb {Z}^{\infty }$
.
Note that Theorem A(1) implies the following.
Theorem B. For each
![]() $\lambda \in \Lambda $
, there is an infinite collection of topologically slice knots
$\lambda \in \Lambda $
, there is an infinite collection of topologically slice knots
![]() $\{K_{\lambda ,i}\}_{i=1}^{\infty }$
with
$\{K_{\lambda ,i}\}_{i=1}^{\infty }$
with
![]() $\Delta _{K_{\lambda ,i}}$
a power of
$\Delta _{K_{\lambda ,i}}$
a power of
![]() $\lambda \lambda ^*$
, such that any nontrivial linear combination of the
$\lambda \lambda ^*$
, such that any nontrivial linear combination of the
![]() $K_{\lambda ,i}$
is not smoothly concordant to any knot J with
$K_{\lambda ,i}$
is not smoothly concordant to any knot J with
![]() $\Delta _J$
relatively prime to
$\Delta _J$
relatively prime to
![]() $\lambda $
.
$\lambda $
.
Indeed, Theorem B is equivalent to Theorem A, by an elementary formal argument.
Proof that Theorem B implies Theorem A. Suppose that Theorem B holds. Let
![]() ${\mathcal S}$
be the subgroup in
${\mathcal S}$
be the subgroup in
![]() ${\mathcal T}$
that is generated by
${\mathcal T}$
that is generated by
![]() $\Delta $
and the two-parameter family
$\Delta $
and the two-parameter family
![]() $\{K_{\lambda ,i}\}_{\lambda \in \Lambda , i\in {\mathbb N}}$
given by Theorem B.
$\{K_{\lambda ,i}\}_{\lambda \in \Lambda , i\in {\mathbb N}}$
given by Theorem B.
We claim that, for each
![]() $\lambda \in \Lambda $
,
$\lambda \in \Lambda $
,
![]() ${\mathcal S}_{\lambda }$
is equal to the subgroup generated by
${\mathcal S}_{\lambda }$
is equal to the subgroup generated by
![]() $\Delta $
and the one-parameter family
$\Delta $
and the one-parameter family
![]() $\{K_{\lambda ,i}\}_{i\in {\mathbb N}}$
. To see this, first observe that for irreducibles
$\{K_{\lambda ,i}\}_{i\in {\mathbb N}}$
. To see this, first observe that for irreducibles
![]() $\lambda $
and
$\lambda $
and
![]() $\mu $
that are not
$\mu $
that are not
![]() $*$
-associates,
$*$
-associates,
![]() ${\mathcal S}_{\lambda }\subset {\mathcal S}^{\mu }$
, and so the composition
${\mathcal S}_{\lambda }\subset {\mathcal S}^{\mu }$
, and so the composition
is zero. If a linear combination
![]() $[J] + \sum _{\mu } \sum _i r_{\mu ,i} [K_{\mu ,i}]$
(
$[J] + \sum _{\mu } \sum _i r_{\mu ,i} [K_{\mu ,i}]$
(
![]() $[J]\in \Delta $
,
$[J]\in \Delta $
,
![]() $r_{\mu ,i} \in \mathbb {Z}$
) lies in
$r_{\mu ,i} \in \mathbb {Z}$
) lies in
![]() ${\mathcal S}_{\lambda }$
, then for each
${\mathcal S}_{\lambda }$
, then for each
![]() $\mu \ne \lambda $
, the image of the linear combination in
$\mu \ne \lambda $
, the image of the linear combination in
![]() ${\mathcal S}/{\mathcal S}^{\mu }$
, which is represented by
${\mathcal S}/{\mathcal S}^{\mu }$
, which is represented by
![]() $\sum _{i} r_{\mu ,i} [K_{\mu ,i}]$
, should be zero by the observation. Therefore,
$\sum _{i} r_{\mu ,i} [K_{\mu ,i}]$
, should be zero by the observation. Therefore,
![]() $r_{\mu ,i}=0$
for all i and
$r_{\mu ,i}=0$
for all i and
![]() $\mu \ne \lambda $
, by the conclusion of Theorem B that the classes
$\mu \ne \lambda $
, by the conclusion of Theorem B that the classes
![]() $[K_{\mu ,i}]$
are linearly independent in
$[K_{\mu ,i}]$
are linearly independent in
![]() ${\mathcal S}/{\mathcal S}^{\mu }$
. This proves the claim.
${\mathcal S}/{\mathcal S}^{\mu }$
. This proves the claim.
Fix
![]() $\lambda \in \Lambda $
and temporarily denote by
$\lambda \in \Lambda $
and temporarily denote by
![]() $\mathbb {Z}^{\infty }$
the free abelian group generated by the collection
$\mathbb {Z}^{\infty }$
the free abelian group generated by the collection
![]() $\{K_{\lambda ,i}\}_i$
. The assignment
$\{K_{\lambda ,i}\}_i$
. The assignment
![]() $K_{\lambda ,i} \mapsto [K_{\lambda ,i}]$
gives rise to an epimorphism
$K_{\lambda ,i} \mapsto [K_{\lambda ,i}]$
gives rise to an epimorphism
![]() $\mathbb {Z}^{\infty } \twoheadrightarrow {\mathcal S}_{\lambda }/\Delta $
by the claim. Because
$\mathbb {Z}^{\infty } \twoheadrightarrow {\mathcal S}_{\lambda }/\Delta $
by the claim. Because
![]() ${\mathcal S}$
is generated by
${\mathcal S}$
is generated by
![]() $\{K_{\lambda ,i}\}_{\lambda ,i}$
and
$\{K_{\lambda ,i}\}_{\lambda ,i}$
and
![]() $[K_{\mu ,i}]=0$
in
$[K_{\mu ,i}]=0$
in
![]() ${\mathcal S}/{\mathcal S}^{\lambda }$
for
${\mathcal S}/{\mathcal S}^{\lambda }$
for
![]() $\mu \ne \lambda $
, the composition
$\mu \ne \lambda $
, the composition
is surjective. Moreover, by the linear independence of
![]() $[K_{\lambda ,i}]$
in
$[K_{\lambda ,i}]$
in
![]() ${\mathcal S}/{\mathcal S}^{\lambda }$
, (1.4) is an isomorphism. From this, it follows that both
${\mathcal S}/{\mathcal S}^{\lambda }$
, (1.4) is an isomorphism. From this, it follows that both
![]() $\mathbb {Z}^{\infty } \to {\mathcal S}_{\lambda }/\Delta $
and
$\mathbb {Z}^{\infty } \to {\mathcal S}_{\lambda }/\Delta $
and
![]() ${\mathcal S}_{\lambda }/\Delta \to {\mathcal S}/{\mathcal S}^{\lambda }$
are isomorphisms. This shows that Theorem A(1) holds.
${\mathcal S}_{\lambda }/\Delta \to {\mathcal S}/{\mathcal S}^{\lambda }$
are isomorphisms. This shows that Theorem A(1) holds.
Because (1.3) is zero for
![]() $\mu \ne \lambda \in \Lambda $
, the composition of two horizontal arrows on the top row of (1.2) is the direct sum of the isomorphisms
$\mu \ne \lambda \in \Lambda $
, the composition of two horizontal arrows on the top row of (1.2) is the direct sum of the isomorphisms
![]() ${\mathcal S}_{\lambda }/\Delta \to {\mathcal S}/{\mathcal S}^{\lambda }$
. So the top row composition in (1.2) is an isomorphism. Also, the first horizontal arrow in the top row is surjective by the definition of
${\mathcal S}_{\lambda }/\Delta \to {\mathcal S}/{\mathcal S}^{\lambda }$
. So the top row composition in (1.2) is an isomorphism. Also, the first horizontal arrow in the top row is surjective by the definition of
![]() ${\mathcal S}$
. From this, it follows that Theorem A(2) and (3) hold.
${\mathcal S}$
. From this, it follows that Theorem A(2) and (3) hold.
1.2. Primary decomposition for the bipolar filtration
The method of this article provides further information on the structure of
![]() ${\mathcal T}$
. To discuss this, we consider the bipolar filtration of
${\mathcal T}$
. To discuss this, we consider the bipolar filtration of
![]() ${\mathcal T}$
, which was defined by Cochran, Harvey and Horn [Reference Cochran, Harvey and Horn11]. It is a descending filtration
${\mathcal T}$
, which was defined by Cochran, Harvey and Horn [Reference Cochran, Harvey and Horn11]. It is a descending filtration
where the subgroup
![]() ${\mathcal T}_n$
consists of concordance classes of certain knots called n-bipolar (see Definition 2.1). It is known that various modern smooth invariants vanish for knots in the subgroups
${\mathcal T}_n$
consists of concordance classes of certain knots called n-bipolar (see Definition 2.1). It is known that various modern smooth invariants vanish for knots in the subgroups
![]() ${\mathcal T}_0$
and
${\mathcal T}_0$
and
![]() ${\mathcal T}_1$
, but the associated graded groups
${\mathcal T}_1$
, but the associated graded groups
![]() $\mathrm {gr}_n({\mathcal T}\kern3pt):={\mathcal T}_n/{\mathcal T}_{n+1}$
are nontrivial for all n [Reference Cochran, Harvey and Horn11, Reference Cha and Kim6]. Indeed, the abelian group
$\mathrm {gr}_n({\mathcal T}\kern3pt):={\mathcal T}_n/{\mathcal T}_{n+1}$
are nontrivial for all n [Reference Cochran, Harvey and Horn11, Reference Cha and Kim6]. Indeed, the abelian group
![]() $\mathrm {gr}_n({\mathcal T}\kern3pt)$
is known to have infinite rank for
$\mathrm {gr}_n({\mathcal T}\kern3pt)$
is known to have infinite rank for
![]() $n=0$
[Reference Cochran and Horn15] and for all
$n=0$
[Reference Cochran and Horn15] and for all
![]() $n\ge 2$
[Reference Cha and Kim6].
$n\ge 2$
[Reference Cha and Kim6].
As an attempt to understand the structure of the filtration, we formulate and study the primary decomposition of
![]() $\mathrm {gr}_n({\mathcal T}\kern3pt)$
. For an n-bipolar knot K, denote its class in
$\mathrm {gr}_n({\mathcal T}\kern3pt)$
. For an n-bipolar knot K, denote its class in
![]() $\mathrm {gr}_n({\mathcal T}\kern3pt)$
by
$\mathrm {gr}_n({\mathcal T}\kern3pt)$
by
![]() $[K]$
. Similar to the case of
$[K]$
. Similar to the case of
![]() ${\mathcal T}$
, for an irreducible element
${\mathcal T}$
, for an irreducible element
![]() $\lambda $
in
$\lambda $
in
![]() $\mathbb {Q}[t^{\pm 1}]$
, consider the following subgroups of
$\mathbb {Q}[t^{\pm 1}]$
, consider the following subgroups of
![]() $\mathrm {gr}_n({\mathcal T}\kern3pt)$
:
$\mathrm {gr}_n({\mathcal T}\kern3pt)$
:
 $$ \begin{align*} \mathrm{gr}_n({\mathcal T}\kern3pt)_{\lambda} &:=\{[K] \in \mathrm{gr}_n({\mathcal T}\kern3pt) \mid \Delta_K = (\lambda\lambda^*)^k \text{ for some } k \ge 0\}, \\ \mathrm{gr}_n({\mathcal T}\kern3pt)^{\lambda} &:= \{[K] \in \mathrm{gr}_n({\mathcal T}\kern3pt) \mid \Delta_K \text{ is relatively prime to }\lambda\}. \end{align*} $$
$$ \begin{align*} \mathrm{gr}_n({\mathcal T}\kern3pt)_{\lambda} &:=\{[K] \in \mathrm{gr}_n({\mathcal T}\kern3pt) \mid \Delta_K = (\lambda\lambda^*)^k \text{ for some } k \ge 0\}, \\ \mathrm{gr}_n({\mathcal T}\kern3pt)^{\lambda} &:= \{[K] \in \mathrm{gr}_n({\mathcal T}\kern3pt) \mid \Delta_K \text{ is relatively prime to }\lambda\}. \end{align*} $$
Also, let
![]() $\mathrm {gr}_n(\Delta ) =\{[K] \in \mathrm {gr}_n({\mathcal T}\kern3pt) \mid \Delta _K\ \text{is trivial}\}$
. The injections
$\mathrm {gr}_n(\Delta ) =\{[K] \in \mathrm {gr}_n({\mathcal T}\kern3pt) \mid \Delta _K\ \text{is trivial}\}$
. The injections
![]() $\mathrm {gr}_n({\mathcal T}\kern3pt)_{\lambda }/\mathrm {gr}_n(\Delta ) \hookrightarrow \mathrm {gr}_n({\mathcal T}\kern3pt)/\mathrm {gr}_n(\Delta )$
and the surjections
$\mathrm {gr}_n({\mathcal T}\kern3pt)_{\lambda }/\mathrm {gr}_n(\Delta ) \hookrightarrow \mathrm {gr}_n({\mathcal T}\kern3pt)/\mathrm {gr}_n(\Delta )$
and the surjections
![]() $\mathrm {gr}_n({\mathcal T}\kern3pt)/\mathrm {gr}_n(\Delta ) \twoheadrightarrow \mathrm {gr}_n({\mathcal T}\kern3pt)/\mathrm {gr}_n({\mathcal T}\kern3pt)^{\lambda }$
induce homomorphisms
$\mathrm {gr}_n({\mathcal T}\kern3pt)/\mathrm {gr}_n(\Delta ) \twoheadrightarrow \mathrm {gr}_n({\mathcal T}\kern3pt)/\mathrm {gr}_n({\mathcal T}\kern3pt)^{\lambda }$
induce homomorphisms
 $$ \begin{align*} \Phi^n_L\colon & \bigoplus\nolimits_{[\lambda]} \mathrm{gr}_n({\mathcal T}\kern3pt)_{\lambda}/\mathrm{gr}_n(\Delta) \longrightarrow \mathrm{gr}_n({\mathcal T}\kern3pt)/\mathrm{gr}_n(\Delta), \\ \Phi^n_R\colon & \mathrm{gr}_n({\mathcal T}\kern3pt)/\mathrm{gr}_n(\Delta) \longrightarrow \bigoplus\nolimits_{[\lambda]} \mathrm{gr}_n({\mathcal T}\kern3pt)/\mathrm{gr}_n({\mathcal T}\kern3pt)^{\lambda}. \end{align*} $$
$$ \begin{align*} \Phi^n_L\colon & \bigoplus\nolimits_{[\lambda]} \mathrm{gr}_n({\mathcal T}\kern3pt)_{\lambda}/\mathrm{gr}_n(\Delta) \longrightarrow \mathrm{gr}_n({\mathcal T}\kern3pt)/\mathrm{gr}_n(\Delta), \\ \Phi^n_R\colon & \mathrm{gr}_n({\mathcal T}\kern3pt)/\mathrm{gr}_n(\Delta) \longrightarrow \bigoplus\nolimits_{[\lambda]} \mathrm{gr}_n({\mathcal T}\kern3pt)/\mathrm{gr}_n({\mathcal T}\kern3pt)^{\lambda}. \end{align*} $$
The following is an analogue of Question 1.1.
Question 1.2 Primary decomposition for the associated graded
-
(1) Is
 $\Phi ^n_L$
an isomorphism?
$\Phi ^n_L$
an isomorphism? -
(2) Is
 $\Phi ^n_R$
an isomorphism?
$\Phi ^n_R$
an isomorphism? -
(3) Are
 $\mathrm {gr}_n({\mathcal T}\kern3pt)_{\lambda }/\mathrm {gr}_n(\Delta )$
and
$\mathrm {gr}_n({\mathcal T}\kern3pt)_{\lambda }/\mathrm {gr}_n(\Delta )$
and
 $\mathrm {gr}_n({\mathcal T}\kern3pt)/\mathrm {gr}_n({\mathcal T}\kern3pt)^{\lambda }$
nontrivial for every irreducible
$\mathrm {gr}_n({\mathcal T}\kern3pt)/\mathrm {gr}_n({\mathcal T}\kern3pt)^{\lambda }$
nontrivial for every irreducible
 $\lambda $
that arises as a factor of an Alexander polynomial of a knot?
$\lambda $
that arises as a factor of an Alexander polynomial of a knot? -
(4) Is the following composition an isomorphism?
 $$ \begin{align*} \mathrm{gr}_n({\mathcal T}\kern3pt)_{\lambda}/\mathrm{gr}_n(\Delta) \hookrightarrow \mathrm{gr}_n({\mathcal T}\kern3pt)/\mathrm{gr}_n(\Delta) \twoheadrightarrow \mathrm{gr}_n({\mathcal T}\kern3pt)/\mathrm{gr}_n({\mathcal T}\kern3pt)^{\lambda}. \end{align*} $$
$$ \begin{align*} \mathrm{gr}_n({\mathcal T}\kern3pt)_{\lambda}/\mathrm{gr}_n(\Delta) \hookrightarrow \mathrm{gr}_n({\mathcal T}\kern3pt)/\mathrm{gr}_n(\Delta) \twoheadrightarrow \mathrm{gr}_n({\mathcal T}\kern3pt)/\mathrm{gr}_n({\mathcal T}\kern3pt)^{\lambda}. \end{align*} $$
The following result supports affirmative answers. Similar to the case of
![]() ${\mathcal T}$
, for a subgroup
${\mathcal T}$
, for a subgroup
![]() ${\mathcal S}$
in
${\mathcal S}$
in
![]() $\mathrm {gr}_n({\mathcal T}\kern3pt)$
, let
$\mathrm {gr}_n({\mathcal T}\kern3pt)$
, let
![]() ${\mathcal S}_{\lambda }={\mathcal S}\cap \mathrm {gr}_n({\mathcal T}\kern3pt)_{\lambda }$
and
${\mathcal S}_{\lambda }={\mathcal S}\cap \mathrm {gr}_n({\mathcal T}\kern3pt)_{\lambda }$
and
![]() ${\mathcal S}^{\lambda }={\mathcal S}\cap \mathrm {gr}_n({\mathcal T}\kern3pt)^{\lambda }$
. Recall that the collection
${\mathcal S}^{\lambda }={\mathcal S}\cap \mathrm {gr}_n({\mathcal T}\kern3pt)^{\lambda }$
. Recall that the collection
![]() $\Lambda $
has been defined in (1.1) above.
$\Lambda $
has been defined in (1.1) above.
Theorem C. Let
![]() $n\ge 2$
. Then there is a subgroup
$n\ge 2$
. Then there is a subgroup
![]() ${\mathcal S}$
in
${\mathcal S}$
in
![]() $\mathrm {gr}_n({\mathcal T}\kern3pt)$
that contains
$\mathrm {gr}_n({\mathcal T}\kern3pt)$
that contains
![]() $\mathrm {gr}_n(\Delta )$
such that
$\mathrm {gr}_n(\Delta )$
such that
 $$ \begin{align*} \bigoplus_{\lambda\in\Lambda} {\mathcal S}_{\lambda}/\mathrm{gr}_n(\Delta) \xrightarrow{\cong} {\mathcal S}/\mathrm{gr}_n(\Delta) \xrightarrow{\cong} \bigoplus_{\lambda\in\Lambda} {\mathcal S} / {\mathcal S}^{\lambda} \end{align*} $$
$$ \begin{align*} \bigoplus_{\lambda\in\Lambda} {\mathcal S}_{\lambda}/\mathrm{gr}_n(\Delta) \xrightarrow{\cong} {\mathcal S}/\mathrm{gr}_n(\Delta) \xrightarrow{\cong} \bigoplus_{\lambda\in\Lambda} {\mathcal S} / {\mathcal S}^{\lambda} \end{align*} $$
and
![]() ${\mathcal S}_{\lambda }/\mathrm {gr}_n(\Delta ) \cong \mathbb {Z}^{\infty } \cong {\mathcal S} / {\mathcal S}^{\lambda }$
for every
${\mathcal S}_{\lambda }/\mathrm {gr}_n(\Delta ) \cong \mathbb {Z}^{\infty } \cong {\mathcal S} / {\mathcal S}^{\lambda }$
for every
![]() $\lambda \in \Lambda $
.
$\lambda \in \Lambda $
.
By the same argument as the proof that Theorem A is equivalent to Theorem B, it is seen that Theorem C is equivalent to the following statement.
Theorem D. Let
![]() $n\ge 2$
. Then for each
$n\ge 2$
. Then for each
![]() $\lambda \in \Lambda $
, there are infinitely many topologically slice n-bipolar knots
$\lambda \in \Lambda $
, there are infinitely many topologically slice n-bipolar knots
![]() $K_{\lambda ,i}$
(
$K_{\lambda ,i}$
(
![]() $i=1,2,\ldots $
) with
$i=1,2,\ldots $
) with
![]() $\Delta _{K_{\lambda ,i}}$
a power of
$\Delta _{K_{\lambda ,i}}$
a power of
![]() $\lambda \lambda ^*$
that are linearly independent in
$\lambda \lambda ^*$
that are linearly independent in
![]() $\mathrm {gr}_n({\mathcal T}\kern3pt)/\mathrm {gr}_n({\mathcal T}\kern3pt)^{\lambda }$
.
$\mathrm {gr}_n({\mathcal T}\kern3pt)/\mathrm {gr}_n({\mathcal T}\kern3pt)^{\lambda }$
.
Also, Theorem D implies Theorem B. Indeed, if a linear combination
![]() $\#_i\, a_i K_{\lambda ,i}$
of the knots
$\#_i\, a_i K_{\lambda ,i}$
of the knots
![]() $K_{\lambda ,i}$
in Theorem D is smoothly concordant to a knot L with
$K_{\lambda ,i}$
in Theorem D is smoothly concordant to a knot L with
![]() $\Delta _L$
relatively prime to
$\Delta _L$
relatively prime to
![]() $\lambda $
, then the class
$\lambda $
, then the class
![]() $[L]$
automatically lies in the subgroup
$[L]$
automatically lies in the subgroup
![]() ${\mathcal T}_n$
of
${\mathcal T}_n$
of
![]() ${\mathcal T}$
because so are
${\mathcal T}$
because so are
![]() $K_{\lambda ,i}$
, and thus
$K_{\lambda ,i}$
, and thus
![]() $[L]$
is zero in the quotient
$[L]$
is zero in the quotient
![]() $\mathrm {gr}_n({\mathcal T}\kern3pt)/\mathrm {gr}_n({\mathcal T}\kern3pt)^{\lambda }$
. It follows that
$\mathrm {gr}_n({\mathcal T}\kern3pt)/\mathrm {gr}_n({\mathcal T}\kern3pt)^{\lambda }$
. It follows that
![]() $a_i=0$
for all i, by Theorem D. Therefore, to obtain Theorems A, B and C, it suffices to prove Theorem D.
$a_i=0$
for all i, by Theorem D. Therefore, to obtain Theorems A, B and C, it suffices to prove Theorem D.
The remaining part of this article is organised as follows. Sections 2–4 are devoted to the proof of Theorem D. In the appendix, we discuss a general formulation of the notion of primary decomposition.
1.2.1. Ingredients of the proof
The proof of the above results uses (the ideas of) several results in the literature. To extract obstructions to smooth concordance, we combine the Cheeger-Gromov
![]() $L^2 \ \rho $
-invariants or, equivalently,
$L^2 \ \rho $
-invariants or, equivalently,
![]() $L^2$
-signature defects and the Ozsváth-Szabó d-invariant defined from Heegaard Floer homology, following the approach of [Reference Cha and Kim6], which was motivated by earlier work of Cochran, Harvey and Horn [Reference Cochran, Harvey and Horn11]. The amenable signature theorem developed in [Reference Cha and Orr8, Reference Cha3] and Ozsváth-Szabó’s d-invariant inequality for definite 4-manifolds [Reference Ozsváth and Szabó40] are among the key ingredients. We develop and use a localisation technique inspired by work of Cochran, Harvey and Leidy [Reference Cochran, Harvey and Leidy14, Reference Cochran, Harvey and Leidy13], to produce representations of the fundamental group to which our
$L^2$
-signature defects and the Ozsváth-Szabó d-invariant defined from Heegaard Floer homology, following the approach of [Reference Cha and Kim6], which was motivated by earlier work of Cochran, Harvey and Horn [Reference Cochran, Harvey and Horn11]. The amenable signature theorem developed in [Reference Cha and Orr8, Reference Cha3] and Ozsváth-Szabó’s d-invariant inequality for definite 4-manifolds [Reference Ozsváth and Szabó40] are among the key ingredients. We develop and use a localisation technique inspired by work of Cochran, Harvey and Leidy [Reference Cochran, Harvey and Leidy14, Reference Cochran, Harvey and Leidy13], to produce representations of the fundamental group to which our
![]() $\rho $
-invariants are associated. Also, to compute and estimate d-invariants of infinitely many branched covers of the infinitely many topologically slice knots in Theorems B and D, we use Némethi’s work [Reference Némethi38] on Heegaard Floer homology of negative definite plumbed 3-manifolds.
$\rho $
-invariants are associated. Also, to compute and estimate d-invariants of infinitely many branched covers of the infinitely many topologically slice knots in Theorems B and D, we use Némethi’s work [Reference Némethi38] on Heegaard Floer homology of negative definite plumbed 3-manifolds.
2. The first step of the proof of Theorem D
As a preliminary of the proof of Theorem D, we recall the definition of the bipolar filtration from [Reference Cochran, Harvey and Horn11]. Let
![]() $M(K)$
be the zero framed surgery manifold of a knot K in
$M(K)$
be the zero framed surgery manifold of a knot K in
![]() $S^3$
.
$S^3$
.
Definition 2.1 [Reference Cochran, Harvey and Horn11, Definition 5.1]
Let
![]() $n\ge 0$
be an integer. A compact connected 4-manifold V bounded by
$n\ge 0$
be an integer. A compact connected 4-manifold V bounded by
![]() $M(K)$
is an n-negaton if the following are satisfied:
$M(K)$
is an n-negaton if the following are satisfied:
-
(1) The inclusion induces an isomorphism on
 $H_1(M(K))\to H_1(V)$
, and a meridian of K normally generates
$H_1(M(K))\to H_1(V)$
, and a meridian of K normally generates
 $\pi _1(V)$
.
$\pi _1(V)$
. -
(2) There are disjointly embedded closed connected surfaces
 $S_i$
in V that form a basis for
$S_i$
in V that form a basis for
 $H_2(V)$
and have self-intersection
$H_2(V)$
and have self-intersection
 $-1$
or, equivalently, the normal bundle of
$-1$
or, equivalently, the normal bundle of
 $S_i$
has Euler class
$S_i$
has Euler class
 $-1$
.
$-1$
. -
(3) For each i, the image of
 $\pi _1(S_i)$
lies in the nth derived subgroup
$\pi _1(S_i)$
lies in the nth derived subgroup
 $\pi _1(V)^{(n)}$
.
$\pi _1(V)^{(n)}$
.
If there is an n-negaton bounded by
![]() $M(K)$
, then K is called n-negative. An n-positon and an n-positive knot are defined by replacing
$M(K)$
, then K is called n-negative. An n-positon and an n-positive knot are defined by replacing
![]() $-1$
by
$-1$
by
![]() $+1$
in condition (2) above. A knot K is n-bipolar if K is n-positive and n-negative.
$+1$
in condition (2) above. A knot K is n-bipolar if K is n-positive and n-negative.
Recall that
![]() ${\mathcal T}$
is the smooth concordance group of topologically slice knots. The bipolar filtration
${\mathcal T}$
is the smooth concordance group of topologically slice knots. The bipolar filtration
![]() $\{{\mathcal T}_n\}_{n\ge 0}$
of
$\{{\mathcal T}_n\}_{n\ge 0}$
of
![]() ${\mathcal T}$
is defined by
${\mathcal T}$
is defined by
Because an
![]() $(n+1)$
-bipolar knot is n-bipolar,
$(n+1)$
-bipolar knot is n-bipolar,
![]() $\{{\mathcal T}_n\}_{n\ge 0}$
is a descending filtration. It is an open problem whether
$\{{\mathcal T}_n\}_{n\ge 0}$
is a descending filtration. It is an open problem whether
![]() $\bigcap _{n\ge 0} {\mathcal T}_n=\{0\}$
.
$\bigcap _{n\ge 0} {\mathcal T}_n=\{0\}$
.
2.1. Construction of a family of knots
 $\{K_i\}$
$\{K_i\}$
We start the proof of Theorem D with a construction of knots that will be shown to generate the promised infinite rank free abelian subgroup.
Fix an integer
![]() $n\ge 2$
, as in Theorem D. Also, fix another integer
$n\ge 2$
, as in Theorem D. Also, fix another integer
![]() $m\ge 1$
. Several objects we will use below depend on
$m\ge 1$
. Several objects we will use below depend on
![]() $(n,m)$
, but we omit it from notation because
$(n,m)$
, but we omit it from notation because
![]() $(m,n)$
is fixed in our arguments. Let
$(m,n)$
is fixed in our arguments. Let
For each
![]() $(n,m)$
, we will construct an infinite family of knots
$(n,m)$
, we will construct an infinite family of knots
![]() $\{K_i\}$
indexed by integers
$\{K_i\}$
indexed by integers
![]() $i>0$
, whose Alexander polynomial is
$i>0$
, whose Alexander polynomial is
![]() $\lambda (t)\lambda (t^{-1})$
. The construction is similar to [Reference Cha and Kim6, Section 2.2]. (See also [Reference Cochran, Harvey and Horn11], which influenced the construction of [Reference Cha and Kim6] and ours.) Let
$\lambda (t)\lambda (t^{-1})$
. The construction is similar to [Reference Cha and Kim6, Section 2.2]. (See also [Reference Cochran, Harvey and Horn11], which influenced the construction of [Reference Cha and Kim6] and ours.) Let
![]() $R(J,D)$
be the knot shown in Figure 1. Here J and D are knots that will be specified later. (For now, ignore the circles
$R(J,D)$
be the knot shown in Figure 1. Here J and D are knots that will be specified later. (For now, ignore the circles
![]() $\alpha _J$
and
$\alpha _J$
and
![]() $\alpha _D$
.) The knot
$\alpha _D$
.) The knot
![]() $R(J,D)$
bounds an obviously seen Seifert surface of genus one, which consists of a 0-handle and two 1-handles. In Figure 1, the two 1-handles are untwisted and cross each other
$R(J,D)$
bounds an obviously seen Seifert surface of genus one, which consists of a 0-handle and two 1-handles. In Figure 1, the two 1-handles are untwisted and cross each other
![]() $2m+1$
times. So,
$2m+1$
times. So,
 $S=\left [\begin {smallmatrix}0 & m+1\\m & 0\end {smallmatrix}\right ]$
is a Seifert matrix. We remark that [Reference Cha and Kim6] and [Reference Cochran, Harvey and Horn11] use the particular case of
$S=\left [\begin {smallmatrix}0 & m+1\\m & 0\end {smallmatrix}\right ]$
is a Seifert matrix. We remark that [Reference Cha and Kim6] and [Reference Cochran, Harvey and Horn11] use the particular case of
![]() $m=1$
.
$m=1$
.

Figure 1 The knot
![]() $R(J,D)$
.
$R(J,D)$
.
Because
![]() $tS-S^T$
presents the Alexander module of
$tS-S^T$
presents the Alexander module of
![]() $R(J,D)$
, a routine computation shows that
$R(J,D)$
, a routine computation shows that
![]() $R(J,D)$
has (integral) Alexander module
$R(J,D)$
has (integral) Alexander module
and the summands
![]() $\mathbb {Z}[t^{\pm 1}]/\langle \lambda (t)\rangle $
and
$\mathbb {Z}[t^{\pm 1}]/\langle \lambda (t)\rangle $
and
![]() $\mathbb {Z}[t^{\pm 1}]/\langle \lambda (t^{-1})\rangle $
are equal to the subgroups
$\mathbb {Z}[t^{\pm 1}]/\langle \lambda (t^{-1})\rangle $
are equal to the subgroups
![]() $\langle \alpha _J\rangle $
and
$\langle \alpha _J\rangle $
and
![]() $\langle \alpha _D\rangle $
generated by the loops
$\langle \alpha _D\rangle $
generated by the loops
![]() $\alpha _J$
and
$\alpha _J$
and
![]() $\alpha _D$
shown in Figure 1. It follows that
$\alpha _D$
shown in Figure 1. It follows that
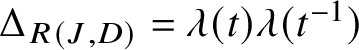 $\Delta _{R(J,D)} = \lambda (t)\lambda (t^{-1})$
. Moreover, the Blanchfield pairing
$\Delta _{R(J,D)} = \lambda (t)\lambda (t^{-1})$
. Moreover, the Blanchfield pairing
on the Alexander module
![]() ${\mathcal A} := H_1(M(R(J,D));\mathbb {Q}[t^{\pm 1}])$
has exactly two metabolisers,
${\mathcal A} := H_1(M(R(J,D));\mathbb {Q}[t^{\pm 1}])$
has exactly two metabolisers,
![]() $\langle \alpha _J\rangle $
and
$\langle \alpha _J\rangle $
and
![]() $\langle \alpha _D\rangle $
. Here, a submodule
$\langle \alpha _D\rangle $
. Here, a submodule
![]() $P\subset {\mathcal A}$
is called a metaboliser if P is equal to
$P\subset {\mathcal A}$
is called a metaboliser if P is equal to
![]() $P^{\perp }:=\{x\in {\mathcal A} \mid B\ell (P,x)=0\}$
. The above observations on
$P^{\perp }:=\{x\in {\mathcal A} \mid B\ell (P,x)=0\}$
. The above observations on
![]() $R(J,D)$
hold for any choice of J and D.
$R(J,D)$
hold for any choice of J and D.
As another ingredient of the construction of the promised knots
![]() $K_i$
, we will use a family of knots
$K_i$
, we will use a family of knots
 $\{J^i_k\}$
, which was given in [Reference Cha and Kim6]. For
$\{J^i_k\}$
, which was given in [Reference Cha and Kim6]. For
![]() $k=0$
, an explicit construction of such
$k=0$
, an explicit construction of such
 $\{J^i_0\}_i$
is given in [Reference Cha and Kim6, Section 4]. We need that
$\{J^i_0\}_i$
is given in [Reference Cha and Kim6, Section 4]. We need that
 $\{J^i_0\}_i$
satisfies the following conditions (J1), (J2) and (J3) for some sequence of increasing primes
$\{J^i_0\}_i$
satisfies the following conditions (J1), (J2) and (J3) for some sequence of increasing primes
![]() $\{p_i\}$
. For a knot J and an integer p, let
$\{p_i\}$
. For a knot J and an integer p, let
![]() $\sigma _J(\omega )\in \mathbb {Z}$
be the Levine-Tristram signature function of J at
$\sigma _J(\omega )\in \mathbb {Z}$
be the Levine-Tristram signature function of J at
![]() $\omega \in S^1\subset \mathbb {C}$
, and let
$\omega \in S^1\subset \mathbb {C}$
, and let
 $$ \begin{align} \rho(J,\mathbb{Z}_d) = \frac1d \sum_{k=0}^{d-1} \sigma_J(e^{2\pi k\sqrt{-1}/d}). \end{align} $$
$$ \begin{align} \rho(J,\mathbb{Z}_d) = \frac1d \sum_{k=0}^{d-1} \sigma_J(e^{2\pi k\sqrt{-1}/d}). \end{align} $$
-
(J1) For each i,
 $J^i_0$
is
$J^i_0$
is
 $0$
-negative.
$0$
-negative. -
(J2) For each i,
 $|\rho (J^i_0,\mathbb {Z}_{p_i})|> 69\,713\,280\cdot (6n+8m+86)$
.
$|\rho (J^i_0,\mathbb {Z}_{p_i})|> 69\,713\,280\cdot (6n+8m+86)$
. -
(J3) For
 $i<j$
,
$i<j$
,
 $\rho (J^j_0,\mathbb {Z}_{p_i})=0$
.
$\rho (J^j_0,\mathbb {Z}_{p_i})=0$
.
For
![]() $k=0,\ldots ,n-2$
,
$k=0,\ldots ,n-2$
,
 $J^i_{k+1}$
is defined inductively by
$J^i_{k+1}$
is defined inductively by
 $J^i_{k+1} = P_k(\eta _k,J^i_k)$
, where
$J^i_{k+1} = P_k(\eta _k,J^i_k)$
, where
 $P_k(\eta _k,J^i_k)$
is the satellite knot shown in the right of Figure 2. The left of Figure 2 shows the pattern
$P_k(\eta _k,J^i_k)$
is the satellite knot shown in the right of Figure 2. The left of Figure 2 shows the pattern
![]() $P_k$
in the exterior of an unknotted circle
$P_k$
in the exterior of an unknotted circle
![]() $\eta _k$
, which is a standard solid torus. The companion is the knot
$\eta _k$
, which is a standard solid torus. The companion is the knot
![]() $J^i_k$
.
$J^i_k$
.

Figure 2 The stevedore’s pattern
![]() $(P_k,\eta _k)$
and the satellite knot
$(P_k,\eta _k)$
and the satellite knot
 $P_k(\eta _k,J^i_k)$
.
$P_k(\eta _k,J^i_k)$
.
Now, let
 $K_i = R(J_{n-1}^i,D)$
, where
$K_i = R(J_{n-1}^i,D)$
, where
![]() $D=\mathrm {Wh}^+(T)$
is the positive Whitehead double of the right-handed trefoil T. Because D is topologically slice [Reference Freedman21],
$D=\mathrm {Wh}^+(T)$
is the positive Whitehead double of the right-handed trefoil T. Because D is topologically slice [Reference Freedman21],
![]() $K_i$
is topologically concordant to
$K_i$
is topologically concordant to
 $R(J_{n-1}^i,U)$
, where U is the trivial knot. Because
$R(J_{n-1}^i,U)$
, where U is the trivial knot. Because
![]() $R(J,U)$
is (smoothly) slice for any J, it follows that
$R(J,U)$
is (smoothly) slice for any J, it follows that
![]() $K_i$
is topologically slice. By [Reference Cha and Kim6, Section 2.2, Lemma 2.3], property (J1) implies that each
$K_i$
is topologically slice. By [Reference Cha and Kim6, Section 2.2, Lemma 2.3], property (J1) implies that each
![]() $K_i$
is n-negative and k-positive for all
$K_i$
is n-negative and k-positive for all
![]() $k\ge 0$
. Because
$k\ge 0$
. Because
![]() $\Delta _{K_i} = \lambda (t)\lambda (t^{-1})$
, it follows that the class
$\Delta _{K_i} = \lambda (t)\lambda (t^{-1})$
, it follows that the class
![]() $[K_i]$
lies in
$[K_i]$
lies in
![]() $\mathrm {gr}_n({\mathcal T}\kern3pt)_{\lambda } = ({\mathcal T}_n\cap {\mathcal T}_{\lambda }) / ({\mathcal T}_{n+1}\cap {\mathcal T}_{\lambda })$
. Therefore, to prove Theorem D, it suffices to show the following statement.
$\mathrm {gr}_n({\mathcal T}\kern3pt)_{\lambda } = ({\mathcal T}_n\cap {\mathcal T}_{\lambda }) / ({\mathcal T}_{n+1}\cap {\mathcal T}_{\lambda })$
. Therefore, to prove Theorem D, it suffices to show the following statement.
Theorem 2.2. Suppose that
 $K=\bigl (\#_{i=1}^r \, a_i K_i\bigr ) \# L$
(
$K=\bigl (\#_{i=1}^r \, a_i K_i\bigr ) \# L$
(
![]() $a_i\in \mathbb {Z}$
) is a linear combination of the knots
$a_i\in \mathbb {Z}$
) is a linear combination of the knots
![]() $K_i$
and a knot L with
$K_i$
and a knot L with
![]() $\Delta _L(t)$
relatively prime to
$\Delta _L(t)$
relatively prime to
![]() $\lambda (t)$
. If
$\lambda (t)$
. If
![]() $a_i\ne 0$
for some i, then K is not
$a_i\ne 0$
for some i, then K is not
![]() $(n+1)$
-bipolar.
$(n+1)$
-bipolar.
For the special case that L is a trivial knot and
![]() $m=1$
, the conclusion of Theorem 2.2 was shown in [Reference Cha and Kim6]. The general case of Theorem 2.2 requires substantially more sophisticated ideas and methods, which will be discussed in Sections 3 and 4.
$m=1$
, the conclusion of Theorem 2.2 was shown in [Reference Cha and Kim6]. The general case of Theorem 2.2 requires substantially more sophisticated ideas and methods, which will be discussed in Sections 3 and 4.
2.2. Construction of a negaton
To prove Theorem 2.2 by contradiction, suppose that the knot K is
![]() $(n+1)$
-bipolar. Recall that
$(n+1)$
-bipolar. Recall that
![]() $K_i$
is n-bipolar. The following observation will be useful. The knot L in the statement of Theorem 2.2 is automatically n-bipolar, because L is concordant to the sum of K,
$K_i$
is n-bipolar. The following observation will be useful. The knot L in the statement of Theorem 2.2 is automatically n-bipolar, because L is concordant to the sum of K,
![]() $-a_1K_1,\ldots$
$-a_1K_1,\ldots$
![]() $-a_{r-1}K_{r-1}$
, and
$-a_{r-1}K_{r-1}$
, and
![]() $-a_rK_r$
and each of K and
$-a_rK_r$
and each of K and
![]() $K_i$
are n-bipolar.
$K_i$
are n-bipolar.
We may assume
![]() $a_i\ne 0$
for all i, by removing
$a_i\ne 0$
for all i, by removing
![]() $K_i$
when
$K_i$
when
![]() $a_i=0$
. In addition, by taking
$a_i=0$
. In addition, by taking
![]() $-K$
instead of K, we may assume that
$-K$
instead of K, we may assume that
![]() $a_1>0$
. Under this assumption, we will prove that K is not
$a_1>0$
. Under this assumption, we will prove that K is not
![]() $(n+1)$
-negative. To derive a contradiction, suppose that K is
$(n+1)$
-negative. To derive a contradiction, suppose that K is
![]() $(n+1)$
-negative. As done in [Reference Cha and Kim6, Section 2.3], we will construct a certain n-negaton for the first summand
$(n+1)$
-negative. As done in [Reference Cha and Kim6, Section 2.3], we will construct a certain n-negaton for the first summand
![]() $K_1$
, which we will call
$K_1$
, which we will call
![]() $X^-$
below. Because the generality of Theorem 2.2 does not cause significant issues in this construction, we will closely follow [Reference Cha and Kim6], with minor additional changes related to L.
$X^-$
below. Because the generality of Theorem 2.2 does not cause significant issues in this construction, we will closely follow [Reference Cha and Kim6], with minor additional changes related to L.
Use the n-bipolarity of L to choose an n-negaton, say,
![]() $Z^-_L$
, bounded by
$Z^-_L$
, bounded by
![]() $-M(L)=M(-L)$
. Use the n-bipolarity of
$-M(L)=M(-L)$
. Use the n-bipolarity of
![]() $K_i$
, choose an n-negaton
$K_i$
, choose an n-negaton
![]() $Z^-_i$
bounded by
$Z^-_i$
bounded by
![]() $-M(K_i)=M(-K_i)$
for each i for which
$-M(K_i)=M(-K_i)$
for each i for which
![]() $a_i>0$
and choose n-negaton
$a_i>0$
and choose n-negaton
![]() $Z^-_i$
bounded by
$Z^-_i$
bounded by
![]() $M(K_i)$
for each i for which
$M(K_i)$
for each i for which
![]() $a_i<0$
. Let
$a_i<0$
. Let
![]() $V^-$
be an
$V^-$
be an
![]() $(n+1)$
-negaton bounded by
$(n+1)$
-negaton bounded by
![]() $M(K)$
. There is a standard cobordism C bounded by the union of
$M(K)$
. There is a standard cobordism C bounded by the union of
![]() $\partial _-C := -M(K)$
and
$\partial _-C := -M(K)$
and
![]() $\partial _+C := \bigl (\bigsqcup _i a_i M(K_i)\bigr ) \sqcup M(L)$
, which is associated with the connected sum expression
$\partial _+C := \bigl (\bigsqcup _i a_i M(K_i)\bigr ) \sqcup M(L)$
, which is associated with the connected sum expression
 $K=\bigl (\#_{i=1}^r \, a_i K_i\bigr ) \# L$
; C is obtained by attaching to
$K=\bigl (\#_{i=1}^r \, a_i K_i\bigr ) \# L$
; C is obtained by attaching to
![]() $\bigl (\bigsqcup _{i=1}^r a_i M(K_i) \times I\bigr ) \sqcup M(L)\times I$
, N 1-handles that connect the component and then attaching N 2-handles that make meridians of the involved
$\bigl (\bigsqcup _{i=1}^r a_i M(K_i) \times I\bigr ) \sqcup M(L)\times I$
, N 1-handles that connect the component and then attaching N 2-handles that make meridians of the involved
![]() $N+1$
knots parallel, where
$N+1$
knots parallel, where
![]() $N=\sum _i |a_i|$
. A detailed description of C can be found, for instance, from [Reference Cochran, Orr and Teichner17, p. 113]. Define
$N=\sum _i |a_i|$
. A detailed description of C can be found, for instance, from [Reference Cochran, Orr and Teichner17, p. 113]. Define
 $$ \begin{align} X^- := V^- \mathbin{\mathop{\cup}\limits_{\partial_-C}} C \mathbin{\mathop{\cup}\limits_{\partial_+C}} \bigg((a_1-1)Z^-_1 \sqcup \Bigl({\textstyle\bigsqcup\limits_{i>1} |a_i| Z^-_i} \Bigr) \sqcup Z^-_L \bigg). \end{align} $$
$$ \begin{align} X^- := V^- \mathbin{\mathop{\cup}\limits_{\partial_-C}} C \mathbin{\mathop{\cup}\limits_{\partial_+C}} \bigg((a_1-1)Z^-_1 \sqcup \Bigl({\textstyle\bigsqcup\limits_{i>1} |a_i| Z^-_i} \Bigr) \sqcup Z^-_L \bigg). \end{align} $$
Figure 3 depicts the construction of
![]() $X^-$
. By (the argument of) [Reference Cha and Kim6, Lemma 2.4],
$X^-$
. By (the argument of) [Reference Cha and Kim6, Lemma 2.4],
![]() $X^-$
is an n-negaton bounded by
$X^-$
is an n-negaton bounded by
![]() $M(K_1)$
.
$M(K_1)$
.

Figure 3 The construction of
![]() $X^-$
. The sign of
$X^-$
. The sign of
![]() $M(K_i)$
equals that of
$M(K_i)$
equals that of
![]() $a_i$
.
$a_i$
.
Now, let
Because
![]() $X^-$
is an n-negaton with
$X^-$
is an n-negaton with
![]() $n\ge 2$
, P is a metaboliser of the Blanchfield pairing on
$n\ge 2$
, P is a metaboliser of the Blanchfield pairing on
![]() $H_1(M(K_1);\mathbb {Q}[t^{\pm 1}])$
, by [Reference Cochran, Harvey and Horn11, Theorem 5.8]. (See also the statement of [Reference Cha and Kim6, Lemma 2.5].) Because
$H_1(M(K_1);\mathbb {Q}[t^{\pm 1}])$
, by [Reference Cochran, Harvey and Horn11, Theorem 5.8]. (See also the statement of [Reference Cha and Kim6, Lemma 2.5].) Because
 $K_1=R(J^1_{n-1},D)$
has exactly two metabolisers
$K_1=R(J^1_{n-1},D)$
has exactly two metabolisers
![]() $\langle \alpha _J\rangle $
and
$\langle \alpha _J\rangle $
and
![]() $\langle \alpha _D\rangle $
, we have the following two cases:
$\langle \alpha _D\rangle $
, we have the following two cases:
![]() $P=\langle \alpha _D\rangle $
or
$P=\langle \alpha _D\rangle $
or
![]() $P=\langle \alpha _J\rangle $
. By deriving a contradiction for each case, the proof of Theorem 2.2 will be completed.
$P=\langle \alpha _J\rangle $
. By deriving a contradiction for each case, the proof of Theorem 2.2 will be completed.
3.
 $L^2$
-signatures and localised mixed-type commutator series
$L^2$
-signatures and localised mixed-type commutator series
In this section, we continue the proof of Theorem 2.2 for the case
![]() $P=\langle \alpha _D\rangle $
.
$P=\langle \alpha _D\rangle $
.
Recall that we constructed an n-negaton
![]() $X^-$
in (2.3) using the negatons
$X^-$
in (2.3) using the negatons
![]() $V^-$
,
$V^-$
,
![]() $Z_L^-$
and
$Z_L^-$
and
![]() $Z_i^-$
. To obtain a hyperbolic intersection form, take the connected sum of the
$Z_i^-$
. To obtain a hyperbolic intersection form, take the connected sum of the
![]() $(n+1)$
-negaton
$(n+1)$
-negaton
![]() $V^-$
and
$V^-$
and
![]() $b_2(V^-)$
copies of
$b_2(V^-)$
copies of
![]() $\mathbb {C} P^2$
and call the result
$\mathbb {C} P^2$
and call the result
![]() $V^0$
. Indeed, by [Reference Cochran, Harvey and Horn11, Proposition 5.5],
$V^0$
. Indeed, by [Reference Cochran, Harvey and Horn11, Proposition 5.5],
![]() $V^0$
is a special type of 4-manifold called an integral
$V^0$
is a special type of 4-manifold called an integral
![]() $(n+1)$
-solution in [Reference Cha3, Definition 3.1], which particularly has a metabolic intersection form over twisted coefficients. We do not describe its definition because we do not use it directly, but we will state and use its properties later. For
$(n+1)$
-solution in [Reference Cha3, Definition 3.1], which particularly has a metabolic intersection form over twisted coefficients. We do not describe its definition because we do not use it directly, but we will state and use its properties later. For
![]() $Z_L^-$
and
$Z_L^-$
and
![]() $Z_i^-$
, define integral n-solutions
$Z_i^-$
, define integral n-solutions
![]() $Z_L^0$
and
$Z_L^0$
and
![]() $Z_i^0$
by taking connected sum with copies of
$Z_i^0$
by taking connected sum with copies of
![]() $\mathbb {C} P^2$
in the same way.
$\mathbb {C} P^2$
in the same way.
Repeat the construction of
![]() $X^-$
but now use
$X^-$
but now use
![]() $V^0$
,
$V^0$
,
![]() $Z_L^0$
and
$Z_L^0$
and
![]() $Z_i^0$
in place of
$Z_i^0$
in place of
![]() $V^-$
,
$V^-$
,
![]() $Z_L^-$
and
$Z_L^-$
and
![]() $Z_i^-$
to obtain a 4-manifold
$Z_i^-$
to obtain a 4-manifold
![]() $X^0$
. By the proof of [Reference Cha and Kim6, Lemma 2.4],
$X^0$
. By the proof of [Reference Cha and Kim6, Lemma 2.4],
![]() $b_2(X^-)$
is equal to the sum of
$b_2(X^-)$
is equal to the sum of
![]() $b_2(V^-)$
,
$b_2(V^-)$
,
![]() $b_2(Z_L^-)$
,
$b_2(Z_L^-)$
,
![]() $(a_1-1)b_2(Z_1^-)$
and
$(a_1-1)b_2(Z_1^-)$
and
![]() $|a_i| b_2(Z_i^-)$
(
$|a_i| b_2(Z_i^-)$
(
![]() $i>1$
). Thus,
$i>1$
). Thus,
![]() $X^0 = X^- \# (b_2(X^-) \mathbb {C} P^2)$
. Because
$X^0 = X^- \# (b_2(X^-) \mathbb {C} P^2)$
. Because
![]() $X^-$
is an n-negaton, it follows that
$X^-$
is an n-negaton, it follows that
![]() $X^0$
is an integral n-solution, again by [Reference Cochran, Harvey and Horn11, Proposition 5.5].
$X^0$
is an integral n-solution, again by [Reference Cochran, Harvey and Horn11, Proposition 5.5].
We will attach additional pieces to
![]() $X^0$
to obtain a sequence of 4-manifolds, essentially following a technique that first appeared in [Reference Cochran, Harvey and Leidy12]; see also [Reference Cochran, Harvey and Leidy14, Reference Cochran, Harvey and Leidy13, Reference Cha3, Reference Cha and Kim6]. The notation used below is close to [Reference Cha3, Reference Cha and Kim6]. Consider the satellite construction
$X^0$
to obtain a sequence of 4-manifolds, essentially following a technique that first appeared in [Reference Cochran, Harvey and Leidy12]; see also [Reference Cochran, Harvey and Leidy14, Reference Cochran, Harvey and Leidy13, Reference Cha3, Reference Cha and Kim6]. The notation used below is close to [Reference Cha3, Reference Cha and Kim6]. Consider the satellite construction
 $J^1_{k+1} = P_k(\eta _k, J^1_k)$
. Due to [Reference Cochran, Harvey and Leidy12], there is a standard cobordism, which we denote by
$J^1_{k+1} = P_k(\eta _k, J^1_k)$
. Due to [Reference Cochran, Harvey and Leidy12], there is a standard cobordism, which we denote by
![]() $E_k$
, from
$E_k$
, from
 $M(J^1_{k+1})$
to
$M(J^1_{k+1})$
to
 $M(J^1_k)\sqcup M(P_k)$
for
$M(J^1_k)\sqcup M(P_k)$
for
![]() $k=0,\ldots$
,
$k=0,\ldots$
,
![]() $n-2$
. In Subsection 3.1, we will use an alternative description given in Figure 4, which illustrates that
$n-2$
. In Subsection 3.1, we will use an alternative description given in Figure 4, which illustrates that
![]() $E_k$
is obtained from
$E_k$
is obtained from
 $M(J^1_{k+1})\times [0,1]$
by attaching a 2-handle and a 3-handle: start with
$M(J^1_{k+1})\times [0,1]$
by attaching a 2-handle and a 3-handle: start with
 $M(J^1_{k+1}) = M(P_k(\eta _k, J^1_k))$
, attach a 2-handle along a zero-framed longitude of
$M(J^1_{k+1}) = M(P_k(\eta _k, J^1_k))$
, attach a 2-handle along a zero-framed longitude of
![]() $J^1_k$
to obtain the second diagram and apply handle slide to obtain the last diagram, which is
$J^1_k$
to obtain the second diagram and apply handle slide to obtain the last diagram, which is
 $M(J^1_k) \# M(P_k)$
. Attach a 3-handle to obtain
$M(J^1_k) \# M(P_k)$
. Attach a 3-handle to obtain
 $M(J^1_k) \sqcup M(P_k)$
.
$M(J^1_k) \sqcup M(P_k)$
.

Figure 4 A handlebody description of the standard cobordism
![]() $E_k$
.
$E_k$
.
View
 $K_1=R(J^1_{n-1},D)$
as the satellite knot
$K_1=R(J^1_{n-1},D)$
as the satellite knot
 $R(U,D)(\alpha _J,J^1_{n-1})$
and apply the same construction to obtain a standard cobordism
$R(U,D)(\alpha _J,J^1_{n-1})$
and apply the same construction to obtain a standard cobordism
![]() $E_{n-1}$
from
$E_{n-1}$
from
![]() $M(K_1)$
to
$M(K_1)$
to
 $M(J^1_{n-1})\sqcup M(R(U,D))$
. Now, define 4-manifolds
$M(J^1_{n-1})\sqcup M(R(U,D))$
. Now, define 4-manifolds
![]() $X_n$
,
$X_n$
,
![]() $X_{n-1},\ldots$
,
$X_{n-1},\ldots$
,
![]() $X_0=X$
as follows:
$X_0=X$
as follows:
 $$ \begin{align*} X_n & := X^0 \\ X_{n-1} & := X_n \mathbin{\mathop{\cup}\limits_{M(K_1)}} E_{n-1} = X^0 \mathbin{\mathop{\cup}\limits_{M(K_1)}} E_{n-1} \\ X_{n-2} & := X_{n-1} \mathbin{\mathop{\cup}\limits_{M(J^1_{n-1})}} E_{n-2} = X^0 \mathbin{\mathop{\cup}\limits_{M(K_1)}} E_{n-1} \mathbin{\mathop{\cup}\limits_{M(J^1_{n-1})}} E_{n-2} \\ &\hphantom{=}\vdots \\ X=X_0 &:= X_1 \mathbin{\mathop{\cup}\limits_{M(J^1_{1})}} E_{0} = X^0 \mathbin{\mathop{\cup}\limits_{M(K_1)}} E_{n-1} \mathbin{\mathop{\cup}\limits_{M(J^1_{n-1})}} E_{n-2} \mathbin{\mathop{\cup}\limits_{M(J^1_{n-2})}} \cdots \mathbin{\mathop{\cup}\limits_{M(J^1_{1})}} E_{0}. \end{align*} $$
$$ \begin{align*} X_n & := X^0 \\ X_{n-1} & := X_n \mathbin{\mathop{\cup}\limits_{M(K_1)}} E_{n-1} = X^0 \mathbin{\mathop{\cup}\limits_{M(K_1)}} E_{n-1} \\ X_{n-2} & := X_{n-1} \mathbin{\mathop{\cup}\limits_{M(J^1_{n-1})}} E_{n-2} = X^0 \mathbin{\mathop{\cup}\limits_{M(K_1)}} E_{n-1} \mathbin{\mathop{\cup}\limits_{M(J^1_{n-1})}} E_{n-2} \\ &\hphantom{=}\vdots \\ X=X_0 &:= X_1 \mathbin{\mathop{\cup}\limits_{M(J^1_{1})}} E_{0} = X^0 \mathbin{\mathop{\cup}\limits_{M(K_1)}} E_{n-1} \mathbin{\mathop{\cup}\limits_{M(J^1_{n-1})}} E_{n-2} \mathbin{\mathop{\cup}\limits_{M(J^1_{n-2})}} \cdots \mathbin{\mathop{\cup}\limits_{M(J^1_{1})}} E_{0}. \end{align*} $$
See the schematic diagram in Figure 5.

Figure 5 A schematic diagram of the 4-manifold X.
We have that
![]() $H_1(X^0)=H_1(X^-)=\mathbb {Z}=\langle t \rangle $
where the generator t is represented by the meridian
$H_1(X^0)=H_1(X^-)=\mathbb {Z}=\langle t \rangle $
where the generator t is represented by the meridian
![]() $\mu _K$
of K, because
$\mu _K$
of K, because
![]() $X^-$
is a negaton bounded by
$X^-$
is a negaton bounded by
![]() $M(K)$
. See Definition 2.3(1). By a Mayer-Vietoris argument using this, it follows that
$M(K)$
. See Definition 2.3(1). By a Mayer-Vietoris argument using this, it follows that
![]() $H_1(X_k)=\mathbb {Z}$
for all
$H_1(X_k)=\mathbb {Z}$
for all
![]() $k=0,\ldots$
, n.
$k=0,\ldots$
, n.
3.1. A localised mixed-type commutator series associated with X
Recall from Subsection 2.1 that
![]() $p_1$
denotes the first prime used in properties (J2) and (J3), and
$p_1$
denotes the first prime used in properties (J2) and (J3), and
![]() $\lambda (t)=(m+1)t-m$
. Let
$\lambda (t)=(m+1)t-m$
. Let
Obviously,
![]() $\Sigma $
is a multiplicative subset. Let
$\Sigma $
is a multiplicative subset. Let
![]() $\mathbb {Q}[t^{\pm }]\Sigma ^{-1}$
be the localisation.
$\mathbb {Q}[t^{\pm }]\Sigma ^{-1}$
be the localisation.
Definition 3.1. Let G be a group endowed with a homomorphism
![]() $G\to \pi _1(X)$
that induces an epimorphism
$G\to \pi _1(X)$
that induces an epimorphism
![]() $H_1(G) \twoheadrightarrow H_1(X)$
. For
$H_1(G) \twoheadrightarrow H_1(X)$
. For
![]() $i=0,1,\ldots ,n+1$
, define subgroups
$i=0,1,\ldots ,n+1$
, define subgroups
![]() ${\mathcal P}^i G$
of G inductively as follows. Let
${\mathcal P}^i G$
of G inductively as follows. Let
![]() ${\mathcal P}^0 G := G$
, and let
${\mathcal P}^0 G := G$
, and let
![]() ${\mathcal P}^1 G$
be the kernel of the composition
${\mathcal P}^1 G$
be the kernel of the composition
Let
![]() ${\mathcal P}^2G$
be the kernel of the composition
${\mathcal P}^2G$
be the kernel of the composition

Here,
 $\operatorname {Im} H_1(Z_L^0;\mathbb {Q}[t^{\pm 1}]\Sigma ^{-1})$
is the image of
$\operatorname {Im} H_1(Z_L^0;\mathbb {Q}[t^{\pm 1}]\Sigma ^{-1})$
is the image of
 $H_1(Z_L^0;\mathbb {Q}[t^{\pm 1}]\Sigma ^{-1}) \to H_1(X;\mathbb {Q}[t^{\pm 1}]\Sigma ^{-1})$
induced by the inclusion.
$H_1(Z_L^0;\mathbb {Q}[t^{\pm 1}]\Sigma ^{-1}) \to H_1(X;\mathbb {Q}[t^{\pm 1}]\Sigma ^{-1})$
induced by the inclusion.
For
![]() $i=2,\ldots$
,
$i=2,\ldots$
,
![]() $n-1$
, let
$n-1$
, let
 $$ \begin{align*} {\mathcal P}^{i+1}G := \operatorname{Ker} \left\{ {\mathcal P}^i G \twoheadrightarrow \frac{{\mathcal P}^i G}{[{\mathcal P}^i G,{\mathcal P}^i G]} \rightarrow \frac{{\mathcal P}^i G}{[{\mathcal P}^i G,{\mathcal P}^i G]} {\mathbin{\mathop{\otimes}_{{\mathbb{Z}}}}} \mathbb{Q} = H_1\bigl(G;\mathbb{Q}[G/{\mathcal P}^i G]\bigr) \right\}. \end{align*} $$
$$ \begin{align*} {\mathcal P}^{i+1}G := \operatorname{Ker} \left\{ {\mathcal P}^i G \twoheadrightarrow \frac{{\mathcal P}^i G}{[{\mathcal P}^i G,{\mathcal P}^i G]} \rightarrow \frac{{\mathcal P}^i G}{[{\mathcal P}^i G,{\mathcal P}^i G]} {\mathbin{\mathop{\otimes}_{{\mathbb{Z}}}}} \mathbb{Q} = H_1\bigl(G;\mathbb{Q}[G/{\mathcal P}^i G]\bigr) \right\}. \end{align*} $$
Finally, define
 $$ \begin{align*} {\mathcal P}^{n+1}G := \operatorname{Ker} \left\{ {\mathcal P}^n G \twoheadrightarrow \frac{{\mathcal P}^n G}{[{\mathcal P}^n G,{\mathcal P}^n G]} \twoheadrightarrow \frac{{\mathcal P}^n G}{[{\mathcal P}^n G,{\mathcal P}^n G]} {\mathbin{\mathop{\otimes}_{{\mathbb{Z}}}}} \mathbb{Z}_{p_1} = H_1\bigl(G;\mathbb{Z}_{p_1}[G/{\mathcal P}^n G]\bigr) \right\}. \end{align*} $$
$$ \begin{align*} {\mathcal P}^{n+1}G := \operatorname{Ker} \left\{ {\mathcal P}^n G \twoheadrightarrow \frac{{\mathcal P}^n G}{[{\mathcal P}^n G,{\mathcal P}^n G]} \twoheadrightarrow \frac{{\mathcal P}^n G}{[{\mathcal P}^n G,{\mathcal P}^n G]} {\mathbin{\mathop{\otimes}_{{\mathbb{Z}}}}} \mathbb{Z}_{p_1} = H_1\bigl(G;\mathbb{Z}_{p_1}[G/{\mathcal P}^n G]\bigr) \right\}. \end{align*} $$
It is straightforward to verify inductively that
![]() ${\mathcal P}^k G$
is a normal subgroup of G and the standard kth derived subgroup
${\mathcal P}^k G$
is a normal subgroup of G and the standard kth derived subgroup
![]() $G^{(k)}$
lies in
$G^{(k)}$
lies in
![]() ${\mathcal P}^k G$
for all k.
${\mathcal P}^k G$
for all k.
We remark that the commutator series
![]() $\{{\mathcal P}^k G\}_k$
in Definition 3.1 is ‘localised at polynomials’ in the sense of [Reference Cochran, Harvey and Leidy14, Sections 3 and 4] and is of ‘mixed-coefficient’ type in the sense that we use both
$\{{\mathcal P}^k G\}_k$
in Definition 3.1 is ‘localised at polynomials’ in the sense of [Reference Cochran, Harvey and Leidy14, Sections 3 and 4] and is of ‘mixed-coefficient’ type in the sense that we use both
![]() $\mathbb {Z}_{p_1}$
and
$\mathbb {Z}_{p_1}$
and
![]() $\mathbb {Q}$
(see [Reference Cha3, Section 4.1]).
$\mathbb {Q}$
(see [Reference Cha3, Section 4.1]).
In particular, define the subgroups
![]() ${\mathcal P}^i\pi _1(X_k)$
, by applying Definition 3.1 to the case
${\mathcal P}^i\pi _1(X_k)$
, by applying Definition 3.1 to the case
![]() $G=\pi _1(X_k) \to \pi _1(X)$
. The following properties, which we will state as Assertions A and B, are essential for our purpose. Let
$G=\pi _1(X_k) \to \pi _1(X)$
. The following properties, which we will state as Assertions A and B, are essential for our purpose. Let
 $\mu _k\subset M(J^1_k)$
be the meridian of
$\mu _k\subset M(J^1_k)$
be the meridian of
![]() $J^1_k$
. By the construction of
$J^1_k$
. By the construction of
![]() $X_k$
,
$X_k$
,
 $M(J^1_k)$
is a component of
$M(J^1_k)$
is a component of
![]() $\partial X_k$
(see Figure 5), and thus
$\partial X_k$
(see Figure 5), and thus
![]() $\mu _k$
represents an element in
$\mu _k$
represents an element in
![]() $\pi _1(X_k)$
for
$\pi _1(X_k)$
for
![]() $k\le n-1$
. For brevity, let
$k\le n-1$
. For brevity, let
![]() $J^1_n := K_1$
, so that the previous sentence holds for
$J^1_n := K_1$
, so that the previous sentence holds for
![]() $k=n$
as well. Also, let
$k=n$
as well. Also, let
![]() $(P_{n-1},\eta _{n-1}):=(R(U,D),\alpha _D)$
, so that
$(P_{n-1},\eta _{n-1}):=(R(U,D),\alpha _D)$
, so that
 $J^1_k = P_{k-1}(\eta _{k-1},J^1_{k-1})$
holds for
$J^1_k = P_{k-1}(\eta _{k-1},J^1_{k-1})$
holds for
![]() $k=n$
as well.
$k=n$
as well.
Assertion A. The class of
![]() $\mu _k$
lies in
$\mu _k$
lies in
![]() $\pi _1(X_k)^{(n-k)}\subset {\mathcal P}^{n-k}\pi _1(X_k)$
and is nontrivial in
$\pi _1(X_k)^{(n-k)}\subset {\mathcal P}^{n-k}\pi _1(X_k)$
and is nontrivial in
![]() ${\mathcal P}^{n-k}\pi _1(X_k)/{\mathcal P}^{n-k+1}\pi _1(X_k)$
for all
${\mathcal P}^{n-k}\pi _1(X_k)/{\mathcal P}^{n-k+1}\pi _1(X_k)$
for all
![]() $k=0$
,
$k=0$
,
![]() $1,\ldots$
, n. In particular, the class
$1,\ldots$
, n. In particular, the class
![]() $\mu _0$
is nontrivial in
$\mu _0$
is nontrivial in
![]() ${\mathcal P}^n\pi _1(X)/{\mathcal P}^{n+1}\pi _1(X)$
.
${\mathcal P}^n\pi _1(X)/{\mathcal P}^{n+1}\pi _1(X)$
.
Assertion B. For
![]() $i= 1,\ldots$
, n, the inclusion-induced map sends
$i= 1,\ldots$
, n, the inclusion-induced map sends
 $\pi _1(Z_L^0)^{(i)}$
to the subgroup
$\pi _1(Z_L^0)^{(i)}$
to the subgroup
![]() ${\mathcal P}^{i+1}\pi _1(X) \subset \pi _1(X)$
. In particular,
${\mathcal P}^{i+1}\pi _1(X) \subset \pi _1(X)$
. In particular,
 $\pi _1(Z_L^0)^{(n)}$
maps to
$\pi _1(Z_L^0)^{(n)}$
maps to
![]() ${\mathcal P}^{n+1}\pi _1(X)$
.
${\mathcal P}^{n+1}\pi _1(X)$
.
Remark 3.2.
-
(1) Analogues of Assertion A for similar situations were established in earlier papers; for instance, in [Reference Cochran, Harvey and Leidy12, Reference Cochran, Harvey and Leidy14, Reference Cha3, Reference Cha4, Reference Cha and Kim6]. We will give a proof for our case, because our series
 ${\mathcal P}^i$
is different (notably at
${\mathcal P}^i$
is different (notably at
 $i=2$
) from those in the literature. Assertion B and its application are new, to the author’s knowledge.
$i=2$
) from those in the literature. Assertion B and its application are new, to the author’s knowledge. -
(2) Note that both
 $\mu _0$
and
$\mu _0$
and
 $\pi _1(Z_L^0)^{(n)}$
map to the nth subgroup
$\pi _1(Z_L^0)^{(n)}$
map to the nth subgroup
 ${\mathcal P}^n \pi _1(X)$
. Due to Assertions A and B, they have opposite nature in the next stage:
${\mathcal P}^n \pi _1(X)$
. Due to Assertions A and B, they have opposite nature in the next stage:
 $\pi _1(Z_L^0)^{(n)}$
lies in
$\pi _1(Z_L^0)^{(n)}$
lies in
 ${\mathcal P}^{n+1} \pi _1(X)$
, whereas
${\mathcal P}^{n+1} \pi _1(X)$
, whereas
 $\mu _0$
does not. This will be crucial in separating the contribution of the unknown knot L from that of
$\mu _0$
does not. This will be crucial in separating the contribution of the unknown knot L from that of
 $K_1$
in the linear combination
$K_1$
in the linear combination
 $K=\bigl (\#_{i=1}^r a_i K_i\bigr ) \# L$
. See Subsection 3.2, particularly the Cheeger-Gromov
$K=\bigl (\#_{i=1}^r a_i K_i\bigr ) \# L$
. See Subsection 3.2, particularly the Cheeger-Gromov
 $\rho $
-invariants in (3.3) and (3.8).
$\rho $
-invariants in (3.3) and (3.8).
In the proof of Assertion A, the following fact will be useful. Let
![]() $\lambda _{k-1}$
be the zero-linking longitude of
$\lambda _{k-1}$
be the zero-linking longitude of
 $J^1_{k-1}$
, which lies in
$J^1_{k-1}$
, which lies in
 $$ \begin{align*} E(J^1_{k-1}) \subset E(J^1_{k-1})\cup E(P_{k-1}\sqcup \eta_{k-1}) = E(J^1_k) \subset M(J^1_k) \subset \partial X_k. \end{align*} $$
$$ \begin{align*} E(J^1_{k-1}) \subset E(J^1_{k-1})\cup E(P_{k-1}\sqcup \eta_{k-1}) = E(J^1_k) \subset M(J^1_k) \subset \partial X_k. \end{align*} $$
Assertion C. The inclusion
![]() $X_k \subset X_{k-1}$
induces an isomorphism
$X_k \subset X_{k-1}$
induces an isomorphism
![]() ${\mathcal P}^i\pi _1(X_k)/\langle \lambda _{k-1} \rangle \cong {\mathcal P}^i\pi _1(X_{k-1})$
for all
${\mathcal P}^i\pi _1(X_k)/\langle \lambda _{k-1} \rangle \cong {\mathcal P}^i\pi _1(X_{k-1})$
for all
![]() $i\le n-k+2$
. Consequently, we have
$i\le n-k+2$
. Consequently, we have
Proof of Assertion C. Because
![]() $E_{k-1}$
is obtained by attaching a 2-handle to
$E_{k-1}$
is obtained by attaching a 2-handle to
 $M(J^1_k)\times [0,1]$
along
$M(J^1_k)\times [0,1]$
along
![]() $\lambda _{k-1}$
and then attaching a 3-handle (see Figure 4),
$\lambda _{k-1}$
and then attaching a 3-handle (see Figure 4),
![]() $X_{k-1}=X_k\cup E_{k-1}$
is obtained from
$X_{k-1}=X_k\cup E_{k-1}$
is obtained from
![]() $X_k$
by the same handle attachments. It follows that
$X_k$
by the same handle attachments. It follows that
![]() $\pi _1(X_{k-1}) \cong \pi _1(X_k)/\langle \lambda _{k-1} \rangle $
. This shows the assertion for
$\pi _1(X_{k-1}) \cong \pi _1(X_k)/\langle \lambda _{k-1} \rangle $
. This shows the assertion for
![]() $i=0$
. Now, to proceed by induction, suppose that
$i=0$
. Now, to proceed by induction, suppose that
![]() $i\ge 1$
and suppose that the assertion holds for
$i\ge 1$
and suppose that the assertion holds for
![]() $i-1$
. If
$i-1$
. If
![]() $i=1$
, we have the following commutative diagram with exact rows:
$i=1$
, we have the following commutative diagram with exact rows:

Because the two rightmost horizontal arrows are to the same target
![]() $H_1(X)$
, there is an induced epimorphism
$H_1(X)$
, there is an induced epimorphism
![]() ${\mathcal P}^i\pi _1(X_k) \twoheadrightarrow {\mathcal P}^i\pi _1(X_{k-1})$
and its kernel is equal to that of the epimorphism
${\mathcal P}^i\pi _1(X_k) \twoheadrightarrow {\mathcal P}^i\pi _1(X_{k-1})$
and its kernel is equal to that of the epimorphism
![]() ${\mathcal P}^{i-1}\pi _1(X_k) \twoheadrightarrow {\mathcal P}^{i-1}\pi _1(X_{k-1})$
. So the assertion holds for
${\mathcal P}^{i-1}\pi _1(X_k) \twoheadrightarrow {\mathcal P}^{i-1}\pi _1(X_{k-1})$
. So the assertion holds for
![]() $i=1$
. For
$i=1$
. For
![]() $i=2$
, replace
$i=2$
, replace
![]() $H_1(X)$
in the above diagram by the quotient
$H_1(X)$
in the above diagram by the quotient
 $$ \begin{align*} H_1\bigl(X;\mathbb{Q}[t^{\pm1}]\Sigma^{-1}\bigr) / \operatorname{Im} H_1\bigl(Z_L^0;\mathbb{Q}[t^{\pm1}]\Sigma^{-1}\bigr) \end{align*} $$
$$ \begin{align*} H_1\bigl(X;\mathbb{Q}[t^{\pm1}]\Sigma^{-1}\bigr) / \operatorname{Im} H_1\bigl(Z_L^0;\mathbb{Q}[t^{\pm1}]\Sigma^{-1}\bigr) \end{align*} $$
and apply the same argument.
For
![]() $i\ge 3$
, we have
$i\ge 3$
, we have

where
![]() $R=\mathbb {Q}$
or
$R=\mathbb {Q}$
or
![]() $\mathbb {Z}_{p_1}$
, depending on i. We claim that the rightmost vertical arrow is an isomorphism. From the claim, it follows that the assertion holds for i, once again by the argument used above. To show the claim, let
$\mathbb {Z}_{p_1}$
, depending on i. We claim that the rightmost vertical arrow is an isomorphism. From the claim, it follows that the assertion holds for i, once again by the argument used above. To show the claim, let
![]() $\gamma _{k-1}$
be the meridian of
$\gamma _{k-1}$
be the meridian of
 $J^1_{k-1}$
in the exterior
$J^1_{k-1}$
in the exterior
 $E(J^1_{k-1}) \subset M(J^1_k) \subset \partial X_k$
. Note that
$E(J^1_{k-1}) \subset M(J^1_k) \subset \partial X_k$
. Note that
![]() $\gamma _{k-1}$
is different from the meridian
$\gamma _{k-1}$
is different from the meridian
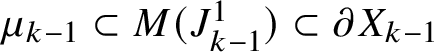 $\mu _{k-1}\subset M(J^1_{k-1})\subset \partial X_{k-1}$
used in the statement of Assertion A, but
$\mu _{k-1}\subset M(J^1_{k-1})\subset \partial X_{k-1}$
used in the statement of Assertion A, but
![]() $\gamma _{k-1}$
and
$\gamma _{k-1}$
and
![]() $\mu _{k-1}$
are isotopic in the cobordism
$\mu _{k-1}$
are isotopic in the cobordism
![]() $E_{k-1}$
. The meridian
$E_{k-1}$
. The meridian
![]() $\gamma _{k-1}$
is identified with the curve
$\gamma _{k-1}$
is identified with the curve
![]() $\eta _{k-1}$
, which lies in the commutator subgroup
$\eta _{k-1}$
, which lies in the commutator subgroup
 $\pi _1(M(J^1_k))^{(1)}$
. Because
$\pi _1(M(J^1_k))^{(1)}$
. Because
 $\pi _1(M(J^1_k))$
is normally generated by the meridian
$\pi _1(M(J^1_k))$
is normally generated by the meridian
![]() $\mu _k$
,
$\mu _k$
,
![]() $\gamma _{k-1}$
lies in
$\gamma _{k-1}$
lies in
![]() $\langle \mu _k\rangle ^{(1)} = \langle \gamma _k\rangle ^{(1)}$
in
$\langle \mu _k\rangle ^{(1)} = \langle \gamma _k\rangle ^{(1)}$
in
![]() $\pi _1(X_k)$
. By induction, it follows that
$\pi _1(X_k)$
. By induction, it follows that
![]() $\gamma _{k-1}$
lies in
$\gamma _{k-1}$
lies in
![]() $\langle \gamma _n\rangle ^{(n-k+1)}$
. Therefore, the image of
$\langle \gamma _n\rangle ^{(n-k+1)}$
. Therefore, the image of
 $\pi _1(E(J^1_{k-1}))$
lies in
$\pi _1(E(J^1_{k-1}))$
lies in
![]() $\pi _1(X_k)^{(n-k+1)}$
. Because the longitude
$\pi _1(X_k)^{(n-k+1)}$
. Because the longitude
![]() $\lambda _{k-1}$
lies in
$\lambda _{k-1}$
lies in
 $\pi _1(E(J^1_{k-1}))^{(1)}$
, it follows that
$\pi _1(E(J^1_{k-1}))^{(1)}$
, it follows that
Because
![]() $i\le n-k+2$
, (3.1) implies that
$i\le n-k+2$
, (3.1) implies that
![]() $\lambda _{k-1} \in \pi _1(X_k)^{(i)} \subset ({\mathcal P}^{i-1}\pi _1(X_k))^{(1)}$
. Also, by the induction hypothesis,
$\lambda _{k-1} \in \pi _1(X_k)^{(i)} \subset ({\mathcal P}^{i-1}\pi _1(X_k))^{(1)}$
. Also, by the induction hypothesis,
![]() ${\mathcal P}^{i-1}\pi _1(X_k) \twoheadrightarrow {\mathcal P}^{i-1}\pi _1(X_{k-1})$
is an epimorphism with kernel
${\mathcal P}^{i-1}\pi _1(X_k) \twoheadrightarrow {\mathcal P}^{i-1}\pi _1(X_{k-1})$
is an epimorphism with kernel
![]() $\langle \lambda _{k-1}\rangle $
. It follows that the rightmost vertical arrow in the above diagram is an isomorphism. This completes the proof of the assertion.
$\langle \lambda _{k-1}\rangle $
. It follows that the rightmost vertical arrow in the above diagram is an isomorphism. This completes the proof of the assertion.
Proof of Assertion A. In the proof of Assertion C, we already showed that
![]() $\mu _k$
lies in
$\mu _k$
lies in
![]() $\pi _1(X_k)^{(n-k)}$
. This is the first part of Assertion A.
$\pi _1(X_k)^{(n-k)}$
. This is the first part of Assertion A.
It remains to show that
![]() $\mu _k$
is nontrivial in
$\mu _k$
is nontrivial in
![]() ${\mathcal P}^{n-k}\pi _1(X_k)/{\mathcal P}^{n-k+1}\pi _1(X_k)$
. We will use reverse induction for
${\mathcal P}^{n-k}\pi _1(X_k)/{\mathcal P}^{n-k+1}\pi _1(X_k)$
. We will use reverse induction for
![]() $k=n$
,
$k=n$
,
![]() $n-1,\ldots$
,
$n-1,\ldots$
,
![]() $0$
. For
$0$
. For
![]() $k=n$
,
$k=n$
,
![]() $\pi _1(X_n)/{\mathcal P}^1\pi _1(X_n) = H_1(X)$
by definition, and the meridian
$\pi _1(X_n)/{\mathcal P}^1\pi _1(X_n) = H_1(X)$
by definition, and the meridian
![]() $\mu _n$
of
$\mu _n$
of
![]() $J^1_n = K_1$
is a generator of
$J^1_n = K_1$
is a generator of
![]() $H_1(X)$
. So the assertion holds.
$H_1(X)$
. So the assertion holds.
For the case
![]() $k=n-1$
, let
$k=n-1$
, let
![]() $\Lambda =\mathbb {Q}[t^{\pm 1}]$
for brevity, and consider the following commutative diagram:
$\Lambda =\mathbb {Q}[t^{\pm 1}]$
for brevity, and consider the following commutative diagram:

Here,
![]() $H_1(X_n;\Lambda \Sigma ^{-1}) \to H_1(X;\Lambda \Sigma ^{-1})$
is an isomorphism, because
$H_1(X_n;\Lambda \Sigma ^{-1}) \to H_1(X;\Lambda \Sigma ^{-1})$
is an isomorphism, because
![]() $\pi _1(X)=\pi _1(X_0)$
is isomorphic to
$\pi _1(X)=\pi _1(X_0)$
is isomorphic to
![]() $\pi _1(X_n)/\langle \lambda _0,\ldots ,\lambda _{n-1}\rangle $
by Assertion C, and the longitudes
$\pi _1(X_n)/\langle \lambda _0,\ldots ,\lambda _{n-1}\rangle $
by Assertion C, and the longitudes
![]() $\lambda _0,\ldots ,\lambda _{n-1}$
lie in
$\lambda _0,\ldots ,\lambda _{n-1}$
lie in
![]() $\pi _1(X_n)^{(2)}$
by (3.1). The same argument shows that the bottom horizontal arrow is an isomorphism. (Alternatively, one may use Mayer-Vietoris arguments to show that they are isomorphisms.) Also, consider the Mayer-Vietoris sequence for
$\pi _1(X_n)^{(2)}$
by (3.1). The same argument shows that the bottom horizontal arrow is an isomorphism. (Alternatively, one may use Mayer-Vietoris arguments to show that they are isomorphisms.) Also, consider the Mayer-Vietoris sequence for
 $X = \overline {X\smallsetminus Z_L^0} \cup _{M(L)} Z_L^0$
:
$X = \overline {X\smallsetminus Z_L^0} \cup _{M(L)} Z_L^0$
:
 $$ \begin{align*} H_1(M(L);\Lambda\Sigma^{-1}) \longrightarrow H_1(X\smallsetminus Z_L^0;\Lambda\Sigma^{-1}) \oplus H_1(Z_L^0;\Lambda\Sigma^{-1}) \longrightarrow H_1(X;\Lambda\Sigma^{-1}) \longrightarrow 0. \end{align*} $$
$$ \begin{align*} H_1(M(L);\Lambda\Sigma^{-1}) \longrightarrow H_1(X\smallsetminus Z_L^0;\Lambda\Sigma^{-1}) \oplus H_1(Z_L^0;\Lambda\Sigma^{-1}) \longrightarrow H_1(X;\Lambda\Sigma^{-1}) \longrightarrow 0. \end{align*} $$
We have
![]() $H_1(M(L);\Lambda \Sigma ^{-1}) = 0$
by the hypothesis that
$H_1(M(L);\Lambda \Sigma ^{-1}) = 0$
by the hypothesis that
![]() $\Delta _L(t)$
is relatively prime to the polynomial
$\Delta _L(t)$
is relatively prime to the polynomial
![]() $\lambda (t)$
. It follows that the diagonal arrow on the right-hand side of the above diagram is an isomorphism.
$\lambda (t)$
. It follows that the diagonal arrow on the right-hand side of the above diagram is an isomorphism.
By our hypothesis, the kernel P of
is equal to the summand
![]() $\langle \alpha _D\rangle $
. So the other summand
$\langle \alpha _D\rangle $
. So the other summand
![]() $\langle \alpha _J\rangle $
injects into
$\langle \alpha _J\rangle $
injects into
![]() $H_1(X_n;\Lambda )$
. Because
$H_1(X_n;\Lambda )$
. Because
![]() $\langle \alpha _J\rangle \cong \Lambda /\langle \lambda \rangle $
is not annihilated by
$\langle \alpha _J\rangle \cong \Lambda /\langle \lambda \rangle $
is not annihilated by
![]() $\Sigma $
, this implies that
$\Sigma $
, this implies that
![]() $\langle \alpha _J\rangle $
injects into
$\langle \alpha _J\rangle $
injects into
![]() $H_1(X_n;\Lambda \Sigma ^{-1}) = H_1(X_n;\Lambda )\Sigma ^{-1}$
. By the above diagram, it follows that
$H_1(X_n;\Lambda \Sigma ^{-1}) = H_1(X_n;\Lambda )\Sigma ^{-1}$
. By the above diagram, it follows that
![]() $\langle \alpha _J\rangle $
injects into
$\langle \alpha _J\rangle $
injects into
 $H_1(X\smallsetminus Z_L^0;\Lambda \Sigma ^{-1})$
. Thus,
$H_1(X\smallsetminus Z_L^0;\Lambda \Sigma ^{-1})$
. Thus,
![]() $\alpha _J$
is nontrivial in
$\alpha _J$
is nontrivial in
 $H_1(X;\Lambda \Sigma ^{-1})/\operatorname {Im} H_1(Z_L^0;\Lambda \Sigma ^{-1})$
. Therefore, by the definition of
$H_1(X;\Lambda \Sigma ^{-1})/\operatorname {Im} H_1(Z_L^0;\Lambda \Sigma ^{-1})$
. Therefore, by the definition of
![]() ${\mathcal P}^2\pi _1(X_n)$
,
${\mathcal P}^2\pi _1(X_n)$
,
![]() $\alpha _J$
is nontrivial in the quotient
$\alpha _J$
is nontrivial in the quotient
 $$ \begin{align*} {\mathcal P}^1\pi_1(X_n)/{\mathcal P}^2\pi_1(X_n) \subset H_1(X;\Lambda\Sigma^{-1})/\operatorname{Im} H_1(Z_L^0;\Lambda\Sigma^{-1}). \end{align*} $$
$$ \begin{align*} {\mathcal P}^1\pi_1(X_n)/{\mathcal P}^2\pi_1(X_n) \subset H_1(X;\Lambda\Sigma^{-1})/\operatorname{Im} H_1(Z_L^0;\Lambda\Sigma^{-1}). \end{align*} $$
By Assertion C,
![]() ${\mathcal P}^1\pi _1(X_n)/{\mathcal P}^2\pi _1(X_n) \cong {\mathcal P}^1\pi _1(X_{n-1})/{\mathcal P}^2\pi _1(X_{n-1})$
. Also,
${\mathcal P}^1\pi _1(X_n)/{\mathcal P}^2\pi _1(X_n) \cong {\mathcal P}^1\pi _1(X_{n-1})/{\mathcal P}^2\pi _1(X_{n-1})$
. Also,
![]() $\alpha _J$
is isotopic to the meridian
$\alpha _J$
is isotopic to the meridian
![]() $\mu _{n-1}$
in
$\mu _{n-1}$
in
![]() $X_{n-1}$
. It follows that
$X_{n-1}$
. It follows that
![]() $\mu _{n-1}$
is nontrivial in the quotient
$\mu _{n-1}$
is nontrivial in the quotient
![]() ${\mathcal P}^1\pi _1(X_{n-1})/{\mathcal P}^2\pi _1(X_{n-1})$
. This is exactly the promised conclusion for
${\mathcal P}^1\pi _1(X_{n-1})/{\mathcal P}^2\pi _1(X_{n-1})$
. This is exactly the promised conclusion for
![]() $k=n-1$
.
$k=n-1$
.
Now, suppose
![]() $0\le k \le n-2$
. The induction hypothesis is that
$0\le k \le n-2$
. The induction hypothesis is that
![]() $\mu _{k+1}$
is nontrivial in the quotient
$\mu _{k+1}$
is nontrivial in the quotient
![]() ${\mathcal P}^{n-k-1}\pi _1(X_{k+1})/{\mathcal P}^{n-k}\pi _1(X_{k+1})$
. To show that
${\mathcal P}^{n-k-1}\pi _1(X_{k+1})/{\mathcal P}^{n-k}\pi _1(X_{k+1})$
. To show that
![]() $\mu _k$
is nontrivial in
$\mu _k$
is nontrivial in
![]() ${\mathcal P}^{n-k}\pi _1(X_k)/{\mathcal P}^{n-k+1}\pi _1(X_k)$
, we use an argument that is essentially the same as [Reference Cha3, Proof of Theorem 4.14], which was influenced by [Reference Cochran, Harvey and Leidy12]. Let
${\mathcal P}^{n-k}\pi _1(X_k)/{\mathcal P}^{n-k+1}\pi _1(X_k)$
, we use an argument that is essentially the same as [Reference Cha3, Proof of Theorem 4.14], which was influenced by [Reference Cochran, Harvey and Leidy12]. Let
![]() $R=\mathbb {Q}$
if
$R=\mathbb {Q}$
if
![]() $k\ge 1$
, and
$k\ge 1$
, and
![]() $R=\mathbb {Z}_{p_1}$
if
$R=\mathbb {Z}_{p_1}$
if
![]() $k=0$
. Let
$k=0$
. Let
 $$ \begin{align*} B \colon H_1(M(J^1_{k+1});R[t^{\pm1}])\times H_1(M(J^1_{k+1});R[t^{\pm1}]) \longrightarrow R(t)/R[t^{\pm1}] \end{align*} $$
$$ \begin{align*} B \colon H_1(M(J^1_{k+1});R[t^{\pm1}])\times H_1(M(J^1_{k+1});R[t^{\pm1}]) \longrightarrow R(t)/R[t^{\pm1}] \end{align*} $$
be the classical Blanchfield pairing of
 $J^1_{k+1}$
over R-coefficients. For brevity, let
$J^1_{k+1}$
over R-coefficients. For brevity, let
![]() $G=\pi _1(X_{k+1})/{\mathcal P}^{n-k}\pi _1(X_{k+1})$
. Consider the noncommutative Alexander module
$G=\pi _1(X_{k+1})/{\mathcal P}^{n-k}\pi _1(X_{k+1})$
. Consider the noncommutative Alexander module
 ${\mathcal A}:= H_1(M(J^1_{k+1}); RG)$
. The noncommutative Blanchfield pairing
${\mathcal A}:= H_1(M(J^1_{k+1}); RG)$
. The noncommutative Blanchfield pairing
![]() ${\mathcal B} \colon {\mathcal A}\times {\mathcal A} \to {\mathcal K}/RG$
is defined following [Reference Cochran, Orr and Teichner16, Theorem 2.13], where
${\mathcal B} \colon {\mathcal A}\times {\mathcal A} \to {\mathcal K}/RG$
is defined following [Reference Cochran, Orr and Teichner16, Theorem 2.13], where
![]() ${\mathcal K}$
is the skew-quotient field of
${\mathcal K}$
is the skew-quotient field of
![]() $RG$
. (For
$RG$
. (For
![]() $R=\mathbb {Z}_{p_1}$
, see also [Reference Cha3, Section 5].) In our case, because
$R=\mathbb {Z}_{p_1}$
, see also [Reference Cha3, Section 5].) In our case, because
![]() $2\le n-k\le n$
, from Definition 3.1 it follows that
$2\le n-k\le n$
, from Definition 3.1 it follows that
![]() $G=\pi _1(X_{k+1})/{\mathcal P}^{n-k}\pi _1(X_{k+1})$
is poly-torsion-free-abelian and, consequently,
$G=\pi _1(X_{k+1})/{\mathcal P}^{n-k}\pi _1(X_{k+1})$
is poly-torsion-free-abelian and, consequently,
![]() $RG$
is an Ore domain due to [Reference Cochran, Orr and Teichner16, Proposition 2.5] and [Reference Cha3, Lemma 5.2]. We will use the following known facts:
$RG$
is an Ore domain due to [Reference Cochran, Orr and Teichner16, Proposition 2.5] and [Reference Cha3, Lemma 5.2]. We will use the following known facts:
-
(1) The nontriviality of
 $\mu _{k+1}$
in
$\mu _{k+1}$
in
 ${\mathcal P}^{n-k-1}\pi _1(X_{k+1})/{\mathcal P}^{n-k}\pi _1(X_{k+1}) \subset G$
implies that
${\mathcal P}^{n-k-1}\pi _1(X_{k+1})/{\mathcal P}^{n-k}\pi _1(X_{k+1}) \subset G$
implies that
 ${\mathcal A} \cong RG {\mathbin {\mathop {\otimes }_{{R[t^{\pm 1}]}}}} H_1(M(J^1_{k+1});R[t^{\pm 1}])$
and that
${\mathcal A} \cong RG {\mathbin {\mathop {\otimes }_{{R[t^{\pm 1}]}}}} H_1(M(J^1_{k+1});R[t^{\pm 1}])$
and that
 ${\mathcal B}(1\otimes x, 1\otimes y) = 0$
if and only if
${\mathcal B}(1\otimes x, 1\otimes y) = 0$
if and only if
 $B(x,y)=0$
. This is due to [Reference Leidy33, Theorem 4.7], [Reference Cha2, Theorem 5.16] and [Reference Cochran, Harvey and Leidy12, Lemma 6.5, Theorem 6.6]. See also [Reference Cha3, Theorem 5.4].
$B(x,y)=0$
. This is due to [Reference Leidy33, Theorem 4.7], [Reference Cha2, Theorem 5.16] and [Reference Cochran, Harvey and Leidy12, Lemma 6.5, Theorem 6.6]. See also [Reference Cha3, Theorem 5.4]. -
(2) The 4-manifold
 $X_{k+1}$
endowed with
$X_{k+1}$
endowed with
 $\pi _1(X_{k+1}) \to G$
is a Blanchfield bordism in the sense of [Reference Cha4, Definition 4.11], due to an argument in [Reference Cha4, p. 3270] that uses [Reference Cha4, Theorem 4.13]. (The 4-manifold
$\pi _1(X_{k+1}) \to G$
is a Blanchfield bordism in the sense of [Reference Cha4, Definition 4.11], due to an argument in [Reference Cha4, p. 3270] that uses [Reference Cha4, Theorem 4.13]. (The 4-manifold
 $W_{k+1}$
in [Reference Cha4] plays the role of our
$W_{k+1}$
in [Reference Cha4] plays the role of our
 $X_{k+1}$
.) The only property of a Blanchfield bordism we need is the following: for all z in
$X_{k+1}$
.) The only property of a Blanchfield bordism we need is the following: for all z in
 $\operatorname {Ker}\{{\mathcal A} \to H_1(X_{k+1};RG)\}$
,
$\operatorname {Ker}\{{\mathcal A} \to H_1(X_{k+1};RG)\}$
,
 ${\mathcal B}(z,z)=0$
by [Reference Cha4, Theorem 4.12].
${\mathcal B}(z,z)=0$
by [Reference Cha4, Theorem 4.12].
Recall that
 $E(P_k\sqcup \eta _k) \cup E(J^1_k) = E(J^1_{k+1}) \subset M(J^1_{k+1})\subset \partial X_{k+1}$
. Denote a zero-linking longitude of
$E(P_k\sqcup \eta _k) \cup E(J^1_k) = E(J^1_{k+1}) \subset M(J^1_{k+1})\subset \partial X_{k+1}$
. Denote a zero-linking longitude of
![]() $\eta _k$
in
$\eta _k$
in
 $E(P_k\sqcup \eta _k)\subset M(J^1_{k+1})$
by
$E(P_k\sqcup \eta _k)\subset M(J^1_{k+1})$
by
![]() $\eta _k$
, abusing notation. If
$\eta _k$
, abusing notation. If
![]() $\eta _k$
is trivial in
$\eta _k$
is trivial in
![]() ${\mathcal P}^{n-k}\pi _1(X_{k+1})/{\mathcal P}^{n-k+1}\pi _1(X_{k+1})$
, then by the definition of
${\mathcal P}^{n-k}\pi _1(X_{k+1})/{\mathcal P}^{n-k+1}\pi _1(X_{k+1})$
, then by the definition of
![]() ${\mathcal P}^{n-k+1}$
,
${\mathcal P}^{n-k+1}$
,
![]() $\eta _k=1\otimes \eta _k$
lies in the kernel of
$\eta _k=1\otimes \eta _k$
lies in the kernel of
![]() ${\mathcal A} \to H_1(X_{k+1};RG)$
. By (2), from this it follows that
${\mathcal A} \to H_1(X_{k+1};RG)$
. By (2), from this it follows that
![]() ${\mathcal B}(1\otimes \eta _k,1\otimes \eta _k) = 0$
and, consequently, by (1),
${\mathcal B}(1\otimes \eta _k,1\otimes \eta _k) = 0$
and, consequently, by (1),
![]() $B(\eta _k,\eta _k)=0$
. Because
$B(\eta _k,\eta _k)=0$
. Because
 $J^1_{k+1} = P_k(\eta _k,J^1_k)$
with
$J^1_{k+1} = P_k(\eta _k,J^1_k)$
with
![]() $k\le n-2$
, the Alexander module
$k\le n-2$
, the Alexander module
 $H_1(M(J^1_{k+1});R[t^{\pm 1}])$
is isomorphic to that of stevedore’s knot
$H_1(M(J^1_{k+1});R[t^{\pm 1}])$
is isomorphic to that of stevedore’s knot
![]() $P_k$
, which is a cyclic module generated by
$P_k$
, which is a cyclic module generated by
![]() $\eta _k$
. It contradicts the nonsingularity of the classical Blanchfield pairing B. This shows that
$\eta _k$
. It contradicts the nonsingularity of the classical Blanchfield pairing B. This shows that
![]() $\eta _k$
is nontrivial in
$\eta _k$
is nontrivial in
![]() ${\mathcal P}^{n-k}\pi _1(X_{k+1})/{\mathcal P}^{n-k+1}\pi _1(X_{k+1})$
, which is isomorphic to
${\mathcal P}^{n-k}\pi _1(X_{k+1})/{\mathcal P}^{n-k+1}\pi _1(X_{k+1})$
, which is isomorphic to
![]() ${\mathcal P}^{n-k}\pi _1(X_k)/{\mathcal P}^{n-k+1}\pi _1(X_k)$
by Assertion C. Because
${\mathcal P}^{n-k}\pi _1(X_k)/{\mathcal P}^{n-k+1}\pi _1(X_k)$
by Assertion C. Because
![]() $\eta _k$
is identified with
$\eta _k$
is identified with
![]() $\mu _k$
, it follows that
$\mu _k$
, it follows that
![]() $\mu _k$
is nontrivial in the quotient
$\mu _k$
is nontrivial in the quotient
![]() ${\mathcal P}^{n-k}\pi _1(X_k)/{\mathcal P}^{n-k+1}\pi _1(X_k)$
. This completes the proof of Assertion A.
${\mathcal P}^{n-k}\pi _1(X_k)/{\mathcal P}^{n-k+1}\pi _1(X_k)$
. This completes the proof of Assertion A.
Proof of Assertion B. Recall that Assertion B says that
 $\pi _1(Z_0^L)^{(i)}$
maps to
$\pi _1(Z_0^L)^{(i)}$
maps to
![]() ${\mathcal P}^{i+1}\pi _1(X)$
for
${\mathcal P}^{i+1}\pi _1(X)$
for
![]() $1\le i \le n$
. To show this for
$1\le i \le n$
. To show this for
![]() $i=1$
, observe that the composition
$i=1$
, observe that the composition
 $$ \begin{align*} \begin{aligned} \frac{\pi_1(Z_L^0)^{(1)}}{\pi_1(Z_L^0)^{(2)}} = H_1(Z_L^0;\mathbb{Z}[t^{\pm1}]) & \longrightarrow H_1(X;\mathbb{Z}[t^{\pm1}]) \longrightarrow H_1(X;\mathbb{Q}[t^{\pm1}]\Sigma^{-1}) \\ & \longrightarrow H_1(X;\mathbb{Q}[t^{\pm1}]\Sigma^{-1})/\operatorname{Im} H_1(Z_L^0;\mathbb{Q}[t^{\pm1}]\Sigma^{-1}) \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \frac{\pi_1(Z_L^0)^{(1)}}{\pi_1(Z_L^0)^{(2)}} = H_1(Z_L^0;\mathbb{Z}[t^{\pm1}]) & \longrightarrow H_1(X;\mathbb{Z}[t^{\pm1}]) \longrightarrow H_1(X;\mathbb{Q}[t^{\pm1}]\Sigma^{-1}) \\ & \longrightarrow H_1(X;\mathbb{Q}[t^{\pm1}]\Sigma^{-1})/\operatorname{Im} H_1(Z_L^0;\mathbb{Q}[t^{\pm1}]\Sigma^{-1}) \end{aligned} \end{align*} $$
is obviously zero. By definition of
![]() ${\mathcal P}^2 \pi _1(X)$
, it follows that
${\mathcal P}^2 \pi _1(X)$
, it follows that
 $\pi _1(Z_L^0)^{(1)}$
maps to
$\pi _1(Z_L^0)^{(1)}$
maps to
![]() ${\mathcal P}^2\pi _1(X)$
. Therefore, for all
${\mathcal P}^2\pi _1(X)$
. Therefore, for all
![]() $1\le i\le n$
,
$1\le i\le n$
,
 $\pi _1(Z_L^0)^{(i)} = (\pi _1(Z_L^0)^{(1)})^{(i-1)}$
maps to
$\pi _1(Z_L^0)^{(i)} = (\pi _1(Z_L^0)^{(1)})^{(i-1)}$
maps to
![]() ${\mathcal P}^2\pi _1(X)^{(i-1)}$
, which is a subgroup of
${\mathcal P}^2\pi _1(X)^{(i-1)}$
, which is a subgroup of
![]() ${\mathcal P}^{i+1}\pi _1(X)$
.
${\mathcal P}^{i+1}\pi _1(X)$
.
3.2. Obstruction from Cheeger-Gromov
 $\rho$
-invariants
$\rho$
-invariants
Now, we will use the Cheeger-Gromov
![]() $\rho $
-invariant to derive a contradiction. We begin with some background. For a connected closed 3-manifold M and a homomorphism
$\rho $
-invariant to derive a contradiction. We begin with some background. For a connected closed 3-manifold M and a homomorphism
![]() $\phi \colon \pi _1(M) \to \Gamma $
with
$\phi \colon \pi _1(M) \to \Gamma $
with
![]() $\Gamma $
arbitrary, the Cheeger-Gromov invariant
$\Gamma $
arbitrary, the Cheeger-Gromov invariant
![]() $\rho ^{(2)}(M,\phi )\in \mathbb {R}$
is defined [Reference Cheeger and Gromov10]. The value of
$\rho ^{(2)}(M,\phi )\in \mathbb {R}$
is defined [Reference Cheeger and Gromov10]. The value of
![]() $\rho ^{(2)}(M,\phi )$
is preserved under composition with automorphisms of
$\rho ^{(2)}(M,\phi )$
is preserved under composition with automorphisms of
![]() $\pi _1(M)$
, so one can view
$\pi _1(M)$
, so one can view
![]() $\rho ^{(2)}(M,\phi )$
as an invariant of M equipped with (the homotopy class of) a map
$\rho ^{(2)}(M,\phi )$
as an invariant of M equipped with (the homotopy class of) a map
![]() $\phi \colon M\to B\Gamma =K(\Gamma ,1)$
, instead of
$\phi \colon M\to B\Gamma =K(\Gamma ,1)$
, instead of
![]() $\pi _1(M) \to \Gamma $
. Even when M is not connected,
$\pi _1(M) \to \Gamma $
. Even when M is not connected,
![]() $\rho ^{(2)}(M,\phi )$
is defined for
$\rho ^{(2)}(M,\phi )$
is defined for
![]() $\phi \colon M\to B\Gamma $
, with additivity under disjoint union:
$\phi \colon M\to B\Gamma $
, with additivity under disjoint union:
![]() $\rho ^{(2)}(M,\phi )=\sum _i\rho ^{(2)}(M_i,\phi |_{M_i})$
where
$\rho ^{(2)}(M,\phi )=\sum _i\rho ^{(2)}(M_i,\phi |_{M_i})$
where
![]() $M=\bigcup _i M_i$
with components
$M=\bigcup _i M_i$
with components
![]() $M_i$
.
$M_i$
.
In this article, we do not use the definition of
![]() $\rho ^{(2)}(M,\rho ^{(2)})$
given in [Reference Cheeger and Gromov10]. Instead, for our purpose, the following
$\rho ^{(2)}(M,\rho ^{(2)})$
given in [Reference Cheeger and Gromov10]. Instead, for our purpose, the following
![]() $L^2$
-signature defect interpretation is useful. If
$L^2$
-signature defect interpretation is useful. If
![]() $M=\bigcup M_i$
bounds a 4-manifold W and
$M=\bigcup M_i$
bounds a 4-manifold W and
![]() $\phi \colon M\to B\Gamma $
factors through W, then
$\phi \colon M\to B\Gamma $
factors through W, then
![]() $\rho ^{(2)}(M,\phi ) = \sum _i\rho ^{(2)}(M_i,\phi |_{M_i})$
is equal to the
$\rho ^{(2)}(M,\phi ) = \sum _i\rho ^{(2)}(M_i,\phi |_{M_i})$
is equal to the
![]() $L^2$
-signature defect
$L^2$
-signature defect
 $\smash {\bar \sigma ^{(2)}_{\Gamma }(W)}:=\smash {\operatorname {sign}^{(2)}_{\Gamma }(W)} -\operatorname {sign}(W)$
, where
$\smash {\bar \sigma ^{(2)}_{\Gamma }(W)}:=\smash {\operatorname {sign}^{(2)}_{\Gamma }(W)} -\operatorname {sign}(W)$
, where
![]() $\operatorname {sign}(W)$
is the ordinary signature and
$\operatorname {sign}(W)$
is the ordinary signature and
 $\smash {\operatorname {sign}^{(2)}_{\Gamma }(W)}$
is the
$\smash {\operatorname {sign}^{(2)}_{\Gamma }(W)}$
is the
![]() $L^2$
-signature of W over the group
$L^2$
-signature of W over the group
![]() $\Gamma $
. We note that this approach can also be used to provide an alternative definition of
$\Gamma $
. We note that this approach can also be used to provide an alternative definition of
![]() $\rho ^{(2)}(M,\phi )$
for arbitrary
$\rho ^{(2)}(M,\phi )$
for arbitrary
![]() $(M,\phi )$
. As references, see, for instance, [Reference Chang and Weinberger9], [Reference Cochran and Teichner18, Section 2], [Reference Harvey23, Section 3], [Reference Cha5, Section 2.1].
$(M,\phi )$
. As references, see, for instance, [Reference Chang and Weinberger9], [Reference Cochran and Teichner18, Section 2], [Reference Harvey23, Section 3], [Reference Cha5, Section 2.1].
For our case, let
![]() $\Gamma := \pi _1(X) / {\mathcal P}^{n+1} \pi _1(X)$
. For a connected 3-dimensional submanifold M in X, denote the composition
$\Gamma := \pi _1(X) / {\mathcal P}^{n+1} \pi _1(X)$
. For a connected 3-dimensional submanifold M in X, denote the composition
![]() $\pi _1(M)\to \pi _1(X)\to \Gamma $
by
$\pi _1(M)\to \pi _1(X)\to \Gamma $
by
![]() $\phi $
, abusing notation.
$\phi $
, abusing notation.
Then, by the
![]() $L^2$
-signature defect interpretation for
$L^2$
-signature defect interpretation for
![]() $\rho ^{(2)}(\partial X,\phi )$
, we have
$\rho ^{(2)}(\partial X,\phi )$
, we have
 $$ \begin{align} \rho^{(2)}(M(J^1_0),\phi) &+ \sum_{k=0}^{n-2} \rho^{(2)}(M(P_k),\phi) + \rho^{(2)}(M(R(U,D)),\phi) = \bar\sigma^{(2)}_{\Gamma}(X) \end{align} $$
$$ \begin{align} \rho^{(2)}(M(J^1_0),\phi) &+ \sum_{k=0}^{n-2} \rho^{(2)}(M(P_k),\phi) + \rho^{(2)}(M(R(U,D)),\phi) = \bar\sigma^{(2)}_{\Gamma}(X) \end{align} $$
 $$\begin{align*} &\quad = \bar\sigma^{(2)}_{\Gamma}(V^0) + \bar\sigma^{(2)}_{\Gamma}(C) + \bar\sigma^{(2)}_{\Gamma}(Z^0_L) + \sum_{i,j} \bar\sigma^{(2)}_{\Gamma}(Z^0_{i,j}) + \sum_{k=0}^{n-1} \bar\sigma^{(2)}_{\Gamma}(E_k),\notag \end{align*}$$
$$\begin{align*} &\quad = \bar\sigma^{(2)}_{\Gamma}(V^0) + \bar\sigma^{(2)}_{\Gamma}(C) + \bar\sigma^{(2)}_{\Gamma}(Z^0_L) + \sum_{i,j} \bar\sigma^{(2)}_{\Gamma}(Z^0_{i,j}) + \sum_{k=0}^{n-1} \bar\sigma^{(2)}_{\Gamma}(E_k),\notag \end{align*}$$
where the 4-manifolds
 $Z^0_{i,j}$
are copies of
$Z^0_{i,j}$
are copies of
![]() $Z^0_i$
used in the construction of X. (See Figure 5.) The second equality is obtained by Novikov additivity of
$Z^0_i$
used in the construction of X. (See Figure 5.) The second equality is obtained by Novikov additivity of
![]() $L^2$
-signatures (for instance, see [Reference Cochran, Orr and Teichner16 Lemma 5.9]).
$L^2$
-signatures (for instance, see [Reference Cochran, Orr and Teichner16 Lemma 5.9]).
Recall that
![]() $\mu _0$
is the meridian of
$\mu _0$
is the meridian of
![]() $J^{1}_{0}$
in
$J^{1}_{0}$
in
 $M(J^{1}_{0})$
. By Assertion A,
$M(J^{1}_{0})$
. By Assertion A,
![]() $\phi (\mu _{0})$
is nontrivial in
$\phi (\mu _{0})$
is nontrivial in
![]() $\Gamma $
. Because
$\Gamma $
. Because
 $\phi (\mu _{J^{1}_{0}})$
lies in the subgroup
$\phi (\mu _{J^{1}_{0}})$
lies in the subgroup
![]() ${\mathcal P}^n\pi _{1}(X)/{\mathcal P}^{n+1} \pi _1(X)$
of
${\mathcal P}^n\pi _{1}(X)/{\mathcal P}^{n+1} \pi _1(X)$
of
![]() $\Gamma $
, which is a vector space over
$\Gamma $
, which is a vector space over
![]() $\mathbb {Z}_{p_1}$
by Definition 3.1, it follows that
$\mathbb {Z}_{p_1}$
by Definition 3.1, it follows that
![]() $\mu _{J^1_0}$
has order
$\mu _{J^1_0}$
has order
![]() $p_1$
. So the image of
$p_1$
. So the image of
 $\pi _1(M(J^1_0))$
in
$\pi _1(M(J^1_0))$
in
![]() $\Gamma $
under
$\Gamma $
under
![]() $\phi $
is isomorphic to
$\phi $
is isomorphic to
![]() $\mathbb {Z}_{p_1}$
. By [Reference Cha and Orr8, Lemma 8.7], this implies that
$\mathbb {Z}_{p_1}$
. By [Reference Cha and Orr8, Lemma 8.7], this implies that
 $$ \begin{align} \rho^{(2)}(M(J^1_0),\phi) = \rho(J^1_0,\mathbb{Z}_{p_1}), \end{align} $$
$$ \begin{align} \rho^{(2)}(M(J^1_0),\phi) = \rho(J^1_0,\mathbb{Z}_{p_1}), \end{align} $$
where
 $\rho (J^1_0,\mathbb {Z}_{p_1})$
is defined by (2.2).
$\rho (J^1_0,\mathbb {Z}_{p_1})$
is defined by (2.2).
By the explicit universal bound for the Cheeger-Gromov invariants given in [Reference Cha5, Theorem 1.9], we have
 $$ \begin{align} \big|\rho^{(2)}\big(M(P_k),\phi\big)\big| \le 6\cdot 69\,713\,280 \end{align} $$
$$ \begin{align} \big|\rho^{(2)}\big(M(P_k),\phi\big)\big| \le 6\cdot 69\,713\,280 \end{align} $$
because stevedore’s knot
![]() $P_k$
has six crossings. Similarly, by [Reference Cha5, Theorem 1.9],
$P_k$
has six crossings. Similarly, by [Reference Cha5, Theorem 1.9],
 $$ \begin{align} \big|\rho^{(2)}\big(M(R(U,D)),\phi\big)\big| \le (8m+92)\cdot 69\,713\,280 \end{align} $$
$$ \begin{align} \big|\rho^{(2)}\big(M(R(U,D)),\phi\big)\big| \le (8m+92)\cdot 69\,713\,280 \end{align} $$
because
![]() $R(U,D)$
has a diagram with
$R(U,D)$
has a diagram with
![]() $8m+92$
crossings (see Figure 1).
$8m+92$
crossings (see Figure 1).
By [Reference Cochran, Harvey and Leidy12, Lemma 2.4], the following holds for each k.
 $$ \begin{align} \bar\sigma^{(2)}_G(C)=0, \quad \bar\sigma^{(2)}_G(E_k)=0. \end{align} $$
$$ \begin{align} \bar\sigma^{(2)}_G(C)=0, \quad \bar\sigma^{(2)}_G(E_k)=0. \end{align} $$
To evaluate the terms
 $\bar \sigma ^{(2)}_{\Gamma }(V^0)$
and
$\bar \sigma ^{(2)}_{\Gamma }(V^0)$
and
 $\bar \sigma ^{(2)}_{\Gamma }(Z^0_L)$
in (3.2), we will use the following result.
$\bar \sigma ^{(2)}_{\Gamma }(Z^0_L)$
in (3.2), we will use the following result.
Theorem 3.3 Amenable Signature Theorem [Reference Cha3, Theorem 3.2]
Suppose that W is an integral
![]() $(n+1)$
-solution bounded by the zero surgery manifold
$(n+1)$
-solution bounded by the zero surgery manifold
![]() $M(K)$
of a knot K. Suppose that
$M(K)$
of a knot K. Suppose that
![]() $\Gamma $
is a group that satisfies
$\Gamma $
is a group that satisfies
![]() $\Gamma ^{(n+1)}=\{1\}$
and lies in Strebel’s class
$\Gamma ^{(n+1)}=\{1\}$
and lies in Strebel’s class
![]() $D(\mathbb {Z}_{p_1})$
in the sense of [Reference Strebel45] (or, equivalently,
$D(\mathbb {Z}_{p_1})$
in the sense of [Reference Strebel45] (or, equivalently,
![]() $\Gamma $
is a locally p-indicable group, due to [Reference Howie and Schneebeli26]). If
$\Gamma $
is a locally p-indicable group, due to [Reference Howie and Schneebeli26]). If
![]() $\phi \colon \pi _1(M(K)) \to \Gamma $
is a homomorphism that factors through
$\phi \colon \pi _1(M(K)) \to \Gamma $
is a homomorphism that factors through
![]() $\pi _1(W)$
and sends the meridian of K to an infinite-order element in
$\pi _1(W)$
and sends the meridian of K to an infinite-order element in
![]() $\Gamma $
, then
$\Gamma $
, then
 $\rho ^{(2)}(M(K),\phi ) = \bar \sigma ^{(2)}_{\Gamma }(W) = 0$
.
$\rho ^{(2)}(M(K),\phi ) = \bar \sigma ^{(2)}_{\Gamma }(W) = 0$
.
In our case,
![]() $V^0$
is an integral
$V^0$
is an integral
![]() $(n+1)$
-solution bounded by
$(n+1)$
-solution bounded by
![]() $M(K)$
. Also, the group
$M(K)$
. Also, the group
![]() $\Gamma $
lies in
$\Gamma $
lies in
![]() $D(\mathbb {Z}_{p_1})$
by [Reference Cha and Orr8, Lemma 6.8], and we have
$D(\mathbb {Z}_{p_1})$
by [Reference Cha and Orr8, Lemma 6.8], and we have
![]() $\Gamma ^{(n+1)}=\{1\}$
because
$\Gamma ^{(n+1)}=\{1\}$
because
![]() $\pi _1(X)^{(n+1)} \subset {\mathcal P}^{n+1}\pi _1(X)$
. The meridian of K has infinite order in
$\pi _1(X)^{(n+1)} \subset {\mathcal P}^{n+1}\pi _1(X)$
. The meridian of K has infinite order in
![]() $\Gamma $
because
$\Gamma $
because
![]() $\Gamma $
surjects onto
$\Gamma $
surjects onto
![]() $H_1(X)=\mathbb {Z}$
generated by the meridian. By Amenable Signature Theorem 3.3, it follows that
$H_1(X)=\mathbb {Z}$
generated by the meridian. By Amenable Signature Theorem 3.3, it follows that
 $$ \begin{align} \bar\sigma^{(2)}_{\Gamma}(V^0) = \rho^{(2)}(M(K),\phi)=0. \end{align} $$
$$ \begin{align} \bar\sigma^{(2)}_{\Gamma}(V^0) = \rho^{(2)}(M(K),\phi)=0. \end{align} $$
Now we will evaluate
 $\bar \sigma ^{(2)}_{\Gamma }(Z^0_L)$
, using the Amenable Signature Theorem again. Note that
$\bar \sigma ^{(2)}_{\Gamma }(Z^0_L)$
, using the Amenable Signature Theorem again. Note that
 $\partial Z^0_L=M(L)$
. An important difference from the above paragraph is that the 4-manifold
$\partial Z^0_L=M(L)$
. An important difference from the above paragraph is that the 4-manifold
![]() $Z^0_L$
is an integral n-solution, not
$Z^0_L$
is an integral n-solution, not
![]() $n+1$
. So, the Amenable Signature Theorem does not apply directly over
$n+1$
. So, the Amenable Signature Theorem does not apply directly over
![]() $\Gamma $
, because
$\Gamma $
, because
![]() $\Gamma ^{(n)}$
is not necessarily trivial. Instead, we proceed as follows.
$\Gamma ^{(n)}$
is not necessarily trivial. Instead, we proceed as follows.
Note that the map
 $\phi \colon \pi _1(M(L)) \to \pi _1(Z_L^0) \to \Gamma $
factors through
$\phi \colon \pi _1(M(L)) \to \pi _1(Z_L^0) \to \Gamma $
factors through
 $\pi _1(Z_L^0)/\pi _1(Z_L^0)^{(n)}$
, by Assertion B. Let G be the image of
$\pi _1(Z_L^0)/\pi _1(Z_L^0)^{(n)}$
, by Assertion B. Let G be the image of
 $\pi _1(Z_L^0)/\pi _1(Z_L^0)^{(n)}$
in
$\pi _1(Z_L^0)/\pi _1(Z_L^0)^{(n)}$
in
![]() $\Gamma $
, and let
$\Gamma $
, and let
![]() $\psi \colon \pi _1(M(L)) \to G$
be the map induced by
$\psi \colon \pi _1(M(L)) \to G$
be the map induced by
![]() $\phi $
. Because G injects into
$\phi $
. Because G injects into
![]() $\Gamma $
, we have
$\Gamma $
, we have
![]() $\rho ^{(2)}(M(L),\phi ) = \rho ^{(2)}(M(L),\psi )$
, by the
$\rho ^{(2)}(M(L),\phi ) = \rho ^{(2)}(M(L),\psi )$
, by the
![]() $L^2$
-induction property (for instance, see [Reference Cheeger and Gromov10, Eq. 2.3]). Now, because G is a subgroup of
$L^2$
-induction property (for instance, see [Reference Cheeger and Gromov10, Eq. 2.3]). Now, because G is a subgroup of
![]() $\Gamma $
that is in
$\Gamma $
that is in
![]() $D(\mathbb {Z}_{p_1})$
, G is in Strebel’s class
$D(\mathbb {Z}_{p_1})$
, G is in Strebel’s class
![]() $D({\mathbb {Z}}_{p_1})$
, too. Also,
$D({\mathbb {Z}}_{p_1})$
, too. Also,
![]() $G^{(n)}$
is trivial because it is the image of
$G^{(n)}$
is trivial because it is the image of
 $\pi _1(Z_L^0)/\pi _1(Z_L^0)^{(n)}$
. The meridian
$\pi _1(Z_L^0)/\pi _1(Z_L^0)^{(n)}$
. The meridian
![]() $\mu _L$
of L has infinite order in G, because G surjects onto
$\mu _L$
of L has infinite order in G, because G surjects onto
![]() $H_1(X)=\mathbb {Z}$
, which
$H_1(X)=\mathbb {Z}$
, which
![]() $\mu _L$
generates. Therefore, Amenable Signature Theorem 3.3 (with n in place of
$\mu _L$
generates. Therefore, Amenable Signature Theorem 3.3 (with n in place of
![]() $n+1$
) applies to
$n+1$
) applies to
![]() $(M(L),\psi )$
to conclude that
$(M(L),\psi )$
to conclude that
 $$ \begin{align} \bar\sigma^{(2)}_{\Gamma}(Z^0_L) = \rho^{(2)}(M(L),\phi) = \rho^{(2)}(M(L),\psi) = 0. \end{align} $$
$$ \begin{align} \bar\sigma^{(2)}_{\Gamma}(Z^0_L) = \rho^{(2)}(M(L),\phi) = \rho^{(2)}(M(L),\psi) = 0. \end{align} $$
By [Reference Cha and Kim6, Lemma 3.3], we may assume that each
 $Z^0_{i,j}$
has the property that
$Z^0_{i,j}$
has the property that
 $\bar \sigma ^{(2)}_{\Gamma }(Z^0_{i,j})$
is equal to either
$\bar \sigma ^{(2)}_{\Gamma }(Z^0_{i,j})$
is equal to either
![]() $0$
or
$0$
or
 $\rho (J^i_0,\mathbb {Z}_{p_1})$
. (Indeed, [Reference Cha and Kim6, Lemma 3.3] applies when every
$\rho (J^i_0,\mathbb {Z}_{p_1})$
. (Indeed, [Reference Cha and Kim6, Lemma 3.3] applies when every
![]() $J^i_0$
is
$J^i_0$
is
![]() $0$
-negative; it is the case by property (J1) in Subsection 2.1.) Moreover, by property (J3) in Subsection 2.1, we have
$0$
-negative; it is the case by property (J1) in Subsection 2.1.) Moreover, by property (J3) in Subsection 2.1, we have
 $$ \begin{align} \bar\sigma^{(2)}_{\Gamma}(Z^0_{i,j}) = \begin{cases} 0 \text{ or } \rho(J^1_0,\mathbb{Z}_{p_1}) &\text{if }i=1, \\ 0 &\text{if }i>1. \end{cases} \end{align} $$
$$ \begin{align} \bar\sigma^{(2)}_{\Gamma}(Z^0_{i,j}) = \begin{cases} 0 \text{ or } \rho(J^1_0,\mathbb{Z}_{p_1}) &\text{if }i=1, \\ 0 &\text{if }i>1. \end{cases} \end{align} $$
Now, combine (3.2)–(3.9) to obtain
 $$ \begin{align*} N\cdot |\rho^{(2)}(J^1_0,\mathbb{Z}_{p_1})| \le (6n+8m+86)\cdot 69\;713\;280, \end{align*} $$
$$ \begin{align*} N\cdot |\rho^{(2)}(J^1_0,\mathbb{Z}_{p_1})| \le (6n+8m+86)\cdot 69\;713\;280, \end{align*} $$
where N is one plus the number of the 4-manifolds
 $Z^0_{1,j}$
such that
$Z^0_{1,j}$
such that
 $\bar \sigma ^{(2)}(Z^0_{1,j})\ne 0$
. Because
$\bar \sigma ^{(2)}(Z^0_{1,j})\ne 0$
. Because
![]() $N\ge 1$
, it contradicts property (J2) in Subsection 2.1. This completes the proof that P cannot be equal to
$N\ge 1$
, it contradicts property (J2) in Subsection 2.1. This completes the proof that P cannot be equal to
![]() $\langle \alpha _D \rangle $
. That is, P must be
$\langle \alpha _D \rangle $
. That is, P must be
![]() $\langle \alpha _J \rangle $
.
$\langle \alpha _J \rangle $
.
4. Computing and estimating d-invariants
In this section, we will continue the proof of Theorem 2.2, to reach a contradiction under the hypothesis that
![]() $P=\langle \alpha _J\rangle $
.
$P=\langle \alpha _J\rangle $
.
4.1. Finite cyclic covers and their d-invariants
We begin by applying a trick introduced in [Reference Cochran, Harvey and Horn11], which we describe below. Let
![]() $K_1=K_0(\alpha ,J)$
be a satellite knot, where the pattern satisfies
$K_1=K_0(\alpha ,J)$
be a satellite knot, where the pattern satisfies
![]() $\mathrm {lk}(K_0,\alpha )=0$
. Then, the identity on
$\mathrm {lk}(K_0,\alpha )=0$
. Then, the identity on
![]() $E(K\sqcup \alpha )$
extends to a map
$E(K\sqcup \alpha )$
extends to a map
![]() $E(K_1)=E(K\sqcup \alpha )\cup E(J) \to E(K\sqcup \alpha ) \cup E(U)=E(K_0)$
that induces an isomorphism
$E(K_1)=E(K\sqcup \alpha )\cup E(J) \to E(K\sqcup \alpha ) \cup E(U)=E(K_0)$
that induces an isomorphism
![]() $H_1(M(K_1);\mathbb {Q}[t^{\pm 1}]) \to H_1(M(K_0);\mathbb {Q}[t^{\pm 1}])$
, under which we will identify the Alexander modules. Essentially, [Reference Cochran, Harvey and Horn11, Lemma 8.2] says the following (see also [Reference Cha and Kim6, Lemma 5.1]): if
$H_1(M(K_1);\mathbb {Q}[t^{\pm 1}]) \to H_1(M(K_0);\mathbb {Q}[t^{\pm 1}])$
, under which we will identify the Alexander modules. Essentially, [Reference Cochran, Harvey and Horn11, Lemma 8.2] says the following (see also [Reference Cha and Kim6, Lemma 5.1]): if
![]() $K_1=K_0(\alpha ,J)$
admits a
$K_1=K_0(\alpha ,J)$
admits a
![]() $1$
-negaton
$1$
-negaton
![]() $X_1$
bounded by
$X_1$
bounded by
![]() $M(K_1)$
and if J is unknotted by changing some positive crossings to negative, then
$M(K_1)$
and if J is unknotted by changing some positive crossings to negative, then
![]() $K_0$
has a
$K_0$
has a
![]() $1$
-negaton
$1$
-negaton
![]() $X_0$
bounded by
$X_0$
bounded by
![]() $M(K_0)$
such that the two maps
$M(K_0)$
such that the two maps
have the identical kernel. In particular, this applies to the satellite knot
 $K_1 = R(U,D)(\alpha _D,J^1_{n-1})$
defined in Subsection 2.1, because
$K_1 = R(U,D)(\alpha _D,J^1_{n-1})$
defined in Subsection 2.1, because
 $J^1_{n-1}=P_{n-2}(\eta _n, J^1_{n-2})$
is unknotted by changing a single positive crossing (see Figure 2). Note that here we use that
$J^1_{n-1}=P_{n-2}(\eta _n, J^1_{n-2})$
is unknotted by changing a single positive crossing (see Figure 2). Note that here we use that
![]() $n\ge 2$
. Therefore, in our case, the knot
$n\ge 2$
. Therefore, in our case, the knot
![]() $K_0 := R(U,D)$
admits a
$K_0 := R(U,D)$
admits a
![]() $1$
-negaton bounded by
$1$
-negaton bounded by
![]() $M(K_0)$
, say, W, such that
$M(K_0)$
, say, W, such that
We will derive a contradiction from the existence of this 1-negaton W for
![]() $K_0$
.
$K_0$
.
The next step is to pass to finite-degree branched cyclic covers, to which Heegaard Floer homology machinery applies, following [Reference Cha and Kim6, Section 5.1]. Let
![]() $\Sigma _r$
be the r-fold branched cyclic cover of
$\Sigma _r$
be the r-fold branched cyclic cover of
![]() $(S^3,K_0)$
. The curves
$(S^3,K_0)$
. The curves
![]() $\alpha _J$
and
$\alpha _J$
and
![]() $\alpha _D$
in Figure 1 represent homology classes in
$\alpha _D$
in Figure 1 represent homology classes in
![]() $\Sigma _r$
, say,
$\Sigma _r$
, say,
![]() $x_1$
and
$x_1$
and
![]() $x_2\in H_1(\Sigma _r)$
, respectively. (The classes
$x_2\in H_1(\Sigma _r)$
, respectively. (The classes
![]() $x_1$
and
$x_1$
and
![]() $x_2$
are defined up to covering transformation, but it will cause no problem in our argument.) Due to [Reference Milnor37], we have
$x_2$
are defined up to covering transformation, but it will cause no problem in our argument.) Due to [Reference Milnor37], we have
![]() $H_1(\Sigma _r) = H_1(M(K_0);\mathbb {Z}[t^{\pm 1}])/\langle t^r-1\rangle $
. Recall that
$H_1(\Sigma _r) = H_1(M(K_0);\mathbb {Z}[t^{\pm 1}])/\langle t^r-1\rangle $
. Recall that
![]() $H_1(M(K_0);\mathbb {Z}[t^{\pm 1}])$
is given by (2.1). From this, by elementary computation, it follows that
$H_1(M(K_0);\mathbb {Z}[t^{\pm 1}])$
is given by (2.1). From this, by elementary computation, it follows that
![]() $H_1(\Sigma _r)=\mathbb {Z}_{(m+1)^r-m^r} \oplus \mathbb {Z}_{(m+1)^r-m^r}$
and the summands are generated by
$H_1(\Sigma _r)=\mathbb {Z}_{(m+1)^r-m^r} \oplus \mathbb {Z}_{(m+1)^r-m^r}$
and the summands are generated by
![]() $x_1$
and
$x_1$
and
![]() $x_2$
. In particular,
$x_2$
. In particular,
![]() $\Sigma _r$
is a
$\Sigma _r$
is a
![]() $\mathbb {Z}_2$
-homology sphere.
$\mathbb {Z}_2$
-homology sphere.
For a rational homology 3-sphere Y and a spin
![]() $^c$
structure
$^c$
structure
![]() $\mathfrak {t}$
on Y, Ozsváth and Szabó defined a correction term invariant
$\mathfrak {t}$
on Y, Ozsváth and Szabó defined a correction term invariant
![]() $d(Y,\mathfrak {t})$
using the Heegaard Floer chain complex [Reference Ozsváth and Szabó40]. In case of a
$d(Y,\mathfrak {t})$
using the Heegaard Floer chain complex [Reference Ozsváth and Szabó40]. In case of a
![]() $\mathbb {Z}_2$
-homology sphere Y, the unique spin structure determines a canonical spin
$\mathbb {Z}_2$
-homology sphere Y, the unique spin structure determines a canonical spin
![]() $^c$
structure on Y, which we denote by
$^c$
structure on Y, which we denote by
![]() $\mathfrak {s}_Y$
, and all spin
$\mathfrak {s}_Y$
, and all spin
![]() $^c$
structures of Y are given in the form
$^c$
structures of Y are given in the form
![]() $\mathfrak {s}_Y+c$
, where
$\mathfrak {s}_Y+c$
, where
![]() $c\in H^2(Y)$
and
$c\in H^2(Y)$
and
![]() $+$
designates the action of
$+$
designates the action of
![]() $H^2(Y)$
on the set of spin
$H^2(Y)$
on the set of spin
![]() $^c$
structures. For
$^c$
structures. For
![]() $x\in H_1(Y)$
, let
$x\in H_1(Y)$
, let
![]() $\widehat x\in H^2(Y)$
be the Poincaré dual of x. Techniques used in [Reference Cha and Kim6, Reference Cochran, Harvey and Horn11] give us the following d-invariant obstruction.
$\widehat x\in H^2(Y)$
be the Poincaré dual of x. Techniques used in [Reference Cha and Kim6, Reference Cochran, Harvey and Horn11] give us the following d-invariant obstruction.
Lemma 4.1. Suppose that
![]() $M(K_0)$
bounds a
$M(K_0)$
bounds a
![]() $1$
-negaton that satisfies (4.1). If r is sufficiently large, then
$1$
-negaton that satisfies (4.1). If r is sufficiently large, then
![]() $d(\Sigma _r, \mathfrak {s}_{\Sigma _r}+ k\cdot \widehat {x_1})\ge 0$
for all
$d(\Sigma _r, \mathfrak {s}_{\Sigma _r}+ k\cdot \widehat {x_1})\ge 0$
for all
![]() $k\in \mathbb {Z}$
.
$k\in \mathbb {Z}$
.
Proof. Attach a 2-handle to a given
![]() $1$
-negaton W, along the zero-framed meridian of
$1$
-negaton W, along the zero-framed meridian of
![]() $K_0$
, to obtain a 4-manifold, which we temporarily call V. Note that
$K_0$
, to obtain a 4-manifold, which we temporarily call V. Note that
![]() $\partial V = S^3$
and the cocore of the 2-handle is a slicing disk
$\partial V = S^3$
and the cocore of the 2-handle is a slicing disk
![]() $\Delta \subset V$
bounded by
$\Delta \subset V$
bounded by
![]() $K_0$
. Take the r-fold branched cyclic cover of
$K_0$
. Take the r-fold branched cyclic cover of
![]() $(V,\Delta )$
and call it
$(V,\Delta )$
and call it
![]() $V_r$
. Here the r-fold branched cyclic cover is defined because, using that W is a
$V_r$
. Here the r-fold branched cyclic cover is defined because, using that W is a
![]() $1$
-negaton, we see that
$1$
-negaton, we see that
![]() $H_1(W\smallsetminus \Delta )=\mathbb {Z}$
generated by a meridian of
$H_1(W\smallsetminus \Delta )=\mathbb {Z}$
generated by a meridian of
![]() $\Delta $
. Indeed, if we denote by
$\Delta $
. Indeed, if we denote by
![]() $W_r$
the r-fold cyclic cover of W, then
$W_r$
the r-fold cyclic cover of W, then
![]() $V_r$
is obtained by attaching a 2-handle to
$V_r$
is obtained by attaching a 2-handle to
![]() $W_r$
. The 4-manifold
$W_r$
. The 4-manifold
![]() $V_r$
is bounded by
$V_r$
is bounded by
![]() $\Sigma _r$
.
$\Sigma _r$
.
The first key step is to relate the hypothesis
![]() $P=\langle \alpha _J\rangle $
, which is associated with the infinite cyclic cover, to the kernel
$P=\langle \alpha _J\rangle $
, which is associated with the infinite cyclic cover, to the kernel
associated with finite covers. The following is a modified version of [Reference Cha and Kim6, Lemma 5.2].
Assertion. Under the hypothesis that
![]() $P=\langle \alpha _J\rangle $
,
$P=\langle \alpha _J\rangle $
,
![]() $x_1\in G$
for all large primes r.
$x_1\in G$
for all large primes r.
Although we do not use it, we remark that the assertion implies that
![]() $G=\langle x_1\rangle $
, because it is known that
$G=\langle x_1\rangle $
, because it is known that
![]() $|G|$
is equal to
$|G|$
is equal to
![]() $|H_1(\Sigma _m)|^{1/2} = (m+1)^r-m^r\!.$
$|H_1(\Sigma _m)|^{1/2} = (m+1)^r-m^r\!.$
Proof of Assertion. Let
![]() $E_r$
be the r-fold cyclic cover of the exterior
$E_r$
be the r-fold cyclic cover of the exterior
![]() $E(K_0)$
for
$E(K_0)$
for
![]() $r \le \infty $
. Consider the following commutative diagram:
$r \le \infty $
. Consider the following commutative diagram:

The vertical arrows are induced by coverings and inclusions. Because
![]() $\alpha _J$
lies in the kernel of the composition of the top row by the hypothesis,
$\alpha _J$
lies in the kernel of the composition of the top row by the hypothesis,
![]() $\alpha _J$
is
$\alpha _J$
is
![]() $\mathbb {Z}$
-torsion in
$\mathbb {Z}$
-torsion in
![]() $H_1(W;\mathbb {Z}[t^{\pm 1}])$
. That is,
$H_1(W;\mathbb {Z}[t^{\pm 1}])$
. That is,
![]() $a\cdot \alpha _j=0$
in
$a\cdot \alpha _j=0$
in
![]() $H_1(W;\mathbb {Z}[t^{\pm 1}])$
for some nonzero
$H_1(W;\mathbb {Z}[t^{\pm 1}])$
for some nonzero
![]() $a\in \mathbb {Z}$
. By the above diagram, it follows that
$a\in \mathbb {Z}$
. By the above diagram, it follows that
![]() $a\cdot x_1 \in H_1(\Sigma _r)$
lies in the kernel G of
$a\cdot x_1 \in H_1(\Sigma _r)$
lies in the kernel G of
![]() $H_1(\Sigma _r)\to H_1(V_r)$
.
$H_1(\Sigma _r)\to H_1(V_r)$
.
Suppose that r is a prime not smaller than any prime factor of a. Under this assumption, we claim that
![]() $\gcd (a, (m+1)^r - m^r)=1$
. From this it follows that
$\gcd (a, (m+1)^r - m^r)=1$
. From this it follows that
![]() $x_1$
lies in G, because
$x_1$
lies in G, because
![]() $x_1$
has order
$x_1$
has order
![]() $(m+1)^r - m^r$
in
$(m+1)^r - m^r$
in
![]() $H_1(\Sigma _r)$
. This proves the assertion, modulo the proof of the claim.
$H_1(\Sigma _r)$
. This proves the assertion, modulo the proof of the claim.
To show the claim, it suffices to show that every prime factor q of a is relatively prime to
![]() $(m+1)^r - m^r\!.$
It is obviously true, if
$(m+1)^r - m^r\!.$
It is obviously true, if
![]() $q\mid m$
or
$q\mid m$
or
![]() $q\mid m+1$
. So, suppose that q divides neither m nor
$q\mid m+1$
. So, suppose that q divides neither m nor
![]() $m+1$
but q divides
$m+1$
but q divides
![]() $(m+1)^r - m^r\!.$
Let
$(m+1)^r - m^r\!.$
Let
![]() $u=m^*(m+1)$
, where
$u=m^*(m+1)$
, where
![]() $m^*$
is an arithmetic inverse of
$m^*$
is an arithmetic inverse of
![]() $m \bmod q$
. We have
$m \bmod q$
. We have
![]() $u^r \equiv 1 \bmod q$
by the hypothesis and
$u^r \equiv 1 \bmod q$
by the hypothesis and
![]() $u^{q-1} \equiv 1 \bmod q$
by Fermat’s little theorem. Because r is a prime and
$u^{q-1} \equiv 1 \bmod q$
by Fermat’s little theorem. Because r is a prime and
![]() $u\not \equiv 1 \bmod q$
, it follows that
$u\not \equiv 1 \bmod q$
, it follows that
![]() $r\mid q-1$
. This contradicts the assumption that
$r\mid q-1$
. This contradicts the assumption that
![]() $r\ge q$
. This completes the proof of the claim.
$r\ge q$
. This completes the proof of the claim.
The assertion enables us to invoke a result of Cochran, Harvey and Horn [Reference Cochran, Harvey and Horn11, Theorem 6.5], which says the following: if W is a
![]() $1$
-negaton bounded by
$1$
-negaton bounded by
![]() $M(K_0)$
, then
$M(K_0)$
, then
![]() $d(\Sigma _r,\widehat x)\ge 0$
for all x lying in
$d(\Sigma _r,\widehat x)\ge 0$
for all x lying in
![]() $G=\operatorname {Ker}\{H_1(\Sigma _r) \to H_1(V_r)\}$
. Applying this to
$G=\operatorname {Ker}\{H_1(\Sigma _r) \to H_1(V_r)\}$
. Applying this to
![]() $x=k\cdot x_1$
, the proof of Lemma 4.1 is completed.
$x=k\cdot x_1$
, the proof of Lemma 4.1 is completed.
Theorem 4.2. Let
![]() $m\ge 1$
be an odd integer and
$m\ge 1$
be an odd integer and
![]() $r\ge 1$
be an odd prime power. Let k be the arithmetic inverse of
$r\ge 1$
be an odd prime power. Let k be the arithmetic inverse of
![]() $2 \bmod (m+1)^r-m^r\!.$
Then
$2 \bmod (m+1)^r-m^r\!.$
Then
 $d(\Sigma _r, \mathfrak {s}_{\Sigma _r} + k\widehat x_1) \le -\frac 32$
.
$d(\Sigma _r, \mathfrak {s}_{\Sigma _r} + k\widehat x_1) \le -\frac 32$
.
On the other hand, Lemma 4.1 says that
![]() $d(\Sigma _r, \mathfrak {s}_{\Sigma _r} + k\widehat x_1)$
must be nonnegative. This contradiction implies that the kernel P defined in (2.4) cannot be equal to
$d(\Sigma _r, \mathfrak {s}_{\Sigma _r} + k\widehat x_1)$
must be nonnegative. This contradiction implies that the kernel P defined in (2.4) cannot be equal to
![]() $\langle \alpha _J\rangle $
. This completes the proof of Theorem 2.2.
$\langle \alpha _J\rangle $
. This completes the proof of Theorem 2.2.
For
![]() $m=1$
, Theorem 4.2 was already shown in [Reference Cha and Kim6, Theorem 5.4]. (We remark that the symbol m in [Reference Cha and Kim6] denotes our r.) So, in the remaining part of this article, we will assume that
$m=1$
, Theorem 4.2 was already shown in [Reference Cha and Kim6, Theorem 5.4]. (We remark that the symbol m in [Reference Cha and Kim6] denotes our r.) So, in the remaining part of this article, we will assume that
![]() $m>1$
.
$m>1$
.
Proof of Theorem 4.2. Let A and B be the 3-manifolds given by the surgery presentations in Figure 6. Let
![]() $Y_r$
be the connected sum of A, B and
$Y_r$
be the connected sum of A, B and
![]() $r-3$
copies of the lens space
$r-3$
copies of the lens space
![]() $L_{2m+1,1}$
. (We use the orientation convention that
$L_{2m+1,1}$
. (We use the orientation convention that
![]() $L_{p,1}$
is the p-framed surgery on the trivial knot U in
$L_{p,1}$
is the p-framed surgery on the trivial knot U in
![]() $S^3$
.) Then, arguments in [Reference Cha and Kim6, Section 6.1] construct a negative definite 4-manifold W with
$S^3$
.) Then, arguments in [Reference Cha and Kim6, Section 6.1] construct a negative definite 4-manifold W with
![]() $\partial W = Y_r \sqcup -\Sigma _r$
and
$\partial W = Y_r \sqcup -\Sigma _r$
and
![]() $b_2(W)=(2m+1)r-4m+1$
and construct a spin
$b_2(W)=(2m+1)r-4m+1$
and construct a spin
![]() $^c$
structure
$^c$
structure
![]() $\mathfrak {t}$
on W such that
$\mathfrak {t}$
on W such that
![]() $c_1(\mathfrak {t})^2 = -r$
,
$c_1(\mathfrak {t})^2 = -r$
,
![]() $c_1(\mathfrak {t}|_{\Sigma _r}) = \widehat {x_1}$
and
$c_1(\mathfrak {t}|_{\Sigma _r}) = \widehat {x_1}$
and
![]() $c_1(\mathfrak {t}|_{Y_r}) = 0$
. Indeed, [Reference Cha and Kim6, Section 6.1] is the case of
$c_1(\mathfrak {t}|_{Y_r}) = 0$
. Indeed, [Reference Cha and Kim6, Section 6.1] is the case of
![]() $m=1$
. We do not repeat the details here, because exactly the same method works under our assumption that
$m=1$
. We do not repeat the details here, because exactly the same method works under our assumption that
![]() $m\ge 1$
is odd. Perhaps the least obvious part is that the inverse matrix
$m\ge 1$
is odd. Perhaps the least obvious part is that the inverse matrix
![]() $P^{-1}$
in [Reference Cha and Kim6, Eq. (6.10)] should be replaced with a block matrix
$P^{-1}$
in [Reference Cha and Kim6, Eq. (6.10)] should be replaced with a block matrix
![]() $P^{-1}=(R_{ij})_{1\le i,j\le r-1}$
with
$P^{-1}=(R_{ij})_{1\le i,j\le r-1}$
with
 $$ \begin{align*} R_{ij} = \frac{((m+1)^i-m^i)((m+1)^{r-j}-m^{r-j})}{(m+1)^r-m^r} \begin{bmatrix} 0 & (m+1)^{i-j} \\ m^{i-j} & 0 \end{bmatrix} \text{ for } i\ge j, \end{align*} $$
$$ \begin{align*} R_{ij} = \frac{((m+1)^i-m^i)((m+1)^{r-j}-m^{r-j})}{(m+1)^r-m^r} \begin{bmatrix} 0 & (m+1)^{i-j} \\ m^{i-j} & 0 \end{bmatrix} \text{ for } i\ge j, \end{align*} $$
and
 $R_{ij}=R^T_{ji}$
for
$R_{ij}=R^T_{ji}$
for
![]() $i<j$
.
$i<j$
.

Figure 6 The 3-manifolds A and B. The box
![]() $2m+1$
represents
$2m+1$
represents
![]() $2m+1$
right-handed full twists between vertical strands.
$2m+1$
right-handed full twists between vertical strands.
By applying Ozsváth-Szabó’s d-invariant inequality [Reference Ozsváth and Szabó40, Theorem 9.6] to the negative definite 4-manifold W, and by using additivity of the d-invariant under connected sum, we have
 $$ \begin{align*} \begin{aligned} d(\Sigma_r,\mathfrak{t}|_{\Sigma_r}) & \le d(Y_r,\mathfrak{t}|_{Y_r}) - \frac{c_1(\mathfrak{t})^2 + b_2(W)}{4} \\ & = d(A,\mathfrak{t}|_{A}) + d(B,\mathfrak{t}|_{B}) + (r-3)d(L_{2m+1,1},\mathfrak{t}|_{L_{2m+1,1}}) - \frac{2mr-4m+1}{4}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} d(\Sigma_r,\mathfrak{t}|_{\Sigma_r}) & \le d(Y_r,\mathfrak{t}|_{Y_r}) - \frac{c_1(\mathfrak{t})^2 + b_2(W)}{4} \\ & = d(A,\mathfrak{t}|_{A}) + d(B,\mathfrak{t}|_{B}) + (r-3)d(L_{2m+1,1},\mathfrak{t}|_{L_{2m+1,1}}) - \frac{2mr-4m+1}{4}. \end{aligned} \end{align*} $$
Because
![]() $c_1(\mathfrak {t}|_{Y_r})=0$
, we have
$c_1(\mathfrak {t}|_{Y_r})=0$
, we have
![]() $\mathfrak {t}|_{L_{2m+1,1}}= \mathfrak {s}_{L_{2m+1,1}}$
. By a d-invariant formula for lens spaces given in [Reference Ozsváth and Szabó40, Proposition 4.8],
$\mathfrak {t}|_{L_{2m+1,1}}= \mathfrak {s}_{L_{2m+1,1}}$
. By a d-invariant formula for lens spaces given in [Reference Ozsváth and Szabó40, Proposition 4.8],
![]() $d(L_{2m+1,1},\mathfrak {s}_{L_{2m+1,1}})=m/2$
. By Lemmas 4.3 and 4.4, which we will prove below, we have
$d(L_{2m+1,1},\mathfrak {s}_{L_{2m+1,1}})=m/2$
. By Lemmas 4.3 and 4.4, which we will prove below, we have
![]() $d(A,\mathfrak {t}|_A) \le (m-7)/4$
and
$d(A,\mathfrak {t}|_A) \le (m-7)/4$
and
![]() $d(B,\mathfrak {t}|_B) \le (m+2)/4$
. Combine them with the above inequality to obtain
$d(B,\mathfrak {t}|_B) \le (m+2)/4$
. Combine them with the above inequality to obtain
 $d(\Sigma _r, \mathfrak {t}|_{\Sigma _r}) \le -\frac 32$
. Observe that
$d(\Sigma _r, \mathfrak {t}|_{\Sigma _r}) \le -\frac 32$
. Observe that
![]() $c_1(\mathfrak {t}|_{\Sigma _r})=\widehat {x_1} = 2k \widehat {x_1} = c_1(\mathfrak {s}_{\Sigma _r} + k \widehat {x_1})$
, because
$c_1(\mathfrak {t}|_{\Sigma _r})=\widehat {x_1} = 2k \widehat {x_1} = c_1(\mathfrak {s}_{\Sigma _r} + k \widehat {x_1})$
, because
![]() $2k\equiv 1\bmod (m+1)^r-m^r$
and
$2k\equiv 1\bmod (m+1)^r-m^r$
and
![]() $x_1$
has order
$x_1$
has order
![]() $(m+1)^r-m^r\!.$
It follows that
$(m+1)^r-m^r\!.$
It follows that
![]() $\mathfrak {t}|_{\Sigma _r} = \mathfrak {s}_{\Sigma _r}$
, because
$\mathfrak {t}|_{\Sigma _r} = \mathfrak {s}_{\Sigma _r}$
, because
![]() $\Sigma _r$
is a
$\Sigma _r$
is a
![]() $\mathbb {Z}_2$
-homology sphere.
$\mathbb {Z}_2$
-homology sphere.
Note that
 $|H_1(A)| = \bigl |\det \left [\begin {smallmatrix}m & -2m-1 \\ -2m-1 & m+1\end {smallmatrix}\right ]\bigr | = 3m^2+3m+1$
is odd, so there is a unique spin
$|H_1(A)| = \bigl |\det \left [\begin {smallmatrix}m & -2m-1 \\ -2m-1 & m+1\end {smallmatrix}\right ]\bigr | = 3m^2+3m+1$
is odd, so there is a unique spin
![]() $^c$
structure
$^c$
structure
![]() $\mathfrak {s}$
of A such that
$\mathfrak {s}$
of A such that
![]() $c_1(\mathfrak {s}) = 0$
.
$c_1(\mathfrak {s}) = 0$
.
Lemma 4.3. For the spin
![]() $^c$
structure
$^c$
structure
![]() $\mathfrak {s}$
on A with
$\mathfrak {s}$
on A with
![]() $c_1(\mathfrak {s}) = 0$
,
$c_1(\mathfrak {s}) = 0$
,
![]() $d(A,\mathfrak {s}) \le (m-7)/4$
.
$d(A,\mathfrak {s}) \le (m-7)/4$
.
For the case of B, because
 $|H_1(B)| = \bigl |\det \left [\begin {smallmatrix}m & -2m-1 \\ -2m-1 & m+2\end {smallmatrix}\right ] \bigr | = 3m^2+2m+1$
is even, there are exactly two spin
$|H_1(B)| = \bigl |\det \left [\begin {smallmatrix}m & -2m-1 \\ -2m-1 & m+2\end {smallmatrix}\right ] \bigr | = 3m^2+2m+1$
is even, there are exactly two spin
![]() $^c$
structures
$^c$
structures
![]() $\mathfrak {s}$
of B such that
$\mathfrak {s}$
of B such that
![]() $c_1(\mathfrak {s}) = 0$
.
$c_1(\mathfrak {s}) = 0$
.
Lemma 4.4. If
![]() $\mathfrak {s}$
is a spin
$\mathfrak {s}$
is a spin
![]() $^c$
structure of B such that
$^c$
structure of B such that
![]() $c_1(\mathfrak {s}) = 0$
, then
$c_1(\mathfrak {s}) = 0$
, then
![]() $d(B,\mathfrak {s}) \le (m+2)/4$
.
$d(B,\mathfrak {s}) \le (m+2)/4$
.
Proof of Lemma 4.3. Let
![]() $A'$
be the 3-manifold obtained by
$A'$
be the 3-manifold obtained by
![]() $(m+6)$
-surgery on the knot
$(m+6)$
-surgery on the knot
![]() $T\#-D$
. See Figure 7. Let Y be the 3-manifold given by the last surgery diagram in Figure 7. The four diagrams in Figure 7 describe a cobordism from
$T\#-D$
. See Figure 7. Let Y be the 3-manifold given by the last surgery diagram in Figure 7. The four diagrams in Figure 7 describe a cobordism from
![]() $A\# A'$
to Y. More precisely, start by taking
$A\# A'$
to Y. More precisely, start by taking
![]() ${(A\# A') \times I}$
. Attach a 2-handle to obtain a cobordism, say, V, from
${(A\# A') \times I}$
. Attach a 2-handle to obtain a cobordism, say, V, from
![]() $A\#A'$
to the second surgery diagram in Figure 7. Apply handle slide, to change the second surgery diagram to the third. Observe that in the third surgery diagram, the two components with framing
$A\#A'$
to the second surgery diagram in Figure 7. Apply handle slide, to change the second surgery diagram to the third. Observe that in the third surgery diagram, the two components with framing
![]() $m+6$
and
$m+6$
and
![]() $0$
give a
$0$
give a
![]() $S^3$
summand, whereas the two components with framing m and
$S^3$
summand, whereas the two components with framing m and
![]() $2m+7$
form a link concordant to the link in the last surgery diagram, which describes Y. It follows that there is a homology cobordism, say,
$2m+7$
form a link concordant to the link in the last surgery diagram, which describes Y. It follows that there is a homology cobordism, say,
![]() $V'$
, from the third surgery diagram to Y. Now
$V'$
, from the third surgery diagram to Y. Now
![]() $V\cup V'$
is a cobordism from
$V\cup V'$
is a cobordism from
![]() $A\#A'$
to Y.
$A\#A'$
to Y.

Figure 7 A cobordism from
![]() $A\# A'$
to Y.
$A\# A'$
to Y.
We claim that V is negative definite. To see this, view the surgery diagram of the 3-manifold
![]() $A\# A'$
as a Kirby diagram of a 4-manifold
$A\# A'$
as a Kirby diagram of a 4-manifold
![]() $V_0$
. That is,
$V_0$
. That is,
![]() $V_0$
consists of one 0-handle and three 2-handles attached along the framed link diagram of
$V_0$
consists of one 0-handle and three 2-handles attached along the framed link diagram of
![]() $A\# A'$
in Figure 7. We have
$A\# A'$
in Figure 7. We have
![]() $\partial V_0=A\# A'$
. The second diagram in Figure 7 or, equivalently, the third diagram, is a Kirby diagram of the 4-manifold
$\partial V_0=A\# A'$
. The second diagram in Figure 7 or, equivalently, the third diagram, is a Kirby diagram of the 4-manifold
![]() $V_0\cup _{A\# A'} V$
. The Kirby diagram of
$V_0\cup _{A\# A'} V$
. The Kirby diagram of
![]() $V_0$
has linking matrix
$V_0$
has linking matrix
 $$ \begin{align*} L = \begin{bmatrix} m & -2m-1 & 0 \\ -2m-1 & m & 0 \\ 0 & 0 & m+6 \end{bmatrix}, \end{align*} $$
$$ \begin{align*} L = \begin{bmatrix} m & -2m-1 & 0 \\ -2m-1 & m & 0 \\ 0 & 0 & m+6 \end{bmatrix}, \end{align*} $$
which has signature
![]() $1$
because
$1$
because
![]() $m>0$
and the top upper
$m>0$
and the top upper
![]() $2\times 2$
submatrix has negative determinant. It follows that
$2\times 2$
submatrix has negative determinant. It follows that
![]() $\operatorname {sign} V_0 = 1$
. The third diagram in Figure 7 has linking matrix
$\operatorname {sign} V_0 = 1$
. The third diagram in Figure 7 has linking matrix
 $$ \begin{align*} \begin{bmatrix} m & -2m-1 & 0 & 0\\ -2m-1 & 2m+7 & 0 & 0 \\ 0 & 0 & 0 & -1 \\ 0 & 0 & -1 & m+6 \end{bmatrix}, \end{align*} $$
$$ \begin{align*} \begin{bmatrix} m & -2m-1 & 0 & 0\\ -2m-1 & 2m+7 & 0 & 0 \\ 0 & 0 & 0 & -1 \\ 0 & 0 & -1 & m+6 \end{bmatrix}, \end{align*} $$
which has vanishing signature. So
![]() $\operatorname {sign} V_0\cup V = 0$
. By Novikov additivity, it follows that
$\operatorname {sign} V_0\cup V = 0$
. By Novikov additivity, it follows that
![]() $\operatorname {sign} V=-1$
. Because
$\operatorname {sign} V=-1$
. Because
![]() $b_2(V)=1$
, this proves the claim that V is negative definite.
$b_2(V)=1$
, this proves the claim that V is negative definite.
Because
![]() $V'$
is a homology cobordism,
$V'$
is a homology cobordism,
![]() $H_*(V\cup V')=H_*(V)$
. Consequently,
$H_*(V\cup V')=H_*(V)$
. Consequently,
![]() $V\cup V'$
is negative definite.
$V\cup V'$
is negative definite.
We will construct a generator of
![]() $H_2(V\cup V') = H_2(V)$
and use it to describe a certain spin
$H_2(V\cup V') = H_2(V)$
and use it to describe a certain spin
![]() $^c$
structure on
$^c$
structure on
![]() $V\cup V'$
. Let
$V\cup V'$
. Let
![]() $\sigma $
be the core of the 2-handle of
$\sigma $
be the core of the 2-handle of
![]() $(V,A\#A')$
, and let
$(V,A\#A')$
, and let
![]() $\alpha =\partial \sigma $
be its attaching circle, which lies in
$\alpha =\partial \sigma $
be its attaching circle, which lies in
![]() $A\#A'$
. See the second diagram in Figure 7, in which
$A\#A'$
. See the second diagram in Figure 7, in which
![]() $\alpha $
is the zero-framed circle. Because the linking matrix L is a presentation for
$\alpha $
is the zero-framed circle. Because the linking matrix L is a presentation for
![]() $H_1(A\#A')$
, it is seen that
$H_1(A\#A')$
, it is seen that
![]() $H_1(A\#A')=\mathbb {Z}_{3m^2+3m+1}\oplus \mathbb {Z}_{m+6}$
, and
$H_1(A\#A')=\mathbb {Z}_{3m^2+3m+1}\oplus \mathbb {Z}_{m+6}$
, and
![]() $\alpha = (1,1)$
in
$\alpha = (1,1)$
in
![]() $H_1(A\#A')$
. So, the order of
$H_1(A\#A')$
. So, the order of
![]() $\alpha $
in
$\alpha $
in
![]() $H_1(A\#A')$
is
$H_1(A\#A')$
is
![]() $(3m^2+3m+1)(m+6)/d$
, where
$(3m^2+3m+1)(m+6)/d$
, where
![]() $d:=\gcd (3m^2+3m+1, m+6)$
. (Indeed, it can be seen that d is either
$d:=\gcd (3m^2+3m+1, m+6)$
. (Indeed, it can be seen that d is either
![]() $91$
or
$91$
or
![]() $1$
.) From this, it follows that there is a 2-cycle z in
$1$
.) From this, it follows that there is a 2-cycle z in
![]() $A\#A'$
such that
$A\#A'$
such that
 $$ \begin{align*} \partial z= \frac{(3m^2+3m+1)(m+6)}{d}\cdot \alpha. \end{align*} $$
$$ \begin{align*} \partial z= \frac{(3m^2+3m+1)(m+6)}{d}\cdot \alpha. \end{align*} $$
Moreover, the 2-chain
 $$ \begin{align*} E:= \frac{(3m^2+3m+1)(m+6)}{d} \cdot \sigma - z \end{align*} $$
$$ \begin{align*} E:= \frac{(3m^2+3m+1)(m+6)}{d} \cdot \sigma - z \end{align*} $$
is a generator of
![]() $H_2(V)=\mathbb {Z}$
, by a standard Mayer-Vietoris argument for the 2-handle attachment.
$H_2(V)=\mathbb {Z}$
, by a standard Mayer-Vietoris argument for the 2-handle attachment.
The self-intersection number
![]() $E\cdot E$
is equal to the intersection number (in
$E\cdot E$
is equal to the intersection number (in
![]() $A\#A'$
) of z and a pushoff of
$A\#A'$
) of z and a pushoff of
![]() $\partial z$
, say,
$\partial z$
, say,
![]() $\partial z'$
, taken along the 2-handle attachment framing (which is the zero framing in Figure 7). So
$\partial z'$
, taken along the 2-handle attachment framing (which is the zero framing in Figure 7). So
![]() $E\cdot E$
is equal to the linking number of
$E\cdot E$
is equal to the linking number of
![]() $\partial z$
and its pushoff in the rational homology sphere
$\partial z$
and its pushoff in the rational homology sphere
![]() $A\#A'$
. In addition, the linking number can be computed using the linking matrix L (for instance, see [Reference Cha and Ko7, Theorem 3.1]):
$A\#A'$
. In addition, the linking number can be computed using the linking matrix L (for instance, see [Reference Cha and Ko7, Theorem 3.1]):
 $$ \begin{align*} \begin{aligned} E\cdot E &= \mathrm{lk}_{A\#A'}(\partial z,\partial z') = \frac{(3m^2+3m+1)^2(m+6)^2}{d^2} \cdot \begin{bmatrix} 0 & -1 & 1 \end{bmatrix} L^{-1} \begin{bmatrix} 0 \\ -1 \\ 1 \end{bmatrix} \\ & = \frac{(3m^2+3m+1)(m+6)(-2m^2+3m-1)}{d^2}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} E\cdot E &= \mathrm{lk}_{A\#A'}(\partial z,\partial z') = \frac{(3m^2+3m+1)^2(m+6)^2}{d^2} \cdot \begin{bmatrix} 0 & -1 & 1 \end{bmatrix} L^{-1} \begin{bmatrix} 0 \\ -1 \\ 1 \end{bmatrix} \\ & = \frac{(3m^2+3m+1)(m+6)(-2m^2+3m-1)}{d^2}. \end{aligned} \end{align*} $$
Because the factor
![]() $-2m^2+3m-1$
of the numerator is even and d is odd,
$-2m^2+3m-1$
of the numerator is even and d is odd,
![]() $E\cdot E$
is even. From this, it follows that
$E\cdot E$
is even. From this, it follows that
![]() $0\in H^2(V\cup V')$
is characteristic. Therefore, there is a spin
$0\in H^2(V\cup V')$
is characteristic. Therefore, there is a spin
![]() $^c$
structure
$^c$
structure
![]() $\mathfrak {t}$
on
$\mathfrak {t}$
on
![]() $V\cup V'$
such that
$V\cup V'$
such that
![]() $c_1(\mathfrak {t})=0$
. By the Ozsváth-Szabó inequality [Reference Ozsváth and Szabó40, Theorem 9.6], we have
$c_1(\mathfrak {t})=0$
. By the Ozsváth-Szabó inequality [Reference Ozsváth and Szabó40, Theorem 9.6], we have
 $$ \begin{align*} d(Y,\mathfrak{t}|_Y) - d(A,\mathfrak{t}|_A) - d(A',\mathfrak{t}|_{A'}) \ge \frac 14. \end{align*} $$
$$ \begin{align*} d(Y,\mathfrak{t}|_Y) - d(A,\mathfrak{t}|_A) - d(A',\mathfrak{t}|_{A'}) \ge \frac 14. \end{align*} $$
Note that
![]() $A'$
is the
$A'$
is the
![]() $(m+6)$
-surgery on the knot
$(m+6)$
-surgery on the knot
![]() $T\# -D$
, and
$T\# -D$
, and
![]() $c_1(\mathfrak {t}|_{A'})=0$
because
$c_1(\mathfrak {t}|_{A'})=0$
because
![]() $c_1(\mathfrak {t})=0$
. By techniques of [Reference Cochran, Harvey and Horn11, p. 2150-2151] and [Reference Hedden, Kim and Livingston24, Appendix A],
$c_1(\mathfrak {t})=0$
. By techniques of [Reference Cochran, Harvey and Horn11, p. 2150-2151] and [Reference Hedden, Kim and Livingston24, Appendix A],
![]() $d(A',\mathfrak {t}|_{A'}) = d(L_{m+6},\mathfrak {s}_{L_{m+6}})$
. By Ozsváth-Szabó’s formula for lens spaces [Reference Ozsváth and Szabó40, Proposition 4.8], we have
$d(A',\mathfrak {t}|_{A'}) = d(L_{m+6},\mathfrak {s}_{L_{m+6}})$
. By Ozsváth-Szabó’s formula for lens spaces [Reference Ozsváth and Szabó40, Proposition 4.8], we have
![]() $d(L_{m+6},\mathfrak {s}_{L_{m+6}}) = (m+5)/4$
. By Lemma 4.8, which we will prove below, we have
$d(L_{m+6},\mathfrak {s}_{L_{m+6}}) = (m+5)/4$
. By Lemma 4.8, which we will prove below, we have
![]() $d(Y,\mathfrak {t}|_Y) \le (2m-1)/4$
. (Note that
$d(Y,\mathfrak {t}|_Y) \le (2m-1)/4$
. (Note that
![]() $c_1(\mathfrak {t}|_Y)=0$
because
$c_1(\mathfrak {t}|_Y)=0$
because
![]() $c_1(\mathfrak {t})=0$
.) Combining these with the above inequality, it follows that
$c_1(\mathfrak {t})=0$
.) Combining these with the above inequality, it follows that
![]() $d(A,\mathfrak {s}) \le (m-7)/4$
.
$d(A,\mathfrak {s}) \le (m-7)/4$
.
4.2. A quick summary of Némethi’s method for Seifert 3-manifolds
For the reader’s convenience, we provide a summary of Némethi’s method to compute d-invariants [Reference Némethi38], which we will use in Subsection 4.3. We focus on the case of Seifert 3-manifolds, which is treated in [Reference Némethi38, Section 11], and [Reference Némethi38] provides techniques for a larger class of certain plumbed 3-manifolds.
Let Y be a Seifert 3-manifold. It is well known that Y admits a surgery presentation of a specific form, which is shown in the left side of Figure 8. The associated star-shaped plumbing graph, which is shown in the right side of Figure 8, is often used to describe the 3-manifold Y, as the boundary of a plumbed 4-manifold X: for each vertex, take a disk bundle over a 2-sphere whose Euler number is the integer decoration of the vertex. For each edge, perform
![]() $+1$
plumbing between the two disk bundles corresponding to the endpoints. The result is a 4-manifold X with
$+1$
plumbing between the two disk bundles corresponding to the endpoints. The result is a 4-manifold X with
![]() $\partial X=Y$
.
$\partial X=Y$
.

Figure 8 A Seifert 3-manifold and its plumbing graph.
Let
![]() $\nu $
be the number of branches of the star-shaped graph in Figure 8. In this subsection, we assume that
$\nu $
be the number of branches of the star-shaped graph in Figure 8. In this subsection, we assume that
![]() $\nu \ge 3$
and that X is negative definite. (We remark that not all Seifert 3-manifolds Y are described by a plumbing graph satisfying this assumption.)
$\nu \ge 3$
and that X is negative definite. (We remark that not all Seifert 3-manifolds Y are described by a plumbing graph satisfying this assumption.)
We use the following notation. Let
![]() $e_0$
be the decoration of the root vertex. Let
$e_0$
be the decoration of the root vertex. Let
![]() $s_{\ell }$
be the number of (non-root) vertices on the
$s_{\ell }$
be the number of (non-root) vertices on the
![]() $\ell $
th branch, and let
$\ell $
th branch, and let
![]() $e_{\ell ,1},\ldots$
,
$e_{\ell ,1},\ldots$
,
![]() $e_{\ell ,s_{\ell }}$
be the decorations of those
$e_{\ell ,s_{\ell }}$
be the decorations of those
![]() $s_{\ell }$
vertices. See Figure 8. We may assume that
$s_{\ell }$
vertices. See Figure 8. We may assume that
![]() $e_{\ell ,j}\le -2$
for all
$e_{\ell ,j}\le -2$
for all
![]() $\ell $
, j (for instance, see [Reference Neumann39]). Let
$\ell $
, j (for instance, see [Reference Neumann39]). Let
![]() $b_0$
and
$b_0$
and
![]() $b_{\ell ,j} \in H_2(X)$
be the classes of 2-spheres corresponding to vertices with decoration
$b_{\ell ,j} \in H_2(X)$
be the classes of 2-spheres corresponding to vertices with decoration
![]() $e_0$
and
$e_0$
and
![]() $e_{\ell ,j}$
respectively (
$e_{\ell ,j}$
respectively (
![]() $1\le \ell \le \nu $
,
$1\le \ell \le \nu $
,
![]() $1\le j\le s_{\ell }$
). They form a basis for the free abelian group
$1\le j\le s_{\ell }$
). They form a basis for the free abelian group
![]() $H_2(X)$
. Let
$H_2(X)$
. Let
![]() $b^*_0$
and
$b^*_0$
and
 $b^*_{\ell ,j}\in H^2(X)$
be basis elements (hom) dual to
$b^*_{\ell ,j}\in H^2(X)$
be basis elements (hom) dual to
![]() $b_0$
and
$b_0$
and
![]() $b_{\ell ,j}$
. With respect to these bases, the intersection form
$b_{\ell ,j}$
. With respect to these bases, the intersection form
![]() $\lambda \colon H_2(X)\times H_2(X) \to X$
or its adjoint
$\lambda \colon H_2(X)\times H_2(X) \to X$
or its adjoint
![]() $\lambda \colon H_2(X) \to \mathrm {Hom}(H_2(X),\mathbb {Z}) = H^2(X)$
is given as follows:
$\lambda \colon H_2(X) \to \mathrm {Hom}(H_2(X),\mathbb {Z}) = H^2(X)$
is given as follows:
![]() $\lambda (b_0,b_0)=e_0$
,
$\lambda (b_0,b_0)=e_0$
,
![]() $\lambda (b_{\ell ,j}, b_{\ell ,j}) = e_{\ell ,j}$
, and for
$\lambda (b_{\ell ,j}, b_{\ell ,j}) = e_{\ell ,j}$
, and for
![]() $b\ne b'$
,
$b\ne b'$
,
![]() $\lambda (b,b')=1$
if
$\lambda (b,b')=1$
if
![]() $\{b,b'\}=\{b_0,b_{\ell ,1}\}$
or
$\{b,b'\}=\{b_0,b_{\ell ,1}\}$
or
![]() $\{b_{\ell ,j},b_{\ell ,j+1}\}$
, and
$\{b_{\ell ,j},b_{\ell ,j+1}\}$
, and
![]() $\lambda (b,b')=0$
otherwise. For
$\lambda (b,b')=0$
otherwise. For
![]() $1\le \ell \le \nu $
, define a continued fraction by
$1\le \ell \le \nu $
, define a continued fraction by
 $$ \begin{align*} \frac{\alpha_{\ell}}{\omega_{\ell}} := [-e_{\ell,1},\ldots,-e_{\ell,s_{\ell}}] = -e_{\ell,1} - \cfrac{1}{-e_{\ell,2} - \cfrac{1}{\,\,\,\vdots\,\,\,}}. \end{align*} $$
$$ \begin{align*} \frac{\alpha_{\ell}}{\omega_{\ell}} := [-e_{\ell,1},\ldots,-e_{\ell,s_{\ell}}] = -e_{\ell,1} - \cfrac{1}{-e_{\ell,2} - \cfrac{1}{\,\,\,\vdots\,\,\,}}. \end{align*} $$
The condition
![]() $e_{\ell ,j}\le -2$
implies that
$e_{\ell ,j}\le -2$
implies that
![]() $\alpha _{\ell }/\omega _{\ell }>1$
. So we may assume
$\alpha _{\ell }/\omega _{\ell }>1$
. So we may assume
![]() $0\le \omega _{\ell } < \alpha _{\ell }$
. Then, a standard diagonalisation process applied to the intersection form
$0\le \omega _{\ell } < \alpha _{\ell }$
. Then, a standard diagonalisation process applied to the intersection form
![]() $\lambda $
gives us a diagonal matrix whose all diagonals are easily seen to be negative, possibly except one, which is equal to
$\lambda $
gives us a diagonal matrix whose all diagonals are easily seen to be negative, possibly except one, which is equal to
 $$ \begin{align*} e := e_0 + \sum_{\ell=1}^{\nu} \omega_{\ell}/\alpha_{\ell}. \end{align*} $$
$$ \begin{align*} e := e_0 + \sum_{\ell=1}^{\nu} \omega_{\ell}/\alpha_{\ell}. \end{align*} $$
So, X is negative definite if and only if
![]() $e<0$
.
$e<0$
.
The set of characteristic elements in
![]() $H^2(X)$
is defined to be
$H^2(X)$
is defined to be
 $$ \begin{align*} \operatorname{Char}(X) := \{\xi \in H^2(X) \mid \xi(b_j)\equiv \lambda(b_j,b_j) \bmod 2 \text{ for all } j\}. \end{align*} $$
$$ \begin{align*} \operatorname{Char}(X) := \{\xi \in H^2(X) \mid \xi(b_j)\equiv \lambda(b_j,b_j) \bmod 2 \text{ for all } j\}. \end{align*} $$
The Chern class
![]() $c_1\colon \operatorname {\mathrm {Spin}}^c(X) \to \operatorname {Char}(X)$
is bijective, because
$c_1\colon \operatorname {\mathrm {Spin}}^c(X) \to \operatorname {Char}(X)$
is bijective, because
![]() $H^2(X)$
does not have any 2-torsion. Under the identification via
$H^2(X)$
does not have any 2-torsion. Under the identification via
![]() $c_1$
, the action of an element
$c_1$
, the action of an element
![]() $c\in H^2(X)$
on
$c\in H^2(X)$
on
![]() $\operatorname {\mathrm {Spin}}^c(X)$
is given by
$\operatorname {\mathrm {Spin}}^c(X)$
is given by
![]() $\xi \mapsto \xi +2c$
for
$\xi \mapsto \xi +2c$
for
![]() $\xi \in \operatorname {Char}(X)=\operatorname {\mathrm {Spin}}^c(X)$
. In particular, the action of
$\xi \in \operatorname {Char}(X)=\operatorname {\mathrm {Spin}}^c(X)$
. In particular, the action of
![]() $x\in H_2(X)$
on
$x\in H_2(X)$
on
![]() $\operatorname {Char}(X)=\operatorname {\mathrm {Spin}}^c(X)$
via
$\operatorname {Char}(X)=\operatorname {\mathrm {Spin}}^c(X)$
via
![]() $\lambda \colon H_2(X)\to H^2(X)$
is given by
$\lambda \colon H_2(X)\to H^2(X)$
is given by
![]() $\xi \mapsto \xi +2\lambda (x)$
.
$\xi \mapsto \xi +2\lambda (x)$
.
The Chern class
![]() $c_1\colon \operatorname {\mathrm {Spin}}^c(Y)\to H^2(Y)$
is not injective in general, so the standard identification of spin
$c_1\colon \operatorname {\mathrm {Spin}}^c(Y)\to H^2(Y)$
is not injective in general, so the standard identification of spin
![]() $^c$
structures of Y is given indirectly using X: we have a bijection
$^c$
structures of Y is given indirectly using X: we have a bijection
Here, for a spin
![]() $^c$
structure
$^c$
structure
![]() $\xi \in \operatorname {\mathrm {Spin}}^c(X)=\operatorname {Char}(X)$
, the coset
$\xi \in \operatorname {\mathrm {Spin}}^c(X)=\operatorname {Char}(X)$
, the coset
![]() $[\xi ] = \xi +2\lambda (H_2(X))$
in
$[\xi ] = \xi +2\lambda (H_2(X))$
in
![]() $\operatorname {Char}(X)/2\lambda (H_2(X))$
corresponds to the restriction of
$\operatorname {Char}(X)/2\lambda (H_2(X))$
corresponds to the restriction of
![]() $\xi $
on Y. Essentially, the bijectivity is a consequence of the fact that
$\xi $
on Y. Essentially, the bijectivity is a consequence of the fact that
![]() $H^2(Y)$
is the cokernel of
$H^2(Y)$
is the cokernel of
![]() $\lambda \colon H_2(X) \to H^2(X)$
.
$\lambda \colon H_2(X) \to H^2(X)$
.
In [Reference Némethi38], the notion of a distinguished representative is used to express a spin
![]() $^c$
structure of Y. Instead of the original definition (see Section 5, especially Definition 5.1 of [Reference Némethi38]), we will use a characterisation theorem as a definition. We need the following notation. For
$^c$
structure of Y. Instead of the original definition (see Section 5, especially Definition 5.1 of [Reference Némethi38]), we will use a characterisation theorem as a definition. We need the following notation. For
![]() $1\le i\le j\le s_{\ell }$
, let
$1\le i\le j\le s_{\ell }$
, let
 $n^{\ell }_{i,j}/d^{\ell }_{i,j} := [-e^{\ell }_i, \ldots , -e^{\ell }_j]$
, where
$n^{\ell }_{i,j}/d^{\ell }_{i,j} := [-e^{\ell }_i, \ldots , -e^{\ell }_j]$
, where
 $n^{\ell }_{i,j}> 0$
and
$n^{\ell }_{i,j}> 0$
and
 $\gcd (n^{\ell }_{i,j}, d^{\ell }_{i,j}) = 1$
. Note that
$\gcd (n^{\ell }_{i,j}, d^{\ell }_{i,j}) = 1$
. Note that
 $\alpha _{\ell }/\omega _{\ell } = n^{\ell }_{1,s_{\ell }}/d^{\ell }_{1,s_{\ell }}$
. Define an element
$\alpha _{\ell }/\omega _{\ell } = n^{\ell }_{1,s_{\ell }}/d^{\ell }_{1,s_{\ell }}$
. Define an element
![]() $K\in \operatorname {\mathrm {Spin}}^c(X) = \operatorname {Char}(X)\subset H^2(X)$
by
$K\in \operatorname {\mathrm {Spin}}^c(X) = \operatorname {Char}(X)\subset H^2(X)$
by
The element K is characteristic because
![]() $K(b_0) \equiv \lambda (b_0,b_0)$
and
$K(b_0) \equiv \lambda (b_0,b_0)$
and
![]() $K(b_{\ell ,j}) \equiv \lambda (b_{\ell ,j},b_{\ell ,j}) \bmod 2$
. In [Reference Némethi38], K is called the canonical spin
$K(b_{\ell ,j}) \equiv \lambda (b_{\ell ,j},b_{\ell ,j}) \bmod 2$
. In [Reference Némethi38], K is called the canonical spin
![]() $^c$
structure. We have
$^c$
structure. We have
![]() $\operatorname {Char}(X) = K + 2H^2(X)$
. Consider a class
$\operatorname {Char}(X) = K + 2H^2(X)$
. Consider a class
![]() $k_r\in \operatorname {Char}(X)$
of the form
$k_r\in \operatorname {Char}(X)$
of the form
 $$ \begin{align} k_r = K - 2 \bigg( a_0^{\vphantom{1}} b^*_0 + \sum_{\ell,j} a_{\ell,j}^{\vphantom{1}} b_{\ell,j}^* \bigg), \end{align} $$
$$ \begin{align} k_r = K - 2 \bigg( a_0^{\vphantom{1}} b^*_0 + \sum_{\ell,j} a_{\ell,j}^{\vphantom{1}} b_{\ell,j}^* \bigg), \end{align} $$
where
![]() $a_0$
and
$a_0$
and
![]() $a_{\ell ,j}$
are integers. Let
$a_{\ell ,j}$
are integers. Let
 $$ \begin{align} a_{\ell} = \sum_{t=1}^{s_{\ell}-1} n^{\ell}_{t+1,s_{\ell}} a_{\ell,t}. \end{align} $$
$$ \begin{align} a_{\ell} = \sum_{t=1}^{s_{\ell}-1} n^{\ell}_{t+1,s_{\ell}} a_{\ell,t}. \end{align} $$
Definition 4.5 [Reference Némethi38, Corollary 11.7]
The class
![]() $k_r$
in (4.3) called a distinguished representative if
$k_r$
in (4.3) called a distinguished representative if
![]() $0\le a_{\ell } < \alpha _{\ell }$
for all
$0\le a_{\ell } < \alpha _{\ell }$
for all
![]() $\ell $
and if
$\ell $
and if
 $$ \begin{align} 0\le a_0 \le -1 -i e_0 - \sum_{\ell=1}^{\nu} \Bigl[ \frac{i\omega_{\ell} + a_{\ell}}{\alpha_{\ell}} \Bigr] \end{align} $$
$$ \begin{align} 0\le a_0 \le -1 -i e_0 - \sum_{\ell=1}^{\nu} \Bigl[ \frac{i\omega_{\ell} + a_{\ell}}{\alpha_{\ell}} \Bigr] \end{align} $$
for all
![]() $i>0$
. Here
$i>0$
. Here
![]() $[x]$
is the largest integer not greater than x.
$[x]$
is the largest integer not greater than x.
To state Némethi’s formula for the d-invariant, we need one more notation. Let
 $$ \begin{align} \tau(i) = \sum_{t=0}^{i-1} \bigg(a_0+1-te_0 + \sum_{\ell=1}^{\nu} \Bigl[ \frac{-t\omega_{\ell} + a_{\ell}}{\alpha_{\ell}} \Bigr] \bigg). \end{align} $$
$$ \begin{align} \tau(i) = \sum_{t=0}^{i-1} \bigg(a_0+1-te_0 + \sum_{\ell=1}^{\nu} \Bigl[ \frac{-t\omega_{\ell} + a_{\ell}}{\alpha_{\ell}} \Bigr] \bigg). \end{align} $$
In particular,
![]() $\tau (0)=0$
.
$\tau (0)=0$
.
Theorem 4.5 Némethi [Reference Némethi38, p. 1038]
Suppose that X is negative definite and
![]() $\nu \ge 3$
. Suppose that the class
$\nu \ge 3$
. Suppose that the class
![]() $k_r$
given in (4.3) is a distinguished representative. Then, for the spin
$k_r$
given in (4.3) is a distinguished representative. Then, for the spin
![]() $^c$
structure
$^c$
structure
![]() $[k_r]$
of Y, the d-invariant is given by
$[k_r]$
of Y, the d-invariant is given by
 $$ \begin{align*} d(Y,[k_r]) = \frac{k_r^2+b_2(X)}{4} - 2\cdot \min \{ \tau(i) \mid i\ge 0\}. \end{align*} $$
$$ \begin{align*} d(Y,[k_r]) = \frac{k_r^2+b_2(X)}{4} - 2\cdot \min \{ \tau(i) \mid i\ge 0\}. \end{align*} $$
Remark 4.6.
-
(1) For each
 $k_r$
given by (4.3), the minimum in Theorem 4.6 can be found in finite steps. To see this, let
$k_r$
given by (4.3), the minimum in Theorem 4.6 can be found in finite steps. To see this, let
 $\Delta _i = \tau (i+1)-\tau (i)$
. Then we have if i is not smaller than
$\Delta _i = \tau (i+1)-\tau (i)$
. Then we have if i is not smaller than $$ \begin{align*} \Delta_i & \ge a_0 + 1 - ie_0 + \sum_{\ell=1}^{\nu} \frac{- i \omega_{\ell} + a_{\ell} + \alpha_{\ell} - 1}{\alpha_{\ell}} \\ & = -e\cdot i + \bigg( 1+a_0 + \sum_{\ell=1}^{\nu} \frac{a_{\ell}-\alpha_{\ell}+1}{\alpha_{\ell}} \bigg) \ge 0 \end{align*} $$
Here we use that e is negative because X is negative definite. So, the minimum in Theorem 4.6 can be taken over
$$ \begin{align*} \Delta_i & \ge a_0 + 1 - ie_0 + \sum_{\ell=1}^{\nu} \frac{- i \omega_{\ell} + a_{\ell} + \alpha_{\ell} - 1}{\alpha_{\ell}} \\ & = -e\cdot i + \bigg( 1+a_0 + \sum_{\ell=1}^{\nu} \frac{a_{\ell}-\alpha_{\ell}+1}{\alpha_{\ell}} \bigg) \ge 0 \end{align*} $$
Here we use that e is negative because X is negative definite. So, the minimum in Theorem 4.6 can be taken over $$ \begin{align*} R := \bigg( 1+a_0 + \sum_{\ell=1}^{\nu} \frac{a_{\ell}-\alpha_{\ell}+1}{\alpha_{\ell}} \bigg) \Big/ (-e). \end{align*} $$
$$ \begin{align*} R := \bigg( 1+a_0 + \sum_{\ell=1}^{\nu} \frac{a_{\ell}-\alpha_{\ell}+1}{\alpha_{\ell}} \bigg) \Big/ (-e). \end{align*} $$
 $0\le i \le \max \{0,R\}$
.
$0\le i \le \max \{0,R\}$
.
-
(2) A similar argument shows that it can be determined in finite steps whether a class
 $k_r$
given by (4.3) satisfies Definition 4.5. Indeed, the right- hand side of (4.5) is bounded from below by
$k_r$
given by (4.3) satisfies Definition 4.5. Indeed, the right- hand side of (4.5) is bounded from below by
 $-(1+\sum a_{\ell }/\alpha _{\ell })-ei$
. Because
$-(1+\sum a_{\ell }/\alpha _{\ell })-ei$
. Because
 $e<0$
, (4.5) is satisfied for all large i, and thus it suffices to check (4.5) for only finitely many i.
$e<0$
, (4.5) is satisfied for all large i, and thus it suffices to check (4.5) for only finitely many i.
Using (1) and (2), it is straightforward to write a practically efficient algorithm (and computer code) to find distinguished representatives of all spin
![]() $^c$
structures of Y and compute the associated d-invariants.
$^c$
structures of Y and compute the associated d-invariants.
4.3. d-invariants of the 3-manifolds Y and B
Let Y be the 3-manifold given by the last surgery diagram in Figure 7 or, equivalently, by the first surgery diagram in Figure 9. The following lemma gives an estimate of the d-invariant of Y, which is used to complete the proof of Lemma 4.3. Note that there are two spin
![]() $^c$
structures on Y satisfying
$^c$
structures on Y satisfying
![]() $c_1(\mathfrak {s})=0$
, because
$c_1(\mathfrak {s})=0$
, because
![]() $|H_1(Y)| = 2m^2-3m+1$
is even.
$|H_1(Y)| = 2m^2-3m+1$
is even.

Figure 9 Surgery diagram calculus that gives a plumbing tree for Y. The symbol
![]() $(*)$
means handle slides and elimination of components with 0-framed meridians.
$(*)$
means handle slides and elimination of components with 0-framed meridians.
Lemma 4.8. If
![]() $\mathfrak {s}$
is a spin
$\mathfrak {s}$
is a spin
![]() $^c$
structure on Y such that
$^c$
structure on Y such that
![]() $c_1(\mathfrak {s})=0$
, then
$c_1(\mathfrak {s})=0$
, then
![]() $d(Y,\mathfrak {s}) \le (2m-1)/4$
.
$d(Y,\mathfrak {s}) \le (2m-1)/4$
.
Proof. The surgery diagram calculus in Figure 9 shows that Y is a Seifert 3-manifold. The last plumbing graph in Figure 9 describes a plumbed 4-manifold X with
![]() $\partial X=Y$
.
$\partial X=Y$
.
To compute the d-invariant, we will apply the method discussed in Subsection 4.2. Using the notation in Subsection 4.2, denote the basis of
![]() $H_2(X)$
by
$H_2(X)$
by
![]() $\{b_0$
,
$\{b_0$
,
![]() $b_{1,1},\ldots$
,
$b_{1,1},\ldots$
,
![]() $b_{1,2m}$
,
$b_{1,2m}$
,
![]() $b_{2,1}$
,
$b_{2,1}$
,
![]() $b_{3,1}$
,
$b_{3,1}$
,
![]() $b_{4,1}\}$
and the dual basis of
$b_{4,1}\}$
and the dual basis of
![]() $H^2(X)$
by
$H^2(X)$
by
![]() $\{b^*_0$
,
$\{b^*_0$
,
![]() $b^*_{1,1},\ldots$
,
$b^*_{1,1},\ldots$
,
![]() $b^*_{1,2m}$
,
$b^*_{1,2m}$
,
![]() $b^*_{2,1}$
,
$b^*_{2,1}$
,
![]() $b^*_{3,1}$
,
$b^*_{3,1}$
,
 $b^*_{4,1}\}$
. The intersection form
$b^*_{4,1}\}$
. The intersection form
![]() $\lambda \colon H_2(X)\times H_2(X)\to \mathbb {Z}$
is computed straightforwardly from the plumbing graph:
$\lambda \colon H_2(X)\times H_2(X)\to \mathbb {Z}$
is computed straightforwardly from the plumbing graph:
 $$ \begin{align*} \lambda = \left[ \begin{array}{c|ccccc|c|c|c} -2 & 1 & & & & & 1 & 1 & 1 \\ \hline 1 & -2 & 1 & & & & & & \\ & 1 & -2 & 1 & & & & & \\ & & \ddots & \ddots & \ddots & & & \\ & & & 1 & -2 & 1 & & & \\ & & & & 1 & -2 & & & \\ \hline 1 & & & & & & -2 & & \\ \hline 1 & & & & & & & -3 & \\ \hline 1 & & & & & & & & -m-1 \end{array} \right]_{(2m+4)\times(2m+4)}. \end{align*} $$
$$ \begin{align*} \lambda = \left[ \begin{array}{c|ccccc|c|c|c} -2 & 1 & & & & & 1 & 1 & 1 \\ \hline 1 & -2 & 1 & & & & & & \\ & 1 & -2 & 1 & & & & & \\ & & \ddots & \ddots & \ddots & & & \\ & & & 1 & -2 & 1 & & & \\ & & & & 1 & -2 & & & \\ \hline 1 & & & & & & -2 & & \\ \hline 1 & & & & & & & -3 & \\ \hline 1 & & & & & & & & -m-1 \end{array} \right]_{(2m+4)\times(2m+4)}. \end{align*} $$
Also, using the definition in Subsection 4.2, it is routine to compute the following:
 $$ \begin{align*} \Bigl( \frac{\alpha_1}{\omega_1},\, \frac{\alpha_2}{\omega_2},\, \frac{\alpha_3}{\omega_3},\, \frac{\alpha_4}{\omega_4} \Bigr) = \Bigl( \frac{2m+1}{2m},\,\frac21,\,\frac31,\,\frac{m+1}{1} \Bigr). \end{align*} $$
$$ \begin{align*} \Bigl( \frac{\alpha_1}{\omega_1},\, \frac{\alpha_2}{\omega_2},\, \frac{\alpha_3}{\omega_3},\, \frac{\alpha_4}{\omega_4} \Bigr) = \Bigl( \frac{2m+1}{2m},\,\frac21,\,\frac31,\,\frac{m+1}{1} \Bigr). \end{align*} $$
So, the orbifold Euler number is given by
 $$ \begin{align*} e = -2 + \frac{2m}{2m+1} + \frac{1}{2} + \frac{1}{3} + \frac{1}{m+1} = -\frac{(m-1)(2m-1)}{6(m+1)(2m+1)}. \end{align*} $$
$$ \begin{align*} e = -2 + \frac{2m}{2m+1} + \frac{1}{2} + \frac{1}{3} + \frac{1}{m+1} = -\frac{(m-1)(2m-1)}{6(m+1)(2m+1)}. \end{align*} $$
For
![]() $m>1$
, we have
$m>1$
, we have
![]() $e<0$
, so X is negative definite.
$e<0$
, so X is negative definite.
We will describe two spin
![]() $^c$
structures
$^c$
structures
![]() $[k_1]$
and
$[k_1]$
and
![]() $[k_2]\in \operatorname {Char}(X)/2\lambda (H_2(X))$
. Let
$[k_2]\in \operatorname {Char}(X)/2\lambda (H_2(X))$
. Let
 $$ \begin{align*} k_1 &:= -2 b^*_{1,2m} - b^*_{3,1} + 2b^*_{4,1}, \\ k_2 &:= -2 b^*_{1,2m-1} + b^*_{3,1} - 2b^*_{4,1}. \end{align*} $$
$$ \begin{align*} k_1 &:= -2 b^*_{1,2m} - b^*_{3,1} + 2b^*_{4,1}, \\ k_2 &:= -2 b^*_{1,2m-1} + b^*_{3,1} - 2b^*_{4,1}. \end{align*} $$
It is straightforward to show that
![]() $k_1$
and
$k_1$
and
![]() $k_2$
are distinguished representatives in the sense of Definition 4.5. Indeed, in our case, the canonical spin
$k_2$
are distinguished representatives in the sense of Definition 4.5. Indeed, in our case, the canonical spin
![]() $^c$
structure described in (4.2) is given by
$^c$
structure described in (4.2) is given by
 $K= b^*_{3,1} -(m+1) b^*_{4,1}$
, and
$K= b^*_{3,1} -(m+1) b^*_{4,1}$
, and
![]() $k_1$
is of the form (4.3), where
$k_1$
is of the form (4.3), where
By (4.4), we have
 $(a_0,a_1,a_2,a_3,a_4) = (0,1,0,1,\tfrac {m-3}{2})$
. This satisfies the conditions in Definition 4.5, so
$(a_0,a_1,a_2,a_3,a_4) = (0,1,0,1,\tfrac {m-3}{2})$
. This satisfies the conditions in Definition 4.5, so
![]() $k_1$
is a distinguished representative. The class
$k_1$
is a distinguished representative. The class
![]() $k_2$
is shown to be a distinguished representative, too, by similar computation. In this case, we have
$k_2$
is shown to be a distinguished representative, too, by similar computation. In this case, we have
and
![]() $(a_0,a_1,a_2,a_3,a_4) = (0,2,0,0,m-2)$
.
$(a_0,a_1,a_2,a_3,a_4) = (0,2,0,0,m-2)$
.
Under the adjoint
![]() $\lambda \colon H_2(X) \to H^2(X)=\mathrm {Hom}(H_2(X),\mathbb {Z})$
of the intersection form of X,
$\lambda \colon H_2(X) \to H^2(X)=\mathrm {Hom}(H_2(X),\mathbb {Z})$
of the intersection form of X,
![]() $k_1$
and
$k_1$
and
![]() $k_2$
are respectively the images of
$k_2$
are respectively the images of
 $$ \begin{align*} x_1 &= 2b_0 + 2b_{1,1}+\cdots+2b_{1,2m} + b_{2,1} + b_{3,1}, \\ x_2 &= 4b_1 + 4b_{1,1}+\cdots+4b_{1,2m-1}+2b_{1,2m} + 2b_{2,1} + 2b_{3,1} + 2b_{4,1}. \end{align*} $$
$$ \begin{align*} x_1 &= 2b_0 + 2b_{1,1}+\cdots+2b_{1,2m} + b_{2,1} + b_{3,1}, \\ x_2 &= 4b_1 + 4b_{1,1}+\cdots+4b_{1,2m-1}+2b_{1,2m} + 2b_{2,1} + 2b_{3,1} + 2b_{4,1}. \end{align*} $$
Recall that
![]() $\operatorname {Char}(X)\subset H^2(X)$
is identified with
$\operatorname {Char}(X)\subset H^2(X)$
is identified with
![]() $\operatorname {\mathrm {Spin}}^c(X)$
via
$\operatorname {\mathrm {Spin}}^c(X)$
via
![]() $c_1$
, and thus for a spin
$c_1$
, and thus for a spin
![]() $^c$
structure
$^c$
structure
![]() $[k] \in \operatorname {Char}(X)/2\lambda (H_2(X))$
of Y, we have
$[k] \in \operatorname {Char}(X)/2\lambda (H_2(X))$
of Y, we have
![]() $c_1([k]) = k|_Y$
. So,
$c_1([k]) = k|_Y$
. So,
![]() $c_1([k]) = 0$
if and only if k lies in the kernel of
$c_1([k]) = 0$
if and only if k lies in the kernel of
![]() $H^2(X) \to H^2(Y)$
or, equivalently, k lies in the image of
$H^2(X) \to H^2(Y)$
or, equivalently, k lies in the image of
![]() $\lambda \colon H_2(X) \to H^2(X)$
. From this observation, it follows that
$\lambda \colon H_2(X) \to H^2(X)$
. From this observation, it follows that
![]() $c_1([k_i]) = 0$
for
$c_1([k_i]) = 0$
for
![]() $i=1,2$
, because
$i=1,2$
, because
![]() $k_i = \lambda (x_i)$
. Also,
$k_i = \lambda (x_i)$
. Also,
![]() $[k_1] \ne [k_2]$
because
$[k_1] \ne [k_2]$
because
![]() $x_1-x_2\notin 2H_2(X)$
. Therefore, to complete the proof, it suffices to show
$x_1-x_2\notin 2H_2(X)$
. Therefore, to complete the proof, it suffices to show
![]() $d(Y,[k_i]) \le (2m-1)/4$
for
$d(Y,[k_i]) \le (2m-1)/4$
for
![]() $i=1,2$
.
$i=1,2$
.
We have
 $$ \begin{align*} k_1^2 = \lambda(x_1,x_1) = -3, \quad k_2^2 = \lambda(x_2,x_2) = -m-4. \end{align*} $$
$$ \begin{align*} k_1^2 = \lambda(x_1,x_1) = -3, \quad k_2^2 = \lambda(x_2,x_2) = -m-4. \end{align*} $$
The last thing we need is the minimum of the values of
![]() $\tau (i)$
defined in (4.6). Recall the notation
$\tau (i)$
defined in (4.6). Recall the notation
![]() $\Delta _i = \tau (i+1)-\tau (i)$
from Remark 4.7.
$\Delta _i = \tau (i+1)-\tau (i)$
from Remark 4.7.
Assertion. For both
![]() $k_1$
and
$k_1$
and
![]() $k_2$
and for all
$k_2$
and for all
![]() $i\ge 0$
,
$i\ge 0$
,
![]() $\Delta _i \ge 0$
.
$\Delta _i \ge 0$
.
We will provide a proof of the assertion for
![]() $m\ge 23$
. For
$m\ge 23$
. For
![]() $m<23$
, the assertion is verified by direct inspection using Remark 4.7 (indeed, the author used a computer program), so we omit details for
$m<23$
, the assertion is verified by direct inspection using Remark 4.7 (indeed, the author used a computer program), so we omit details for
![]() $m<23$
. Note that it suffices to use
$m<23$
. Note that it suffices to use
![]() $m\ge 23$
to prove the main results of this article, Theorems A, B, C and D.
$m\ge 23$
to prove the main results of this article, Theorems A, B, C and D.
For the case of
![]() $k_1$
, by Remark 4.7, we have
$k_1$
, by Remark 4.7, we have
![]() $\Delta _i\ge 0$
for
$\Delta _i\ge 0$
for
![]() $i\ge R$
, where
$i\ge R$
, where
Because
![]() $m\ge 23$
,
$m\ge 23$
,
![]() $R\le 10$
. So,
$R\le 10$
. So,
![]() $\Delta _i\ge 0$
for
$\Delta _i\ge 0$
for
![]() $i\ge 10$
. For
$i\ge 10$
. For
![]() $i\le 10$
, using (4.6), we have
$i\le 10$
, using (4.6), we have
 $$ \begin{align*} \Delta_i &= 1 + 2i + \bigg[ \frac{-2mi+1}{2m+1} \bigg] + \bigg[ \frac{-i}{2} \bigg] + \bigg[ \frac{-i+1}{3} \bigg] + \bigg[ \frac{-i+(m-3)/2}{m+1} \bigg] \\ & \ge 1+2i-i+\frac{-i-1}{2} + \frac{-i-1}{3} = \frac{i+1}{6} \ge 0. \end{align*} $$
$$ \begin{align*} \Delta_i &= 1 + 2i + \bigg[ \frac{-2mi+1}{2m+1} \bigg] + \bigg[ \frac{-i}{2} \bigg] + \bigg[ \frac{-i+1}{3} \bigg] + \bigg[ \frac{-i+(m-3)/2}{m+1} \bigg] \\ & \ge 1+2i-i+\frac{-i-1}{2} + \frac{-i-1}{3} = \frac{i+1}{6} \ge 0. \end{align*} $$
This shows the claim for
![]() $k_1$
. For the case of
$k_1$
. For the case of
![]() $k_2$
, we proceed in the same way. We have
$k_2$
, we proceed in the same way. We have
Because
![]() $m\ge 23$
,
$m\ge 23$
,
![]() $R\ge 10$
, and thus
$R\ge 10$
, and thus
![]() $\Delta _i\ge 0$
for
$\Delta _i\ge 0$
for
![]() $i\ge 10$
by Remark 4.7. For
$i\ge 10$
by Remark 4.7. For
![]() $1\le i\le 10$
, using (4.6), we have
$1\le i\le 10$
, using (4.6), we have
 $$ \begin{align*} \Delta_i &= 1 + 2i + \bigg[ \frac{-2mi+1}{2m+1} \bigg] + \bigg[ \frac{-i}{2} \bigg] + \bigg[ \frac{-i}{3} \bigg] + \bigg[ \frac{-i+m-2}{m+1} \bigg] \\ & \ge 1+2i-i+\frac{-i-1}{2} + \frac{-i-2}{3} = \frac{i-1}{6} \ge 0. \end{align*} $$
$$ \begin{align*} \Delta_i &= 1 + 2i + \bigg[ \frac{-2mi+1}{2m+1} \bigg] + \bigg[ \frac{-i}{2} \bigg] + \bigg[ \frac{-i}{3} \bigg] + \bigg[ \frac{-i+m-2}{m+1} \bigg] \\ & \ge 1+2i-i+\frac{-i-1}{2} + \frac{-i-2}{3} = \frac{i-1}{6} \ge 0. \end{align*} $$
For
![]() $i=0$
, a direct computation using (4.6) gives
$i=0$
, a direct computation using (4.6) gives
![]() $\Delta _0=1$
. This completes the proof of the assertion.
$\Delta _0=1$
. This completes the proof of the assertion.
From the assertion, it follows that
![]() $\min \{\tau (i)\mid i\ge 0\}=0$
because
$\min \{\tau (i)\mid i\ge 0\}=0$
because
![]() $\tau (0)=0$
. So, by Némethi’s Theorem 4.6,
$\tau (0)=0$
. So, by Némethi’s Theorem 4.6,
 $$ \begin{align*} d(Y,[k_i]) = \frac{k_i^2 + 2m+4}{4} = \begin{cases} (2m-1)/4 &\text{for } i=1, \\ m/4 &\text{for } i=2. \end{cases} \end{align*} $$
$$ \begin{align*} d(Y,[k_i]) = \frac{k_i^2 + 2m+4}{4} = \begin{cases} (2m-1)/4 &\text{for } i=1, \\ m/4 &\text{for } i=2. \end{cases} \end{align*} $$
Therefore
![]() $d(Y,[k_i]) \le (2m-1)/4$
holds for
$d(Y,[k_i]) \le (2m-1)/4$
holds for
![]() $i=1,2$
.
$i=1,2$
.
Now, to complete the proof of Theorem 2.2, it only remains to prove of Lemma 4.4, which estimates d-invariants of the 3-manifold B in Figure 6. In the proof below, we will use that B is a Seifert 3-manifold as well.
Proof of Lemma 4.4. Recall that B is the 3-manifold described in Figure 6. Let
![]() $\mathfrak {s}$
be a spin
$\mathfrak {s}$
be a spin
![]() $^c$
structure of B satisfying
$^c$
structure of B satisfying
![]() $c_1(\mathfrak {s})=0$
. The goal is to show that
$c_1(\mathfrak {s})=0$
. The goal is to show that
![]() $d(B,\mathfrak {s})\le (m+2)/4$
.
$d(B,\mathfrak {s})\le (m+2)/4$
.
As we will see in what follows, it will be useful to consider
![]() $-B$
instead of B. That is, we will show
$-B$
instead of B. That is, we will show
![]() $d(-B,\mathfrak {s})\ge -(m+2)/4$
. Figure 10 shows that
$d(-B,\mathfrak {s})\ge -(m+2)/4$
. Figure 10 shows that
![]() $-B$
is a Seifert 3-manifold. We use the notation of Subsection 4.2. The associated plumbed 4-manifold X has
$-B$
is a Seifert 3-manifold. We use the notation of Subsection 4.2. The associated plumbed 4-manifold X has
![]() $H_2(X)=\mathbb {Z}^{2m}$
, with basis elements
$H_2(X)=\mathbb {Z}^{2m}$
, with basis elements
![]() $b_0$
,
$b_0$
,
![]() $b_{1,1},\ldots$
,
$b_{1,1},\ldots$
,
![]() $b_{1,m}$
,
$b_{1,m}$
,
![]() $b_{2,1},\ldots$
,
$b_{2,1},\ldots$
,
![]() $b_{2,m-2}$
,
$b_{2,m-2}$
,
![]() $b_{3,1}$
. The associated decorations are
$b_{3,1}$
. The associated decorations are
![]() $e_0=-2$
,
$e_0=-2$
,
![]() $e_{1,j} = -2$
for all j,
$e_{1,j} = -2$
for all j,
![]() $e_{2,j}=-2$
for all j and
$e_{2,j}=-2$
for all j and
![]() $e_{3,1}=-2m-1$
. Let
$e_{3,1}=-2m-1$
. Let
![]() $b^*_0$
,
$b^*_0$
,
 $b^*_{\ell ,j}$
be the dual basis elements in
$b^*_{\ell ,j}$
be the dual basis elements in
![]() $H^2(X)$
. Because
$H^2(X)$
. Because
 $$ \begin{align*} e = -2 + \frac{m}{m+1} + \frac{m-2}{m-1} + \frac{1}{2m+1} = \frac{-3m^2 -2m -1}{(m^2-1)(2m+1)} < 0, \end{align*} $$
$$ \begin{align*} e = -2 + \frac{m}{m+1} + \frac{m-2}{m-1} + \frac{1}{2m+1} = \frac{-3m^2 -2m -1}{(m^2-1)(2m+1)} < 0, \end{align*} $$
the 4-manifold X is negative definite. This is why we use
![]() $-B$
instead of B.
$-B$
instead of B.

Figure 10 Surgery diagram calculus showing that
![]() $-B$
is a Seifert 3-manifold. The symbol
$-B$
is a Seifert 3-manifold. The symbol
![]() $(*)$
means handle slides (or Rolfsen twist [Reference Rolfsen41, p. 264]) followed by elimination of a component together with a 0-framed meridian.
$(*)$
means handle slides (or Rolfsen twist [Reference Rolfsen41, p. 264]) followed by elimination of a component together with a 0-framed meridian.
The canonical spin
![]() $^c$
structure K of X is given by
$^c$
structure K of X is given by
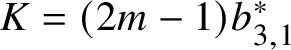 $K=(2m-1)b^*_{3,1}$
. Let
$K=(2m-1)b^*_{3,1}$
. Let
 $$ \begin{align*} x_1 &= b_{1,1} + b_{1,3} + \cdots + b_{1,m} + b_{3,1}, \\ x_2 &= b_{2,1} + b_{2,3} + \cdots + b_{2,m-2} + b_{3,1}, \end{align*} $$
$$ \begin{align*} x_1 &= b_{1,1} + b_{1,3} + \cdots + b_{1,m} + b_{3,1}, \\ x_2 &= b_{2,1} + b_{2,3} + \cdots + b_{2,m-2} + b_{3,1}, \end{align*} $$
and let
![]() $k_i = \lambda (x_i) \in H^2(X)$
for
$k_i = \lambda (x_i) \in H^2(X)$
for
![]() $i=1$
,
$i=1$
,
![]() $2$
. Then
$2$
. Then
![]() $k_i \in \operatorname {Char}(X)=K+2H^2(X)$
, so that
$k_i \in \operatorname {Char}(X)=K+2H^2(X)$
, so that
![]() $[k_i] \in \operatorname {Char}(X)/2\lambda (H_2(X))=\operatorname {\mathrm {Spin}}^c(-B)$
is a spin
$[k_i] \in \operatorname {Char}(X)/2\lambda (H_2(X))=\operatorname {\mathrm {Spin}}^c(-B)$
is a spin
![]() $^c$
structure of
$^c$
structure of
![]() $-B$
. Similar to the proof of Lemma 4.8,
$-B$
. Similar to the proof of Lemma 4.8,
![]() $c_1([k_i]) = k_i|_{-B} = 0$
. Also,
$c_1([k_i]) = k_i|_{-B} = 0$
. Also,
![]() $[k_1] \ne [k_2]$
in
$[k_1] \ne [k_2]$
in
![]() $\operatorname {\mathrm {Spin}}^c(-B)$
because
$\operatorname {\mathrm {Spin}}^c(-B)$
because
![]() $x_1-x_2 \notin 2H_2(X)$
. It follows that
$x_1-x_2 \notin 2H_2(X)$
. It follows that
![]() $[k_1]$
and
$[k_1]$
and
![]() $[k_2]$
are the two spin
$[k_2]$
are the two spin
![]() $^c$
structures of
$^c$
structures of
![]() $-B$
with
$-B$
with
![]() $c_1=0$
. So, it suffices to show that
$c_1=0$
. So, it suffices to show that
![]() $d(-B,[k_i])\ge -(m+2)/4$
for
$d(-B,[k_i])\ge -(m+2)/4$
for
![]() $i=1$
,
$i=1$
,
![]() $2$
. Instead of determining the values exactly, we will present a simpler argument that gives the promised estimate. We have
$2$
. Instead of determining the values exactly, we will present a simpler argument that gives the promised estimate. We have
 $k_1^2 = \lambda (x_1,x_1) = -3m-2$
. So, by Ozsváth-Szabó’s inequality [Reference Ozsváth and Szabó40, Theorem 9.6],
$k_1^2 = \lambda (x_1,x_1) = -3m-2$
. So, by Ozsváth-Szabó’s inequality [Reference Ozsváth and Szabó40, Theorem 9.6],
 $$ \begin{align} d(-B,[k_1]) \ge \frac{k_1^2 + b_2(X)}{4} = \frac{-m-2}{4}. \end{align} $$
$$ \begin{align} d(-B,[k_1]) \ge \frac{k_1^2 + b_2(X)}{4} = \frac{-m-2}{4}. \end{align} $$
Similarly, because
 $k_2^2 = \lambda (x_2,x_2) = -3m$
, we have
$k_2^2 = \lambda (x_2,x_2) = -3m$
, we have
 $$ \begin{align} d(-B,[k_2]) \ge \frac{k_2^2 + b_2(X)}{4} = \frac{-m}{4}. \end{align} $$
$$ \begin{align} d(-B,[k_2]) \ge \frac{k_2^2 + b_2(X)}{4} = \frac{-m}{4}. \end{align} $$
So, we have
![]() $d(-B,[k_i]) \ge -(m+2)/4$
for
$d(-B,[k_i]) \ge -(m+2)/4$
for
![]() $i=1$
,
$i=1$
,
![]() $2$
. (Indeed, it can be shown that the equality holds in (4.7) and (4.8), by using the technique described in Subsection 4.2, as we did in the proof of Lemma 4.8.)
$2$
. (Indeed, it can be shown that the equality holds in (4.7) and (4.8), by using the technique described in Subsection 4.2, as we did in the proof of Lemma 4.8.)
Appendix General primary decomposition
The goal of this appendix is to present an abstract formulation of the notion of primary decomposition along an invariant with values in an unique factorisation domain. We also discuss questions in specific cases and earlier related results in the literature from our viewpoint. The organisation is as follows. In Subsection A.1, we describe the definition of general primary decomposition and present basic observations. In Subsection A.2, we investigate primary decomposition of extensions. In Subsection A.3, we discuss specialisations to various knot concordance groups (e.g., smooth/topological) and related filtrations. In Subsection A.4, we discuss the case of rational homology cobordism group of rational homology 3-spheres.
A.1. Definitions and basic observations
Let
![]() ${\mathbb K}$
be an abelian monoid and
${\mathbb K}$
be an abelian monoid and
![]() $\sim $
be an equivalence relation on
$\sim $
be an equivalence relation on
![]() ${\mathbb K}$
. Suppose that the monoid structure on
${\mathbb K}$
. Suppose that the monoid structure on
![]() ${\mathbb K}$
descends to an abelian group structure on the set
${\mathbb K}$
descends to an abelian group structure on the set
![]() ${\mathcal C} := {\mathbb K}/{\sim }$
of equivalence classes. Denote the equivalence class of
${\mathcal C} := {\mathbb K}/{\sim }$
of equivalence classes. Denote the equivalence class of
![]() $K\in {\mathbb K}$
by
$K\in {\mathbb K}$
by
![]() $[K] \in {\mathcal C}$
.
$[K] \in {\mathcal C}$
.
Let R be a unique factorisation domain with involution
![]() $r \mapsto r^*$
. Main examples are
$r \mapsto r^*$
. Main examples are
![]() $\mathbb {Z}$
with a trivial involution and the Laurent polynomial ring
$\mathbb {Z}$
with a trivial involution and the Laurent polynomial ring
![]() $\mathbb {Q}[t^{\pm 1}]$
with the standard involution
$\mathbb {Q}[t^{\pm 1}]$
with the standard involution
![]() $\bigl (\sum a_i t^i\bigr )^* = \sum a_i t^{-i}$
. For r,
$\bigl (\sum a_i t^i\bigr )^* = \sum a_i t^{-i}$
. For r,
![]() $s\in R$
, write
$s\in R$
, write
![]() $r\doteq s$
if r and s in R are associates; that is,
$r\doteq s$
if r and s in R are associates; that is,
![]() $r=us$
for some unit u in R. We say that two irreducibles
$r=us$
for some unit u in R. We say that two irreducibles
![]() $\lambda $
and
$\lambda $
and
![]() $\mu $
in R are
$\mu $
in R are
![]() $*$
-associates if either
$*$
-associates if either
![]() $\lambda \doteq \mu $
or
$\lambda \doteq \mu $
or
![]() $\lambda ^*\doteq \mu $
. We say that
$\lambda ^*\doteq \mu $
. We say that
![]() $r\in R$
is self-dual if
$r\in R$
is self-dual if
![]() $r\doteq r^*$
.
$r\doteq r^*$
.
Suppose that
![]() $\chi \colon {\mathbb K} \to (R\smallsetminus \{0\}) / {\doteq }$
is a function. We will denote a representative of
$\chi \colon {\mathbb K} \to (R\smallsetminus \{0\}) / {\doteq }$
is a function. We will denote a representative of
![]() $\chi (K)$
by
$\chi (K)$
by
![]() $\Delta _K\in R\smallsetminus \{0\}$
. Suppose that the following hold for all K,
$\Delta _K\in R\smallsetminus \{0\}$
. Suppose that the following hold for all K,
![]() $K'$
in
$K'$
in
![]() ${\mathbb K}$
:
${\mathbb K}$
:
-
(
 $\Delta 1$
)
$\Delta 1$
)
 $\Delta _K$
is self-dual.
$\Delta _K$
is self-dual. -
(
 $\Delta 2$
)
$\Delta 2$
)
 $\Delta _{K+K'} \doteq \Delta _K\cdot \Delta _{K'}$
.
$\Delta _{K+K'} \doteq \Delta _K\cdot \Delta _{K'}$
. -
(
 $\Delta 3$
)
$\Delta 3$
)
 $-[K] = [J]$
for some J in
$-[K] = [J]$
for some J in
 ${\mathbb K}$
such that
${\mathbb K}$
such that
 $\Delta _J \doteq \Delta _K$
.
$\Delta _J \doteq \Delta _K$
.
In particular, writing
![]() ${\mathcal S}(R)=\{r\in R\mid r\ne 0$
is self-dual
${\mathcal S}(R)=\{r\in R\mid r\ne 0$
is self-dual
![]() $\}$
,
$\}$
,
 ${\mathbb K} \xrightarrow {\chi } {\mathcal S}(R)/{\doteq }$
is a homomorphism between abelian monoids.
${\mathbb K} \xrightarrow {\chi } {\mathcal S}(R)/{\doteq }$
is a homomorphism between abelian monoids.
Of course, the main example that one may keep in mind is the case that
![]() ${\mathbb K}$
is the monoid of knots under connected sum,
${\mathbb K}$
is the monoid of knots under connected sum,
![]() ${\sim }$
is concordance and
${\sim }$
is concordance and
![]() $\Delta _K$
is the Alexander polynomial in
$\Delta _K$
is the Alexander polynomial in
![]() $R=\mathbb {Q}[t^{\pm 1}]$
. Including this, we will discuss various specific examples in Subsections A.3 and A.4.
$R=\mathbb {Q}[t^{\pm 1}]$
. Including this, we will discuss various specific examples in Subsections A.3 and A.4.
Let
![]() $\Delta = \{[K] \in {\mathcal C} \mid \Delta _K \doteq 1 \}$
. For an irreducible
$\Delta = \{[K] \in {\mathcal C} \mid \Delta _K \doteq 1 \}$
. For an irreducible
![]() $\lambda $
in R, let
$\lambda $
in R, let
![]() $S(\lambda )=\lambda $
if
$S(\lambda )=\lambda $
if
![]() $\lambda $
is self-dual, and
$\lambda $
is self-dual, and
![]() $S(\lambda )=\lambda \lambda ^*$
otherwise. Let
$S(\lambda )=\lambda \lambda ^*$
otherwise. Let
 $$ \begin{align*} {\mathcal C}_{\lambda} &:= \{[K] \in {\mathcal C} \mid \Delta_K \doteq S(\lambda)^k \text{ for some } k\ge 0\}, \\ {\mathcal C}^{\lambda} &:= \{[K] \in {\mathcal C} \mid \Delta_K \text{ is relatively prime to } \lambda\}. \end{align*} $$
$$ \begin{align*} {\mathcal C}_{\lambda} &:= \{[K] \in {\mathcal C} \mid \Delta_K \doteq S(\lambda)^k \text{ for some } k\ge 0\}, \\ {\mathcal C}^{\lambda} &:= \{[K] \in {\mathcal C} \mid \Delta_K \text{ is relatively prime to } \lambda\}. \end{align*} $$
It is straightforward to verify that
![]() ${\mathcal C}_{\lambda }$
,
${\mathcal C}_{\lambda }$
,
![]() ${\mathcal C}^{\lambda }$
and
${\mathcal C}^{\lambda }$
and
![]() $\Delta $
are subgroups of
$\Delta $
are subgroups of
![]() ${\mathcal C}$
, using (
${\mathcal C}$
, using (
![]() $\Delta 2$
) and (
$\Delta 2$
) and (
![]() $\Delta 3$
). Also, using (
$\Delta 3$
). Also, using (
![]() $\Delta 1$
), it is seen that
$\Delta 1$
), it is seen that
![]() $[K]\in {\mathcal C}_{\lambda }$
if and only if
$[K]\in {\mathcal C}_{\lambda }$
if and only if
![]() $K\sim J$
for some J with
$K\sim J$
for some J with
![]() $\Delta _J$
lying in the multiplicative subset generated by
$\Delta _J$
lying in the multiplicative subset generated by
![]() $\lambda $
,
$\lambda $
,
![]() $\lambda ^*$
and the units in R. We have
$\lambda ^*$
and the units in R. We have
![]() $\Delta \subset {\mathcal C}_{\lambda }$
,
$\Delta \subset {\mathcal C}_{\lambda }$
,
![]() ${\mathcal C}_{\lambda }={\mathcal C}_{\lambda ^*}$
and
${\mathcal C}_{\lambda }={\mathcal C}_{\lambda ^*}$
and
![]() ${\mathcal C}^{\lambda }={\mathcal C}^{\lambda ^*}$
. Use
${\mathcal C}^{\lambda }={\mathcal C}^{\lambda ^*}$
. Use
![]() $S(\lambda )=S(\lambda ^*)$
and (
$S(\lambda )=S(\lambda ^*)$
and (
![]() $\Delta 1$
) to verify the two equalities respectively.
$\Delta 1$
) to verify the two equalities respectively.
Note that though
![]() $\Delta _K$
is self-dual, irreducible factors of
$\Delta _K$
is self-dual, irreducible factors of
![]() $\Delta _K$
are not necessarily self-dual. For instance, in
$\Delta _K$
are not necessarily self-dual. For instance, in
![]() $R=\mathbb {Q}[t^{\pm 1}]$
, we have
$R=\mathbb {Q}[t^{\pm 1}]$
, we have
![]() $-2t+5-2t^{-1}=(t-2)(t^{-1}-2)$
. By the above definition, a class
$-2t+5-2t^{-1}=(t-2)(t^{-1}-2)$
. By the above definition, a class
![]() $[K]$
with
$[K]$
with
![]() $\Delta _K=-2t+5-2t^{-1}$
lies in
$\Delta _K=-2t+5-2t^{-1}$
lies in
![]() ${\mathcal C}_{\lambda }$
for
${\mathcal C}_{\lambda }$
for
![]() $\lambda =t-2$
.
$\lambda =t-2$
.
Definition A.1. Let
![]() ${\mathbb P}$
be the set of
${\mathbb P}$
be the set of
![]() $*$
-associate classes of irreducibles in R.
$*$
-associate classes of irreducibles in R.
-
(1) We say that
 $({\mathbb K},\sim ,\chi )$
is left primary decomposable if the sum of the inclusions
$({\mathbb K},\sim ,\chi )$
is left primary decomposable if the sum of the inclusions $$ \begin{align*} \Phi_L\colon \bigoplus_{[\lambda]\in {\mathbb P}} {\mathcal C}_{\lambda}/\Delta \longrightarrow {\mathcal C}/\Delta \end{align*} $$
$$ \begin{align*} \Phi_L\colon \bigoplus_{[\lambda]\in {\mathbb P}} {\mathcal C}_{\lambda}/\Delta \longrightarrow {\mathcal C}/\Delta \end{align*} $$
 ${\mathcal C}_{\lambda }/\Delta \hookrightarrow {\mathcal C}/\Delta $
is an isomorphism.
${\mathcal C}_{\lambda }/\Delta \hookrightarrow {\mathcal C}/\Delta $
is an isomorphism.
-
(2) We say that
 $({\mathbb K},\sim ,\chi )$
is right primary decomposable if the surjections
$({\mathbb K},\sim ,\chi )$
is right primary decomposable if the surjections
 ${\mathcal C}/\Delta \twoheadrightarrow {\mathcal C}/{\mathcal C}^{\lambda }$
induce an isomorphism
${\mathcal C}/\Delta \twoheadrightarrow {\mathcal C}/{\mathcal C}^{\lambda }$
induce an isomorphism  $$ \begin{align*} \Phi_R\colon {\mathcal C}/\Delta \longrightarrow \bigoplus_{[\lambda]\in{\mathbb P}} {\mathcal C}/{\mathcal C}^{\lambda}. \end{align*} $$
$$ \begin{align*} \Phi_R\colon {\mathcal C}/\Delta \longrightarrow \bigoplus_{[\lambda]\in{\mathbb P}} {\mathcal C}/{\mathcal C}^{\lambda}. \end{align*} $$
Because each
![]() $\Delta _K$
has finitely many irreducible factors, it follows that the product
$\Delta _K$
has finitely many irreducible factors, it follows that the product
 ${\mathcal C}/\Delta \to \prod _{[\lambda ]\in {\mathbb P}} {\mathcal C}/{\mathcal C}^{\lambda }$
of the surjections
${\mathcal C}/\Delta \to \prod _{[\lambda ]\in {\mathbb P}} {\mathcal C}/{\mathcal C}^{\lambda }$
of the surjections
![]() ${\mathcal C}/\Delta \twoheadrightarrow {\mathcal C}/{\mathcal C}^{\lambda }$
has image in the direct sum
${\mathcal C}/\Delta \twoheadrightarrow {\mathcal C}/{\mathcal C}^{\lambda }$
has image in the direct sum
 $\bigoplus _{[\lambda ]\in {\mathbb P}}{\mathcal C}/{\mathcal C}^{\lambda }$
. That is,
$\bigoplus _{[\lambda ]\in {\mathbb P}}{\mathcal C}/{\mathcal C}^{\lambda }$
. That is,
![]() $\Phi _R$
is always a well-defined homomorphism.
$\Phi _R$
is always a well-defined homomorphism.
We remark that taking the quotient by
![]() $\Delta $
may be viewed as an analogue of ignoring units in the primary decomposition in a unique factorisation domain.
$\Delta $
may be viewed as an analogue of ignoring units in the primary decomposition in a unique factorisation domain.
For brevity, when the choice of
![]() $({\mathbb K},\sim ,\chi )$
is clearly understood from the context, we will simply say that
$({\mathbb K},\sim ,\chi )$
is clearly understood from the context, we will simply say that
![]() ${\mathcal C}$
is left or right primary decomposable.
${\mathcal C}$
is left or right primary decomposable.
From the definition, it is straightforward to see that
![]() ${\mathcal C}$
is left primary decomposable if only if the following two conditions (LP1) and (LP2) hold. More precesly, (LP1) and (LP2) are respectively equivalent to the surjectivity and injectivity of
${\mathcal C}$
is left primary decomposable if only if the following two conditions (LP1) and (LP2) hold. More precesly, (LP1) and (LP2) are respectively equivalent to the surjectivity and injectivity of
![]() $\Phi _L$
.
$\Phi _L$
.
-
(LP1) Existence: for every
 $K\in {\mathbb K}$
, there exist irreducibles
$K\in {\mathbb K}$
, there exist irreducibles
 $\lambda _1,\ldots$
,
$\lambda _1,\ldots$
,
 $\lambda _n$
and
$\lambda _n$
and
 $[K_1]\in {\mathcal C}_{\lambda _1},\ldots ,[K_n]\in {\mathcal C}_{\lambda _n}$
such that
$[K_1]\in {\mathcal C}_{\lambda _1},\ldots ,[K_n]\in {\mathcal C}_{\lambda _n}$
such that
 $[K] \equiv [K_1]+\cdots +[K_n]\bmod \Delta $
.
$[K] \equiv [K_1]+\cdots +[K_n]\bmod \Delta $
. -
(LP2) Uniqueness: if
 $[K_1]+\cdots +[K_n] \equiv 0 \bmod \Delta $
and
$[K_1]+\cdots +[K_n] \equiv 0 \bmod \Delta $
and
 $[K_i]\in {\mathcal C}_{\lambda _i}$
for some pairwise distinct
$[K_i]\in {\mathcal C}_{\lambda _i}$
for some pairwise distinct
 $[\lambda _1],\ldots$
,
$[\lambda _1],\ldots$
,
 $[\lambda _n] \in {\mathbb P}$
, then
$[\lambda _n] \in {\mathbb P}$
, then
 $[K_i]\equiv 0 \bmod \Delta $
for all i.
$[K_i]\equiv 0 \bmod \Delta $
for all i.
The following examples illustrate that the left and right primary decomposabilities are independent of each other.
Example A.2. Let
be the free abelian monoid generated by four generators K,
![]() $K'$
, J and
$K'$
, J and
![]() $J'$
. Define
$J'$
. Define
![]() $\sim $
on
$\sim $
on
![]() ${\mathbb K}$
by
${\mathbb K}$
by
and let
![]() ${\mathcal C} = {\mathbb K}/{\sim }$
. Then
${\mathcal C} = {\mathbb K}/{\sim }$
. Then
![]() ${\mathcal C}$
is the infinite cyclic group, and
${\mathcal C}$
is the infinite cyclic group, and
![]() $[K]=-[K']=[J]=-[J']$
is a generator. Fix R that has three distinct self-dual irreducibles
$[K]=-[K']=[J]=-[J']$
is a generator. Fix R that has three distinct self-dual irreducibles
![]() $\lambda $
,
$\lambda $
,
![]() $\mu $
and
$\mu $
and
![]() $\nu $
. Define
$\nu $
. Define
In particular,
![]() $\Delta _K = \lambda $
and
$\Delta _K = \lambda $
and
![]() $\Delta _J=\mu \nu $
. It is straightforward to verify that (
$\Delta _J=\mu \nu $
. It is straightforward to verify that (
![]() $\Delta 1$
), (
$\Delta 1$
), (
![]() $\Delta 2$
) and (
$\Delta 2$
) and (
![]() $\Delta 3$
) are satisfied and that the subgroup
$\Delta 3$
) are satisfied and that the subgroup
![]() $\Delta $
is trivial.
$\Delta $
is trivial.
We claim that
![]() ${\mathcal C}$
is left primary decomposable. Indeed, it is straightforward to see that for
${\mathcal C}$
is left primary decomposable. Indeed, it is straightforward to see that for
![]() $L\in {\mathbb K}$
,
$L\in {\mathbb K}$
,
![]() $\Delta _L$
is a power of an irreducible if and only if
$\Delta _L$
is a power of an irreducible if and only if
![]() $L=aK+bK'$
(and thus
$L=aK+bK'$
(and thus
![]() $\Delta _L=\lambda ^{a+b}$
). It follows that for any irreducible
$\Delta _L=\lambda ^{a+b}$
). It follows that for any irreducible
![]() $\zeta $
in R,
$\zeta $
in R,
![]() ${\mathcal C}_{\zeta }={\mathcal C}$
if
${\mathcal C}_{\zeta }={\mathcal C}$
if
![]() $\zeta =\lambda $
, and
$\zeta =\lambda $
, and
![]() ${\mathcal C}_{\zeta }=0$
otherwise. So
${\mathcal C}_{\zeta }=0$
otherwise. So
 $\Phi _L\colon \bigoplus _{[\zeta ]} {\mathcal C}_{\zeta }/\Delta \to {\mathcal C}/\Delta $
is an isomorphism.
$\Phi _L\colon \bigoplus _{[\zeta ]} {\mathcal C}_{\zeta }/\Delta \to {\mathcal C}/\Delta $
is an isomorphism.
On the other hand,
![]() ${\mathcal C}$
is not right primary decomposable. To see this, observe that
${\mathcal C}$
is not right primary decomposable. To see this, observe that
![]() $[K]\in {\mathcal C}^{\zeta }$
for all
$[K]\in {\mathcal C}^{\zeta }$
for all
![]() $\zeta \ne \lambda $
, because
$\zeta \ne \lambda $
, because
![]() $\Delta _K=\lambda $
. Also,
$\Delta _K=\lambda $
. Also,
![]() $[K]=[J]\in {\mathcal C}^{\lambda }$
because
$[K]=[J]\in {\mathcal C}^{\lambda }$
because
![]() $\Delta _J=\mu \nu $
. Because
$\Delta _J=\mu \nu $
. Because
![]() $[K]$
generates
$[K]$
generates
![]() ${\mathcal C}$
, it follows that
${\mathcal C}$
, it follows that
![]() ${\mathcal C}^{\zeta }={\mathcal C}$
for all
${\mathcal C}^{\zeta }={\mathcal C}$
for all
![]() $\zeta $
. So
$\zeta $
. So
 $\Phi _R\colon {\mathcal C}/\Delta \to \bigoplus _{[\zeta ]} {\mathcal C}/{\mathcal C}^{\zeta }=0$
is not injective.
$\Phi _R\colon {\mathcal C}/\Delta \to \bigoplus _{[\zeta ]} {\mathcal C}/{\mathcal C}^{\zeta }=0$
is not injective.
Example A.3. Let
![]() ${\mathbb K}$
,
${\mathbb K}$
,
![]() $\sim $
,
$\sim $
,
![]() ${\mathcal C}$
, R,
${\mathcal C}$
, R,
![]() $\lambda $
,
$\lambda $
,
![]() $\mu $
and
$\mu $
and
![]() $\nu $
be as in Example A.2, but define
$\nu $
be as in Example A.2, but define
Note that (
![]() $\Delta 1$
), (
$\Delta 1$
), (
![]() $\Delta 2$
) and (
$\Delta 2$
) and (
![]() $\Delta 3$
) are satisfied,
$\Delta 3$
) are satisfied,
![]() $\Delta _K = \lambda \mu $
,
$\Delta _K = \lambda \mu $
,
![]() $\Delta _J=\mu \nu $
and
$\Delta _J=\mu \nu $
and
![]() $\Delta $
is trivial.
$\Delta $
is trivial.
First we will show that
![]() ${\mathcal C}$
is not left primary decomposable. For
${\mathcal C}$
is not left primary decomposable. For
![]() $L\in {\mathbb K}$
, either
$L\in {\mathbb K}$
, either
![]() $L=0$
or
$L=0$
or
![]() $\Delta _L$
is not a power of
$\Delta _L$
is not a power of
![]() $S(\zeta )$
for any irreducible
$S(\zeta )$
for any irreducible
![]() $\zeta $
. Therefore,
$\zeta $
. Therefore,
![]() ${\mathcal C}_{\zeta }=0$
for all
${\mathcal C}_{\zeta }=0$
for all
![]() $\zeta $
. It follows that
$\zeta $
. It follows that
 $\Phi _L\colon \bigoplus _{[\zeta ]} {\mathcal C}_{\zeta }/\Delta = 0 \to {\mathcal C}/\Delta $
is not surjective.
$\Phi _L\colon \bigoplus _{[\zeta ]} {\mathcal C}_{\zeta }/\Delta = 0 \to {\mathcal C}/\Delta $
is not surjective.
On the other hand,
![]() ${\mathcal C}$
is right primary decomposable. To prove this, observe that
${\mathcal C}$
is right primary decomposable. To prove this, observe that
![]() $\Delta _L$
is relatively prime to
$\Delta _L$
is relatively prime to
![]() $\mu $
if and only if
$\mu $
if and only if
![]() $L=0$
. That is,
$L=0$
. That is,
![]() ${\mathcal C}^{\mu }=0$
. Also,
${\mathcal C}^{\mu }=0$
. Also,
![]() $[K] \in {\mathcal C}^{\zeta }$
for
$[K] \in {\mathcal C}^{\zeta }$
for
![]() $\zeta \ne \lambda ,\mu $
, and
$\zeta \ne \lambda ,\mu $
, and
![]() $[J] \in {\mathcal C}^{\zeta }$
for
$[J] \in {\mathcal C}^{\zeta }$
for
![]() $\zeta \ne \mu ,\nu $
. Because
$\zeta \ne \mu ,\nu $
. Because
![]() ${\mathcal C}$
is generated by
${\mathcal C}$
is generated by
![]() $[K]=[J]$
, it follows that
$[K]=[J]$
, it follows that
![]() ${\mathcal C}^{\zeta }={\mathcal C}$
for
${\mathcal C}^{\zeta }={\mathcal C}$
for
![]() $\zeta \ne \mu $
. Therefore,
$\zeta \ne \mu $
. Therefore,
 $\Phi _R\colon {\mathcal C}/\Delta \to \bigoplus _{[\zeta ]} {\mathcal C}/{\mathcal C}^{\zeta }$
is an isomorphism.
$\Phi _R\colon {\mathcal C}/\Delta \to \bigoplus _{[\zeta ]} {\mathcal C}/{\mathcal C}^{\zeta }$
is an isomorphism.
Though the above examples tell us that the bijectivity of
![]() $\Phi _L$
does not imply the bijectivity of
$\Phi _L$
does not imply the bijectivity of
![]() $\Phi _R$
or vice versa, the following observations provide partial relationships between the surjectivity and injectivity of
$\Phi _R$
or vice versa, the following observations provide partial relationships between the surjectivity and injectivity of
![]() $\Phi _L$
and
$\Phi _L$
and
![]() $\Phi _R$
.
$\Phi _R$
.
Lemma A.4.
-
(1) If
 $\Phi _L$
is surjective, then
$\Phi _L$
is surjective, then
 $\Phi _R$
is surjective.
$\Phi _R$
is surjective. -
(2) Suppose that
 $\Phi _R$
is injective. Then the following splitting property holds: if
$\Phi _R$
is injective. Then the following splitting property holds: if
 $\Delta _K$
and
$\Delta _K$
and
 $\Delta _J$
are relatively prime and
$\Delta _J$
are relatively prime and
 $[K]+[J]\equiv 0 \bmod \Delta $
, then
$[K]+[J]\equiv 0 \bmod \Delta $
, then
 $[K]\equiv [J]\equiv 0 \bmod \Delta $
. In particular,
$[K]\equiv [J]\equiv 0 \bmod \Delta $
. In particular,
 $\Phi _L$
is injective.
$\Phi _L$
is injective.
Proof. (1) The homomorphism
![]() $\Phi _R$
is surjective if and only if for every given
$\Phi _R$
is surjective if and only if for every given
![]() $[K]\in {\mathcal C}$
and
$[K]\in {\mathcal C}$
and
![]() $[\lambda ]\in {\mathbb P}$
there exists
$[\lambda ]\in {\mathbb P}$
there exists
![]() $[J] \in {\mathcal C}$
such that
$[J] \in {\mathcal C}$
such that
![]() $[J] \equiv [K] \bmod {\mathcal C}^{\lambda }$
and
$[J] \equiv [K] \bmod {\mathcal C}^{\lambda }$
and
![]() $[J] \equiv 0 \bmod {\mathcal C}^{\mu }$
for all
$[J] \equiv 0 \bmod {\mathcal C}^{\mu }$
for all
![]() $[\mu ] \ne [\lambda ]$
. By the surjectivity of
$[\mu ] \ne [\lambda ]$
. By the surjectivity of
![]() $\Phi _L$
or, equivalently, (LP1),
$\Phi _L$
or, equivalently, (LP1),
![]() $[K] \equiv [K_1]+\cdots +[K_n] \bmod \Delta $
for some
$[K] \equiv [K_1]+\cdots +[K_n] \bmod \Delta $
for some
![]() $[K_i]\in {\mathcal C}_{\lambda _i}$
, where
$[K_i]\in {\mathcal C}_{\lambda _i}$
, where
![]() $[\lambda _i]\ne [\lambda _j]$
for
$[\lambda _i]\ne [\lambda _j]$
for
![]() $i\ne j$
. If
$i\ne j$
. If
![]() $[\lambda ]=[\lambda _i]$
for some i, then let
$[\lambda ]=[\lambda _i]$
for some i, then let
![]() $[J] = [K_i]$
. Otherwise, let
$[J] = [K_i]$
. Otherwise, let
![]() $[J]=0$
. Then, because
$[J]=0$
. Then, because
![]() ${\mathcal C}_{\lambda _i} \subset {\mathcal C}^{\mu }$
whenever
${\mathcal C}_{\lambda _i} \subset {\mathcal C}^{\mu }$
whenever
![]() $[\mu ] \ne [\lambda _i]$
, it follows that
$[\mu ] \ne [\lambda _i]$
, it follows that
![]() $[J]$
has the desired property.
$[J]$
has the desired property.
(2) Suppose that
![]() $\gcd (\Delta _K,\Delta _J)=1$
and
$\gcd (\Delta _K,\Delta _J)=1$
and
![]() $[K]+[J]\equiv 0 \bmod \Delta $
. If an irreducible
$[K]+[J]\equiv 0 \bmod \Delta $
. If an irreducible
![]() $\lambda $
divides
$\lambda $
divides
![]() $\Delta _J$
, then
$\Delta _J$
, then
![]() $\gcd (\lambda ,\Delta _K)=1$
and so
$\gcd (\lambda ,\Delta _K)=1$
and so
![]() $[K] \equiv 0 \bmod {\mathcal C}^{\lambda }$
. If
$[K] \equiv 0 \bmod {\mathcal C}^{\lambda }$
. If
![]() $\gcd (\lambda ,\Delta _J)=1$
, then
$\gcd (\lambda ,\Delta _J)=1$
, then
![]() $[K] \equiv [K]+[J] \equiv 0 \bmod {\mathcal C}^{\lambda }$
. So
$[K] \equiv [K]+[J] \equiv 0 \bmod {\mathcal C}^{\lambda }$
. So
![]() $[K]\equiv 0\bmod {\mathcal C}^{\lambda }$
for all
$[K]\equiv 0\bmod {\mathcal C}^{\lambda }$
for all
![]() $\lambda $
, and thus
$\lambda $
, and thus
![]() $[K]\equiv 0\bmod \Delta $
by the injectivity of
$[K]\equiv 0\bmod \Delta $
by the injectivity of
![]() $\Phi _R$
. The same argument shows
$\Phi _R$
. The same argument shows
![]() $[J]\equiv 0 \bmod \Delta $
. From this, (LP2) immediately follows. That is,
$[J]\equiv 0 \bmod \Delta $
. From this, (LP2) immediately follows. That is,
![]() $\Phi _L$
is injective.
$\Phi _L$
is injective.
Remark A.5. As seen in the last sentence of the above proof of Lemma A.4(1), the composition
![]() ${\mathcal C}_{\lambda }/\Delta \hookrightarrow {\mathcal C}/\Delta \twoheadrightarrow {\mathcal C}/{\mathcal C}^{\mu }$
is zero if
${\mathcal C}_{\lambda }/\Delta \hookrightarrow {\mathcal C}/\Delta \twoheadrightarrow {\mathcal C}/{\mathcal C}^{\mu }$
is zero if
![]() $[\lambda ]\ne [\mu ]$
. Consequently, the composition
$[\lambda ]\ne [\mu ]$
. Consequently, the composition
 $$ \begin{align*} \Phi_R \circ \Phi_L \colon \bigoplus_{[\lambda]\in {\mathbb P}} {\mathcal C}_{\lambda}/\Delta \longrightarrow \bigoplus_{[\lambda]\in {\mathbb P}} {\mathcal C}/{\mathcal C}^{\lambda} \end{align*} $$
$$ \begin{align*} \Phi_R \circ \Phi_L \colon \bigoplus_{[\lambda]\in {\mathbb P}} {\mathcal C}_{\lambda}/\Delta \longrightarrow \bigoplus_{[\lambda]\in {\mathbb P}} {\mathcal C}/{\mathcal C}^{\lambda} \end{align*} $$
is the orthogonal direct sum of the compositions
![]() ${\mathcal C}_{\lambda }/\Delta \hookrightarrow {\mathcal C}/\Delta \twoheadrightarrow {\mathcal C}/{\mathcal C}^{\lambda }$
. It follows that
${\mathcal C}_{\lambda }/\Delta \hookrightarrow {\mathcal C}/\Delta \twoheadrightarrow {\mathcal C}/{\mathcal C}^{\lambda }$
. It follows that
![]() ${\mathcal C}_{\lambda }/\Delta \hookrightarrow {\mathcal C}/\Delta \twoheadrightarrow {\mathcal C}/{\mathcal C}^{\lambda }$
is an isomorphism for each irreducible
${\mathcal C}_{\lambda }/\Delta \hookrightarrow {\mathcal C}/\Delta \twoheadrightarrow {\mathcal C}/{\mathcal C}^{\lambda }$
is an isomorphism for each irreducible
![]() $\lambda $
if and only if
$\lambda $
if and only if
![]() $\Phi _R\circ \Phi _L$
is an isomorphism. Consequently,
$\Phi _R\circ \Phi _L$
is an isomorphism. Consequently,
![]() ${\mathcal C}_{\lambda }/\Delta \hookrightarrow {\mathcal C}/\Delta \twoheadrightarrow {\mathcal C}/{\mathcal C}^{\lambda }$
is an isomorphism if
${\mathcal C}_{\lambda }/\Delta \hookrightarrow {\mathcal C}/\Delta \twoheadrightarrow {\mathcal C}/{\mathcal C}^{\lambda }$
is an isomorphism if
![]() ${\mathcal C}$
is left primary decomposable and right primary decomposable.
${\mathcal C}$
is left primary decomposable and right primary decomposable.
Recall that
![]() ${\mathcal C}$
is left primary decomposable if and only if (LP1) and (LP2) hold. The following is a stronger variation of (LP1):
${\mathcal C}$
is left primary decomposable if and only if (LP1) and (LP2) hold. The following is a stronger variation of (LP1):
-
(LP1) Strong existence: for every
 $K\in {\mathbb K}$
, there exist irreducible factors
$K\in {\mathbb K}$
, there exist irreducible factors
 $\lambda _1,\ldots$
,
$\lambda _1,\ldots$
,
 $\lambda _n$
of
$\lambda _n$
of
 $\Delta _K$
and
$\Delta _K$
and
 $[K_1]\in {\mathcal C}_{\lambda _1},\ldots ,[K_n]\in {\mathcal C}_{\lambda _n}$
such that
$[K_1]\in {\mathcal C}_{\lambda _1},\ldots ,[K_n]\in {\mathcal C}_{\lambda _n}$
such that
 $[K] \equiv [K_1]+\cdots +[K_n]\bmod \Delta $
.
$[K] \equiv [K_1]+\cdots +[K_n]\bmod \Delta $
.
Definition A.6. We say that
![]() ${\mathcal C}={\mathbb K}/{\sim }$
is strongly primary decomposable if (LP1) and (LP2) hold.
${\mathcal C}={\mathbb K}/{\sim }$
is strongly primary decomposable if (LP1) and (LP2) hold.
Proposition A.7. If
![]() ${\mathcal C}$
is strongly primary decomposable, then
${\mathcal C}$
is strongly primary decomposable, then
![]() ${\mathcal C}$
is left primary decomposable and right primary decomposable.
${\mathcal C}$
is left primary decomposable and right primary decomposable.
Proof. If
![]() ${\mathcal C}$
is strongly primary decomposable,
${\mathcal C}$
is strongly primary decomposable,
![]() ${\mathcal C}$
is obviously left primary decomposable. Also,
${\mathcal C}$
is obviously left primary decomposable. Also,
![]() $\Phi _R$
is surjective by Lemma A.4(1). So it remains to show that
$\Phi _R$
is surjective by Lemma A.4(1). So it remains to show that
![]() $\Phi _R$
is injective.
$\Phi _R$
is injective.
Suppose that
![]() $[K]$
lies in
$[K]$
lies in
![]() ${\mathcal C}^{\lambda }$
for all irreducibles
${\mathcal C}^{\lambda }$
for all irreducibles
![]() $\lambda $
. The goal is to show that
$\lambda $
. The goal is to show that
![]() $[K]\in \Delta $
. We claim that the given
$[K]\in \Delta $
. We claim that the given
![]() $[K]$
can be assumed to lie in
$[K]$
can be assumed to lie in
![]() ${\mathcal C}_{\mu }$
for some
${\mathcal C}_{\mu }$
for some
![]() $[\mu ]\in {\mathbb P}$
. To prove this, first use (LP1) (or the surjectivity of
$[\mu ]\in {\mathbb P}$
. To prove this, first use (LP1) (or the surjectivity of
![]() $\Phi _L$
) to write
$\Phi _L$
) to write
![]() $[K] \equiv [K_1]+\cdots +[K_n] \bmod \Delta $
for some
$[K] \equiv [K_1]+\cdots +[K_n] \bmod \Delta $
for some
![]() $K_i\in {\mathcal C}_{\lambda _i}$
, where
$K_i\in {\mathcal C}_{\lambda _i}$
, where
![]() $[\lambda _i]\ne [\lambda _j]$
for
$[\lambda _i]\ne [\lambda _j]$
for
![]() $i\ne j$
. Fix i. We have that
$i\ne j$
. Fix i. We have that
![]() $[K_i] \equiv [K]-\sum _{j\ne i} [K_j] \bmod \Delta $
,
$[K_i] \equiv [K]-\sum _{j\ne i} [K_j] \bmod \Delta $
,
 $[K_j]\in {\mathcal C}_{\lambda _j} \subset {\mathcal C}^{\lambda _i}$
for all
$[K_j]\in {\mathcal C}_{\lambda _j} \subset {\mathcal C}^{\lambda _i}$
for all
![]() $j\ne i$
, and
$j\ne i$
, and
![]() $[K]\in {\mathcal C}^{\lambda _i}$
. It follows that
$[K]\in {\mathcal C}^{\lambda _i}$
. It follows that
![]() $[K_i] \in {\mathcal C}^{\lambda _i}$
. Because
$[K_i] \in {\mathcal C}^{\lambda _i}$
. Because
![]() $[K_i]\in {\mathcal C}_{\lambda _i}$
,
$[K_i]\in {\mathcal C}_{\lambda _i}$
,
![]() $[K_i]\in {\mathcal C}^{\lambda }$
for
$[K_i]\in {\mathcal C}^{\lambda }$
for
![]() $[\lambda ]\ne [\lambda _i]$
. So,
$[\lambda ]\ne [\lambda _i]$
. So,
![]() $[K_i]$
lies in
$[K_i]$
lies in
![]() ${\mathcal C}^{\lambda }$
for all
${\mathcal C}^{\lambda }$
for all
![]() $\lambda $
. Note that it suffices to show that
$\lambda $
. Note that it suffices to show that
![]() $[K_i]\in \Delta $
for all i, to conclude that
$[K_i]\in \Delta $
for all i, to conclude that
![]() $[K]\in \Delta $
. This proves the claim.
$[K]\in \Delta $
. This proves the claim.
Now, fix an irreducible
![]() $\mu $
. Suppose that
$\mu $
. Suppose that
![]() $[K] \in {\mathcal C}_{\mu }$
and
$[K] \in {\mathcal C}_{\mu }$
and
![]() $[K]\in {\mathcal C}^{\lambda }$
for all
$[K]\in {\mathcal C}^{\lambda }$
for all
![]() $\lambda $
. Because
$\lambda $
. Because
![]() $[K]\in {\mathcal C}^{\mu }$
, we have
$[K]\in {\mathcal C}^{\mu }$
, we have
![]() $[K]=[J]$
for some
$[K]=[J]$
for some
![]() $J\in {\mathbb K}$
such that
$J\in {\mathbb K}$
such that
![]() $\gcd (\Delta _J,\mu )=1$
. By (
$\gcd (\Delta _J,\mu )=1$
. By (
![]() $\textrm{LP1}'$
),
$\textrm{LP1}'$
),
![]() $[J] \equiv [J_1]+\cdots [J_m] \bmod \Delta $
for some
$[J] \equiv [J_1]+\cdots [J_m] \bmod \Delta $
for some
![]() $[J_k]\in {\mathcal C}_{\mu _k}$
, where the
$[J_k]\in {\mathcal C}_{\mu _k}$
, where the
![]() $\mu _k$
are irreducible factors of
$\mu _k$
are irreducible factors of
![]() $\Delta _J$
. In particular, every
$\Delta _J$
. In particular, every
![]() $\mu _k$
is relatively prime to
$\mu _k$
is relatively prime to
![]() $\mu $
. Also,
$\mu $
. Also,
![]() $\mu _k^*$
is relatively prime to
$\mu _k^*$
is relatively prime to
![]() $\mu $
, because
$\mu $
, because
![]() $\mu _k^*$
divides
$\mu _k^*$
divides
![]() $\Delta _J^* \doteq \Delta _J$
, which is relatively prime to
$\Delta _J^* \doteq \Delta _J$
, which is relatively prime to
![]() $\mu $
. So
$\mu $
. So
![]() $[\mu _k] \ne [\mu ]$
in
$[\mu _k] \ne [\mu ]$
in
![]() ${\mathbb P}$
for all k. Because
${\mathbb P}$
for all k. Because
![]() $-[K] + [J_1] + \cdots + [J_m]\in \Delta $
and
$-[K] + [J_1] + \cdots + [J_m]\in \Delta $
and
![]() $[K]\in {\mathcal C}_{\mu }$
, it follows that
$[K]\in {\mathcal C}_{\mu }$
, it follows that
![]() $[K]$
lies in
$[K]$
lies in
![]() $\Delta $
by (LP2).
$\Delta $
by (LP2).
A.2. Extensions
Suppose that
![]() $({\mathbb K},\sim ,\chi )$
is as in Subsection A.1 and
$({\mathbb K},\sim ,\chi )$
is as in Subsection A.1 and
![]() ${\mathcal A}$
is a subgroup of
${\mathcal A}$
is a subgroup of
![]() ${\mathcal C}={\mathbb K}/{\sim }$
. We have
${\mathcal C}={\mathbb K}/{\sim }$
. We have
![]() ${\mathcal A}={\mathbb A}/{\sim }$
for the submonoid
${\mathcal A}={\mathbb A}/{\sim }$
for the submonoid
![]() ${\mathbb A}:=\{K\in {\mathbb K}\mid [K]\in {\mathcal A}\}$
. Or, conversely, if
${\mathbb A}:=\{K\in {\mathbb K}\mid [K]\in {\mathcal A}\}$
. Or, conversely, if
![]() ${\mathbb A}$
is a submonoid of
${\mathbb A}$
is a submonoid of
![]() ${\mathbb K}$
such that
${\mathbb K}$
such that
![]() $K+J\sim 0$
and
$K+J\sim 0$
and
![]() $K\in {\mathbb A}$
imply
$K\in {\mathbb A}$
imply
![]() $J\in {\mathbb A}$
, then
$J\in {\mathbb A}$
, then
![]() ${\mathcal A} := {\mathbb A}/{\sim }$
is a subgroup of
${\mathcal A} := {\mathbb A}/{\sim }$
is a subgroup of
![]() ${\mathcal C}$
. Let
${\mathcal C}$
. Let
![]() ${\mathcal G}={\mathcal C}/{\mathcal A}$
be the quotient group. We have
${\mathcal G}={\mathcal C}/{\mathcal A}$
be the quotient group. We have
![]() ${\mathcal G} = {\mathbb K}/{\approx }$
, where the equivalence relation
${\mathcal G} = {\mathbb K}/{\approx }$
, where the equivalence relation
![]() $\approx $
is defined by
$\approx $
is defined by
![]() $K\approx J$
if and only if
$K\approx J$
if and only if
![]() $K\sim J+L$
for some
$K\sim J+L$
for some
![]() $L\in {\mathbb A}$
.
$L\in {\mathbb A}$
.
We will relate primary decompositions of
![]() ${\mathcal A}$
,
${\mathcal A}$
,
![]() ${\mathcal C}$
and
${\mathcal C}$
and
![]() ${\mathcal G}$
. To avoid confusion, for
${\mathcal G}$
. To avoid confusion, for
![]() ${\mathcal A}$
,
${\mathcal A}$
,
![]() ${\mathcal C}$
and
${\mathcal C}$
and
![]() ${\mathcal G}$
respectively, denote by
${\mathcal G}$
respectively, denote by
![]() $\Delta ({\mathcal A})$
,
$\Delta ({\mathcal A})$
,
![]() $\Delta ({\mathcal C})$
and
$\Delta ({\mathcal C})$
and
![]() $\Delta ({\mathcal G})$
their subgroups of classes represented by K with
$\Delta ({\mathcal G})$
their subgroups of classes represented by K with
![]() $\Delta _K\doteq 1$
. We have
$\Delta _K\doteq 1$
. We have
![]() $\Delta ({\mathcal A})=\Delta ({\mathcal C})\cap {\mathcal A}$
and
$\Delta ({\mathcal A})=\Delta ({\mathcal C})\cap {\mathcal A}$
and
![]() $\Delta ({\mathcal G}) = (\Delta ({\mathcal C})+{\mathcal A})/{\mathcal A} \subset {\mathcal G}={\mathcal C}/{\mathcal A}$
. It is straightforward to verify that the exact sequence
$\Delta ({\mathcal G}) = (\Delta ({\mathcal C})+{\mathcal A})/{\mathcal A} \subset {\mathcal G}={\mathcal C}/{\mathcal A}$
. It is straightforward to verify that the exact sequence
gives rise to an exact sequence
and induces the following exact sequences for all irreducibles
![]() $\lambda $
in
$\lambda $
in
![]() $\mathbb {Q}[t^{\pm 1}]$
:
$\mathbb {Q}[t^{\pm 1}]$
:
 $$ \begin{align*} 0 &\longrightarrow {\mathcal A}_{\lambda} \longrightarrow {\mathcal C}_{\lambda} \longrightarrow {\mathcal G}_{\lambda} \longrightarrow 0 \\ 0 &\longrightarrow {\mathcal A}^{\lambda} \longrightarrow {\mathcal C}^{\lambda} \longrightarrow {\mathcal G}^{\lambda} \longrightarrow 0 \end{align*} $$
$$ \begin{align*} 0 &\longrightarrow {\mathcal A}_{\lambda} \longrightarrow {\mathcal C}_{\lambda} \longrightarrow {\mathcal G}_{\lambda} \longrightarrow 0 \\ 0 &\longrightarrow {\mathcal A}^{\lambda} \longrightarrow {\mathcal C}^{\lambda} \longrightarrow {\mathcal G}^{\lambda} \longrightarrow 0 \end{align*} $$
Consequently, rows of the following commutative diagram are exact:

For
![]() $\bullet =L$
and R, (A.1) gives rise to an exact sequence
$\bullet =L$
and R, (A.1) gives rise to an exact sequence
 $$ \begin{align} \begin{aligned} 0 \longrightarrow \operatorname{Ker} \Phi^{\mathcal A}_{\bullet} & \longrightarrow \operatorname{Ker} \Phi^{\mathcal C}_{\bullet} \longrightarrow \operatorname{Ker} \Phi^{{\mathcal G}}_{\bullet} \\ &\longrightarrow \operatorname{Coker} \Phi^{\mathcal A}_{\bullet} \longrightarrow \operatorname{Coker} \Phi^{\mathcal C}_{\bullet} \longrightarrow \operatorname{Coker} \Phi^{{\mathcal G}}_{\bullet} \longrightarrow 0 \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} 0 \longrightarrow \operatorname{Ker} \Phi^{\mathcal A}_{\bullet} & \longrightarrow \operatorname{Ker} \Phi^{\mathcal C}_{\bullet} \longrightarrow \operatorname{Ker} \Phi^{{\mathcal G}}_{\bullet} \\ &\longrightarrow \operatorname{Coker} \Phi^{\mathcal A}_{\bullet} \longrightarrow \operatorname{Coker} \Phi^{\mathcal C}_{\bullet} \longrightarrow \operatorname{Coker} \Phi^{{\mathcal G}}_{\bullet} \longrightarrow 0 \end{aligned} \end{align} $$
by the snake lemma. It follows that
![]() $\Phi ^{\mathcal C}_{\bullet }$
is an isomorphism if and only if
$\Phi ^{\mathcal C}_{\bullet }$
is an isomorphism if and only if
![]() $\Phi ^{\mathcal A}_{\bullet }$
is injective,
$\Phi ^{\mathcal A}_{\bullet }$
is injective,
![]() $\Phi ^{{\mathcal G}}_{\bullet }$
is surjective and the connecting map
$\Phi ^{{\mathcal G}}_{\bullet }$
is surjective and the connecting map
![]() $\operatorname {Ker} \Phi ^{{\mathcal G}}_{\bullet } \to \operatorname {Coker} \Phi ^{\mathcal A}_{\bullet }$
is an isomorphism. The following is an immediate consequence.
$\operatorname {Ker} \Phi ^{{\mathcal G}}_{\bullet } \to \operatorname {Coker} \Phi ^{\mathcal A}_{\bullet }$
is an isomorphism. The following is an immediate consequence.
Theorem A.8. The group
![]() ${\mathcal C}$
is left (respectively right) primary decomposable if both
${\mathcal C}$
is left (respectively right) primary decomposable if both
![]() ${\mathcal A}$
and
${\mathcal A}$
and
![]() ${\mathcal G}$
are left (respectively right) primary decomposable.
${\mathcal G}$
are left (respectively right) primary decomposable.
Theorem A.9. The group
![]() ${\mathcal C}$
is strongly primary decomposable if both
${\mathcal C}$
is strongly primary decomposable if both
![]() ${\mathcal A}$
and
${\mathcal A}$
and
![]() ${\mathcal G}$
are strongly primary decomposable.
${\mathcal G}$
are strongly primary decomposable.
Proof. Suppose that
![]() ${\mathcal A}$
and
${\mathcal A}$
and
![]() ${\mathcal G}$
are strongly primary decomposable. Then by Proposition A.7 and Theorem A.8,
${\mathcal G}$
are strongly primary decomposable. Then by Proposition A.7 and Theorem A.8,
![]() ${\mathcal C}$
satisfies the uniqueness condition (LP2). So, it remains to verify the strong existence condition (
${\mathcal C}$
satisfies the uniqueness condition (LP2). So, it remains to verify the strong existence condition (
![]() $\textrm{LP1}'$
) for
$\textrm{LP1}'$
) for
![]() ${\mathcal C}$
.
${\mathcal C}$
.
Fix
![]() $[K]\in {\mathcal C}$
. Because
$[K]\in {\mathcal C}$
. Because
![]() ${\mathcal G}$
satisfies (
${\mathcal G}$
satisfies (
![]() $\textrm{LP1}'$
), we have
$\textrm{LP1}'$
), we have
![]() $[K] \equiv [J_1]+\cdots +[J_n] \bmod \Delta ({\mathcal C})+{\mathcal A}$
for some
$[K] \equiv [J_1]+\cdots +[J_n] \bmod \Delta ({\mathcal C})+{\mathcal A}$
for some
![]() $[J_1]\in {\mathcal C}_{\lambda _1},\ldots$
,
$[J_1]\in {\mathcal C}_{\lambda _1},\ldots$
,
![]() $[J_n]\in {\mathcal C}_{\lambda _n}$
, where each
$[J_n]\in {\mathcal C}_{\lambda _n}$
, where each
![]() $\lambda _i$
is an irreducible factor of
$\lambda _i$
is an irreducible factor of
![]() $\Delta _K$
and
$\Delta _K$
and
![]() $\Delta _{J_i}$
is a power of
$\Delta _{J_i}$
is a power of
![]() $S(\lambda _i)$
. So, for some
$S(\lambda _i)$
. So, for some
![]() $[J]\in {\mathcal C}$
with
$[J]\in {\mathcal C}$
with
![]() $\Delta _J \doteq 1$
, we have
$\Delta _J \doteq 1$
, we have
Using property (
![]() $\Delta 3$
), choose
$\Delta 3$
), choose
![]() $J_1',\ldots$
,
$J_1',\ldots$
,
![]() $J_n'$
such that
$J_n'$
such that
![]() $[J_i']=-[J_i]$
and
$[J_i']=-[J_i]$
and
![]() $\Delta _{J_i'} \doteq \Delta _{J_i}$
, and let
$\Delta _{J_i'} \doteq \Delta _{J_i}$
, and let
![]() $L=K+J_1'+\cdots +J_n'+J$
. Then
$L=K+J_1'+\cdots +J_n'+J$
. Then
![]() $[L]\in {\mathcal A}$
by (A.3) and
$[L]\in {\mathcal A}$
by (A.3) and
![]() $\Delta _L \doteq \Delta _K\cdot \prod \Delta _{J_i}$
by (
$\Delta _L \doteq \Delta _K\cdot \prod \Delta _{J_i}$
by (
![]() $\Delta 2$
). In particular, irreducibles dividing
$\Delta 2$
). In particular, irreducibles dividing
![]() $\Delta _L$
divide
$\Delta _L$
divide
![]() $\Delta _K$
. Because
$\Delta _K$
. Because
![]() ${\mathcal A}$
satisfies (
${\mathcal A}$
satisfies (
![]() $\textrm{LP1}'$
), there is a decomposition
$\textrm{LP1}'$
), there is a decomposition
where
![]() $[L_j] \in {\mathcal A}_{\mu _j}$
and each
$[L_j] \in {\mathcal A}_{\mu _j}$
and each
![]() $\mu _j$
is an irreducible factor of
$\mu _j$
is an irreducible factor of
![]() $\Delta _K$
. It follows that
$\Delta _K$
. It follows that
Recall that
![]() $[J_i] \in {\mathcal C}_{\lambda _i}$
,
$[J_i] \in {\mathcal C}_{\lambda _i}$
,
![]() $[L_j]\in {\mathcal A}_{\mu _j} \subset {\mathcal C}_{\mu _j}$
and
$[L_j]\in {\mathcal A}_{\mu _j} \subset {\mathcal C}_{\mu _j}$
and
![]() $\lambda _i$
and
$\lambda _i$
and
![]() $\mu _j$
are factors of
$\mu _j$
are factors of
![]() $\Delta _K$
. So, (
$\Delta _K$
. So, (
![]() $\textrm{LP1}'$
) is satisfied for the given
$\textrm{LP1}'$
) is satisfied for the given
![]() $[K]\in {\mathcal C}$
.
$[K]\in {\mathcal C}$
.
A.3. Knot concordance and primary decomposition
Algebraic concordance over
 $\mathbb {Q}$
$\mathbb {Q}$
Levine’s work on knot concordance provides an algebraic analogue of the knot concordance group, which is now called the algebraic concordance group [Reference Levine35, Reference Levine34]. The algebraic concordance group over
![]() $\mathbb {Q}$
is known to be left and right primary decomposable in our sense. We describe this using Blanchfield linking forms over
$\mathbb {Q}$
is known to be left and right primary decomposable in our sense. We describe this using Blanchfield linking forms over
![]() $\mathbb {Q}[t^{\pm 1}]$
, whereas Levine’s original papers [Reference Levine35, Reference Levine34] use Seifert matrices.
$\mathbb {Q}[t^{\pm 1}]$
, whereas Levine’s original papers [Reference Levine35, Reference Levine34] use Seifert matrices.
Let
![]() $\mathbb {Q}(t)$
be the rational function field. A
$\mathbb {Q}(t)$
be the rational function field. A
![]() $(\mathbb {Q}(t)/\mathbb {Q}[t^{\pm 1}])$
-valued linking form is defined to be a map
$(\mathbb {Q}(t)/\mathbb {Q}[t^{\pm 1}])$
-valued linking form is defined to be a map
![]() $B\colon V\times V\to \mathbb {Q}(t)/\mathbb {Q}[t^{\pm 1}]$
, with V a finitely generated
$B\colon V\times V\to \mathbb {Q}(t)/\mathbb {Q}[t^{\pm 1}]$
, with V a finitely generated
![]() $\mathbb {Q}[t^{\pm 1}]$
-module such that
$\mathbb {Q}[t^{\pm 1}]$
-module such that
![]() $V\otimes _{\mathbb {Q}[t^{\pm 1}]} \mathbb {Q}(t)=0$
, which is sesquilinear and nonsingular. That is,
$V\otimes _{\mathbb {Q}[t^{\pm 1}]} \mathbb {Q}(t)=0$
, which is sesquilinear and nonsingular. That is,
![]() $B(x,y)=B(y,x)^*$
,
$B(x,y)=B(y,x)^*$
,
![]() $y\mapsto B(x,-)$
is
$y\mapsto B(x,-)$
is
![]() $\mathbb {Q}[t^{\pm 1}]$
-linear for all
$\mathbb {Q}[t^{\pm 1}]$
-linear for all
![]() $x\in V$
, and the adjoint
$x\in V$
, and the adjoint
 $V\to \mathrm {Hom}_{\mathbb {Q}[t^{\pm 1}]}(V,\mathbb {Q}(t)/\mathbb {Q}[t^{\pm 1}])$
is an isomorphism. Let
$V\to \mathrm {Hom}_{\mathbb {Q}[t^{\pm 1}]}(V,\mathbb {Q}(t)/\mathbb {Q}[t^{\pm 1}])$
is an isomorphism. Let
![]() ${\mathbb K}$
be the monoid of
${\mathbb K}$
be the monoid of
![]() $(\mathbb {Q}(t)/\mathbb {Q}[t^{\pm 1}])$
-valued linking forms (under direct sum operation), and define
$(\mathbb {Q}(t)/\mathbb {Q}[t^{\pm 1}])$
-valued linking forms (under direct sum operation), and define
![]() $\chi \colon {\mathbb K} \to \mathbb {Q}[t^{\pm 1}]/{\doteq }$
by
$\chi \colon {\mathbb K} \to \mathbb {Q}[t^{\pm 1}]/{\doteq }$
by
![]() $\chi (B)=\Delta _B(t)$
, where the Alexander polynomial
$\chi (B)=\Delta _B(t)$
, where the Alexander polynomial
![]() $\Delta _B(t)$
is defined to be the order of the torsion module V over
$\Delta _B(t)$
is defined to be the order of the torsion module V over
![]() $\mathbb {Q}[t^{\pm 1}]$
. A linking form B is metabolic if there is a submodule
$\mathbb {Q}[t^{\pm 1}]$
. A linking form B is metabolic if there is a submodule
![]() $P\subset V$
such that
$P\subset V$
such that
![]() $P=\{x\in V\mid B(x,P)=0\}$
. We say that B and
$P=\{x\in V\mid B(x,P)=0\}$
. We say that B and
![]() $B'$
are Witt equivalent if there are metabolic linking forms H and
$B'$
are Witt equivalent if there are metabolic linking forms H and
![]() $H'$
such that the orthogonal sums
$H'$
such that the orthogonal sums
![]() $B\oplus H$
and
$B\oplus H$
and
![]() $B'\oplus H$
are isomorphic. The set
$B'\oplus H$
are isomorphic. The set
![]() ${\mathcal G}$
of Witt equivalence classes of linking forms is an abelian group under orthogonal sum.Footnote
1
The conditions (
${\mathcal G}$
of Witt equivalence classes of linking forms is an abelian group under orthogonal sum.Footnote
1
The conditions (
![]() $\Delta 1$
), (
$\Delta 1$
), (
![]() $\Delta 2$
) and (
$\Delta 2$
) and (
![]() $\Delta 3$
) stated in Subsection A.1 hold. By definition,
$\Delta 3$
) stated in Subsection A.1 hold. By definition,
![]() $\Delta _B(t)$
is trivial if and only if V is trivial. It follows that the subgroup
$\Delta _B(t)$
is trivial if and only if V is trivial. It follows that the subgroup
![]() $\Delta =\{[B]\in {\mathcal G} \mid \Delta _B \doteq 1\}$
is trivial.
$\Delta =\{[B]\in {\mathcal G} \mid \Delta _B \doteq 1\}$
is trivial.
The following result is essentially due to Levine [Reference Levine34].
Theorem A.10 Levine [Reference Levine34]
The group
![]() ${\mathcal G}$
is left and right primary decomposable.
${\mathcal G}$
is left and right primary decomposable.
 $$ \begin{align*} \bigoplus_{[\lambda]} {\mathcal G}_{\lambda} \xrightarrow[\cong]{\Phi_L} {\mathcal G} \xrightarrow[\cong]{\Phi_R} \bigoplus_{[\lambda]} {\mathcal G}/{\mathcal G}^{\lambda} \end{align*} $$
$$ \begin{align*} \bigoplus_{[\lambda]} {\mathcal G}_{\lambda} \xrightarrow[\cong]{\Phi_L} {\mathcal G} \xrightarrow[\cong]{\Phi_R} \bigoplus_{[\lambda]} {\mathcal G}/{\mathcal G}^{\lambda} \end{align*} $$
Indeed,
![]() ${\mathcal G}$
is strongly primary decomposable. An elegant generalisation of Levine’s Theorem A.10 to the case of the group ring of a (noncommutative) free group was developed in work of Sheiham [Reference Sheiham43, Section 3]. See also [Reference Sheiham42].
${\mathcal G}$
is strongly primary decomposable. An elegant generalisation of Levine’s Theorem A.10 to the case of the group ring of a (noncommutative) free group was developed in work of Sheiham [Reference Sheiham43, Section 3]. See also [Reference Sheiham42].
Algebraic concordance over
 $\mathbb {Z}$
$\mathbb {Z}$
For a knot K in
![]() $S^3$
, the Blanchfield form [Reference Blanchfield1]
$S^3$
, the Blanchfield form [Reference Blanchfield1]
![]() $B_K$
defined on the Alexander module
$B_K$
defined on the Alexander module
![]() $H_1(S^3\smallsetminus K;\mathbb {Q}[t^{\pm 1}])$
is a linking form in the above sense. We have
$H_1(S^3\smallsetminus K;\mathbb {Q}[t^{\pm 1}])$
is a linking form in the above sense. We have
![]() $\Delta _K = \Delta _{B_K}$
. The association
$\Delta _K = \Delta _{B_K}$
. The association
![]() $K\mapsto B_K$
induces a homomorphism of the (topological and smooth) knot concordance group into
$K\mapsto B_K$
induces a homomorphism of the (topological and smooth) knot concordance group into
![]() ${\mathcal G}$
. The image of this homomorphism is characterised as follows. By replacing
${\mathcal G}$
. The image of this homomorphism is characterised as follows. By replacing
![]() $(\mathbb {Q}[t^{\pm 1}],\mathbb {Q}(t))$
with
$(\mathbb {Q}[t^{\pm 1}],\mathbb {Q}(t))$
with
![]() $(\mathbb {Z}[t^{\pm 1}],S^{-1}\mathbb {Z}[t^{\pm 1}])$
where
$(\mathbb {Z}[t^{\pm 1}],S^{-1}\mathbb {Z}[t^{\pm 1}])$
where
![]() $S=\{f(t)\in \mathbb {Z}[t^{\pm 1}] \,|\, f(1)=\pm 1\}$
, one constructs an integral analogue of
$S=\{f(t)\in \mathbb {Z}[t^{\pm 1}] \,|\, f(1)=\pm 1\}$
, one constructs an integral analogue of
![]() ${\mathcal G}$
, say,
${\mathcal G}$
, say,
![]() ${\mathcal G}(\mathbb {Z})$
. It is known that the natural map
${\mathcal G}(\mathbb {Z})$
. It is known that the natural map
![]() ${\mathcal G}(\mathbb {Z})\to {\mathcal G}$
is injective [Reference Levine34], and the subgroup
${\mathcal G}(\mathbb {Z})\to {\mathcal G}$
is injective [Reference Levine34], and the subgroup
![]() ${\mathcal G}(\mathbb {Z})$
of
${\mathcal G}(\mathbb {Z})$
of
![]() ${\mathcal G}$
is exactly the image of the concordance group of knots in
${\mathcal G}$
is exactly the image of the concordance group of knots in
![]() $S^3$
. A knot K such that
$S^3$
. A knot K such that
![]() $[B_K]=0$
in
$[B_K]=0$
in
![]() ${\mathcal G}(\mathbb {Z}) \subset {\mathcal G}$
is said to be algebraically slice.
${\mathcal G}(\mathbb {Z}) \subset {\mathcal G}$
is said to be algebraically slice.
Levine showed that both
![]() ${\mathcal G}$
and
${\mathcal G}$
and
![]() ${\mathcal G}(\mathbb {Z})$
are isomorphic to
${\mathcal G}(\mathbb {Z})$
are isomorphic to
![]() $\mathbb {Z}^{\infty } \oplus (\mathbb {Z}_2)^{\infty } \oplus (\mathbb {Z}_4)^{\infty }$
[Reference Levine34]. The difference of the structures of
$\mathbb {Z}^{\infty } \oplus (\mathbb {Z}_2)^{\infty } \oplus (\mathbb {Z}_4)^{\infty }$
[Reference Levine34]. The difference of the structures of
![]() ${\mathcal G}$
and
${\mathcal G}$
and
![]() ${\mathcal G}(\mathbb {Z})$
was studied in work of Stoltzfus [Reference Stoltzfus44]. Among his main results, it was shown that
${\mathcal G}(\mathbb {Z})$
was studied in work of Stoltzfus [Reference Stoltzfus44]. Among his main results, it was shown that
 $\Phi _L\colon \bigoplus _{[\lambda ]} {\mathcal G}(\mathbb {Z})_{\lambda } \to {\mathcal G}(\mathbb {Z})$
is not surjective (whereas it is injective due to Levine’s work [Reference Levine35]). In particular,
$\Phi _L\colon \bigoplus _{[\lambda ]} {\mathcal G}(\mathbb {Z})_{\lambda } \to {\mathcal G}(\mathbb {Z})$
is not surjective (whereas it is injective due to Levine’s work [Reference Levine35]). In particular,
![]() ${\mathcal G}(\mathbb {Z})$
is not left primary decomposable. (To the author’s knowledge, it was not addressed in the literature whether
${\mathcal G}(\mathbb {Z})$
is not left primary decomposable. (To the author’s knowledge, it was not addressed in the literature whether
![]() ${\mathcal G}(\mathbb {Z})$
is right primary decomposable.)
${\mathcal G}(\mathbb {Z})$
is right primary decomposable.)
Topological knot concordance and algebraically slice knots
Let
![]() ${\mathbb K}$
be the set of isotopy classes of oriented knots in
${\mathbb K}$
be the set of isotopy classes of oriented knots in
![]() $S^3$
, with connected sum as a monoid operation. If K,
$S^3$
, with connected sum as a monoid operation. If K,
![]() $K' \in {\mathbb K}$
are topologically concordant, write
$K' \in {\mathbb K}$
are topologically concordant, write
![]() ${K\sim K'}$
. The set of equivalence classes
${K\sim K'}$
. The set of equivalence classes
![]() ${\mathcal C}^{\mathrm {top}} = {\mathbb K}/{\sim }$
is the topological knot concordance group. Define
${\mathcal C}^{\mathrm {top}} = {\mathbb K}/{\sim }$
is the topological knot concordance group. Define
![]() $\chi \colon {\mathbb K} \to \mathbb {Q}[t^{\pm 1}]/{\doteq }$
by
$\chi \colon {\mathbb K} \to \mathbb {Q}[t^{\pm 1}]/{\doteq }$
by
![]() $\chi (K) = \Delta _K(t)$
, the Alexander polynomial of K. The assumptions (
$\chi (K) = \Delta _K(t)$
, the Alexander polynomial of K. The assumptions (
![]() $\Delta 1$
), (
$\Delta 1$
), (
![]() $\Delta 2$
) and (
$\Delta 2$
) and (
![]() $\Delta 3$
) in Subsection A.1 are standard properties of the Alexander polynomial. By work of Freedman [Reference Freedman21], the subgroup
$\Delta 3$
) in Subsection A.1 are standard properties of the Alexander polynomial. By work of Freedman [Reference Freedman21], the subgroup
![]() $\Delta =\{[K]\in {\mathcal C}^{\mathrm {top}} \mid \Delta _K \doteq 1\}$
is trivial.
$\Delta =\{[K]\in {\mathcal C}^{\mathrm {top}} \mid \Delta _K \doteq 1\}$
is trivial.
Let
![]() ${\mathcal A}^{\mathrm {top}}$
be the topological concordance group of algebraically slice knots. Then, because
${\mathcal A}^{\mathrm {top}}$
be the topological concordance group of algebraically slice knots. Then, because
is exact,
![]() ${\mathcal C}^{\mathrm {top}}$
is right primary decomposable if so are both
${\mathcal C}^{\mathrm {top}}$
is right primary decomposable if so are both
![]() ${\mathcal A}^{\mathrm {top}}$
and
${\mathcal A}^{\mathrm {top}}$
and
![]() ${\mathcal G}^{\mathbb {Z}}$
. Regarding left primary decomposability, because
${\mathcal G}^{\mathbb {Z}}$
. Regarding left primary decomposability, because
 $\bigoplus _{[\lambda ]} {\mathcal G}^{\mathbb {Z}}_{\lambda } \to {\mathcal G}^{\mathbb {Z}}$
is not surjective due to Stoltzfus [Reference Stoltzfus44],
$\bigoplus _{[\lambda ]} {\mathcal G}^{\mathbb {Z}}_{\lambda } \to {\mathcal G}^{\mathbb {Z}}$
is not surjective due to Stoltzfus [Reference Stoltzfus44],
 $\Phi _L^{\mathrm {top}}\colon \bigoplus _{[\lambda ]} {\mathcal C}^{\mathrm {top}}_{\lambda } \to {\mathcal C}^{\mathrm {top}}$
is not surjective by the exact sequence (A.2). In particular,
$\Phi _L^{\mathrm {top}}\colon \bigoplus _{[\lambda ]} {\mathcal C}^{\mathrm {top}}_{\lambda } \to {\mathcal C}^{\mathrm {top}}$
is not surjective by the exact sequence (A.2). In particular,
![]() ${\mathcal C}^{\mathrm {top}}$
is not left primary decomposable. The following appear to be interesting.
${\mathcal C}^{\mathrm {top}}$
is not left primary decomposable. The following appear to be interesting.
Question A.11.
-
(1) Is
 $\Phi _L^{\mathrm {top}}\colon \bigoplus _{[\lambda ]} {\mathcal C}^{\mathrm {top}}_{\lambda } \to {\mathcal C}^{\mathrm {top}}$
injective?
$\Phi _L^{\mathrm {top}}\colon \bigoplus _{[\lambda ]} {\mathcal C}^{\mathrm {top}}_{\lambda } \to {\mathcal C}^{\mathrm {top}}$
injective? -
(2) Is
 ${\mathcal C}^{\mathrm {top}}$
right primary decomposable?
${\mathcal C}^{\mathrm {top}}$
right primary decomposable?
By Lemma A.4(2), an affirmative answer to Question A.11(2) implies that the answer to Question A.11(1) is affirmative and that the splitting property in Lemma A.4(2) holds.
In the literature, there are related results that provide affirmative answers to the following splitting question for certain concordance invariants (or obstructions): if K and J have relatively prime Alexander polynomials and if the invariant vanishes for
![]() $K\# J$
, then does the invariant vanish for each of K and J? See work of S.-G. Kim [Reference Kim28], which addresses the case of Casson-Gordon invariants, and work of and S.-G. Kim and T. Kim [Reference Kim and Kim29, Reference Kim and Kim30] on
$K\# J$
, then does the invariant vanish for each of K and J? See work of S.-G. Kim [Reference Kim28], which addresses the case of Casson-Gordon invariants, and work of and S.-G. Kim and T. Kim [Reference Kim and Kim29, Reference Kim and Kim30] on
![]() $L^2$
-signature defects. These may be viewed as evidence supporting an affirmative answer to the injectivity part for
$L^2$
-signature defects. These may be viewed as evidence supporting an affirmative answer to the injectivity part for
 $\Phi _R^{\mathrm {top}}$
in Question A.11(2), which implies the splitting property stated in Lemma A.4(2). Also, T. Kim [Reference Kim32] proved results related to primary decomposition structures in
$\Phi _R^{\mathrm {top}}$
in Question A.11(2), which implies the splitting property stated in Lemma A.4(2). Also, T. Kim [Reference Kim32] proved results related to primary decomposition structures in
![]() ${\mathcal A}^{\mathrm {top}}$
.
${\mathcal A}^{\mathrm {top}}$
.
Smooth concordance and topologically slice knots
Let
![]() ${\mathbb K}$
and
${\mathbb K}$
and
![]() $\chi $
be as above but now write
$\chi $
be as above but now write
![]() $K\sim K'$
if K and
$K\sim K'$
if K and
![]() $K'$
are smoothly concordant. Then
$K'$
are smoothly concordant. Then
![]() ${\mathcal C}^{\mathrm {sm}}={\mathbb K}/{\sim }$
is the smooth knot concordance group.
${\mathcal C}^{\mathrm {sm}}={\mathbb K}/{\sim }$
is the smooth knot concordance group.
Similar to the case of
![]() ${\mathcal C}^{\mathrm {top}}$
, the homomorphism
${\mathcal C}^{\mathrm {top}}$
, the homomorphism
 $ \Phi ^{\mathrm {sm}}_L\colon \bigoplus _{[\lambda ]} {\mathcal C}^{\mathrm {sm}}_{\lambda }/\Delta \to {\mathcal C}^{\mathrm {sm}}/\Delta $
is not surjective because
$ \Phi ^{\mathrm {sm}}_L\colon \bigoplus _{[\lambda ]} {\mathcal C}^{\mathrm {sm}}_{\lambda }/\Delta \to {\mathcal C}^{\mathrm {sm}}/\Delta $
is not surjective because
 $\bigoplus _{[\lambda ]} {\mathcal G}^{\mathbb {Z}}_{\lambda } \to {\mathcal G}^{\mathbb {Z}}$
is not surjective. So
$\bigoplus _{[\lambda ]} {\mathcal G}^{\mathbb {Z}}_{\lambda } \to {\mathcal G}^{\mathbb {Z}}$
is not surjective. So
![]() ${\mathcal C}^{\mathrm {sm}}$
is not left primary decomposable.
${\mathcal C}^{\mathrm {sm}}$
is not left primary decomposable.
Question A.12.
-
(1) Is
 $\Phi _L^{\mathrm {sm}} \colon \bigoplus _{[\lambda ]} {\mathcal C}^{\mathrm {sm}}_{\lambda }/\Delta \to {\mathcal C}^{\mathrm {sm}}/\Delta $
injective?
$\Phi _L^{\mathrm {sm}} \colon \bigoplus _{[\lambda ]} {\mathcal C}^{\mathrm {sm}}_{\lambda }/\Delta \to {\mathcal C}^{\mathrm {sm}}/\Delta $
injective? -
(2) Is
 ${\mathcal C}^{\mathrm {sm}}$
right primary decomposable?
${\mathcal C}^{\mathrm {sm}}$
right primary decomposable?
Again by Lemma A.4(2), an affirmative answer to Question A.12(2) implies that the answer to Question A.12(1) is affimative and that the splitting property stated in Lemma A.4(2) holds.
The smooth concordance group of topologically slice knots
![]() ${\mathcal T}$
is the kernel of the natural homomorphism
${\mathcal T}$
is the kernel of the natural homomorphism
![]() ${\mathcal C}^{\mathrm {sm}} \to {\mathcal C}^{\mathrm {top}}$
. By Theorem A.8,
${\mathcal C}^{\mathrm {sm}} \to {\mathcal C}^{\mathrm {top}}$
. By Theorem A.8,
![]() ${\mathcal C}^{\mathrm {sm}}$
is right primary decomposable if both
${\mathcal C}^{\mathrm {sm}}$
is right primary decomposable if both
![]() ${\mathcal T}$
and
${\mathcal T}$
and
![]() ${\mathcal C}^{\mathrm {top}}$
are right primary decomposable.
${\mathcal C}^{\mathrm {top}}$
are right primary decomposable.
Question 1.1 in the Introduction asks whether
![]() ${\mathcal T}$
is left and right primary decomposable in the sense of Definition A.1, and Theorem A provides supporting evidence for affirmative answers.
${\mathcal T}$
is left and right primary decomposable in the sense of Definition A.1, and Theorem A provides supporting evidence for affirmative answers.
Recall that the definition in Subsection A.1 says that
![]() $[K]\in {\mathcal T}_{\lambda }$
if
$[K]\in {\mathcal T}_{\lambda }$
if
![]() $\Delta _K \doteq S(\lambda )^k$
for some
$\Delta _K \doteq S(\lambda )^k$
for some
![]() $k\ge 0$
. For topologically slice K,
$k\ge 0$
. For topologically slice K,
![]() $\Delta _K \doteq ff^*$
for some
$\Delta _K \doteq ff^*$
for some
![]() $f\in \mathbb {Q}[t^{\pm 1}]$
, due to Fox and Milnor [Reference Fox and Milnor20]. From this it follows that
$f\in \mathbb {Q}[t^{\pm 1}]$
, due to Fox and Milnor [Reference Fox and Milnor20]. From this it follows that
![]() $\Delta _K \doteq S(\lambda )^k$
for some
$\Delta _K \doteq S(\lambda )^k$
for some
![]() $k\ge 0$
if and only if
$k\ge 0$
if and only if
![]() $\Delta _K \doteq (\lambda \lambda ^*)^{\ell }$
for some
$\Delta _K \doteq (\lambda \lambda ^*)^{\ell }$
for some
![]() $\ell \ge 0$
. Thus, the definition of
$\ell \ge 0$
. Thus, the definition of
![]() ${\mathcal T}_{\lambda }$
in Subsection A.1 agrees with that in Subsection 1.1.
${\mathcal T}_{\lambda }$
in Subsection A.1 agrees with that in Subsection 1.1.
Livingston informed us that the techniques of [Reference Hedden, Livingston and Ruberman25] can be used to show the following: there are nonassociate self-dual irreducible polynomials
![]() $\lambda _1$
,
$\lambda _1$
,
![]() $\lambda _2$
and
$\lambda _2$
and
![]() $\lambda _3$
and a topologically slice knot K with
$\lambda _3$
and a topologically slice knot K with
![]() $\Delta _K=(\lambda _1\lambda _2\lambda _3)^2$
that is not smoothly concordant to a connected sum
$\Delta _K=(\lambda _1\lambda _2\lambda _3)^2$
that is not smoothly concordant to a connected sum
![]() $K_1\#K_2\#K_3$
for any knots
$K_1\#K_2\#K_3$
for any knots
![]() $K_1$
,
$K_1$
,
![]() $K_2$
and
$K_2$
and
![]() $K_3$
with
$K_3$
with
![]() $\Delta _{K_i}$
a power of
$\Delta _{K_i}$
a power of
![]() $\lambda _i$
. It says that
$\lambda _i$
. It says that
![]() ${\mathcal T}$
does not satisfy the strong existence condition (
${\mathcal T}$
does not satisfy the strong existence condition (
![]() $\textrm{LP1}'$
). This method does not provide counterexamples to the left/right primary decomposability of
$\textrm{LP1}'$
). This method does not provide counterexamples to the left/right primary decomposability of
![]() ${\mathcal T}$
.
${\mathcal T}$
.
Filtrations of the knot concordance groups
For the bipolar filtration
![]() $\{{\mathcal T}_n\}$
of
$\{{\mathcal T}_n\}$
of
![]() ${\mathcal T}$
defined by Cochran, Harvey and Horn [Reference Cochran, Harvey and Horn11], Question 1.2 in the Introduction asks whether the associated graded
${\mathcal T}$
defined by Cochran, Harvey and Horn [Reference Cochran, Harvey and Horn11], Question 1.2 in the Introduction asks whether the associated graded
![]() $\mathrm {gr}_n({\mathcal T}\kern3pt)={\mathcal T}_n/{\mathcal T}_{n+1}$
is left and right primary decomposable in the sense of Definition A.1. Theorem C supports an affirmative answer, by presenting a large subgroup that is left and right (indeed strongly) primary decomposable into infinitely many infinite rank primary parts.
$\mathrm {gr}_n({\mathcal T}\kern3pt)={\mathcal T}_n/{\mathcal T}_{n+1}$
is left and right primary decomposable in the sense of Definition A.1. Theorem C supports an affirmative answer, by presenting a large subgroup that is left and right (indeed strongly) primary decomposable into infinitely many infinite rank primary parts.
In addition, whether
![]() ${\mathcal T}_n$
is left/right primary decomposable appears to be an interesting problem. By Theorems A.8 and A.9,
${\mathcal T}_n$
is left/right primary decomposable appears to be an interesting problem. By Theorems A.8 and A.9,
![]() ${\mathcal T}_n$
is left/right primary decomposable if so are both
${\mathcal T}_n$
is left/right primary decomposable if so are both
![]() ${\mathcal T}_{n+1}$
and
${\mathcal T}_{n+1}$
and
![]() $\mathrm {gr}_n({\mathcal T}\kern3pt)$
.
$\mathrm {gr}_n({\mathcal T}\kern3pt)$
.
In [Reference Cochran, Orr and Teichner16], Cochran, Orr and Teichner introduced a descending filtration
of the topological knot concordance group
![]() ${\mathcal C}^{\mathrm {top}}$
. A knot K represents an element of
${\mathcal C}^{\mathrm {top}}$
. A knot K represents an element of
![]() ${\mathcal F}_h$
(
${\mathcal F}_h$
(
 $h\in \frac 12\mathbb {Z}_{\ge 0}$
) if K is h-solvable in the sense of [Reference Cochran, Orr and Teichner16, Definitions 8.5 and 8.7].
$h\in \frac 12\mathbb {Z}_{\ge 0}$
) if K is h-solvable in the sense of [Reference Cochran, Orr and Teichner16, Definitions 8.5 and 8.7].
Question A.13. Are
![]() ${\mathcal F}_h$
and
${\mathcal F}_h$
and
![]() ${\mathcal F}_h/{\mathcal F}_{h+0.5}$
left and/or right primary decomposable?
${\mathcal F}_h/{\mathcal F}_{h+0.5}$
left and/or right primary decomposable?
Once again by Theorem A.8,
![]() ${\mathcal F}_h$
is left/right primary decomposable if so are both
${\mathcal F}_h$
is left/right primary decomposable if so are both
![]() ${\mathcal F}_{h+0.5}$
and
${\mathcal F}_{h+0.5}$
and
![]() ${\mathcal F}_n/{\mathcal F}_{h+0.5}$
. For integers
${\mathcal F}_n/{\mathcal F}_{h+0.5}$
. For integers
![]() $n>0$
, it is unknown whether
$n>0$
, it is unknown whether
![]() ${\mathcal F}_{n.5}/{\mathcal F}_{n+1}$
is nontrivial. Recently, Davis, Martin, Otto and Park showed that elements in
${\mathcal F}_{n.5}/{\mathcal F}_{n+1}$
is nontrivial. Recently, Davis, Martin, Otto and Park showed that elements in
![]() ${\mathcal F}_{0.5}$
represented by a genus one knot are contained in
${\mathcal F}_{0.5}$
represented by a genus one knot are contained in
![]() ${\mathcal F}_1$
[Reference Davis, Martin, Otto and Park19]. For the other half of the associated graded
${\mathcal F}_1$
[Reference Davis, Martin, Otto and Park19]. For the other half of the associated graded
![]() ${\mathcal F}_n/{\mathcal F}_{n.5}$
, Cochran, Harvey and Leidy provided strong evidence that supports the conjecture that the associated graded
${\mathcal F}_n/{\mathcal F}_{n.5}$
, Cochran, Harvey and Leidy provided strong evidence that supports the conjecture that the associated graded
![]() ${\mathcal F}_n/{\mathcal F}_{n.5}$
is right primary decomposable for all integers
${\mathcal F}_n/{\mathcal F}_{n.5}$
is right primary decomposable for all integers
![]() ${n\ge 0}$
[Reference Cochran, Harvey and Leidy14, Reference Cochran, Harvey and Leidy13]. Indeed, they proposed a highly refined primary decomposition conjecture for the associated graded
${n\ge 0}$
[Reference Cochran, Harvey and Leidy14, Reference Cochran, Harvey and Leidy13]. Indeed, they proposed a highly refined primary decomposition conjecture for the associated graded
![]() ${\mathcal F}_n/{\mathcal F}_{n.5}$
, using noncommutative localisations [Reference Cochran, Harvey and Leidy14, p. 444], and they showed that refined primary parts reveal interesting structures [Reference Cochran, Harvey and Leidy14, Reference Cochran, Harvey and Leidy13]. We remark that aforementioned earlier works of S.-G. Kim and T. Kim [Reference Kim28, Reference Kim and Kim29] also provide supporting evidence for the case of
${\mathcal F}_n/{\mathcal F}_{n.5}$
, using noncommutative localisations [Reference Cochran, Harvey and Leidy14, p. 444], and they showed that refined primary parts reveal interesting structures [Reference Cochran, Harvey and Leidy14, Reference Cochran, Harvey and Leidy13]. We remark that aforementioned earlier works of S.-G. Kim and T. Kim [Reference Kim28, Reference Kim and Kim29] also provide supporting evidence for the case of
![]() ${\mathcal F}_1/{\mathcal F}_{1.5}$
.
${\mathcal F}_1/{\mathcal F}_{1.5}$
.
A.4. Rational homology 3-spheres and primary decomposition
Let
 $\Theta ^{\mathrm {top}}_{\mathbb {Q}}$
and
$\Theta ^{\mathrm {top}}_{\mathbb {Q}}$
and
 $\Theta ^{\mathrm {sm}}_{\mathbb {Q}}$
be the topological and smooth rational homology cobordism groups of rational homology 3-spheres, respectively. For a rational homology 3-sphere Y, let
$\Theta ^{\mathrm {sm}}_{\mathbb {Q}}$
be the topological and smooth rational homology cobordism groups of rational homology 3-spheres, respectively. For a rational homology 3-sphere Y, let
![]() $\Delta _Y = |H_1(Y)|\in \mathbb {Z}$
, the order of the first homology with integral coefficients. The association
$\Delta _Y = |H_1(Y)|\in \mathbb {Z}$
, the order of the first homology with integral coefficients. The association
![]() $\chi \colon Y \mapsto \Delta _Y = |H_1(Y)|$
satisfies conditions (
$\chi \colon Y \mapsto \Delta _Y = |H_1(Y)|$
satisfies conditions (
![]() $\Delta 1$
), (
$\Delta 1$
), (
![]() $\Delta 2$
) and (
$\Delta 2$
) and (
![]() $\Delta 3$
). So, our general definition of primary decomposition applies to
$\Delta 3$
). So, our general definition of primary decomposition applies to
 $\Theta ^{\mathrm {top}}_{\mathbb {Q}}$
and
$\Theta ^{\mathrm {top}}_{\mathbb {Q}}$
and
 $\Theta ^{\mathrm {sm}}_{\mathbb {Q}}$
.
$\Theta ^{\mathrm {sm}}_{\mathbb {Q}}$
.
For the topological case, the subgroup
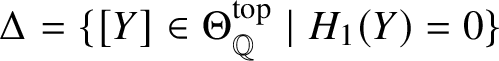 $\Delta =\{[Y] \in \Theta ^{\mathrm {top}}_{\mathbb {Q}} \mid H_1(Y)=0\}$
is trivial, because every integral homology 3-sphere bounds a contractible compact 4-manifold [Reference Freedman and Quinn22, Section 9.3C]. So, the left and right primary decompositions concern the homomorphisms
$\Delta =\{[Y] \in \Theta ^{\mathrm {top}}_{\mathbb {Q}} \mid H_1(Y)=0\}$
is trivial, because every integral homology 3-sphere bounds a contractible compact 4-manifold [Reference Freedman and Quinn22, Section 9.3C]. So, the left and right primary decompositions concern the homomorphisms
 $$ \begin{align*} \Phi_L\colon \bigoplus_p (\Theta^{\mathrm{top}}_{\mathbb{Q}})_p \longrightarrow \Theta^{\mathrm{top}}_{\mathbb{Q}}, \quad \Phi_R\colon \Theta^{\mathrm{top}}_{\mathbb{Q}} \longrightarrow \bigoplus_p \Theta^{\mathrm{top}}_{\mathbb{Q}}/(\Theta^{\mathrm{top}}_{\mathbb{Q}})^p, \end{align*} $$
$$ \begin{align*} \Phi_L\colon \bigoplus_p (\Theta^{\mathrm{top}}_{\mathbb{Q}})_p \longrightarrow \Theta^{\mathrm{top}}_{\mathbb{Q}}, \quad \Phi_R\colon \Theta^{\mathrm{top}}_{\mathbb{Q}} \longrightarrow \bigoplus_p \Theta^{\mathrm{top}}_{\mathbb{Q}}/(\Theta^{\mathrm{top}}_{\mathbb{Q}})^p, \end{align*} $$
where p varies over primes in
![]() $\mathbb {Z}$
. Here, the primary part
$\mathbb {Z}$
. Here, the primary part
 $(\Theta ^{\mathrm {top}}_{\mathbb {Q}})_p$
is generated by
$(\Theta ^{\mathrm {top}}_{\mathbb {Q}})_p$
is generated by
 $\mathbb {Z}[\frac 1p]$
-homology spheres, and
$\mathbb {Z}[\frac 1p]$
-homology spheres, and
 $(\Theta ^{\mathrm {top}}_{\mathbb {Q}})^p$
is generated by
$(\Theta ^{\mathrm {top}}_{\mathbb {Q}})^p$
is generated by
![]() $\mathbb {Z}_p$
-homology spheres.
$\mathbb {Z}_p$
-homology spheres.
The linking form
![]() $L_Y\colon H_1(Y)\times H_1(Y)\to \mathbb {Q}/\mathbb {Z}$
of a rational homology 3-sphere Y gives fundamental information. Algebraically, a
$L_Y\colon H_1(Y)\times H_1(Y)\to \mathbb {Q}/\mathbb {Z}$
of a rational homology 3-sphere Y gives fundamental information. Algebraically, a
![]() $(\mathbb {Q}/\mathbb {Z})$
-valued linking form is a nonsingular symmetric bilinear form
$(\mathbb {Q}/\mathbb {Z})$
-valued linking form is a nonsingular symmetric bilinear form
![]() $L\colon A \times A\to \mathbb {Q}/\mathbb {Z}$
with A a finite abelian group. The Witt group of
$L\colon A \times A\to \mathbb {Q}/\mathbb {Z}$
with A a finite abelian group. The Witt group of
![]() $(\mathbb {Q}/\mathbb {Z})$
-valued linking forms, which we denote by
$(\mathbb {Q}/\mathbb {Z})$
-valued linking forms, which we denote by
![]() $W(\mathbb {Q}/\mathbb {Z})$
, is defined in the standard manner. There is a homomorphism
$W(\mathbb {Q}/\mathbb {Z})$
, is defined in the standard manner. There is a homomorphism
 $\Theta ^{\mathrm {top}}_{\mathbb {Q}} \to W(\mathbb {Q}/\mathbb {Z})$
that sends the class of a rational homology sphere Y to the Witt class of the associated linking form
$\Theta ^{\mathrm {top}}_{\mathbb {Q}} \to W(\mathbb {Q}/\mathbb {Z})$
that sends the class of a rational homology sphere Y to the Witt class of the associated linking form
![]() $L_Y$
. This is surjective due to [Reference Kawauchi and Kojima27]. The following is a well-known conjecture [Reference Kim and Livingston31, p. 4].
$L_Y$
. This is surjective due to [Reference Kawauchi and Kojima27]. The following is a well-known conjecture [Reference Kim and Livingston31, p. 4].
Conjecture A.14. The homomorphism
 $\Theta ^{\mathrm {top}}_{\mathbb {Q}} \to W(\mathbb {Q}/\mathbb {Z})$
is an isomorphism.
$\Theta ^{\mathrm {top}}_{\mathbb {Q}} \to W(\mathbb {Q}/\mathbb {Z})$
is an isomorphism.
Also, it is a standard fact that the Witt group
![]() $W(\mathbb {Q}/\mathbb {Z})$
is left and right primary decomposable. (Indeed, the strong existence condition (
$W(\mathbb {Q}/\mathbb {Z})$
is left and right primary decomposable. (Indeed, the strong existence condition (
![]() $\textrm{LP1}'$
) is also satisfied.) The primary part
$\textrm{LP1}'$
) is also satisfied.) The primary part
![]() $W(\mathbb {Q}/\mathbb {Z})_p$
is the Witt group of linking forms defined on p-torsion finite abelian groups. So, an affirmative answer to the above conjecture implies that
$W(\mathbb {Q}/\mathbb {Z})_p$
is the Witt group of linking forms defined on p-torsion finite abelian groups. So, an affirmative answer to the above conjecture implies that
![]() $\Theta ^{\mathrm {top}}$
is left and right primary decomposable.
$\Theta ^{\mathrm {top}}$
is left and right primary decomposable.
For the smooth case, the left and right primary decompositions concern the homomorphisms
 $$ \begin{align*} \Phi_L\colon \bigoplus_p (\Theta^{\mathrm{sm}}_{\mathbb{Q}})_p/\Delta \longrightarrow \Theta^{\mathrm{sm}}_{\mathbb{Q}}/\Delta, \quad \Phi_R\colon \Theta^{\mathrm{sm}}_{\mathbb{Q}}/\Delta \longrightarrow \bigoplus_p \Theta^{\mathrm{sm}}_{\mathbb{Q}}/(\Theta^{\mathrm{sm}}_{\mathbb{Q}})^p, \end{align*} $$
$$ \begin{align*} \Phi_L\colon \bigoplus_p (\Theta^{\mathrm{sm}}_{\mathbb{Q}})_p/\Delta \longrightarrow \Theta^{\mathrm{sm}}_{\mathbb{Q}}/\Delta, \quad \Phi_R\colon \Theta^{\mathrm{sm}}_{\mathbb{Q}}/\Delta \longrightarrow \bigoplus_p \Theta^{\mathrm{sm}}_{\mathbb{Q}}/(\Theta^{\mathrm{sm}}_{\mathbb{Q}})^p, \end{align*} $$
where
 $\Delta \subset \Theta ^{\mathrm {sm}}_{\mathbb {Q}}$
is the subgroup generated by the classes of integral homology 3-spheres. A result of S.-G. Kim and Livingston [Reference Kim and Livingston31, Proposition, p. 184] says that this
$\Delta \subset \Theta ^{\mathrm {sm}}_{\mathbb {Q}}$
is the subgroup generated by the classes of integral homology 3-spheres. A result of S.-G. Kim and Livingston [Reference Kim and Livingston31, Proposition, p. 184] says that this
![]() $\Phi _L$
is not surjective, and thus
$\Phi _L$
is not surjective, and thus
 $\Theta ^{\mathrm {sm}}_{\mathbb {Q}}$
is not left primary decomposable. We have the following questions.
$\Theta ^{\mathrm {sm}}_{\mathbb {Q}}$
is not left primary decomposable. We have the following questions.
Question A.15.
-
(1) Is
 $\Phi _L\colon \bigoplus _p (\Theta ^{\mathrm {sm}}_{\mathbb {Q}})_p/\Delta \to \Theta ^{\mathrm {sm}}_{\mathbb {Q}} / \Delta $
injective?
$\Phi _L\colon \bigoplus _p (\Theta ^{\mathrm {sm}}_{\mathbb {Q}})_p/\Delta \to \Theta ^{\mathrm {sm}}_{\mathbb {Q}} / \Delta $
injective? -
(2) Is
 $\Theta ^{\mathrm {sm}}_{\mathbb {Q}}$
right primary decomposable?
$\Theta ^{\mathrm {sm}}_{\mathbb {Q}}$
right primary decomposable?
By Theorem A.8,
 $\Theta ^{\mathrm {sm}}_{\mathbb {Q}}$
is right primary decomposable if Conjecture A.14 is true and the rational homology cobordism group of rational homology 3-spheres bounding a topological rational homology 4-ball is right primary decomposable.
$\Theta ^{\mathrm {sm}}_{\mathbb {Q}}$
is right primary decomposable if Conjecture A.14 is true and the rational homology cobordism group of rational homology 3-spheres bounding a topological rational homology 4-ball is right primary decomposable.
Acknowledgements
The author is indebted to Min Hoon Kim, Se-Goo Kim and Taehee Kim for discussions that led him to prove the results described in the Introduction. The author thanks Chuck Livingston for his extremely helpful comments. Many results in this article were obtained during the author’s visit to Max Planck Institute for Mathematics in 2017–2018. The author is grateful to the institute and Peter Teichner for the invitation and hospitality. Finally, the author thanks an anonymous referee for comments that were very helpful in improving the exposition.
Conflict of Interest
None.
Financial support
This work was partly supported by NRF grant 2019R1A3B2067839.