Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-12-01T00:16:40.659Z Has data issue: false hasContentIssue false
  • English
  • Français

THE POLYTABLOID BASIS EXPANDS POSITIVELY INTO THE WEB BASIS

Part of: Algebraic combinatorics

Published online by Cambridge University Press:  19 August 2019

BRENDON RHOADES
BRENDON RHOADES*
Affiliation:
Department of Mathematics, University of California, San Diego, La Jolla, CA, 92093, USA; [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We show that the transition matrix from the polytabloid basis to the web basis of the irreducible 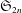$\mathfrak{S}_{2n}$-representation of shape 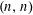$(n,n)$ has nonnegative integer entries. This proves a conjecture of Russell and Tymoczko [Int. Math. Res. Not., 2019(5) (2019), 1479–1502].

MSC classification

Primary: 05E10: Combinatorial aspects of representation theory
Secondary: 05E40: Combinatorial aspects of commutative algebra
Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 7 , 2019 , e26
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author 2019

References

Ariki, S., Terasoma, T. and Yamada, H.-F., ‘Higher Specht polynomials’, Hiroshima Math. J. 27(1) (1997), 177–188.Google Scholar
Garsia, A. M. and McLarnan, T. J., ‘Relations between Young’s natural and the Kazhdan–Lusztig representations of S n ’, Adv. Math. 69(1) (1988), 32–92.Google Scholar
Kazhdan, D. and Lusztig, G., ‘Representations of Coxeter groups and Hecke algebras’, Invent. Math. 53 (1979), 165–184.Google Scholar
Kung, J. P. S. and Rota, G.-C., ‘The invariant theory of binary forms’, Bull. Amer. Math. Soc. (N.S.) 10(1) (1984), 27–85.Google Scholar
Petersen, K., Pylyavskyy, P. and Rhoades, B., ‘Promotion and cyclic sieving via webs’, J. Algebraic Combin. 30(1) (2009), 19–41.Google Scholar
Rhoades, B., ‘A skein action of the symmetric group on noncrossing partitions’, J. Algebraic Combin. 45(1) (2017), 81–127.Google Scholar
Russell, H. and Tymoczko, J., ‘The transition matrix between the Specht and web bases is unipotent with additional vanishing entries’, Int. Math. Res. Not. IMRN 2019(5) (2019), 1479–1502.Google Scholar
Specht, W., ‘Die irreduziblen Darstellungen der symmetrischen Gruppe’, Math. Z. 39(1) (1935), 696–711.Google Scholar
Young, A., The Collected Papers of Alfred Young 1873–1940, Math. Expositions, No. 21 , (University of Toronto Press, 1977).Google Scholar