Hostname: page-component-6bf8c574d5-mggfc Total loading time: 0 Render date: 2025-02-17T18:28:54.588Z Has data issue: false hasContentIssue false
  • English
  • Français

Pencils on Surfaces with Normal Crossings and the Kodaira Dimension of 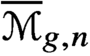$\overline {\mathcal {M}}_{g,n}$

Part of: Special varieties Curves

Published online by Cambridge University Press:  12 April 2021

Daniele Agostini  and
Ignacio Barros
Daniele Agostini
Affiliation:
MPI for Mathematics in the Sciences, Inselstraße 22, 04103Leipzig, Germany; E-mail: [email protected].
Ignacio Barros
Affiliation:
Laboratoire de mathématiques d’Orsay, Université Paris-Saclay, Rue Michel Magat, Bât. 307, Orsay91405, France; E-mail: [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study smoothing of pencils of curves on surfaces with normal crossings. As a consequence we show that the canonical divisor of 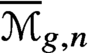$\overline {\mathcal {M}}_{g,n}$ is not pseudoeffective in some range, implying that 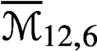$\overline {\mathcal {M}}_{12,6}$, 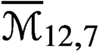$\overline {\mathcal {M}}_{12,7}$, 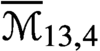$\overline {\mathcal {M}}_{13,4}$ and 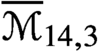$\overline {\mathcal {M}}_{14,3}$ are uniruled. We provide upper bounds for the Kodaira dimension of 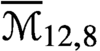$\overline {\mathcal {M}}_{12,8}$ and 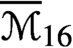$\overline {\mathcal {M}}_{16}$. We also show that the moduli space of 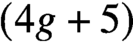$(4g+5)$-pointed hyperelliptic curves 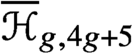$\overline {\mathcal {H}}_{g,4g+5}$ is uniruled. Together with a recent result of Schwarz, this concludes the classification of moduli of pointed hyperelliptic curves with negative Kodaira dimension.

MSC classification

Primary: 14H10: Families, moduli (algebraic)
Secondary: 14H45: Special curves and curves of low genus 14M20: Rational and unirational varieties
Type
Algebraic and Complex Geometry
Information
Forum of Mathematics, Sigma , Volume 9 , 2021 , e31
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited
Copyright
© The Author(s), 2021. Published by Cambridge University Press

References

Agostini, D. and Barros, I., ‘Auxiliary Macaulay2 code’, 2020. URL: https://personal-homepages.mis.mpg.de/agostini/.Google Scholar
Arbarello, E., Cornalba, M. and Griffiths, P. A., Geometry of Algebraic Curves, Vol. II, Grundlehren Math. Wiss. vol. 267 (Springer-Verlag, New York, 2011).CrossRefGoogle Scholar
Barros, I. and Mullane, S., ‘Two moduli spaces of Calabi-Yau type’, Int. Math. Res. Not. IMRN, to appear, (2019) Published online.CrossRefGoogle Scholar
Beltrametti, M. and Lanteri, A., ‘On the 2 and the 3-connectedness of ample divisors on a surface’, Manuscripta Math. 58 (1987), 109–128.CrossRefGoogle Scholar
Benzo, L., ‘Uniruledness of some moduli spaces of stable pointed curves’, J. Pure Appl. Algebra 218(3) (2014), 395–404.CrossRefGoogle Scholar
Boucksom, S., Demailly, J.-P., Păun, M. and Peternell, T., ‘The pseudoeffective cone of a compact Kähler manifold and varieties of negative Kodaira dimension’, J. Algebraic Geom. 22 (2013), 201–248.CrossRefGoogle Scholar
Bruno, A. and Verra, A., ‘${{\mathcal{M}}}_{15}$ is rationally connected’, in Projective Varieties with Unexpected Properties, (Walter de Gruyter GmbH, Berlin, 2005), 51–65.Google Scholar
Casnati, G., ‘On the rationality of moduli spaces of pointed hyperelliptic curves’, Rocky Mountain J. Math. 42(2) (2012), 491–498.CrossRefGoogle Scholar
Chang, M. C. and Ran, Z., ‘Unirationality of the moduli space of curves of genus $11,13$ (and $12$)’, Invent. Math. 76 (1984), 41–54.CrossRefGoogle Scholar
Chang, M. C. and Ran, Z., ‘The Kodaira dimension of the moduli space of curves of genus $15$’, J. Differential Geom. 24 (1986), 205–220.CrossRefGoogle Scholar
Chang, M. C. and Ran, Z., ‘On the slope and Kodaira dimension of ${\overline{{\mathcal{M}}}}_g$for small $g$’, J. Differential Geom. 34 (1991), 267–274.CrossRefGoogle Scholar
di Rocco, S., ‘k-Very ample line bundles on del Pezzo surfaces’, Math. Nachr. 179 (1996), 47–56.CrossRefGoogle Scholar
Eisenbud, D. and Harris, J., ‘Limit linear series: Basic theory’, Invent. Math. 85 (1986), 337–371.CrossRefGoogle Scholar
Eisenbud, D. and Harris, J., ‘The Kodaira dimension of the moduli space of curves of genus $\ge 23$’, Invent. Math. 90 (1987), 359–387.CrossRefGoogle Scholar
Farkas, G., ‘Koszul divisors on moduli spaces of curves’, Amer. J. Math. 131 (2009), 819–867.CrossRefGoogle Scholar
Farkas, G., Jensen, D. and Payne, S., ‘The Kodaira dimensions of ${\overline{{\mathcal{M}}}}_{22}$ and ${\overline{{\mathcal{M}}}}_{23}$’, Preprint, 2020, arXiv: 2005.00622.Google Scholar
Farkas, G. and Popa, M., ‘Effective divisors on ${\overline{{\mathcal{M}}}}_g$, curves on $K3$ surfaces and the Slope Conjecture’, J. Algebraic Geom. 14 (2005), 151–174.CrossRefGoogle Scholar
Farkas, G. and Verra, A., ‘The classification of universal Jacobians over the moduli space of curves’, Comment. Math. Helv. 88 (2013), 587–611.CrossRefGoogle Scholar
Farkas, G. and Verra, A., ‘On the Kodaira dimension of ${\overline{{\mathcal{M}}}}_{16}$’, Preprint, 2020, arXiv: 2008.08852.Google Scholar
Friedman, R., ‘Global smoothings of varieties with normal crossings’, Ann. of Math. (2) 118(1) (1983), 75–114.CrossRefGoogle Scholar
Grayson, D. and Stillman, M., ‘Macaulay2, a software system for research in algebraic geometry’. URL: http://www.math.uiuc.edu/Macaulay2/.Google Scholar
Hacking, P., ‘Compact moduli of surfaces of general type’, Contemp. Math. 564 (2012), 1–18.CrossRefGoogle Scholar
Harris, J. and Mumford, D., ‘On the Kodaira dimension of ${\overline{{\mathcal{M}}}}_g$’, Invent. Math. 67 (1982), 23–88.CrossRefGoogle Scholar
Keneshlou, H. and Tanturri, F., ‘On the unirationality of moduli spaces of pointed curves’, Preprint, 2020, arXiv: 2003.07888.Google Scholar
Lipman, J., ‘Notes on derived functors and Grothendieck duality’, in Foundations of Grothendieck Duality for Diagrams of Schemes, Lecture Notes in Mathematics vol. 1960 (Springer-Verlag, Berlin Heidelberg, 2009), 1–259.CrossRefGoogle Scholar
Logan, A., ‘The Kodaira dimension of moduli spaces of curves with marked points’, Amer. J. Math. 125(1) (2003), 105–138.CrossRefGoogle Scholar
Mukai, S., ‘Curves and K3 surfaces of genus eleven’, in Moduli of Vector Bundles, Lecture Notes in Pure and Applied Mathematics vol. 179 (CRC Press, Boca Raton, 1996), 189–197.Google Scholar
Schwarz, I., ‘On the Kodaira dimension of the moduli space of hyperelliptic curves with marked points’, Preprint, 2020, arXiv: 2002.03417.Google Scholar
Sernesi, E., Deformations of Algebraic Schemes, Grundlehren der Mathematischen Wissenschaften vol. 334 (Springer-Verlag, Berlin Heidelber, 2006).Google Scholar
The Stacks project authors, ‘The Stacks project’ (2020). URL: https://stacks.math.columbia.edu.Google Scholar
Tseng, D., ‘On the slope of the moduli space of genus $15$ and $16$ curves. Preprint, 2019, arXiv: 1905.00449.Google Scholar
Verra, A., ‘The unirationality of the moduli space of curves of genus $14$ and lower’, Compos. Math. 141 (2005), 1425–1444.CrossRefGoogle Scholar