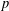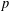Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Bhatt, Bhargav
2018.
On the direct summand conjecture and its derived variant.
Inventiones mathematicae,
Vol. 212,
Issue. 2,
p.
297.
Deninger, Christopher
and
Werner, Annette
2019.
Parallel transport for vector bundles on 𝑝-adic varieties.
Journal of Algebraic Geometry,
Vol. 29,
Issue. 1,
p.
1.