Article contents
Overconvergent modular forms are highest-weight vectors in the Hodge-Tate weight zero part of completed cohomology
Published online by Cambridge University Press: 02 March 2021
Abstract
We construct a 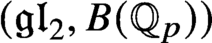 $(\mathfrak {gl}_2, B(\mathbb {Q}_p))$ and Hecke-equivariant cup product pairing between overconvergent modular forms and the local cohomology at
$(\mathfrak {gl}_2, B(\mathbb {Q}_p))$ and Hecke-equivariant cup product pairing between overconvergent modular forms and the local cohomology at 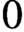 $0$ of a sheaf on
$0$ of a sheaf on 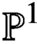 $\mathbb {P}^1$, landing in the compactly supported completed
$\mathbb {P}^1$, landing in the compactly supported completed 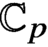 $\mathbb {C}_p$-cohomology of the modular curve. The local cohomology group is a highest-weight Verma module, and the cup product is non-trivial on a highest-weight vector for any overconvergent modular form of infinitesimal weight not equal to
$\mathbb {C}_p$-cohomology of the modular curve. The local cohomology group is a highest-weight Verma module, and the cup product is non-trivial on a highest-weight vector for any overconvergent modular form of infinitesimal weight not equal to 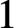 $1$. For classical weight
$1$. For classical weight 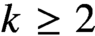 $k\geq 2$, the Verma has an algebraic quotient
$k\geq 2$, the Verma has an algebraic quotient 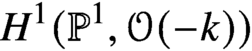 $H^1(\mathbb {P}^1, \mathcal {O}(-k))$, and on classical forms, the pairing factors through this quotient, giving a geometric description of ‘half’ of the locally algebraic vectors in completed cohomology; the other half is described by a pairing with the roles of
$H^1(\mathbb {P}^1, \mathcal {O}(-k))$, and on classical forms, the pairing factors through this quotient, giving a geometric description of ‘half’ of the locally algebraic vectors in completed cohomology; the other half is described by a pairing with the roles of 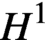 $H^1$ and
$H^1$ and 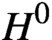 $H^0$ reversed between the modular curve and
$H^0$ reversed between the modular curve and 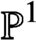 $\mathbb {P}^1$. Under minor assumptions, we deduce a conjecture of Gouvea on the Hodge-Tate-Sen weights of Galois representations attached to overconvergent modular forms. Our main results are essentially a strict subset of those obtained independently by Lue Pan, but the perspective here is different, and the proofs are short and use simple tools: a Mayer-Vietoris cover, a cup product, and a boundary map in group cohomology.
$\mathbb {P}^1$. Under minor assumptions, we deduce a conjecture of Gouvea on the Hodge-Tate-Sen weights of Galois representations attached to overconvergent modular forms. Our main results are essentially a strict subset of those obtained independently by Lue Pan, but the perspective here is different, and the proofs are short and use simple tools: a Mayer-Vietoris cover, a cup product, and a boundary map in group cohomology.
MSC classification
- Type
- Number Theory
- Information
- Creative Commons
- This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
References
- 3
- Cited by



