Hostname: page-component-f554764f5-fr72s Total loading time: 0 Render date: 2025-04-09T23:18:52.009Z Has data issue: false hasContentIssue false
  • English
  • Français

On n-dependent groups and fields II

Published online by Cambridge University Press:  07 May 2021

Artem Chernikov  and
Nadja Hempel
Artem Chernikov
Affiliation:
Department of Mathematics, University of California Los Angeles, Los Angeles, CA90095-1555, USA; E-mail: [email protected].
Nadja Hempel
Affiliation:
Mathematisches Institut, Albert-Ludwigs-Universität Freiburg, Ernst-Zermelo-Str. 1, 79104Freiburg, Deutschland; E-mail: [email protected].

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We continue the study of n-dependent groups, fields and related structures, largely motivated by the conjecture that every n-dependent field is dependent. We provide evidence toward this conjecture by showing that every infinite n-dependent valued field of positive characteristic is henselian, obtaining a variant of Shelah’s Henselianity Conjecture in this case and generalizing a recent result of Johnson for dependent fields. Additionally, we prove a result on intersections of type-definable connected components over generic sets of parameters in n-dependent groups, generalizing Shelah’s absoluteness of 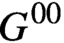$G^{00}$ in dependent theories and relative absoluteness of 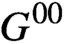$G^{00}$ in $2$-dependent theories. In an effort to clarify the scope of this conjecture, we provide new examples of strictly $2$-dependent fields with additional structure, showing that Granger’s examples of non-degenerate bilinear forms over dependent fields are 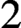$2$-dependent. Along the way, we obtain some purely model-theoretic results of independent interest: we show that n-dependence is witnessed by formulas with all but one variable singletons; provide a type-counting criterion for 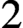$2$-dependence and use it to deduce 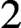$2$-dependence for compositions of dependent relations with arbitrary binary functions (the Composition Lemma); and show that an expansion of a geometric theory T by a generic predicate is dependent if and only if it is n-dependent for some n, if and only if the algebraic closure in T is disintegrated. An appendix by Martin Bays provides an explicit isomorphism in the Kaplan-Scanlon-Wagner theorem.

Keywords

03C4503C60
Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 9 , 2021 , e38
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s), 2021. Published by Cambridge University Press

References

Arnol’d, Vladimir Igorevich. On functions of three variables. In Doklady Akademii Nauk, volume 114, pages 679–681. Russian Academy of Sciences, 1957.Google Scholar
Baldwin, John T and Saxl, Jan. Logical stability in group theory. Journal of the Australian Mathematical Society, 21(3):267–276, 1976.CrossRefGoogle Scholar
Baudisch, Andreas. Mekler’s construction preserves CM-triviality. Annals of Pure and Applied Logic, 115(1-3):115–173, 2002.CrossRefGoogle Scholar
Baudisch, Andreas. Neostability-properties of Fraïssé limits of 2-nilpotent groups of exponent $p>2$. Archive for Mathematical Logic, 55(3-4):397–403, 2016.CrossRefGoogle Scholar
Berenstein, Alexander and Vassiliev, Evgueni. Geometric structures with a dense independent subset. Selecta Mathematica, 22(1):191–225, 2016.CrossRefGoogle Scholar
Chatzidakis, Zoé and Pillay, Anand. Generic structures and simple theories. Annals of Pure and Applied Logic, 95(1-3):71–92, 1998.CrossRefGoogle Scholar
Chatzidakis, Zoé and Pillay, Anand. Errata of the paper “Generic structures and simple theories”, Annals of Pure and Applied Logic 95 (1998) 71 – 92. https://www.math.ens.fr/~zchatzid/papiers/errtpta.pdf, 2020.Google Scholar
Cherlin, Gregory and Hrushovski, Ehud. Finite structures with few types, volume 152 of Annals of Mathematics Studies. Princeton University Press, Princeton, NJ, 2003.Google Scholar
Cherlin, Gregory and Shelah, Saharon. Superstable fields and groups. Annals of mathematical logic, 18(3):227–270, 1980.CrossRefGoogle Scholar
Chernikov, Artem. Lecture notes on stability theory. AMS Open Math Notes (OMN:201905.110792), 2019.Google Scholar
Chernikov, Artem and Hempel, Nadja. Mekler’s construction and generalized stability. Israel Journal of Mathematics, 230(2):745–769, 2019.CrossRefGoogle Scholar
Chernikov, Artem and Hempel, Nadja. On $n$-dependent groups and fields III. In preparation, 2021+.Google Scholar
Chernikov, Artem, Kaplan, Itay, and Shelah, Saharon. On non-forking spectra. Journal of the European Mathematical Society, 18(12):2821–2848, 2016.CrossRefGoogle Scholar
Chernikov, Artem, Palacin, Daniel, and Takeuchi, Kota. On $n$-dependence. Notre Dame J. Form. Log., 60(2):195–214, 2019.CrossRefGoogle Scholar
Chernikov, Artem and Ramsey, Nicholas. On model-theoretic tree properties. Journal of Mathematical Logic, 16(02):1650009, 2016.CrossRefGoogle Scholar
Chernikov, Artem and Shelah, Saharon. On the number of Dedekind cuts and two-cardinal models of dependent theories. Journal of the Institute of Mathematics of Jussieu, 15(4):771–784, 2016.CrossRefGoogle Scholar
Chernikov, Artem and Towsner, Henry. Hypergraph regularity and higher arity VC-dimension. Preprint, arXiv:2010.00726, 2020.Google Scholar
Dobrowolski, Jan. Sets, groups, and fields definable in vector spaces with a bilinear form. Preprint, arXiv:2004.07238, 2020.Google Scholar
Duret, Jean-Louis. Les corps faiblement algébriquement clos non séparablement clos ont la propriété d’indépendance. In Model theory of algebra and arithmetic, pages 136–162. Springer, 1980.CrossRefGoogle Scholar
Gismatullin, Jakub. Model theoretic connected components of groups. Israel J. Math., 184:251–274, 2011.CrossRefGoogle Scholar
Granger, Nicolas Mark. Stability, simplicity and the model theory of bilinear forms. PhD thesis, University of Manchester, 1999.Google Scholar
Hempel, Nadja. On $n$-dependent groups and fields. Mathematical Logic Quarterly, 62(3):215–224, 2016.CrossRefGoogle Scholar
Hrushovski, Ehud. Unidimensional theories are superstable. Annals of Pure and Applied Logic, 50(2):117–137, 1990.CrossRefGoogle Scholar
Hrushovski, Ehud. The Mordell-Lang conjecture for function fields. Journal of the American mathematical society, 9(3):667–690, 1996.CrossRefGoogle Scholar
Hrushovski, Ehud. Pseudo-finite fields and related structures. In Model theory and applications, volume 11 of Quad. Mat., pages 151–212. Aracne, Rome, 2002.Google Scholar
Ivanov, A. The structure of superflat graphs. Fundamenta Mathematicae, 143(2):107–117, 1993.Google Scholar
Johnson, Will. Dp-finite fields I (A): The infinitesimals. Annals of Pure and Applied Logic, page 102947, 2021.CrossRefGoogle Scholar
Johnson, Will. Dp-finite fields I (B): Positive characteristic. Annals of Pure and Applied Logic, page 102949, 2021.CrossRefGoogle Scholar
Johnson, Will, Tran, Chieu-Minh, Walsberg, Erik, and Ye, Jinhe. Étale-open topology and the stable field conjecture. Preprint, arXiv:2009.02319, 2020.Google Scholar
Johnson, William Andrew. Fun with Fields. ProQuest LLC, Ann Arbor, MI, 2016. PhD thesis, University of California, Berkeley.Google Scholar
Kaplan, Itay, Scanlon, Thomas, and Wagner, Frank O. Artin-Schreier extensions in NIP and simple fields. Israel Journal of Mathematics, 185(1):141–153, 2011.CrossRefGoogle Scholar
Kruckman, Alex, Tran, Minh Chieu, and Walsberg, Erik. Interpolative fusions. Preprint, arXiv:1811.06108, 2018.Google Scholar
Macintyre, Angus. On ${\omega}_1$-categorical theories of fields. Fundamenta Mathematicae, 1(71):1–25, 1971.CrossRefGoogle Scholar
Marker, David. Model theory: An introduction, volume 217 of Graduate Texts in Mathematics. Springer-Verlag, New York, 2002.Google Scholar
Mitchell, William. Aronszajn trees and the independence of the transfer property. Annals of Mathematical Logic, 5(1):21–46, 1972.CrossRefGoogle Scholar
Pillay, A., Scanlon, T., and Wagner, F. O.. Supersimple fields and division rings. Math. Res. Lett., 5(4):473–483, 1998.CrossRefGoogle Scholar
Podewski, Klaus-Peter. Minimale ringe. Math. Phys. Semesterberichte, 22:193–197, 1973.Google Scholar
Shelah, S.. Classification theory and the number of nonisomorphic models, volume 92 of Studies in Logic and the Foundations of Mathematics. North-Holland Publishing Co., Amsterdam, second edition, 1990.Google Scholar
Shelah, Saharon. Minimal bounded index subgroup for dependent theories. Proceedings of the American Mathematical Society, 136(3):1087–1091, 2008.CrossRefGoogle Scholar
Shelah, Saharon. Strongly dependent theories. Israel Journal of Mathematics, 204(1):1–83, 2014.CrossRefGoogle Scholar
Shelah, Saharon. Definable groups for dependent and 2-dependent theories. Sarajevo J. Math., 13(25)(1):3–25, 2017.Google Scholar
Simon, Pierre. A guide to NIP theories, volume 44 of Lecture Notes in Logic. Association for Symbolic Logic, Chicago, IL; Cambridge Scientific Publishers, Cambridge, 2015.CrossRefGoogle Scholar
Tent, Katrin and Ziegler, Martin. A course in model theory, volume 40 of Lecture Notes in Logic. Association for Symbolic Logic, La Jolla, CA; Cambridge University Press, Cambridge, 2012.CrossRefGoogle Scholar
Terry, Caroline. VC$_{\ell }$ -dimension and the jump to the fastest speed of a hereditary $\mathbf{\mathcal{L}}$-property. Proceedings of the American Mathematical Society, 146(7):3111–3126, 2018.CrossRefGoogle Scholar
Laurentius Petrus Dignus van den Dries. Model Theory of Fields: Decidability and Bounds for Polynomial Ideals. PhD thesis, Rijksuniversiteit Utrecht, 1978.Google Scholar
Winkler, Peter M.. Model-completeness and Skolem expansions. In Model theory and algebra (memorial tribute to Abraham Robinson), pages 408–463. Lecture Notes in Math., Vol. 498. 1975.CrossRefGoogle Scholar
Zilber, Boris. Uncountably categorical theories, volume 117 of Translations of Mathematical Monographs. American Mathematical Society, Providence, RI, 1993. Translated from the Russian by Louvish, D..CrossRefGoogle Scholar