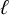1 Introduction
Let X be a smooth variety over a field k and let
![]() $\ell $
be a prime invertible in k. In this paper, we study the
$\ell $
be a prime invertible in k. In this paper, we study the
![]() $\ell $
-power torsion subgroup
$\ell $
-power torsion subgroup
![]() $\operatorname {CH}^i(X)[\ell ^{\infty }]$
of the Chow group
$\operatorname {CH}^i(X)[\ell ^{\infty }]$
of the Chow group
![]() $\operatorname {CH}^i(X)$
of codimension-i cycles on X. Following some constructions in [Reference BlochBlo79, Reference SchreiederSch21b], we define a cycle map
$\operatorname {CH}^i(X)$
of codimension-i cycles on X. Following some constructions in [Reference BlochBlo79, Reference SchreiederSch21b], we define a cycle map

where
![]() $M^{2i-1}(X)\subset H^{2i-1}(X_{\acute{\mathrm{e}}\text{t}},{\mathbb Q}_{\ell }/\mathbb {Z}_{\ell }(i))$
is defined as follows: we pick a finitely generated subfield
$M^{2i-1}(X)\subset H^{2i-1}(X_{\acute{\mathrm{e}}\text{t}},{\mathbb Q}_{\ell }/\mathbb {Z}_{\ell }(i))$
is defined as follows: we pick a finitely generated subfield
![]() $k_0\subset k$
such that there is a
$k_0\subset k$
such that there is a
![]() $k_0$
-variety
$k_0$
-variety
![]() $X_0$
with
$X_0$
with
![]() $X=X_0\times _{k_0}k$
and let
$X=X_0\times _{k_0}k$
and let

where
![]() $k'$
runs through all finitely generated subfields of k that contain
$k'$
runs through all finitely generated subfields of k that contain
![]() $k_0$
, and
$k_0$
, and
![]() $N^{\ast }$
denotes the coniveau filtration (cf. (2.2) below).
$N^{\ast }$
denotes the coniveau filtration (cf. (2.2) below).
If k is algebraically closed and X is projective, then
![]() $M^{2i-1}(X)=0$
by weight reasons (see Lemma 4.1 below) and the above map coincides with Bloch’s map [Reference BlochBlo79]; see Lemma 4.5 below. If, moreover,
$M^{2i-1}(X)=0$
by weight reasons (see Lemma 4.1 below) and the above map coincides with Bloch’s map [Reference BlochBlo79]; see Lemma 4.5 below. If, moreover,
![]() $k=\mathbb C$
, the map agrees on the subgroup of homologically trivial
$k=\mathbb C$
, the map agrees on the subgroup of homologically trivial
![]() $\ell $
-power torsion cycles with Griffiths’ Abel–Jacobi map [Reference GriffithsGri69]; see [Reference BlochBlo79, Proposition 3.7].
$\ell $
-power torsion cycles with Griffiths’ Abel–Jacobi map [Reference GriffithsGri69]; see [Reference BlochBlo79, Proposition 3.7].
Bloch’s map over algebraically closed fields is injective on torsion cycles of codimension
![]() $\leq 2$
; the non-trivial case
$\leq 2$
; the non-trivial case
![]() $i=2$
is a theorem of Bloch and Merkurjev–Suslin; see [Reference Merkurjev and SuslinMS83, §18]. Moreover, for any ground field k, Colliot-Thélène–Sansuc–Soulé showed in [Reference Colliot- Thélène, Sansuc and SouléCTSS83, Corollaire 3] that
$i=2$
is a theorem of Bloch and Merkurjev–Suslin; see [Reference Merkurjev and SuslinMS83, §18]. Moreover, for any ground field k, Colliot-Thélène–Sansuc–Soulé showed in [Reference Colliot- Thélène, Sansuc and SouléCTSS83, Corollaire 3] that
![]() $\operatorname {CH}^2(X)[\ell ^{\infty }]$
is isomorphic to a subquotient of
$\operatorname {CH}^2(X)[\ell ^{\infty }]$
is isomorphic to a subquotient of
![]() $H^3(X_{\acute{\mathrm{e}}\text{t}},{\mathbb Q}_{\ell }/\mathbb {Z}_{\ell }(2))$
. The following result generalizes the injectivity theorem of Bloch and Merkurjev–Suslin over algebraically closed fields by making the aforementioned result in [Reference Colliot- Thélène, Sansuc and SouléCTSS83] more precise; the argument relies on some results from [Reference SchreiederSch21b].
$H^3(X_{\acute{\mathrm{e}}\text{t}},{\mathbb Q}_{\ell }/\mathbb {Z}_{\ell }(2))$
. The following result generalizes the injectivity theorem of Bloch and Merkurjev–Suslin over algebraically closed fields by making the aforementioned result in [Reference Colliot- Thélène, Sansuc and SouléCTSS83] more precise; the argument relies on some results from [Reference SchreiederSch21b].
Theorem 1.1. Let X be a smooth variety over a field k and let
![]() $\ell $
be a prime invertible in k. Then
$\ell $
be a prime invertible in k. Then
![]() $\lambda _{X}^i$
from (1.1) is injective for
$\lambda _{X}^i$
from (1.1) is injective for
![]() $i=1,2$
and induces the following isomorphisms:
$i=1,2$
and induces the following isomorphisms:
In the body of this paper, we prove a version of the above theorem that works for arbitrary algebraic schemes; see Theorem 4.2 and Corollary 4.4. To this end, one has to replace in the above discussion ordinary cohomology by Borel–Moore cohomology; cf. [Reference SchreiederSch21b, §4].
Using some Lefschetz hyperplane argument, Bloch shows that the injectivity of
![]() $\lambda _{X}^2$
implies the injectivity of
$\lambda _{X}^2$
implies the injectivity of
![]() $\lambda _{X}^{\dim X}$
over algebraically closed fields (see [Reference BlochBlo79]), hence Roitman’s theorem [Reference RoitmanRoi80] away from the characteristic. Similarly,
$\lambda _{X}^{\dim X}$
over algebraically closed fields (see [Reference BlochBlo79]), hence Roitman’s theorem [Reference RoitmanRoi80] away from the characteristic. Similarly,
![]() $\lambda _{X}^{\dim X}$
is known to be injective over finite fields; see, for example, [Reference Kato and SaitoKS83, Reference Colliot- Thélène, Sansuc and SouléCTSS83]. However, even over algebraically closed fields, the map
$\lambda _{X}^{\dim X}$
is known to be injective over finite fields; see, for example, [Reference Kato and SaitoKS83, Reference Colliot- Thélène, Sansuc and SouléCTSS83]. However, even over algebraically closed fields, the map
![]() $\lambda _{X}^i$
is for
$\lambda _{X}^i$
is for
![]() $2<i<\dim X $
, in general, not injective (e.g., [Reference SchoenSchoe00, Reference TotaroTot97, Reference Soulé and VoisinSV05, Reference Rosenschon and SrinivasRS10, Reference TotaroTot16, Reference SchreiederSch21c, Reference Scavia and SuzukiSS23]).
$2<i<\dim X $
, in general, not injective (e.g., [Reference SchoenSchoe00, Reference TotaroTot97, Reference Soulé and VoisinSV05, Reference Rosenschon and SrinivasRS10, Reference TotaroTot16, Reference SchreiederSch21c, Reference Scavia and SuzukiSS23]).
Roitman’s theorem on the injectivity of
![]() $\lambda _{X}^{\dim X}$
over algebraically closed fields turned out to be a very robust statement, with generalizations to non-proper and even singular spaces (e.g., [Reference LevineLev85, Reference Krishna and SrinivasKS02, Reference GeisserGei10]). As mentioned above, there is also a generalization to finite fields [Reference Kato and SaitoKS83, Reference Colliot- Thélène, Sansuc and SouléCTSS83]. In light of the injectivity of
$\lambda _{X}^{\dim X}$
over algebraically closed fields turned out to be a very robust statement, with generalizations to non-proper and even singular spaces (e.g., [Reference LevineLev85, Reference Krishna and SrinivasKS02, Reference GeisserGei10]). As mentioned above, there is also a generalization to finite fields [Reference Kato and SaitoKS83, Reference Colliot- Thélène, Sansuc and SouléCTSS83]. In light of the injectivity of
![]() $\lambda _{X}^2$
over arbitrary fields, it is natural to wonder if Roitman’s theorem admits also a generalization to arbitrary fields (i.e., is
$\lambda _{X}^2$
over arbitrary fields, it is natural to wonder if Roitman’s theorem admits also a generalization to arbitrary fields (i.e., is
![]() $\lambda _{X}^{\dim X}$
always injective?) The main result of this paper answers this question negatively.
$\lambda _{X}^{\dim X}$
always injective?) The main result of this paper answers this question negatively.
Theorem 1.2. Let
![]() $\ell $
be a prime and let k be a field of characteristic different from
$\ell $
be a prime and let k be a field of characteristic different from
![]() $\ell $
. Then there is a finitely generated field extension
$\ell $
. Then there is a finitely generated field extension
![]() $K/k$
and a smooth projective threefold X over K such that
$K/k$
and a smooth projective threefold X over K such that
![]() $\lambda _{X}^3$
from (1.1) is not injective.
$\lambda _{X}^3$
from (1.1) is not injective.
The proof of the above result will rely on an adaptation of Schoen’s argument in [Reference SchoenSchoe00], together with some results on the integral Hodge and Tate conjecture due to Kollár, Hassett–Tschinkel and Totaro. Taking products with projective spaces, we get the following.
Corollary 1.3. Let
![]() $i\leq n$
be positive integers, let k be a field and let
$i\leq n$
be positive integers, let k be a field and let
![]() $\ell $
be a prime invertible in k. Then the map
$\ell $
be a prime invertible in k. Then the map
![]() $\lambda _{X}^i$
from (1.1) is injective for all smooth projective varieties X of dimension n over all finitely generated field extension of k if and only if
$\lambda _{X}^i$
from (1.1) is injective for all smooth projective varieties X of dimension n over all finitely generated field extension of k if and only if
![]() $i\leq 2$
.
$i\leq 2$
.
We will see in Lemma 4.7 below that over any field, the restriction of Jannsen’s cycle class map in continuous étale cohomology [Reference JannsenJan88] to
![]() $\ell $
-power torsion cycles,
$\ell $
-power torsion cycles,
factors through
![]() $\lambda _{X}^i$
. In particular, (1.1) refines Jannsen’s cycle class map on torsion cycles. As a consequence of Theorem 1.2, we immediately get the following, which answers [Reference Scavia and SuzukiSS23, Question 1.7(a)].
$\lambda _{X}^i$
. In particular, (1.1) refines Jannsen’s cycle class map on torsion cycles. As a consequence of Theorem 1.2, we immediately get the following, which answers [Reference Scavia and SuzukiSS23, Question 1.7(a)].
Corollary 1.4. For any
![]() $n\geq 3$
and any prime
$n\geq 3$
and any prime
![]() $\ell $
, there is a smooth projective n-fold X over a finitely generated field of characteristic different from
$\ell $
, there is a smooth projective n-fold X over a finitely generated field of characteristic different from
![]() $\ell $
such that Jannsen’s cycle class map
$\ell $
such that Jannsen’s cycle class map
is not injective on the subgroup of
![]() $\ell $
-power torsion classes.
$\ell $
-power torsion classes.
Jannsen showed that in the case of divisors (i.e., codimension one cycles) his cycle class map for smooth projective varieties over finitely generated fields is injective integrally; see [Reference JannsenJan88, Remark 6.15(a)] and [Reference SchreiederSch21b, (P7.2) in Proposition 6.6]. He further conjectured that after tensoring with
![]() ${\mathbb Q}$
, his cycle class map is injective for cycles of arbitrary codimension over finitely generated fields. Scavia and Suzuki exhibited in [Reference Scavia and SuzukiSS23] several interesting examples that show that tensoring with
${\mathbb Q}$
, his cycle class map is injective for cycles of arbitrary codimension over finitely generated fields. Scavia and Suzuki exhibited in [Reference Scavia and SuzukiSS23] several interesting examples that show that tensoring with
![]() ${\mathbb Q}$
is really necessary (i.e., the integral Jannsen conjecture fails in general). The main case left open by [Reference Scavia and SuzukiSS23] is that of zero-cycles, that we deal with in this paper. The case of zero-cycles is of particular importance because injectivity of
${\mathbb Q}$
is really necessary (i.e., the integral Jannsen conjecture fails in general). The main case left open by [Reference Scavia and SuzukiSS23] is that of zero-cycles, that we deal with in this paper. The case of zero-cycles is of particular importance because injectivity of
![]() $\lambda _{X}^{\dim X}$
on
$\lambda _{X}^{\dim X}$
on
![]() $\ell $
-power torsion zero-cycles for all smooth projective varieties X over finitely generated fields would imply the Rost nilpotence conjecture in characteristic zero by [Reference DiazDia22] and the arguments in [Reference SchreiederSch21b, §9.4] and [Reference SchreiederSch22, §B.2] (see also [Reference Rosenschon and SawantRS18]).
$\ell $
-power torsion zero-cycles for all smooth projective varieties X over finitely generated fields would imply the Rost nilpotence conjecture in characteristic zero by [Reference DiazDia22] and the arguments in [Reference SchreiederSch21b, §9.4] and [Reference SchreiederSch22, §B.2] (see also [Reference Rosenschon and SawantRS18]).
For the aforementioned application to the Rost nilpotence conjecture, it would be enough to prove injectivity of
![]() $\lambda _{X}^{\dim X}$
for varieties with a k-rational point (essentially because the argument in [Reference DiazDia22] proceeds via base change to the function field, where a rational point is automatic). The examples in Theorem 1.2 have no rational point. However, a variant of our construction gives (at least for the prime
$\lambda _{X}^{\dim X}$
for varieties with a k-rational point (essentially because the argument in [Reference DiazDia22] proceeds via base change to the function field, where a rational point is automatic). The examples in Theorem 1.2 have no rational point. However, a variant of our construction gives (at least for the prime
![]() $\ell =2$
) examples with rational points as well, which puts an end to the hope that the Rost nilpotence conjecture may be a consequence of the injectivity of
$\ell =2$
) examples with rational points as well, which puts an end to the hope that the Rost nilpotence conjecture may be a consequence of the injectivity of
![]() $\lambda ^{\dim X}$
on smooth projective varieties with a rational point.
$\lambda ^{\dim X}$
on smooth projective varieties with a rational point.
Theorem 1.5. There is a finitely generated field k of characteristic zero and a smooth projective threefold X over k such that X has a k-rational point and
![]() $\lambda _{X}^3$
from (1.1) is not injective for the prime
$\lambda _{X}^3$
from (1.1) is not injective for the prime
![]() $\ell =2$
.
$\ell =2$
.
The examples in Theorem 1.2 have Kodaira dimension 2, while those in Theorem 1.5 have negative Kodaira dimension, as they are conic bundles over surfaces of positive Kodaira dimension. The question whether
![]() $\lambda _{X}^{\dim X}$
is injective for smooth projective varieties X that are geometrically rationally connected remains open (this question is interesting for the base change
$\lambda _{X}^{\dim X}$
is injective for smooth projective varieties X that are geometrically rationally connected remains open (this question is interesting for the base change
![]() $X_{k(X)}$
of any rationally connected variety X over an algebraically closed field k which does not admit an integral decomposition of the diagonal; for examples of the latter, see the survey [Reference Schreieder and FarkasSch21a] and the references therein).
$X_{k(X)}$
of any rationally connected variety X over an algebraically closed field k which does not admit an integral decomposition of the diagonal; for examples of the latter, see the survey [Reference Schreieder and FarkasSch21a] and the references therein).
2 Preliminaries
We recall some of the notation and conventions from [Reference SchreiederSch21b] that we will use. An algebraic scheme is a separated scheme of finite type over a field. A variety is an integral algebraic scheme. A field is finitely generated if it is finitely generated over its prime field. The n-torsion subgroup of an abelian group G is denoted by
![]() $G[n]$
; the subgroup of elements annihilated by some power of n is denoted by
$G[n]$
; the subgroup of elements annihilated by some power of n is denoted by
![]() $G[n^{\infty }]$
. If
$G[n^{\infty }]$
. If
![]() $\varphi :H\to G$
is a morphism of abelian groups, we denote by slight abuse of notation
$\varphi :H\to G$
is a morphism of abelian groups, we denote by slight abuse of notation
![]() $G/H:=\operatorname {coker}(\varphi )$
.
$G/H:=\operatorname {coker}(\varphi )$
.
We fix a field k and a prime
![]() $\ell $
invertible in k. For an algebraic scheme X of dimension
$\ell $
invertible in k. For an algebraic scheme X of dimension
![]() $d_X$
over k, we denote by
$d_X$
over k, we denote by
![]() $\operatorname {CH}^i(X):=\operatorname {CH}_{d_X-i}(X)$
the Chow group of cycles of dimension
$\operatorname {CH}^i(X):=\operatorname {CH}_{d_X-i}(X)$
the Chow group of cycles of dimension
![]() $d_X-i$
on X. For
$d_X-i$
on X. For
![]() $A\in \{\mathbb {Z}/\ell ^r,\mathbb {Z}_{\ell },{\mathbb Q}_{\ell },{\mathbb Q}_{\ell }/\mathbb {Z}_{\ell }\}$
, we let
$A\in \{\mathbb {Z}/\ell ^r,\mathbb {Z}_{\ell },{\mathbb Q}_{\ell },{\mathbb Q}_{\ell }/\mathbb {Z}_{\ell }\}$
, we let
be twisted Borel–Moore pro-étale cohomology; see [Reference SchreiederSch21b, (6.13)-(6.15)] and [Reference SchreiederSch21b, Proposition 6.6]. Some of the most important properties of this functor are collected in [Reference SchreiederSch21b, Section 4]. If X is smooth and equi-dimensional, then we have canonical identifications
see [Reference SchreiederSch21b, Lemma 6.5].
For
![]() $j\geq 0$
, we denote by
$j\geq 0$
, we denote by
![]() $F_jX$
the pro-scheme given by the inverse limit of all open subsets
$F_jX$
the pro-scheme given by the inverse limit of all open subsets
![]() $U\subset X$
with
$U\subset X$
with
![]() $\dim (X\setminus U)<\dim X-j$
. If
$\dim (X\setminus U)<\dim X-j$
. If
![]() $U\hookrightarrow X$
is an open immersion with
$U\hookrightarrow X$
is an open immersion with
![]() $\dim U=\dim X$
, then there are restriction maps
$\dim U=\dim X$
, then there are restriction maps
![]() $H^i(X,A(n))\to H^i(U,A(n))$
. As in [Reference SchreiederSch21b, Section 5], we define
$H^i(X,A(n))\to H^i(U,A(n))$
. As in [Reference SchreiederSch21b, Section 5], we define
where U runs through all open subsets of X that make up the pro-scheme
![]() $F_jX$
above. The coniveau filtration
$F_jX$
above. The coniveau filtration
![]() $N^{\ast }$
on
$N^{\ast }$
on
![]() $H^i(X,A(n))$
is then given by
$H^i(X,A(n))$
is then given by
see [Reference SchreiederSch21b, (5.1)].
For
![]() $m\geq j$
, there are natural restriction maps
$m\geq j$
, there are natural restriction maps
![]() $ H^i(F_mX,A(n))\to H^i(F_jX,A(n)) $
, and we denote the image of this map by
$ H^i(F_mX,A(n))\to H^i(F_jX,A(n)) $
, and we denote the image of this map by
![]() $F^m H^i(F_jX,A(n))$
; see [Reference SchreiederSch21b, Definition 5.3]. For a scheme point
$F^m H^i(F_jX,A(n))$
; see [Reference SchreiederSch21b, Definition 5.3]. For a scheme point
![]() $x\in X$
, we let
$x\in X$
, we let
![]() $H^i(x,A(n)):=H^i(F_0\overline {\{ x\}},A(n))$
, where
$H^i(x,A(n)):=H^i(F_0\overline {\{ x\}},A(n))$
, where
![]() $\overline {\{ x\}}\subset X$
denotes the closure of x; note that
$\overline {\{ x\}}\subset X$
denotes the closure of x; note that
![]() $H^0(x,A(0))=A\cdot [x]$
, where
$H^0(x,A(0))=A\cdot [x]$
, where
![]() $[x]\in H^0(x,A(0))$
denotes the fundamental class of x; cf. [Reference SchreiederSch21b, (P3) in Definition 4.2 and Proposition 6.6].
$[x]\in H^0(x,A(0))$
denotes the fundamental class of x; cf. [Reference SchreiederSch21b, (P3) in Definition 4.2 and Proposition 6.6].
The Gysin sequence induces the following important long exact sequence (see [Reference SchreiederSch21b, Lemma 5.8]):
Since
![]() $H^i(x,A(n))=0$
for
$H^i(x,A(n))=0$
for
![]() $i<0$
, we deduce
$i<0$
, we deduce
![]() $H^i(X,A(n))=H^i(F_jX,A(n))$
for
$H^i(X,A(n))=H^i(F_jX,A(n))$
for
![]() $j\geq \lceil i/2\rceil $
; see [Reference SchreiederSch21b, Corollary 5.10].
$j\geq \lceil i/2\rceil $
; see [Reference SchreiederSch21b, Corollary 5.10].
Let
![]() $\operatorname {CH}^i(X)_{\mathbb {Z}_{\ell }}:=\operatorname {CH}^i(X)\otimes _{\mathbb {Z}} \mathbb {Z}_{\ell }$
. Then there is a cycle class map
$\operatorname {CH}^i(X)_{\mathbb {Z}_{\ell }}:=\operatorname {CH}^i(X)\otimes _{\mathbb {Z}} \mathbb {Z}_{\ell }$
. Then there is a cycle class map
see [Reference SchreiederSch21b, (7.1)]. This map is induced by the following pushforward map that appears in the above long exact sequence (2.3):
If X is smooth and equi-dimensional, then the above cycle class map agrees with Jannsen’s cycle class map in continuous étale cohomology from [Reference JannsenJan88]; see [Reference SchreiederSch21b, Lemma 9.1].
There is a natural coniveau filtration
![]() $N^{\ast }$
on
$N^{\ast }$
on
![]() $\operatorname {CH}^i(X)_{\mathbb {Z}_{\ell }}$
, given by the condition that a cycle
$\operatorname {CH}^i(X)_{\mathbb {Z}_{\ell }}$
, given by the condition that a cycle
![]() $[z]$
lies in
$[z]$
lies in
![]() $N^j$
if and only if there is a closed subset
$N^j$
if and only if there is a closed subset
![]() $Z\subset X$
of codimension j such that z is rationally equivalent to a homologously trivial cycle on Z; that is,
$Z\subset X$
of codimension j such that z is rationally equivalent to a homologously trivial cycle on Z; that is,
see [Reference SchreiederSch21b, Definition 7.3]. In view of [Reference SchreiederSch21b, Definition 7.2 and Lemma 7.4], we define
If the field k is finitely generated, then
![]() $A^i(X)_{\mathbb {Z}_{\ell }}=\operatorname {CH}^i(X)_{\mathbb {Z}_{\ell }}$
by [Reference SchreiederSch21b, Lemma 7.5].
$A^i(X)_{\mathbb {Z}_{\ell }}=\operatorname {CH}^i(X)_{\mathbb {Z}_{\ell }}$
by [Reference SchreiederSch21b, Lemma 7.5].
Remark 2.1. Let X be an algebraic k-scheme of dimension
![]() $d_X$
. Assume that there is a closed embedding
$d_X$
. Assume that there is a closed embedding
![]() $\iota :X\hookrightarrow Y$
into a smooth equi-dimensional algebraic k-scheme Y of dimension
$\iota :X\hookrightarrow Y$
into a smooth equi-dimensional algebraic k-scheme Y of dimension
![]() $d_Y$
. Then the Borel–Moore cohomology groups
$d_Y$
. Then the Borel–Moore cohomology groups
![]() $ H^i(X,A(n)) =H_{BM}^i(X,A(n)) $
above may be identified with ordinary cohomology groups with support as follows:
$ H^i(X,A(n)) =H_{BM}^i(X,A(n)) $
above may be identified with ordinary cohomology groups with support as follows:
where
![]() $c=d_Y-d_X$
; see also [Reference SchreiederSch22, Appendix A]. We explain the above identification in the case where
$c=d_Y-d_X$
; see also [Reference SchreiederSch22, Appendix A]. We explain the above identification in the case where
![]() $A=\mathbb {Z}_{\ell }$
; the general case is similar. To this end, let
$A=\mathbb {Z}_{\ell }$
; the general case is similar. To this end, let
![]() $\pi _X:X\to \operatorname {Spec} k$
be the structure map and note that by definition in [Reference SchreiederSch21b, (6.13)-(6.15)], we have
$\pi _X:X\to \operatorname {Spec} k$
be the structure map and note that by definition in [Reference SchreiederSch21b, (6.13)-(6.15)], we have
If
![]() $\pi _Y:Y\to \operatorname {Spec} k$
denotes the structure morphism, then
$\pi _Y:Y\to \operatorname {Spec} k$
denotes the structure morphism, then
![]() $\pi _X=\pi _Y\circ \iota $
and so
$\pi _X=\pi _Y\circ \iota $
and so
where we used that
![]() $\pi _Y^!=\pi _Y^{\ast }(d_Y)[2d_Y]$
by Poincaré duality; see, for example, [Reference SchreiederSch21b, Lemma 6.1(4)]. Hence,
$\pi _Y^!=\pi _Y^{\ast }(d_Y)[2d_Y]$
by Poincaré duality; see, for example, [Reference SchreiederSch21b, Lemma 6.1(4)]. Hence,
where
![]() $c:=d_Y-d_X$
, and where the above right-hand side denotes ordinary pro-étale cohomology with support; see [Reference SchreiederSch22, (A.6)] and [Reference Bhatt and ScholzeBS15].
$c:=d_Y-d_X$
, and where the above right-hand side denotes ordinary pro-étale cohomology with support; see [Reference SchreiederSch22, (A.6)] and [Reference Bhatt and ScholzeBS15].
3 An auxiliary cycle map
3.1 Construction of
 $\tilde {\lambda }_{tr}^i$
$\tilde {\lambda }_{tr}^i$
In this subsection, we construct a map
![]() $\tilde {\lambda }_{tr}^i$
which is closely related to the transcendental Abel–Jacobi map in [Reference SchreiederSch21b] and which will be used in Section 4.1 below to construct
$\tilde {\lambda }_{tr}^i$
which is closely related to the transcendental Abel–Jacobi map in [Reference SchreiederSch21b] and which will be used in Section 4.1 below to construct
![]() $\lambda _{X}^i$
from (1.1).
$\lambda _{X}^i$
from (1.1).
To begin, we will need the following simple lemma.
Lemma 3.1. Let X be an algebraic scheme over a field k and let
![]() $A\in \{\mathbb {Z}/\ell ^r,\mathbb {Z}_{\ell },{\mathbb Q}_{\ell },{\mathbb Q}_{\ell }/\mathbb {Z}_{\ell }\}$
, where
$A\in \{\mathbb {Z}/\ell ^r,\mathbb {Z}_{\ell },{\mathbb Q}_{\ell },{\mathbb Q}_{\ell }/\mathbb {Z}_{\ell }\}$
, where
![]() $\ell $
is a prime invertible in k. Then the natural restriction map
$\ell $
is a prime invertible in k. Then the natural restriction map
![]() $H^{2i-1}(X,A(i))\to H^{2i-1}(F_{i-1}X,A(i)) $
is injective. Using this to identify each
$H^{2i-1}(X,A(i))\to H^{2i-1}(F_{i-1}X,A(i)) $
is injective. Using this to identify each
![]() $N^jH^{2i-1}(X,A(i))$
with a subgroup of
$N^jH^{2i-1}(X,A(i))$
with a subgroup of
![]() $H^{2i-1}(F_{i-1}X,A(i))$
, we get a natural isomorphism
$H^{2i-1}(F_{i-1}X,A(i))$
, we get a natural isomorphism
 $$ \begin{align} \iota_{\ast} \left( \ker\left(\partial\circ \iota_{\ast}:\bigoplus_{x\in X^{(i-1)}}H^1( x,A(1)) \to \bigoplus_{x\in X^{(i)}}[x]A \right) \right)\simeq N^{i-1}H^{2i-1}(X,A(i)). \end{align} $$
$$ \begin{align} \iota_{\ast} \left( \ker\left(\partial\circ \iota_{\ast}:\bigoplus_{x\in X^{(i-1)}}H^1( x,A(1)) \to \bigoplus_{x\in X^{(i)}}[x]A \right) \right)\simeq N^{i-1}H^{2i-1}(X,A(i)). \end{align} $$
Proof. By (2.3),
![]() $H^{2i-1}(F_{j}X,A(i))\to H^{2i-1}(F_{j-1}X,A(i)) $
is injective for all
$H^{2i-1}(F_{j}X,A(i))\to H^{2i-1}(F_{j-1}X,A(i)) $
is injective for all
![]() $j\geq i$
, as
$j\geq i$
, as
![]() $H^{l}(x,A(n))=0$
for
$H^{l}(x,A(n))=0$
for
![]() $l<0$
and
$l<0$
and
![]() $x\in X$
. Since
$x\in X$
. Since
![]() $F_{j}X=X$
for
$F_{j}X=X$
for
![]() $j>\dim X$
, we deduce that
$j>\dim X$
, we deduce that
![]() $H^{2i-1}(X,A(i))\to H^{2i-1}(F_{i-1}X,A(i)) $
is injective, which proves the injectivity claim in the lemma.
$H^{2i-1}(X,A(i))\to H^{2i-1}(F_{i-1}X,A(i)) $
is injective, which proves the injectivity claim in the lemma.
Note next that the following sequence is exact by (2.3):
By the compatibility of the Gysin long exact sequence with proper pushforwards (see [Reference SchreiederSch21b, (P2)]), we find that
 $$ \begin{align*}\iota_{\ast} \left( \ker\left(\partial\circ \iota_{\ast}:\bigoplus_{x\in X^{(i-1)}}H^1( x,A(1)) \to \bigoplus_{x\in X^{(i)}}[x]A \right) \right)\subset H^{2i-1}(F_{i-1}X,A(i)) \end{align*} $$
$$ \begin{align*}\iota_{\ast} \left( \ker\left(\partial\circ \iota_{\ast}:\bigoplus_{x\in X^{(i-1)}}H^1( x,A(1)) \to \bigoplus_{x\in X^{(i)}}[x]A \right) \right)\subset H^{2i-1}(F_{i-1}X,A(i)) \end{align*} $$
agrees with the image of the map
![]() $N^{i-1}H^{2i-1}(X,A(i))\to H^{2i-1}(F_{i-1}X,A(i))$
. This concludes the proof of the lemma.
$N^{i-1}H^{2i-1}(X,A(i))\to H^{2i-1}(F_{i-1}X,A(i))$
. This concludes the proof of the lemma.
Let X be an algebraic k-scheme and let
![]() $\ell $
be a prime invertible in k. By [Reference SchreiederSch21b, Lemma 8.1], there is a canonical isomorphism
$\ell $
be a prime invertible in k. By [Reference SchreiederSch21b, Lemma 8.1], there is a canonical isomorphism

which we describe in what follows explicitly. To this end, note that an
![]() $\ell ^r$
-torsion class in
$\ell ^r$
-torsion class in
![]() $A^i(X)_{\mathbb {Z}_{\ell }}$
corresponds to a cycle
$A^i(X)_{\mathbb {Z}_{\ell }}$
corresponds to a cycle
![]() $[z]\in \operatorname {CH}^i(X)_{\mathbb {Z}_{\ell }}$
such that
$[z]\in \operatorname {CH}^i(X)_{\mathbb {Z}_{\ell }}$
such that
![]() $\ell ^r[z]\in N^{i-1}\operatorname {CH}^i(X)_{\mathbb {Z}_{\ell }}$
. By [Reference SchreiederSch21b, Definition 7.2 and Lemma 7.4], this means that there is a class
$\ell ^r[z]\in N^{i-1}\operatorname {CH}^i(X)_{\mathbb {Z}_{\ell }}$
. By [Reference SchreiederSch21b, Definition 7.2 and Lemma 7.4], this means that there is a class
with
![]() $\partial (\iota _{\ast }\xi )=\ell ^r \cdot z$
. It follows that the reduction
$\partial (\iota _{\ast }\xi )=\ell ^r \cdot z$
. It follows that the reduction
![]() $\bar \xi $
of
$\bar \xi $
of
![]() $\xi $
modulo
$\xi $
modulo
![]() $\ell ^r$
has trivial residues and we have
$\ell ^r$
has trivial residues and we have
![]() $\psi _r([z])=[\bar {\xi }]$
.
$\psi _r([z])=[\bar {\xi }]$
.
Since
![]() $\xi $
has trivial residues modulo
$\xi $
has trivial residues modulo
![]() $\ell ^r$
, there is a class
$\ell ^r$
, there is a class
![]() $\gamma \in H^{2i-1}(X,\mu _{\ell ^r}^{\otimes i})$
with
$\gamma \in H^{2i-1}(X,\mu _{\ell ^r}^{\otimes i})$
with
Note that
![]() $\gamma $
is uniquely determined by
$\gamma $
is uniquely determined by
![]() $\bar \xi $
because the map
$\bar \xi $
because the map
is injective by Lemma 3.1. Using this, we will, in what follows, implicitly identify
![]() $ \iota _{\ast } \bar \xi $
and
$ \iota _{\ast } \bar \xi $
and
![]() $\gamma $
with each other.
$\gamma $
with each other.
The image of
![]() $\gamma = \iota _{\ast } \bar \xi $
in
$\gamma = \iota _{\ast } \bar \xi $
in
![]() $H^{2i-1}(X,{\mathbb Q}_{\ell }/\mathbb {Z}_{\ell }(i))$
is well-defined (i.e., depends only on the class
$H^{2i-1}(X,{\mathbb Q}_{\ell }/\mathbb {Z}_{\ell }(i))$
is well-defined (i.e., depends only on the class
![]() $[z]$
) up to elements of the form
$[z]$
) up to elements of the form
![]() $\iota _{\ast } \bar \zeta $
for
$\iota _{\ast } \bar \zeta $
for

By Lemma 3.1, the subgroup of
![]() $H^{2i-1}(X,{\mathbb Q}_{\ell }/\mathbb {Z}_{\ell }(i))$
generated by classes of the form
$H^{2i-1}(X,{\mathbb Q}_{\ell }/\mathbb {Z}_{\ell }(i))$
generated by classes of the form
![]() $\iota _{\ast } \bar \zeta $
with
$\iota _{\ast } \bar \zeta $
with
![]() $\zeta $
as in (3.3) agrees with the image of
$\zeta $
as in (3.3) agrees with the image of
![]() $N^{i-1}H^{2i-1}(X,{\mathbb Q}_{\ell }(i))$
, and so we find that the class
$N^{i-1}H^{2i-1}(X,{\mathbb Q}_{\ell }(i))$
, and so we find that the class
is well-defined, giving rise to a map
(The minus sign is necessary to make our map compatible with Bloch’s map; cf. [Reference BlochBlo79, p. 112] and [Reference SchreiederSch21b, Proposition 8.3].)
3.2 Basic properties of
 $\tilde {\lambda }_{tr}^i$
$\tilde {\lambda }_{tr}^i$
Lemma 3.2. The restriction of
![]() $ \tilde {\lambda }_{tr}^i$
to the subgroup of classes
$ \tilde {\lambda }_{tr}^i$
to the subgroup of classes
![]() $[z]\in A^i(X)[\ell ^{\infty }]$
with
$[z]\in A^i(X)[\ell ^{\infty }]$
with
![]() $\operatorname {cl}_{X}^i(z)=0$
coincides with the transcendental Abel–Jacobi map
$\operatorname {cl}_{X}^i(z)=0$
coincides with the transcendental Abel–Jacobi map
![]() $\lambda _{tr}^i$
from [Reference SchreiederSch21b, §7.5].
$\lambda _{tr}^i$
from [Reference SchreiederSch21b, §7.5].
Proof. Assume that
![]() $\operatorname {cl}_{X}^i(z)=0$
. Following the construction in [Reference SchreiederSch21b, §7.5], there is a class
$\operatorname {cl}_{X}^i(z)=0$
. Following the construction in [Reference SchreiederSch21b, §7.5], there is a class
![]() $\alpha \in H^{2i-1}(F_{i-1}X,\mathbb {Z}_{\ell }(i))$
with
$\alpha \in H^{2i-1}(F_{i-1}X,\mathbb {Z}_{\ell }(i))$
with
![]() $\partial \alpha =z$
and a class
$\partial \alpha =z$
and a class
![]() $\beta \in H^{2i-1}(X,\mathbb {Z}_{\ell }(i))$
with
$\beta \in H^{2i-1}(X,\mathbb {Z}_{\ell }(i))$
with
for some
![]() $\xi \in \bigoplus _{x\in X^{(i-1)}}H^1(x,\mathbb {Z}_{\ell }(1))$
. We then think about
$\xi \in \bigoplus _{x\in X^{(i-1)}}H^1(x,\mathbb {Z}_{\ell }(1))$
. We then think about
![]() $\beta /\ell ^r$
as a class in
$\beta /\ell ^r$
as a class in
![]() $H^{2i-1}(X,{\mathbb Q}_{\ell }(i))$
and project this further to a class
$H^{2i-1}(X,{\mathbb Q}_{\ell }(i))$
and project this further to a class
![]() $[\beta /\ell ^r]\in H^{2i-1}(X,{\mathbb Q}_{\ell }/\mathbb {Z}_{\ell }(i))$
. By definition in loc. cit., this class represents
$[\beta /\ell ^r]\in H^{2i-1}(X,{\mathbb Q}_{\ell }/\mathbb {Z}_{\ell }(i))$
. By definition in loc. cit., this class represents
![]() $\lambda _{tr}^i([z])$
:
$\lambda _{tr}^i([z])$
:
 $$ \begin{align*}\lambda_{tr}^i([z])=[\beta/\ell^r] \in \frac{H^{2i-1}(X,{\mathbb Q}_{\ell}/\mathbb{Z}_{\ell}(i))}{N^{i-1}H^{2i-1}(X,{\mathbb Q}_{\ell}(i) )}. \end{align*} $$
$$ \begin{align*}\lambda_{tr}^i([z])=[\beta/\ell^r] \in \frac{H^{2i-1}(X,{\mathbb Q}_{\ell}/\mathbb{Z}_{\ell}(i))}{N^{i-1}H^{2i-1}(X,{\mathbb Q}_{\ell}(i) )}. \end{align*} $$
We aim to see that this coincides with
![]() $\tilde {\lambda }_{tr}^i([z])$
defined above. To this end, note that (3.5) implies
$\tilde {\lambda }_{tr}^i([z])$
defined above. To this end, note that (3.5) implies
![]() $\partial \iota _{\ast } \xi =\ell ^r\partial \alpha =\ell ^r\cdot z$
and so
$\partial \iota _{\ast } \xi =\ell ^r\partial \alpha =\ell ^r\cdot z$
and so
where
![]() $\bar \xi $
is the reduction modulo
$\bar \xi $
is the reduction modulo
![]() $\ell ^r$
of
$\ell ^r$
of
![]() $\xi \in \bigoplus _{x\in X^{(i-1)}}H^1(x,\mathbb {Z}_{\ell }(1))$
. By (3.5), we have
$\xi \in \bigoplus _{x\in X^{(i-1)}}H^1(x,\mathbb {Z}_{\ell }(1))$
. By (3.5), we have
![]() $\bar \beta =-\iota _{\ast } \bar \xi $
and so the claim in the lemma reduces to the simple observation that the following diagram is commutative:
$\bar \beta =-\iota _{\ast } \bar \xi $
and so the claim in the lemma reduces to the simple observation that the following diagram is commutative:

This concludes the proof of the lemma.
It is shown in [Reference SchreiederSch21b] that
![]() $\lambda _{tr}^i$
is injective for
$\lambda _{tr}^i$
is injective for
![]() $i\leq 2$
; cf. [Reference SchreiederSch21b, Theorem 9.4 and Corollary 9.5] or [Reference SchreiederSch21b, Theorem 1.8(2)]. The following result extends this to
$i\leq 2$
; cf. [Reference SchreiederSch21b, Theorem 9.4 and Corollary 9.5] or [Reference SchreiederSch21b, Theorem 1.8(2)]. The following result extends this to
![]() $\tilde {\lambda }_{tr}^i$
as follows.
$\tilde {\lambda }_{tr}^i$
as follows.
Proposition 3.3. Let X be an algebraic scheme over a finitely generated field k and let
![]() $\ell $
be a prime invertible in k. Then
$\ell $
be a prime invertible in k. Then
is injective for
![]() $i\leq 2$
.
$i\leq 2$
.
Proof. Let
![]() $[z_{0}]\in \ker (\tilde {\lambda }_{tr}^i)$
. We first show that
$[z_{0}]\in \ker (\tilde {\lambda }_{tr}^i)$
. We first show that
![]() $[z_0]$
lies in the kernel of the cycle class map. By (3.2), we find that there is a class
$[z_0]$
lies in the kernel of the cycle class map. By (3.2), we find that there is a class
![]() $\xi \in \bigoplus _{x\in X^{(i-1)}}H^{1}(x,\mathbb {Z}_{\ell }(1))$
such that
$\xi \in \bigoplus _{x\in X^{(i-1)}}H^{1}(x,\mathbb {Z}_{\ell }(1))$
such that
![]() $\ell ^{r}z_{0}=\partial (\iota _{\ast }\xi )$
and such that
$\ell ^{r}z_{0}=\partial (\iota _{\ast }\xi )$
and such that
![]() $\tilde {\lambda }_{tr}^i([z_{0}])=-[\iota _{\ast }\overline {\xi }]=0$
. Especially, we may assume
$\tilde {\lambda }_{tr}^i([z_{0}])=-[\iota _{\ast }\overline {\xi }]=0$
. Especially, we may assume
and so by (3.1), we obtain
![]() $\iota _{\ast }\overline {\xi }=\iota _{\ast }\overline {\zeta }$
for some
$\iota _{\ast }\overline {\xi }=\iota _{\ast }\overline {\zeta }$
for some

Exactness of the Bockstein sequence then gives
![]() $\iota _{\ast }\xi =\iota _{\ast }\zeta +\ell ^{r}\alpha $
for some
$\iota _{\ast }\xi =\iota _{\ast }\zeta +\ell ^{r}\alpha $
for some
![]() $\alpha \in H^{2i-1}(F_{i-1}X,\mathbb {Z}_{\ell }(i))$
. Since
$\alpha \in H^{2i-1}(F_{i-1}X,\mathbb {Z}_{\ell }(i))$
. Since
![]() $\partial \iota _{\ast } \zeta =0$
, we get that
$\partial \iota _{\ast } \zeta =0$
, we get that
![]() $z_{0}=\partial \alpha $
and so
$z_{0}=\partial \alpha $
and so
![]() $\operatorname {cl}^{i}_{X}([z_{0}])=\iota _{\ast }[z_0]=0$
by exactness of (2.3). Hence,
$\operatorname {cl}^{i}_{X}([z_{0}])=\iota _{\ast }[z_0]=0$
by exactness of (2.3). Hence,
![]() $z_0$
has trivial cycle class on X, as claimed. By Lemma 3.2, it then follows that
$z_0$
has trivial cycle class on X, as claimed. By Lemma 3.2, it then follows that
![]() $z_0$
lies in the kernel of the transcendental Abel–Jacobi map from [Reference SchreiederSch21b]:
$z_0$
lies in the kernel of the transcendental Abel–Jacobi map from [Reference SchreiederSch21b]:
![]() $\lambda _{tr}^i([z_0])=0$
. In other words, we have proved that
$\lambda _{tr}^i([z_0])=0$
. In other words, we have proved that
![]() $\ker (\tilde {\lambda }_{tr}^i)=\ker ( \lambda _{tr}^i)$
(but note that the two maps are defined on different domains:
$\ker (\tilde {\lambda }_{tr}^i)=\ker ( \lambda _{tr}^i)$
(but note that the two maps are defined on different domains:
![]() $\lambda _{tr}^i$
is defined on homologically trivial
$\lambda _{tr}^i$
is defined on homologically trivial
![]() $\ell ^{\infty }$
-torsion cycles, while
$\ell ^{\infty }$
-torsion cycles, while
![]() $\tilde {\lambda }_{tr}^i$
is defined on arbitrary
$\tilde {\lambda }_{tr}^i$
is defined on arbitrary
![]() $\ell ^{\infty }$
-torsion cycles). Since
$\ell ^{\infty }$
-torsion cycles). Since
![]() $\ker (\tilde {\lambda }_{tr}^i)=\ker ( \lambda _{tr}^i)$
, [Reference SchreiederSch21b, Theorem 1.8(2)] yields
$\ker (\tilde {\lambda }_{tr}^i)=\ker ( \lambda _{tr}^i)$
, [Reference SchreiederSch21b, Theorem 1.8(2)] yields
where
![]() $H^i_{j,nr}(X,A(n))=\operatorname {im}(H^i(F_{j+1}X,A(n))\to H^i(F_{j}X,A(n)))$
denotes the j-th refined unramified cohomology; cf. [Reference SchreiederSch21b]. Since
$H^i_{j,nr}(X,A(n))=\operatorname {im}(H^i(F_{j+1}X,A(n))\to H^i(F_{j}X,A(n)))$
denotes the j-th refined unramified cohomology; cf. [Reference SchreiederSch21b]. Since
![]() $F_jX=\emptyset $
for
$F_jX=\emptyset $
for
![]() $j<0$
, we get that
$j<0$
, we get that
![]() $H^i_{j,nr}(X,A(n))=0$
for
$H^i_{j,nr}(X,A(n))=0$
for
![]() $j<0$
and so
$j<0$
and so
![]() $ \ker (\tilde {\lambda }_{tr}^i)=0 $
for
$ \ker (\tilde {\lambda }_{tr}^i)=0 $
for
![]() $i<3$
. This proves the proposition.
$i<3$
. This proves the proposition.
The following result is motivated by the description of the image of
![]() $\lambda _{tr}^i$
in [Reference SchreiederSch21b, Proposition 7.16].
$\lambda _{tr}^i$
in [Reference SchreiederSch21b, Proposition 7.16].
Proposition 3.4. Let X be an algebraic k-scheme and let
![]() $\ell $
be a prime invertible in k. Then the map
$\ell $
be a prime invertible in k. Then the map
![]() $\tilde {\lambda }^{i}_{tr}$
from (3.4) satisfies
$\tilde {\lambda }^{i}_{tr}$
from (3.4) satisfies
 $$ \begin{align*}\operatorname{im}(\tilde{\lambda}^{i}_{tr})=\frac{N^{i-1}H^{2i-1}(X,{\mathbb Q}_{\ell}/\mathbb{Z}_{\ell}(i))}{N^{i-1}H^{2i-1}(X,{\mathbb Q}_{\ell}(i))}.\end{align*} $$
$$ \begin{align*}\operatorname{im}(\tilde{\lambda}^{i}_{tr})=\frac{N^{i-1}H^{2i-1}(X,{\mathbb Q}_{\ell}/\mathbb{Z}_{\ell}(i))}{N^{i-1}H^{2i-1}(X,{\mathbb Q}_{\ell}(i))}.\end{align*} $$
Proof. Recall from Section 3.1 that
![]() $\tilde {\lambda }^{i}_{tr}$
was constructed as the direct limit of maps
$\tilde {\lambda }^{i}_{tr}$
was constructed as the direct limit of maps

over all positive integers
![]() $r\geq 1$
. As taking direct limits is an exact functor, it suffices to show that
$r\geq 1$
. As taking direct limits is an exact functor, it suffices to show that
 $$ \begin{align} \operatorname{im}(\tilde{\lambda}^{i}_{r})=\frac{N^{i-1}H^{2i-1}(X,\mu^{\otimes i}_{\ell^{r}})}{N^{i-1}H^{2i-1}(X,\mathbb{Z}_{\ell}(i))}\ \ \ \text{for all}\ r\geq 1. \end{align} $$
$$ \begin{align} \operatorname{im}(\tilde{\lambda}^{i}_{r})=\frac{N^{i-1}H^{2i-1}(X,\mu^{\otimes i}_{\ell^{r}})}{N^{i-1}H^{2i-1}(X,\mathbb{Z}_{\ell}(i))}\ \ \ \text{for all}\ r\geq 1. \end{align} $$
Let
![]() $[z_{0}]\in A^{i}(X)[\ell ^{r}]$
. Then by (3.2) and the construction in Section 3.1, there is a class
$[z_{0}]\in A^{i}(X)[\ell ^{r}]$
. Then by (3.2) and the construction in Section 3.1, there is a class
such that
![]() $\partial (\iota _{\ast }\xi )=\ell ^{r}z_{0}$
and such that
$\partial (\iota _{\ast }\xi )=\ell ^{r}z_{0}$
and such that
![]() $\tilde {\lambda }^{i}_{r}([z_{0}])=-[\iota _{\ast }\overline {\xi }]$
. Since the following sequence
$\tilde {\lambda }^{i}_{r}([z_{0}])=-[\iota _{\ast }\overline {\xi }]$
. Since the following sequence
is exact by (2.3), we find
![]() $\iota _{\ast }\overline {\xi }\in N^{i-1}H^{2i-1}(X,\mu ^{\otimes i}_{\ell ^{r}})$
. This proves the inclusion “
$\iota _{\ast }\overline {\xi }\in N^{i-1}H^{2i-1}(X,\mu ^{\otimes i}_{\ell ^{r}})$
. This proves the inclusion “
![]() $\subseteq $
” for (3.6).
$\subseteq $
” for (3.6).
However, if
![]() $\beta \in N^{i-1}H^{2i-1}(X,\mu ^{\otimes i}_{\ell ^{r}})$
then, by (3.1), we can pick
$\beta \in N^{i-1}H^{2i-1}(X,\mu ^{\otimes i}_{\ell ^{r}})$
then, by (3.1), we can pick

such that
![]() $\iota _{\ast }\overline {\xi }=\beta $
. Hilbert 90 implies that
$\iota _{\ast }\overline {\xi }=\beta $
. Hilbert 90 implies that
![]() $H^1(x,\mathbb {Z}_{\ell }(1))\to H^{1}(x,\mu ^{\otimes i}_{\ell ^{r}})$
is surjective for all
$H^1(x,\mathbb {Z}_{\ell }(1))\to H^{1}(x,\mu ^{\otimes i}_{\ell ^{r}})$
is surjective for all
![]() $x\in X$
; see [Reference SchreiederSch21b, (P6) in Definition 4.4 and Proposition 6.6]. Hence, there is a class
$x\in X$
; see [Reference SchreiederSch21b, (P6) in Definition 4.4 and Proposition 6.6]. Hence, there is a class
![]() $\xi \in \bigoplus _{x\in X^{(i-1)}} H^{1}(x,\mathbb {Z}_{\ell }(1))$
whose reduction modulo
$\xi \in \bigoplus _{x\in X^{(i-1)}} H^{1}(x,\mathbb {Z}_{\ell }(1))$
whose reduction modulo
![]() $\ell ^{r}$
is
$\ell ^{r}$
is
![]() $\overline {\xi }\in \bigoplus _{x\in X^{(i-1)}}H^{1}(x,\mu ^{\otimes i}_{\ell ^{r}})$
. In particular,
$\overline {\xi }\in \bigoplus _{x\in X^{(i-1)}}H^{1}(x,\mu ^{\otimes i}_{\ell ^{r}})$
. In particular,
![]() $0=\partial \beta =\partial (\iota _{\ast }\overline {\xi })$
yields
$0=\partial \beta =\partial (\iota _{\ast }\overline {\xi })$
yields
![]() $\partial (\iota _{\ast }\xi )=\ell ^{r}z_{0}$
for some
$\partial (\iota _{\ast }\xi )=\ell ^{r}z_{0}$
for some
![]() $z_{0}\in \bigoplus _{x\in X^{(i)}}[x]\mathbb {Z}_{\ell }$
and thus,
$z_{0}\in \bigoplus _{x\in X^{(i)}}[x]\mathbb {Z}_{\ell }$
and thus,
![]() $\tilde {\lambda }^{i}_{r}(-[z_{0}])=[\iota _{\ast }\overline {\xi }]=[\beta ]$
. This finishes the proof of the proposition.
$\tilde {\lambda }^{i}_{r}(-[z_{0}])=[\iota _{\ast }\overline {\xi }]=[\beta ]$
. This finishes the proof of the proposition.
By Lemma 3.2,
![]() $\tilde {\lambda }^i_{tr}$
and
$\tilde {\lambda }^i_{tr}$
and
![]() $\lambda _{tr}^i$
agree on
$\lambda _{tr}^i$
agree on
![]() $\ell $
-power torsion classes with trivial cycle class. Moreover, in the proof of Proposition 3.3, we showed that
$\ell $
-power torsion classes with trivial cycle class. Moreover, in the proof of Proposition 3.3, we showed that
![]() $\tilde {\lambda }^i_{tr}$
and
$\tilde {\lambda }^i_{tr}$
and
![]() $\lambda _{tr}^i$
have the same kernel. The following lemma shows more generally that
$\lambda _{tr}^i$
have the same kernel. The following lemma shows more generally that
![]() $\tilde {\lambda }^i_{tr}$
factors through the cycle class map.
$\tilde {\lambda }^i_{tr}$
factors through the cycle class map.
Lemma 3.5. Let X be an algebraic k-scheme which admits a closed embedding into a smooth equi-dimensional algebraic k-scheme (e.g., X is quasi-projective). Then the composition of
![]() $ \tilde {\lambda }_{tr}^i$
from (3.4) with the negative of the Bockstein map
$ \tilde {\lambda }_{tr}^i$
from (3.4) with the negative of the Bockstein map
agrees with the cycle class map
.
Proof. We follow the proof of [Reference Colliot- Thélène, Sansuc and SouléCTSS83, Proposition 1]. By topological invariance of the pro-étale site, we may up to replacing k by its perfect closure assume that k is perfect (cf. [Reference Bhatt and ScholzeBS15, Lemma 5.4.2]).
Let
![]() $[z_{0}]\in A^{i}(X)[\ell ^{\infty }]$
. Then there is a closed subset
$[z_{0}]\in A^{i}(X)[\ell ^{\infty }]$
. Then there is a closed subset
![]() $W\subset X$
of pure codimension
$W\subset X$
of pure codimension
![]() $i-1$
and a class
$i-1$
and a class
![]() $\xi \in H^{1}(F_{0}W,\mathbb {Z}_{\ell }(1))$
such that
$\xi \in H^{1}(F_{0}W,\mathbb {Z}_{\ell }(1))$
such that
![]() $\partial \xi =\ell ^{r}z_{0}$
for some integer
$\partial \xi =\ell ^{r}z_{0}$
for some integer
![]() $r\geq 0$
. In particular,
$r\geq 0$
. In particular,
![]() $\tilde {\lambda }^{i}_{tr}([z_{0}])=-[\iota _{\ast }\overline {\xi }],$
where
$\tilde {\lambda }^{i}_{tr}([z_{0}])=-[\iota _{\ast }\overline {\xi }],$
where
![]() $\overline {\xi }\in H^{1}(W,\mu _{\ell ^{r}})$
is the reduction of
$\overline {\xi }\in H^{1}(W,\mu _{\ell ^{r}})$
is the reduction of
![]() $\xi $
modulo
$\xi $
modulo
![]() $\ell ^{r}$
and
$\ell ^{r}$
and
![]() $\iota \colon W\hookrightarrow X$
the obvious closed embedding. Since the Bockstein map is compatible with proper pushforwards (cf. [Reference SchreiederSch21b, (P5) in Definition 4.4 and Proposition 6.6]), the lemma follows if we can show that
$\iota \colon W\hookrightarrow X$
the obvious closed embedding. Since the Bockstein map is compatible with proper pushforwards (cf. [Reference SchreiederSch21b, (P5) in Definition 4.4 and Proposition 6.6]), the lemma follows if we can show that
The above statement does not depend on the ambient space X. Since X can be embedded into a smooth equi-dimensional k-scheme by assumption, we may thus from now on assume without loss of generality that X is smooth and equi-dimensional.
In what follows, for a closed subset
![]() $Z\subset X$
and
$Z\subset X$
and
![]() $A\in \{\mathbb {Z}/\ell ^r,\mathbb {Z}_{\ell },{\mathbb Q}_{\ell },{\mathbb Q}_{\ell }/\mathbb {Z}_{\ell }\}$
, the group
$A\in \{\mathbb {Z}/\ell ^r,\mathbb {Z}_{\ell },{\mathbb Q}_{\ell },{\mathbb Q}_{\ell }/\mathbb {Z}_{\ell }\}$
, the group
![]() $H^{i}_{Z}(X,A(n))$
stands for ordinary pro-étale cohomology with support; if
$H^{i}_{Z}(X,A(n))$
stands for ordinary pro-étale cohomology with support; if
![]() $c=\dim X-\dim Z$
, then
$c=\dim X-\dim Z$
, then
by Remark 2.1. The equation (3.7) then translates into the claim that
We aim to describe the class
![]() $\alpha _{2}=\operatorname {cl}_W^1(z_0)$
. Since
$\alpha _{2}=\operatorname {cl}_W^1(z_0)$
. Since
![]() $\xi \in H^{1}(F_{0}W,\mathbb {Z}_{\ell }(1)),$
we may pick a closed subset
$\xi \in H^{1}(F_{0}W,\mathbb {Z}_{\ell }(1)),$
we may pick a closed subset
![]() $W'\subset W$
of pure codimension one such that
$W'\subset W$
of pure codimension one such that
![]() $\xi $
admits a lift to
$\xi $
admits a lift to
![]() $H^{1}(W\setminus W',\mathbb {Z}_{\ell }(1))=H^{2i-1}_{W\setminus W'}(X\setminus W',\mathbb {Z}_{\ell }(i))$
. Then
$H^{1}(W\setminus W',\mathbb {Z}_{\ell }(1))=H^{2i-1}_{W\setminus W'}(X\setminus W',\mathbb {Z}_{\ell }(i))$
. Then
![]() $\partial \xi =\ell ^{r}z_{0}\in H^{2i}_{W'}(X,\mathbb {Z}_{\ell }(i))=\bigoplus _{x\in W^{\prime (0)}}[x]\mathbb {Z}_{\ell }$
, and
$\partial \xi =\ell ^{r}z_{0}\in H^{2i}_{W'}(X,\mathbb {Z}_{\ell }(i))=\bigoplus _{x\in W^{\prime (0)}}[x]\mathbb {Z}_{\ell }$
, and
![]() $\alpha _{2}$
is the image of
$\alpha _{2}$
is the image of
![]() $z_{0}$
in
$z_{0}$
in
![]() $H^{2i}_{W}(X,\mathbb {Z}_{\ell }(i))$
.
$H^{2i}_{W}(X,\mathbb {Z}_{\ell }(i))$
.
In order to show
![]() $\alpha _1=\alpha _2$
, we take a Cartan-Eilenberg injective resolution
$\alpha _1=\alpha _2$
, we take a Cartan-Eilenberg injective resolution
for the following short exact sequence of sheaves on
![]() $X_{\text {pro}\acute{\mathrm{e}}\text{t}}$
$X_{\text {pro}\acute{\mathrm{e}}\text{t}}$
and we consider the following commutative diagram of complexes of abelian groups.

As higher cohomology (with support) of injective objects vanishes, we find that both the rows and columns of the above diagram are exact. We shall denote the differential of these complexes by the letter d.
Let
![]() $\eta \in H^{0}_{W}(X,K^{2i-1})$
be a lift of
$\eta \in H^{0}_{W}(X,K^{2i-1})$
be a lift of
![]() $\overline {\xi }\in H^{2i-1}_{W}(X,\mu ^{\otimes i}_{\ell ^{r}})$
. We claim that there exists a lift
$\overline {\xi }\in H^{2i-1}_{W}(X,\mu ^{\otimes i}_{\ell ^{r}})$
. We claim that there exists a lift
![]() $\omega \in H^{0}_{W}(X,J^{2i-1})$
of
$\omega \in H^{0}_{W}(X,J^{2i-1})$
of
![]() $\eta $
such that the image
$\eta $
such that the image
![]() $\omega '$
of
$\omega '$
of
![]() $\omega $
in
$\omega $
in
![]() $H^{0}_{W\setminus W'}(X\setminus W',J^{2i-1})$
satisfies
$H^{0}_{W\setminus W'}(X\setminus W',J^{2i-1})$
satisfies
![]() $d\omega '=0$
. Indeed, let
$d\omega '=0$
. Indeed, let
![]() $\eta '$
denote the image of
$\eta '$
denote the image of
![]() $\eta $
in
$\eta $
in
![]() $H^{0}_{W\setminus W'}(X\setminus W',K^{2i-1})$
. Since
$H^{0}_{W\setminus W'}(X\setminus W',K^{2i-1})$
. Since
![]() $\overline {\xi }$
is the reduction modulo
$\overline {\xi }$
is the reduction modulo
![]() $\ell ^{r}$
of a class
$\ell ^{r}$
of a class
![]() $\xi \in H^{2i-1}_{W\setminus W'}(X\setminus W',\mathbb {Z}_{\ell }(i))$
and the reduction map
$\xi \in H^{2i-1}_{W\setminus W'}(X\setminus W',\mathbb {Z}_{\ell }(i))$
and the reduction map
is induced by
we can find a class
![]() $\tau ^{\prime }_{1}\in H^{0}_{W\setminus W'}(X\setminus W',J^{2i-1})$
with
$\tau ^{\prime }_{1}\in H^{0}_{W\setminus W'}(X\setminus W',J^{2i-1})$
with
![]() $d\tau ^{\prime }_{1}=0$
such that
$d\tau ^{\prime }_{1}=0$
such that
![]() $p(\tau ^{\prime }_{1})=\eta '+d(\kappa ')$
for some
$p(\tau ^{\prime }_{1})=\eta '+d(\kappa ')$
for some
![]() $\kappa \in H^{0}_{W}(X,K^{2i-2})$
with image
$\kappa \in H^{0}_{W}(X,K^{2i-2})$
with image
![]() $\kappa '\in H^{0}_{W\setminus W'}(X\setminus W',K^{2i-2})$
. Replacing
$\kappa '\in H^{0}_{W\setminus W'}(X\setminus W',K^{2i-2})$
. Replacing
![]() $\eta $
with
$\eta $
with
![]() $\eta +d\kappa ,$
we may assume
$\eta +d\kappa ,$
we may assume
![]() $p(\tau ^{\prime }_{1})=\eta '$
. Let
$p(\tau ^{\prime }_{1})=\eta '$
. Let
![]() $\tau _{1}\in H^{0}_{W}(X,J^{2i-1})$
be a lift of
$\tau _{1}\in H^{0}_{W}(X,J^{2i-1})$
be a lift of
![]() $\tau _{1} '$
. Exactness of the above diagram yields
$\tau _{1} '$
. Exactness of the above diagram yields
![]() $\eta -p(\tau _{1})=p(\iota _{\ast }\tau _{2})$
for some
$\eta -p(\tau _{1})=p(\iota _{\ast }\tau _{2})$
for some
![]() $\tau _{2}\in H^{0}_{W'}(X,J^{2i-1})$
and we take
$\tau _{2}\in H^{0}_{W'}(X,J^{2i-1})$
and we take
![]() $\omega :=\tau _{1}+\iota _{\ast } \tau _{2}$
, where
$\omega :=\tau _{1}+\iota _{\ast } \tau _{2}$
, where
![]() $\iota _{\ast } \tau _2$
denotes the image of
$\iota _{\ast } \tau _2$
denotes the image of
![]() $\tau _2$
in
$\tau _2$
in
![]() $H^{0}_{W}(X,J^{2i-1})$
. Then
$H^{0}_{W}(X,J^{2i-1})$
. Then
![]() $p(\omega )=\eta $
and the image
$p(\omega )=\eta $
and the image
![]() $\omega '$
of
$\omega '$
of
![]() $\omega $
in
$\omega $
in
![]() $H^{0}_{W\setminus W'}(X\setminus W',J^{2i-1})$
satisfies
$H^{0}_{W\setminus W'}(X\setminus W',J^{2i-1})$
satisfies
![]() $d\omega '=d\tau _1'=0$
, as claimed above.
$d\omega '=d\tau _1'=0$
, as claimed above.
Using that the Bockstein map
![]() is the coboundary map of the middle vertical short exact sequence in the diagram above, we deduce
is the coboundary map of the middle vertical short exact sequence in the diagram above, we deduce
![]() $\alpha _{1}=[d\omega ]$
, where we regard
$\alpha _{1}=[d\omega ]$
, where we regard
![]() $d\omega $
as an element in
$d\omega $
as an element in
![]() $H^{0}_{W}(X,I^{2i})$
.
$H^{0}_{W}(X,I^{2i})$
.
Finally, we recall the construction of the class
![]() $\alpha _{2},$
so as to verify our claim (i.e.,
$\alpha _{2},$
so as to verify our claim (i.e.,
![]() $\alpha _{1}=\alpha _{2}$
). Indeed, the class
$\alpha _{1}=\alpha _{2}$
). Indeed, the class
![]() $\omega '$
corresponds to a lift
$\omega '$
corresponds to a lift
![]() $\xi $
of
$\xi $
of
![]() $\overline {\xi }\in H^{2i-1}_{W\setminus W'}(X\setminus W',\mu ^{\otimes i}_{\ell ^{r}})$
in
$\overline {\xi }\in H^{2i-1}_{W\setminus W'}(X\setminus W',\mu ^{\otimes i}_{\ell ^{r}})$
in
![]() $ H^{2i-1}_{W\setminus W'}(X\setminus W',\mathbb {Z}_{\ell }(i))$
, and an easy diagram chase gives that
$ H^{2i-1}_{W\setminus W'}(X\setminus W',\mathbb {Z}_{\ell }(i))$
, and an easy diagram chase gives that
![]() $\partial \xi \in H^{2i}_{W'}(X,\mathbb {Z}_{\ell }(i))$
is the cohomology class of
$\partial \xi \in H^{2i}_{W'}(X,\mathbb {Z}_{\ell }(i))$
is the cohomology class of
![]() $d\omega \in H^{0}_{W'}(X,J^{2i})$
. Since
$d\omega \in H^{0}_{W'}(X,J^{2i})$
. Since
![]() $p(d\omega )=d\eta =0$
, we deduce
$p(d\omega )=d\eta =0$
, we deduce
![]() $d\omega \in H^{0}_{W'}(X,I^{2i})$
and the corresponding class in
$d\omega \in H^{0}_{W'}(X,I^{2i})$
and the corresponding class in
![]() $H^{2i}_{W'}(X,\mathbb {Z}_{\ell }(i))$
agrees with
$H^{2i}_{W'}(X,\mathbb {Z}_{\ell }(i))$
agrees with
![]() $z_{0}$
. Hence, the image of
$z_{0}$
. Hence, the image of
![]() $z_{0}$
in
$z_{0}$
in
![]() $H^{2i}_{W}(X,\mathbb {Z}_{\ell }(i))$
is the cohomology class of
$H^{2i}_{W}(X,\mathbb {Z}_{\ell }(i))$
is the cohomology class of
![]() $d\omega \in H^{0}_{W}(X,I^{2i})$
, showing
$d\omega \in H^{0}_{W}(X,I^{2i})$
, showing
![]() $\alpha _{1}=\alpha _{2},$
as we want. This concludes the proof of the lemma.
$\alpha _{1}=\alpha _{2},$
as we want. This concludes the proof of the lemma.
Lemma 3.6. Let
![]() $X_j$
for
$X_j$
for
![]() $j=1,2$
be smooth projective k-varieties and let
$j=1,2$
be smooth projective k-varieties and let
![]() $\ell $
be a prime invertible in k. Let
$\ell $
be a prime invertible in k. Let
![]() $z_j\in \operatorname {CH}^{i_j}(X_j)$
be classes such that
$z_j\in \operatorname {CH}^{i_j}(X_j)$
be classes such that
![]() $z_2$
is
$z_2$
is
![]() $\ell ^r$
-torsion. Then
$\ell ^r$
-torsion. Then
where
![]() $\overline { \operatorname {cl}_{X_1}^{i_1}(z_1)}\in H^{2i_1}(X_1,{\mathbb Q}_{\ell }/\mathbb {Z}_{\ell }(i_1))$
denotes the reduction modulo
$\overline { \operatorname {cl}_{X_1}^{i_1}(z_1)}\in H^{2i_1}(X_1,{\mathbb Q}_{\ell }/\mathbb {Z}_{\ell }(i_1))$
denotes the reduction modulo
![]() $\ell ^r$
of
$\ell ^r$
of
![]() $ \operatorname {cl}_{X_1}^{i_1}(z_1)$
, that is, the image of
$ \operatorname {cl}_{X_1}^{i_1}(z_1)$
, that is, the image of
![]() $ \operatorname {cl}_{X_1}^{i_1}(z_1)$
via the composition
$ \operatorname {cl}_{X_1}^{i_1}(z_1)$
via the composition
Proof. By topological invariance of the étale, resp. pro-étale site, we may up to replacing k by its perfect closure assume that k is perfect (cf. [Reference Bhatt and ScholzeBS15, Lemma 5.4.2]).
We will frequently cite properties of cohomology with support from [Reference SchreiederSch22, Appendix A], which applies to our setting by Remark 2.1 above.
There is a closed subset
![]() $W_2\subset X$
of pure codimension
$W_2\subset X$
of pure codimension
![]() $i_2-1$
and a class
$i_2-1$
and a class
![]() $\xi \in H^1(F_0W_2,\mathbb {Z}_{\ell }(1))$
such that
$\xi \in H^1(F_0W_2,\mathbb {Z}_{\ell }(1))$
such that
![]() $\partial \xi =\ell ^r z_2$
. We then have
$\partial \xi =\ell ^r z_2$
. We then have
![]() $\tilde {\lambda }_{tr}^{i_2}([z_2]) = -[(\iota _2)_{\ast } \overline {\xi }]$
, where
$\tilde {\lambda }_{tr}^{i_2}([z_2]) = -[(\iota _2)_{\ast } \overline {\xi }]$
, where
![]() $\overline \xi $
denotes the reduction of
$\overline \xi $
denotes the reduction of
![]() $\xi $
modulo
$\xi $
modulo
![]() $\ell ^r$
and
$\ell ^r$
and
![]() $(\iota _2)_{\ast }$
denotes the pushforward induced by the closed embedding
$(\iota _2)_{\ast }$
denotes the pushforward induced by the closed embedding
![]() $\iota _2:W_2\hookrightarrow X_2$
. If
$\iota _2:W_2\hookrightarrow X_2$
. If
![]() $\iota _1:W_1\hookrightarrow X_1$
denotes the inclusion of the support of
$\iota _1:W_1\hookrightarrow X_1$
denotes the inclusion of the support of
![]() $z_1$
, then
$z_1$
, then
![]() $c:=\operatorname {cl}_{W_1}^0(z_{1})\in H^0(W_1,\mathbb {Z}_{\ell }(0))=H^0(F_{0}W_1,\mathbb {Z}_{\ell }(0))$
satisfies
$c:=\operatorname {cl}_{W_1}^0(z_{1})\in H^0(W_1,\mathbb {Z}_{\ell }(0))=H^0(F_{0}W_1,\mathbb {Z}_{\ell }(0))$
satisfies
![]() $\operatorname {cl}_{X_1}^{i_1}([z_1])=(\iota _1)_{\ast } c$
. We may then consider the class
$\operatorname {cl}_{X_1}^{i_1}([z_1])=(\iota _1)_{\ast } c$
. We may then consider the class
where
![]() $p_i^{\ast }$
denotes the pullback induced by the projection map
$p_i^{\ast }$
denotes the pullback induced by the projection map
![]() $p_i:W_1\times W_2\to W_i$
. Note that we use here the reduction step that k is perfect as it implies that for each i,
$p_i:W_1\times W_2\to W_i$
. Note that we use here the reduction step that k is perfect as it implies that for each i,
![]() $W_i$
is generically smooth and equi-dimensional, in which case Borel–Moore cohomology agrees with ordinary cohomology. In particular, the cup product used above exists.
$W_i$
is generically smooth and equi-dimensional, in which case Borel–Moore cohomology agrees with ordinary cohomology. In particular, the cup product used above exists.
The residue of the above class is given by
cf. [Reference Schreieder and FarkasSch21a, Lemma 2.4]. Hence,
In particular, the lemma follows once we have proven the following claim:
where
![]() $\operatorname {pr}_i^{\ast }$
denotes the pullback induced by the projection
$\operatorname {pr}_i^{\ast }$
denotes the pullback induced by the projection
![]() $\operatorname {pr}_i:X_1\times X_2\to X_i$
. The second equality in (3.9) is clear and so it suffices to prove the first. By linearity, it suffices to prove this in the case where
$\operatorname {pr}_i:X_1\times X_2\to X_i$
. The second equality in (3.9) is clear and so it suffices to prove the first. By linearity, it suffices to prove this in the case where
![]() $W_1$
is irreducible and
$W_1$
is irreducible and
![]() $c=1\cdot [W_1]\in H^0(W_1,\mathbb {Z}_{\ell }(0))$
is the fundamental class. It then suffices to prove
$c=1\cdot [W_1]\in H^0(W_1,\mathbb {Z}_{\ell }(0))$
is the fundamental class. It then suffices to prove
We consider the closed embeddings
Note that
![]() $\iota _1\times \iota _2=g\circ f$
. Let further
$\iota _1\times \iota _2=g\circ f$
. Let further
![]() $q_1: X_1\times W_2 \to X_1$
and
$q_1: X_1\times W_2 \to X_1$
and
![]() $q_2:X_1\times W_2\to W_2$
denote the projections. Then
$q_2:X_1\times W_2\to W_2$
denote the projections. Then
![]() $p_2=q_2\circ f$
and so
$p_2=q_2\circ f$
and so
By the projection formula (see, for example, [Reference SchreiederSch22, Lemma A.19]), applied to f, we thus get
Note that in the above equation,
Hence,
Applying the projection formula with respect to g thus yields
To prove (3.10), it thus suffices to show that
The first identity follows directly by the compatibility of pullbacks in cohomology and Chow groups via the cycle class map (see, for example, [Reference SchreiederSch22, Lemma A.21]). The second identity follows from the compatibility of pullbacks and pushforwards as outlined, for example, in [Reference SchreiederSch22, Lemma A.12(2)], applied to the commutative diagram

where
![]() $Z_2\subset W_2$
is a closed subset that is nowhere dense and which contains the singular locus of
$Z_2\subset W_2$
is a closed subset that is nowhere dense and which contains the singular locus of
![]() $W_2$
. This concludes the proof of the lemma.
$W_2$
. This concludes the proof of the lemma.
Corollary 3.7. Let
![]() $X_j$
for
$X_j$
for
![]() $j=1,2$
be smooth projective k-varieties and let
$j=1,2$
be smooth projective k-varieties and let
![]() $\ell $
be a prime invertible in k. Let
$\ell $
be a prime invertible in k. Let
![]() $z_j\in \operatorname {CH}^{i_j}(X_j)$
be classes such that
$z_j\in \operatorname {CH}^{i_j}(X_j)$
be classes such that
![]() $z_2$
is
$z_2$
is
![]() $\ell ^r$
-torsion for some positive integer r. Assume that
$\ell ^r$
-torsion for some positive integer r. Assume that
![]() $\operatorname {cl}^{i_1}_{X_1}(z_1)$
is zero modulo
$\operatorname {cl}^{i_1}_{X_1}(z_1)$
is zero modulo
![]() $\ell ^r$
. Then the
$\ell ^r$
. Then the
![]() $\ell ^r$
-torsion cycle
$\ell ^r$
-torsion cycle
lies in the kernel of
![]() $\tilde {\lambda }_{tr}^{i_1+i_2}$
.
$\tilde {\lambda }_{tr}^{i_1+i_2}$
.
Proof. This is an immediate consequence of Lemma 3.6.
4 Passing to the limit over finitely generated subfields
4.1 Construction of
 $\lambda _{X}^i$
$\lambda _{X}^i$
Let X be an algebraic scheme over a field k and let
![]() $k_0\subset k$
be a finitely generated subfield such that there is a variety
$k_0\subset k$
be a finitely generated subfield such that there is a variety
![]() $X_0$
over
$X_0$
over
![]() $k_0$
with
$k_0$
with
![]() $X=X_0\times _{k_0} k$
. For any finitely generated subfield
$X=X_0\times _{k_0} k$
. For any finitely generated subfield
![]() $k'\subset k$
with
$k'\subset k$
with
![]() $k_0\subset k'$
, we consider
$k_0\subset k'$
, we consider
![]() $X_{k'}:=X_0\times _{k_0}k'$
. We then have
$X_{k'}:=X_0\times _{k_0}k'$
. We then have
where the limit runs through all finitely generated subfields
![]() $k'\subset k$
with
$k'\subset k$
with
![]() $k_0\subset k'$
and where we used
$k_0\subset k'$
and where we used
![]() $\operatorname {CH}^i(X_{k'})_{\ \mathbb {Z}_{\ell }}=A^i(X_{k'})_{\ \mathbb {Z}_{\ell }}$
for
$\operatorname {CH}^i(X_{k'})_{\ \mathbb {Z}_{\ell }}=A^i(X_{k'})_{\ \mathbb {Z}_{\ell }}$
for
![]() $k'$
finitely generated; cf. [Reference SchreiederSch21b, Lemma 7.5]. Using this, we define
$k'$
finitely generated; cf. [Reference SchreiederSch21b, Lemma 7.5]. Using this, we define
![]() $\lambda _{X}^i$
as the direct limit of
$\lambda _{X}^i$
as the direct limit of
![]() $\tilde {\lambda }_{tr}^i$
(see Section 3.1), applied to
$\tilde {\lambda }_{tr}^i$
(see Section 3.1), applied to
![]() $X_{k'}$
for all finitely generated fields
$X_{k'}$
for all finitely generated fields
![]() $k'$
as above:
$k'$
as above:

where we use that
and where

If X is smooth and equi-dimensional (e.g., a smooth variety), then Borel–Moore cohomology agrees with ordinary cohomology (see (2.1)) and the above map yields a cycle map as in (1.1).
Lemma 4.1. Assume that X is a smooth projective k-variety. In the following special cases, the group
![]() $M^{2i-1}(X)$
can be computed explicitly as follows:
$M^{2i-1}(X)$
can be computed explicitly as follows:
-
(1) If k is algebraically closed, then
 $M^{2i-1}(X)=0$
for all i;
$M^{2i-1}(X)=0$
for all i; -
(2) If k is a finite field, then
 $M^{2i-1}(X)=0$
for all i;
$M^{2i-1}(X)=0$
for all i; -
(3) If
 $i=1$
, k is arbitrary and X is geometrically integral, then
$i=1$
, k is arbitrary and X is geometrically integral, then  $$ \begin{align*}M^1(X)=\operatorname{im}(H^1(\operatorname{Spec} k,{\mathbb Q}_{\ell}/\mathbb{Z}_{\ell}(1))\to H^1(X,{\mathbb Q}_{\ell}/\mathbb{Z}_{\ell}(1))).\end{align*} $$
$$ \begin{align*}M^1(X)=\operatorname{im}(H^1(\operatorname{Spec} k,{\mathbb Q}_{\ell}/\mathbb{Z}_{\ell}(1))\to H^1(X,{\mathbb Q}_{\ell}/\mathbb{Z}_{\ell}(1))).\end{align*} $$
Proof. Assume first that k is algebraically closed. By the Weil conjectures proven by Deligne, the group
![]() $H^{2i-1}(X,{\mathbb Q}_{\ell } (i))$
does not contain any nontrivial element that is fixed by the absolute Galois group of a finitely generated subfield
$H^{2i-1}(X,{\mathbb Q}_{\ell } (i))$
does not contain any nontrivial element that is fixed by the absolute Galois group of a finitely generated subfield
![]() $k'\subset k$
. Hence, the natural map
$k'\subset k$
. Hence, the natural map
![]() $ H^{2i-1}(X_{k'},{\mathbb Q}_{\ell }(i))\to H^{2i-1}(X,{\mathbb Q}_{\ell } (i)) $
is zero for any finitely generated field
$ H^{2i-1}(X_{k'},{\mathbb Q}_{\ell }(i))\to H^{2i-1}(X,{\mathbb Q}_{\ell } (i)) $
is zero for any finitely generated field
![]() $k'\subset k$
. This implies
$k'\subset k$
. This implies
![]() $M^{2i-1}(X)=0$
as we want in (1).
$M^{2i-1}(X)=0$
as we want in (1).
Assume now that k is a finite field. The Weil conjectures imply that
![]() $H^{2i-1}(X,{\mathbb Q}_{\ell }/\mathbb {Z}_{\ell }(i))$
is a finite group (see [Reference Colliot- Thélène, Sansuc and SouléCTSS83, Théorème 2]) and so the map
$H^{2i-1}(X,{\mathbb Q}_{\ell }/\mathbb {Z}_{\ell }(i))$
is a finite group (see [Reference Colliot- Thélène, Sansuc and SouléCTSS83, Théorème 2]) and so the map
![]() $H^{2i-1}(X,{\mathbb Q}_{\ell }(i))\to H^{2i-1}(X,{\mathbb Q}_{\ell }/\mathbb {Z}_{\ell }(i))$
is zero. This implies
$H^{2i-1}(X,{\mathbb Q}_{\ell }(i))\to H^{2i-1}(X,{\mathbb Q}_{\ell }/\mathbb {Z}_{\ell }(i))$
is zero. This implies
![]() $M^{2i-1}(X)=0$
, as claimed.
$M^{2i-1}(X)=0$
, as claimed.
It suffices by a limit argument to prove the last claim in the case where k is an arbitrary finitely generated field. Let
![]() $G=\operatorname {Gal}_k$
be the absolute Galois group of k and let
$G=\operatorname {Gal}_k$
be the absolute Galois group of k and let
![]() $\bar k$
be an algebraic (or separable) closure of k. Then the Hochschild–Serre spectral sequence from [Reference JannsenJan88] yields an exact sequence
$\bar k$
be an algebraic (or separable) closure of k. Then the Hochschild–Serre spectral sequence from [Reference JannsenJan88] yields an exact sequence
where we use that
![]() $H^0(X_{\bar k},{\mathbb Q}_{\ell }(1))={\mathbb Q}_{\ell }(1)$
because X is geometrically integral. The Weil conjectures proven by Deligne [Reference DeligneDel74] imply that
$H^0(X_{\bar k},{\mathbb Q}_{\ell }(1))={\mathbb Q}_{\ell }(1)$
because X is geometrically integral. The Weil conjectures proven by Deligne [Reference DeligneDel74] imply that
![]() $H^1(X_{\bar k},{\mathbb Q}_{\ell }(1))^G=0$
and so the first map in the above sequence is surjective. Moreover, Kummer theory implies that
$H^1(X_{\bar k},{\mathbb Q}_{\ell }(1))^G=0$
and so the first map in the above sequence is surjective. Moreover, Kummer theory implies that
![]() $H^1(\operatorname {Spec} k,{\mathbb Q}_{\ell }(1))\to H^1(\operatorname {Spec} k,{\mathbb Q}_{\ell }/\mathbb {Z}_{\ell }(1)) $
is surjective. Since
$H^1(\operatorname {Spec} k,{\mathbb Q}_{\ell }(1))\to H^1(\operatorname {Spec} k,{\mathbb Q}_{\ell }/\mathbb {Z}_{\ell }(1)) $
is surjective. Since
![]() $N^0H^1(X,{\mathbb Q}_{\ell }(1))=H^1(X,{\mathbb Q}_{\ell }(1))$
, we finally conclude
$N^0H^1(X,{\mathbb Q}_{\ell }(1))=H^1(X,{\mathbb Q}_{\ell }(1))$
, we finally conclude
as we want. This finishes the proof of the lemma.
4.2 Basic properties of
 $\lambda _{X}^i$
$\lambda _{X}^i$
Theorem 4.2. Let X be an algebraic scheme over a field k and let
![]() $\ell $
be a prime invertible in k. Then the cycle map
$\ell $
be a prime invertible in k. Then the cycle map

is injective for
![]() $i\leq 2$
.
$i\leq 2$
.
Proof. This follows from Proposition 3.3, where we recall our convention that
![]() $ H^{\ast } (X ,A(n))=H^{\ast }_{BM}(X ,A(n))$
denotes Borel–Moore cohomology.
$ H^{\ast } (X ,A(n))=H^{\ast }_{BM}(X ,A(n))$
denotes Borel–Moore cohomology.
The following result generalizes [Reference Merkurjev and SuslinMS83, (18.4)].
Lemma 4.3. Let X be an algebraic scheme over a field k and let
![]() $\ell $
be a prime invertible in k. Then the image of
$\ell $
be a prime invertible in k. Then the image of
![]() $\lambda ^{i}_{X}$
is given by
$\lambda ^{i}_{X}$
is given by
 $$ \begin{align*}\operatorname{im}(\lambda^{i}_{X})=\frac{N^{i-1} H^{2i-1}_{BM}(X ,{\mathbb Q}_{\ell}/\mathbb{Z}_{\ell}(i))}{M^{2i-1}(X)}.\end{align*} $$
$$ \begin{align*}\operatorname{im}(\lambda^{i}_{X})=\frac{N^{i-1} H^{2i-1}_{BM}(X ,{\mathbb Q}_{\ell}/\mathbb{Z}_{\ell}(i))}{M^{2i-1}(X)}.\end{align*} $$
Proof. This follows from Proposition 3.4, together with the construction of
![]() $\lambda _{X}^i$
via direct limit in Section 4.1.
$\lambda _{X}^i$
via direct limit in Section 4.1.
Corollary 4.4. Let X be an algebraic scheme over a field k and let
![]() $\ell $
be a prime invertible in k. Then
$\ell $
be a prime invertible in k. Then
![]() $\lambda _{X}^i$
induces for
$\lambda _{X}^i$
induces for
![]() $i\in \{1,2\}$
isomorphisms
$i\in \{1,2\}$
isomorphisms
 $$ \begin{align*}\operatorname{CH}^1(X)[\ell^{\infty}] \simeq \frac{ H^{1}_{BM}(X ,{\mathbb Q}_{\ell}/\mathbb{Z}_{\ell}(1))}{M^{1}(X)}\ \ \text{and}\ \ \operatorname{CH}^2(X)[\ell^{\infty}] \simeq \frac{N^{1} H^{3}_{BM}(X ,{\mathbb Q}_{\ell}/\mathbb{Z}_{\ell}(2))}{M^{3}(X)}. \end{align*} $$
$$ \begin{align*}\operatorname{CH}^1(X)[\ell^{\infty}] \simeq \frac{ H^{1}_{BM}(X ,{\mathbb Q}_{\ell}/\mathbb{Z}_{\ell}(1))}{M^{1}(X)}\ \ \text{and}\ \ \operatorname{CH}^2(X)[\ell^{\infty}] \simeq \frac{N^{1} H^{3}_{BM}(X ,{\mathbb Q}_{\ell}/\mathbb{Z}_{\ell}(2))}{M^{3}(X)}. \end{align*} $$
Proof. By Lemma 4.3,
![]() $ \operatorname {im}(\lambda _{X}^i)= N^{i-1} H^{2i-1}_{BM}(X ,{\mathbb Q}_{\ell }/\mathbb {Z}_{\ell }(i))/ M^{2i-1}(X). $
Hence, the result is an immediate consequence of Theorem 4.2.
$ \operatorname {im}(\lambda _{X}^i)= N^{i-1} H^{2i-1}_{BM}(X ,{\mathbb Q}_{\ell }/\mathbb {Z}_{\ell }(i))/ M^{2i-1}(X). $
Hence, the result is an immediate consequence of Theorem 4.2.
Comparing the above construction with Bloch’s map from [Reference BlochBlo79], we get the following.
Lemma 4.5. If k is algebraically closed and X is a smooth projective variety over k, then
![]() $M^{2i-1}(X)=0$
for all i and the map
$M^{2i-1}(X)=0$
for all i and the map
agrees with Bloch’s map from [Reference BlochBlo79]. In particular, if
![]() $k=\mathbb C$
, then
$k=\mathbb C$
, then
![]() $\lambda _{X}^i$
restricted to the subgroup of homologically trivial cycles can be identified with Griffiths Abel–Jacobi map from [Reference GriffithsGri69].
$\lambda _{X}^i$
restricted to the subgroup of homologically trivial cycles can be identified with Griffiths Abel–Jacobi map from [Reference GriffithsGri69].
Proof. The vanishing of
![]() $M^{2i-1}(X)$
follows from Lemma 4.1. Using this, it is straightforward to check that our map
$M^{2i-1}(X)$
follows from Lemma 4.1. Using this, it is straightforward to check that our map
![]() $\lambda _{X}^i$
coincides over algebraically closed fields with Bloch’s map from [Reference BlochBlo79]. The comparison with Griffiths’ map thus follows from [Reference BlochBlo79, Proposition 3.7]. This concludes the proof of the lemma.
$\lambda _{X}^i$
coincides over algebraically closed fields with Bloch’s map from [Reference BlochBlo79]. The comparison with Griffiths’ map thus follows from [Reference BlochBlo79, Proposition 3.7]. This concludes the proof of the lemma.
Lemma 4.6. Let X be an algebraic scheme over a field k and let
![]() $k_0\subset k$
be a finitely generated subfield such that there is a variety
$k_0\subset k$
be a finitely generated subfield such that there is a variety
![]() $X_0$
over
$X_0$
over
![]() $k_0$
with
$k_0$
with
![]() $X=X_0\times _{k_0} k$
. Let
$X=X_0\times _{k_0} k$
. Let
![]() $\ell $
be a prime invertible in k. Assume that
$\ell $
be a prime invertible in k. Assume that
![]() $\lambda _{X}^i$
is not injective. Let
$\lambda _{X}^i$
is not injective. Let
![]() $L\subset k$
be any subfield with
$L\subset k$
be any subfield with
![]() $k_0\subset L$
. Then there is a subfield
$k_0\subset L$
. Then there is a subfield
![]() $k'\subset k$
with
$k'\subset k$
with
![]() $L\subset k'$
, such that
$L\subset k'$
, such that
![]() $k'/L$
is finitely generated and
$k'/L$
is finitely generated and

is not injective, where
![]() $X':=X_{0}\times _{k_0}k'$
.
$X':=X_{0}\times _{k_0}k'$
.
Proof. By assumption, there is a nontrivial element
![]() $[z]\in \operatorname {CH}^i(X)[\ell ^{\infty }]$
with
$[z]\in \operatorname {CH}^i(X)[\ell ^{\infty }]$
with
![]() $\lambda _{X}^i([z])=0$
. We can choose a finitely generated extension
$\lambda _{X}^i([z])=0$
. We can choose a finitely generated extension
![]() $k'/L$
such that z is defined over
$k'/L$
such that z is defined over
![]() $k'$
and so we get a class
$k'$
and so we get a class
where
![]() $X'=X_{0}\times _{k_0}k'$
. Up to possibly replacing
$X'=X_{0}\times _{k_0}k'$
. Up to possibly replacing
![]() $k'$
by a larger finitely generated extension of L, we can assume that
$k'$
by a larger finitely generated extension of L, we can assume that
![]() $[z']$
is
$[z']$
is
![]() $\ell ^{\infty }$
-torsion and so there is a class
$\ell ^{\infty }$
-torsion and so there is a class
 $$ \begin{align*}\lambda_{X'}^i([z'])\in \frac{ H^{2i-1}(X' ,{\mathbb Q}_{\ell}/\mathbb{Z}_{\ell}(i))}{M^{2i-1}(X')}. \end{align*} $$
$$ \begin{align*}\lambda_{X'}^i([z'])\in \frac{ H^{2i-1}(X' ,{\mathbb Q}_{\ell}/\mathbb{Z}_{\ell}(i))}{M^{2i-1}(X')}. \end{align*} $$
Note that
![]() $[z^{\prime }_k]=[z]$
lies in the kernel of
$[z^{\prime }_k]=[z]$
lies in the kernel of
![]() $\lambda _{X}^i$
. Since
$\lambda _{X}^i$
. Since
![]() $\lambda _{X}^i$
and
$\lambda _{X}^i$
and
![]() $\lambda _{X'}^i$
are defined via direct limits over all finitely generated subfields of k and
$\lambda _{X'}^i$
are defined via direct limits over all finitely generated subfields of k and
![]() $k'$
, respectively, we see that up to possibly replacing
$k'$
, respectively, we see that up to possibly replacing
![]() $k'$
by a larger finitely generated extension of L, we may assume that
$k'$
by a larger finitely generated extension of L, we may assume that
![]() $\lambda _{X'}^i([z'])=0$
while
$\lambda _{X'}^i([z'])=0$
while
![]() $[z']\in \operatorname {CH}^i(X')$
is still nontrivial because its base change to k is nontrivial. This proves the lemma.
$[z']\in \operatorname {CH}^i(X')$
is still nontrivial because its base change to k is nontrivial. This proves the lemma.
Next, we have the following.
Lemma 4.7. Let X be an algebraic k-scheme which admits a closed embedding into a smooth equi-dimensional algebraic k-scheme (e.g., X is quasi-projective) and let
![]() $\ell $
be a prime invertible in k. The composition of
$\ell $
be a prime invertible in k. The composition of
![]() $\lambda _{X}^i$
with the projection
$\lambda _{X}^i$
with the projection

followed by the injection
 $$ \begin{align*}-\delta: \frac{ H^{2i-1}(X ,{\mathbb Q}_{\ell}/\mathbb{Z}_{\ell}(i))}{ H^{2i-1}(X ,{\mathbb Q}_{\ell} (i))} \hookrightarrow H^{2i}(X,\mathbb{Z}_{\ell}(i)) \end{align*} $$
$$ \begin{align*}-\delta: \frac{ H^{2i-1}(X ,{\mathbb Q}_{\ell}/\mathbb{Z}_{\ell}(i))}{ H^{2i-1}(X ,{\mathbb Q}_{\ell} (i))} \hookrightarrow H^{2i}(X,\mathbb{Z}_{\ell}(i)) \end{align*} $$
induced by the Bockstein map
![]() $\delta $
, agrees with the cycle class map
$\delta $
, agrees with the cycle class map
.
Proof. This is a direct consequence of Lemma 3.5.
Lemma 4.8. Let
![]() $X_j$
for
$X_j$
for
![]() $j=1,2$
be smooth projective k-varieties and let
$j=1,2$
be smooth projective k-varieties and let
![]() $\ell $
be a prime invertible in k. Let
$\ell $
be a prime invertible in k. Let
![]() $z_j\in \operatorname {CH}^{i_j}(X_j)$
be classes such that
$z_j\in \operatorname {CH}^{i_j}(X_j)$
be classes such that
![]() $z_2$
is
$z_2$
is
![]() $\ell ^r$
-torsion for some positive integer r. Assume that
$\ell ^r$
-torsion for some positive integer r. Assume that
![]() $\operatorname {cl}^{i_1}_{X_1}(z_1)$
is zero modulo
$\operatorname {cl}^{i_1}_{X_1}(z_1)$
is zero modulo
![]() $\ell ^r$
. Then the
$\ell ^r$
. Then the
![]() $\ell ^r$
-torsion cycle
$\ell ^r$
-torsion cycle
lies in the kernel of the cycle map
![]() $ \lambda _{X}^{i_1+i_2}$
from (1.1).
$ \lambda _{X}^{i_1+i_2}$
from (1.1).
Proof. Let
![]() $k_0$
be a finitely generated subfield over which
$k_0$
be a finitely generated subfield over which
![]() $X_j$
and the cycle
$X_j$
and the cycle
![]() $z_j$
are both defined for
$z_j$
are both defined for
![]() $j=1,2$
. Since
$j=1,2$
. Since
![]() $z_2$
is
$z_2$
is
![]() $\ell ^r$
-torsion, we may assume that it is already
$\ell ^r$
-torsion, we may assume that it is already
![]() $\ell ^r$
-torsion on
$\ell ^r$
-torsion on
![]() $X_0$
(i.e., when viewed as a cycle over
$X_0$
(i.e., when viewed as a cycle over
![]() $k_0$
). Note, moreover, that
$k_0$
). Note, moreover, that
where
![]() $k'$
runs through all finitely generated subfields of k that contain
$k'$
runs through all finitely generated subfields of k that contain
![]() $k_0$
, and
$k_0$
, and
![]() ${X_1}_{k'}$
denotes the base change to
${X_1}_{k'}$
denotes the base change to
![]() $k'$
of a fixed form of
$k'$
of a fixed form of
![]() $X_1$
over
$X_1$
over
![]() $k_0$
. We can therefore also assume that the cycle class of
$k_0$
. We can therefore also assume that the cycle class of
![]() $z_1$
over
$z_1$
over
![]() $k_0$
is zero modulo
$k_0$
is zero modulo
![]() $\ell ^r$
. The claim in the lemma follows then from Corollary 3.7.
$\ell ^r$
. The claim in the lemma follows then from Corollary 3.7.
5 Schoen’s argument over non-closed fields
The following proposition extends (some version of) the main result from [Reference SchoenSchoe00] to non-closed fields.
Proposition 5.1. Let k be an algebraically closed field and let C be a smooth irreducible curve over k. Let
![]() $\ell $
be a prime and let r be a positive integer. Let E be an elliptic curve over
$\ell $
be a prime and let r be a positive integer. Let E be an elliptic curve over
![]() $k(C)$
whose j-invariant is transcendental over k. Up to replacing C by a (possibly ramified) finite cover, the following holds for any k-variety B, where we denote by
$k(C)$
whose j-invariant is transcendental over k. Up to replacing C by a (possibly ramified) finite cover, the following holds for any k-variety B, where we denote by
![]() $K=k(B\times C)$
the function field of
$K=k(B\times C)$
the function field of
![]() $B\times C$
: There is a class
$B\times C$
: There is a class
![]() $\tau \in \operatorname {CH}_0(E_K)$
of order
$\tau \in \operatorname {CH}_0(E_K)$
of order
![]() $\ell ^r$
such that for any smooth projective variety Y over
$\ell ^r$
such that for any smooth projective variety Y over
![]() $k(B)$
, the kernel of the exterior product map
$k(B)$
, the kernel of the exterior product map
is contained in the image of
Proof. Replacing C by the normalization of a projective closure, we may assume that C is smooth and projective. Note that k is algebraically closed and that the j-invariant of E is transcendental over k. Using this, the same argument as in [Reference SchoenSchoe00, Lemma 2.7] shows that up to replacing C by a finite cover, we may assume that the curve
![]() $E_K$
admits a regular projective model
$E_K$
admits a regular projective model
![]() $\mathcal E$
over
$\mathcal E$
over
![]() $C_{k(B)}:=C\times _kk(B)$
, with the following properties:
$C_{k(B)}:=C\times _kk(B)$
, with the following properties:
-
(i)
 $\mathcal E\to C_{k(B)}$
is a minimal elliptic surface over
$\mathcal E\to C_{k(B)}$
is a minimal elliptic surface over
 $k(B)$
;
$k(B)$
; -
(ii) there is a k-rational point on C with induced point
 $0\in C_{k(B)}$
, such that the fibre F of
$0\in C_{k(B)}$
, such that the fibre F of
 $\mathcal E\to C_{k(B)}$
above
$\mathcal E\to C_{k(B)}$
above
 $0$
is of type
$0$
is of type
 $I_{\ell ^rN}$
for some
$I_{\ell ^rN}$
for some
 $N\geq 1$
;
$N\geq 1$
; -
(iii) if we denote by
 $F_i$
,
$F_i$
,
 $i=0,1,\dots , \ell ^rN-1$
the components of F, then
$i=0,1,\dots , \ell ^rN-1$
the components of F, then
 $F_i^2=-2$
for all i and
$F_i^2=-2$
for all i and
 $F_i\cdot F_{i-1}=1$
for all i if
$F_i\cdot F_{i-1}=1$
for all i if
 $\ell ^rN\neq 2$
and
$\ell ^rN\neq 2$
and
 $F_0F_1=2$
if
$F_0F_1=2$
if
 $\ell ^rN= 2$
, where the index has to be read modulo
$\ell ^rN= 2$
, where the index has to be read modulo
 $ \ell ^rN$
;
$ \ell ^rN$
; -
(iv) the model
 $\mathcal E\to C_{k(B)}$
admits two sections
$\mathcal E\to C_{k(B)}$
admits two sections
 $s_0,s_1$
such that
$s_0,s_1$
such that
 $s_1-s_0$
restricts to a zero-cycle
$s_1-s_0$
restricts to a zero-cycle
 $\tau \in \operatorname {CH}_0(E_K)$
of order
$\tau \in \operatorname {CH}_0(E_K)$
of order
 $\ell ^r$
and such that
$\ell ^r$
and such that
 $s_0$
meets
$s_0$
meets
 $F_0$
, while the (unique) component of F that meets
$F_0$
, while the (unique) component of F that meets
 $s_1$
is of the form
$s_1$
is of the form
 $F_{mN}$
with m coprime to
$F_{mN}$
with m coprime to
 $\ell $
.
$\ell $
.
The same argument as in [Reference SchoenSchoe00, Lemma 2.8] then shows that there is a divisor D on
![]() $\mathcal E$
which is supported on the special fibre F and such that the following holds.
$\mathcal E$
which is supported on the special fibre F and such that the following holds.
-
(v) if
 $D'$
is another divisor on
$D'$
is another divisor on
 $\mathcal E$
that is supported on some fibres of
$\mathcal E$
that is supported on some fibres of
 $\mathcal E\to C_{k(B)}$
, then
$\mathcal E\to C_{k(B)}$
, then
 $D'\cdot D\equiv 0 \mod \ell ^r N$
;
$D'\cdot D\equiv 0 \mod \ell ^r N$
; -
(vi)
 $(s_1-s_0)\cdot D=mN \cdot \chi $
for some integer m that is coprime to
$(s_1-s_0)\cdot D=mN \cdot \chi $
for some integer m that is coprime to
 $\ell ^r$
and some zero-cycle
$\ell ^r$
and some zero-cycle
 $\chi \in \operatorname {CH}_0(F)$
of degree 1.
$\chi \in \operatorname {CH}_0(F)$
of degree 1.
To conclude the argument, we consider the model
with special fibre
![]() $X_0=Y\times _{k(B)} F$
and generic fibre
$X_0=Y\times _{k(B)} F$
and generic fibre
![]() $X_{\eta }=Y_K\times _KE_K$
. Since Y is smooth over
$X_{\eta }=Y_K\times _KE_K$
. Since Y is smooth over
![]() $k(B)$
and
$k(B)$
and
![]() $\mathcal E$
is regular, the model
$\mathcal E$
is regular, the model
![]() $\mathcal X$
is regular as well. Let
$\mathcal X$
is regular as well. Let
![]() $z\in \operatorname {CH}^i(Y)$
. Since
$z\in \operatorname {CH}^i(Y)$
. Since
![]() $s_1-s_0$
is a divisor class on
$s_1-s_0$
is a divisor class on
![]() $\mathcal E$
, we can consider the exterior product cycle
$\mathcal E$
, we can consider the exterior product cycle
The restriction
![]() $\xi _{\eta }\in \operatorname {CH}^{i+1}(Y_K\times _KE_K)$
of this cycle to the generic fibre of
$\xi _{\eta }\in \operatorname {CH}^{i+1}(Y_K\times _KE_K)$
of this cycle to the generic fibre of
![]() $\mathcal X\to C_{k(B)}$
agrees with
$\mathcal X\to C_{k(B)}$
agrees with
where
![]() $ z_K\in \operatorname {CH}^i(Y_K)$
denotes the base change of z and
$ z_K\in \operatorname {CH}^i(Y_K)$
denotes the base change of z and
![]() $\tau \in \operatorname {CH}_0(E_K)$
is the class of order
$\tau \in \operatorname {CH}_0(E_K)$
is the class of order
![]() $\ell ^r$
from (iv).
$\ell ^r$
from (iv).
To prove the proposition, we assume that
![]() $\xi _{\eta }=0$
, and we then aim to show that z is the sum of a torsion class and a class that is
$\xi _{\eta }=0$
, and we then aim to show that z is the sum of a torsion class and a class that is
![]() $\ell ^r$
-divisible. To this end, note that the localization formula together with the assumption
$\ell ^r$
-divisible. To this end, note that the localization formula together with the assumption
![]() $\xi _{\eta }=0$
implies that there are closed points
$\xi _{\eta }=0$
implies that there are closed points
![]() $c_1,\dots ,c_n\in C_{k(B)}$
with
$c_1,\dots ,c_n\in C_{k(B)}$
with
![]() $c_j\neq 0$
for all j such that
$c_j\neq 0$
for all j such that

Hence,

Note that
![]() $X_0=Y\times _{k(B)} F$
. Since F is a cycle of smooth rational curves, the natural map
$X_0=Y\times _{k(B)} F$
. Since F is a cycle of smooth rational curves, the natural map
is surjective. It follows that we can write
for some
![]() $\xi _{1j}\in \operatorname {CH}^{i}(Y)$
,
$\xi _{1j}\in \operatorname {CH}^{i}(Y)$
,
![]() $D^{\prime }_j\in \operatorname {CH}^0(F)$
,
$D^{\prime }_j\in \operatorname {CH}^0(F)$
,
![]() $\xi _2\in \operatorname {CH}^{i-1}(Y)$
, and
$\xi _2\in \operatorname {CH}^{i-1}(Y)$
, and
![]() $\zeta \in \operatorname {CH}^1(F)$
. Let
$\zeta \in \operatorname {CH}^1(F)$
. Let
![]() $Y\times D$
denote the pullback of the divisor D via the natural projection
$Y\times D$
denote the pullback of the divisor D via the natural projection
![]() $\operatorname {pr}_2:\mathcal X\to \mathcal E$
. Since
$\operatorname {pr}_2:\mathcal X\to \mathcal E$
. Since
![]() $\mathcal X$
is regular, we may consider the intersection product
$\mathcal X$
is regular, we may consider the intersection product
![]() $\xi \cdot (Y\times D) \in \operatorname {CH}^{i+2}(\mathcal X)$
. Since D is supported on the special fibre F, the support of
$\xi \cdot (Y\times D) \in \operatorname {CH}^{i+2}(\mathcal X)$
. Since D is supported on the special fibre F, the support of
![]() $\xi "$
is disjoint from the support of
$\xi "$
is disjoint from the support of
![]() $Y\times D$
and so
$Y\times D$
and so
![]() $\xi "\cdot (Y\times D)=0$
. Hence,
$\xi "\cdot (Y\times D)=0$
. Hence,
 $$ \begin{align*}\xi\cdot (Y\times D)=\left(\sum_j \xi_{1j}\times D_j'+\xi_2\times \zeta\right)\cdot (Y\times D) \in \operatorname{CH}^{i+2}(\mathcal X). \end{align*} $$
$$ \begin{align*}\xi\cdot (Y\times D)=\left(\sum_j \xi_{1j}\times D_j'+\xi_2\times \zeta\right)\cdot (Y\times D) \in \operatorname{CH}^{i+2}(\mathcal X). \end{align*} $$
By item (v),
![]() $(\xi _{1j}\times D^{\prime }_j)\cdot (Y\times D)\equiv 0\mod \ell ^rN $
for all j and so
$(\xi _{1j}\times D^{\prime }_j)\cdot (Y\times D)\equiv 0\mod \ell ^rN $
for all j and so
because
![]() $\zeta \cdot D=0$
for degree reasons. Hence,
$\zeta \cdot D=0$
for degree reasons. Hence,
However,
![]() $\xi = z \times (s_1-s_0)$
and so item (vi) implies
$\xi = z \times (s_1-s_0)$
and so item (vi) implies
Consider the natural proper map
of
![]() $k(B)$
-varieties. Then the above computations show that
$k(B)$
-varieties. Then the above computations show that
for some
![]() $z'\in \operatorname {CH}^i(Y)$
. Hence,
$z'\in \operatorname {CH}^i(Y)$
. Hence,
is N-torsion. Since m is coprime to
![]() $\ell $
, we find that the class of z in
$\ell $
, we find that the class of z in
![]() $\operatorname {CH}^i(Y)/\ell ^r$
may be represented by a torsion class, as we want. This concludes the proof of the proposition.
$\operatorname {CH}^i(Y)/\ell ^r$
may be represented by a torsion class, as we want. This concludes the proof of the proposition.
For later use, we record here the following variant of the above argument.
Proposition 5.2. Let k be an arbitrary field. Let Y be a smooth projective k-variety. Then there is an elliptic curve E over
![]() $K=k(\mathbb P^1)$
(in fact, the Legendre elliptic curve
$K=k(\mathbb P^1)$
(in fact, the Legendre elliptic curve
![]() $y^2=x(x-1)(x-t)$
) and a class
$y^2=x(x-1)(x-t)$
) and a class
![]() $\tau \in \operatorname {CH}_{0}(E)$
of order
$\tau \in \operatorname {CH}_{0}(E)$
of order
![]() $2$
such that the exterior product map
$2$
such that the exterior product map
is injective.
Proof. We let E be the generic fibre of the Legendre family
![]() $y^2=x(x-1)(x-t)$
, where t denotes an affine coordinate on
$y^2=x(x-1)(x-t)$
, where t denotes an affine coordinate on
![]() $\mathbb P^1$
. Let
$\mathbb P^1$
. Let
![]() $\mathcal E\to \mathbb P^1$
be a minimal elliptic surface whose generic fibre is E. The special fibre F above
$\mathcal E\to \mathbb P^1$
be a minimal elliptic surface whose generic fibre is E. The special fibre F above
![]() $t=0$
is then of type
$t=0$
is then of type
![]() $I_2$
:
$I_2$
:
![]() $F=F_0\cup F_1$
with
$F=F_0\cup F_1$
with
![]() $F_j^2=-2$
and
$F_j^2=-2$
and
![]() $F_0\cdot F_1=2$
. Note further that each
$F_0\cdot F_1=2$
. Note further that each
![]() $2$
-torsion point of E is K-rational (see [Reference IgusaIG59]) and it extends to a section of
$2$
-torsion point of E is K-rational (see [Reference IgusaIG59]) and it extends to a section of
![]() $\mathcal E\to \mathbb P^1$
. It follows, in particular, that there are sections
$\mathcal E\to \mathbb P^1$
. It follows, in particular, that there are sections
![]() $s_0,s_1$
of
$s_0,s_1$
of
![]() $\mathcal E\to \mathbb P^1$
such that
$\mathcal E\to \mathbb P^1$
such that
![]() $s_j$
meets
$s_j$
meets
![]() $F_j$
and such that
$F_j$
and such that
![]() $s_1-s_0$
restricts to a zero-cycle
$s_1-s_0$
restricts to a zero-cycle
![]() $\tau \in \operatorname {CH}_0(E)$
of order
$\tau \in \operatorname {CH}_0(E)$
of order
![]() $2$
. Let
$2$
. Let
![]() $z\in \operatorname {CH}^i(Y)$
be nonzero modulo
$z\in \operatorname {CH}^i(Y)$
be nonzero modulo
![]() $2$
. Let
$2$
. Let
![]() $z_K\in \operatorname {CH}^i(Y_K)$
denote the base change of z. To prove the proposition, it is then enough to show that the
$z_K\in \operatorname {CH}^i(Y_K)$
denote the base change of z. To prove the proposition, it is then enough to show that the
![]() $2$
-torsion class
$2$
-torsion class
is nonzero. This follows by exactly the same argument as in the proof of Proposition 5.1 above. The main difference is that in the current situation, the special fibre F is of type
![]() $I_2$
and so the integer N in the proof of Proposition 5.1 equals
$I_2$
and so the integer N in the proof of Proposition 5.1 equals
![]() $1$
, so that the class t in (5.1) is not only torsion, but in fact zero.
$1$
, so that the class t in (5.1) is not only torsion, but in fact zero.
Remark 5.3. Let C be a smooth irreducible projective curve over a field k and let
![]() $\ell $
be a prime. The proof of Proposition 5.2 shows more generally that if E is an elliptic curve over
$\ell $
be a prime. The proof of Proposition 5.2 shows more generally that if E is an elliptic curve over
![]() $K=k(C)$
whose
$K=k(C)$
whose
![]() $\ell $
-torsion points are all K-rational and, in addition, there is a K-rational point
$\ell $
-torsion points are all K-rational and, in addition, there is a K-rational point
![]() $0\in C$
so that the fibre F of the minimal model
$0\in C$
so that the fibre F of the minimal model
![]() $\mathcal E\to C$
above
$\mathcal E\to C$
above
![]() $t=0$
is of type
$t=0$
is of type
![]() $I_{\ell }$
, then there is a class
$I_{\ell }$
, then there is a class
![]() $\tau \in \operatorname {CH}_{0}(E)$
of order
$\tau \in \operatorname {CH}_{0}(E)$
of order
![]() $\ell $
such that for any smooth projective k-variety Y, the exterior product map
$\ell $
such that for any smooth projective k-variety Y, the exterior product map
is injective.
A concrete example for the prime
![]() $\ell =3$
is given by the elliptic curve E over
$\ell =3$
is given by the elliptic curve E over
![]() $\mathbb {Q}(\omega )(\mathbb P^{1}) \ (\omega ^{3}=1,\omega \neq 1)$
defined by the degree
$\mathbb {Q}(\omega )(\mathbb P^{1}) \ (\omega ^{3}=1,\omega \neq 1)$
defined by the degree
![]() $3$
equation
$3$
equation
in
![]() $\mathbb P^{2}$
; see [Reference IgusaIG59].
$\mathbb P^{2}$
; see [Reference IgusaIG59].
6 A construction of Kollár, Hassett–Tschinkel and Totaro
In this section, we use some arguments of Kollár [Reference KollárKo92], Hassett–Tschinkel (cf. [Reference TotaroTot13, Introduction]) and Totaro [Reference TotaroTot13] to prove the following.
Proposition 6.1. Let k be an algebraically closed field and let
![]() $\ell $
be a prime invertible in k. If the characteristic of k is positive, assume that k has positive transcendence degree over its prime field. There is smooth projective hypersurface
$\ell $
be a prime invertible in k. If the characteristic of k is positive, assume that k has positive transcendence degree over its prime field. There is smooth projective hypersurface
![]() $S\subset \mathbb P^3_{k(\mathbb P^1)}$
such that the cycle class map
$S\subset \mathbb P^3_{k(\mathbb P^1)}$
such that the cycle class map
is not injective up to torsion. That is, there is a zero-cycle
![]() $z\in \operatorname {CH}_0(S) $
with trivial cycle class in
$z\in \operatorname {CH}_0(S) $
with trivial cycle class in
![]() $H^4(S,\mu _{\ell }^{\otimes 2})$
such that
$H^4(S,\mu _{\ell }^{\otimes 2})$
such that
![]() $z\notin \operatorname {CH}_0(S)_{\operatorname {tors}}+\ell \cdot \operatorname {CH}_0(S)$
.
$z\notin \operatorname {CH}_0(S)_{\operatorname {tors}}+\ell \cdot \operatorname {CH}_0(S)$
.
Proof. Our examples arise due to the failure of the integral Hodge and Tate conjectures for certain hypersurfaces in
![]() $\mathbb P_{k}^{1}\times _{k}\mathbb P_{k}^{3}$
of bidegree
$\mathbb P_{k}^{1}\times _{k}\mathbb P_{k}^{3}$
of bidegree
![]() $(3,\ell ^{2})$
. To this end, let
$(3,\ell ^{2})$
. To this end, let
![]() $\lambda \in k$
be transcendental over the prime field if k has positive characteristic and let
$\lambda \in k$
be transcendental over the prime field if k has positive characteristic and let
![]() $\lambda :=\ell $
if k has characteristic zero. We then consider the smooth hypersurface
$\lambda :=\ell $
if k has characteristic zero. We then consider the smooth hypersurface
![]() $\mathcal {X}\subset \mathbb P^{1}_{u,t}\times \mathbb P^{3}_{x_{0},x_{1},x_{2},x_{3}}$
over k, defined by the equation
$\mathcal {X}\subset \mathbb P^{1}_{u,t}\times \mathbb P^{3}_{x_{0},x_{1},x_{2},x_{3}}$
over k, defined by the equation
Let
![]() $S:=\mathcal {X}_{\eta }$
be the generic fibre of the first projection
$S:=\mathcal {X}_{\eta }$
be the generic fibre of the first projection
![]() $\operatorname {pr}_{1}\colon \mathcal {X}\to \mathbb P_{k}^{1}$
. We aim to show that the cycle class map
$\operatorname {pr}_{1}\colon \mathcal {X}\to \mathbb P_{k}^{1}$
. We aim to show that the cycle class map
![]() is not injective up to torsion.
is not injective up to torsion.
Step 1. Let
![]() $n:=\gcd \{\deg (z)|z\in \operatorname {CH}_{0}(S)\}$
be the index of S. If
$n:=\gcd \{\deg (z)|z\in \operatorname {CH}_{0}(S)\}$
be the index of S. If
![]() $\mathcal {Z}^{4}(\mathcal {X})$
denotes the cokernel of the cycle class map
$\mathcal {Z}^{4}(\mathcal {X})$
denotes the cokernel of the cycle class map
![]() $\operatorname {cl}^{2}_{\mathcal {X}}\colon \operatorname {CH}^{2}(\mathcal {X})_{\mathbb {Z}_{\ell }}\to H^{4}(\mathcal {X},\mathbb {Z}_{\ell }(2))$
, then
$\operatorname {cl}^{2}_{\mathcal {X}}\colon \operatorname {CH}^{2}(\mathcal {X})_{\mathbb {Z}_{\ell }}\to H^{4}(\mathcal {X},\mathbb {Z}_{\ell }(2))$
, then
![]() $\mathcal {Z}^{4}(\mathcal {X})\simeq \mathbb {Z}_{\ell }/n\mathbb {Z}_{\ell }$
.
$\mathcal {Z}^{4}(\mathcal {X})\simeq \mathbb {Z}_{\ell }/n\mathbb {Z}_{\ell }$
.
Proof. We have the following commutative diagram

where
![]() $i_{*}\colon H^{4}(\mathcal {X},\mathbb {Z}_{\ell }(2))\to H^{6}(\mathbb P^{1}\times _{k}\mathbb P^{3},\mathbb {Z}_{\ell }(3))$
is an isomorphism by the Weak Lefschetz theorem [Reference MilneMil80, Theorem VI.7.1]. Recall that
$i_{*}\colon H^{4}(\mathcal {X},\mathbb {Z}_{\ell }(2))\to H^{6}(\mathbb P^{1}\times _{k}\mathbb P^{3},\mathbb {Z}_{\ell }(3))$
is an isomorphism by the Weak Lefschetz theorem [Reference MilneMil80, Theorem VI.7.1]. Recall that
![]() $H^{6}(\mathbb P^{1}\times _{k}\mathbb P^{3},\mathbb {Z}_{\ell }(3))$
is the free
$H^{6}(\mathbb P^{1}\times _{k}\mathbb P^{3},\mathbb {Z}_{\ell }(3))$
is the free
![]() $\mathbb {Z}_{\ell }$
-module of rank
$\mathbb {Z}_{\ell }$
-module of rank
![]() $2$
generated by
$2$
generated by
![]() $\ell _{1}:=\operatorname {cl}^{3}(\mathbb P_{k}^{1}\times pt)$
and
$\ell _{1}:=\operatorname {cl}^{3}(\mathbb P_{k}^{1}\times pt)$
and
![]() $\ell _{2}:=\operatorname {cl}^{3}(pt\times L)$
, where
$\ell _{2}:=\operatorname {cl}^{3}(pt\times L)$
, where
![]() $L\subset \mathbb P^{3}_{k}$
is any one-dimensional linear subspace. Let
$L\subset \mathbb P^{3}_{k}$
is any one-dimensional linear subspace. Let
![]() $L\subset \mathbb P^{3}_{k}$
be the subspace defined by the equations
$L\subset \mathbb P^{3}_{k}$
be the subspace defined by the equations
![]() $x_{0}=0$
and
$x_{0}=0$
and
![]() $x_{3}=\zeta x_{2}$
, where
$x_{3}=\zeta x_{2}$
, where
![]() $\zeta \in k$
with
$\zeta \in k$
with
![]() $\zeta ^{\ell ^{2}}=-1$
. An easy check shows
$\zeta ^{\ell ^{2}}=-1$
. An easy check shows
![]() $(1:0)\times L\subset \mathcal {X}$
. The
$(1:0)\times L\subset \mathcal {X}$
. The
![]() $1$
-cycle
$1$
-cycle
![]() $\tilde {\ell _{2}}:=[(1:0)\times L]\in \operatorname {CH}^{2}(\mathcal {X})$
clearly then satisfies
$\tilde {\ell _{2}}:=[(1:0)\times L]\in \operatorname {CH}^{2}(\mathcal {X})$
clearly then satisfies
![]() $i_{*}\operatorname {cl}^{2}_{\mathcal {X}}(\tilde {\ell _{2}})=\ell _{2}$
. Pick
$i_{*}\operatorname {cl}^{2}_{\mathcal {X}}(\tilde {\ell _{2}})=\ell _{2}$
. Pick
![]() $z\in \operatorname {CH}^{2}(\mathcal {X})$
such that
$z\in \operatorname {CH}^{2}(\mathcal {X})$
such that
![]() $\deg (z|_{S})=n$
. By replacing z with
$\deg (z|_{S})=n$
. By replacing z with
![]() $z':=z-m\tilde {\ell _{2}}$
, where the integer m is determined by
$z':=z-m\tilde {\ell _{2}}$
, where the integer m is determined by
![]() ${\operatorname {pr}_{2}}_{*}(z)=m[L]$
with
${\operatorname {pr}_{2}}_{*}(z)=m[L]$
with
![]() $\operatorname {pr}_2:\mathcal X\to \mathbb P^3$
, we may assume that
$\operatorname {pr}_2:\mathcal X\to \mathbb P^3$
, we may assume that
![]() ${\operatorname {pr}_{2}}_{*}(z)=0$
. It follows that
${\operatorname {pr}_{2}}_{*}(z)=0$
. It follows that
![]() $i_{*}\operatorname {cl}^{2}_{\mathcal {X}}(z)=n\ell _{1}$
. To conclude, we notice that the image of the composite
$i_{*}\operatorname {cl}^{2}_{\mathcal {X}}(z)=n\ell _{1}$
. To conclude, we notice that the image of the composite
is
![]() $n\mathbb {Z}_{\ell }$
, where n is the index of S.
$n\mathbb {Z}_{\ell }$
, where n is the index of S.
Step 2. We have
![]() $n\in \ell \mathbb {Z}_{\ell }$
.
$n\in \ell \mathbb {Z}_{\ell }$
.
Proof. The proof is essentially the same as in [Reference TotaroTot13, Theorem 2.1], where the case
![]() $\ell =2$
and
$\ell =2$
and
![]() $k=\bar {\mathbb {Q}}$
is treated. We briefly recall the argument for the reader’s convenience.
$k=\bar {\mathbb {Q}}$
is treated. We briefly recall the argument for the reader’s convenience.
Note that
![]() $\mathcal {X}$
degenerates via
$\mathcal {X}$
degenerates via
![]() $\lambda \to 0$
to the hypersurface
$\lambda \to 0$
to the hypersurface
in
![]() $\mathbb P^{1}\times \mathbb P^{3}$
over some algebraically closed field extension
$\mathbb P^{1}\times \mathbb P^{3}$
over some algebraically closed field extension
![]() $F/\bar {\mathbb {F}}_{q}$
, where
$F/\bar {\mathbb {F}}_{q}$
, where
![]() $q=\ell $
if
$q=\ell $
if
![]() $\operatorname {char}(k)=0$
and
$\operatorname {char}(k)=0$
and
![]() $q=\operatorname {char}(k),$
otherwise. A straightforward specialization argument enables us to reduce our task to proving that the hypersurface
$q=\operatorname {char}(k),$
otherwise. A straightforward specialization argument enables us to reduce our task to proving that the hypersurface
in
![]() $\mathbb P^{3}$
over
$\mathbb P^{3}$
over
![]() $F((t))$
has no rational point over any extension
$F((t))$
has no rational point over any extension
![]() $F((s))$
of
$F((s))$
of
![]() $F((t))$
whose degree is not divisible by
$F((t))$
whose degree is not divisible by
![]() $\ell $
. For a contradiction, we assume that there is an extension
$\ell $
. For a contradiction, we assume that there is an extension
![]() $F((s))/F((t))$
of degree d with
$F((s))/F((t))$
of degree d with
![]() $\gcd (d,\ell )=1$
and Laurent series
$\gcd (d,\ell )=1$
and Laurent series
![]() $t(s),x_{i}(s)\in F((s))$
satisfying the equation of Y. Then the valuations of the
$t(s),x_{i}(s)\in F((s))$
satisfying the equation of Y. Then the valuations of the
![]() $4$
terms in the equation, given by
$4$
terms in the equation, given by
![]() $\operatorname {ord}_{s}(t^{i}x^{\ell ^{2}}_{i})\equiv id \mod \ell ^{2}$
, are all different, forcing all the
$\operatorname {ord}_{s}(t^{i}x^{\ell ^{2}}_{i})\equiv id \mod \ell ^{2}$
, are all different, forcing all the
![]() $x_{i}(s)$
to be zero. This certainly cannot be a point of the projective space, contradicting our hypothesis.
$x_{i}(s)$
to be zero. This certainly cannot be a point of the projective space, contradicting our hypothesis.
Finally, we are in the position to conclude the proof of Proposition 6.1. By Step 1, we can pick a
![]() $1$
-cycle
$1$
-cycle
![]() $\alpha \in \operatorname {CH}^{2}(\mathcal {X})$
such that
$\alpha \in \operatorname {CH}^{2}(\mathcal {X})$
such that
![]() $\operatorname {cl}^{2}_{\mathcal {X}}(\alpha )=n\ell _{1}$
. We set
$\operatorname {cl}^{2}_{\mathcal {X}}(\alpha )=n\ell _{1}$
. We set
![]() $z:=\alpha |_{S}\in \operatorname {CH}^{2}(S)$
and note that
$z:=\alpha |_{S}\in \operatorname {CH}^{2}(S)$
and note that
![]() $\operatorname {cl}^{2}_{S}(z)=0\in H^{4}(S,\mu _{\ell }^{\otimes 2})$
because
$\operatorname {cl}^{2}_{S}(z)=0\in H^{4}(S,\mu _{\ell }^{\otimes 2})$
because
![]() $n\in \ell \mathbb {Z}_{\ell }$
by Step 2. We claim that
$n\in \ell \mathbb {Z}_{\ell }$
by Step 2. We claim that
![]() $z\notin \operatorname {CH}^{2}(S)_{\operatorname {tors}}+\ell \operatorname {CH}^{2}(S)$
. Indeed, if we write
$z\notin \operatorname {CH}^{2}(S)_{\operatorname {tors}}+\ell \operatorname {CH}^{2}(S)$
. Indeed, if we write
![]() $z=z_{1}+\ell z_{2}$
for some
$z=z_{1}+\ell z_{2}$
for some
![]() $z_{1}\in \operatorname {CH}^{2}(S)_{\operatorname {tors}}$
and
$z_{1}\in \operatorname {CH}^{2}(S)_{\operatorname {tors}}$
and
![]() $z_{2}\in \operatorname {CH}^{2}(S)$
, then
$z_{2}\in \operatorname {CH}^{2}(S)$
, then
![]() $n=\deg (z)=\ell \deg (z_{2})$
. This yields a contradiction, as the integer n is the index of S.
$n=\deg (z)=\ell \deg (z_{2})$
. This yields a contradiction, as the integer n is the index of S.
7 Proof of the main results
Proof of Theorem 1.1.
The injectivity of
![]() $\lambda _{X}^i$
for
$\lambda _{X}^i$
for
![]() $i=1,2$
follows from Theorem 4.2. The isomorphisms in question then follow from the description of the image of
$i=1,2$
follows from Theorem 4.2. The isomorphisms in question then follow from the description of the image of
![]() $\lambda _{X}^i$
in Corollary 4.4. In the case
$\lambda _{X}^i$
in Corollary 4.4. In the case
![]() $i=1$
, we note in addition that
$i=1$
, we note in addition that
![]() $N^0H^i(X,A(n))=H^i(X,A(n))$
.
$N^0H^i(X,A(n))=H^i(X,A(n))$
.
Proof of Theorem 1.2.
Let
![]() $\ell $
be a prime and let k be a field of characteristic different from
$\ell $
be a prime and let k be a field of characteristic different from
![]() $\ell $
. We aim to construct a finitely generated field extension
$\ell $
. We aim to construct a finitely generated field extension
![]() $K/k$
and a smooth projective threefold X over K such that
$K/k$
and a smooth projective threefold X over K such that
is not injective. To prove this, we are free to replace k by a finitely generated field extension and so we can assume that k has positive transcendence degree over its prime field. Lemma 4.6 allows us to reduce further to the case where k is algebraically closed and of positive transcendence degree over its prime field. It then follows from Proposition 6.1 that there is a smooth projective hypersurface
![]() $S\subset \mathbb P^3_{k(\mathbb P^1)}$
which carries a zero-cycle
$S\subset \mathbb P^3_{k(\mathbb P^1)}$
which carries a zero-cycle
![]() $z_1\in \operatorname {CH}_0(S)$
with trivial cycle class in
$z_1\in \operatorname {CH}_0(S)$
with trivial cycle class in
![]() $ H^4(S,\mu _{\ell }^{\otimes 2})$
such that
$ H^4(S,\mu _{\ell }^{\otimes 2})$
such that
Let C be any smooth curve over k and let E be an elliptic curve over
![]() $k(C)$
whose j-invariant is transcendental over k (e.g., we could take
$k(C)$
whose j-invariant is transcendental over k (e.g., we could take
![]() $C=\mathbb P^1$
and let E be the Legendre elliptic curve). We then apply Proposition 5.1 to C, E,
$C=\mathbb P^1$
and let E be the Legendre elliptic curve). We then apply Proposition 5.1 to C, E,
![]() $B:=\mathbb P^1$
, and to the
$B:=\mathbb P^1$
, and to the
![]() $k(B)$
-variety
$k(B)$
-variety
![]() $Y:=S$
. We let
$Y:=S$
. We let
![]() $K:=k(B\times C)$
and find that up to replacing C by a finite cover, there is a zero-cycle
$K:=k(B\times C)$
and find that up to replacing C by a finite cover, there is a zero-cycle
![]() $\tau \in \operatorname {CH}^1(E_K)$
of order
$\tau \in \operatorname {CH}^1(E_K)$
of order
![]() $\ell $
such that the kernel of the exterior product map
$\ell $
such that the kernel of the exterior product map
is contained in the image of
We finally set
![]() $X:= S_{K}\times _{K}E_{K}$
and consider the zero-cycle
$X:= S_{K}\times _{K}E_{K}$
and consider the zero-cycle
Since
![]() $\tau $
has order
$\tau $
has order
![]() $\ell $
, the zero-cycle z is
$\ell $
, the zero-cycle z is
![]() $\ell $
-torsion. By (7.1) and the above description of the kernel of the exterior product map in (7.2), we find that z is nontrivial. However, since the cycle class of
$\ell $
-torsion. By (7.1) and the above description of the kernel of the exterior product map in (7.2), we find that z is nontrivial. However, since the cycle class of
![]() $z_1$
in
$z_1$
in
![]() $ H^4(S,\mu _{\ell }^{\otimes 2})$
vanishes while
$ H^4(S,\mu _{\ell }^{\otimes 2})$
vanishes while
![]() $\tau $
is
$\tau $
is
![]() $\ell $
-torsion, Lemma 4.8 implies that
$\ell $
-torsion, Lemma 4.8 implies that
This concludes the proof of the theorem.
Proof of Corollary 1.3.
One direction is Theorem 1.1. The other direction follows from Theorem 1.2 by taking products with projective spaces.
Proof of Theorem 1.5.
By [Reference Parimala and SureshPS96, Theorem 8.5], there is a smooth projective surface Y (given as a conic fibration over a hyperelliptic curve) over a field k such that
![]() $Y(k)\neq \emptyset $
and such that the cycle class map
$Y(k)\neq \emptyset $
and such that the cycle class map
![]() $\operatorname {CH}^2(Y)/2\to H^4(Y,\mu _{2}^{\otimes 2})$
is not injective. In loc. cit., the example is defined over
$\operatorname {CH}^2(Y)/2\to H^4(Y,\mu _{2}^{\otimes 2})$
is not injective. In loc. cit., the example is defined over
![]() ${\mathbb Q}_3$
; a straightforward limit argument then allows us to assume that
${\mathbb Q}_3$
; a straightforward limit argument then allows us to assume that
![]() $k\subset {\mathbb Q}_3$
is a finitely generated subfield. We pick a zero-cycle
$k\subset {\mathbb Q}_3$
is a finitely generated subfield. We pick a zero-cycle
![]() $z\in \operatorname {CH}^{2}(Y)$
that is nonzero modulo
$z\in \operatorname {CH}^{2}(Y)$
that is nonzero modulo
![]() $2$
but its cycle class
$2$
but its cycle class
![]() $\operatorname {cl}^{2}_{Y}(z)$
is zero modulo
$\operatorname {cl}^{2}_{Y}(z)$
is zero modulo
![]() $2$
. Let now
$2$
. Let now
![]() $K=k(\mathbb P^1)$
. Then Proposition 5.2 implies that there is an elliptic curve E over K (in fact, the Legendre elliptic curve) and a class
$K=k(\mathbb P^1)$
. Then Proposition 5.2 implies that there is an elliptic curve E over K (in fact, the Legendre elliptic curve) and a class
![]() $\tau \in \operatorname {CH}_{0}(E)$
of order
$\tau \in \operatorname {CH}_{0}(E)$
of order
![]() $2$
such that the cycle
$2$
such that the cycle
![]() $z_{K}\times \tau \in \operatorname {CH}^{3}(X)[2]$
is nonzero, where X is the smooth projective threefold
$z_{K}\times \tau \in \operatorname {CH}^{3}(X)[2]$
is nonzero, where X is the smooth projective threefold
![]() $Y_K\times _K E$
. It follows from Lemma 4.8 that
$Y_K\times _K E$
. It follows from Lemma 4.8 that
![]() $\lambda _{X}^3(z_{K}\times \tau )=0$
, proving the noninjectivity of
$\lambda _{X}^3(z_{K}\times \tau )=0$
, proving the noninjectivity of
![]() $\lambda _{X}^3$
for the prime
$\lambda _{X}^3$
for the prime
![]() $\ell =2$
. Since E is an elliptic curve, it has a rational point, and since Y has a rational point as well, we find that
$\ell =2$
. Since E is an elliptic curve, it has a rational point, and since Y has a rational point as well, we find that
![]() $X(K)\neq \emptyset $
, as we want.
$X(K)\neq \emptyset $
, as we want.
Acknowledgements
We thank the referee for his or her useful comments. This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme under grant agreement No 948066 (ERC-StG RationAlgic).
Competing interest
The authors have no competing interest to declare.