Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-28T15:37:06.620Z Has data issue: false hasContentIssue false
  • English
  • Français

ON BINARY CORRELATIONS OF MULTIPLICATIVE FUNCTIONS

Part of: Multiplicative number theory Exponential sums and character sums

Published online by Cambridge University Press:  28 June 2018

JONI TERÄVÄINEN

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study logarithmically averaged binary correlations of bounded multiplicative functions 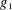$g_{1}$ and 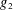$g_{2}$. A breakthrough on these correlations was made by Tao, who showed that the correlation average is negligibly small whenever 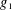$g_{1}$ or 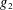$g_{2}$ does not pretend to be any twisted Dirichlet character, in the sense of the pretentious distance for multiplicative functions. We consider a wider class of real-valued multiplicative functions 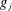$g_{j}$, namely those that are uniformly distributed in arithmetic progressions to fixed moduli. Under this assumption, we obtain a discorrelation estimate, showing that the correlation of 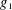$g_{1}$ and 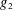$g_{2}$ is asymptotic to the product of their mean values. We derive several applications, first showing that the numbers of large prime factors of $n$ and 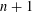$n+1$ are independent of each other with respect to logarithmic density. Secondly, we prove a logarithmic version of the conjecture of Erdős and Pomerance on two consecutive smooth numbers. Thirdly, we show that if 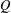$Q$ is cube-free and belongs to the Burgess regime 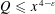$Q\leqslant x^{4-\unicode[STIX]{x1D700}}$, the logarithmic average around $x$ of the real character 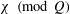$\unicode[STIX]{x1D712}\hspace{0.6em}({\rm mod}\hspace{0.2em}Q)$ over the values of a reducible quadratic polynomial is small.

MSC classification

Primary: 11N37: Asymptotic results on arithmetic functions
Secondary: 11N60: Distribution functions associated with additive and positive multiplicative functions 11L40: Estimates on character sums
Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 6 , 2018 , e10
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author 2018

References

Burgess, D. A., ‘On character sums and L-series. II’, Proc. Lond. Math. Soc. (3) 13 (1963), 524–536.CrossRefGoogle Scholar
Burgess, D. A., ‘On Dirichlet characters of polynomials’, Proc. Lond. Math. Soc. (3) 13 (1963), 537–548.CrossRefGoogle Scholar
Daboussi, H. and Sárközy, A., ‘On the correlation of the truncated Liouville function’, Acta Arith. 108(1) (2003), 61–76.Google Scholar
De Koninck, J.-M. and Doyon, N., ‘On the distance between smooth numbers’, Integers 11(A25) (2011), 22.Google Scholar
de la Bretèche, R., Pomerance, C. and Tenenbaum, G., ‘Products of ratios of consecutive integers’, Ramanujan J. 9(1–2) (2005), 131–138.CrossRefGoogle Scholar
Elliott, P. D. T. A., ‘Extrapolating the mean-values of multiplicative functions’, Nederl. Akad. Wetensch. Indag. Math. 51(4) (1989), 409–420.CrossRefGoogle Scholar
Elliott, P. D. T. A., ‘On the correlation of multiplicative functions’, Notas Soc. Math. Chile 11(1) (1992), 1–11.Google Scholar
Elliott, P. D. T. A., ‘On the correlation of multiplicative and the sum of additive arithmetic functions’, Mem. Amer. Math. Soc. 112(538) (1994), viii+88.Google Scholar
Erdős, P., ‘Some unconventional problems in number theory’, inJournées Arithmétiques de Luminy (Colloq. Internat. CNRS, Centre Univ. Luminy, Luminy, 1978), Astérisque, 61 (Soc. Math. France, Paris, 1979), 73–82.Google Scholar
Erdős, P. and Pomerance, C., ‘On the largest prime factors of n and n + 1’, Aequationes Math. 17(2–3) (1978), 311–321.Google Scholar
Frantzikinakis, N., ‘An averaged Chowla and Elliott conjecture along independent polynomials’, Int. Math. Res. Not. IMRN 2018(12) (2018), 3721–3743.Google Scholar
Frantzikinakis, N., ‘Ergodicity of the Liouville system implies the Chowla conjecture’, Discrete Anal. 19 (2017), 41pp.Google Scholar
Granville, A. and Soundararajan, K., ‘The spectrum of multiplicative functions’, Ann. of Math. (2) 153(2) (2001), 407–470.CrossRefGoogle Scholar
Granville, A. and Soundararajan, K., ‘Decay of mean values of multiplicative functions’, Canad. J. Math. 55(6) (2003), 1191–1230.Google Scholar
Halász, G., ‘Über die Mittelwerte multiplikativer zahlentheoretischer Funktionen’, Acta Math. Acad. Sci. Hungar. 19 (1968), 365–403.Google Scholar
Hall, R. R., ‘A sharp inequality of Halász type for the mean value of a multiplicative arithmetic function’, Mathematika 42(1) (1995), 144–157.CrossRefGoogle Scholar
Hildebrand, A., ‘On a conjecture of Balog’, Proc. Amer. Math. Soc. 95(4) (1985), 517–523.Google Scholar
Hildebrand, A. and Tenenbaum, G., ‘Integers without large prime factors’, J. Théor. Nombres Bordeaux 5(2) (1993), 411–484.Google Scholar
Iwaniec, H. and Kowalski, E., Analytic Number Theory, American Mathematical Society Colloquium Publications, 53 (American Mathematical Society, Providence, RI, 2004).Google Scholar
Klurman, O., ‘Correlations of multiplicative functions and applications’, Compos. Math. 153(8) (2017), 1622–1657.CrossRefGoogle Scholar
Mangerel, A. P., On the Bivariate Erdős–Kac Theorem and Correlations of the Möbius Function, ArXiv e-prints, 2016.Google Scholar
Matomäki, K. and Radziwiłł, M., ‘Multiplicative functions in short intervals’, Ann. of Math. (2) 183(3) (2016), 1015–1056.Google Scholar
Matomäki, K., Radziwiłł, M. and Tao, T., ‘An averaged form of Chowla’s conjecture’, Algebra Number Theory 9(9) (2015), 2167–2196.CrossRefGoogle Scholar
Matomäki, K., Radziwiłł, M. and Tao, T., ‘Sign patterns of the Liouville and Möbius functions’, Forum Math. Sigma 4(e14) (2016), 44.Google Scholar
Matthiesen, L., ‘Generalized Fourier coefficients of multiplicative functions’, Algebra Number Theory, to appear.Google Scholar
Pollack, P., ‘Arithmetic properties of polynomial specializations over finite fields’, Acta Arith. 136(1) (2009), 57–79.Google Scholar
Shparlinski, I. E., ‘Open problems on exponential and character sums’, inNumber Theory, Series on Number Theory and its Applications, 6 (World Scientific Publishing, Hackensack, NJ, 2010), 222–242.Google Scholar
Sós, V. T., ‘Turbulent years: Erdős in his correspondence with Turán from 1934 to 1940’, inPaul Erdős and his Mathematics, I (Budapest, 1999), Bolyai Soc. Math. Stud., 11 (János Bolyai Math. Soc., Budapest, 2002), 85–146.Google Scholar
Tao, T., A small remark on the Elliott conjecture. http://terrytao.wordpress.com/2015/09/18.Google Scholar
Tao, T., ‘The logarithmically averaged Chowla and Elliott conjectures for two-point correlations’, Forum Math. Pi 4(e8) (2016), 36.Google Scholar
Tao, T., ‘Equivalence of the logarithmically averaged Chowla and Sarnak conjectures’, inNumber Theory—Diophantine Problems, Uniform Distribution and Applications (Springer, Cham, 2017), 391–421.Google Scholar
Tao, T. and Teräväinen, J., ‘Odd order cases of the logarithmically averaged Chowla conjecture’, J. Théor. Nombres Bordeaux, to appear.Google Scholar
Tao, T. and Teräväinen, J., The structure of logarithmically averaged correlations of multiplicative functions, with applications to the Chowla and Elliott conjectures, ArXiv e-prints, 2017.Google Scholar
Tenenbaum, G., Introduction to Analytic and Probabilistic Number Theory, 3rd edn, Graduate Studies in Mathematics, 163 (American Mathematical Society, Providence, RI, 2015), Translated from the 2008 French edition by Patrick D. F. Ion.Google Scholar
Wang, Z., ‘On the largest prime factors of consecutive integers in short intervals’, Proc. Amer. Math. Soc. 145(8) (2017), 3211–3220.Google Scholar
Wang, Z., ‘Sur les plus grands facteurs premiers d’entiers consécutifs’, Mathematika 64(2) (2018), 343–379.Google Scholar