Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2025-01-06T03:37:08.041Z Has data issue: false hasContentIssue false
  • English
  • Français

Motivic Steenrod operations in characteristic p

Part of: Homotopy theory $K$-theory in geometry (Co)homology theory

Published online by Cambridge University Press:  13 November 2020

Eric Primozic
Eric Primozic*
Affiliation:
Mathematical and Statistical Sciences, University of Alberta, Edmonton, AB, Canada; E-mail: [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For a prime p and a field k of characteristic 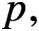$p,$ we define Steenrod operations 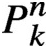$P^{n}_{k}$ on motivic cohomology with 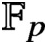$\mathbb {F}_{p}$ -coefficients of smooth varieties defined over the base field 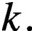$k.$ We show that 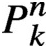$P^{n}_{k}$ is the pth power on 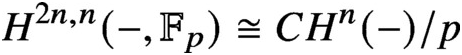$H^{2n,n}(-,\mathbb {F}_{p}) \cong CH^{n}(-)/p$ and prove an instability result for the operations. Restricted to mod p Chow groups, we show that the operations satisfy the expected Adem relations and Cartan formula. Using these new operations, we remove previous restrictions on the characteristic of the base field for Rost’s degree formula. Over a base field of characteristic 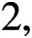$2,$ we obtain new results on quadratic forms.

MSC classification

Primary: 14F42: Motivic cohomology; motivic homotopy theory 19E15: Algebraic cycles and motivic cohomology
Secondary: 55P43: Spectra with additional structure ($E_infty$, $A_infty$, ring spectra, etc.)
Type
Topology
Information
Forum of Mathematics, Sigma , Volume 8 , 2020 , e52
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s), 2020. Published by Cambridge University Press

References

Brosnan, P., ‘Steenrod operations in Chow theory’, Trans. Amer. Math. Soc. 355(5) (2003), 1869–1903.CrossRefGoogle Scholar
Chevalley, C., ‘Sur les décompositions cellulaires des espaces G/B’, in Proc. Sympos. Pure Math., 56, Part 1—Algebraic Groups and Their Generalizations: Classical Methods (American Mathematical Society, University Park, PA, 1994), 1–23.Google Scholar
Cisinski, D.-C. and Déglise, F., ‘Triangulated categories of mixed motives’, Preprint, 2012, arxiv.org/abs/0912.2110.Google Scholar
Conrad, B., ‘Reductive group schemes’, in Autour des schémas en groupes, Vol. I: Panoramas et synthèses 42-43 (Société mathematiques de France, Paris, 2014), 94-444.Google Scholar
Demazure, M., ‘Invariants symétriques entiers des groupes de Weyl et torsion’, Invent. Math. 21 (1973), 287–302.CrossRefGoogle Scholar
Elman, R., Karpenko, N. and Merkurjev, A., The Algebraic and Geometric Theory of Quadratic Forms, Vol. 56 (American Mathematical Society, Providence, RI, 2008).Google Scholar
Elmanto, E., Hoyois, M., Khan, A. A., Sosnilo, V. and Yakerson, M., ‘Motivic infinite loop spaces’, Preprint, 2018, arxiv.org/abs/1711.05248.Google Scholar
Frankland, M. and Spitzweck, M., ‘Towards the dual motivic Steenrod algebra in positive characteristic’, Preprint, 2018, arxiv.org/pdf/1711.05230.pdf.Google Scholar
Friedlander, E. M. and Suslin, A., ‘The spectral sequence relating algebraic $K$ -theory to motivic cohomology’, Ann. Sci. Éc. Norm. Supér. (4) 35 (2002), 773–875.CrossRefGoogle Scholar
Fulton, W., Intersection Theory (Springer, New York, 1998).CrossRefGoogle Scholar
Geisser, T., ‘Motivic cohomology over Dedekind rings’, Math. Z. 248 (2004), 773–794.CrossRefGoogle Scholar
Haution, O., ‘Integrality of the Chern character in small codimension’, Adv. Math. 231(2) (2012), 855–878.CrossRefGoogle Scholar
Haution, O., ‘Duality and the topological filtration’, Math. Ann. 357(4) (2013), 1425–1454.CrossRefGoogle Scholar
Haution, O., ‘On the first Steenrod square for Chow groups’, Amer. J. Math. 135(1) (2013), 53–63.CrossRefGoogle Scholar
Haution, O., ‘Detection by regular schemes in degree two’, Algebr. Geom. 2(1) (2015), 44–61.CrossRefGoogle Scholar
Haution, O., ‘Involutions of varieties and Rost’s degree formula’, J. Reine Angew. Math. 745 (2018), 231–252.CrossRefGoogle Scholar
Hoyois, M., Kelly, S. and stvr, P. A., ‘The motivic Steenrod algebra in positive characteristic’, J. Eur. Math. Soc. (JEMS) 19(12) (2017), 3813–3849.CrossRefGoogle Scholar
Karpenko, N., ‘On the first Witt index of quadratic forms’, Invent. Math. 153(2) (2003), 455–462.CrossRefGoogle Scholar
Karpenko, N., ‘Variations on a theme of rationality of cycles’, Cent. Eur. J. Math . 11(6) (2013), 1056–1067.Google Scholar
Karpenko, N., ‘An ultimate proof of Hoffmann–Totaro’s conjecture’, Preprint, 2019, https://sites.ualberta.ca/~karpenko/ publ/ultimate05.pdf.Google Scholar
Köck, B., ‘Chow motif and higher Chow theory of G/P’, Manuscripta Math. 70(4) (1991), 363–372.CrossRefGoogle Scholar
Kondo, S. and Yasuda, S., ‘Product structures in motivic cohomology and higher Chow groups’, J. Pure Appl. Algebra 215 (2011), 511–522.CrossRefGoogle Scholar
Levine, M., ‘Techniques of localization in the theory of algebraic cycles’, J. Algebraic Geom. 10 (2001), 299–363.Google Scholar
Merkurjev, A., ‘Steenrod operations and degree formulas’, J. Reine Angew. Math. 565 (2003), 12–26.Google Scholar
Morel, F. and Voevodsky, V., ‘A1-homotopy theory of schemes’, Publ. Math. Inst. Hautes Études Sci. 90 (1999), 45–143.CrossRefGoogle Scholar
Panin, I., ‘Riemann-Roch theorems for oriented cohomology’, in NATO Science Series II: Mathematics, Physics and Chemistry, Vol. 131—Axiomatic, Enriched and Motivic Homotopy Theory, edited by Greenlees, J. P. C. (Kluwer Academic Publishing, Dordrecht, the Netherlands, 2004), 261–334.CrossRefGoogle Scholar
Riou, J., ‘Opérations de Steenrod motiviques’, Preprint, 2012, https://www.math.u-psud.fr/~riou/doc/steenrod.pdf.Google Scholar
Scully, S., ‘Hoffmann’s conjecture for totally singular forms of prime degree’, Algebra Number Theory 10(5) (2016), 1091–1132.CrossRefGoogle Scholar
Seshadri, C. S., ‘Standard monomial theory and the work of Demazure’, in Algebraic Varieties and Analytic Varieties (Mathematical Society of Japan, Tokyo, Japan, 1983), 355–384.CrossRefGoogle Scholar
Spitzweck, M., ‘A commutative ${\mathbb{P}}^1$ -spectrum representing motivic cohomology over Dedekind domains’, Mém. Soc. Math. Fr. (N.S.) 157 (2018), 1–110.Google Scholar
Totaro, B., ‘Birational geometry of quadrics in characteristic $2$ ’, J. Algebraic Geom. 17 (2008), 577–597.CrossRefGoogle Scholar
Vishik, A., ‘Fields of $u$ -invariant ${2}^r+1$ ’, Progr. Math. 270 (2009), 661–685.Google Scholar
Voevodsky, V., ‘A1 -homotopy theory’, in Proc. Int. Congr. Mathematicians , Vol. I (Doc. Math. 1998, Extra Vol. I), 579–604.Google Scholar
Voevodsky, V., ‘Motivic cohomology groups are isomorphic to higher Chow groups in any characteristic’, Int. Math. Res. Not. IMRN 7 (2002), 351–355.CrossRefGoogle Scholar
Voevodsky, V., ‘Reduced power operations in motivic cohomology’, Publ. Math. Inst. Hautes Études Sci. 98 (2003), 1–57.CrossRefGoogle Scholar