More on zeros and approximation of the Ising partition function

Abstract

We consider the problem of computing the partition function 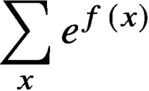$\sum _x e^{f(x)}$ , where 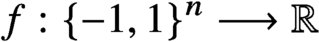$f: \{-1, 1\}^n \longrightarrow {\mathbb R}$ is a quadratic or cubic polynomial on the Boolean cube 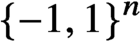$\{-1, 1\}^n$ . In the case of a quadratic polynomial f, we show that the partition function can be approximated within relative error 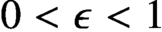$0 < \epsilon < 1$ in quasi-polynomial 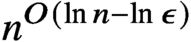$n^{O(\ln n - \ln \epsilon )}$ time if the Lipschitz constant of the non-linear part of f with respect to the 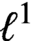$\ell ^1$ metric on the Boolean cube does not exceed 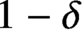$1-\delta $ , for any 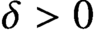$\delta>0$ , fixed in advance. For a cubic polynomial f, we get the same result under a somewhat stronger condition. We apply the method of polynomial interpolation, for which we prove that 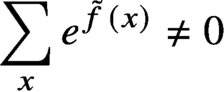$\sum _x e^{\tilde {f}(x)} \ne 0$ for complex-valued polynomials 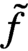$\tilde {f}$ in a neighborhood of a real-valued f satisfying the above mentioned conditions. The bounds are asymptotically optimal. Results on the zero-free region are interpreted as the absence of a phase transition in the Lee–Yang sense in the corresponding Ising model. The novel feature of the bounds is that they control the total interaction of each vertex but not every single interaction of sets of vertices.