Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Prince, Thomas
2018.
Smoothing toric Fano surfaces using the Gross-Siebert algorithm.
Proceedings of the London Mathematical Society,
Vol. 117,
Issue. 3,
p.
617.
Oneto, Alessandro
and
Petracci, Andrea
2018.
On the quantum periods of del Pezzo surfaces with ⅓ (1, 1) singularities.
Advances in Geometry,
Vol. 18,
Issue. 3,
p.
303.
Qureshi, Muhammad Imran
2020.
Polarized Rigid Del Pezzo Surfaces in Low Codimension.
Mathematics,
Vol. 8,
Issue. 9,
p.
1567.
CAVEY, Daniel
and
PRINCE, Thomas
2020.
Del Pezzo surfaces with a single $1/k(1,1)$ singularity.
Journal of the Mathematical Society of Japan,
Vol. 72,
Issue. 2,
Cavey, Daniel
and
Higashitani, Akihiro
2021.
Winding number of $r$-modular sequences and applications to the singularity content of a fano polygon.
Tohoku Mathematical Journal,
Vol. 73,
Issue. 1,
Coates, Tom
Kasprzyk, Alexander M.
Pitton, Giuseppe
and
Tveiten, Ketil
2021.
Maximally mutable Laurent polynomials.
Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences,
Vol. 477,
Issue. 2254,
Casals, Roger
and
Vianna, Renato
2022.
Full ellipsoid embeddings and toric mutations.
Selecta Mathematica,
Vol. 28,
Issue. 3,
Prince, Thomas
2022.
Interactions with Lattice Polytopes.
Vol. 386,
Issue. ,
p.
315.
Cavey, Daniel
and
Kutas, Edwin
2022.
Interactions with Lattice Polytopes.
Vol. 386,
Issue. ,
p.
115.
Petracci, Andrea
2023.
Birational Geometry, Kähler–Einstein Metrics and Degenerations.
Vol. 409,
Issue. ,
p.
709.
Mizuno, Yuma
2024.
q-Painlevé equations on cluster Poisson varieties via toric geometry.
Selecta Mathematica,
Vol. 30,
Issue. 2,
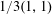 $1/3(1,1)$.
$1/3(1,1)$.