Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-28T15:08:30.764Z Has data issue: false hasContentIssue false
  • English
  • Français

LOCAL SYSTEMS ON COMPLEMENTS OF ARRANGEMENTS OF SMOOTH, COMPLEX ALGEBRAIC HYPERSURFACES

Part of: Homology and cohomology theories Singularities Low-dimensional topology Homotopy theory Holomorphic convexity Special varieties Applied homological algebra and category theory Fiber spaces and bundles Connections with homological algebra and category theory

Published online by Cambridge University Press:  23 May 2018

GRAHAM DENHAM  and
ALEXANDER I. SUCIU
GRAHAM DENHAM
Affiliation:
Department of Mathematics, University of Western Ontario, London, ON N6A 5B7, Canada; [email protected]
ALEXANDER I. SUCIU
Affiliation:
Department of Mathematics, Northeastern University, Boston, MA 02115, USA; [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We consider smooth, complex quasiprojective varieties 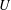$U$ that admit a compactification with a boundary, which is an arrangement of smooth algebraic hypersurfaces. If the hypersurfaces intersect locally like hyperplanes, and the relative interiors of the hypersurfaces are Stein manifolds, we prove that the cohomology of certain local systems on 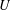$U$ vanishes. As an application, we show that complements of linear, toric, and elliptic arrangements are both duality and abelian duality spaces.

MSC classification

Primary: 55N25: Homology with local coefficients, equivariant cohomology
Secondary: 14M27: Compactifications; symmetric and spherical varieties 20J05: Homological methods in group theory 32E10: Stein spaces, Stein manifolds 32S22: Relations with arrangements of hyperplanes 55P62: Rational homotopy theory 55R80: Discriminantal varieties, configuration spaces 55U30: Duality 57M07: Topological methods in group theory
Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 6 , 2018 , e6
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2018

References

Azam, H., ‘Cohomology groups of configuration spaces of Riemann surfaces’, Bull. Math. Soc. Sci. Math. Roumanie (N.S.) 58(1) (2015), 33–47.Google Scholar
Bibby, C., ‘Cohomology of abelian arrangements’, Proc. Amer. Math. Soc. 144(7) (2016), 3093–3104.Google Scholar
Bieri, R. and Eckmann, B., ‘Groups with homological duality generalizing Poincaré duality’, Invent. Math. 20 (1973), 103–124.Google Scholar
Budur, N., ‘Complements and higher resonance varieties of hyperplane arrangements’, Math. Res. Lett. 18(5) (2011), 859–873.Google Scholar
Casto, K., ‘ $\text{FI}_{g}$ -modules, orbit configuration spaces, and complex reflection groups’, Preprint, 2016, arXiv:1608.06317v1.Google Scholar
Cohen, F. R., Kohno, T. and Xicoténcatl, M. A., ‘Orbit configuration spaces associated to discrete subgroups of PSL(2, ℝ)’, J. Pure Appl. Algebra 213(12) (2009), 2289–2300.Google Scholar
Davis, M. W., Januszkiewicz, T. and Leary, I. J., ‘The l 2 -cohomology of hyperplane complements’, Groups Geom. Dyn. 1(3) (2007), 301–309.Google Scholar
Davis, M. W., ‘Complements of hyperplane arrangements as posets of spaces’, Preprint, 2015, arXiv:1502.03650v2, comment and abstract.Google Scholar
Davis, M. W., Januszkiewicz, T., Leary, I. J. and Okun, B., ‘Cohomology of hyperplane complements with group ring coefficients’, Int. Math. Res. Not. IMRN 9 (2011), 2110–2116.Google Scholar
Davis, M. W. and Settepanella, S., ‘Vanishing results for the cohomology of complex toric hyperplane complements’, Publ. Mat. 57(2) (2013), 379–392.Google Scholar
De Concini, C. and Gaiffi, G., ‘Projective wonderful models for toric arrangements’, Preprint, 2016, arXiv:1608.08746v1.Google Scholar
De Concini, C. and Procesi, C., ‘Wonderful models of subspace arrangements’, Selecta Math. (N.S.) 1(3) (1995), 459–494.Google Scholar
Denham, G., Suciu, A. I. and Yuzvinsky, S., ‘Combinatorial covers and vanishing of cohomology’, Selecta Math. (N.S.) 22(2) (2016), 561–594.Google Scholar
Denham, G., Suciu, A. I. and Yuzvinsky, S., ‘Abelian duality and propagation of resonance’, Selecta Math. (N.S.) 23(4) (2017), 2331–2367.Google Scholar
Docquier, F. and Grauert, H., ‘Levisches Problem und Rungescher Satz für Teilgebiete Steinscher Mannigfaltigkeiten’, Math. Ann. 140 (1960), 94–123.Google Scholar
Dupont, C., ‘The Orlik–Solomon model for hypersurface arrangements’, Ann. Inst. Fourier (Grenoble) 65(6) (2015), 2507–2545.Google Scholar
Eckmann, B., ‘Introduction to ℓ 2 -methods in topology: reduced ℓ 2 -homology, harmonic chains, ℓ 2 -Betti numbers’, Israel J. Math. 117(1) (2000), 183–219.Google Scholar
Esnault, H., Schechtman, V. and Viehweg, E., ‘Cohomology of local systems on the complement of hyperplanes’, Invent. Math. 109(3) (1992), 557–561.Google Scholar
Esterov, A. and Takeuchi, K., ‘On vanishing theorems for local systems associated to Laurent polynomials’, Nagoya J. Math. (2017), 1–22. doi:10.1017/nmj.2017.8.Google Scholar
Fadell, E. and Neuwirth, L., ‘Configuration spaces’, Math. Scand. 10 (1962), 111–118.Google Scholar
Feichtner, E. M., ‘De Concini-Procesi wonderful arrangement models: a discrete geometer’s point of view’, inCombinatorial and Computational Geometry, Mathematical Sciences Research Institute Publications, 52 (Cambridge University Press, Cambridge, 2005), 333–360.Google Scholar
Feichtner, E. M. and Yuzvinsky, S., ‘Chow rings of toric varieties defined by atomic lattices’, Invent. Math. 155(3) (2004), 515–536.Google Scholar
Feichtner, E. M. and Ziegler, G. M., ‘The integral cohomology algebras of ordered configuration spaces of spheres’, Doc. Math. 5 (2000), 115–139.Google Scholar
Félix, Y., Halperin, S. and Thomas, J.-C., Rational Homotopy Theory, Graduate Texts in Mathematics, 205 (Springer, New York, 2001).Google Scholar
Félix, Y. and Thomas, J.-C., ‘Rational Betti numbers of configuration spaces’, Topology Appl. 102(2) (2000), 139–149.Google Scholar
Forstnerič, F., Stein Manifolds and Holomorphic Mappings. The Homotopy Principle in Complex Analysis, Ergebnisse der Mathematik und ihrer Grenzgebiete, 56 (Springer, Heidelberg, 2011).Google Scholar
Fritzsche, K. and Grauert, H., From Holomorphic Functions to Complex Manifolds, Graduate Texts in Mathematics, 213 (Springer, New York, 2002).Google Scholar
Griffiths, P. and Morgan, J., Rational Homotopy Theory and Differential Forms, second edition, Progress in Mathematics, 16 (Springer, New York, 2013).Google Scholar
Kohno, T., ‘Homology of a local system on the complement of hyperplanes’, Proc. Japan Acad. Ser. A Math. Sci. 62(4) (1986), 144–147.Google Scholar
Levin, A. and Varchenko, A., Cohomology of the Complement to an Elliptic Arrangement, Configuration spaces, CRM Series, 14 (2012), 373–388. Ed. Norm., Pisa.Google Scholar
Li, L., ‘Wonderful compactification of an arrangement of subvarieties’, Michigan Math. J. 58(2) (2009), 535–563.Google Scholar
Liu, Y., Maxim, L. and Wang, B., ‘Topology of subvarieties of complex semi-abelian varieties’, Preprint, 2017, arXiv:1706.07491v1.Google Scholar
Liu, Y., Maxim, L. and Wang, B., ‘Mellin transformation, propagation, and abelian duality spaces’, Preprint, 2017, arXiv:1709.02870v2.Google Scholar
Lück, W., L 2 -invariants: Theory and Applications to Geometry and K-theory, Ergebnisse der Mathematik und ihrer Grenzgebiete. (3), 44 (Springer, Berlin, 2002).Google Scholar
Maguire, M., ‘Computing cohomology of configuration spaces (with an appendix by Matthew Christie and Derek Francour)’, Preprint, 2016, arXiv:1612.06314v1.Google Scholar
Schechtman, V., Terao, H. and Varchenko, A., ‘Local systems over complements of hyperplanes and the Kac-Kazhdan conditions for singular vectors’, J. Pure Appl. Algebra 100(1–3) (1995), 93–102.Google Scholar
Suciu, A. I. and Wang, H., ‘Formality properties of finitely generated groups and Lie algebras’, Preprint, 2015, arXiv:1504.08294.Google Scholar
Totaro, B., ‘Configuration spaces of algebraic varieties’, Topology 35(4) (1996), 1057–1067.Google Scholar
Xicoténcatl Merino, M. A., ‘Orbit configuration spaces, infinitesimal braid relations in homology and equivariant loop spaces’, PhD Thesis, University of Rochester, 1997.Google Scholar
Yakovleva, O. V., ‘On the Stein property of the complement of an algebraic surface in a toric manifold’, Sibirsk. Mat. Zh. 39(3) (1998), 703–713.Google Scholar