Hostname: page-component-745bb68f8f-l4dxg Total loading time: 0 Render date: 2025-02-06T16:04:16.014Z Has data issue: false hasContentIssue false
  • English
  • Français

THE LIPMAN–ZARISKI CONJECTURE IN GENUS ONE HIGHER

Part of: Surfaces and higher-dimensional varieties Differential algebra Local theory Singularities

Published online by Cambridge University Press:  23 April 2020

HANNAH BERGNER  and
PATRICK GRAF
HANNAH BERGNER
Affiliation:
Mathematisches Institut, Albert-Ludwigs-Universität Freiburg, Ernst-Zermelo-Straße 1, 79104Freiburg im Breisgau, Germany; [email protected]
PATRICK GRAF
Affiliation:
Department of Mathematics, University of Utah, 155 South 1400 East, Salt Lake City, UT84112, USA; [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We prove the Lipman–Zariski conjecture for complex surface singularities with 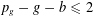$p_{g}-g-b\leqslant 2$. Here 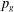$p_{g}$ is the geometric genus, 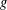$g$ is the sum of the genera of exceptional curves and 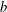$b$ is the first Betti number of the dual graph. This improves on a previous result of the second author. As an application, we show that a compact complex surface with a locally free tangent sheaf is smooth as soon as it admits two generically linearly independent twisted vector fields and its canonical sheaf has at most two global sections.

MSC classification

Primary: 14B05: Singularities
Secondary: 14J17: Singularities 32S25: Surface and hypersurface singularities 13N15: Derivations
Type
Algebraic and Complex Geometry
Information
Forum of Mathematics, Sigma , Volume 8 , 2020 , e21
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2020

References

Akhiezer, D. N., Lie Group Actions in Complex Analysis, Aspects of Mathematics, E27 (Friedr. Vieweg & Sohn, Braunschweig, 1995).CrossRefGoogle Scholar
Barth, W. P., Hulek, K., Peters, C. A. M. and Van de Ven, A., Compact Complex Surfaces, second edn, Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge. A Series of Modern Surveys in Mathematics [Results in Mathematics and Related Areas. 3rd Series. A Series of Modern Surveys in Mathematics], 4 (Springer, Berlin, 2004).CrossRefGoogle Scholar
Becker, J., ‘Higher derivations and integral closure’, Amer. J. Math. 100(3) (1978), 495–521.Google Scholar
Burns, D. M. and Wahl, J. M., ‘Local contributions to global deformations of surfaces’, Invent. Math. 26 (1974), 67–88.CrossRefGoogle Scholar
Campana, F., Demailly, J.-P. and Peternell, Th., ‘The algebraic dimension of compact complex threefolds with vanishing second Betti number’, Compos. Math. 112(1) (1998), 77–91.CrossRefGoogle Scholar
Flenner, H., ‘Extendability of differential forms on non-isolated singularities’, Invent. Math. 94(2) (1988), 317–326.CrossRefGoogle Scholar
Graf, P., The Lipman–Zariski conjecture in low genus, published electronically in IMRN, July 2019.Google Scholar
Graf, P. and Kovács, S. J., ‘An optimal extension theorem for 1-forms and the Lipman–Zariski Conjecture’, Doc. Math. 19 (2014), 815–830.Google Scholar
Kodaira, K., ‘On the structure of compact complex analytic surfaces, II’, Amer. J. Math. 88 (1966), 682–721.Google Scholar
Kollár, J., Lectures on Resolution of Singularities, Annals of Mathematics Studies, 166 (Princeton University Press, Princeton, NJ, 2007).Google Scholar
Kollár, J. and Mori, S., Birational Geometry of Algebraic Varieties, Cambridge Tracts in Mathematics, 134 (Cambridge University Press, Cambridge, 1998).CrossRefGoogle Scholar
Lipman, J., ‘Free derivation modules on algebraic varieties’, Amer. J. Math. 87(4) (1965), 874–898.Google Scholar
Seidenberg, A., ‘Differential ideals in rings of finitely generated type’, Amer. J. Math. 89 (1967), 22–42.CrossRefGoogle Scholar
van Straten, D. and Steenbrink, J. H. M., ‘Extendability of holomorphic differential forms near isolated hypersurface singularities’, Abh. Math. Semin. Univ. Hambg. 55 (1985), 97–110.CrossRefGoogle Scholar