Article contents
LIFTING TORSION GALOIS REPRESENTATIONS
Published online by Cambridge University Press: 24 August 2015
Abstract
Let 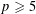 $p\geqslant 5$ be a prime, and let
$p\geqslant 5$ be a prime, and let 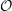 ${\mathcal{O}}$ be the ring of integers of a finite extension
${\mathcal{O}}$ be the ring of integers of a finite extension 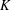 $K$ of
$K$ of 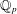 $\mathbb{Q}_{p}$ with uniformizer
$\mathbb{Q}_{p}$ with uniformizer  ${\it\pi}$. Let
${\it\pi}$. Let 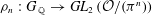 ${\it\rho}_{n}:G_{\mathbb{Q}}\rightarrow \mathit{GL}_{2}\left({\mathcal{O}}/({\it\pi}^{n})\right)$ have modular mod-
${\it\rho}_{n}:G_{\mathbb{Q}}\rightarrow \mathit{GL}_{2}\left({\mathcal{O}}/({\it\pi}^{n})\right)$ have modular mod- ${\it\pi}$ reduction
${\it\pi}$ reduction 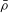 $\bar{{\it\rho}}$, be ordinary at
$\bar{{\it\rho}}$, be ordinary at 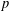 $p$, and satisfy some mild technical conditions. We show that
$p$, and satisfy some mild technical conditions. We show that 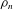 ${\it\rho}_{n}$ can be lifted to an
${\it\rho}_{n}$ can be lifted to an 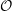 ${\mathcal{O}}$-valued characteristic-zero geometric representation which arises from a newform. This is new in the case when
${\mathcal{O}}$-valued characteristic-zero geometric representation which arises from a newform. This is new in the case when 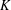 $K$ is a ramified extension of
$K$ is a ramified extension of 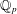 $\mathbb{Q}_{p}$. We also show that a prescribed ramified complete discrete valuation ring
$\mathbb{Q}_{p}$. We also show that a prescribed ramified complete discrete valuation ring 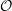 ${\mathcal{O}}$ is the weight-
${\mathcal{O}}$ is the weight-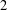 $2$ deformation ring for
$2$ deformation ring for 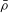 $\bar{{\it\rho}}$ for a suitable choice of auxiliary level. This implies that the field of Fourier coefficients of newforms of weight 2, square-free level, and trivial nebentype that give rise to semistable
$\bar{{\it\rho}}$ for a suitable choice of auxiliary level. This implies that the field of Fourier coefficients of newforms of weight 2, square-free level, and trivial nebentype that give rise to semistable 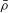 $\bar{{\it\rho}}$ of weight 2 can have arbitrarily large ramification index at
$\bar{{\it\rho}}$ of weight 2 can have arbitrarily large ramification index at 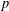 $p$.
$p$.
- Type
- Research Article
- Information
- Creative Commons
- This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
- Copyright
- © The Author(s) 2015
References
A correction has been issued for this article:
- 4
- Cited by
Linked content
Please note a has been issued for this article.



