Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-24T11:36:47.477Z Has data issue: false hasContentIssue false
  • English
  • Français

INVARIANT MEASURES CONCENTRATED ON COUNTABLE STRUCTURES

Part of: Model theory Graph theory Stochastic processes Infinite-dimensional dissipative dynamical systems Distribution theory

Published online by Cambridge University Press:  28 June 2016

NATHANAEL ACKERMAN ,
CAMERON FREER  and
REHANA PATEL
NATHANAEL ACKERMAN
Affiliation:
Department of Mathematics, Harvard University, One Oxford Street, Cambridge, MA 02138, USA; [email protected]
CAMERON FREER
Affiliation:
Computer Science and Artificial Intelligence Laboratory, Massachusetts Institute of Technology, 32 Vassar Street, Cambridge, MA 02139, USA; [email protected]
REHANA PATEL
Affiliation:
Franklin W. Olin College of Engineering, 1000 Olin Way, Needham, MA 02492, USA; [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 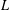$L$ be a countable language. We say that a countable infinite 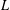$L$ -structure 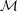${\mathcal{M}}$ admits an invariant measure when there is a probability measure on the space of 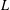$L$ -structures with the same underlying set as 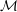${\mathcal{M}}$ that is invariant under permutations of that set, and that assigns measure one to the isomorphism class of 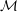${\mathcal{M}}$ . We show that 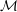${\mathcal{M}}$ admits an invariant measure if and only if it has trivial definable closure, that is, the pointwise stabilizer in $\text{Aut}({\mathcal{M}})$ of an arbitrary finite tuple of ${\mathcal{M}}$ fixes no additional points. When 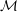${\mathcal{M}}$ is a Fraïssé limit in a relational language, this amounts to requiring that the age of 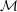${\mathcal{M}}$ have strong amalgamation. Our results give rise to new instances of structures that admit invariant measures and structures that do not.

MSC classification

Primary: 03C98: Applications of model theory
Secondary: 60G09: Exchangeability 37L40: Invariant measures 05C80: Random graphs 03C75: Other infinitary logic 62E10: Characterization and structure theory 05C63: Infinite graphs
Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 4 , 2016 , e17
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2016

References

Ackerman, N., Freer, C., Nešetřil, J. and Patel, R., ‘Invariant measures via inverse limits of finite structures’, European J. Combin. 52(2016) 248–289.CrossRefGoogle Scholar
Ackerman, N. L., ‘A characterization of quasitrivial $n$ -semigroups’, Algebra Universalis, to appear.Google Scholar
Ahlbrandt, G. and Ziegler, M., ‘Quasi-finitely axiomatizable totally categorical theories’, Ann. Pure Appl. Logic 30(1) (1986), 63–82.CrossRefGoogle Scholar
Aldous, D. J., ‘Representations for partially exchangeable arrays of random variables’, J. Multivariate Anal. 11(4) (1981), 581–598.CrossRefGoogle Scholar
Austin, T., ‘On exchangeable random variables and the statistics of large graphs and hypergraphs’, Probab. Surv. 5(2008) 80–145.Google Scholar
Austin, T., ‘Razborov flag algebras as algebras of measurable functions’, Preprint, 2008, arXiv:0801.1538.Google Scholar
Barwise, J., Admissible Sets and Structures: An Approach to Definability Theory, Perspectives in Mathematical Logic (Springer, Berlin, 1975).CrossRefGoogle Scholar
Becker, H. and Kechris, A. S., The Descriptive Set Theory of Polish Group Actions, London Mathematical Society Lecture Note Series, 232 (Cambridge University Press, Cambridge, 1996).Google Scholar
Cameron, P. J., Oligomorphic Permutation Groups, London Mathematical Society Lecture Note Series, 152 (Cambridge University Press, Cambridge, 1990).Google Scholar
Cameron, P. J., ‘Homogeneous permutations’, Electron. J. Combin. 9(2) (2002/03), Research paper 2.Google Scholar
Cameron, P. J. and Vershik, A. M., ‘Some isometry groups of the Urysohn space’, Ann. Pure Appl. Logic 143(1–3) (2006), 70–78.Google Scholar
Cherlin, G., ‘Homogeneous directed graphs. The imprimitive case’, inLogic Colloquium ’85 (Orsay, 1985), Studies in Logic and the Foundations of Mathematics, 122 (North-Holland, Amsterdam, 1987), 67–88.Google Scholar
Cherlin, G., The Classification of Countable Homogeneous Directed Graphs and Countable Homogeneous n-Tournaments, Memoirs of the American Mathematical Society, 131 (American Mathematical Society, Providence, RI, 1998).Google Scholar
Cherlin, G., ‘Two problems on homogeneous structures, revisited’, inModel-Theoretic Methods in Finite Combinatorics, Contemporary Mathematics, 558 (American Mathematical Society, Providence, RI, 2011), 319–415.Google Scholar
Cherlin, G., Shelah, S. and Shi, N., ‘Universal graphs with forbidden subgraphs and algebraic closure’, Adv. Appl. Math. 22(4) (1999), 454–491.CrossRefGoogle Scholar
Cherlin, G. and Tallgren, L., ‘Universal graphs with a forbidden near-path or 2-bouquet’, J. Graph Theory 56(1) (2007), 41–63.Google Scholar
Diaconis, P. and Janson, S., ‘Graph limits and exchangeable random graphs’, Rend. Mat. Appl. (7) 28(1) (2008), 33–61.Google Scholar
Dolinka, I. and Mašulović, D., ‘Properties of the automorphism group and a probabilistic construction of a class of countable labeled structures’, J. Combin. Theory Ser. A 119(5) (2012), 1014–1030.Google Scholar
Droste, M. and Kuske, D., ‘On random relational structures’, J.  Combin. Theory Ser. A 102(2) (2003), 241–254.Google Scholar
Erdős, P., Kleitman, D. J. and Rothschild, B. L., ‘Asymptotic enumeration of K n -free graphs’, inColloquio Internazionale sulle Teorie Combinatorie (Rome, 1973), Tomo II, Atti dei Convegni Lincei, 17 (Accad. Naz. Lincei, Rome, 1976), 19–27.Google Scholar
Erdős, P. and Rényi, A., ‘On random graphs. I’, Publ. Math. Debrecen 6(1959) 290–297.Google Scholar
Gaifman, H., ‘Concerning measures in first order calculi’, Israel J. Math. 2(1964) 1–18.Google Scholar
Gao, S., ‘Complexity ranks of countable models’, Notre Dame J. Form. Log. 48(1) (2007), 33–48.Google Scholar
Gilbert, E. N., ‘Random graphs’, Ann. Math. Statist. 30(1959) 1141–1144.Google Scholar
Henson, C. W., ‘A family of countable homogeneous graphs’, Pacific J. Math. 38(1971) 69–83.Google Scholar
Henson, C. W., ‘Countable homogeneous relational structures and ℵ 0 -categorical theories’, J. Symbolic Logic 37(1972) 494–500.Google Scholar
Hodges, W., Model Theory, Encyclopedia of Mathematics and its Applications, 42 (Cambridge University Press, Cambridge, 1993).CrossRefGoogle Scholar
Hoover, D. N., ‘Relations on probability spaces and arrays of random variables’, Preprint, 1979, Institute for Advanced Study, Princeton, NJ.Google Scholar
Hoppen, C., Kohayakawa, Y., Moreira, C. G., Ráth, B., Menezes, R. and Sampaio, ‘Limits of permutation sequences’, J. Combin. Theory Ser. B 103(1) (2013), 93–113.Google Scholar
Hubička, J. and Nešetřil, J., ‘Homomorphism and embedding universal structures for restricted classes’, Preprint, 2014, arXiv:0909.4939.Google Scholar
Janson, S., ‘Poset limits and exchangeable random posets’, Combinatorica 31(5) (2011), 529–563.Google Scholar
Janson, S., Graphons, Cut Norm and Distance, Couplings and Rearrangements, New York Journal of Mathematics NYJM Monographs, 4 (State University of New York, University at Albany, Albany, NY, 2013).Google Scholar
Kallenberg, O., ‘Symmetries on random arrays and set-indexed processes’, J. Theoret. Probab. 5(4) (1992), 727–765.Google Scholar
Kallenberg, O., ‘Multivariate sampling and the estimation problem for exchangeable arrays’, J. Theoret. Probab. 12(3) (1999), 859–883.Google Scholar
Kallenberg, O., Foundations of Modern Probability, 2nd edn, Probability and its Applications (Springer, New York, 2002).Google Scholar
Kallenberg, O., Probabilistic Symmetries and Invariance Principles, Probability and its Applications (Springer, New York, 2005).Google Scholar
Kechris, A. S., Classical Descriptive Set Theory, Graduate Texts in Mathematics, 156 (Springer, New York, 1995).Google Scholar
Keisler, H. J., Model Theory for Infinitary Logic: Logic with Countable Conjunctions and Finite Quantifiers, Studies in Logic and the Foundations of Mathematics, 62 (North-Holland Publishing Co., Amsterdam, 1971).Google Scholar
Keisler, H. J. and Knight, J. F., ‘Barwise: infinitary logic and admissible sets’, Bull. Symbolic Logic 10(1) (2004), 4–36.Google Scholar
Kolaitis, P. G., Prömel, H. J. and Rothschild, B. L., ‘ K l+1 -free graphs: asymptotic structure and a 0–1 law’, Trans. Amer. Math. Soc. 303(2) (1987), 637–671.Google Scholar
Komjáth, P., ‘Some remarks on universal graphs’, Discrete Math. 199(1–3) (1999), 259–265.Google Scholar
Krauss, P. H., ‘Representation of symmetric probability models’, J. Symbolic Logic 34(1969) 183–193.Google Scholar
Lachlan, A. H., ‘Countable homogeneous tournaments’, Trans. Amer. Math. Soc. 284(2) (1984), 431–461.Google Scholar
Lachlan, A. H. and Woodrow, R. E., ‘Countable ultrahomogeneous undirected graphs’, Trans. Amer. Math. Soc. 262(1) (1980), 51–94.Google Scholar
Lovász, L., Large Networks and Graph Limits, American Mathematical Society. Colloquium Publications, 60 (American Mathematical Society, Providence, RI, 2012).CrossRefGoogle Scholar
Lovász, L. and Szegedy, B., ‘Limits of dense graph sequences’, J. Combin. Theory Ser. B 96(6) (2006), 933–957.Google Scholar
Lovász, L. and Szegedy, B., ‘Regularity partitions and the topology of graphons’, inAn Irregular Mind, Bolyai Society Mathematical Studies, 21 (János Bolyai Mathematical Society, Budapest, 2010), 415–446.CrossRefGoogle Scholar
Lovász, L. and Szegedy, B., ‘Random graphons and a weak Positivstellensatz for graphs’, J. Graph Theory 70(2) (2012), 214–225.Google Scholar
Macpherson, D., ‘A survey of homogeneous structures’, Discrete Math. 311(15) (2011), 1599–1634.CrossRefGoogle Scholar
Marker, D., Model Theory, Graduate Texts in Mathematics, 217 (Springer, New York, 2002).Google Scholar
Montalbán, A. and Nies, A., ‘Borel structures: a brief survey’, inEffective Mathematics of the Uncountable, Lecture Notes in Logic, 41 (Association for Symbolic Logic, La Jolla, CA, 2013), 124–134.Google Scholar
Petrov, F. and Vershik, A., ‘Uncountable graphs and invariant measures on the set of universal countable graphs’, Random Structures Algorithms 37(3) (2010), 389–406.Google Scholar
Rado, R., ‘Universal graphs and universal functions’, Acta Arith. 9(1964) 331–340.Google Scholar
Razborov, A. A., ‘Flag algebras’, J. Symbolic Logic 72(4) (2007), 1239–1282.Google Scholar
Schmerl, J. H., ‘Countable homogeneous partially ordered sets’, Algebra Universalis 9(3) (1979), 317–321.Google Scholar
Scott, D. and Krauss, P., ‘Assigning probabilities to logical formulas’, inAspects of Inductive Logic (eds. Hintikka, J. and Suppes, P.) Studies in Logic and the Foundations of Mathematics (North-Holland, Amsterdam, 1966), 219–259.Google Scholar
Steinhorn, C. I., ‘Borel structures and measure and category logics’, inModel-Theoretic Logics, Perspectives in Mathematical Logic (Springer, New York, 1985), 579–596.Google Scholar
Usvyatsov, A., ‘Generic separable metric structures’, Topology Appl. 155(14) (2008), 1607–1617.Google Scholar
Vershik, A. M., ‘Classification of measurable functions of several arguments, and invariantly distributed random matrices’, Funktsional. Anal. i Prilozhen. 36(2) (2002), 12–27. 95.Google Scholar
Vershik, A. M., ‘A random metric space is a Urysohn space’, Dokl. Akad. Nauk 387(6) (2002), 733–736.Google Scholar
Vershik, A. M., ‘Random metric spaces and universality’, Uspekhi Mat. Nauk 59(2(356)) (2004), 65–104.Google Scholar
Williams, D., Probability with Martingales (Cambridge University Press, Cambridge, 1991).Google Scholar