Hostname: page-component-5cf477f64f-xc2pj Total loading time: 0 Render date: 2025-04-07T12:30:28.217Z Has data issue: false hasContentIssue false
  • English
  • Français

THE INTERSECTION MOTIVE OF THE MODULI STACK OF SHTUKAS

Part of: Linear algebraic groups and related topics $K$-theory in geometry Special varieties

Published online by Cambridge University Press:  03 February 2020

TIMO RICHARZ  and
JAKOB SCHOLBACH Open the ORCID record for JAKOB SCHOLBACH [Opens in a new window]
TIMO RICHARZ
Affiliation:
TU Darmstadt, Germany; [email protected]
JAKOB SCHOLBACH
Affiliation:
Universität Münster, Germany; [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For a split reductive group 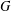$G$ over a finite field, we show that the intersection (cohomology) motive of the moduli stack of iterated 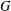$G$-shtukas with bounded modification and level structure is defined independently of the standard conjectures on motivic $t$-structures on triangulated categories of motives. This is in accordance with general expectations on the independence of 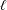$\ell$ in the Langlands correspondence for function fields.

MSC classification

Primary: 20G05: Representation theory
Secondary: 14M15: Grassmannians, Schubert varieties, flag manifolds 19E15: Algebraic cycles and motivic cohomology
Type
Algebra
Information
Forum of Mathematics, Sigma , Volume 8 , 2020 , e8
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2020

References

Artin, D. M., Grothendieck, A. and Verdier, J. L., Théorie des topos et cohomologie étale des schémas. Tome 3. Lecture Notes in Mathematics, 305. Springer, Berlin, 1973. Séminaire de Géométrie Algébrique du Bois-Marie 1963–1964 (SGA 4). Avec la collaboration de P. Deligne et B. Saint-Donat.Google Scholar
Ayoub, J., ‘Les six opérations de Grothendieck et le formalisme des cycles évanescents dans le monde motivique. I’, Astérisque 314 (2008), x+466 pp, 2007.Google Scholar
Ayoub, J., ‘Les six opérations de Grothendieck et le formalisme des cycles évanescents dans le monde motivique. II’, Astérisque (315) (2008), vi+364 pp, 2007.Google Scholar
Ayoub, J., ‘La réalisation étale et les opérations de Grothendieck’, Annales Scientifiques de L’ens 47(1) (2014), 1–145. doi:10.24033/asens.2210.Google Scholar
Bachmann, T., ‘Affine Grassmannians in 𝔸1 -homotopy theory’, Selecta Math. (N.S.) 25(2) (2019), Art. 25, 14. doi:10.1007/s00029-019-0471-1.CrossRefGoogle Scholar
Beĭlinson, A. A., Bernstein, J. and Deligne, P., ‘Faisceaux pervers’, inAnalysis and Topology on Singular Spaces, I (Luminy, 1981), Astérisque, 100 (Soc. Math. France, Paris, 1982), 5–171.Google Scholar
Beilinson, A. and Drinfeld, V., ‘Quantization of Hitchin’s integrable system and Hecke eigensheaves’. (1999). URL: http://www.math.utexas.edu/users/benzvi/Langlands.html.Google Scholar
Bousfield, A. K. and Kan, D. M., Homotopy Limits, Completions and Localizations, Lecture Notes in Mathematics, 304 (Springer, Berlin, 1972).CrossRefGoogle Scholar
Bondarko, M. V. and Luzgarev, A. Y., ‘On relative $K$-motives, weights for them, and negative $K$-groups’. Preprint, 2016, arXiv:1605.08435.Google Scholar
Bloch, S., ‘Algebraic cycles and higher K-theory’, Adv. Math. 61(3) (1986), 267–304.CrossRefGoogle Scholar
Bosch, S., Lütkebohmert, W. and Raynaud, M., Néron Models, Ergebnisse der Mathematik und ihrer Grenzgebiete (3) [Results in Mathematics and Related Areas (3)], 21 (Springer, Berlin, 1990), doi:10.1007/978-3-642-51438-8.CrossRefGoogle Scholar
Bunke, U. and Nikolaus, T., ‘Twisted differential cohomology’, Algebr. Geom. Topol. 19(4) (2019), 1631–1710.CrossRefGoogle Scholar
Bondarko, M. V., ‘Weight structures and ‘weights’ on the hearts of t-structures’, Homology, Homotopy Appl. 14(1) (2012), 239–261.CrossRefGoogle Scholar
Bondarko, M. V., ‘Weights for relative motives: relation with mixed complexes of sheaves’, Int. Math. Res. Not. IMRN (17) (2014), 4715–4767.CrossRefGoogle Scholar
Bourbaki, N., Éléments de mathématique. Fasc. XXXIV. Groupes et algèbres de Lie. Chapitre IV: Groupes de Coxeter et systèmes de Tits. Chapitre V: Groupes engendrés par des réflexions. Chapitre VI: systèmes de racines. Actualités Scientifiques et Industrielles, 1337. Hermann, Paris, 1968.Google Scholar
Bondarko, M. V. and Sosnilo, V. A., ‘On purely generated 𝛼-smashing weight structures and weight-exact localizations’, J. Algebra 535 (2019), 407–455.CrossRefGoogle Scholar
Bruhat, F. and Tits, J., ‘Groupes réductifs sur un corps local. II. Schémas en groupes. Existence d’une donnée radicielle valuée’, Publ. Math. Inst. Hautes Études Sci. (60) (1984), 197–376. URL: http://www.numdam.org/item/PMIHES_1984__60__5_0/.Google Scholar
Cisinski, D.-C. and Déglise, F., ‘Triangulated categories of mixed motives’. Preprint, 2009, arXiv:0912.2110.Google Scholar
Cisinski, D.-C. and Déglise, F., ‘Étale motives’, Compos. Math. 152(3) (2016), 556–666.CrossRefGoogle Scholar
Conrad, B., ‘Reductive group schemes’, inAutour des schémas en groupes, Vol. I, Panor. Synthèses, 42/43 (Soc. Math. France, Paris, 2014), 93–444.Google Scholar
de Cataldo, M. A., Haines, T. J. and Li, L., ‘Frobenius semisimplicity for convolution morphisms’, Math. Z. 289(1–2) (2018), 119–169.CrossRefGoogle Scholar
Déglise, F., ‘Around the Gysin triangle. II’, Doc. Math. 13 (2008), 613–675.Google Scholar
Deligne, P. and Goncharov, A. B., ‘Groupes fondamentaux motiviques de Tate mixte’, Ann. Sci. Éc. Norm. Supér. (4) 38(1) (2005), 1–56.CrossRefGoogle Scholar
Dugger, D. and Isaksen, D. C., ‘Motivic cell structures’, Algebr. Geom. Topol. 5 (2005), 615–652.CrossRefGoogle Scholar
Deligne, P. and Lusztig, G., ‘Representations of reductive groups over finite fields’, Ann. of Math. (2) 103(1) (1976), 103–161.CrossRefGoogle Scholar
Edidin, D. and Graham, W., ‘Equivariant intersection theory’, Invent. Math. 131(3) (1998), 595–634.CrossRefGoogle Scholar
Emerton, M. and Gee, T., “‘Scheme-theoretic images” of morphisms of stacks’. Preprint, 2015, arXiv:1506.06146.Google Scholar
Eberhardt, J. N. and Kelly, S., ‘Mixed motives and geometric representation theory in equal characteristic’, Selecta Math. (N.S.) 25(2) Art. 30, 54, 2019. doi:10.1007/s00029-019-0475-x.Google Scholar
Faltings, G., ‘Algebraic loop groups and moduli spaces of bundles’, J. Eur. Math. Soc. (JEMS) 5(1) (2003), 41–68.CrossRefGoogle Scholar
Gaitsgory, D., ‘Notes on geometric Langlands: Generalities on DG categories’. Preprint, available at the web site of the author.Google Scholar
Giraud, J., Cohomologie non abélienne, Die Grundlehren der mathematischen Wissenschaften, Band 179 (Springer, New York, 1971).Google Scholar
Goerss, P. G. and Jardine, J. F., Simplicial Homotopy Theory, Modern Birkhäuser Classics (Birkhäuser Verlag, Basel, 2009), Reprint of the 1999 edition. doi:10.1007/978-3-0346-0189-4.CrossRefGoogle Scholar
Gaitsgory, D. and Rozenblyum, N., ‘A study in derived algebraic geometry’, inCorrespondences and Duality, Vol. I, Mathematical Surveys and Monographs, 221 (American Mathematical Society, Providence, RI, 2017).Google Scholar
Grothendieck, A., ‘Éléments de géométrie algébrique: II. Étude globale élémentaire de quelques classes de morphismes’, Publ. Math. Inst. Hautes Études Sci. (8) (1961), 222 URL: http://www.numdam.org/item/PMIHES_1961__8__5_0/.Google Scholar
Habibi, S., On the motive of a bundle, 2011. Thesis at the Universitá di Milano. URL: https://air.unimi.it/retrieve/handle/2434/212311/197090/phd_unimi_R08381.pdf.Google Scholar
Haines, T. J. and Richarz, T., ‘On the normality of Schubert varieties: remaining cases in positive characteristic’. Preprint, 2018, arXiv:1806.11001.Google Scholar
Haines, T. J. and Richarz, T., ‘The test function conjecture for local models of weil-restricted groups’. Preprint, 2018, arXiv:1805.07081.Google Scholar
Haines, T. J. and Richarz, T., ‘The test function conjecture for parahoric local models’. Preprint, 2018. arXiv:1801.07094.Google Scholar
Hanamura, M., ‘Mixed motives and algebraic cycles. I’, Math. Res. Lett. 2(6) (1995), 811–821.CrossRefGoogle Scholar
Haugseng, R., ‘Rectification of enriched ∞-categories’, Algebr. Geom. Topol. 15(4) (2015), 1931–1982.CrossRefGoogle Scholar
Hébert, D., ‘Structure de poids à la Bondarko sur les motifs de Beilinson’, Compos. Math. 147(5) (2011), 1447–1462.CrossRefGoogle Scholar
Heinloth, J., ‘Uniformization of 𝓖-bundles’, Math. Ann. 347(3) (2010), 499–528.CrossRefGoogle Scholar
Heinloth, J., ‘Langlands parameterization over function fields following V. Lafforgue’, Acta Math. Vietnam 43(1) (2018), 45–66.CrossRefGoogle Scholar
Hoskins, V. and Lehalleur, S. P., ‘A formula for the Voevodsky motive of the moduli stack of vector bundles on a curve’. Preprint, 2018, arXiv:1809.02150.Google Scholar
Hoyois, M., ‘The six operations in equivariant motivic homotopy theory’, Adv. Math. 305 (2017), 197–279. doi:10.1016/j.aim.2016.09.031.CrossRefGoogle Scholar
Illusie, L., Laszlo, Y. and Orgogozo, F., Travaux de Gabber sur l’uniformisation locale et la cohomologie étale des schémas quasi-excellents. Séminaire à l’École polytechnique 2006–2008. available at http://www.math.polytechnique.fr/∼orgogozo/, 2012.Google Scholar
Jantzen, J. C., Representations of Algebraic Groups, 2nd edn, Mathematical Surveys and Monographs, 107 (American Mathematical Society, Providence, RI, 2003).Google Scholar
Khan, A., Motivic homotopy theory in derived algebraic geometry, 2016. PhD thesis, Universität Duisburg-Essen. URL: https://duepublico.uni-duisburg-essen.de/servlets/DerivateServlet/Derivate-42021/Diss_Khan.pdf.Google Scholar
Kiehl, R. and Weissauer, R., Weil Conjectures, Perverse Sheaves and l’adic Fourier Transform, Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge. A Series of Modern Surveys in Mathematics [Results in Mathematics and Related Areas. 3rd Series. A Series of Modern Surveys in Mathematics], 42 (Springer, Berlin, 2001), doi:10.1007/978-3-662-04576-3.CrossRefGoogle Scholar
Kottwitz, R. and Rapoport, M., ‘On the existence of F-crystals’, Comment. Math. Helv. 78(1) (2003), 153–184.CrossRefGoogle Scholar
Lafforgue, V., ‘Chtoucas pour les groupes réductifs et paramétrisation de Langlands globale’, J. Amer. Math. Soc. 31(3) (2018), 719–891.CrossRefGoogle Scholar
Levin, B., ‘Local models for Weil-restricted groups’, Compos. Math. 152(12) (2016), 2563–2601.CrossRefGoogle Scholar
Levine, M., ‘Tate motives and the vanishing conjectures for algebraic K-theory’, inAlgebraic K-theory and Algebraic Topology (Lake Louise, AB, 1991), NATO Adv. Sci. Inst. Ser. C Math. Phys. Sci., 407 (Kluwer Academic Publishers, Dordrecht, 1993), 167–188.CrossRefGoogle Scholar
Levine, M., Mixed Motives, Mathematical Surveys and Monographs, 57 (American Mathematical Society, Providence, RI, 1998).CrossRefGoogle Scholar
Laszlo, Y. and Olsson, M., ‘The six operations for sheaves on Artin stacks. II. Adic coefficients’, Publ. Math. Inst. Hautes Études Sci. (107) (2008), 169–210, doi:10.1007/s10240-008-0012-5.CrossRefGoogle Scholar
Liu, Y. and Zheng, W., ‘Enhanced six operations and base change theorem for higher Artin stacks’. Preprint, 2011, arXiv:1211.5948.Google Scholar
Liu, Y. and Zheng, W., ‘Enhanced adic formalism and perverse $t$-structures for higher Artin stacks’. Preprint, 2014, arXiv:1404.1128.Google Scholar
Lurie, J., Higher Topos Theory, Annals of Mathematics Studies, 170 (Princeton University Press, Princeton, NJ, 2009).CrossRefGoogle Scholar
Lurie, J., ‘Higher Algebra’. 2017. URL: http://www.math.harvard.edu/∼lurie/.Google Scholar
Mirković, I. and Vilonen, K., ‘Geometric Langlands duality and representations of algebraic groups over commutative rings’, Ann. of Math. (2) 166(1) (2007), 95–143.CrossRefGoogle Scholar
Nikolaus, T., Schreiber, U. and Stevenson, D., ‘Principal ∞-bundles: general theory’, J. Homotopy Relat. Struct. 10(4) (2015), 749–801.CrossRefGoogle Scholar
Pappas, G. and Rapoport, M., ‘Twisted loop groups and their affine flag varieties’, Adv. Math. 219(1) (2008), 118–198. With an appendix by T. Haines and Rapoport.CrossRefGoogle Scholar
Pappas, G. and Zhu, X., ‘Local models of Shimura varieties and a conjecture of Kottwitz’, Invent. Math. 194(1) (2013), 147–254.CrossRefGoogle Scholar
Raskin, S., ‘D-modules on infinite dimensional varieties’. Preprint, available at the web site of the author.Google Scholar
Revêtements étales et groupe fondamental (SGA 1). Documents Mathématiques (Paris) [Mathematical Documents (Paris)], 3. Société Mathématique de France, Paris, 2003. Séminaire de géométrie algébrique du Bois Marie 1960–61. [Algebraic Geometry Seminar of Bois Marie 1960–61], Directed by A. Grothendieck, With two papers by M. Raynaud, Updated and annotated reprint of the 1971 original [Lecture Notes in Mathematics, 224, Springer, Berlin; MR0354651 (50 #7129)].Google Scholar
Richarz, T., ‘Schubert varieties in twisted affine flag varieties and local models’, J. Algebra 375 (2013), 121–147. doi:10.1016/j.jalgebra.2012.11.013.CrossRefGoogle Scholar
Richarz, T., ‘Affine Grassmannians and geometric Satake equivalences’, Int. Math. Res. Not. IMRN (12) (2016), 3717–3767. doi:10.1093/imrn/rnv226.CrossRefGoogle Scholar
Richarz, T., ‘On the Iwahori Weyl group’, Bull. Soc. Math. France 144(1) (2016), 117–124.CrossRefGoogle Scholar
Richarz, T. and Scholbach, J., ‘The motivic Satake isomorphism’. Preprint, 2019, arXiv:1909.08322.Google Scholar
Rozenblyum, N., Filtered colimits of $\infty$-categories. Harvard seminar notes.Google Scholar
Rydh, D., ‘Submersions and effective descent of étale morphisms’, Bull. Soc. Math. France 138(2) (2010), 181–230.CrossRefGoogle Scholar
Scholze, P., ‘Etale cohomology of diamonds’. Preprint, 2017, arXiv:1709.07343.Google Scholar
Soergel, W., ‘On the relation between intersection cohomology and representation theory in positive characteristic’, J. Pure Appl. Algebra 152(1–3) (2000), 311–335. Commutative algebra, homological algebra and representation theory (Catania/Genoa/Rome, 1998).CrossRefGoogle Scholar
The Stacks Project Authors. Stacks Project. http://stacks.math.columbia.edu, 2017.Google Scholar
Soergel, W., Virk, R. and Wendt, M., ‘Equivariant motives and geometric representation theory (with an appendix by F. Hörmann and M. Wendt)’. Preprint, 2018, arXiv:1809.05480.Google Scholar
Scholze, P. and Weinstein, J., ‘Moduli of p-divisible groups’, Camb. J. Math. 1(2) (2013), 145–237.CrossRefGoogle Scholar
Soergel, W. and Wendt, M., ‘Perverse motives and graded derived category 𝓞’, J. Inst. Math. Jussieu 17(2) (2018), 347–395.CrossRefGoogle Scholar
Tits, J., ‘Reductive groups over local fields’, inAutomorphic Forms, Representations and L-functions (Proc. Sympos. Pure Math., Oregon State Univ., Corvallis, OR, 1977), Part 1, Proceedings of Symposia in Pure Mathematics, XXXIII (American Mathematical Society, Providence, RI, 1979), 29–69.Google Scholar
Toën, B. and Vezzosi, G., ‘Homotopical algebraic geometry. II. Geometric stacks and applications’, Mem. Amer. Math. Soc. 193(902) (2008), x+224.Google Scholar
Totaro, B., ‘The Chow ring of a classifying space’, inAlgebraic K-theory (Seattle, WA, 1997), Proceedings of Symposia in Pure Mathematics, 67 (American Mathematical Society, Providence, RI, 1999), 249–281. doi:10.1090/pspum/067/1743244.Google Scholar
Totaro, B., ‘The motive of a classifying space’, Geom. Topol. 20(4) (2016), 2079–2133.CrossRefGoogle Scholar
Varshavsky, Y., ‘Moduli spaces of principal F-bundles’, Sel. Math., New Ser. 10(1) (2004), 131–166.CrossRefGoogle Scholar
Voevodsky, V., ‘Triangulated categories of motives over a field’, inCycles, Transfers, and Motivic Homology Theories, Annals of Mathematics Studies, 143 (Princeton University Press, Princeton, NJ, 2000), 188–238.Google Scholar
Wildeshaus, J., ‘Notes on Artin-Tate motives’, inAutour des motifs, Vol. III, Panorama et Synthèses, 49 (2016), 101–131.Google Scholar
Wildeshaus, J., ‘Pure motives, mixed motives and extensions of motives associated to singular surfaces’, inAutour des motifs—École d’été Franco-Asiatique de Géométrie Algébrique et de Théorie des Nombres/Asian-French Summer School on Algebraic Geometry and Number Theory. Vol. III, Panoramas et Synthèses, 49 (Soc. Math. France, Paris, 2016), 65–100.Google Scholar
Zhu, X., ‘Affine Grassmannians and the geometric Satake in mixed characteristic’, Ann. of Math. (2) 185(2) (2017), 403–492.CrossRefGoogle Scholar