Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-27T09:02:46.197Z Has data issue: false hasContentIssue false
  • English
  • Français

Hyperbolic tessellations and generators of 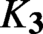${K}_{\textbf {3}}$ for imaginary quadratic fields

Part of: $K$-theory in number theory Higher algebraic $K$-theory Algebraic number theory: global fields Arithmetic algebraic geometry Real and complex geometry Other groups of matrices

Published online by Cambridge University Press:  24 May 2021

David Burns Open the ORCID record for David Burns [Opens in a new window] ,
Rob de Jeu Open the ORCID record for Rob de Jeu [Opens in a new window] ,
Herbert Gangl Open the ORCID record for Herbert Gangl [Opens in a new window] ,
Alexander D. Rahm Open the ORCID record for Alexander D. Rahm [Opens in a new window]  and
Dan Yasaki Open the ORCID record for Dan Yasaki [Opens in a new window]
David Burns
Affiliation:
King’s College London, Dept. of Mathematics, LondonWC2R 2LS, United Kingdom; E-mail: [email protected]
Rob de Jeu
Affiliation:
Faculteit der Bètawetenschappen, Afdeling Wiskunde, Vrije Universiteit Amsterdam, De Boelelaan 1111, 1081HV, Amsterdam, The Netherlands; E-mail: [email protected]
Herbert Gangl
Affiliation:
Department of Mathematical Sciences, Stockton Road, DurhamDH1 3LE, United Kingdom; E-mail: [email protected]
Alexander D. Rahm
Affiliation:
Laboratoire de mathématiques GAATI, Université de la Polynésie française, BP6570, 98702Faaa, French Polynesia; E-mail: [email protected]
Dan Yasaki
Affiliation:
Department of Mathematics and Statistics, University of North Carolina at Greensboro, PO Box 26170, Greensboro, NC27402-6170, USA; E-mail: [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We develop methods for constructing explicit generators, modulo torsion, of the 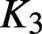$K_3$-groups of imaginary quadratic number fields. These methods are based on either tessellations of hyperbolic 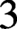$3$-space or on direct calculations in suitable pre-Bloch groups and lead to the very first proven examples of explicit generators, modulo torsion, of any infinite 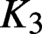$K_3$-group of a number field. As part of this approach, we make several improvements to the theory of Bloch groups for 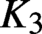$ K_3 $ of any field, predict the precise power of 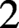$2$ that should occur in the Lichtenbaum conjecture at 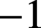$ -1 $ and prove that this prediction is valid for all abelian number fields.

MSC classification

Primary: 11G55: Polylogarithms and relations with $K$-theory 11R70: $K$-theory of global fields 19F27: Étale cohomology, higher regulators, zeta and $L$-functions 19D45: Higher symbols, Milnor $K$-theory
Secondary: 11R42: Zeta functions and $L$-functions of number fields 20H20: Other matrix groups over fields 51M20: Polyhedra and polytopes; regular figures, division of spaces
Type
Algebra
Information
Forum of Mathematics, Sigma , Volume 9 , 2021 , e40
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BYCreative Common License - NCCreative Common License - ND
This is an Open Access article, distributed under the terms of the Creative Commons Attribution-NonCommercial-NoDerivatives licence (http://creativecommons.org/licenses/by-nc-nd/4.0/), which permits non-commercial re-use, distribution, and reproduction in any medium, provided the original work is unaltered and is properly cited. The written permission of Cambridge University Press must be obtained for commercial re-use or in order to create a derivative work.
Copyright
© The Author(s), 2021. Published by Cambridge University Press

References

Ash, A., Mumford, D., Rapoport, M. and Tai, Y.-S., Smooth Compactifications of Locally Symmetric Varieties, second ed. (Cambridge Mathematical Library, Cambridge University Press, Cambridge, 2010). With the collaboration of Peter Scholze.CrossRefGoogle Scholar
Belabas, K. and Gangl, H., ‘Generators and relations for ${{K}}_2{{\mathcal{O}}}_{{F}}$’, ${K}\!$-Theory 31(3) (2004), 195–231.Google Scholar
Benois, D. and Nguyen Quang Do, T., ‘Les nombres de Tamagawa locaux et la conjecture de Bloch et Kato pour les motifs $\mathbb{Q}({m})$sur un corps abélien’, Ann. Sci. École Norm. Sup. (4) 35(5) (2002), 641–672.CrossRefGoogle Scholar
Bergeron, N., Falbel, E. and Guilloux, A., ‘Tetrahedra of flags, volume and homology of $\mathrm{SL}(3)$’, Geom. Topol. 18(4) (2014), 1911–1971.CrossRefGoogle Scholar
Bloch, S., ‘Higher regulators, algebraic ${K}\!$-theory, and zeta functions of elliptic curves’, Manuscript (‘Irvine notes’, 1978). Published as CRM Monograph Series, Vol. 11 (American Mathematical Society, Providence, RI, 2000).Google Scholar
Bloch, S. and Kato, K., $`$$\mathrm{L}$-functions and Tamagawa numbers of motives’, in The Grothendieck Festschrift I, Progress in Mathematics, Vol. 86 (Birkhäuser, Boston, 1990), 333–400.Google Scholar
Borel, A., ‘Stable real cohomology of arithmetic groups’, Ann. Sci. ENS 4 (1974), 235–272.Google Scholar
Borel, A., ‘Cohomologie de ${{SL}}_{\mathrm{n}}$ et valeurs de fonctions zêta aux points entiers’, Ann. Scuola Norm. Sup. Pisa Cl. Sci. (4) 4(4) (1977), 613–636. Errata in Ann. Scuola Norm. Sup. Pisa Cl. Sci. (4) 7(2) (1980), 373.Google Scholar
Borel, A., ‘Commensurability classes and volumes of hyperbolic $3$-manifolds’, Ann. Scuola Norm. Sup. Pisa Cl. Sci. (4) 8(1) (1981), 1–33.Google Scholar
Bosma, W., Cannon, J. and Playoust, C., ‘The Magma algebra system. I. The user language’, J. Symbolic Comput. 24(3–4) (1997), 235–265.CrossRefGoogle Scholar
Browkin, J., ‘The functor ${{K}}_2$ for the ring of integers of a number field’, in Universal Algebra and Applications (Warsaw, 1978), Banach Center Publ., Vol. 9 (PWN, Warsaw, Poland 1982), 187–195.Google Scholar
Browkin, J. and Gangl, H., ‘Tame and wild kernels of quadratic imaginary number fields’, Math. Comp. 68(225) (1999), 291–305.CrossRefGoogle Scholar
Burgos Gil, J. I., The Regulators of Beilinson and Borel, CRM Monograph Series, Vol. 15 (American Mathematical Society, Providence, RI, 2002).Google Scholar
Burns, D., de Jeu, R. and Gangl, H., ‘On special elements in higher algebraic ${K}\!$-theory and the Lichtenbaum-Gross conjecture’, Adv. Math. 230(3) (2012), 1502–1529.CrossRefGoogle Scholar
Burns, D. and Flach, M., ‘On Galois structure invariants associated to Tate motives’, Amer. J. Math. 120(6) (1998), 1343–1397.CrossRefGoogle Scholar
Burns, D. and Flach, M., ‘Tamagawa numbers for motives with (non-commutative) coefficients’, Doc. Math. 6 (2001), 501–570.Google Scholar
Burns, D. and Greither, C., ‘On the equivariant Tamagawa number conjecture for Tate motives’, Invent. Math. 153(2) (2003), 303–359.CrossRefGoogle Scholar
Cisneros-Molina, J. L. and Jones, J. D. S., ‘The Bloch invariant as a characteristic class in ${B}({{SL}}_2(\mathbb{C}),\mathbf{\mathcal{T}})$’, Homology Homotopy Appl. 5(1) (2003), 325–344.CrossRefGoogle Scholar
de Jeu, R., ‘Zagier’s conjecture and wedge complexes in algebraic ${K}\!$-theory’, Compos. Math. 96 (1995), 197–247.Google Scholar
de Jeu, R., ‘Towards regulator formulae for the ${K}\!$-theory of curves over number fields’, Compos. Math. 124(2) (2000), 137–194.CrossRefGoogle Scholar
Dupont, J. L. and Sah, C. H., ‘Scissors congruences, II’, J. Pure Appl. Algebra 25(2) (1982), 159–195.CrossRefGoogle Scholar
Dutour Sikirić, M., Gangl, H., Gunnells, P. E., Hanke, J., Schürmann, A. and Yasaki, D., ‘On the cohomology of linear groups over imaginary quadratic fields’, J. Pure Appl. Algebra 220(7) (2016), 2564–2589.CrossRefGoogle Scholar
Dwyer, W. and Friedlander, E., ‘Algebraic and étale $\mathrm{K}$-theory’, Trans. Amer. Math. Soc. 292(1) (1985), 247–280.Google Scholar
Elstrodt, J., Grunewald, F. and Mennicke, J., Groups Acting on Hyperbolic Space: Harmonic Analysis and Number Theory, Springer Monographs in Mathematics (Springer, Berlin, 1998).CrossRefGoogle Scholar
Flach, M., ‘On the cyclotomic main conjecture at the prime $2$’, J. Reine Angew. Math. 661 (2011), 1–36.CrossRefGoogle Scholar
Fontaine, J.-M., ‘Valeurs spéciales des fonctions ${L}$ des motifs’, Astérisque, tome 206 (1992), Séminaire Bourbaki, exp. no. 751, p. 205–249.Google Scholar
Fontaine, J.-M. and Perrin-Riou, B., ‘Autour des conjectures de Bloch et Kato: cohomologie galoisienne et valeurs de fonctions ${L}$’, in Motives (Seattle, WA, 1991), Proc. Sympos. Pure Math., Vol. 55 (American Mathematical Society, Providence, RI, 1994), 599–706.Google Scholar
Gangl, H., Werte von Dedekindschen Zetafunktionen, Dilogarithmuswerte und Pflasterungen des hyperbolischen Raumes (Diploma Thesis, Bonn, Germany, 1989).Google Scholar
Goncharov, A. B., ‘Polylogarithms and motivic Galois groups’, in Motives (Seattle, WA, 1991), Proc. Sympos. Pure Math., Vol. 55 (American Mathematical Society, Providence, RI, 1994), 43–96.Google Scholar
Goncharov, A. B., ‘Volumes of hyperbolic manifolds and mixed Tate motives’, J. Amer. Math. Soc. 12(2) (1999), 569–618.CrossRefGoogle Scholar
Hecke, E., Vorlesungen über die Theorie der algebraischen Zahlen (Chelsea Publishing Co., Bronx, NY, 1970). Second edition of the 1923 original, with an index.Google Scholar
Huber, A. and Kings, G., ‘Bloch-Kato conjecture and main conjecture of Iwasawa theory for Dirichlet characters’, Duke Math. J. 119(3) (2003), 393–464.CrossRefGoogle Scholar
Huber, A. and Wildeshaus, J., ‘Classical motivic polylogarithm according to Beilinson and Deligne’, Doc. Math. 3 (1998), 27–133. Erratum pp. 297–299.Google Scholar
Kahn, B., ‘The Quillen-Lichtenbaum conjecture at the prime 2’, preprint (1997). URL: http://www.math.uiuc.edu/K-theory/208.Google Scholar
Klein, F., ‘Ueber binäre Formen mit linearen Transformationen in sich selbst’, Math. Ann. 9(2) (1875), 183–208.CrossRefGoogle Scholar
Knudsen, F. and Mumford, D., ‘The projectivity of the moduli space of stable curves. I. Preliminaries on “det” and “Div”’, Math. Scand. 39(1) (1976), 19–55.CrossRefGoogle Scholar
Koecher, M., ‘Beiträge zu einer Reduktionstheorie in Positivitätsbereichen. I’, Math. Ann. 141 (1960), 384–432.CrossRefGoogle Scholar
Kolster, M., Nguyen Quang Do, T. and Fleckinger, V., ‘Twisted ${S}$-units, ${p}$-adic class number formulas, and the Lichtenbaum conjectures’, Duke Math. J. 84(3) (1996), 679–717.CrossRefGoogle Scholar
Krämer, N., ‘Imaginärquadratische Einbettung von Ordnungen rationaler Quaternionenalgebren, und die nichtzyklischen endlichen Untergruppen der Bianchi-Gruppen’, preprint (2015). URL: https://hal.archives-ouvertes.fr/hal-00720823/en/.Google Scholar
Le Floc’h, M., Movahhedi, A. and Nguyen Quang Do, T., ‘On capitulation cokernels in Iwasawa theory’, Amer. J. Math. 127(4) (2005), 4, 851–877.CrossRefGoogle Scholar
Levine, M., ‘The indecomposable ${{K}}_3$ of fields’, Ann. Sci. École Norm. Sup. (4) 22(2) (1989), 255–344.CrossRefGoogle Scholar
Lichtenbaum, S., ‘Values of zeta-functions, étale cohomology, and algebraic ${K}\!$-theory’, in Algebraic${K}\!$-Theory, II: “Classical” Algebraic ${K}\!$-Theory and Connections with Arithmetic (Proc. Conf., Battelle Memorial Inst., Seattle, Wash., 1972), Lecture Notes in Mathematics, Vol. 342 (Springer, Berlin, 1973), 489–501.Google Scholar
Mellit, A., ‘Angle structure on $3$-manifolds’, preprint (2020). URL: https://arxiv.org/abs/2011.12279.Google Scholar
Mendoza, E. R., Cohomology of${PGL}_2$ over Imaginary Quadratic Integers (Dissertation, Rheinische Friedrich-Wilhelms-Universität, Bonn, Germany, 1979).Google Scholar
Milne, J., Arithmetic Duality Theorems, Perspectives in Mathematics (Academic Press, Orlando, FL, 1986).Google Scholar
Neumann, W. and Yang, J., ‘Bloch invariants of hyperbolic $3$-manifolds’, Duke Math. J. 96(1) (1999), 29–59.CrossRefGoogle Scholar
Neumann, W. D. and Zagier, D., ‘Volumes of hyperbolic three-manifolds’, Topology 24 (1985), no. 3, 307–332.CrossRefGoogle Scholar
The PARI Group, ‘PARI/GP version 2.11.0’ (2018). URL: http://pari.math.u-bordeaux.fr/.Google Scholar
Quillen, D., ‘Finite generation of the groups ${{K}}_{{i}}$ of rings of algebraic integers’, in Algebraic ${K}\!$-Theory 1, Lecture Notes in Mathematics, Vol. 341 (Springer, Berlin, 1973), 179–198.Google Scholar
Rognes, J. and Weibel, C., ‘Two-primary algebraic ${K}\!$-theory of rings of integers in number fields’, J. Amer. Math. Soc. 13(1) (2000), 1–54. Appendix A by Manfred Kolster.CrossRefGoogle Scholar
Schneider, P., ‘Über gewisse Galoiscohomologiegruppen’, Math. Z. 168(2) (1979), 181–205.CrossRefGoogle Scholar
Soulé, C., ‘K-théorie des anneaux d’entiers de corps de nombres et cohomologie étale’, Invent. Math. 55 (1979), 251–295.CrossRefGoogle Scholar
Soulé, C., ‘Operations on etale ${K}\!$-theory. Applications’, in Algebraic K-Theory, Lecture Notes in Mathematics, Vol. 966 (Springer, Berlin, 1982), 271–303.CrossRefGoogle Scholar
Srinivas, V., Algebraic ${K}\!$-Theory, second ed., Progress in Mathematics, Vol. 90 (Birkhäuser, Boston, 1996).Google Scholar
Suslin, A. A., ‘{{K}}_3$ of a field, and the Bloch group’, Trudy Mat. Inst. Steklov. 183 (1990), 180–199. Translated in Proc. Steklov Inst. Math. 1991, no. 4, 217–239, Galois theory, rings, algebraic groups and their applications (Russian).Google Scholar
Voronoi, G., ‘Nouvelles applications des paramètres continus à la théorie des formes quadratiques. Premier mémoire. Sur quelques propriétés des formes quadratiques positives parfaites’, J. Reine Angew. Math. 133 (1908), 97–102.CrossRefGoogle Scholar
Washington, L., Introduction to Cyclotomic Fields, second ed., Graduate Texts in Mathematics, Vol. 83 (Springer, New York, 1997).CrossRefGoogle Scholar
Weibel, C., ‘Étale Chern classes at the prime $2$’, in Algebraic ${K}\!$-Theory and Algebraic Topology (Lake Louise, AB, 1991), NATO Adv. Sci. Inst. Ser. C Math. Phys. Sci., Vol. 407 (Kluwer Academic, Dordrecht, The Netherlands, 1993), 249–286.Google Scholar
Weibel, C., ‘Algebraic ${K}\!$-theory of rings of integers in local and global fields’, in Handbook of ${K}\!$-Theory, Vols. 1, 2 (Springer, Berlin, 2005), 139–190.Google Scholar
Weibel, C., ‘The norm residue isomorphism theorem’, Topology 2 (2009), 346–372.CrossRefGoogle Scholar
Weibel, C., The K-book: An Introduction to Algebraic K-theory, Graduate Studies in Mathematics, Vol. 145 (American Mathematical Society, Providence, RI, 2013).Google Scholar
Yasaki, D., ‘Database of generators for ${{K}}_3$ of imaginary quadratic number fields’, URL: https://mathstats.uncg.edu/yasaki/data.Google Scholar
Yasaki, D., ‘Hyperbolic tessellations associated to Bianchi groups’, in Algorithmic Number Theory, Lecture Notes in Computer Science, Vol. 6197 (Springer, Berlin, 2010), 385–396.CrossRefGoogle Scholar
Zagier, D., ‘Hyperbolic manifolds and special values of Dedekind zeta-functions’, Invent. Math. 83(2) (1986), 285–301.CrossRefGoogle Scholar
Zagier, D., ‘The remarkable dilogarithm’, J. Math. Phys. Sci. 22(1) (1988), 131–145.Google Scholar
Zagier, D., ‘Polylogarithms, Dedekind zeta functions and the algebraic ${K}\!$-theory of fields’, in Arithmetic Algebraic Geometry (Texel, 1989), Progress in Mathematics, Vol. 89 (Birkhäuser, Boston, 1991), 391–430.CrossRefGoogle Scholar