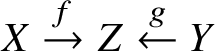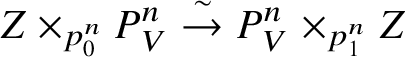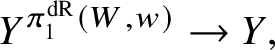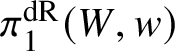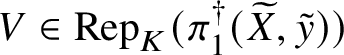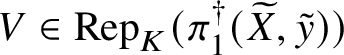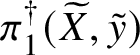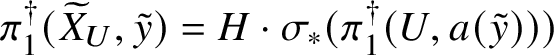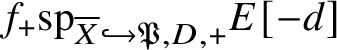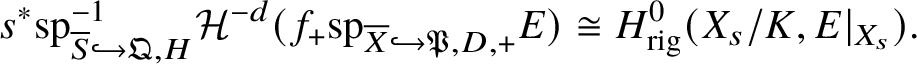1 Introduction
One of the basic principles in ‘algebraic’ approaches to homotopy theory is that a smooth and proper morphism ![]() $f:X\rightarrow S$ of schemes (in any characteristic) should behave like a Serre fibration of topological spaces. In particular, for any reasonable definition of homotopy groups, one expects a long exact sequence relating the homotopy groups of the base S, the total space X and the fibre
$f:X\rightarrow S$ of schemes (in any characteristic) should behave like a Serre fibration of topological spaces. In particular, for any reasonable definition of homotopy groups, one expects a long exact sequence relating the homotopy groups of the base S, the total space X and the fibre ![]() $X_s$ over some point
$X_s$ over some point ![]() $s\in S$. For étale homotopy groups, for example, this was proved in [Reference FriedlanderFri73], at least after completing away from the residue characteristics of S.
$s\in S$. For étale homotopy groups, for example, this was proved in [Reference FriedlanderFri73], at least after completing away from the residue characteristics of S.
While the étale fundamental group controls the category of ![]() $\ell $-adic local systems on varieties in characteristics different from
$\ell $-adic local systems on varieties in characteristics different from ![]() $\ell $, the same is certainly not true for p-adic local systems in characteristic p. In this situation, the version of the fundamental group that is usually considered is the one defined using Tannakian duality; this is somewhat analogous to the full pro-algebraic completion of the topological fundamental group
$\ell $, the same is certainly not true for p-adic local systems in characteristic p. In this situation, the version of the fundamental group that is usually considered is the one defined using Tannakian duality; this is somewhat analogous to the full pro-algebraic completion of the topological fundamental group ![]() $\pi _1(X)$ of a complex algebraic variety. (For now, we omit base points from the notation.) In this world of ‘pro-algebraic homotopy theory’ much less is known than in étale homotopy theory, even in the case of smooth varieties over the complex numbers.
$\pi _1(X)$ of a complex algebraic variety. (For now, we omit base points from the notation.) In this world of ‘pro-algebraic homotopy theory’ much less is known than in étale homotopy theory, even in the case of smooth varieties over the complex numbers.
For example, it is not completely clear what the correct analogues of the higher homotopy groups are (although see [Reference ToënToë00] for some work in this direction), and hence even formulating the analogue of the homotopy long exact sequence is problematic. Even if one sticks to the well-understood terms – that is, to the sequence
then showing exactness has in general proved to be rather difficult. If we work with de Rham fundamental groups of complex varieties and assume that the base S and fibre ![]() $X_s$ are connected, then exactness follows from ‘right exactness of the pro-algebraic completion functor’. More generally, it was shown for fields of characteristic
$X_s$ are connected, then exactness follows from ‘right exactness of the pro-algebraic completion functor’. More generally, it was shown for fields of characteristic ![]() $0$ using a mixture of algebraic and transcendental methods in [Reference ZhangZha14]. Similar exact sequences for logarithmic and/or unipotent fundamental groups have been proved in [Reference Chiarellotto, Di Proietto and ShihoCDPS, Reference Di Proietto and ShihoDPS18, Reference LazdaLaz15] and a version ‘over the generic point of S’ in [Reference Esnault and HaiEH06].
$0$ using a mixture of algebraic and transcendental methods in [Reference ZhangZha14]. Similar exact sequences for logarithmic and/or unipotent fundamental groups have been proved in [Reference Chiarellotto, Di Proietto and ShihoCDPS, Reference Di Proietto and ShihoDPS18, Reference LazdaLaz15] and a version ‘over the generic point of S’ in [Reference Esnault and HaiEH06].
A major new approach to these sorts of problems was introduced in [Reference dos SantosdS15], where the author showed how to construct pushforwards of certain kinds of ‘non-linear ![]() $\mathcal {D}$-modules’; that is, stratified schemes over the total space X. He then used this construction to give a completely algebraic proof of exactness of the
$\mathcal {D}$-modules’; that is, stratified schemes over the total space X. He then used this construction to give a completely algebraic proof of exactness of the ![]() $\pi _1$-part of the sequence, assuming geometric connectedness of
$\pi _1$-part of the sequence, assuming geometric connectedness of ![]() $X_s$ and S. One of the crucial insights of his article is that by replacing linear representations with projective representations, one can avoid completely one of the major difficulties in proving exactness of these sorts of ‘homotopy sequences’ (see Section 3).
$X_s$ and S. One of the crucial insights of his article is that by replacing linear representations with projective representations, one can avoid completely one of the major difficulties in proving exactness of these sorts of ‘homotopy sequences’ (see Section 3).
Inspired by dos Santos’s methods, in this article we prove the following result.
Theorem 8.3. Let ![]() $f:X\rightarrow S$ be a smooth, projective morphism of smooth varieties over a perfect field k of characteristic
$f:X\rightarrow S$ be a smooth, projective morphism of smooth varieties over a perfect field k of characteristic ![]() $p>0$, with geometrically connected fibres and base. Let
$p>0$, with geometrically connected fibres and base. Let ![]() $s\in S(k)$. Then the sequence of fundamental groups
$s\in S(k)$. Then the sequence of fundamental groups
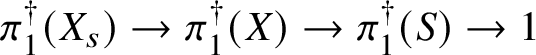 $$ \begin{align*} \pi_1^\dagger(X_s) \rightarrow \pi_1^\dagger(X) \rightarrow \pi_1^\dagger(S) \rightarrow 1 \\[-17pt]\end{align*} $$
$$ \begin{align*} \pi_1^\dagger(X_s) \rightarrow \pi_1^\dagger(X) \rightarrow \pi_1^\dagger(S) \rightarrow 1 \\[-17pt]\end{align*} $$classifying overconvergent isocrystals is exact.
If one tries to directly transport dos Santos’s construction to the overconvergent setting, one is very quickly confronted by a seemingly insurmountable list of problems and subtleties: even in the linear case the problem of constructing ![]() $\mathbf {R}^0f_*$ of an overconvergent isocrystal (without F-structure!) along a smooth and proper morphism is unreasonably difficult (see Section 9). Instead, we proceed in a much more roundabout fashion, advancing via a lengthy chain of reductions, which here we present in reverse order to that found in the body of the article.
$\mathbf {R}^0f_*$ of an overconvergent isocrystal (without F-structure!) along a smooth and proper morphism is unreasonably difficult (see Section 9). Instead, we proceed in a much more roundabout fashion, advancing via a lengthy chain of reductions, which here we present in reverse order to that found in the body of the article.
First we cut our given morphism ![]() $f:X\rightarrow S$ by a sequence of hyperplane sections, which by some diagram chasing and a very weak form of the Lefschetz hyperplane theorem for fundamental groups allows us to reduce to the case of a family of curves. In this case, our morphism arises via pullback from the universal curve
$f:X\rightarrow S$ by a sequence of hyperplane sections, which by some diagram chasing and a very weak form of the Lefschetz hyperplane theorem for fundamental groups allows us to reduce to the case of a family of curves. In this case, our morphism arises via pullback from the universal curve

and hence by lifting the morphism ![]() $S\rightarrow \mathcal {M}_g$ along some smooth lift of S (at least locally) we can assume that the whole family of smooth projective curves lifts to characteristic
$S\rightarrow \mathcal {M}_g$ along some smooth lift of S (at least locally) we can assume that the whole family of smooth projective curves lifts to characteristic ![]() $0$. (This is not quite what we do, but this is the basic idea.)
$0$. (This is not quite what we do, but this is the basic idea.)
In this case we can write the overconvergent fundamental group 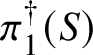 $\pi _1^\dagger (S)$ as a quotient
$\pi _1^\dagger (S)$ as a quotient
 $$ \begin{align*} \varprojlim_\lambda \pi_1^{\mathrm{dR}}(V_\lambda) \twoheadrightarrow \pi_1^\dagger(S) \end{align*} $$
$$ \begin{align*} \varprojlim_\lambda \pi_1^{\mathrm{dR}}(V_\lambda) \twoheadrightarrow \pi_1^\dagger(S) \end{align*} $$of the inverse limit of the de Rham fundamental groups 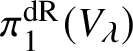 $\pi _1^{\mathrm {dR}}(V_\lambda )$ as
$\pi _1^{\mathrm {dR}}(V_\lambda )$ as ![]() $V_\lambda $ ranges over all strict neighbourhoods of the tube
$V_\lambda $ ranges over all strict neighbourhoods of the tube ![]() $]S[$ inside the generic fibre of the given lift. (Again, this is not strictly what we do, but this is the essential idea.) Moreover, the same is true for
$]S[$ inside the generic fibre of the given lift. (Again, this is not strictly what we do, but this is the essential idea.) Moreover, the same is true for 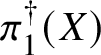 $\pi _1^\dagger (X)$, and in fact we can choose a cofinal system
$\pi _1^\dagger (X)$, and in fact we can choose a cofinal system ![]() $\{W_\lambda \}$ of strict neighbourhoods of
$\{W_\lambda \}$ of strict neighbourhoods of ![]() $]X[$ such that each
$]X[$ such that each ![]() $W_\lambda $ is smooth and projective over
$W_\lambda $ is smooth and projective over ![]() $V_\lambda $. Some more diagram chasing then allows us to reduce to the following result in rigid analytic geometry.
$V_\lambda $. Some more diagram chasing then allows us to reduce to the following result in rigid analytic geometry.
Theorem 2.5. Let ![]() $f:W\rightarrow V$ be a smooth, projective morphism of smooth analytic varieties over a p-adic field K, with geometrically connected fibres and base. Let
$f:W\rightarrow V$ be a smooth, projective morphism of smooth analytic varieties over a p-adic field K, with geometrically connected fibres and base. Let ![]() $v\in V(K)$. Then the sequence of fundamental groups
$v\in V(K)$. Then the sequence of fundamental groups
 $$ \begin{align*} \pi_1^{\mathrm{dR}}(W_v) \rightarrow \pi_1^{\mathrm{dR}}(W) \rightarrow \pi_1^{\mathrm{dR}}(V) \rightarrow 1 \end{align*} $$
$$ \begin{align*} \pi_1^{\mathrm{dR}}(W_v) \rightarrow \pi_1^{\mathrm{dR}}(W) \rightarrow \pi_1^{\mathrm{dR}}(V) \rightarrow 1 \end{align*} $$classifying coherent modules with integrable connection is exact.
The point is that now we have reduced to a statement solely concerning smooth projective morphisms of analytic K-varieties, with no reference to tubes or overconvergence. We are therefore in a situation where we really can directly apply dos Santos’s ideas and arguments, as essentially all of the difficulties we originally faced have disappeared. This is now what we do: the proof of this ‘de Rham’ homotopy exact sequence consists entirely of translating dos Santos’s proof from [Reference dos SantosdS15] into the analytic context.
In actual fact, we do much less than this. Rather than reprove analytically all of dos Santos’s results on ‘pushforwards’ of stratified schemes, we instead use various tricks to be able to reduce to cases where we can in fact apply his results. The basic idea is that it in fact suffices to show that for a stratified variety Z over W, the unit map ![]() $f^*f_{\mathrm {dR}*} Z \rightarrow Z$ for the relative pushforward is a closed immersion, and the image is stable under the stratification on Z. But now, by relative rigid analytic GAGA, these relative pushforwards simply arise as the analytification of those considered in [Reference dos SantosdS15]. Moreover, that the image is stable under the stratification can be checked after passing to the completed local ring at any rigid point and hence to the various infinitesimal neighbourhoods of this point. The situation is now completely algebraic over the ground field K, and so once more we can use dos Santos’s results. In fact, a little care is needed, since these infinitesimal neighbourhoods will not be smooth over K, so a priori the results of [Reference dos SantosdS15] do not apply. However, it is straightforward to show that the proofs of these results apply in the situation we are interested in.
$f^*f_{\mathrm {dR}*} Z \rightarrow Z$ for the relative pushforward is a closed immersion, and the image is stable under the stratification on Z. But now, by relative rigid analytic GAGA, these relative pushforwards simply arise as the analytification of those considered in [Reference dos SantosdS15]. Moreover, that the image is stable under the stratification can be checked after passing to the completed local ring at any rigid point and hence to the various infinitesimal neighbourhoods of this point. The situation is now completely algebraic over the ground field K, and so once more we can use dos Santos’s results. In fact, a little care is needed, since these infinitesimal neighbourhoods will not be smooth over K, so a priori the results of [Reference dos SantosdS15] do not apply. However, it is straightforward to show that the proofs of these results apply in the situation we are interested in.
Finally, in Section 13, we discuss some applications of the homotopy exact sequence for overconvergent fundamental groups. First of all, we prove a Lefschetz hyperplane theorem, stating that if ![]() $Y\subset X$ is a smooth hyperplane section inside a smooth projective variety, then the induced map
$Y\subset X$ is a smooth hyperplane section inside a smooth projective variety, then the induced map
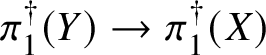 $$ \begin{align*} \pi_1^\dagger(Y)\rightarrow \pi_1^\dagger(X) \end{align*} $$
$$ \begin{align*} \pi_1^\dagger(Y)\rightarrow \pi_1^\dagger(X) \end{align*} $$on convergent fundamental groups is surjective. We are then able to use this to show that when the ground field is algebraically closed and X is smooth and projective, there is a canonical isomorphism
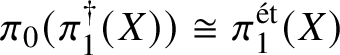 $$ \begin{align*} \pi_0(\pi_1^\dagger(X)) \cong \pi_1^{\mathrm{\acute{e}t}}(X)\end{align*} $$
$$ \begin{align*} \pi_0(\pi_1^\dagger(X)) \cong \pi_1^{\mathrm{\acute{e}t}}(X)\end{align*} $$between the component group of the convergent fundamental group and the pro-finite étale fundamental group. This generalises a result of Crew [Reference CrewCre92, Proposition 4.4], in which objects were assumed to have Frobenius structures.
Notations and conventions
• We will denote by k a perfect field of characteristic
 $p>0$,
$p>0$,  $\mathcal {V}$ a complete DVR with residue field k and fraction field K of characteristic
$\mathcal {V}$ a complete DVR with residue field k and fraction field K of characteristic  $0$. We will let
$0$. We will let  $\varpi $ denote a choice of uniformiser for
$\varpi $ denote a choice of uniformiser for  $\mathcal {V}$.
$\mathcal {V}$.• An algebraic variety over k (respectively K) will mean a separated scheme of finite type, the category of which will be denoted
 $\mathbf {Var}_{k}$ (respectively
$\mathbf {Var}_{k}$ (respectively  $\mathbf {Var}_K$). If V is an algebraic variety over either k or K, we will denote by
$\mathbf {Var}_K$). If V is an algebraic variety over either k or K, we will denote by  $\mathbf {Var}_V$ the slice category of varieties over V.
$\mathbf {Var}_V$ the slice category of varieties over V.• An analytic variety over K will mean an adic space, separated and locally of finite type over
 $\mathrm {Spa}\left (K,\mathcal {V}\right )$. Since all rigid spaces will be locally of finite type over K, we may, without ambiguity, denote an affinoid adic space
$\mathrm {Spa}\left (K,\mathcal {V}\right )$. Since all rigid spaces will be locally of finite type over K, we may, without ambiguity, denote an affinoid adic space  $\mathrm {Spa}\left (A,A^+\right )$ simply by
$\mathrm {Spa}\left (A,A^+\right )$ simply by  $\mathrm {Spa}\left (A\right )$. We will let
$\mathrm {Spa}\left (A\right )$. We will let  $\mathbf {Rig}_{K}$ denote the category of analytic varieties over K, and for any such V the slice category will be denoted
$\mathbf {Rig}_{K}$ denote the category of analytic varieties over K, and for any such V the slice category will be denoted  $\mathbf {Rig}_V$. The analytification of an algebraic variety over K will always be considered as an adic space. Throughout, we will implicitly use [Reference Fujiwara and KatoFK18, Theorem II.A.5.2] to apply the results of [Reference Fujiwara and KatoFK18] to objects of
$\mathbf {Rig}_V$. The analytification of an algebraic variety over K will always be considered as an adic space. Throughout, we will implicitly use [Reference Fujiwara and KatoFK18, Theorem II.A.5.2] to apply the results of [Reference Fujiwara and KatoFK18] to objects of  $\mathbf {Rig}_K$.
$\mathbf {Rig}_K$.• If Y is a k-variety, we will denote by
 $\mathrm {Isoc}^\dagger (Y/K)$ the category of overconvergent isocrystals on
$\mathrm {Isoc}^\dagger (Y/K)$ the category of overconvergent isocrystals on  $Y/K$.
$Y/K$.• A closed subgroup of an affine group scheme will always mean a closed subscheme that is also a subgroup, and a surjective homomorphism will be a group scheme homomorphism which is faithfully flat.
• Unadorned tensor or fibre products will be over
 $k,K$ or
$k,K$ or  $\mathcal {V}$, which will be clear which from the context. Sometimes, in order to avoid confusion, we will denote the fibre product of a diagram
$\mathcal {V}$, which will be clear which from the context. Sometimes, in order to avoid confusion, we will denote the fibre product of a diagram  $X\overset {f}{\rightarrow } Z \overset {g}{\leftarrow } Y$ by one of
$X\overset {f}{\rightarrow } Z \overset {g}{\leftarrow } Y$ by one of  $X\times _{f,Z,g} Y$,
$X\times _{f,Z,g} Y$,  $X\times _{f,Z}Y$ or
$X\times _{f,Z}Y$ or  $X\times _{Z,g}Y$, depending on which structure morphism needs clarifying.
$X\times _{Z,g}Y$, depending on which structure morphism needs clarifying.
2 The homotopy sequence for analytic  $\boldsymbol {K}$-varieties
$\boldsymbol {K}$-varieties
The first goal of this article will be the proof of a homotopy exact sequence for certain classes of families of smooth analytic K-varieties. To start with, we will need to define the de Rham fundamental group of such spaces. So let V be an analytic variety over K.
Proposition 2.1. Assume that V is smooth, geometrically connected and admits a rational point ![]() $v\in V(K)$. Then the category
$v\in V(K)$. Then the category ![]() $\mathrm {MIC}(V/K)$ of coherent
$\mathrm {MIC}(V/K)$ of coherent ![]() $\mathcal {O}_V$-modules with integrable connection is neutral Tannakian over K, with fibre functor
$\mathcal {O}_V$-modules with integrable connection is neutral Tannakian over K, with fibre functor ![]() $v^*$.
$v^*$.
Proof. We first claim that any coherent module with integrable connection is locally free. Indeed, this question is local, and we may assume ![]() $V=\mathrm {Spa}\left (A\right )$ to be affinoid. In particular, E comes from a coherent sheaf
$V=\mathrm {Spa}\left (A\right )$ to be affinoid. In particular, E comes from a coherent sheaf ![]() $E^a$ on
$E^a$ on ![]() $\mathrm {Spec}\left (A\right )$ and it suffices to prove that
$\mathrm {Spec}\left (A\right )$ and it suffices to prove that ![]() $E^a$ is locally free. But this may be checked after passing to the completed local ring
$E^a$ is locally free. But this may be checked after passing to the completed local ring ![]() $\widehat {A}_{\mathfrak {m}}$ at any closed point
$\widehat {A}_{\mathfrak {m}}$ at any closed point ![]() $\mathfrak {m}\in \mathrm {Spec}\left (A\right )$, which by enlarging K can be assumed to be K-valued. Now choosing étale co-ordinates
$\mathfrak {m}\in \mathrm {Spec}\left (A\right )$, which by enlarging K can be assumed to be K-valued. Now choosing étale co-ordinates ![]() $\mathrm {Spa}\left (A\right )\rightarrow {\mathbb D}^n_K$ in some neighbourhood of this given K-point induces an isomorphism
$\mathrm {Spa}\left (A\right )\rightarrow {\mathbb D}^n_K$ in some neighbourhood of this given K-point induces an isomorphism ![]() $\widehat {A}_{\mathfrak {m}}\cong K[\![ x_1,\ldots ,x_n ]\!]$. Moreover, the integrable connection on E induces a formal integrable connection on
$\widehat {A}_{\mathfrak {m}}\cong K[\![ x_1,\ldots ,x_n ]\!]$. Moreover, the integrable connection on E induces a formal integrable connection on ![]() $E^a\otimes _A \widehat {A}_{\mathfrak {m}}$. Hence, we may apply [Reference KatzKat70, Proposition 8.9].
$E^a\otimes _A \widehat {A}_{\mathfrak {m}}$. Hence, we may apply [Reference KatzKat70, Proposition 8.9].
It therefore follows that
is a faithful, K-linear, exact tensor functor, and since V is connected, we can see that if ![]() $v^*(E)$ has dimension
$v^*(E)$ has dimension ![]() $1$, then E is a line bundle. Hence, applying [Reference Deligne, Milne, Ogus and ShihDMOS82, Ch. II, Proposition 1.20], it suffices to prove that the natural map
$1$, then E is a line bundle. Hence, applying [Reference Deligne, Milne, Ogus and ShihDMOS82, Ch. II, Proposition 1.20], it suffices to prove that the natural map
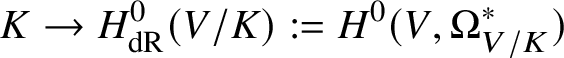 $$ \begin{align*} K\rightarrow H^0_{\mathrm{dR}}(V/K):=H^0(V,\Omega^*_{V/K}) \end{align*} $$
$$ \begin{align*} K\rightarrow H^0_{\mathrm{dR}}(V/K):=H^0(V,\Omega^*_{V/K}) \end{align*} $$is an isomorphism. Applying ![]() $v^*$ we obtain a retraction
$v^*$ we obtain a retraction
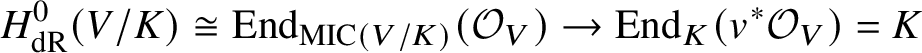 $$ \begin{align*} H^0_{\mathrm{dR}}(V/K)\cong \mathrm{End}_{\mathrm{MIC}(V/K)}(\mathcal{O}_V) \rightarrow \mathrm{End}_K(v^*\mathcal{O}_V)=K \end{align*} $$
$$ \begin{align*} H^0_{\mathrm{dR}}(V/K)\cong \mathrm{End}_{\mathrm{MIC}(V/K)}(\mathcal{O}_V) \rightarrow \mathrm{End}_K(v^*\mathcal{O}_V)=K \end{align*} $$of this map. In particular, if 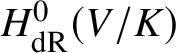 $H^0_{\mathrm {dR}}(V/K)$ were strictly bigger than K, then
$H^0_{\mathrm {dR}}(V/K)$ were strictly bigger than K, then ![]() $\Gamma (V,\mathcal {O}_V)$ would contain a nontrivial idempotent element, contradicting the connectedness of V.
$\Gamma (V,\mathcal {O}_V)$ would contain a nontrivial idempotent element, contradicting the connectedness of V.
Definition 2.2. Let ![]() $(V,v)$ be as in Proposition 2.1. Then we define the de Rham fundamental group
$(V,v)$ be as in Proposition 2.1. Then we define the de Rham fundamental group 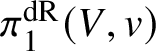 $\pi _1^{\mathrm {dR}}(V,v)$ of V to be the Tannaka dual of
$\pi _1^{\mathrm {dR}}(V,v)$ of V to be the Tannaka dual of ![]() $\mathrm {MIC}(V/K)$ with respect to the fibre functor
$\mathrm {MIC}(V/K)$ with respect to the fibre functor
Now let ![]() $f:W\rightarrow V$ be a proper morphism of analytic K-varieties. Recall from [Reference ConradCon06] that a line bundle
$f:W\rightarrow V$ be a proper morphism of analytic K-varieties. Recall from [Reference ConradCon06] that a line bundle ![]() $\mathcal {L}$ on W is said to be f-ample if it is so on each fibre
$\mathcal {L}$ on W is said to be f-ample if it is so on each fibre ![]() $W_v$ over a rigid point
$W_v$ over a rigid point ![]() $v\in V$. In other words, for each rigid point
$v\in V$. In other words, for each rigid point ![]() $v\in V$, some tensor power
$v\in V$, some tensor power 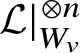 $\mathcal {L}|_{W_v}^{\otimes {n}}$ defines a closed immersion
$\mathcal {L}|_{W_v}^{\otimes {n}}$ defines a closed immersion 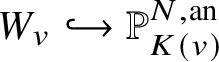 $W_v\hookrightarrow {\mathbb P}^{N,\mathrm {an}}_{K(v)}$.
$W_v\hookrightarrow {\mathbb P}^{N,\mathrm {an}}_{K(v)}$.
Definition 2.3. We say that a proper morphism ![]() $f:W\rightarrow V$ of analytic K-varieties is projective if W admits an f-ample line bundle.
$f:W\rightarrow V$ of analytic K-varieties is projective if W admits an f-ample line bundle.
Remark 2.4. With this definition, a projective morphism admits a closed immersion 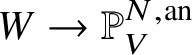 $W\rightarrow {\mathbb P}^{N,\mathrm {an}}_V$ locally on the base V, by [Reference ConradCon06, Theorem 3.2.7]. Such an embedding need not exist globally, although it will if the base is affinoid or itself projective over
$W\rightarrow {\mathbb P}^{N,\mathrm {an}}_V$ locally on the base V, by [Reference ConradCon06, Theorem 3.2.7]. Such an embedding need not exist globally, although it will if the base is affinoid or itself projective over ![]() $\mathrm {Spa}\left (K\right )$. Note also that with this definition, a composition of projective morphisms is projective, but projectivity is not necessarily local on the base.
$\mathrm {Spa}\left (K\right )$. Note also that with this definition, a composition of projective morphisms is projective, but projectivity is not necessarily local on the base.
Suppose that ![]() $f:W\rightarrow V$ is a morphism of smooth, geometrically connected K-varieties and
$f:W\rightarrow V$ is a morphism of smooth, geometrically connected K-varieties and ![]() $w\in W(K)$ is a K-valued point, and set
$w\in W(K)$ is a K-valued point, and set ![]() $v=f(w)$. If the fibre
$v=f(w)$. If the fibre ![]() $W_v$ is also smooth and geometrically connected, then we call the sequence
$W_v$ is also smooth and geometrically connected, then we call the sequence
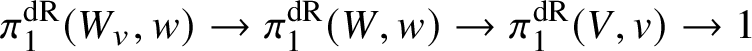 $$ \begin{align*} \pi_1^{\mathrm{dR}}(W_v,w)\rightarrow \pi_1^{\mathrm{dR}}(W,w)\rightarrow \pi_1^{\mathrm{dR}}(V,v)\rightarrow 1 \end{align*} $$
$$ \begin{align*} \pi_1^{\mathrm{dR}}(W_v,w)\rightarrow \pi_1^{\mathrm{dR}}(W,w)\rightarrow \pi_1^{\mathrm{dR}}(V,v)\rightarrow 1 \end{align*} $$of affine group schemes the homotopy sequence associated to the pair ![]() $(f,w)$. Then the main result of the first part of this article is the following.
$(f,w)$. Then the main result of the first part of this article is the following.
Theorem 2.5. Let ![]() $f:W\rightarrow V$ be a smooth projective morphism of smooth analytic K-varieties, with geometrically connected fibres and base, and let
$f:W\rightarrow V$ be a smooth projective morphism of smooth analytic K-varieties, with geometrically connected fibres and base, and let ![]() $w\in W(K)$. Then the homotopy sequence of the pair
$w\in W(K)$. Then the homotopy sequence of the pair ![]() $(f,w)$ is exact.
$(f,w)$ is exact.
3 Exactness criteria and polarisable  $\boldsymbol {G}$-varieties
$\boldsymbol {G}$-varieties
The strategy to prove Theorem 2.5 is essentially to translate dos Santos’s proof of exactness of the homotopy sequence in [Reference dos SantosdS15] from the algebraic to the analytic setting. The need to work analytically will present us with several difficulties and, consequently, at many points we will prove weaker results, and with extra hypotheses, than those obtained in [Reference dos SantosdS15]. In order to be able to get away with this, we will need to combine the ‘projective’ criteria for exactness of a sequence of affine group schemes discussed in [Reference dos SantosdS15, §4] with more traditional ‘linear’ versions considered for example in [Reference Esnault, Hai and SunEHS08, Appendix A]. To begin with, let us quickly recall how these criteria work.
Theorem 3.1 [Reference dos SantosdS15], Lemma 4.3
Let
be a sequence of affine group schemes such that p is faithfully flat. Then the sequence is exact if and only if for all ![]() $V\in \mathrm {Rep}(G)$ the inclusion
$V\in \mathrm {Rep}(G)$ the inclusion
of K-points on the fixed schemes is an equality.
Theorem 3.2 [Reference Esnault, Hai and SunEHS08], Theorem A.1(iii)
Let
be a sequence of affine group schemes, such that q is a closed immersion and p is faithfully flat. Then the sequence is exact if and only if the following three conditions hold:
1. If
 $V\in \mathrm {Rep}(G)$, then
$V\in \mathrm {Rep}(G)$, then  $q^*(V)$ is trivial in
$q^*(V)$ is trivial in  $\mathrm {Rep}(L)$ if and only if
$\mathrm {Rep}(L)$ if and only if  $V\cong p^*(W)$ for some
$V\cong p^*(W)$ for some  $W\in \mathrm {Rep}(A)$;
$W\in \mathrm {Rep}(A)$;2. for any
 $V\in \mathrm {Rep}(G)$, if
$V\in \mathrm {Rep}(G)$, if  $W_0\subset q^*(V)$ is the maximal trivial subobject in
$W_0\subset q^*(V)$ is the maximal trivial subobject in  $\mathrm {Rep}(L)$, then there exists
$\mathrm {Rep}(L)$, then there exists  $W\subset V \in \mathrm {Rep}(G)$ such that
$W\subset V \in \mathrm {Rep}(G)$ such that  $q^*(W)=W_0\subset q^*(V)$;
$q^*(W)=W_0\subset q^*(V)$;3. any object of
 $\mathrm {Rep}(L)$ is a subobject of one in the essential image of
$\mathrm {Rep}(L)$ is a subobject of one in the essential image of  $q^*$.
$q^*$.
In practice, the first two of the conditions in Theorem 3.2 are (conceptually at least) very easy to verify and the third is extremely difficult. It will therefore be useful to see what happens when we drop it. Note that the intersection of any collection of closed normal subgroups of an affine group scheme G is also a closed normal subgroup; hence, we may define the normal closure ![]() $H^{\mathrm {norm}}\subset G$ of a closed subgroup
$H^{\mathrm {norm}}\subset G$ of a closed subgroup ![]() $H\subset G$ as the intersection of all closed normal subgroups containing it.
$H\subset G$ as the intersection of all closed normal subgroups containing it.
Definition 3.3. We say that a sequence of affine group schemes
is weakly exact if ![]() $G\overset {p}{\rightarrow } A$ is surjective, the composition
$G\overset {p}{\rightarrow } A$ is surjective, the composition ![]() $L\overset {p\circ q}{\rightarrow } A$ is trivial and if
$L\overset {p\circ q}{\rightarrow } A$ is trivial and if ![]() $\ker (p)=q(L)^{\mathrm {norm}}$. In other words, the sequence
$\ker (p)=q(L)^{\mathrm {norm}}$. In other words, the sequence
is exact.
Weak exactness turns out to be exactly what we can prove without the third condition in Theorem 3.2.
Theorem 3.4. Let ![]() $L\overset {q}{\rightarrow } G \overset {p}{\rightarrow } A \rightarrow 1 $ be a sequence of affine group schemes over K such that p is faithfully flat. Assume that
$L\overset {q}{\rightarrow } G \overset {p}{\rightarrow } A \rightarrow 1 $ be a sequence of affine group schemes over K such that p is faithfully flat. Assume that
1. if
 $V\in \mathrm {Rep}(G)$, then
$V\in \mathrm {Rep}(G)$, then  $q^*(V)$ is trivial in
$q^*(V)$ is trivial in  $\mathrm {Rep}(L)$ if and only if
$\mathrm {Rep}(L)$ if and only if  $V\cong p^*(W)$ for some
$V\cong p^*(W)$ for some  $W\in \mathrm {Rep}(A)$;
$W\in \mathrm {Rep}(A)$;2. for any
 $V\in \mathrm {Rep}(G)$, if
$V\in \mathrm {Rep}(G)$, if  $W_0\subset q^*(V)$ is the maximal trivial subobject in
$W_0\subset q^*(V)$ is the maximal trivial subobject in  $\mathrm {Rep}(L)$, then there exists
$\mathrm {Rep}(L)$, then there exists  $W\subset V \in \mathrm {Rep}(G)$ such that
$W\subset V \in \mathrm {Rep}(G)$ such that  $q^*(W)=W_0\subset q^*(V)$.
$q^*(W)=W_0\subset q^*(V)$.
Then ![]() $L \rightarrow G \rightarrow A \rightarrow 1$ is weakly exact.
$L \rightarrow G \rightarrow A \rightarrow 1$ is weakly exact.
Proof. First note that by [Reference Esnault, Hai and SunEHS08, Theorem A.1] we may describe ![]() $\mathrm {Rep}(q(L))$ as the full subcategory of
$\mathrm {Rep}(q(L))$ as the full subcategory of ![]() $\mathrm {Rep}(L)$ consisting of objects which are subquotients of objects in the essential image of
$\mathrm {Rep}(L)$ consisting of objects which are subquotients of objects in the essential image of ![]() $q^*:\mathrm {Rep}(G)\rightarrow \mathrm {Rep}(L)$. In particular, it is straightforward to verify that both conditions continue to hold if we replace L by
$q^*:\mathrm {Rep}(G)\rightarrow \mathrm {Rep}(L)$. In particular, it is straightforward to verify that both conditions continue to hold if we replace L by ![]() $q(L)$, in other words, we may assume that q is a closed immersion and L is in fact a closed subgroup of G.
$q(L)$, in other words, we may assume that q is a closed immersion and L is in fact a closed subgroup of G.
We next claim that, moreover, the conditions continue to hold if we replace L by the normal subgroup ![]() $L^{\mathrm {norm}}$ it generates, the nontrivial one is (2). In this case, we know from condition (2) applied to L that for any representation V of G, the subspace
$L^{\mathrm {norm}}$ it generates, the nontrivial one is (2). In this case, we know from condition (2) applied to L that for any representation V of G, the subspace ![]() $V^L$ is in fact stable by G. Since
$V^L$ is in fact stable by G. Since ![]() $V^L$ is therefore a G-representation on which L acts trivially, it follows that
$V^L$ is therefore a G-representation on which L acts trivially, it follows that ![]() $L^{\mathrm {norm}}$ acts trivially; in particular, we have
$L^{\mathrm {norm}}$ acts trivially; in particular, we have ![]() $V^L=V^{L^{\mathrm {norm}}}$, which suffices to prove that (2) also holds for
$V^L=V^{L^{\mathrm {norm}}}$, which suffices to prove that (2) also holds for ![]() $L^{\mathrm {norm}}$.
$L^{\mathrm {norm}}$.
In other words, we may in fact assume that ![]() $L=L^{\mathrm {norm}}$ and, in particular, that L is a normal subgroup of G. But now we note that by [Reference Esnault, Hai and SunEHS08, Theorem A.1(ii)] any object of
$L=L^{\mathrm {norm}}$ and, in particular, that L is a normal subgroup of G. But now we note that by [Reference Esnault, Hai and SunEHS08, Theorem A.1(ii)] any object of ![]() $\mathrm {Rep}(L)$ is a subobject of one in the essential image of
$\mathrm {Rep}(L)$ is a subobject of one in the essential image of ![]() $q^*$; hence, applying Theorem 3.2 we can see that the sequence
$q^*$; hence, applying Theorem 3.2 we can see that the sequence
is exact.
As mentioned before, the conditions of Theorem 3.4 are often easy to verify, and in the situation of Theorem 2.5 we may do so as follows. Let ![]() $f:W\rightarrow V$,
$f:W\rightarrow V$, ![]() $w\in W(K)$ be as in Theorem 2.5, and suppose we are given
$w\in W(K)$ be as in Theorem 2.5, and suppose we are given ![]() $E\in \mathrm {MIC}(W/K)$. We define
$E\in \mathrm {MIC}(W/K)$. We define
 $$ \begin{align*} f_{\mathrm{dR}*}E&:= \mathbf{R}^0f_*\left(E\otimes_{\mathcal{O}_W}\Omega^*_{W/V} \right) \\ &= \ker\left(f_*E \rightarrow f_*(E\otimes \Omega^1_{W/V}) \right) \\ &= f_*\ker\left(E\rightarrow E\otimes \Omega^1_{W/V} \right) \end{align*} $$
$$ \begin{align*} f_{\mathrm{dR}*}E&:= \mathbf{R}^0f_*\left(E\otimes_{\mathcal{O}_W}\Omega^*_{W/V} \right) \\ &= \ker\left(f_*E \rightarrow f_*(E\otimes \Omega^1_{W/V}) \right) \\ &= f_*\ker\left(E\rightarrow E\otimes \Omega^1_{W/V} \right) \end{align*} $$to be the sheaf of relative horizontal sections. Since f is proper, ![]() $f_{\mathrm {dR}*}E$ is a coherent sheaf on V, and exactly as in [Reference Katz and OdaKO68, §2], we may endow it with an integrable connection. One easily verifies that
$f_{\mathrm {dR}*}E$ is a coherent sheaf on V, and exactly as in [Reference Katz and OdaKO68, §2], we may endow it with an integrable connection. One easily verifies that
are adjoint functors and that for any K-valued point ![]() $v\in V(K)$ there is a natural isomorphism
$v\in V(K)$ there is a natural isomorphism
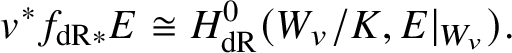 $$ \begin{align*} v^*f_{\mathrm{dR}*}E \cong H^0_{\mathrm{dR}}(W_v/K,E|_{W_v}). \end{align*} $$
$$ \begin{align*} v^*f_{\mathrm{dR}*}E \cong H^0_{\mathrm{dR}}(W_v/K,E|_{W_v}). \end{align*} $$Lemma 3.5. In the situation of Theorem 2.5 the sequence
 $$ \begin{align*} \pi_1^{\mathrm{dR}}(W_v,w)\rightarrow \pi_1^{\mathrm{dR}}(W,w)\rightarrow \pi_1^{\mathrm{dR}}(V,v) \rightarrow 1 \end{align*} $$
$$ \begin{align*} \pi_1^{\mathrm{dR}}(W_v,w)\rightarrow \pi_1^{\mathrm{dR}}(W,w)\rightarrow \pi_1^{\mathrm{dR}}(V,v) \rightarrow 1 \end{align*} $$is weakly exact.
Proof. Using the fact that 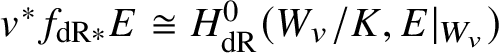 $v^*f_{\mathrm {dR}*}E \cong H^0_{\mathrm {dR}}(W_v/K,E|_{W_v})$, one easily checks that the adjunction map
$v^*f_{\mathrm {dR}*}E \cong H^0_{\mathrm {dR}}(W_v/K,E|_{W_v})$, one easily checks that the adjunction map ![]() $F\rightarrow f_{\mathrm {dR}*}f^*F$ is an isomorphism for any
$F\rightarrow f_{\mathrm {dR}*}f^*F$ is an isomorphism for any ![]() $F\in \mathrm {MIC}(V/K)$; thus, the functor
$F\in \mathrm {MIC}(V/K)$; thus, the functor ![]() $f^*$ is fully faithful. If we are given a subobject
$f^*$ is fully faithful. If we are given a subobject ![]() $E\subset f^*F$, then again applying
$E\subset f^*F$, then again applying ![]() $f^*f_{\mathrm {dR}*}$ we obtain
$f^*f_{\mathrm {dR}*}$ we obtain
and we claim that in fact ![]() $ f^*f_{\mathrm {dR}*}E = E$. But since this can be checked on fibres, it follows from the fact that any subobject of a trivial object in
$ f^*f_{\mathrm {dR}*}E = E$. But since this can be checked on fibres, it follows from the fact that any subobject of a trivial object in ![]() $\mathrm {MIC}(W_v/K)$ is itself trivial.
$\mathrm {MIC}(W_v/K)$ is itself trivial.
Hence, the map 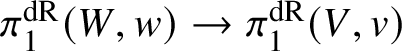 $\pi _1^{\mathrm {dR}}(W,w)\rightarrow \pi _1^{\mathrm {dR}}(V,v)$ is faithfully flat. To show that condition (1) in Theorem 3.4 holds, we note that for
$\pi _1^{\mathrm {dR}}(W,w)\rightarrow \pi _1^{\mathrm {dR}}(V,v)$ is faithfully flat. To show that condition (1) in Theorem 3.4 holds, we note that for ![]() $E\in \mathrm {MIC}(W/K)$ the adjunction map
$E\in \mathrm {MIC}(W/K)$ the adjunction map ![]() $f^*f_{\mathrm {dR}*}E\rightarrow E$ is an isomorphism iff it is so on fibres, which happens iff
$f^*f_{\mathrm {dR}*}E\rightarrow E$ is an isomorphism iff it is so on fibres, which happens iff ![]() $E|_{W_v}$ is trivial. Similarly, for (2) we can take
$E|_{W_v}$ is trivial. Similarly, for (2) we can take ![]() $f^*f_{\mathrm {dR}*} E\subset E$ as the required subobject.
$f^*f_{\mathrm {dR}*} E\subset E$ as the required subobject.
The reason that this is useful is that now we can formulate an alternative version of dos Santos’s criterion (Theorem 3.1).
Proposition 3.6. Let ![]() $L\overset {q}{\rightarrow } G \overset {p}{\rightarrow } A \rightarrow 1 $ be a weakly exact sequence of affine group schemes. Then the sequence is exact if and only if for any
$L\overset {q}{\rightarrow } G \overset {p}{\rightarrow } A \rightarrow 1 $ be a weakly exact sequence of affine group schemes. Then the sequence is exact if and only if for any ![]() $V\in \mathrm {Rep}(G)$ the fixed scheme
$V\in \mathrm {Rep}(G)$ the fixed scheme
is invariant under G.
Proof. By Theorem 3.1 we must prove that the inclusion ![]() ${\mathbb P}(V)^{\ker p}(K) \subset {\mathbb P}(V)^L(K)$ of K-points on the fixed scheme is an equality. If
${\mathbb P}(V)^{\ker p}(K) \subset {\mathbb P}(V)^L(K)$ of K-points on the fixed scheme is an equality. If ![]() ${\mathbb P}(V)^L$ is invariant under G, then we obtain a homomorphism
${\mathbb P}(V)^L$ is invariant under G, then we obtain a homomorphism
of functors on K-schemes that by definition satisfies ![]() $q(L)\subset \ker \rho $. Since
$q(L)\subset \ker \rho $. Since ![]() ${\mathbb P}(V)^L$ is a projective variety, the functor
${\mathbb P}(V)^L$ is a projective variety, the functor ![]() $\mathbf {Aut}_K({\mathbb P}(V)^L)$ is representable by a group scheme over K; hence,
$\mathbf {Aut}_K({\mathbb P}(V)^L)$ is representable by a group scheme over K; hence, ![]() $\ker \rho $ is a closed normal subgroup of G. Since it contains
$\ker \rho $ is a closed normal subgroup of G. Since it contains ![]() $q(L)$, it must also contain
$q(L)$, it must also contain ![]() $q(L)^{\mathrm {norm}}$, from which we deduce that
$q(L)^{\mathrm {norm}}$, from which we deduce that ![]() $\ker p$ must act trivially on
$\ker p$ must act trivially on ![]() ${\mathbb P}(V)^L$. Hence, the claimed equality does indeed hold.
${\mathbb P}(V)^L$. Hence, the claimed equality does indeed hold.
This shows the importance of considering projective schemes together with actions of the fundamental group, and many results from [Reference dos SantosdS15] involve extending the classical Tannakian duality to include these sorts of objects. We expect many of these results to also hold in the analytic context, but in our impatience to prove Theorem 2.5 (and consequently Theorem 8.3) we have not investigated this fully. Instead, we will stick to the more restrictive category of varieties together with a polarisable action.
Definition 3.7. Let G be an affine group scheme over K, Y a proper K-variety and ![]() $\rho :G\rightarrow \mathbf {Aut}_K(Y)$ an action of G on Y. We say that the action is polarisable if
$\rho :G\rightarrow \mathbf {Aut}_K(Y)$ an action of G on Y. We say that the action is polarisable if
1.
 $\rho $ factors through an algebraic quotient
$\rho $ factors through an algebraic quotient  $G\twoheadrightarrow H$;
$G\twoheadrightarrow H$;2. there exists an ample line bundle
 $\mathcal {L}$ on Y admitting a H-linearisation.
$\mathcal {L}$ on Y admitting a H-linearisation.
Note that ‘polarisable’ simply means that such an H and ![]() $\mathcal {L}$ exist; we do not specify them as part of the data.
$\mathcal {L}$ exist; we do not specify them as part of the data.
Lemma 3.8. A G-action on Y is polarisable if and only if there exists some ![]() $V\in \mathrm {Rep}(G)$ and a G-equivariant closed embedding
$V\in \mathrm {Rep}(G)$ and a G-equivariant closed embedding
Proof. Since the action on any such V must factor through an algebraic quotient, the existence of such an embedding clearly implies polarisability. For the converse, we may assume that G is algebraic and that the line bundle ![]() $\mathcal {L}$ in condition (2) is very ample. In this situation,
$\mathcal {L}$ in condition (2) is very ample. In this situation, ![]() $H^0(Y,\mathcal {L})$ is a finite-dimensional representation of G and the natural map
$H^0(Y,\mathcal {L})$ is a finite-dimensional representation of G and the natural map
is G-equivariant.
Remark 3.9. In fact, the proof of this lemma shows that the condition in Definition 3.7 that the action of G on either Y or the ample line bundle ![]() $\mathcal {L}$ factors through some algebraic quotient is redundant.
$\mathcal {L}$ factors through some algebraic quotient is redundant.
Corollary 3.10. If ![]() $G\rightarrow H$ is a homomorphism of affine group schemes and Y is a proper K-variety with a polarisable H-action, then the induced G-action is also polarisable.
$G\rightarrow H$ is a homomorphism of affine group schemes and Y is a proper K-variety with a polarisable H-action, then the induced G-action is also polarisable.
4 Stratified analytic spaces
The proof of Lemma 3.5 demonstrates that the problem of proving weak exactness of the homotopy sequence is more or less that of constructing well-behaved ‘pushforwards’ of coherent modules with integrable connections along the given map ![]() $f:W\rightarrow V$. Similarly, one of the key insights of [Reference dos SantosdS15] is that the problem of proving that the conditions of Theorem 3.1 hold is essentially one of constructing pushforwards of more general, nonlinear fibre bundles over W, endowed with ‘nonlinear connections’. The construction of such pushforwards is exactly what we will want to imitate in the analytic setting. First, however, we will need to discuss the concept of a stratification on an analytic variety over some given base, which is the correct way to generalise integrable connections to nonlinear objects.
$f:W\rightarrow V$. Similarly, one of the key insights of [Reference dos SantosdS15] is that the problem of proving that the conditions of Theorem 3.1 hold is essentially one of constructing pushforwards of more general, nonlinear fibre bundles over W, endowed with ‘nonlinear connections’. The construction of such pushforwards is exactly what we will want to imitate in the analytic setting. First, however, we will need to discuss the concept of a stratification on an analytic variety over some given base, which is the correct way to generalise integrable connections to nonlinear objects.
So let ![]() $V/K$ be an analytic variety, which for now we will not necessarily assume to be smooth. Let
$V/K$ be an analytic variety, which for now we will not necessarily assume to be smooth. Let ![]() $P_V^n$ denote the nth-order infinitesimal neighbourhood of V inside
$P_V^n$ denote the nth-order infinitesimal neighbourhood of V inside ![]() $V\times V$ and
$V\times V$ and ![]() $p_i^n:P_V^n\rightarrow V$ for
$p_i^n:P_V^n\rightarrow V$ for ![]() $i=0,1$ the projection maps.
$i=0,1$ the projection maps.
Definition 4.1. Let ![]() $Z\rightarrow V$ be an analytic variety over V. Then a stratification on Z is a collection of compatible isomorphisms
$Z\rightarrow V$ be an analytic variety over V. Then a stratification on Z is a collection of compatible isomorphisms
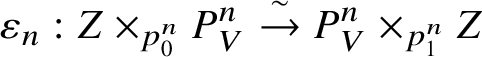 $$ \begin{align*} \varepsilon_n: Z\times_{p_0^n} P^n_V \overset{\sim}{\rightarrow} P^n_V \times_{p_1^n} Z\end{align*} $$
$$ \begin{align*} \varepsilon_n: Z\times_{p_0^n} P^n_V \overset{\sim}{\rightarrow} P^n_V \times_{p_1^n} Z\end{align*} $$of ![]() $P^n_V$-varieties such that
$P^n_V$-varieties such that ![]() $\epsilon _0=\mathrm {id}$ and which satisfy the cocyle condition (see, for example, [Reference BerthelotBer74, Ch. II, §1]). A morphism of stratified varieties is simply a morphism compatible with the maps
$\epsilon _0=\mathrm {id}$ and which satisfy the cocyle condition (see, for example, [Reference BerthelotBer74, Ch. II, §1]). A morphism of stratified varieties is simply a morphism compatible with the maps ![]() $\varepsilon _n$, and the category of such objects will be denoted
$\varepsilon _n$, and the category of such objects will be denoted ![]() $\mathbf {Str}(V/K)$. We will denote the full subcategory of
$\mathbf {Str}(V/K)$. We will denote the full subcategory of ![]() $\mathbf {Str}(V/K)$ consisting of varieties
$\mathbf {Str}(V/K)$ consisting of varieties ![]() $Z\rightarrow V$ which are projective over V by
$Z\rightarrow V$ which are projective over V by ![]() $\mathbf {StrP}(V/K)$.
$\mathbf {StrP}(V/K)$.
Example 4.2. Assume that V is smooth.
1. If
 $Z\rightarrow V$ is a bundle of analytic affine spaces – in other words, is locally isomorphic to the projection
$Z\rightarrow V$ is a bundle of analytic affine spaces – in other words, is locally isomorphic to the projection  ${\mathbb A}^{n,\mathrm {an}}_V \rightarrow V$ (with linear transition maps) – and the stratification maps are linear, then we recover the notion of a coherent module with integrable connection on V.
${\mathbb A}^{n,\mathrm {an}}_V \rightarrow V$ (with linear transition maps) – and the stratification maps are linear, then we recover the notion of a coherent module with integrable connection on V. $$ \begin{align*} Z\times_{p_0^n} P^n_V \overset{\sim}{\rightarrow} P^n_V \times_{p_1^n} Z \end{align*} $$
$$ \begin{align*} Z\times_{p_0^n} P^n_V \overset{\sim}{\rightarrow} P^n_V \times_{p_1^n} Z \end{align*} $$2. If E is a coherent
 $\mathcal {O}_V$-module with integrable connection, with associated affine bundle
$\mathcal {O}_V$-module with integrable connection, with associated affine bundle  $\mathbf {E}\rightarrow V$, then the projectivisation
$\mathbf {E}\rightarrow V$, then the projectivisation  ${\mathbb P}(E)\rightarrow V$ of
${\mathbb P}(E)\rightarrow V$ of  $\mathbf {E}$ inherits a stratification from that on E.
$\mathbf {E}$ inherits a stratification from that on E.
More generally, a natural source of stratified varieties will be varieties equipped with an action of the fundamental group. From now on we will assume that V is smooth, connected and equipped with a K-rational point ![]() $v\in V(K)$.
$v\in V(K)$.
Definition 4.3. We will denote the category of proper K-varieties together with a polarisable 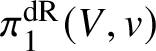 $\pi _1^{\mathrm {dR}}(V,v)$-action by
$\pi _1^{\mathrm {dR}}(V,v)$-action by ![]() $\mathcal {R}_V$.
$\mathcal {R}_V$.
It is worth pointing out that the category we have denoted ![]() $\mathcal {R}_V$ is not the direct analogue in the analytic context of dos Santos’s category of the same name considered in [Reference dos SantosdS15, §6.2]. Our conditions are rather more restrictive; however,
$\mathcal {R}_V$ is not the direct analogue in the analytic context of dos Santos’s category of the same name considered in [Reference dos SantosdS15, §6.2]. Our conditions are rather more restrictive; however, ![]() $\mathcal {R}_V$ will still have enough objects for our purposes.
$\mathcal {R}_V$ will still have enough objects for our purposes.
The construction of objects in ![]() $\mathbf {StrP}(V/K)$ from those in
$\mathbf {StrP}(V/K)$ from those in ![]() $\mathcal {R}_V$ is relatively straightforward. Indeed, if
$\mathcal {R}_V$ is relatively straightforward. Indeed, if ![]() $(Y,\rho ) \in \mathcal {R}_V$, then we may choose an equivariant embedding
$(Y,\rho ) \in \mathcal {R}_V$, then we may choose an equivariant embedding 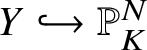 $Y\hookrightarrow {\mathbb P}^N_K$ for some linear action of
$Y\hookrightarrow {\mathbb P}^N_K$ for some linear action of 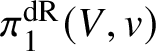 $\pi _1^{\mathrm {dR}}(V,v)$ on
$\pi _1^{\mathrm {dR}}(V,v)$ on 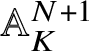 ${\mathbb A}^{N+1}_K$. Via this embedding we may view the projective co-ordinate ring
${\mathbb A}^{N+1}_K$. Via this embedding we may view the projective co-ordinate ring
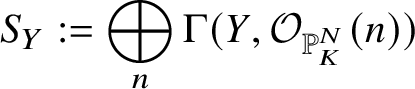 $$ \begin{align*} S_Y := \bigoplus_n \Gamma(Y,\mathcal{O}_{{\mathbb P}^N_K}(n) ) \end{align*} $$
$$ \begin{align*} S_Y := \bigoplus_n \Gamma(Y,\mathcal{O}_{{\mathbb P}^N_K}(n) ) \end{align*} $$as a 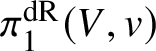 $\pi _1^{\mathrm {dR}}(V,v)$-representation. By construction, we know that
$\pi _1^{\mathrm {dR}}(V,v)$-representation. By construction, we know that ![]() $S_Y$ is the colimit of its finite-dimensional subrepresentations, and hence via the usual Tannakian correspondence we can construct an associated ind-coherent sheaf
$S_Y$ is the colimit of its finite-dimensional subrepresentations, and hence via the usual Tannakian correspondence we can construct an associated ind-coherent sheaf ![]() $\mathcal {S}_Y$ of graded rings on V, equipped with an integrable connection. We now define
$\mathcal {S}_Y$ of graded rings on V, equipped with an integrable connection. We now define
via the relative Proj construction of [Reference ConradCon06]. The integrable connection on ![]() $\mathcal {S}_Y$ induces a stratification on
$\mathcal {S}_Y$ induces a stratification on ![]() $\mathcal {U}_V(Y,\rho )$, making it into an object of
$\mathcal {U}_V(Y,\rho )$, making it into an object of ![]() $\mathbf {StrP}(V/K)$. This generalises Example 4.2(2) in that if
$\mathbf {StrP}(V/K)$. This generalises Example 4.2(2) in that if ![]() $Y={\mathbb P}(E_v)$ for some
$Y={\mathbb P}(E_v)$ for some ![]() $E\in \mathrm {MIC}(V/K)$, then
$E\in \mathrm {MIC}(V/K)$, then ![]() $\mathcal {U}_V(Y)\cong {\mathbb P}(E)$.
$\mathcal {U}_V(Y)\cong {\mathbb P}(E)$.
Proposition 4.4. This construction induces a functor ![]() $\mathcal {U}_V:\mathcal {R}_V\rightarrow \mathbf {StrP}(V/K)$ from polarisable
$\mathcal {U}_V:\mathcal {R}_V\rightarrow \mathbf {StrP}(V/K)$ from polarisable 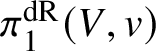 $\pi _1^{\mathrm {dR}}(V,v)$-varieties to projective stratified V-varieties. It is compatible with pullback via morphisms
$\pi _1^{\mathrm {dR}}(V,v)$-varieties to projective stratified V-varieties. It is compatible with pullback via morphisms ![]() $f:W\rightarrow V$ in the sense that the diagram
$f:W\rightarrow V$ in the sense that the diagram
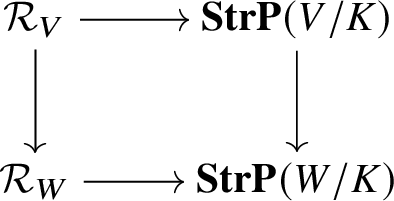
is 2-commutative.
Proof. There are two things to check: firstly, that ![]() $\mathcal {U}_V(Y,\rho )$ does not depend on the choice of
$\mathcal {U}_V(Y,\rho )$ does not depend on the choice of 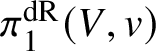 $\pi _1^{\mathrm {dR}}(V,v)$-linearised ample line bundle
$\pi _1^{\mathrm {dR}}(V,v)$-linearised ample line bundle ![]() $\mathcal {L}$ and, secondly, that we can make the association functorial in
$\mathcal {L}$ and, secondly, that we can make the association functorial in ![]() $(Y,\rho )$. For the first claim, we note that given two equivariant embeddings
$(Y,\rho )$. For the first claim, we note that given two equivariant embeddings ![]() $Y\rightarrow {\mathbb P}(E_v)$ and
$Y\rightarrow {\mathbb P}(E_v)$ and ![]() $Y\rightarrow {\mathbb P}(F_v)$, giving rise to polarised
$Y\rightarrow {\mathbb P}(F_v)$, giving rise to polarised 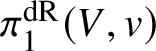 $\pi _1^{\mathrm {dR}}(V,v)$-varieties
$\pi _1^{\mathrm {dR}}(V,v)$-varieties ![]() $(Y,\rho )$ and
$(Y,\rho )$ and ![]() $(Y,\sigma )$, we can simply consider their product
$(Y,\sigma )$, we can simply consider their product
as a polarised 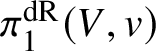 $\pi _1^{\mathrm {dR}}(V,v)$-variety
$\pi _1^{\mathrm {dR}}(V,v)$-variety ![]() $(Y,\tau )$ and show that the two projection maps induce isomorphisms
$(Y,\tau )$ and show that the two projection maps induce isomorphisms
Similarly, to obtain functoriality, we factor a given map ![]() $Y\rightarrow Y'$ of polarisable
$Y\rightarrow Y'$ of polarisable 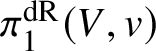 $\pi _1^{\mathrm {dR}}(V,v)$-varieties into the closed immersion
$\pi _1^{\mathrm {dR}}(V,v)$-varieties into the closed immersion ![]() $Y\hookrightarrow Y\times _K Y'$ followed by the projection
$Y\hookrightarrow Y\times _K Y'$ followed by the projection ![]() $Y\times _K Y' \rightarrow Y'$ to reduce to considering either the case of a closed immersion or that of a projection. These can both be very easily handled.
$Y\times _K Y' \rightarrow Y'$ to reduce to considering either the case of a closed immersion or that of a projection. These can both be very easily handled.
Finally, functoriality in ![]() $f:W\rightarrow V$ follows from the facts that the homomorphism
$f:W\rightarrow V$ follows from the facts that the homomorphism 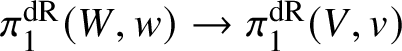 $\pi _1^{\mathrm {dR}}(W,w)\rightarrow \pi _1^{\mathrm {dR}}(V,v)$ corresponds to
$\pi _1^{\mathrm {dR}}(W,w)\rightarrow \pi _1^{\mathrm {dR}}(V,v)$ corresponds to ![]() $f^*$ on the level of modules with integrable connection and that
$f^*$ on the level of modules with integrable connection and that ![]() $\mathbf {Proj}$ commutes with pullback of ind-coherent modules by [Reference ConradCon06, Theorem 2.3.6].
$\mathbf {Proj}$ commutes with pullback of ind-coherent modules by [Reference ConradCon06, Theorem 2.3.6].
With additional polarisability assumptions, ‘Tannakian reconstruction’ theorems are very easy to prove using the classical linear versions.
Definition 4.5. We say that ![]() $Z\in \mathbf {StrP}(V/K)$ is polarisable if there exists
$Z\in \mathbf {StrP}(V/K)$ is polarisable if there exists ![]() $E\in \mathrm {MIC}(V/K)$ and a closed embedding
$E\in \mathrm {MIC}(V/K)$ and a closed embedding ![]() $Z\hookrightarrow {\mathbb P}(E)$ of stratified V-varieties.
$Z\hookrightarrow {\mathbb P}(E)$ of stratified V-varieties.
Clearly, the functor ![]() $\mathcal {R}_V$ lands inside the full subcategory
$\mathcal {R}_V$ lands inside the full subcategory ![]() $\mathbf {StrPol}(V/K)\subset \mathbf {StrP}(V/K)$ consisting of polarisable stratified V-varieties. For us, polarisable stratified varieties will always assumed to be projective, although this is not clear from the terminology.
$\mathbf {StrPol}(V/K)\subset \mathbf {StrP}(V/K)$ consisting of polarisable stratified V-varieties. For us, polarisable stratified varieties will always assumed to be projective, although this is not clear from the terminology.
Theorem 4.6. The functor
is an equivalence of categories.
Proof. This follows very easily from ordinary Tannakian duality and the relative Proj construction introduced in [Reference ConradCon06]. We first claim that given ![]() $(Y,\rho )\in \mathcal {R}_V$, the functor
$(Y,\rho )\in \mathcal {R}_V$, the functor ![]() $\mathcal {U}_V$ induces a bijection between
$\mathcal {U}_V$ induces a bijection between 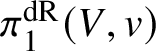 $\pi _1^{\mathrm {dR}}(V,v)$-invariant subschemes of Y and closed stratified subvarieties of
$\pi _1^{\mathrm {dR}}(V,v)$-invariant subschemes of Y and closed stratified subvarieties of ![]() $\mathcal {U}_V(Y,\rho )$. Indeed, injectivity is clear, since for
$\mathcal {U}_V(Y,\rho )$. Indeed, injectivity is clear, since for ![]() $T\subset Y$ closed and
$T\subset Y$ closed and 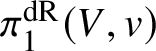 $\pi _1^{\mathrm {dR}}(V,v)$-invariant we may recover T as the fibre of
$\pi _1^{\mathrm {dR}}(V,v)$-invariant we may recover T as the fibre of ![]() $\mathcal {U}_V(T,\rho )$ over v.
$\mathcal {U}_V(T,\rho )$ over v.
For surjectivity, we note that by construction ![]() $\mathcal {U}_V(Y,\rho )=\mathbf {Proj}_{\mathcal {O}_V}(\mathcal {S}_Y)$ for some ind-coherent graded
$\mathcal {U}_V(Y,\rho )=\mathbf {Proj}_{\mathcal {O}_V}(\mathcal {S}_Y)$ for some ind-coherent graded ![]() $\mathcal {O}_V$-algebra
$\mathcal {O}_V$-algebra ![]() $\mathcal {S}_Y$, equipped with an integrable connection. The closed subvariety
$\mathcal {S}_Y$, equipped with an integrable connection. The closed subvariety ![]() $\mathcal {T}\hookrightarrow \mathcal {U}_V(Y,\rho )$ is therefore given by some quotient
$\mathcal {T}\hookrightarrow \mathcal {U}_V(Y,\rho )$ is therefore given by some quotient
which, since T is a stratified subvariety, must be horizontal. There is therefore an induced integrable connection on ![]() $\mathcal {S}_{\mathcal {T}}$. Moreover, since
$\mathcal {S}_{\mathcal {T}}$. Moreover, since ![]() $\mathcal {S}_Y$ is the colimit of its coherent, horizontal subbundles, the same is true of
$\mathcal {S}_Y$ is the colimit of its coherent, horizontal subbundles, the same is true of ![]() $\mathcal {S}_{\mathcal {T}}$. Hence, by the usual Tannakian correspondence this has to come from some
$\mathcal {S}_{\mathcal {T}}$. Hence, by the usual Tannakian correspondence this has to come from some 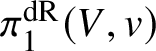 $\pi _1^{\mathrm {dR}}(V,v)$-invariant quotient
$\pi _1^{\mathrm {dR}}(V,v)$-invariant quotient ![]() $S_Y:=\mathcal {S}_{Y,v}\rightarrow S_T:=\mathcal {S}_{\mathcal {T},v}$. Then
$S_Y:=\mathcal {S}_{Y,v}\rightarrow S_T:=\mathcal {S}_{\mathcal {T},v}$. Then ![]() $T=\mathrm {Proj}(S_T)$ is the required invariant closed subscheme of Y.
$T=\mathrm {Proj}(S_T)$ is the required invariant closed subscheme of Y.
This immediately implies essential surjectivity of ![]() $\mathcal {U}_V$ and in fact also implies full faithfulness. Indeed, as in Proposition 4.4, to prove full faithfulness it suffices via the graph construction to treat closed immersions and projections from products. The latter is obvious, and we have just proved the former.
$\mathcal {U}_V$ and in fact also implies full faithfulness. Indeed, as in Proposition 4.4, to prove full faithfulness it suffices via the graph construction to treat closed immersions and projections from products. The latter is obvious, and we have just proved the former.
5 Relative stratifications and pushforwards
To construct appropriate ‘pushforwards’ of smooth, projective stratified varieties along a smooth and projective morphism in [Reference dos SantosdS15], dos Santos proceeds in two stages. First of all, he considers the pushforward of a ‘relatively stratified variety’ Z and then shows that when this arises from a variety with an ‘absolute’ stratification, there is a canonical induced stratification on this pushforward. The analogy to bear in mind from the linear case is that the pushforward ![]() $f_{\mathrm {dR}*}E$ of some module with integrable connection
$f_{\mathrm {dR}*}E$ of some module with integrable connection ![]() $E\in \mathrm {MIC}(W/K)$ is constructed by first viewing it as an object in
$E\in \mathrm {MIC}(W/K)$ is constructed by first viewing it as an object in ![]() $\mathrm {MIC}(W/V)$; one then puts a connection on
$\mathrm {MIC}(W/V)$; one then puts a connection on ![]() $f_{\mathrm {dR}*}E$ by using the fact that E came from
$f_{\mathrm {dR}*}E$ by using the fact that E came from ![]() $\mathrm {MIC}(W/K)$.
$\mathrm {MIC}(W/K)$.
In this section we will achieve the first step for stratified analytic varieties by appealing to GAGA. This will tell us that we can actually apply dos Santos’s results to provide the required pushforwards. In Section 7 we will then find another way to complete the proof of Theorem 2.5 without having to develop the analytic analogue of the ‘infinitesimal equivalence relations’ used in [Reference dos SantosdS15], instead by reducing to the situation over the formal polydisc ![]() $\mathrm {Spf}\left (K[\![ x_1,\ldots ,x_n ]\!]\right )$. We start by introducing certain ‘formal adic spaces’, which will allow a slightly better way of talking about stratifications.
$\mathrm {Spf}\left (K[\![ x_1,\ldots ,x_n ]\!]\right )$. We start by introducing certain ‘formal adic spaces’, which will allow a slightly better way of talking about stratifications.
Definition 5.1. Let ![]() $T\hookrightarrow V$ be a closed immersion of analytic K-varieties; it is therefore by [Reference Fujiwara and KatoFK18, Proposition II.7.3.5] defined by a coherent ideal sheaf
$T\hookrightarrow V$ be a closed immersion of analytic K-varieties; it is therefore by [Reference Fujiwara and KatoFK18, Proposition II.7.3.5] defined by a coherent ideal sheaf ![]() $\mathcal {I}_T\subset \mathcal {O}_V$. Let
$\mathcal {I}_T\subset \mathcal {O}_V$. Let 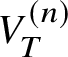 $V^{(n)}_T$ denote the closed subvariety of V defined by the ideal sheaf
$V^{(n)}_T$ denote the closed subvariety of V defined by the ideal sheaf  $\mathcal {I}_T^{n+1}$ (i.e.,
$\mathcal {I}_T^{n+1}$ (i.e., 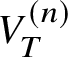 $V_T^{(n)}$ is the nth infinitesimal neighbourhood of T in V). We define the ‘formal completion of V along T’ to be the ind-object
$V_T^{(n)}$ is the nth infinitesimal neighbourhood of T in V). We define the ‘formal completion of V along T’ to be the ind-object 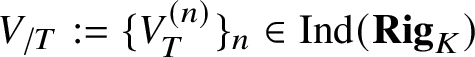 $V_{/T}:=\{ V^{(n)}_T \}_n\in \mathrm {Ind}(\mathbf {Rig}_K)$ in the category of analytic K-varieties.
$V_{/T}:=\{ V^{(n)}_T \}_n\in \mathrm {Ind}(\mathbf {Rig}_K)$ in the category of analytic K-varieties.
Let ![]() $\mathrm {Sh}(\mathbf {Rig}_K)$ denote the category of sheaves on
$\mathrm {Sh}(\mathbf {Rig}_K)$ denote the category of sheaves on ![]() $\mathbf {Rig}_K$ for the analytic topology. Since objects of
$\mathbf {Rig}_K$ for the analytic topology. Since objects of ![]() $\mathbf {Rig}_K$ are locally quasi-compact, we have a fully faithful embedding
$\mathbf {Rig}_K$ are locally quasi-compact, we have a fully faithful embedding
and we will use this to view ![]() $V_{/T}$ as such a sheaf.
$V_{/T}$ as such a sheaf.
Example 5.2. If ![]() $V=\mathrm {Spa}\left (K\langle x \rangle ,\mathcal {V}\langle x \rangle \right )$ and
$V=\mathrm {Spa}\left (K\langle x \rangle ,\mathcal {V}\langle x \rangle \right )$ and ![]() $T\hookrightarrow V$ is the zero section, then
$T\hookrightarrow V$ is the zero section, then
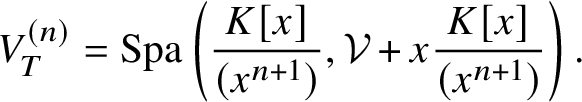 $$ \begin{align*} V^{(n)}_T = \mathrm{Spa}\left(\frac{K[x]}{(x^{n+1})},\mathcal{V}+x\frac{K[x]}{(x^{n+1})}\right). \end{align*} $$
$$ \begin{align*} V^{(n)}_T = \mathrm{Spa}\left(\frac{K[x]}{(x^{n+1})},\mathcal{V}+x\frac{K[x]}{(x^{n+1})}\right). \end{align*} $$So we should think of ![]() $V_{/T}$ as being given by something like
$V_{/T}$ as being given by something like
where the topology on ![]() $K[\![ x ]\!]$ has a basis of open subgroups of the form
$K[\![ x ]\!]$ has a basis of open subgroups of the form ![]() $\varpi ^m\mathcal {V}[\![ x ]\!]+x^nK[\![ x ]\!]$. Note that with this topology,
$\varpi ^m\mathcal {V}[\![ x ]\!]+x^nK[\![ x ]\!]$. Note that with this topology, ![]() $K[\![ x ]\!]$ is not an f-adic ring, and hence the pair
$K[\![ x ]\!]$ is not an f-adic ring, and hence the pair ![]() $(K[\![ x ]\!],\mathcal {V}+xK[\![ x ]\!])$ is not an affinoid ring in the sense of [Reference HuberHub96, §1.1]. It would be interesting to see if there is a more general category of adic spaces in which things like
$(K[\![ x ]\!],\mathcal {V}+xK[\![ x ]\!])$ is not an affinoid ring in the sense of [Reference HuberHub96, §1.1]. It would be interesting to see if there is a more general category of adic spaces in which things like ![]() $\mathrm {Spa}\left (K[\![ x ]\!],\mathcal {V}+xK[\![ x ]\!]\right )$ make sense.
$\mathrm {Spa}\left (K[\![ x ]\!],\mathcal {V}+xK[\![ x ]\!]\right )$ make sense.
By considering the diagonal ![]() $\Delta :V\rightarrow V^2$ of an analytic K-variety, we obtain the ind-variety that we will denote by
$\Delta :V\rightarrow V^2$ of an analytic K-variety, we obtain the ind-variety that we will denote by ![]() $\widehat {P}_V$, which comes equipped with two ‘projection’ maps
$\widehat {P}_V$, which comes equipped with two ‘projection’ maps ![]() $p_i:\widehat {P}_V\rightarrow V$. With this language, we can rephrase the data of a stratification on some variety
$p_i:\widehat {P}_V\rightarrow V$. With this language, we can rephrase the data of a stratification on some variety ![]() $Z \rightarrow V$ as an isomorphism
$Z \rightarrow V$ as an isomorphism
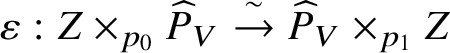 $$ \begin{align*}\varepsilon: Z \times_{p_0} \widehat{P}_V \overset{\sim}{\rightarrow} \widehat{P}_V \times_{p_1} Z \end{align*} $$
$$ \begin{align*}\varepsilon: Z \times_{p_0} \widehat{P}_V \overset{\sim}{\rightarrow} \widehat{P}_V \times_{p_1} Z \end{align*} $$in the slice category 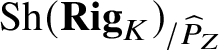 $\mathrm {Sh}(\mathbf {Rig}_K)_{/\widehat {P}_Z}$ of sheaves over
$\mathrm {Sh}(\mathbf {Rig}_K)_{/\widehat {P}_Z}$ of sheaves over ![]() $\widehat {P}_V$, subject to certain obvious conditions. If we let
$\widehat {P}_V$, subject to certain obvious conditions. If we let ![]() $s: \widehat {P}_V\rightarrow \widehat {P}_V$ denote the map switching the factors and
$s: \widehat {P}_V\rightarrow \widehat {P}_V$ denote the map switching the factors and 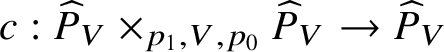 $c :\widehat {P}_V\times _{p_1,V,p_0} \widehat {P}_V \rightarrow \widehat {P}_V$ the map induced by
$c :\widehat {P}_V\times _{p_1,V,p_0} \widehat {P}_V \rightarrow \widehat {P}_V$ the map induced by ![]() $((v_0,v_1),(v_1,v_2))\mapsto (v_0,v_2)$, then exactly as in [Reference BerthelotBer74, Ch. II, §1] we can show that the data
$((v_0,v_1),(v_1,v_2))\mapsto (v_0,v_2)$, then exactly as in [Reference BerthelotBer74, Ch. II, §1] we can show that the data
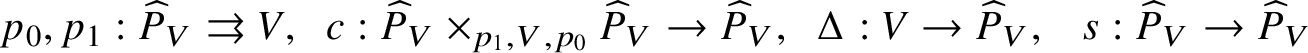 $$ \begin{align*} p_0,p_1:\widehat{P}_V \rightrightarrows V,\;\; c :\widehat{P}_V\times_{p_1,V,p_0} \widehat{P}_V \rightarrow \widehat{P}_V ,\;\;\Delta: V\rightarrow\widehat{P}_V,\;\;\ s:\widehat{P}_V\rightarrow \widehat{P}_V\end{align*} $$
$$ \begin{align*} p_0,p_1:\widehat{P}_V \rightrightarrows V,\;\; c :\widehat{P}_V\times_{p_1,V,p_0} \widehat{P}_V \rightarrow \widehat{P}_V ,\;\;\Delta: V\rightarrow\widehat{P}_V,\;\;\ s:\widehat{P}_V\rightarrow \widehat{P}_V\end{align*} $$forms a ‘formal groupoid’ over ![]() $\mathrm {Spa}\left (K\right )$ and that a stratification on a V-variety Z is equivalent to an action of this groupoid.
$\mathrm {Spa}\left (K\right )$ and that a stratification on a V-variety Z is equivalent to an action of this groupoid.
Similarly, if we are given some morphism ![]() $f:W\rightarrow V$, then we may consider the formal completion
$f:W\rightarrow V$, then we may consider the formal completion 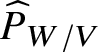 $\widehat {P}_{W/V}$ along the diagonal
$\widehat {P}_{W/V}$ along the diagonal ![]() $\Delta :W\rightarrow W\times _V W$. We have
$\Delta :W\rightarrow W\times _V W$. We have
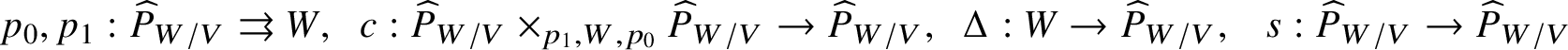 $$ \begin{align*} p_0,p_1:\widehat{P}_{W/V} \rightrightarrows W,\;\; c :\widehat{P}_{W/V}\times_{p_1,W,p_0} \widehat{P}_{W/V} \rightarrow \widehat{P}_{W/V} ,\;\;\Delta: W\rightarrow\widehat{P}_{W/V},\;\;\ s:\widehat{P}_{W/V}\rightarrow \widehat{P}_{W/V}\end{align*} $$
$$ \begin{align*} p_0,p_1:\widehat{P}_{W/V} \rightrightarrows W,\;\; c :\widehat{P}_{W/V}\times_{p_1,W,p_0} \widehat{P}_{W/V} \rightarrow \widehat{P}_{W/V} ,\;\;\Delta: W\rightarrow\widehat{P}_{W/V},\;\;\ s:\widehat{P}_{W/V}\rightarrow \widehat{P}_{W/V}\end{align*} $$exactly as before, giving rise to a formal groupoid over V.
Definition 5.3. A V-linear stratification on a W-variety Z is an action of the groupoid 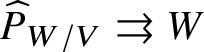 $\widehat {P}_{W/V}\rightrightarrows W$. We denote the category of W-varieties with a V-linear stratification by
$\widehat {P}_{W/V}\rightrightarrows W$. We denote the category of W-varieties with a V-linear stratification by ![]() $\mathbf {Str}(W/V)$ and the full subcategory of objects which are projective over W by
$\mathbf {Str}(W/V)$ and the full subcategory of objects which are projective over W by ![]() $\mathbf {StrP}(W/V)$.
$\mathbf {StrP}(W/V)$.
These notions satisfy all of the usual functorialities, which can be summarised by saying that for any commutative square

there is an induced morphism
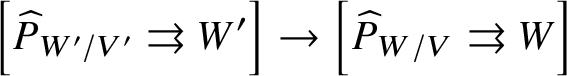 $$ \begin{align*} \left[ \widehat{P}_{W'/V'}\rightrightarrows W' \right] \rightarrow \left[ \widehat{P}_{W/V}\rightrightarrows W \right] \end{align*} $$
$$ \begin{align*} \left[ \widehat{P}_{W'/V'}\rightrightarrows W' \right] \rightarrow \left[ \widehat{P}_{W/V}\rightrightarrows W \right] \end{align*} $$of formal groupoids, and hence a pullback functor ![]() $\mathbf {Str}(W/V)\rightarrow \mathbf {Str}(W'/V')$. This is transitive in the obvious manner. For example, taking the diagram
$\mathbf {Str}(W/V)\rightarrow \mathbf {Str}(W'/V')$. This is transitive in the obvious manner. For example, taking the diagram

we obtain the forgetful functor ![]() $\mathbf {Str}(W/K)\rightarrow \mathbf {Str}(W/V)$.
$\mathbf {Str}(W/K)\rightarrow \mathbf {Str}(W/V)$.
Now let us suppose that we have a smooth, projective morphism ![]() $f:W\rightarrow V$ of analytic K-varieties, with geometrically connected fibres. Note that we do not assume at this point that the base V is smooth. If
$f:W\rightarrow V$ of analytic K-varieties, with geometrically connected fibres. Note that we do not assume at this point that the base V is smooth. If ![]() $\mathbf {P}(V)=\mathbf {StrP}(V/V)$ denotes the category of projective V-varieties, then, as we have just seen, there is a pullback functor
$\mathbf {P}(V)=\mathbf {StrP}(V/V)$ denotes the category of projective V-varieties, then, as we have just seen, there is a pullback functor
We wish to construct an ‘adjoint’ to ![]() $f^*$, at least under certain extra conditions on objects in
$f^*$, at least under certain extra conditions on objects in ![]() $\mathbf {StrP}(W/V)$. To do so, suppose therefore that we are given some
$\mathbf {StrP}(W/V)$. To do so, suppose therefore that we are given some ![]() $Z\in \mathbf {StrP}(W/V)$. Define a functor
$Z\in \mathbf {StrP}(W/V)$. Define a functor
 $$ \begin{align*} f_*Z :\mathbf{Rig}_V &\rightarrow \mathbf{Sets} \\ T/V &\mapsto \left\{ \text{sections of } Z \times_V T \rightarrow W\times_V T \right\} \end{align*} $$
$$ \begin{align*} f_*Z :\mathbf{Rig}_V &\rightarrow \mathbf{Sets} \\ T/V &\mapsto \left\{ \text{sections of } Z \times_V T \rightarrow W\times_V T \right\} \end{align*} $$where sections are considered as certain closed subvarieties of ![]() $Z \times _V T$. (Thus,
$Z \times _V T$. (Thus, ![]() $f_*Z$ is a subfunctor of the Hilbert functor and the usual flatness condition is redundant for
$f_*Z$ is a subfunctor of the Hilbert functor and the usual flatness condition is redundant for ![]() $f_*Z$, since W is flat over V.)
$f_*Z$, since W is flat over V.)
Proposition 5.4. The functor ![]() $f_*Z$ is representable by an analytic variety over V which has the following property: for each open affinoid
$f_*Z$ is representable by an analytic variety over V which has the following property: for each open affinoid ![]() $\mathrm {Spa}\left (A\right )\subset V$, the restriction of
$\mathrm {Spa}\left (A\right )\subset V$, the restriction of ![]() $f_*Z \times _V \mathrm {Spa}\left (A\right )\rightarrow \mathrm {Spa}\left (A\right )$ to each of its connected components arises as the analytification of a quasi-projective A-scheme.
$f_*Z \times _V \mathrm {Spa}\left (A\right )\rightarrow \mathrm {Spa}\left (A\right )$ to each of its connected components arises as the analytification of a quasi-projective A-scheme.
Proof. This is similar in spirit to [Reference ConradCon06, Theorem 4.1.3]. Since ![]() $f_*Z$ is clearly a sheaf for the analytic topology on
$f_*Z$ is clearly a sheaf for the analytic topology on ![]() $\mathbf {Rig}_K$, we may in fact assume that
$\mathbf {Rig}_K$, we may in fact assume that ![]() $V=\mathrm {Spa}\left (A\right )$ is affinoid. Hence, by relative rigid analytic GAGA [Reference ConradCon06, Example 3.2.6], W is the analytification of a smooth projective A-scheme
$V=\mathrm {Spa}\left (A\right )$ is affinoid. Hence, by relative rigid analytic GAGA [Reference ConradCon06, Example 3.2.6], W is the analytification of a smooth projective A-scheme ![]() $W^a$, and
$W^a$, and ![]() $Z\rightarrow W$ is the analyitification of a projective morphism
$Z\rightarrow W$ is the analyitification of a projective morphism ![]() $Z^a\rightarrow W^a$. We consider the corresponding functor
$Z^a\rightarrow W^a$. We consider the corresponding functor
 $$ \begin{align*} f^a_*Z^a :\mathbf{Sch}_A &\rightarrow \mathbf{Sets} \\ T/A &\mapsto \left\{ \text{sections of } Z^a \times_{A} T \rightarrow W^a \times_A T \right\} \end{align*} $$
$$ \begin{align*} f^a_*Z^a :\mathbf{Sch}_A &\rightarrow \mathbf{Sets} \\ T/A &\mapsto \left\{ \text{sections of } Z^a \times_{A} T \rightarrow W^a \times_A T \right\} \end{align*} $$of locally Noetherian A-schemes, which by [Reference GrothendieckGro61, §4, Variant c.] is representable by a disjoint union of quasi-projective A-schemes. It therefore suffices to show that the analytification of ![]() $f^a_*Z^a$ represents the functor
$f^a_*Z^a$ represents the functor ![]() $f_*Z$. Since both are sheaves for the analytic topology, it suffices to check this on affinoids
$f_*Z$. Since both are sheaves for the analytic topology, it suffices to check this on affinoids ![]() $\mathrm {Spa}\left (B\right )\rightarrow \mathrm {Spa}\left (A\right )$. In this case, we can again appeal to rigid analytic GAGA, which says that any closed subvariety of
$\mathrm {Spa}\left (B\right )\rightarrow \mathrm {Spa}\left (A\right )$. In this case, we can again appeal to rigid analytic GAGA, which says that any closed subvariety of ![]() $Z\times _{\mathrm {Spa}\left (A\right )} \mathrm {Spa}\left (B\right )$ is algebraic; that is, comes from a unique closed subscheme of
$Z\times _{\mathrm {Spa}\left (A\right )} \mathrm {Spa}\left (B\right )$ is algebraic; that is, comes from a unique closed subscheme of ![]() $Z^a_{B}$.
$Z^a_{B}$.
Let ![]() $b:T\rightarrow f_*Z$ be a point of
$b:T\rightarrow f_*Z$ be a point of ![]() $f_*Z$, corresponding to a section
$f_*Z$, corresponding to a section ![]() $\tau _b:W\times _V T \rightarrow Z\times _V T$. Pulling back by the two projections
$\tau _b:W\times _V T \rightarrow Z\times _V T$. Pulling back by the two projections 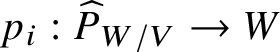 $p_i:\widehat {P}_{W/V}\rightarrow W$ – that is, applying
$p_i:\widehat {P}_{W/V}\rightarrow W$ – that is, applying 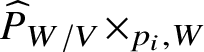 $\widehat {P}_{W/V}\times _{p_i,W}$ – we obtain sections
$\widehat {P}_{W/V}\times _{p_i,W}$ – we obtain sections
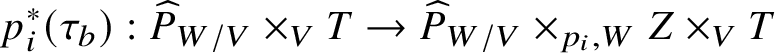 $$ \begin{align*}p_i^*(\tau_b): \widehat{P}_{W/V} \times_V T \rightarrow \widehat{P}_{W/V}\times_{p_i,W}Z\times_V T \end{align*} $$
$$ \begin{align*}p_i^*(\tau_b): \widehat{P}_{W/V} \times_V T \rightarrow \widehat{P}_{W/V}\times_{p_i,W}Z\times_V T \end{align*} $$of ![]() $\mathrm {id}\times _{p_i,W}g$. We say that b is horizontal if
$\mathrm {id}\times _{p_i,W}g$. We say that b is horizontal if ![]() $\epsilon (p^*_0(\tau _b))=p^*_1(\tau _b)$, where
$\epsilon (p^*_0(\tau _b))=p^*_1(\tau _b)$, where ![]() $\epsilon $ is the stratification on Z.
$\epsilon $ is the stratification on Z.
Definition 5.5. We define ![]() $f_{\mathrm {dR}*}Z\subset f_*Z$ to be the subfunctor of horizontal sections.
$f_{\mathrm {dR}*}Z\subset f_*Z$ to be the subfunctor of horizontal sections.
Proposition 5.6. The subfunctor ![]() $f_{\mathrm {dR}*}Z$ is representable by a closed analytic subvariety of
$f_{\mathrm {dR}*}Z$ is representable by a closed analytic subvariety of ![]() $f_*Z$. If Z is smooth over W, then for any open affinoid
$f_*Z$. If Z is smooth over W, then for any open affinoid ![]() $\mathrm {Spa}\left (A\right )\subset V$ the restriction of
$\mathrm {Spa}\left (A\right )\subset V$ the restriction of ![]() $f_{\mathrm {dR}*}Z \times _V \mathrm {Spa}\left (A\right )\rightarrow \mathrm {Spa}\left (A\right )$ to each of its connected components is projective.
$f_{\mathrm {dR}*}Z \times _V \mathrm {Spa}\left (A\right )\rightarrow \mathrm {Spa}\left (A\right )$ to each of its connected components is projective.
Proof. Being a closed subvariety is local, and hence we may in fact assume that ![]() $V=\mathrm {Spa}\left (A\right )$ is affinoid. Now again the whole situation algebrises: we have some smooth projective
$V=\mathrm {Spa}\left (A\right )$ is affinoid. Now again the whole situation algebrises: we have some smooth projective ![]() $f^a:W^a\rightarrow \mathrm {Spec}\left (A\right )$ and some projective
$f^a:W^a\rightarrow \mathrm {Spec}\left (A\right )$ and some projective ![]() $Z^a\rightarrow W^a$ giving rise to Z upon analytification. Moreover, since the algebraic infinitesimal neighbourhoods give rise to the analytic ones upon analytification, it follows that the analytic stratification on Z comes from a unique A-linear algebraic stratification on
$Z^a\rightarrow W^a$ giving rise to Z upon analytification. Moreover, since the algebraic infinitesimal neighbourhoods give rise to the analytic ones upon analytification, it follows that the analytic stratification on Z comes from a unique A-linear algebraic stratification on ![]() $Z^a$. Now we simply note that the results of [Reference dos SantosdS15, §10] apply over any separated, Noetherian base scheme; for example,
$Z^a$. Now we simply note that the results of [Reference dos SantosdS15, §10] apply over any separated, Noetherian base scheme; for example, ![]() $\mathrm {Spec}\left (A\right )$. Translated into algebraic terms, what we have termed ‘horizontal’ corresponds exactly to what dos Santos calls ‘tangential’; hence, we may again use rigid analytic GAGA to show that our functor
$\mathrm {Spec}\left (A\right )$. Translated into algebraic terms, what we have termed ‘horizontal’ corresponds exactly to what dos Santos calls ‘tangential’; hence, we may again use rigid analytic GAGA to show that our functor ![]() $ f_{\mathrm {dR}*}Z$ is simply the analytification of dos Santos’s scheme
$ f_{\mathrm {dR}*}Z$ is simply the analytification of dos Santos’s scheme ![]() $H_{f^a}(Z^a)$.
$H_{f^a}(Z^a)$.
The defining property of ![]() $f_{\mathrm {dR}*}Z$ gives a section
$f_{\mathrm {dR}*}Z$ gives a section ![]() $W\times _V f_{\mathrm {dR}*}Z \rightarrow Z\times _V f_{\mathrm {dR}*}Z$, and by composing with the first projection, we therefore obtain a morphism
$W\times _V f_{\mathrm {dR}*}Z \rightarrow Z\times _V f_{\mathrm {dR}*}Z$, and by composing with the first projection, we therefore obtain a morphism ![]() $\varepsilon _Z: f^*f_{\mathrm {dR}*}Z\rightarrow Z$ of W-varieties. Essentially all of the main properties of
$\varepsilon _Z: f^*f_{\mathrm {dR}*}Z\rightarrow Z$ of W-varieties. Essentially all of the main properties of ![]() $f_{\mathrm {dR}*}Z$ can then be deduced from those proved in [Reference dos SantosdS15].
$f_{\mathrm {dR}*}Z$ can then be deduced from those proved in [Reference dos SantosdS15].
Proposition 5.7. Let ![]() $Z\in \mathbf {StrP}(W/V)$ be smooth over W.
$Z\in \mathbf {StrP}(W/V)$ be smooth over W.
1. The map
 $\varepsilon _Z: f^*f_{\mathrm {dR}*}Z\rightarrow Z$ is horizontal with respect to the pullback (V-linear) stratification on
$\varepsilon _Z: f^*f_{\mathrm {dR}*}Z\rightarrow Z$ is horizontal with respect to the pullback (V-linear) stratification on  $f_{\mathrm {dR}*}Z$ and the given (V-linear) stratification on Z.
$f_{\mathrm {dR}*}Z$ and the given (V-linear) stratification on Z.2. Formation of
 $f_{\mathrm {dR}*}Z$ is compatible with base change: if
$f_{\mathrm {dR}*}Z$ is compatible with base change: if  $V'\rightarrow V$ is a morphism of K-varieties, then
$V'\rightarrow V$ is a morphism of K-varieties, then  $(f_{\mathrm {dR}*}Z)\times _V V' \cong f_{\mathrm {dR}*}(Z\times _V V')$ and, via this isomorphism,
$(f_{\mathrm {dR}*}Z)\times _V V' \cong f_{\mathrm {dR}*}(Z\times _V V')$ and, via this isomorphism,  $\varepsilon _{Z\times _V V'} = \varepsilon _Z \times _V V'$.
$\varepsilon _{Z\times _V V'} = \varepsilon _Z \times _V V'$.3. If the base
 $V=\mathrm {Spa}\left (K\right )$ is a point,
$V=\mathrm {Spa}\left (K\right )$ is a point,  $w\in W(K)$ is a rational point and
$w\in W(K)$ is a rational point and  $Z=\mathcal {U}_W(Y,\rho )$ for some
$Z=\mathcal {U}_W(Y,\rho )$ for some  $(Y,\rho )\in \mathcal {R}_W$, smooth over K, then
$(Y,\rho )\in \mathcal {R}_W$, smooth over K, then  $\varepsilon _Z: f^*f_{\mathrm {dR}*}Z \rightarrow Z$ is obtained by applying
$\varepsilon _Z: f^*f_{\mathrm {dR}*}Z \rightarrow Z$ is obtained by applying  $\mathcal {U}_W$ to the closed immersion considered as a morphism of
$\mathcal {U}_W$ to the closed immersion considered as a morphism of $$ \begin{align*} Y^{\pi_1^{\mathrm{dR}}(W,w)}\rightarrow Y, \end{align*} $$
$$ \begin{align*} Y^{\pi_1^{\mathrm{dR}}(W,w)}\rightarrow Y, \end{align*} $$ $\pi _1^{\mathrm {dR}}(W,w)$-varieties.
$\pi _1^{\mathrm {dR}}(W,w)$-varieties.
Proof. Note that the first two are local on V and therefore follow from their algebraic versions [Reference dos SantosdS15, Proposition 12.1, Corollary 12.4]. For the third, we wish to algebrise and apply [Reference dos SantosdS15, Proposition 14.5]; the point is to check that the induced (algebraic) stratification on Z is simple. This follows from the argument in the paragraph preceding the proof of [Reference dos SantosdS15, Proposition 14.5].
6 Formal stratifications, integrability and base change
It will be necessary for us to have a formal analogue of the above constructions, working for now over an arbitrary field F. Since the basic ideas are essentially identical to those in the previous section, we will not give too many details. Let ![]() $t=(t_1,\ldots ,t_d)$ be a collection of variables and set
$t=(t_1,\ldots ,t_d)$ be a collection of variables and set ![]() $S=\mathrm {Spf}\left (F[\![ t ]\!]\right )$ to be the d-dimensional formal polydisc over F (using the t-adic topology). We will let
$S=\mathrm {Spf}\left (F[\![ t ]\!]\right )$ to be the d-dimensional formal polydisc over F (using the t-adic topology). We will let ![]() $f:X\rightarrow S$ be a smooth morphism of finite type. In this situation we may define the formal groupoids
$f:X\rightarrow S$ be a smooth morphism of finite type. In this situation we may define the formal groupoids
 $$ \begin{align*}\widehat{P}_X \rightrightarrows X,\;\; \widehat{P}_{X/S} \rightrightarrows X,\;\; \widehat{P}_S \rightrightarrows S \end{align*} $$
$$ \begin{align*}\widehat{P}_X \rightrightarrows X,\;\; \widehat{P}_{X/S} \rightrightarrows X,\;\; \widehat{P}_S \rightrightarrows S \end{align*} $$exactly as before. If ![]() $g:Z\rightarrow X$ is a morphism of formal schemes, then an F-linear (respectively S-linear) stratification on Z is then an action of the groupoid
$g:Z\rightarrow X$ is a morphism of formal schemes, then an F-linear (respectively S-linear) stratification on Z is then an action of the groupoid ![]() $\widehat {P}_X \rightrightarrows X$ (respectively
$\widehat {P}_X \rightrightarrows X$ (respectively  $\widehat {P}_{X/S} \rightrightarrows X$). We similarly have the notion of an F-linear stratification on some formal S-scheme.
$\widehat {P}_{X/S} \rightrightarrows X$). We similarly have the notion of an F-linear stratification on some formal S-scheme.
If ![]() $X/S$ is projective and
$X/S$ is projective and ![]() $g:Z\rightarrow X$ is a projective formal X-scheme equipped with an S-linear stratification, then we may define the pushforward
$g:Z\rightarrow X$ is a projective formal X-scheme equipped with an S-linear stratification, then we may define the pushforward ![]() $f_*Z$ as a disjoint union of formal schemes over S, as well as the closed subscheme
$f_*Z$ as a disjoint union of formal schemes over S, as well as the closed subscheme ![]() $f_{\mathrm {dR}*}Z\subset f_{*}Z$, exactly as in the previous section. If we let
$f_{\mathrm {dR}*}Z\subset f_{*}Z$, exactly as in the previous section. If we let ![]() $S_n,X_n,Z_n$ denote the mod
$S_n,X_n,Z_n$ denote the mod ![]() $t^{n+1}$-reductions, then we could equally well construct
$t^{n+1}$-reductions, then we could equally well construct ![]() $f_{\mathrm {dR}*}Z$ and
$f_{\mathrm {dR}*}Z$ and ![]() $f_{*}Z$ as the limits
$f_{*}Z$ as the limits
of the algebraic pushforwards along ![]() $f_n:X_n\rightarrow S_n$, as considered by dos Santos in [Reference dos SantosdS15, §10] (and that he terms
$f_n:X_n\rightarrow S_n$, as considered by dos Santos in [Reference dos SantosdS15, §10] (and that he terms ![]() $H_0(Z_n)$ and
$H_0(Z_n)$ and ![]() $H_{f_n}(Z_n)$, respectively). The following represents a simple extension to formal schemes of the results of [Reference dos SantosdS15].
$H_{f_n}(Z_n)$, respectively). The following represents a simple extension to formal schemes of the results of [Reference dos SantosdS15].
Theorem 6.1. Assume that X is projective over S and that Z is smooth and projective over X, equipped with an F-linear stratification. Then there exists an F-linear stratification on ![]() $f_{\mathrm {dR}*}Z$ as a formal S-scheme such that the map
$f_{\mathrm {dR}*}Z$ as a formal S-scheme such that the map
is compatible with the F-linear stratifications on both sides.
Proof. This essentially follows from [Reference dos SantosdS15] upon taking the limit in n, although a little care is needed to achieve this. Consider for all n the mod ![]() $t^{n+1}$ reduction
$t^{n+1}$ reduction  $Z_n \overset {g_n}{\rightarrow } X_n \overset {f_n}{\rightarrow } S_n$ of everything in sight, we wish to construct a stratification on
$Z_n \overset {g_n}{\rightarrow } X_n \overset {f_n}{\rightarrow } S_n$ of everything in sight, we wish to construct a stratification on ![]() $f_{n,\mathrm {dR}*}Z_n$ as an
$f_{n,\mathrm {dR}*}Z_n$ as an ![]() $S_n$-scheme such that
$S_n$-scheme such that ![]() $f_n^*f_{n,\mathrm {dR}*}Z_n \rightarrow Z_n$ is compatible with the stratifications. We cannot directly apply the results of [Reference dos SantosdS15] since
$f_n^*f_{n,\mathrm {dR}*}Z_n \rightarrow Z_n$ is compatible with the stratifications. We cannot directly apply the results of [Reference dos SantosdS15] since ![]() $S_n$ is not smooth over F, but we can get around this as follows.
$S_n$ is not smooth over F, but we can get around this as follows.
Firstly, let us recall that dos Santos views stratifications as particular kinds of ‘infinitesimal equivalence relations’, and without using any smoothness assumptions on the ‘base’ of the fibration (in our case ![]() $S_n$) he constructs an infinitesimal equivalence relation on
$S_n$) he constructs an infinitesimal equivalence relation on ![]() $f_{n,\mathrm {dR}*}Z_n$ such that
$f_{n,\mathrm {dR}*}Z_n$ such that ![]() $f_n^*f_{n,\mathrm {dR}*}Z_n \rightarrow Z_n$ intertwines these two equivalence relations. The point is then to try to prove that this equivalence relation on
$f_n^*f_{n,\mathrm {dR}*}Z_n \rightarrow Z_n$ intertwines these two equivalence relations. The point is then to try to prove that this equivalence relation on ![]() $f_{n,\mathrm {dR}*}Z_n$ actually comes from a stratification. This is the content of [Reference dos SantosdS15, Proposition 13.4], and this proposition is the only place where smoothness assumptions are used.
$f_{n,\mathrm {dR}*}Z_n$ actually comes from a stratification. This is the content of [Reference dos SantosdS15, Proposition 13.4], and this proposition is the only place where smoothness assumptions are used.
But here we can exploit the fact that our situation arises as the mod ![]() $t^{n+1}$ reduction of
$t^{n+1}$ reduction of 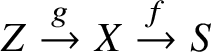 $Z\overset {g}{\rightarrow } X \overset {f}{\rightarrow } S$ with S formally smooth over K. In particular, if we choose local étale co-ordinates
$Z\overset {g}{\rightarrow } X \overset {f}{\rightarrow } S$ with S formally smooth over K. In particular, if we choose local étale co-ordinates ![]() $x=(x_1,\ldots , x_k)$ for
$x=(x_1,\ldots , x_k)$ for ![]() $X/S$ and
$X/S$ and ![]() $z=(z_1,\ldots ,z_m)$ for
$z=(z_1,\ldots ,z_m)$ for ![]() $Z/X$, then the stratification on Z corresponds to some section
$Z/X$, then the stratification on Z corresponds to some section ![]() $\mathcal {O}_Z[\![ dt,dx,dz ]\!] \rightarrow \mathcal {O}_Z[\![ dt,dx ]\!]$ of the natural inclusion
$\mathcal {O}_Z[\![ dt,dx,dz ]\!] \rightarrow \mathcal {O}_Z[\![ dt,dx ]\!]$ of the natural inclusion ![]() $\mathcal {O}_Z[\![ dt,dx ]\!] \rightarrow \mathcal {O}_Z[\![ dt,dx,dz ]\!]$. In particular, we may therefore choose m elements
$\mathcal {O}_Z[\![ dt,dx ]\!] \rightarrow \mathcal {O}_Z[\![ dt,dx,dz ]\!]$. In particular, we may therefore choose m elements ![]() $F_1,\ldots ,F_m$ generating the kernel, locally on X and Z. Now reducing mod
$F_1,\ldots ,F_m$ generating the kernel, locally on X and Z. Now reducing mod ![]() $t^{n+1}$ we can follow the proof of [Reference dos SantosdS15, Proposition 13.4] word for word to conclude.
$t^{n+1}$ we can follow the proof of [Reference dos SantosdS15, Proposition 13.4] word for word to conclude.
For this to be useful, we will need to compare this with the setup considered previously. Let us therefore return to that situation. So we have some smooth projective map ![]() $f:W\rightarrow V$ of analytic K-varieties, with geometrically connected fibres, and
$f:W\rightarrow V$ of analytic K-varieties, with geometrically connected fibres, and ![]() $g:Z\rightarrow W$ some smooth and projective stratified variety over W. If
$g:Z\rightarrow W$ some smooth and projective stratified variety over W. If ![]() $v\in V$ is a smooth rigid point of V, then we may consider the various infinitesimal neighbourhoods
$v\in V$ is a smooth rigid point of V, then we may consider the various infinitesimal neighbourhoods 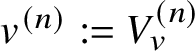 $v^{(n)}:=V_{v}^{(n)}$ as before. The point is that now the base change
$v^{(n)}:=V_{v}^{(n)}$ as before. The point is that now the base change ![]() $Z_{v^{(n)}}\rightarrow W_{v^{(n)}} \rightarrow v^{(n)}$ algebrises relative to the ground field K, so we may consider
$Z_{v^{(n)}}\rightarrow W_{v^{(n)}} \rightarrow v^{(n)}$ algebrises relative to the ground field K, so we may consider ![]() $Z_{v^{(n)}}\rightarrow W_{v^{(n)}}$ as a projective morphism of projective K-schemes, equipped with a K-linear stratification. Thus, taking the limit in n we obtain a smooth projective stratified formal scheme
$Z_{v^{(n)}}\rightarrow W_{v^{(n)}}$ as a projective morphism of projective K-schemes, equipped with a K-linear stratification. Thus, taking the limit in n we obtain a smooth projective stratified formal scheme  $\widehat {Z}_v\overset {g_v}{\rightarrow } \widehat {W}_v \overset {f_v}{\rightarrow } \mathrm {Spf}(\widehat {\mathcal {O}}_{V,v})$, where
$\widehat {Z}_v\overset {g_v}{\rightarrow } \widehat {W}_v \overset {f_v}{\rightarrow } \mathrm {Spf}(\widehat {\mathcal {O}}_{V,v})$, where  $\widehat {\mathcal {O}}_{V,v}$ is simply considered with the maximal-adic topology (not any kind of p-adic topology). Since v was chosen to be a smooth point, we therefore find ourselves in the situation of Theorem 6.1.
$\widehat {\mathcal {O}}_{V,v}$ is simply considered with the maximal-adic topology (not any kind of p-adic topology). Since v was chosen to be a smooth point, we therefore find ourselves in the situation of Theorem 6.1.
Hence, we have some projective stratified formal scheme 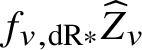 $f_{v,\mathrm {dR}*}\widehat {Z}_v$ over
$f_{v,\mathrm {dR}*}\widehat {Z}_v$ over 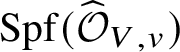 $\mathrm {Spf}(\widehat {\mathcal {O}}_{V,v})$. Alternatively, since the base change of
$\mathrm {Spf}(\widehat {\mathcal {O}}_{V,v})$. Alternatively, since the base change of ![]() $f_{\mathrm {dR}*}Z$ to
$f_{\mathrm {dR}*}Z$ to ![]() $v^{(n)}$ is a disjoint union of projective
$v^{(n)}$ is a disjoint union of projective ![]() $v^{(n)}$-schemes, we may take the limit in n to obtain
$v^{(n)}$-schemes, we may take the limit in n to obtain 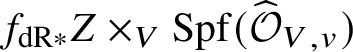 $f_{\mathrm {dR}*}Z \times _V \mathrm {Spf}(\widehat {\mathcal {O}}_{V,v})$ which is a disjoint union of projective formal
$f_{\mathrm {dR}*}Z \times _V \mathrm {Spf}(\widehat {\mathcal {O}}_{V,v})$ which is a disjoint union of projective formal 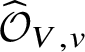 $\widehat {\mathcal {O}}_{V,v}$-schemes. Note that this is simply notation, since there is no actual map
$\widehat {\mathcal {O}}_{V,v}$-schemes. Note that this is simply notation, since there is no actual map 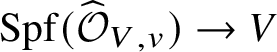 $\mathrm {Spf}(\widehat {\mathcal {O}}_{V,v}) \rightarrow V$ of locally ringed spaces.
$\mathrm {Spf}(\widehat {\mathcal {O}}_{V,v}) \rightarrow V$ of locally ringed spaces.
Proposition 6.2. There is a natural isomorphism
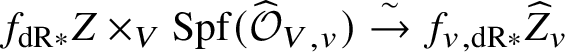 $$ \begin{align*} f_{\mathrm{dR}*}Z \times_V \mathrm{Spf}(\widehat{\mathcal{O}}_{V,v}) \overset{\sim}{\rightarrow} f_{v,\mathrm{dR}*}\widehat{Z}_v \end{align*} $$
$$ \begin{align*} f_{\mathrm{dR}*}Z \times_V \mathrm{Spf}(\widehat{\mathcal{O}}_{V,v}) \overset{\sim}{\rightarrow} f_{v,\mathrm{dR}*}\widehat{Z}_v \end{align*} $$of disjoint unions of projective formal schemes over 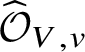 $\widehat {\mathcal {O}}_{V,v}$, such that the diagram
$\widehat {\mathcal {O}}_{V,v}$, such that the diagram
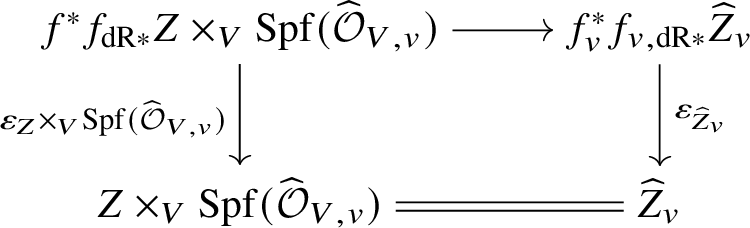
of formal schemes with ![]() $\widehat {V}_v$-linear stratifications commutes.
$\widehat {V}_v$-linear stratifications commutes.
Proof. This simply follows from applying Proposition 5.7(2) to the various infinitesimal neighbourhoods ![]() $v^{(n)}\rightarrow V$ and then taking the limit in n.
$v^{(n)}\rightarrow V$ and then taking the limit in n.
Corollary 6.3. If ![]() $Z\in \mathbf {StrP}(W/K)$ is smooth over W, then for each connected open affinoid
$Z\in \mathbf {StrP}(W/K)$ is smooth over W, then for each connected open affinoid ![]() $\mathrm {Spa}\left (A\right )\subset V$ the fibre product
$\mathrm {Spa}\left (A\right )\subset V$ the fibre product
is flat and projective over ![]() $\mathrm {Spa}\left (A\right )$.
$\mathrm {Spa}\left (A\right )$.
Proof. We may assume that ![]() $V=\mathrm {Spa}\left (A\right )$ and that
$V=\mathrm {Spa}\left (A\right )$ and that ![]() $f,g$ come from algebraic maps
$f,g$ come from algebraic maps
of projective A-schemes. We have already observed in Propostion 5.6 that in this situation ![]() $f_{\mathrm {dR}*}Z $ is the analytification of a disjoint union
$f_{\mathrm {dR}*}Z $ is the analytification of a disjoint union ![]() $f^a_{\mathrm {dR}*}Z^a$ of projective A-schemes. Moreover, for any closed point
$f^a_{\mathrm {dR}*}Z^a$ of projective A-schemes. Moreover, for any closed point ![]() $\mathfrak {m}\in \mathrm {Spec}\left (A\right )$, we know by Theorem 6.1 that the base change
$\mathfrak {m}\in \mathrm {Spec}\left (A\right )$, we know by Theorem 6.1 that the base change 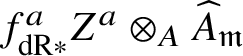 $f^a_{\mathrm {dR}*}Z^a \otimes _A \widehat {A}_{\mathfrak {m}}$ admits a formal stratification. In particular, by applying [Reference dos SantosdS15, Lemma 6.2], we can see that
$f^a_{\mathrm {dR}*}Z^a \otimes _A \widehat {A}_{\mathfrak {m}}$ admits a formal stratification. In particular, by applying [Reference dos SantosdS15, Lemma 6.2], we can see that 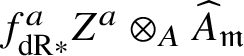 $f^a_{\mathrm {dR}*}Z^a \otimes _A \widehat {A}_{\mathfrak {m}}$ must be flat over
$f^a_{\mathrm {dR}*}Z^a \otimes _A \widehat {A}_{\mathfrak {m}}$ must be flat over ![]() $\widehat {A}_{\mathfrak {m}}$.
$\widehat {A}_{\mathfrak {m}}$.
Since this is true for all ![]() $\mathfrak {m}$, it follows that
$\mathfrak {m}$, it follows that ![]() $f^a_{\mathrm {dR}*}Z^a$ is flat over A, so the restriction of
$f^a_{\mathrm {dR}*}Z^a$ is flat over A, so the restriction of ![]() $f^a_{\mathrm {dR}*}Z^a\rightarrow \mathrm {Spec}\left (A\right )$ to each of its connected components is flat and projective. Since
$f^a_{\mathrm {dR}*}Z^a\rightarrow \mathrm {Spec}\left (A\right )$ to each of its connected components is flat and projective. Since ![]() $\mathrm {Spec}\left (A\right )$ is connected, each of these components must be set theoretically surjective over
$\mathrm {Spec}\left (A\right )$ is connected, each of these components must be set theoretically surjective over ![]() $\mathrm {Spec}\left (A\right )$, so each has a nonempty fibre over
$\mathrm {Spec}\left (A\right )$, so each has a nonempty fibre over ![]() $\mathfrak {m}$. Hence, the map
$\mathfrak {m}$. Hence, the map
on connected components is surjective. Now applying [Reference dos SantosdS15, Proposition 6.4] and Proposition 5.7(3) to the fibre ![]() $f^a_{\mathrm {dR}*}Z^a \otimes _A A/\mathfrak {m}$, we know that this it has only finitely many connected components. Therefore, so does
$f^a_{\mathrm {dR}*}Z^a \otimes _A A/\mathfrak {m}$, we know that this it has only finitely many connected components. Therefore, so does ![]() $f^a_{\mathrm {dR}*}Z^a$ and it is thus flat and projective over A. The claim now follows by taking the analytification.
$f^a_{\mathrm {dR}*}Z^a$ and it is thus flat and projective over A. The claim now follows by taking the analytification.
7 Invariance under the stratification and exactness of the homotopy sequence
Having constructed the relative pushforwards in Section 5, what we should do next is emulate the construction of [Reference dos SantosdS15, §13] to endow ![]() $f_{\mathrm {dR}*}Z$ with a stratification, at least when
$f_{\mathrm {dR}*}Z$ with a stratification, at least when ![]() $Z/W$ is smooth and comes from an object of
$Z/W$ is smooth and comes from an object of ![]() $\mathbf {StrP}(W/K)$. We should then show that
$\mathbf {StrP}(W/K)$. We should then show that ![]() $f_{\mathrm {dR}*}$ is a ‘weak adjoint’ to
$f_{\mathrm {dR}*}$ is a ‘weak adjoint’ to ![]() $f^*$. In fact, to obtain the proof of Theorem 2.5 we can get away with the formal version of this result, namely, Theorem 6.1.
$f^*$. In fact, to obtain the proof of Theorem 2.5 we can get away with the formal version of this result, namely, Theorem 6.1.
Let us put ourselves in the situation of Theorem 2.5, so that ![]() $f:W\rightarrow V$ is smooth with geometrically connected fibres and V is smooth and geometrically connected. Fix
$f:W\rightarrow V$ is smooth with geometrically connected fibres and V is smooth and geometrically connected. Fix ![]() $w\in W(K)$ and set
$w\in W(K)$ and set ![]() $v=f(w)$. Let
$v=f(w)$. Let ![]() $(Y,\rho )\in \mathcal {R}_W$ and assume that Y is smooth over K. Let
$(Y,\rho )\in \mathcal {R}_W$ and assume that Y is smooth over K. Let ![]() $Z=\mathcal {U}_W(Y,\rho )\in \mathbf {StrP}(W/K)$. By applying the forgetful functor
$Z=\mathcal {U}_W(Y,\rho )\in \mathbf {StrP}(W/K)$. By applying the forgetful functor ![]() $\mathbf {StrP}(W/K)\rightarrow \mathbf {StrP}(W/V)$ we may construct
$\mathbf {StrP}(W/K)\rightarrow \mathbf {StrP}(W/V)$ we may construct ![]() $\varepsilon _Z: f^*f_{\mathrm {dR}*}Z\rightarrow Z$ as in the previous section.
$\varepsilon _Z: f^*f_{\mathrm {dR}*}Z\rightarrow Z$ as in the previous section.
Proposition 7.1. The map ![]() $\varepsilon _Z:f^*f_{\mathrm {dR}*}Z\rightarrow Z$ is a closed immersion.
$\varepsilon _Z:f^*f_{\mathrm {dR}*}Z\rightarrow Z$ is a closed immersion.
Proof. We first note that by Proposition 5.7 the given map ![]() $\varepsilon _Z:f^*f_{\mathrm {dR}*}Z\rightarrow Z$ becomes a closed immersion on the fibre
$\varepsilon _Z:f^*f_{\mathrm {dR}*}Z\rightarrow Z$ becomes a closed immersion on the fibre ![]() $W_v$ over the given K-valued point
$W_v$ over the given K-valued point ![]() $v\in V(K)$. By letting v vary and possibly increase the base field K, we deduce that the same is true over any rigid point of V. Moreover, we know from Corollary 6.3 that on any connected open affinoid
$v\in V(K)$. By letting v vary and possibly increase the base field K, we deduce that the same is true over any rigid point of V. Moreover, we know from Corollary 6.3 that on any connected open affinoid ![]() $\mathrm {Spa}\left (A\right )\subset V$, the base change
$\mathrm {Spa}\left (A\right )\subset V$, the base change
is projective over A. Since ![]() $\varepsilon _Z$ being a closed immersion is local on V, we therefore find ourselves in the following general situation. We have a smooth projective morphism
$\varepsilon _Z$ being a closed immersion is local on V, we therefore find ourselves in the following general situation. We have a smooth projective morphism ![]() $f:W\rightarrow \mathrm {Spa}\left (A\right )$ over an affinoid base and a morphism
$f:W\rightarrow \mathrm {Spa}\left (A\right )$ over an affinoid base and a morphism ![]() $T\rightarrow Z$ of projective W-varieties, which is a closed immersion after passing to any rigid point of
$T\rightarrow Z$ of projective W-varieties, which is a closed immersion after passing to any rigid point of ![]() $\mathrm {Spa}\left (A\right )$. We wish to show that
$\mathrm {Spa}\left (A\right )$. We wish to show that ![]() $T\rightarrow Z$ is a closed immersion. This is now a situation which can be algebrised, since by rigid analytic GAGA all three of
$T\rightarrow Z$ is a closed immersion. This is now a situation which can be algebrised, since by rigid analytic GAGA all three of ![]() $W,T,Z$ come from projective A-schemes, as do all of the morphisms between them.
$W,T,Z$ come from projective A-schemes, as do all of the morphisms between them.
Since the role of W can now be ignored, we can reduce to the following. Let A be a Noetherian ring and ![]() $i:T^a\rightarrow Z^a$ a morphism of projective A-schemes, which is a closed immersion on the fibres over all closed points of A. Then we wish to show that i is an closed immersion. To see this, note that the quasi-finite locus of i must contain every closed point of
$i:T^a\rightarrow Z^a$ a morphism of projective A-schemes, which is a closed immersion on the fibres over all closed points of A. Then we wish to show that i is an closed immersion. To see this, note that the quasi-finite locus of i must contain every closed point of ![]() $Z^a$; it must therefore be equal to
$Z^a$; it must therefore be equal to ![]() $Z^a$ by [Reference GrothendieckGro66, Théorème 13.1.5]. Therefore, i is quasi-finite and projective, and hence finite, say locally of the form
$Z^a$ by [Reference GrothendieckGro66, Théorème 13.1.5]. Therefore, i is quasi-finite and projective, and hence finite, say locally of the form ![]() $\mathrm {Spec}\left (C\right )\rightarrow \mathrm {Spec}\left (B\right )$. Moreover, for any maximal ideal
$\mathrm {Spec}\left (C\right )\rightarrow \mathrm {Spec}\left (B\right )$. Moreover, for any maximal ideal ![]() $\mathfrak {m}$ of B, the induced map
$\mathfrak {m}$ of B, the induced map 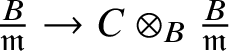 $\frac {B}{\mathfrak {m}} \rightarrow C\otimes _B \frac {B}{\mathfrak {m}}$ is either the zero map or an isomorphism and, in particular, it is surjective. Hence, i is a closed immersion as claimed.
$\frac {B}{\mathfrak {m}} \rightarrow C\otimes _B \frac {B}{\mathfrak {m}}$ is either the zero map or an isomorphism and, in particular, it is surjective. Hence, i is a closed immersion as claimed.
Definition 7.2. We say that a closed subvariety ![]() $T\hookrightarrow Z$ is stable under the (K-linear) stratification if the composite map
$T\hookrightarrow Z$ is stable under the (K-linear) stratification if the composite map
 $$ \begin{align*} T \times_{W,p_0} \widehat{P}_W \rightarrow Z \times_{W,p_0} \widehat{P}_W \overset{\mathrm{pr}_Z\circ \epsilon}{\longrightarrow} Z \end{align*} $$
$$ \begin{align*} T \times_{W,p_0} \widehat{P}_W \rightarrow Z \times_{W,p_0} \widehat{P}_W \overset{\mathrm{pr}_Z\circ \epsilon}{\longrightarrow} Z \end{align*} $$factors through T.
Theorem 7.3. Let ![]() $Z=\mathcal {U}_W(Y,\rho )$ for some
$Z=\mathcal {U}_W(Y,\rho )$ for some ![]() $(Y,\rho ) \in \mathcal {R}_W$ smooth over K. Then the closed immersion
$(Y,\rho ) \in \mathcal {R}_W$ smooth over K. Then the closed immersion
is stable under the K-linear stratification on Z.
Proof. Let us write T for ![]() $f^*f_{\mathrm {dR}*}Z$ to save on notation. First of all, the claim is local on V, which we may therefore assume to be affinoid,
$f^*f_{\mathrm {dR}*}Z$ to save on notation. First of all, the claim is local on V, which we may therefore assume to be affinoid, ![]() $V=\mathrm {Spa}\left (A\right )$. Applying Theorem 6.1 and Proposition 6.2, we know that for any rigid point
$V=\mathrm {Spa}\left (A\right )$. Applying Theorem 6.1 and Proposition 6.2, we know that for any rigid point ![]() $v\in V$ the base change
$v\in V$ the base change 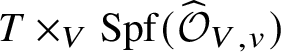 $T \times _V \mathrm {Spf}(\widehat {\mathcal {O}}_{V,v})$ (again, this is just notation) is stable under the pullback stratification. Now, since we are in characteristic zero, stability under the stratification (of either T or
$T \times _V \mathrm {Spf}(\widehat {\mathcal {O}}_{V,v})$ (again, this is just notation) is stable under the pullback stratification. Now, since we are in characteristic zero, stability under the stratification (of either T or 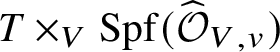 $ T \times _V \mathrm {Spf}(\widehat {\mathcal {O}}_{V,v})$) amounts simply to stability under the induced action of
$ T \times _V \mathrm {Spf}(\widehat {\mathcal {O}}_{V,v})$) amounts simply to stability under the induced action of ![]() $\mathcal {D}er_K(\mathcal {O}_W)$. Therefore, what we need to show is that for any local section
$\mathcal {D}er_K(\mathcal {O}_W)$. Therefore, what we need to show is that for any local section ![]() $\partial \in \mathcal {D}er_K(\mathcal {O}_W)$ and any local section
$\partial \in \mathcal {D}er_K(\mathcal {O}_W)$ and any local section ![]() $f\in \mathcal {I}_T$ of the ideal of T in Z, the section
$f\in \mathcal {I}_T$ of the ideal of T in Z, the section ![]() $\partial (f)$ is also in
$\partial (f)$ is also in ![]() $\mathcal {I}_T$; that is, maps to zero in
$\mathcal {I}_T$; that is, maps to zero in ![]() $\mathcal {O}_T$.
$\mathcal {O}_T$.
Since Z is projective over ![]() $\mathrm {Spa}(A)$, we may algebrise Z to produce a projective scheme
$\mathrm {Spa}(A)$, we may algebrise Z to produce a projective scheme ![]() $Z^a$ over
$Z^a$ over ![]() $\mathrm {Spec}\left (A\right )$ and replace f by an local section of
$\mathrm {Spec}\left (A\right )$ and replace f by an local section of ![]() $\mathcal {O}_{Z^a}$, as well as
$\mathcal {O}_{Z^a}$, as well as ![]() $\partial $ by a suitable algebraic derivation. Since
$\partial $ by a suitable algebraic derivation. Since 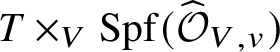 $T\times _V \mathrm {Spf}(\widehat {\mathcal {O}}_{V,v})$ is stable under the connection, we know that
$T\times _V \mathrm {Spf}(\widehat {\mathcal {O}}_{V,v})$ is stable under the connection, we know that ![]() $\partial (f)$ restricts to zero as a local section of
$\partial (f)$ restricts to zero as a local section of 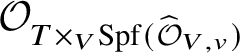 $\mathcal {O}_{T\times _V \mathrm {Spf}(\widehat {\mathcal {O}}_{V,v})}$. Hence, we are reduced to the following situation: A is a regular Noetherian ring, T is a flat and projective scheme over A Footnote 1 and
$\mathcal {O}_{T\times _V \mathrm {Spf}(\widehat {\mathcal {O}}_{V,v})}$. Hence, we are reduced to the following situation: A is a regular Noetherian ring, T is a flat and projective scheme over A Footnote 1 and ![]() $g\in \mathcal {O}_T$ is some local section of the structure sheaf of T.Footnote 2 We are given that, for any maximal ideal
$g\in \mathcal {O}_T$ is some local section of the structure sheaf of T.Footnote 2 We are given that, for any maximal ideal ![]() $\mathfrak {m}$ of A, g vanishes as a local section of
$\mathfrak {m}$ of A, g vanishes as a local section of 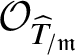 $\mathcal {O}_{\widehat {T}_{/\mathfrak {m}}}$, the structure sheaf of the formal completion of Z along
$\mathcal {O}_{\widehat {T}_{/\mathfrak {m}}}$, the structure sheaf of the formal completion of Z along ![]() $\mathfrak {m}$. We wish to show that in fact
$\mathfrak {m}$. We wish to show that in fact ![]() $g=0$.
$g=0$.
If g is nonzero, there exists some closed point ![]() $t\in T$ such that g is nonzero in
$t\in T$ such that g is nonzero in ![]() $\mathcal {O}_{T,t}$. Since
$\mathcal {O}_{T,t}$. Since ![]() $\mathcal {O}_{T,t}$ is Noetherian, the map
$\mathcal {O}_{T,t}$ is Noetherian, the map 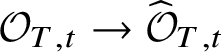 $\mathcal {O}_{T,t}\rightarrow \widehat {\mathcal {O}}_{T,t}$ is faithfully flat, and hence g is nonzero in
$\mathcal {O}_{T,t}\rightarrow \widehat {\mathcal {O}}_{T,t}$ is faithfully flat, and hence g is nonzero in 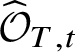 $\widehat {\mathcal {O}}_{T,t}$. But now if
$\widehat {\mathcal {O}}_{T,t}$. But now if ![]() $\mathfrak {m}$ is the image of t in
$\mathfrak {m}$ is the image of t in ![]() $\mathrm {Spec}\left (A\right )$, we have the factorisation
$\mathrm {Spec}\left (A\right )$, we have the factorisation 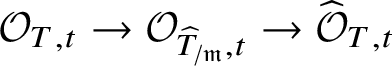 $\mathcal {O}_{T,t}\rightarrow \mathcal {O}_{\widehat {T}_{/\mathfrak {m}},t}\rightarrow \widehat {\mathcal {O}}_{T,t}$ and so g must be nonzero in
$\mathcal {O}_{T,t}\rightarrow \mathcal {O}_{\widehat {T}_{/\mathfrak {m}},t}\rightarrow \widehat {\mathcal {O}}_{T,t}$ and so g must be nonzero in 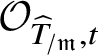 $\mathcal {O}_{\widehat {T}_{/\mathfrak {m}},t}$, which is a contradiction. Hence, we do indeed have
$\mathcal {O}_{\widehat {T}_{/\mathfrak {m}},t}$, which is a contradiction. Hence, we do indeed have ![]() $g=0$ as required.
$g=0$ as required.
We can now complete the proof of Theorem 2.5.
Proof of Theorem 2.5. Suppose that we have some ![]() $E\in \mathrm {MIC}(W/K)$. Then applying Theorem 7.3, we obtain a closed subvariety
$E\in \mathrm {MIC}(W/K)$. Then applying Theorem 7.3, we obtain a closed subvariety
which is stable under the stratification and by Proposition 5.7 recovers the inclusion
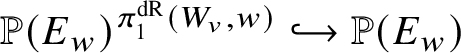 $$ \begin{align*} {\mathbb P}(E_w)^{\pi_1^{\mathrm{dR}}(W_v,w)} \hookrightarrow {\mathbb P}(E_w) \end{align*} $$
$$ \begin{align*} {\mathbb P}(E_w)^{\pi_1^{\mathrm{dR}}(W_v,w)} \hookrightarrow {\mathbb P}(E_w) \end{align*} $$on the fibre over w. Since ![]() $f^*f_{\mathrm {dR}*}{\mathbb P}(E)$ is stable under the stratification on
$f^*f_{\mathrm {dR}*}{\mathbb P}(E)$ is stable under the stratification on ![]() ${\mathbb P}(E)$, it therefore acquires an induced stratification such that
${\mathbb P}(E)$, it therefore acquires an induced stratification such that
is a closed immersion of stratified W-varieties. We now apply Theorem 4.6 to deduce that the closed immersion ![]() $f^*f_{\mathrm {dR}*}{\mathbb P}(E) \hookrightarrow {\mathbb P}(E)$ must come from a unique
$f^*f_{\mathrm {dR}*}{\mathbb P}(E) \hookrightarrow {\mathbb P}(E)$ must come from a unique 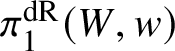 $\pi _1^{\mathrm {dR}}(W,w)$-invariant closed subscheme of
$\pi _1^{\mathrm {dR}}(W,w)$-invariant closed subscheme of ![]() ${\mathbb P}(E_w)$. Put differently, we can see that the closed subscheme
${\mathbb P}(E_w)$. Put differently, we can see that the closed subscheme 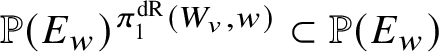 ${\mathbb P}(E_w)^{\pi _1^{\mathrm {dR}}(W_v,w)} \subset {\mathbb P}(E_w)$ is invariant under
${\mathbb P}(E_w)^{\pi _1^{\mathrm {dR}}(W_v,w)} \subset {\mathbb P}(E_w)$ is invariant under 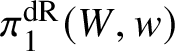 $\pi _1^{\mathrm {dR}}(W,w)$. Hence, we may conclude by applying Proposition 3.6.
$\pi _1^{\mathrm {dR}}(W,w)$. Hence, we may conclude by applying Proposition 3.6.
8 The homotopy sequence for algebraic  $\boldsymbol {k}$-varieties
$\boldsymbol {k}$-varieties
In the second part of this article, we will use Theorem 2.5 to deduce a corresponding result for algebraic k-varieties. The particular positive characteristic analogue of the category ![]() $\mathrm {MIC}(W/K)$ that we will be interested in is the category
$\mathrm {MIC}(W/K)$ that we will be interested in is the category ![]() $\mathrm {Isoc}^\dagger (X/K)$ of overconvergent isocrystals on a k-variety X, and to begin with we will quickly recall the basic definitions and constructions. The interested reader should consult [Reference BerthelotBer96a, Reference Le StumLS07] for more details.
$\mathrm {Isoc}^\dagger (X/K)$ of overconvergent isocrystals on a k-variety X, and to begin with we will quickly recall the basic definitions and constructions. The interested reader should consult [Reference BerthelotBer96a, Reference Le StumLS07] for more details.
Definition 8.1. A frame over ![]() $\mathcal {V}$ is a triple
$\mathcal {V}$ is a triple ![]() $(X,Y,\mathfrak {P})$ consisting of an open immersion
$(X,Y,\mathfrak {P})$ consisting of an open immersion ![]() $X\hookrightarrow Y$ of k-varieties and a closed immersion
$X\hookrightarrow Y$ of k-varieties and a closed immersion ![]() $Y\hookrightarrow \mathfrak {P}$ of formal
$Y\hookrightarrow \mathfrak {P}$ of formal ![]() $\mathcal {V}$-schemes of finite type. We say that it is proper if Y is proper over k and smooth if
$\mathcal {V}$-schemes of finite type. We say that it is proper if Y is proper over k and smooth if ![]() $\mathfrak {P}$ is smooth over
$\mathfrak {P}$ is smooth over ![]() $\mathcal {V}$ in a neighbourhood of X.
$\mathcal {V}$ in a neighbourhood of X.
In this situation we have a (continuous) specialisation map
where ![]() $\mathfrak {P}_K$ is the generic fibre of
$\mathfrak {P}_K$ is the generic fibre of ![]() $\mathfrak {P}$, considered as an (adic) analytic variety over K. We define the tube
$\mathfrak {P}$, considered as an (adic) analytic variety over K. We define the tube
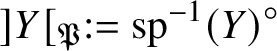 $$ \begin{align*} ]Y[_{\mathfrak{P}}:= \mathrm{sp}^{-1}(Y)^\circ \end{align*} $$
$$ \begin{align*} ]Y[_{\mathfrak{P}}:= \mathrm{sp}^{-1}(Y)^\circ \end{align*} $$of Y to be the topological interior of the inverse image under ![]() $\mathrm {sp}$. As an open subset of
$\mathrm {sp}$. As an open subset of ![]() $\mathfrak {P}_K$, the tube
$\mathfrak {P}_K$, the tube ![]() $]Y[_{\mathfrak {P}}$ naturally admits the structure of an analytic variety over K. There is, moreover, an induced map
$]Y[_{\mathfrak {P}}$ naturally admits the structure of an analytic variety over K. There is, moreover, an induced map ![]() $\mathrm {sp}_Y:]Y[_{\mathfrak {P}}\rightarrow Y$ and we define the tube
$\mathrm {sp}_Y:]Y[_{\mathfrak {P}}\rightarrow Y$ and we define the tube
 $$ \begin{align*} ]X[_{\mathfrak{P}}:= \overline{\mathrm{sp}^{-1}_Y(X)} \end{align*} $$
$$ \begin{align*} ]X[_{\mathfrak{P}}:= \overline{\mathrm{sp}^{-1}_Y(X)} \end{align*} $$of X to be the topological closure of the inverse image under ![]() $\mathrm {sp}_Y$. Note that, in general,
$\mathrm {sp}_Y$. Note that, in general, ![]() $]X[_{\mathfrak {P}}$ is not necessarily an adic space but simply a closed subset of one. We let
$]X[_{\mathfrak {P}}$ is not necessarily an adic space but simply a closed subset of one. We let ![]() $j:]X[_{\mathfrak {P}}\rightarrow ]Y[_{\mathfrak {P}}$ denote the natural inclusion, and for any sheaf
$j:]X[_{\mathfrak {P}}\rightarrow ]Y[_{\mathfrak {P}}$ denote the natural inclusion, and for any sheaf ![]() $\mathcal {F}$ on
$\mathcal {F}$ on ![]() $]Y[_{\mathfrak {P}}$ we define
$]Y[_{\mathfrak {P}}$ we define
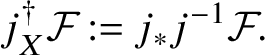 $$ \begin{align*} j_X^\dagger\mathcal{F}:= j_*j^{-1}\mathcal{F} .\end{align*} $$
$$ \begin{align*} j_X^\dagger\mathcal{F}:= j_*j^{-1}\mathcal{F} .\end{align*} $$We let 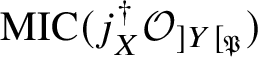 $ \mathrm {MIC}(j_X^\dagger \mathcal {O}_{]Y[_{\mathfrak {P}}})$ denote the category of coherent
$ \mathrm {MIC}(j_X^\dagger \mathcal {O}_{]Y[_{\mathfrak {P}}})$ denote the category of coherent 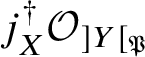 $j_X^\dagger \mathcal {O}_{]Y[_{\mathfrak {P}}}$-modules with integrable connection. If
$j_X^\dagger \mathcal {O}_{]Y[_{\mathfrak {P}}}$-modules with integrable connection. If ![]() $(X,Y,\mathfrak {P})$ is a smooth and proper frame, then by definition
$(X,Y,\mathfrak {P})$ is a smooth and proper frame, then by definition
 $$ \begin{align*} \mathrm{Isoc}^\dagger(X/K) \subset \mathrm{MIC}(j_X^\dagger\mathcal{O}_{]Y[_{\mathfrak{P}}}) \end{align*} $$
$$ \begin{align*} \mathrm{Isoc}^\dagger(X/K) \subset \mathrm{MIC}(j_X^\dagger\mathcal{O}_{]Y[_{\mathfrak{P}}}) \end{align*} $$is the full subcategory consisting of those objects which satisfy a suitable convergence condition on their Taylor isomorphisms. We will not describe this condition explicitly here, but it can be found, for example, in [Reference Le StumLS07, Theorem 4.3.9]. We can summarise the main properties of ![]() $\mathrm {Isoc}^\dagger (X/K)$ as follows (again, proofs of all of these claims can be found in either of [Reference BerthelotBer96a, Reference Le StumLS07]).
$\mathrm {Isoc}^\dagger (X/K)$ as follows (again, proofs of all of these claims can be found in either of [Reference BerthelotBer96a, Reference Le StumLS07]).
Theorem. The category ![]() $\mathrm {Isoc}^\dagger (X/K)$ does not depend on the choice of smooth and proper frame
$\mathrm {Isoc}^\dagger (X/K)$ does not depend on the choice of smooth and proper frame ![]() $(X,Y,\mathfrak {P})$, is functorial in X and K and glues over a Zariski open cover of X (it is therefore defined for varieties which do not necessarily admit such a frame).
$(X,Y,\mathfrak {P})$, is functorial in X and K and glues over a Zariski open cover of X (it is therefore defined for varieties which do not necessarily admit such a frame).
Then ![]() $\mathrm {Isoc}^\dagger (X/K)$ is the category of local systems for the theory of rigid cohomology. When X is geometrically connected, it is Tannakian over K by [Reference CrewCre92, Lemma 1.8]. Moreover, if
$\mathrm {Isoc}^\dagger (X/K)$ is the category of local systems for the theory of rigid cohomology. When X is geometrically connected, it is Tannakian over K by [Reference CrewCre92, Lemma 1.8]. Moreover, if ![]() $x\in X(k)$ is a rational point, then
$x\in X(k)$ is a rational point, then ![]() $\mathrm {Isoc}^\dagger (X/K)$ is neutral Tannakian over K and
$\mathrm {Isoc}^\dagger (X/K)$ is neutral Tannakian over K and
provides a fibre functor.
Definition 8.2. We define the overconvergent fundamental group 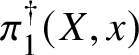 $\pi _1^\dagger (X,x)$ of X with base point x to be the Tannaka dual of
$\pi _1^\dagger (X,x)$ of X with base point x to be the Tannaka dual of ![]() $\mathrm {Isoc}^\dagger (X/K)$ with respect to
$\mathrm {Isoc}^\dagger (X/K)$ with respect to ![]() $x^*$. It is an affine group scheme over K.
$x^*$. It is an affine group scheme over K.
For brevity, we have not included K in the notation for the overconvergent fundamental group; this should not present to much of a problem. Suppose now that we are given a morphism ![]() $f:X\rightarrow S$ of geometrically connected k-varieties and
$f:X\rightarrow S$ of geometrically connected k-varieties and ![]() $x\in X(k)$. Write
$x\in X(k)$. Write ![]() $s=f(x)$. If the fibre
$s=f(x)$. If the fibre ![]() $X_s$ is also geometrically connected, then we call the sequence
$X_s$ is also geometrically connected, then we call the sequence
 $$ \begin{align*}\pi_1^\dagger(X_s,x) \rightarrow\pi_1^\dagger(X,x)\rightarrow\pi_1^\dagger(S,s)\rightarrow 1\end{align*} $$
$$ \begin{align*}\pi_1^\dagger(X_s,x) \rightarrow\pi_1^\dagger(X,x)\rightarrow\pi_1^\dagger(S,s)\rightarrow 1\end{align*} $$the homotopy sequence associated to the pair ![]() $(f,x)$. The positive characteristic analogue of Theorem 2.5 is then the following.
$(f,x)$. The positive characteristic analogue of Theorem 2.5 is then the following.
Theorem 8.3. Let ![]() $f:X\rightarrow S$ be a smooth and projective morphism of smooth k-varieties, with geometrically connected fibres and base, and let
$f:X\rightarrow S$ be a smooth and projective morphism of smooth k-varieties, with geometrically connected fibres and base, and let ![]() $x\in X(k)$. Then the homotopy sequence of the pair
$x\in X(k)$. Then the homotopy sequence of the pair ![]() $(f,x)$ is exact.
$(f,x)$ is exact.
The basic idea of the proof will be to reduce to the situation when X is a family of smooth projective curves. In this case we may lift the whole family to characteristic ![]() $0$, and then standard results in rigid cohomology will enable us to deduce the exactness we require from Theorem 2.5. Let us note now that formation of
$0$, and then standard results in rigid cohomology will enable us to deduce the exactness we require from Theorem 2.5. Let us note now that formation of ![]() $\pi _1^\dagger $ commutes with taking finite extension of K (and hence of k), and exactness of a sequence of affine group schemes can be checked after such a finite extension. We will make use of this to freely take finite extensions of k throughout the proof.
$\pi _1^\dagger $ commutes with taking finite extension of K (and hence of k), and exactness of a sequence of affine group schemes can be checked after such a finite extension. We will make use of this to freely take finite extensions of k throughout the proof.
Our first task in the proof of Theorem 8.3 will be to show the overconvergent analogue of Lemma 3.5; that is, that the homotopy sequence of a smooth projective morphism is always weakly exact. While conceptually simple, the proof will require the existence of pushforwards for overconvergent isocrystals, and showing this will require some rather daunting heavy machinery from the theory of arithmetic ![]() $\mathcal {D}^\dagger $-modules.
$\mathcal {D}^\dagger $-modules.
Proposition 8.4. Let ![]() $f:X\rightarrow S$ be a smooth and projective morphism of smooth k-varieties, of constant relative dimension d. Then there exists a functor
$f:X\rightarrow S$ be a smooth and projective morphism of smooth k-varieties, of constant relative dimension d. Then there exists a functor
right adjoint to
such that for any ![]() $s\in S(k)$ we have
$s\in S(k)$ we have 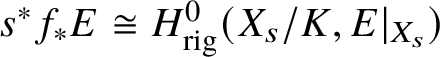 $s^*f_*E \cong H^0_{\mathrm {rig}}(X_s/K,E|_{X_s})$.
$s^*f_*E \cong H^0_{\mathrm {rig}}(X_s/K,E|_{X_s})$.
The proof will be postponed until Section 9, and for now we will deduce several important consequences.
Corollary 8.5. Let ![]() $f:X\rightarrow S$,
$f:X\rightarrow S$, ![]() $x\in X(k)$,
$x\in X(k)$, ![]() $s=f(x)$ be as in Theorem 8.3. Then the sequence
$s=f(x)$ be as in Theorem 8.3. Then the sequence
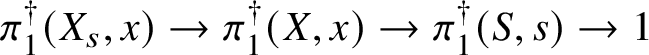 $$ \begin{align*} \pi_1^\dagger(X_s,x)\rightarrow \pi_1^\dagger(X,x)\rightarrow \pi_1^\dagger(S,s)\rightarrow 1\end{align*} $$
$$ \begin{align*} \pi_1^\dagger(X_s,x)\rightarrow \pi_1^\dagger(X,x)\rightarrow \pi_1^\dagger(S,s)\rightarrow 1\end{align*} $$of affine group schemes is weakly exact.
This will enable us to make some rather major simplifying assumptions in the proof of Theorem 8.3, in particular by combining it with the following elementary lemma.
Lemma 8.6. Let
be a commutative diagram of sequences of affine group schemes, with surjective vertical maps. Assume that the top sequence is exact and that the bottom sequence is weakly exact. Then the bottom sequence is in fact exact.
Proof. Follows from the fact that the image of a normal subgroup under a surjective group homomorphism is again a normal subgroup.
Another corollary of weak exactness that will play an important role is the following very weak version of the Lefschetz hyperplane theorem for overconvergent fundamental groups.
Theorem 8.7. Let ![]() $X\subset {\mathbb P}^n_k$ be smooth, projective and geometrically connected. Assume that
$X\subset {\mathbb P}^n_k$ be smooth, projective and geometrically connected. Assume that ![]() $\dim X\geq 2$ and let
$\dim X\geq 2$ and let ![]() $Y=H\cap X$ be a smooth hyperplane section. Let
$Y=H\cap X$ be a smooth hyperplane section. Let ![]() $y\in Y(k)$. Then the normal closure of the image of
$y\in Y(k)$. Then the normal closure of the image of
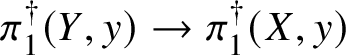 $$ \begin{align*} \pi_1^\dagger(Y,y)\rightarrow \pi_1^\dagger(X,y)\end{align*} $$
$$ \begin{align*} \pi_1^\dagger(Y,y)\rightarrow \pi_1^\dagger(X,y)\end{align*} $$is the whole of 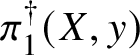 $\pi _1^\dagger (X,y)$.
$\pi _1^\dagger (X,y)$.
Proof. After possibly extending k we may assume (by Bertini’s hyperplane section theorem) that there exists a hyperplane ![]() $H'\subset \mathbb {P}^n_k$ distinct from H such that
$H'\subset \mathbb {P}^n_k$ distinct from H such that ![]() $y\in Y\cap H'$ and
$y\in Y\cap H'$ and ![]() $Z=Y\cap H'$ is smooth. Let
$Z=Y\cap H'$ is smooth. Let ![]() $g:\widetilde {X}\rightarrow X$ be the blow-up of X along Z and
$g:\widetilde {X}\rightarrow X$ be the blow-up of X along Z and ![]() $\widetilde {Y}\subset \widetilde {X}$ the strict transform of Y. Thus,
$\widetilde {Y}\subset \widetilde {X}$ the strict transform of Y. Thus, ![]() $\widetilde {Y}\cong Y$ and, in particular, we may lift y canonically to a point
$\widetilde {Y}\cong Y$ and, in particular, we may lift y canonically to a point ![]() $\tilde {y}$ of
$\tilde {y}$ of ![]() $\widetilde {Y}$.
$\widetilde {Y}$.
Claim. The induced map 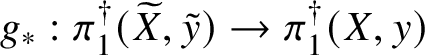 $g_*:\pi _1^{\dagger }(\widetilde {X},\tilde {y})\rightarrow \pi _1^{\dagger }(X,y) $ is an isomorphism.
$g_*:\pi _1^{\dagger }(\widetilde {X},\tilde {y})\rightarrow \pi _1^{\dagger }(X,y) $ is an isomorphism.
Proof of claim. We want to show that the functor ![]() $\mathrm {Isoc}^\dagger (X/K)\rightarrow \mathrm {Isoc}^\dagger (\widetilde {X}/K)$ is an equivalence of categories. According to [Reference KedlayaKed07, Proposition 5.3.6], the functor is essentially surjective. It is automatically faithful; hence, we must demonstrate that it is full. So let
$\mathrm {Isoc}^\dagger (X/K)\rightarrow \mathrm {Isoc}^\dagger (\widetilde {X}/K)$ is an equivalence of categories. According to [Reference KedlayaKed07, Proposition 5.3.6], the functor is essentially surjective. It is automatically faithful; hence, we must demonstrate that it is full. So let ![]() $g^*E\rightarrow g^*F$ be a morphism. Since
$g^*E\rightarrow g^*F$ be a morphism. Since ![]() $g:\widetilde {X}\setminus g^{-1}(Z)\rightarrow X\setminus Z$ is an isomorphism, this induces a morphism
$g:\widetilde {X}\setminus g^{-1}(Z)\rightarrow X\setminus Z$ is an isomorphism, this induces a morphism ![]() $E|_{X\setminus Z}\rightarrow F|_{X\setminus Z}$ which by [Reference KedlayaKed07, Theorem 5.2.1] must come from a morphism
$E|_{X\setminus Z}\rightarrow F|_{X\setminus Z}$ which by [Reference KedlayaKed07, Theorem 5.2.1] must come from a morphism ![]() $E\rightarrow F$.
$E\rightarrow F$.
Clearly, the claim also holds for ![]() $\widetilde {Y}\rightarrow Y$; hence, it suffices to show that the normal closure of the image of
$\widetilde {Y}\rightarrow Y$; hence, it suffices to show that the normal closure of the image of
 $$ \begin{align*} \pi_1^{\dagger}(\widetilde{Y},\tilde{y})\rightarrow \pi_1^{\dagger}(\widetilde{X},\tilde{y}) \end{align*} $$
$$ \begin{align*} \pi_1^{\dagger}(\widetilde{Y},\tilde{y})\rightarrow \pi_1^{\dagger}(\widetilde{X},\tilde{y}) \end{align*} $$is the whole of 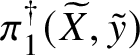 $\pi _1^{\dagger }(\widetilde {X},\tilde {y})$. The pencil of hyperplane sections spanned by
$\pi _1^{\dagger }(\widetilde {X},\tilde {y})$. The pencil of hyperplane sections spanned by ![]() $Y=X\cap H$ and
$Y=X\cap H$ and ![]() $X\cap H'$ furnishes a projective map
$X\cap H'$ furnishes a projective map 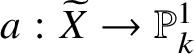 $a:\widetilde {X}\rightarrow \mathbb {P}^1_k$ whose generic fibre is smooth, and the pre-image of y with respect to g is a closed subscheme of
$a:\widetilde {X}\rightarrow \mathbb {P}^1_k$ whose generic fibre is smooth, and the pre-image of y with respect to g is a closed subscheme of ![]() $\widetilde {X}$ mapped isomorphically onto
$\widetilde {X}$ mapped isomorphically onto ![]() ${\mathbb P}^1_k$ by a. Thus, we obtain a section
${\mathbb P}^1_k$ by a. Thus, we obtain a section ![]() $\sigma $ of a, and it is easy to check that
$\sigma $ of a, and it is easy to check that ![]() $\sigma (a(\tilde {y}))=\tilde {y}$.
$\sigma (a(\tilde {y}))=\tilde {y}$.
Let ![]() $b:\widetilde {X}_U\rightarrow U$ be the smooth locus of a and note that
$b:\widetilde {X}_U\rightarrow U$ be the smooth locus of a and note that ![]() $\widetilde {Y}\subset \widetilde {X}_U$ is a fibre of b. Since b has geometrically connected fibres, Corollary 8.5 implies that the induced sequence of group schemes
$\widetilde {Y}\subset \widetilde {X}_U$ is a fibre of b. Since b has geometrically connected fibres, Corollary 8.5 implies that the induced sequence of group schemes
 $$ \begin{align*} \pi_1^{\dagger}(\widetilde{Y},\tilde{y})\rightarrow \pi_1^\dagger(\widetilde{X}_U,\tilde y) \rightarrow \pi_1^{\dagger}(U,a(\tilde{y}))\rightarrow 1 \end{align*} $$
$$ \begin{align*} \pi_1^{\dagger}(\widetilde{Y},\tilde{y})\rightarrow \pi_1^\dagger(\widetilde{X}_U,\tilde y) \rightarrow \pi_1^{\dagger}(U,a(\tilde{y}))\rightarrow 1 \end{align*} $$is weakly exact. We also have a commutative diagram of affine group schemes
such that the middle vertical arrow arrow is surjective by [Reference KedlayaKed07, Theorem 5.2.1, Proposition 5.3.1].
Note that 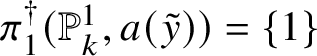 $\pi _1^\dagger ({\mathbb P}^1_k,a(\tilde y))=\{1\}$ by Lemma 8.8. Hence, applying Theorem 3.4 with
$\pi _1^\dagger ({\mathbb P}^1_k,a(\tilde y))=\{1\}$ by Lemma 8.8. Hence, applying Theorem 3.4 with ![]() $A=\{1\}$ we must show that
$A=\{1\}$ we must show that
1. an object
 $V\in \mathrm {Rep}_K(\pi _1^\dagger (\widetilde X,\tilde y))$ is trivial if and only if it is trivial in
$V\in \mathrm {Rep}_K(\pi _1^\dagger (\widetilde X,\tilde y))$ is trivial if and only if it is trivial in  $\mathrm {Rep}_K(\pi _1^\dagger (\widetilde Y,\tilde y))$;
$\mathrm {Rep}_K(\pi _1^\dagger (\widetilde Y,\tilde y))$;2. for any object
 $V\in \mathrm {Rep}_K(\pi _1^\dagger (\widetilde X,\tilde y))$,
$V\in \mathrm {Rep}_K(\pi _1^\dagger (\widetilde X,\tilde y))$,  $V^{\pi _1^\dagger (\widetilde Y,\tilde y)}$ is stable under
$V^{\pi _1^\dagger (\widetilde Y,\tilde y)}$ is stable under  $\pi _1^\dagger (\widetilde X,\tilde y)$.
$\pi _1^\dagger (\widetilde X,\tilde y)$.
Note that the ‘only if’ part of (1) is trivial, and in the situation of (2) it follows from weak exactness of
 $$ \begin{align*} \pi_1^{\dagger}(\widetilde{Y},\tilde{y})\rightarrow \pi_1^\dagger(\widetilde{X}_U,\tilde y) \rightarrow \pi_1^{\dagger}(U,a(\tilde{y}))\rightarrow 1 \end{align*} $$
$$ \begin{align*} \pi_1^{\dagger}(\widetilde{Y},\tilde{y})\rightarrow \pi_1^\dagger(\widetilde{X}_U,\tilde y) \rightarrow \pi_1^{\dagger}(U,a(\tilde{y}))\rightarrow 1 \end{align*} $$that ![]() $V^{\pi _1^\dagger (\widetilde Y,\tilde y)}$ is stable under
$V^{\pi _1^\dagger (\widetilde Y,\tilde y)}$ is stable under 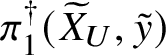 $\pi _1^\dagger (\widetilde {X}_U,\tilde y)$. By surjectivity of
$\pi _1^\dagger (\widetilde {X}_U,\tilde y)$. By surjectivity of 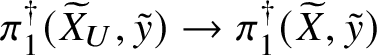 $\pi _1^\dagger (\widetilde {X}_U,\tilde y)\rightarrow \pi _1^\dagger (\widetilde {X},\tilde y)$ it is therefore stable under
$\pi _1^\dagger (\widetilde {X}_U,\tilde y)\rightarrow \pi _1^\dagger (\widetilde {X},\tilde y)$ it is therefore stable under 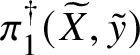 $\pi _1^\dagger (\widetilde {X},\tilde y)$.
$\pi _1^\dagger (\widetilde {X},\tilde y)$.
It remains to show the ‘if’ part of (1); therefore, let us assume that we have some 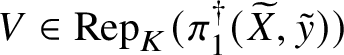 $V\in \mathrm {Rep}_K(\pi _1^\dagger (\widetilde X,\tilde y))$ on which
$V\in \mathrm {Rep}_K(\pi _1^\dagger (\widetilde X,\tilde y))$ on which 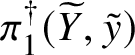 $\pi _1^\dagger (\widetilde Y,\tilde y)$ acts trivially. Let H be the normal closure of the image of
$\pi _1^\dagger (\widetilde Y,\tilde y)$ acts trivially. Let H be the normal closure of the image of
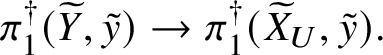 $$ \begin{align*} \pi_1^\dagger(\widetilde Y,\tilde y) \rightarrow \pi_1^\dagger(\widetilde{X}_U,\tilde y). \end{align*} $$
$$ \begin{align*} \pi_1^\dagger(\widetilde Y,\tilde y) \rightarrow \pi_1^\dagger(\widetilde{X}_U,\tilde y). \end{align*} $$We therefore know that
•
 $\pi _1^\dagger (\widetilde {X}_U,\tilde y)= H\cdot \sigma _*(\pi _1^\dagger (U,a(\tilde y)))$;
$\pi _1^\dagger (\widetilde {X}_U,\tilde y)= H\cdot \sigma _*(\pi _1^\dagger (U,a(\tilde y)))$;• H acts trivially on V.
Since  $\sigma _*(\pi _1^\dagger (U,a(\tilde y)))$ has trivial image in
$\sigma _*(\pi _1^\dagger (U,a(\tilde y)))$ has trivial image in 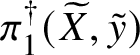 $\pi _1^\dagger (\widetilde {X},\tilde {y})$, it follows that
$\pi _1^\dagger (\widetilde {X},\tilde {y})$, it follows that 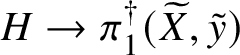 $H\rightarrow \pi _1^\dagger (\widetilde {X},\tilde {y})$ is surjective; hence,
$H\rightarrow \pi _1^\dagger (\widetilde {X},\tilde {y})$ is surjective; hence, 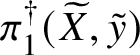 $\pi _1^\dagger (\widetilde X,\tilde y)$ acts trivially on V as required.
$\pi _1^\dagger (\widetilde X,\tilde y)$ acts trivially on V as required.
Lemma 8.8. Let ![]() $f:Y\rightarrow Z$ be a map which Zariski-locally on Z is a product of projective bundles. Then the induced map
$f:Y\rightarrow Z$ be a map which Zariski-locally on Z is a product of projective bundles. Then the induced map
is an equivalence of categories.
Proof. Applying Proposition 8.4 we get unit and counit maps
 $$ \begin{align*} f^*f_*E &\rightarrow E,\;\;E\in \mathrm{Isoc}^\dagger(Y/K) \\ F &\rightarrow f_*f^*F,\;\;F\in \mathrm{Isoc}^\dagger(Z/K); \end{align*} $$
$$ \begin{align*} f^*f_*E &\rightarrow E,\;\;E\in \mathrm{Isoc}^\dagger(Y/K) \\ F &\rightarrow f_*f^*F,\;\;F\in \mathrm{Isoc}^\dagger(Z/K); \end{align*} $$we must prove that these are isomorphisms. But this can be checked fibre by fibre, and we are therefore reduced to the case of the structure map ![]() ${\mathbb P}^{n_1}_k \times _k \ldots \times _k {\mathbb P}^{n_r}_k \rightarrow \mathrm {Spec}\left (k\right )$. Hence, using GAGA we may reduce to the statement that over a field K of characteristic
${\mathbb P}^{n_1}_k \times _k \ldots \times _k {\mathbb P}^{n_r}_k \rightarrow \mathrm {Spec}\left (k\right )$. Hence, using GAGA we may reduce to the statement that over a field K of characteristic ![]() $0$, every vector bundle with integrable connection on
$0$, every vector bundle with integrable connection on ![]() ${\mathbb P}^{n_1}_K \times _K \ldots \times _K {\mathbb P}^{n_r}_K$ is trivial.
${\mathbb P}^{n_1}_K \times _K \ldots \times _K {\mathbb P}^{n_r}_K$ is trivial.
9 Pushforward of overconvergent isocrystals
The purpose of this section is to prove Proposition 8.4, stating that if ![]() $f:X\rightarrow S$ is a smooth and proper morphism of k-varieties, then
$f:X\rightarrow S$ is a smooth and proper morphism of k-varieties, then ![]() $f^*:\mathrm {Isoc}^\dagger (S/K)\rightarrow \mathrm {Isoc}^\dagger (X/K)$ has a right adjoint
$f^*:\mathrm {Isoc}^\dagger (S/K)\rightarrow \mathrm {Isoc}^\dagger (X/K)$ has a right adjoint ![]() $f_*:\mathrm {Isoc}^\dagger (X/K)\rightarrow \mathrm {Isoc}^\dagger (S/K)$, which commutes with base change and on fibres recovers the zeroeth cohomology group
$f_*:\mathrm {Isoc}^\dagger (X/K)\rightarrow \mathrm {Isoc}^\dagger (S/K)$, which commutes with base change and on fibres recovers the zeroeth cohomology group 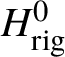 $H^0_{\mathrm {rig}}$ with coefficients. This will require some heavy machinery from the theory of arithmetic
$H^0_{\mathrm {rig}}$ with coefficients. This will require some heavy machinery from the theory of arithmetic ![]() $\mathcal {D}$-modules, as developed by Berthelot and Caro, and while the result we require is essentially contained in work of Caro, it will take a little care to extract it in the form that we need. This section is rather technical, and the casual reader will gain little from going through it in detail; they are advised to simply take Proposition 8.4 on trust.
$\mathcal {D}$-modules, as developed by Berthelot and Caro, and while the result we require is essentially contained in work of Caro, it will take a little care to extract it in the form that we need. This section is rather technical, and the casual reader will gain little from going through it in detail; they are advised to simply take Proposition 8.4 on trust.
With these warnings out of the way, let us begin. To start with, by uniqueness of adjoints, the question is local on the base S, which we may therefore assume to be affine. Hence, we may assume that there exists a smooth and proper formal scheme ![]() $\mathfrak {Q}$ over W, a divisor
$\mathfrak {Q}$ over W, a divisor ![]() $H\subset \mathfrak {Q} \times _{\mathcal {V}} k$ and a locally closed immersion
$H\subset \mathfrak {Q} \times _{\mathcal {V}} k$ and a locally closed immersion ![]() $S\hookrightarrow \mathfrak {Q}$ such that
$S\hookrightarrow \mathfrak {Q}$ such that ![]() $S=\overline {S}\setminus H$. In other words,
$S=\overline {S}\setminus H$. In other words, ![]() $(\mathfrak {Q},H,\overline {S})$ is a ‘triplet lisse en dehors du diviseur’ in the sense of [Reference CaroCar11, Définition 3.1.6]. By choosing a projective embedding of X over S, we may construct another smooth and proper formal scheme
$(\mathfrak {Q},H,\overline {S})$ is a ‘triplet lisse en dehors du diviseur’ in the sense of [Reference CaroCar11, Définition 3.1.6]. By choosing a projective embedding of X over S, we may construct another smooth and proper formal scheme ![]() $\mathfrak {P}$ over W together with a commutative diagram of embeddings
$\mathfrak {P}$ over W together with a commutative diagram of embeddings
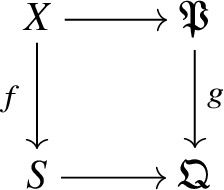
such that ![]() $\mathfrak {P}\rightarrow \mathfrak {Q}$ is smooth, and
$\mathfrak {P}\rightarrow \mathfrak {Q}$ is smooth, and ![]() $X=\overline {X}\setminus g^{-1}(H)$. Set
$X=\overline {X}\setminus g^{-1}(H)$. Set ![]() $T=g^{-1}(H)$, so that again
$T=g^{-1}(H)$, so that again ![]() $(\mathfrak {P},T,\overline {X})$ is a ‘triplet lisse en dehors du diviseur’.
$(\mathfrak {P},T,\overline {X})$ is a ‘triplet lisse en dehors du diviseur’.
We will let  $D^b_{\mathrm {surcoh}}(\mathfrak {P},T,\overline {X}/K)$ denote the category of bounded complexes of overcoherent
$D^b_{\mathrm {surcoh}}(\mathfrak {P},T,\overline {X}/K)$ denote the category of bounded complexes of overcoherent ![]() $\mathcal {D}^\dagger $-modules on the triple
$\mathcal {D}^\dagger $-modules on the triple ![]() $(\mathfrak {P},T,\overline {X})$ in the sense of [Reference CaroCar15, Notations 1.2.3], in other words overcoherent complexes of
$(\mathfrak {P},T,\overline {X})$ in the sense of [Reference CaroCar15, Notations 1.2.3], in other words overcoherent complexes of  $\mathcal {D}^\dagger _{\mathfrak {P},{\mathbb Q}}(^\dagger T)$-modules
$\mathcal {D}^\dagger _{\mathfrak {P},{\mathbb Q}}(^\dagger T)$-modules ![]() $\mathcal {E}$ such that
$\mathcal {E}$ such that 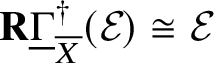 $\mathbf {R}\underline {\Gamma }^\dagger _{\overline {X}}(\mathcal {E})\cong \mathcal {E}$. We will similarly denote by
$\mathbf {R}\underline {\Gamma }^\dagger _{\overline {X}}(\mathcal {E})\cong \mathcal {E}$. We will similarly denote by 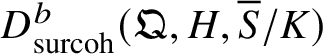 $D^b_{\mathrm {surcoh}}(\mathfrak {Q},H,\overline {S}/K)$ the category of bounded complexes of overcoherent
$D^b_{\mathrm {surcoh}}(\mathfrak {Q},H,\overline {S}/K)$ the category of bounded complexes of overcoherent ![]() $\mathcal {D}^\dagger $-modules on the triple
$\mathcal {D}^\dagger $-modules on the triple ![]() $(\mathfrak {Q},H,\overline {S})$. Following [Reference CaroCar15, Définition 1.2.5], we have full subcategories
$(\mathfrak {Q},H,\overline {S})$. Following [Reference CaroCar15, Définition 1.2.5], we have full subcategories
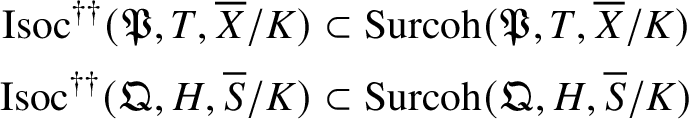 $$ \begin{align*} \mathrm{Isoc}^{\dagger\dagger}(\mathfrak{P},T,\overline{X}/K) &\subset \mathrm{Surcoh}(\mathfrak{P},T,\overline{X}/K) \\ \mathrm{Isoc}^{\dagger\dagger}(\mathfrak{Q},H,\overline{S}/K) &\subset \mathrm{Surcoh}(\mathfrak{Q},H,\overline{S}/K) \end{align*} $$
$$ \begin{align*} \mathrm{Isoc}^{\dagger\dagger}(\mathfrak{P},T,\overline{X}/K) &\subset \mathrm{Surcoh}(\mathfrak{P},T,\overline{X}/K) \\ \mathrm{Isoc}^{\dagger\dagger}(\mathfrak{Q},H,\overline{S}/K) &\subset \mathrm{Surcoh}(\mathfrak{Q},H,\overline{S}/K) \end{align*} $$consisting of ‘overcoherent isocrystals’ and by [Reference CaroCar11, Corollaire 3.5.10, Théorème 4.2.2] canonical equivalences of categories
 $$ \begin{align*} \mathrm{sp}_{\overline{X}\hookrightarrow \mathfrak{P},T,+}:\mathrm{Isoc}^\dagger(X/K) &\overset{\sim}{\rightarrow} \mathrm{Isoc}^{\dagger\dagger}(\mathfrak{P},T,\overline{X}/K) \\ \mathrm{sp}_{\overline{S}\hookrightarrow \mathfrak{Q},H,+}:\mathrm{Isoc}^\dagger(S/K) &\overset{\sim}{\rightarrow} \mathrm{Isoc}^{\dagger\dagger}(\mathfrak{Q},H,\overline{S}/K), \end{align*} $$
$$ \begin{align*} \mathrm{sp}_{\overline{X}\hookrightarrow \mathfrak{P},T,+}:\mathrm{Isoc}^\dagger(X/K) &\overset{\sim}{\rightarrow} \mathrm{Isoc}^{\dagger\dagger}(\mathfrak{P},T,\overline{X}/K) \\ \mathrm{sp}_{\overline{S}\hookrightarrow \mathfrak{Q},H,+}:\mathrm{Isoc}^\dagger(S/K) &\overset{\sim}{\rightarrow} \mathrm{Isoc}^{\dagger\dagger}(\mathfrak{Q},H,\overline{S}/K), \end{align*} $$we will denote inverse functors by ![]() $\mathrm {sp}^{-1}_{-}$. There are full subcategories
$\mathrm {sp}^{-1}_{-}$. There are full subcategories
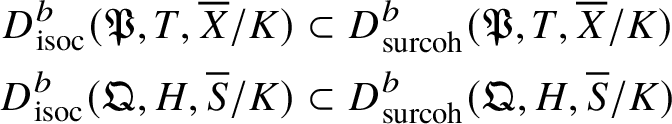 $$ \begin{align*} D^b_{\mathrm{isoc}}(\mathfrak{P},T,\overline{X}/K) &\subset D^b_{\mathrm{surcoh}}(\mathfrak{P},T,\overline{X}/K) \\ D^b_{\mathrm{isoc}}(\mathfrak{Q},H,\overline{S}/K) &\subset D^b_{\mathrm{surcoh}}(\mathfrak{Q},H,\overline{S}/K) \end{align*} $$
$$ \begin{align*} D^b_{\mathrm{isoc}}(\mathfrak{P},T,\overline{X}/K) &\subset D^b_{\mathrm{surcoh}}(\mathfrak{P},T,\overline{X}/K) \\ D^b_{\mathrm{isoc}}(\mathfrak{Q},H,\overline{S}/K) &\subset D^b_{\mathrm{surcoh}}(\mathfrak{Q},H,\overline{S}/K) \end{align*} $$consisting of objects whose cohomology sheaves are overcoherent isocrystals.
Let d denote the relative dimension of f, ![]() $\mathbf {D}_T$ (respectively
$\mathbf {D}_T$ (respectively ![]() $\mathbf {D}_H$) the
$\mathbf {D}_H$) the 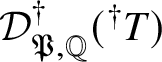 $\mathcal {D}^\dagger _{\mathfrak {P},{\mathbb Q}}(^\dagger T)$-linear (respectively
$\mathcal {D}^\dagger _{\mathfrak {P},{\mathbb Q}}(^\dagger T)$-linear (respectively 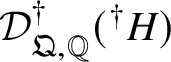 $\mathcal {D}^\dagger _{\mathfrak {Q},{\mathbb Q}}(^\dagger H)$-linear) dual functor and
$\mathcal {D}^\dagger _{\mathfrak {Q},{\mathbb Q}}(^\dagger H)$-linear) dual functor and ![]() $g_+, g^!$ the direct and inverse image functors between
$g_+, g^!$ the direct and inverse image functors between 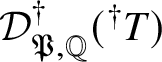 $\mathcal {D}^\dagger _{\mathfrak {P},{\mathbb Q}}(^\dagger T)$ and
$\mathcal {D}^\dagger _{\mathfrak {P},{\mathbb Q}}(^\dagger T)$ and 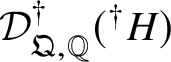 $\mathcal {D}^\dagger _{\mathfrak {Q},{\mathbb Q}}(^\dagger H)$-modules. Applying [Reference CaroCar11, Proposition 3.1.7, Corollaire 3.5.10] and [Reference CaroCar15, Théorème 3.3.1] we have factorisations
$\mathcal {D}^\dagger _{\mathfrak {Q},{\mathbb Q}}(^\dagger H)$-modules. Applying [Reference CaroCar11, Proposition 3.1.7, Corollaire 3.5.10] and [Reference CaroCar15, Théorème 3.3.1] we have factorisations
 $$ \begin{align*} f^!:=\mathbf{R}\underline{\Gamma}^\dagger_{\overline{X}}\circ g^! : D^b_{\mathrm{isoc}}(\mathfrak{Q},H,\overline{S}/K)&\rightarrow D^b_{\mathrm{isoc}}(\mathfrak{P},T,\overline{X}/K) \\ f_+:=g_+: D^b_{\mathrm{isoc}}(\mathfrak{P},T,\overline{X}/K)&\rightarrow D^b_{\mathrm{isoc}}(\mathfrak{Q},H,\overline{S}/K) \\ \mathbf{D}:=\mathbf{D}_T:D^b_{\mathrm{isoc}}(\mathfrak{P},T,\overline{X}/K)&\rightarrow D^b_{\mathrm{isoc}}(\mathfrak{P},T,\overline{X}/K) \\ \mathbf{D}:=\mathbf{D}_H:D^b_{\mathrm{isoc}}(\mathfrak{Q},H,\overline{S}/K)&\rightarrow D^b_{\mathrm{isoc}}(\mathfrak{Q},H,\overline{S}/K). \end{align*} $$
$$ \begin{align*} f^!:=\mathbf{R}\underline{\Gamma}^\dagger_{\overline{X}}\circ g^! : D^b_{\mathrm{isoc}}(\mathfrak{Q},H,\overline{S}/K)&\rightarrow D^b_{\mathrm{isoc}}(\mathfrak{P},T,\overline{X}/K) \\ f_+:=g_+: D^b_{\mathrm{isoc}}(\mathfrak{P},T,\overline{X}/K)&\rightarrow D^b_{\mathrm{isoc}}(\mathfrak{Q},H,\overline{S}/K) \\ \mathbf{D}:=\mathbf{D}_T:D^b_{\mathrm{isoc}}(\mathfrak{P},T,\overline{X}/K)&\rightarrow D^b_{\mathrm{isoc}}(\mathfrak{P},T,\overline{X}/K) \\ \mathbf{D}:=\mathbf{D}_H:D^b_{\mathrm{isoc}}(\mathfrak{Q},H,\overline{S}/K)&\rightarrow D^b_{\mathrm{isoc}}(\mathfrak{Q},H,\overline{S}/K). \end{align*} $$Set ![]() $f^+:=\mathbf {D}\circ f^!\circ \mathbf {D}$. By [Reference CaroCar11, Proposition 4.2.4] the diagram
$f^+:=\mathbf {D}\circ f^!\circ \mathbf {D}$. By [Reference CaroCar11, Proposition 4.2.4] the diagram

is 2-commutative, and by combining [Reference CaroCar06, Théorèmes 1.2.7, 1.2.9] we can see that ![]() $f_+$ and
$f_+$ and ![]() $f^+$ are adjoint functors. Putting this all together, we obtain a natural isomorphism
$f^+$ are adjoint functors. Putting this all together, we obtain a natural isomorphism
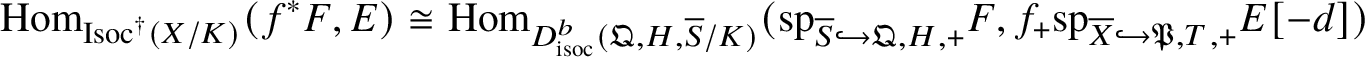 $$ \begin{align*} \mathrm{Hom}_{\mathrm{Isoc}^\dagger(X/K)}(f^*F,E)\cong \mathrm{Hom}_{D^b_{\mathrm{isoc}}(\mathfrak{Q},H,\overline{S}/K)}(\mathrm{sp}_{\overline{S}\hookrightarrow \mathfrak{Q},H,+}F,f_+\mathrm{sp}_{\overline{X}\hookrightarrow \mathfrak{P},T,+}E[-d]) \end{align*} $$
$$ \begin{align*} \mathrm{Hom}_{\mathrm{Isoc}^\dagger(X/K)}(f^*F,E)\cong \mathrm{Hom}_{D^b_{\mathrm{isoc}}(\mathfrak{Q},H,\overline{S}/K)}(\mathrm{sp}_{\overline{S}\hookrightarrow \mathfrak{Q},H,+}F,f_+\mathrm{sp}_{\overline{X}\hookrightarrow \mathfrak{P},T,+}E[-d]) \end{align*} $$for any ![]() $E\in \mathrm {Isoc}^\dagger (X/K)$ and
$E\in \mathrm {Isoc}^\dagger (X/K)$ and ![]() $F\in \mathrm {Isoc}^\dagger (S/K)$. To complete the proof of Proposition 8.4, it suffices to show that
$F\in \mathrm {Isoc}^\dagger (S/K)$. To complete the proof of Proposition 8.4, it suffices to show that
1.
 $f_+\mathrm {sp}_{\overline {X}\hookrightarrow \mathfrak {P},D,+}E[-d]$ is concentrated in degrees
$f_+\mathrm {sp}_{\overline {X}\hookrightarrow \mathfrak {P},D,+}E[-d]$ is concentrated in degrees  $\geq 0$;
$\geq 0$;2. we have
 $$ \begin{align*} s^*\mathrm{sp}^{-1}_{\overline{S}\hookrightarrow \mathfrak{Q},H}\mathcal{H}^{-d}(f_+\mathrm{sp}_{\overline{X}\hookrightarrow \mathfrak{P},D,+}E) \cong H^0_{\mathrm{rig}}(X_s/K,E|_{X_s}). \end{align*} $$
$$ \begin{align*} s^*\mathrm{sp}^{-1}_{\overline{S}\hookrightarrow \mathfrak{Q},H}\mathcal{H}^{-d}(f_+\mathrm{sp}_{\overline{X}\hookrightarrow \mathfrak{P},D,+}E) \cong H^0_{\mathrm{rig}}(X_s/K,E|_{X_s}). \end{align*} $$
Indeed, this will imply that
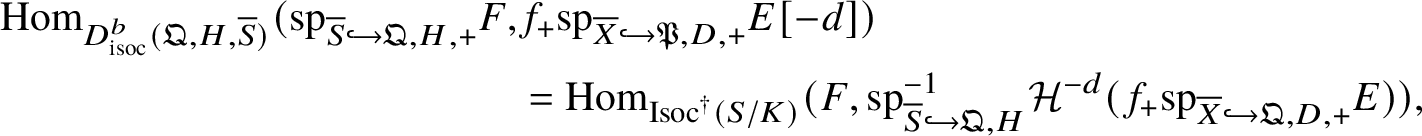 $$ \begin{align*} \mathrm{Hom}_{D^b_{\mathrm{isoc}}(\mathfrak{Q},H,\overline{S})}(\mathrm{sp}_{\overline{S}\hookrightarrow \mathfrak{Q},H,+}F,&f_+\mathrm{sp}_{\overline{X}\hookrightarrow \mathfrak{P},D,+}E[-d]) \\ &= \mathrm{Hom}_{\mathrm{Isoc}^\dagger(S/K)}(F,\mathrm{sp}^{-1}_{\overline{S}\hookrightarrow \mathfrak{Q},H}\mathcal{H}^{-d}(f_+\mathrm{sp}_{\overline{X}\hookrightarrow \mathfrak{Q},D,+}E)),\end{align*} $$
$$ \begin{align*} \mathrm{Hom}_{D^b_{\mathrm{isoc}}(\mathfrak{Q},H,\overline{S})}(\mathrm{sp}_{\overline{S}\hookrightarrow \mathfrak{Q},H,+}F,&f_+\mathrm{sp}_{\overline{X}\hookrightarrow \mathfrak{P},D,+}E[-d]) \\ &= \mathrm{Hom}_{\mathrm{Isoc}^\dagger(S/K)}(F,\mathrm{sp}^{-1}_{\overline{S}\hookrightarrow \mathfrak{Q},H}\mathcal{H}^{-d}(f_+\mathrm{sp}_{\overline{X}\hookrightarrow \mathfrak{Q},D,+}E)),\end{align*} $$and therefore taking
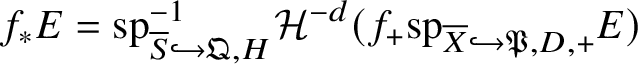 $$ \begin{align*} f_*E=\mathrm{sp}^{-1}_{\overline{S}\hookrightarrow \mathfrak{Q},H}\mathcal{H}^{-d}(f_+\mathrm{sp}_{\overline{X}\hookrightarrow \mathfrak{P},D,+}E) \end{align*} $$
$$ \begin{align*} f_*E=\mathrm{sp}^{-1}_{\overline{S}\hookrightarrow \mathfrak{Q},H}\mathcal{H}^{-d}(f_+\mathrm{sp}_{\overline{X}\hookrightarrow \mathfrak{P},D,+}E) \end{align*} $$will do the trick. To prove these, we note that by combining [Reference CaroCar11, Proposition 4.2.4, Théorème 5.2.5] and [Reference CaroCar15, Théorème 4.4.2], we have an isomorphism
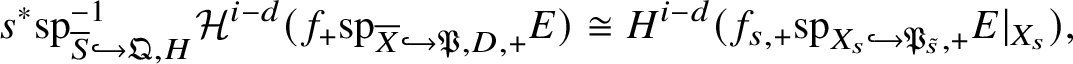 $$ \begin{align*} s^*\mathrm{sp}^{-1}_{\overline{S}\hookrightarrow \mathfrak{Q},H}\mathcal{H}^{i-d}(f_+\mathrm{sp}_{\overline{X}\hookrightarrow \mathfrak{P},D,+}E) \cong H^{i-d}(f_{s,+}\mathrm{sp}_{X_s\hookrightarrow \mathfrak{P}_{\tilde{s}},+}E|_{X_s}), \end{align*} $$
$$ \begin{align*} s^*\mathrm{sp}^{-1}_{\overline{S}\hookrightarrow \mathfrak{Q},H}\mathcal{H}^{i-d}(f_+\mathrm{sp}_{\overline{X}\hookrightarrow \mathfrak{P},D,+}E) \cong H^{i-d}(f_{s,+}\mathrm{sp}_{X_s\hookrightarrow \mathfrak{P}_{\tilde{s}},+}E|_{X_s}), \end{align*} $$where ![]() $\tilde {s}$ denotes some lift of s to a
$\tilde {s}$ denotes some lift of s to a ![]() $\mathcal {V}$-point of
$\mathcal {V}$-point of ![]() $\mathfrak {Q}$ and
$\mathfrak {Q}$ and ![]() $\mathfrak {P}_{\tilde s}$ the fibre of g over
$\mathfrak {P}_{\tilde s}$ the fibre of g over ![]() $\tilde {s}$. We may therefore reduce to Lemma 9.1.
$\tilde {s}$. We may therefore reduce to Lemma 9.1.
Lemma 9.1. Let ![]() $X\hookrightarrow \mathfrak {P}$ be a closed embedding of a smooth d-dimensional k-variety into a smooth formal
$X\hookrightarrow \mathfrak {P}$ be a closed embedding of a smooth d-dimensional k-variety into a smooth formal ![]() $\mathcal {V}$-scheme, and let
$\mathcal {V}$-scheme, and let ![]() $f:\mathfrak {P}\rightarrow \mathrm {Spf}\left (\mathcal {V}\right )$ denote the structure morphism. Let E be a convergent isocrystal on X. Then for all
$f:\mathfrak {P}\rightarrow \mathrm {Spf}\left (\mathcal {V}\right )$ denote the structure morphism. Let E be a convergent isocrystal on X. Then for all ![]() $i\in {\mathbb Z}$ we have
$i\in {\mathbb Z}$ we have
 $$ \begin{align*}H^{i-d}(f_+ \mathrm{sp}_{X\hookrightarrow \mathfrak{P},+}E) \cong \begin{cases} H^0_{\mathrm{conv}}(X/K,E) & i=0 \\ 0 & i<0. \end{cases} \end{align*} $$
$$ \begin{align*}H^{i-d}(f_+ \mathrm{sp}_{X\hookrightarrow \mathfrak{P},+}E) \cong \begin{cases} H^0_{\mathrm{conv}}(X/K,E) & i=0 \\ 0 & i<0. \end{cases} \end{align*} $$Proof. By considering suitable spectral sequences arising from an open cover of ![]() $\mathfrak {P}$, the question is local on
$\mathfrak {P}$, the question is local on ![]() $\mathfrak {P}$, so we may reduce to the corresponding question for both
$\mathfrak {P}$, so we may reduce to the corresponding question for both ![]() $\mathfrak {P}$ and X affine, and we may therefore assume that
$\mathfrak {P}$ and X affine, and we may therefore assume that ![]() $X\hookrightarrow \mathfrak {P}$ lifts to a closed embedding of smooth formal
$X\hookrightarrow \mathfrak {P}$ lifts to a closed embedding of smooth formal ![]() $\mathcal {V}$-schemes
$\mathcal {V}$-schemes ![]() $i:\mathfrak {X}\hookrightarrow \mathfrak {P}$.
$i:\mathfrak {X}\hookrightarrow \mathfrak {P}$.
In this case, we can describe Caro’s functor ![]() $\mathrm {sp}_{X\hookrightarrow \mathfrak {P},+}$, constructed in [Reference CaroCar09, §2.5], very explicitly. Indeed, what Caro does is take an open cover of
$\mathrm {sp}_{X\hookrightarrow \mathfrak {P},+}$, constructed in [Reference CaroCar09, §2.5], very explicitly. Indeed, what Caro does is take an open cover of ![]() $\mathfrak {P}$ by affines
$\mathfrak {P}$ by affines ![]() $\mathfrak {P}_\alpha $ and chooses a lift of each inclusion
$\mathfrak {P}_\alpha $ and chooses a lift of each inclusion ![]() $X\cap \mathfrak {P}_\alpha \hookrightarrow \mathfrak {P}_\alpha $ to a closed immersion of smooth formal schemes
$X\cap \mathfrak {P}_\alpha \hookrightarrow \mathfrak {P}_\alpha $ to a closed immersion of smooth formal schemes ![]() $i_\alpha : \mathfrak {X}_\alpha \rightarrow \mathfrak {P}_\alpha $. The restriction of E to each
$i_\alpha : \mathfrak {X}_\alpha \rightarrow \mathfrak {P}_\alpha $. The restriction of E to each ![]() $X\cap \mathfrak {P}_\alpha $ is then realised on
$X\cap \mathfrak {P}_\alpha $ is then realised on ![]() $\mathfrak {X}_{\alpha K}$ as a module with convergent integrable connection
$\mathfrak {X}_{\alpha K}$ as a module with convergent integrable connection ![]() $E_{\mathfrak {X}_\alpha }$. Thus,
$E_{\mathfrak {X}_\alpha }$. Thus, ![]() $\mathrm {sp}_*E_{\mathfrak {X}_\alpha }$ is a coherent
$\mathrm {sp}_*E_{\mathfrak {X}_\alpha }$ is a coherent 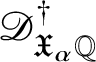 $\mathscr {D}^\dagger _{\mathfrak {X}_\alpha {\mathbb Q}}$-module by [Reference BerthelotBer96b, Proposition 4.1.4], and Caro shows that the modules
$\mathscr {D}^\dagger _{\mathfrak {X}_\alpha {\mathbb Q}}$-module by [Reference BerthelotBer96b, Proposition 4.1.4], and Caro shows that the modules ![]() $i_{\alpha +}\mathrm {sp}_*E_{\mathfrak {X}_\alpha }$ glue together to give a coherent
$i_{\alpha +}\mathrm {sp}_*E_{\mathfrak {X}_\alpha }$ glue together to give a coherent  $\mathscr {D}^\dagger _{\mathfrak {P}{\mathbb Q}}$-module
$\mathscr {D}^\dagger _{\mathfrak {P}{\mathbb Q}}$-module ![]() $\mathrm {sp}_{X\hookrightarrow \mathfrak {P},+}E$. (Note that in our situation, the ‘divisor at
$\mathrm {sp}_{X\hookrightarrow \mathfrak {P},+}E$. (Note that in our situation, the ‘divisor at ![]() $\infty $’, denoted by T in [Reference CaroCar09], is empty.)
$\infty $’, denoted by T in [Reference CaroCar09], is empty.)
Since we are already in the affine case, the whole construction simplifies to give ![]() $\mathrm {sp}_{X\hookrightarrow \mathfrak {P},+}E\cong i_+\mathrm {sp}_*E_{\mathfrak {X}}$, where
$\mathrm {sp}_{X\hookrightarrow \mathfrak {P},+}E\cong i_+\mathrm {sp}_*E_{\mathfrak {X}}$, where ![]() $E_{\mathfrak {X}}$ denotes the realisation of E on
$E_{\mathfrak {X}}$ denotes the realisation of E on ![]() $\mathfrak {X}_K$. If we therefore let
$\mathfrak {X}_K$. If we therefore let ![]() $g:\mathfrak {X}\rightarrow \mathrm {Spf}\left (\mathcal {V}\right )$ denote the structure morphism of
$g:\mathfrak {X}\rightarrow \mathrm {Spf}\left (\mathcal {V}\right )$ denote the structure morphism of ![]() $\mathfrak {X}$, we obtain
$\mathfrak {X}$, we obtain ![]() $f_+\mathrm {sp}_{X\hookrightarrow \mathfrak {P},+}E\cong g_+\mathrm {sp}_*E_{\mathfrak {X}}$ by [Reference BerthelotBer02, (4.3.6.1)]. Finally, the overconvergent Spencer resolution [Reference BerthelotBer02, (4.2.1.1)] shows that
$f_+\mathrm {sp}_{X\hookrightarrow \mathfrak {P},+}E\cong g_+\mathrm {sp}_*E_{\mathfrak {X}}$ by [Reference BerthelotBer02, (4.3.6.1)]. Finally, the overconvergent Spencer resolution [Reference BerthelotBer02, (4.2.1.1)] shows that
 $$ \begin{align*} g_+{\mathrm{sp}}_*E_{\mathfrak{X}}\cong \mathbf{R}\Gamma(\mathfrak{X},\mathrm{sp}_*E_{\mathfrak{X}}\otimes_{\mathcal{O}_{\mathfrak{X}}} \Omega^{\bullet}_{\mathfrak{X}})[d] \cong \mathbf{R}\Gamma(\mathfrak{X}_K,E_{\mathfrak{X}}\otimes_{\mathcal{O}_{\mathfrak{X}_K}} \Omega^{\bullet}_{\mathfrak{X}_K})[d]= \mathbf{R}\Gamma_{\mathrm{conv}}(X/K,E)[d] \end{align*} $$
$$ \begin{align*} g_+{\mathrm{sp}}_*E_{\mathfrak{X}}\cong \mathbf{R}\Gamma(\mathfrak{X},\mathrm{sp}_*E_{\mathfrak{X}}\otimes_{\mathcal{O}_{\mathfrak{X}}} \Omega^{\bullet}_{\mathfrak{X}})[d] \cong \mathbf{R}\Gamma(\mathfrak{X}_K,E_{\mathfrak{X}}\otimes_{\mathcal{O}_{\mathfrak{X}_K}} \Omega^{\bullet}_{\mathfrak{X}_K})[d]= \mathbf{R}\Gamma_{\mathrm{conv}}(X/K,E)[d] \end{align*} $$as required.
10 Exactness for liftable morphisms
In this and the following sections, we will build up to the proof of Theorem 8.3 in stages, starting from very particular situations and then reducing the general case to these. The first situation in which we will prove Theorem 8.3 is under some very strong liftability assumptions on the morphism f.
So suppose that we have some smooth affine variety ![]() $S=\mathrm {Spec}\left (A_0\right )$ over k. Then by [Reference ElkikElk73, Théorème 6] we know that S lifts to a smooth and affine
$S=\mathrm {Spec}\left (A_0\right )$ over k. Then by [Reference ElkikElk73, Théorème 6] we know that S lifts to a smooth and affine ![]() $\mathcal {V}$-scheme
$\mathcal {V}$-scheme ![]() $\mathcal {S}=\mathrm {Spec}\left (A\right )$. Choosing a presentation of A gives us embeddings
$\mathcal {S}=\mathrm {Spec}\left (A\right )$. Choosing a presentation of A gives us embeddings
and we let ![]() $\mathfrak {S}$ denote the completion of the closure of
$\mathfrak {S}$ denote the completion of the closure of ![]() $\mathcal {S}$ inside
$\mathcal {S}$ inside 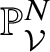 ${\mathbb P}^N_{\mathcal {V}}$. Let
${\mathbb P}^N_{\mathcal {V}}$. Let ![]() $\overline {S}$ denote the closure of S inside
$\overline {S}$ denote the closure of S inside ![]() $\mathfrak {S}\times _{\mathcal {V}} k$, so we have a smooth and proper frame
$\mathfrak {S}\times _{\mathcal {V}} k$, so we have a smooth and proper frame ![]() $(S,\overline {S},\mathfrak {S})$ over
$(S,\overline {S},\mathfrak {S})$ over ![]() $\mathcal {V}$, in the sense of Definition 8.1.
$\mathcal {V}$, in the sense of Definition 8.1.
Definition 10.1. We will call any frame of the form ![]() $(S,\overline {S},\mathfrak {S})$, as just constructed, a Monsky–Washnitzer frame.
$(S,\overline {S},\mathfrak {S})$, as just constructed, a Monsky–Washnitzer frame.
The main result of this section is then the following.
Theorem 10.2. Let ![]() $f:X\rightarrow S$,
$f:X\rightarrow S$, ![]() $x\in X(k)$ and
$x\in X(k)$ and ![]() $s=f(x)$ be as in Theorem 8.3. Assume that S is affine and that there exists a morphism of frames
$s=f(x)$ be as in Theorem 8.3. Assume that S is affine and that there exists a morphism of frames
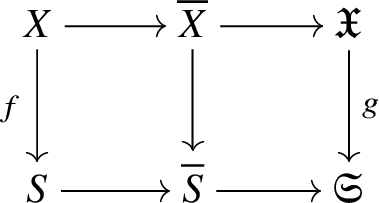
extending f such that
1.
 $(S,\overline {S},\mathfrak {S})$ is a Monsky–Washnitzer frame;
$(S,\overline {S},\mathfrak {S})$ is a Monsky–Washnitzer frame;2. both squares in the above diagram are Cartesian;
3.
 $\mathfrak {X}\rightarrow \mathfrak {S}$ is projective and smooth in a neighbourhood of X.
$\mathfrak {X}\rightarrow \mathfrak {S}$ is projective and smooth in a neighbourhood of X.
Then the homotopy sequence for ![]() $(f,x)$ is exact.
$(f,x)$ is exact.
Remark 10.3. Note that by GFGA [Reference GrothendieckGro61, §5.1] together with the Monsky–Washnitzer assumption on ![]() $(S,\overline {S},\mathfrak {S})$, the morphism
$(S,\overline {S},\mathfrak {S})$, the morphism ![]() $g:\mathfrak {X}\rightarrow \mathfrak {S}$ in the statement of the theorem arises as the formal completion of a morphism of projective
$g:\mathfrak {X}\rightarrow \mathfrak {S}$ in the statement of the theorem arises as the formal completion of a morphism of projective ![]() $\mathcal {V}$-schemes.
$\mathcal {V}$-schemes.
In the situation of Theorem 10.2 we may choose a cofinal system of neighbourhoods ![]() $V_\lambda $ of
$V_\lambda $ of ![]() $]S[_{\mathfrak {S}}$ inside
$]S[_{\mathfrak {S}}$ inside ![]() $\mathfrak {S}_K$, for
$\mathfrak {S}_K$, for ![]() $\lambda \rightarrow 1^-$, such that each
$\lambda \rightarrow 1^-$, such that each ![]() $V_\lambda $ is smooth and geometrically connected over K. Since the diagram
$V_\lambda $ is smooth and geometrically connected over K. Since the diagram

is Cartesian, it follows that ![]() $W_\lambda :=g^{-1}(V_\lambda )$ form a cofinal system of neighbourhoods of
$W_\lambda :=g^{-1}(V_\lambda )$ form a cofinal system of neighbourhoods of ![]() $]X[_{\mathfrak {X}}$ inside
$]X[_{\mathfrak {X}}$ inside ![]() $\mathfrak {X}_K$. Again, by choosing
$\mathfrak {X}_K$. Again, by choosing ![]() $\lambda $ close enough to
$\lambda $ close enough to ![]() $1$ we can assume that all of the induced maps
$1$ we can assume that all of the induced maps
are smooth and projective. Let
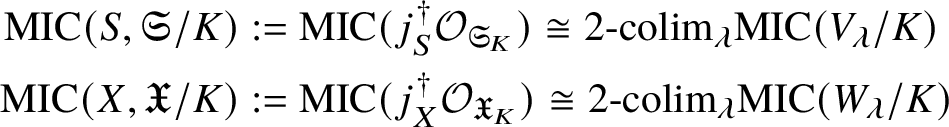 $$ \begin{align*} \mathrm{MIC}(S,\mathfrak{S}/K)&:=\mathrm{MIC}(j_S^\dagger\mathcal{O}_{\mathfrak{S}_K}) \cong 2\text{-}\mathrm{colim}_\lambda\mathrm{MIC}(V_\lambda/K) \\ \mathrm{MIC}(X,\mathfrak{X}/K)&:=\mathrm{MIC}(j_X^\dagger\mathcal{O}_{\mathfrak{X}_K}) \cong 2\text{-}\mathrm{colim}_\lambda\mathrm{MIC}(W_\lambda/K) \end{align*} $$
$$ \begin{align*} \mathrm{MIC}(S,\mathfrak{S}/K)&:=\mathrm{MIC}(j_S^\dagger\mathcal{O}_{\mathfrak{S}_K}) \cong 2\text{-}\mathrm{colim}_\lambda\mathrm{MIC}(V_\lambda/K) \\ \mathrm{MIC}(X,\mathfrak{X}/K)&:=\mathrm{MIC}(j_X^\dagger\mathcal{O}_{\mathfrak{X}_K}) \cong 2\text{-}\mathrm{colim}_\lambda\mathrm{MIC}(W_\lambda/K) \end{align*} $$denote the category of coherent 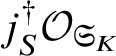 $j_S^\dagger \mathcal {O}_{\mathfrak {S}_K}$-modules (respectively
$j_S^\dagger \mathcal {O}_{\mathfrak {S}_K}$-modules (respectively 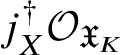 $j_X^\dagger \mathcal {O}_{\mathfrak {X}_K}$-modules) with integrable connection (for the claimed equivalences with the 2-colimit categories, see [Reference Le StumLS07, Proposition 6.1.15]).
$j_X^\dagger \mathcal {O}_{\mathfrak {X}_K}$-modules) with integrable connection (for the claimed equivalences with the 2-colimit categories, see [Reference Le StumLS07, Proposition 6.1.15]).
Proposition 10.4. Choose a lift ![]() $\tilde x\in ]X[_{\mathfrak {X}}(K)$ of
$\tilde x\in ]X[_{\mathfrak {X}}(K)$ of ![]() $x\in X(k)$, and let
$x\in X(k)$, and let ![]() $\tilde s=g(\tilde x)$. Then the categories
$\tilde s=g(\tilde x)$. Then the categories ![]() $\mathrm {MIC}(X,\mathfrak {X}/K)$ and
$\mathrm {MIC}(X,\mathfrak {X}/K)$ and ![]() $\mathrm {MIC}(S,\mathfrak {S}/K)$ are neutral Tannakian over K, with fibre functors provided by
$\mathrm {MIC}(S,\mathfrak {S}/K)$ are neutral Tannakian over K, with fibre functors provided by ![]() $\tilde {x}^*$ and
$\tilde {x}^*$ and ![]() $\tilde {s}^*$, respectively.
$\tilde {s}^*$, respectively.
Proof. By 2.1 we know that the coherent 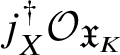 $j^\dagger _X\mathcal {O}_{\mathfrak {X}_K}$-module underlying any object in
$j^\dagger _X\mathcal {O}_{\mathfrak {X}_K}$-module underlying any object in ![]() $\mathrm {MIC}(X,\mathfrak {X}/K)$ is locally free, and similarly for
$\mathrm {MIC}(X,\mathfrak {X}/K)$ is locally free, and similarly for ![]() $\mathrm {MIC}(S,\mathfrak {S}/K)$. The rest of the proof is word for word the same as the proof of Proposition 2.1.
$\mathrm {MIC}(S,\mathfrak {S}/K)$. The rest of the proof is word for word the same as the proof of Proposition 2.1.
We will let 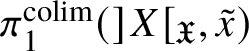 $\pi _1^{\mathrm {colim}}(]X[_{\mathfrak {X}},\tilde {x})$ and
$\pi _1^{\mathrm {colim}}(]X[_{\mathfrak {X}},\tilde {x})$ and 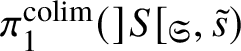 $\pi _1^{\mathrm {colim}}(]S[_{\mathfrak {S}},\tilde {s})$ denote the corresponding Tannaka duals.
$\pi _1^{\mathrm {colim}}(]S[_{\mathfrak {S}},\tilde {s})$ denote the corresponding Tannaka duals.
Proposition 10.5. The sequence of affine group schemes
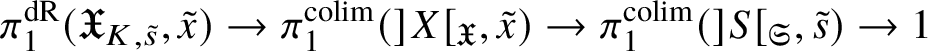 $$ \begin{align*} \pi_1^{\mathrm{dR}}(\mathfrak{X}_{K,\tilde{s}},\tilde{x})\rightarrow \pi_1^{\mathrm{colim}}(]X[_{\mathfrak{X}},\tilde{x})\rightarrow \pi_1^{\mathrm{colim}}(]S[_{\mathfrak{S}},\tilde{s}) \rightarrow 1 \end{align*} $$
$$ \begin{align*} \pi_1^{\mathrm{dR}}(\mathfrak{X}_{K,\tilde{s}},\tilde{x})\rightarrow \pi_1^{\mathrm{colim}}(]X[_{\mathfrak{X}},\tilde{x})\rightarrow \pi_1^{\mathrm{colim}}(]S[_{\mathfrak{S}},\tilde{s}) \rightarrow 1 \end{align*} $$is exact.
Proof. By combining the pushforward functors ![]() $g_{\mathrm {dR}*}:\mathrm {MIC}(W_\lambda /K)\rightarrow \mathrm {MIC}(V_\lambda /K)$ considered in the proof of Lemma 3.5, it is entirely straightforward to construct a pushforward functor
$g_{\mathrm {dR}*}:\mathrm {MIC}(W_\lambda /K)\rightarrow \mathrm {MIC}(V_\lambda /K)$ considered in the proof of Lemma 3.5, it is entirely straightforward to construct a pushforward functor
which is adjoint to ![]() $g^*$ and which on fibres recovers
$g^*$ and which on fibres recovers 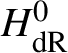 $H^0_{\mathrm {dR}}$. Now arguing exactly as in the proof of Lemma 3.5 we can see that the claimed sequence is weakly exact. Let
$H^0_{\mathrm {dR}}$. Now arguing exactly as in the proof of Lemma 3.5 we can see that the claimed sequence is weakly exact. Let ![]() $K_{\mathrm {colim}}$ denote the kernel of
$K_{\mathrm {colim}}$ denote the kernel of
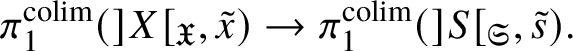 $$ \begin{align*} \pi_1^{\mathrm{colim}}(]X[_{\mathfrak{X}},\tilde{x})\rightarrow \pi_1^{\mathrm{colim}}(]S[_{\mathfrak{S}},\tilde{s}). \end{align*} $$
$$ \begin{align*} \pi_1^{\mathrm{colim}}(]X[_{\mathfrak{X}},\tilde{x})\rightarrow \pi_1^{\mathrm{colim}}(]S[_{\mathfrak{S}},\tilde{s}). \end{align*} $$By Theorem 3.1 it therefore suffices to show that for any ![]() $E\in \mathrm {MIC}(X,\mathfrak {X}/K)$, with associated monodromy representation
$E\in \mathrm {MIC}(X,\mathfrak {X}/K)$, with associated monodromy representation
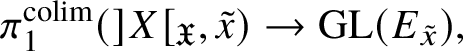 $$ \begin{align*}\pi_1^{\mathrm{colim}}(]X[_{\mathfrak{X}},\tilde{x})\rightarrow \mathrm{GL}(E_{\tilde{x}}), \end{align*} $$
$$ \begin{align*}\pi_1^{\mathrm{colim}}(]X[_{\mathfrak{X}},\tilde{x})\rightarrow \mathrm{GL}(E_{\tilde{x}}), \end{align*} $$the inclusion
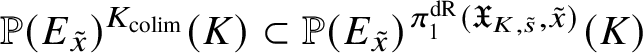 $$ \begin{align*} {\mathbb P}(E_{\tilde{x}})^{K_{\mathrm{colim}}}(K)\subset {\mathbb P}(E_{\tilde{x}})^{\pi_1^{\mathrm{dR}}(\mathfrak{X}_{K,\tilde{s}},\tilde{x})}(K) \end{align*} $$
$$ \begin{align*} {\mathbb P}(E_{\tilde{x}})^{K_{\mathrm{colim}}}(K)\subset {\mathbb P}(E_{\tilde{x}})^{\pi_1^{\mathrm{dR}}(\mathfrak{X}_{K,\tilde{s}},\tilde{x})}(K) \end{align*} $$is in fact an equality. Note that any such object is pulled back from some ![]() $W_\lambda $ via the map
$W_\lambda $ via the map ![]() $]X[_{\mathfrak {X}}\rightarrow W_\lambda $ and let
$]X[_{\mathfrak {X}}\rightarrow W_\lambda $ and let ![]() $K_\lambda $ the kernel of
$K_\lambda $ the kernel of 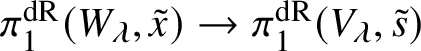 $ \pi _1^{\mathrm {dR}}(W_\lambda ,\tilde {x}) \rightarrow \pi _1^{\mathrm {dR}}(V_\lambda ,\tilde {s})$. We therefore have a natural map
$ \pi _1^{\mathrm {dR}}(W_\lambda ,\tilde {x}) \rightarrow \pi _1^{\mathrm {dR}}(V_\lambda ,\tilde {s})$. We therefore have a natural map ![]() $K_{\mathrm {colim}}\rightarrow K_\lambda $. Applying Theorem 2.5, the sequence
$K_{\mathrm {colim}}\rightarrow K_\lambda $. Applying Theorem 2.5, the sequence
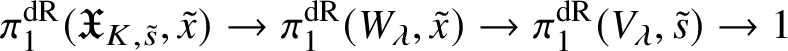 $$ \begin{align*} \pi_1^{\mathrm{dR}}(\mathfrak{X}_{K,\tilde{s}},\tilde{x})\rightarrow \pi_1^{\mathrm{dR}}(W_\lambda,\tilde{x}) \rightarrow \pi_1^{\mathrm{dR}}(V_\lambda,\tilde{s}) \rightarrow 1 \end{align*} $$
$$ \begin{align*} \pi_1^{\mathrm{dR}}(\mathfrak{X}_{K,\tilde{s}},\tilde{x})\rightarrow \pi_1^{\mathrm{dR}}(W_\lambda,\tilde{x}) \rightarrow \pi_1^{\mathrm{dR}}(V_\lambda,\tilde{s}) \rightarrow 1 \end{align*} $$is exact and hence, again applying Theorem 3.1, we can deduce that
 $$ \begin{align*} {\mathbb P}(E_{\tilde{x}})^{\pi_1^{\mathrm{dR}}(\mathfrak{X}_{K,\tilde{s}},\tilde{x})}(K) = {\mathbb P}(E_{\tilde{x}})^{K_\lambda}(K).\end{align*} $$
$$ \begin{align*} {\mathbb P}(E_{\tilde{x}})^{\pi_1^{\mathrm{dR}}(\mathfrak{X}_{K,\tilde{s}},\tilde{x})}(K) = {\mathbb P}(E_{\tilde{x}})^{K_\lambda}(K).\end{align*} $$But since we have ![]() $K_{\mathrm {colim}}\rightarrow K_\lambda $, it follows that
$K_{\mathrm {colim}}\rightarrow K_\lambda $, it follows that
 $$ \begin{align*} {\mathbb P}(E_{\tilde{x}})^{\pi_1^{\mathrm{dR}}(\mathfrak{X}_{K,\tilde{s}},\tilde{x})}(K) = {\mathbb P}(E_{\tilde{x}})^{K_\lambda}(K) \subset {\mathbb P}(E_{\tilde{x}})^{K_{\mathrm{colim}}}(K)\end{align*} $$
$$ \begin{align*} {\mathbb P}(E_{\tilde{x}})^{\pi_1^{\mathrm{dR}}(\mathfrak{X}_{K,\tilde{s}},\tilde{x})}(K) = {\mathbb P}(E_{\tilde{x}})^{K_\lambda}(K) \subset {\mathbb P}(E_{\tilde{x}})^{K_{\mathrm{colim}}}(K)\end{align*} $$and the proof is complete.
Proof of Theorem 10.2. It follows from [Reference BerthelotBer96a, Proposition 2.2.7] that the functors
 $$ \begin{align*} \mathrm{Isoc}^\dagger(X/K) & \rightarrow \mathrm{MIC}(X,\mathfrak{X}/K) \\ \mathrm{Isoc}^\dagger(S/K) & \rightarrow \mathrm{MIC}(S,\mathfrak{S}/K) \\ \mathrm{Isoc}^\dagger(X_s/K) & \rightarrow \mathrm{MIC}(\mathfrak{X}_{\tilde{s}}/K) \end{align*} $$
$$ \begin{align*} \mathrm{Isoc}^\dagger(X/K) & \rightarrow \mathrm{MIC}(X,\mathfrak{X}/K) \\ \mathrm{Isoc}^\dagger(S/K) & \rightarrow \mathrm{MIC}(S,\mathfrak{S}/K) \\ \mathrm{Isoc}^\dagger(X_s/K) & \rightarrow \mathrm{MIC}(\mathfrak{X}_{\tilde{s}}/K) \end{align*} $$are all fully faithful with image stable by subquotients. In particular, in the commutative diagram
all of the vertical maps are surjective. Since the top sequence is exact and the bottom sequence is weakly exact, we may apply Lemma 8.6.
11 The case of a smooth family of curves
While the liftability condition in Theorem 10.2 is extremely strong, it will always hold for a family of curves over a smooth affine base. That this is true is the key result of this section; we will then use this to deduce Theorem 8.3 in relative dimension 1. In order to do so, we will need to show Theorem 8.3 ‘localises on the base’, which is the content of the following lemma. Throughout, let ![]() $f:X\rightarrow S$,
$f:X\rightarrow S$, ![]() $x\in X(k)$ and
$x\in X(k)$ and ![]() $s=f(x)$ be as in the statement of Theorem 8.3.
$s=f(x)$ be as in the statement of Theorem 8.3.
Lemma 11.1. Let ![]() $U\subset S$ be an open subset containing s and
$U\subset S$ be an open subset containing s and ![]() $f_U:X_U\rightarrow U$ the base change. If the homotopy sequence for
$f_U:X_U\rightarrow U$ the base change. If the homotopy sequence for ![]() $(f_U,x)$ is exact, then so is the homotopy sequence for
$(f_U,x)$ is exact, then so is the homotopy sequence for ![]() $(f,x)$.
$(f,x)$.
Proof. We consider the diagram
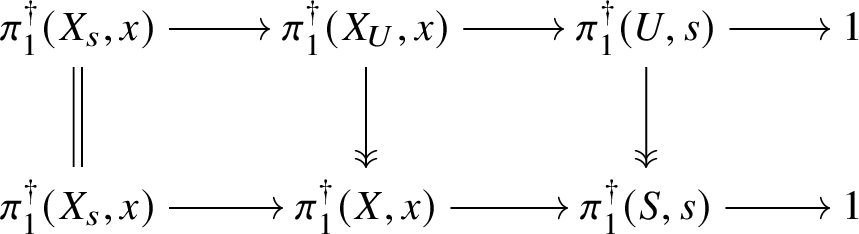
where the vertical arrows are surjective by [Reference KedlayaKed07, Theorem 5.2.1, Proposition 5.3.1]. Since the bottom sequence is always weakly exact, we may apply Lemma 8.6 to conclude.
This enables us to prove exactness of the homotopy sequence for curves.
Theorem 11.2. Theorem 8.3 is true if ![]() $f:X\rightarrow S$ has relative dimension
$f:X\rightarrow S$ has relative dimension ![]() $1$.
$1$.
Proof. Let g denote the genus of f. If ![]() $g=0$, then we are done by the proof of Lemma 8.8. To make the argument work, we only need a rational point on the fibre over s, which we have by assumption. We will treat the case
$g=0$, then we are done by the proof of Lemma 8.8. To make the argument work, we only need a rational point on the fibre over s, which we have by assumption. We will treat the case ![]() $g\geq 2$ in detail and then point out where the argument needs to be modified to work for
$g\geq 2$ in detail and then point out where the argument needs to be modified to work for ![]() $g=1$.
$g=1$.
By Proposition 11.1 we are free to replace S by any open subscheme containing s; in particular, we may assume that ![]() $S=\mathrm {Spec}\left (A_0\right )$ is affine, and
$S=\mathrm {Spec}\left (A_0\right )$ is affine, and ![]() $f:X\rightarrow S$ can be tri-canonically embedded in
$f:X\rightarrow S$ can be tri-canonically embedded in 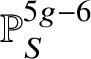 ${\mathbb P}^{5g-6}_S$. If we let
${\mathbb P}^{5g-6}_S$. If we let ![]() $H_g^0$ denote the moduli scheme (over
$H_g^0$ denote the moduli scheme (over ![]() ${\mathbb Z}$) of such tri-canonically embedded curves and
${\mathbb Z}$) of such tri-canonically embedded curves and 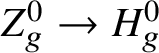 $Z_g^0\rightarrow H_g^0$ the universal curve, then we obtain a Cartesian diagram of schemes
$Z_g^0\rightarrow H_g^0$ the universal curve, then we obtain a Cartesian diagram of schemes
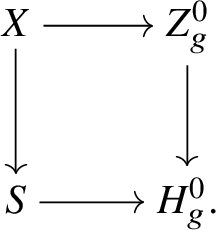
After possibly shrinking S further, we may assume that there exists an open affine subscheme 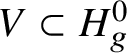 $V\subset H_g^0$ through which
$V\subset H_g^0$ through which 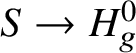 $S\rightarrow H_g^0$ factors.
$S\rightarrow H_g^0$ factors.
Now by [Reference ElkikElk73, Théorème 6] we may lift ![]() $A_0$ to a smooth
$A_0$ to a smooth ![]() $\mathcal {V}$-algebra A, let
$\mathcal {V}$-algebra A, let ![]() $A^h$ denote the
$A^h$ denote the ![]() $\varpi $-adic Henselisation of A. Since V is smooth and affine over
$\varpi $-adic Henselisation of A. Since V is smooth and affine over ![]() ${\mathbb Z}$ [Reference Deligne and MumfordDM69, Corollary 1.7] we may apply [Reference RaynaudRay72, Théorème 2] to deduce that the given morphism
${\mathbb Z}$ [Reference Deligne and MumfordDM69, Corollary 1.7] we may apply [Reference RaynaudRay72, Théorème 2] to deduce that the given morphism ![]() $S\rightarrow V$ lifts to a morphism
$S\rightarrow V$ lifts to a morphism
 $$ \begin{align*} \mathrm{Spec}\left(A^h\right)\rightarrow V. \end{align*} $$
$$ \begin{align*} \mathrm{Spec}\left(A^h\right)\rightarrow V. \end{align*} $$Since V is of finite type over ![]() ${\mathbb Z}$, it follows that after possibly passing to some étale A-algebra with the same special fibre, we may assume that the family of curves
${\mathbb Z}$, it follows that after possibly passing to some étale A-algebra with the same special fibre, we may assume that the family of curves ![]() $X\rightarrow S$ lifts to a family
$X\rightarrow S$ lifts to a family ![]() $\mathcal {X}\rightarrow \mathcal {S}=\mathrm {Spec}\left (A\right )$ over A, which is, moreover, a closed subscheme of
$\mathcal {X}\rightarrow \mathcal {S}=\mathrm {Spec}\left (A\right )$ over A, which is, moreover, a closed subscheme of  ${\mathbb P}^{5g-6}_{\mathcal {S}}$. Now choose a projective embedding
${\mathbb P}^{5g-6}_{\mathcal {S}}$. Now choose a projective embedding
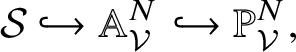 $$ \begin{align*} \mathcal{S} \hookrightarrow {\mathbb A}^N_{\mathcal{V}} \hookrightarrow {\mathbb P}^N_{\mathcal{V}}, \end{align*} $$
$$ \begin{align*} \mathcal{S} \hookrightarrow {\mathbb A}^N_{\mathcal{V}} \hookrightarrow {\mathbb P}^N_{\mathcal{V}}, \end{align*} $$ let ![]() $\overline {\mathcal {S}}$ be the closure of
$\overline {\mathcal {S}}$ be the closure of ![]() $\mathcal {S}$ inside
$\mathcal {S}$ inside 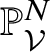 ${\mathbb P}^N_{\mathcal {V}}$ and let
${\mathbb P}^N_{\mathcal {V}}$ and let ![]() $\overline {\mathcal {X}}$ be the closure of
$\overline {\mathcal {X}}$ be the closure of ![]() $\mathcal {X}$ inside
$\mathcal {X}$ inside 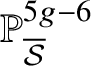 ${\mathbb P}^{5g-6}_{\overline {\mathcal {S}}}$. Setting
${\mathbb P}^{5g-6}_{\overline {\mathcal {S}}}$. Setting 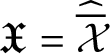 $\mathfrak {X}=\widehat {\overline {\mathcal {X}}}$ and
$\mathfrak {X}=\widehat {\overline {\mathcal {X}}}$ and 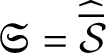 $\mathfrak {S}=\widehat {\overline {\mathcal {S}}}$ we find ourselves in the situation of Theorem 10.2.
$\mathfrak {S}=\widehat {\overline {\mathcal {S}}}$ we find ourselves in the situation of Theorem 10.2.
When ![]() $g=1$ we can argue as follows. First of all, we consider the base change
$g=1$ we can argue as follows. First of all, we consider the base change ![]() $X\times _S X\rightarrow X$ of f by itself, equipped with the rational point
$X\times _S X\rightarrow X$ of f by itself, equipped with the rational point ![]() $(x,x)$. Then we have a commutative diagram
$(x,x)$. Then we have a commutative diagram
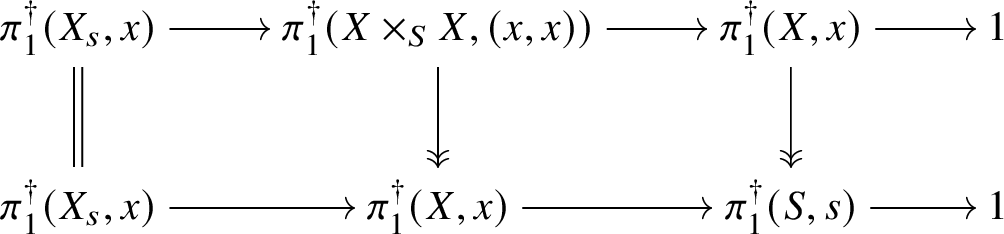
where the surjectivity of the vertical arrows follows from Corollary 8.5. If the top sequence is exact, then again the bottom sequence is exact by Lemma 8.6. In particular, after replacing ![]() $X\rightarrow S$ by
$X\rightarrow S$ by ![]() $X\times _S X\rightarrow X$, we may assume that
$X\times _S X\rightarrow X$, we may assume that ![]() $f:X\rightarrow S$ admits a section; that is, is an elliptic curve.
$f:X\rightarrow S$ admits a section; that is, is an elliptic curve.
Hence, after possibly localising on S and again using Lemma 11.1, we may assume that we have a smooth Weierstrass model 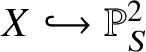 $X\hookrightarrow {\mathbb P}^2_S$ of X. We now replace the scheme
$X\hookrightarrow {\mathbb P}^2_S$ of X. We now replace the scheme ![]() $H^0_g$ in the previous argument with the smooth moduli scheme over
$H^0_g$ in the previous argument with the smooth moduli scheme over ![]() ${\mathbb Z}$ parametrising Weierstrass models of elliptic curves.
${\mathbb Z}$ parametrising Weierstrass models of elliptic curves.
12 Cutting a smooth projective morphism by curves
Using Theorem 8.7, we can now finally complete the proof of Theorem 8.3 by reducing to the case of a family of smooth projective curves, and hence to Theorem 11.2.
Suppose that we are in the situation of Theorem 8.3. Let d be the relative dimension of ![]() $X/S$ and assume that
$X/S$ and assume that ![]() $d\geq 2$. Assume, moreover, that S is quasi-projective over k. There therefore exists a global closed immersion
$d\geq 2$. Assume, moreover, that S is quasi-projective over k. There therefore exists a global closed immersion ![]() $X\hookrightarrow {\mathbb P}^n_S$. Let
$X\hookrightarrow {\mathbb P}^n_S$. Let ![]() $\widetilde {S}$ denote the dual projective space
$\widetilde {S}$ denote the dual projective space ![]() $\check {{\mathbb P}}^n_S$ and define
$\check {{\mathbb P}}^n_S$ and define
to be the subscheme of pairs ![]() $(x,H)$ such that
$(x,H)$ such that ![]() $x\in H$. We therefore have a diagram
$x\in H$. We therefore have a diagram

such that ![]() $\widetilde {f}$ is projective, with generic fibre smooth, projective and geometrically connected of dimension
$\widetilde {f}$ is projective, with generic fibre smooth, projective and geometrically connected of dimension ![]() $d-1$. Choose an open subscheme
$d-1$. Choose an open subscheme ![]() $U\subset \widetilde {S}$, surjective over S, such that the pullback
$U\subset \widetilde {S}$, surjective over S, such that the pullback ![]() $\tilde {f}_U:\widetilde {X}_U\rightarrow U$ is smooth with geometrically connected fibres. After possibly making a finite extension of k, we may moreover assume that there exists some k-rational point
$\tilde {f}_U:\widetilde {X}_U\rightarrow U$ is smooth with geometrically connected fibres. After possibly making a finite extension of k, we may moreover assume that there exists some k-rational point ![]() $u\in U$ lifting
$u\in U$ lifting ![]() $s\in S(k)$ and some
$s\in S(k)$ and some ![]() $\tilde {x}\in \widetilde {X}_U(k)$ such that
$\tilde {x}\in \widetilde {X}_U(k)$ such that ![]() $\tilde {f}_U(\tilde {x})=u$.
$\tilde {f}_U(\tilde {x})=u$.
In particular, combining Lemma 8.8 with [Reference KedlayaKed07, Theorem 5.2.1, Proposition 5.3.1], we have a commutative diagram

Proposition 12.1. If the homotopy sequence of ![]() $(\tilde {f}_U,\tilde x)$ is exact, then so is that of
$(\tilde {f}_U,\tilde x)$ is exact, then so is that of ![]() $(f,x)$.
$(f,x)$.
Proof. We first claim that under the hypothesis of the proposition, the sequence
 $$ \begin{align*} \pi_1^\dagger(\widetilde{X}_{u},\tilde x) \rightarrow \pi_1^\dagger(\widetilde{X},\tilde x) \rightarrow \pi_1^\dagger(\widetilde S,u)\rightarrow 1\\[-17pt]\end{align*} $$
$$ \begin{align*} \pi_1^\dagger(\widetilde{X}_{u},\tilde x) \rightarrow \pi_1^\dagger(\widetilde{X},\tilde x) \rightarrow \pi_1^\dagger(\widetilde S,u)\rightarrow 1\\[-17pt]\end{align*} $$satisfies the conditions of Theorem 3.4 (note that this does not follow from Corollary 8.5). Indeed, surjectivity of 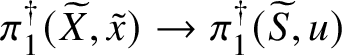 $\pi _1^\dagger (\widetilde {X},\tilde x) \rightarrow \pi _1^\dagger (\widetilde S,u)$ follows from that of
$\pi _1^\dagger (\widetilde {X},\tilde x) \rightarrow \pi _1^\dagger (\widetilde S,u)$ follows from that of 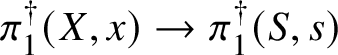 $\pi _1^\dagger (X,x) \rightarrow \pi _1^\dagger (S,s)$, and one half of (1) is clear.
$\pi _1^\dagger (X,x) \rightarrow \pi _1^\dagger (S,s)$, and one half of (1) is clear.
For the other half of (1), suppose that ![]() $E\in \mathrm {Isoc}^\dagger (\widetilde {X}/K)$ is such that
$E\in \mathrm {Isoc}^\dagger (\widetilde {X}/K)$ is such that ![]() $E|_{\widetilde {X}_u}$ is trivial. We may assume by Lemma 8.8 that E comes from an object
$E|_{\widetilde {X}_u}$ is trivial. We may assume by Lemma 8.8 that E comes from an object ![]() $E'$ of
$E'$ of ![]() $\mathrm {Isoc}^\dagger (X/K)$. Applying Theorem 8.7 to the map
$\mathrm {Isoc}^\dagger (X/K)$. Applying Theorem 8.7 to the map ![]() $\widetilde {X}_u \rightarrow X_s$ we can see that in fact
$\widetilde {X}_u \rightarrow X_s$ we can see that in fact ![]() $E'\mid _{X_s}$ is trivial, and so by weak exactness of
$E'\mid _{X_s}$ is trivial, and so by weak exactness of
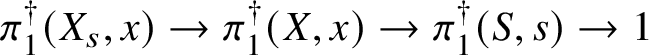 $$ \begin{align*} \pi_1^\dagger(X_s,x) \rightarrow \pi_1^\dagger(X,x) \rightarrow \pi_1^\dagger(S,s)\rightarrow 1 \\[-17pt]\end{align*} $$
$$ \begin{align*} \pi_1^\dagger(X_s,x) \rightarrow \pi_1^\dagger(X,x) \rightarrow \pi_1^\dagger(S,s)\rightarrow 1 \\[-17pt]\end{align*} $$we know that ![]() $E'\cong f^*(F')$ for some
$E'\cong f^*(F')$ for some ![]() $F'\in \mathrm {Isoc}^\dagger (S/K)$. Hence,
$F'\in \mathrm {Isoc}^\dagger (S/K)$. Hence, ![]() $E\cong \tilde {f}^*(F)$ for some
$E\cong \tilde {f}^*(F)$ for some ![]() $F\in \mathrm {Isoc}^\dagger (\widetilde S/K)$ as required. To prove (2) we note that if the top sequence is exact, then the image of
$F\in \mathrm {Isoc}^\dagger (\widetilde S/K)$ as required. To prove (2) we note that if the top sequence is exact, then the image of
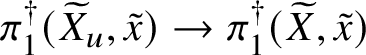 $$ \begin{align*} \pi_1^\dagger(\widetilde{X}_{u},\tilde x) \rightarrow \pi_1^\dagger(\widetilde{X},\tilde x) \end{align*} $$
$$ \begin{align*} \pi_1^\dagger(\widetilde{X}_{u},\tilde x) \rightarrow \pi_1^\dagger(\widetilde{X},\tilde x) \end{align*} $$is a normal subgroup, and hence for any representation V of 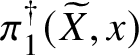 $\pi _1^\dagger (\widetilde {X},x)$, we know that
$\pi _1^\dagger (\widetilde {X},x)$, we know that ![]() $V^{\pi _1^\dagger (\widetilde {X}_u,\tilde x)}$ must be stable under
$V^{\pi _1^\dagger (\widetilde {X}_u,\tilde x)}$ must be stable under 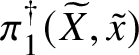 $\pi _1^\dagger (\widetilde {X},\tilde x)$.
$\pi _1^\dagger (\widetilde {X},\tilde x)$.
Hence, the top sequence is weakly exact. Since we have already noted that the image of 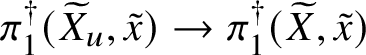 $\pi _1^\dagger (\widetilde {X}_{u},\tilde x) \rightarrow \pi _1^\dagger (\widetilde {X},\tilde x)$ is a normal subgroup, it is in fact exact. The exactness of
$\pi _1^\dagger (\widetilde {X}_{u},\tilde x) \rightarrow \pi _1^\dagger (\widetilde {X},\tilde x)$ is a normal subgroup, it is in fact exact. The exactness of
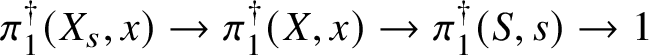 $$ \begin{align*} \pi_1^\dagger(X_s,x) \rightarrow \pi_1^\dagger(X,x) \rightarrow \pi_1^\dagger(S,s)\rightarrow 1\end{align*} $$
$$ \begin{align*} \pi_1^\dagger(X_s,x) \rightarrow \pi_1^\dagger(X,x) \rightarrow \pi_1^\dagger(S,s)\rightarrow 1\end{align*} $$now follows from a simple diagram chase.
We can now complete the proof of Theorem 8.3.
13 Applications
In this final section we deduce a couple of corollaries of Theorem 8.3.
Theorem 13.1. Let ![]() $X\subset {\mathbb P}^n_k$ be smooth, projective and geometrically connected. Assume that
$X\subset {\mathbb P}^n_k$ be smooth, projective and geometrically connected. Assume that ![]() $\dim X\geq 2$ and let
$\dim X\geq 2$ and let ![]() $Y=H\cap X$ be a smooth hyperplane section. Let
$Y=H\cap X$ be a smooth hyperplane section. Let ![]() $y\in Y(k)$. Then the map
$y\in Y(k)$. Then the map
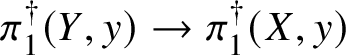 $$ \begin{align*} \pi_1^\dagger(Y,y)\rightarrow \pi_1^\dagger(X,y)\end{align*} $$
$$ \begin{align*} \pi_1^\dagger(Y,y)\rightarrow \pi_1^\dagger(X,y)\end{align*} $$is surjective.
Proof. We simply copy the proof of Theorem 8.7, replacing all instances of Corollary 8.5 with Theorem 8.3.
We can also show a version of the Kunneth formula, when one of the varieties is projective.
Proposition 13.2. Let ![]() $X,Y$ be smooth and geometrically connected over k,
$X,Y$ be smooth and geometrically connected over k, ![]() $x\in X(k)$,
$x\in X(k)$, ![]() $y\in Y(k)$. If either X or Y is projective, then the natural map
$y\in Y(k)$. If either X or Y is projective, then the natural map
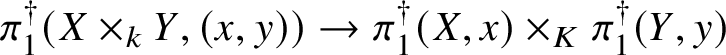 $$ \begin{align*} \pi_1^\dagger(X\times_k Y,(x,y))\rightarrow \pi_1^\dagger(X,x)\times _K \pi_1^\dagger(Y,y) \end{align*} $$
$$ \begin{align*} \pi_1^\dagger(X\times_k Y,(x,y))\rightarrow \pi_1^\dagger(X,x)\times _K \pi_1^\dagger(Y,y) \end{align*} $$is an isomorphism.
Proof. Assume that Y is projective. Then by Theorem 8.3 the sequence
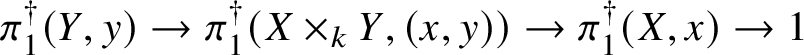 $$ \begin{align*} \pi_1^\dagger(Y,y)\rightarrow \pi_1^\dagger(X\times_k Y,(x,y)) \rightarrow \pi_1^\dagger(X,x)\rightarrow 1 \end{align*} $$
$$ \begin{align*} \pi_1^\dagger(Y,y)\rightarrow \pi_1^\dagger(X\times_k Y,(x,y)) \rightarrow \pi_1^\dagger(X,x)\rightarrow 1 \end{align*} $$is exact, and the first map is split by the projection 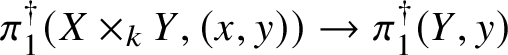 $\pi _1^\dagger (X\times _k Y,(x,y))\rightarrow \pi _1^\dagger (Y,y)$.
$\pi _1^\dagger (X\times _k Y,(x,y))\rightarrow \pi _1^\dagger (Y,y)$.
We can also use Theorem 8.3 to compare the (over)convergent fundamental group 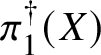 $\pi _1^\dagger (X)$ with the étale one
$\pi _1^\dagger (X)$ with the étale one 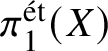 $\pi _1^{\mathrm {\acute {e}t}}(X)$.
$\pi _1^{\mathrm {\acute {e}t}}(X)$.
Assumption. We will assume for the remainder of this section that the ground field k is algebraically closed.
Let X be a smooth, projective, connected k-variety and ![]() $x\in X(k)$. Then there is a functor
$x\in X(k)$. Then there is a functor
from the category of finite étale covers of X to (over)convergent isocrystals which sends ![]() $f:Y\rightarrow X$ to
$f:Y\rightarrow X$ to 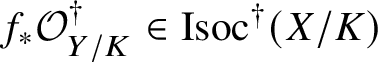 $f_*\mathcal {O}_{Y/K}^\dagger \in \mathrm {Isoc}^\dagger (X/K)$. This gives rise to a homomorphism of pro-algebraic groups
$f_*\mathcal {O}_{Y/K}^\dagger \in \mathrm {Isoc}^\dagger (X/K)$. This gives rise to a homomorphism of pro-algebraic groups
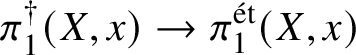 $$ \begin{align*} \pi_1^\dagger(X,x)\rightarrow \pi_1^{\mathrm{\acute{e}t}}(X,x) \end{align*} $$
$$ \begin{align*} \pi_1^\dagger(X,x)\rightarrow \pi_1^{\mathrm{\acute{e}t}}(X,x) \end{align*} $$and hence to a homomorphism of pro-finite groups
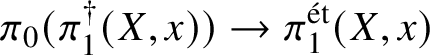 $$ \begin{align*} \pi_0(\pi_1^\dagger(X,x))\rightarrow \pi_1^{\mathrm{\acute{e}t}}(X,x)\end{align*} $$
$$ \begin{align*} \pi_0(\pi_1^\dagger(X,x))\rightarrow \pi_1^{\mathrm{\acute{e}t}}(X,x)\end{align*} $$where the former is the component group of 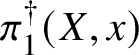 $\pi _1^\dagger (X,x)$. The following strengthens a result of Crew [Reference CrewCre92, Proposition 4.4].
$\pi _1^\dagger (X,x)$. The following strengthens a result of Crew [Reference CrewCre92, Proposition 4.4].
Theorem 13.3. The map 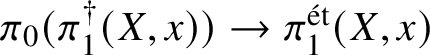 $\pi _0(\pi _1^\dagger (X,x))\rightarrow \pi _1^{\mathrm {\acute {e}t}}(X,x)$ is an isomorphism.
$\pi _0(\pi _1^\dagger (X,x))\rightarrow \pi _1^{\mathrm {\acute {e}t}}(X,x)$ is an isomorphism.
We can translate this into Tannakian terms as follows. Let ![]() $E\in \mathrm {Isoc}^\dagger (X/K)$, and consider the associated monodromy representation
$E\in \mathrm {Isoc}^\dagger (X/K)$, and consider the associated monodromy representation
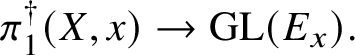 $$ \begin{align*} \pi_1^\dagger(X,x)\rightarrow \mathrm{GL}(E_x). \end{align*} $$
$$ \begin{align*} \pi_1^\dagger(X,x)\rightarrow \mathrm{GL}(E_x). \end{align*} $$By definition, the image of this homomorphism is the monodromy group ![]() $\mathrm {DGal}_x(E)$ of E. Then Theorem 13.3 is equivalent to the following.
$\mathrm {DGal}_x(E)$ of E. Then Theorem 13.3 is equivalent to the following.
Theorem 13.4. If ![]() $E\in \mathrm {Isoc}^\dagger (X/K)$ has finite monodromy group, then it is trivialised by some finite étale cover
$E\in \mathrm {Isoc}^\dagger (X/K)$ has finite monodromy group, then it is trivialised by some finite étale cover ![]() $f:Y\rightarrow X$
$f:Y\rightarrow X$
Remark 13.5. Note that the condition of having finite monodromy group is independent of the choice of base point x.
The following lemma will play an important role in the proof of Theorem 13.3.
Lemma 13.6. Let ![]() $f:Y\rightarrow X$ be a morphism of connected k-varieties, with Y a smooth curve. Let
$f:Y\rightarrow X$ be a morphism of connected k-varieties, with Y a smooth curve. Let ![]() $y\in Y(k)$, and set
$y\in Y(k)$, and set ![]() $x=f(y)$. Assume that the induced homomorphism
$x=f(y)$. Assume that the induced homomorphism
 $$ \begin{align*} \pi_1^\dagger(Y,y)\rightarrow \pi_1^\dagger(X,x) \end{align*} $$
$$ \begin{align*} \pi_1^\dagger(Y,y)\rightarrow \pi_1^\dagger(X,x) \end{align*} $$is surjective, and let ![]() $E\in \mathrm {Isoc}^\dagger (X/K)$ be simple. If there exists
$E\in \mathrm {Isoc}^\dagger (X/K)$ be simple. If there exists ![]() $E'\in F\text {-}\mathrm {Isoc}^\dagger (Y/K)$ and an injection of isocrystals
$E'\in F\text {-}\mathrm {Isoc}^\dagger (Y/K)$ and an injection of isocrystals ![]() $f^*E\hookrightarrow E'$, then there exists
$f^*E\hookrightarrow E'$, then there exists ![]() $E'' \in F\text {-}\mathrm {Isoc}^\dagger (X/K)$ and an injection of isocrystals
$E'' \in F\text {-}\mathrm {Isoc}^\dagger (X/K)$ and an injection of isocrystals ![]() $E\hookrightarrow E''$.
$E\hookrightarrow E''$.
Proof. Write ![]() $f^*(-)=(-)|_Y$. For all
$f^*(-)=(-)|_Y$. For all ![]() $n\geq 0$ we can view the Frobenius pullback
$n\geq 0$ we can view the Frobenius pullback ![]() $(F^n)^*E|_Y$ as lying inside
$(F^n)^*E|_Y$ as lying inside ![]() $E'$ via the Frobenius
$E'$ via the Frobenius ![]() $\varphi ^n$ on
$\varphi ^n$ on ![]() $E'$. Let
$E'$. Let ![]() $E^{\prime }_0\subset E'$ denote the sum of all the
$E^{\prime }_0\subset E'$ denote the sum of all the ![]() $(F^n)^*E|_Y$; this is therefore stable by
$(F^n)^*E|_Y$; this is therefore stable by ![]() $\varphi $, and we can thus view it as an F-isocrystal. Since E is simple, surjectivity of the map
$\varphi $, and we can thus view it as an F-isocrystal. Since E is simple, surjectivity of the map
 $$ \begin{align*} \pi_1^\dagger(Y,y)\rightarrow \pi_1^\dagger(X,x)\end{align*} $$
$$ \begin{align*} \pi_1^\dagger(Y,y)\rightarrow \pi_1^\dagger(X,x)\end{align*} $$implies that ![]() $E|_Y$ is simple. Moreover, since Y is a smooth curve, we know that there exists a good compactification
$E|_Y$ is simple. Moreover, since Y is a smooth curve, we know that there exists a good compactification ![]() $\overline {Y}$ which lifts to a smooth and proper curve over
$\overline {Y}$ which lifts to a smooth and proper curve over ![]() $\mathcal {V}$. Thus, we may apply [Reference BerthelotBer96b, Théorème 4.4.5] together with [Reference BerthelotBer00, Théorème 2.3.6] to deduce that the Frobenius pullback functor
$\mathcal {V}$. Thus, we may apply [Reference BerthelotBer96b, Théorème 4.4.5] together with [Reference BerthelotBer00, Théorème 2.3.6] to deduce that the Frobenius pullback functor
is an equivalence of categories. In particular, each ![]() $(F^n)^*E|_Y$ is simple. Hence,
$(F^n)^*E|_Y$ is simple. Hence, ![]() $E^{\prime }_0$ is semi-simple and, moreover, we can write
$E^{\prime }_0$ is semi-simple and, moreover, we can write
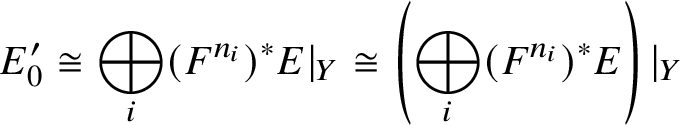 $$ \begin{align*} E^{\prime}_0\cong \bigoplus_i (F^{n_i})^*E|_Y \cong \left(\bigoplus_i (F^{n_i})^*E\right)|_Y \end{align*} $$
$$ \begin{align*} E^{\prime}_0\cong \bigoplus_i (F^{n_i})^*E|_Y \cong \left(\bigoplus_i (F^{n_i})^*E\right)|_Y \end{align*} $$for some ![]() $n_i$. Hence,
$n_i$. Hence, ![]() $E^{\prime }_0$ extends to some
$E^{\prime }_0$ extends to some ![]() $E''$ on X, and since
$E''$ on X, and since
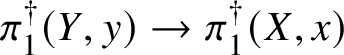 $$ \begin{align*} \pi_1^\dagger(Y,y)\rightarrow \pi_1^\dagger(X,x)\end{align*} $$
$$ \begin{align*} \pi_1^\dagger(Y,y)\rightarrow \pi_1^\dagger(X,x)\end{align*} $$is surjective, both the induced Frobenius on ![]() $E^{\prime }_0=E''|_Y$ and the injection
$E^{\prime }_0=E''|_Y$ and the injection ![]() $E|_Y\hookrightarrow E''|_Y$ also extend to X.
$E|_Y\hookrightarrow E''|_Y$ also extend to X.
We can now begin the proof of Theorem 13.3 in earnest. Our first step is to show a slightly weaker version of Theorem 13.4 when X is a curve.
Lemma 13.7. Let C be a smooth, projective, connected curve over k, and let ![]() $E\in \mathrm {Isoc}^\dagger (C/K)$ be simple with finite monodromy group. Then there exists a smooth, projective, connected curve D and a nonconstant, separable morphism
$E\in \mathrm {Isoc}^\dagger (C/K)$ be simple with finite monodromy group. Then there exists a smooth, projective, connected curve D and a nonconstant, separable morphism ![]() $f:D\rightarrow C$ such that
$f:D\rightarrow C$ such that ![]() $f^*E$ is trivial.
$f^*E$ is trivial.
Proof. Choose a lift ![]() $\mathcal {C}$ of C to
$\mathcal {C}$ of C to ![]() $\mathcal {V}$, with generic fibre
$\mathcal {V}$, with generic fibre ![]() $\mathcal {C}_K$ a smooth, projective, geometrically connected curve over K. Then E corresponds to a module with overconvergent connection on
$\mathcal {C}_K$ a smooth, projective, geometrically connected curve over K. Then E corresponds to a module with overconvergent connection on ![]() $\mathcal {C}_K$. Choose a point
$\mathcal {C}_K$. Choose a point ![]() $\tilde {c}$ of
$\tilde {c}$ of ![]() $\mathcal {C}_K$ specialising to some
$\mathcal {C}_K$ specialising to some ![]() $c\in C(k)$. Combining the defintion of
$c\in C(k)$. Combining the defintion of ![]() $\mathrm {Isoc}^\dagger (C/K)$ with GAGA, we can see that
$\mathrm {Isoc}^\dagger (C/K)$ with GAGA, we can see that ![]() $\mathrm {Isoc}^\dagger (C/K)$ is a full subcategory of the category
$\mathrm {Isoc}^\dagger (C/K)$ is a full subcategory of the category ![]() $\mathrm {MIC}(\mathcal {C}_K/K)$ of modules with integrable connection on the algebraic curve
$\mathrm {MIC}(\mathcal {C}_K/K)$ of modules with integrable connection on the algebraic curve ![]() $\mathcal {C}_K$, and this subcategory is stable under taking subquotients. We therefore get a surjective map
$\mathcal {C}_K$, and this subcategory is stable under taking subquotients. We therefore get a surjective map 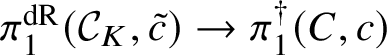 $\pi _1^{\mathrm {dR}}(\mathcal {C}_K,\tilde {c})\rightarrow \pi _1^\dagger (C,c)$.
$\pi _1^{\mathrm {dR}}(\mathcal {C}_K,\tilde {c})\rightarrow \pi _1^\dagger (C,c)$.
Hence, E also has finite monodromy when considered as a representation of 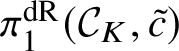 $\pi _1^{\mathrm {dR}}(\mathcal {C}_K,\tilde {c})$. If we now choose a finitely generated subfield
$\pi _1^{\mathrm {dR}}(\mathcal {C}_K,\tilde {c})$. If we now choose a finitely generated subfield ![]() $K_0\subset K$ over which
$K_0\subset K$ over which ![]() $\mathcal {C}_K$,
$\mathcal {C}_K$, ![]() $\tilde {c}$ and E are all defined and then embed this field into
$\tilde {c}$ and E are all defined and then embed this field into ![]() ${\mathbb C}$, we have an isomorphism between
${\mathbb C}$, we have an isomorphism between 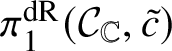 $\pi _1^{\mathrm {dR}}(\mathcal {C}_{{\mathbb C}},\tilde {c})$ and the
$\pi _1^{\mathrm {dR}}(\mathcal {C}_{{\mathbb C}},\tilde {c})$ and the ![]() ${\mathbb C}$-valued pro-algebraic completion of the abstract group
${\mathbb C}$-valued pro-algebraic completion of the abstract group ![]() $\pi _1(\mathcal {C}({\mathbb C}),\tilde {c})$. Thus,
$\pi _1(\mathcal {C}({\mathbb C}),\tilde {c})$. Thus, ![]() $E_{{\mathbb C}}$ has finite monodromy as a representation of
$E_{{\mathbb C}}$ has finite monodromy as a representation of ![]() $\pi _1(\mathcal {C}({\mathbb C}),\tilde {c})$ and so is trivialised by a finite étale cover of
$\pi _1(\mathcal {C}({\mathbb C}),\tilde {c})$ and so is trivialised by a finite étale cover of ![]() $\mathcal {C}_{{\mathbb C}}$. Descending down to
$\mathcal {C}_{{\mathbb C}}$. Descending down to ![]() $K_0$ and then re-ascending to K, we can see that after possibly replacing K by a finite extension (this does not change the problem) there exists a finite, étale, geometrically connected cover
$K_0$ and then re-ascending to K, we can see that after possibly replacing K by a finite extension (this does not change the problem) there exists a finite, étale, geometrically connected cover ![]() $\mathcal {C}^{\prime }_K\rightarrow \mathcal {C}_K$ trivialising E as a module with integrable connection. Let
$\mathcal {C}^{\prime }_K\rightarrow \mathcal {C}_K$ trivialising E as a module with integrable connection. Let ![]() $\mathcal {C}'$ denote the normalisation of
$\mathcal {C}'$ denote the normalisation of ![]() $\mathcal {C}$ inside the function field extension
$\mathcal {C}$ inside the function field extension ![]() $K(\mathcal {C}_K)\rightarrow K(\mathcal {C}^{\prime }_K)$.
$K(\mathcal {C}_K)\rightarrow K(\mathcal {C}^{\prime }_K)$.
By de Jong’s theorem on alterations [Reference de JongdJ96, Theorem 8.2] we can find (after possibly further increasing K) some alteration ![]() $\mathcal {C}''\rightarrow \mathcal {C}'$ with strictly semistable reduction; let
$\mathcal {C}''\rightarrow \mathcal {C}'$ with strictly semistable reduction; let ![]() $C''$ denote the special fibre. Then the map from the smooth locus of
$C''$ denote the special fibre. Then the map from the smooth locus of ![]() $C''$ to C is dominant, so we may choose some connected component
$C''$ to C is dominant, so we may choose some connected component ![]() $C'''$ of
$C'''$ of ![]() $\mathrm {sm}(C'')$ which is nonconstant over C. Then the formal completion
$\mathrm {sm}(C'')$ which is nonconstant over C. Then the formal completion ![]() $\widehat {\mathcal {C}}''$ is smooth over
$\widehat {\mathcal {C}}''$ is smooth over ![]() $\mathcal {V}$ in a neighbourhood of
$\mathcal {V}$ in a neighbourhood of ![]() $C'''$, and so the pullback of isocrystals along
$C'''$, and so the pullback of isocrystals along ![]() $C'''\rightarrow C$ can be identified with the pullback of modules with integrable connection along
$C'''\rightarrow C$ can be identified with the pullback of modules with integrable connection along
 $$ \begin{align*} ]C'''[_{\widehat{\mathcal{C}}''} \subset {\mathcal{C}_K''}^{\mathrm{an}}\rightarrow{\mathcal{C}_K'}^{\mathrm{an}} \rightarrow \mathcal{C}_K^{\mathrm{an}}. \end{align*} $$
$$ \begin{align*} ]C'''[_{\widehat{\mathcal{C}}''} \subset {\mathcal{C}_K''}^{\mathrm{an}}\rightarrow{\mathcal{C}_K'}^{\mathrm{an}} \rightarrow \mathcal{C}_K^{\mathrm{an}}. \end{align*} $$Thus, E becomes trivial after pulling back by ![]() $C'''\rightarrow C$. Let
$C'''\rightarrow C$. Let ![]() $D'$ denote the smooth compactification of
$D'$ denote the smooth compactification of ![]() $C'''$; applying [Reference KedlayaKed07, Theorem 5.2.1] we therefore know that E becomes trivial after pulling back by
$C'''$; applying [Reference KedlayaKed07, Theorem 5.2.1] we therefore know that E becomes trivial after pulling back by ![]() $D'\rightarrow C$. Finally, factor
$D'\rightarrow C$. Finally, factor ![]() $D'\rightarrow D\rightarrow C$ into a totally inseparable morphism
$D'\rightarrow D\rightarrow C$ into a totally inseparable morphism ![]() $D'\rightarrow D$ followed by a separable morphism
$D'\rightarrow D$ followed by a separable morphism ![]() $D\rightarrow C$. Since E is trivial when pulled back to
$D\rightarrow C$. Since E is trivial when pulled back to ![]() $D'$, it follows from [Reference OgusOgu84, Corollary 4.10] that it is trivial when pulled back to D.
$D'$, it follows from [Reference OgusOgu84, Corollary 4.10] that it is trivial when pulled back to D.
We can now prove Theorem 13.4, and hence Theorem 13.3.
Proof of Theorem 13.4. Let ![]() $E\in \mathrm {Isoc}^\dagger (X/K)$ have finite monodromy group. Since finite groups are reductive, E is therefore semi-simple, and by working one simple factor at a time we may assume that E is simple. Choose an iterated hyperplane section
$E\in \mathrm {Isoc}^\dagger (X/K)$ have finite monodromy group. Since finite groups are reductive, E is therefore semi-simple, and by working one simple factor at a time we may assume that E is simple. Choose an iterated hyperplane section ![]() $C\rightarrow X$ which is a smooth, projective, connected curve over k. By Theorem 13.1 we know that
$C\rightarrow X$ which is a smooth, projective, connected curve over k. By Theorem 13.1 we know that ![]() $E|_C$ is simple with finite monodromy, and therefore by Lemma 13.7 we can find some finite separable morphism
$E|_C$ is simple with finite monodromy, and therefore by Lemma 13.7 we can find some finite separable morphism ![]() $D\rightarrow C$ such that
$D\rightarrow C$ such that ![]() $E|_D$ is trivial.
$E|_D$ is trivial.
Let ![]() $D_U\rightarrow U$ be the étale locus of
$D_U\rightarrow U$ be the étale locus of ![]() $D\rightarrow C$. Then since
$D\rightarrow C$. Then since ![]() $E|_{D_U}$ is trivial, we know by taking the pushforward along
$E|_{D_U}$ is trivial, we know by taking the pushforward along ![]() $D_U\rightarrow U$ that we can find some
$D_U\rightarrow U$ that we can find some ![]() $E'\in F\text {-}\mathrm {Isoc}^\dagger (U/K)$ and an injection of isocrystals
$E'\in F\text {-}\mathrm {Isoc}^\dagger (U/K)$ and an injection of isocrystals ![]() $E|_U\hookrightarrow E'$. Using Theorem 13.1 together with [Reference KedlayaKed07, Theorem 5.2.1, Proposition 5.3.1] we may apply Lemma 13.6 above to the map
$E|_U\hookrightarrow E'$. Using Theorem 13.1 together with [Reference KedlayaKed07, Theorem 5.2.1, Proposition 5.3.1] we may apply Lemma 13.6 above to the map ![]() $U\rightarrow X$. We can therefore find some
$U\rightarrow X$. We can therefore find some ![]() $E''\in F\text {-}\mathrm {Isoc}^\dagger (X/K)$ and an injection of isocrystals
$E''\in F\text {-}\mathrm {Isoc}^\dagger (X/K)$ and an injection of isocrystals ![]() $E\hookrightarrow E''$. We can now apply [Reference CrewCre92, Proposition 4.3] to conclude. (Note the remark following the proof of this result that you do not need to assume X is a curve for the implication (iv)
$E\hookrightarrow E''$. We can now apply [Reference CrewCre92, Proposition 4.3] to conclude. (Note the remark following the proof of this result that you do not need to assume X is a curve for the implication (iv)![]() $\Rightarrow $(ii), which is the one we are interested in.)
$\Rightarrow $(ii), which is the one we are interested in.)
Acknowledgements
The authors thank Imperial College London, Università Degli Studi di Padova, the Centre International de Rencontres Mathematiques in Marseille and the Mittag-Leffler Institute in Stockholm for hospitality during the writing of this article. We also thank the anonymous referee for a careful reading of the article. Finally, we owe a huge amount to the work of J.P. dos Santos, in particular the article [Reference dos SantosdS15], which pointed the way towards a solution to a problem we had been considering for a number of years. The first author was supported by a Marie Curie fellowship of the Istituto Nazionale di Alta Matematica ‘F. Severi’. The second author was partially supported by the EPSRC Grant P36794. Open access funding was provided by the University of Warwick Open Access Fund.
Conflicts of interest
None.