Hostname: page-component-f554764f5-44mx8 Total loading time: 0 Render date: 2025-04-20T08:54:37.542Z Has data issue: false hasContentIssue false
  • English
  • Français

HIGHER RANDOMNESS AND GENERICITY

Part of: Rings and algebras with additional structure Modules, bimodules and ideals

Published online by Cambridge University Press:  10 December 2017

NOAM GREENBERG  and
BENOIT MONIN
NOAM GREENBERG
Affiliation:
Department of Mathematics, Victoria University of Wellington, New Zealand; [email protected]
BENOIT MONIN
Affiliation:
LACL, Université Paris Est-Créteil, France; [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We use concepts of continuous higher randomness, developed in Bienvenu et al. [‘Continuous higher randomness’, J. Math. Log. 17(1) (2017).], to investigate 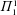$\unicode[STIX]{x1D6F1}_{1}^{1}$-randomness. We discuss lowness for 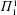$\unicode[STIX]{x1D6F1}_{1}^{1}$-randomness, cupping with 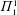$\unicode[STIX]{x1D6F1}_{1}^{1}$-random sequences, and an analogue of the Hirschfeldt–Miller characterization of weak 2-randomness. We also consider analogous questions for Cohen forcing, concentrating on the class of 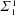$\unicode[STIX]{x1D6F4}_{1}^{1}$-generic reals.

MSC classification

Primary: 16W10: Rings with involution; Lie, Jordan and other nonassociative structures
Secondary: 16D50: Injective modules, self-injective rings
Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 5 , 2017 , e31
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2017

References

Baire, R., ‘Sur les fonctions de variables réelles’, Ann. Mat. Pura Appl. (4) 3(1) (1899), 1–123.Google Scholar
Bienvenu, L., Greenberg, N. and Monin, B., ‘Bad oracles’, in preparation.Google Scholar
Bienvenu, L., Greenberg, N. and Monin, B., ‘Continuous higher randomness’, J. Math. Log. 17(1) (2017).Google Scholar
Chong, C. T., Nies, A. and Yu, L., ‘Lowness of higher randomness notions’, Israel J. Math. 166(1) (2008), 39–60.Google Scholar
Chong, C. T. and Yu, L., ‘Randomness in the higher setting’, J. Symbolic Logic 80(4) (2015), 1131–1148.CrossRefGoogle Scholar
Day, A. R. and Dzhafarov, D. D., ‘Limits to joining with generics and randoms’, inProceedings of the 12th Asian Logic Conference (World Scientific Publishing, Hackensack, NJ, 2013), 76–88.Google Scholar
Day, A. R. and Miller, J. S., ‘Cupping with random sets’, Proc. Amer. Math. Soc. 142(8) (2014), 2871–2879.Google Scholar
Downey, R., Nies, A., Weber, R. and Lowness, L. Y., ‘𝛱2 0 nullsets’, J. Symbolic Logic 71(3) (2006), 1044–1052.Google Scholar
Feferman, S., ‘Some applications of the notions of forcing and generic sets’, Fund. Math. 56(3) (1964), 325–345.Google Scholar
Franklin, J. and Ng, K. M., ‘Difference randomness’, Proc. Amer. Math. Soc. 139(1) (2011), 345–360.CrossRefGoogle Scholar
Greenberg, N. and Miller, J. S., ‘Lowness for Kurtz randomness’, J. Symbolic Logic 74(2) (2009), 665–678.Google Scholar
Greenberg, N., Miller, J., Monin, B. and Turetsky, D., ‘Two more characterizations of k-triviality’, Notre Dame J. Form. Log. (to appear).Google Scholar
Hjorth, G. and Nies, A., ‘Randomness via effective descriptive set theory’, J. Lond. Math. Soc. (2) 75(2) (2007), 495–508.Google Scholar
Jockusch, C. G. Jr., ‘Degrees of generic sets’, inRecursion Theory: its Generalisation and Applications (Proc. Logic Colloq., Univ. Leeds, Leeds, 1979), London Mathematical Society Lecture Note Series, 45 (Cambridge University Press, Cambridge, 1980), 110–139.Google Scholar
Kechris, A. S., ‘The theory of countable analytical sets’, Trans. Amer. Math. Soc. 202 (1975), 259–297.Google Scholar
Kjos-Hanssen, B., ‘Low for random reals and positive-measure domination’, Proc. Amer. Math. Soc. 135(11) (2007), 3703–3709.Google Scholar
Kjos-Hanssen, B., Merkle, W. and Stephan, F., ‘Kolmogorov complexity and the recursion theorem’, Trans. Amer. Math. Soc. 363 (2011), 5465–5480.Google Scholar
Kjos-Hanssen, B., Nies, A., Stephan, F. and Yu, L., ‘Higher Kurtz randomness’, Ann. Pure Appl. Logic 161(10) (2010), 1280–1290.Google Scholar
Kihara, T, ‘Higher randomness and limsup forcing within and beyond hyperarithmetic’, inSets and Computation (World Scientific) 117–155. (seehttp://www.worldscientific.com/doi/abs/10.1142/9789813223523_0006.Google Scholar
Kolmogorov, A. N., ‘Three approaches to the quantitative definition of information’, Prob. Inform. Trans. 1(1) (1965), 1–7.Google Scholar
Kučera, A., ‘Measure, 𝛱1 0 -classes and complete extensions of PA’, inRecursion theory week (Oberwolfach, 1984), Lecture Notes in Mathematics, 1141 (Springer, Berlin, 1985), 245–259.Google Scholar
Kurtz, S., ‘Randomness and genericity in the degrees of unsolvability’, Dissertation Abstracts International Part B: Science and Engineering 42 9, University of Illinois, Urbana–Champaign, 1982.Google Scholar
Kurtz, S., ‘Notions of weak genericity’, J. Symbolic Logic 48(03) (1983), 764–770.Google Scholar
Lebesgue, H., ‘Sur les fonctions représentables analytiquement’, J. Math. Pures Appl. (9) (1905), 139–216.Google Scholar
Martin-Löf, P., ‘The definition of random sequences’, Inform. Control 9 (1966), 602–619.Google Scholar
Monin, B., ‘Higher randomness and forcing with closed sets’, in31st International Symposium on Theoretical Aspects of Computer Science (STACS 2014), (eds. Mayr, E. W. and Portier, N.) Leibniz International Proceedings in Informatics (LIPIcs), 25 (Schloss Dagstuhl, Leibniz-Zentrum für Informatik, Dagstuhl, Germany, 2014), 566–577.Google Scholar
Moschovakis, Y., Descriptive Set Theory (Elsevier, 1987).Google Scholar
Nies, A., ‘Computability and randomness’, inOxford Logic Guides (Oxford University Press, New York, NY, USA, 2009).Google Scholar
Nies, A., ‘Logic blog 2013’, Preprint, 2014, arXiv:1403.5719.Google Scholar
Posner, D. B. and Robinson, R. W., ‘Degrees joining to 0’, J. Symbolic Logic 46(04) (1981), 714–722.Google Scholar
Sacks, G. E., ‘Higher recursion theory’, inPerspectives in Mathematical Logic (Springer, Berlin, 1990).Google Scholar
Solomonoff, R. J., ‘A formal theory of inductive inference. Part I’, Inform. Control 7(1) (1964), 1–22.Google Scholar
Shore, R. A. and Slaman, T. A., ‘Defining the Turing jump’, Math. Res. Lett. 6(5–6) (1999), 711–722.Google Scholar
Stern, J., ‘Réels aléatoires et ensembles de mesure nulle en théorie descriptive des ensembles’, C. R. Acad. Sci. Paris Sér. A–B 276 (1973), A1249–A1252.Google Scholar
Stern, J., ‘Some measure theoretic results in effective descriptive set theory’, Israel J. Math. 20(2) (1975), 97–110.Google Scholar
Stephan, F. and Yu, L., ‘Lowness for weakly 1-generic and Kurtz-random’, inTheory and Applications of Models of Computation, Third International Conference, TAMC 2006, Beijing, China, May 15–20, 2006, Proceedings (eds. Cai, Jin-Yi, Cooper, Barry S. and Li, Angsheng) (Springer, 2006), 756–764.Google Scholar
Yu, L., ‘Lowness for genericity’, Arch. Math. Logic 45(2) (2006), 233–238.Google Scholar