Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-14T05:20:22.521Z Has data issue: false hasContentIssue false
  • English
  • Français

HIGH ORDER PARACONTROLLED CALCULUS

Part of: Stochastic analysis Miscellaneous topics - Partial differential equations

Published online by Cambridge University Press:  02 December 2019

ISMAËL BAILLEUL  and
FRÉDÉRIC BERNICOT
ISMAËL BAILLEUL
Affiliation:
Univ Rennes, CNRS, IRMAR – UMR 6625, F-35000Rennes, France; [email protected]
FRÉDÉRIC BERNICOT
Affiliation:
Laboratoire de Mathématiques Jean Leray, CNRS – Université de Nantes, 2 Rue de la Houssinière 44322 Nantes Cedex 03, France; [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We develop in this work a general version of paracontrolled calculus that allows to treat analytically within this paradigm a whole class of singular partial differential equations with the same efficiency as regularity structures. This work deals with the analytic side of the story and offers a toolkit for the study of such equations, under the form of a number of continuity results for some operators, while emphasizing the simple and systematic mechanics of computations within paracontrolled calculus, via the introduction of two model operations 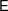$\mathsf{E}$ and 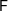$\mathsf{F}$. We illustrate the efficiency of this elementary approach on the example of the generalized parabolic Anderson model equation

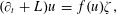$$\begin{eqnarray}(\unicode[STIX]{x2202}_{t}+L)u=f(u)\unicode[STIX]{x1D701},\end{eqnarray}$$
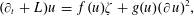on a 3-dimensional closed manifold, and the generalized KPZ equation
$$\begin{eqnarray}(\unicode[STIX]{x2202}_{t}+L)u=f(u)\unicode[STIX]{x1D701}+g(u)(\unicode[STIX]{x2202}u)^{2},\end{eqnarray}$$
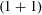 driven by a $(1+1)$-dimensional space/time white noise.

MSC classification

Primary: 60H15: Stochastic partial differential equations
Secondary: 35R60: Partial differential equations with randomness, stochastic partial differential equations 35R01: Partial differential equations on manifolds
Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 7 , 2019 , e44
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2019

References

Bailleul, I. and Bernicot, F., ‘Heat semigroup and singular PDEs’, J. Funct. Anal. 270 (2016), 3344–3452.Google Scholar
Bailleul, I., Bernicot, F. and Frey, D., ‘Space-time paraproducts for paracontrolled calculus, 3D-PAM and multiplicative Burgers equations’, Ann. Sci. Éc. Norm. Supér. (4) 51(6) (2018), 1399–1457.Google Scholar
Bailleul, I., Debussche, A. and Hofmanovà, M., ‘Quasilinear generalised parabolic Anderson model equation’, Stoch. Part. Diff. Eq.: Anal. Comput. 7(1) (2018), 40–63.Google Scholar
Bailleul, I. and Hoshino, M., ‘Paracontrolled calculus and regularity structures (I)’, J. Math. Soc. Japan, to appear. Preprint, 2020, arXiv:1812.07919.Google Scholar
Bruned, Y., Chandra, A., Chevyrev, I. and Hairer, M., ‘Renormalising SPDEs in regularity structures’, J. Eur. Math. Soc. (2020), (to appear).Google Scholar
Bruned, Y., Gabriel, F., Hairer, M. and Zambotti, L., ‘Geometric stochastic heat equations’, Preprint, 2019, arXiv:1902.02884.Google Scholar
Bruned, Y., Hairer, M. and Zambotti, L., ‘Algebraic renormalisation of regularity structures’, Invent. Math. 215(3) (2019), 1039–1156.Google Scholar
Caruana, M., Lévy, T. and Lyons, T., Differential Equations Driven by Rough Paths, Lecture Notes in Mathematics 1908 (Springer-Verlag, Berlin Heidelberg, 2006).Google Scholar
Catellier, R. and Chouk, K., ‘Paracontrolled distributions and the 3-dimensional stochastic quantization equation’, Ann. Probab. 46(5) (2018), 2621–2679.Google Scholar
Chandra, A. and Hairer, M., ‘An analytic BPHZ theorem for regularity structures’, Preprint, 2016, arXiv:1612.08138.Google Scholar
Chemin, J.-Y., ‘Calcul paradifférentiel précisé et applications à des équations aux dérivées partielles non semilinéaires’, Duke Math. J. 56(3) (1988), 431–469.Google Scholar
Chemin, J.-Y., ‘Interaction contrôlée dans les équations aux dérivées partielles non linéaires’, Bull. Soc. Math. France 116(3) (1988), 341–383.Google Scholar
Chouk, K. and Allez, R., ‘The continuous Anderson hamiltonian in dimension two’, Preprint, 2015, arXiv:1511.02718.Google Scholar
Chouk, K. and Cannizzaro, G., ‘Multidimensional SDEs with singular drift and universal construction of the polymer measure with white noise potential’, Ann. Probab. 46(3) (2018), 1710–1763.Google Scholar
Dahlqvist, A., Diehl, J. and Driver, B., ‘The parabolic Anderson model on Riemann surfaces’, Probab. Theory Related Fields 174(1-2) (2019), 369–444.Google Scholar
Duong, X. T. and McIntosh, A., ‘Functional calculi of second-order elliptic partial differential operators with bounded measurable coefficients’, J. Geom. Anal. 6(2) (1996), 181–205.Google Scholar
Gubinelli, M., Imkeller, P. and Perkowski, N., ‘Paracontrolled distributions and singular PDEs’, Forum Math. Pi 3(e6) (2015), 75 pages.Google Scholar
Gubinelli, M. and Perkowski, N., ‘KPZ reloaded’, Comm. Math. Phys. 349(1) (2017), 165–269.Google Scholar
Hairer, M., ‘A theory of regularity structures’, Invent. Math. 198(2) (2014), 269–504.Google Scholar
Hairer, M., ‘The motion of a random string’, Preprint, 2016, arXiv:1605.02192.Google Scholar
Hairer, M. and Pardoux, E., ‘A Wong–Zakai theorem for stochastic PDEs’, J. Math. Soc. Japan 67(4) (2015), 1551–1604.Google Scholar
Lyons, T., ‘Differential equations driven by rough signals’, Rev. Mat. Iberoam. 14(2) (1998), 215–310.Google Scholar
Perkowski, N., ‘Paracontrolled distributions and singular SPDEs’, https://personal-homepages.mis.mpg.de/perkow/paracontrolled-leipzig.pdf, 2019.Google Scholar
Zhu, R. and Zhu, X., ‘Three-dimensional Navier–Stokes equations driven by space-time white noise’, J. Differential Equations 259(9) (2015), 4443–4506.Google Scholar
Zhu, R. and Zhu, X., ‘Approximating three-dimensional Navier–Stokes equations driven by space-time white noise’, Inf. Dim. Anal., Quantum Probab. Rel. Topics 20(4)1750020 (2017).Google Scholar
Zhu, R. and Zhu, X., ‘Lattice approximation to the dynamical 𝛷3 4 model’, Ann. Probab. 46(1) (2018), 397–455.Google Scholar