Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Bodnár, J.
2016.
Classification of rational unicuspidal curves with two Newton pairs.
Acta Mathematica Hungarica,
Vol. 148,
Issue. 2,
p.
294.
Wang, Shida
2016.
On the first singularity for the Upsilon invariant of algebraic knots.
Bulletin of the London Mathematical Society,
Vol. 48,
Issue. 2,
p.
349.
Borodzik, Maciej
and
Livingston, Charles
2016.
Semigroups,d-invariants and deformations of cuspidal singular points of plane curves.
Journal of the London Mathematical Society,
Vol. 93,
Issue. 2,
p.
439.
Borodzik, Maciej
and
Moe, Torgunn Karoline
2016.
Topological obstructions for rational cuspidal curves in Hirzebruch surfaces.
Michigan Mathematical Journal,
Vol. 65,
Issue. 4,
Bodnár, József
Celoria, Daniele
and
Golla, Marco
2016.
Cuspidal curves and Heegaard Floer homology.
Proceedings of the London Mathematical Society,
Vol. 112,
Issue. 3,
p.
512.
Bodnár, József
and
Némethi, András
2017.
Singularities and Computer Algebra.
p.
173.
Bodnár, József
Celoria, Daniele
and
Golla, Marco
2017.
A note on cobordisms of algebraic knots.
Algebraic & Geometric Topology,
Vol. 17,
Issue. 4,
p.
2543.
Aceto, Paolo
and
Golla, Marco
2017.
Dehn surgeries and rational homology balls.
Algebraic & Geometric Topology,
Vol. 17,
Issue. 1,
p.
487.
Palka, Karol
and
Pełka, Tomasz
2017.
Classification of planar rational cuspidal curves I. C∗∗-fibrations.
Proceedings of the London Mathematical Society,
Vol. 115,
Issue. 3,
p.
638.
Baranowski, Adam
Borodzik, Maciej
and
Serrano de Rodrigo, Juan
2017.
Heegaard Floer Homologies and Rational Cuspidal Curves. Lecture notes..
Winter Braids Lecture Notes,
Vol. 3,
Issue. ,
p.
1.
Borodzik, Maciej
2017.
Rational cuspidal curves in projective surfaces. Topological versus algebraic obstructions.
International Journal of Mathematics,
Vol. 28,
Issue. 14,
p.
1750106.
Koras, Mariusz
and
Palka, Karol
2017.
The Coolidge–Nagata conjecture.
Duke Mathematical Journal,
Vol. 166,
Issue. 16,
Krcatovich, David
2018.
A restriction on the Alexander polynomials of
L-space knots.
Pacific Journal of Mathematics,
Vol. 297,
Issue. 1,
p.
117.
BORODZIK, MACIEJ
and
HEDDEN, MATTHEW
2018.
The ϒ function ofL–space knots is a Legendre transform.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 164,
Issue. 3,
p.
401.
Aceto, Paolo
Golla, Marco
and
Lecuona, Ana
2018.
Handle decompositions of rational homology balls and Casson–Gordon invariants.
Proceedings of the American Mathematical Society,
Vol. 146,
Issue. 9,
p.
4059.
Park, Kyungbae
2018.
On independence of iterated Whitehead doubles in the knot concordance group.
Journal of Knot Theory and Its Ramifications,
Vol. 27,
Issue. 01,
p.
1850003.
Golla, Marco
and
Marengon, Marco
2018.
Correction Terms and the Nonorientable Slice Genus.
Michigan Mathematical Journal,
Vol. 67,
Issue. 1,
Gorsky, E. A.
2019.
Introduction to Heegaard Floer homology.
Russian Mathematical Surveys,
Vol. 74,
Issue. 1,
p.
1.
Celoria, Daniele
and
Golla, Marco
2019.
Heegaard Floer homology and concordance bounds on the Thurston norm.
Transactions of the American Mathematical Society,
Vol. 373,
Issue. 1,
p.
295.
Palka, Karol
2019.
Cuspidal curves, minimal models and Zaidenberg’s finiteness conjecture.
Journal für die reine und angewandte Mathematik (Crelles Journal),
Vol. 2019,
Issue. 747,
p.
147.
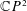 $\mathbb{C}P^{2}$. As one application, we resolve an open
conjecture that constrains the Alexander polynomial of the link of the singular point
of the curve in the case that there is exactly one singular point, having connected
link, and the curve is of genus zero. Generalizations apply in the case of multiple
singular points.
$\mathbb{C}P^{2}$. As one application, we resolve an open
conjecture that constrains the Alexander polynomial of the link of the singular point
of the curve in the case that there is exactly one singular point, having connected
link, and the curve is of genus zero. Generalizations apply in the case of multiple
singular points.

