Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-30T23:18:59.478Z Has data issue: false hasContentIssue false
  • English
  • Français

GL-EQUIVARIANT MODULES OVER POLYNOMIAL RINGS IN INFINITELY MANY VARIABLES. II

Published online by Cambridge University Press:  12 March 2019

STEVEN V SAM  and
ANDREW SNOWDEN
STEVEN V SAM
Affiliation:
Department of Mathematics, University of California, San Diego, CA, USA; [email protected]; http://math.ucsd.edu/∼ssam/
ANDREW SNOWDEN
Affiliation:
Department of Mathematics, University of Michigan, Ann Arbor, MI, USA; [email protected]; http://www-personal.umich.edu/∼asnowden/

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

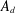Twisted commutative algebras (tca’s) have played an important role in the nascent field of representation stability. Let $A_{d}$ be the tca freely generated by 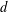$d$ indeterminates of degree 1. In a previous paper, we determined the structure of the category of 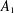$A_{1}$-modules (which is equivalent to the category of 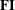$\mathbf{FI}$-modules). In this paper, we establish analogous results for the category of 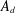$A_{d}$-modules, for any 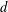$d$. Modules over 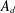$A_{d}$ are closely related to the structures used by the authors in previous works studying syzygies of Segre and Veronese embeddings, and we hope the results of this paper will eventually lead to improvements on those works. Our results also have implications in asymptotic commutative algebra.

Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 7 , 2019 , e5
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution-NonCommercial-ShareAlike licence (http://creativecommons.org/licenses/by-nc-sa/4.0/), which permits non-commercial re-use, distribution, and reproduction in any medium, provided the same Creative Commons licence is included and the original work is properly cited. The written permission of Cambridge University Press must be obtained for commercial re-use.
Copyright
© The Author(s) 2019

References

Akin, K. and Weyman, J., ‘Minimal free resolutions of determinantal ideals and irreducible representations of the Lie superalgebra gl (m|n)’, J. Algebra 197(2) (1997), 559–583.Google Scholar
Assmus, E. F. Jr, ‘On the homology of local rings’, Illinois J. Math. 3 (1959), 187–199.Google Scholar
Church, T. and Ellenberg, J. S., ‘Homological properties of FI-modules and stability’, Geom. Topol. to appear, arXiv:1506.01022v2.Google Scholar
Church, T., Ellenberg, J. S. and Farb, B., ‘FI-modules and stability for representations of symmetric groups’, Duke Math. J. 164(9) (2015), 1833–1910.Google Scholar
Church, T. and Farb, B., ‘Representation theory and homological stability’, Adv. Math. (2013), 250–314. arXiv:1008.1368v3.Google Scholar
Dade, E. C., ‘Localization of injective modules’, J. Algebra 69(2) (1981), 416–425.Google Scholar
de Concini, C., Eisenbud, David and Procesi, C., ‘Young diagrams and determinantal varieties’, Invent. Math. 56(2) (1980), 129–165.Google Scholar
Gabriel, P., ‘Des catégories abéliennes’, Bull. Soc. Math. France 90 (1962), 323–448.Google Scholar
Hartshorne, R., Residues and Duality, Lecture Notes in Mathematics, 20 (Springer, Berlin–New York, 1966).Google Scholar
Jantzen, J. C., Representations of Algebraic Groups, Pure and Applied Mathematics, 131 , (Academic Press, Boston, MA, 1987).Google Scholar
Kapranov, M. M., ‘On the derived categories of coherent sheaves on some homogeneous spaces’, Invent. Math. 92(3) (1988), 479–508.Google Scholar
Nagpal, R., Sam, S. V. and Snowden, A., ‘Noetherianity of some degree two twisted commutative algebras’, Selecta Math. (N.S.) 22(2) (2016), 913–937.Google Scholar
Raicu, C., ‘Regularity and cohomology of determinantal thickenings’, arXiv:1611.00415v1.Google Scholar
Ramos, Eric, ‘Generalized representation stability and FI d -modules’, Proc. Amer. Math. Soc. (2016), to appear, arXiv:1606.02673v4.Google Scholar
Ramos, E., ‘Configuration spaces of graphs with certain permitted collisions’, arXiv:1703.05535v1.Google Scholar
Raicu, C. and Weyman, J., ‘Local cohomology with support in generic determinantal ideals’, Algebra Number Theory 8(5) (2014), 1231–1257.Google Scholar
Raicu, C. and Weyman, J., ‘The syzygies of some thickenings of determinantal varieties’, Proc. Amer. Math. Soc. 145(1) (2017), 49–59.Google Scholar
Steven, V Sam, ‘Ideals of bounded rank symmetric tensors are generated in bounded degree’, Invent. Math. 207(1) (2017), 1–21.Google Scholar
Sam, S. V., ‘Syzygies of bounded rank symmetric tensors are generated in bounded degree’, Math. Ann. 368(3) (2017), 1095–1108.Google Scholar
Steven, V Sam and Snowden, Andrew, ‘GL-equivariant modules over polynomial rings in infinitely many variables’, Trans. Amer. Math. Soc. 368 (2016), 1097–1158.Google Scholar
Sam, S. V. and Snowden, A., ‘Introduction to twisted commutative algebras’, arXiv:1209.5122v1.Google Scholar
Sam, S. V. and Snowden, A., ‘Gröbner methods for representations of combinatorial categories’, J. Amer. Math. Soc. 30 (2017), 159–203.Google Scholar
Sam, S. V. and Snowden, A., ‘Hilbert series for twisted commutative algebras’, Algebraic Combin. 1(1) (2018), 147–172.Google Scholar
Sam, S. V. and Snowden, A., Depth and local cohomology of twisted commutative algebras; in preparation.Google Scholar
Sam, S. V. and Snowden, A., ‘Regularity bounds for twisted commutative algebras’, arXiv:1704.01630v1.Google Scholar
Snowden, Andrew, ‘Syzygies of Segre embeddings and 𝛥-modules’, Duke Math. J. 162(2) (2013), 225–277.Google Scholar
Stacks Project, http://stacks.math.columbia.edu, 2017.Google Scholar
Weyman, J., Cohomology of Vector Bundles and Syzygies 149 (Cambridge University Press, Cambridge, 2003).Google Scholar