Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-24T15:11:37.291Z Has data issue: false hasContentIssue false
  • English
  • Français

GENERATING MAXIMAL SUBGROUPS OF FINITE ALMOST SIMPLE GROUPS

Part of: Representation theory of groups Structure and classification of infinite or finite groups Special aspects of infinite or finite groups

Published online by Cambridge University Press:  30 June 2020

ANDREA LUCCHINI ,
CLAUDE MARION  and
GARETH TRACEY
ANDREA LUCCHINI
Affiliation:
Dipartimento di Matematica Tullio Levi-Civita, Università degli Studi di Padova, 35121-IPadova, Italy; [email protected]
CLAUDE MARION
Affiliation:
CMUP, Departamento de Matemática, Universidade do Porto, 4169-007Porto, Portugal; [email protected]
GARETH TRACEY
Affiliation:
Department of Mathematical Sciences, University of Bath, BathBA2 7AY, UK; [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For a finite group 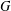$G$, let 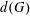$d(G)$ denote the minimal number of elements required to generate 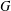$G$. In this paper, we prove sharp upper bounds on 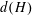$d(H)$ whenever 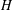$H$ is a maximal subgroup of a finite almost simple group. In particular, we show that 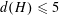$d(H)\leqslant 5$ and that 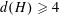$d(H)\geqslant 4$ if and only if 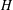$H$ occurs in a known list. This improves a result of Burness, Liebeck and Shalev. The method involves the theory of crowns in finite groups.

MSC classification

Primary: 20F05: Generators, relations, and presentations
Secondary: 20D05: Finite simple groups and their classification 20E28: Maximal subgroups
Type
Algebra
Information
Forum of Mathematics, Sigma , Volume 8 , 2020 , e32
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2020

References

Aschbacher, M., ‘On the maximal subgroups of the finite classical groups’, Invent. Math. 76 (1984), 469–514.CrossRefGoogle Scholar
Aschbacher, M. and Guralnick, R., ‘Some applications of the first cohomology group’, J. Algebra 90 (1984), 446–460.CrossRefGoogle Scholar
Aschbacher, M. and Scott, L., ‘Maximal subgroups of finite groups’, J. Algebra 92 (1985), 44–80.CrossRefGoogle Scholar
Aschbacher, M. and Seitz, G. M., ‘Involutions in Chevalley groups over fields of even order’, Nagoya Math. J. 63 (1976), 1–91.CrossRefGoogle Scholar
Azad, H., Barry, M. and Seitz, G., ‘On the structure of parabolic subgroups’, Comm. Algebra 18(2) (1990), 551–562.CrossRefGoogle Scholar
Ballester-Bolinches, A. and Ezquerro, L. M., Classes of Finite Groups, Mathematics and Its Applications (Springer), 584 (Springer, Dordrecht, 2006).Google Scholar
Bosma, W., Cannon, J. and Playoust, C., ‘The Magma algebra system. I. The user language’, J. Symbolic Comput. 24 (1997), 235–265.CrossRefGoogle Scholar
Bourbaki, N., Groupes et algèbres de Lie - Chapitres 4,5, et 6, 2nd edn, (Springer, Berlin, Heidelberg, Paris, 1972).Google Scholar
Bray, J. N., Holt, D. F. and Roney-Dougal, C. M., The Maximal Subgroups of the Low-Dimensional Finite Classical Groups, Lecture Note Series, 407 (London Mathematical Society, Cambridge, 2013).CrossRefGoogle Scholar
Burness, T., Liebeck, M. and Shalev, A., ‘Generation and random generation: From simple groups to maximal subgroups’, Adv. Math. 248 (2013), 59–95.CrossRefGoogle Scholar
Cameron, P., Lucchini, A. and Roney-Dougal, C., ‘Generating sets of finite groups’, Trans. Amer. Math. Soc. 370(9) (2018), 6751–6770.CrossRefGoogle Scholar
Carter, R., ‘Centralizers of semisimple elements in finite groups of Lie type’, Proc. Lond. Math. Soc. 37 (1978), 491–507.CrossRefGoogle Scholar
Cohen, A., Liebeck, M., Saxl, J. and Seitz, G., ‘The local maximal subgroups of the exceptional groups of Lie type, finite and algebraic’, Proc. Lond. Math. Soc. 64(3) (1992), 21–48.CrossRefGoogle Scholar
Connor, T. and Leemans, D., ‘An atlas of subgroup lattices of finite almost simple groups’, Ars Math. Contemp. 8 (2015), 259–266.CrossRefGoogle Scholar
Conway, J., Curtis, R., Norton, S., Parker, R. and Wilson, R., Atlas of Finite Groups, (Oxford University Press, Eynsham, 1985).Google Scholar
Curtis, C. W. and Reiner, I., Representation Theory of Finite Groups and Associative Algebras, (AMS Chelsea Publishing, Providence, RI, 2006), Reprint of the 1962 original.CrossRefGoogle Scholar
Dalla Volta, F. and Lucchini, A., ‘Generation of almost simple groups’, J. Algebra 178 (1995), 194–223.CrossRefGoogle Scholar
Dalla Volta, F. and Lucchini, A., ‘Finite groups that need more generators than any proper quotient’, J. Aust. Math. Soc. 64 (1998), 82–91.Google Scholar
Dalla Volta, F., Lucchini, A. and Morini, F., ‘On the probability of generating a minimal d-generated group’, J. Aust. Math. Soc. 71 (2001), 177–185.CrossRefGoogle Scholar
Detomi, E. and Lucchini, A., ‘Crowns and factorization of the probabilistic zeta function of a finite group’, J. Algebra 265 (2003), 651–668.CrossRefGoogle Scholar
Detomi, E. and Lucchini, A., ‘Probabilistic generation of finite groups with a unique minimal normal subgroup’, J. Lond. Math. Soc. 87 (2013), 689–706.CrossRefGoogle Scholar
Flaass, D., ‘2-local subgroups of Fischer’s groups’, Mat. Zametki 35 (1984), 333–342.Google Scholar
Förster, P., ‘Chief factors, crowns, and the generalized Jordan–Hölder theorem’, Comm. Algebra 16 (1988), 1627–1638.CrossRefGoogle Scholar
Gaschütz, W., ‘Praefrattinigruppen’, Arch. Math. 13 (1962), 418–426.CrossRefGoogle Scholar
Gorenstein, D. and Lyons, R., ‘The local structure of finite groups of characteristic 2 type’, Mem. Amer. Math. Soc. 42 (1983), 1–731.Google Scholar
Gorenstein, D., Lyons, R. and Solomon, R., The Classification of the Finite Simple Groups Number Three, Mathematical Surveys and Monographs, 40 (3) (American Mathematical Society, Providence, 1991).Google Scholar
Holmes, P. E. and Wilson, R. A., ‘A new computer construction of the Monster using 2-local subgroups’, J. Lond. Math. Soc. 67 (2003), 349–364.CrossRefGoogle Scholar
Humphreys, J., Linear Algebraic Groups, (Springer, New York, 1975).CrossRefGoogle Scholar
Jiménez-Seral, P. and Lafuente, J. P., ‘On complemented non-abelian chief factors of a finite group’, Israel J. Math. 106 (1998), 177–188.CrossRefGoogle Scholar
Kleidman, P., ‘The maximal subgroups of the finite 8-dimensional orthogonal groups P𝛺8+(q) and of their automorphism groups’, J. Algebra 110 (1987), 173–242.CrossRefGoogle Scholar
Kleidman, P. and Liebeck, M., The Subgroup Structure of the Finite Classical Groups, London Mathematical Society Lecture Note Series, 129 (Cambridge University Press, 1990).CrossRefGoogle Scholar
Kleidman, P., Parker, R. and Wilson, R., ‘The maximal subgroups of the Fisher group Fi 23’, J. Lond. Math. Soc. 39 (1989), 89–101.CrossRefGoogle Scholar
Kleidman, P. and Wilson, R., ‘The maximal subgroups of Fi 22’, Math. Proc. Cambridge Philos. Soc. 102 (1987), 17–23.CrossRefGoogle Scholar
Liebeck, M., Saxl, J. and Seitz, G., ‘Subgroups of maximal rank in finite exceptional groups of Lie type’, Proc. Lond. Math. Soc. (3) 65 (1992), 297–325.CrossRefGoogle Scholar
Liebeck, M. and Seitz, G., ‘Maximal subgroups of exceptional groups of Lie type, finite and algebraic’, Geom. Dedicata 35(1–3) (1990), 353–387.CrossRefGoogle Scholar
Linton, S. and Wilson, R., ‘The maximal subgroups of the Fischer groups Fi 24 and Fi 24′’, Proc. Lond. Math. Soc. 63 (1991), 113–164.CrossRefGoogle Scholar
Lucchini, A. and Menegazzo, F., ‘Generators for finite groups with a unique minimal normal subgroup’, Rend. Semin. Mat. Univ. Padova 98 (1997), 173–191.Google Scholar
Lucchini, A. and Morini, F., ‘On the probability of generating finite groups with a unique minimal normal subgroup’, Pac. J. Math. 203 (2002), 429–440.CrossRefGoogle Scholar
Lyndon, R. and Schupp, P., Combinatorial Group Theory (Springer, Berlin, 1977).Google Scholar
Malle, G. and Testerman, D., Linear Algebraic Groups and Finite Groups of Lie Type, Cambridge Studies in Advanced Mathematics, 133 (Cambridge University Press, Cambridge, 2011).CrossRefGoogle Scholar
Meierfrankenfeld, U. and Shpectorov, S. V., ‘Maximal 2-local subgroups of the Monster and Baby Monster’, Preprint, 2002. Michigan State University, Available from http://www.mth.msu.edu/meier/Preprints/2monster/maxmon.pdf.Google Scholar
Menezes, N., Quick, M. and Roney-Dougal, C., ‘The probability of generating a finite simple group’, Israel J. Math. 198(1) (2013), 371–392.CrossRefGoogle Scholar
Miller, G., ‘On the groups generated by two operators’, Bull. Amer. Math. Soc. 7 (1901), 424–426.CrossRefGoogle Scholar
Norton, S. and Wilson, R., ‘Maximal subgroups of the Harada–Norton Group’, J. Algebra 103 (1986), 362–376.CrossRefGoogle Scholar
Norton, S. and Wilson, R., ‘A correction to the 41-structure of the Monster, a construction of a new maximal subgroup Ł 2(41) and a new Moonshine phenomenon’, J. Lond. Math. Soc. 87 (2013), 943–962.CrossRefGoogle Scholar
Seitz, G., ‘Generation of finite groups of Lie type’, Trans. Amer. Math. Soc. 271 (1982), 351–407.CrossRefGoogle Scholar
Steinberg, R., ‘Generators for simple groups’, Canad. J. Math. 14 (1962), 277–283.CrossRefGoogle Scholar
Wilson, R., ‘The maximal subgroups of Conway’s group Co 1’, J.  Algebra 85 (1983), 144–165.CrossRefGoogle Scholar
Wilson, R., ‘Some subgroups of the Baby Monster’, Invent. Math. 89 (1987), 197–218.CrossRefGoogle Scholar
Wilson, R., ‘The local subgroups of the Fischer groups’, J. Lond. Math. Soc. (2) 36 (1987), 77–94.CrossRefGoogle Scholar
Wilson, R., ‘The maximal subgroups of the Baby Monster, I’, J. Algebra 211 (1999), 1–14.CrossRefGoogle Scholar
Wilson, R., Parker, R., Nickerson, S., Breuer, T. and Bray, J., ‘AtlasRep, A GAP Interface to the Atlas of Group Representations’, Version 1.5.1 (2016), http://www.math.rwth-aachen.de/∼Thomas.Breuer/atlasrep.Google Scholar
Wilson, R. et al. , ‘A World-Wide-Web Atlas of finite group representations’,http://brauer.maths.qmul.ac.uk/Atlas/v3/.Google Scholar